Hillslope subsurface flow is driven by vegetation more than soil properties in colonized valley moraines along a humid mountain elevation

Valley moraines along an elevation gradient are colonized by different climax vegetation; here, preferential flow paths (PFPs) and ground layers, as important hillslope structures, critically influence hillslope flow. However, the roles of these hillslope structures in flow dynamics, and their mechanisms in contrasting forest types within moraines, remain enigmatic. To this end, we conceptualized PFPs and ground layers as explicit elements in HYDRUS 2D, constructing set-ups of hillslope internal structures that incorporated an optional ground layer and varying intensities of PFPs using a random placement method to represent the shallow root zone (0–50 cm) of vegetated moraines. The results showed that, out of the 50 set-ups for each forest type, only 3 set-ups for the coniferous forest and 2 for the broadleaf forest successfully predicted the flow dynamics and water balance of the hydrological response at the event scale. Notably, all 5 successful set-ups featured below-average vertically connected PFPs that covered only 5 % of the total spatial area in both forests, following the principle of maximum free energy dissipation, which is achieved when flow passes through a network composed of partial PFPs and a steepened soil matrix gradient. The similar intensity of PFPs across forest types is attributed to the occurrence of similar coarse-textured soils, resulting from frequent precipitation and clay washout, as well as comparable fine root biomass, both contributing to the connectivity of vertical PFPs, which governs subsurface flow in shallow soil hillslopes. In addition, a linear relationship between vertically connected PFPs and subsurface flow was observed in both forests, with the coniferous forest being more sensitive to changes in PFPs due to its lower soil organic matter content. The presence of the ground layer caused the PFPs to be buried and trigged rapid lateral flow within the ground layer towards downslope positions, reducing the spatial homogeneity of the water exchange between PFPs and the soil matrix, leading to earlier peak flow timing and increased peak flow magnitude. This study highlights the role of vegetation-related processes in influencing subsurface flow, advancing our understanding of hillslope structures and runoff evolution over time in humid valley moraines.

1 Introduction

The hillslope, as the basic functional component of catchments, strongly influences the hydrological responses of stream water (Anderson et al., 2009; Angermann et al., 2017; Loritz et al., 2017; Hartmann and Blume, 2024). These hydrological responses depend on the hillslope/soil structure and further determine soil water dynamics, subsurface flow paths, and flow fluxes (Wienhöfer et al., 2009; Jackisch et al., 2017; Hartmann et al., 2020b; Jarvis et al., 2024). Structural features, such as macropores formed by roots, soil fauna, fractures, and cracks, serve as effective and efficient means to in situ determine hillslope/soil structures and flow dynamics (Uchida et al., 2002; Graham and Lin, 2012; Beven and Germann, 2013; Cheng et al., 2017; Jackisch et al., 2017).

Preferential flow refers to the rapid movement of water through preferred pathways, with velocities and fluxes orders of magnitude higher than that through the soil matrix, effectively bypassing much of the soil matrix. Preferential flow, and the associated preferential flow paths (PFPs), have been proved to be the rule rather than the exception (Jarvis, 2007; Beven and Germann, 2013; Jarvis et al., 2016). The ubiquitous phenomenon of preferential flow in soil can be understood from a thermodynamic perspective (Lin, 2010) – water tends to flow through paths that minimize resistance, thereby enabling more efficient water redistribution and free energy dissipation. Water flow through PFPs adheres to the principle of minimizing resistance, primarily imposed by friction and capillary forces, which explains the prevalence of preferential flow across different soil types. This also supports the observation that only a small fraction of PFPs is actively involved in water movement; yet they are responsible for a substantial portion of water transport across various soil types, which is primarily attributed either to isolated PFPs disconnected from the flow network or to air entrapment during infiltration (Jarvis et al., 2016). The phenomenon has been observed in a wide range of soils, including agricultural silt loam (Luo et al., 2008), grassy coarse sandy loam (Sněhota et al., 2010), silty clay soil developed from postglacial lake sediments (Koestel and Larsbo, 2014), and cultivated silt clay loam developed from Loess (Sammartino et al., 2015). Additionally, such behaviour has also been observed in connected PFPs, which are considered the dominant continuum for water flow in heterogeneous soils. Koestel and Larsbo (2014) identified that solute transport predominantly occurred through two cylindrical PFPs. Similarly, Sammartino et al. (2015) showed that a single dominant flow network, largely composed of active macropores, was responsible for water flow. However, how vegetation and soil type influence the PFPs involved in water flow, as well as the underlying causes, remain questions yet to be explored.

In alpine mountains, moraines resulting from widespread glacier retreat have undergone successive colonization by vegetation. Deciduous or evergreen forests typically represent the final and stable stage of vegetation succession (Huggett, 1998; Hartmann and Blume, 2024), which provides an ideal platform to investigate the intricate interactions between environment, vegetation, soil properties, and the associated runoff processes. Two distinct features arise from vegetation colonization: ground layer generation and soil formation processes (Laine-Kaulio et al., 2015; Hartmann et al., 2020b; Hartmann et al., 2022). The ground layer can intercept falling rainfall (Zhu et al., 2020) and disconnect PFPs from the soil surface. The former function determines the net rainfall input and the timing of water entry into the soil, thereby significantly influencing hydrological processes such as runoff generation, peak flow magnitude, and peak flow timing (Gomyo and Kuraji, 2016). The latter function is comparable to tilled soil, where transport processes are partly disrupted due to the burial of PFPs beneath the plough pan during tillage operations (Akay and Fox, 2007; Bogner et al., 2013). While, many studies have focused on the interception capacity of the ground layer, such as its maximum and minimum storage (Guevara-Escobar et al., 2007; Li et al., 2017), they largely overlook its crucial role in disconnecting macropores from the soil surface. Soil formation processes primarily manifest as changes in the soil structure, significantly altered due to the presence of PFPs in the form of macropore channels created by roots and soil fauna, whose critical role in influencing both surface and subsurface water flow has been the focus of numerous studies on glacial sandy till soils and vegetation-colonized moraines in various regions (Laine-Kaulio et al., 2015; Hartmann and Blume, 2024). However, only a few studies specifically focused on the PFPs involved in water transport, particularly in hillslopes developed from moraines where subsurface flow is dominant. Advancing this research would certainly promote our understanding of the underlying mechanisms and improve the accuracy of runoff predictions in alpine mountains where preferential flow is significant.

The methods employed to investigate PFPs involved in water flow include X-ray computed tomography (X-ray CT), magnetic resonance imaging (MRI), positron emission tomography (PET), and numerical modelling, all of which require reconciling scales with the precision of the study (Jarvis et al., 2016). Moreover, many of these methods are unsuitable for the forest ground layer due to its loose structure, making numerical models the most suitable approach for accounting for both the ground layer and PFPs, as they can represent these features either implicitly or explicitly (Šimùnek et al., 2003; Rasoulzadeh and Homapoor Ghoorabjiri, 2013; Kirchner et al., 2023). In addition, explicit models consider porous media as fine-scale elements, allowing the geometrical separation of PFPs from the soil matrix, and thereby clarifying the interplay between soil structures and model outputs. Though acquiring detailed hillslope subsurface structural data is difficult, previous studies have demonstrated the feasibility of using random placement of structures and genetic modelling of structure formation, with parameters derived from detailed plot-scale observations (Vogel et al., 2006; Weiler and McDonnell, 2007; Klaus and Zehe, 2011; Wienhöfer and Zehe, 2014). These modelling approaches enable us to evaluate the extent to which field evidence can effectively constrain and elucidate the role of PFPs in runoff processes.

In this study, we selected typical evergreen coniferous and deciduous broadleaf forests along an elevation gradient in a humid mountainous area, representing the ultimate stages of vegetation colonization on moraines. Compared to the coniferous forest at higher elevations, the broadleaf forest at lower and warmer elevations is characterized by more active biological and geochemical processes, which tends to accelerate moraine weathering and the accumulation of clay-sized particles as well as enhance ground litter and organic matter buildup during soil formation. These processes potentially increase soil water-holding capacity and promote macropore formation, thereby contributing to differences in hillslope outflow across the forest types. At the same time, humidity also influences the initial soil wetness and hydraulic conductivity of both the soil and ground layer, limiting the extent of water deficit and favouring preferential flow initiation, thereby potentially reducing forest-type effects on flow dynamics. Thus, we hypothesize that (1) the forest ground layer significantly influence hillslope outflow dynamics by intercepting rainfall and disconnecting PFPs from the soil surface; (2) there are more PFPs involved in hillslope outflow in the broadleaf forest due to increased biological activities at a lower elevation; (3) the coniferous forest is less sensitive to changes in PFPs because of low soil water-holding capacity. To address these hypotheses, field and laboratory experiments on PFPs, soil properties, and ground layers were conducted or collected. The data were then explicitly represented in HYDRUS 2D to investigate the interplay between hillslope structures and outflows in two colonized forests on moraines. The results of this study will help inform the conceptualization of numerical models of hillslope runoff using field evidences and promote our understanding of hydrological processes during moraines colonization and ongoing forest transformation under global climate change.

2 Materials and methods

2.1 Study sites description

2.1.1 Description of the valley moraines

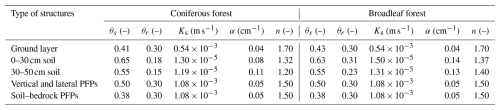
Gongga Mountain, located on the east edge of the Tibetan Plateau, experienced extensive and repeated glaciation during the Quaternary glacial-interglacial cycles (Wang et al., 2012). Hailuo Valley, one of five distinctive sets of preserved moraines in the Gongga Mountain, features varying forest types along the retreat moraines due to a dramatic elevation rise by 6400 m over a short horizontal distance of 29 km. We selected two typical forest types in the Hailuo Valley (Fig. S1): a coniferous forest at 3020 m a.s.l., developed from neoglacial moraines, with Abies fabri and Picea brachytyla as climax vegetation; and a broadleaf forest at 2060 m a.s.l., developed from MIS2 moraines, with Lithocarpus cleistocarpus and Cercidiphyllum japonicum as climax vegetation (Wang et al., 2012; Hu et al., 2018). The soils in both forests are classified as Cambisols according to the International Union of Soil Sciences (IUSS) working group, World Reference Base for Soil Resources (WRB) (2022). In the root zone (0–50 cm), the upper soil layer (0–30 cm) is organic-rich with low bulk density (mean values of 0.82 g cm⁻³ in the coniferous forest and 0.78 g cm⁻³ in the broadleaf forest). Soil bulk density increases below 30 cm in both forests (0.98 g cm⁻³ and 1.15 g cm⁻³ in the coniferous and broadleaf forests, respectively). The mean sand content exceeds 85 % in both forests, while the clay content is less than 4 %, with no significant difference between the forest types. Additionally, both forests have a ground layer with a mean thickness of ∼ 3 cm, consisting of a mixture of moss and litter in the coniferous forest and primarily litter in the broadleaf forest (Fig. S2). Higher root biomass, residual soil water content, and saturated soil hydraulic conductivity were observed in the broadleaf forest compared with the coniferous forest (Wang et al., 2022; Wang et al., 2023). The mean rock fragment content was 7.77 ± 2.54 cm³ cm⁻³ in the coniferous forest and 6.50 ± 2.91 cm³ cm⁻³ in the broadleaf forest, showing no significant difference between the forest types (p>0.05).

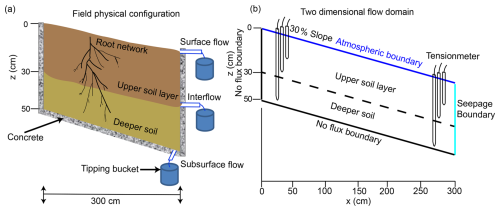
2.1.2 Artificial field configuration

Field observations of the rainfall runoff process were carried out using two isolated soil blocks extracted from the field, each representing one of the two typical forest types. This approach was designed to exclude potential confounding factors such as slope gradient, rainfall input heterogeneity, and slope orientation. The soil blocks, each measuring $\mathrm{300}\times \mathrm{100}\times \mathrm{50}$ cm³ (projected length × width × height) and inclined at 30°, were refilled with field soil transferred using cutting boxes, with minimal disturbance to mimic field conditions. A 3 cm thick gravel drainage layer was placed between the soil volume and underlying bedrock to act as a soil–bedrock interface that facilitates lateral preferential flow on hillslopes (Graham and Lin, 2012). Both blocks were equipped with identical monitoring devices for measuring water balance, including soil water potential sensors and outflow gauges (Figs. 1a; S1). Natural rainfall was recorded using tipping buckets deployed nearby. The monitored outflows included surface runoff, interflow, and subsurface flow (Fig. 1a and b). However, only subsurface flow was observed throughout the entire monitoring period in both forest types.

Figure 1 Artificial field configurations (a) and flow domain with boundary conditions in the numerical model (b).

2.2 Field experiments and previous studies

2.2.1 Field experiments on ground layers and soils

The interception capacity of forest ground layers was measured using simulated rainfall experiments conducted on artificial field configurations. Each experiment lasted 150 min, with simulated rainfall at a constant intensity of 5, 10, 20, and 40 mm h⁻¹. Five groups of T4e sensors were evenly distributed along the hillslope for the soil water storage calculation, which was then used to calculate the interception capacity based on the water balance equation.

To determine the saturated hydraulic conductivity of the soil matrix (K_ms), a tension infiltrometer called “hood infiltrometer” was used (Demand et al., 2019). For every measurement location, infiltration rates with at least three tensions between 0.4 and 5.9 hPa were recorded, allowing an exponential function to be fitted to calculate K_ms at a tension of 6 hPa (Gardner, 1958). At this tension, pores with diameters greater than 0.5 mm are excluded from flow, so the measured hydraulic conductivity represents the soil matrix infiltration capacity (Jarvis, 2007). However, due to high macroporosity at many locations, adjusting the pressure in the hood was difficult, and measurements were only possible at tensions of 1–4 hPa. Therefore, for some sites, the K_ms values are extrapolated from the Gardner fit to a tension of 6 hPa (Demand et al., 2019).

2.2.2 Previous studies on PFPs

Dye tracer experiments demonstrated that prominent PFPs were in the form of macropores within the root zone. Moreover, these experiments revealed that PFPs are well-connected in the vertical direction but are discrete in the lateral direction (Wang et al., 2022). The connected PFPs were constituted by several individual macropores, such as decayed root channels, soil–root interface spaces, and animal burrows. The mean lateral transport distance of a tracer was around 25 cm. It is believed that the abundant root distribution, presence of rock fragments, and coarse soil texture contribute to the vertically connected flow paths within the root zone of both forests; this is also confirmed by the similar occurrence frequency of preferential flow in both forests (Wang et al., 2022). Intact soil cores (50 mm in diameter and height) were sampled by depth and scanned to determine the macroporosity, defined as the ratio of pores with a diameter greater than 30 µm to the total soil column. The results showed that macroporosity ranged from 3 % to 16 %, with mean values of approximately 8 % in the coniferous forest and 9 % in the broadleaf forest (Ruxin Yang, 2023, personal communication).

2.3 Numerical modelling

2.3.1 Numerical model and model set-up

The HYDRUS 2D software is a physically based finite-element model for simulating two-dimensional water movement in variably saturated media by numerically solving the Richards' equation (Šimùnek et al., 2012; Šimùnek et al., 2016). It also enables the explicit representation and adjustment of different soil structures (i.e. PFPs and ground layers).

A 2D flow model identical to the artificial field configuration was established (Fig. 1a and b), with a constant 3 cm thick soil–bedrock PFP. The hillslope cross-section was discretized at 5×5 mm to balance the need to represent PFPs and minimize computational costs (Fig. 2). A no flux boundary condition was imposed at the bottom bedrock boundary and the up vertical boundary, while a seepage face boundary condition and an atmospheric boundary condition were specified at the lower vertical boundary and the soil surface, respectively (Fig. 1b).

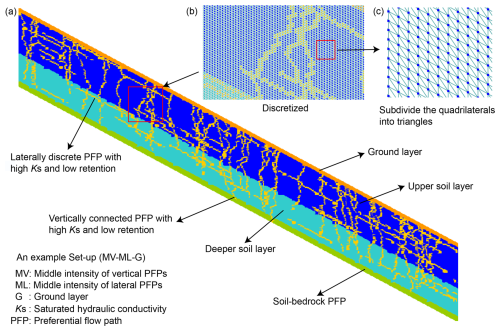
Figure 2 A hillslope set-up with explicit structures (a) and discretization of the flow domain (b, c) in the numerical model.

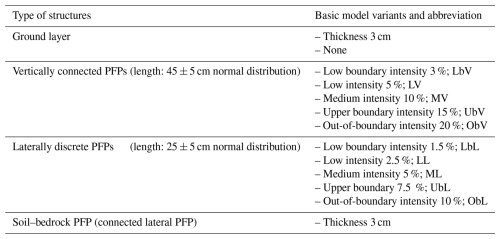
Within the soil, PFPs were conceptualized as vertically connected PFPs (vPFPs) and laterally discrete PFPs (lPFPs) in the 2D cross-section, based on prior knowledge. To represent the PFPs in the model, a random placement method was applied. Five different macroporosities were used for vPFPs: 3 % for lower boundary intensity (Lb), 5 % for low intensity (L), 10 % for medium intensity (M), 15 % for upper boundary intensity (Ub), and 20 % for out-of-boundary intensity (Ob). Due to the observed half-length of lPFPs compared to vPFPs, half of these intensities were assigned to discrete lPFP: 1.5 %, 2.5 %, 5 %, 7.5 %, 10 % (Table 1). Since the explicit spatial distribution of PFPs in soil remains unknown, they were generated using random components. The starting points of the vPFPs were appointed using a Poisson process and extended stepwise into the soil to lengths sampled from a normal distribution with a mean of 45 cm and a standard deviation of 5 cm. The lPFPs were generated similarly, with starting points randomly assigned and extended downslope to lengths sampled from a normal distribution with a mean of 25 cm and a standard deviation of 5 cm. To examine the role of the ground layer in determining subsurface flow, it was optionally included in the topmost row of the 2D flow domain.

Table 1 Different types of structures and variants for the numerical model set-up: four different types of structures.

2.3.2 Model parameters and evaluation

We assigned an effective porous medium with low water retention properties to the meshes representing PFPs to minimize capillary forces. Partial parameters for the PFPs were retrieved from a meta-analysis, using a mean macropore flow velocity of $\mathrm{1.08}\times {\mathrm{10}}^{-\mathrm{3}}$ m s⁻¹ (Gao et al., 2018). For the soil matrix, parameters except saturated hydraulic conductivity were determined using multistep-outflow experiments on undisturbed soil columns under unsaturated conditions to exclude the hydraulic effects of macropores. The hydraulic properties of the different soil layers were modelled with van Genuchten–Mualem parameterization (Table 2). The ground layer was likewise parameterized as a highly conductive medium with high porosity. It was treated as an equivalent soil layer, with a high residual water content, and the saturated water content was defined as the sum of the residual water content and the equivalent interception capacity. The soil–bedrock interface was also conceptualized as a highly conductive medium with a low retention capacity, akin to the PFPs (Table 2).

Table 2 Parameters for different structures in the numerical model.

To investigate the role of PFPs and the ground layer in subsurface flow, and to identify the active PFPs involved in subsurface flow, we first performed a short-term simulation of a typical rainfall event representative of local rainfall characteristics. This initial simulation allowed us to examine how the hillslope structure (i.e. PFPs and the ground layer) affects subsurface flow and to identify set-ups that meet evaluation criteria. Subsequently, a long-term simulation covering the growing season was conducted to further refine the candidate set-ups identified at the event scale because of equifinality and to identify the active PFPs involved in surface flow in both forests. The simulated subsurface flow was compared with observed flow data, and set-ups were deemed acceptable if they met the following evaluation criteria: a Nash–Sutcliffe efficiency (NSE) greater than 0.75, a root mean square error (RMSE) less than half of the standard deviation of the observed subsurface flow, and a water balance deviation within 10 % (Wienhöfer and Zehe, 2014).

3 Results

3.1 Hillslope subsurface flow at even scale

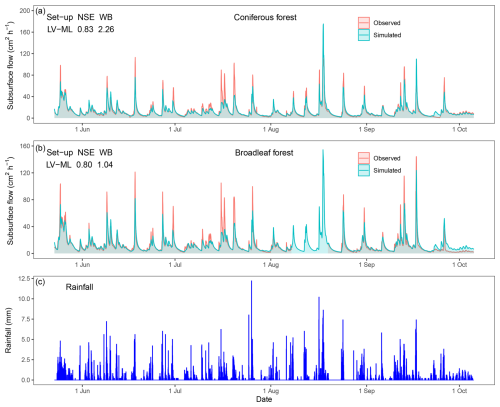
The selected rainfall event lasted from 7 June 2020 17:00 to 11 June 17:00 UTC+08:00, spanning 97 h, with multiple peaks and a mean intensity of 0.88 mm h⁻¹ (69 mm in total), which was close to the mean intensity of 0.85 mm h⁻¹ for the entire monitoring period. During the event, subsurface flow ranged from 4.24 to 91.59 cm² h⁻¹ in the broadleaf forest, with a standard deviation of 17.81 cm² h⁻¹, and from 4.40 to 77.92 cm² h⁻¹ in the coniferous forest, with a standard deviation of 15.69 cm² h⁻¹.

Overall, the model evaluation criteria for 50 set-ups per forest type were summarized (Table 3). A total of 36 set-ups in the coniferous forest and 39 in the broadleaf forest achieved an NSE greater than 0.75, with maximum NSE values of 0.86 and 0.88, respectively. Under the LbV and LV conditions, all set-ups that included a ground layer met the NSE criterion. However, as the intensity of vPFPs increased, the number of set-ups meeting the NSE criterion decreased sharply. Furthermore, 31 set-ups in the coniferous forest and 35 in the broadleaf forest met the RMSE criterion, displaying significant variability with no discernible patterns. Regarding the water balance criterion, only 6 set-ups in the coniferous forest and 5 in the broadleaf forest matched the observed water balance within an error margin of ±10 %, with minimum errors of 0.52 % and 2.12 %, respectively. Notably, these acceptable set-ups were observed only under LbV and LV conditions without the ground layer (Table 3; Fig. 3). Ultimately, only 3 set-ups in the coniferous forest and 2 in the broadleaf forest fulfilled all three elevation criteria – specifically, LV-LbL, LV-LL, and LV-ML in the coniferous forest, and LV-LL and LV-ML in the broadleaf forest – and were considered acceptable set-ups (Table 3).

Figure 3 Observed and simulated hydrographs of the acceptable set-ups and their counterparts with a ground layer in the coniferous forest (a, c) and broadleaf forest (b, d) at the event scale (e, f).

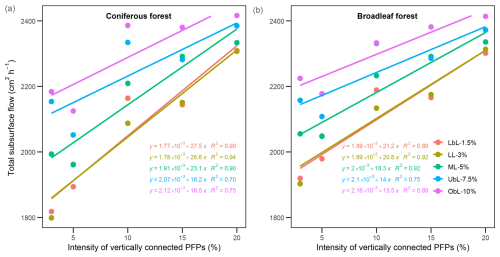
Figure 4 Relationships between total subsurface flow and the intensity of vertically connected PFPs in the coniferous forest (a) and broadleaf forest (b).

The simulation results of the acceptable set-ups with and without the additional ground layer were displayed against the observed hydrographs (Fig. 3). These results demonstrated that only partial PFPs were involved or active in the runoff processes in both forests. Notably, none of the 5 set-ups included a ground layer. However, simulations incorporating a ground layer exhibited an elevated NSE (mean NSE of 0.86 with a ground layer versus 0.79 without a ground layer) under LV conditions in the broadleaf forest, while the coniferous forest showed no significant difference (mean NSE of 0.81 with a ground layer versus 0.82 without a ground layer, respectively). When the ground layer is excluded, a positive linear relationship between subsurface flow and the intensity of vertically connected PFPs was observed in both forests (Fig. 4). The coniferous forest exhibited higher fitted slopes across all the set-ups (Fig. 3), indicating the higher sensitivity of subsurface flow to changes in PFPs in the coniferous forest compared to the broadleaf forest. In addition, as the intensity of PFPs increases, the variability of the subsurface flow decreases among set-ups (Fig. 3).

Furthermore, to assess the robustness of the approach under consistent PFP intensity but varying spatial distribution, multiple runs were conducted for each acceptable set-up with an additional ML-LL set-up. The results revealed significant differences between set-ups (p<0.01), but no significant differences within set-ups, except for the ML-LL set-up in the coniferous forest (Fig. S3). These findings suggest that the set-ups were generally robust against spatial heterogeneity in PFPs, thereby indicating their reliability in representing the underlying hydrological processes. Particularly, the ML-LL set-up in the coniferous forest was the first to exhibit differences among replicates of the same set-up (Fig. S3), further supporting its greater sensitivity to changes in PFPs. Since the saturated hydraulic conductivity of PFPs (Ks_pfps) is a key factor controlling water flow and was retrieved from a meta-analysis study, we conducted a sensitivity analysis to clarify its effect on model performance. The analysis revealed an exponential relationship between Ks_pfps and NSE and demonstrated that the broadleaf forest was more sensitive to macropore flow velocity in the range of $\mathrm{2.22}\times {\mathrm{10}}^{-\mathrm{5}}$ to $\mathrm{1.83}\times {\mathrm{10}}^{-\mathrm{1}}$ m s⁻¹ (Fig. S4).

3.2 Hillslope subsurface flow at seasonal scale

The simulation period at the seasonal scale spanned from 23 May 2020 00:00 to 5 October 2020 16:00 UTC+08:00, covering a total of 3257 h (∼ 136 d) and 1412.95 mm of rainfall. The acceptable 3 and 2 set-ups that met all model evaluation criteria at the event scale were used to simulate long-term subsurface flow dynamics. The results showed a reduction in the number of acceptable set-ups: from 3 to 2 in the coniferous forest, and from 2 to 1 in the broadleaf forest. This reduction indicated that long-term simulation helps constrain model equifinality and improves the congruence of set-ups to actual hillslope structures. The final set-ups meeting all 3 evaluation criteria at the seasonal scale were LV-ML (NSE = 0.83, RMSE = 6.06, and water balance (WB) = 1.04 %) and LV-LbL (NSE = 0.80, RMSE = 6.66, and WB = 0.95 %) in the coniferous forest, and LV-ML (NSE = 0.80, RMSE = 6.59, and WB = 2.26 %) in the broadleaf forest. The reduced set-up was LV-LL (NSE = 0.69, RMSE = 8.12, and WB = 1.17 %) in the coniferous forest and LV-LL (NSE = 0.74, RMSE = 7.47, and WB = 2.16 %) in the broadleaf forest. Hydrographs of the best-performing set-ups (with the highest NSE values) were displayed against the observed hydrographs (Fig. 5). While these set-ups successfully reproduced seasonal subsurface flow dynamics, there were noticeable deviations between simulated and observed peak subsurface flows following heavy rainfall events, particularly during continuous heavy rainfall events within a short time frame.

Figure 5 Observed and simulated hydrographs of the set-ups with the highest NSE in the coniferous forest (a) and broadleaf forest (b) during the growing season (c).

4 Discussion

4.1 Role of the ground layer in runoff processes

The forest ground layer significantly influences hillslope flow dynamics at the event scale. Specifically, we found that the first simulated peak flow in set-ups with a ground layer was higher in magnitude and occurred earlier compared to those set-ups without a ground layer (Fig. 4; Table S1). This is because the ground layer tends to retain rainfall and delay water entry into PFPs, thereby advancing peak flow timing. In contrast, the set-ups without a ground layer exhibited even more delayed peak flow timing. This can be attributed to more PFPs being directly connected to the atmosphere, leading to greater water retention in soil due to increased exchange between PFPs and the soil matrix; therefore, we observed a consistently delayed peak flow timing in both forest types (Fig. 4; Table S1). Meanwhile, set-ups with a ground layer produced higher peak flows that were closer to the observed values, which aligns with previous findings that the litter layer enhanced flood peak flows during short-duration storms (Zhu et al., 2020). Due to the high flow velocity in the ground layer, water is rapidly transported downslope, where it infiltrates into the soil, leading to increases in soil moisture and thereby soil hydraulic conductivity. This process allows water to discharge more quickly and in greater volume at the downslope of hillslope, as recognized in a previous study (Klaus and Jackson, 2018), rather than being distributed relatively homogeneously over the whole hillslope as observed in set-ups without a ground layer.

Table 3 Summary table of the simulations in different set-ups in relation to the three model evaluation criteria (“N”: NSE greater than 0.75, “–” less than 0.75; “R”: RMSE less than half of standard deviation; and “W”: water balance error less than 10 %). Letters indicate which criteria were fulfilled, and bold and italic text indicates that all criteria were fulfilled. The abbreviations Lb, L, M, Ub, and Ob represent the PFPs intensities level: Lb (lower boundary), L (low), M (middle), Ub (upper boundary), and Ob (out-of-boundary); the letters “L” and “V” following the intensity indicate the directions of PFPs – lateral and vertical, respectively).

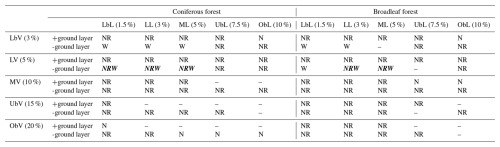
Besides, only the set-ups without a ground layer met the water balance criterion (Table 3). This may be ascribed to the rainfall characteristics and the high hydraulic conductivity of the ground layer in this study: low rainfall intensity means low infiltration capacity, causing water to remain longer in the ground layer, where high hydraulic conductivity facilitates rapid lateral flow. Additionally, the buried PFPs resemble those in agricultural fields, where macropores started below a tilled topsoil layer (Akay and Fox, 2007; Holbak et al., 2021). Agricultural fields with buried macropores exhibit a higher peak flow amount than those with surface-connected macropores under flat terrain, where the hydraulic conductivity of the “material” above macropores was 1.60 cm h⁻¹ (Akay and Fox, 2007) and 1.47 cm h⁻¹ (Holbak et al., 2021). These values are much less than that of the ground layer in this study; and slope negatively affects ground layer interception regardless of vegetation types and increases lateral flow, particularly when it a threshold value of 15° (Du et al., 2019; Zhao et al., 2022). Therefore, the high hydraulic conductivity of the ground layer and steep slope together facilitate lateral flow and amplify the unpredictability of water flow behaviour, which likely explains why simulations without a ground layer performed better at both the event and seasonal scales. Overall, these findings recognize the need to account for the ground layer by considering not only its interception capacity and hydraulic conductivity, which facilitate lateral flow within it, but also its role as a cover layer, which disconnects PFPs from the atmosphere, an aspect often ignored or simplified as a bucket in the runoff processes of many earth system and hydrological models.

4.2 The PFPs involved in runoff processes in moraines

Previous studies have shown that over long periods of soil development spanning thousands of years, moraines commonly exhibit decreases in bulk density, increases in clay-sized particles, and the accumulation of organic matter. These factors are known to influence soil hydrology by shaping soil structure (Hartmann et al., 2020a). In this study, glacial retreat in alpine mountains formed elevation-dependent moraines that primarily differ in temperature. Soil at lower elevations experiences stronger weathering due to higher temperatures; thus, lower bulk density and higher clay content were expected in the broadleaf forest. However, moraines distributed along the valley had a mean slope of over 30° (Fig. S5), and frequent precipitation and scouring had carried away large amounts of fine particles in the early bare and later vegetated phases of the moraines, thus altering the traditional trend of clay accumulation (Li et al., 1986). Hence, both forests had coarse-textured soil with sand content over 85 %, but the broadleaf forest had relatively higher soil organic matter content due to the higher temperature, leading to increased residual soil water content and field capacity (Table 2; Fig. S6). Thus, stronger soil suction under lower soil water content conditions in the coniferous forest allowed more water absorption by the soil matrix, consistent with the observed lower total subsurface flow at low PFPs intensity (Fig. 4). In contrast, the broadleaf forest, characterized by higher soil residual water content and organic matter content, attenuated lateral water dispersion due to organic matter coating, which reduced permeability and promoted rapid water accumulation in PFPs due to the fast attainment of soil field capacity, exhibiting a buffering effect on changes in PFPs (Fig. S6). Consequently, the coniferous forest exhibited greater sensitivity to changes in PFPs.

Land cover plays a key role in shaping hillslope internal structures and especially influences the number and type of PFPs (Luo et al., 2010; Benegas et al., 2014; Guo and Lin, 2018; Demand et al., 2019). This is especially true on forested hillslopes with thin soil – preferential flow usually develops vertically through the entire soil profile via a connected flow network of soil–root interfaces, decayed root channels, animal burrows, fissures, and cracks, allowing for the fast movement of infiltrated rainfall to the soil–bedrock interface. Subsequently, lateral flow at the soil–bedrock interface transmits water downslope and generates subsurface flow (Tromp-Van Meerveld and McDonnell, 2006; McDonnell et al., 2021; Zhang et al., 2025). Meanwhile, flow in the lateral PFPs within the forest soil is restricted by relatively impermeable organic coatings, which limits lateral connectivity, and the flow usually converges into vertically connected PFPs that extend through the entire soil profile (Jarvis, 2007), supporting the dominant role of vertically connected PFPs in subsurface flow. In this study, the broadleaf forest was hypothesized to engage more PFPs in subsurface flow due to its more intensive biophysical activities, driven by its lower elevation and relatively higher average temperature compared with the coniferous forest. However, the modelling results rejected the hypothesis, as set-ups with a low intensity of vertically connected PFPs best matched observed flow dynamics at both the event and seasonal scales in both forests, manifesting only partial PFP involvement. The underlying reasons involve several aspects. First, vertically connected PFPs may be mainly attributed to fine roots (< 2 mm in diameter). Studies have shown that fine roots account for over 90 % of total roots in both deciduous broadleaf and evergreen coniferous forests, creating connected PFPs through an intensified network of interconnected void pores driven by the roots' fast turnover (Luo et al., 2019). This aligns with the consistently positive relationship between fine root density and subsurface flow across different land covers (Nespoulous et al., 2019). Accordingly, the comparable fine root content across forest types, of 77.5 ± 6.3 g kg⁻¹ for the broadleaf forest and 65.4 ± 7.6 g kg⁻¹ for the coniferous forest (p>0.05) in this study (Xiong et al., 2024), contributed to the comparable PFPs involved in water flow. Second, similar soil properties, including soil bulk density, porosity, texture, and rock fragment content, were observed across the forest types. This is primarily due to the comparable rainfall pattern, which is recognized as the main factor influencing soil variation (van der Meij et al., 2020). Furthermore, studies in the Central Swiss Alps showed that only macropore flow via root channels was observed in the deeper parts of the soil at the oldest moraine (aged 10 millennia), where prostrate shrubs and small trees have colonized (Hartmann et al., 2020b); sprinkling experiments in the moraine further confirmed that PFPs are more closely related to soil layering, organic matter content, root biomass, and root length density than soil texture (Hartmann et al., 2022). Our previous study also revealed a comparable preferential flow occurrence and runoff coefficient of the shallow root zone, despite significant differences in the total root biomass between forest types (Wang et al., 2022; Wang et al., 2024). Overall, these findings, together with supporting evidence from the literature, suggest that PFPs associated with fine roots, rather than total macroporosity, should be the primary focus, as increases in macroporosity or total root biomass do not necessarily enhance hillslope subsurface flow.

Next, we explored the mechanism of preferential flow from a thermodynamic perspective, which provides insight into its nature. Zehe et al. (2010) and Lin (2010) propose that water flow organizes itself to maximize the dissipation of free energy, the energy capable of performing work, thereby driving the system toward local thermodynamic equilibrium and enhancing mechanic stability by reducing hydro-mechanical stress (Ehlers et al., 2011; Zehe et al., 2013). In this study, soil matrix hydraulic conductivity was relatively higher (on the order of 10⁻⁵ m s⁻¹) than rainfall intensity (Wang et al., 2022), and soil moisture remained persistently high (Wang et al., 2023). These conditions suggest that the dissipation of free energy via surface flow is uncommon (Anderson et al., 2009; Angermann et al., 2017; Wang et al., 2024), whereas water through PFPs efficiently depletes free energy by facilitating the export of potential energy via subsurface flow (Zehe et al., 2013). This mechanism is consistent with the high frequency of preferential flow observed in our earlier study (Wang et al., 2022).

A soil-mantled hillslope functions as an open thermodynamic system that exchanges mass, energy, and entropy with the surroundings to maintain a far-from-equilibrium, stable, and steady state (Lin, 2010; Zehe et al., 2013). This concept supports the idea that hillslope evolution tends toward optimal structures, in which materials with different properties are rearranged/arranged to maximize entropy production and energy dissipation (Lin, 2010; Zehe et al., 2019). Overall, water flowing through soil creates network-like subsurface pathways and arranges soil properties, such as soil texture, soil layering, organic matter, soil structure, and other features, to reduce flow resistance, thus forming a preferential flow network with the least global flow resistance (Lin, 2010). In this study, the primary difference between the two analysed hillslope arises from variations in temperature caused by decreasing atmospheric pressure with elevation, which in turn has led to divergent vegetation. While the most frequent inputs of mass and energy, solar radiation and rainfall, were similar for both forests, temperature-induced vegetation appears to play a key role in directing hillslope evolution toward structures that optimize the depletion of free energy. This highlights a close relationship between vegetation and soil structures, specifically PFPs, contributing to convergent hillslope structures. This is consistent with research showing that the macroporosity calculated using the maximum reduction rate of the free energy of soil water enables long-term water balance simulation as well as provides the best fit when macroporosity is calibrated to match rainfall–runoff (Zehe et al., 2013; Zehe et al., 2019). These findings and literature potentially elucidate the dominant role of vegetation in shaping moraine hillslope structures and thereby subsurface flow dynamics in steep terrain with a humid climate.

Despite the propensity of preferential flow to rapidly reduce free energy, the flow network formed by PFPs in soil do not always achieve the maximum local reduction of free energy. Studies show that only a limited number of particle paths pass through high conductivity zones (e.g. PFPs), and that the connectivity of rapid PFPs does not require connected zones of continuously high hydraulic conductivity (Bianchi et al., 2011; Edery et al., 2014). Indeed, water particles emerge near the vicinity of bottlenecks with low hydraulic conductivity, where considerable energy is required to propel fluid, resulting in significant free energy depletion (Bejan, 2007; Bianchi et al., 2011; Edery et al., 2014; Zehe et al., 2021). This suggests that water flow through a network of limited PFPs and soil matrix facilitates the maximum dissipation of free energy at the entire hillslope hydrological system level, indicating that PFPs are partially involved in subsurface flow.

4.3 Uncertainties and future outlook

In this study, certain uncertainties related to model conceptualization and methodology still exist, which also point toward promising directions for further research.

Uncertainties of conceptualization: With regards the PFPs, their intensities/numbers were derived from CT-imaged macropores, which were classified based on pore diameter exceeding a certain threshold, for which no consensus has been reached (Jarvis, 2007). A more accurate estimate of PFPs could be achieved if the extent to which critical pore diameter is governed by gravity were known. Further, we assumed a vertically and laterally uniform macropore diameter/aperture, disregarding its inherent nonuniformity (Luo et al., 2010). Moreover, PFPs were represented as explicit elements in the flow domain following specific rules, but it cannot be ruled out that a more regular or irregular way would achieve better simulation results (Wienhöfer and Zehe, 2014). More importantly, we explicitly represented the hillslope using pore-scale PFPs, as this pore system was identified as dominant at this scale and was deemed appropriate for better representing soil heterogeneity given the relatively uniform soil phases in this study. Despite the fact that the pore system fundamentally determines the structure of porous media and governs water flow (Vogel, 2019), it remains necessary to account for the formation processes of the pore system with respect to the studied medium to enable the accurate representation of PFPs in physically based models. For example, PFPs in the form of wormholes (common in gypsum or limestone karst), created by flow and dissolution, have lengths following a power law distribution (Li et al., 2022), while PFPs in calcite are dynamic through reaction–transport coupling (Shavelzon et al., 2025). However, extending pore-scale representations to larger spatial scales entails prohibitive computational demands. Nevertheless, as most flow processes scale up, the influence of small-scale perturbations diminishes, reducing the necessity to represent fine-scale complexity. For example, representing PFPs as the most permeable alluvial facies, delineated by gridded cells, achieved satisfactory results in a glaciofluvial sedimentary basin (Schiavo, 2022, 2023). These points emphasize the importance of representing heterogeneity with respect to site-specific processes and the scale of investigation.

Uncertainties of methodology: As to the medium parameters, we fixed parameters with some existing data to guide the conceptualization of both PFPs and the ground layer. Specifically, the parameters for the ground layer were acquired through rainfall simulation, conducted at intensities far exceeding the regional average. The ground layer was further simplified as an isotropic media, which oversimplified its distinct stratification, decomposition stages, and substantial spatial variability along hillslopes. Moreover, the complex and often unpredictable phases of the ground layer's storage and release response to rainfall (Guevara-Escobar et al., 2007; Li et al., 2017; Du et al., 2019) cannot be adequately captured by an equivalent water retention curve. As for the numerical model, we used HYDRUS 2D, which solves water flow using Richards' equation. However, this approach does not capture pore-scale processes, such as observed finger flow, which is often observed in heterogeneous moraine soils (Hartmann et al., 2020b; Nimmo, 2021; Hartmann et al., 2022). Additionally, PFPs are emptied more rapidly, causing a lag in water content related to water potential. Thus, they do not follow a unique water retention curve as typically assumed when applying Richards' equation (Vogel et al., 2023).

Specifically, there are noticeable deviations between the simulated and observed subsurface flow under heavy rainfall conditions (Fig. 5). Although these deviations may appear rather small given the complexity and heterogeneity of natural hillslopes, we nevertheless delve into them in light of the aforementioned uncertainties, aiming to provide insights for improving model conceptualization and predictive accuracy. First, we defined macropores as pores with a diameter or aperture over 30 µm; however, it is evident that fracture apertures less than 30 µm can still transmit preferential flow in the form of film or rivulet flow (Tokunaga and Wan, 2001; Lange et al., 2009); Secondly, although the model reproduced acceptable results using a fixed and below-average number of PFPs, increased soil wetness during continuous rainfall promotes the self-organization of PFPs into larger flow networks, thereby engaging more PFPs in subsurface flow (Sidle et al., 2001; Nieber and Sidle, 2010; Zehe et al., 2013). Finally, the potential initiation of other preferential flow types, such as finger flow and funnel flow induced by heterogeneity in soil moisture, soil hydraulic conductivity, or water flux, was not considered (Hartmann et al., 2020b; Nimmo, 2021). In summary, the simplified conception of PFPs, the assumption of their static nature during rainfall, and the omission of other preferential flow regimes collectively contribute to the underestimation of subsurface flow under heavy rainfall conditions. Addressing these limitations in numerical models would help improve simulation accuracy, particularly for flood prediction during extreme rainfall events.

5 Conclusions

This study simulated subsurface flow using HYDRUS 2D, explicitly accounting for PFPs and ground layers in forested hillslopes on valley moraines along an alpine mountain elevation, focusing on two climax vegetation types – coniferous and broadleaf forests. The hillslope structure set-ups that successfully reproduced the field-observed hydrological responses were identified at both the event and seasonal scales, and the underlying mechanisms were interpreted using available field data and a thermodynamic perspective to emphasize the synergy between vegetation and soil properties.

The configuration of the successful set-ups consistently showed that the intensity/number of the vertically connected PFPs involved in the subsurface flow were low, representing 5 % of total spatial area at both the event and seasonal scales in both coniferous and broadleaf forests. The low intensity of vertically connected PFPs stems from the principle of least global flow resistance and maximum dissipation of free energy. This is achieved by water flowing through a combination of partial PFPs and the soil matrix, rather than relying on all PFPs within the hillslope. The similar involvement of PFPs across forest types was largely attributed to the occurrence of similar coarse-texture soil resulting from frequent precipitation and washout of clay-sized particles, as well as comparable fine root content, both of which contribute to the connectivity of vertical PFPs, which dominates subsurface flow in thin soil hillslopes. The coniferous forest is more sensitive to changes in PFPs due to lower organic matter content in the soil profile. In addition, the ground layer significantly influences subsurface flow by disconnecting PFPs from the soil surface, promoting faster and greater water accumulation in the downslope area of hillslopes, thereby decreasing peak flow timing and increasing peak flow magnitude in both forests. This study elucidated the feasibility of conceptualizing numerical models based on field evidence of PFPs and ground layers to successfully predict hillslope flow, and revealed that vegetation (i.e. organic matter content, fine roots, and ground layers) plays a more dominant role in controlling water flow than soil properties (e.g. bulk density, texture, and rock fragments), advancing our knowledge of hillslope structures and runoff evolution over time in humid valley moraines.