Improved representation of soil moisture processes through incorporation of cosmic-ray neutron count measurements in a large-scale hydrologic model

Profound knowledge of soil moisture and its variability plays a crucial role in hydrological modelling to support agricultural management, flood and drought monitoring and forecasting, and groundwater recharge estimation. Cosmic-ray neutron sensing (CRNS) has been recognised as a promising tool for soil moisture monitoring due to its hectare-scale footprint and decimetre-scale measurement depth. But since CRNS provides an integral measurement over several soil horizons, a direct comparison of observed and simulated soil moisture products is not possible. This study establishes a framework to assess the accuracy of soil moisture simulated by the mesoscale Hydrologic Model (mHM) by generating simulated neutron counts and comparing these with observed neutron measurements for the first time. We included three different approaches to estimate CRNS neutron counts in the mHM as a function of the simulated soil moisture profiles: two methods based on the Desilets equation and one based on the forward operator COSMIC (COsmic-ray Soil Moisture Interaction Code). For the Desilets method, we tested two different approaches to average the vertical soil moisture profiles: a uniform vs. a non-uniform weighting scheme depending on the CRNS measurement depth. The methods were tested at two agricultural sites, namely one pasture site and one forest site, in Germany. To explore the prior and posterior distributions of the mHM parameters when constrained by CRNS observations, we used a Monte Carlo method based on Latin hypercube sampling with a large sample size (S = 100 000). We found that all three methods performed well, with a Kling–Gupta efficiency > 0.75 and a percent bias < ± 10 % across the majority of investigated sites and for the best 1 % of parameter sets. The performance of the neutron forward models varied slightly across different land cover types. The non-uniform approach generally showed good performance, particularly at the agricultural sites. On the other hand, the COSMIC method performed slightly better at the forest site. The uniform approach showed slightly better results at the grassland site. We also demonstrated for the first time that the incorporation of CRNS measurements into the mHM could improve both the soil moisture and the evapotranspiration products of the mHM. This suggests that CRNS is capable of improving the model parameter space in general and adds a broader perspective on the potential of CRNS to support large-scale hydrological and land surface models.

1 Introduction

Soil moisture is a key terrestrial climate variable because it controls the mass and energy exchange between the Earth's surface, the groundwater, the vegetation, and the atmosphere. Understanding soil moisture levels with changes in temperature is crucial for enhancing the predictability of climate patterns on inter-seasonal and annual timescales, as highlighted in previous studies (Santanello et al., 2011; Seneviratne et al., 2006). Moreover, soil moisture variability also plays a significant role in a wide range of applications, including flood forecasting, weather forecasting, climate modelling, agricultural management, and groundwater recharge (Van Steenbergen and Willems, 2013; Albergel et al., 2010; Jablonowski, 2004; Wahbi et al., 2018; Samaniego et al., 2019; Barbosa et al., 2021). In hydrological modelling, soil moisture is a key variable controlling the partitioning of precipitation into evapotranspiration, infiltration, and runoff (Fuamba et al., 2019; Zhuo et al., 2020). Proper initialisation and modelling of soil moisture are crucial for predicting other hydrologic processes (e.g. runoff, evapotranspiration). Nevertheless, uncertainties in input data and model parameters, along with limitations in the representation of subsurface processes, can impede the reliability of soil moisture estimation (Chen et al., 2011). Obtaining accurate soil moisture measurements at the field scale is challenging due to current measurement limitations and subsurface complexity (Dong and Ochsner, 2018). Estimating average soil moisture at the mesoscale (≈ 1–100 km) is particularly difficult due to measurement technique limitations in terms of their “footprint” and due to the limitations of the measurement methods used to bridge the scale gap between point-scale and areal average measurements for hydrologic modelling (Chan et al., 2018).

One promising approach to infer soil moisture at the field scale is the cosmic-ray neutron sensing (CRNS) technique (Zreda et al., 2008; Desilets et al., 2010; Zreda et al., 2012). It is based on a neutron detector that counts the average number of neutrons in the air above the ground, which represents the average hydrogen content in the environment. The method has demonstrated potential for estimating average soil moisture over areas of several hectares in size and tens of decimetres in depth (Köhli et al., 2015; Schrön et al., 2017). CRNS probes are typically calibrated locally using soil samples within their support volume (Franz et al., 2012; Schrön et al., 2017). CRNS data are used in various studies, including land surface modelling, vegetation dynamics, and catchment hydrology, as well as in supporting the agriculture sector with soil and climate data (Franz et al., 2020). Moreover, CRNS-derived soil moisture has been valuable in water balance studies, aiding in estimating infiltration and evapotranspiration (Schreiner-McGraw et al., 2015; Foolad et al., 2017; Wang et al., 2018).

When it comes to the comparison of observed CRNS soil moisture with the results from a hydrological model, a major challenge is to select the right vertical scale. A CRNS measurement is an integral value over a measurement volume, and the depth of this volume depends on the soil moisture profile in a non-linear way (Köhli et al., 2015). While it is well understood at which depth the measured neutrons probed the soil, it is not directly clear how to compare the CRNS soil moisture product with several soil layers in a model. Shuttleworth et al. (2013) argued that the direct comparison of the raw product – the neutron counts – would be the favourable way to compare simulations with observations instead. By simulating neutrons directly, one could emulate the neutron counts per grid cell based on its soil moisture profile in the model and then compare the result directly with the corresponding neutron measurement.

One way to calculate neutrons within the model is to use established empirical relationships between average soil moisture and neutrons (Desilets et al., 2010; Köhli et al., 2021). Another way is to employ the neutron forward operator COSMIC (COsmic-ray Soil Moisture Interaction Code) introduced by Shuttleworth et al. (2013). It emulates the effective vertical neutron transport through the soil and thereby enables a comprehensive representation of the neutron generation process. Although this operator can only be a simplification of the actual physical processes as modelled by, for example, URANOS (Köhli et al., 2023), its higher complexity still comes with higher computational demand compared to the mentioned analytical relationships.

Previous studies, such as Barbosa et al. (2021) and Brunetti et al. (2019), have recognised the importance of CRNS over traditional invasive point-scale techniques and have utilised the HYDRUS-1D model to simulate soil moisture at the field scale. HYDRUS-1D offers a valuable framework for modelling soil moisture dynamics and has been particularly useful in addressing the subsurface processes. These studies incorporated a neutron forward operator COSMIC to simulate the neutron counts based on soil moisture profiles. They inversely calibrated soil hydraulic parameters by comparing observed and simulated neutron count rates, whereas, beforehand, this was limited to being done via comparison of depth-averaged soil moisture values (Rivera Villarreyes et al., 2014). The potential utility of using CRNS data to calculate volumetric soil water content (SWC) and to improve soil hydraulic parameters within land surface models has also been observed previously, as highlighted by Rosolem et al. (2014). In Iwema et al. (2017), a land surface model investigated the impact of reducing scale mismatch between energy flux and soil moisture observations using CRNS data. Patil et al. (2021) employed a distributed land surface model, the Data Assimilation Research Testbed (DART) with CRNS time series, and an ensemble adjustment Kalman filter to simulate water and energy balances. Both studies focused on analysing land surface water and the energy balance, exploring data assimilation and calibration techniques.

The Hydrologiska Bryans Vattenbalansavdelning (HBV) model, as studied by Dimitrova-Petrova et al. (2020), employed CRNS data in a mixed-agriculture landscape to explore the water balance on the land surface. On the other hand, Beck et al. (2021) used remote sensing products and groundwater level measurements to temporally calibrate the HBV model, emphasising the challenge of comparing satellite-derived soil moisture with point-scale in situ measurements. Additionally, the study by Baatz et al. (2017) was the first that utilised spatially distributed hydrological modelling, integrating CRNS data, FAO and BK50 soil maps, and other soil data in the Community Land Model (CLM). They demonstrated that assimilating CRNS data improved catchment-scale soil water content characterisation by updating spatially distributed soil hydraulic parameters. Furthermore, Zhao et al. (2021) assessed the significance of CRNS data in CLM version 3.5, conducting simulations based on 13 CRNS stations over 2017–2018. Despite employing a simplified Richards equation, limitations included the absence of lateral flows and groundwater representation.

The mesoscale Hydrologic Model (mHM; Samaniego et al., 2010b; Kumar et al., 2013b) is known for its spatially distributed hydrologic predictions at a large scale, incorporated with the multiscale parameter regionalisation (MPR) technique. We chose the mHM in this study for its efficient parameterisation approach that allows for a seamless prediction of water fluxes at different spatial resolutions (Samaniego et al., 2017; Zink et al., 2017; Jing et al., 2018; Schweppe et al., 2022). This feature allows the model to scale its applications from a locally relevant scale to regional and continental scales (Kumar et al., 2013b; Huang et al., 2017; Rakovec et al., 2019). One of the promising applications of the mHM is the operational German Drought Monitor (GDM) that provides daily updates on the soil-moisture-related drought status (Samaniego et al., 2013; Moravec et al., 2019; Pohl et al., 2023). Previous evaluation of the GDM for soil moisture focuses on assessing the skill of the model in reproducing soil moisture anomalies based on point-scale soil moisture observations (Zink et al., 2016, 2018; Rakovec et al., 2022; Scharnweber et al., 2020; Boeing et al., 2022). Such an evaluation is fraught with uncertainties due to the scale mismatch between limited point-scale observations versus grid-scale modelled estimates. In contrast, CRNS has been recognised as a promising tool for soil moisture monitoring due to its hectare-scale footprint and decimetre-scale measurement depth. Therefore, by including a CRNS neutron count framework within the mHM, it could better handle the scale mismatch issue and represent the soil moisture dynamics. The widespread availability of observed CRNS data opens up new opportunities to develop and implement novel methods and hypotheses to improve soil moisture representation in hydrologic models.

In this study, we established a framework to incorporate CRNS data into the mesoscale Hydrologic Model (mHM) to compare empirical and forward-modelling approaches for neutron count estimation to improve soil water content parameters in the mHM across different vegetation types in Germany. To do this, we compared modelled with measured neutron counts to infer optimal model parameters, such as soil hydraulic conductivity. Here, we test three approaches: (i) the direct calculation of neutrons from the equal-average SWC profiles based on Desilets et al. (2010), (ii) the same with weighted-average soil moisture profiles based on Schrön et al. (2017), and (iii) the neutron forward operator COSMIC by Shuttleworth et al. (2013). We evaluate the simulation of neutron counts at scales of 1.2 km × 1.2 km, comparing the results to observed neutron counts from three different sites including agriculture, deciduous forests, and grasslands. The goal of this study is to investigate the potential of using CRNS probes and measured neutron counts to improve soil moisture predictions through simulations in the mHM across different land covers and soil properties and to evaluate the feasibility of incorporating neutron count measurements into the modelling scheme. We employ a (calibration) framework by applying a Monte Carlo experiment to account for parameter uncertainties. We further cross-evaluate our simulations and test the reliability of the CRNS soil moisture scheme incorporated into the mHM for simulating other variables by utilising available time series of observed evapotranspiration from an eddy covariance station. Finally, we discuss and provide guidelines (challenges and limitations) for incorporating CRNS measurements into a large-scale hydrologic model. In summary, the present paper aims to answer the following research questions:

• What is the best approach to simulate CRNS neutron counts in a hydrological model considering the heterogeneity of vertical soil moisture profiles?

• What is the impact of model calibration with CRNS observations on simulated evapotranspiration at Hohes Holz?

• Is the mHM capable of capturing the dynamics of hectare-scale CRNS measurements at approx. 1 km resolution at different land cover sites in a grid, including two agriculture sites, one forest site, and one meadow site?

Table 1 Geographical characteristics of study sites: site names, geographic coordinates, climatic data (annual precipitation in mm yr⁻¹, annual mean temperature in °C), and the periods covered in observed and simulated datasets.

2 Materials and methods

2.1 Experimental site description

For this study, we select four sites (shown in Fig. 1) with CRNS sensors, namely Grosses Bruch, Hohes Holz, Hordorf, and Cunnersdorf in northern Germany, as provided already within COSMOS EU (Bogena et al., 2021) with particularly long time series and with different land covers, i.e. agriculture, forest, and meadow (see Table 1). The first three sites belong to the TERENO Harz/Central German Lowland Observatory (Zacharias et al., 2011), while the fourth site is part of an agricultural research farm operated by the German Weather Service (DWD). The Grosses Bruch site is a meadow/grassland that is usually flooded naturally once or twice a year. The meadows have sandy loam Fluvisol–Gleysol soil, which is 1.5 m deep and partially covered with a layer of peat (Wollschläger et al., 2017). Meteorological conditions like soil moisture and temperature at various depths are continuously monitored by a wireless soil moisture monitoring network (Schrön, 2017). Hohes Holz is a deciduous forest site, and the performance of the CRNS sensor there is highly dependent on dynamic effects such as tree canopy water or seasonal fluctuations in wet biomass. Water trapped in leaves and litter can present a particular challenge for CRNS measurements, especially at forest stations (Bogena et al., 2013). Also, Bogena et al. (2021) indicated that the influence of seasonal changes of biomass on the CRNS signal is much less important than the influence of changing soil moisture, even in Hohes Holz, as changes in soil moisture are the much larger source of variation represented by the CRNS measurements. The mean annual air temperature for each site ranges from 10.0 to 10.9 °C, and the average yearly precipitation ranges from 458 to 535 mm.

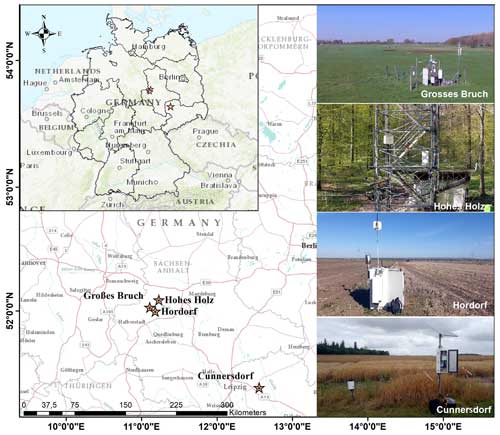
Figure 1 Study area map of Germany, highlighting the four test sites where observed neutron count rates from CRNS are utilised to evaluate the performance of the mHM. The figure utilises OSM basemap layers from OpenStreetMap contributors (2020) (© OpenStreetMap contributors 2021; distributed under the Open Data Commons Open Database License (ODbL) v1.0).

2.2 The mesoscale Hydrologic Model (mHM)

The mHM is a spatially distributed process-based hydrologic model capable of representing processes such as canopy interception; snow accumulation and melting; soil moisture dynamics; infiltration and surface runoff; evaporation; underground storage; and runoff generation, deep infiltration, and baseflow, as well as runoff attenuation and flood routing (Samaniego et al., 2010a; Kumar et al., 2013a). The mHM is flexible for hydrological simulations at different spatial scales due to its novel multiscale parameter regionalisation approach (MPR; Samaniego et al., 2010b), and it has demonstrated applicability in diverse settings (Samaniego et al., 2010a; Kumar et al., 2013a; Rakovec et al., 2016a; Samaniego et al., 2017). The MPR's basic concept is to estimate parameters (e.g. porosity) based on soil properties (e.g. sand and clay content) using transfer functions at a fine spatial resolution (e.g. 100 m) and upscaling them to modelling resolutions (e.g. 1 km). In the MPR, transfer functions (e.g. pedo-transfer functions to estimate soil parameters) are combined with morphological inputs (e.g. soil texture properties) and thus lead to model hydrologic parameters (e.g. porosity or hydraulic conductivity of the soil) (Livneh et al., 2015; Zacharias and Wessolek, 2007). In the mHM, the soil moisture horizons and/or profile can be divided into several horizons, all of which are sensitive to root water uptake and evapotranspiration processes. The mHM simulates the daily dynamics of soil moisture at different depths considering the incoming water (e.g. rainfall plus snowmelt for the topmost layer and infiltration from above layers for other layers) and outgoing evapotranspiration (ET) and ex-filtration fluxes. Further details on the mHM code can be found at https://mhm-ufz.org/news/ (last access: 2 June 2023).

2.3 Model setup

The latest version (5.12) of the mHM is used in this study (see Samaniego et al., 2023, and https://github.com/mhm-ufz/mHM/tree/v5.13.1, last access: 12 December 2024). The model was set up for a period of 6 years (2014–2020) with a daily time step, and the spatial resolution of the mHM grid cells was fixed at 0.01562° × 0.01562° (∼ 1.2 km × 1.2 km using the WGS84 coordinate system). In the mHM, level 1 (L1) denotes the spatial resolution at which dominant hydrological processes are modelled, and level 2 (L2) denotes the resolution of the meteorological forcing data. The finest resolved spatial level, L0 (0.001953125° × 0.001953125°), denotes the subgrid variability of relevant basin characteristics, which include information on the soil, as well as on land use, topography, and geology.

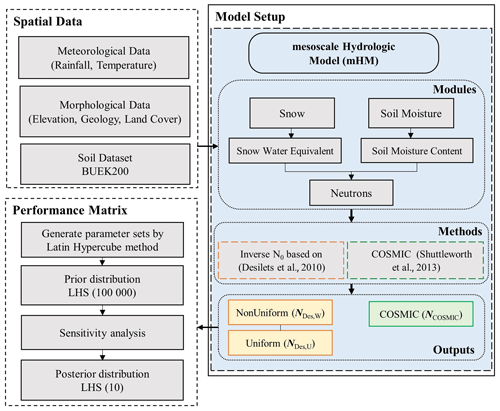
Figure 2 Flowchart depicting the methodology employed for calculating CRNS neutron counts through the utilisation of the Latin hypercube sampling (LHS) technique for parameterisation in the mHM. The computation of the CRNS neutron count is carried out using three distinct approaches: N_Des,U, N_Des,W, and N_COSMIC.

Figure 2 shows the flow diagram depicting the basic methodology of our study, which includes the calculation of CRNS neutron count rates based on daily soil moisture values simulated with mHM. The model boundary conditions, such as precipitation and temperature, for the mHM are acquired from the German Weather Service (DWD) station closest to the test site. The potential evapotranspiration required by the mHM is estimated using the Hargreaves–Samani method (Hargreaves and Samani, 1985). The model setup and parameterisation for the soil moisture module use the scheme optimised by Boeing et al. (2022). A raster dataset describing the distribution of the soils in the model area and a corresponding lookup table with the attributes of depth, soil texture (sand and clay fraction), and bulk density are required as soil input data and are derived from national digital soil maps provided by the Federal Institute for Geosciences and Natural Resources (BGR, 2020). The dataset contains the physical and chemical properties for soil at different layers, and these are available at a resolution of $\mathrm{1}:\mathrm{250},\mathrm{000}$ (BUEK 200; BGR, 2020). The mHM uses three dominant land cover classes (forest, permeable, and impervious) that were retrieved by a GlobCover database (ESA, 2009). Furthermore, vegetation characteristics like leaf area index (LAI) and the fraction of roots for different vegetation types are prescribed in the model. The mHM soil domain is divided into three horizons with depths of 0–5, 5–25, and 25–60 cm. The upper two model layers are parameterised using the topsoil layer properties, while, for the lower model layer, the subsoil properties are used. More details on the underlying input data for the mHM can be obtained from Boeing et al. (2022).

In our study, we utilised three distinct modules of parameters, namely snow, soil moisture, and neutrons, with a total of 28 parameters being employed for the Desilets method and 30 parameters being employed for the COSMIC method. The simulation of soil water content is processed through these three modules to estimate neutron counts. To comprehensively cover the parameter set ranges, we employed 100 000 iterations. Finally, we selected the top 10 optimised parameter sets based on the objective function KGE_αβ (where KGE denotes Kling–Gupta efficiency) for further analysis and evaluation.

2.4 Conversion of soil moisture to neutron count rate

In this study, we compared observed neutron counts from CRNS data with simulated neutron counts estimated from modelled soil moisture with the goal of optimising the parameterisation of soil water content from the mHM shown in Fig. 3. By incorporating the approaches from Desilets et al. (2010) and Shuttleworth et al. (2013) directly into the mHM, we are also able to account for the uncertainty in the model predictions and test their feasibility across four distinct sites. We analysed the soil water content data at different soil layers (0–5, 5–25, and 25–60 cm) in the mHM, as utilised in the study by Boeing et al. (2022). The accuracy of numerical calculations would benefit from more highly resolved soil profiles; however, our experiments demonstrated that varying soil depths from three to six layers did not have a substantial impact on the simulated neutron count results in the mHM. We used BGR (2020), which is a global dataset that is not detailed enough to allow for a finer vertical resolution. Our main objective is to optimise the parameterisation of soil hydraulic properties in the mHM based on the comparison between measurement and modelled neutron counts.

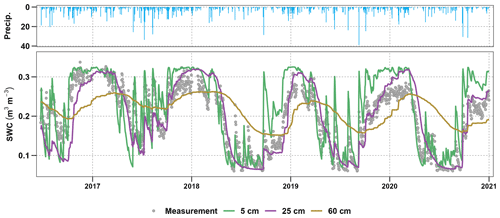
Figure 3 Daily time series of soil water content (cm³ cm⁻³) at the Cunnersdorf site. The graph shows a comparison between the measured SWC from CRNS data representing an integral over the first decimetres and the simulated data derived from the mHM for three distinct soil depths at 0–5 cm (green), 5–25 cm (purple), and 25–60 cm (brown).

2.4.1 Desilets-based method

In the present study, we utilise the soil moisture information from the mHM to convert it into neutron counts using the empirically based approach by Desilets et al. (2010). We also added lattice water and bulk density information following the suggestions from Dong et al. (2014) and Hawdon et al. (2014), respectively. This empirical approach makes use of a free scaling parameter N₀, which represents the neutron count rate of a particular CRNS probe under dry soil conditions. This parameter is typically site-specific but does not change over time, as noted by Franz et al. (2013) and Hawdon et al. (2014). It is also specific to the particular CRNS detector and may be influenced by factors such as terrain (topography), local soil, vegetation characteristics, and additional hydrogen pools (e.g. from organic matter) at each observation site. Therefore, the determination of N₀ by local soil sampling campaigns is necessary. Once determined, the parameter N₀ should be kept constant or carefully calibrated within limits of not more than ± 5 %. As a sensitive parameter, N₀ strongly influences the accuracy of the mHM soil moisture results.

Soil moisture for three vertical mHM soil layers is used as input for both the Desilets method and the COSMIC operator. To improve comparability between measurements and modelling techniques, Schrön et al. (2017) proposed weighting the soil moisture values of each layer by their depth. This approach results in a depth-weighted average SWC θ_avg that better represents the complex behaviour of neutrons in probing the soil.

$$\begin{array}{}\text{(1)}& N_{\text{Des}}=N_{\text{0,Des}}\left({\displaystyle \frac{a_{\mathrm{0}}}{({\mathit{\theta }}_{\text{avg}}+{\mathit{\theta }}_{\text{lw}})/({\mathit{\varrho }}_{\mathrm{b}}/{\mathit{\varrho }}_{\mathrm{w}})+a_{\mathrm{2}}}}+a_{\mathrm{1}}\right)\end{array}$$

Among the four parameters, values of a_0…2 were determined empirically by Desilets et al. (2010). The authors derived a₀=0.0808, a₁=0.372, and a₂=0.115 for θ > 0.02 g g⁻¹. The fourth parameter, N_0,Des, is fixed based on field measurements, with its value being taken from Bogena et al. (2021). Since neutrons are sensitive to all kinds of hydrogen in the footprint, the variable θ does not only denote soil moisture; rather, it is assumed to also include lattice water θ_lw, as well as the water equivalent from soil organic carbon and vegetation biomass. More precisely, θ_lw is the grid average volumetric water content of the equivalent lattice water content of the CRNS area (cm³ cm⁻³); ϱ_b (g cm⁻³) is the bulk density of the dry soil, usually determined from soil samples; and ϱ_w = 1 g cm⁻³ is the density of water. Regarding the variables of soil organic carbon (SOC) and biomass, it is important to note that these variables are often not readily available, especially when it comes to biomass data. For lattice water, we assume a linear relationship to clay content (Avery et al., 2016):

$$\begin{array}{}\text{(2)}& {\mathit{\theta }}_{\text{lw}}={\mathit{\theta }}_{\text{lw0}}\cdot C+{\mathit{\theta }}_{\text{lw1}},\end{array}$$

where C denotes the clay fraction in percent (Greacen, 1981). The derived quantity of lattice water θ_lw is regionalised based on C and varies between 0.0 and 0.1 m³ m⁻³. In order to obtain the average soil moisture for a layered soil moisture profile within mHM, the following averaging equation is employed:

$$\begin{array}{}\text{(3)}& {\mathit{\theta }}_{\text{avg}}(w,\mathit{\theta })={\displaystyle \frac{{\sum }_{i=\mathrm{1}}^n{w}_i{\mathit{\theta }}_i}{{\sum }_{i=\mathrm{1}}^n{w}_i}},\end{array}$$

where the volumetric soil water content at a specific layer of the mHM in a given profile is denoted by θ_i (m³ m⁻³). The total number of layers in all soil sampling profiles is represented by the variable n, and the weight assigned to layer i is denoted by w_i. In the uniformly weighted approach, all weights equal 1:

$$\begin{array}{}\text{(4)}& N_{\text{Des,U}}=N_{\text{Des}}(w_i=\mathrm{1})\forall i.\end{array}$$

In the weighted-averaging approach, the weights are determined based on Schrön et al. (2017):

$$\begin{array}{ll}\text{(5)}& {\displaystyle }{N}_{\text{Des,W}}=& {\displaystyle }{N}_{\text{Des}}\left({\mathit{\theta }}_{\text{avg}}\right(w,\mathit{\theta }\left)\right),{\displaystyle }\text{where }{w}_i=& {\displaystyle }\int {z_{i,\text{min}}}^{z_{i,\text{max}}}{e}^{-\mathrm{2}z/D}\mathrm{d}z\\ {\displaystyle }& {\displaystyle }\propto e^{-\mathrm{2}{z}_{i,\text{min}}/D}-e^{-\mathrm{2}{z}_{i,\text{max}}/D}\\ \text{(6)}& {\displaystyle }\text{and }D=& {\displaystyle }{\mathit{\varrho }}_{\mathrm{b}}^{-\mathrm{1}}\left(p_{\mathrm{0}}+p_{\mathrm{1}}\left(p_{\mathrm{2}}+{\text{e}}^{-p_{\mathrm{3}}r}\right){\displaystyle \frac{p_{\mathrm{4}}+\mathit{\theta }}{p_{\mathrm{5}}+\mathit{\theta }}}\right).\end{array}$$

Here, the integral goes through each horizon from z_i,min to z_i,max in 10 mm steps and sums up the weight over the whole layer. z_i is the depth of the given soil moisture layer i, D is the average vertical footprint depth of the neutrons, p_i denotes numerical parameters presented in Schrön et al. (2017), and r (m) represents the distance from the sensor. It should be noted that the equation for D is valid for ϱ_b > 1.0 g cm⁻³ and soil moisture contents above θ > 2 % (Kasner et al., 2022). In our model, we set r = 1 m, which is sufficient to represent the average depth across the footprint radius within the model grid. The soil moisture profile is converted to a single average neutron count per grid cell using Eqs. (1)–(5).

2.4.2 COsmic-ray Soil Moisture Interaction Code (COSMIC)

The COsmic-ray Soil Moisture Interaction Code (COSMIC) is a neutron forward operator that has been developed for data assimilation applications (Shuttleworth et al., 2013). The model aims to mimic the physical processes of neutron transport in the vertical dimension of the soil using a simplified analytical formulation of the most relevant mechanisms and their effective parameterisations. Shuttleworth et al. (2013) reported that this lack of complexity might introduce systematic errors for typical soil moisture profiles on the order of 2 % compared to physics-based models (e.g. Köhli et al., 2023). However, the simplified approach allows us to estimate neutron counts with a computational efficiency that is several orders of magnitude faster.

The COSMIC model assumes a downward attenuation of incoming high-energy neutrons with soil depth, the production of fast neutrons in each soil layer, and an isotropic scattering of the resulting fast neutrons that is projected upwards. These processes exhibit a parametric dependency on soil properties and water content and lead to a resulting neutron count value for each grid cell in the mHM.

$$\begin{array}{}\text{(7)}& {\displaystyle }{N}_{\text{COSMIC}}={\displaystyle }{N}_{\text{0,COSMIC}}\sum A_{\text{high}}\left(z\right)X_{\text{eff}}\left(z\right)A_{\text{fast}}\left(z\right)\end{array}$$

In the above, A_high(z) $=e^{-{\mathrm{\Lambda }}_{\text{high}}\left(z\right)}$, A_fast(z) $=\frac{\mathrm{2}}{\mathit{\pi }}{\int }_{\mathrm{0}}^{\mathit{\pi }/\mathrm{2}}{e}^{-{\mathrm{\Lambda }}_{\text{fast}}\left(z\right)}$ (cos φ)⁻¹ dφ, and X_eff(z) $={\mathit{\alpha }}_{\text{COSMIC}}{X}_{\text{soil}}+X_{\text{water}}$.

We used soil samples from the COSMOS-Europe paper (Bogena et al., 2021) to run the COSMIC model in order to determine the scaling factor N_0,COSMIC, following the established strategies (Shuttleworth et al., 2013; Patil et al., 2021; Baatz et al., 2014). In Eq. (7), A_high represents the high-energy neutron attenuation, A_fast represents the fast neutron attenuation, and X_eff represents the production of fast neutrons from high-energy neutrons at any level in the soil. It takes into account the different mechanisms in both water and soil, where the soil is typically less effective in producing fast neutrons by a factor of α_COSMIC ≈ 0.24 (g cm³ g⁻¹), depending on bulk density.

$$\begin{array}{}\text{(8)}& {\displaystyle }{X}_{\text{soil}}\left(z\right)& {\displaystyle }=\mathrm{\Delta }z{\mathit{\varrho }}_{\mathrm{b}}\text{(9)}& {\displaystyle }{X}_{\text{water}}\left(z\right)& {\displaystyle }=\mathrm{\Delta }z{\mathit{\varrho }}_{\text{water}}({\mathit{\theta }}_z+{\mathit{\theta }}_{\text{lw}})\end{array}$$

The effective attenuation of high-energy and fast neutrons in the soil–water composite is described by physically motivated functional relationships with effective length scales L_i.

$$\begin{array}{}\text{(10)}& {\displaystyle }{\mathrm{\Lambda }}_{\text{high}}\left(z\right)& {\displaystyle }={\displaystyle \frac{X_{\text{soil}}\left(z\right)}{L_{\mathrm{1}}}}+{\displaystyle \frac{X_{\text{water}}\left(z\right)}{L_{\mathrm{2}}}}\text{(11)}& {\displaystyle }{\mathrm{\Lambda }}_{\text{fast}}\left(z\right)& {\displaystyle }={\displaystyle \frac{X_{\text{soil}}\left(z\right)}{L_{\mathrm{3}}}}+{\displaystyle \frac{X_{\text{water}}\left(z\right)}{L_{\mathrm{4}}}}\end{array}$$

The length constants L₁, L₂, L₃, and L₄ (in g cm⁻²) are related to local soil properties. COSMIC uses several time-invariant, site-independent, and site-specific parameters, including L₁ = 162.0 (g cm⁻²), L₂ = 129.1 (g cm⁻²), and L₄ = 3.16 (g cm⁻²), as reported by Shuttleworth et al. (2013), regardless of location. However, the L₃ (g cm⁻²) parameter varies with soil bulk density ϱ_b, which may change with depth. In the mHM, this is expressed by a linear relationship of regionalised parameters L₃₀ and L₃₁:

$$\begin{array}{}\text{(12)}& {\displaystyle }{L}_{\mathrm{3}}=L_{\mathrm{30}}{\mathit{\varrho }}_{\mathrm{b}}-L_{\mathrm{31}}.\end{array}$$

The original formulation of the COSMIC method has been further extended by the inclusion of layer-wise lattice water content and bulk density. Furthermore, COSMIC inside the mHM has been numerically optimised to substantially increase the computational performance. This includes the calculation of the projected integral (Eq. 7) based on lookup tables.

2.5 Constraining the model parameterisation

In this study, we employ a model calibration technique to identify the most suitable parameter values for the mHM. Specifically, we utilise a total of 28 parameters for the Desilets-based method and 30 parameters for the COSMIC method; these include hydrologic processes related to snow, soil moisture, and neutron count dynamics. The process of model calibration involves modifying the parameter values of the model to achieve a satisfactory standard for an objective function by comparing the predicted output with the observed data (James, 1982). We use the general concept of the KGE as a weighted combination of the three components (bias, variability, and correlation terms) to evaluate our simulation (Gupta et al., 2009). We excluded the correlation component from the Gupta et al. (2009) equation as our simulation already exhibited satisfactory correlation due to strong seasonality; we opted not to consider it in our assessment (objective function) as it accounted for 33 % of the total weighting in the overall KGE score. Seasonality is an inherent characteristic in the Northern Hemisphere, where precipitation minus evaporation is mostly driven by evapotranspiration. Even if a random parameter is selected, correlation will always be higher because the meteorological forcing is the precipitation − evaporation, which is seasonal. This modified KGE_αβ only depends on variability (α) and bias (β), and variants of it have also been used in other studies (see, for example, Martinez and Gupta, 2010; Mai, 2023). We utilise observed neutron count data from CRNS and estimated neutron count data from the mHM to calculate various metrics such as the modified Kling–Gupta efficiency coefficient (KGE_αβ), the root mean square error (RMSE), and the percentage bias (PBIAS) by Gupta et al. (1999). The optimal PBIAS value is 0, with lower values indicating more accurate model simulations. Positive values indicate underestimation by the model, while negative values indicate overestimation. This approach allows us to minimise uncertainty in the simulated neutron count data by comparing them to observed data and determining the optimal parameter values for the mHM . A summary of the individual parameters and their ranges can be found in Table S3 in the Supplement.

3 Results

3.1 Analysis of posterior parameters across the study sites

Figure 4 shows the normalised range of posterior parameter sets of the mHM compared across the four study sites: Grosses Bruch, Hohes Holz, Hordorf, and Cunnersdorf. Out of 30 parameters, the 10 most relevant parameters for root zone soil moisture dynamics are presented (see Table 2 for parameter description and ranges). The other parameters are shown in the Supplement. Figure 4 indicates that the selected parameters showed a well-constrained distribution within their allowed range across the study sites. Among them, at the Grosses Bruch site, we find the most stable parameter distribution, with low variability (small error bars) across most of the inferred parameters, including vertical root fractions of different vegetation types (rotfrcoffore, rotfrcofperv). A relatively higher variability (large error bars) in the posterior parameter distributions is noticed for ptflw0, ptflw1, and ptfhigdb – these parameters are related to the estimation of lattice water and bulk density. Parameters related to the pedo-transfer function (PTF) parameters that control the saturated soil water content (ptflowconst, ptflw1, ptflw0) at the Hohes Holz site showed the lowest variability, reflecting a consistent behaviour in inferring these parameters at this site. The site at Hordorf shows moderate variability across most of the analysed parameters, especially for orgmatperv, pfthighdb, ptflw1, and ptflw0. Overall across all the study sites, the posterior distribution of parameter ptflowdb exhibits high variability, reflecting the importance of further constraining this parameter. There is a varying degree of sensitivity across the parameters, but certain parameters consistently demonstrate sensitivity across the site (rotfrcoffore, ptflowdb, ptfhigclay, ptflowconst). This finding aligns with previous studies (Cuntz et al., 2015; Koch et al., 2022; Demirci and Demirel, 2023), which also identified these parameters as being sensitive in the mHM across various study locations.

Table 2 Description of 10 selected parameters and their ranges in the mHM.

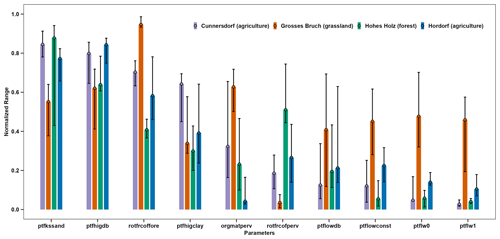
Figure 4 Bar plot showing posterior distribution of model parameters across three land cover types, calibrated using cosmic-ray neutron sensing data. Parameter values are scaled between 0 and 1. The whiskers represent the upper and lower limits of the inter-quartile range, while the dots represent the median values of the normalised range for each parameter.

3.2 Time series analysis of simulated neutron counts

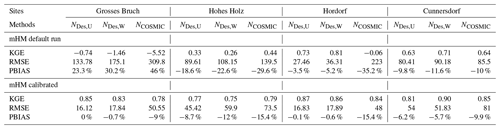
The study conducts simulations of neutron counts in the mHM using soil moisture parameterisations, with results presented in Figs. 5 and 6 for different land cover sites. In these figures, the grey dots represent the CRNS soil moisture measurements. The N₀ parameter values, taken from field measurement, are documented for each site, including Grosses Bruch, Hohes Holz, Hordorf, and Cunnersdorf. We utilised measurement data from COSMOS Europe (Bogena et al., 2021), where neutron counts were converted to soil moisture θ(N) using the methodology from Desilets et al. (2010). The simulated neutron counts were based on the simulated soil moisture content at the modelled soil horizons, i.e. 0–5, 5–25, and 25–60 cm. The results of the ensemble runs show that the precision is higher for the behavioural simulation ensembles at 0.1 % (represented by dark-grey shaded areas) than in the unconstrained simulated data at 1 % (represented by light-grey shaded areas). We select the best 0.1 % with the highest KGE from 100 000 model runs, and the results are presented in Table 3. However, a larger discrepancy was noted at Hohes Holz, a dense forest site, across all three methods. This difference could be attributed to the leaf area index (LAI), biomass, and vegetation dynamics, which are currently not integrated into the mHM. Recent efforts by Bahrami et al. (2022) aim to address vegetation dynamics in the mHM, but this integration is still incomplete. Among the methods, the N_COSMIC method performs best at the forest site (Hohes Holz), whereas, at the agricultural sites (Hordorf and Cunnersdorf), the N_Des,W method performs slightly better. In the grassland site (Grosses Bruch), the uniform method N_Des,U slightly outperforms the other two methods, i.e. N_Des,W and N_COSMIC. In general, we observe good model performance for all methods, as indicated by a Kling–Gupta efficiency greater than 0.75 and a percent bias (PBIAS) below ± 10 % across the majority of investigated sites and methods. These results suggest that the neutron forward models match the observed neutron counts well. However, the mean ensemble had difficulties reproducing the neutron counts for the Hohes Holz site in all three methods.

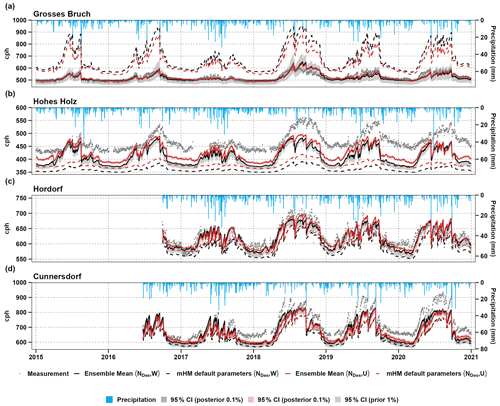
Figure 5 Simulated daily time series of N_Des,W (black) and N_Des,U (red) (counts per hour, cph) for the four sites. The black lines represent the median of the behavioural simulation ensembles that satisfy the objective function, which are LHS10 ensemble members. The light-grey shaded areas represent the 95 % confidence interval (CI) of the simulation ensembles corresponding to different levels of constraining, which are LHS1000 ensemble members, and the observation is shown in grey points. Precipitation is shown in blue at the top.

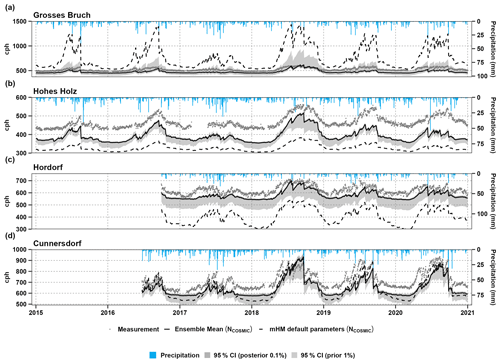
Figure 6 Simulated daily time series of N_COSMIC (counts per hour, cph) for the four sites. The black lines represent the median of the behavioural simulation ensembles that satisfy the objective function, which are LHS10 ensemble members. The light-grey shaded areas represent the 95 % CI of the simulation ensembles corresponding to different levels of constraining, which are LHS1000 ensemble members, and the observation is shown in grey points.

Table 3 Performance metrics for model calibration (2014–2021) using various methods, namely Kling–Gupta efficiency (KGE), root mean square error (RMSE), and percentage bias (PBIAS), across different sites. The observed neutron counts were compared with the simulated neutron counts from the mHM.

The incorporation of dynamic vegetation into models is important as it can impact the model parameter LAI, which in turn can affect root water uptake and soil water content. Currently, these factors are not considered in the models, leading to a permanent and systematic shift in these variables each year (Zink et al., 2017; Massoud et al., 2019).

The results also highlight the uncertainties associated with model simulations and the sensitivity of the objective function. We find that 10 soil-moisture-related parameters, mentioned in Table 2, have the most significant impact on the objective function KGE_αβ compared to the other parameters of the mHM. The parameter lw (lattice water) directly affects the neutron count simulations, while the other parameters correspond to the fractions of vegetation roots in different soil layers that directly affect the water-availability-related stress for the estimation of actual evapotranspiration and, thereby, the soil–water dynamics (Samaniego et al., 2010b; Kumar et al., 2013b). The best parameter set values in the mHM across all sites and methods are provided (see Table S3).

3.3 Model calibration statistics and evaluation

In addition to KGE_αβ, the three metrics KGE, RMSE, and PBIAS are used to further evaluate the mHM neutron counts simulated with observed CRNS data. We employ Latin hypercube sampling (LHS) to generate a parameter sample of 100 000 for the three methods, namely N_Des,U, N_Des,W, and N_COSMIC, by uniformly distributing the ranges provided in Table S2. The top 10 parameter sets are found to perform satisfactorily, with a KGE range of 0.75 to 0.9, as demonstrated in Table 3. The calibrated parameter sets obtained from different objective functions are also evaluated and compared using various statistical indices, as shown in Fig. 7. The results for the COSMIC method indicate that the main contribution to poorer results during the evaluation period was due to the variability term (α). The boxplot displayed in Fig. 7 illustrates the threshold achieved by the top 1000, 100, and 10 LHS members, along with the corresponding percentage of the best 10 LHS parameter sets that meet the threshold. Among the 30 parameters selected to simulate neutron counts, this plot provides an overview of the distribution of results and their variability with respect to the threshold criteria.

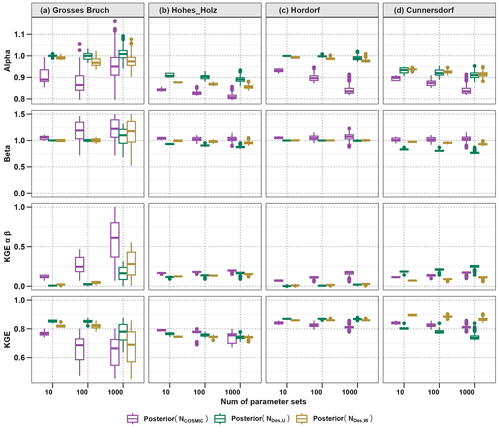
Figure 7 Evaluation of model performance using boxplots constraining 1000 members to the best 10 parameters set at four different sites using three different methods, namely N_Des,W in brown, N_Des,U in green, and N_COSMIC in purple. The figure presents four subplots, where the top row represents alpha; the second row represents beta; the third row represents KGE_αβ; and the fourth row represents the Kling–Gupta efficiency (KGE) and its components, i.e. the variability term (perfect value: 1) and bias term (perfect value: 1).

3.4 Comparing evapotranspiration at Hohes Holz: eddy covariance observed data vs. the mHM simulation

The ensemble model of simulations (10 members) is further validated with actual evapotranspiration (ETa) data to assess the model's ability to represent other fluxes and states in addition to neutron counts. This validation uses ETa observational data from eddy covariance measurements provided by the Integrated Carbon Observation System (ICOS) at Hohes Holz (Warm Winter, 2022). In terms of temporal dynamics, the model is capable of capturing the observed ETa quite well at the study site, as shown in Fig. 8. Figure 8c displays the scatterplot incorporating linear regression models to quantify the relationships between observed and mHM-simulated ETa during both the growing and non-growing seasons. This plot provides insights into the seasonal variations in the relationship between observed and simulated ETa. It suggests that the model performs best during winter, while its performance during summer is comparatively weaker. The correlation coefficients (r values) for each season are as follows: autumn (SON) r = 0.72, spring (MAM) r = 0.75, summer (JJA) r = 0.35, and winter (DJF) r = 0.85. It is worth noting that winter shows the highest correlation between observed and simulated ETa, while summer exhibits the lowest correlation. The most significant deviation in terms of RMSE is evident during the summer, when ETa is highest, while the smallest difference is in winter when ETa has less impact. The model slightly overestimates ETa in summer and spring, possibly because of the absence of a dynamic vegetation growth module in the mHM, also discussed for evapotranspiration by Zink et al. (2017). The temporal dynamics of the model-simulated evapotranspiration are in good agreement with the observed data from the Hohes Holz forest eddy covariance site, taken from Warm Winter (2022), as illustrated in Fig. 8a. The daily correlation between observed and simulated evapotranspiration is observed to be high in the growing season at r = 0.8, whereas the lowest correlation is found in the non-growing season at r = 0.53 in Fig. 8c. The highest deviation in terms of RMSE is observed during summer when the highest fluxes occur, and the lowest is observed during winter, during which the contribution of ETa is lowest.

Figure 8 (a) Comparison of weekly observed actual evapotranspiration (grey dots) and simulated actual evapotranspiration using the default mHM parameters by Boeing et al. (2022) (red line), the calibrated simulation (blue lines), and the prior range of 100 000 realisations (red) over the Hohes Holz site. (b) Boxplot of daily actual evapotranspiration (ETa) differences between the growing and non-growing seasons, comparing two selected previously with 100 000 simulations; the values represent the mean of the statistical metrics and the posterior with 10 ensemble member distributions using the root mean square error (RMSE) as the evaluation metric (mm d⁻¹). (c) Scatterplots of modelled vs. observed ETa on a daily basis from ICOS during the growing season from March to August (green) and during the non-growing season from September to February (orange) at Hohes Holz eddy covariance station in a forest.

In Fig. 8b, the prior and posterior parameter distributions of evapotranspiration for Hohes Holz are displayed. The prior distribution represents the 100 000 parameter set utilised for the neutron count simulation under Latin hypercube sampling (LHS). The results demonstrate that the ensemble model of 10-member simulations (posterior) for neutron counts can also effectively capture evapotranspiration, exhibiting a root mean square error (RMSE) of 0.76 mm d⁻¹ during the growing season and 0.25 mm d⁻¹ during the non-growing season when compared to observed ICOS data and the simulated mHM. When compared to the model simulations with prior parameter sets, we notice a substantial improvement in ET simulations (mean RMSE of 0.85 to 0.76 mm d⁻¹). Furthermore, the RMSE range is also narrower for the posterior simulations compared to the prior ones, which further demonstrated the additional value of incorporating CRNS measurements in improving the consistency of both modelled soil moisture and evapotranspiration estimates. Nevertheless, the overall agreement between modelled and observed ETa is reasonably good, and the analysis reveals further improvements in terms of model performance in the growing season.

4 Discussion

This study assessed the suitability of CRNS observations at four sites to enhance soil moisture representation in the mHM. The theoretical measurement depth for the cosmic-ray probe varies, ranging from ∼ 12 cm in wet soils to ∼ 76 cm in dry soils (Zreda et al., 2008, 2012; Rosolem et al., 2014).

To improve the soil moisture profile representation within the mHM, it is a major challenge to use a single vertically integrated CRNS measurement. In order to have a fair comparison between the model and observed CRNS data, two conceptually different approaches were integrated into the mHM to calculate neutron counts from different SWC horizon depths, i.e. an empirical method based on Desilets et al. (2010) and the neutron forward operator (COSMIC) based on Shuttleworth et al. (2013). Since the empirical method is described by an analytical expression, taking into account the uniform average of the soil moisture layers, it is straightforward to implement and is therefore most commonly used (Zreda et al., 2012; Rivera Villarreyes et al., 2011; Andreasen et al., 2017; Bogena et al., 2021). However, the method comes with the risk of missing a representation of the vertical profile of soil properties and water content. Therefore, we extended this uniform-averaging scheme with a vertical weighting scheme to mimic the sensitivity of the neutrons to the upper layers; both weighted and non-weighted soil moisture approaches in the context of CRNS have been discussed (Rivera Villarreyes et al., 2014; Baroni and Oswald, 2015; Schreiner-McGraw et al., 2015; Zreda, 2016; Schrön et al., 2017; Vather et al., 2019; Barbosa et al., 2021). The COSMIC operator also accounts for the full soil moisture profile, following the track and attenuation of the neutrons in and out of the soil column. The mHM is now able to simulate neutrons directly with all three approaches. The presented results confirmed general consistency with CRNS observations at four sites in Germany (Figs. 5 and 6).

Agricultural land presents a valuable opportunity to examine the interaction between soil moisture dynamics, crop growth, irrigation methods, and vegetation dynamics. Hordorf and Cunnersdorf are specific agricultural sites where seasonal changes in aboveground biomass are expected to be larger due to crop growth and harvest compared to grassland and forest sites. The study by Schrön et al. (2017) found that the revised weighting strategy for CRNS data improved the accuracy of soil moisture predictions at agriculture sites, but there is still room for improvement in capturing local dynamics through revised parameters in the CRNS model. Our results also showed that, at the agriculture site, the N_Des,U methods in the mHM outperformed the other methods slightly.

We also investigated Hohes Holz, a forest site, and observed an early simulation of approximately 28 d in the simulation of neutron counts compared to the observations. The early simulation phase could be attributed to the limitation of the mHM in simulating the dynamics of detailed vegetation mechanisms (Zink et al., 2017). While CRNS and time domain reflectometers (TDRs) generally agree at this site, the discrepancy shown in our results could be attributed to issues related to process representation in the mHM (Boeing et al., 2022). The simulation of neutron data within the mHM and subsequently comparing them with observed counts can enhance the accuracy and precision of soil moisture measurements. Future research can focus on exploring the potential relationships between CRNS data and soil moisture anomalies, thus furthering our understanding of the dynamics of drought and assisting in the development of efficient drought monitoring and mitigation strategies.

To cross-evaluate our results, we generated and filtered the 100 000 regionalised parameter sets based on observed neutron counts for behavioural solutions. After selecting the most effective solutions, we conduct cross-validation by comparing the mHM simulations of evapotranspiration against observational data from eddy covariance measurements by ICOS (Warm Winter, 2022; Pohl et al., 2023) at Hohes Holz. Figure 8 shows the scatter, including the seasonal correlation coefficient at the forest site. The results indicate low correlations in summer, likely due to the mHM's limitations in capturing evapotranspiration values with its static vegetation module. However, the model performs well in winter, with a high correlation between observed and simulated values of evapotranspiration; the results confirm the findings from Zink et al. (2017), who used the mHM to estimate evapotranspiration, groundwater recharge, soil moisture, and runoff with 4 km spatial and daily temporal resolutions (1951–2010). They utilised soil moisture observations from eddy covariance stations employing time domain reflectometer (TDR) or frequency domain reflectometer (FDR) sensors. Due to disparities in spatial representativeness and sampling depth, a direct comparison between observed and simulated soil moisture was not feasible; the findings of Zink et al. (2017) revealed deviations in evapotranspiration during spring and in cropland areas, while soil moisture estimations exhibited good agreement with observed dynamics. The study highlights the importance of considering seasonal variations when analysing the results. Discrepancies, such as low correlations in summer, indicate the need for improvements in capturing evapotranspiration dynamics under varying environmental conditions. Refining vegetation dynamics representation could enhance the simulation of evapotranspiration processes. Additionally, the agreement between the mHM and observed soil moisture dynamics suggests variable model performance for different hydrological variables, emphasising the need for a comprehensive assessment of its capabilities across various environmental conditions and spatiotemporal scales. The accuracy of modelled evapotranspiration is linked to soil parameterisation because soil water is the main source of evaporative water. During the growing season (summer), the model exhibited the largest variability in modelled ETa (see Fig. 8c). This can be associated with, among other things, a lack of a dynamic vegetation growth module in the mHM, which may not capture the onset of the vegetation period adequately. This variability could also be attributed to seasonal changes in the vapour pressure difference (VPD) or more localised processes occurring at the forest site (e.g. vegetation dynamics), which are currently not considered in the model.

The Grosses Bruch site stands out as a mesophilic grassland site with a nearby water channel, shallow groundwater, regular cattle grazing, and seasonal flooding (Hermanns et al., 2021). We find the uniformly weighted approach N_Des,U shows a slightly better performance than the other two methods N_Des,W and N_COSMIC (see Table 3). The behaviour may result in a missing representation of locally significant hydrological components, such as dynamic biomass, snow, shallow groundwater, or nearby surface ponding (Schrön et al., 2017). Döpper et al. (2022) mentioned the high impact of grazing on the plant traits and soil properties at this site. Additionally, the use of one grid cell measurement by the mHM in our study may have limited the accuracy of our results as the depth of the measurement may not be representative of the entire soil profile. Notably, neutron counts were found to provide a more accurate representation of soil water content during June, July, August, and September, when levels tend to be lower. Further exploration of neutron counts may yield additional improvements to model performance.

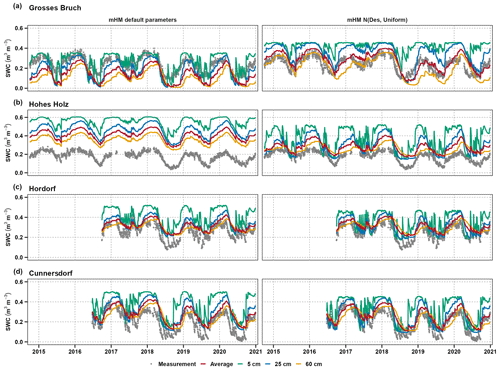
Figure 9 Comparison of soil water content (SWC) time series from 2015 to 2021 across all sites. The left panel illustrates the default simulation from the mHM using parameters from Boeing et al. (2022), while the right panel presents the calibrated simulation based on the N_Des,U method. Both panels compare CRNS-derived soil moisture data (grey dots) with simulated values from the mHM. The best 10 calibrated mean SWC values across different soil layers are shown, with the total average soil moisture represented by the red line.

Overall, the three methods (N_Des,U, N_Des,W, and N_COSMIC) in the mHM were able to consistently simulate the neutron count variability throughout the available data period, with the exception of the Hohes Holz site. However, a broader confidence interval is observed, indicating a greater range of variations, which implies a higher degree of uncertainty in N_COSMIC. The COSMIC approach is more complex than the Desilets approach and, as such, depends on more detailed additional information about the soil properties, vegetation interception, layering, etc. If the model input data are not known in such detail, we would expect the COSMIC model to provide more uncertain results. Moreover, all three approaches are rough approximations of the actual physical processes of neutron transport, which could contribute to systematic biases of around 2 % compared to exact physics-based models (Shuttleworth et al., 2013). The simulated time series tended to underestimate the CRNS neutron count rate slightly, particularly during the dry season. This effect could be explained by the known limitations of the equations under very dry conditions, while recent approaches exist (Köhli et al., 2021) that could lead to further improvement in future studies. Nevertheless, the results generally confirmed the slightly better performance of the weighted approach N_Des,W compared to the uniform N_Des,U, because of its more realistic representation of neutron propagation with depth. After optimising the soil hydraulic properties based on CRNS data, the integrated signal was reproduced very well (Fig. 5). Previous studies, such as McJannet et al. (2014) or Baatz et al. (2014), have noted low experimental performance for the universal calibration function (UCF) method described by Franz et al. (2013). However, we have selected the Desilets method, known as the N₀ method, and the COSMIC method for specific reasons. Both methods require information from soil profiles, which is readily available in the mHM. In contrast, the universal transport solution (UTS) function couples soil moisture with air humidity in a non-separable way, while no atmospheric information about air humidity is available in the distributed hydrological model that is the mHM. The same holds for the UCF function, which additionally requires a number of parameters related to hydrogen pools not represented by the mHM. In using the CRNS soil moisture measurement, the drier locations show larger deviations than the wetter locations (Iwema et al., 2015). The possibility of using simulated high-resolution soil moisture profiles instead of a few measurements at different soil depths could further increase the accuracy of the model predictions (Brunetti et al., 2019).

Table 4 Performance metrics (KGE, RMSE, and PBIAS) for soil moisture simulations across four sites from 2014 to 2021 in relation to θ_CRNS against simulated data from the mHM: Grosses Bruch, Hohes Holz, Hordorf, and Cunnersdorf. We compare the results of the default mHM run and three calibration methods (N_Des,U, N_Des,W, and N_COSMIC).

Previous studies by Smith et al. (2019) and Liu et al. (2022) address the challenges of using the original KGE in Markov chain Monte Carlo (MCMC) methods, offering insights into accurate parameter estimation and posterior distribution exploration. To address this issue, it is recommended that one use adaptations to the LHS method instead of directly using the original KGE to improve the exploration of the posterior distributions. Our approach can estimate the posterior distributions of model parameters based on the objective function KGE_αβ by taking the variance and bias. We compared soil moisture before and after calibrating neutron counts in the mHM at four sites shown in Fig. 9. The left panel shows the mHM default simulation using the default parameter set from Boeing et al. (2022), whereas the right panel shows the calibrated simulation based on the N_Des,U method. The results presented depict the CRNS soil moisture measurements (grey dots) versus the soil moisture derived from the mHM at different depths (colours). Table 4 shows the corresponding performance measures. It is important to acknowledge that the optimisation of observed neutron counts did not only improve the soil moisture representation in the mHM. At the same time, it also improved the simulated evapotranspiration, as shown in the example of Hohes Holz (see Fig. 8a). The KGE value between modelled and measured ETa by eddy covariance observations improved significantly from 0.74 to 0.83. This provides evidence that CRNS data have the potential to improve hydrological process understanding as a whole.

5 Conclusion and future outlook

This study evaluates the potential of cosmic-ray neutron observations to improve soil moisture and model parameters in the mesoscale Hydrologic Model, the mHM, at the 1.2 km × 1.2 km scale across different land cover sites for the period 2014–2021. For this, we derived the neutron counts from simulated soil moisture profiles directly in the model using three different approaches: two based on an empirical function with uniform and non-uniform weighting of soil horizons and one more complex approach based on the neutron forward operator COSMIC. Then, observed neutron counts from four sites in Germany were used to calibrate the mHM parameters. Based on the KGE_αβ between simulated and observed neutrons, the best 1 % of parameter sets out of 100 000 model realisations were used to investigate the impact on the posterior parameter distribution and on the simulated neutrons, soil moisture, and evapotranspiration.

The evaluation of neutron counts yielded KGE values > 0.75 at all four sites, indicating a satisfactory representation of the neutron counts in the model compared to the observations for the best 1 % of ensemble parameter sets. The performance of the neutron-counting methods varied across different land cover types. The non-uniform N_Des,W method generally showed good performance, particularly at the agricultural sites. On the other hand, the N_COSMIC method performed slightly better at the forest site. The uniform N_Des,U method showed slightly better results at the grassland site.

There is still room for improvement in the model representation of complex sites, for example, to better address the special site-specific conditions of the forest or grassland site, especially when using the COSMIC method. On the one hand, it is a method that aims to mimic the physical processes of neutron transport in the soil in detailed way, but, on the other hand, it relies on the detailed representation of the site characteristics in the hydrological model. This complexity could introduce additional uncertainties and limitations into the model, potentially affecting its performance, especially when the actual site is more complex than it has been modelled to be. The study suggests that the observed discrepancies between the model and observations may be attributed to the representation of dynamic biomass, snow, surface ponding, and shallow groundwater dynamics, which are present at the grassland site, for instance. Addressing these features could further enhance the model's accuracy.

The calibration of neutron counts not only improved the soil moisture estimation but also improved the simulation of evapotranspiration at the Hohes Holz station. The evaluation with evapotranspiration data from eddy covariance observations indicated some deficiencies in the mHM with regard to dealing with forest systems but also indicated great potential for CRNS measurements to improve the water partitioning in the model as a whole. In the growing season (March–August), deviations of the modelled and observed ETa indicate that there is room for better representation of mixed soils and dynamic vegetation modules at the local scale within the mHM.

In conclusion, the incorporation of neutron count estimation into the mHM by accounting for vertical soil moisture profiles improves the model's accuracy and provides a more realistic representation of soil moisture dynamics at all four study sites and even of evapotranspiration at the Hohes Holz site. This research presents a direction for future studies to explore. Next steps could be the evaluation of neutrons and soil moisture in the mHM by means of a large-scale soil moisture monitoring initiative, for example, by utilising more stationary CRNS networks (e.g. Heistermann et al., 2021; Bogena et al., 2021) or large-scale mobile CRNS campaigns (McJannet et al., 2017; Altdorff et al., 2023). To further increase the accuracy and general understanding of hydrological processes, we recommend integrating both CRNS and satellite remote sensing data into the mHM (e.g. based on recent insights from Schmidt et al., 2024; Zheng et al., 2024; Rakovec et al., 2016b). Improving the model predictions will contribute to reducing the uncertainties associated with drought and flood management strategies and informed agricultural decisions.