Deducing land–atmosphere coupling regimes from SMAP soil moisture

In recent years, there has been a growing recognition of the significance of land–atmosphere (L–A) interactions and feedback mechanisms in understanding and predicting Earth's water and energy cycles. Soil moisture plays a critical role in mediating the strength of L–A interactions and is important for understanding the complex and governing processes across this interface. This study aims to identify the significance of soil moisture in identifying L–A coupling strength within the convective triggering potential (CTP) and humidity index (HI) framework. To address this, a consistent and reliable dataset of atmospheric profiles is created by merging CTP and HI using triple collocation (TC) with three reanalysis datasets. The merged CTP and HI product demonstrates enhanced performance globally compared to the individual datasets when validated with radiosonde and satellite observations. This merged product of CTP and HI is then used to compare the L–A coupling strength based on Soil Moisture Active Passive Level 3 (SMAPL3) and SMAP Level 4 (SMAPL4) over 2 decades (2003–2022) where L–A coupling strength is defined as the persistence probability within the dry and wet coupling regimes. Results indicate that the persistency-based coupling strength is related to the ability of soil moisture to predict future atmospheric humidity and dry vs. wet coupling state. The coupling strength in SMAPL4 is consistently stronger than in SMAPL3 and is likely due to its reliance on a land surface model and reduced susceptibility to random noise. The difference in coupling strength based on the same CTP–HI underscores the importance of soil moisture data in estimating coupling strength within the CTP–HI framework. These findings lay the groundwork for understanding the role of L–A interactions and drought evolution due to soil moisture variations by providing insight into the quantification of coupling strength and its role in drought monitoring and forecast efforts.

1 Introduction

Land–atmosphere (L–A) interactions are critical to Earth's complex climate processes and environmental sustainability (Seo and Dirmeyer, 2022; Seneviratne and Stöckli, 2008). These interactions are primarily driven by the two-way energy, momentum, and mass exchanges between the land surface and the overlying atmosphere (Hsu and Dirmeyer, 2023). Among the many components influencing L–A interactions, soil moisture is a critical element (Zhou et al., 2019; Santanello et al., 2018; Saini et al., 2016; Alexander et al., 2022; Wakefield et al., 2019; Findell et al., 2024). Soil moisture is not merely a passive participant but an active modifier of water and heat transfer between the land and the atmosphere (Qi et al., 2023). It serves as a vital component in the climate system and is considered an essential climate variable (ECV) (Liu et al., 2020; Miranda Espinosa et al., 2020; Pratola et al., 2015).

Soil moisture is a critical intermediary in L–A feedbacks, affecting a wide range of atmospheric processes at local and regional scales (Seo and Ha, 2022). Its influence on partitioning energy at the land surface into sensible and latent heat fluxes directly impacts weather patterns, climate variability, and extreme meteorological events (Zhou et al., 2019). L–A interactions are often separated into different regimes (Bennet et al., 2023), such as dry and wet coupling regimes. Dry coupling refers to conditions where the land's dryness limits moisture availability to the atmosphere, typically resulting in less cloud formation and precipitation, leading to hotter, drier conditions that exacerbate droughts. Conversely, wet coupling describes a scenario where abundant soil moisture enhances evaporation and transpiration, increasing humidity, cloud formation, and potentially precipitation. Understanding these interactions is crucial to diagnosing and predicting how the land condition may affect weather and climate.

Classifying L–A coupling regimes requires characterizing both the land state and the atmosphere. An integrated approach, highlighted by Findell and Eltahir (2003), provides a framework for understanding the complex exchanges and feedback loops between the Earth's surface and the air above. Specifically, this framework uses the convective triggering potential (CTP) and humidity index (HI) as metrics to classify L–A feedback based on the likelihood of convective precipitation. The CTP is critical in gauging the potential for convection by assessing atmospheric stability, while the HI quantifies the moisture content in the lower troposphere. The CTP–HI framework was further developed by Roundy et al. (2013), which added the use of soil moisture within the CTP–HI framework. This eliminated the need for a model-based approach for linking the thermodynamic preconditioning of the lower troposphere to the triggering or suppression of convective activities in response to surface conditions. This method underscores the critical role of soil moisture as a crucial driver influencing convective dynamics and provides a means for understanding and predicting weather patterns and regimes based on L–A interactions (Roundy and Wood, 2015; Roundy et al., 2014).

Despite this, the sensitivity of the classification system to soil moisture remains largely unexplored, especially relative to satellite-based observations of soil moisture. Furthermore, quantifying the impact of soil moisture within the CTP–HI framework requires a consistent and reliable dataset of atmospheric profiles (i.e., for CTP and HI). However, this is not straightforward, as global observations of lower-tropospheric temperature and humidity are limited (Teixeira et al., 2021). Reanalysis data provide the best global estimate of atmospheric data for quantifying the CTP–HI, yet inherent uncertainties in the data cannot be overlooked. These uncertainties often arise from varied data sources, measurement approaches, and spatial and temporal resolution. These factors, along with diverse data assimilation techniques, can contribute to biases and uncertainties within climate reanalysis, thus complicating the quantification of land–atmosphere dynamics, as highlighted by both Jach et al. (2022) and Mukherjee and Mishra (2022).

One way to address the challenge of uncertainties in reanalysis datasets is to employ data merging techniques, as suggested by Sun and Fu (2021), Lu et al. (2021), and Feng and Wang (2018), to create a more reliable dataset of CTP and HI based on multiple reanalysis data. Many merging techniques exist, including M-kernel merging (Zhou et al., 2003), optimal interpolation (Lorenzo et al., 2017), random forest algorithms (Nguyen et al., 2021), and approaches rooted in Bayesian analysis (Wilson and Fronczyk, 2016) to name a few. However, the triple collocation (TC) method has emerged as an invaluable technique for estimating error variances within datasets, as evidenced by research from Gruber et al. (2017, 2020), Stoffelen (1998), and Saha et al. (2020). The widespread application of the TC method is primarily due to its effectiveness in utilizing the statistical attributes of multiple datasets to reduce the bias and quantify the uncertainties associated with each dataset. Consequently, the TC method is an ideal choice to create a more robust merged CTP and HI metric for analysis of L–A coupling strength.

This study aims to enhance our understanding of L–A coupling classification by developing and applying a merged CTP and HI dataset to isolate the impact of different soil moisture products on the CTP–HI framework and the associated coupling strength. Specifically, it focuses on the L–A coupling that results from using either the Soil Moisture Active Passive Level 3 (SMAPL3; Entekhabi et al., 2016) or SMAP Level 4 (SMAPL4; Reichle et al., 2021) soil moisture products in the CTP–HI framework. The goal of this comparative study is to uncover how soil moisture, as detected through direct satellite observations (SMAPL3) and assimilated data products (SMAPL4), influences L–A coupling strength across the globe. The anticipated insights into how soil moisture variability influences coupling strength will provide critical advancements for assessing hydrological extremes. The comprehensive analysis of the coupling series, detailed in the Results section and the Discussion section, underscores the contributions of this study towards improving predictive models for weather and climate applications.

2 Methodology

2.1 L–A coupling classification

To quantify the L–A coupling, the observational-based CTP–HI framework developed by Roundy et al. (2013) is used. This framework is similar to the Findell and Eltahir (2003) framework in that it utilizes measures of atmospheric stability (CTP) and humidity (HI), but it goes a step further by using soil moisture (SM) to classify the CTP–HI into coupling regimes. The use of soil moisture to classify the CTP–HI space provides an observationally based approach to L–A classification, which is different from the Findell and Eltahir (2003) approach that utilized model simulations to classify the CTP–HI space. A brief overview of the classification methodology from Roundy et al. (2013) is given below, organized into three sections. First, the input variables are discussed. Next, a description of the methodology used to classify the CTP–HI space into coupling regimes is presented. Finally, the development of a daily time series of L–A coupling classification and its use in creating a measure of coupling strength is described. A conceptual diagram of this process is given in Fig. 1.

Figure 1 A visual representation of the soil moisture (SM), convective triggering potential (CTP), and humidity index (HI) on a thermodynamic diagram, along with a joint probability space of CTP–HI–SM at a specific grid location (38.89, −115.59). The CTP–HI framework is depicted after applying a two-sample Kolmogorov–Smirnov test to the joint probability space of CTP–HI–SM for the classification period from April 2015 to 2022.

2.1.1 Classification input variables

The left panel in Fig. 1 shows a conceptual diagram of the input variables required and includes an atmospheric thermodynamic diagram showing the CTP (atmospheric stability) and HI (atmospheric moisture) as well as a representation of SM (surface moisture). The CTP is the integrated area between the temperature profile and a moist adiabat between 100 and 300 hPa above the surface. It quantifies the stability of the atmosphere, where a more negative value indicates stable conditions, and a more positive value indicates unstable conditions. The HI quantifies moisture content in the lower atmosphere, explicitly reflecting the lower-tropospheric dew point depression. The HI is calculated as the sum of the dew point depressions at 50 and 150 hPa above the surface. A large value of HI indicates a dry atmosphere as there is a significant difference between the temperature and the dew point temperature at the specified pressure levels. As the dew point temperature approaches the temperature, the HI decreases and eventually reaches zero when the atmosphere is saturated. SM is a measure of surface wetness and is usually taken as the top-level soil moisture, thus making satellite remote sensing estimates an ideal input. Daily values of each of the three input variables are typically taken before sunrise to capture the state of the land and atmosphere prior to the impact of solar radiation. It is not always possible to have estimates right before sunrise, especially for remote sensing variables which are available only at a fixed overpass time. For these cases, any observation obtained before sunrise may be used, but care must be taken when comparing datasets with inconsistent measurement times (Roundy and Santanello, 2017).

2.1.2 Classification of the CTP–HI space

The classification process relies on daily values of the early morning estimates of CTP, HI, and SM over a classification period. In this work, the classification period was selected as April 2015 to December 2022 to be consistent with the SMAP observational record. An example of the joint probability space, with the CTP on the x axis, the HI on the y axis, and the SM averaged over bins in the CTP–HI space, is given in the middle panel of Fig. 1. This joint probability space is then used to define L–A coupling regimes within the two-dimensional CTP–HI space based on the distribution of soil moisture. This is done by comparing the soil moisture in each bin to the climatological soil moisture using the two-sample Kolmogorov–Smirnov test. Bins with soil moisture distributions significantly wetter than the climatological distribution are classified as a wet regime bin, while those with significantly drier soil moisture distributions are classified as a dry regime bin. This process is repeated using multiple bin sizes and statistical significance thresholds within the CTP–HI space to arrive at a probabilistic classification considering algorithmic uncertainty (see Roundy et al., 2013, for more details) as shown in the right panel. The fundamental underpinning of this approach is that consistent areas within the CTP–HI space with fundamentally different distributions of soil moisture represent a persistent coupling between the land and the atmosphere. Wet coupling regions in the CTP–HI framework are typified by a positive feedback loop through higher surface moisture, which results in increased latent heat fluxes that can initiate convection through an increase in moist static energy and a lower lifting condensation level. On the other hand, the dry coupling regime is identified in regions of drier soil moisture within the CTP–HI framework and is characteristic of high sensible heat fluxes, leading to strong boundary layer growth and possibly convection, thus causing negative feedback. However, this regime is often associated with less frequent and smaller precipitation events, resulting in an overall drying effect. Locations with a non-dominant combination of wet and dry classification based on the uncertainty parameters are considered to be in a transitional L–A coupling regime. Lastly, areas in the CTP–HI framework that do not show a significantly different distribution of soil moisture relative to the climatology are classified as atmospherically controlled, signifying that the convective processes are predominantly driven by atmospheric factors rather than land surface feedback. To simplify the analysis and to emphasize the crucial role that soil moisture plays in defining the dry and wet regimes, the atmospherically controlled and transitional regimes are merged into a single category termed “atmospherically controlled” for this analysis. The classification process is done for each dataset of CTP–HI–SM at the grid scale, thus allowing the coupling classification to account for the difference in climatology across datasets and regions around the globe, overcoming a limitation of the original Findell and Eltahir (2003) framework (Ferguson and Wood, 2011).

2.1.3 L–A coupling strength

Once the CTP–HI space is classified based on estimates of morning observations of CTP, HI, and SM, a daily coupling time series can be generated. The daily coupling is determined by mapping the CTP and HI values for a day onto the classified CTP–HI space (right panel in Fig. 1). For example, if the CTP and HI for a particular day map to a wet coupling regime, then that day is classified as a wet coupling regime day. This process is repeated for every day where there is an estimate of CTP and HI. Since the process for determining the daily coupling regime does not require the SM variable, the coupling time series can extend beyond the availability of SM data if there are CTP and HI data. Therefore, even though the CTP–HI space was classified based on data from 2015–2022, the time series of daily coupling was extended to 2003 based on the availability of CTP and HI data from remote sensing. This extended period provides for a more robust analysis of L–A coupling strength. Within this context, coupling strength is defined as the persistency of a specific coupling regime over the derived time series. The coupling strength is calculated by applying a first-order three-state (dry, wet, and atmospherically controlled) Markov chain model to the time series. A first-order three-state Markov chain describes the evolution of the coupling state through three persistence probabilities and six transitional probabilities based on a 1 d lag (i.e., tomorrow's coupling state is only dependent on the current coupling state). Of the nine probabilities calculated, only the two persistence probabilities for the dry and wet regimes are used to define the coupling strength (i.e., the probability that it remains in its current state). Since coupling strength is a probability expressed as a percentage (ranging from 0 % to 100 %, with 100 % indicating strong coupling or persistence), higher percentages signify a stable interaction between the land and the atmosphere that can impact weather patterns and short-term climate variability. In contrast, low values of coupling strength indicate weaker L–A interactions.

2.2 Merged CTP and HI

Evaluating the sensitivity of the coupling strength to different soil moisture datasets requires a consistent dataset of CTP–HI. The only global CTP and HI datasets available are from reanalysis or satellites. Relying solely on a single reanalysis dataset for CTP–HI could introduce biases and limit the comparability when evaluated alongside multiple soil moisture products. Moreover, satellite-derived CTP–HI estimates face significant challenges, such as missing observations and lower vertical resolution (Roundy and Santanello, 2017), which can impact the quality and reliability of the data.

To address the limitations inherent in single-source CTP–HI estimates, a merged CTP–HI product is developed from three different reanalysis datasets. This approach aims to provide a more comprehensive and reliable benchmark for comparing the impact of soil moisture dynamics on L–A coupling strength. Previous research has shown that the triple collocation (TC) data merging methodology is reliable for combining hydrologic variables without requiring ground-based observational data (Yilmaz et al., 2012). This study uses a 30 d centered window (15 d on either side of the day) that removes the effect of seasonality. To reduce complexity due to leap years, the analysis only considers 28 d in February for each year. The TC technique employs a least-squares approach to calculate weight distributions for each dataset based on the root mean square error (RMSE). A core assumption of this method is the independence of each dataset – that is, a lack of correlated errors between the datasets. This condition ensures the accuracy of the TC method, as otherwise the merged estimate is prone to biases. Mathematically, the errors within each dataset can be articulated as a linear combination of mutually independent error terms, as mentioned in Eq. (1) (Wu et al., 2020):

$$\begin{array}{}\text{(1)}& {\mathit{\theta }}_i=a_i+b_i\mathit{\theta }+{\mathit{\epsilon }}_i,\end{array}$$

where θ_i represents collocated measurements of an arbitrary variable (here CTP and HI) for i= 1, 2, and 3 related to the true value θ with ε_i as random errors, and a_i and, b_i correspond to the intercept and slope obtained through ordinary least-squares regression. Considering these assumptions and their potential implications, the resulting merged dataset provides a more comprehensive and accurate representation of the underlying physical phenomenon.

The TC methodology is employed to create a merged CTP and HI dataset from three reanalysis products: the Modern-Era Retrospective Analysis for Research and Application version 2 (MERRA-2), the Climate Forecast System Reanalysis (CFSR), and the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis v5 (ERA5). The TC method requires choosing a reference dataset (used to estimate the true values of the measured physical phenomenon). MERRA-2 is selected to be the reference dataset; however, it is worth noting that previous studies have indicated that the choice of reference dataset does not impact the outcome of TC error variance (Anderson et al., 2012). The first step involves converting the CFSR and ERA5 estimates (θ) into the MERRA-2 climatology (θ^′) using Eqs. (2) and (3) to establish a common reference framework for the datasets.

$$\begin{array}{}\text{(2)}& {\displaystyle }{{\mathit{\theta }}^{\prime }}_{\mathrm{CFSR}}={\mathit{\mu }}_{\mathrm{MERRA}\text{-}\mathrm{2}}+({\mathit{\theta }}_{\mathrm{CFSR}}-{\mathit{\mu }}_{\mathrm{CFSR}})\left({\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{MERRA}\text{-}\mathrm{2}}}{{\mathit{\sigma }}_{\mathrm{CFSR}}}}\right)\text{(3)}& {\displaystyle }{{\mathit{\theta }}^{\prime }}_{\mathrm{ERA}\mathrm{5}}={\mathit{\mu }}_{\mathrm{MERRA}\text{-}\mathrm{2}}+({\mathit{\theta }}_{\mathrm{ERA}\mathrm{5}}-{\mathit{\mu }}_{\mathrm{ERA}\mathrm{5}})\left({\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{MERRA}\text{-}\mathrm{2}}}{{\mathit{\sigma }}_{\mathrm{ERA}\mathrm{5}}}}\right)\end{array}$$

In the above step, μ represents the mean and σ is the standard deviation of the respective datasets. The normalized composites are linearly scaled and used as input in TC analysis, as described below in Eqs. (4)–(6). Each dataset was rescaled to a consistent grid resolution of 1° × 1° before applying the TC method and was evaluated from 2003 to 2022 to calculate the TC error value (ε²).

$$\begin{array}{}\text{(4)}& {\displaystyle }{\mathit{\epsilon }}_{\mathrm{MERRA}\text{-}\mathrm{2}}^{\mathrm{2}}=\left\{\left({\mathit{\theta }}_{\mathrm{MERRA}\text{-}\mathrm{2}}-{{\mathit{\theta }}^{\prime }}_{\mathrm{CFSR}}\right)({\mathit{\theta }}_{\mathrm{MERRA}\text{-}\mathrm{2}}-{{\mathit{\theta }}^{\prime }}_{\mathrm{ERA}\mathrm{5}})\right\}\text{(5)}& {\displaystyle }{\mathit{\epsilon }}_{\mathrm{CFSR}}^{\mathrm{2}}=\left\{\left({\mathit{\theta }}_{\mathrm{CFSR}}-{{\mathit{\theta }}^{\prime }}_{\mathrm{MERRA}\text{-}\mathrm{2}}\right)({\mathit{\theta }}_{\mathrm{CFSR}}-{{\mathit{\theta }}^{\prime }}_{\mathrm{ERA}\mathrm{5}})\right\}\text{(6)}& {\displaystyle }{\mathit{\epsilon }}_{\mathrm{ERA}\mathrm{5}}^{\mathrm{2}}=\left\{\left({\mathit{\theta }}_{\mathrm{ERA}\mathrm{5}}-{{\mathit{\theta }}^{\prime }}_{\mathrm{CFSR}}\right)({\mathit{\theta }}_{\mathrm{ERA}\mathrm{5}}-{{\mathit{\theta }}^{\prime }}_{\mathrm{MERRA}\text{-}\mathrm{2}})\right\}\end{array}$$

The above equation brackets indicate the temporal average of differences between two datasets over the study area. Mathematically, the ideal merger of a variable from numerous datasets requires information regarding errors such that a highly accurate data source receives the larger weight for merging and vice versa (Chen et al., 2022). To generate an unbiased merged data product from the three datasets, the sum of individual weights at each grid cell should be 1 ($w_{\mathrm{MERRA}\text{-}\mathrm{2}}+w_{\mathrm{CFSR}}+w_{\mathrm{ERA}\mathrm{5}}=\mathrm{1})$ (Gruber et al., 2017). The merged outcome or cost function is calculated using Eqs. (7)–(9), which minimizes the error variance in the merged outcome obtained from the least-squares approach and highly depends on the TC error (Lyu et al., 2021).

$$\begin{array}{}\text{(7)}& {\displaystyle }\begin{array}{rl}& w_{\mathrm{MERRA}\text{-}\mathrm{2}}=\\ & {\displaystyle \frac{{\mathit{\epsilon }}_{\mathrm{CFSR}}^{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{ERA}\mathrm{5}}^{\mathrm{2}}}{{\mathit{\epsilon }}_{\mathrm{MERRA}\text{-}\mathrm{2}}^{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{CFSR}}^{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{MERRA}\text{-}\mathrm{2}}^{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{ERA}\mathrm{5}}^{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{CFSR}}^{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{ERA}\mathrm{5}}^{\mathrm{2}}}}\end{array}\text{(8)}& {\displaystyle }\begin{array}{rl}& w_{\mathrm{CFSR}}=\\ & {\displaystyle \frac{{\mathit{\epsilon }}_{\mathrm{MERAR}\text{-}\mathrm{2}}^{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{ERA}\mathrm{5}}^{\mathrm{2}}}{{\mathit{\epsilon }}_{\mathrm{MERRA}\text{-}\mathrm{2}}^{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{CFSR}}^{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{MERRA}\text{-}\mathrm{2}}^{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{zERA}\mathrm{5}}^{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{CFSR}}^{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{ERA}\mathrm{5}}^{\mathrm{2}}}}\end{array}\end{array}$$

$$\begin{array}{}\text{(10)}& {\displaystyle }\begin{array}{rl}& w_{\mathrm{ERA}\mathrm{5}}=\\ & {\displaystyle \frac{{\mathit{\epsilon }}_{\mathrm{MERRA}\text{-}\mathrm{2}}^{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{CFRS}}^{\mathrm{2}}}{{\mathit{\epsilon }}_{\mathrm{MERRA}\text{-}\mathrm{2}}^{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{CFSR}}^{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{MERRA}\text{-}\mathrm{2}}^{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{ERA}\mathrm{5}}^{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{CFSR}}^{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{ERA}\mathrm{5}}^{\mathrm{2}}}}\end{array}\end{array}$$

The merged CTP is then calculated using the weighted sum of the individual datasets.

$$\begin{array}{}\text{(11)}& {\displaystyle }\begin{array}{rl}{\mathrm{CTP}}_{\mathrm{merged}}& =w_{\mathrm{MERRA}\text{-}\mathrm{2}}{\mathrm{CTP}}_{\mathrm{MERRA}\text{-}\mathrm{2}}+w_{\mathrm{CFSR}}{\mathrm{CTP}}_{\mathrm{CFSR}}\\ & +w_{\mathrm{ERA}\mathrm{5}}{\mathrm{CTP}}_{\mathrm{ERA}\mathrm{5}}\end{array}\text{(12)}& {\displaystyle }\begin{array}{rl}{\mathrm{HI}}_{\mathrm{merged}}& =w_{\mathrm{MERRA}\text{-}\mathrm{2}}{\mathrm{HI}}_{\mathrm{MERRA}\text{-}\mathrm{2}}+w_{\mathrm{CFSR}}{\mathrm{HI}}_{\mathrm{CFSR}}\\ & +w_{\mathrm{ERA}\mathrm{5}}{\mathrm{HI}}_{\mathrm{ERA}\mathrm{5}}\end{array}\end{array}$$

The weights remain consistent with the three datasets. The resulting merged CTP and HI, as well as the individual reanalysis products (MERRA-2, CFSR, and ERA5), are evaluated against estimates of CTP and HI from in situ radiosondes and satellite remote sensing based on several summary metrics, including the mean absolute error (MAE), bias, and the correlation coefficient (CC) as discussed in Sect. 4.1.

3 Dataset description

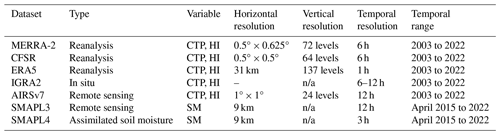
This study utilizes datasets that include soil moisture products derived from satellite remote sensing, as well as atmospheric profiles for calculating the CTP and HI metrics. The computation of CTP and HI requires surface pressure, 2 m temperature (T2m) and dew point temperature (DP2M), and vertical profiles of humidity (q) and temperature (T). A summary of these datasets, including their horizontal and temporal resolutions and coverage, is presented in Table 1.

Table 1 Description of the dataset for convective triggering potential (CTP), humidity index (HI), and soil moisture (SM) used in this study.

n/a: not applicable

Satellite remote sensing and in situ data are used to assess the performance of the merged CTP–HI dataset. Specifically, CTP and HI are calculated using data from the Atmospheric Infrared Sounder Version 7 (AIRSv7) as well as radiosonde observations from Integrated Global Radiosonde Archive Version 2 (IGRA2). To ensure spatial consistency in the study, all datasets were standardized to a uniform spatial resolution of 1° × 1°, which aligns the analysis with the spatial and temporal coverage of the AIRSv7 from 2003 to 2022.

The merged product is validated using the AIRS overpass time (∼ 01:30 local time) to leverage the benefits of remote sensing data (i.e., global coverage). However, the theoretical basis for the CTP–HI framework relies on early morning observations of CTP and HI (Findell and Eltair, 2003; Roundy et al., 2013), which more closely align with the SMAP overpass time (∼ 06:00 local time). Estimates of CTP and HI calculated from reanalysis at 01:30 and 06:30 reveal variations that suggest that the timing of data acquisition may influence these measurements. Therefore, the merged product is created at two different times: the AIRS overpass time (∼ 01:30) and at sunrise. The validation of the merged product is based on CTP and HI calculated at the AIRS overpass time so that it can be directly compared to AIRS, while the merged sunrise CTP and HI product is used for the analysis of coupling strength to be consistent with previous L–A coupling work.

3.1 CTP and HI datasets

The CTP and HI are calculated using three reanalysis datasets (MERRA-2, CFSR, and ERA5), satellite estimates, and in situ observations. When performing TC analysis, it is crucial to consider the presence of biases and errors in the datasets across different variables and applications. For instance, Park et al. (2020), Dong et al. (2020), Arshad et al. (2021), and Kozubek et al. (2020) have observed variations among these reanalysis datasets in their respective studies. Yingshan et al. (2022) found seasonal trend variations in all three datasets and concluded that ERA5 demonstrated superior performance in shortwave and longwave radiation compared to MERRA-2. Zhang et al. (2021) evaluated the surface air temperature in China and reported significant interannual variability in the MERRA-2, CFSR, and ERA5 datasets. Hassler and Lauer (2021) noted that performance in tropical areas varies depending on the subset of data used, such as land only, ocean only, or land–atmosphere–ocean. Santanello et al. (2015) reported a dry bias in CFSR and a wet bias in MERRA in the overall surface planetary boundary layer (PBL) based on local land–atmosphere coupling (LoCo) analyses over the US Southern Great Plains. A description of each of the CTP–HI datasets is given below.

3.1.1 The Modern-Era Retrospective Analysis for Research and Application version 2 (MERRA-2)

NASA's Global Modelling and Assimilation Office (GMAO) developed MERRA-2 as an atmospheric reanalysis dataset, employing the Goddard Earth Observing System (GEOS) atmospheric general circulation model (AGCM) (GMAO, 2015). The AGCM is a sophisticated numerical model that simulates the Earth's atmospheric processes, providing a comprehensive framework for understanding climate dynamics and variability. MERRA-2 provides 6-hourly observations with an approximate spatial resolution of 0.5° × 0.625° and includes 72 hybrid pressure levels ranging from the surface to 0.01 hPa (Gelaro et al., 2017). The data assimilation system of MERRA-2 utilizes the 3D-Var algorithm and spans from 1980 to the present. Gelaro et al. (2017) describe how the dataset incorporates observation-based precipitation to force the land model, ensuring realistic precipitation inputs, along with advancements and improvements made in the system.

3.1.2 The Climate Forecast System Reanalysis (CFSR)

The Climate Forecast System Reanalysis (CFSR) is developed by the National Center for Environmental Prediction (NCEP). It covers the period from 1979 to the present. It provides 6-hourly variable estimations, including 64 atmospheric levels at a 0.5° × 0.5° horizontal resolution (Saha et al., 2011). Operating as a global coupled atmosphere–ocean–land surface–sea ice system, CFSR incorporates satellite radiance data and employs the Integrated Forecasting System (IFS) Cycle 41r2 with the 3D-Var data assimilation system. Observations are carefully considered for each component during the assimilation process of the CFSR dataset; however, CFSR uses observation-based precipitation to force the land model, enhancing precipitation accuracy, as highlighted in Saha et al. (2010).

3.1.3 European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis v5 (ERA5)

ERA5, the fifth ECMWF reanalysis of global climate, is accessible from January 1959 to the present and produced by the Copernicus Climate Change Service (C3S) (Hersbach et al., 2023). ERA5 provides hourly land and atmospheric climate variable estimations at approximately a 31 km spatial resolution and 137 levels from the surface to 80 km (Bell et al., 2021). It employs the Integrated Forecasting System (IFS) Cycle 41r2 and assimilates satellite and in situ observations. ERA5 includes advanced screen-level assimilation for 2 m temperature and relative humidity components, where the soil moisture is nudged to better match the 2 m observations. ERA5 assimilates soil moisture from spaceborne scatterometers and integrates various precipitation data sources, improving soil moisture and precipitation estimates. Hersbach et al. (2020) compared ERA5 with radiosonde data and showed temperature, wind, and humidity improvements in the troposphere for the latest version.

Differences in land surface observations among these datasets can impact atmospheric variables and introduce biases. Soil moisture influences evaporation and humidity, while observation-based precipitation enhances land model accuracy, influencing atmospheric moisture and stability. ERA5 benefits from direct soil moisture assimilation, which potentially reduces bias. In contrast, MERRA-2 and CFSR use observation-based precipitation to force their land models and rely on model-generated soil moisture. This approach can introduce bias in temperature and humidity profiles due to uncertainties in the modeled soil moisture.

3.1.4 The Integrated Global Radiosonde Archive (IGRA) Version 2

The Integrated Global Radiosonde Archive Version 2 (IGRA2) is a comprehensive dataset provided by the National Center for Environmental Information (NCEI) of the National Oceanic and Atmospheric Administration (NOAA) in the United States (Durre et al., 2016). It offers access to high-quality radiosonde observations over 1500 stations worldwide from 1905 to the present (Durre and Yin, 2008). The dataset has undergone quality control and adjustments to correct instrument biases across various regions. These procedures ensure that the IGRA records are homogeneous and robust, making them valuable for long-term climate studies.

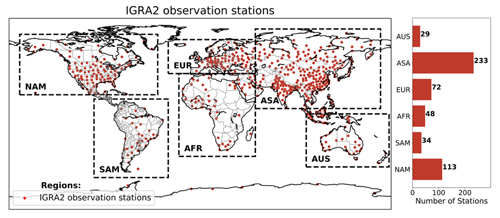
Despite its comprehensive coverage, the IGRA2 dataset presents challenges, including nonuniform data distribution across the world due to variable observation frequencies. Although radiosonde observations are typically recorded twice daily at 00:00 and 12:00 Coordinated Universal Time (UTC), in some regions, additional observations are taken at 06:00 and 18:00 UTC. Therefore, the frequency and timing of these observations differ among stations and locations. In this study, calculations for CTP and HI are performed using radiosonde data that fall within a ±3 h window of the nighttime AIRS overpass (∼ 01:30 local time). This targeted approach aligns CTP and HI calculations with the same observation time during the merging and validation process. Also, when multiple observations are available for a single grid cell, the selection criteria prioritize the station offering the most frequent data. A map of the geographic location of the IGRA2 radiosonde observation sites, along with regional totals in North America (NAM), South America (SAM), Africa (AFR), Europe (EUR), Asia (ASA), and Australia (AUS), is given in Fig. 2. Across the world, 534 locations have data available from 2003 to 2022. Most observations are in Asia, followed by North America and Europe.

Figure 2 IGRA2 observation stations across the globe, along with regions selected for further analysis and the number of observation stations in each region.

3.1.5 Atmospheric Infrared Sounder Version 7 (AIRSv7)

AIRS was launched in 2002 on NASA's Aqua satellite. AIRS retrieved thermodynamic profiles (temperature and humidity) using passive radiance observations. This study focuses on the descending orbit, covering Northern to Southern Hemisphere movement with an Equator crossing at ∼ 01:30 local time. Data have a twice-daily temporal resolution, capturing half of the 8 d Aqua orbit repeat cycle. Level 3 files contain averaged quality and geophysical parameters in 1° × 1° grid cells, including humidity and temperature profiles at 24 pressure levels from 1 to 1000 hPa (AIRS Project, 2019). In Version 7, shortwave exclusion in the retrieval algorithm reduces bias, and targeted channel selection focused on water vapor retrieval improves temperature and water vapor profile performance (Zhang et al., 2023a). It should be noted that for the processing and analysis of the AIRSv7 data, no alterations were made to the predefined quality control (QC) flags.

3.2 Soil Moisture Active Passive (SMAP)

NASA's Soil Moisture Active Passive (SMAP) mission provides global monitoring of soil moisture content. The enhanced SMAP Level 3 (SMAPL3) product, derived from the foundational Level 1 and 2 data, provides standardized, gridded global soil moisture at 9 km resolution with the capability to observe the entirety of the Earth's surface every 2–3 d (O'Neill et al., 2021). While the enhanced SMAP Level 3 is provided at a 9 km resolution, it should be noted that the native radiometer footprint is at ∼ 36 km and the brightness temperatures are interpolated to the 9 km resolution using an optimally localized average method. SMAP Level 4 (SMAPL4) data are produced using a land surface modeling system that assimilates SMAP brightness temperatures. SMAPL4 integrates SMAP Level 2 brightness temperature measurements, along with initialization and forcing inputs from the Catchment Land Surface Model (CLSM) (Reichle et al., 2017), thus producing 3-hourly, comprehensive estimates of surface and root-zone soil moisture at a 9 km spatial resolution (Qiu et al., 2021). SMAPL3 provides direct satellite remote sensing retrievals of surface soil moisture, while SMAPL4 uses a sophisticated data assimilation system within a modeling framework to create a more comprehensive (i.e., in time and space) soil moisture record. This differentiation is the basis of the analysis, providing a contrasting comparison of the impact of different estimates of soil moisture on the L–A coupling framework and the resulting impact on L–A coupling strength. The morning overpass is used for SMAPL3, while the sunrise soil moisture is estimated through linear interpolation from the 3 h data for SMAPL4. All available SMAPL3 data are used without filtering based on the quality flags in order to maintain a larger dataset for a comprehensive analysis. SMAPL3 also has missing observations due to the satellite's orbital constraints, which is not the case with the SMAPL4 dataset due to its reliance on the land surface model. This difference in data completeness may affect the comparative analysis. To quantify this impact, a dataset called SMAPL4_L3 is also included, which utilizes SMAPL4 but with the temporal coverage of SMAPL3 data, ensuring a comparison with equal samples of soil moisture estimates.

4 Results

4.1 Evaluation of merged CTP–HI

The foundational concept of the TC method emphasizes that inaccuracies in individual datasets should remain uncorrelated to avoid errors in the merged product. However, in practice, it is likely that the three reanalysis datasets will exhibit correlated errors. In Fig. 3a, the scatterplots show the correlated errors between different reanalysis datasets (MERRA-2, CFSR, and ERA5) with respect to the IGRA2 observations at a location in Kansas, United States (coordinates 39.96, −95.26). For instance, MERRA-2 vs. CFSR represents the errors in MERRA-2 plotted against the errors in CFSR, both with respect to the IGRA2 observations. These errors are analyzed at the AIRS overpass (∼ 01:30 local time). The analysis indicates a significant correlation of errors, with a correlation coefficient of ∼ 0.85 when assessed against IGRA2 data. This correlation appears more pronounced for the CTP than the HI, suggesting a stronger association of errors within the stability metric (CTP). This is further seen at the global scale in Fig. 3b, showing box plots for observed error correlation across the 534 IGRA2 locations. Most locations have a correlation exceeding 0.7. This high correlation points to similar error sources in the datasets for CTP and HI across the three datasets considered. This may stem from similar approaches and data used in assimilating temperature and humidity profiles or their radiances, while HI may be influenced more by differences in model physics and parameters, as well as screen-level nudging (in ERA5), compounded by challenges in assimilating near-surface humidity data. Even though the datasets employ diverse methods of data assimilation (DA) and feature distinct physics and parameters, the common input of in situ and satellite data likely contributes to this correlation. These correlated errors may affect the accuracy of the resulting merged dataset, which is validated against observations in Sect. 4.1.2.

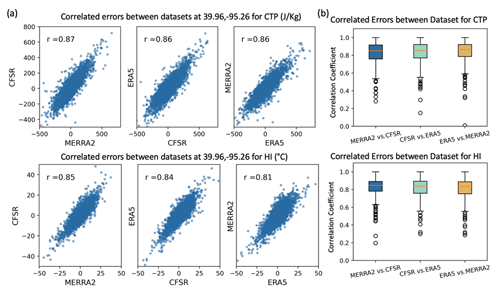
Figure 3 (a) Observed errors between IGRA2 and reanalysis datasets at a location in Kansas, United States (latitude: 39.96, longitude: −95.26), for CTP and HI from 2003 to 2022, along with the Pearson correlation displayed in the upper left corner. (b) Observed error correlation between reanalysis datasets at IGRA2 stations across the globe (529 sites).

The triple-collocation-based error (TC error) using Eqs. (4)–(6) given in the Supplement (Fig. S1) reveals a remarkably high TC error for the CTP within the MERRA-2 and CFSR datasets, most notably over the Northern Hemisphere and South America. The merged product is constructed based on the weights derived from the error variance calculated by Eqs. (7)–(9). Locations with a higher error variance are assigned lower weights, reflecting their reduced reliability. Conversely, locations with lower error variance are deemed more reliable and are thus given greater weights in the grid-level merging process.

Table 2 demonstrates the distribution of TC-based weights for CTP and HI across various global regions for the three datasets. The spatial maps in the Supplement (Fig. S2) detail the weights for each reanalysis product for CTP and HI globally. These weights are directly proportional to the relative error variance; areas where MERRA-2 and CFSR show larger variances (Fig. S3), especially in the Northern Hemisphere and South America, tend to favor ERA5 for the weighting of the merged CTP. Based on Table 2, ERA5 emerges as the leading dataset for CTP, being allocated the highest weight in most regions. However, in Europe and Africa, the weight distribution for CTP is almost similar among the three datasets, indicating a balanced reliance on each dataset within these continents.

Table 2 Average weight across North America (NAM), South America (SAM), Africa (AFR), Europe (EUR), Asia (ASA), and Australia (AUS). The color gradient is applied based on the minimum value (yellow color) to the maximum value (green color) for CTP and HI for AIRS overpass.

The weight allocation for the HI shows considerable regional variation. In South America, the MERRA-2 dataset is assigned the lowest weight, implying that it contributes less to the combined HI product. Conversely, in Europe, it is the ERA5 dataset that receives the lowest weight, signifying its reduced contribution to the HI variable in this region. These regional differences in the weighting of datasets underscore the merging process, allowing for a location-specific approach to creating a merged product.

4.1.1 Performance of merged CTP–HI

The data are merged following Eqs. (10a) and (10b), and the resultant spatial distribution of average CTP and HI during the summer season (June, July, and August of JJA) for the year 2012 is portrayed in the Supplement (Figs. S3 and S4). These figures compare the CTP and HI values derived from the MERRA-2, CFSR, and ERA5 alongside the merged product.

The accuracy of the merged data, along the individual reanalysis datasets MERRA-2, CFSR, and ERA5, is evaluated through a comparison with IGRA2 radiosonde and AIRSv7 satellite observations, as depicted in Figs. 4 and 5. The evaluation utilizes the mean absolute error (MAE), bias, and correlation coefficient (CC) across major global regions. The results indicate that the merged dataset consistently achieves the lowest MAE for CTP and HI variables, outperforming the individual reanalysis datasets. This improvement in accuracy suggests that the merging process effectively consolidates the strengths of the individual datasets while mitigating their respective biases despite the correlated errors seen in Fig. 3.

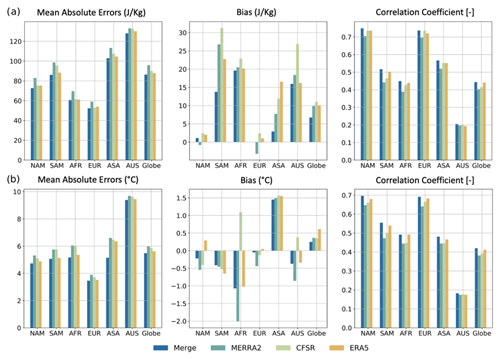
Figure 4 Bar plot of performance metrics and intercomparison of merged data and reanalysis with radiosonde observations from IGRA2 in different regions and globally for (a) CTP and (b) HI.

The merged product compensates for these inaccuracies in regions where the MERRA-2 dataset exhibits substantial discrepancies with observational data, demonstrating a practical approach that improves the overall metric. Furthermore, the merged dataset shows a considerable reduction in positive bias for CTP across South America, Europe, and Asia, as well as a decrease in negative bias for HI in most regions, except for Asia. These improvements highlight the efficacy of the merging process in yielding a more reliable dataset, which is especially beneficial for L–A coupling studies in regions challenged by less accurate reanalysis data.

Figure 5 presents the same set of performance metrics as in Fig. 4 but compared against the AIRSv7 data. The result indicates a general trend of overestimation for CTP and HI by the reanalysis and merged datasets across all regions compared to AIRSv7. It is essential to acknowledge the limitations in measurement capabilities and inherent biases of AIRSv7, particularly in terms of lower-troposphere retrieval due to limited vertical resolution in AIRS, which is different from those in the reanalysis datasets. Specifically, the limited sensitivity and vertical resolution of AIRSv7 in the PBL might lead to positive biases, resulting in discrepancies with the reanalysis datasets vs. that observed with radiosonde data as the reference.

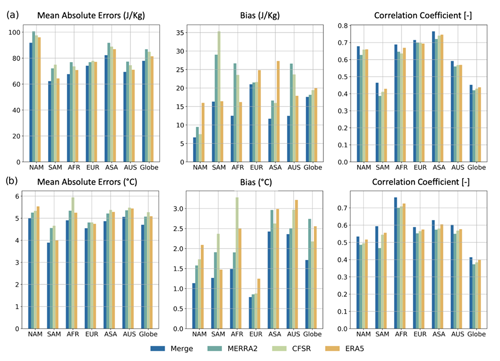
Figure 5 Bar plot of performance metrics and intercomparison of merged data and reanalysis with satellite remote sensing from AIRSv7 in different regions and globally for (a) CTP and (b) HI.

Regarding temporal correlation, the merged dataset and the ERA5 reanalysis score the highest values, reflecting a consistent signal with observations from IGRA2 and AIRSv7 (as shown in Figs. 4 and 5). When evaluated against both ground-based observations and satellite remote sensing, there is a noticeable improvement in the performance of the merged product compared to the individual reanalysis datasets. The merged product demonstrates a closer alignment with the ground truth, as represented by IGRA2, capturing the observed signal with greater accuracy. Overall, the outcome remains consistent across the globe when validating the merged product and individual reanalysis datasets with respect to IGRA2 and AIRSv7 for CTP and HI.

The previous evaluation of the CTP and HI products was done at the AIRS overpass time (∼ 01:30 local time); however, the theory of the CTP–HI framework for classifying coupling relies on early morning observations of the CTP and HI (Findell and Eltair, 2003), which also aligns with the SMAP overpass time (∼ 06:00 local time). Table S5 gives the weights for the merged product at sunrise. Compared to the AIRS overpass weights (Table 2), the sunrise weights show similar spatial patterns with marginal variations. This is consistent with previous research by Roundy and Santanello (2017) that demonstrated the application of the CTP–HI framework with AIRS estimates and demonstrated similarity in the overarching pattern of L–A coupling classification. Thus, the remainder of the analysis will use the sunrise merged CTP and HI products to classify and analyze L–A coupling.

4.2 Coupling strength in the contiguous United States

The sunrise merged CTP and HI products and three different datasets of soil moisture (SMAPL3, SMAPL4_L3, and SMAPL4) are used to classify the CTP–HI space and create a time series of L–A coupling from 2003–2022. The time series is then used to quantify the L–A coupling strength based on the persistence probabilities from a first-order three-state Markov chain. Figure 6 examines the coupling strength over the contiguous United States using the same CTP–HI data but with different soil moisture datasets. Figure 6a reveals a consistent pattern of a persistent dry regime in the inter-mountain west region and a persistent wet regime in the northwestern and eastern parts of the country. A side-by-side evaluation shows that the SMAPL4 dataset displays a more persistent pattern under dry and wet regimes. This indicates a stronger representation of L–A coupling in SMAPL4 that may be due to the strong vertical coupling of soil moisture in the catchment assimilation processes. On the other hand, SMAPL4_L3 data show less persistence than SMAPL4, suggesting that part of observed difference between SMAPL3 and SMAPL4 is due to sample size. Despite these differences, the overarching spatial pattern remains consistent across all datasets except over the northern Great Lakes for SMAPL4 where it shows a persistent wet coupling regime.

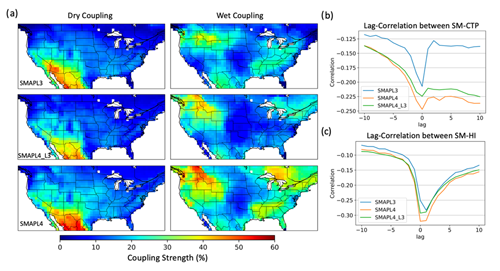
Figure 6 Comparative analysis of L–A coupling strength using SMAPL3, SMAPL4_L3, and SMAPL4 data. (a) Coupling strength for the dry and wet coupling regime and (b, c) lag correlation between soil moisture and CTP and HI averaged over the contiguous United States.

To delve deeper into the noted differences in coupling strength, the lagged correlation between the three sets of soil moisture and the CTP and HI over 2015–2022 is analyzed. Lag correlation is employed to identify the relationship between soil moisture and future CTP and HI and vice versa. While previous work has discussed the potential for soil moisture predictability out to 60 d (Dirmeyer et al., 2018), this analysis uses a 10 d lag to capture the role of soil moisture in predicting the atmospheric state (CTP and HI) and the atmospheric state in predicting soil moisture on timescales relative to typical weather predictability. Within this setup, the ability of soil moisture to predict future CTP and HI is given as a positive lag correlation and the ability of the CTP and HI to predict future soil moisture is given as a negative lag. For both the CTP and HI, the correlation with soil moisture is negative due to the relationship between SM–CTP and SM–HI. Wet soil typically results in surface cooling when solar radiation is limited, leading to a more stable temperature profile in the lower atmosphere. This stability restricts vertical movement and consequently leads to a lower CTP, thus creating a negative correlation. HI, on the other hand, measures atmospheric moisture content. Higher HI values signify drier air, while lower values indicate moisture-rich air closer to saturation. High soil moisture enhances evaporation, which adds water vapor to the atmosphere, reducing the gap between temperature and dew point and thus lowering the HI, resulting in a negative correlation.

Figure 6b and c show the average lag correlation out to 10 d over the contiguous US and indicate that soil moisture has a stronger predictive influence on CTP and HI as shown by the larger magnitudes of correlations over positive lags, which suggest that while CTP and HI are not as strong in predicting soil moisture (lower magnitude of correlations over negative lags), soil moisture is more effective in predicting changes in CTP and HI. This is particularly noticeable for shorter lags, suggesting a more immediate impact of soil moisture on atmospheric stability and humidity. Conversely, the decrease in correlation magnitude with longer lags highlights the diminishing influence of L–A interaction over time. For the different datasets, SMAPL4 consistently shows higher correlations at all lag intervals for both CTP and HI. However, the sample size does play a role in this assessment as noticed by a decrease in the magnitude of correlation for the SMAPL4_L3. Despite this, the SMAPL4_L3 dataset still shows a higher magnitude in lag correlation compared SMAPL3, particularly for CTP. This suggests that the assimilation of SMAP observations into a model, as in SMAPL4, may yield a stronger relationship in the temporal dynamics between the land surface and the atmosphere. In contrast, the pattern of a stronger L–A connection for SMAPL4 is less evident for HI.

To further analyze the impact of soil moisture on coupling strength, Fig. 7 delves into a grid-scale analysis at a location in Nevada, USA (38.89, −115.59). Figure 7a illustrates the classified CTP–HI space based on SMAPL3, SMAPL4_L3, and SMAPL4 datasets. The coupling regimes are clearly distinguished within the CTP–HI framework across the datasets, highlighting the variations and interactions between soil moisture and atmospheric conditions. SMAPL4 indicates more bins assigned to wet and dry coupling regimes, thereby resulting in an increased coupling strength within the time series. In Fig. 7b, the joint probability of CTP–HI–SM space illustrates the bin average SM within the CTP–HI space based on historical observations and helps to identify patterns in the CTP–HI–SM relationship. States of wet coupling are associated with higher soil moisture levels in the combined probability space of CTP–HI–SM, whereas dry states are linked to consistent lower moisture levels within the CTP–HI space. While the overall disparities between SMAPL3 and SMAPL4 in the distribution of soil moisture are quite evident in Fig. 7c, there is also very little difference in soil moisture distribution due to sample size (difference between SMAPL4 and SMAPL4_L3). Given that the classification algorithm accounts for climatological difference in the soil moisture datasets, the difference stems from the shape of the soil moisture distribution and its projection on to the CTP–HI space. The SMAPL3 dataset shows a tendency for observations to skew toward the lower end of the soil moisture spectrum, while the SMAPL4 tends to exhibit a clustering of observations in the mid-range between 0.4 and 0.8. These differences in both the soil moisture distribution and its projection in the CTP–HI space affect the classification of coupling regimes and therefore the coupling strength of the time series. Figure 7d depicts the daily coupling classification for an arbitrary month (May 2010). The SMAPL4 dataset, with its higher number of wet regime classifications, demonstrates a greater likelihood of days being categorized as a wet regime. This is evidenced in the time series, where most days are classified under wet conditions in SMAPL4, in contrast to the SMAPL3 dataset, which indicates more days in an atmospherically controlled regime. Sample size has a small impact on the classification, with only 2 d being different between SMAPL4_L3 and SMAPL4. This difference underscores the influence of soil moisture on the daily classification of L–A coupling within the CTP–HI framework, even though it is not directly used in creating daily time series.

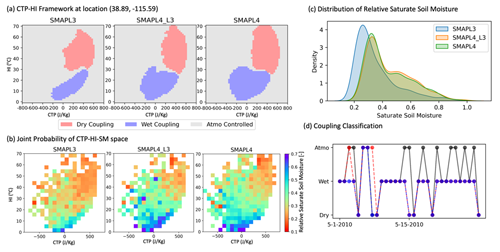
Figure 7 Multifaceted assessment of coupling classification influenced by soil moisture across SMAPL3, SMAPL4_L3, and SMAPL4 data at a specific grid location (38.89, −115.59) situated in Nevada, USA. (a) CTP–HI framework. (b) A joint probability space of CTP–HI–SM. (c) Saturated soil moisture distribution. (d) Coupling classification time series for May 2010.

4.3 Global coupling strength

The previous section highlighted the connection between coupling strength and the lag correlation between SM and the CTP and HI. To explore this further, Fig. 8 presents the average coupling strength (for both dry and wet regimes) on the x axis and the average positive (soil moisture predicts CTP–HI) lag correlation out to 10 d on the y axis for all land grid cells across the globe. Overall, all soil moisture datasets show a nonlinear relationship between coupling strength and lag correlation, with little relationship between the variables for low coupling strength that transitions into a stronger relationship as coupling strength increases. To help quantify this, the data are fit to a quadratic model, and the R² for this relationship is shown. The R² value is calculated to measure how well the variance in the observed data can be explained by the quadratic model. As indicated in Fig. 8a, all soil moisture datasets show a weaker relationship between average coupling strength and average lag correlation for CTP, as indicated by a lower R² (explained variance by the regression line) and a shallower slope in the regression line. In contrast, Fig. 8b shows that the SM–HI relationship is stronger, with higher R² values and a more pronounced nonlinear relationship. This indicates that persistency as a measure of coupling strength is predominantly driven by the SM–HI relationship, suggesting a direct influence of soil moisture on lower-level humidity and its correlation over time. In contrast, the SM–CTP relations is more complex due to the indirect influence on atmospheric stability, which may be more influenced by larger-scale atmospheric conditions. Furthermore, SMAPL4 shows a stronger relationship compared to SMAPL3 that is only slightly impacted by the difference in sample size between SMAPL3 and SMAPL4.

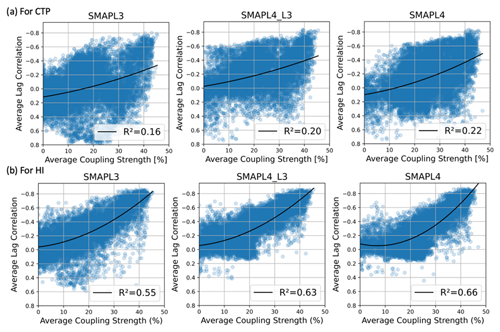
Figure 8 Comparative analysis of average dry and wet coupling strength and 10 d lag correlation using SMAPL3, SMAPL4_L3, and SMAPL4 soil moisture datasets for (a) CTP and (b) HI.

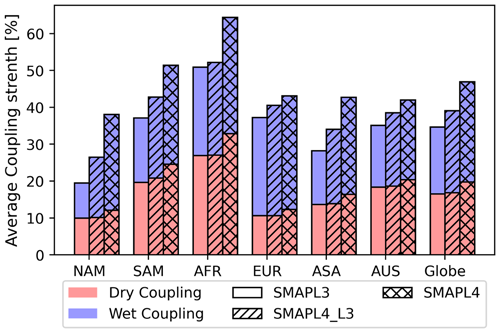
The average coupling strength for dry and wet regimes across the different regions and globally using SMAPL3, SMAPL4_L3, and SMAPL4 is given in Fig. 9. All datasets are consistent in showing that Africa has the largest average coupling strength, while North America has the smallest average coupling strength. Yet, there are differences in the relative strength for other regions. Notably, the SMAPL4 dataset demonstrates a stronger coupling strength in both the dry and wet regimes, indicating a stronger temporal persistence in the coupling regime. The variation in coupling strength becomes noticeable when the sample size is considered. This is particularly true for Africa, where there is little difference between the average coupling strength between SMAPL3 and SMAPL4_L3. In contrast, North America shows the largest difference in coupling strength between SMAPL3 and SMAPL4_L3. As with other regions of the globe, there is little difference in the coupling strength for the dry regime, as differences are predominantly seen in the wet regime coupling strength. This outcome is consistent with Fig. 6, which shows the spatial variability of coupling strength over the contiguous United States.

Figure 9 Comparative analysis of land–atmosphere average coupling strength using different soil moisture from SMAPL3, SMAPL4_L3, and SMAPL4 data across various regions and globally.

5 Discussion

An important aspect of this analysis is the development of the merged CTP and HI product. The merging process employs the triple collocation method based on the relative errors among the MERRA-2, CFSR, and ERA5 datasets. The variations in the weight distributions for CTP and the HI reflect the inherent differences in the datasets. In the merged dataset, the ERA5 reanalysis had the highest weight, which may be a result of improved representations of tropospheric temperature and humidity (Hersbach et al., 2020). Nonetheless, it is critical to understand that a higher weight for ERA5 does not mean that the merged product will closely resemble ERA5 in its characteristics. The merging process involves integrating information from multiple datasets, and the resulting merged product is a distinct and independent entity. Figure 3 also reveals the presence of correlated errors when compared with radiosonde observations, suggesting the potential for a biased merged product. However, the merged product outperformed the individual reanalysis datasets when compared to radiosondes and satellite-based estimates of CTP and HI (Figs. 4 and 5). This suggests that the merging process reduces the bias arising from the individual reanalysis products and provides a more accurate product. While this validation of the merged product is robust, it is not without its flaws. The differences in spatial and temporal resolutions between the merged product and the IGRA2 radiosonde and AIRSv7 observations are prone to uncertainty. Despite this, the merged dataset demonstrates a more accurate reflection of in situ and satellite observations of CTP and HI compared to individual datasets, thus providing a temporal and spatially consistent dataset for analyzing L–A coupling.

The merged CTP–HI product was used to investigate how soil moisture from SMAP contributes to quantifying L–A coupling strength globally. As depicted in Figs. 6 through 9, the findings underscore the pivotal role of soil moisture in the representation of L–A coupling strength within the CTP–HI framework developed by Roundy et al. (2013). The coupling strength is quantified as the persistence in the wet and dry coupling regimes defined using a three-state Markov chain model. Figures 6 and 8 demonstrate the ability of soil moisture to predict future CTP and HI through lag correlation analysis and its direct relationship with coupling strength. The observed lag correlation is most pronounced for the SM–HI relation, indicating the direct influence of soil moisture on lower-tropospheric humidity. In contrast, there is a weaker relationship between soil moisture and atmospheric stability, as indicated by the SM–CTP lag correlation. Reinforcing this point, Entekhabi et al. (1996) discussed the significant feedback mechanisms between soil moisture and atmospheric processes, highlighting how changes in soil moisture can directly impact the atmospheric environment. Wang et al. (2024) further substantiate this argument, which demonstrates the potential for soil moisture to predict the future coupling state and the utility of the persistence in the coupling regime as a measure of coupling strength.

The SMAPL4 dataset exhibits higher coupling strength in both the wet and dry regimes across the globe (Fig. 9). This indicates that SMAPL4 would give stronger short-term predictions of future coupling states using the Coupling Stochastic Model (CSM) developed by Roundy and Wood (2015) compared to the SMAPL3 product. However, it is unclear if the stronger coupling predictions would lead to more skillful predictions, and this topic is left to future research. One possible reason for the weaker coupling strength in SMAPL3 is that all available SMAPL3 data points were used to maintain a larger dataset without considering the quality flags. Dong and Crow (2019) highlight the importance of high signal-to-noise ratios in L-band SMAP soil moisture data for accurately quantifying L–A coupling strength. However, reducing the SMAPL3 sample size by filtering out data based on quality flags may introduce additional variability and noise, potentially impacting the coupling strength, especially in regions with variable data quality. This could potentially be teased out with a longer SMAP data record that would allow greater scrutiny of the retrievals without compromising the sample size.

The higher coupling strength observed in SMAPL4 is attributed to the reliance on a land surface model and assimilation process. The constraints of a deterministic model, based on fixed equations, make a land surface model less susceptible to variation and random noise and thus create a higher autocorrelation compared to SMAPL3. While this is a unique characteristic of SMAPL4, it is important to remember that the strong coupling may not accurately mirror the complexities of real-world conditions (Van Vuuren et al., 2012). The accuracy of the stronger coupling in SMAPL4 is difficult to quantity due to the scarcity of in situ observations across the globe where simultaneous atmospheric profile and soil moisture measurements can be obtained. The limitation of comprehensive ground-based observations poses a significant challenge in validating the true representation of coupling and understanding the intricate interplay between soil moisture and atmospheric conditions (Santanello et al., 2018; Beamesderfer et al., 2022). This conclusion also aligns with the insight provided by Findell et al. (2024), who emphasized the importance of high-frequency data for accurately assessing land–atmosphere coupling in climate models. Consequently, our ability to ascertain which dataset offers a more accurate representation of L–A coupling remains a subject of ongoing investigation.

Figure 7c shows that differences between the SMAPL3 and SMAPL4 coupling strengths are mainly due to the shape of the distribution of soil moisture and its projection in the CTP–HI space. A minor difference in soil moisture distribution is observed in Fig. 7c when comparing SMAPL4 and SMAPL4_L3, though this difference is more notable in the joint probability space of CTP–HI–SM (Fig. 7a and b). Soil moisture estimates from SMAPL3 tend to skew towards drier values, likely due to the retrieval of the topsoil layer, which tends to dry quickly after rainfall events. This skew is influenced by fixed conditions in the retrieval process such as the prescribed freeze–thaw condition, as well as land surface characteristics like vegetation cover and soil properties. In contrast, SMAPL4, which uses observations from the same satellite, employs model-based soil hydraulic parameters, providing a greater range in the depiction of soil moisture variations across different landscapes. Studies by Reichle et al. (2017) and Reichle et al. (2019, 2021) have shown a reduced bias and expanded dynamic range of surface soil moisture in SMAPL4 compared to in situ observations and the previous version of SMAPL4. These differences highlight the varying methodologies and characteristics of SMAPL3 and SMAPL4, resulting in distinct soil moisture estimates.

Recent research underscores the vital role of the SMAPL3 soil moisture product in agricultural applications, as demonstrated by Zhu et al. (2024). The accuracy of soil moisture measurement is crucial, and Tavakol et al. (2019) highlighted that the SMAPL3 and SMAPL4 soil moisture products are at the forefront of soil moisture accuracy. For instance, Xu (2020) concluded that the SMAPL4 surface soil moisture product is more accurate, with lower errors (ubRMSE < 0.04 m³ m⁻³), compared to the SMAPL3 product (∼ 0.06 m³ m⁻³). Moreover, SMAP outperforms other soil moisture products, such as AMSR2 L3 and SMOS-IC, across most of the global land surface (Kim et al., 2021). This enhanced accuracy has been corroborated by Zhang et al. (2017), who showed that SMAPL4 captures spatial and temporal soil moisture variations more reliably than the Advanced Microwave Scanning Radiometer (AMSR2) across the United States. Reichle et al. (2017) have shown that the version 4 SMAPL4 bias is significantly reduced compared to version 3, exhibiting a 46 % decrease in surface soil moisture uncertainty. Considering the above points, SMAP observations could improve drought monitoring and provide detailed insight into drought conditions, as demonstrated in studies by Mishra et al. (2017), Velpuri et al. (2016), and Mladenova et al.(2020). This work further demonstrates the particular relevance of SMAP observations for studies of drought and L–A interaction, providing deeper insights into how land surface conditions influence atmospheric responses (Zhang et al., 2023b) and how it could potentially improve drought monitoring and prediction using statistical modeling (Roundy and Wood, 2015).

6 Conclusion

This work developed a merged reanalysis-based product for CTP and HI, which outperforms individual reanalysis products when validated against radiosonde and satellite observations. The merged CTP and HI product was used in combination with two different SMAP soil moisture products to analyze the coupling strength across the globe. Coupling strength is defined by the persistence probability for wet and dry coupling regimes as given by a first-order three-state Markov chain model and is directly related to the ability of soil moisture to predict future atmospheric states out to 10 d. It is demonstrated that the measure of coupling strength is primarily driven by the SM–HI relationship, suggesting a direct influence of soil moisture on lower-tropospheric humidity over time. In contrast, the SM–CTP relationship is more complex and likely influenced by larger-scale atmospheric conditions.

Another key conclusion is that SMAPL4 consistently presents a stronger representation of coupling strength compared to SMAPL3. While some of the difference in coupling strength can be attributed to the limited sample size of SMAPL3, analyzing similar samples from both SMAP products still demonstrates stronger persistence in the wet coupling regimes in SMAPL4. The increased coupling strength in SMAPL4 may result from SMAPL4's reliance on a land surface model, which reduces susceptibility to random noise compared to SMAPL3. The difference in coupling strength in the two soil moisture datasets using the same CTP–HI underscores the importance of soil moisture data in estimating coupling strength using the CTP–HI framework. Nevertheless, it is not clear which of the two SMAP measures of coupling strength provide a better representation of the “real-world coupling” as enhanced observation networks (i.e., collocated ground and atmospheric profile measurements) are needed to assess the accuracy of L–A interactions on a global scale.

Future work will investigate how the differences and similarities in the SMAP coupling strength may influence the ability to monitor and forecast the initiation, intensification, and abatement of drought conditions using methods such as the L–A-coupling-based drought index (Roundy et al., 2014) and coupling stochastic model (Roundy and Wood, 2015). Such work may lead to potential improvements to drought monitoring and forecasting, strengthening the capacity for effective drought preparedness and response.