the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Simulation-based inference for parameter estimation of complex watershed simulators
Elena Leonarduzzi
Luis De La Fuente
Hoang Viet Tran
Andrew Bennett
Peter Melchior
Reed M. Maxwell
Laura E. Condon
High-resolution, spatially distributed process-based (PB) simulators are widely employed in the study of complex catchment processes and their responses to a changing climate. However, calibrating these PB simulators using observed data remains a significant challenge due to several persistent issues, including the following: (1) intractability stemming from the computational demands and complex responses of simulators, which renders infeasible calculation of the conditional probability of parameters and data, and (2) uncertainty stemming from the choice of simplified representations of complex natural hydrologic processes. Here, we demonstrate how simulation-based inference (SBI) can help address both of these challenges with respect to parameter estimation. SBI uses a learned mapping between the parameter space and observed data to estimate parameters for the generation of calibrated simulations. To demonstrate the potential of SBI in hydrologic modeling, we conduct a set of synthetic experiments to infer two common physical parameters – Manning's coefficient and hydraulic conductivity – using a representation of a snowmelt-dominated catchment in Colorado, USA. We introduce novel deep-learning (DL) components to the SBI approach, including an “emulator” as a surrogate for the PB simulator to rapidly explore parameter responses. We also employ a density-based neural network to represent the joint probability of parameters and data without strong assumptions about its functional form. While addressing intractability, we also show that, if the simulator does not represent the system under study well enough, SBI can yield unreliable parameter estimates. Approaches to adopting the SBI framework for cases in which multiple simulator(s) may be adequate are introduced using a performance-weighting approach. The synthetic experiments presented here test the performance of SBI, using the relationship between the surrogate and PB simulators as a proxy for the real case.
- Article
(4581 KB) - Full-text XML
- BibTeX
- EndNote
Robust hydrologic tools are necessary to understand and predict watershed (catchment) behavior in a changing climate (Condon, 2022). This need is underscored by long-term drought in the American West (Williams et al., 2022), which has led to the withering of water supplies from the Colorado River (Santos and Patno, 2022), increased groundwater pumping (Castle et al., 2014), and uncertainty about what is next (Tenney, 2022). Hydrologic simulators that represent physical processes and connections within the hydrologic cycle (Paniconi and Putti, 2015) are very commonly used tools to address these needs. These process-based (PB) simulators explicitly represent hydrologic states and fluxes at multiple scales based upon the physics first principles (Fatichi et al., 2016). Catchment scientists often use PB simulators to answer “what if” questions about the behavior of the catchment snowpack, soil moisture, and streamflow in a changed future, as they encode fundamental processes, not just historical data (Maxwell et al., 2021).
The behavior and skill of these PB catchment simulators (henceforth referred to as PB simulators) strongly depend on spatially varying parameters (Tsai et al., 2021). Parameters represent the structure and physical properties of the hydrologic system, such as the roughness of the land surface (i.e., Manning's coefficient, M) or the water-transmitting properties of the subsurface (i.e., hydraulic conductivity, K). There are many approaches to determine parameters in hydrology (Beven and Binley, 1992; Gupta et al., 1998; Bastidas et al., 1999; Hunt et al., 2007; Vrugt and Sadegh, 2013; White et al., 2020; Tsai et al., 2021). The variety of approaches and long history of research in this area underscores that there is “no obvious formulation [of parameter determination] that previous generations of modelers have overlooked” (Hunt et al., 2007). However, the question of how best to infer parameters for PB simulators remains unsettled.
Parameter determination remains a challenge with respect to catchment PB simulators, thereby resulting in an impediment to robust, physics-informed hydrologic predictions. There are two related and ongoing difficulties that make parameter determination a very challenging problem. The first is the problem of intractability. For a dynamical catchment simulator with a range of possible configurations, many combinations of parameters may be plausible given observed data (Beven, 2012; Nearing et al., 2016). Therefore, many have argued that it may be preferable to simulate distributions of hydrologic variables and the underlying parameters that give rise to them (e.g., Vrugt and Sadegh, 2013). Intractability arises when these distributions cannot be approximated for theoretical or computational reasons. For example, large-scale, high-resolution PB simulations can require massively parallel, high-performance computing (e.g., Maxwell et al., 2015), limiting the number of exploratory simulations due to computational demands. A solution to the problem of intractability needs to efficiently approximate complex distributions of probable parameters given observations with a sufficient level of accuracy and precision.
Deep learning (DL) may provide new opportunities vis-à-vis the intractability problem in parameter determination. In DL, behaviors are learned from data, as opposed to PB approaches, which derive behavior from established theory. The Earth sciences have recently seen greater adoption of DL approaches (Wilkinson et al., 2016), for example, in streamflow prediction (Kratzert et al., 2018). However, DL methods are not widely used in the prediction of distributed catchment variables due to the “inadequacy of available data in representing the complex spaces of hypotheses” (Karpatne et al., 2017), such as catchment observations. Recently, there has been a push for methods that can incorporate process understanding into DL approaches (e.g., Zhao et al., 2019; Jiang et al., 2020). Still, studies that employ DL to improve PB simulator performance by aiding in the hunt for better parameters are rare1. Tsai et al. (2021) used a neural network to learn the mapping between observable attributes and unobserved physical parameters, for a set of catchment rainfall–runoff simulators optimized to a regional loss function. This “differentiable learning” approach can effectively find parameter sets that yield continuity across neighboring domains. While the approach is strong for the spatial generalization of lumped catchment simulators, it does not explicitly address the case in which many parameter sets may be plausible (the equifinality problem), nor does it provide a mechanism to constrain the role of deficiencies in the simulator on parameter estimates.
Simulation-based inference (SBI) is a DL-informed approach to PB parameter determination that has shown promise in particle physics (Cranmer et al., 2020), cosmology (Alsing et al., 2019), and neural dynamics (Lueckmann et al., 2017). In SBI, a neural network is employed to approximate the conditional density of parameters and simulated outputs from the behavior of a simulator. The learned conditional relationship can then be evaluated using observations to estimate a set of probable parameters. Surrogate simulators are neural networks that emulate the complex interdependence of variables, inputs, and parameters encoded in PB simulators, such as catchment simulators (Maxwell et al., 2021; Tran et al., 2021). Once trained, surrogate simulators can closely mimic the PB simulator, run at a fraction of the cost, and speed up the exploration of parameter space. Restated, this approach uses one neural network (the “surrogate”) to quickly generate thousands of simulations that are utilized to train another neural network (via conditional density estimation) to develop a statistical representation of the relationship between parameters and simulated data. Via SBI, this statistical representation can be used to infer distributions of PB parameter values based on observed data. Assuming that the model is correctly specified, the inferred set of parameters accurately and precisely reflects the uncertainty in the parameter estimate (Cranmer et al., 2020). To our knowledge, applications of SBI in hydrology have been limited (e.g., Maxwell et al., 2021). A brief introduction to SBI is presented in Sect. 2.
A second challenge to parameter determination is the problem of epistemic uncertainty arising from limited knowledge, data, and understanding of complex hydrologic processes. The sources of epistemic uncertainty in the modeling process are various and include the following: uncertainties in data (for example, in simulator inputs and misleading information in observed data used to train and assess simulators); uncertainties derived from performance measures and information to omit; and uncertainty about what the structure of the simulator should be, which arises from the inherent challenge of choosing simplified representations of complex processes (Leamer, 1978; Beven and Binley, 1992; Draper, 1995; Gupta et al., 2012; Nearing et al., 2016). For example, the structure of PB catchment simulators is defined by the mathematical description of hydrologic flows, state variables, and parameters. This description may or may not be able to represent catchment behavior without error. DL surrogate simulators trained to mimic PB behavior inherit this assumed structure, in addition to error from imperfect training. In other words, uncertainty about structure arises from both the relationship between the PB simulator and the catchment under study and the relationship between the surrogate and the PB simulators. In this work, we focus on a subclass of epistemic uncertainty in the appropriate simulator (both PB and surrogate) structure(s) known as “misspecification”, in which a unique and optimal description of the catchment is assumed to exist but is unknown. Discounting the role of uncertainty about the appropriate simulator structure can have profound consequences regarding the insights that we draw from inference tasks like parameter determination.
A common challenge is the potential underrepresentation of uncertainty stemming from the choice of simulator structure. This issue becomes evident when inference yields parameter estimates that are overly confident, which can be problematic when a more conservative estimate that accounts for the inherent uncertainties about simulator structure is preferred (Beven, 2012; Cranmer et al., 2020; Hermans, 2022). One potential remedy is to perform inference using multiple simulators, with different underlying structures and fit quality. Once a set of competing simulator structures is assembled, the challenge then becomes deciding how to combine them. Generalized likelihood uncertainty estimation, or GLUE (Beven and Binley, 1992, 2014), associates a measure of belief with each selected simulator structure and parameter configuration, forming a conceptually simple way of weighting ensembles of predictions to estimate uncertainty stemming from various sources. A similar principle underlies Bayesian model averaging, or BMA (Leamer, 1978; Hoeting et al., 1999; Raftery et al., 2005; Duan et al., 2007). While GLUE and BMA differ with respect to their implementations, they both adhere to the principle that simulator structures capable of generating simulation results closely aligned with observations should hold stronger credibility and carry greater significance within an ensemble, whereas simulator structures less capable of producing behavioral simulations should be assigned a low probability or rejected. In the case of GLUE, this measure of credibility is derived from a modeler's choice of metric, or informal likelihood function (e.g., Smith et al., 2008). GLUE and BMA are further described in Sect. 2.
The primary objective of this work is to demonstrate an approach to generating accurate and precise estimates of the spatially distributed parameters of a PB hydrologic simulator where conventional methods might struggle due to the intractability problem. A secondary goal is to explore how this workflow could be extended to yield meaningful parameter estimates considering uncertainty about the appropriate simulator (surrogate or PB) structure. Surrogate-derived SBI is utilized to address the problem of intractability in complex parameter spaces using a statistical, deep-learning approach. The problem of simulator misspecification is confronted using a quasi-BMA approach that utilizes an informal likelihood to weight the credibility of parameter estimates from SBI.
We use synthetic test cases with diagnosable degrees of error to test the performance of the inference workflow. Here, we determine the physical parameters of a headwater subcatchment of the upper Colorado River basin by calibrating a PB simulator to streamflow observations. We utilize SBI in tandem with a long short-term memory (LSTM) surrogate (henceforth referred to as the surrogate simulator) for the PB simulator ParFlow (Jones and Woodward, 2001; Maxwell and Kollet, 2006; Maxwell et al., 2015a) to rapidly generate probable configurations of the hydraulic conductivity (K) and Manning's coefficient (M). Furthermore, we use the inferred distribution of parameters to generate streamflow predictions. The experiments presented use the relationship between the surrogate and PB simulators as a proxy for the real case. We explore the influence of synthetic observations on parameter inference with a set of experiments that systematically vary the degree of error in the simulator (i.e., misspecification). In the latter experiments, a form of BMA is utilized to improve the robustness of the parameter estimates to misspecification; in the extreme case, this is done by assigning zero probability to all models in the set. The experiments are outlined in Sect. 3.1.
Novel aspects of the present analysis that bear noting include the following: (1) the usage of DL in conjunction with a PB catchment simulator to improve its performance; (2) the novel application of density-based SBI to the scientific domain of hydrology; and (3) the usage of informal likelihood measures to directly assign model probabilities to parameter estimates made by SBI in a manner similar to BMA. The significance of this work is to develop a framework to tackle harder inference problems in catchment modeling and in other domains of the Earth sciences where complex PB simulators are used.
This section provides a brief background of methods used for parameter determination in catchment simulation. Context is provided relevant to understanding the “point of convergence” (Cranmer et al., 2020), which we call simulation-based inference (SBI), and how it is similar to and different from some other approaches to inference. We start with a general overview of inference. Next, we discuss the traditional formulation of the inference of parameters using Bayes' theorem (Sect. 2.1). We then introduce what sets SBI apart from these traditional approaches (Sect. 2.2). Next, we discuss the role of machine learning in SBI (Sect. 2.3). Finally, we introduce some approaches to parameter estimation under epistemic uncertainty that have been applied in hydrology (Sect. 2.4). In this section, “simulator” generically refers to a computer program that requires some number of parameters and produces output data; this term encompasses most PB simulators (as well as their surrogates) used in hydrology and other research domains. The term “model” refers to the statistical relationship between parameters and outputs, which is defined implicitly by a simulator (PB or surrogate). We define “inference” as using observations (data) and the statistical model defined by a simulator to describe unobserved characteristics (parameters) of the system that we are interested in (Cranmer et al., 2020; Wikle and Berliner, 2007).
2.1 Bayesian inference
Bayesian inference is a common method to extract information from observations. The essence of this formulation of inference unfolds in three steps (Wikle and Berliner, 2007): (1) formulation of a “full probability model”, which emerges from the joint probability distribution of observable and unobservable parameters; (2) inference of the conditional distribution of the parameters given observed data; (3) evaluation of the fit of the simulator (given parameters inferred in step 2) and its ability to adequately characterize the process(es) of interest.
Traditionally, we apply Bayes' theorem to tackle inference problems. For illustration, let θ denote unobserved parameters of interest (such as hydraulic conductivity) and let Y represent simulated or observed data of the variable of interest (such as streamflow). The joint probability p(θ,Y) can be factored into the conditional and marginal distribution by applying Bayes' rule, such that we obtain
The terms in this expression are as follows:
-
The data distribution, p(Y|θ), is the distribution of data given unobservable parameters. This distribution is referred to as the likelihood when viewed as a function of θ for a fixed Y. The likelihood function of “implicit” simulators (such as those used in catchment hydrology) is often regarded as “intractable”; i.e., its form cannot be evaluated (integrated), at least not in a computationally feasible way (Cranmer et al., 2020).
-
The prior distribution, p(θ), is our a priori understanding of unobservable parameters. The prior often results from a choice made by the domain expert. For example, in catchment simulation, the prior distribution arises from a belief about the possible structures and magnitudes of parameters (for example, hydraulic conductivity) in a study domain as well as the probability that they could be observed.
-
The marginal distribution, p(Y), can be thought of as a normalizing constant or “evidence”. In practice, this distribution is rarely computed, as it contains no information about the parameters. As such, we do not include P(Y) and instead work with the unnormalized density provided by
-
The posterior distribution, p(θ|Y), which is the distribution of unobservable parameters given the data. The posterior is the primary goal of Bayesian inference; it is proportional to the product of our prior knowledge of parameters and the information provided in our observations.
Inference conducted using a Bayesian paradigm has a long history in computational hydrology (Vrugt and Sadegh, 2013). However, applications have been somewhat limited due to challenges centered on the intractability of the data distribution, p(Y|θ), for catchment simulators with many parameters.
2.2 Simulation-based inference
SBI is a set of methods that attempt to overcome the intractability of the data distribution by learning the form of the posterior distribution directly from the behavior of the simulator itself (Tejero-Cantero et al., 2020). There are a range of SBI approaches, some of which include deep learning, although deep learning has traditionally not been part of SBI workflows. The classic approach is approximate Bayesian computation (ABC), which compares observed and simulated data, rejecting and accepting simulation results based on some distance measure (Fenicia et al., 2018; Vrugt and Sadegh, 2013; Weiss and von Haeseler, 1998). While this approach has been widely used, it suffers from a range of issues, including poor scaling to high-dimensional problems (resulting in the need for summary statistics) and uncertainty arising from the selection of a distance threshold (Alsing et al., 2019). Additionally, in traditional ABC, it is necessary to restart the inference process as new data become available (Papamakarios and Murray, 2016), making it inefficient to evaluate large numbers of observations (Cranmer et al., 2020).
SBI methods predicated on density estimation enable an alternative that does not suffer from the same shortcomings as ABC. The density estimation approach aims to train a flexible density estimator of the posterior parameter distribution from a set of simulated data–parameter pairs (Alsing et al., 2019). Some of the key advantages of a density estimation approach over ABC are as follows: (a) it parametrically (as a trained neural network) represents the posterior2 distribution that can be reused to evaluate new data as they become available; (b) it drops the need for a distance threshold by targeting an “exact” approximation of the posterior; (c) it more efficiently uses simulations by adaptively focusing on the plausible parameter region (Papamakarios and Murray, 2016).
One general-purpose workflow that we employ in this paper uses a neural density estimator to learn the distribution of streamflow data as a function of the physical parameters of the simulator and employs active learning to run simulations in the most relevant regions of parameter space (Alsing et al., 2019; Lueckmann et al., 2017). The SBI workflow is further described in Sect. 3.5, while the neural density estimator is described in Sect. 3.6.
2.3 The role of machine learning in SBI
Due to advances in the capacity of neural networks to learn complex relationships, we can learn high-dimensional probability distributions from data in a way that was previously not really possible (Cranmer et al., 2020). This has led to strong claims in other fields, including cosmology and computational neuroscience, regarding the potential of SBI to “shift the way observational [science] is done in practice” (Alsing et al., 2019). While our implementation is described in more detail in Sect. 3, we direct readers to the literature for a broader (Cranmer et al., 2020) and deeper (Papamakarios and Murray, 2016) understanding of density-based SBI.
Learning the full conditional density p(θ|Y) requires many simulated parameter–data pairs: thousands (or hundreds of thousands) of forward simulations. This presents a challenge with some high-resolution PB simulators, as each forward simulation can take hours of computer time to run. Many have noted that surrogate simulators trained using deep learning can help; after an initial simulation and training phase, these simulators can be run forward very efficiently. “Surrogate-derived approaches benefit from imposing suitable inductive bias for a given problem” (Cranmer et al., 2020). In our case, this “inductive bias” is applied by learning the rainfall–runoff response of our PB domain using a long short-term memory (LSTM) simulator, a type of neural network that is suited for learning temporal patterns in data (Kratzert et al., 2018). The surrogate simulator is described in more detail in Sect. 3.3. Surrogate simulators can be used directly in the construction of viable posterior distributions of physical parameters and run at a low cost relative to the PB simulator.
It should be noted that inference is always done within the context of a simulator (Cranmer, 2022). As such, if the simulator structure is not adequate, it will affect inference in undesirable ways. Simulator structural inadequacy arises when a simulator does not capture the behavior of the dynamical system, giving rise to a mismatch between the simulated and observed data (Cranmer et al., 2020). SBI conducted with structurally inadequate simulators can result in overly precise and otherwise erroneous inference. Similar concerns about the quality of inference arise from other potential sources of epistemic uncertainty in the modeling process, such as undiagnosed error in the data used to condition the model.
2.4 Model combination and parameter determination in hydrology
As simulator structural adequacy is not guaranteed, basing inference on one simulator structure alone is risky (Hoeting et al., 1999). Bayesian model averaging (BMA) is an approach developed in the statistical literature (Madigan and Raftery, 1994) to address this problem. BMA creates an updated statistical model by combining two or more competing ones (Roberts, 1965); in the case of dynamical systems, the competing models are defined implicitly by simulators with differing underlying structures. For example, BMA has been adopted to create weighted averages of climate forecasts derived from multiple simulators, each with a different quality of fit to observed data (i.e., Raftery et al., 2005). Similarly, BMA has been used to generate streamflow forecasts taken from several structurally distinct rainfall–runoff simulators (Duan et al., 2006). Results from these analyses show that the weighted combination yields more accurate inference and descriptions of uncertainty than those derived from any one simulator.
BMA is introduced here generically and extended to the current analysis at the end of the section. Consider YObs to be observed data, such as a streamflow time series; a quantity of interest Δ to be inferred, such as a prediction or underlying set of parameters θ; and the set of competing models M1, …, MK. Each model Mk is defined by a simulator with a unique underlying structure, which encodes the simulated data Y for possible values of θ. The probability of Δ in the presence of YObs can be represented as a weighted average, such that
The terms in this expression are as follows:
-
is the posterior distribution of Δ given the model under consideration Mk and YObs, which can be interpreted as the conditional probability of Δ given that Mk is the best model in the set (Raftery et al., 2005);
-
wk is the posterior model probability, or the model weight. This can be interpreted as the posterior probability that model Mk is the best one (Raftery et al., 2005).
Even in relatively simple test cases (i.e., Raftery et al., 1997), the calculation of p(Δ|YObs) is difficult due to the large number of possible models and the computational and conceptual challenges related to wk; therefore, defensible approximation methods are required (Hoeting, 1999). In dynamical systems simulation (i.e., Raftery et al., 2005; Duan et al., 2007), this problem has typically been solved iteratively as an expectation-maximization problem that simultaneously maximizes the likelihood of both and wk, although other approaches have been employed in other domains (i.e., Liu and Ker, 2020).
Generalized likelihood uncertainty estimation (GLUE) is an approach to uncertainty estimation with wide use in hydrology (Beven and Binley, 2014). GLUE recognizes that discrepancies between observed and simulated data often exhibit nonrandom patterns, reflecting the presence of heteroscedasticity and autocorrelation resulting from errors in simulator structure, inputs, and data (Beven, 2012). To account for these uncertainties, GLUE assigns a “measure of belief” to each simulation result, reflecting confidence in its validity. This measure of belief, or likelihood function, may not be formal in the statistical sense, but it serves to express the practitioner's subjective judgment (Beven, 2012). The selection of an appropriate likelihood is crucial, often relying on performance metrics such as the Nash–Sutcliffe efficiency (NSE) coefficient , but its choice depends on the study objective (Smith et al., 2008). Likelihoods are used to develop acceptability limits, weight a set of simulation results, and approximate the uncertainty associated with the inference of parameters. By allowing consideration of multiple simulator structures and developing a clear metric by which to evaluate them, GLUE provides a holistic and flexible framework for parameter estimation in the presence of error related to simulator structure and other epistemic uncertainties (Beven, 2012).
The current analysis adopts a strategy that combines SBI with informal likelihood weighting to address the error related to the simulator structure. This approach involves generating weighted averages of estimated parameter distributions from a set of simulators with different underlying structures using a form of BMA (Eq. 3). Specifically, we take the weighted average of the conditional estimates of p(θ|Y) (Eq. 2) obtained through SBI for a set of surrogate rainfall–runoff simulators. As in GLUE, weights are calculated from a selected performance metric, reflecting the suitability of simulated values given the observed data; simulation results below a predefined limit of acceptability are not considered. The claim is that this method of combination mitigates overconfident inference due to simulator structural inadequacy without diluting the valuable information in the parameter estimates made by SBI. The broader implication is an approach to extend the usage of SBI to situations in which some structural error related to the simulator is inevitable, as is often the case for real systems. We believe that being able to extend SBI in this way could, broadly speaking, be part of a strategy to build a more comprehensive understanding of the inherent uncertainties associated with hydrological modeling approaches. Experiment 4 evaluates whether BMA produces more accurate parameter estimates and realistic parameter spreads compared with standalone SBI. The reader is referred to Sect. 3.8 for implementation details.
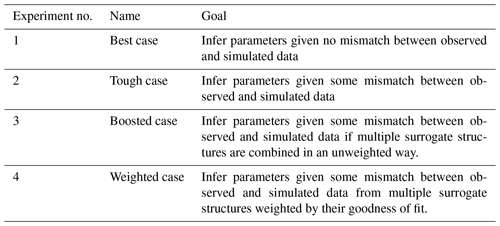
This section describes our implementation of surrogate-derived SBI and the four experiments undertaken to test it. We first introduce those experiments and the goals associated with them (Sect. 3.1). Then, we describe the domain of interest, the Taylor River catchment (Sect. 3.2). The rest of the methods subsections describe the components, implementation, and validation of SBI, as outlined in Table 1.
Figure 1 shows how the components of surrogate-derived SBI are interrelated. In Fig. 1a, a small set of process-based simulations are generated by ParFlow. A LSTM neural network learns from these simulations to mimic the behavior of ParFlow, interpolating the relationship between climate forcings, catchment parameters M and K, and output streamflow time series. The LSTM network can be used as a ParFlow surrogate to quickly explore the streamflow response to different parameter configurations and forcing scenarios. Throughout the rest of the paper, we will refer to ParFlow as the PB simulator and the LSTM network as the surrogate simulator or the LSTM.
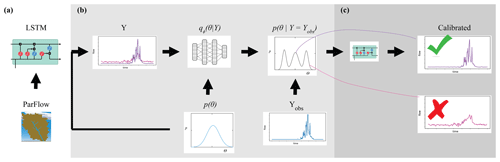
Figure 1An illustration of surrogate-derived simulation-based inference (SBI). In subplot (a), a long short-term memory (LSTM) neural network learns catchment behavior from ParFlow, a process-based simulator. The implementation of SBI is shown in subplot (b), where the objective is to estimate catchment parameters θ given an observation YObs. This parameter estimate is formally known as the posterior parameter distribution . We randomly sample many parameter configurations from a prior distribution p(θ) and, from the LSTM, simulate an equivalent number of streamflow time series Y. This set of simulated parameter–data pairs is used to train a neural density estimator qϕ(θ|Y). Subplot (c) shows the posterior predictive check, which involves using the parameter estimate to (ideally) generate a calibrated set of simulations.
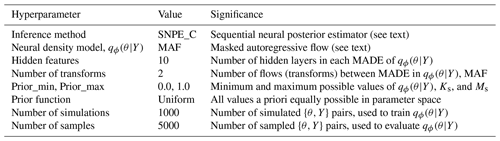
We leverage the efficiency of the surrogate to conduct SBI on parameters, as depicted in Fig. 1b. Our goal with SBI is to estimate probable values for the catchment parameters M and K given the occurrence of a particular streamflow observation. To that end, we randomly sample many (n=5000) parameter configurations from a prior distribution p(θ) and, from the LSTM, simulate an equivalent number of streamflow time series Y. This set of simulated parameter–data pairs is used to train a neural density estimator qϕ(θ|Y), which is a deep learning model of the full conditional density of parameters given data p(θ|Y). Once trained, the neural density estimator is evaluated with a given observation to produce a distribution of parameters, the posterior distribution , which represents our “best guess” of what the parameters should be. The prior distribution and other details of the density estimation approach are described in Table C1 and Sect. 3.5.
Finally, a predictive check (Fig. 1c) ensures that the parameter estimates generate a calibrated surrogate simulator. The simplest version of this check is to put the estimates of parameters from the previous step back into the LSTM, which generates a new ensemble of streamflow simulations. The simulations should resemble the observation closely if the simulator captures the behavior of the dynamical system well and if the parameter inference was done correctly. Optionally, the parameter estimates may be weighted using a performance evaluation of the predictive check.
3.1 Experiments
We explore the performance of SBI using four experiments. The subject of interest is the ability of SBI to accurately and precisely estimate parameters given observations under varying conditions of uncertainty. The uncertainty comes from error related to the structure of the surrogate simulator. Synthetic observations with known parameters are used to conduct the experiments, as they are easier to benchmark; for completeness, the analysis is extended to actual catchment data in Appendix E. To test SBI, we first draw the synthetic observations from the surrogate simulator and then from the harder-to-match PB simulator. Strategies to address uncertainty regarding the simulator structure and the effect on parameter estimates are presented in the final experiments. The experiments are further described in Table 2 and below, while the results are explored in Sect. 4.
Briefly, the four experimental cases are as follows:
-
“Best” case – find . We use the streamflow generated by a surrogate simulator (e.g., with a given combination of parameters) as the observation and employ SBI to infer the parameters. Because we are treating the simulator as observations in this case (i.e., we assume that the simulator can generate data identical to the observation), no uncertainty exists about the structural adequacy of the simulator. This experiment serves as a baseline check for our SBI workflow.
-
“Tough” case – find . We use a ParFlow simulation as the observation and employ SBI to infer the values of the parameters. As there is a slight mismatch between observed (in this case ParFlow simulation) and simulated (i.e., the surrogate simulator) data, there is some uncertainty about the structural adequacy of the surrogate simulator. This experiment tests whether the proposed framework, where SBI is carried out with the surrogate simulator, can be successful given misspecification of the surrogate.
-
“Boosted” case – find more accurate . Building from the Tough case, we again use a ParFlow simulation as the observation but, instead, employ an ensemble (“boosted”) surrogate simulator to infer the known parameters. Unlike in the Tough case, multiple forms of the surrogate simulator are considered to represent uncertainty about the appropriate structure. In this case, we are testing whether the proposed framework can be made more robust to surrogate misspecification if multiple surrogate structures are combined in an unweighted way.
-
“Weighted” case – find the Bayesian-model-averaged , w). Building from the Boosted case, we add a performance measure (e.g., informal likelihood) to emphasize (“weight”) credible and reject implausible forms of the surrogate simulator that have been identified by SBI. Unlike in the Boosted case, uncertainty regarding the adequacy of surrogate simulator structures and configurations is explicitly evaluated using the likelihood weighting. This experiment tests whether the proposed framework is more robust to surrogate misspecification if competing surrogate structures are weighted based on the fit between simulated and observed data.
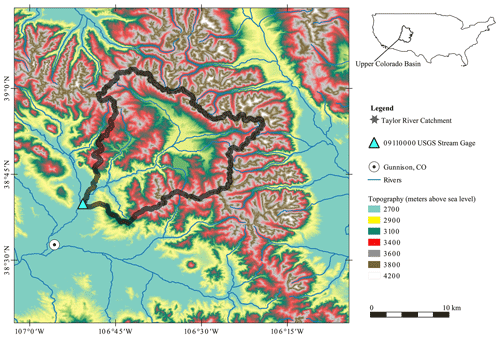
3.2 Taylor River – the domain
The physical area of study is the Taylor River headwater catchment located in the upper Colorado River catchment (Fig. 2). The Taylor is an important mountain headwater system for flood control and water supply in the upper Colorado River catchment (Leonarduzzi et al., 2022). This catchment is at an elevation of between 2451 and 3958 m above mean sea level and has a surface area of around 1144 km2. This catchment is a snowmelt-dominated regime in summer. The geographical extent of the catchment is defined by the United States Geological Survey (USGS) streamflow gage in Almont (ID 09110000), Colorado, at the catchment outlet. Over the full period of record (1910–2022), the lowest average monthly discharges were recorded in January and February, with values of approximately 100 cfs (cubic feet per second; equal to approximately 3 m3 s−1), after which there was a steady increase in discharge and general wetness in the catchment up until June, when an average discharge of approximately 900 cfs (25 m3 s−1) was recorded. Synthetic data corresponding to the Almont gage (ID 09110000) location are used for experiments 1–4, as described in Sect. 3.1. Observed streamflow data from water year 1995 are revisited in Sect. 5 and Appendix E.
3.3 The process-based simulations (ParFlow)
We use the integrated hydrologic simulator ParFlow-CLM to simulate groundwater and surface water flow in our domain. ParFlow-CLM is designed to capture dynamically evolving interactions among groundwater, surface water, and land surface fluxes (Jones and Woodward, 2001; Maxwell and Kollet, 2006; Maxwell et al., 2015a). In the subsurface, variably saturated flow is solved using the mixed form of Richards equation. Overland flow is solved by the kinematic wave approximation and Manning's equation. ParFlow is coupled to the Common Land Model (CLM). The CLM is a land surface model that handles the surface water–energy balance (Maxwell and Miller, 2005; Kollet and Maxwell, 2008). Thus, it is well-suited to examine evolving catchment dynamics at the large scales (e.g., Maxwell et al., 2015b), as in the Taylor River catchment in Colorado, USA.
The Taylor catchment is represented by ParFlow at a 1 km resolution, comprising five vertical layers with a total depth of 102 m (Leonarduzzi et al., 2022). As in Leonarduzzi et al. (2022), all of the required input files – including soil properties, land cover, and meteorological forcings – are subset from upper Colorado River catchment ParFlow-CLM simulations of Tran et al. (2022). The subsurface contains 23 separate soil and geological units.
We explore the sensitivity of streamflow to an ensemble of different configurations of Manning's roughness coefficient (M) and the hydraulic conductivity (K). For the baseline configuration of the simulator, K ranges between and (m h−1) across the 23 spatial units; M is constant across the domain surface at (h m). An ensemble of 183 simulations is generated by systematically varying M and K. For M, as the values are spatially constant, it is easy to adjust this single value. K is spatially variable; therefore, we apply a single scaling factor to all three dimensions (Table A1). To make the distinction clear, we call these “single” scalar representations Ks and Ms, respectively. The values Ks and Ms used in this study are shown in Table A2. A sensitivity analysis of streamflow to parameter configurations is shown in Fig. A1.
All simulations are run for a 1-year period (8760 h) using forcings from water year 1995 taken from Tran et al. (2020). Surface pressure outputs are converted to runoff using the overland flow utility built into ParFlow. This study focuses on runoff at the cell closest to USGS gage ID 09110000. We convert to cubic feet per second for direct comparison to gaged data and rescale from zero to one. Streamflow simulations from ParFlow are relatively more sensitive to changes in K compared with changes in M, as shown in Fig. A1. The relatively small size of the ensemble is due, in part, to the computational demand of ParFlow. The time for each ParFlow simulation was 28 min. As there are 183 simulations in the ensemble, the total simulation time was about 85 h. All simulations were undertaken in the Princeton Hydrologic Data Center (PHDC) on NVIDIA A100 GPUs. The purpose of generating this ParFlow ensemble is not to create the most diverse set of system realizations; rather, we seek to provide a foundation from which to train the surrogate simulator and test performance of the simulation-based inference approach.
3.4 The surrogate simulator (LSTM)
We employ a long short-term memory (LSTM) network to learn from our process-based simulator ParFlow. LSTM networks are neural networks that are designed to learn temporal relationships (Rumelhart et al., 1986; Hochreiter and Schmidhuber, 1997). These networks are widely used for predictive tasks in hydrology, for example, to relate meteorological forcing sequences (Kratzert et al., 2018) to catchment streamflow. In our study, an LSTM network learns the response of streamflow at gaged location ID 09110000 to forcings and parameters in the Taylor River catchment, as defined by the ensemble of ParFlow simulations described in Sect. 3.3.
Throughout our experiments, we used an LSTM network with 10 input features, containing forcings X and parameters θ, and one output class, containing streamflow Y. As in Kratzert et al. (2018), we employ a “look-back” approach. For each sample, the LSTM network ingests a sequence length of “l” =14 d of previous forcings weighted by scalar representations of ParFlow parameters (Ks and Ms) and returns streamflow the next day. More explicitly,
where Yt+1 is the streamflow the next day; l is the look back, which controls the length of the input sequence used for prediction; are vectors containing sequences of forcing data from today (i.e., day t) back to day t minus l for each of the eight forcing variables; and Ks and Ms are scalar representations of the ParFlow parameters' hydraulic conductivity (K) and Manning's roughness (M), respectively. As these values do not vary over time, each is ingested as a vector repeated l times by the LSTM model.
The relevant hyperparameters used to fit the LSTM surrogate are further defined in Tables A1 and B1. The computational cost of the LSTM is much less than the cost of ParFlow. The time for training the LSTM is around 15 min in the PHDC. Once trained, simulation from the LSTM is low cost (less than s). Figure B1a shows the distribution of training–validation and test sets across parameter space, and the performance of the LSTM relative to ParFlow on a streamflow time series generated by a randomly selected test parameter set, θA, is used throughout the results section for benchmarking. Hyperparameters were determined by trial and error. The LSTM captures the general streamflow behavior quite well, although not quite perfectly (Fig. B1b). The Kling–Gupta efficiency (KGE) exceeds 0.7 for test data reserved from ParFlow. We emphasize that the goal here is to produce a surrogate simulator adequate for the simulation-based inference of parameters Ks and Ms.
3.5 Implementation of simulation-based inference
The goal of SBI is to infer appropriate values flexibly and efficiently for simulator parameters, given a particular observation. SBI is illustrated in Fig. 1b. Take θ to be a vector of parameters that control a simulator, and let Y be a vector of simulated data. The simulator implicitly defines a conditional probability p(Y|θ), which may be analytically intractable. p(θ) encodes our prior beliefs about parameters. We are interested in inferring the parameter θ given an observation YObs, i.e., we would like to know the posterior probability density , following Papamakarios and Murray (2016):
where θ contains Ks and Ms, and YObs is an observed streamflow time series. Y is a set of simulated outputs that are formally equivalent but not identical to the observation YObs. Here, parameter–data pairs are simulated by a surrogate (Sect. 3.4) of ParFlow. Simulations are drawn from the same forcing scenario to limit the degrees of freedom of parameter inference.
A conditional density estimator qϕ(θ|Y) learns the posterior density directly from simulations generated by the surrogate. qϕ is a learnable model – often a neural network – that fits to p(θ|Y) and can be evaluated to approximate ; the reader is referred to Sect. 3.6 for details about qϕ. The procedure can be summarized as follows, after Papamakarios and Murray (2016):
-
Propose a prior set of parameter vectors {θ}, sampled from p(θ).
-
For each θ, run the simulator to obtain the corresponding data vector, Y.
-
Train the neural density estimator qϕ(θ|Y) on the simulated set from {θ,Y}.
-
Evaluate qϕ at observed data vector YObs to generate a posterior set of parameter vectors {θ} proportional to .
The SBI workflow and architectures used in this study are derived from a Python toolbox for simulation-based inference (Tejero-Cantero et al., 2020). We direct the reader to Papamakarios and Murray (2016) for a detailed description of the structure, training, and evaluation of a neural conditional density estimator for simulation-based inference. Others (Lueckmann et al., 2017; Greenberg et al., 2019) have built on this idea to introduce Markov chain Monte Carlo (MCMC)-like approaches to sequential learning of the posterior at observations to make inference more efficient. We employ a sequential learning procedure in our workflow, as described in Appendix C2. The hyperparameters and architectures used in SBI are shown in Table C1.
3.6 Neural conditional density estimators for SBI
The conditional density estimator qϕ(θ|Y) is an essential ingredient of SBI. The neural conditional density estimator differs from conventional neural networks (such as the LSTM) in two important ways: first, it learns a conditional probability distribution, as opposed to a function; second, it represents the inverse model – the probability of parameters given data p(θ|Y) – as opposed to the dependency of data on parameters, which is encoded in “forward” simulators like ParFlow and its surrogate, the LSTM. Once trained, the neural conditional density estimator is evaluated with an observation to infer a distribution of plausible parameters, the posterior distribution (Fig. 1b).
Conditional density estimators create a model for “a flexible family of conditional densities”, parameterized by a vector of parameters (ϕ) (Papamakarios and Murray, 2016). Density estimator parameters are not to be confused with the parameters of PB simulators, θ. The latter are the target of inference, whereas the former parameterize the density-estimated posterior probability and must be learned or derived to conduct inference of simulation parameters. Deep neural networks provide new opportunities to learn ϕ for complex classes of densities, which gives rise to the term neural conditional density estimator.
Mixture density networks (MDNs) are an intuitive class of conditional density estimators capable of modeling any arbitrary conditional density (Bishop, 1994). They take the form of a mixture of k (not hydraulic conductivity, K) Gaussian components, as shown below.
where the mixing coefficients (α), means (m), and covariance matrices (S) comprise the neural density parameterization, ϕ. They can be computed by a feedforward neural network.
Training an MDN is a maximum likelihood optimization problem (Bishop, 1994). Given a training set of N simulation parameters and data pairs, {θ,Y}, the objective is to maximize the average log probability (or minimize the negative log probability) with respect to the parameters, ϕ.
For a fuller description of the parameterization and training of neural density estimators, the reader is referred to the supplementary material in Papamakarios and Murray (2016) or the original write-up in Bishop (1994). This study uses a specialization of this family of neural networks called a masked autoencoder for density estimation (further described in Appendix C1).
3.7 Posterior predictive check
A crucial diagnostic step in the SBI workflow is to check the ability of the simulator to characterize process(es) of interest after inference has been conducted (Cranmer et al., 2020). To be more explicit, this step checks that parameters from the inferred posterior can simulate streamflow data (Y) consistent with the observation (YObs) when plugged back into the simulator. The simulated data should “look similar” to the observation (Tejero-Cantero et al., 2020). Gabry et al. (2019) describe this type of evaluation as a posterior predictive check. This predictive check is represented by Fig. 1c.
Here, we conduct posterior predictive checks by drawing a small number of parameter sets from our inferred parameter posterior density. In our workflow, the inferred posterior parameter density is represented by an array containing thousands (n=5000) of plausible parameter sets. The frequency of their occurrence is probability weighted, in the sense that there are very few occurrences of parameter sets in the tails of the distribution and many occurrences close to the mean, and improbable parameter sets do not exist at all. For our posterior predictive check, we randomly sample (n= 50) parameter sets from this frequency-weighted parameter posterior array. We use these parameter samples to generate an ensemble of predicted streamflow time series using the LSTM.
3.8 Calculation of weights
Bayesian model averaging (BMA) is a method of combining different simulator structures to reduce the risk of overfitting on prediction or inference (Madigan and Raftery, 1994). The implementation explored here uses an informal likelihood measure to assign probabilities, or weights, to the SBI-derived parameter estimates of some number of simulators. Note that the simulators could be PB or surrogates. The structure of each simulator may be unique, in that the mathematical description of the relationship between streamflow and the parameters θ differs. Specifically, the sets of parameters estimated by SBI are resampled using weights based on the fit of observed and simulated streamflow to estimate a new probability density. Given a set of K models ( defined implicitly by the simulators considered, this weighted estimated density p(θ|YObs, wk) is as follows:
where is equivalent to the posterior parameter density, from SBI (Eq. 5), and wk is the model probability or weight, which is based on the goodness of fit of simulated data from the posterior predictive check. All probabilities are implicitly conditional on the set of all models considered.
In the current application, weights are calculated using the informal likelihood Lik for simulations drawn from the posterior predictive check. Simulations are defined as values for the parameters θ and resulting simulated data Y. The informal likelihood is a measure of acceptability for each simulation result based on its error relative to observed data. Simulations with likelihood measures below a predefined limit of acceptability are rejected; the set of remaining simulations is assumed to be equally probable prior to weighting. Weights for each simulator in the set K of structures, each composed of a set of I simulations, is equal to
The informed reader will recognize disagreement and inconsistent usage in the literature about the likelihood function (Beven, 2012; Nearing et al., 2016). We acknowledge legitimacy in all camps, but we adopt a subjective, or informal, likelihood here, as sometimes used in generalized likelihood uncertainty estimation (GLUE). We choose to use the Kling–Gupta efficiency (KGE; Gupta et al., 2009) as the likelihood metric due to its utility and history with respect to rainfall–runoff simulation. Furthermore, we note that the method is not dependent on a specific metric, and others could apply this approach using a different metric if they choose. The KGE metric is computed using the following equation:
where α is the ratio of the standard deviation of simulated and observed streamflow data, respectively; β is the ratio of their means; and ρ is the correlation coefficient in time.
The weighted probability density is estimated using a distribution-sampling algorithm, where the distribution represents the weights of each simulation i under each simulator k. Simulation indices are sampled by mapping a random target probability between zero and one to the cumulative distribution of simulation weights. This approach can be used to sample sets of parameters from the SBI-inferred posterior parameter density weighted to high-likelihood simulations identified by the posterior predictive check.
3.9 Evaluation metrics
The performance of simulation-based inference is evaluated in terms of accuracy and precision. First, we evaluate performance with respect to the parameter posterior (the inferred parameters). Following this, we evaluate it with respect to the posterior predictive check (the ability to generate realistic data using the inferred parameters).
3.9.1 Evaluating the posterior parameter density
Accuracy of parameter inference is evaluated using the Mahalanobis distance, DM(θTrue). The Mahalanobis distance measures the distance between a point and a distribution of values, following Maesschalck et al. (2000), such that
where θTrue is the set of observed or “true” parameters, θμ is the mean of the posterior distribution , and Σ is the covariance matrix of . In essence, the Mahalanobis distance measures how far off our parameter estimate is from the “truth”. For this study, values less than 2 are defined as acceptable (within ∼ 2 standard deviations); this threshold was identified via trial and error.
The precision of parameter inference is evaluated in terms of the determinant of the covariance matrix of the inferred parameter posterior, . The determinant can be interpreted geometrically as the “volume” contained by the covariance matrix (and, by extension, the inferred parameter posterior distribution). Larger determinant values are less precise, whereas smaller values more precise (Margalit and Rabinoff, 2017). In this study, we define values of less than 10−6 as acceptable; this threshold was identified via trial and error.
3.9.2 Evaluating the posterior predictive check
We evaluate the ability of the simulated ensemble of streamflow to adequately characterize the observed streamflow using the root-mean-square error (RMSE) between each (n=50) simulated streamflow time series (Y) and the observed streamflow time series (YObs). The RMSE is calculated for each predication as the square root of the mean-squared error, such that
where is the simulator-predicted streamflow at time t, taken from Ypred; is the observed or true streamflow at time t, taken from YObs; and T is the number of times (days) in the streamflow time series.
Accuracy of the simulator characterization of streamflow is assessed as the mean of the RMSE calculated for all (n=50) Y relative to YObs (RMSEAve). Precision of the simulator characterization of streamflow is assessed as the standard deviation of the RMSE calculated for all (n=50) Ypred relative to YObs (RMSESD). For both the mean and variance, RMSE values of less than 0.01 (scaled streamflow units), identified via trial and error, are acceptable. The RMSE was selected to evaluate the posterior prediction out of convenience. Other metrics, such as the KGE, could also be used.
Here, we present the outcomes of the three experiments described in Sect. 3.1. The first two experiments showcase inference problems that increase in difficulty from the easy Best case (Sect. 4.1) to the hard Tough case (Sect. 4.2). The final experiments offer workarounds by way of the Boosted case (Sect. 4.3) and Weighted case (Sect. 4.4). The performance of the methods explored in the three experiments is first discussed in terms of one shared benchmark scenario. Then, we show the results of the three experiments on a larger shared set (n= 18) of benchmark scenarios (Sect. 4.5).
4.1 Experiment 1 – Best case
For the Best scenario, we attempt to infer the parameters of synthetic observation(s) taken from the trained surrogate simulator, such that . We first infer the parameters of just one randomly selected streamflow observation, denoted with an “A” (YObs_LSTM_A). The set of benchmark parameters (θA) used to generate the underlying simulation are approximately 0.60 for Ks and 0.85 for Ms. θA is also our benchmark in parameter space for experiments 2 and 3.
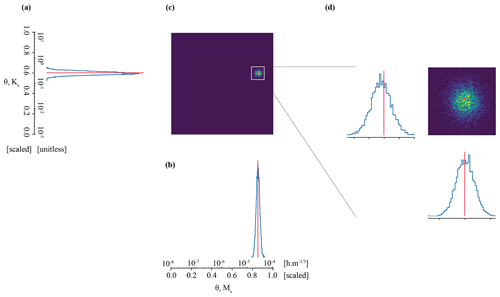
Figure 3The posterior parameter estimate for observation YObs_LSTM_A closely matches the true parameter values in the Best case. Subplots (a), (b), and (c) comprise a pair plot of posterior densities across the full possible parameter space; subplot (d) is zoomed in for detail. The posterior density of (a) MS and (b) Ks are shown individually; they are also shown together in subplot (c). Axes are expressed in both the scale/transformed and unscaled units of the parameters. The “true” parameters are denoted by the red line or circle.
We accurately and precisely estimate parameters for our benchmark case (Fig. 3). The pair plot approximates the posterior parameter density evaluated by the neural density estimator at the observation. In individual parameter space, narrower peaks (in blue) correspond to more confident and precise parameter estimates. In shared parameter space (Fig. 3c), zones of deep purple are effectively zones of no probability; zones of blue–green–yellow are zones of high probability. The benchmark parameters (i.e., the parameters used to generate the simulation) are denoted by the red line or circle. Accuracy is evaluated by the Mahalanobis distance, which is ; thus, the true parameter set can be thought of as less than 1 standard deviation from the central tendency of the inferred distribution. Precision is estimated by taking the determinant of the covariance matrix. The determinant of the covariance matrix is . This is well below our threshold of for sufficiently precise parameter inference.
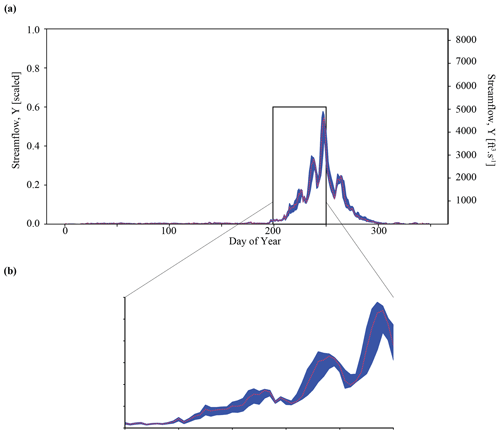
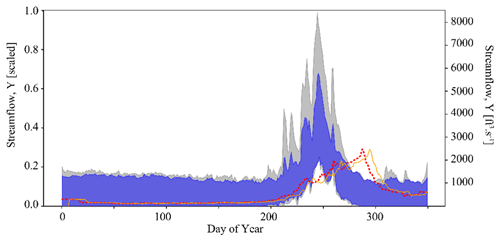
Figure 4Results of the posterior predictive check on synthetic observation YObs_LSTM_A in Experiment 1 (Best case). Subplot (a) shows streamflow simulations resulting from inference of . The ensemble of predictions is bounded by blue, whereas observations are shown in red. Blue lines represent time series of upper and lower streamflow values in this ensemble, and the red line represents the observation YObs_LSTM_A. In subplot (b), we zoom into the area of greatest uncertainty between days 200 and 300, corresponding to the spring snowmelt.
Taking this one step further, we can use the inferred parameter distributions to generate an ensemble of streamflow simulations using the LSTM and compare this to the observed streamflow (referred to as our posterior predictive check). As show in Fig. 4a, the inferred parameters generate simulation results that characterize the observed streamflow observation reasonably well. Greater uncertainty exists around higher streamflow values over the course of the water year, as shown by the increasing width of the uncertainty envelope after day 200 (Fig. 4b). Note that this is the time of year during which snowmelt occurs in the Taylor River catchment. The mean and standard deviation of streamflow error are approximately and (scaled streamflow units), respectively.
Inference for many observations
In addition to conducting this analysis for one observation (as described), an advantage of SBI is the low computational expense of evaluating new observations. Process-based simulations (i.e., ParFlow) are slow and scale linearly with the number of simulations. It takes ∼105 times longer to generate a ParFlow simulation (1680 s) than to evaluate one observation YObs using a trained neural density estimator (0.045 s) on a high-performance computer system allocation of one CPU node with 4 GB of working memory. Put another way, after an upfront sunk cost to learn the distributions, we can evaluate new observations, YObs, practically for free. Many other parameter determination techniques are not “amortized” in this way (Cranmer et al., 2020). For example, approximate Bayesian computation (ABC) requires restarting most steps in the inference process when new data become available (Vrugt and Sadegh, 2013). This property of SBI can be handy in domains where the system structure (parameters) stays the same but new observations become available all the time – as can be the case in catchment hydrology. In Appendix D, we extend Experiment 1 to evaluate the posterior parameter density for many synthetic observations (YObs_LSTM_i).
4.2 Experiment 2 – Tough case
Experiment 2 is our Tough case. We attempt to infer the parameters of synthetic observations from ParFlow, such that . We do this using the same realization of the neural density estimator from Experiment 1 (the Best case). The Tough case is a realistic test of the robustness of parameter inference. Specifically, it tests our ability to evaluate data from a different source. In contrast to the Best case, we must deal with uncertainties related to the goodness of fit between the simulator (the LSTM surrogate) and observation (the underlying ParFlow simulator). We generate the posterior parameter and predictive densities for the benchmark case (θA) explored in Experiment 1. The only difference is that YObs_ParFlow_A is a simulation generated by ParFlow, not by the surrogate.
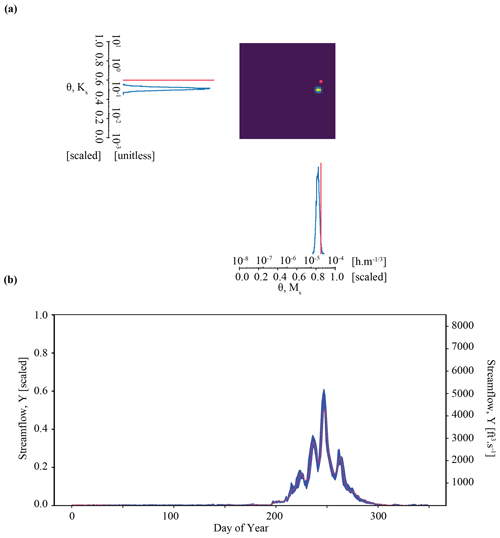
Figure 5Results of the parameter inference and posterior predictive check on synthetic observation YObs_ParFlow_A in Experiment 2 (Tough case). Subplots (a) and (b) show an overconfident parameter inference that still results in a well-constrained posterior predictive check.
Figure 5 plots the results of Experiment 2. Here, we see that the quality of inference is somewhat degraded for the Tough case compared with the Best case. Parameter inference here is overconfident; it is precise but biased, as indicated by the tight probability distributions and the difference between the peak probability and the observation (indicted by the red line in Fig. 7a). The true parameter value does not plot in the area corresponding to highest probability. The determinant is , which is within the same order of magnitude as the Best case. However, the Mahalanobis distance is much higher, at 7. Thus, the true parameter set can be thought of heuristically as approximately 7 “standard deviations” from the central tendency of the inferred distribution. Visual inspection of Fig. 7b shows that streamflow simulations yielded by inferred parameters still characterize the synthetic streamflow observation well. However, average error is roughly twice as high for the Tough case compared with the Best case ( compared to ), which is approximately equal to the acceptability criterion described in Sect. 3.7.
Overconfident posterior estimates are a result of the misfit between our LSTM surrogate and ParFlow (Fig. B1b). One interpretation of overconfident parameter inference is that the relationship between data (streamflow) and parameters (Ms, Ks) in the LSTM surrogate does not quite represent their relationship as it exists in ParFlow. These differences are not unexpected, because ParFlow has parameters that vary across a 3D domain but are lumped together in the LSTM (see also Appendix A). This bias in the surrogate simulator increases the possibility of overconfidence in the conditional density learned by the neural density estimator. We consider this suboptimal performance in parameter inference a consequence of surrogate misspecification, as described further in Sect. 6.
4.3 Experiment 3 – Boosted case
To prevent overfitting by the neural density estimator and circumvent overconfident parameter posteriors, we may use multiple “weak” LSTM surrogates as opposed to one “strong” surrogate. We utilize an ensemble of surrogate LSTM simulators with distinct bias stemming from surrogate misspecification subject to the initialization and selection of training data. That ensemble is then used to generate the set of simulated pairs {θ,Y} to train a new neural density estimator. The underlying principle is that the overall behavior of an ensemble of surrogate simulators in aggregate may not be biased, even if each individual simulator has its own bias.
Experiment 3 is our Boosted case. As in Experiment 2, we attempt to infer the parameters of synthetic observation(s) reserved from ParFlow, . As opposed to experiments 1 and 2, we learn the conditional probability from an ensemble of 10 surrogate LSTM simulators instead of just 1. We refer to the LSTM ensemble as a boosted surrogate. Compared with the LSTM used in experiments 1 and 2, these LSTM networks are trained for fewer epochs (100 compared with 300) and on a smaller random split of the data (0.7 compared with 0.6). The reserved test data are the same across the LSTM networks for experiments 1, 2, and 3. Note that we do not use an adaptive learning algorithm such as AdaBoost (Freund and Schapire, 1997); instead, we equally weight each weak LSTM simulator. The neural conditional density estimator is trained by taking a random draw from the ensemble of LSTM networks and using the selected LSTM network to generate a forward simulation of streamflow from a randomized parameter combination. Thousands of such draws are repeated until the conditional density has been sufficiently learned (see Appendix B for details), at which point it can be utilized for parameter inference.
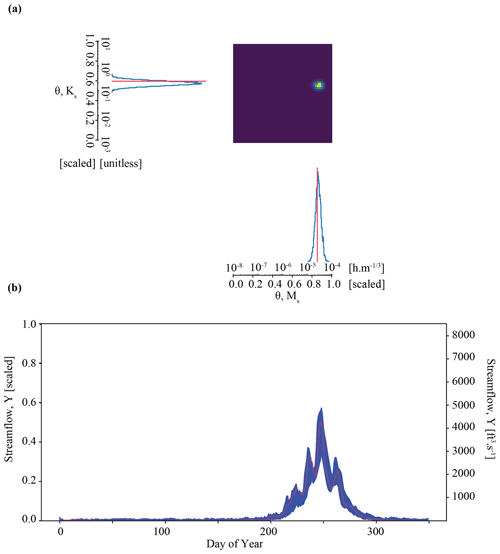
Figure 6Results of the parameter inference and posterior predictive check on synthetic observation YObs_ParFlow_A in Experiment 3 (Boosted case). Subplots (a) and (b) show an accurate parameter inference that is somewhat less precise, resulting in a wider, although still well-constrained, posterior predictive check.
Results of the Boosted case in Experiment 3 show that we may be able to work around the issue of overconfident posteriors encountered in the Tough case in Experiment 2. Figure 6a shows precise and accurate parameter inference for our benchmark case in Experiment 3. The benchmark parameter values are in the area identified by the highest probability, as opposed to in Experiment 2. We note that the area of highest density is somewhat larger than in Experiment 2. The determinant is , which is about an order of magnitude higher than the Tough case (). The Mahalanobis distance is 1. For comparison, the Mahalanobis distance in the previous “overconfident” experiment was 7. The inferred parameters generate streamflow simulations that characterize the synthetic streamflow observation well, as shown by the posterior predictive check (Fig. 6b). We note that, compared with Experiment 2 (Fig. 5b), our simulations are somewhat more variable, as shown by the larger distance between the minimum and maximum simulated data. The average streamflow error is about twice as high for the Boosted case compared with the Tough case ( compared with ). The standard deviation of the error is also greater ( compared with ). The sacrifice of precision with respect to both parameter inference and the posterior prediction is a consequence of using an ensemble of surrogates to simulate each parameter set.
4.4 Experiment 4 – Weighted case
In the preceding experiment, we aimed to rectify overconfident parameter estimates arising from SBI due to surrogate misspecification. Adding an informal likelihood measure to the inferential paradigm may help to address the issue of overconfident parameter estimates by decreasing the importance of low-credibility simulator structures. Experiment 4 demonstrates our Weighted case. As in experiments 2 and 3, we attempt to infer the parameters of synthetic observation(s) reserved from ParFlow, . We extend the competing set of surrogate simulators from Experiment 3, each with distinct misspecification relative to ParFlow, to train a set of neural density estimators. These are evaluated with the synthetic observations to generate posterior parameter estimates and the associated posterior predictive check for each simulator considered. As opposed to experiments 1, 2, and 3, we use the KGE of the simulated data drawn from the posterior predictive check to weight the importance of each set of inferred parameters. The added metric, the informal likelihood, emphasizes credible simulator structures and simulations (values for parameters θ and resulting simulated data Y) and safeguards against those that deviate significantly from observations. Simulations scoring less than persistence (defined by setting next week's predicted data equal to today's observed data) are considered not to be credible and are assigned a weight of zero. The weights, w, are used to condition sampling from . Weighted sampling yields a new set of inferred parameters , w). We term this quantity the weighted posterior parameter density, an output of the methodology described in Sect. 3.8.
Table 3 characterizes the parameter estimates from the set of competing surrogate simulators and posterior density estimates for the benchmark scenario, YObs_ParFlow and θA. Each simulator is a separate row, with the resultant weighted outcome last. Some surrogate simulators are more credible than others, where credibility is represented by the average KGE of simulated data taken from the posterior predictive check for each surrogate. The average KGE (second column in Table 3) for most simulators clusters above 0.90, and this value is near a perfect match (value of 1) for simulators 7 and 9. Simulators 3 and 6, with average KGE values below 0.80, are generally less credible. The weighted KGE of 0.94 (bottom row in Table 3) indicates that the performance of the weighted outcome most closely resembles the most-credible simulators, but it also incorporates information from less-credible ones.
Table 3Calculation of the weighted posterior density from a set of competing surrogates for baseline synthetic observation YObs_ParFlow_A.
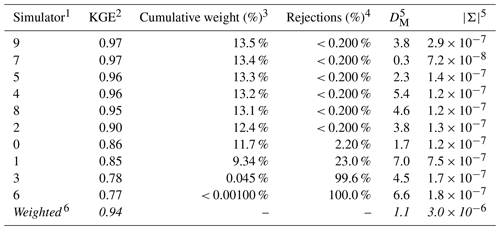
1 Competing surrogate simulators and the probability densities that they implicitly define (n=10). 2 Average Kling–Gupta efficiency (KGE) calculated from unweighted posterior predictions. 3 Each posterior predictive simulation is weighted by the associated KGE; simulation weights are zero if values are poorer than persistence (KGE < 0.81). The value in this column is the sum of the individual weights of 5000 predictive simulations taken for each surrogate. 4 Count of rejected (zero-weight) simulations divided by the total number of simulations for each surrogate. 5 The Mahalanobis distance, DM, and determinant, , calculated by comparing θ, Ms= 0.85, and θAKs= 0.60 to the unweighted parameter posterior for each surrogate 6 The weighted posterior parameter density , derived by resampling the posterior densities using individual weights. The use of italics indicates a summary value for each column of the other rows.
The simulator weights, which are calculated from individual simulation KGE values, are presented in the third column of Table 3. The simulators that produce many credible simulations have a higher weight. Because predictive checks from simulators 8, 4, 5, 7, and 9 contain an equivalent number of credible simulations, they are nearly equally weighted. Surrogates 1, 3, and 6 have many rejected simulations, which are assigned a weight of zero. The percentage of simulations drawn from the posterior predictive check for each simulator with a KGE value less than the limit of acceptability (0.81) is shown in the fourth column.
The relative accuracy of parameter estimates is presented in the fifth column of Table 3 as the Mahalanobis distance, DM, of the posterior parameter density for each surrogate. The parameter estimates derived from the weighted posterior density are more accurate than those drawn from all but Simulator 7. This increase in accuracy reflects, in part, that more highly weighted members are associated with more-accurate parameter estimates compared with those with lower weights. Note that the weighted parameter estimate is also less precise compared with that of the individual surrogates, as represented by the determinant in column six of Table 3.
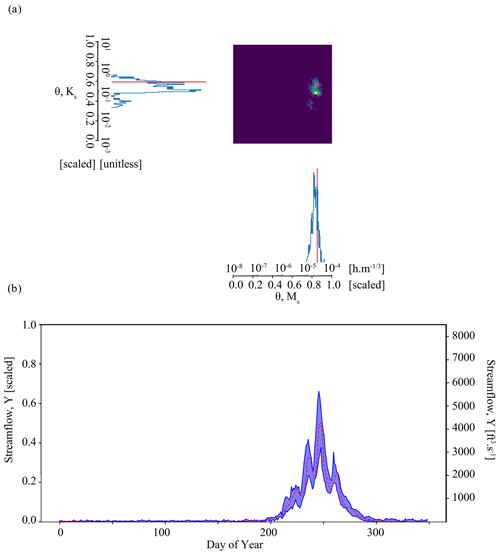
Figure 7Results of the parameter inference and posterior predictive check on synthetic observation in Experiment 4 (Weighted case). Subplot (a) shows an accurate parameter inference that is somewhat less precise and discontinuous, focused on simulator structures that are associated with a higher informal likelihood. The result is a narrow, well-constrained posterior predictive check in subplot (b).
Results of the Weighted case in Experiment 4 demonstrate that it is a viable approach to the issue of overconfident posteriors encountered in the Tough case in Experiment 2. Figure 7a shows accurate parameter inference for our benchmark case in Experiment 4. As in Experiment 3, the benchmark parameter values are in the area identified by the highest probability. The Mahalanobis distance, 1.1, is like that of Experiment 3. The geometry of the area of the highest density differs from Experiment 3, covering a larger area due to differences in the unweighted parameter estimates associated with each surrogate. As a result, the parameter estimate is less precise: the determinant is , which is about an order of magnitude higher than the Boosted case (). The inferred parameters generate streamflow simulations that characterize the synthetic streamflow observation well, as shown by the posterior predictive check (Fig. 7b). We note that, compared to Experiment 3 (Fig. 6b), our simulations are about as variable. The average streamflow RMSE is similar for the Boosted case and the Weighted case (). The standard deviation of the error is also very similar ( compared to ).
4.5 Summary of experiments 1–4
Previously, we compared the performance of simulation-based inference in experiments 1 (Best case), 2 (Tough case), 3 (Boosted case), and 4 (Weighted case) on only one benchmark parameter set. In this section, we expand the comparison of SBI across the experiments to a larger number (n= 18) of parameter sets and corresponding observations. In the case of experiments 1 and 2, the same neural density estimator was utilized to conduct inference. For Experiment 3, an ensemble approach was used to create one new neural density estimator. For Experiment 4, likelihood-weighted parameter estimates from an ensemble of neural density estimators was used. In the case of experiments 2, 3, and 4, the mock data are the same benchmark streamflow simulations from ParFlow; for Experiment 1, the observations are taken from the surrogate. All four experiments utilize mock data corresponding to the same test parameter sets, to make an apples-to-apples comparison. For reference, those test parameter sets are plotted relative to parameter space in Fig. B1a. The results of the analysis of multiple (n= 18) parameter sets are shown by the box plots in Fig. 8.
4.5.1 The precision and accuracy of parameter inference
In general, the parameter estimates from the four experiments are accurate and precise, as shown in Fig. 8a and b. The Best case (Experiment 1) tends to be both precise and accurate. Compared with Experiment 1, the Tough case (Experiment 2) tends to be just as precise but less accurate. This is to be expected, as we made the problem harder for experiments 2, 3, and 4 by not assuming a perfect surrogate. Experiment 3 tends to be less precise but more accurate than Experiment 2. Compared with Experiment 3, the Weighted case (Experiment 4) tends to be even less precise and more accurate. A couple of second-order discussion points arise from Fig. 8a and b.
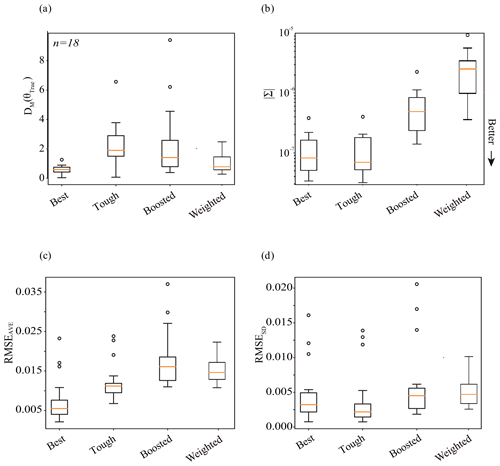
Figure 8Comparative plots showing the performance of the simulation-based inference of parameters and predicted quantities across a set of n= 18 test data. We compare the results of experiments 1 (Best case), 2 (Tough case), 3 (Boosted case), and 4 (Weighted case). Subplots (a) and (b) show the respective accuracy and precision of parameter inference: accuracy is shown in subplot (a) via the Mahalanobis distance of the posterior parameter density; precision is shown in subplot (b) via the determinant, . Subplots (c) and (d) show the respective accuracy and precision of the posterior predictive check: subplot (c) shows the average of the error, RMSEAve, of streamflow ensembles relative to “truth”, which can be thought of as a measure of accuracy; subplot (d) shows the standard deviation of the error, RMSESD, of streamflow ensembles, which can be thought of as a measure of precision. Values closer to the x axis are more desirable.
The resulting box plots of the determinant, a metric for the precision of inference, are shown in Fig. 8b. Here, we see that the training of the conditional density estimator – and not the source of the observations – seems to define the precision of inference. The box plots show that parameter inference is more precise (i.e., the determinant smaller) for experiments 1 and 2, compared with experiments 3 and 4. Experiments 1 and 2 use synthetic observations from different sources (the LSTM surrogate and ParFlow, respectively); however, they are both evaluated using the same neural conditional density estimator: note the similar behavior of the determinant in the first two experiments. On the other hand, the determinant behaves quite differently in Experiment 2 compared with experiments 3 and 4; all three experiments use synthetic observations from ParFlow but use different configurations of the neural conditional density estimator. In the case of Experiment 3 (the Boosted case), differences within an ensemble of LSTM surrogates are lumped into the training of one neural density estimator; in the case of Experiment 4 (the Weighted case), those differences are incorporated in the training of separate neural density estimators. Results show that Experiment 3 is associated with greater precision in parameter inference (i.e., smaller determinant) compared with Experiment 4, as shown by the expanded volume of the parameter estimates in Figs. 7a compared with 6a. The lumping approach in the Boosted case may smooth differences between the surrogates, de-emphasizing parameter combinations in the tails of the separated posterior densities used in the Weighted case. The likelihood-weighting and limits of acceptability also influence the distribution of the parameter estimate, although not in a manner that significantly decreases its precision. More fundamentally, the precision of parameter inference for those methods seems to reflect the simulator(s) (i.e., the variety in simulated responses, Y, to parameter configurations, θ) and not contain much, if any, information about the goodness of fit between observations, YObs, and simulated data, Y.3
Box plots of the Mahalanobis distance4, a metric of the accuracy of inference, are shown in Fig. 8a. The box plots show that parameter inference in experiments 2 and 3 degrades with respect to accuracy compared with Experiment 1, whereas parameter inference from Experiment 4 is nearly as accurate. The box plots also demonstrate that parameter inference is generally more accurate for the Boosted case (Experiment 3) compared with the Tough case (Experiment 2). However, the Mahalanobis distance is greater at some outlier points in the Boosted case (Fig. 7b). This means is that, although it yields more accurate inference in some parts of parameter space (for example, the benchmark parameter set θA explored throughout the earlier results sections), the Boosted case implementation is no silver bullet for averting overconfident parameter estimates. On the other hand, the Weighted case introduced in Experiment 4 is consistently associated with much smaller Mahalanobis distances compared with either the Tough or Boosted cases. The apparent accuracy of the Weighted case can be attributed to the likelihood-based weighting and limits of acceptability methodology as well as to the decrease in precision due to drawing from a set of competing density estimates.
4.5.2 The precision and accuracy of posterior predictions
Taking this one step further, we can use the inferred parameter distributions to generate an ensemble of streamflow simulations using the LSTM and compare this to the observed streamflow (referred to as our posterior predictive check). As shown in Fig. 8c and d, the posterior predictions are precise, and generally fairly accurate. Figure 8c shows the average of the error (RMSEAve) between the simulated streamflow time series and the observed time series, with lower average error corresponding to greater accuracy. Streamflow prediction accuracy decreases between experiments 1, 2, and 3. This is represented by the fact that the RMSEAVE increases nearly 3-fold across each of our experiments (median of ∼0.005 in the Best case, ∼0.010 in the Tough case, and ∼0.015 in Boosted case, in scaled streamflow units). The degradation of the posterior predictive accuracy is related to the degradation of the accuracy of parameter inference (Fig. 8a). Figure 8d shows the variability in the error (RMSESTD) between the simulated streamflow time series and the observed time series, with lower error variability corresponding to greater precision. We see that the central tendency of the RMSESTD of streamflow simulations for the Best, Tough, and Boosted cases are all similar. Streamflow posterior predictions across all three experiments remained precise, in spite of the breakdown in the accuracy.
In Experiment 4 (the Weighted case), the posterior predictive accuracy (RMSEAVE) and the average variability (RMSESTD) is improved compared with Experiment 3. Improvement is seen in the outliers, where simulator configurations with a poor fit relative to observed data are assigned low or no weight in Experiment 4 based on the informal likelihood. Importantly, the KGE was used in the calculation of the informal likelihood. Therefore, conclusions about the accuracy and precision of posterior predictions associated with the four experiments may differ as measured by the KGE as opposed to the RMSE.
The multi-observation comparison helps us to generalize some insights. Briefly, these are as follows:
-
Inference results are often desirable; in particular, SBI seems to result in precise parameter inference across all conditions.
-
Parameter inference with a well-trained surrogate simulator is precise, but it is not always suited to conducting inference on observations with an uncertain relationship to simulated data (as in Experiment 2).
-
The performance of posterior predictive checks is dependent on both the performance of the simulator and the neural density estimator. As such, it can be a valuable tool in assessing the performance of parameter inference.
-
Although a density estimate derived from an ensemble of simulators (as in Experiment 3) may yield more accurate parameter inference, overconfident parameter estimates are a recalcitrant problem for some observed data.
-
In Experiment 4, an approach to likelihood-weighting parameter estimates from SBI was demonstrated to overcome the problem of overconfidence in these controlled experiments.
As users of hydrologic tools such as high-fidelity, process-based simulators, we are often interested in finding simulator configuration(s) most consistent with catchment observations and established physical theory. In practice, this gives rise to uncertainty about whether a simulator is “adequate”, as measured by its predictive ability and structural interpretability (Gupta et al., 2012). In the special case where a correct simulator structure exists, the practitioner's task is to conduct a specification search (Leamer, 1978) to identify it; other candidate simulators inconsistent with observations and theory can be said to be misspecified (Cranmer et al., 2020). One example of misspecification in this work is underscored by the misfit between the process-based ParFlow and the surrogate LSTM simulators. We call this special situation surrogate misspecification.
Our research shows that using a misspecified surrogate to conduct simulation-based inference for a process-based hydrologic simulator can yield erroneous parameter estimates. These overconfident estimates occur because the neural density estimator learns the conditional relationship between parameters and data only from the surrogate simulator. Thus, SBI explicitly infers inputs to the surrogate and not parameters of the process-based simulator. Given surrogate misspecification, the inferred values of parameters may not retain their physical significance with respect to the process-based simulator; this can be a barrier to the interpretability of those simulator configurations identified by inference.
We demonstrate that erroneous parameter estimates due to surrogate misspecification can be addressed through informal Bayesian model averaging (BMA). This approach to BMA applies a performance check – the informal likelihood – to weight and reject simulator configurations identified by SBI. Notably, the likelihood and related limits of acceptability are chosen by the practitioner based on simulation goals. Thus, broadly, informal BMA belongs to the class of approaches to encode expert/domain knowledge into a deep-learning framework (e.g., Reichstein et al., 2019). More specifically, SBI conducts a preliminary search of parameter space for plausible simulator structures and configurations, and the likelihood test incorporates expert-defined information about simulator adequacy into the parameter estimates. Overconfident parameter estimates carry the risk of underrepresenting the uncertainty in the inferences that we draw form simulators. Our work shows that, with these two methods in combination, erroneously overconfident parameter estimates are less likely to occur, compared with standalone SBI.
In our experiments, we focused investigation on SBI and not the process-based simulator. Extending this methodology to observed data requires consideration of many additional sources of uncertainty compared with the synthetic case. Among these is much deeper uncertainty about which simulator structure(s) is (are) appropriate. In the synthetic experiments presented, the relationship between the simulator (the surrogate) and the data-generating process (ParFlow) is well-defined; the surrogate is learned directly from ParFlow. However, for real hydrologic problems, physics-based simulators are nearly always simplified representations of real data-generating processes; stumbling upon a true representation is unlikely or even impossible. Moreover, physical parameters like the hydraulic conductivity (K) and Manning's roughness (M) are themselves conceptual quantities and are almost never known at the scale that we care about, making estimates difficult to validate (Oreskes et al., 1994). In this real-world case, the practitioner's search may be for a set of adequate simulator structures and configurations (i.e., Gupta et al., 2012), where adequacy is subjectively defined. Here, a reasonably good estimate of the hydrologic variable (i.e., streamflow) is often what catchment scientists strive for (van Fraassen, 1980). For completeness, a worked example demonstrating the estimation of parameters using the current simulator formulation and observed streamflow data from the Taylor River catchment is presented in Appendix E. The critic might suggest that not enough was done to tailor the present analysis to real-world data. We disagree on the grounds that our purpose here is to rigorously present and evaluate a method for parameter inference given well-defined constraints. The challenge of this goal is real and relevant. In fact, this work seems to show an upper bound for the performance of SBI where undiagnosed structural error exists. A novel simulation-averaging approach inspired by approximate Bayesian averaging (BMA) and general likelihood uncertainty estimation (GLUE) (Hoeting, 1999; Beven and Binley, 1992) is demonstrated to be an important check to SBI, in presented synthetic and real examples. Further comparison to observations would instead shift the focus of this work from the quality of the SBI and BMA methods to the quality of the underlying hydrologic simulator.
At the core of the challenge of extending SBI is the development of simulators that adequately capture hydrologic behavior. These challenges arise in both the surrogate and the PB simulators. For example, the LSTM surrogate simulator in this study is relatively effective at mimicking ParFlow. This is understandable because the catchment is dominated by snowmelt, which the LSTM mimics well due to its strong memory capabilities. However, in arid catchments, streamflow dynamics are often driven more strongly by short-term reactions to acute rainfall events, and LSTM networks may struggle to represent these processes (Feng et al., 2020). Additionally, PB simulators are not perfect; for example, Richard's equation may not adequately represent groundwater flow through fractured bedrock (Ofterdinger et al., 2019) or preferential unsaturated zone flow (Vriens et al., 2021). Inadequate surrogate and PB simulator structures may yield erroneous parameter estimates when coupled with SBI.
A more nuanced question regarding simulator adequacy is “How good is good enough?”. For example, when should an LSTM trained on PB simulator representations of arid catchment conditions be used with SBI for parameter estimation? The informal performance-weighting approach defines simulator adequacy to exclude poorly performing surrogate simulator structures from the parameter estimation process. Here, the practitioner's belief in each simulation defines its adequacy. This performance-weighted approach within the SBI framework can mitigate issues arising from mismatches between the system of interest and the surrogate simulator. If a surrogate trained on arid catchment conditions fails to meet the acceptability criteria, SBI will yield no viable parameter estimates, signaling the need for simulator reevaluation (as explored in Appendix E). This outcome highlights the necessity for practitioners to reconsider the assumed simulator structures, whether surrogate or process based.
The development of robust simulator structures, both surrogate and process-based, remains a central challenge in hydrology. Advances in surrogates capable of representing spatially distributed hydrologic systems and the use of high-fidelity PB simulators, like ParFlow, which capture a broad range of hydrologic processes across various scales, continue to enhance our ability to simulate real hydrologic conditions. As these simulators improve, so too will the overall effectiveness of SBI. Logical next steps to further extend this methodology to the real case are outlined below.
Adding additional complexity to the training set for the surrogate simulator (i.e., exploring a larger number of parameters configurations, their spatial variability, or multiple forcing scenarios) may help yield better estimates and associated predictions. Many of the practitioners of simulation-based inference advocate packing as much complexity into simulators as possible (Alsing and Wandelt, 2019). High-resolution process-based simulators (such as ParFlow) can be used to explore the realistic behaviors of catchments across a great number of variable and parameter configurations by leveraging surrogate simulators trained using deep learning and SBI. Beyond the informal BMA evaluation of SBI presented here, it may also be important to control for the trade-off between complexity and parsimony in this expanded set of simulator structures and configurations. This could be achieved using a framework similar to the Akaike information criterion (e.g., Schoups et al., 2008), which adds a penalty term related to the number of estimated physical parameters in the likelihood evaluation. A similar “penalty for complexity” concept was explored in traditional applications of Bayesian simulator averaging for statistical models through Occam's window (Madigan and Raftery, 1994).
SBI is well-suited for inference in high-dimensional space, and has had many adaptations (Cranmer et al., 2020). As with any approach to inference, scaling to a greater number of parameters will bump into computational constraints. Those constraints come from the cost of simulation (i.e., in the present work, the cost of our PB simulations) and the cost of inference (i.e., the cost of training and evaluating the neural density estimator). In our study, the cost of PB simulation is high, and this has a compounding effect on the cost of inference. Utilizing a surrogate can reduce the cost of inference by reducing the need to resort to the PB simulator; however, we show that the resulting parameter estimates may not be accurate if the surrogate is not perfect. Focusing inference on the most informative parts of higher-dimensional parameter space is important if SBI is conducted directly with a costly simulator. Papamarkarios' early work with SBI developed sequential neural sampling techniques that might be less wasteful than other approaches to sampling parameter space (i.e., Papamakarios et al., 2018; Lueckmann et al., 2017; Greenberg et al., 2019). Tsai et al. (2021) used a neural network to learn the mapping between physical parameters and outputs only for PB simulator configurations that corresponded closely to observations; SBI can be implemented similarly. However, any framework for parameter learning focused only on observed behavior needs to be updated as new observations become available and may omit reasonable model configurations from the parameter estimates. Lastly is the option of compressing or reducing the dimensionality, which could be important for estimating distributed parameters. The topic of compression and SBI is explored by Asling and Wandelt (2019).
Including additional catchment observation types (i.e., groundwater and soil moisture) in the inference workflow could also improve estimates of the physical parameters for real systems as well as for the predictions associated with complex simulators. However, observations in hydrology – particularly of groundwater systems – are generally sparse. This presents a problem. One option is to better observe that complexity. New spatially distributed “big data” products that leverage remote sensing offer new opportunities to observe hydrologic variables like soil moisture (Mohanty et al., 2017; Petropoulos et al., 2015). The extension of the methodology to real-world observations will also need to consider the role of data quality, adequacy (Gupta et al., 2012), and disinformation (Beven and Westerberg, 2011) as well as the challenge of defining limits of acceptability regarding model performance.
Our investigation implements simulation-based inference (SBI) to determine parameters for a spatially distributed, process-based catchment simulator. We believe that this research is among the first to apply contemporary SBI to catchment modeling. The implementation employed here has a couple of noteworthy features, which are outlined in the following.
-
We use deep learning to train a surrogate long short-term memory (LSTM) network on the original physically based simulations (from ParFlow). This allows for quick and comprehensive exploration of simulation results for which we have corresponding observations, such as streamflow at a catchment outflow in a catchment.
-
A density-based neural network leverages the capacity of the surrogate to generate simulations quickly to learn a representation of the full conditional density, p(θ|Y), of parameters given data. This learned conditional density can be evaluated using observations to determine the parameter posterior density, . This parameter posterior represents our best guess of what the parameters for our simulator should be.
We demonstrate that this approach to SBI can generate reasonable estimates of the parameters of a hydrologic simulator, ParFlow, through a set of synthetic experiments. In Experiment 1 (the Best case), we show that SBI works well in controlled settings in which we assume that our surrogate LSTM simulator is accurate. Moreover, this experiment highlights how, once learned, the model of the conditional density can be used to determine the process-based parameters rapidly and effectively for many observations without the need for additional process-based simulations. That is particularly valuable when simulations are costly, as is often the case with high-resolution, transient simulators used in the field of catchment modeling.
In Experiment 2 (the Tough case), we show that SBI produces a set of probable parameters with precision in settings where the simulator does not represent the underlying system generating the observation perfectly. These inferred parameters are used to generate reasonable streamflow simulations relative to observations. However, the Tough case shows that parameter inference is not always accurate with respect to the physics-based simulator that was used to train the surrogate. This undesirable characteristic (of precision but not accuracy, or overconfidence) arises from issues related to the structural adequacy of the simulator, which is well-recognized in the literature as an impediment for accurate parameter inference (Cranmer et al., 2020). The controlled nature of Experiment 2 explores the special case of surrogate misspecification. This special case arises from a mismatch between the surrogate and the process-based simulations from ParFlow. In inference, surrogate misspecification gives rise to error in estimates of the physical parameters. We show that sources of this error can be quite difficult to diagnose, although conducting a posterior predictive check is a qualitative way of ascertaining the extent of simulator bias.
In experiments 3 and 4 (the Boosted and Weighted cases, respectively), we attempt to address the issue of overconfident parameter inference due to misspecification. In Experiment 3, we use an ensemble of weak surrogate simulators (instead of just one strong surrogate simulator) to learn the full conditional density. The underlying principle is that the behavior of an ensemble of surrogate simulators in aggregate may not be biased, even if each individual simulator has its own bias. This may “wash out” the negative effects of surrogate misspecification on parameter inference. Evidence from the Boosted case shows that this approach reduces the occurrence of overconfident parameter estimates, but it is not a silver bullet for conducting accurate inference.
In Experiment 4 (the Weighted case), the practitioner assigns a measure of belief to parameter estimates from a set of competing surrogate simulators, reflecting their confidence in its validity. This measure of belief – or informal likelihood (i.e., Beven and Binley, 1992) – is used to weight and reject simulator configurations identified by SBI. The underlying principle is that SBI conducts a preliminary search of parameter space for plausible simulator structures and configurations, and the likelihood test incorporates expert-defined information about simulator adequacy into the parameter estimates. The Weighted case is demonstrated to solve the problem of overconfident parameter estimates introduced by surrogate misspecification.
The results of experiments 2, 3, and 4 demonstrate progress towards being able to implement SBI in hydrological domains subject to uncertainty that we can benchmark (i.e., the misspecification of the surrogate). Additional work is needed to address deeper uncertainty about the structural adequacy of the underlying physics-based simulator. This uncertainty often exists in catchment modeling – due to factors such as natural heterogeneities in the subsurface, approximations in process parameterizations, and bias in the meteorological input data – that can seldom be fully accounted for. Thus, the notion of structural “adequacy” is nearly always subjective (Gupta et al., 2012). In many real-world applications, a calibrated estimate of the hydrologic variable (i.e., streamflow) is what catchment scientists strive for. Enhancing standalone SBI with the likelihood-weighting methodology introduced in Experiment 4 embraces this principle of subjective adequacy and is broadly extendable to more complex inference problems in catchment modeling. When no simulators are identified as adequate, an obvious next step is to expand the simulator to explore more and different configurations of parameters and input variables.
Table A1The relationship between ParFlow and LSTM static inputs (e.g., parameters, θ), dynamic inputs (e.g., meteorological forcings, X), and dynamic outputs (e.g., streamflow, Y). ParFlow variables must be compressed into lower-dimensional representations in order to be used in the LSTM. Non-italicized content constitutes the general descriptions of the parameters, inputs, and outputs of the table. Italicized content is further commentary.

Table A2ParFlow was run many times under different parameter configurations. This table shows the scalar factors used to modify the spatially distributed Manning coefficient and hydraulic conductivity. We call these factors Ks and Ms, respectively, to keep the distinction between them and ParFlow's parameters clear.

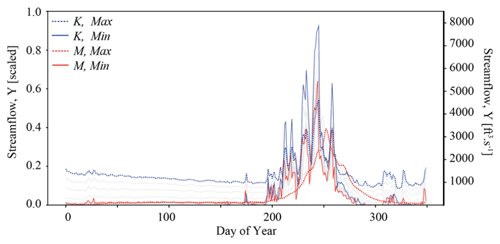
Figure A1Sensitivity of ParFlow-generated streamflow time series for water year 1995 to perturbations in the hydraulic conductivity and Manning's coefficient. We show the sensitivity of holding Ks and Ms constant at 0.1 and , respectively, while varying the other values across the range of parameters explored in Table A2.
Table B1Relevant notes on the architecture, training, and hyperparameters for the surrogate LSTM simulator.
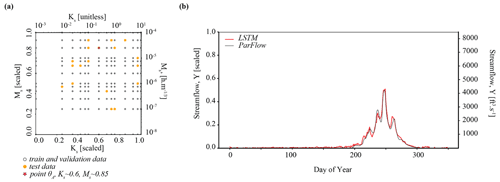
Figure B1Plots show the training–validation and test split for the LSTM surrogate trained on n= 183 ParFlow simulations. In subplot (a), the locations in parameter space where ParFlow simulations were run are shown. The surrogate was trained and tested at the orange dots. In subplot (b), a comparison of ParFlow to LSTM streamflow simulation generated at benchmark parameter set θA, Ks∼0.6, and Ms∼0.85 is shown. The fit between ParFlow and LSTM is explored more in Sect. 4 of the paper.
Deriving implicit statistical models using density estimation techniques is not new (Diggle and Gratton, 1984). However, these traditional approaches suffer from some shortcomings, including sample efficiency and inference quality, as described further in Cranmer et al. (2020). We show two components of the density-based SBI workflow utilized here that have benefited due to recent innovations: masked autoencoder for density estimation (MADE) and sequential neural posterior sampling.
C1 Masked autoencoder for density estimation (MADE)
While mixture density networks have a long operational history, there have been more recent innovations in using neural networks to learn and represent conditional probability distributions. This study utilizes a class of neural density estimators called masked autoregressive flows (Alsing et al., 2019), which shares some of the underlying principles described for mixture density networks. Masked autoregressive flows arise from the principle that “any probability density can be factorized as a product of one-dimensional conditionals” via the chain rule (Alsing et al., 2019); these 1D conditionals are parameterized by a fully connected neural network known as a masked autoencoder for density estimation (MADE) (Uria et al., 2016). Masked autoregressive flows are composed of “stacks” of masked autoencoder for density estimations, to add flexibility (Papamakarios et al., 2018). A detailed description of these methods is beyond the scope of this paper.
C2 Sequential neural posterior estimation
We use a sampling technique called sequential neural posterior estimation (SNPE) to speed up and improve the evaluation of a trained neural conditional density estimator. By evaluation, we mean using data Y (most typically observed data, YObs) to generate a posterior estimate here (step 4 in Sect. 3.5). The need for SNPE arises from the challenge that drawing simulation parameters from the full prior distribution is wasteful (Papamakarios et al., 2018; Lueckmann et al., 2017; Greenberg et al., 2019). This is due to the fact that data simulated from some parts of parameter space have higher or lower posterior density for YObs. SNPE iteratively refines the posterior estimate to make inference more efficient and flexible, as described by Greenberg et al. (2019).
Details related to the architectures, hyperparameters, training, and evaluation of neural density estimators are shown in Table C1. Decisions about hyperparameters were made via trial and error. It is important to note that the goal of our work is not to create the most robust neural density estimator model; rather, we aim to explore inference under a variety of different conditions.
A trained neural density estimator can be used to infer the parameters of an observation without the need for additional simulation runs. In this section, we extend Experiment 1 (the Best case) to quickly and effectively evaluate the posterior parameter density for many synthetic observations (YObs_LSTM_i). We use many parameter sets (θi) of Ks and Ms sampled uniformly across parameter space to generate an equivalent number of synthetic observations, where i= 1, 2, …, 441.
SBI can infer the parameters from many diverse and different synthetic observations well, as shown in Fig. D1. The precision of inference of the posterior parameter densities is explored in Fig. D1a as a map of determinants across parameter space. Parameter inference is more precise (with a smaller determinant) in the center than at the edges of the parameter space; it is below our precision threshold of everywhere. Parameter inference is accurate across parameter space, as shown by the map of the Mahalanobis distance in Fig. D1B. There are some pockets of parameter space characterized by more- and less-accurate parameter inference. The structure of the Mahalanobis distances across parameter space does not seem to be as well-defined as that of the determinant; this is likely a consequence of randomness in the initialization of the neural density estimator (confirmed by many independent trials). We note that evaluating each of the synthetic observations in Fig. D1 took only a few seconds.
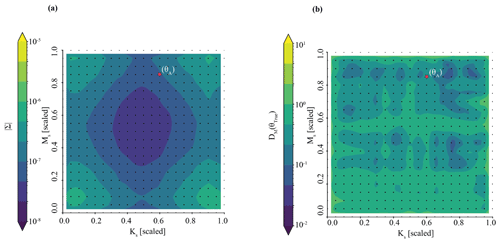
Figure D1Once the neural conditional density estimator is trained, it can be evaluated quickly and effectively given new data. This figure shows the performance of SBI of Manning's coefficient (Ms) and the hydraulic conductivity (Ks) given synthetic streamflow data generated by the surrogate from across 441 locations across parameter space. Subplot (a) shows the determinant, , of the posterior parameter estimate, which quantifies the precision of parameter inference. Subplot (b) shows the Mahalanobis distance, DM (θTrue), between the inferred distribution and true parameter values, which quantifies the accuracy of the inference. These values are shown across the entirety of the parameter space investigated, where purple is better. The red star in the subplots corresponds to the benchmark location θA in the parameter space of the analysis shown in Fig. 3.
The posterior predictive check shows that streamflow characterization is generally both precise and accurate. This required drawing a subset of parameters from each of the 441 posterior parameter densities represented as points in Fig. D1 and generating an ensemble of simulated streamflow time series using the surrogate simulator. The accuracy of the posterior predictions is explored in Fig. D2A as a map across parameter space. In general, the posterior predictions have an average error of less than 0.01. Accuracy is highest in the middle of the parameter space and seems to degrade towards the upper boundaries where the parameters Ks and Ms are large. The precision of the posterior predictions is explored in Fig. D2B as a map across parameter space. In general, the posterior predictions are precise, with standard deviation of the error less than 0.01. We note that both the average and standard deviation of error increase at large parameter values, in particular large values of hydraulic conductivity. Overall, Figs. D1 and D2 show that SBI can reliably infer parameters and characterize streamflow processes for many streamflow observations that span the parameter space that we investigated.
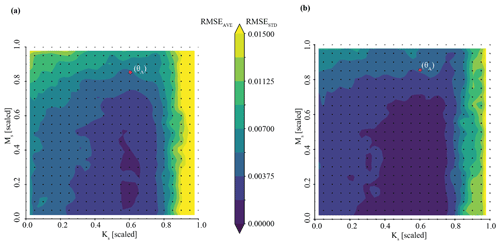
Figure D2Posterior predictive check for many observations: once parameters are inferred, the posterior can be drawn (n= 50) to generate probabilistic streamflow ensembles. This figure shows the performance of streamflow ensembles derived from SBI at 441 locations across parameter space. Subplot (a) shows the average of the error (RMSEAve) of streamflow ensembles relative to the “truth”, which can be thought of as a measure of accuracy. Subplot (b) shows the standard deviation of the error (RMSESD) of streamflow ensembles, which can be thought of as a measure of precision. Streamflow ensembles are evaluated against the “true” synthetic streamflow time series generated by the surrogate simulator, where blue is better.
The informal BMA methodology is suited to assessing the adequacy of model structures and configurations in the real-world case. In Fig. E1, inference is conducted on the observed streamflow time series for water year 1995 from the Taylor River gage ID 09110000 (red). Figure E1 shows the posterior predictive check with confidence intervals from standalone SBI (blue) as well as the “persistence” baseline (orange). Model configurations scoring less than persistence (defined by setting next week's predicted data equal to today's observed data) are considered not to be credible and are assigned a weight of zero. Note that standalone SBI does not perform well relative to persistence (KGE = 0.94). The culprit is the timing of peak simulated flows, which occur on average some 44 d before the peak observation and 51 d before persistence. With no models superior to persistence, the BMA methodology returns an empty set; no model structures (LSTM surrogates) or configurations (parameter sets) yield predications that are “reasonably good”. In fact, no model structures or configurations superior to persistence exist in the full space of possible combinations of M and K, as shown by the confidence intervals in gray. We emphasize to the reader that the BMA methodology results in a desirable outcome: all models identified by standalone SBI are rejected, while overconfident predictions and parameter estimates are avoided.
The repository containing the scripts used to create the LSTM surrogate simulator and infer parameters by SBI was created by Robert Hull and can be accessed at https://github.com/rhull21/sbi_taylor/ (last access: 11 July 2024; https://doi.org/10.5281/zenodo.13899823, Hull, 2024).
The repository containing the scripts to create inputs and forcing scenarios and run Parflow-CLM for the Taylor catchment in Colorado was created by Elena Leonarduzzi and can be accessed at https://github.com/HydroGEN-pubs/Taylor_CO (last access: 11 July 2024; Leonarduzzi et al., 2022).
RH, LEC, and PM: conceptualization and formal analysis. RH: data curation, visualization, and writing (original draft). LEC and RMM: funding acquisition. RH, EL, LDLF, HVT, AB, PM, LEC, and RMM: investigation and validation. RH, EL, LDLF, HVT, AB, PM, LEC, and RMM: methodology. LEC and RMM: project administration. EL and RH: software. LEC, PM, and RMM: supervision. RH, EL, LDLF, HVT, AB, PM, LEC, and RMM: writing (review and editing). All authors contributed to the article and approved the submitted version.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
Vineet Bansal and Calla Chennault are acknowledged for infrastructure and software support.
This research has been supported by the National Science Foundation (grant nos. 1835794 and 2040542).
This paper was edited by Manuela Irene Brunner and reviewed by Shijie Jiang and Uwe Ehret.
Alsing, J. and Wandelt, B.: Nuisance Hardened Data Compression for Fast Likelihood-Free Inference, Mon. Not. R. Astron. Soc., 488, 5093–5103, https://doi.org/10.1093/mnras/stz1900, 2019.
Alsing, J., Charnock, T., Feeney, S., and Wandelt, B.: Fast likelihood-free cosmology with neural density estimators and active learning, Mon. Not. R. Astron. Soc., 488, 4440–458, https://doi.org/10.1093/mnras/stz1960, 2019.
Bastidas, L., Gupta, H., Sorooshian, S., Shuttleworth, W., and Yang, Z.-L.: Sensitivity analysis of a land surface scheme using multicriteria methods, J. Geophys. Res., 104, 19481–19490, https://doi.org/10.1029/1999JD900155, 1999.
Beven, K.: Parameter Estimation and Predictive Uncertainty, in: Rainfall‐Runoff Modelling, John Wiley & Sons, Ltd, 231–287, https://doi.org/10.1002/9781119951001.ch7, 2012.
Beven, K. and Binley, A.: The future of distributed models: Model calibration and uncertainty prediction, Hydrol. Process., 6, 279–298, https://doi.org/10.1002/hyp.3360060305, 1992.
Beven, K. and Binley, A.: GLUE: 20 years on, Hydrol. Process., 28, 5897–5918, https://doi.org/10.1002/hyp.10082, 2014.
Beven, K. and Westerberg, I.: On red herrings and real herrings: disinformation and information in hydrological inference, Hydrol. Process., 25, 1676–1680, https://doi.org/10.1002/hyp.7963, 2011.
Bishop, C.: Mixture Density Networks, Neural Computing Research Group Report, Department of Computer Science and Applied Mathematics: Aston University, https://www.microsoft.com/en-us/research/publication/mixture-density-networks/ (last access: 12 September 2024), 1994.
Castle, S. L., Thomas, B. F., Reager, J. T., Rodell, M., Swenson, S. C., and Famiglietti, J. S.: Groundwater depletion during drought threatens future water security of the Colorado River Catchment, Geophys. Res. Lett., 41, 5904–5911, https://doi.org/10.1002/2014GL061055, 2014.
Condon, L. E.: Scientist Spotlight: Laura Condon, University of Arizona, https://science.arizona.edu/news/2022/06/scientist-spotlight-laura-condon (last access: 11 July 2024), 2022.
Cranmer, K.: A3D3 Seminar: Accelerating Simulation-based Inference | Kyle S. Cranmer, YouTube, https://www.youtube.com/watch?v=3ULdEHaAWJQ (last access: 12 September 2024), 2022.
Cranmer, K., Brehmer, J., and Louppe, G.: The frontier of simulation-based inference, P. Natl. Acad. Sci. USA, 117, 30055–30062, https://doi.org/10.1073/pnas.1912789117, 2020.
Diggle, P. J. and Gratton, R. J.: Monte Carlo methods of inference for implicit statistical models, J. R. Stat. Soc.-B, 46, 193–212, 1984.
Draper, D.: Assessment and Propagation of Model Uncertainty, J. R. Stat. Soc.-B, 57, 45–70, https://doi.org/10.1111/j.2517-6161.1995.tb02015.x, 1995.
Duan, Q., Ajami, N. K., Gao, X., and Sorooshian, S.: Multi-model ensemble hydrologic prediction using Bayesian model averaging, Adv. Water Resour., 30, 1371–1386, https://doi.org/10.1016/j.advwatres.2006.11.014, 2007.
Fatichi, S., Vivoni, E. R., Ogden, F. L., Ivanov, V. Y., Mirus, B., Gochis, D., Downer, C. W., Camporese, M., Davison, J. H., Ebel, B., Jones, N., Kim, J., Mascaro, G., Niswonger, R., Restrepo, P., Rigon, R., Shen, C., Sulis, M., and Tarboton, D.: An overview of current applications, challenges, and future trends in distributed process-based models in hydrology, J. Hydrol., 537, 45–60, https://doi.org/10.1016/j.jhydrol.2016.03.026, 2016.
Feng, D., Fang, K., and Shen, C.: Enhancing Streamflow Forecast and Extracting Insights Using Long-Short Term Memory Networks With Data Integration at Continental Scales, Water Resour. Res., 56, e2019WR026793, https://doi.org/10.1029/2019WR026793, 2020.
Fenicia, F., Kavetski, D., Reichert, P., and Albert, C.: Signature-Domain Calibration of Hydrological Models Using Approximate Bayesian Computation: Empirical Analysis of Fundamental Properties, Water Resour. Res., 54, 3958–3987, https://doi.org/10.1002/2017WR021616, 2018.
Freund, Y. and Schapire, R. E.: A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting, J. Comput. Syst. Sci., 55, 119–139, https://doi.org/10.1006/jcss.1997.1504, 1997.
Gabry, J., Simpson, D., Vehtari, A., Betancourt, M., and Gelman, A.: Visualization in Bayesian workflow, J. R. Stat. Soc.-A Stat., 182, 389–402, https://doi.org/10.1111/rssa.12378, 2019.
Greenberg, D. S., Nonnenmacher, M., and Macke, J. H.: Automatic Posterior Transformation for Likelihood-Free Inference, arXiv [preprint], https://doi.org/10.48550/ARXIV.1905.07488, 2019.
Gupta, H. V., Sorooshian, S., and Yapo, P. O.: Toward improved calibration of hydrologic models: Multiple and noncommensurable measures of information, Water Resour. Res., 34, 751–763, https://doi.org/10.1029/97WR03495, 1998.
Gupta, H. V., Kling, H., Yilmaz, K. K., and Martinez, G. F.: Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling, J. Hydrol., 377, 80–91, https://doi.org/10.1016/j.jhydrol.2009.08.003, 2009.
Gupta, H. V., Clark, M. P., Vrugt, J. A., Abramowitz, G., and Ye, M.: Towards a comprehensive assessment of model structural adequacy, Water Resour. Res., 48, W08301, https://doi.org/10.1029/2011WR011044, 2012.
Hermans, J., Delaunoy, A., Rozet, F., Wehenkel, A., and Louppe, G.: A Crisis In Simulation-Based Inference? Beware, Your Posterior Approximations Can Be Unfaithful, Transactions on Machine Learning Research, https://openreview.net/pdf?id=LHAbHkt6Aq (last access: 12 September 2024), 2022.
Hochreiter, S. and Schmidhuber, J.: Long Short-Term Memory, Neural Comput., 1735–1780, https://doi.org/10.1162/neco.1997.9.8.1735, 1997.
Hoeting, J. A., Madigan, D., Raftery, A. E., and Volinsky, C. T.: Bayesian model averaging: a tutorial (with comments by: M. Clyde, David Draper and E. I. George, and a rejoinder by the authors), Stat. Sci., 14, 382–417, https://doi.org/10.1214/ss/1009212519, 1999.
Hunt, R. J., Doherty, J., and Tonkin, M. J.: Are Models Too Simple? Arguments for Increased Parameterization, Groundwater, 45, 254–262, https://doi.org/10.1111/j.1745-6584.2007.00316.x, 2007.
Jiang, S., Zheng, Y., and Solomatine, D.: Improving AI system awareness of geoscience knowledge: Symbiotic integration of physical approaches and deep learning, Geophys. Res. Lett., 47, e2020GL088229, https://doi.org/10.1029/2020GL088229, 2020.
Jones, J. E. and Woodward, C. S.: Newton-Krylov-multigrid solvers for large-scale, highly heterogenous, variably saturated flow problems, Adv. Water Resour., 24, 763–774, https://doi.org/10.1016/S0309-1708(00)00075-0, 2001.
Karpatne, A., Atluri, G., Faghmous, J. H., Steinbach, M., Banerjee, A., Ganguly, A., Shekhar, S., Samatova, N., and Kumar, V.: Theory-guided data science: A new paradigm for scientific discovery from data, IEEE T. Knowl. Data Eng., 29, 2318–2331, 2017.
Kollet, S. J. and Maxwell, R. M.: Capturing the influence of groundwater dynamics on land surface processes using an integrated, distributed catchment model, Water Resour. Res., 44, W02402, https://doi.org/10.1029/2007wr006004, 2008.
Kratzert, F., Klotz, D., Brenner, C., Schulz, K., and Herrnegger, M.: Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks, Hydrol. Earth Syst. Sci., 22, 6005–6022, https://doi.org/10.5194/hess-22-6005-2018, 2018.
Leonarduzzi, E., Tran, H., Bansal, V., Hull, R. B., De la Fuente, L., Bearup, L. A. , Melchior, P., Condon, L. E., and Maxwell, R. M.: Training Machine Learning with Physics-Based Simulations to Predict 2D Soil Moisture Fields in a Changing Climate, Frontiers in Water, 4, 92711, https://doi.org/10.3389/frwa.2022.927113, 2022.
Leamer, E. E.: Specification searches: ad hoc inference with nonexperimental data, Wiley, https://www.anderson.ucla.edu/faculty/edward.leamer/books/specification_searches/specification_searches.htm (last access: 18 September 2024), 1978.
Liu, Y. and Ker, A. P.: Rating Crop Insurance Contracts with Nonparametric Bayesian Model Averaging, J. Agr. Resour. Econ., 45,244–64, 2020.
Lueckmann, J.-M., Goncalves, P. J., Bassetto, G., Öcal, K., Nonnenmacher, M., and Macke, J. H.: Flexible statistical inference for mechanistic models of neural dynamics, arXiv [preprint], https://doi.org/10.48550/ARXIV.1711.01861, 2017.
Madigan, D. and Raftery, A. E.: Model Selection and Accounting for Model Uncertainty in Graphical Models Using Occam's Window, J. Am. Stat. Assoc., 89, 1535–1546, https://doi.org/10.1080/01621459.1994.10476894, 1994.
Maesschalck, R. D., Jouan-Rimbaud, D., and Massart, D. L.: The Mahalanobis distance, Chemometr. Intell. Lab., 50, 1–18, https://doi.org/10.1016/S0169-7439(99)00047-7, 2000.
Margalit, D. and Rabinoff, J.: Determinants and Volumes, in: Interactive Linear Algebra, Georgia Institute of Technology, 222–235, https://textbooks.math.gatech.edu/ila/determinants-volumes.html (last access: 12 September 2024), 2017.
Maxwell, R. M. and Kollet, S. J.: Integrated surface–groundwater flow modeling: A free-surface overland flow boundary condition in a parallel groundwater flow model, Adv. Water Resour., 945–958, https://doi.org/10.1016/j.advwatres.2005.08.006, 2006.
Maxwell, R. M. and Miller, N. L.: Development of a Coupled Land Surface and Groundwater Model, J. Hydrometeorol., 233–247, https://doi.org/10.1175/JHM422.1, 2005.
Maxwell, R. M., Condon, L. E., and Kollet, S. J.: A high-resolution simulation of groundwater and surface water over most of the continental US with the integrated hydrologic model ParFlow v3, Geosci. Model Dev., 8, 923–937, https://doi.org/10.5194/gmd-8-923-2015, 2015.
Maxwell, R. M., Condon, L. E., and Melchior, P.: A Physics-Informed, Machine Learning Emulator of a 2D Surface Water Model: What Temporal Networks and Simulation-Based Inference Can Help Us Learn about Hydrologic Processes, Water, 13, 3633, https://doi.org/10.3390/w13243633, 2021.
Mohanty, B. P., Cosh, M. H., Lakshmi, V., and Montzka, C.: Soil moisture remote sensing: State-of-the-science, Vadose Zone J., 16, 1–9, 2017.
Nearing, G. S., Tian, Y., Gupta, H. V., Clark, M. P., Harrison, K. W., and Weijs, S. V.: A philosophical basis for hydrological uncertainty, Hydrolog. Sci. J., 61, 1666–1678, https://doi.org/10.1080/02626667.2016.1183009, 2016.
Ofterdinger, U., A. M. MacDonald, J.-C. Comte, and M. E. Young. “Groundwater in Fractured Bedrock Environments: Managing Catchment and Subsurface Resources – an Introduction.” In Groundwater in Fractured Bedrock Environments: Managing Catchment and Subsurface Resources, edited by: Ofterdinger, U., MacDonald, A. M., Comte, J.-C., and Young, M. E., 479, Geological Society of London, https://doi.org/10.1144/SP479-2018-170, 2019.
Oreskes, N., Shrader-Frechette, K., and Belitz, K.: Verification, Validation, and Confirmation of Numerical Models in the Earth Science, Science (New York, N.Y.), 263, 641–646, https://doi.org/10.1126/science.263.5147.641, 1994.
Paniconi, C. and Putti, M.: Physically based modeling in catchment hydrology at 50: Survey and outlook, Water Resour. Res., 51, 7090–7129, https://doi.org/10.1002/2015WR017780, 2015.
Papamakarios, G. and Murray, I.: Fast ε-free Inference of Simulation Models with Bayesian Conditional Density Estimation, arXiv [preprint], https://doi.org/10.48550/ARXIV.1605.06376, 2016.
Papamakarios, G., Sterratt, D. C., and Murray, I.: Sequential Neural Likelihood: Fast Likelihood-free Inference with Autoregressive Flows, arXiv [preprint], https://doi.org/10.48550/ARXIV.1805.07226, 2018.
Petropoulos, G. P., Ireland, G., and Barrett, B.: Surface soil moisture retrievals from remote sensing: Current status, products & future trends, Phys. Chem. Earth, Parts A/B/C, 83, 36–56, 2015.
Raftery, A. E., Madigan, D., and Hoeting, J. A.: Bayesian Model Averaging for Linear Regression Models, J. Am. Stat. Assoc., 92, 179–191, https://doi.org/10.1080/01621459.1997.10473615, 1997.
Raftery, A. E., Gneiting, T., Balabdaoui, F., and Polakowski, M.: Using Bayesian Model Averaging to Calibrate Forecast Ensembles, Mon. Weather Rev., 133, 1155–1174, https://doi.org/10.1175/MWR2906.1, 2005.
Reichstein, M., Camps-Valls, G., Stevens, B., Jung, M., Denzler, J., Carvalhais, N., and Prabhat: Deep learning and process understanding for data-driven Earth system science, Nature, 566, 195–204, https://doi.org/10.1038/s41586-019-0912-1, 2019.
Hull, R.: Code and resources supporting the paper. “Simulation-based Inference for Parameter Estimation of Complex Watershed Simulators”, Zenodo [code], https://doi.org/10.5281/zenodo.13899823, 2024.
Roberts, H. V.: Probabilistic Prediction, J. Am. Stat. Assoc., 60, 50–62, https://doi.org/10.1080/01621459.1965.10480774, 1965.
Rumelhart, D. E., Hinton, G. E., and Williams, R. J.: Learning representations by back-propagating errors, Nature, 323, 533–536, https://doi.org/10.1038/323533a0, 1986.
Santos, N. and Patno, H.: Operations Plan for Colorado River Reservoirs from the Bureau of Reclamation, https://www.usbr.gov/lc/region/g4000/24mo/2022/AUG22_MIN.pdf (last access: 12 September 2024), 2022
Schoups, G., van de Giesen, N. C., and Savenije, H. H. G.: Model complexity control for hydrologic prediction, Water Resour. Res., 44, W00B03, https://doi.org/10.1029/2008WR006836, 2008.
Smith, P., Beven, K. J., and Tawn, J. A.: Informal likelihood measures in model assessment: Theoretic development and investigation, Adv. Water Resour., 31, 1087–1100, https://doi.org/10.1016/j.advwatres.2008.04.012, 2008.
Tejero-Cantero, A., Boelts, J., Deistler, M., Lueckmann, J.-M., Durkan, C., Gonçalves, P. J., Greenberg, D. S., and Macke, J. H.: sbi: A toolkit for simulation-based inference, Journal of Open Source Software, 5, 2505, https://doi.org/10.21105/joss.02505, 2020.
Tenney, W.: A Tier 2a Shortage Is Confirmed, but Uncertainty Remains, Arizona Municipal Water Users Association (blog), https://www.amwua.org/blog/a-tier-2a-shortage-is-confirmed-but-uncertainty-remains (last access: 12 September 2024), 2022.
Tran, H., Leonarduzzi, E., De la Fuente, L., Hull, R. B., Bansal, V., Chennault, C., Gentine, P., Melchior, P., Condon, L. E., and Maxwell, R. M.: Development of a Deep Learning Emulator for a Distributed Groundwater-Surface Water Model: ParFlow-ML, Water, 13, 3393, https://doi.org/10.3390/w13233393, 2021.
Tran, H., Zhang, J., O'Neill, M. M., Ryken, A., Condon, L. E., and Maxwell, R. M.: A hydrological simulation dataset of the Upper Colorado River Catchment from 1983 to 2019, Scientific Data, 9, 16, https://doi.org/10.1038/s41597-022-01123-w, 2022.
Tsai, W.-P., Feng, D., Pan, M., Beck, H., Lawson, K., Yang, Y., Liu, J., and Shen, C.: From calibration to parameter learning: Harnessing the scaling effects of big data in geoscientific modeling, Nat. Commun., 12, 5988, https://doi.org/10.1038/s41467-021-26107-z, 2021.
Uria, B., Côté, M.-A., Gregor, K., Murray, I., and Larochelle, H.: Neural Autoregressive Distribution Estimation, J. Mach. Learn. Res., 17, 1–37, 2016.
van Fraassen, B. C.: The Scientific Image, Clarendon Library of Logic and Philosophy (Oxford), Oxford Academic, https://doi.org/10.1093/0198244274.001.0001, 1980.
Vriens, B., Plante, B., Seigneur, N., and Jamieson, H.: Mine Waste Rock: Insights for Sustainable Hydrogeochemical Management, Minerals, 10, 728, https://doi.org/10.3390/min10090728, 2021.
Vrugt, J. A. and Sadegh, M.: Toward diagnostic model calibration and evaluation: Approximate Bayesian computation, Water Resour. Res., 49, 4335–4345, https://doi.org/10.1002/wrcr.20354, 2013.
Weiss, G. and von Haeseler, A.: Inference of Population History Using a Likelihood Approach, Genetics, 149, 1539–1546, https://doi.org/10.1093/genetics/149.3.1539, 1998.
White, J. T., Hunt, R. J., Fienen, M. N., and Doherty, J. E.: Approaches to highly parameterized inversion: PEST Version 5, a software suite for parameter estimation, uncertainty analysis, management optimization and sensitivity analysis, Reston, VA, https://doi.org/10.3133/tm7C26, 2020.
Wikle, C. K. and Berliner, L. M.: A Bayesian tutorial for data assimilation, Physica D, 230, 1–16, https://doi.org/10.1016/j.physd.2006.09.017, 2007.
Wilkinson, M. D., Dumontier, M., Aalbersberg, I. J. J., Appleton, G., Axton, M., Baak, A., Blomberg, N., Boiten, J.-W., da Silva Santos, L. B., Bourne, P. E., Bouwman, J., Brookes, A. J., Clark, T., Crosas, M., Dillo, I., Dumon, O., Edmunds, S., Evelo, C. T., Finkers, R., Gonzalez-Beltran, A., Gray, A. J. G., Groth, P., Goble, C., Grethe, J. S., Heringa, J., 't Hoen, P. A. C., Hooft, R., Kuhn, T., Kok, R., Kok, J., Lusher, S. J., Martone, M. E., Mons, A., Packer, A. L., Persson, B., Rocca-Serra, P., Roos, M., van Schaik, R., Sansone, S.-A., Schultes, E., Sengstag, T., Slater, T., Strawn, G., Swertz, M. A., Thompson, M., van der Lei, J., van Mulligen, E., Velterop, J., Waagmeester, A., Wittenburg, P., Wolstencroft, K., Zhao, J., and Mons, B.: The FAIR Guiding Principles for scientific data management and stewardship., Sci. Data, 3, 160018, https://doi.org/10.1038/sdata.2016.18, 2016.
Williams, A. P., Cook, B. I., and Smerdon, J. E.: Rapid intensification of the emerging southwestern North American megadrought in 2020–2021, Nat. Clim. Change, 12, 232–234, https://doi.org/10.1038/s41558-022-01290-z, 2022.
Zhao, W. L., Gentine, P., Reichstein, M., Zhang, Y., Zhou, S., Wen, Y., Lin, C., Li, X., and Qiu, G. Y.: Physics-constrained machine learning of evapotranspiration, Geophys. Res. Lett., 46, 14496–14507, 2019.
We make a distinction between the parameters of PB simulators and the parameters embedded in neural networks, which are optimized during training by backpropagation. In this report, we almost exclusively refer to the parameters of PB simulators, even as we discuss the capacity of neural networks to learn and represent them.
We share the literature's tendency to use “conditional” and “posterior” density interchangeably; denotations of , for the posterior density evaluated at an observation YObs, and for conditional density representative of a large set of simulated {θ,Y}, are used when possible to reduce ambiguity.
This behavior is also observed in Fig. D1a, which shows that the determinant exhibits a fixed pattern across parameter space.
Note that the Mahalanobis distance is a precision-weighted metric of distance, unlike Euclidean distance. These numbers should not be considered raw distance.
- Abstract
- Introduction
- Background of inference-based approaches to hydrologic parameter determination
- Materials and methods
- Results
- Discussion
- Conclusion
- Appendix A: The process-based simulations (ParFlow)
- Appendix B: The surrogate simulator (LSTM)
- Appendix C: Improved components for SBI
- Appendix D: Inference for many observations, YObs_LSTM_i
- Appendix E: Inference on non-synthetic observations at the Taylor River
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Background of inference-based approaches to hydrologic parameter determination
- Materials and methods
- Results
- Discussion
- Conclusion
- Appendix A: The process-based simulations (ParFlow)
- Appendix B: The surrogate simulator (LSTM)
- Appendix C: Improved components for SBI
- Appendix D: Inference for many observations, YObs_LSTM_i
- Appendix E: Inference on non-synthetic observations at the Taylor River
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References