Solutions and case studies for thermally driven reactive transport and porosity evolution in geothermal systems (reactive Lauwerier problem)

Subsurface non-isothermal fluid injection is a ubiquitous scenario in energy and water resource applications, which can lead to geochemical disequilibrium and thermally driven solubility changes and reactions. Depending on the nature of the solubility of a mineral, the thermal change can lead to either mineral dissolution or precipitation (due to undersaturation or supersaturation conditions). Here, by considering this thermo-hydro-chemical (THC) scenario and by calculating the temperature-dependent solubility using a non-isothermal solution (the so-called Lauwerier solution), thermally driven reactive transport solutions are derived for a confined aquifer. The coupled solutions, hereafter termed the “reactive Lauwerier problem”, are developed for axisymmetric and Cartesian symmetries and additionally provide the porosity evolution in the aquifer. The solutions are then used to study two common cases: (I) hot CO₂-rich water injection into a carbonate aquifer and (II) hot silica-rich water injection into a sandstone aquifer, leading to mineral dissolution and precipitation, respectively. We discuss the timescales of such fluid–rock interactions and the changes in hydraulic system properties. The solutions and findings contribute to the understanding and management of subsurface energy and water resources, such as aquifer thermal energy storage, aquifer storage and recovery and reinjection of used geothermal water. The solutions are also useful for developing and benchmarking complex coupled numerical codes.

1 Introduction

The recharge or injection of fluids in constrained physical and chemical states in geothermal systems and aquifers is a common phenomenon in both natural and applied systems (Phillips, 2009; Stauffer et al., 2013). In many instances, thermal changes within these systems can shift the system from a state of geochemical equilibrium to disequilibrium and lead to chemical reactions over extensive distances determined by the variations in temperature. These perturbations result from the changes in the solubility of minerals in groundwater, which can become supersaturated or undersaturated in response to thermal changes. These thermally driven reactions cause progressive changes in the rock porosity and hydraulic properties that result from accumulation, removal, or replacement of solid minerals and the accompanied volumetric changes (Phillips, 2009; Woods, 2015). Such processes are responsible for the natural transformations of rocks from diagenesis and metamorphism (Jamtveit and Yardley, 1996; Yardley et al., 2011) to the evolution of aquifers and reservoirs (Andre and Rajaram, 2005; Jones and Xiao, 2006) and melt migration in the Earth's mantle (Aharonov et al., 1995; Kelemen et al., 1995). In applied systems, fluid–rock interactions can significantly impact hydrothermal performance at a timescale of years (Huenges et al., 2013; Pandey et al., 2018).

Depending on the natural solubility of the minerals in the system, an increase in temperature can induce either dissolution or precipitation. This is because mineral solubilities can either increase with temperature (“prograde solubility”) or decrease with it (“retrograde solubility”; Jamtveit and Yardley, 1996; Woods, 2015). Flow and transport commonly influence the state of saturation by continuously introducing thermally disequilibriated fluid, which subsequently becomes geochemically disequilibriated. This occurs because, in many cases, advection serves as the dominant transport mechanism, characterized by a shorter timescale (t_A) compared to diffusive heat (t_C) or diffusive solute transport (t_D). These timescales are represented by $t_{\mathrm{A}}=l_{\mathrm{A}}/u_{\mathrm{A}}$, $t_{\mathrm{C}}=l_{\mathrm{C}}^{\mathrm{2}}/{\mathit{\alpha }}_{\mathrm{b}}$, and $t_{\mathrm{D}}=l_{\mathrm{D}}^{\mathrm{2}}/D$ , where l_A, l_C, and l_D are characteristic length scales of advection, heat conduction, and ionic diffusion, respectively. Here, u_A denotes the characteristic Darcy flux [L T⁻¹], while α_b and D are the bulk thermal diffusivity and ionic diffusion coefficient, respectively. The ratio of these timescales defines the thermal Péclet number (${\mathit{Pe}}_{\mathrm{T}}=t_{\mathrm{C}}/t_{\mathrm{A}}$) and the solute Péclet number (${\mathit{Pe}}_{\mathrm{s}}=t_{\mathrm{D}}/t_{\mathrm{A}}$), which are used to characterize the transport regime in these systems. When Pe_T and Pe_s are high (i.e., ≫1), advective transport prevails (Ladd and Szymczak, 2021; Nield and Bejan, 2017; Roded et al., 2020).

The overall integrated action of these mechanisms results in a coupled thermo-hydro-chemical (THC) process (Huenges et al., 2013; Pandey et al., 2018; Phillips, 2009; Regenauer-Lieb et al., 2013). The tightly coupled feedbacks in THC processes commonly render them highly nonlinear. Fluid flow and diffusive heat and solute transport induce chemical reactions, which alter the pore structure and its transport properties, leading to further feedback on flow and transport (Chaudhuri et al., 2013; Phillips, 2009; Woods, 2015). Studying these coupled feedback alterations improves the understanding of reactive transport processes taking place in the Earth's upper crust. Specifically, these studies are integral to the sustainable planning and long-term management of water resources (Andre and Rajaram, 2005; Phillips, 2009), geothermal energy systems (on the scale of tens of years; Frick et al., 2011; Huenges et al., 2013; Pandey et al., 2018), and CO₂ geo-sequestration (Dávila et al., 2020; Steefel et al., 2013; Tutolo et al., 2015).

In enhanced geothermal systems (EGSs) in particular, channelized dissolution can create a short circuit and reduce the heat exchange between the rock and the fluid. Conversely, precipitation can significantly reduce permeability, leading to reduced production and potentially sealing reservoirs (Huenges et al., 2013; Olasolo et al., 2016; Pandey et al., 2018). Another challenge associated with geothermal utilization is the risk of groundwater contamination, where thermal changes can lead to the leaching of undesired chemical species from the rocks. Specifically, contamination may arise from the reinjection of fluids required to maintain reservoir pressure from aquifer thermal energy storage (ATES) systems that leverage seasonal temperature fluctuations (Bonte et al., 2014; Glassley, 2014; Possemiers et al., 2014). It may also result from substantial injections of hotter or colder water for groundwater management practices, such as aquifer storage and recovery (ASR) (Maliva, 2019; Zheng et al., 2021).

In terms of mineralogy, a range of thermally driven reactions occurs in the previously mentioned systems. Commonly reported precipitates accumulating in geothermal plant piping loops and natural spring deposits include carbonates (e.g., calcite, dolomite, and siderite), sulfates (e.g., gypsum and baryte), and amorphous silica (Glassley, 2014; Huenges et al., 2013). Particularly, geothermal systems composed of sandstones and carbonates are ubiquitous in the Earth's crust and are prone to alterations (Goldscheider et al., 2010; Pandey et al., 2018; Wood and Hewett, 1984). The solubility of silica is proportional to temperature (i.e., prograde solubility), and water pumping or injection can lead to substantial changes in reservoir transmissivity that can affect heat extraction (Pandey et al., 2018; Rawal and Ghassemi, 2014; Taron and Elsworth, 2009). In particular, silica precipitation can occur several orders of magnitude faster than the dissolution of either quartz minerals or amorphous silica (Rimstidt and Barnes, 1980). The exception is the dissolution of unconsolidated amorphous silica sediments (e.g., diatomite). Due to the high specific reactive surface area of the material, these sediments can be intensely dissolved when steam and hot water undersaturated with respect to silica are injected (Bhat and Kovscek, 1998). In contrast to silica, carbonate minerals demonstrate an inverse relation (i.e., retrograde solubility), which is often strong and influenced by CO₂ content. Consequently, limestone and dolomite aquifers and reservoirs subjected to geothermal flows, commonly rich in CO₂, can evolve at relatively short timescales. Either rapid dissolution or rapid precipitation can occur in such systems depending on conditions (Andre and Rajaram, 2005; Coudrain-Ribstein et al., 1998; Roded et al., 2023).

Investigating the multi-physical systems of THC processes is complex and relies on numerical models facilitated by ongoing advancements in computational capabilities (Kolditz et al., 2016; Pandey et al., 2018; Steefel et al., 2015). Over recent decades, these models have improved the understanding of subsurface processes (Niemi et al., 2017; Regenauer-Lieb et al., 2013; Seigneur et al., 2019; Steefel et al., 2013); however, the validity of such models remains questionable if the results cannot be rigorously tested (Kolditz et al., 2016; Nield and Bejan, 2017). Particularly, analytical solutions allow for the establishment of functional relationships between variables and physical properties and provide robust reliability and accuracy tests for numerical models (Bear and Cheng, 2010; Diersch and Kolditz, 2002; Nield and Bejan, 2017). However, comprehensive testing of multi-coupled THC codes is often mathematically cumbersome and precluded by many different approaches. This limitation arises because existing theoretical solutions focus solely on scenarios related to heat and/or solute transport (Diersch and Kolditz, 2002; Nield and Bejan, 2017; Stauffer et al., 2013; Turcotte and Schubert, 2002) or reactive solute transport (Bear and Cheng, 2010; Nield and Bejan, 2017) and because complete solutions that involve coupled THC processes are scarce (White et al., 2018). To the best of the authors' knowledge, coupled THC solutions are limited to two scenarios: thermally driven reactive front development (Jupp and Woods, 2003, 2004) and thermal and/or solutal convection in a reactive medium (e.g., Rayleigh–Bénard equivalent in a reactive porous medium; Al-Sulaimi, 2015; Corson and Pritchard, 2017). Solutions for fundamental and practical situations in geothermal and groundwater systems, such as non-isothermal injection into a reservoir and consequent matrix modifications, are missing. This is despite the existence of the so-called “Lauwerier solution” (Lauwerier, 1955), which analytically predicts the thermal field resulting from hot (or cold) fluid injection into a thin non-reactive confined layer system. The Lauwerier solution has served as the basis for the development of multiple modified heat transport solutions, accounting for various boundary conditions and system geometries, considering conduction and dispersion, and even accommodating fractured media (Abbasi et al., 2017; Chen and Reddell, 1983; Lin et al., 2019; Shaw-Yang and Hund-Der, 2008; Voigt and Haefner, 1987; Yang et al., 2010; Zhou et al., 2019; Ziagos and Blackwell, 1986; see review in Stauffer et al., 2013).

In the present work, we present analytical solutions, invoking non-isothermal fluid injection from a point or planar source into a thin confined aquifer (essentially the same scenario as of the Lauwerier problem). However, in this study, thermal changes drive the reactions and porosity evolution. Here, we define and solve the coupled physics of the “reactive Lauwerier problem”. To achieve this, we employ a temperature-dependent solubility in a reactive-flow formulation, while accounting for the thermal field following the Lauwerier formulation. The equations are solved for radial and planar flows, and the general solutions are applied to two common scenarios: carbonate dissolution and silica precipitation with respective permeability evolutions of each.

2 Mathematical analyses

2.1  Reactive Lauwerier scenario and the conceptual model

We consider Lauwerier problem settings (Lauwerier, 1955; Stauffer et al., 2013) involving the injection of hot (or cold) fluid into a confined aquifer located between bedrock and caprock, with lateral flow along the coordinate φ. The latter can represent the radial coordinate in an axisymmetric setting or x in Cartesian coordinates; i.e., φ=r or x. Figure 1 illustrates a summary of the problem, while Appendix F provides a summary of the nomenclature.

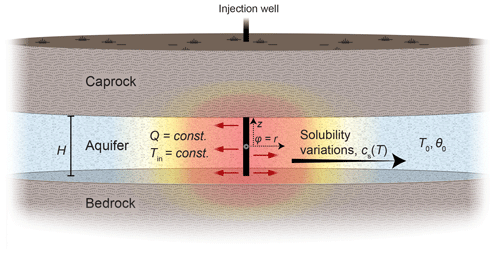
Figure 1 Sketch of the reactive Lauwerier problem and the conceptual model for thermally driven reactive transport in geothermal systems (the radial case). Hot (or cold) fluid is injected into a confined aquifer between aquiclude bedrock and caprock at a constant flow rate, Q, and temperature, T_in. The initial temperature of the aquifer is T₀, and its thickness is H. Downstream, along the flow path, heat is conducted from the aquifer through the confining layers. Thermal variations in the aquifer (color gradients) induce a change in solubility, c_s(T), and hence disequilibrium and reaction, which in turn drive the evolution of the porosity of the aquifer from its initial value, θ₀. z represents the vertical coordinate. In the main text, both polar and Cartesian geometries are considered, with φ=r or x, respectively. The origin of φ and z is defined at the center of the injection well. The injection well exhibits either axial (as shown in the sketch) or planar symmetry if Cartesian geometry is considered.

Downstream, along the flow path away from the injection point, heat is exchanged between the aquifer and the impermeable confining rock layers. Within the confining layers, heat is transported by conduction alone. The heat exchange and thermal variations in the aquifer induce changes in the solubility of the minerals (i.e., saturation concentration, c_s(T)), which in turn trigger undersaturation and dissolution reactions or, conversely, supersaturation and precipitation reactions that modify the aquifer porosity, θ. Both removal or accumulation of minerals can occur depending on the injection temperature (colder or warmer than ambient) and the prograde or retrograde nature of the reactive minerals. Our radial setup pertains to injection from a single well or mimics natural localized thermal upwelling in fractured/faulted media of deep origin, discharging into the shallower aquifer (Craw, 2000; Micklethwaite and Cox, 2006; Roded et al., 2013, 2023; Tripp and Vearncombe, 2004). The planar source setup simulates injection wells arranged in a straight line (Lauwerier, 1955).

2.2 Main model assumptions

Here, the THC conceptual model shown in Fig. 1 is mathematically described using conservation equations for heat and reactive transport along with initial and boundary conditions. The thermal Lauwerier solution and the mathematical model involve several simplifying assumptions, the major ones of which are listed below. For a more comprehensive overview, expanded versions of the conservation equations are provided in Appendix A.

The underlying thermal assumptions include negligible basal (background) geothermal heat flow and an initial geothermal gradient compared to the heat input by the injected fluid. The aquifer is located at a significant depth, preventing heat transport to the surface; otherwise, greater heat exchange would occur between the aquifer and the caprock. This assumption regarding the depth also depends on the timescale of interest: the thermal front, which ascends with time, may not reach the surface on a short timescale. However, it may transport heat to the surface after a longer time (which can be estimated using t_C).

Heat transport in the layers confining the aquifer is described by conduction and only in the vertical direction (z), neglecting lateral (φ) heat conduction. This assumption limits the applicability of the solution to scenarios involving large injected fluid fluxes. To assess the validity of this assumption, a thermal Péclet number, which compares heat advection in the aquifer to lateral heat conduction, ${\mathit{Pe}}_{\mathrm{T}}=u_{\mathrm{A}}l/{\mathit{\alpha }}_{\mathrm{b}}$, is used. Pe_T involves a length scale, l, at which substantial temperature variation occurs (e.g., larger than 2 % from the total temperature change, ΔT). An analysis using the parameter values in Table 1 and the results in Sect. 3 (i.e., a posteriori inspection) confirm that Pe_T≫1 at all times. Additionally, beyond the very early moments, the length scale of l should be larger than the vertical dimension of the aquifer, H, at which complete thermal mixing is assumed (l≫H). This assumption may not be applicable if a thick aquifer (i.e., large H) is considered and substantial vertical temperature gradients are expected to develop.

Furthermore, conduction and solute diffusion within the aquifer groundwater are neglected because the respective thermal (Pe_T) and solute (Pe_s) Péclet numbers are assumed to be large. Fluid and solid properties, such as density and heat conductivity, are considered constant and independent of temperature. It is noted that for CO₂ applications, the assumption of constant density and incompressibility may not be appropriate for a CO₂-rich phase (supercritical or gas) with moderate temperature changes (e.g., ΔT>40 °C).

Furthermore, the specific reactive surface area, A_s (L² to L⁻³ of the porous medium), is considered constant here and assumed not to change as reaction progresses. In most instances, this assumption does not weaken the applicability of the solution since A_s may vary widely across different rock lithologies, e.g., from 10⁻¹ m⁻¹ in fractured media (Deng and Spycher, 2019; Pacheco and Van der Weijden, 2014) to above 10⁵ m⁻¹ for porous rocks (Mostaghimi et al., 2013; Noiriel et al., 2012; Seigneur et al., 2019) and can often only be estimated very roughly (e.g., within an order of magnitude accuracy). Furthermore, A_s can evolve with the reactive flow in a way that is difficult to estimate (Noiriel, 2015; Seigneur et al., 2019). If large porosity changes occur, the inherent assumption of a constant A_s can limit the applicability of the solutions.

2.3 The basic conservation equations

Neglecting heat conduction in the radial direction, r, the heat conduction equation in the rock confining the aquifer above and below is given by

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\partial T}{\partial t}}={\mathit{\alpha }}_{\mathrm{b}}{\displaystyle \frac{{\partial }^{\mathrm{2}}T}{\partial z^{\mathrm{2}}}}\left\{\begin{array}{l}z\le -\frac{H}{\mathrm{2}},\\ z\ge \frac{H}{\mathrm{2}},\end{array}\right.\end{array}$$

where T represents temperature; t denotes time; z is the vertical coordinate, with its origin at the center of the injection well; and H is the aquifer thickness (see Fig. 1). The quantity ${\mathit{\alpha }}_{\mathrm{b}}=K_{\mathrm{b}}/C_{{\mathrm{p}}_{\mathrm{b}}}$ is the thermal diffusivity [L² T⁻¹], where the subscript b indicates bulk rock, K is the thermal conductivity, and C_p is the volumetric heat capacity (Chen and Reddell, 1983; Stauffer et al., 2013).

Assuming that heat transport in the fluid along the aquifer is governed by advection and that complete mixing occurs in the aquifer transverse direction (z), a depth-averaged heat-transport equation can then be formulated for the aquifer region:

$$\begin{array}{}\text{(2)}& C_{{\mathrm{p}}_{\mathrm{b}}}H{\displaystyle \frac{\partial T}{\partial t}}=-C_{{\mathrm{p}}_{\mathrm{f}}}H{\displaystyle \frac{\mathrm{1}}{r}}{\displaystyle \frac{\partial \left(ruT\right)}{\partial r}}-\mathrm{\Theta }(r,t)\mathrm{for}-{\displaystyle \frac{H}{\mathrm{2}}}\le z\le {\displaystyle \frac{H}{\mathrm{2}}},\end{array}$$

where subscript f denotes fluid and u(r) is the radial superficial velocity (or Darcy flux), which can be determined from the total volumetric flow rate, Q, using $u=Q/\left(H\mathrm{2}\mathit{\pi }r\right)$ (assuming u to be uniform along the z direction of the aquifer; Andre and Rajaram, 2005; Lauwerier, 1955). Function Θ accounts for the heat exchange between the aquifer and the confining rock located above and below, calculated using Fourier's law, with continuous temperature assumed at the interfaces:

$$\begin{array}{}\text{(3)}& \mathrm{\Theta }=-\mathrm{2}{K}_{\mathrm{b}}{\left.{\displaystyle \frac{\partial T}{\partial z}}\right|}_{z=\frac{H}{\mathrm{2}}}.\end{array}$$

The factor of 2 accounts for the rock both above and below the horizon (Stauffer et al., 2013).

The solute transport advection–reaction equation in the aquifer is

$$\begin{array}{}\text{(4)}& \mathrm{0}=-u{\displaystyle \frac{\partial c}{\partial r}}-\mathrm{\Omega }(r,t)\mathrm{for}-{\displaystyle \frac{H}{\mathrm{2}}}\le z\le {\displaystyle \frac{H}{\mathrm{2}}}.\end{array}$$

Here, c is the solute concentration [M L⁻³] and Ω is the reaction term (Chaudhuri et al., 2013; Szymczak and Ladd, 2012). Equation (4) is derived by neglecting transient and diffusive terms in the advection–diffusion–reaction equation (Eq. A3). The justification for the quasi-static approximation used when deriving Eq. (4) lies in the separation of timescales between heat conduction (t_C) in the confining rocks and mineral alteration (t_M) and the relaxation of solute concentration (t_A) (for in-depth analysis and discussion, see Appendix B and, e.g., Detwiler and Rajaram, 2007; Ladd and Szymczak, 2017; Lichtner, 1991; Roded et al., 2020; Sanford and Konikow, 1989).

Here, we assume a surface-controlled reaction and first-order kinetics:

$$\begin{array}{}\text{(5)}& \mathrm{\Omega }=A_{\mathrm{s}}\mathit{\lambda }\mathrm{\Lambda },\end{array}$$

where A_s is the specific reactive surface area and λ is the kinetic reaction rate coefficient [L T⁻¹], here assumed to be constant (Dreybrodt et al., 2005; Seigneur et al., 2019). Λ is denoted as the solute disequilibrium and is defined as the difference between the concentration of dissolved ions and saturation (equilibrium) concentrations, c_s,

$$\begin{array}{}\text{(6)}& \mathrm{\Lambda }=c-c_{\mathrm{s}}\left(T\right).\end{array}$$

Thus, the solute disequilibrium, Λ, is negative for undersaturation and positive for supersaturation. c_s is calculated as follows:

$$\begin{array}{}\text{(7)}& c_{\mathrm{s}}\left(T\right)=c_{\mathrm{s}}\left(T_{\mathrm{0}}\right)+\mathit{\beta }\left(T-T_{\mathrm{0}}\right).\end{array}$$

Here, T₀ represents the initial temperature in the aquifer and the parameter $\mathit{\beta }=\partial c_{\mathrm{s}}/\partial T$. Equation (7) assumes a linear relationship between c_s and T, with a constant proportionality factor, β, which is positive for minerals of prograde solubility and negative for minerals of retrograde solubility (Al-Sulaimi, 2015; Corson and Pritchard, 2017; Woods, 2015).

Given the reaction rate (Eq. 5), the change in porosity, θ, can be calculated as follows:

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{\partial \mathit{\theta }}{\partial t}}=-{\displaystyle \frac{\mathrm{\Omega }}{\mathit{\nu }{c}_{\mathrm{sol}}}}\mathrm{for}-{\displaystyle \frac{H}{\mathrm{2}}}\le z\le {\displaystyle \frac{H}{\mathrm{2}}},\end{array}$$

where c_sol is the concentration of the soluble solid mineral and ν accounts for the stoichiometry of the reaction. In the case of planar flow and Cartesian coordinates, r can be replaced by x in the equations above, while Eq. (2) takes the following form:

$$\begin{array}{}\text{(9)}& C_{{\mathrm{p}}_{\mathrm{b}}}{\displaystyle \frac{\partial \left(HT\right)}{\partial t}}=-u{C}_{{\mathrm{p}}_{\mathrm{f}}}H{\displaystyle \frac{\partial T}{\partial x}}-\mathrm{\Theta }(x,t)\mathrm{for}-{\displaystyle \frac{H}{\mathrm{2}}}\le z\le {\displaystyle \frac{H}{\mathrm{2}}},\end{array}$$

where u here is the spatially uniform fluid velocity in the x direction.

2.4 Initial and boundary conditions

The initial conditions involve a uniform value of temperature T₀ throughout the medium. The boundary conditions at the injection well (φ=0) include a constant rate of fluid injection at temperature T_in and initially zero solute disequilibrium, Λ=0 (Eq. 6). The caprock and bedrock thickness and aquifer extent are assumed to be infinite.

2.5 Solution of the reactive Lauwerier problem

2.5.1 Axisymmetric (radial) flow

Aquifer temperature

The solution of Eqs. (1) and (2) for the temperature distribution in the aquifer (known as the Lauwerier solution) for the radial case is given by

$$\begin{array}{}\text{(10)}& T(r,t)=T_{\mathrm{0}}+\mathrm{\Delta }T\mathrm{erfc}\left[\mathit{\zeta }(r,t)r^{\mathrm{2}}\right].\end{array}$$

Here, erfc is the complementary error function, $\mathrm{\Delta }T=T_{\mathrm{in}}-T_{\mathrm{0}}$ is the difference between injection and initial aquifer temperature, and ζ is defined as

$$\begin{array}{}\text{(11)}& \mathit{\zeta }(r,t)={\displaystyle \frac{\mathit{\pi }\sqrt{K_{\mathrm{b}}{C}_{{\mathrm{p}}_{\mathrm{b}}}}}{Q{C}_{{\mathrm{p}}_{\mathrm{f}}}\sqrt{t^{\prime }}}}.\end{array}$$

The time variable, $t^{\prime }=t-\mathrm{2}r{C}_{{\mathrm{p}}_{\mathrm{b}}}/\left(C_{{\mathrm{p}}_{\mathrm{f}}}u\right)$, and the solution given by Eq. (10) holds when $t^{\prime }>\mathrm{0}$ (Stauffer et al., 2013). We additionally assume long enough time and conditions where $t^{\prime }\approx t$ (see Appendix C for analysis of the validity of this assumption). Furthermore, to simplify the equations, we assume equal heat capacities for both the confining rocks and the aquifer. To account for non-uniform heat capacities alternative form of Eq. (10) can be used (refer to Eqs. 3.122 and 3.131 and associated definitions in Stauffer et al., 2013).

Reactive solute transport

We begin by substituting Eq. (6) into Eq. (4) to obtain

$$\begin{array}{}\text{(12)}& \mathrm{0}=-u\left({\displaystyle \frac{\partial \mathrm{\Lambda }}{\partial r}}+{\displaystyle \frac{\partial c_{\mathrm{s}}}{\partial r}}\right)-\mathrm{\Omega }.\end{array}$$

The derivative $\partial c_{\mathrm{s}}/\partial r$ can then be expressed by differentiating the relationship in Eq. (7),

$$\begin{array}{}\text{(13)}& {\displaystyle \frac{\partial c_{\mathrm{s}}}{\partial r}}={\displaystyle \frac{\mathit{\beta }\partial T}{\partial r}},\end{array}$$

and further substituting Lauwerier solution (Eq. 10), which provides

$$\begin{array}{}\text{(14)}& {\displaystyle \frac{\mathit{\beta }\partial T}{\partial r}}=\mathrm{4}\mathrm{\Delta }T{\displaystyle \frac{\mathit{\beta }\mathit{\zeta }r}{\sqrt{\mathit{\pi }}}}{e}^{\left(-{\mathit{\zeta }}^{\mathrm{2}}{r}^{\mathrm{4}}\right)}.\end{array}$$

Next, substituting Eq. (14) into Eqs. (13) and (12) results in a linear inhomogeneous differential equation. Assuming saturation conditions at the inlet and the boundary condition of $\mathrm{\Lambda }(r=\mathrm{0})=\mathrm{0}$ leads to the following solution:

$$\begin{array}{}\text{(15)}& \mathrm{\Lambda }=\mathrm{\Delta }T\mathit{\beta }{e}^{\left(\frac{{\mathit{\eta }}^{\mathrm{2}}}{\mathrm{4}{\mathit{\zeta }}^{\mathrm{2}}}-\mathit{\eta }{r}^{\mathrm{2}}\right)}\left(\mathrm{erf}\left[\mathit{\zeta }{r}^{\mathrm{2}}-{\displaystyle \frac{\mathit{\eta }}{\mathrm{2}\mathit{\zeta }}}\right]+\mathrm{erf}\left[{\displaystyle \frac{\mathit{\eta }}{\mathrm{2}\mathit{\zeta }}}\right]\right),\end{array}$$

where erf is the error function and $\mathit{\eta }=H\mathit{\pi }{A}_{\mathrm{s}}\mathit{\lambda }/Q$. Appendix D presents an approximation for Eq. (15) which is useful for efficient computation and prevents integer overflow (Press et al., 2007).

Given the reaction rate (Eq. 5), the erosion and porosity change can be calculated using the solid erosion equation (Eq. 8). Substituting Eq. (15) into Eq. (8), integrating over time, and using the initial condition of $\mathit{\theta }(t=\mathrm{0})={\mathit{\theta }}_{\mathrm{0}}$ results in a closed-form expression for the temporal and spatial evolution of porosity, θ:

$$\begin{array}{}\text{(16)}& \begin{array}{rl}\mathit{\theta }(r,t)& ={\mathit{\theta }}_{\mathrm{0}}+\mathrm{4}{\displaystyle \frac{{\mathit{\zeta }}^{\mathrm{2}}t}{{\mathit{\eta }}^{\mathrm{2}}}}{\displaystyle \frac{\mathit{\lambda }{A}_{\mathrm{s}}\mathrm{\Delta }T\mathit{\beta }}{\mathit{\nu }{c}_{\mathrm{sol}}}}\left(-e^{\mathit{\eta }/\mathrm{4}\left(\frac{\mathit{\eta }}{{\mathit{\zeta }}^{\mathrm{2}}}-\mathrm{4}{r}^{\mathrm{2}}\right)}\right.\\ & \left(\mathrm{erf}\left[\mathit{\zeta }{r}^{\mathrm{2}}-{\displaystyle \frac{\mathit{\eta }}{\mathrm{2}\mathit{\zeta }}}\right]+\mathrm{erf}\left[{\displaystyle \frac{\mathit{\eta }}{\mathrm{2}\mathit{\zeta }}}\right]\right)+{\displaystyle \frac{\mathit{\eta }}{\mathit{\zeta }\sqrt{\mathit{\pi }}}}{e}^{-\mathit{\eta }{r}^{\mathrm{2}}}\\ & \left.+\mathrm{erf}\left[\mathit{\zeta }{r}^{\mathrm{2}}\right]\left(\mathrm{1}-\mathit{\eta }{r}^{\mathrm{2}}\right)-{\displaystyle \frac{\mathit{\eta }}{\mathit{\zeta }\sqrt{\mathit{\pi }}}}{e}^{-{\mathit{\zeta }}^{\mathrm{2}}{r}^{\mathrm{4}}}+\mathit{\eta }{r}^{\mathrm{2}}-\mathrm{1}\right).\end{array}\end{array}$$

2.5.2 Planar flow

In the Cartesian case, with injection along a line, the Lauwerier solution is

$$\begin{array}{}\text{(17)}& T(x,t)=T_{\mathrm{0}}+\mathrm{\Delta }T\mathrm{erfc}\left[\mathit{\omega }\right(x,t\left)x\right],\end{array}$$

where ω is defined as

$$\begin{array}{}\text{(18)}& \mathit{\omega }(x,t)={\displaystyle \frac{\sqrt{K_{\mathrm{b}}{C}_{{\mathrm{p}}_{\mathrm{b}}}}}{H{C}_{{\mathrm{p}}_{\mathrm{f}}}u\sqrt{t^{\prime }}}},\end{array}$$

and $t^{\prime }=t-x{C}_{{\mathrm{p}}_{\mathrm{b}}}/\left(C_{{\mathrm{p}}_{\mathrm{f}}}u\right)$. Similarly, to the radial case, the solution holds at sufficiently long times, for which $t^{\prime }\approx t$.

Following the analogous steps as in the radial case, the solution is derived by

$$\begin{array}{}\text{(19)}& \mathrm{\Lambda }=\mathrm{\Delta }T\mathit{\beta }{e}^{\left(\frac{{\mathit{\sigma }}^{\mathrm{2}}}{\mathrm{4}{\mathit{\omega }}^{\mathrm{2}}}-\mathit{\sigma }x\right)}\left(\mathrm{erf}\left[\mathit{\omega }x-{\displaystyle \frac{\mathit{\sigma }}{\mathrm{2}\mathit{\omega }}}\right]+\mathrm{erf}\left[{\displaystyle \frac{\mathit{\sigma }}{\mathrm{2}\mathit{\omega }}}\right]\right),\end{array}$$

and

$$\begin{array}{}\text{(20)}& \begin{array}{rl}\mathit{\theta }(x,t)& ={\mathit{\theta }}_{\mathrm{0}}+\mathrm{4}{\displaystyle \frac{{\mathit{\omega }}^{\mathrm{2}}t}{{\mathit{\sigma }}^{\mathrm{2}}}}{\displaystyle \frac{\mathit{\lambda }{A}_{\mathrm{s}}\mathrm{\Delta }T\mathit{\beta }}{\mathit{\nu }{c}_{\mathrm{sol}}}}\left(-e^{\mathit{\sigma }/\mathrm{4}\left(\frac{\mathit{\sigma }}{{\mathit{\omega }}^{\mathrm{2}}}-\mathrm{4}x\right)}\right.\\ & \left(\mathrm{erf}\left[\mathit{\omega }x-{\displaystyle \frac{\mathit{\sigma }}{\mathrm{2}\mathit{\omega }}}\right]+\mathrm{erf}\left[{\displaystyle \frac{\mathit{\sigma }}{\mathrm{2}\mathit{\omega }}}\right]\right)+{\displaystyle \frac{\mathit{\sigma }}{\mathit{\omega }\sqrt{\mathit{\pi }}}}{e}^{-\mathit{\sigma }x}\\ & \left.+\mathrm{erf}\left[\mathit{\omega }x\right](\mathrm{1}-\mathit{\sigma }x)-{\displaystyle \frac{\mathit{\sigma }}{\mathit{\omega }\sqrt{\mathit{\pi }}}}{e}^{-{\mathit{\omega }}^{\mathrm{2}}{x}^{\mathrm{2}}}+\mathit{\sigma }x-\mathrm{1}\right),\end{array}\end{array}$$

where $\mathit{\sigma }=A_{\mathrm{s}}\mathit{\lambda }/u$.

3 Thermally driven reactive flow in geothermal systems

In this section, we use the radial solutions presented in the previous section to examine two common scenarios: (I) injection of CO₂-rich hot water into a carbonate aquifer and (II) injection of silica-rich hot water into a sandstone aquifer. These scenarios result in cooling-induced calcite dissolution and silica precipitation, respectively. The subsequent porosity evolution within these systems (Eqs. 16 and 20) is then used to estimate the evolution of aquifer permeability. These scenarios are pertinent, for instance, in aquifer thermal storage, reinjection of geothermal water at shallow depths, or applications of groundwater storage and recovery (Diaz et al., 2016; Fleuchaus et al., 2018; Maliva, 2019).

3.1 Aquifer properties and injection conditions

Here, we discuss conditions for thermally induced reactivity in carbonates and sandstone aquifers and the parameter values assigned in the simulations (Table 1). Regarding the description of the kinetics of these systems, calcite dissolution can often be complex, involving various chemical species and reactions of varying orders (Dreybrodt, 1988; Plummer et al., 1978). However, for a wide range of pH values, it can be simplified and described by assuming a linear dependence on undersaturation or acid concentration. Specifically, first-order kinetics are commonly employed to study natural karst formations (pH ∼ 6; Dreybrodt et al., 2005; Palmer, 1991), and dissolution under the acidic conditions common in engineering applications (pH ∼ 3; Hoefner and Fogler, 1988; Peng et al., 2015) or in geothermal systems of high CO₂ partial pressure, PCO₂ (pH∼ 5; Coudrain-Ribstein et al., 1998; Lu et al., 2020; Roded et al., 2023). Silica precipitation can be well described by first-order kinetics (Carroll et al., 1998; Ji et al., 2023; Pandey et al., 2015; Rimstidt and Barnes, 1980).

Table 1 Parameter values used in the simulations.

^a Glassley (2014). ^b Huenges and Ledru (2011). ^c Palmer (1991). ^d Rimstidt and Barnes (1980). ^e See text. ^f Hussaini and Dvorkin (2021) and Lai et al. (2015). ^g Roded et al. (2023).

We also exploit approximately linear temperature–solubility dependence over the temperature range studied here (between T₀=20 °C and T_in=60 °C) and assign a constant value to β (Eq. 7; Andre and Rajaram, 2005; Glassley, 2014; Rimstidt and Barnes, 1980; Roded et al., 2023). Additionally, it should be noted that in carbonates, the temperature–solubility relation strongly depends on PCO₂: higher PCO₂ values result in larger increases in c_s as the water cools (i.e., the magnitude of β is larger; see Fig. 2b in Roded et al., 2023, and Andre and Rajaram, 2005; Palmer, 1991). Here, in accordance with typical conditions in geothermal systems, we consider injection of water with PCO₂ = 0.03 MPa (Coudrain-Ribstein et al., 1998; Lu et al., 2020).

In the simulations, we assign characteristic porosity (θ) and reactive surface area (A_s) for the different aquifer types. In accordance with common field observations, we consider a carbonate aquifer in which flow and dissolution are focused in the permeable fracture network and a porous sandstone aquifer characterized by high intergranular permeability (Bear and Cheng, 2010; Jamtveit and Yardley, 1996). The different aquifer characteristics are reflected in significant differences in θ and A_s for the different aquifer types. Specifically, carbonates are often characterized by permeability contrasts spanning orders of magnitudes between the fractures and the rock matrix (Dreybrodt et al., 2005; Lucia, 2007). Consequently, transport in the matrix occurs mostly by slow diffusion, and the reaction within the matrix can be neglected. Hence, only the reactive surface area, A_s, of the fractures effectively participates in the reaction (Deng and Spycher, 2019; Maher et al., 2006; Pacheco and Alencoão, 2006; Seigneur et al., 2019). In this case, θ can be minimal (Lucia, 2007) and A_s is orders of magnitude smaller compared to its value in porous sandstones (Hussaini and Dvorkin, 2021; Lai et al., 2015; Pacheco and Alencoão, 2006; Pacheco and Van der Weijden, 2014; Seigneur et al., 2019). This disparity can lead to substantial differences in characteristic alteration rates and Damköhler numbers in these systems (Ladd and Szymczak, 2021; Lucia, 2007; Seigneur et al., 2019).

Specifically, in the case of fractured rocks as described above, we calculate the reactive surface area using $A_{\mathrm{s}}=\mathrm{2}\cdot \mathit{\kappa }\cdot \mathrm{RF}$, where κ is the fracture density (defined as the number of fractures per unit volume), the factor of 2 accounts for the presence of two surfaces, and RF is the roughness factor (Deng et al., 2018). Assuming $\mathit{\kappa }=\mathrm{1}/{\mathrm{3}}^{\mathrm{3}}$ m⁻³ and RF = 1.35 results in A_s=0.1 m⁻¹. Typical values of κ and fracture spacing can span a substantial range and may be higher or lower (Narr and Suppe, 1991; Scholz, 2019). Here, it is further assumed that the fracture density is high and the network is of high connectivity, allowing it to be treated as a continuum (Anderson et al., 2015; Sahimi, 2011). We consider here an injection flow rate of Q=500 m³ d⁻¹, which falls within the typical range of flow rates observed in relevant applications, such as geothermal systems (Glassley, 2014) or groundwater storage and recovery (Maliva, 2019). The injection temperature is set to T_in=60 °C, and aquifer ambient temperature is set to T₀=20 °C (ΔT=40 °C). To obtain the results, in this section, the solutions were implemented in MATLAB code (MATLAB, 2022). Appendix D details the use of the approximated Eq. (D2) in calculating the results in Figs. 2 and 3.

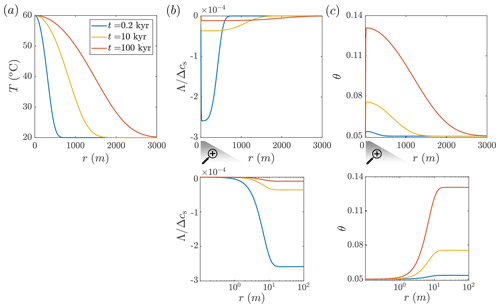
Figure 2 Carbonate aquifer dissolution by cooling hot water. Temperature, T; solute disequilibrium, Λ; and porosity, θ, in the aquifer are plotted as functions of the radial position, r, at different times (computed using Eqs. 10, 16, and D2). (a) The hot flow cools gradually as it travels through the aquifer, transferring heat to the confining rocks, thereby causing them to warm over time and the thermal front to progress downstream. (b) Cooling induces undersaturation (negative disequilibrium, Λ; see Eq. 6), which is of a relatively small magnitude due to the rapid kinetics of calcite dissolution. Λ is normalized by the total solubility change in the system, Δc_s (refer to the text for the definition of Δc_s). The water is hot and saturated at the inlet, c=c_s(T_in). Undersaturation quickly develops near the inlet (r≈20 m, as shown in the magnification) and then gradually diminishes due to dissolution reactions further along the flow path (Λ approaches zero). As the thermal front propagates over time, and thermal gradients diminish, the Λ curves also flatten. (c) Corresponding to Λ variations, a porosity profile develops over time (see the magnification for the inlet-adjacent region).

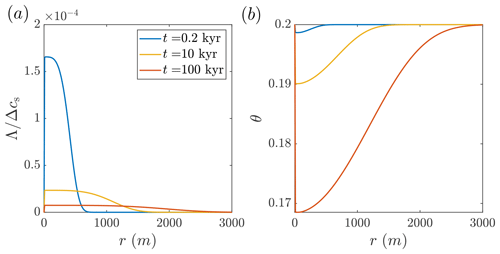
Figure 3 Silica precipitation in a sandstone aquifer by cooling hot water. The calculated solute disequilibrium, Λ, and porosity, θ, as functions of the lateral position, r, are shown at different times since the beginning of the injection (calculated using Eqs. 16 and D2; the temperature profile is given in Fig. 2a). The reactive transport processes in this case are similar to the carbonate dissolution system shown in Fig. 2, with insets Fig. 2b and c being approximately mirror images of panels (a) and (b), showing supersaturation and porosity reduction. (a) As a result of cooling, solute disequilibrium corresponding to supersaturation (Λ; Eq. 6) develops, which is of a small magnitude due to the high reaction rates (Λ is scaled by the total solubility change in the system, Δc_s; refer to the text for the definition of Δc_s). The water enters hot and saturated at the inlet, c=c_s(T_in), and, subsequently, Λ increases rapidly and then gradually diminishes downstream due to the reaction. The advancement of the thermal front over time and lower gradients lead to the flattening of Λ curves. (b) In accordance with Λ, an extensive porosity profile develops over time.

3.2 Carbonate aquifer dissolution by cooling water

In Fig. 2, the results of CO₂-rich hot water injection into a carbonate aquifer at successive times since the beginning of the injection are shown (Eqs. 10, 16, and D2 are solved for t=0.2, 10, and 100 kyr). During the radial flow within the aquifer, the hot fluid cools by transferring heat into the confining layers, which heat up with time, resulting in the gradual advancement of the thermal front downstream (Fig. 2a). The cooling induces solute disequilibrium (Λ) associated with undersaturation (note that Λ is negative for undersaturation and positive for supersaturation; see Eq. 6). The magnitude of Λ in the aquifer is small compared to the absolute solubility change in the system, $\mathrm{\Delta }{c}_{\mathrm{s}}=\left|c_{\mathrm{s}}\right(T_{\mathrm{in}})-c_{\mathrm{s}}(T_{\mathrm{0}}\left)\right|$, i.e., between c_s(T_in) at the injection point and c_s(T₀) at ambient conditions ($\left|\mathrm{\Lambda }\right|/\mathrm{\Delta }{c}_{\mathrm{s}}\ll \mathrm{1}$ %; see Fig. 2b). The small magnitude of disequilibrium is associated with relatively high PCO₂ considered here (0.03 MPa) and rapid kinetics under these conditions. The quasi-equilibrium conditions may allow for the simplification and calculation of the local reaction rate from transport processes alone, regardless of kinetics, referred to as the so-called “equilibrium model” (Andre and Rajaram, 2005; Bekri et al., 1995; Golfier et al., 2002; Lichtner, 1991), which will be the subject of a future research.

Although the magnitude of disequilibrium, Λ, is small, it controls the alteration of the aquifer and the evolution of its properties. Significantly, because the water at the inlet is hot and saturated with calcite, c=c_s(T_in), disequilibrium, and reaction rate are zero at the inlet, leading to no change in the porosity there (see Figs. 2b and 3c and their magnifications). Disequilibrium (undersaturation) sharply develops downstream of the injection site, first forming a small minimum (at r≈20 m) and gradually increasing to zero at greater distances. Undersaturation and dissolution along the flow path are controlled by the interplay of three processes: (I) dissolution reducing undersaturation (i.e., Λ becomes closer to zero), (II) progressive cooling increasing undersaturation, and (III) advection–transport–reaction products (i.e., calcium ions) radially outward from the well, helping maintain undersaturation. Here, the effect of fluid velocity and advection decays with a distance of $\mathrm{1}/r$.

High advection and cooling rates near the inlet result in the abrupt formation of undersaturation (i.e., negative Λ). Further downstream, undersaturation diminishes due to dissolution reactions. As the thermal front advances downstream over time and the temperature gradients diminish along the aquifer, the Λ curve flattens and becomes more elongated (see curves for t=10 and 100 kyr in Fig. 2b). Due to the disequilibrium, porosity grows with time. The porosity sharply increases near the inlet and then gradually decreases downstream (Fig. 2c). The porosity changes are extensive and take place over an aquifer area of ∼30 km² within a relatively short geological timescale of 100 kyr, resulting in the addition of significant void space of thousands of cubic meters ($\sim \mathrm{5}\times {\mathrm{10}}^{\mathrm{3}}$ m³).

An essential assumption underlying the solutions in Sect. 2 and the results depicted in Fig. 2 is the assumption of spatial uniformity and symmetry of reactive flow. In practical scenarios, however, dissolution instabilities can emerge at the reaction front. These instabilities, owing to the positive feedback between reaction and transport, may evolve into dissolution channels, often referred to as wormholes (Aharonov et al., 1997; Budek and Szymczak, 2012; Chadam et al., 1986; Ortoleva et al., 1987; Roded et al., 2018, 2021). The wormholes concentrate reactive flow, resulting in heterogeneous flow fields that cannot be accurately represented by assuming symmetry and uniformity. In such a case, the results of Fig. 2 can only be regarded as an average solution, which is not accurate locally.

Isothermal dissolution, driven by undersaturation of the incoming solution is known to be unstable in the radial geometry for a large-enough solute Péclet number, Pe_s, and intermediate Damköhler numbers. The Damköhler number here is given by $Da=A_{\mathrm{s}}\mathit{\lambda }{l}_{\mathrm{A}}/u_{\mathrm{A}}$ and represents the ratio between advective and reactive timescales (Daccord, 1987; Grodzki and Szymczak, 2019; Kalia and Balakotaiah, 2007; Xu et al., 2020). However, in our case, the cooling of the solution renews its aggressiveness, hence extending the penetration length in the system which may influence the stability of the reactive front (Xu et al., 2020). The effect of renewed aggressiveness by considering solubility gradients was studied for planar reactive flow in Aharonov et al. (1997) and Spiegelman et al. (2001) but requires further investigation for radial flow and taking into account coupling with heat transfer.

3.3 Silica precipitation by cooling water

Here, we consider the injection of hot silica-rich water that cools, becoming supersaturated and leading to silica precipitation, consequently reducing void space and permeability. While the previous case involved dissolution, this one involves precipitation; however, the thermal and reactive transport processes are similar in both cases (with approximately mirror-image Λ and θ profiles; see Figs. 2b, c and 3a, b).

Similarly to the previous section, the low magnitude of Λ suggests that the reaction rate (Eq. 5) is relatively high compared to transport processes, effectively reducing disequilibrium, Λ. It is noted that the reaction rates are high in both systems despite the orders-of-magnitude differences in the kinetic rate coefficient ($\mathit{\lambda }={\mathrm{10}}^{-\mathrm{6}}$ m s⁻¹ for calcite dissolution compared to $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{10}}$ m s⁻¹ for silica precipitation). However, this difference is largely compensated by the contrast between the reactive surface area of the porous sandstone and fractured carbonate aquifers (A_s=10⁴ m⁻¹ compared to 10 m⁻¹, respectively). It should also be noted that while precipitation of crystalline and non-crystalline (amorphous) silica is characterized by relatively high rates, dissolution of quartz and silica polymorphs is typically slower by several orders of magnitude (Rimstidt and Barnes, 1980).

While the reaction rates are high in both systems, differences exist in the absolute magnitude of porosity change resulting from the injection. For example, the maximal porosity change in the aquifer due to silica precipitation is approximately Δθ_max≈0.03, whereas for the carbonate case it is around Δθ_max≈0.08 (where $\mathrm{\Delta }{\mathit{\theta }}_{\max }=\left|{\mathit{\theta }}_{\max }\right(t=\mathrm{100}\mathrm{kyr})-{\mathit{\theta }}_{\mathrm{0}}|$ and θ_max denote the maximal porosity change along the profile). The predicted lower porosity change in silica arises mostly due to its lower total solubility change, Δc_s, and the reduced dependence of mineral solubility on temperature, expressed here by the β parameter (see Table 1). This conclusion is further supported by the fact that no disequilibriated fluid exits the system: the fluid flows out from the system at r=3000 m at a temperature that is close to the ambient temperature, T₀ (Fig. 2a), and chemically equilibrated (Λ=0; Figs. 2b and 3a).

3.4 Permeability evolution of the aquifers

The porosity changes affect the aquifer hydraulics. Here, we calculate the effective aquifer permeability, k_eff, within a distance, R, around the well. k_eff is calculated based on the relationship between the local porosity and permeability, utilizing the power-law relation $k\left(r\right)/k_{\mathrm{0}}=\left(\mathit{\theta }\right(r)/{\mathit{\theta }}_{\mathrm{0}}{)}^n$, where k₀ and θ₀ are the initial permeability and porosity (the steps for the calculation of k_eff are presented in Appendix E). The exponent n depends on various factors, such as medium microstructural details and the nature of the alteration processes (Seigneur et al., 2019; Steefel et al., 2015; Vafaie et al., 2023). The limited predictive capabilities of k–θ relations, including instances where counter trends of porosity and permeability changes occur (Garing et al., 2015), have been previously noted (e.g., Sabo and Beckingham, 2021). Here, it is applied to evaluate general trends, which, with the exception of unique cases, remain valid regardless of the porosity–permeability relation used.

The wide range of heterogeneous microstructures in rocks and sediments and their response to different reactive-flow regimes lead to a large variability in the exponent n values. For example, for relatively uniform spatial dissolution, n can range from ∼3 to a few dozen for the early stages of flow or when wormholes develop (Hao et al., 2013; Roded et al., 2020; Vafaie et al., 2023). For precipitation, n typically ranges from ∼2 up to above 10 (Aharonov et al., 1998; Hommel et al., 2018; Seigneur et al., 2019).

Figure 4 shows k_eff evolution over time for representative exponent values within a distance of R=3 km. The rapid increase in carbonate aquifer permeability indicates (in agreement with previous works, Agar and Geiger, 2015; Andre and Rajaram, 2005; Dreybrodt et al., 2005) that k_eff can be substantially altered within relatively short geological timescales. Specifically, the results suggest that k_eff can even increase by several tens of percents within tens to hundreds of years. Conversely, significant k_eff alterations due to silica precipitations (10 %–50 % reduction) involve typical timescales of tens of thousands of years. These findings are consistent with previous observations of dissolution and precipitation driven by a solubility gradient (e.g., Aharonov et al., 1997), emphasizing differences between these processes, as embodied in the exponent n. Moreover, under constant pressure (instead of constant flux) boundary conditions, this effect will be enhanced due to a positive (negative) feedback during dissolution (precipitation) (Aharonov et al., 1997).

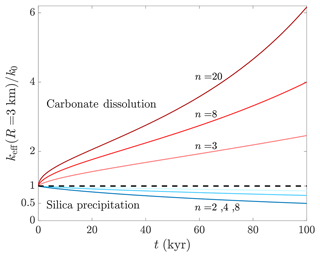
Figure 4 Evolution of aquifer effective permeability due to dissolution and precipitation. The effective permeability is k_eff, and t is time; red and blue curves designate carbonate dissolution and silica precipitation, respectively. k_eff is calculated within a radius of R=3 km from the well and is normalized by its initial value, k₀. The power-law θ–k relation is used to determine k_eff from the local porosity, θ(r), and permeability, k(r), with typical exponent values of n=3–20 for dissolution and n=2–8 for precipitation. k_eff can be substantially altered in carbonate aquifers due to dissolution even within tens to hundreds of years, while tens of thousands of years are required for similar magnitudes of change caused by silica precipitation.

4 Summary and conclusions

In this paper, we considered non-isothermal injection into a confined aquifer and the settings and solution of the so-called Lauwerier problem to derive coupled thermally driven reactive transport solutions (reactive Lauwerier problem). The presented solution is among the very limited number of analytical solutions available in the field of thermo-hydro-chemical (THC) flows in porous media. The THC scenarios considered here involved geochemical disequilibrium and reactions induced by thermally driven solubility changes, leading to mineral dissolution or precipitation. In the first section, solutions were derived for the evolution of solute concentration in radial and planar cases. These derivations utilized the non-isothermal Lauwerier solution to calculate the temperature-dependent solubility, which was then substituted into the reactive transport equation. Subsequently, the obtained concentration closed-form solutions were used to derive expressions for the porosity change in the aquifer.

In the second section, these solutions were employed to study two common cases in geothermal and water resource systems, exhibiting opposite feedback on porosity evolution: (I) injection of hot CO₂-rich water into a fractured carbonate aquifer, leading to cooling and dissolution, and (II) injection of hot silica-rich water into a sandstone aquifer, leading to silica precipitation. The resulting porosity profiles were then used to calculate the hydraulic changes and effective aquifer permeabilities. The results show that the timescale of porosity development in these systems is on the order of thousands to tens of thousands of years depending on the THC conditions (in agreement with previous works, Andre and Rajaram, 2005; Roded et al., 2023). Despite the often faster kinetics of carbonate dissolution compared to silica precipitation, similar timescales are observed in both systems. This is attributed to the high specific reactive surface area of sandstones, which enhances the reaction rate, compensating for the differences in kinetics between carbonate dissolution and silica precipitation. However, substantial hydraulic changes occur much faster in dissolving carbonate aquifers, possibly within tens to hundreds of years, primarily due to the rapid enhancement of permeability resulting from dissolution and a flow-enhanced feedback.

It is worth noting that under the typical conditions considered, the reaction rates are high and the geochemical disequilibrium in these systems is minimal (i.e., quasi-equilibrium). In such conditions, the equilibrium assumption, which simplifies calculations in the reactive Lauwerier problem and comprises an ongoing area of inquiry, may be applied. The solutions and analyses provided contribute to the understanding of natural and engineered hydrothermal systems, such as aquifer storage and recovery (ASR) and thermal energy storage (ATES) applications. Additionally, these solutions can aid in the development and benchmarking of coupled numerical models.

Appendix A: An extended form of the conservation equations

A1 Aquifer temperature

Assuming radial symmetry and that heat transport through the rocks confining the aquifer is governed by conduction, the heat equation in polar coordinates becomes

$$\begin{array}{}\text{(A1)}& {\displaystyle \frac{\partial T}{\partial t}}={\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{b}}}{r}}{\displaystyle \frac{\partial }{\partial r}}\left(r{\displaystyle \frac{\partial T}{\partial r}}\right)+{\mathit{\alpha }}_{\mathrm{b}}{\displaystyle \frac{{\partial }^{\mathrm{2}}T}{\partial z^{\mathrm{2}}}}\left\{\begin{array}{c}z\le -\frac{H}{\mathrm{2}},\\ z\ge \frac{H}{\mathrm{2}},\end{array}\right.\end{array}$$

where T is the temperature; t is time; r and z are the radial and vertical coordinates, respectively, with their origin at the injection well center; and H is aquifer thickness (see Fig. 1). The quantity ${\mathit{\alpha }}_{\mathrm{b}}=K_{\mathrm{b}}/C_{{\mathrm{p}}_{\mathrm{b}}}$ is the thermal diffusivity, where the subscript b denotes bulk rock, K is the thermal conductivity, and C_p is the volumetric heat capacity (Stauffer et al., 2013).

Assuming that heat transport in the fluid within the aquifer is governed by advection and conduction, the heat-transport equation can then be expressed as

$$\begin{array}{}\text{(A2)}& \begin{array}{rl}{C}_{{\mathrm{p}}_{\mathrm{b}}}{\displaystyle \frac{\partial T}{\partial t}}=& -C_{{\mathrm{p}}_{\mathrm{f}}}{\displaystyle \frac{\mathrm{1}}{r}}{\displaystyle \frac{\partial \left(ruT\right)}{\partial r}}+K_{\mathrm{b}}\left({\displaystyle \frac{\mathrm{1}}{r}}{\displaystyle \frac{\partial }{\partial r}}\left(r{\displaystyle \frac{\partial T}{\partial r}}\right)+{\displaystyle \frac{{\partial }^{\mathrm{2}}T}{\partial z^{\mathrm{2}}}}\right)\\ & \mathrm{for}-{\displaystyle \frac{H}{\mathrm{2}}}\le z\le {\displaystyle \frac{H}{\mathrm{2}}},\end{array}\end{array}$$

where subscript f denotes fluid and u(r) is the radial superficial velocity (or Darcy flux) and can be calculated from the total volumetric flow rate, Q, using $u=Q/\left(H\mathrm{2}\mathit{\pi }r\right)$ (assuming uniformity of u along the z direction of the aquifer; Andre and Rajaram, 2005; Chaudhuri et al., 2013).

Assuming complete thermal mixing in the transverse direction (z) of the aquifer allows us to establish the depth-averaged Eq. (2) in the main text. In this case, the heat exchange between the aquifer and the confining rocks is integrated within the heat exchange term (Θ).

A2 Reactive transport

Similarly, the solute transport advection–diffusion–reaction equation in the aquifer is

$$\begin{array}{}\text{(A3)}& \begin{array}{rl}{\displaystyle \frac{\partial c}{\partial t}}=& -u{\displaystyle \frac{\partial c}{\partial r}}+D\left({\displaystyle \frac{\mathrm{1}}{r}}{\displaystyle \frac{\partial }{\partial r}}\left(r{\displaystyle \frac{\partial c}{\partial r}}\right)+{\displaystyle \frac{{\partial }^{\mathrm{2}}c}{\partial z^{\mathrm{2}}}}\right)-\mathrm{\Omega }(r,t)\\ & \mathrm{for}-{\displaystyle \frac{H}{\mathrm{2}}}\le z\le {\displaystyle \frac{H}{\mathrm{2}}},\end{array}\end{array}$$

where c is the solute concentration [M L⁻³], D is the molecular diffusion coefficient, and Ω is the reaction term (Chaudhuri et al., 2013; Szymczak and Ladd, 2012). The equations describing the reaction term, Ω; saturation concentration, c_s; dependence on the temperature; and porosity change are given in Sect. 2.3 in the main text (Eqs. 5, 7, and 8, respectively).

In the case of planar flow and Cartesian coordinates, Eqs. (A1)–(A3) above take the following form:

$$\begin{array}{}\text{(A4)}& {\displaystyle }{\displaystyle \frac{\partial T}{\partial t}}={\mathit{\alpha }}_{\mathrm{b}}\left({\displaystyle \frac{{\partial }^{\mathrm{2}}T}{\partial x^{\mathrm{2}}}}+{\displaystyle \frac{{\partial }^{\mathrm{2}}T}{\partial z^{\mathrm{2}}}}\right)\left\{\begin{array}{c}z\le -\frac{H}{\mathrm{2}},\\ z\ge \frac{H}{\mathrm{2}},\end{array}\right.\text{(A5)}& {\displaystyle }\begin{array}{rl}{C}_{{\mathrm{p}}_{\mathrm{b}}}{\displaystyle \frac{\partial T}{\partial t}}=& -u{C}_{{\mathrm{p}}_{\mathrm{f}}}{\displaystyle \frac{\partial T}{\partial x}}+K_{\mathrm{b}}\left({\displaystyle \frac{{\partial }^{\mathrm{2}}T}{\partial x^{\mathrm{2}}}}+{\displaystyle \frac{{\partial }^{\mathrm{2}}T}{\partial z^{\mathrm{2}}}}\right)\\ & \mathrm{for}-{\displaystyle \frac{H}{\mathrm{2}}}\le z\le {\displaystyle \frac{H}{\mathrm{2}}},\end{array}\end{array}$$

and

$$\begin{array}{}\text{(A6)}& \begin{array}{rl}{\displaystyle \frac{\partial c}{\partial t}}=& -u{\displaystyle \frac{\partial c}{\partial x}}+D\left({\displaystyle \frac{{\partial }^{\mathrm{2}}c}{\partial x^{\mathrm{2}}}}+{\displaystyle \frac{{\partial }^{\mathrm{2}}c}{\partial z^{\mathrm{2}}}}\right)-\mathrm{\Omega }(x,t)\\ & \mathrm{for}-{\displaystyle \frac{H}{\mathrm{2}}}\le z\le {\displaystyle \frac{H}{\mathrm{2}}}.\end{array}\end{array}$$

Here u is the constant velocity in the x direction.

Appendix B: Timescale analysis to validate the quasi-static assumption

In our reactive transport calculations and Eq. (4) used for developing the solutions in Sect. 2, we adopt the quasi-static approach (Detwiler and Rajaram, 2007; Ladd and Szymczak, 2017; Lichtner, 1991; Roded et al., 2020; Sanford and Konikow, 1989) and neglect the transient term (present in Eqs. A3 and A6). However, it is noted that temporal variations may take place due to changes in the temperature field and their effect on the solubility, as arises from Eq. (7).

The justification for the quasi-static assumption lies in the significant separation of characteristic timescales in the system. There are three important timescales in our problem: (I) the timescale governing reactant transport (t_A), (II) the timescale of mineral chemical alteration (t_M), and (III) the characteristic timescale of conductive heat transport (t_C). The latter affects the solubility of aquifer minerals, thus influencing reaction and solute transport. Specifically, the conditions for the validity of quasi-static assumption are that t_C and t_M are several orders of magnitude larger compared to reactant transport relaxation time, t_A (i.e., t_A≪t_M and t_A≪t_C).

For example, in relatively fast-reacting natural carbonate systems, the doubling of initial pore size or fracture aperture due to dissolution typically occurs over a timescale of months to years. In silicate minerals, these timescales are of the order of thousands of years (Dove and Crerar, 1990; Ladd and Szymczak, 2021; Szymczak and Ladd, 2012; Zhu, 2005). Similarly, the characteristic timescale for the conduction processes in the confining rocks (t_C) is commonly several orders of magnitude longer than the relaxation time for reactant transport (t_A), which essentially maintains a steady state throughout the aquifer evolution. These timescales are given by

$$\begin{array}{}\text{(B1)}& t_{\mathrm{A}}={\displaystyle \frac{l_{\mathrm{A}}}{u_{\mathrm{A}}}},t_{\mathrm{C}}={\displaystyle \frac{l_{\mathrm{C}}^{\mathrm{2}}}{{\mathit{\alpha }}_{\mathrm{b}}}},\mathrm{and}{t}_{\mathrm{M}}={\displaystyle \frac{{\mathit{\theta }}_{\mathrm{0}}}{\mathit{\gamma }{A}_{\mathrm{s}}\mathit{\lambda }}},\end{array}$$

where l_A and l_C are characteristic length scales of advection and heat conduction, respectively, u_A denotes the characteristic Darcy flux [L T⁻¹], α_b is the bulk thermal diffusivity, θ₀ represents the initial porosity, A_s stands for the specific surface area of the reacting mineral [L² L⁻³], and λ is the kinetic reaction rate coefficient [L T⁻¹]. Here, $\mathit{\gamma }=\mathrm{\Delta }{c}_{\mathrm{s}}/c_{\mathrm{sol}}\mathit{\nu }$, where c_sol is the mineral concentration in the solid, ν accounts for the stoichiometry of the reaction, and Δc_s is the variation in solubility induced by thermal changes along the flow path. Δc_s is calculated here using the difference between the injected saturated fluid concentration, $c(\mathit{\phi }=\mathrm{0})=c_{\mathrm{s}}\left(T_{\mathrm{in}}\right)$, and the downstream saturation at the background aquifer temperature, c=c_s(T₀) (i.e., $\mathrm{\Delta }{c}_{\mathrm{s}}=\left|c_{\mathrm{s}}\right(T_{\mathrm{in}})-c_{\mathrm{s}}(T_{\mathrm{0}}\left)\right|$). γ is often referred to as the acid capacity number, representing the ratio between (I) under(super)-saturation created when cooling or heating the solution from T_in to T₀ and (II) the number of molecules in a unit volume of a mineral, c_sol (see parameter values in Table 1; Ladd and Szymczak, 2017; Roded et al., 2020).

In the calculation of timescale t_A, the characteristic length scale, l_A, can be set to be equal to the reactive front length, which in turn is affected by the thermal front length along the aquifer (φ direction). The length scale, l_C (used in t_C calculation) corresponds to the thermal front that develops in the confining insulating layers in the z direction, which elongates over time. In practice, the timescale separation between t_A and t_M and t_C can also be validated a posteriori. Under a large set of conditions, the reaction rate is limited solely by advective transport (i.e., regardless of kinetics), which leads to small geochemical disequilibrium (Andre and Rajaram, 2005). In such conditions, the actual timescale of matrix deformation will be much longer than predicted by the expression given above for t_M.

Appendix C: Lauwerier solution validity assuming $t^{\prime }\approx t$

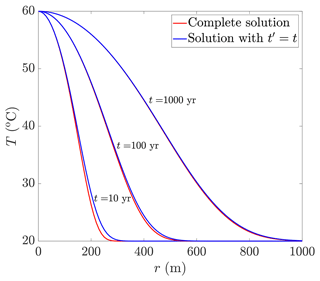
In this Appendix, the solution of Eq. (10) is compared to its approximated solution, when $t^{\prime }\approx t$ is assumed (Fig. C1). The results demonstrate that for times longer than 100 years, the differences between the solutions diminish, with a maximal error of 1.5 %, where the error is defined as $\mathrm{err}=\mathrm{100}\cdot \left(\right|T_{\mathrm{Ext}}-T_{\mathrm{Apr}}\left|\right)/\mathrm{\Delta }T$, with T_Ext and T_Apr being the exact and approximated solutions. These results confirm the validity of the assumption of $t^{\prime }\approx t$ and the derived solutions for times longer than 100 years under the conditions considered.

Figure C1 Comparison of the full and approximate solution for the temperature profile. The approximate solution considers $t^{\prime }=t$ (Eq. 10). The results demonstrate that for times longer than 100 years, the differences between the solutions diminish, with a maximal error of 1.5 % (see text).

Appendix D: Asymptotic expansion for the disequilibrium solutions

To obtain a solution by computational means and prevent an integer overflow (Press et al., 2007), it is useful to derive an approximate solution for Eq. (15) using the first-order asymptotic expansion of erf. Substituting this expansion into Eq. (15) leads to

$$\begin{array}{}\text{(D1)}& \begin{array}{rl}\mathrm{\Lambda }& ={\displaystyle \frac{\mathrm{\Delta }T\mathit{\beta }}{\sqrt{\mathit{\pi }}}}{e}^{\left(\frac{{\mathit{\eta }}^{\mathrm{2}}}{\mathrm{4}{\mathit{\zeta }}^{\mathrm{2}}}-\mathit{\eta }{r}^{\mathrm{2}}\right)}\left(-e^{\left(-\frac{{\mathit{\eta }}^{\mathrm{2}}}{\mathrm{4}{\mathit{\zeta }}^{\mathrm{2}}}\right)}{\displaystyle \frac{\mathrm{2}\mathit{\zeta }}{\mathit{\eta }}}\right.\\ & \left.+e^{-\left(\frac{{\mathit{\eta }}^{\mathrm{2}}}{\mathrm{4}{\mathit{\zeta }}^{\mathrm{2}}}-\mathit{\eta }{r}^{\mathrm{2}}+{\mathit{\zeta }}^{\mathrm{2}}{r}^{\mathrm{4}}\right)}{\displaystyle \frac{\mathrm{1}}{\frac{\mathit{\eta }}{\mathrm{2}\mathit{\zeta }}-\mathit{\zeta }{r}^{\mathrm{2}}}}\right),\end{array}\end{array}$$

and after further rearrangement, we finally arrive at

$$\begin{array}{}\text{(D2)}& \mathrm{\Lambda }={\displaystyle \frac{\mathrm{\Delta }T\mathit{\beta }}{\sqrt{\mathit{\pi }}}}{e}^{\left(-\mathit{\eta }{r}^{\mathrm{2}}\right)}\left({\displaystyle \frac{{\mathrm{e}}^{\left(\mathit{\eta }{r}^{\mathrm{2}}-{\mathit{\zeta }}^{\mathrm{2}}{r}^{\mathrm{4}}\right)}}{\frac{\mathit{\eta }}{\mathrm{2}\mathit{\zeta }}-\mathit{\zeta }{r}^{\mathrm{2}}}}-{\displaystyle \frac{\mathrm{2}\mathit{\zeta }}{\mathit{\eta }}}\right).\end{array}$$

For the planar injection case, we obtain the following from Eq. (19):

$$\begin{array}{}\text{(D3)}& \mathrm{\Lambda }={\displaystyle \frac{\mathrm{\Delta }T\mathit{\beta }}{\sqrt{\mathit{\pi }}}}{e}^{(-\mathit{\sigma }x)}\left({\displaystyle \frac{e^{\left(\mathit{\sigma }x-{\mathit{\omega }}^{\mathrm{2}}{x}^{\mathrm{2}}\right)}}{\frac{\mathit{\sigma }}{\mathrm{2}\mathit{\omega }}-\mathit{\omega }x}}-{\displaystyle \frac{\mathrm{2}\mathit{\omega }}{\mathit{\sigma }}}\right).\end{array}$$

To avoid integer overflow errors, Eq. (D2) is used to obtain the undersaturation profiles in Figs. 2b and 3a and is numerically iterated to solve for the porosity profile at later times (t≈100 kyr). The accuracy of the approximation of Eq. (D2) was verified by comparing it to the full solution in Eq. (15), which can be solved for early times (t≈1 yr). Furthermore, the accuracy of Eq. (D2) and the iterative solutions was further confirmed by solving for the porosity profile and comparing these results to those obtained using the full solution in Eq. (16) for t=10 kyr.

Appendix E: Permeability of an aquifer with non-uniform porosity profile

Using Darcy's law, we calculate an effective permeability, k_eff, for the aquifer around the well within a radius of r=R. The Darcy's law under these conditions is

$$\begin{array}{}\text{(E1)}& u\left(r\right)=-{\displaystyle \frac{k\left(r\right)}{\mathit{\mu }}}{\displaystyle \frac{\mathrm{d}p}{\mathrm{d}r}},\end{array}$$

where p and μ are the fluid pressure and viscosity and k the permeability. Integrating Eq. (E1) between r=0 and r=R leads to

$$\begin{array}{}\text{(E2)}& u\left(R\right)=-{\displaystyle \frac{R}{\mathit{\mu }\underset{\mathrm{0}}{\overset{R}{\int }}\frac{\mathrm{d}r}{k\left(r\right)}}}\left({\displaystyle \frac{\mathrm{\Delta }p}{R}}\right),\end{array}$$

and the effective permeability is

$$\begin{array}{}\text{(E3)}& k_{\mathrm{eff}}={\displaystyle \frac{R}{\underset{\mathrm{0}}{\overset{R}{\int }}\frac{\mathrm{d}r}{k\left(r\right)}}},\end{array}$$

which is calculated by numerical integration over the porosity profile and the power law given in Sect. 3.4.

Appendix F: Nomenclature

Roman		T	Temperature [°C]
As	Specific reactive surface area [m2 m−3]	u	Fluid velocity [m s−1]
c	Solute concentration [mol m−3]	uA	Characteristic velocity [m s−1]
cs	Saturation concentration [mol m−3]	x	Coordinate [m]
csol	Concentration of soluble solid [mol m−3]	y	Coordinate [m]
Cp	Volumetric heat capacity [J m−3 °C−1]	z	Coordinate [m]
D	Diffusion coefficient [m2 s−1]	Greek
Da	Damköhler number	α	Thermal diffusivity [m2 s−1]
erf	Error function	β	Solubility change parameter [mol m−3 °C−1]
erfc	Complementary error function	γ	Acid capacity number
err	Error	Δ	Total difference
H	Aquifer thickness [m]	η	Parameter group [m−2]
k	Permeability [m2]	θ	Porosity
keff	Effective permeability [m2]	Θ	Heat exchange term [W m−2]
K	Thermal conductivity [W m−1 °C−1]	κ	Fracture density
l	Characteristic length scale [m]	λ	Reaction rate coefficient [m s−1]
lA	Characteristic length scale of advection [m]	Λ	Solute disequilibrium [mol m−3]
lC	Characteristic length scale of conduction [m]	μ	Fluid viscosity [Pa s]
lD	Characteristic length scale of diffusion [m]	ν	Stoichiometric coefficient
n	Exponent of θ–k relation	ζ	Parameter group [m−2]
p	Fluid pressure [Pa]	ρ	Density [kg m−3]
Pes	Solute Péclet number	σ	Parameter group [m−1]
PeT	Thermal Péclet number	φ	Lateral coordinate φ=r or x [m]
Q	Total volumetric flow rate [m3 s−1]	ω	Parameter group [m−1]
r	Coordinate [m]	Ω	Reaction rate [mol m−3 s−1])
R	Effective permeability radius [m]	Subscripts
RF	Roughness factor	Apr	Approximated value
t	Time [s]	b	Bulk rock
tA	Characteristic timescale of advection [s]	Ext	Exact value
tC	Characteristic timescale of conduction [s]	f	Fluid
tD	Characteristic timescale of diffusion [s]	in	Inlet
tM	Characteristic timescale of mineral alteration [s]	max	Maximum
t′	Time parameter [s]	0	Initial average quantity