Hydro-pedotransfer functions: a roadmap for future development

Hydro-pedotransfer functions (PTFs) relate easy-to-measure and readily available soil information to soil hydraulic properties (SHPs) for applications in a wide range of process-based and empirical models, thereby enabling the assessment of soil hydraulic effects on hydrological, biogeochemical, and ecological processes. At least more than 4 decades of research have been invested to derive such relationships. However, while models, methods, data storage capacity, and computational efficiency have advanced, there are fundamental concerns related to the scope and adequacy of current PTFs, particularly when applied to parameterise models used at the field scale and beyond. Most of the PTF development process has focused on refining and advancing the regression methods, while fundamental aspects have remained largely unconsidered. Most soil systems are not represented in PTFs, which have been built mostly for agricultural soils in temperate climates. Thus, existing PTFs largely ignore how parent material, vegetation, land use, and climate affect processes that shape SHPs. The PTFs used to parameterise the Richards–Richardson equation are mostly limited to predicting parameters of the van Genuchten–Mualem soil hydraulic functions, despite sufficient evidence demonstrating their shortcomings. Another fundamental issue relates to the diverging scales of derivation and application, whereby PTFs are derived based on laboratory measurements while often being applied at the field to regional scales. Scaling, modulation, and constraining strategies exist to alleviate some of these shortcomings in the mismatch between scales. These aspects are addressed here in a joint effort by the members of the International Soil Modelling Consortium (ISMC) Pedotransfer Functions Working Group with the aim of systematising PTF research and providing a roadmap guiding both PTF development and use. We close with a 10-point catalogue for funders and researchers to guide review processes and research.

1 Introduction

Spatiotemporal variations in soil moisture contents and water fluxes affect soil biogeochemistry, soil–plant interactions, solute transport, and heat flow, thereby controlling a myriad of processes in Earth's critical zone (Vereecken et al., 2016, 2022). The prediction of these fluxes and states is crucial in multiple disciplines, such as hydrology, ecology, agriculture, climate, or soil science. Different theories have been proposed to model water flow in soils, but until today the Richards–Richardson equation (RRE), with its clear physical basis, has undoubtedly remained the most popular one (Raats and Knight, 2018). The equation finds wide application in numerical models in environmental (Vanclooster et al., 2000), agricultural (Asseng et al., 2015; Jarvis et al., 2022), and geoengineering (Chen et al., 2019) simulation studies. It is applied at different spatial scales, from a few centimetres (e.g. Weller et al., 2011), up to metres (Groh et al., 2020) and grid cells of kilometres (Ashby and Falgout, 1996; Kuffour et al., 2020), and at temporal scales ranging from days (Schelle et al., 2010) to seasons and years (Brandhorst et al., 2021; Wöhling et al., 2009; Warrach-Sagi et al., 2022) and decades (Basso et al., 2018; Riedel et al., 2023). The RRE is based on continuum theory and requires averaging of pore-scale variables to macroscopic state variables such as water content θ and pressure head h (Bear, 1988). The outcome of this averaging yields the soil water retention curve (WRC), θ(h), and the hydraulic conductivity curve (HCC), K(h). These continuous soil hydraulic properties (SHPs) are described using hydraulic functions or SHP models over the entire pressure head range, where the often easy-to-measure WRC is used to predict the HCC. An adequate representation of SHPs is crucial for reliable descriptions of soil water dynamics and the related processes. Water flow in soils is also described by simple models based on basic mass balance calculations (capacity models) (Gilding, 1992). These also require knowledge of SHPs, i.e. water content at specific pressure heads such as field capacity (FC), permanent wilting points or head ranges such as available water capacity. In principle, these can all be calculated using SHP functions.

Traditionally, SHPs are determined in the laboratory with different methods generally involving small-scale soil columns (typically 100–1000 cm³). SHPs are also derived at the lysimeter scale or the scale of individual pedons (Wöhling and Vrugt, 2008; Schelle et al., 2012; Over et al., 2015), typically in the range of several cubic metres. Beyond those scales, direct determination of SHPs becomes technically difficult. Instead, SHPs are commonly estimated using hydro-pedotransfer functions (PTFs). PTFs refer to linear or non-linear regression relationships between explanatory and predictor variables that allow the estimation of SHPs from basic soil data, such as texture data or easy-to-measure soil properties (Wösten et al., 2001). Thus, provided that the spatiotemporal states of soils are known (Gerke et al., 2022), which is still a great challenge in itself, PTFs can be used to relate the basic soil information contained in soil maps or easy-to-measure soil properties to derive the SHP of interest for use in numerical models, such as land surface models (LSMs).

The development of PTFs relies mostly on the derivation of relationships between predictors and response variables (Patil and Singh, 2016; van Looy et al., 2017), using, in increasing complexity, soil texture-based look-up tables (e.g. Schaap et al., 2001; Renger et al., 2008), regression approaches (e.g. Carsel and Parrish, 1988; Weynants et al., 2009, Weber et al., 2020), or more advanced machine learning (ML) methods (e.g. Szabó et al., 2021). Predictors generally include sand, silt, clay content, soil texture classes, bulk density (BD), and soil organic carbon (SOC). Some attempts have been made to include additional chemical and morphological properties and soil structure information (see van Looy et al., 2017) or water retention properties such as water content at field capacity (FC) and wilting point (WP) (Schaap et al., 2001).

The majority of PTFs predict parameters of the Brooks–Corey or van Genuchten (Brooks and Corey, 1964; van Genuchten, 1980) and capillary conductivity functions (Mualem, 1976). These PTFs have been developed mainly on the small scale, or scale of derivation, with the development mainly led by soil physicists working on experimental data from the laboratory. However, the scale of application typically ranges from field or pedon scales of several metres (Vogel, 2019) to regional or global scales where applications are typically done at a grid resolution much larger than 1 km, typically by modellers interested in the representation of different Earth system processes (e.g. Pinnington et al., 2021). This results in a striking dichotomy between both the scale of derivation and the scale of application and between the disciplines involved in the development and use of PTFs. Moreover, the evaluation of the performance of a given PTF across the different spatial (and temporal) scales is not necessarily based on the same criteria. In fact, from a modelling perspective, the characterisation of PTF performance depends on the scale of application and the specific process being modelled. In these regards, PTF evaluation restricted solely to laboratory-derived datasets entails several shortcomings with respect to the overall effectiveness of PTFs and confidence in their application at larger spatial scales. Obtaining effective soil parameters from small-scale measurements remains fraught with difficulty.

While this study does not provide technical details on how to build a PTF (for more detailed overviews of the topic, we refer the reader to Pachepsky and Rawls, 2004, and van Looy et al., 2017), we briefly point out that, quite generally, the relationship between predictor and predicted variables can be non-linear (Jarvis et al., 2013), and linear models may lead to underfitting even after the transformation of variables and parameters. ML approaches (e.g. random forests, gradient boosting, or neural networks) can deal with non-linearities at the price of being susceptible to overfitting, so that rigorous model validation schemes need to be used when employing them, such as block or stratified cross-validation (Jorda et al., 2015; Roberts et al., 2017). Nevertheless, ML techniques are the methods of choice for building modern PTFs provided that either the amount of available data is large enough to build the PTF model or, ideally, adequate ways of regularisation are available.

The aims of this article are to (i) summarise the state of research on SHP description for derivation of PTFs, (ii) discuss issues arising from the dichotomy between PTF developers and users, (iii) identify problems relating to measurements and currently available databases of soil (hydraulic) properties, (iv) provide a blueprint for the inference of soil hydraulic function parameters including evaluation at the appropriate scale and options for plausibility constraint, and (v) propose a roadmap for future research directions for the definition of a more robust and versatile next generation of PTFs. These aims are addressed by the following structure in Sects. 2–7.

In Sect. 2, we present the most commonly adopted SHP models and discuss potential improvements, inherently keeping PTF development in mind. Instead of giving a full review of SHP model development, it targets the most prominent aspects. In Sect. 2.1 we discuss issues related to the dominance of the van Genuchten–Mualem model, in Sect. 2.2 the lack of consideration of non-uniform pore size density distributions, and in Sect. 2.3 problems related to the deficiency in the capillary bundle model. The non-consideration of capillary hysteresis and dynamic non-equilibrium and transient SHPs is addressed in Sect. 2.4 and 2.5, respectively.

Section 3 is intended to assist the reader in the choice of PTFs for modelling applications while presenting the numerous limitations surrounding PTFs. Particular attention is devoted to the spatial validity and transferability of PTFs and highlighting key gaps in the data availability for specific biomes. We discuss the challenges related to the use of PTFs for large-scale application and the need to account for the temporal evolution of SHPs in climate and land use change studies. Lastly, we present various software and web-based tools for using PTFs. Specifically, there are words of caution in applying PTFs in land surface models (Sect. 3.1), especially regarding the spatial appropriateness and spatial validity of PTFs for large-scale application as well as methods of modulation to better suit the natural soil systems. The next four subsections deal with obvious gaps in PTFs for specific soils, substrate types, and land uses (Sect. 3.2); transient PTFs, accounting for the time dependency of SHPs (Sect. 3.3); regionalisation and upscaling (Sect. 3.4); and SHP maps (Sect. 3.5). Section 3 closes with a call for harmonising PTFs in model inter-comparison studies (Sect. 3.6), acknowledging that SHPs are an important contributor to uncertainties in modelling water fluxes in the Earth system, and finally there are guidance and tools to facilitate the use of PTFs (Sect. 3.7).

Section 4 is dedicated to the requirements of measurements and auxiliary information when compiling and harmonising datasets intended for PTF development (Sect. 4.1–4.3). Section 4.4 and 4.5 deal with the inclusion of soil structure characterisation and new opportunities for using in situ sensing.

While Sects. 1–4 address limitations and data needs surrounding PTF development and use, Sects. 5 and 6 address some key considerations regarding PTF development. Neither section intends to give a review of the technical methods to build PTFs but rather intends to address the fact that PTFs have to lead to predicted SHPs which lead to consistent and comprehensive simulations of water fluxes. As such, Sect. 5 presents concepts of constraint-based SHP parameterisation for plausible modelling with a list of some concrete examples to ensure that SHPs honour physical constraints. This section precedes Sect. 6, which substantially discusses the evaluation of PTFs, addressing the gap between the scale of derivation and the scale of application in PTF development and use (Sect. 6.1–6.3), and closes with a proposal for a standardised pedon-scale experiment to overcome the gap (Sect. 6.4) in scales.

Lastly, the paper closes with Sect. 7, a manifesto for future development and use, which we think is a solid basis for developers and reviewers of PTFs to refer to.

A glossary of abbreviations and variables is given in Table 1.

Table 1 Glossary of abbreviations used in the main text.

2 SHP models and egregious shortcomings

2.1 Issues related to the dominance of the van Genuchten–Mualem (VGM) model

A large number of SHP models have been proposed in the literature (as reviewed by Assouline and Or, 2013, and developments since). If we combine just the 22 water retention models listed in Du (2020) with the 9 models of relative conductivity collated by Assouline and Or (2013), we easily obtain around 200 SHP model combinations. This number includes purely empirical models (van Genuchten, 1980; Gardner, 1958), physically based models (Mualem, 1976), models with a low number of parameters (Brooks and Corey, 1966), and very flexible models with many parameters (Gwo et al., 1996).

Among all the different SHP models, the most popular is arguably the VGM model based on the capillary bundle concept. Here, the soil is represented by a “bundle” of vertical parallel pores of different sizes (capillaries are interconnected to pairs in the HCC model). For the WRC, the VGM model assumes that the effective saturation S_e (L³ L⁻³) is a simple sigmoidal function of the pressure head h (L):

$$\begin{array}{}\text{(1)}& S_{\mathrm{e}}\left(h\right)={\left[\mathrm{1}+(\mathit{\alpha }\left|h\right|{)}^n\right]}^{-m},\end{array}$$

where α (L⁻¹) is inversely correlated with the air entry value of the soil, and n (–) and m (–) are shape parameters related to the pore size distribution. In terms of pore size distribution, this function reflects a smooth unimodal equivalent pore size distribution, which is typical of well-sorted materials. The WRC is then given by

$$\begin{array}{}\text{(2)}& \mathit{\theta }\left(h\right)={\mathit{\theta }}_{\mathrm{r}}+\left({\mathit{\theta }}_{\mathrm{s}}-{\mathit{\theta }}_{\mathrm{r}}\right)S_{\mathrm{e}}\left(h\right),\end{array}$$

where θ_s (L³ L⁻³) is the saturated water content and θ_r (L³ L⁻³) is the “residual” or “irreducible” water content. Theoretically, for a fully saturated soil, θ_s is nearly equal to the porosity of the soil φ (L³ L⁻³). By constraining $m=\mathrm{1}-\mathrm{1}/n$ in Eq. (1), the conductivity model of Mualem (1976) yields (van Genuchten, 1980)

$$\begin{array}{}\text{(3)}& K\left(h\right)=K_{\mathrm{s}}{K}_{\mathrm{r}}\left(h\right)=K_{\mathrm{s}}{S}_{\mathrm{e}}^{\mathit{\tau }}{\left(\mathrm{1}-{\left[\mathrm{1}-S_{\mathrm{e}}^{\mathrm{1}/m}\right]}^m\right)}^{\mathrm{2}},\end{array}$$

where K(h) (L T⁻¹) is the saturated (for h=0) or unsaturated (for h<0) conductivity function, K_r(h) (–) is the relative conductivity function, ranging between 0 and 1, and K_s (L T⁻¹) is the saturated conductivity which, in principle, is the hydraulic conductivity for a fully saturated soil system where $K_{\mathrm{r}}(h=\mathrm{0})=\mathrm{1}$ and $\mathit{\theta }(h=\mathrm{0})={\mathit{\theta }}_{\mathrm{s}}\cong \mathit{\phi }$. According to Mualem (1976), τ (–) may be positive or negative and accounts for the connection between pores and for the flow path tortuosity. Based on regression with data from 45 soils, Mualem (1976) found that a value of 0.5 for the so-called tortuosity parameter is a suitable choice and has been used in the predominant cases.

The VGM model has become so widely used because (i) it is relatively flexible in describing WRC data, especially in the wet and mid-pressure head range; (ii) it is continuously differentiable over the full-pressure head range, something very useful for the numerical solution of the pressure head-based RRE; (iii) coupled with the Mualem (1976) theory, it does not require any measurement of unsaturated HCC; and finally (iv) it has been implemented in many soil process modelling tools such as HYDRUS (Šimùnek et al., 2016), SWAP (Kroes et al., 2017), or Expert-N (Priesack, 2006), hydrological models such as SWAT (Arnold et al., 2013), and many LSMs such as JULES (Best et al., 2011), to name a few examples. However, these highly attractive attributes as well as the early and widespread adoption of the VGM model, followed by a large number of VGM PTFs, is a bane to progress and has hampered adoption of more comprehensive SHP modelling approaches. Some of the most important shortcomings of the VGM model are mentioned in the following subsections.

2.2 Non-uniform pore size density distributions

In spite of its wide adoption, the use of the VGM model to represent SHPs is challenged as the underlying assumption of unimodal pore size distribution may be invalid since natural soils often exhibit bi- or multi-modal pore size distributions (e.g. Hadas, 1987; Dexter et al., 2008; Oades and Waters, 1991; Ippisch et al., 2006). Particularly in the presence of distinct soil structural elements such as aggregates, two distinct pore spaces can be identified: intra-aggregate and inter-aggregate pore spaces in mineral soils (Nimmo, 2005). Also, peat soils have been shown to exhibit multi-modal pore size distributions as a consequence of plant structure and decomposition effects (Weber et al., 2017b). The effect of neglecting multi-modality can be small in estimating the WRC, but it may be significant in the HCC, which drops by orders of magnitude as the large water-conducting pores empty (Durner, 1994).

Evidence suggests that HCC data are often better described by scaling K_r(h) using an estimated K_s in the equation rather than using its measured counterpart (denoted here as K_sat; L T⁻¹); this is an indication of bi-modality occurring in the pressure head range near saturation. A number of approaches exist in which all conductivities measured at pressure heads larger than −6 cm were excluded. The motivation is that the remaining data are related to the soil matrix only, discarding data related to the conductivity of the macropores. The subsequent model fitting requires a saturated hydraulic conductivity parameter, which is then termed the matching point conductivity (K₀ (L T⁻¹); Weynants et al., 2009; Zhang and Schaap, 2017). This matching point conductivity is the saturated hydraulic conductivity of the soil matrix. This also indicates the presence of bi-modality, something which has been corroborated by a systematic analyses of some databases by Zhang et al. (2022). Although these models are often needed to adequately describe tabulated data of WRC and HCC (Zhang et al., 2022; Volk et al., 2016), there are currently no PTFs for multi-modal VGM.

However, there remains a more fundamental problem, since it is still not clear whether the effective SHP description should be achieved directly with the unimodal RRE or by coupling variations of the RRE that represent dual- or multi-modal porosity. The reason for this is that, for systems with large pore diameters, the RRE is not valid, due to the violation of the laminar flow assumption in the Darcy equation for which an alternative theory is needed (Gerke and van Genuchten, 1993; Jarvis, 2007; Jarvis et al., 2016).

2.3 Deficiency in the capillary bundle model

Several studies have illustrated the inability of capillary bundle models, such as the VGM model, to describe water content and hydraulic conductivity data over the full pressure head range. More specifically, there is strong evidence that a residual water content (θ_r, Eq. 2) has little physical justification as the water content of drying soils approaches zero (Schofield, 1935). However, other researchers justified the concept of residual water content as the point at which water loses its ability to respond to hydraulic gradients (Nimmo, 1991; Luckner, 2017; Cornelis et al., 2005). Nonetheless, many different modelling approaches have been proposed to incorporate different forms of non-capillary water storage and conductivity (Peters, 2013; Weber et al., 2019; Scarfone et al., 2020; Chen and Chen, 2020; Aubertin et al., 2003; Wang et al., 2013; Tuller and Or, 2001; Diamantopoulos et al., 2024), with very few available PTFs for these physically more comprehensive models. An example is Weber et al. (2020), who proposed a meta-PTF for the Brunswick SHP model system (Weber et al., 2019). This PTF translates any set of VGM parameters to the Brunswick parameters, and it was shown that it could outperform the VGM model, even if the model was not directly fitted to training data.

2.4 Capillary hysteresis

It is well known that the WRC, as defined above in Eqs. (1) and (2), is not a single monotonic curve, mainly due to capillary hysteresis (Fig. 1; Poulovassilis and Childs, 1971; Pham et al., 2005), which refers to the non-uniqueness of the WRC and its dependence on the history of soil wetting and drying. Capillary hysteresis results from pore-scale processes, mainly due to the irregular shapes of pores (ink bottle effect; Haines, 1930), the hysteresis of contact angles between soil water and the solid soil particles (Bachmann et al., 2003; Diamantopoulos et al., 2013), and shrinking or swelling effects (Hillel, 1998). Modelling capillary hysteresis in soils has been a research topic for more than half a century, and we refer to Pham et al. (2005) for a review. It is recognised that neglecting hysteresis from simulation of field-scale data under realistic transient boundary conditions may lead to significant errors, especially during water redistribution (Dane and Wierenga, 1975), as hysteresis has been shown to impact water fluxes and storage in the soil. For example, van Dam et al. (1996) tested alternative simulation runs with the SWAP93 model using data from two experimental sites and reported noticeably changed patterns in simulated soil water regimes on both daily and annual simulation timescales when accounting for hysteresis. Basile et al. (2003) also stressed the significance of hysteretic soil behaviour when interpreting laboratory- and field-measured SHPs.

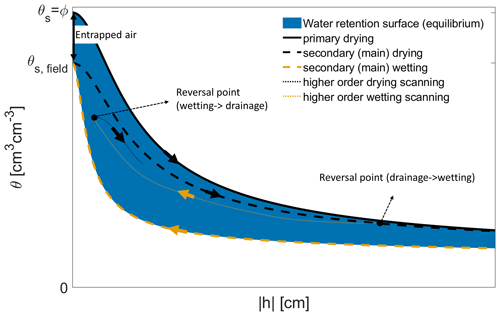
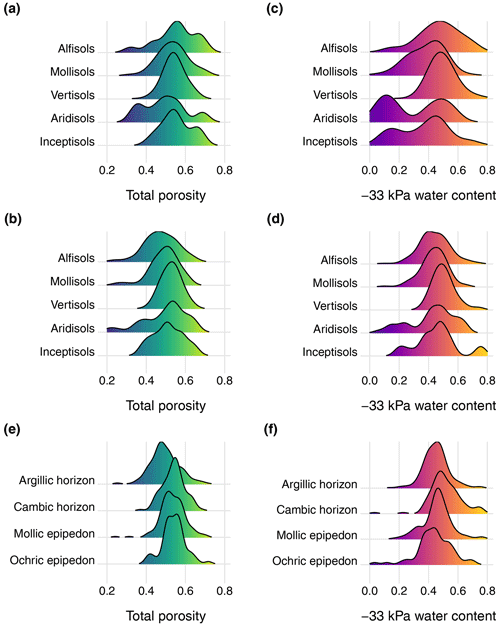
Figure 1 The traditional concept of equilibrium capillary hysteresis. The equilibrium water retention surface (WRS) is bounded by the equilibrium (or static) primary drying curve, starting from 100 % saturation and the equilibrium (or static) main wetting curve.

Capillary hysteresis in soils is generally modelled using either physically based (e.g. Poulovassilis, 1962; Philip, 1964; Poulovassilis and Childs, 1971; Poulovassilis and Kargas, 2000; Mualem, 1984) or empirical models (e.g. Scott, 1983; Kool and Parker, 1987; Huang et al., 2005). Although hysteresis is still a topic of research and in general recognised as a key process to consider (Hannes et al., 2016), it is rarely accounted for in modelling applications. The reason is that it requires extensive laboratory measurements to determine the boundary curves (drying and wetting curves, Fig. 1) and that, at larger scales (pedon and above), model parameterisation is mainly based on the use of “effective properties”, whereby effective WRC and HCC models are calibrated to match observed average state variables (e.g. water content) and water fluxes. For the incorporation of hysteresis into numerical models, PTFs should be able to predict both the primary drying and wetting curves for the same soil.

The existence of hysteresis affects the development of PTFs. It directly affects laboratory experiments, since for a drainage experiment the starting saturation point influences the resulting drying curve. All currently available PTFs target the primary or main drying curve, and the underlying data do not contain information on how sample saturation was achieved (i.e. these PTFTs ignore the scanning curves in Fig. 1). Also, creating a PTF based on measurements performed on ideally fully saturated soil samples may bias simulations of real field conditions (θ_field in Fig. 2), where such fully saturated conditions may occur very rarely. Figure 2 shows the retention curves from the laboratory with fully saturated samples and the field retention curve analysed in this study.

Figure 2 In situ (field) and laboratory measurements of water retention made at the same soil layer in a loamy sand. Field measurement of volumetric water content was made using four TDR-310S sensors (Acclima, Meridian, USA) installed with a 50 cm horizontal distance and a single T8 tensiometer for water potential measurements (METER Group, Munich, Germany). Field data were collected during a dry period in May and June 2019 below a spring barley crop and during a wet winter period with bare soil conditions from January to April 2020. Laboratory measurements were made on five undisturbed soil samples collected using ring cores (250 cm³ in volume) in the same soil layer before sensor installation. The water retention curve was measured using evaporation experiments (METER Group, Munich, Germany). The solid line shows the estimated water retention curve based on soil bulk density and texture (USDA) using a PTF (Wösten et al., 1999).

2.5 Dynamic non-equilibrium and transient soil hydraulic properties

The study of capillary hysteresis in porous media is also affected by dynamic non-equilibrium (DNE) effects. DNE refers to the apparent flow-rate dependence of the WRC under transient conditions. In other words, under transient conditions, the water phase is not instantaneously equilibrated with the pressure head and water content in soil which is continuously drained (wetting), attaining the equilibrium curve described by the WRC. (e.g. Diamantopoulos and Durner, 2012; Hassanizadeh et al., 2002). For example, in the case of drainage, more water is held by the soil matrix when water is moving, in contrast to the case where equilibrium has been reached (Hannes et al., 2016; Diamantopoulos et al., 2012). This means the volumetric water content is still tightly coupled with the pressure head, but only as a long-term limit that is reached after (considerable) equilibration time. Many experimental studies have shown the existence of DNE, especially in laboratory experiments and for different boundary conditions (Diamantopoulos et al., 2015). Similarly to hysteresis, macroscopic observation of DNE is mainly due to pore-scale processes, since pore geometry (especially pore connectivity) determines how quickly some equilibration is reached. The existence of DNE complicates the study of the traditional concept of capillary hysteresis (Funk, 2014, 2015) or quasi-equilibrium hysteresis (Hannes et al., 2016), because DNE is expected to give rise to apparent dynamic hysteresis (Diamantopoulos et al., 2015) when water is flowing. Consequently, it is difficult to separate the effects of capillary hysteresis and dynamic non-equilibrium when examining experimental data.

To date, it is not clear whether DNE should be incorporated into field-scale simulations and consequently into the development of new PTFs. However, identifying those effects in the evaluation of laboratory experiments may lead to less noisy experimental datasets for PTF construction. Furthermore, accounting for hysteresis and DNE may improve the translation from laboratory data to field-scale soil hydraulic parameters and the performance of water flow simulations, particularly at short timescales (hours to days). However, when the temporal scale of the simulation increases (years to decades), other processes become equally (or more) important, as SHPs are expected to vary with land use (Meurer et al., 2020a, b) and tillage practices (Vereecken et al., 2010) (see Sect. 3.2). The quantification of these processes requires long-term experiments where “the drifting” of the SHPs may be monitored so that transient SHPs can be derived. As Vereecken et al. (2010) envisioned, this may require the use of time-dependent PTFs accounting for the soil management history. Soil tillage operations, cryoturbation and bioturbation, root growth, microbial activity, and “post-event” pedogenic processes which lead to transient SHPs are time-dependent features in many current policy incentives in agriculture.

3 Guidance for the use of PTFs and critical limitations

3.1 Some words of caution in applying PTFs in LSMs

Far from being the only community, LSM users have been applying PTFs globally for decades. This community has also seen rapid development of their models in recent years, for example in the context of the move towards kilometre-scale modelling, which has brought with it continual efforts to improve the representation of soil processes, and soil hydraulics in particular (Gudmundsson and Cuntz, 2016; Fisher and Koven, 2020). Here we briefly list and discuss limitations of currently available soil hydraulic parameterisations with a particular focus on the issue of spatial transferability. We note that, in this paper, we use the terminology LSM in a broad sense. This is meant to include numerical or analytical process models which describe the variably saturated water flow in soils. The governing equations may in turn be coupled with other processes such as plant and root growth dynamics or solute and heat flow. The commonality, which is of importance here, is that these models require effective descriptions of SHPs, either in the form of point estimates or parametric functions.

3.1.1 Spatial appropriateness

Most of the PTFs currently used in LSMs are regression models derived from studies with samples from specific geographical locations. For example, the widely used Cosby et al. (1984) PTFs are based on data from soil samples from 23 states in the US. Therefore, it is highly debatable whether it is appropriate to use this PTF in a global model simulation including grid cells with dominant soil types (e.g. highly organic permafrost soils, tropical soils) other than those covered by the US data. Similarly, the Saxton and Rawls (2006) PTF was derived from soil samples excluding organic soils and soils with bulk densities outside the range of 1.0–1.8 g cm⁻³, yet these are widely applied in global LSM simulations regardless. Barros et al. (2013) stated that “In a review on PTFs, Pachepsky and Rawls (1999) and Pachepsky and Rawls (2004) recommended the use of PTFs for regions or soil types similar to those in which they were developed”. Gerke et al. (2022) also point out that “If we only have training data from a certain geographical region, machine learning (ML) models will probably produce poor results for other regions”. However, what exactly is meant by “similar” and “other” in this context? In a data-poor high-elevation location in the Andes, for example, would it be better to use a European PTF derived from the same soil type and a similar mountain environment (i.e. sharing common soil types and climates but not geographical locations and not necessarily mineralogy), or should we rather use a Brazilian PTF derived from the same soil type but a lowland forest environment (i.e. matching soil type and continent but not climate)? We remind the reader that soil type is a taxonomic soil unit in soil science and is often used for soil maps. Defining soil types is based on one of various existing taxonomic rules which may differ considerably. Soil types (and their sub-types) may therefore group soils into one type but with largely different hydraulic functioning. Only very few studies have systematically investigated the relevant dimensions which determine the non-stationarity of PTFs in regard to soil-forming factors (Jenny, 1941), including soil properties, climate, organisms, topography, and landscape attributes, which determine SHPs. A common issue that arises when using PTFs is that data from the locations where the predictions are desired are often not well represented (or even completely absent) in the training dataset used to develop PTFs.

However, there is evidence that it might be possible to use PTFs outside of the geographical location in which the PTF was developed (in this case, different continents) provided that the soil type and climate are comparable. Wösten et al. (2013) explicitly studied this using PTFs derived from a specific set of soil types from one geographical location (South America; Hodnett and Tomasella, 2002) and predicted measured data from similar soil types in the Limpopo catchment of South Africa. In a similar study addressing the appropriateness of translocated PTFs, Fuentes-Guevara et al. (2022) examined input–input and input–output correlation structures in databases underlying the development of four PTFs and compared them to the data of their application catchment. They found that similarities in the correlation of the data, rather than climate, source area, database size, or spatial extent, could explain PTF performance best. More studies are needed to substantiate and verify transfer learning as used in soil mapping (Malone et al., 2016) and also the use of meta-models (Grunwald et al., 2016). This might allow us to understand under which system conditions PTFs are expected to be similar beyond the limit of local specificity.

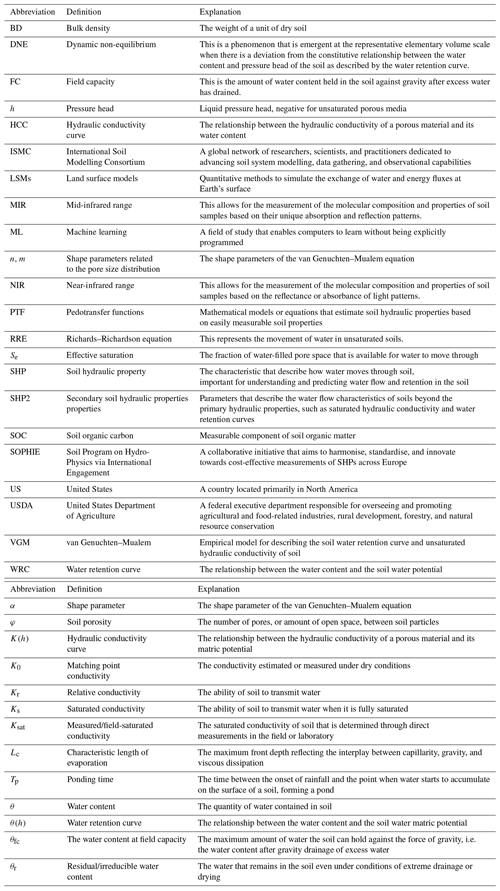
Of course, better geographic coverage of the data is highly desirable, but this is labour-intensive and costly. Due to the large effort required, it may take decades until this is realisable. An alternative approach to tackling this lack of site-specific data is to develop PTFs that explicitly incorporate soil taxonomic classes and/or diagnostic horizons (i.e. pedological information) as suggested by Pachepsky and Rawls (1999) and Gatzke et al. (2011). Incorporating information from soil profile characterisation and classification has the advantage that it allows for an improved taxonomic coverage by accounting for pedogenetic similarities, even in the absence of broad geographic coverage. As an example, we plot two hydraulic properties – total porosity and water content at −33 kPa – for selected A and B horizons of five US Soil Taxonomy (Soil Survey Staff, 2014) orders and four diagnostic horizons in Fig. 3. These probability density ridgeline plots help diagnose differences in the central tendency, spread, skewness, and kurtosis present in several of these taxonomic categories (e.g. Aridisols or Inceptisols). Accounting for these pedogenetic differences by incorporating taxonomic information may improve the applicability of PTFs in regions with poor spatial resolution and data quality. Soil taxonomy relates to the classification system of profiles found in the environment. Soil texture relates to the specific textural composition (sand, silt, clay) of a soil.

Figure 3 Total porosity and water content at −33 kPa for A horizons (a, c), B horizons (b, d) of selected soil orders, and diagnostic horizons (e, f) as defined by the US Soil Taxonomy. Data are from the Pedogenic and Environmental Data Set (PEDS).

3.1.2 Spatial validity and methods of modulation

Most SHP models applied in spatially explicit modelling assume a unimodal pore size distribution. This may be an oversimplification in LSM application, especially in forested areas where biopores created by tree roots or bioturbation commonly occur (Fatichi et al., 2020). Although dual- or multi-porosity SHP models are available (see Sect. 2.2), PTFs for bi-modal or multi-modal soils are currently not available (Zhang et al., 2022). Therefore, modulation of current PTFs may be achieved by using vegetation indices to account for biologically induced soil structure (Fatichi et al., 2020; Bonetti et al., 2021). Similarly, in arid and semi-arid environments it might be instrumental to include models which also account for non-capillary storage and hydraulic conductivity (Weber et al., 2019), since in these areas water fluxes may be dominated by non-capillary processes. While this has thus far never been included directly, a PTF was developed by Weber et al. (2020) to predict the standard model parameters of VGM and then extend them to a model variant, which includes stored and conducted water explained by forces other than capillary theory.

Many LSMs include deep vadose zones and groundwater components including river and lake beds (Condon et al., 2021). For simplicity and due to a lack of knowledge, these LSMs often apply the same soil hydraulic parameterisation as used for the rest of the terrestrial surface, even though sediments and unsaturated rocks may show substantial differences in SHPs compared to the soils located close to the surface. Deep sediments are generally not just more compacted but have also not undergone pedogenic processes (Marthews et al., 2014) and lack the impact of vegetation and bioturbation as a pore-space-forming process, leading to differences in the hydraulic parameters compared to soils that developed close to the surface. Thus, at the field scale, this requires extrapolation of hydraulic properties to larger depths at which very few observational data have been collected (Marthews et al., 2014), thereby making this approach highly questionable.

3.2 Obvious gaps in PTFs for specific soils, substrate types, and land uses

As stated, parent material, climatology, and land use are important drivers that determine SHPs. However, measuring soil properties continuously at each location across the globe is currently unfeasible, as it is far too laborious, expensive, and time-consuming (Rustanto et al., 2017). Globally, soil research is advancing rapidly and researchers have begun to publish many PTFs and databases for regions other than temperate and agriculture-dominated areas. However, the use of existing PTFs for global applications is still limited as PTFs have been predominantly developed on samples from specific regions and transfer learning studies are very limited (see Sect. 3.1). Furthermore, PTFs may be restricted in use due to highly specific input data (Patil and Singh, 2016) which may not be readily available. In the following, we identify the most prominent list of missing PTFs and call for the development of PTFs for specific soils and substrate types.

3.2.1 PTFs for tropical regions

The absence of glaciations has resulted in Precambrian surfaces in tropical regions. Together with predominant high rainfall and temperature, this resulted in a distinct soil structure at different scales including different clay mineralogy (Ottoni et al., 2018; Botula et al., 2013; Nguyen et al., 2015). Unlike the predominantly 2:1 clays of temperate regions, tropical regions are dominated by 1:1 (mainly kaolinite) clay minerals which result in substantially different hydraulic properties in many tropical soils (Sharma and Uehara, 1968). Next to differences in clay mineralogy, BD and cation exchange capacities are other relevant differences between climatic regions (Minasny and Hartemink, 2011), thus serving as viable candidates as predictor variables. Recently, Lehmann et al. (2021) developed a model that used clay mineral maps from Ito and Wagai (2017) to estimate hydrological and mechanical properties for many soil types and concluded that clay-mineral-informed PTFs improve regional SHP prediction. An example is provided by Gupta et al. (2021a), who showed that use of clay fractions without consideration of mineralogy as a predictor of SHPs leads to underestimation of K_sat and may lead to important effects on the partitioning of water at the land surface (Lehmann et al., 2021). This has been corroborated by Gupta et al. (2021a), whose prediction of K_sat improved for tropical regions when explicitly considering data from tropical soils.

Ottoni et al. (2018) introduced the Hydrophysical Database for Brazilian Soils (HYBRAS), Gunarathna et al. (2019) developed PTFs for tropical Sri Lankan soils, while Gebauer et al. (2020) developed PTFs for two remote tropical mountain regions dominated by organic soils under volcanic influence (Mosquera et al., 2021) and tropical mineral soils in southern Ecuador. Thus, data are becoming increasingly available and opportunities have never been greater for collaborative research to develop a bridge between temperate and tropical PTFs. Ways forward are generally better data coverage and the inclusion of more auxiliary information such as clay mineralogy and land cover.

3.2.2 PTFs for forest systems

SHPs are controlled considerably by plant root processes shaping soil structure. In this respect, forest soils are markedly different from other land use types with respect to root size and depth distribution while exhibiting low bulk densities in the topsoil, since trafficking is generally low. Several studies have shown that hydraulic properties of forest soils differ from soils with other vegetation (Jülich et al., 2021; Pirastru et al., 2013). In particular, the effect of forest root systems on soil structure and the resulting abundance of large pores challenges the application of PTFs that are typically trained using samples from arable land. Some forest PTF examples are those provided by Teepe et al. (2003), Puhlmann and von Wilpert (2012), and Lim et al. (2020) – these works showed that, in forest soils, established PTFs fail to describe SHPs in the wet range and that new PTFs must include additional local site information to capture the variation of soil formation processes. In response to the current lack of land-use-specific PTFs, Robinson et al. (2022) performed a global meta-analysis of hydraulic conductivity data measured under different land uses on the same soil type and developed response ratios that relate the K_sat in woodland and grassland to that of arable land. Until land-use-specific PTFs become more widely available, such approaches may assist soil parameterisation in LSMs.

3.2.3 PTFs for litter layers and mulches

Most Earth system models do not explicitly represent the litter layer (the so-called “O horizon”) of natural vegetated areas (e.g. forests or grasslands) or litter layers of agricultural land (e.g. in pastures after mowing or mulches covering cropped soils, e.g. to reduce soil evaporation), even though some approaches have been proposed (Gonzalez-Sosa et al., 1999; Oge and Brunet, 2002). This means that the part of the soil profile that is in direct contact with the atmosphere is not represented, although it can have a substantial effect on controlling the soil water balance by impacting below-canopy interception, runoff–infiltration partitioning, and soil evaporation. A common solution to account for litter layers is to parameterise them as a “pseudo-litter” soil layer by reducing the BD and estimating the SHP from given PTFs (e.g. Montaldo and Albertson, 2001). This pseudo-litter layer SHP approach is utilitarian and does not truly represent the SHPs, which are markedly different because they contain only a few to no mineral particles and the structure of the litter layers greatly differs from that of the soil matrix, causing this layer to have very low water retention and unsaturated hydraulic conductivity (Zagyvai-Kiss et al., 2019). We think this is mostly related to the lack of experimental data as a consequence of a highly demanding experimental methodology for materials with such little structural cohesion and low temporal dynamics. A concerted effort is required to establish methods which can be applied to litter and humus layers and test whether the theory underlying the RRE is applicable in such contexts, which includes testing whether approaches other than simulation with the RRE are more suitable.

3.2.4 PTFs for peat soils

Peat soils are characterised by an organic-rich surface layer that contains, depending on its definition, about 30 % (or more) soil organic matter and that is at least 30 cm thick. This soil organic matter range is typically not included in commonly used PTFs that were developed with a focus on mineral soils (e.g. Wösten et al., 2001; Saxton and Rawls, 2006). To date, there is no PTF for peat soils that would allow derivation of hydraulic properties from readily available regional or global spatial input data. As a consequence, peat soils are currently represented in LSMs with a single set of peat parameters and some specified vertical change in properties to account for the increasing peat decomposition with depth (Letts et al., 2000; Bechtold et al., 2019; Qiu et al., 2018).

Several studies have shown that BD can serve as a good predictor of K_sat, total porosity, and the van Genuchten retention parameters α and n in peat soils (Liu et al., 2020; Liu and Lennartz, 2019; Morris et al., 2022). The degradation state (Wallor et al., 2018; Weber et al., 2017b) as well as the drainage history and type of land use (Liu et al., 2020) have emerged as useful predictors for peat SHPs. Apart from the strong impact of land use on peat properties, they naturally depend on the specific mixture of parent materials and, in particular, on the different peat-forming plant substrates. In this context, there are large structural differences between the most common peatland types at high latitudes with mostly low vegetation such as mosses and in tropical regions with mostly swamp forest. As such, vegetation type, or even latitude, could be used as a predictor of PTF development for peat soils (McCarter and Price, 2012; Apers et al., 2022).

The modelling of peatlands could benefit from PTFs mainly tailored for two different scales of application. At the level of individual peatlands, a PTF based on easily measurable parameters such as BD and/or porosity could be used to parameterise SHPs in spatially distributed peatland hydrological models (Jaenicke et al., 2010). At the scale of LSMs, peatland maps are being developed that focus on spatial distribution (Xu et al., 2018) but not on their local properties, so that spatially distributed information on potentially useful input parameters (e.g. BD, soil organic matter content) is not yet available. In this context, the accuracy of machine-learning-based maps of soil properties such as those provided by SoilGrids (Poggio et al., 2021) for peatlands is currently debatable. As data become increasingly available for PTF development for peat soils, additional research should also investigate the most adequate level of PTF complexity for proper parameterisation of peat SHPs.

3.3 Transient PTFs: accounting for the time dependency of SHPs

There is evidence that SHPs vary considerably during the course of a year, especially for soil layers close to the surface. Technical operations such as repeated tillage, re-compaction, and harvest lead to soil compaction or loosening, changes in aggregate stability, soil faunal activity, development and dying of roots, and silting processes that may even influence the SHPs multiple times within a year or seasons (Messing and Jarvis, 1993; Horn et al., 1994; Bodner et al., 2013; Sandin et al., 2017). Also, animal hooves lead to mechanical-stress-induced soil compaction (Keller and Or, 2022). Other abiotic pressures affect the pore size distribution, such as freeze–thaw cycles (e.g. Ren and Vanapalli, 2019) or hardened pans due to water droplets or chemical dissolution. These effects cannot be modelled with the current approaches that assume a rigid porous medium.

On larger timescales, changing climatic, land use, or management conditions impact the soil chemical, biological, and physical conditions (Hirmas et al., 2018). SOC influences soil structure by aggregation as a binding agent between minerals (Beare et al., 1994; Lal and Shukla, 2013) and plays an important role in shaping SHPs (Rawls et al., 2004). For example, Bellamy et al. (2005) analysed the SOC loss in England and Wales in the years between 1978 and 2003 and calculated carbon loss ratios of 0.6 % yr⁻¹ which were independent of land use, suggesting a link to climate change. Nevertheless, the effect of temporal changes in SOC content on WRC and HCC remains almost always unconsidered in hydrological models and LSMs (see, however, Jha et al., 2023). Soil management is also expected to change in future climates. New cultivations (Sloat et al., 2020) and modified tillage practices, such as no till or minimum till (Hodde et al., 2019), alter SHPs (Fu et al., 2021; Bouma, 2000; Strudley et al., 2008), contrary to the typical assumption that they remain unchanged over simulation times, spanning many decades to hundreds of years, as done in climate change and land use change projections (Eyring et al., 2016; Murphy et al., 2004). Currently, there is a lack of data to properly account for possible impacts of climate change and land use on SHPs. To fill this gap, long-term field trials (e.g. Schmidt et al., 2019) and observatories (Späth et al., 2023) need to be maintained and/or established to allow for a systematic evaluation of the impact of climatic and anthropogenic changes on SHPs.

Swelling and shrinking processes may change soil-saturated and near-saturated hydraulic conductivity radically within a few hours (Stewart et al., 2016). Burrowing of soil macrofauna like earthworms can increase hydraulic conductivity by orders of magnitude in a matter of weeks (Bottinelli et al., 2017). Several studies have meanwhile provided evidence of seasonal dynamics, which may be strongly modified on a temporal scale of days to months to years (Messing and Jarvis, 1993; Horn et al., 1994; Bodner et al., 2013; Sandin et al., 2017). Droughts have also been found to alter SHPs significantly (Robinson et al., 2016; Gimbel et al., 2016), too.

3.4 Regionalisation and upscaling

SHPs are highly variable in space. This is true over all relevant spatial scales, from the centimetre scale to the global scale. At the centimetre scale, this high variability casts doubts on the existence of representative elementary volumes in soil (Koestel et al., 2020) – this alone makes the use of laboratory data from small soil samples to infer to SHPs at larger scales debatable (see Sect. 6.3). At larger scales, several soil types (differing in soil textural properties, BD, SOC content as well as the number and type of soil horizons) can be found within a single model grid cell, with clear implications for SHP characterisation and layer discretisation.

For distributed LSMs or hydrological models, the fine-scale information available from high-resolution soil maps has to be upscaled to the grid scale at which the model will be employed. The general problem of upscaling has been a topic of considerable discussion over the past 4 decades (e.g. Cale et al., 1983; Rastetter et al., 1992; Pierce and Running, 1995; Constantin et al., 2019; Vereecken et al., 2019). The most straightforward method to aggregate fine-scale input data to a larger-scale extent would be spatial averaging, which can be done for certain kinds of soil information, e.g. SOC content, BD, or soil depth. For soil textural information this kind of approach is generally unsuitable. For example, if a grid cell is composed of 50 % clay soil and 50 % sandy soil, direct averaging by texture would yield a sandy clay, which does not reflect the properties of the sand or the clay. Besides, averaging sand, silt, and clay fractions (%) can cause problems in closing the textural mass balance (Montzka et al., 2017). Such averaging procedures generally result in a “loamification” in the parameter space. Alternatively, the PTF output (e.g. van Genuchten parameters), rather than the input, may be averaged. However, some SHPs do not behave linearly over different scales, especially the (unsaturated) hydraulic conductivity or the van Genuchten shape parameters α and n, resulting in considerable uncertainties in water flow predictions (Zhu and Mohanty, 2002; Montzka et al., 2017).

Another commonly used approach for upscaling is aggregation by the dominant soil type within a grid cell. The removal of non-dominant soils, which may have contrasting properties to the dominant soil type, may lead to a loss of sensitive information, particularly concerning sub-grid variability. Additionally, when soil information is aggregated by the dominant soil class, in most cases the 12 United States Department of Agriculture (USDA) soil classes are used (van Looy et al., 2017), resulting in a limited number of soil types actually being represented.

The impact of different soil maps on LSM-predicted terrestrial water budget components was studied by Tafasca et al. (2020) at a grid resolution of 0.5°. They found that the use of three different realistic soil texture maps resulted in rather similar spatial patterns of the simulated water fluxes. The reason behind this could again be the way soil texture was aggregated using the dominant soil class. This approach is taken globally irrespective of the resolution of the soil map. Therefore, one can argue that not only the choice of PTF impacts the simulated targets but also the way the soil inputs are aggregated prior to applying any PTF.

Montzka et al. (2017) proposed a more consistent approach to upscaling SHPs based on Miller–Miller scaling (Miller and Miller, 1956). First, they generated synthetic WRCs based on PTF-predicted SHP parameters for each sub-grid point within a single grid. Then, they fitted a SHP model to all synthetic data points; this can be considered a suitable averaging procedure and has also been used by Weber et al. (2017a). Thus, Montzka et al. (2017) were able to derive a scaling parameter to preserve the information on the sub-grid variability of the WRC, which becomes a measure for the spatial variability to describe SHP uncertainty.

3.5 SHP maps

Spatially distributed global maps of SHPs with high spatial resolution are highly desirable for LSM applications (Montzka et al., 2017). Such SHP maps are predominantly developed using PTFs – for example, Zhang and Schaap (2017) and Dai et al. (2019) used the ROSETTA3 PTFs to produce global maps of SHPs at 1 km resolution. Similarly, euptf (v1) by Tóth et al. (2015) was used to produce SHP maps at 250 m resolution for Europe (Tóth et al., 2017). However, these maps are inherently limited as their representativeness is subjected to the quality of the soil property maps used for their derivation, the appropriateness of the applied PTFs, and the models used to describe the SHP (e.g. most PTFs are suitable for either the (unimodal) VGM or Brooks–Corey types of hydraulic functions). A continuous effort should be made to provide and revise such global maps. As PTFs become increasingly more available for specific regions, SHP maps may be created based on different PTFs, each representative of local conditions.

Gupta et al. (2021a, 2022) recently provided global maps of K_sat and VGM parameters using a ML framework in which local information on topography, climate, and vegetation was included in addition to traditional easy-to-measure soil properties. In this approach, soil samples from both temperate and tropical climate regions were considered to improve the model's predictions across different biomes. However, the spatial distribution and coverage of available soil samples for model training are still a major limitation – global spatial predictions will benefit from continuous efforts in data collection from underrepresented areas.

3.6 Call for harmonising PTFs in model inter-comparison studies

The choice of PTF has been shown to considerably affect simulated water fluxes, regardless of model configuration, for example considering bare soil or vegetation or free drainage vs. soil profiles influenced by groundwater (Weihermüller et al., 2021). Similarly, Paschalis et al. (2022) found that PTF uncertainties for a given soil type are higher than uncertainties across soil types in both hydrological and ecosystem dynamics. Thus, Weihermüller et al. (2021) strongly recommend harmonising the PTFs used in model inter-comparison studies to avoid artefacts originating from the choice of PTF rather than from the actual studied model structures. This is important to note since prominent model inter-comparison efforts, such as the Agricultural Model Intercomparison and Improvement Project (AgMIP) in which the performance of soil–crop models is compared, mostly ignore the effect of PTFs. In the Agricultural Model Intercomparison and Improvement Project model with inter-comparison studies that look at crop yield (e.g. Asseng et al., 2013; Bassu et al., 2014), climate change impact on crop growth and water use (Durand et al., 2018), or actual evapotranspiration (Kimball et al., 2019), SHP parameters are generally estimated using different PTFs in the various models. To rectify this, Groh et al. (2022), in a model inter-comparison study on crop growth and water fluxes in different lysimeters, directly provided SHPs to the group of modellers involved in the study.

Table 2 Tools that facilitate the use of available PTFs.

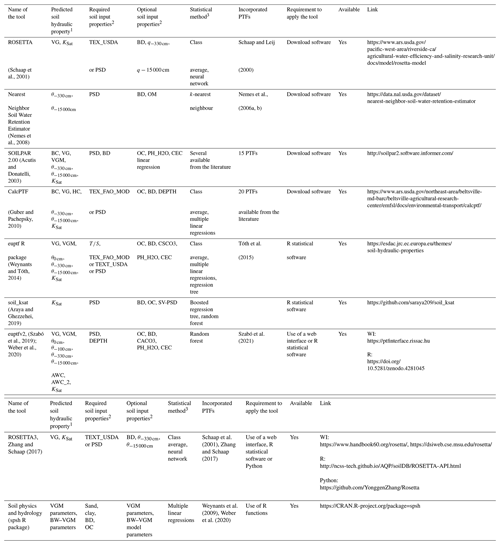
¹ θ: water content; K_Sat: saturated hydraulic conductivity; VG: parameters of the van Genuchten (1980) function to describe the water retention curve; BC: parameters of the Brooks and Corey function (Brooks and Corey, 1964) to describe water retention; C: parameters of the Campbell function (Campbell, 1974) to describe water retention; HC: parameters of the Hutson and Cass modified Campbell function (Hutson and Cass, 1987); VGM: parameters of the Mualem–van Genuchten function to describe the water retention and hydraulic conductivity curve; AWC_2: plant-available water content based on q at a −100 cm matric potential head; AWC: plant-available water content based on θ at a −330 cm pressure head. The BW–VGM model refers to the physically comprehensive Brunswick (BW) model framework in the van Genuchten–Mualem model variant (Streck and Weber, 2020; Weber et al., 2019). ² TEX_FAO_MOD: modified FAO texture class; TEX_USDA: USDA texture class; $T/S$: topsoil and subsoil; PSD: particle size distribution (sand, 50–2000 µm; silt, 2–50 µm; clay, <2 µm – mass %); SV-PSD: secondary variables computed from the particle size distribution; DEPTH: mean soil depth; OC: organic carbon content (mass %); BD: bulk density; CACO3: calcium carbonate content; PH_H2O: pH in water; CEC: cation exchange capacity. ³ Class average: the mean value of a given soil hydraulic property by the soil textural class. WI: web interface. Note that all links were accessed on 19 June 2024.

Based on informal communications, various land surface modellers have indicated that they deem the harmonisation of PTFs to be inappropriate, as they argue that harmonisation will lead to the loss of model diversity, which will subsequently collapse the ensemble spread of LSM outputs and thus bias the ensemble means as the best average representation of “reality”. This argument holds true as long as it does not hinder adoption of more physically comprehensive SHP models, which is the core element of model improvement. Moreover, this perceived lack of adoption undoubtedly hampers our understanding of whether the model output diversities originate from model structure and physics or from the choice of different PTFs. This is especially relevant in model inter-comparison studies dedicated to analysis of soil model structural differences. This picture is exacerbated by the non-harmonised use of soil maps (i.e. the PTF model input).

If the aim is to understand how different model physics (in terms of various soil processes: infiltration, (un)coupled soil heat and water transfer, soil–root hydraulics, etc.) cause model diversities and impact the process-level understanding of land–atmosphere interactions (e.g. via land surface fluxes), one consistent set of SHP functions, PTFs, and a soil property map is a prerequisite (Zeng et al., 2021). Therefore, within SoilWat, a joint GEWEX–ISMC initiative, the Soil Parameter Model Intercomparison Project, has been conducted to approach the question of the degree to which the LSM spread is related to choices pertaining to SHPs by designing controlled multi-model experiments with coordinated inputs of basic soil properties and PTFs (Gudmundsson and Cuntz, 2016).

It is noteworthy that harmonising PTFs may come at a price. As presented, PTF choice may be very sensitive to modelled output. For example, implementing novel and versatile PTFs likely improves weather and climate model predictions through more realistic partitioning of precipitation inputs over the various hydrological flows and stores. However, it needs to be kept in mind that those models have often been tuned (e.g. to decrease near-surface atmospheric temperature biases). This means that initial tests with these improved PTFs may not deliver the expected improvements in model performance until parameters for other soil and land surface processes have been updated too.

3.7 Guidance and tools to facilitate the use of PTFs

From the 2000s onwards, the statistical methods used to describe the relationship between SHPs and other readily available soil information became increasingly more complex, with additional constraints in software specificity often addressed by publishing the software for PTF calculation. Table 2 provides an overview of software and web interfaces that facilitate the use of existing PTFs. PTFs derived with multiple linear regressions or providing mean SHP, WRC, and HCC parameters of specific soil groups (i.e. class PTFs) do not need specific software or web applications to facilitate their use. Collections of selected equations available from the literature can be found in Guber et al. (2006), who listed 22 published PTFs for the prediction of WRC, Dai et al. (2019), who present 20 published PTFs for both the WRC and HCC, and Zhang and Schaap (2019), who provided four ways of predicting K_s based on effective porosity and six PTFs to estimate K_s based on basic soil properties. Nasta et al. (2021) collected 11 PTFs to predict WRC and 10 PTFs for K_sat, which are expected to perform well for European applications.

However, many global regions remain inaccessible for intensive soil sampling, and therefore the worldwide coverage of soil information remains incomplete (Omuto et al., 2013; Batjes et al., 2020). A workflow for modellers to obtain soil hydraulic parameter values is presented in Figs. 4 and 5.

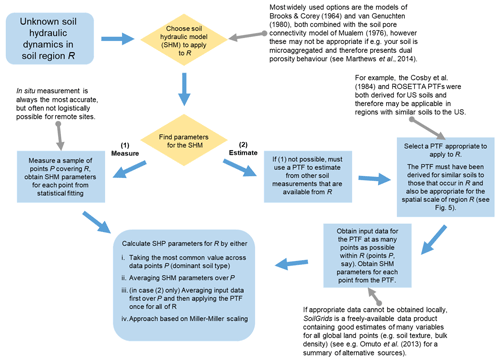
Figure 4 A protocol for the selection of an appropriate set of pedotransfer functions for use in any global soil region R. For Miller–Miller scaling, see Miller and Miller (1956).

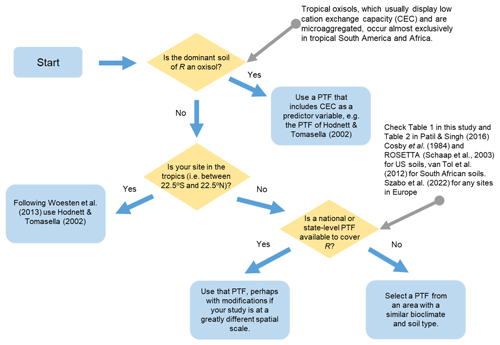
Figure 5 Workflow for acquiring a model representation of soil hydraulic dynamics within an unsampled soil region R. Both “soil hydraulic model” (SHM) and “soil hydraulic dynamics” refer to a set of equations that describe the relationships between volumetric soil water content, soil matric suction, and soil hydraulic conductivity. For example, for van Genuchten (1980), these are two closely related curves called the soil water characteristic (SWC) and the hydraulic conductivity curve (HCC).

4 Requirements of measurements and auxiliary information

4.1 Databases and the impact of different measurement methods

Currently available PTFs have been developed based on datasets from different sources and obtained by varying methodologies. This approach has been successful to the extent that these databases provided a first source of input data for large-scale model applications. However, uncertainty and variation in collated data for large-scale applications may introduce errors. Harmonisation and standardisation to provide reliable SHPs has not received much attention so far, leading to added uncertainties in model outcomes that do not necessarily correspond to real system variability. Data inconsistencies due to a lack of protocol and uniform standards necessarily lead to differences in PTF prediction, particularly when considering the laboratory and field dichotomy (Gupta et al., 2021b). To exemplify the variability that may be produced by different measurement methods, we explored the European Hydro-pedological Data Inventory (EU-HYDI; Weynants et al., 2013). We first note that access to the data inventory is restricted to the data contributors, complicating efforts to exploit the data richness, and to certain data locations. From the data inventory, we selected those SHP records that included information on soil texture, BD, and organic matter. Multiple linear regression PTFs were fitted separately for saturated hydraulic conductivity and water contents at particular pressure heads. We then subtracted the observed retention and hydraulic conductivity values from their estimated counterparts and grouped the residuals by measurement methodologies. Figures 6 and 7 show the results for water retention at a suction of −100 cm and K_sat, respectively. The distribution of residuals indicates that there is a dependency on the methodology as well as on sample sizes used to obtain the WRCs and HCCs in the laboratory. We do note, however, that potential effects of soil texture have not been disentangled here. Noise introduced by the different measurement methods or protocols may impose a ceiling on the prediction quality of PTFs. Efforts such as the Soil Program on Hydro-Physics via International Engagement (SOPHIE) initiative (Bakker et al., 2019) that aim to harmonise, standardise, and innovate soil hydro-physical measurements should be further expanded in the future.

4.2 Harmonisation and standardisation of methods

Issues that have hampered every past effort to develop PTFs are the use of different measurement methods, the amount and method of data reporting, and the classification standards and/or systems. These can even exist within the same dataset. In some cases, this has caused misunderstanding or misrepresentation of data (Nemes et al., 2009). In other cases, conversion or interpolation solutions had to be sought (e.g. Wösten et al., 1999; Nemes et al., 1999) to make the available data compatible, introducing additional uncertainty. Still, Nemes and Rawls (2004) concluded that such conversion is preferable for the purposes of PTF cross-testing and use because the conversion helps reduce or remove bias in the data even if this introduces additional noise.

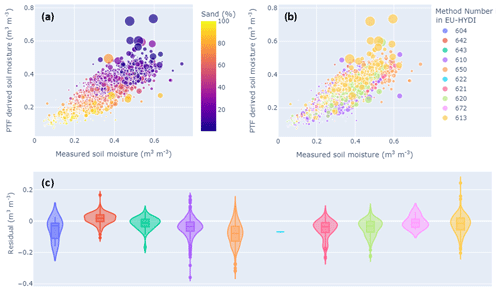
Figure 6 PTF fitting of the water retention data obtained from the EU-HYDI database at a soil suction of −100 cm. (a) Comparison between measured soil moisture and PTF-derived soil moisture by multiple linear regression (adjusted R²: 0.64); the colour is related to the percentage of sand in the sample, and the data point size is related to the organic matter content. (b) Same as (a) the colour related to the method number: the data point size is related to the organic matter content. (c) Residuals plotted per method. Method 604: unknown; sand or kaolin box method with undisturbed soil core. Method 610: 100 cm³, 613: 222 cm³; pressure plate method with undisturbed soil core. Methods 620: 100 cm³, 621: 200 cm³, and 622: 250 cm³. Method 642: pressure membrane method on undisturbed soil clods. Method 642: 3–5 cm³ with estimation of the soil volume on undisturbed soil core (500 cm³). Method 643: 3–5 cm³. Hanging water column method with undisturbed soil core, method 650: 250 cm³. Evaporation method on undisturbed soil core, method 672: 630 cm³, with tensiometers at four depths (1, 3, 5, and 7 cm). Further details on the methods and data can be found in EU-HYDI (Weynants et al., 2013).

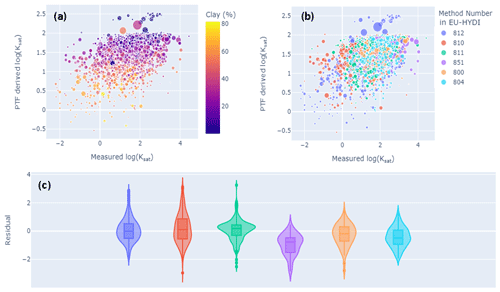
Figure 7 PTF fitting of the saturated hydraulic conductivity (K_sat) data obtained from the EU-HYDI database. (a) Comparison between the measured log (K_sat) and PTF-derived log (K_sat) by multiple linear regression (adjusted R²: 0.21): colour is related to the percentage of clay in a sample, and data point size is related to organic matter content. (b) Same as (a) the colour related to the method number; the data point size is related to the organic matter content. (c) Residuals plotted per method. Saturated hydraulic conductivity methods: constant head method with undisturbed samples; methods 800: 100 cm³ and 804: 630–4700 cm³ sample volume. Falling head method with undisturbed samples; methods 810: 100 cm³, 811: 221–530 cm³, and 812: unspecified sample volume. In situ falling head method, single-ring infiltrometer; method 851: ring 30 cm diameter, inserted 12 cm into the soil. Further details on the methods and data can be found in EU-HYDI (Weynants et al., 2013).

Typical examples are different soil particle size standards. Some countries, like Russia and some central and eastern European countries, apply an upper bound for sand content at 1 mm (whereas most standards use 2 mm). This divergence leaves data from a vast and relatively intensely surveyed land area incompatible with that of the rest of the world. The main issue is that the 1–2 mm coarse sand fraction is absent from the analysis and follow-up calculations; therefore, a conversion would not entail interpolation, but extrapolation.

Another, subtler example is from the USDA Natural Resources Conservation Service's National Cooperative Soil Survey Soil Characterization Database (http://ncsslabdatamart.sc.egov.usda.gov/, last access: 10 June 2024), which has data on BD. The values are determined using different methods or standards for the same soil sample. The lack of convertibility between the methods is visible in Fig. 8, which presents a comparison of BD on a dry-mass basis determined on soil clods that were equilibrated at −33 kPa water content and oven-dried with the volumes determined separately. Because most data plot above the 1:1 line, the deviation indicates a loss in sample volume during oven drying, in comparison to a wet clod equilibrated at −33 kPa. Due to the shape of the point cloud in Fig. 8, there appears to be no option to calculate one from the other. The same is expected when attempting to compare soil-core- and soil-clod-based BDs, in which case the latter does not account for the between-clod pore system. European data collections typically report BDs determined on soil cores (e.g. the Hydraulic Properties of European Soils – HYPRES – and the European Hydro-pedological Data Inventory databases). This is a concrete example hindering international data comparability.

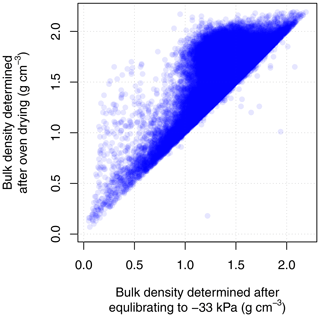
Figure 8 Soil bulk density determined at −33 kPa water content and after oven drying, using data of the USDA Natural Resources Conservation Service's National Cooperative Soil Survey Soil Characterization Database (N=57 512). Each dot represents one soil sample.

Although it is important to harmonise new measurements with historic measurements, there seems to be little willingness to change long-established protocols, especially if that implies additional costs. As a positive precedent, Hungary already transitioned from the International Society of Soil Science particle size classification system to that of the USDA Agricultural Research Service in the 1990s. This was simply achieved by adding an additional measurement of the texture fraction at a particle diameter of 50 µm to the measurement sequence, allowing both backward and forward compatibility at little extra cost. At present, the Food and Agricultural Organization is also engaged in developing recommended measurement protocols for future measurement of various soil properties with the expectation that it will help reduce some sources of variability due to differences in, for example, sample preparation.

New methodologies to measure soil properties keep emerging, and this is to be encouraged, even if it leads to both challenges and opportunities. For example, the measurement of soil particle size distribution by laser diffraction has high upfront investment costs, while the measurement itself is significantly cheaper and quicker than with the pipette or hydrometer methods. At the same time, it has been recognised that the obtained data from these methods are not directly compatible with one another, and the conversion between them is not trivial (Bieganowski et al., 2018). However, methods that provide quasi-continuous data, i.e. data with a high measurement resolution within minutes, are attractive because their data efficiency is higher; the same measurement effort provides data that are compatible with multiple standards. To that end, while it comes with new investment costs and potentially new structural errors dependent on the measurement technique, the integral suspension method (Durner and Iden, 2021) has desirable features in that it reports quasi-continuous data – while it is based on the same theory as the pipette and hydrometer methods, promising good data compatibility and convertibility. At the time of writing, the latter has yet to be widely confirmed, like the added benefit of the quasi-continuous data for building PTFs.

X-ray tomography imaging or spectral properties are gaining popularity and may be used as input data to PTFs. Measurements are usually conducted in small-scale single studies with isolated datasets. Data collection is rarely standardised and is often dependent on technical capabilities, practical cost–benefit choices, and undoubtedly the personal preferences of the involved scientists. In X-ray tomography, this problem of standardisation is particularly abundant, where hardware differs, leading to differences in image resolution and choices of image processing and segmentation, also leading to large impacts on the results. Non-standardised moisture states of the samples at the time of scanning may induce inter-laboratory uncertainties, even when reported.

Furthermore, while X-ray tomography is also sometimes used to infer WRCs, it is unlikely that these data are directly comparable with, for example, data from pressure plate experiments. The reasoning is that the water volume removed from the sample emptied using pressure plates depends on the pore architecture, while X-ray image-derived data depend strongly on the image processing pipeline and the selected segmentation approach (Gackiewicz et al., 2019).

It is desirable that respective research groups summon and establish measurement standards and minimum requirements early and before phasing in larger volumes of measurements internationally, to help prevent fragmentation and incompatibility of data. This would enhance the communal effort to develop PTFs with broader validity. As image processing capabilities have improved steadily and as we understand their effects on the result, publishing 3-D image data in data repositories prior to processing may be desirable, so they can be analysed uniformly by potential future users when new analytical approaches emerge. Still, describing and linking structural information as a further proxy for PTFs is an ongoing challenge.

No systematic standardisation exists in determining SHPs either. However, in one inter-laboratory comparison of physical water retention properties and saturated hydraulic conductivity (Buchter et al., 2015) performed by laboratories all in Switzerland, the results showed significant differences between the laboratories used. These results call into question the concept of comparability between laboratories. For example, the degree of soil saturation and the saturation method prior to the experiment are not always quantified. Furthermore, other hydro-physical characteristics of a given soil may change over time (e.g. Young et al., 2004; Bens et al., 2007; Eppes et al., 2008) as a result of many factors. Ideally, these should be captured as metadata as soil samples are analysed.

Sample preparation conditions such as the saturation method (with or without vacuum) or saturation solution (distilled water or saline solution to limit colloid dispersion, antimicrobial solution to avoid biofilm development) can also influence the measurement result (Klute and Dirksen, 1986; Dane and Topp, 2002; Cresswell et al., 2008). Air entrapment is known to have a large impact on soil-saturated hydraulic conductivity (Faybishenko, 1995). Methods that aim to reduce air entrapment (saturation from below, with or without vacuum) will lead to overestimation of field-saturated hydraulic conductivity. The use of contact materials between the sample and the pressure plate and/or weights on top of the sample may also affect the retention measurement (Klute and Dirksen, 1986). These contact materials can be filter paper or woven materials such as polyester fabric, synthetic knitwear, cheesecloth, kaolinite (Reynolds and Topp, 2008), or silt (Klute and Dirksen, 1986). Gee et al. (2002) demonstrated that neither kaolinite nor adding weights improved the contact between the samples and plates. However, Gubiani et al. (2013) recommend the use of filter paper under high pressure, and McCarter et al. (2017) developed a measurement method particularly suited for peat soils. Laboratory practices differ between laboratories and often change over time in a single laboratory as a result of a change in equipment or technician. Furthermore, the temperature and relative humidity in the laboratory impact the measurements by altering the surface tension of the water and the vapour fluxes in the sample during equilibration (Hopmans and Dane, 1986). In a recent study on the reproducibility of the wet part of the soil WRC, Guillaume et al. (2023) conducted an inter- and intra-laboratory method comparison and found that inter- and intra-laboratory variability can be a substantial source of scatter and error in the data, even when the methods have been harmonised.

With regard to the hydraulic conductivity of soils, the considerations regarding sample saturation remain valid. Javaux and Vanclooster (2006) demonstrated that hydraulic conductivity estimates may be influenced by the sample size. Deb and Shukla (2012) reviewed the multiple factors that can impact the measurement and highlight differences in the device used, the sample support, and the number of replications, among others. They concluded that comparing data produced in different studies is almost impossible. The effect on PTFs, however, remains largely unknown. While inter-laboratory comparisons exist for textural analysis, the same is very rare for hydro-physical properties such as the retention curve or hydraulic conductivity (Guillaume et al., 2023). This type of exercise requires reference samples, which drain over predefined pressure head ranges sufficiently so that inter- and intra-laboratory measurement uncertainty may be disentangled.

In contrast to the environmental chemistry-related sciences, standards, ring tests, and blanks are rarely used in the field of soil physics, a discipline which is rooted in traditional local country-level protocols. For the notion of improving PTFs, it is highly desirable to harmonise and standardise measurement protocols.

4.3 Required and auxiliary data

What do we need to reach higher-quality PTF prediction, especially for larger-scale modelling? Clearly, we need to aim at establishing best practices for measuring and reporting data to be used for PTF development. Open-source data policies are instrumental in that respect. To be able to produce meaningful and high-quality syntheses from models that need soil parameterisations, the quality of the underlying data needs to be ensured. PTF quality is hampered by a lack of “best practices”. In other research fields the need for harmonisation and standardisation has been recognised and dealt with either through formalised networks (e.g. WEPAL, https://www.wepal.nl/en/wepal.htm, last access: 10 June 2024) or management plans for collaborative research (Finkel et al., 2020) or standardised handbooks (e.g. Halbritter et al., 2020). Finally, it has to be mentioned that developments for standardisation of measurement methodologies for PTF development have been initiated by, for example, the Food and Agricultural Organization Global Soil Laboratory Network (https://www.fao.org/global-soil-partnership/glosolan/en/, last access: 10 June 2024) and the earlier-cited SOPHIE initiative (https://www.wur.nl/en/article/Soil-Program-on-Hydro-Physics-via-International, last access: 10 June 2024; Bakker et al., 2019).

Moreover, we should make sure that repositories containing data for properties traditionally used for PTF development would benefit from a checklist containing minimal data requirements and reported auxiliary information in soil surveys. In the following, we present a number of suggestions for what a checklist with metadata should include.

• Soil age and pedogenic development. Assessing the soil age or, more directly, the pedogenic development would likely enhance predictions of SHPs. For example, age along a chronosequence has been strongly linked to significant changes in soil hydraulic conductivity (Young et al., 2004). Although quantitative pedogenic development indices have been difficult to generalise given their dependence on knowledge of the parent material, recent work has shown that these indices can be reconstructed to examine relative differences between illuvial and eluvial horizons, removing the need for lithologic information (Koop et al., 2020).

• Soil geomorphic description. Information on local topography (e.g. slope, aspect, or curvature) and land surface age would likely assist in comparisons between predictions of SHPs for different geomorphic environments and serve as a grouping basis for the development of class-based PTFs.

• Information on current land use (e.g. tillage practices), known history of land use changes, soil age since land use change, and evidence of land degradation characteristics (e.g. erosion).

• Details on vegetation (e.g. above- and below-ground biomass, leaf area index) and soil fauna, soil type together with horizon, soil depth, root zone depth, and groundwater depth.

As such it would be desirable if funding agencies were aware of standards regarding collection, curation, and storage and actively included this.

Two notable data and knowledge gaps are field-measured SHPs – especially hydraulic conductivity – and the wetting branch of the hysteretic WRC that is relevant under field conditions (see Sects. 2 and 6). Careful consideration of the use of hydraulic conductivity in models is warranted though, as it is impacted by the scale of observation (Roth, 2008) and possibly by atmospheric conditions (Oosterwoud et al., 2017) or seasonal effects (Suwardji and Eberbach, 1998; Farkas et al., 2006; Bormann and Klaassen, 2008). It can be difficult to determine the HCC for soils and pressure heads with very low conductivities. Moreover, its non-standardised quantification methods can introduce variation (Fodor et al., 2011). Field hydraulic conductivity under relatively wet conditions can be obtained through measurements of infiltration. Examples of a global database are presented by Rahmati et al. (2018).

Since data on the wetting branch of the WRC are rarely available in sizeable (international) soil hydraulic data collections of the databases known and frequently used, the Unsaturated Soil Hydraulic Database (UNSODA) (Leij, 1996; Nemes et al., 2001) is the only one that has separately collected and stored water retention data measured on the wetting branch. However, data are scarce: while there are 730 laboratory-measured WRCs in the database that were determined during drying, only 33 were determined during wetting. Field-measured WRCs are even more scarce: only 137 and 2, respectively. There is clearly a gap in our quantitative knowledge of soil water retention behaviour under field conditions, while we are aware of the dichotomy between laboratory-measured data and field-observed effective soil hydraulic behaviour. We understand that this dichotomy is driven by multiple factors, among them the non-representativeness of field conditions by laboratory experiments, the scale of the measurement, typically the scale of PTF derivation (see Sect. 6), and the omission of the effect of neighbouring soil layers when working with a centimetre-scale soil sample. Therefore, it would be desirable to routinely complement laboratory data with auxiliary information and field measurements.

Although the scale of measurement is still not comparable to grid cells within LSMs or global circulation models, aquifer conductivity can provide an interesting additional data source when the soils resemble the aquifer materials, such as in uniform sedimentary systems. Pelletier et al. (2016) provide a database containing 1 km gridded thickness of soil, regolith, and sedimentary deposit layers that can inform the application of aquifer conductivity as a proxy for larger-scale PTF estimates.

Furthermore, with the expansion of proximal and remote sensing, larger-scale approaches may become available to estimate hydraulic conductivity. For example, Francos et al. (2021) used uncrewed aerial vehicle hyperspectral data to map water infiltration, and Rezaei et al. (2016) measured apparent electrical conductivity and found a good correlation with the saturated hydraulic conductivity and soil properties and subsequently hydrologic fluxes.

4.4 Characterising and considering soil structure

Soil structure has long been recognised as a missing key determinant of SHPs in PTFs (Lin, 2003; Terribile et al., 2011; Pachepsky and Rawls, 2003). Lack of predictors quantifying relevant soil structures explains the poor performance of PTFs for saturated and near-saturated hydraulic conductivity (Vereecken et al., 2010; Jorda et al., 2015; Gupta et al., 2021b). To fill this gap, using the information on aggregates from field soil surveys is particularly attractive (Pachepsky and Rawls, 2003). Here, the morphology and stability of the soil pore network are fundamental. Due to the opaque nature of soil, quantifying relevant soil structures has proven difficult. During the last 20 years, non-invasive imaging methods have become available and have led to fundamental progress in this field of research, first and foremost 3-D X-ray imaging. From this evidence it has been concluded that the critical pore diameter correlates well with the saturated hydraulic conductivity in undisturbed soil (Koestel et al., 2018). Conceptually speaking, the critical pore diameter is the size of the bottleneck in the pore-to-pore connections from the top to the bottom of a soil sample. In freshly tilled soil, it is macro-porosity that strongly controls the saturated hydraulic conductivity (Schlüter et al., 2020). While acquiring X-ray image data is restricted to sample diameters of less than 20 cm and requires great efforts as direct SHP measurements, it may be useful to identify auxiliary variables and then to link them to SHPs. For example, it will allow one to investigate how soil aggregates relate to soil pore network morphologies (Koestel et al., 2021), which in turn determine SHPs. Deriving a PTF for bi-modal SHP models requires robust measurements of near-saturation unsaturated hydraulic conductivity. If we think of the soil matrix and the macro pores as two domains, measurements near saturation (e.g. $>-\mathrm{6}$ cm) are required to obtain conductivity. In principle, such data may be obtained using multi-step flux experiments and tension-disc infiltrometer measurements. A meta-database of the one used in Jarvis et al. (2013) was recently published (Blanchy et al., 2023). However, the majority of published tension-disc infiltrometer data do not sample sufficient numbers of support tensions for parameterising bi-modality in HCCs.

Progress in quantifying soil structure has been especially slow at the pedon and field scales (Letey, 1991; Eck et al., 2013). Data on soil structure often reflect properties of aggregates (e.g. aggregate–size distributions, aggregate stability). In turn, it is still difficult to relate these directly to soil pore structure due to the lack of information on how aggregates are arranged and packed within a representative soil volume (Sullivan et al., 2022). Where these data exist, they often describe aggregate properties from relatively shallow depths and small samples (e.g. ∼25 g; Nimmo and Perkins, 2002) that do not capture the morphological structure of the soil horizon and, thus, miss the connectivity of pore networks and spatial heterogeneity of SHPs at larger scales (Rabot et al., 2018). Additionally, transferability to other soil samples, even when collected nearby, is still problematic. Additionally, quantitative aggregate data are often only collected for particular research studies as opposed to soil survey efforts, limiting their distribution and availability for inclusion in PTFs. Also, information on the larger soil aggregate structure is often obtained from field descriptions, which are represented by categorical, subjective, and discrete data (Terribile et al., 2011; Eck et al., 2013). Moreover, soil aggregate structure can occur in a nested, hierarchical arrangement within a horizon, and the qualitative data for each representative structural unit need to be combined appropriately to provide information on the overall structural character of the material (Hirmas and Gimenez, 2017).

Despite these issues, several recent promising developments allow us to project a roadmap for the inclusion of soil structure in the generation of PTFs. Probably the lowest-hanging fruit is the use of historic field description data as inputs into PTFs (Lin et al., 1999). Although we collect these data as categorical, recent work has shown that they can be quantified on a ratio scale (Mohammed et al., 2020). For example, Mohammed et al. (2016) combined image analysis of hundreds of structural silhouettes taken from high-resolution photographs with a survey of 78 soil scientists with experience in the field to classify each structural unit in its ped type (i.e. shape, blocky, prism shape, etc.). This allowed each ped type to be assigned a shape metric derived from the image analysis. Hirmas and Gimenez (2017) showed how this information could be combined in soil horizons where multiple and compound structures were described. Because these data are recorded in standard soil survey efforts (e.g. Soil Science Division Staff, 2017), the ability to convert them to quantitative metrics opens the door to including them as input variables in PTFs and widens the range of possible machine learning algorithms used in PTF development.

Other techniques based on images have been developed that address the quantification and the pore aggregate problem described above (e.g. computed tomography; Abrosimov et al., 2021; Koestel et al., 2021) as well as the scale issue (e.g. multi-stripe laser triangulation scanning; Hirmas et al., 2016; Bagnall et al., 2020). However, these techniques are currently not routinely applied in soil survey efforts and, thus, remain restricted to relatively small numbers of samples without wide geographic and soil-geomorphic representation. Because including these data will doubtlessly improve predictions of PTFs, we agree with the recommendation by Rabot et al. (2018) that a coordinated effort should be established to obtain this information at a wider scale (i.e. development of a soil structure library). More urgently, data from these techniques should be used to create better predictions of quantitative structural metrics from readily available soil property information. These predicted structural parameters can then be used to improve predictions of hydraulic properties from PTFs.

A blueprint for rectifying soil structure omission in current PTFs was recently proposed by Bonetti et al. (2021), who suggested the use of vegetation metrics (in combination with soil textural information) to directly modulate PTF-derived SHPs and to account for the effect of biologically induced soil structure on the soil saturated hydraulic conductivity (see also Fatichi et al., 2020; Fan et al., 2022). While this study still relies on empirical relations to link vegetation and soil structure, it offers a systematic and physically based approach to model parameterisation that goes beyond ad hoc parameter tuning. To overcome biases introduced by the limited number and types of predictors commonly employed, additional information should be included in the derivation of PTFs (Vereecken et al., 2010). In these regards, capitalising on the ever-increasing availability of spatially resolved remote sensing information could offer new opportunities to concomitantly include additional local information in PTFs and provide estimates of SHPs at scales relevant to land surface and Earth system models (Bonetti et al., 2021). The recent availability of the global-scale digital maps of soil physical and chemical properties – despite their uncertainties – provides high-spatial-resolution information to support the implementation of PTFs for modelling applications, starting from products such as SoilGrids 250 m (Hengl et al., 2017), its recently updated version, SoilGrids 2.0 (Poggio et al., 2021), or OpenLandMap (https://openlandmap.org, last access: 10 June 2024). For example, Gupta et al. (2021a) harnessed the availability of spatially distributed surface and climate attributes to derive maps of soil-saturated hydraulic conductivity and WRC parameters at 1 km resolution within a ML framework. This novel approach to predictive SHP mapping was named the “covariate-based GeoTransfer function” to highlight differences with previous maps solely based on soil information (i.e. traditional PTFs) and generally neglecting additional environmental covariates.

4.5 New opportunities for in situ sensing

Sensors exist that can indirectly infer basic soil properties rapidly as an alternative to direct measurement of soil physical and hydraulic properties by relating the spectra to the measured soil properties by (multivariate) regression functions. These sensors usually involve the application of some wavelengths of the electromagnetic spectrum to the soil and measuring the response. In particular, soil responds uniquely to the infrared spectrum. Infrared spectrometers can measure soil responses to infrared radiation rapidly and non-destructively. One of the first applications of near-infrared spectrometry in soil science was to measure the soil water content (Bowers and Hanks, 1965), but research into field and laboratory-based infrared soil spectrometry has become increasingly popular over the past 2 decades due to the availability of the sensors and mathematical techniques to process the spectra. Studies have found that soil spectra in the visible and near-infrared range (NIR, 400–2500 nm) and mid-infrared range (MIR, 2500–25 000 nm) can characterise a range of physical, chemical, and biological properties via multivariate prediction functions (Reeves, 2010; Soriano-Disla et al., 2014). The sensors can be operated in the laboratory or the field. For example, the near-infrared sensor can be mounted in a penetrometer to measure soil spectra with depth. Some infrared hyperspectral sensors can be attached to satellite, aircraft, or uncrewed aerial vehicles, offering detailed soil surface spectrum reflectance (e.g. Lagacherie et al., 2020).

Soil infrared spectra can predict several fundamental soil properties very well, including soil particle size distribution, organic and inorganic carbon content, cation exchange capacity, exchangeable cations, pH, mineralogy, and the total elemental concentrations of major elements (Ng et al., 2022). Many of these soil properties are key inputs to PTFs and may be used as predictors for published PTFs (Tranter et al., 2008). There are also several studies that suggest that soil NIR and MIR spectra can predict directly points on the WRC and HCC (e.g. Pittaki-Chrysodonta et al., 2018) too. These are termed spectra PTFs (Santra et al., 2009).

However, as infrared spectrometry only measures the reflectance of the soil matrix (usually in the laboratory on sieved soil samples) and cannot sense any pores or pore size distributions, it has proven performant in predicting water retention in the dry range where water adsorption to mineral surfaces dominates but has low predictive capability related to water stored in aggregates or capillary pores. The infrared spectra can predict water retention measured using sieved soil samples at all moisture ranges, but the predictions of the volumetric water content of soil clods at −60, −100, and −330 hPa were not as accurate as in the sieved samples due to missing information on soil structure. Pittaki-Chrysodonta et al. (2018) stressed that soil-structure-dependent water content will typically be poorly related to basic texture properties and, thus, poorly predicted from NIR spectra.

This factor seems to be disregarded in many publications that promote NIR and MIR as effective proxies to the whole retention curve or hydraulic conductivity. Nevertheless, the use of MIR and NIR for predicting SHPs can be more accurate than traditional PTFs since the spectra contain better information on mineral and organic components of the soil (Pittaki-Chrysodonta et al., 2018). Incorporating information on soil structure into the infrared spectra may overcome these limitations and can open new directions in inferring soil (hydraulic) properties. At the landscape level one can also think about sensor technologies to estimate either soil properties such as soil texture by electromagnetic induction (e.g. Hedley et al., 2004; Heil and Schmidhalter, 2012; Michael Mertens et al., 2008), gamma ray spectroscopy or EMI for determination of field-scale bulk density (e.g. Reinhardt and Herrmann, 2019; Schmäck et al., 2022), or use of either stationary or mobile cosmic ray neutron detectors for estimating field-scale water content dynamics and hydraulic properties using inverse modelling within the HYDRUS COSMIC module (e.g. Brunetti et al., 2019). While these are promising methods, they are still far from operational, requiring fundamental research to integrate them into field-derived PTF development.

5 Constraint-based SHP parameterisation for plausible modelling

Before building a parametric PTF (i.e. a PTF to predict SHP model parameters), the parameters of the SHP model have to be estimated using measured WRC and HCC data by inverse modelling (SHP model calibration). In this section, we present a method and examples of how SHP models may be parameterised to ensure physical plausibility. As discussed earlier, the sample volumes and measuring devices used to obtain the WRC and HCC data may differ and induce uncertainties in the data (Sect. 4). It is expected that this will propagate to the calibrated SHP model parameters and ultimately to the built PTF. Additionally, a given SHP model might not actually be the correct description for the data-generating process – in other words, the model structure may not be able to describe the data or might simply be incomplete (Sect. 2) for a given model use (Sect. 3). The aforementioned reasons may lead to the estimation of physically implausible SHP model parameters and PTFs. One method to ensure physically plausible SHP models during the inverse modelling step is to use additional knowledge and physical constraints in the inference process (Wöhling and Vrugt, 2011; Zhang et al., 2016; Lehmann et al., 2020). We do not discuss outlier detection or the propagation of uncertainties to the PTFs.

5.1 Parameter estimation in a Bayesian framework to integrate constraints

Most commonly, SHP model parameters are estimated using a cost function which is used to minimise the difference between observations and predictions (typically the measured and modelled WRC and HCC data). Frequently, some form of maximum likelihood estimation (Hopmans et al., 2002) or the related minimisation of least squares is used. Equivalently to this common approach, Bayesian inference can identify the maximum a posteriori probability estimates of the model parameters. Beyond such a point estimate, Bayesian inference provides robust information on parameter uncertainty and auxiliary (physical) constraints during which the inference process may be incorporated. We explicitly introduce the Bayesian inference scheme here to highlight its suitability in the context of building physically consistent (Sect. 5.2) and functionally evaluated (Sect. 6) PTFs.

According to Bayes' theorem, the posterior probability p(x|y) of a parameter set x given data y is formulated by the proportionality $p\left(\mathit{x}\mathrm{|}y\right)\propto p\left(y\right|\mathit{x}\left)p\right(\mathit{x})$. The first factor on the right-hand side, the proportionality p(y|x), is the conditional probability of a model with its corresponding parameter vector x having produced the observed data y. This is often termed the likelihood model. The second factor, p(x), is the prior parameter probability. For this frequently weak information, bounded uniform priors are used. We note that the adequacy of the statistical assumptions in the likelihood model p(y|x) (e.g. independently and identically distributed errors which are described by a known distribution) is important for both the accuracy and particularly for the precision of the estimated parameter posterior probability. For methodologies and methods to quantify the posterior, we refer to standard textbooks (e.g. Gelman et al., 2013).

Bayes' theorem will yield identical results to maximum likelihood estimation when non-informative priors are used. This is most commonly done, and the maximum likelihood estimator or best-fit parameter set $\widehat{x}$ is used in the subsequent building process of the PTF. However, it is by use of informative priors that constraints can be directly considered a priori, meaning before the fitting process. This constrains the admissible parameter space to a plausible space. Methodologically, this can be achieved by constraint-based parameter sampling approaches (Chavez Rodriguez et al., 2022; Gharari et al., 2014). Note that this step is taken before fitting WRC and HCC functions to data. The aim is to obtain a prior that fulfils a list of “minimum necessary requirements” or “constraints” (see Sect. 5.2), either evidence-based or expert-elicited for both model parameters and the corresponding model outputs. This may be achieved by drawing parameter vectors from an originally non-informative prior p⁰(θ). Then, before simulating the prior predictive of the SHP model, the parameter samples are subject to fulfilling all the constraints directly (i.e. parameter relationships and plausibility constraints). Subsequently, two more categories of constraints related to the model outputs may be included. First, the simulated prior prediction may be analysed directly (e.g. monotonicity in the modelled HCC). Secondly, the sampled SHP model parameters may be used to parameterise the RRE and simulate water fluxes (e.g. using HYDRUS) or, for example, infiltration experiments (Lassabatère et al., 2006). The simulated state variables may then be compared to measurements or a list of physical plausibilities.

This model-based evaluation of the prior prediction may provide a method to bridge the gap between the laboratory-based measurements commonly used in PTF building and field-scale functional evaluation (Sect. 6). If this approach is done recursively and the sampling process is coupled with a Markov chain Monte Carlo sampler, then the non-informative prior may be turned into a highly informative prior p⁰(θ|M)→p(θ|M) (Chavez Rodriguez et al., 2022) and can be used when fitting the WRC and HCC to ensure physical consistency. We note that, due to the multiplicative nature p(y|x)p(x), this process may be done immediately inside the likelihood model and is straightforward to implement.

To avoid bias in constructing informative priors, constraints should be based on clear empirical evidence from measurements, calculations, and physical theory and careful consideration of uncertainties in observations. Bayesian constraint-based prior modelling approaches also increase the computational efficiency of the subsequent parameter identification and enable consistent quantification of uncertainties and data worth analyses, provided that the statistical assumptions in the likelihood model are met.

5.2 PTFs have to honour physical constraints

The parameters of the SHP that are determined based on fitting experimental data or prediction by PTFs must obey various physical constraints. Straightforward constraints describing the WRC include (i) soil water retention values between 0 and the value of total porosity, (ii) WRC attaining a water content of 0 at oven dryness, and (iii) water retention values monotonically decreasing with decreasing matric potential. While the monotonicity is ensured for parametric models of SHPs (see below), this is not straightforward for PTFs that predict the water content for a few specific matric potential values. In McNeill et al. (2018), the monotonicity was ensured by predicting non-negative water content differences for increasing water potential (starting with a PTF for the wilting point at −150 m). A specific example is point PTFs for the wilting point and FC (and thus the plant-available water). In this case, a possible option is to predict the wilting point and the available water content ≥ 0 with a PTF and to then compute the FC from those to ensure that the difference between the FC and the wilting point will not result in a negative available water capacity value.

The monotonicity is secured when a parametric PTF is applied, providing it was built for that end. In this case, the parameters of the WRC model are predicted, and θ at different h can be computed. However, a more complex approach is required for the derivation of physically constrained WRC or HCC by continuous PTFs. The majority of methods available from the literature predict the parameters of the WRC models but do not consider parameter correlation, thereby being another reason why prediction may lead to physically unrealistic parameter combinations.

Apart from constraining the PTF outputs and hydraulic properties derived from estimated parameters, the user should be clearly advised about the input data range that the PTF has been trained on. To this end, the commonly communicated minimum–maximum range of, for example, sand, silt, and clay content is insufficient, given that the minimum–maximum data range can be nearly identical for temperate and tropical datasets, while their density distribution and related characteristics can differ substantially. More descriptive information is needed that may include, for example, density distribution plots and correlation matrices.

The vast majority of methods used for PTF development are empirical data-driven techniques relying on the derivation of relationships between predictors and response variables (Patil and Singh, 2016; van Looy et al., 2017). The use of limited and only partially representative sets of predictive soil variables combined with the sole reliance on basic goodness-of-fit estimators to evaluate model performance (Vereecken et al., 2010; van Looy et al., 2017) may, however, lead to unphysical parameter combinations and biases in the estimation of SHPs.

In line with Sect. 5.1 and the requirement of constraining, Lehmann et al. (2020) showed that a commonly used metric, the measurable quantity “characteristic length of evaporation”, L_C, is overestimated for about 30 % of the global terrestrial surfaces if it is predicted based on SHPs derived from ROSETTA3 (Zhang and Schaap, 2017) PTFs. Based on the PTF-predicted SHP parameter values, the calculated characteristic length was in many cases several metres, which is unrealistic. The authors thus proposed the use of multiple physical constraints during the PTF construction and fitting of measured SHPs to avoid unphysical parameter combinations (Or, 2019). Specifically, the parameter values of the SHP were fitted to minimise not only the deviation from the measured soil water retention (or hydraulic conductivity) data, but also the expected value of the characteristic length.

The example of the characteristic length of evaporation is one possibility to determine SHP parameter values honouring physical constraints, but such a methodology could be further extended to include additional physical constraints. As examples, the “ponding time T_p” (onset of surface runoff), the “length of evaporation L_C” (maximum length of capillary flow paths to sustain evaporation from the surface), and the “attainment of field capacity θ_FC” (soil water content after gravity drainage) are good candidates and are given in Box 1. In the example of VGM, all these secondary properties (in the following denoted as secondary SHPs, SHP2) can be expressed analytically as a function of the parameters of the SHP (θ_r, θ_s, n, α) and K_sat (see Rahmati et al., 2018; Lehmann et al., 2008; Shokri and Salvucci, 2011; Twarakavi et al., 2009; Assouline and Or, 2014; Assouline, 2013). Both the basic SHP (θ(h) and K(θ(h))) and the SHP2 (T_p, L_C, and θ_FC) are thus functions of the same parameters to be fitted (θ_r, θ_s, n, and α) or predicted by PTFs, meaning that the determination of the parameter values must fulfil constraints related to both SHP and SHP2. In the following, we distinguish between two situations with respect to available information on SHP2.

Box 1 Constraints for the determination of soil hydraulic properties.

Measurements of SHP2 are relatively easy to perform (measuring time and infiltration rate for T_P, evaporation rate and water table depth for L_C, and water content as a function of time for θ_FC). However, values of SHP2 are not routinely measured and must thus be constrained based on literature values and expectations for certain soil textural classes. For example, ponding time T_P is expected to be larger for coarse textures compared to fine materials, and loamy soils must have a greater length of evaporation L_C due to large capillary pressure differences driving flow to the surface. Constraints can thus be defined as a function of soil texture (or other available properties such as BD). Because the shape parameter n changes systematically with texture with small values for fine and large values for coarse textures, constraints can be defined as a function of n. This was done in Lehmann et al. (2020) for L_C and by Twarakavi et al. (2009) for field capacity θ_FC.

Furthermore, as discussed in the previous sections, currently used PTFs generally lack a proper representation of soil structure (Vereecken et al., 2019), strongly affecting the representation of a realistic and reliable hydrologic response, especially in wet and vegetated regions (Or, 2019; Fatichi et al., 2020; Bonetti et al., 2021). An important consequence of this lack of representation of soil structure and macropore flow in PTF-derived SHPs may result in an overestimation of surface runoff (Sobieraj et al., 2001; Du et al., 2016), thus often requiring ad hoc tuning of SHPs to properly model water and energy fluxes (Mascaro et al., 2015; Baroni et al., 2017; Fatichi et al., 2020). Similarly, the use of a clay fraction as a predictor of SHPs irrespective of the dominant type of clay minerals (Gupta et al., 2021b) may lead to an underestimation of the soil-saturated hydraulic conductivity, thus affecting rainfall partitioning and overestimating surface runoff (Lehmann et al., 2021).

Rectifying such biases in current PTF estimates of SHPs requires a paradigm shift to build PTFs that are not purely the result of minimising a cost function but that should be anchored in a modelling framework to obtain physically consistent PTFs using Bayesian inference (see Sect. 5.1 for the methodological framework). This is needed to improve their usefulness and reliability in land surface modelling applications (Or, 2019). In these regards, the injection of additional physical constraints into PTF estimation was recently shown to reduce the occurrence of unphysical parameter combinations (Lehmann et al., 2020).

6 Evaluation of PTFs

Complementary to the constrained PTF derivation, in this section we discuss PTF evaluation. We propose a PTF evaluation scheme that addresses the discrepancy of scales and concepts between PTF derivation and application as a central problem. The overall effectiveness and confidence of PTFs in their application at larger scales are limited, since PTFs are usually only derived with laboratory-measured data. We propose to evaluate PTFs by considering the context and scale of their applications. This includes (i) disentangling different levels of system information, (ii) functional PTF evaluation, and (iii) explicit evaluation of their scaling capability.

6.1 Basic PTF evaluation

Typically, validation of PTFs is done with data of the same structure and scale as the training dataset. In the vast majority of related research papers, the PTF output for specific SHP models (e.g. VGM) is directly evaluated using sampled subsets of the originally available data (e.g. cross-validation) at the laboratory scale. Ideally, independent and external datasets should be used to evaluate PTFs. Most commonly, their performance is expressed in terms of a limited number of general goodness-of-fit metrics (e.g. R², RMSE) of individual soil parameters relating to SHPs. However, when evaluating the regression or ML results with general mean statistics, the performance of the resulting PTF remains opaque since the distribution and auto-correlation of residuals, non-unique variable combinations, or non-linear characteristics are not assessed. However, we have to include analysing residuals against explanatory and predictor variables (see Sect. 5). If we miss this analysis, we risk over-interpreting the information content in the data and ultimately the quality of the PTF.

In principle, the correlation structure in the PTF training data informs about the expected direction in which a predictor will influence a response variable (see also Sect. 5). It can help diagnose reasons for discrepancies between observed and PTF-based predictions (see Fuentes-Guevara et al., 2022). However, the degree of determination and interpretability of the effects of single predictors is reduced by the inherent heterogeneity and collinearity of predictors (Dormann et al., 2013). While advances in basic PTF evaluation of data of the same structure and scale as the training dataset can and should be established directly, the pertinent task is in fact to address and report the PTF uncertainty with respect to its scale of application (Jackisch et al., 2021).

6.2 Gap between scales and levels of information

The choice of the predictor variables is mostly pragmatically defined by established measurement routines and data accessibility in soil maps rather than by considerations of information content. In contrast to the scale and context of development (laboratory), most commonly PTFs are applied to larger spatial scales (pedon scale and beyond) under natural boundary conditions and for large aggregations of soil properties (assuming homogeneity). This creates a mixture of weakly informative predictors, implicit scale transfers, and physically comprehensive predictions outside the training data space and under substantial uncertainty.

Building on the scale triplet (spacing, extent, and support; Blöschl and Sivapalan, 1995), potential reference data and PTF applications can be positioned along a scale axis (Fig. 9, x axis). The scale dependency of inherently non-linear properties and processes in soils has been discussed in numerous studies and concepts (e.g. Vereecken et al., 2007; Vogel, 2019; Vogel and Roth, 2003). Scaling coincides with a change in the type of boundary condition, which is largely ignored during PTF development. Current soil physical theory clearly acknowledges that a change in boundary conditions and hydraulic gradients can fundamentally alter the inferred properties in similar soils at different locations, e.g. in situ field retention curve (Fig. 2) and non-equilibrium water flow observations (Diamantopoulos et al., 2015). Both issues of scale transfer and shift in boundary conditions can alter the effective SHPs (Iiyama, 2017; Hannes et al., 2016), which relates to the fact that the hydraulic properties need to be described with scale- and state-dependent hydraulic functions (see Sect. 4). Inherently, this points to the fact that there is no unifying scale-invariant theory.

Figure 9 Framework for PTF evaluation. Different evaluation approaches are classified by the scale (x axis) and level of system information (y axis) of the observed data used for evaluation.

Moreover, the hydrological system information related to PTF development and application can be classified into different levels with regard to the type of data. We suggest using three consecutive levels of system information to span a second axis (Fig. 9, y axis).

• The first level comprises single parameters of SHP models (e.g. θ_r or n). As discussed, PTF predictions are usually made at this level.

• The second level encompasses SHPs that result from the interaction of the single parameters or from direct point predictor PTFs. Usually, they are expressed by physically interpretable functions (e.g. WRC or HCC). Information directly derived from hydraulic properties like the plant-available water or the air entry value is also assigned to this level. It is the most basic level at which different SHP models can be compared and where an evaluation of the physical consistency of PTFs is meaningful (see Sect. 4).

• The third level encompasses the effects of the parameters and properties assessed in levels 1 and 2 on the hydrological functioning. It comprises any description of system dynamics. Information at this level is usually expressed and communicated as spatial patterns or time series of state variables like soil moisture or matric head. These predictions may involve quantities like runoff, groundwater recharge or evapotranspiration in hydrological models, crop growth and yield in crop models, and soil loss in erosion models.

The resulting framework clearly depicts the gap between common PTF derivation and PTF application with respect to the scale and level of information (Fig. 9).

6.3 Scale- and information-aware PTF evaluation concept

How first-level information is derived under laboratory conditions has been described earlier (see Sect. 5). While remaining at the laboratory scale, the second level of system information unveils a means of analysis for SHPs incorporating the state space spanned by matric potential, soil water content, and hydraulic conductivity, at the very least. The third level of system information refers to actual system dynamics as a means of functional evaluation (Romano and Nasta, 2016; Pringle et al., 2007; Nemes et al., 2003; Vereecken et al., 1992), which is, however, rarely chosen when deriving PTFs. To evaluate the quality of estimated SHPs from PTFs, Vereecken et al. (1992) used a functional evaluation approach based on a soil water balance model to describe system dynamics. In this approach the uncertainty introduced by PTFs in estimating soil hydrological properties such as the moisture supply capacity and the downward flux below the root zone were assessed using a Monte Carlo approach. These analyses were solely based on simulations without using experimental data on terms of the soil water balance. Later, experimental data obtained from transient column experiments (e.g. multi-step outflow, inflow, or flux experiments (Diamantopoulos et al., 2015) or lysimeter data (Groh et al., 2022)) were also used as reference data for functional evaluation. As suggested since Vereecken et al. (1992), simulated time series based on PTF-predicted SHP model parameters can be compared to experimentally observed ones, so that the PTF is evaluated with respect to hydrological functioning. However, the informative value of this evaluation is only based on a confined water flux scenario under very specific boundary conditions. Thus, third-level evaluation is complementary to the other levels because functional evaluation alone involves the pitfalls of high equifinality, physical inconsistencies, and incorrect interpretation of effects from boundary conditions.

PTF application usually takes place at larger scales, where scaled hydrologic soil properties cannot be measured directly. At the pedon scale, examples of first-level information are parameters inversely estimated based on in situ observed data (e.g. soil water retention data). However, the field–laboratory dichotomy, the vague physical meaning of such parameters (Or, 2019), and to some extent the issue of scale in terms of the sample size (Ghanbarian et al., 2017) make such references difficult to serve as a basis for PTF evaluation. At the second level of information, the variability of hydraulic curves within one soil unit can be used as property-based evaluation information. Inverse modelling of observed state dynamics is an example of third-level evaluation. This is an established method and yields effective descriptions of the desired properties and processes (Durner et al., 2007). However, reference data at this level and scale are rare, and derived descriptions are subject to non-unique solutions, considerable uncertainty, and equifinality (Beven, 2006; Pianosi et al., 2016). At larger scales, this is deemed to be even more problematic.

6.4 Proposal for a standardised pedon-scale experiment to overcome the gap

Successful scale-invariant descriptions of SHPs, enabling direct use of PTF predictions, are a rare exception. In addition, required assumptions about homogeneity and a representative elementary volume become ill-posed. Hence, a robust theory for PTF scale transfer appears out of reach as of now. We thus propose to (i) explicitly acknowledge scales and boundary conditions, (ii) use different levels of system information, and (iii) reduce the distance for implicit scaling and information transfer when developing and evaluating PTFs.

Following our proposed evaluation scheme, we call for standardised field experiments, which appear to be the most promising way of acquiring new data for PTF development. Focusing on the pedon scale could be a first step towards a more physically consistent reference of macroscale soil functioning. In contrast to the scale of soil core samples, the pedon scale hosts many hydrological processes, e.g. infiltration and runoff generation, soil water storage, or root water uptake. Furthermore, natural boundary conditions are also effective at the pedon scale.

Building on the experiences with instantaneous profile experiments (field), highly standardised ring sample evaporation experiments (laboratory), and well-equipped lysimeters (field), we suggest designing a smart and repeatable field experiment. With a series of wetting and drying cycles and controlled boundary fluxes, it has to provide sufficient information to derive unique, effective SHPs and reasonable predictors representative of a pedon. Repeating such a standardised in situ experiment at many sites will generate a new homogeneous database to build and validate a new generation of PTFs valid at the relevant scales of application. So far, controlled boundary conditions (irrigation or wetting and drying cycles) and sensors for state dynamics in the soil profile (at least soil water content, matric potential, and temperature) have only existed as experimental setups without any standardisation and with rare links to SHPs and PTFs. Similar to recent advances in laboratory standardisation, the development of such a device has great potential to further the data foundation of PTF development, in particular, and soil system understanding, in general.

7 Manifesto for future PTF development and use

In this study, we reviewed and discussed the current status quo of PTFs from the viewpoints of both developers and users, physical consistency and comprehensiveness in the description of SHPs, and fitting choices and constraint-based estimation of SHPs. We identified the common discrepancy in the scale of derivation against the scale of application. Central to this are aspects of functional evaluation of PTF performance in ecohydrological and terrestrial biosphere models (e.g. Paschalis et al., 2022) and the explicit ability to scale a PTF.

In the light of the presented limitations of current PTFs and available databases (Zhang et al., 2022) and given the importance of modelling soil hydrological processes (Vereecken et al., 2022) and soil functions (Vogel et al., 2018) in a variety of hydrological, climatological, and geomorphological applications, we urgently call for a community effort to establish a new harmonised extensive open-access database. We envision that this database will contain measurements based on undisturbed soil samples including all necessary attributes (physical, chemical, structural, mineralogical, and auxiliary information; see Sect. 4.3). For this it is important to (i) establish measurement protocols and routines to obtain standardised WRC, HCC, and K_sat values (Gupta et al., 2021b), infiltration (Rahmati et al., 2018), and soil structure information (Weller et al., 2022); (ii) ensure worldwide coverage across all soil types; and (iii) close the gap between the scale of derivation and the scale of application. Current databases are still highly fragmented and not harmonised. Setting this up will require extensive collaborative data management structures (Finkel et al., 2020) for which centrally employed data stewards need to be funded who ensure long-term data curation and points of contact for data collection methods. A promising development by Bakker et al. (2019) is underway which has established a portal and started the SOPHIE initiative to help harmonise, standardise, and innovate the measurement and collection of SHPs through international engagement. Until then, the data and data curation methods, as well as the tools and approaches to construct a new PTF, should always be truly reproducible by using data and code repositories. As a manifesto, we advocate 10 points.

1. Standardise the determination methods of SHPs, including the harmonisation of existing databases.

2. Adopt physically comprehensive SHPs in spatially explicit modelling of soil water fluxes.

3. Develop PTFs for unique soil types, climates, and ecosystems (e.g. peat soils, forest soils, and litter layers including mulch, soils with high carbonate content, mulches, salt-affected soils, or volcanic ash soils).

4. Foster the deployment of PTFs through the use of websites and community repositories.

5. Harmonise application of selected PTFs in model inter-comparison studies.

6. Ensure physical consistency by employing constraint-based inverse modelling during the estimation of soil hydraulic model parameters and constraints during the construction of PTFs.

7. Tackle the discrepancy between the scale of derivation and the scale of application by considering functional evaluation at the scale of application and using physical and functional constraint-based simulation during the building and evaluation of PTFs.

8. Evaluate PTFs on uncorrelated leave-out data or on data whose correlation structure is known.

9. Evaluate PTFs functionally by using other levels of system information, such as simulated vs. observed water fluxes or plausibility constraints.

10. Rethink field experiments with the aim of gaining data with a high information content and use easy-to-set-up, standardisable, and ideally low-cost methods.