the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A change in perspective: downhole cosmic-ray neutron sensing for the estimation of soil moisture
Daniel Rasche
Jannis Weimar
Martin Schrön
Markus Köhli
Markus Morgner
Andreas Güntner
Theresa Blume
Above-ground cosmic-ray neutron sensing (CRNS) allows for the non-invasive estimation of the field-scale soil moisture content in the upper decimetres of the soil. However, large parts of the deeper vadose zone remain outside of its observational window. Retrieving soil moisture information from these deeper layers requires extrapolation, modelling or other methods, all of which come with methodological challenges. Against this background, we investigate CRNS for downhole soil moisture measurements in deeper layers of the vadose zone. To render calibration with in situ soil moisture measurements unnecessary, we rescaled neutron intensities observed below the terrain surface with intensities measured above a waterbody.
An experimental set-up with a CRNS sensor deployed at different depths of up to 10 m below the surface in a groundwater observation well combined with particle transport simulations revealed the response of downhole thermal neutron intensities to changes in the soil moisture content at the depth of the downhole neutron detector as well as in the layers above it. The simulation results suggest that the sensitive measurement radius of several decimetres, which depends on soil moisture and soil bulk density, exceeds that of a standard active neutron probe (which is only about 30 cm). We derived transfer functions to estimate downhole neutron signals from soil moisture information, and we describe approaches for using these transfer functions in an inverse way to derive soil moisture from the observed neutron signals. The in situ neutron and soil moisture observations confirm the applicability of these functions and prove the concept of passive downhole soil moisture estimation, even at larger depths, using cosmic-ray neutron sensing.
- Article
(3386 KB) - Full-text XML
- BibTeX
- EndNote
Soil moisture is a key variable in the hydrological cycle (Vereecken et al., 2008, 2014; Seneviratne et al., 2010), as it drives energy and water fluxes, thereby influencing groundwater recharge, runoff generation processes and, subsequently, the local water balance. It influences vegetation growth and vegetation communities which, in turn, influence the local soil moisture and microclimate (e.g. see, Daly and Porporato, 2005; Seneviratne et al., 2010; Wang et al., 2018). Averaged over several ecosystems, approximately 75 % of roots can be found in the upper 40 cm of the soil (Jackson et al., 1996). As a result, soil moisture in these upper decimetres of the root zone exerts an important control on the hydrological cycle. However, the maximum rooting depth largely exceeds the upper decimetres of the soil, depends on the plant species (Canadell et al., 1996) and is driven by local hydrological conditions (e.g. Fan et al., 2017). These deep roots can be of high importance for the water supply of other, more shallow rooting plants through processes such as hydraulic lift (e.g. Neumann and Cardon, 2012; Pierret et al., 2016), especially during dry periods. Additionally, infiltrating water can be diverted along deep roots to greater depths as preferential flow (e.g. see, Nimmo, 2021), potentially leading to increased water storage in deeper layers of the unsaturated zone. Among others, these processes make deeper layers similarly important for the local water balance and the local hydrological processes.
As soil moisture is highly variable, even on small horizontal scales (Vereecken et al., 2014), a large number of point-scale measurements (e.g. in situ sensors) are required to overcome the small-scale variability and derive representative averages. One method to directly measure representative soil moisture averages over several hectares and is cosmic-ray neutron sensing (CRNS; Schrön et al., 2018). This technique was introduced by Zreda et al. (2008) and Desilets et al. (2010) about a decade ago and uses secondary neutrons produced from cosmic rays which are inversely correlated with the amount of hydrogen in the surrounding area. It allows for the non-invasive estimation of average soil moisture contents up to depths of 15–83 cm (Köhli et al., 2015) and, thus, largely covers the shallow soil layers with high root densities.
Despite the large horizontal measurement footprint radius of 130–240 m (Köhli et al., 2015), CRNS lacks an integration depth large enough to cover greater parts of the deeper root zone. Other geophysical methods with a large (hectometre-scale) horizontal measurement area, such as geoelectric approaches (Cimpoiaşu et al., 2020; de Jong et al., 2020) and the observation of integral mass changes by terrestrial gravimetry (Van Camp et al., 2017; Reich et al., 2021), may allow one to infer soil moisture dynamics at larger depths of the vadose zone. However, the separation of the integral gravity signal into different hydrological signatures can be challenging (Van Camp et al., 2017). In addition, depending on the geophysical method chosen, continuous measurements may not be feasible, which would hamper the monitoring of the soil moisture dynamics in the deeper vadose zone.
Another soil moisture measurement technique with a measurement volume smaller than other geophysical methods but larger than that of point-scale sensors is the active neutron probe. Invented in the middle of the previous century (Gardner and Kirkham, 1952), the active neutron probe allows for the estimation of soil moisture at a depth of interest via access tubes. Instead of passively observing the flux of naturally occurring epithermal (0.25 eV–100 keV) neutrons, as is the case for above-ground CRNS, an active neutron source produces fast neutrons (100 keV–10 MeV) and a co-located neutron detector observes the intensity of backscattered slowed-down thermal (below 0.25 eV) neutrons. The intensity of thermal neutrons measured under radiation of a fast-neutron source largely depends on the hydrogen content of the soil due to the decelerating power of hydrogen through elastic collisions and removal of thermal neutrons by absorption (see e.g. IAEA – International Atomic Energy Agency, 1970; Gardner, 1986; Kramer et al., 1992; Ferronsky, 2015, for a detailed review).
An important advantage of downhole soil moisture estimation using active neutron probes is their decimetre-scale measurement volume around the probe in the soil. The Ølgaard (1965) equation in Kristensen (1973) and Gardner (1986) defines the measurement radius in a surrounding soil volume as the radius R95 within which 95 % of the detected thermal neutron signal originates. Accordingly, the radius inversely depends on the soil water content, described as R95 ≈ 53 cm for θ = 0.05 cm3 cm−3 or as R95 ≈ 20 cm for θ = 0.35 cm3 cm−3. As a consequence, the measurement volume of the active neutron probe exceeds the integration volume of standard in situ point-scale sensors and allows for a more representative average soil moisture value at the depth of interest. However, a disadvantage of this method is the precautions that need to be taken when handling active radiation sources (e.g. IAEA – International Atomic Energy Agency, 1970; Gardner, 1986) as well as the typically non-continuous nature of snapshot measurement campaigns with active neutron probes.
Kodama et al. (1985) observed the response of cosmic-ray neutrons to changes in soil moisture at depths down to 40 cm, largely covering the sensitive measurement depth of above-ground CRNS. Against this background, we investigate the possibility of using CRNS as a passive downhole technique (d-CRNS) to estimate soil moisture at different depths below 40 cm, also including the deeper unsaturated zone. For this, we installed CRNS neutron detectors in a standard groundwater observation well, thereby using the well casing above the groundwater level as an access tube.
We hypothesise that a sufficient neutron intensity can be observed by a downhole neutron detector to measure neutron intensity changes caused by soil moisture dynamics at discrete soil depths, thereby taking advantage of both the passive, non-invasive characteristics and continuous monitoring capabilities of CRNS as well as the decimetre-scale measurement volume of sub-surface active neutron probes. Using existing standard groundwater observation wells allows for the multi-purpose use of existing observational infrastructure, as simultaneous groundwater level measurements remain undisturbed.
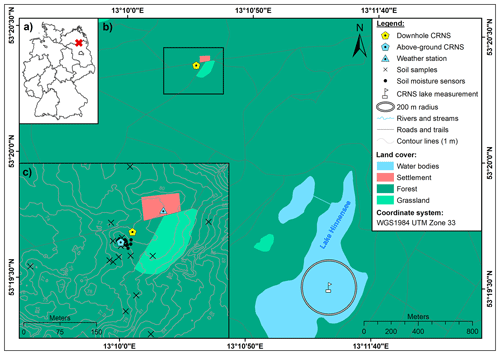
Figure 1Panel (a) presents the location of the study area within Germany, panel (b) shows the location of the study site in relation to the reference lake measurement site and panel (c) displays the details of the CRNS observation site “Serrahn” where the field experiment took place. (The digital elevation model was sourced from LAIV-MV – State Agency for Interior Administration Mecklenburg-Western Pomerania, 2011, and land cover was taken from BKG – German Federal Agency for Cartography and Geodesy, 2018.)
To test our hypotheses, we first conducted particle transport simulations using the Monte Carlo N-Particle (MCNP) particle transport code commonly employed in CRNS research (e.g. Zreda et al., 2008; Franz et al., 2012; Andreasen et al., 2016; Andreasen et al., 2017; Weimar et al., 2020; and Köhli et al., 2021, among others) to investigate the neutron flux at different soil depths. As we expect the neutron response to changes in moisture in the surrounding soil to be different compared with above-ground CRNS or the active neutron probe, we use the particle transport simulations to obtain information on the integration volume and to derive a transfer function from soil moisture to neutron intensities. In a second step, we compare the estimated neutron intensities calculated from reference soil moisture observations based on the derived transfer function with measurements of downhole neutron intensities at different depths. Finally, we illustrate the potential of passive downhole cosmic-ray neutron sensing for the estimation of soil moisture in the vadose zone.
2.1 Study site
The study site comprises the permanent CRNS observation site “Serrahn” (Bogena et al., 2022), located in the Müritz National Park in the lowlands of north-eastern Germany (Fig. 1). The site is of one of three permanently operating CRNS stations (Heidbüchel et al., 2016; Rasche et al., 2021) in the Terrestrial Environmental Observatories TERENO-NE (Zacharias et al., 2011; Heinrich et al., 2018). The observatory is located in the cfb climatic zone following the Köppen–Geiger classification (Bogena et al., 2022), with an average annual temperature of 8.8 ∘C and a precipitation sum of 591 mm yr−1 at the closest long-term weather station in Waren (at a distance of approximately 35 km) operated by the German Weather Service (station ID: 5349, period 1981–2010; DWD - German Weather Service, 2020a, b).
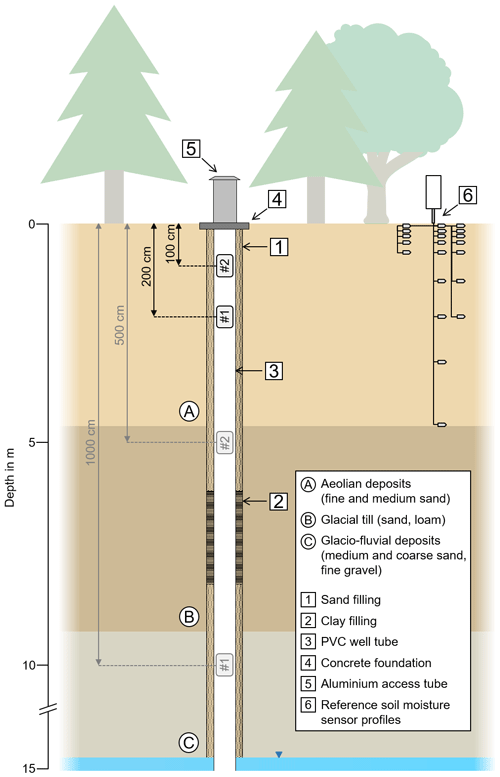
Figure 2Schematic illustration of the experimental set-up at the study site. The thermal (unshielded) neutron detectors no. 1 and no. 2 were simultaneously installed at respective depths of 200 and 100 cm from July to November 2021 and from January to May 2022 and at respective depths of 1000 and 500 cm for the time period in between.
Table 1Soil physical characteristics obtained from laboratory analyses of soil samples taken in February 2019. Soil bulk densities per depth were obtained from oven-drying soil core samples at 105 ∘C for 12 h and subsequent averaging.
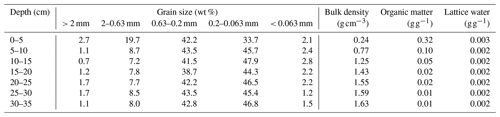
The study site is located on a glacial terminal moraine formed during the Pomeranian phase of the Weichselian glaciation in the Pleistocene (Börner, 2015). The sedimentological profile obtained during the drilling of an on-site groundwater observation well (Fig. 2) with a total depth of 24 m revealed an uppermost layer of aeolian sands deposited during the Holocene reaching a depth of 450 cm followed by a 400 cm thick layer of glacial till which can be attributed to the geological unit of the terminal moraine. From a depth of 850 cm, a layer of glacio-fluvial coarse sands containing fine gravel components extend downward until they reach the glacial till deposited during an earlier phase of the Weichselian glaciation. Regular measurements show a variation in the groundwater level of between 13 and 14 m below the surface. Soil samples collected in the scope of the calibration of the permanent CRNS sensor Serrahn in February 2019 were taken in order to determine the soil physical characteristics, such as the average grain size distributions, soil organic matter and lattice water, via laboratory analyses, as shown in Table 1. Soil organic matter and lattice water contents were obtained from subsamples of bulk samples from all sample locations per depth using 24 h loss-on-ignition analyses at 550 and 1000 ∘C, respectively. Based on the average bulk density at 0–35 cm in the upper soil layer and at 35 cm depth as the representative value for greater depths, soil water contents at field capacity and wilting point were derived for medium fine sand from tabulated values (Sponagel et al., 2005). Accordingly, 0.16 and 0.06 cm3 cm−3 for the upper layer and 0.12 and 0.04 cm3 cm−3 for greater depths were derived for the soil water content at field capacity and wilting point, respectively. Similarly, the soil porosity was estimated based on the material density of quartz (2.65 g cm−3) and corrected for the amount of soil organic matter based on the density of cellulose (1.5 g cm−3). Consequently, we derived a porosity of 0.52 and 0.38 cm3 cm−3 for the upper soil layer and below depths of 35 cm, respectively.
The land cover at the site is mainly a mixed forest dominated by European beech (Fagus sylvatica) and Scots pine (Pinus sylvestris) with a clearing covered by grassy vegetation located a few decametres from the neutron detectors. A vegetation survey was conducted in July 2021 in order estimate the total above-ground biomass at the site. Using allometric regressions for Pinus sylvestris (Urban et al., 2014) and Fagus sylvatica (Chakraborty et al., 2016) revealed a total wet above-ground biomass estimate of 3.73 g cm−2, assuming that other sources of biomass can be neglected.
Along with the stationary CRNS instruments and the groundwater observation well, the study site is equipped with a weather station and a network of in situ point-scale soil moisture sensor profiles (type SMT100; Truebner GmbH, Germany). The soil moisture sensors are installed at depths down to 450 cm along the profiles displayed in Table B1 and continuously monitor the volumetric soil moisture based on the manufacturer's calibration function. The measurement interval is 10 min. The soil moisture profiles are located close to the CRNS instruments and at a distance of 20–40 m from the groundwater observation well (Fig. 1).
2.2 Experimental design
In the scope of this study, we deployed a gas-filled proportional neutron detector of the type CRS1000 (Hydroinnova LCC, USA) inside the on-site groundwater observation well. The detector uses 3He as the converter gas (see Zreda et al., 2012, and Schrön et al., 2018, for details). We disassembled the original set-up and placed two unshielded counter tubes into 50 cm long polypropylene pipes with a wall thickness of 1.9 mm. The relative air humidity in closed groundwater observation wells is constantly close to saturation, making such additional protection of the counter tubes necessary. For the downhole measurements, the CRS1000 counter tubes as well as their readout electronics were lowered into the well to the desired measurement depths by steel ropes. The data logger with its direct-current (DC) power supply remains above the surface.
As shown in the schematic illustration in Fig. 2, the groundwater well itself is composed of an aluminium tube above the surface that is mounted to a small concrete foundation, whereas the below-ground tube is made of 7.5 mm thick PVC (polyvinyl chloride) with an inner diameter of 11 mm. An approximately 100 mm wide gap between the surrounding undisturbed sediment and the well tube was filled with sand and clay (see Fig. 2), depending on the surrounding material, during the installation of the groundwater well in 2014. The presence of filling material as well as the PVC tube material may reduce the response of the sensor to changes in the soil moisture of the surrounding undisturbed soil due to, for example, the high absorption cross section of chlorine and scattering cross section of hydrogen contained in the PVC material. Although some influence on the neutron signal has been described for the active neutron probe (e.g. Keller et al., 1990), the precise influence of both remains unknown for the d-CRNS approach. Following the assumption that the soil moisture dynamics in the porous filling material are similar to those in the surrounding undisturbed material and the sphere of influence largely exceeds the volume of the filling material, we expect the soil moisture signal to dominate the dynamics in the downhole neutron intensity.
Above-ground CRNS relies on epithermal neutrons counted by moderated detector tubes shielded with a 2.5 cm layer of high-density polyethylene (HDPE). In the scope of d-CRNS, we use thermal neutrons counted from unshielded detectors. This is done for different reasons. Firstly, thermal neutrons respond to changes in environmental hydrogen content and, thus, soil moisture (e.g. Hubert et al., 2016; Weimar et al., 2020; Rasche et al., 2021). Secondly, we expect the neutron intensity (i.e. count rate) to decrease strongly with soil depth. A bare counter tube is then more effective, as the HDPE shielding of a moderated tube would not only slow down but would also reflect a certain percentage of potentially countable neutrons away from the instrument and would, thus, reduce the observed intensity. Furthermore, it has been shown that thermal neutrons can potentially be used to obtain soil moisture information from larger depths compared with epithermal neutrons (Rasche et al., 2021). This may be especially useful for downhole measurements in order to increase the potential measurement radius. Lastly, using unshielded detector tubes is of a practical nature, as the removal of the 2.5 cm HDPE shielding reduces the weight and dimensions of the CRS1000 counter tubes, allowing them to fit into standard groundwater well tubes with an inner diameter of 11 cm.
2.3 Neutron measurements and processing
The counter tubes simultaneously measured neutron intensities at 100 cm (tube no. 2) and 200 cm (tube no. 1) depths from July 2021 to November 2021 and from January 2022 to May 2022. In between these two periods, the detectors were placed at 500 cm (tube no. 2) and 1000 cm (tube no. 1) depths.
Following conventional approaches, the observed above-ground epithermal neutron intensities were corrected for variations in atmospheric shielding depth, absolute air humidity and primary neutron flux (Zreda et al., 2012; Rosolem et al., 2013) before being smoothed by a 25 and 49 h moving average in order to reduce the uncertainty in the time series (Schrön et al., 2018). For downhole CRNS applications measuring thermal neutrons, an adjusted correction algorithm for the neutron signal is required. Thermal neutrons detected by a downhole CRNS have not interacted with the atmosphere from the point where they reach water-sensitive energies in the soil to eventually reaching the detector. As a consequence, downhole thermal neutron intensities will be corrected for variations in atmospheric shielding depth and primary neutron influx only. In accordance with Heidbüchel et al. (2016), the required neutron attenuation length was set to 135.9 g cm−2 for the study site. The Neutron Monitor Database (https://www.nmdb.eu, last access: 16 August 2023; station: JUNG – Jungfraujoch) was used to obtain data for the primary neutron flux.
To convert above-ground neutron intensities to soil moisture estimates, a calibration against soil moisture reference measurements is necessary in order to scale the transfer function to possible site-specific characteristics. This is the case for the N0 method (Desilets et al., 2010) as well as for the recently introduced universal transport solution (UTS) (Köhli et al., 2021). Reference soil moisture measurements can be obtained at shallow depths from soil sampling and subsequent laboratory analysis or from point-scale in situ soil moisture sensors. However, using a CRNS detector as a downhole instrument would require reference measurements from greater depths, which are more difficult to acquire. For this reason, we decided to adapt an approach proposed by Franz et al. (2013) for above-ground CRNS applications using epithermal neutrons. It comprises scaling the transfer function by the neutron intensity measured above water instead of above dry soil, as is the case for the N0 method. The count rate above dry soil can be calibrated with reference soil moisture information; however, without this reference information, the count rate above dry soil needs to be measured in order to transfer observed neutron count rates to soil moisture. Measuring neutrons above an (ideal) hydrogen-free soil is practically impossible, whereas the intensity above water can be measured directly and, thus, does not require additional calibration. This approach has been applied in previous studies related to above-ground epithermal CRNS (e.g. McJannet et al., 2014; Andreasen et al., 2016, 2020). We adjusted the approach of above-water measurements for the scaling of thermal neutrons. Therefore, a measurement at 25 cm (detector bottom) above the water surface and of 1.5 h duration was conducted with the two detector tubes on Lake Hinnensee prior to their installation below the ground (Fig. 1). By scaling the downhole neutron intensities with the detector-specific neutron intensity above water by calculating the neutron ratios, Eq. (1) allows for the comparison of observed neutron ratios with simulated neutron ratios. Furthermore, it enables the development of a transfer function from simulations that may be applied without additional calibration against reference soil moisture measurements.
Unlike the measurements below the ground, the neutron intensity above water needs to be corrected for variations in absolute air humidity. A specific humidity correction function has been developed for epithermal neutrons only (Rosolem et al., 2013; Köhli et al., 2021) and may not be valid for thermal neutrons. For this reason, we developed a first equation to correct thermal neutron intensities observed above water to variations in absolute humidity. The observed neutron ratio Nr,
can then be calculated from the downhole thermal neutron intensity (Ns) corrected for variations in atmospheric shielding depth and primary neutron influx only as well as the thermal neutron intensity above water (Nw) corrected for variations in atmospheric shielding depth, primary neutron influx and absolute humidity.
2.4 Particle transport simulations
Several different Monte Carlo-based particle transport simulation toolkits have previously been used for the investigation of secondary cosmic-ray neutrons at the soil–atmosphere interface in the context of CRNS, including GEANT4 (Hubert et al., 2016; Brall et al., 2021), MCNP (Zreda et al., 2008; Franz et al., 2012; Andreasen et al., 2016, 2017; Weimar et al., 2020; Köhli et al., 2021) and URANOS (Köhli et al., 2015, 2021; Li et al., 2019; Rasche et al., 2021), the latter of which only simulates neutrons of different energies. Although simulating only neutrons (and not including protons and muons) might be sufficient at the soil–atmosphere interface with a detector placed above the surface, the simulation of the neutron flux at different depths of the soil requires the inclusion of several other types of particles that may induce neutron production in the deeper soil volume. As the atmospheric neutron flux is attenuated strongly within the soil volume, the in-soil neutron production dominates the thermal neutron flux below soil depths of several decimetres. In-soil neutrons are generated by different cosmic-ray particle species depending on the soil depth. Within the first few metres, the inelastic collisions of high-energy protons and neutrons with atomic nuclei lead to particle production in hadronic showers (e.g. Mollerach and Roulet, 2018). During the collision, neutrons are ejected from the nucleus with energies peaking a few hundred megaelectron volts (e.g. Gudima et al., 1983). The target nucleus remains in an excited state after the impact and deexcites via the emission of lower-energy neutrons with a few megaelectron volts. This process is called evaporation. The hadronic neutron production falls off rapidly with soil depth due to the short penetration length of high-energy neutrons and protons. Below that and down to several tens of metres, hadronic neutron production is significantly lower and is dominated by muons (Heusser, 1996) via capture processes that release neutrons with a few megaelectron volts. Consequently, we used the MCNP v6.2 model (Werner et al., 2018) to simulate the neutron ratios for different soil depths and soil bulk densities, as this model includes, for example, protons, muons and neutrons as source particles within the model domain. Energy spectra and angular distributions of the particle species were set according to Sato (2015, 2016). The starting particles are released 450 m above the soil surface embedded in a cylindrical simulation domain with 6 m radius and reflecting boundaries.
All simulation scenarios described in the following comprise a cutoff rigidity of 2.6 GeV, an absolute humidity of 10 g m−3 and an atmospheric pressure of 1013.25 hPa. The detector has a length of 50 cm and diameter of 5.5 cm. The tube volume is filled with 3He at 1.5 bar, and all neutrons are counted that undergo an absorption process in the simulated detector volume. Thus, the behaviour of an unshielded (bare) proportional neutron detector tube is modelled.
In a first step, the detector was placed 50 cm above an infinite water surface, with the 50 cm being measured from the detector tube centre. The detector volume is slightly larger than the real CRS1000 detector tubes in order to enhance the counting statistics in low-count environments. To estimate the influence of variations in absolute humidity on the thermal neutron intensity above water and in order to develop a correction function, the simulation scenario was repeated with air humidity values of 1, 6, 11, 16, 21 and 26 g m−3.
Neutron responses at different soil depths were modelled with a soil bulk density of 1.43 g cm−3 where the soil material is composed of 75 % SiO2 and 25 % Al2O3. The detector was placed at shielding depths of 75, 100, 150, 200, 250, 300, 350, 400, 500, 750, 1000 and 1500 g cm−2 with 10 different soil moisture contents ranging from 0.005 to 0.5 cm3 cm−3. The shielding depth describes the total amount of matter that a particle has to travel trough. It is influenced by the material dry bulk density, the absolute depth in centimetres and the soil water content (Eq. 9). In the simulation scenarios, the absolute depth of the detector was changed for the different soil moisture states in order to maintain the same simulated shielding depth at the detector centre. In accordance with the set-up of the real groundwater observation well, the virtual detector was placed in a PVC cylinder of the same dimensions. To investigate the influence of the local soil bulk density on the simulated neutron response, a smaller subset of scenarios for all soil moisture states with the shielding depths of 75, 100, 200, 350 and 500 g cm−2 were additionally modelled with soil bulk densities of 1.1 and 1.8 g cm−3.
In order to assess the sphere of influence for the downhole neutron detector, particle tracking simulations for a single shielding depth of 300 g cm−2 and all soil moisture conditions listed above were run. The trajectory of all detected neutrons is traced backwards in order to determine the locations where they probed the soil via scattering. Above 150–200 g cm−2 an increase in the measurement volume can be expected due to an increased contribution from neutrons that previously scattered in the atmospheric layer before entering the soil and eventually being detected. Using the simulations with 300 g cm−2 allows for the isolated characterisation of the measurement volume without the influence of neutrons that previously interacted with the atmosphere. In the scope of this study, the dimensions of the measurement volume are estimated based on the locations of all elastic scattering processes above the thermal energy regime and, thus, the entire moderation process from the point where a detected neutron was generated.
To assess the influence of the well tube material on the neutron ratio as well as on the dimensions of the sphere of influence, we not only simulated a PVC well tube with a wall thickness of 7.5 mm but also a well tube composed of stainless steel of equal wall thickness and a well tube composed of thinner PVC. The additionally simulated PVC material had wall thickness of 5 mm and a density of 1.44 g cm−3, and the steel tube (type X5CrNi18-10) had a wall thickness of 7.5 mm, a density of 7.85 g cm−3, and contained 18 % chromium and 10 % nickel. Particle transport simulations with a shielding depth of 300 g cm−2 were run to investigate the size of the measurement volume for stainless steel, and the neutron ratios were simulated for a soil bulk density of 1.43 g cm−3 and shielding depths from 100 to 400 g cm−2.
3.1 MCNP simulations
3.1.1 Neutron ratio response and sphere of influence
We simulated the detector-specific neutron intensity above water to aid with processing the downhole neutron intensities without the need for calibration based on in situ soil moisture information. The simulation revealed a dependence of thermal neutrons detected above water on absolute air humidity. The thermal neutron intensity decreased approximately linearly by 0.21 % per 1 g m−3 absolute humidity (R2 = 0.93), which is less than half of what has been reported for epithermal neutrons (Rosolem et al., 2013). The correction function developed by Rosolem et al. (2013) for epithermal neutrons can, thus, be adjusted to correcting observed thermal neutron intensities above water by changing the correction factor from the original 0.0054 to the derived 0.0021. It should be noted that the reference absolute humidity for the simulations and the transfer functions was set to an arbitrary 10 g cm−3.
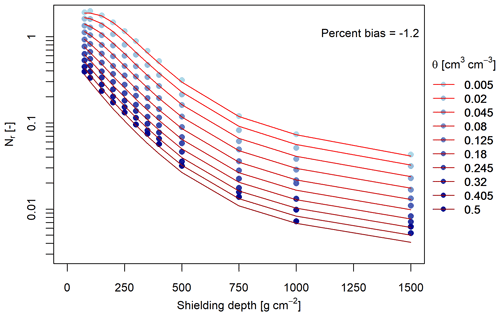
Neutron ratios were calculated for all neutron transport simulations using the reference simulation scenario with the detector placed above a water surface. The simulation results for the first set of scenarios conducted with a soil bulk density of 1.43 g cm−3 are shown in Fig. 3. The response of the simulated neutron ratios observed by the virtual downhole neutron detector to changes in soil moisture differ between the different simulated shielding depths, with generally lower neutron ratios at larger depths. For each simulated shielding depth, the neutron ratio decreases with increasing soil moisture, although a specific behaviour can be observed for shallow shielding depths. From the 75 to the 100 g cm−2 shielding depth scenario, the simulated neutron ratio increases, i.e. the neutron intensity observed by the downhole neutron detector increases, when the soil moisture content is below 0.045 cm3 cm−3. This reveals a peak neutron intensity in shallow soil layers under low-soil-moisture conditions. At higher soil moisture contents, this peak ratio disappears and a continuous decrease in the neutron ratio with increasing shielding depth per simulated soil moisture content can be observed. The simulation sets conducted with lower (1.1 g cm−3) and higher (1.8 g cm−3) soil bulk densities show a similar behaviour, although the absolute values of the neutron ratios change. Higher soil bulk densities result in lower neutron intensities and, thus, lower neutron ratios observed by the virtual downhole neutron detector and vice versa (see Sect. 3.1.2 for details). We also investigated the possible influences of the groundwater observation well tube material by simulating a 5 mm PVC and 7.5 mm stainless-steel tubing. The additional subset of simulations revealed that neutron ratios for a well tube composed of stainless steel are on average 60 % higher compared with a PVC tube with equal wall thickness, but the two materials respond similarly to changes in soil moisture. In addition, a thinner PVC material with a thickness of only 5 mm produces neutron ratios which are on average 28 % higher compared with a PVC tubing with a wall thickness of 7.5 mm.
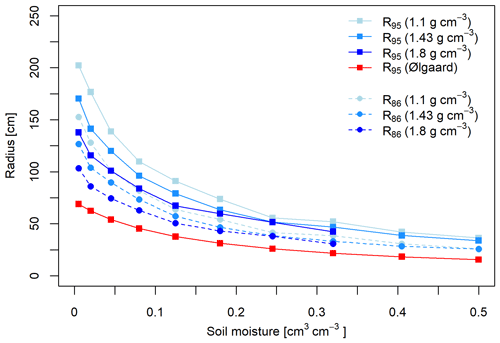
Figure 4Simulated horizontal radii of the sphere of influence defined as the R86 and R95 for different local (at the depth of measurement) soil moisture values θ (see Eq. 8) and soil bulk densities. In addition, the R95 values based on the equation of Ølgaard (1965) in Gardner (1986) for an active neutron probe are displayed for comparison.
In this study, the sphere of influence, i.e. the measurement volume around the downhole neutron detector, is calculated as the 86 % quantile and the 95 % quantile of all locations of elastic collision processes of a detected neutron in the soil. The definition based on the 86 % quantile relies on the convention established for describing the horizontal integration radius and integration depth of above-ground CRNS applications, whereas the 95 % quantile is common for active neutron probe applications. In order to better compare d-CRNS with above-ground CRNS and the traditional active neutron probe, the results of both definitions are shown in Fig. 4.
Table 2Fitted parameters for Eqs. (2)–(7) derived from particle transport simulation scenarios for a PVC well tube with a wall thickness of 7.5 mm.

In line with above-ground CRNS, only the 86 % quantile is used for a mathematical description of the sphere of influence and its dimensions. The shape of the sphere of influence simulated for a neutron detector with a height of 50 cm and diameter of 5.5 cm and for different soil moisture contents at a shielding depth of 300 g cm−2 measured at the detector centre can be described by the following equations. The horizontal sensitive radius of the sphere R86 can be described by the local soil moisture content θ (cm3 cm−3; see Eq. 8) as well as the local soil bulk density ρ (g cm−3) and the fitted parameters p1 to p3 (Table 2) at the depth of the neutron detector via
The simulated horizontal radii of the sphere of influence, defined as the R86 and R95, are shown in Fig. 4 for different soil moisture values and soil bulk densities. Both R86 and R95 decrease with increasing soil moisture and show generally lower values when the soil bulk density is higher. For instance, a bulk density of 1.43 g cm−3 leads to an R95 of 170 cm at 0.005 cm3 cm−3 and to an R95 of 34 cm at 0.5 cm3 cm−3. At the same bulk density and for the same soil moisture values, R86 is generally smaller and decreases from 127 to 26 cm. The values derived from the Ølgaard (1965) equation in Gardner (1986) for the R95 of an active neutron probe reveal respective values of 69 and 16 cm at 0.005 and 0.5 cm3 cm−3 and, hence, smaller radii of the sphere of influence than for a downhole neutron detector for all simulated soil bulk densities and both R95 and R86. Consequently, even for a high bulk density of 1.8 g cm−3, the generally smaller R86 of d-CRNS is approximately 40 % larger than the R95 of an active neutron probe.
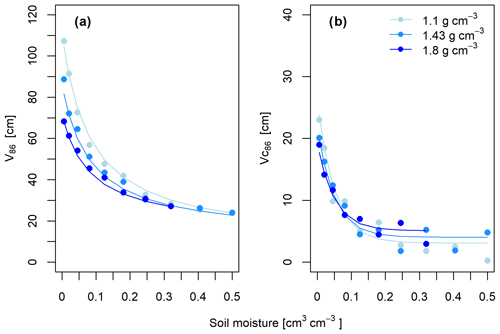
Figure 5(a) Simulated values of the vertical sensitive radius V86 from the detector centre and (b) the position of the most sensitive area relative to the detector centre Vc86 for different local soil moisture values θ (see Eq. 8) and soil bulk densities.

Figure 6Schematic illustration of the sphere of influence described by R86, Vc86 and V86 for a soil with a bulk density of 1.43 g cm−3 and a soil moisture content of 0.10 and 0.35 cm3 cm−3 in the entire soil column. The V86 is different above (upper V86) and below (lower V86) the neutron detector (its centre is marked by an “X” here); thus, V86 represents the average vertical extent. A schematic neutron transport path is displayed with a high-energy particle producing a hydrogen-sensitive and, thus, water-sensitive neutron in the soil which is slowed down to thermal energies by multiple elastic scattering interactions before eventually being detected.
The average vertical sensitive radius of the sphere of influence V86 can be described by Eq. (3) and has a size range of 89–24 cm from the lowest (0.005 cm3 cm−3) to the highest (0.5 cm3 cm−3) simulated soil moisture content at a 1.43 g cm−3 bulk density. In combination with the simulated horizontal radii, an ellipsoidal shape of the sphere of influence can be derived for a downhole neutron detector in d-CRNS applications, with R86 and V86 describing the ellipsoids' semi-axes from the detector centre. However, a vertical shift in the most sensitive area, i.e. the location of the largest horizontal radius relative to the detector centre with varying soil moisture, can be observed. This dimension is described by Eq. (4) and shown in Fig. 5. The vertical sensitive radius V86 increases with decreasing soil moisture, while the most sensitive region Vc86 is always located slightly above the detector centre and shifts upwards with lower soil water contents. For example, for a soil bulk density of 1.43 g cm−3, the most sensitive region of the downhole neutron detector Vc86 is located 5–20 cm (for a 0.5–0.005 cm3 cm−3 soil moisture content) above the detector centre. The fitted parameters p1–p5 required in Eqs. (2)–(4) can be found in Table 2, and a schematic illustration of the sphere of influence for different soil moisture contents can be found in Fig. 6. We define the vertical footprint size as
and the location of the most sensitive region above the detector centre as
The simulation results for a well tube made from stainless steel with a wall thickness of 7.5 mm revealed similar dimensions of the sphere of influence to those derived for PVC with an equal wall thickness. Averaged over the range of simulated soil moisture values and for a soil bulk density of 1.43 g cm−3, R86 is approximately 1.2 cm larger for a well tube made from PVC compared to the steel tube, whereas Vc86 and V86 are 8.2 and 4.5 cm smaller, respectively. The fitted parameters for a well tubing made from stainless steel can be found in Table B2.
3.1.2 Predicting neutron ratios
Our neutron transport simulations revealed a change in the hyperbolic relationship between the neutron ratio Nr and the simulated soil moisture content depending on the shielding depth D measured at the centre of the detector tube (Fig. 3). Therefore, we derived a hyperbolic fit model with the analytical form of Eq. (5) for each shielding depth and subsequently predicted the shape-defining parameters F1 and F2 by shielding depth. A third-order and second-order exponential model resulted in a high goodness of fit for parameters F1 and F2, which lead to the following equations, allowing for the estimation of Nr:
The equation makes use of two key quantities, the local soil water content at the depth of measurement
and the shielding depth
The parameters and variables used in Eqs. (5)–(9) are explained in the following. The fitted parameters p1–p10 can be found in Table 2 for a PVC well tube with a wall thickness of 7.5 mm, in Table B2 for a well tube composed of stainless steel of equal thickness and in Table B3 for a PVC well tube with a thickness of only 5 mm, while the following remaining variables depend on the conditions of the study site. The variable θ describes the total local water content, comprising soil moisture θSM, lattice water θLW and the water equivalent of soil organic matter θSOM (in cm3 cm−3) at the depth of neutron observation measured as the distance from the soil surface to the centre of the detector tube d (in cm). Based on the subset of neutron transport simulations with different soil bulk densities, we found F1 and F2 to be dependent on the ratio between the density ρ at the depth of measurement and the soil density of 1.43 g cm−3 used in the simulations from which the equations were derived.
The second required variable is the shielding depth D describing the total mass neutrons, protons and muons need travel through before reaching the depth of the centre of the detector tube. The shielding depth represents the integral mass from the surface to the detector centre. Thus, it depends on the measurement depth d (in cm) as well as on the average soil bulk density (g cm−3) from the soil surface to the measurement depth. Likewise, the average soil water content (cm3 cm−3) is required, assuming a constant water density ρwater of 1 g cm−3. It should be noted that, for the calculation of the shielding depth, the total mass of material above the centre of the detector tube is required, regardless of its elemental composition. Thus, the mass of soil organic matter and lattice water is already accounted for by the integral soil bulk density. Additionally, as the study site of the present work is located in a mixed forest, the total above-ground mass (DAGM) associated with vegetation needs to be added. Above-ground mass from other sources, such as snow, may also be considered and included in DAGM. Furthermore, it should be noted that, in Eqs. (5)–(7), the parameters p2, p4, p6, p8 and p10 are in square centimetres per gram (inverse shielding depth), whereas the remaining parameters p1, p3, p5, p7 and p9 are dimensionless.
Applying the above equations (Eqs. 5–9) to the input variables of the neutron transport simulation and comparing this prediction with the simulated Nr shows a good overall fit, with a percent bias between the predicted and simulated values of −1.2 % for a bulk density of 1.43 g cm−3 (Fig. 3) and 0.8 % for all modelled densities.
3.1.3 Estimating soil moisture
A key motivation of this study is to derive soil moisture time series by d-CRNS at depths larger than those accessible by surface CRNS. The equations above describe the physical relationships that influence the neutron intensity, and thus Nr, inside the shaft of the groundwater observation well or access tube. They illustrate that both the soil moisture at the local depth of the detector as well as the average soil moisture in the vadose zone above the detector have an effect on the Nr observed at a certain measurement depth. However, estimating two unknown variables, namely θSM and , from Nr (the single known variable) is only possible with further assumptions. One option would be the use of Eqs. (5)–(9) as a forward operator in combination with soil hydraulic models (e.g. HYDRUS-1D; Šimůnek et al., 2008) to model soil moisture time series at different soil depths. The model can then be calibrated by applying Eqs. (5)–(9) with the modelled soil moisture time series and optimising the goodness of fit between the observed and predicted Nr by adjusting the parameters in the soil hydraulic model. However, soil hydraulic models may require further variables, such as rainfall, evapotranspiration and root distributions, which are not always available.
We propose an alternative and more simple approach to estimate the soil moisture time series at the depth of measurement from the observed neutron ratios by using Eqs. (5)–(9). This approach is exemplary in that, while reasonable for the conditions of our study site, the assumed range of soil moisture between the wilting point and field capacity in Eqs. (5)–(9) may need to be modified for other sites. Following these equations, the approach is based on the fact that the influence of θSM on Nr is considerably larger than that of . For example, at a θSM of 0.1 cm3 cm−3, a change in from 0.05 to 0.15 cm3 cm−3 results in a 6 % change in Nr (at a measurement depth of 100 cm). In contrast, changing θSM from 0.05 to 0.15 cm3 cm−3 at a value of 0.1 cm3 cm−3 for leads to a 47 % change in Nr. The higher sensitivity of Nr to changes in the soil moisture content at the depth of measurement allows for its estimation as described in Appendix A.
3.2 Experimental evidence
3.2.1 Observed neutron response
The reference measurement at Lake Hinnensee was conducted in order to the derive the detector-specific raw count rate above water and resulted in values of 315 and 155 cph (counts per hour) for detector tube no. 1 and 2, respectively. The measurement duration of 1.5 h and measurement intervals of 1 min led to a Poisson standard deviation of 14 and 10 cph or a coefficient of variation of 4.6 and 6.6 %, respectively. The average uncorrected downhole neutron count rate was 101 cph for 100 cm (tube no. 2) and 70 cph for 200 cm (tube no. 1), covering the entire measurement period. During about 2 months of measurements at larger depths, the average count rate was significantly lower, with tube no. 2 observing 6 cph for 500 cm and tube no. 1 observing 11 cph for 1000 cm. As a result, the measurement uncertainty increased sharply. For instance, for an observed count rate of 10 cph, the coefficient of variation was 32 %.
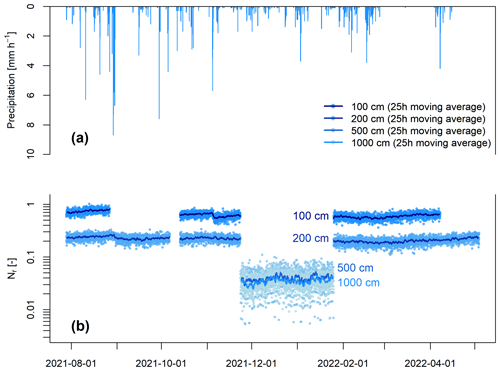
Figure 7Panel (a) presents the hourly precipitation observed at the study site during the experimental period. Panel (b) shows observed time series of Nr at the different measurement depths of 100, 200, 500 and 1000 cm. Points represent the original (not smoothed) neutron ratios from corrected neutron intensities and lines represent the 25 h moving average calculated from corrected neutron intensities.
Nr calculated based on the corrected neutron count rates decreases with increasing measurement and shielding depth (Fig. 7). The average Nr decreases from 0.63 for 100 cm and 0.22 for 200 cm to 0.039 for 500 cm and 0.034 for 1000 cm.

Figure 8Comparison of the hourly corrected neutron intensity Ns smoothed with a 25 h moving average and values from the reference soil moisture sensors with the highest and lowest Pearson correlation coefficient (r) between the observed data and predicted data from a hyperbolic, non-linear, least-squares-fit model in the form of Eq. (5). Panel (a) shows 100 cm depth and reference sensors at 70 and 130 cm depths, whereas panel (b) shows 200 cm depth with the corresponding reference soil moisture sensors also at 200 cm depth.
Figure 8 shows the comparison of the observed neutron intensity corrected for variations in air pressure and primary neutron influx Ns and the local in situ reference soil moisture at depths of 100 and 200 cm. Due to the location of all reference sensors outside the expected sphere of influence of the downhole neutron detector, a comparison with the soil moisture sensor at the respective depth showing the highest Pearson correlation coefficient between the observed and predicted values from a hyperbolic, non-linear, least-squares-fit model in the form of Eq. (5) is shown. In case of the downhole neutron detector installed at 100 cm depth, the reference sensors with the highest and lowest goodness of fit at 70 and 130 cm are considered (due to the lack of sensors at 100 cm depth), whereas reference soil moisture sensors at the same depth are available for the neutron detector at 200 cm depth. Figure 8 illustrates that a distinct neutron intensity response to changes in the local soil moisture following a hyperbolic relationship can be observed at both measurement depths. However, differences occur between the individual in situ reference sensors, including distinct different slopes of the fitted hyperbolic regression model as well as larger deviations from the model fit, indicating different soil moisture dynamics at the individual reference sensor locations.
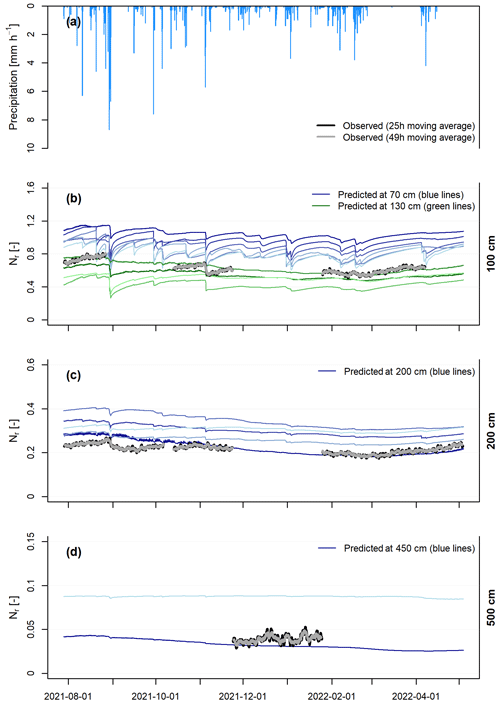
Figure 9Panel (a) shows the hourly precipitation observed at the study site during the experiment. Panels (b)–(d) present the observed (by CRNS detector at 100, 200 and 500 cm depth) and predicted (based on reference soil moisture measurements at similar depths) time series of Nr. The different times series of the predicted Nr at each depth represent the results for every individual soil moisture sensor at that depth (θSM) and the average from the associated sensor profile from the soil surface to the depth of the CRNS ().
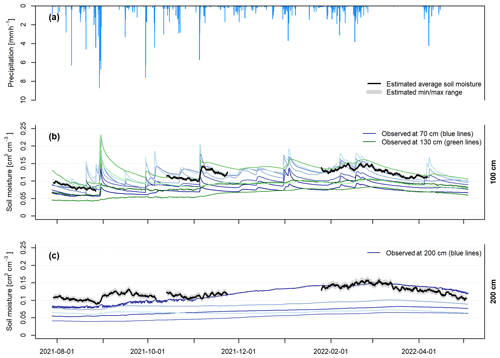
Figure 10The observed time series of θSM from reference soil moisture sensor profiles and estimated time series of θSM from Nr. The different colours indicate the observed time series from individual reference sensors at the respective depths. At both depths, corrected neutron intensities were smoothed with a 49 h moving average prior to calculating Nr and subsequently estimating soil moisture. Panel (a) shows the hourly precipitation observed at the study site during the experiment. Panel (b) presents θSM from reference soil moisture sensors at 70 and 130 cm depths and estimated time series of θSM at 100 cm depth. Panel (c) displays θSM from reference soil moisture sensors and estimated time series of θSM from Nr at 200 cm depth.
3.2.2 Predicting neutron ratios from reference soil moisture observations
In order to provide experimental proof of the proposed downhole application of cosmic-ray thermal neutron sensing (d-CRNS), in a first step, observed soil moisture time series along the different reference sensor profiles are used to predict Nr based on Eqs. (5)–(9). Again, for the measurement depth of 100 cm, we include the sensor profiles with sensors down to depths of 70 and 130 cm, as there are no reference sensors available at the same measurement depth. For each sensor profile, the average soil moisture content is calculated from all sensors along the profile weighted by the depth range covered by each sensor down to the maximum depth of the respective sensor profile (70 and 130 cm) to calculate . Additionally, the soil moisture time series from the sensors installed at depths of 70 and 130 cm are defined as θSM for each individual profile depending on the maximum profile depth. This leads to the set of predicted Nr time series shown in Fig. 9. The observed time series of Nr for the CRNS lies within the range of predicted Nr time series, although the values observed at 100 cm depth are slightly shifted towards the range of the neutron ratios predicted from reference sensor profiles with a depth of 130 cm. Furthermore, the dynamics of the predicted neutron ratios from reference soil moisture sensors match the dynamics of the CRNS-based values, which becomes especially visible during the rainfall event at the beginning of November 2021 (Fig. B1) as well as during the period in March 2022 when very little rainfall was observed. The latter led to a decrease in soil moisture and, hence, an increase in the observed Nr. Additionally, the short-term neutron ratio variations in the observed time series Nr are strongly reduced when the time series is smoothed with a 49 h moving average compared with a 25 h moving average that better corresponds to the Nr time series calculated from reference soil moisture sensors.
Similarly, a set of Nr time series is calculated from the available reference soil moisture sensor profiles with sensors at depths down to 200 and 450 cm. At a measurement depth of 200 cm, reference measurements are available at the exact depth of the detector tube location, whereas the neutron ratios observed at 500 cm are compared to those predicted from sensor profiles with a maximum sensor depth of 450 cm. Figure 9c shows the observed and predicted time series of Nr at 200 cm. The temporal dynamics of the predicted Nr time series are smaller than those predicted from soil moisture sensors at shallower depths. This matches the dynamics of the observed Nr; however, stronger short-term fluctuations become more visible here. Although the dynamics are dampened in both the observed and the different predicted Nr time series, the soil moisture increase caused by the intense rainfall event in late August 2021 is clearly visible (Fig. B2). In contrast, the predicted Nr time series from soil moisture sensors down to 450 cm depth do not show any dynamics over the measurement period (Fig. 9d). However, despite the short-term fluctuations visible in the observed neutron ratio, no trend can be observed, which is in line with the predicted values of Nr. At both measurement depths of 200 and 500 cm, the observed time series of Nr largely lie within the set of time series predicted with different reference soil moisture sensor profiles.
3.2.3 Estimating soil moisture from neutron ratio observations
The soil moisture time series of θSM derived from the observed Nr at depths of 100 and 200 cm are shown in Fig. 10. The estimated soil moisture time series follow the general dynamics of the reference values of θSM at both depths. During the observed intense precipitation events in August and November 2021, θSM at both 100 and 200 cm depth shows a distinct increase, which can also be seen in the soil moisture time series observed by the reference sensors. Similarly, the dry period in March 2022 results in a decrease in soil moisture, as indicated by θSM estimated from Nr at depths of 100 and 200 cm as well as by the in situ reference sensors at the respective depths. While the absolute values of θSM at 100 cm depth lie in the range of observed soil moisture values from the different in situ reference sensors available, the values of θSM at 200 cm depth are at the upper end of the set of time series of reference sensors.
4.1 Feasibility assessment
The particle transport simulations conducted within the scope of this study revealed a distinct relationship of the neutron ratio (Nr) with the local soil moisture content as well as with the shielding depth. As a consequence, changes in both the local soil moisture content at the depth of measurement and in the average soil moisture content above the detector (due to its contribution to the shielding depth) alter the neutron intensity and, thus, Nr observed by a downhole neutron detector. This illustrates the general possibility of deriving soil moisture information from Nr observed in the scope of d-CRNS.
Before neutron ratios can be calculated from downhole neutron intensities and from neutron intensities observed with the same detector above a water surface, the latter need to be corrected for variations in absolute humidity. The response of thermal neutrons to changes in absolute air humidity found here is less than half of the value that was reported by Rosolem et al. (2013) and may be explained by the generally smaller response of thermal neutrons to changes in hydrogen (e.g. Weimar et al., 2020). The rate of change between the thermal neutron intensity and absolute humidity derived in our study can be used to adjust the correction approach described by Rosolem et al. (2013) for epithermal neutrons so that it can be used to correct thermal neutrons observed above water instead. Although this correction approach may also be used as a first approach to correct thermal neutron intensities measured above soils, it should be noted that the response of neutron intensity to absolute humidity may change with soil moisture content, as reported for epithermal neutrons by Köhli et al. (2021). This illustrates the need to develop more sophisticated approaches to the correction of thermal neutron intensities for variations in absolute air humidity.
A specific feature observed in the neutron transport simulations is that, although neutron intensities generally increase with decreasing shielding depths, we find a maximum of the neutron intensity and, hence, the neutron ratio for low soil moisture content at shielding depths between 75 and 100 g cm−2, with lower neutron intensities at shielding depths below 75 g cm−2. A maximum secondary neutron intensity at shallow depths below the surface has been simulated, for example, for the surface of Earth (Phillips et al., 2001; Zweck et al., 2013) or the surface of Mars (Zhang et al., 2022), and it is linked to the production of neutrons in the upper soil layers through nuclear evaporation as well as moderation by elastic scattering and absorption processes. Based on the neutron transport simulations conducted for a soil bulk density of 1.43 g cm−3, an intensity maximum occurs in the soil up to a soil moisture content of 0.045 cm3 cm−3 at a shielding depth of 100 g cm−2 (Fig. 3). At higher soil moisture contents, the maximum disappears. This may be linked to a smaller leakage of neutrons to the atmosphere as more hydrogen causes more elastic scattering in the soil.
The tube and filling materials of the groundwater well noticeably influence the signal of the active neutron probe (e.g. Keller et al., 1990) due to, for example, an influence of material chemistry on thermal neutron intensities (e.g. Quinta-Ferreira et al., 2016). The simulation results of the present study show that the dimensions of the sphere of influence can be comparable for a well tube made of PVC and stainless steel with equal material thickness. As the average difference between a stainless steel and a PVC tube is approximately 1 cm for R86 and between 8 and 5 cm for Vc86 and V86, a small effect of the material composition on the sphere of influence can be identified but may be regarded as negligible. However, a thinner or thicker wall of the tube is likely to have a stronger impact on the measurement volume. For instance, a thicker PVC wall can be expected to reduce the measurement volume.
In contrast, the neutron ratios differ between a well tube composed of stainless steel and PVC. Although the response to changes in soil moisture are similar, the absolute neutron ratios of a PVC well tube compared with a stainless-steel tube of equal thickness are noticeably lower. This may be attributed to the influence of the higher absorption probability of chlorine for thermal neutrons in the PVC material. For the same reason, a thinner PVC material reduces the absolute neutron ratios to a smaller degree compared with a thicker PVC wall tubing.
For similar reasons, the effect of the filling material surrounding the actual tube of the groundwater observation well might be of importance in the scope of d-CRNS and should be assessed in future research. However, at our study site, the width of the filling material around the tube was only 10 cm, and the filling material was similar to the original material of the surrounding undisturbed soils: a sand filling for soil layers composed of sandy soils and clay for less conductive layers at greater depths. Therefore, similar soil moisture dynamics in the refilled material to those of the undisturbed material can be assumed for our test site.
The radius (R95) of the sphere of influence of the d-CRNS approach, even at high soil bulk densities, is larger compared with active neutron probes. For the latter, neutrons have to traverse the soil volume twice: on the way into the soil and back to the detector. In contrast, for passive applications, the water-sensitive neutrons in the fast-energy range are directly generated in the soil by high-energy neutrons, protons and muons, and they only have to traverse the soil volume once. Consequently, secondary cosmic-ray neutrons can reach the downhole neutron detector from origins at greater distances.
According to the particle transport simulation, the most sensitive volume lies above the detector centre. This is related to the source of cosmic-ray neutrons from above the soil surface. Similarly to the measurement footprints of above-ground CRNS, the sphere of influence varies with soil water content and with bulk density, with a higher sensitivity close to the neutron detector. As a consequence, reference soil moisture measurements close to the detector are likely to be more important than those at greater distances of the integration volume when predicting neutron ratios from reference soil moisture observations. Thus, further research may be required in order to assess whether weighting schemes for reference soil moisture measurements similar to those developed for above-ground CRNS are necessary in order to improve predicted neutron ratios. It should be noted that the simulated footprint dimensions are only valid for the modelled detector geometry and may vary with detector size and well or access tube dimensions.
Thermal neutrons detected with an unshielded, bare neutron detector, as is used in the present study, are more sensitive to absorption processes compared with neutrons in the epithermal energy range, which are dominated by moderation processes. As a consequence, soil chemistry influences the observed neutron intensity in the soil and, hence, also the derived neutron ratios from thermal neutrons and the neutron ratio variations with changes in soil moisture contents due to differing nuclear absorption probabilities in soils with different chemical compositions (e.g. Zreda et al., 2008; Quinta-Ferreira et al., 2016). However, we purposely used a simple soil chemistry set-up, which has been used as a standard configuration in several simulation studies, in the particle transport simulations (e.g. Köhli et al., 2015, 2021). This is done in order to derive a first set of equations describing the neutron ratio response and sphere of influence in the scope of the d-CRNS approach that can be applied over wide range of observation sites instead of tailoring the simulation set-up, and thus the derived equations, specifically to the observation site of this study. Although a standard soil chemistry was used to derive the transfer functions, the observed neutron ratios match the dynamics and ranges of predicted neutron ratios from in situ reference sensors, indicating the suitability and applicability of the d-CRNS approach as well as the equations derived at this site. A different soil chemistry may only introduce an overall damping of the measured intensity (Köhli and Schmoldt, 2022). Nonetheless, the conclusions are limited by the single site chosen for this study. Further research is required to test and validate the transferability of the approach and to investigate the influences of, for example, varying soil chemical compositions, access tube and filling materials, and suitable technical set-ups for practicable applications.
4.2 Uncertainties
The experimental set-up of field measurements conducted within the scope of this study comprised the measurement of thermal neutrons with an unshielded proportional detector at 100, 200, 500 and 1000 cm depth with co-located reference in situ soil moisture sensors installed down to 450 cm depth. Observed neutron intensities in the groundwater observation well show a distinct response with changing soil moisture contents at the depth of measurement, indicating the possibility of measuring soil moisture and supporting the results from the various particle transport simulation scenarios.
In line with the exponential decrease in the absolute neutron flux with increasing soil depth, the uncertainty in the neutron intensity as well as the neutron ratio (Nr) increases. In general, the observed downhole neutron intensities are lower than those observed above a water surface and thus, lower compared with the intensities expected for above-ground CRNS applications. As the uncertainty increases with decreasing neutron intensity, the hourly time series needs to be averaged over longer time intervals compared with time series of above-ground neutron detectors. While above-ground neutron time series are typically averaged with a moving average of 13–25 h (e.g. Bogena et al., 2013; Schrön et al., 2018), longer moving average windows of 25–49 h are more suitable for d-CRNS. However, with respect to the passive, continuous nature of d-CRNS as well as the expected smaller soil moisture dynamics at greater depths where soil moisture responses are also more strongly dampened, larger averaging intervals are acceptable.
Additional improvements can be made to reduce the uncertainty in observed downhole neutron time series. For example, detector tube no. 2 showed significantly lower neutron intensities compared with tube no. 1, which can be related to the settings of the instrument electronics. As the detector system used in this study was reassembled from different CRS1000 neutron detector systems, the neutron pulse module settings of tube no. 2 did not match the ideal configuration of the proportional counter tube attached; thus, a large part of potentially countable thermal neutrons were discarded, leading to the lower observed intensities.
In spite of these uncertainties, our study reveals that observed Nr values follow the temporal dynamics of predicted Nr values from Eqs. (5)–(9) and lie within the range of predicted Nr values from in situ reference soil moisture sensor profiles. Both intense rainfall events and gradual soil moisture changes during drying periods could be observed in the downhole measurements. The measurements at 100 cm depth exhibit stronger dynamics compared with those at 200 cm, which is in line with reference soil moisture time series and predicted neutron ratios. The observed Nr time series at 100 cm is closer to that predicted for 130 than for 70 cm depth; this may be explained by the fact that the predicted time series of Nr strongly differ between 70 and 130 cm depth as well as among the sensors within the two depth layers. This is due to markedly different values and dynamics of the individual soil moisture sensors. This marked variability in point-scale soil moisture hampers direct comparison to the results derived from d-CRNS. It should be noted that, especially at large depths of 500 cm, few soil moisture dynamics occur and the d-CRNS uncertainty is high, limiting the range of suitable application depths of d-CRNS. The results of this initial study revealed that the predicted hourly time series of Nr from reference soil moisture sensors at 70 and 130 cm have a coefficient of variation of 5–12 % for the study period. At 200 cm, the coefficients of variation are in a range between 3 and 16 %. The time series of the observed Nr need to be smoothed with a 49 h moving average to suppress noise and to result in coefficients of variation of the same order of magnitude, i.e. a value of 11 % at 100 cm and 9 % at 200 cm depth, respectively. In contrast, the coefficient of variation of the observed Nr at 500 cm depth with the same moving average applied is 4.3 times larger than the maximum coefficient of variation from the predicted Nr time series at 450 cm depth. According to these findings, the d-CRNS observations can be expected to be dominated by noise at the depth of 500 cm, rendering them unable to resolve the small soil moisture variations at this depth. However, the d-CRNS approach may be suitable for resolving the soil moisture dynamics at this site for shielding depths of up to at least 330 g cm−2, which roughly corresponds to a soil depth of at least 200 cm, when a moving average interval of 49 h is applied.
The uncertainties in θSM that are caused by the simplified estimation method used here (Sect. 3.1.3) are comparatively small. Although we allowed the assumed mean soil moisture in the unsaturated zone above the sensor to vary between the wilting point and field capacity when estimating the soil moisture at the sensor depth (which represents the upper bound of the possible uncertainty), the resulting uncertainty bounds of θSM are very small and hardly relevant for the depth of 100 cm, and they are still small for the depth of 200 cm (see Fig. 10).
While it is a major advantage of this study that in situ point-scale soil moisture observations for evaluating the d-CRNS approach are available at the study site at 200 and even at 450 cm depth, all reference sensors are unfortunately located outside the sphere of influence of the downhole neutron detectors in the groundwater observation well (at distances between 20 and 40 m). However, the observed Nr lies within the set of predicted time series of Nr from in situ reference sensor profiles and follows the general temporal dynamics of the predicted time series of Nr, thereby supporting the applicability of d-CRNS.
A key motivation of this study is to provide a new methodological approach to derive soil moisture information from deeper layers of the vadose zone in a larger integration volume compared with point-scale in situ sensors. However, deriving soil moisture from observed Nr is difficult, as two soil moisture variables influence the latter: the soil moisture content at the measurement depth (θSM) and the average soil moisture from the soil surface to the detector centre (). A first option would be the use of Eqs. (5)–(9) as a forward operator in combination with a soil hydraulic model. Similar approaches have been conducted using techniques such as the COSMIC (COsmic-ray Soil Moisture Interaction Code) forward-operator model (Shuttleworth et al., 2013) for above-ground CRNS applications (e.g. Brunetti et al., 2019; Barbosa et al., 2021). Although the application as a forward operator in combination with soil hydraulic modelling may produce more accurate results, as the soil water transport is simulated at different depths, and also allows for the retrieval of soil moisture simulated in several soil layers, a large number of input parameters are required that may not be available at all sites. Furthermore, coupling the derived equations with a soil hydraulic model may introduce additional uncertainties due to the model assumptions and the propagation of uncertainties from input parameters.
In contrast, the simple approach to estimate the local soil moisture content at the depth of measurement (as the most sensitive variable) showed that the resulting soil moisture time series follow the dynamics and also lie in the range of expected values derived from in situ soil moisture sensors. However, it should be noted that this approach may be less accurate and only allows for an estimation of the local soil moisture time series.
As this study is restricted to a single observation site, further research is required to test both the soil hydraulic-model-based approach and the approach used here under different site-specific boundary conditions, set-ups and measurement depths. This also includes the consideration of uncertainties arising from soils with high vertical variability in bulk density (and possibly soil moisture), their impact on predicted neutron ratios and their impact on the estimated soil moisture at the depth of measurement. For example, a lower bulk density and a lower soil water content would lead to more neutrons penetrating into greater depths and, hence, to increased count rates and footprint volumes. Nevertheless, the two mentioned approaches are available for soil moisture retrieval from d-CRNS and could be applied under different soil hydrological conditions in future studies.
In this study, we tested the feasibility of CRNS downhole applications to estimate soil moisture at greater depth by combining particle transport simulations with a first application in the field. Although we used an unshielded neutron detector that was most sensitive to thermal neutrons, a distinct response to changes in the soil moisture content at the observation depth as well as in the shielding depth above the neutron detector was found. This illustrates the possibility to observe soil moisture values at greater depth with d-CRNS without additional soil moisture information for calibration. This is achieved through the calculation of neutron ratios using a measurement above water. The sphere of influence has a unique shape, differing from those expected for active neutron probes, as the neutron source and detector are not co-located. As detected neutrons are produced directly in the soil, the sphere of influence is much larger compared with an active neutron probe; thus, d-CRNS allows one to derive representative average soil moisture information at different depths of the root zone.
Our measurements of downhole neutron intensities and calculated neutron ratios from a groundwater observation well provide experimental evidence that downhole thermal neutron detectors are sensitive to changes in soil moisture contents at the measurement depth. Simultaneously, the results of this study illustrate the opportunity to use existing monitoring infrastructure to retrieve soil moisture information from deeper soil layers. The transfer functions developed from particle transport simulations in the scope of this study can be used as an forward operator to calculate neutron signals from soil moisture information. In combination with soil hydraulic models, the forward operator can then be used to derive soil moisture contents in future applications. When the use of complex models is hampered, for example, by scarce data, a simple approach can be used for a first estimation of the soil moisture at the measurement depth.
In conclusion, we provide both simulation-based and experimental evidence for the feasibility of using downhole secondary cosmic-ray neutrons for the continuous, non-invasive estimation of soil moisture from greater depth. This method has several advantages compared with traditional in situ soil moisture sensors: the larger integration volume of the measurement counteracts the usual problems caused by the high spatial variability in soil moisture, even at small scales as a result of the subsurface heterogeneity. Furthermore, it does not require demanding installation procedures, as it simply uses existing infrastructure (i.e. observation wells) which is readily available in many locations as part of standard monitoring networks. The mathematical relationships presented allow for the prediction of the neutron signal from soil moisture information, and approaches are available to derive soil moisture contents from downhole neutron observations. However, as this study poses several limitations and is only a first proof of concept, further testing and developments will be necessary. This effort is worthwhile, especially as deep soil moisture measurements are becoming increasingly important to monitor subsurface droughts or water stress in forests as well as to validate hydrological models and extrapolation efforts from remote-sensing products.
In order to derive soil moisture information at the depth of measurement from the observed neutron ratios, we propose the following exemplary approach:
-
For , we assign values ranging from the wilting point to the field capacity in steps of 0.001 cm3 cm−3.
-
For each time step of the observed time series of Nr, values of Nr are calculated by assigning values from 0.01 cm3 cm−3 to the soil moisture content at saturation in steps of 0.0001 cm3 cm−3 to θSM.
-
The value of θSM that produces the smallest absolute difference between the observed and calculated Nr at each time step is chosen. This procedure results in a time series of θSM for each value of .
-
Based on this set of time series, we propose averaging the values for θSM for each time step in order to provide a single time series of estimated soil moisture values at the depth of measurement. The minimum and maximum time series can also be calculated to assess the range (uncertainty) of possible θSM values based on the observed Nr.
Table B1Sensor distribution of the reference soil moisture sensor profiles at the study site located at a distance of about 20–30 m from the groundwater observation well.
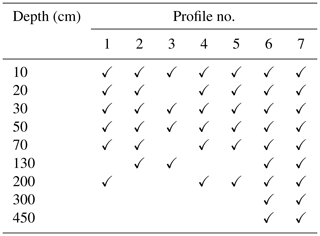
Table B2Fitted parameters for Eqs. (2)–(7) derived from particle transport simulation scenarios for a stainless-steel well tube with a wall thickness of 7.5 mm.

Table B3Fitted parameters for Eq. (6) and (7) derived from particle transport simulation scenarios for a PVC well tube with a wall thickness of 5 mm.

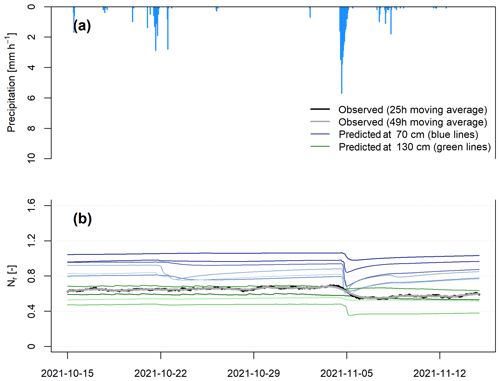
Figure B1Panel (a) shows the hourly precipitation observed at the study site during a detailed period of the experiment in October–November 2021, and panel (b) presents the observed time series of Nr at 100 cm depth and the predicted time series of Nr from reference soil moisture sensor profiles at 70 and 130 cm depths. The different colours indicate the predictions from individual reference sensor profiles.
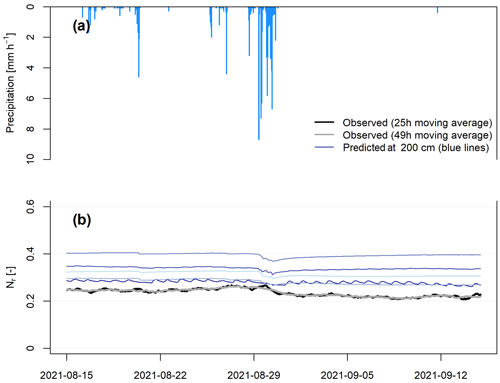
Figure B2Panel (a) shows the hourly precipitation observed at the study site during a detailed period of the experiment in October–November 2021, and panel (b) presents the observed time series of Nr at 200 cm depth and the predicted time series of Nr from reference soil moisture sensor profiles at 200 cm depth. The different colours indicate the predictions from individual reference sensor profiles.
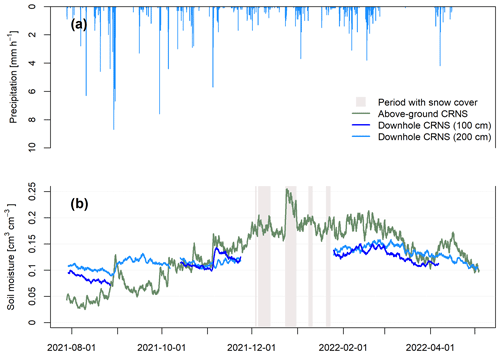
Figure B3Panel (a) shows the hourly precipitation time series, and panel (b) presents the different soil moisture time series derived from CRNS. The neutron observations from above-ground CRNS were processed with standard correction and calibration procedures (site Serrahn; Bogena et al., 2022). A 25 h moving average was applied to the corrected neutron intensities prior to deriving soil moisture from above-ground CRNS observations with the standard transfer function (Desilets et al., 2010; Köhli et al., 2021). Marked periods with snow cover represent periods with fractional to full snow cover and snow depths of up to 10–15 cm.
All data sets are available from the authors upon request.
DR had the idea for this study, designed the experiment, performed the data analysis and wrote the manuscript. JW conducted and analysed the particle transport simulations and wrote the manuscript. MK and MS assisted with performing and analysing neutron transport simulations and provided valuable ideas regarding the manuscript. TB and AG designed the soil moisture and groundwater monitoring network and contributed to writing the manuscript. MM assisted with planning and designing the experimental set-up as well as conducting the field measurements.
Markus Köhli and Jannis Weimar hold a CEO position at StyX Neutronica GmbH. At least one of the (co-)authors is a member of the editorial board of Hydrology and Earth System Sciences. The peer-review process was guided by an independent editor.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This study was conducted as part of the Cosmic Sense research unit, funded by the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG-FOR2694). We gratefully acknowledge technical support from Jörg Wummel and Stephan Schröder, who maintain the TERENO-NE observation sites, funded by the Helmholtz Association. In addition, we would like to thank Paul Voit for his assistance with data acquisition, fieldwork and laboratory analyses. Furthermore, we would like to thank the Müritz National Park for continuing support and collaboration. Lastly, we acknowledge the NMDB database (https://www.nmdb.eu, last access: 16 August 2023), founded under the European Union's FP7 programme (contract no. 213007), and the principal investigators of the individual neutron monitors for providing data.
This research has been supported by the Deutsche Forschungsgemeinschaft (grant no. 357874777).
The article processing charges for this open-access publication were covered by the Helmholtz Centre Potsdam – GFZ German Research Centre for Geosciences.
This paper was edited by Roberto Greco and reviewed by three anonymous referees.
Andreasen, M., Jensen, K. H., Zreda, M., Desilets, D., Bogena, H. R., and Looms, M. C.: Modeling cosmic ray neutron field measurements, Water Resour. Res., 52, 6451–6471, https://doi.org/10.1002/2015wr018236, 2016. a, b, c
Andreasen, M., Jensen, K. H., Desilets, D., Zreda, M., Bogena, H. R., and Looms, M. C.: Cosmic-ray neutron transport at a forest field site: the sensitivity to various environmental conditions with focus on biomass and canopy interception, Hydrol. Earth Syst. Sci., 21, 1875–1894, https://doi.org/10.5194/hess-21-1875-2017, 2017. a, b
Andreasen, M., Jensen, K. H., Bogena, H. R., Desilets, D., Zreda, M., and Looms, M. C.: Cosmic Ray Neutron Soil Moisture Estimation Using Physically Based Site-Specific Conversion Functions, Water Resour. Res., 56, e2019WR026588, https://doi.org/10.1029/2019wr026588, 2020. a
Barbosa, L. R., Coelho, V. H. R., Scheiffele, L. M., Baroni, G., Filho, G. M. R., Montenegro, S. M. G. L., das N. Almeida, C., and Oswald, S. E.: Dynamic groundwater recharge simulations based on cosmic-ray neutron sensing in a tropical wet experimental basin, Vadose Zone J., 20, e20145, https://doi.org/10.1002/vzj2.20145, 2021. a
BKG – German Federal Agency for Cartography and Geodesy: Digital landcover model: ATKIS-Basis-DLM (© GeoBasis-DE/BKG 2018), https://gdz.bkg.bund.de/index.php/default/digitale-geodaten/digitale-landschaftsmodelle/digitales-basis-landschaftsmodell-ebenen-basis-dlm-ebenen.html (last access: 17 August 2023), 2018. a
Bogena, H. R., Huisman, J. A., Baatz, R., Hendricks-Franssen, H.-J., and Vereecken, H.: Accuracy of the cosmic-ray soil water content probe in humid forest ecosystems: The worst case scenario, Water Resour. Res., 49, 5778–5791, https://doi.org/10.1002/wrcr.20463, 2013. a
Bogena, H. R., Schrön, M., Jakobi, J., Ney, P., Zacharias, S., Andreasen, M., Baatz, R., Boorman, D., Duygu, M. B., Eguibar-Galán, M. A., Fersch, B., Franke, T., Geris, J., González Sanchis, M., Kerr, Y., Korf, T., Mengistu, Z., Mialon, A., Nasta, P., Nitychoruk, J., Pisinaras, V., Rasche, D., Rosolem, R., Said, H., Schattan, P., Zreda, M., Achleitner, S., Albentosa-Hernández, E., Akyürek, Z., Blume, T., del Campo, A., Canone, D., Dimitrova-Petrova, K., Evans, J. G., Ferraris, S., Frances, F., Gisolo, D., Güntner, A., Herrmann, F., Iwema, J., Jensen, K. H., Kunstmann, H., Lidón, A., Looms, M. C., Oswald, S., Panagopoulos, A., Patil, A., Power, D., Rebmann, C., Romano, N., Scheiffele, L., Seneviratne, S., Weltin, G., and Vereecken, H.: COSMOS-Europe: a European network of cosmic-ray neutron soil moisture sensors, Earth Syst. Sci. Data, 14, 1125–1151, https://doi.org/10.5194/essd-14-1125-2022, 2022. a, b, c
Börner, A.: Neue Beiträge zum Naturraum und zur Landschaftsgeschichte im Teilgebiet Serrahn des Müritz-Nationalparks - Forschung und Monitoring, vol. 4, chap. Geologische Entwicklung des Gebietes um den Großen Fürstenseer See, Geozon Science Media, Berlin, Germany, 21–29, https://www.mueritz-nationalpark.de/fileadmin/mueritz/Service/Forschung_und_Monitoring/Forschung_u._Monitoring_Band_4.pdf (last access: 18 August 2023), 2015. a
Brall, T., Mares, V., Bütikofer, R., and Rühm, W.: Assessment of neutrons from secondary cosmic rays at mountain altitudes – Geant4 simulations of environmental parameters including soil moisture and snow cover, The Cryosphere, 15, 4769–4780, https://doi.org/10.5194/tc-15-4769-2021, 2021. a
Brunetti, G., Šimůnek, J., Bogena, H. R., Baatz, R., Huisman, J. A., Dahlke, H., and Vereecken, H.: On the Information Content of Cosmic-Ray Neutron Data in the Inverse Estimation of Soil Hydraulic Properties, Vadose Zone J., 18, 1–24, https://doi.org/10.2136/vzj2018.06.0123, 2019. a
Canadell, J., Jackson, R. B., Ehleringer, J. B., Mooney, H. A., Sala, O. E., and Schulze, E.-D.: Maximum rooting depth of vegetation types at the global scale, Oecologia, 108, 583–595, https://doi.org/10.1007/bf00329030, 1996. a
Chakraborty, T., Saha, S., and Reif, A.: Biomass equations for European beech growing on dry sites, iForest, 9, 751–757, https://doi.org/10.3832/ifor1881-009, 2016. a
Cimpoiaşu, M. O., Kuras, O., Pridmore, T., and Mooney, S. J.: Potential of geoelectrical methods to monitor root zone processes and structure: A review, Geoderma, 365, 114232, https://doi.org/10.1016/j.geoderma.2020.114232, 2020. a
Daly, E. and Porporato, A.: A Review of Soil Moisture Dynamics: From Rainfall Infiltration to Ecosystem Response, Environ. Eng. Sci., 22, 9–24, https://doi.org/10.1089/ees.2005.22.9, 2005. a
de Jong, S. M., Heijenk, R. A., Nijland, W., and van der Meijde, M.: Monitoring Soil Moisture Dynamics Using Electrical Resistivity Tomography under Homogeneous Field Conditions, Sensors, 20, 5313, https://doi.org/10.3390/s20185313, 2020. a
Desilets, D., Zreda, M., and Ferré, T. P. A.: Nature's neutron probe: Land surface hydrology at an elusive scale with cosmic rays, Water Resour. Res., 46, W11505, https://doi.org/10.1029/2009wr008726, 2010. a, b, c
DWD – German Weather Service: Multi-annual temperature observations 1981–2010, DWD Climate Data Center, https://opendata.dwd.de/climate_environment/CDC/observations_germany/climate/multi_annual/mean_81-10/Temperatur_1981-2010.txt (last access: 17 August 2023), 2020a. a
DWD - German Weather Service: Multi-annual precipitation observations 1981–2010, DWD Climate Data Center, https://opendata.dwd.de/climate_environment/CDC/observations_germany/climate/multi_annual/mean_81-10/Niederschlag_1981-2010.txt (last access: 17 August 2023), 2020b. a
Fan, Y., Miguez-Macho, G., Jobbágy, E. G., Jackson, R. B., and Otero-Casal, C.: Hydrologic regulation of plant rooting depth, P. Natl. Acad. Sci. USA, 114, 10572–10577, https://doi.org/10.1073/pnas.1712381114, 2017. a
Ferronsky, V.: Nuclear Geophysics; Applications in hydrology, hydrogeology, engineering geology, agriculture and environmental science, Springer Geophysics, Springer International Publishing, Basel, Switzerland, https://doi.org/10.1007/978-3-319-12451-3, 2015. a
Franz, T. E., Zreda, M., Ferré, T. P. A., Rosolem, R., Zweck, C., Stillman, S., Zeng, X., and Shuttleworth, W. J.: Measurement depth of the cosmic ray soil moisture probe affected by hydrogen from various sources, Water Resour. Res., 48, W08515, https://doi.org/10.1029/2012wr011871, 2012. a, b
Franz, T. E., Zreda, M., Rosolem, R., and Ferre, T. P. A.: A universal calibration function for determination of soil moisture with cosmic-ray neutrons, Hydrol. Earth Syst. Sci., 17, 453–460, https://doi.org/10.5194/hess-17-453-2013, 2013. a
Gardner, W. and Kirkham, D.: Determination of Soil Moisture by Neutron Scattering, Soil Sci., 73, 391–402, 1952. a
Gardner, W. H.: Water Content, in: SSSA Book Series, Methods of Soil Analysis, Part 1. Physical and Mineralogical Methods-Agronomy, 2 edn., number 9 in the series Agronomy, American Society of Agronomy, Soil Science Society of America, Madison, USA, https://doi.org/10.2136/sssabookser5.1.2ed.c21, pp. 493–544, 1986. a, b, c, d, e
Gudima, K., Mashnik, S., and Toneev, V.: Cascade-exciton model of nuclear reactions, Nucl. Phys. A, 401, 329–361, https://doi.org/10.1016/0375-9474(83)90532-8, 1983. a
Heidbüchel, I., Güntner, A., and Blume, T.: Use of cosmic-ray neutron sensors for soil moisture monitoring in forests, Hydrol. Earth Syst. Sci., 20, 1269–1288, https://doi.org/10.5194/hess-20-1269-2016, 2016. a, b
Heinrich, I., Balanzategui, D., Bens, O., Blasch, G., Blume, T., Böttcher, F., Borg, E., Brademann, B., Brauer, A., Conrad, C., Dietze, E., Dräger, N., Fiener, P., Gerke, H. H., Güntner, A., Heine, I., Helle, G., Herbrich, M., Harfenmeister, K., Heußner, K.-U., Hohmann, C., Itzerott, S., Jurasinski, G., Kaiser, K., Kappler, C., Koebsch, F., Liebner, S., Lischeid, G., Merz, B., Missling, K. D., Morgner, M., Pinkerneil, S., Plessen, B., Raab, T., Ruhtz, T., Sachs, T., Sommer, M., Spengler, D., Stender, V., Stüve, P., and Wilken, F.: Interdisciplinary Geo-ecological Research across Time Scales in the Northeast German Lowland Observatory (TERENO-NE), Vadose Zone J., 17, 180116, https://doi.org/10.2136/vzj2018.06.0116, 2018. a
Heusser, G.: Cosmic ray interaction study with low-level Ge-spectrometry, Nucl. Instrum. Meth. A, 369, 539–543, https://doi.org/10.1016/s0168-9002(96)80046-5, 1996. a
Hubert, G., Pazianotto, M. T., and Federico, C. A.: Modeling of ground albedo neutrons to investigate seasonal cosmic ray-induced neutron variations measured at high-altitude stations, J. Geophys. Res.-Space, 121, 12,186–12,201, https://doi.org/10.1002/2016ja023055, 2016. a, b
IAEA - International Atomic Energy Agency: Neutron Moisture Gauges – A guide-book on theory and practice, techreport 112, IAEA – International Atomic Energy Agency, Vienna, https://inis.iaea.org/collection/NCLCollectionStore/_Public/01/001/1001730.pdf (last access: 17 August 2023), 1970. a, b
Jackson, R. B., Canadell, J., Ehleringer, J. R., Mooney, H. A., Sala, O. E., and Schulze, E. D.: A global analysis of root distributions for terrestrial biomes, Oecologia, 108, 389–411, https://doi.org/10.1007/bf00333714, 1996. a
Keller, B. R., Everett, L. G., and Marks, R. J.: Effects of Access Tube Material and Grout on Neutron Probe Measurements in the Vadose Zone, Groundwater Monitoring & Remediation, 10, 96–100, https://doi.org/10.1111/j.1745-6592.1990.tb00326.x, 1990. a, b
Kodama, M., Kudo, S., and Kosuge, T.: Application of atmospheric neutrons to soil moisture measurement, Soil Sci., 140, 237–242, 1985. a
Köhli, M. and Schmoldt, J.-P.: Feasibility of UXO detection via pulsed neutron-neutron logging, Appl. Radiat. Isotopes, 188, 110403, https://doi.org/10.1016/j.apradiso.2022.110403, 2022. a
Köhli, M., Schrön, M., Zreda, M., Schmidt, U., Dietrich, P., and Zacharias, S.: Footprint characteristics revised for field-scale soil moisture monitoring with cosmic-ray neutrons, Water Resour. Res., 51, 5772–5790, https://doi.org/10.1002/2015wr017169, 2015. a, b, c, d
Köhli, M., Weimar, J., Schrön, M., Baatz, R., and Schmidt, U.: Soil Moisture and Air Humidity Dependence of the Above-Ground Cosmic-Ray Neutron Intensity, Frontiers in Water, 2, 544847, https://doi.org/10.3389/frwa.2020.544847, 2021. a, b, c, d, e, f, g, h
Kramer, J. H., Cullen, S. J., and Everett, L. G.: Vadose Zone Monitoring with the Neutron Moisture Probe, Groundwater Monitoring & Remediation, 12, 177–187, https://doi.org/10.1111/j.1745-6592.1992.tb00058.x, 1992. a
Kristensen, K. J.: Depth Intervals and Topsoil Moisture Measurement with the Neutron Depth Probe, Hydrol. Res., 4, 77–85, https://doi.org/10.2166/nh.1973.0007, 1973. a
LAIV-MV – State Agency for Interior Administration Mecklenburg-Western Pomerania: Digital elevation model: ATKIS-DEM1 (© GeoBasis-DE/M-V 2011), https://www.laiv-mv.de/Geoinformation/Geobasisdaten/Gelaendemodelle/ (last access: 17 August 2023), 2011. a
Li, D., Schrön, M., Köhli, M., Bogena, H. R., Weimar, J., Bello, M. A. J., Han, X., Gimeno, M. A. M., Zacharias, S., Vereecken, H., and Hendricks-Franssen, H.-J.: Can Drip Irrigation be Scheduled with Cosmic-Ray Neutron Sensing?, Vadose Zone J., 18, 190053, https://doi.org/10.2136/vzj2019.05.0053, 2019. a
McJannet, D., Franz, T., Hawdon, A., Boadle, D., Baker, B., Almeida, A., Silberstein, R., Lambert, T., and Desilets, D.: Field testing of the universal calibration function for determination of soil moisture with cosmic-ray neutrons, Water Resour. Res., 50, 5235–5248, https://doi.org/10.1002/2014wr015513, 2014. a
Mollerach, S. and Roulet, E.: Progress in high-energy cosmic ray physics, Prog. Part. Nucl. Phys., 98, 85–118, https://doi.org/10.1016/j.ppnp.2017.10.002, 2018. a
Neumann, R. B. and Cardon, Z. G.: The magnitude of hydraulic redistribution by plant roots: a review and synthesis of empirical and modeling studies, New Phytol., 194, 337–352, https://doi.org/10.1111/j.1469-8137.2012.04088.x, 2012. a
Nimmo, J. R.: The processes of preferential flow in the unsaturated zone, Soil Sci. Soc. Am. J., 85, 1–27, https://doi.org/10.1002/saj2.20143, 2021. a
Phillips, F. M., Stone, W. D., and Fabryka-Martin, J. T.: An improved approach to calculating low-energy cosmic-ray neutron fluxes near the land/atmosphere interface, Chem. Geol., 175, 689–701, https://doi.org/10.1016/s0009-2541(00)00329-6, 2001. a
Pierret, A., Maeght, J.-L., Clément, C., Montoroi, J.-P., Hartmann, C., and Gonkhamdee, S.: Understanding deep roots and their functions in ecosystems: an advocacy for more unconventional research, Ann. Bot.-London, 118, 621–635, https://doi.org/10.1093/aob/mcw130, 2016. a
Quinta-Ferreira, M., Dias, J. F., and Alija, S.: False low water content in road field compaction control using nuclear gauges: a case study, Environ. Earth Sci., 75, 1114, https://doi.org/10.1007/s12665-016-5901-1, 2016. a, b
Rasche, D., Köhli, M., Schrön, M., Blume, T., and Güntner, A.: Towards disentangling heterogeneous soil moisture patterns in cosmic-ray neutron sensor footprints, Hydrol. Earth Syst. Sci., 25, 6547–6566, https://doi.org/10.5194/hess-25-6547-2021, 2021. a, b, c, d
Reich, M., Mikolaj, M., Blume, T., and Güntner, A.: Field-Scale Subsurface Flow Processes Inferred From Continuous Gravity Monitoring During a Sprinkling Experiment, Water Resour. Res., 57, e2021WR030044, https://doi.org/10.1029/2021wr030044, 2021. a
Rosolem, R., Shuttleworth, W. J., Zreda, M., Franz, T. E., Zeng, X., and Kurc, S. A.: The Effect of Atmospheric Water Vapor on Neutron Count in the Cosmic-Ray Soil Moisture Observing System, J. Hydrometeorol., 14, 1659–1671, https://doi.org/10.1175/jhm-d-12-0120.1, 2013. a, b, c, d, e, f
Sato, T.: Analytical Model for Estimating Terrestrial Cosmic Ray Fluxes Nearly Anytime and Anywhere in the World: Extension of PARMA/EXPACS, PLOS ONE, 10, 1–33, https://doi.org/10.1371/journal.pone.0144679, 2015. a
Sato, T.: Analytical Model for Estimating the Zenith Angle Dependence of Terrestrial Cosmic Ray Fluxes, PLOS ONE, 11, 1–22, https://doi.org/10.1371/journal.pone.0160390, 2016. a
Schrön, M., Zacharias, S., Womack, G., Köhli, M., Desilets, D., Oswald, S. E., Bumberger, J., Mollenhauer, H., Kögler, S., Remmler, P., Kasner, M., Denk, A., and Dietrich, P.: Intercomparison of cosmic-ray neutron sensors and water balance monitoring in an urban environment, Geosci. Instrum. Method. Data Syst., 7, 83–99, https://doi.org/10.5194/gi-7-83-2018, 2018. a, b, c, d
Seneviratne, S. I., Corti, T., Davin, E. L., Hirschi, M., Jaeger, E. B., Lehner, I., Orlowsky, B., and Teuling, A. J.: Investigating soil moisture–climate interactions in a changing climate: A review, Earth-Sci. Rev., 99, 125–161, https://doi.org/10.1016/j.earscirev.2010.02.004, 2010. a, b
Shuttleworth, J., Rosolem, R., Zreda, M., and Franz, T.: The COsmic-ray Soil Moisture Interaction Code (COSMIC) for use in data assimilation, Hydrol. Earth Syst. Sci., 17, 3205–3217, https://doi.org/10.5194/hess-17-3205-2013, 2013. a
Šimůnek, J., van Genuchten, M. T., and Šejna, M.: Development and applications of the HYDRUS and STANMOD software packages and related codes, Vadose Zone J., 7, 587–600, https://doi.org/10.2136/vzj2007.0077, 2008. a
Sponagel, H., Grottenthaler, W., Hartmann, K.-J., Hartwich, R., Janetzko, P., Joisten, H., Kühn, D., Sabel, K.-J., and Traidl, R.: Bodenkundliche Kartieranleitung KA5, 5 edn., BGR – German Federal Institute for Geosciences and Natural Resources, Hannover, Germany, 2005. a
Urban, J., Čermák, J., and Ceulemans, R.: Above- and below-ground biomass, surface and volume, and stored water in a mature Scots pine stand, Eur. J. For. Res., 134, 61–74, https://doi.org/10.1007/s10342-014-0833-3, 2014. a
Van Camp, M., de Viron, O., Watlet, A., Meurers, B., Francis, O., and Caudron, C.: Geophysics From Terrestrial Time-Variable Gravity Measurements, Rev. Geophys., 55, 938–992, https://doi.org/10.1002/2017rg000566, 2017. a, b
Vereecken, H., Huisman, J. A., Bogena, H. R., Vanderborght, J., Vrugt, J. A., and Hopmans, J. W.: On the value of soil moisture measurements in vadose zone hydrology: A review, Water Resour. Res., 44, https://doi.org/10.1029/2008wr006829, 2008. a
Vereecken, H., Huisman, J. A., Pachepsky, Y., Montzka, C., van der Kruk, J., Bogena, H. R., Weihermüller, L., Herbst, M., Martinez, G., and Vanderborght, J.: On the spatio-temporal dynamics of soil moisture at the field scale, J. Hydrol., 516, 76–96, https://doi.org/10.1016/j.jhydrol.2013.11.061, 2014. a, b
Wang, C., Fu, B., Zhang, L., and Xu, Z.: Soil moisture–plant interactions: an ecohydrological review, J. Soils Sediment., 19, 1–9, https://doi.org/10.1007/s11368-018-2167-0, 2018. a
Weimar, J., Köhli, M., Budach, C., and Schmidt, U.: Large-Scale Boron-Lined Neutron Detection Systems as a 3He Alternative for Cosmic Ray Neutron Sensing, Frontiers in Water, 2, 16, https://doi.org/10.3389/frwa.2020.00016, 2020. a, b, c, d
Werner, C. J., Bull, J. S., Solomon, C. J., Brown, F. B., McKinney, G. W., Rising, M. E., Dixon, D. A., Martz, R. L., Hughes, H. G., Cox, L. J., Zukaitis, A. J., Armstrong, J. C., Forster, R. A., and Casswell, L.: MCNP Version 6.2 Release Notes, Tech. Rep. LA-UR-18-20808, Los Alamos National Laboratory, Los Alamos, United States, https://doi.org/10.2172/1419730, 2018. a
Zacharias, S., Bogena, H. R., Samaniego, L., Mauder, M., Fuß, R., Pütz, T., Frenzel, M., Schwank, M., Baessler, C., Butterbach-Bahl, K., Bens, O., Borg, E., Brauer, A., Dietrich, P., Hajnsek, I., Helle, G., Kiese, R., Kunstmann, H., Klotz, S., Munch, J. C., Papen, H., Priesack, E., Schmid, H. P., Steinbrecher, R., Rosenbaum, U., Teutsch, G., and Vereecken, H.: A Network of Terrestrial Environmental Observatories in Germany, Vadose Zone J., 10, 955–973, https://doi.org/10.2136/vzj2010.0139, 2011. a
Zhang, J., Guo, J., Dobynde, M. I., Wang, Y., and Wimmer-Schweingruber, R. F.: From the Top of Martian Olympus to Deep Craters and Beneath: Mars Radiation Environment Under Different Atmospheric and Regolith Depths, J. Geophys. Res.-Planet., 127, e2021JE007157, https://doi.org/10.1029/2021je007157, 2022. a
Zreda, M., Desilets, D., Ferré, T. P. A., and Scott, R. L.: Measuring soil moisture content non-invasively at intermediate spatial scale using cosmic-ray neutrons, Geophys. Res. Lett., 35, L21402, https://doi.org/10.1029/2008gl035655, 2008. a, b, c, d
Zreda, M., Shuttleworth, W. J., Zeng, X., Zweck, C., Desilets, D., Franz, T., and Rosolem, R.: COSMOS: the COsmic-ray Soil Moisture Observing System, Hydrol. Earth Syst. Sci., 16, 4079–4099, https://doi.org/10.5194/hess-16-4079-2012, 2012. a, b
Zweck, C., Zreda, M., and Desilets, D.: Snow shielding factors for cosmogenic nuclide dating inferred from Monte Carlo neutron transport simulations, Earth Planet. Sc. Lett., 379, 64–71, https://doi.org/10.1016/j.epsl.2013.07.023, 2013. a