Hydrological, meteorological, and watershed controls on the water balance of thermokarst lakes between Inuvik and Tuktoyaktuk, Northwest Territories, Canada

Thermokarst lake water balances are becoming increasingly vulnerable to change in the Arctic as air temperature increases and precipitation patterns shift. In the tundra uplands east of the Mackenzie Delta in the Northwest Territories, Canada, previous research has found that lakes responded non-uniformly to year-to-year changes in precipitation, suggesting that lake and watershed properties mediate the response of lakes to climate change. To investigate how lake and watershed properties and meteorological conditions influence the water balance of thermokarst lakes in this region, we sampled 25 lakes for isotope analysis five times in 2018, beginning before snowmelt on 1 May and sampling throughout the remainder of the ice-free season. Water isotope data were used to calculate the average isotope composition of lake source water (δ_I) and the ratio of evaporation to inflow ($E/I$). We identified four distinct water balance phases as lakes responded to seasonal shifts in meteorological conditions and hydrological processes. During the freshet phase from 1 May to 15 June, the median $E/I$ ratio of lakes decreased from 0.20 to 0.13 in response to freshet runoff and limited evaporation due to lake ice presence that persisted for the duration of this phase. During the following warm, dry, and ice-free period from 15 June to 26 July, designated the evaporation phase, the median $E/I$ ratio increased to 0.19. During the brief soil wetting phase, $E/I$ ratios did not respond to rainfall between 26 July and 2 August, likely because watershed soils absorbed most of the precipitation which resulted in minimal runoff to lakes. The median $E/I$ ratio decreased to 0.11 after a cool and rainy August, identified as the recharge phase. Throughout the sampling period, δ_I remained relatively stable and most lakes contained a greater amount of rainfall-sourced water than snow-sourced water, even after the freshet phase, due to snowmelt bypass. The range of average $E/I$ ratios that we observed at lakes (0.00–0.43) was relatively narrow and low compared with thermokarst lakes in other regions, likely owing to the large ratio of watershed area to lake area ($\mathrm{WA}/\mathrm{LA}$), efficient preferential flow pathways for runoff, and a shorter ice-free season. Lakes with smaller $\mathrm{WA}/\mathrm{LA}$ tended to have higher $E/I$ ratios (R² = 0.74). An empirical relationship between $\mathrm{WA}/\mathrm{LA}$ and $E/I$ was derived and used to predict the average $E/I$ ratio of 7340 lakes in the region, which identified that these lakes are not vulnerable to desiccation, given that $E/I$ ratios were < 0.33. If future permafrost thaw and warming cause less runoff to flow into lakes, we expect that lakes with a smaller $\mathrm{WA}/\mathrm{LA}$ will be more influenced by increasing evaporation, while lakes with a larger $\mathrm{WA}/\mathrm{LA}$ will be more resistant to lake-level drawdown. However under wetter conditions, lakes with a larger $\mathrm{WA}/\mathrm{LA}$ will likely experience a greater increases in lake level and could be more susceptible to rapid drainage.

1 Introduction

Thermokarst lakes are common features in ice-rich permafrost terrain, occupying up to 25 % of the land area (Woo, 2012). The water balance of thermokarst lakes is changing as Arctic warming causes precipitation to shift from snowfall to rainfall (Bintanja and Andry, 2017; MacDonald et al., 2021) and permafrost thaw alters the hydrological connectivity of lake watersheds (Wolfe et al., 2011; Walvoord and Kurylyk, 2016; Tananaev and Lotsari, 2022; Koch et al., 2022). Additionally, longer ice-free periods are increasing evaporation (Prowse et al., 2011; Arp et al., 2015), and enhanced vegetation growth is altering snow redistribution and snowmelt timing (Sturm et al., 2001; Essery and Pomeroy, 2004; Pomeroy et al., 2006). In many regions, expansion and contraction of thermokarst lakes has been observed, demonstrating that lake water balances are not responding uniformly to climate change (Smith et al., 2005; Plug et al., 2008; Marsh et al., 2009; Arp et al., 2011; Jones et al., 2011; Andresen and Lougheed, 2015; Travers-Smith et al., 2021).

Previous studies have demonstrated that knowledge of meteorological conditions and lake and watershed attributes, as well as their influence on lake water balance, can explain why thermokarst lakes react non-uniformly to climate change (Wolfe et al., 2011; Turner et al., 2014; Nitze et al., 2017; Wan et al., 2020). Key drivers of lake water balances include the relative size of a lake within its watershed (ratio of watershed area to lake area, $\mathrm{WA}/\mathrm{LA}$), rainfall and snowfall patterns, permafrost dynamics, wildfire, vegetation cover, and ice-free season length (Turner et al., 2014; Arp et al., 2015; MacDonald et al., 2017; Wan et al., 2020). For example, Turner et al. (2014) found that thermokarst lakes in Old Crow Flats, Yukon, with higher evaporation-to-inflow ratios ($E/I$) tended to have smaller $\mathrm{WA}/\mathrm{LA}$ ratios, reflecting the control of watershed area on the amount of inflow a lake receives. Arp et al. (2015) found that lakes in the Alaskan Coastal Plain with bedfast ice became ice-free sooner than lakes with floating ice, causing bedfast lakes to lose more water to evaporation as a result of a longer ice-free season.

In several studies, water isotope (δ¹⁸O and δ²H) analysis has been the primary method used to efficiently characterize the water balance of a large number of thermokarst lakes, as the isotope composition provides an integrated measure of influential hydrological processes (Gibson, 2002; Edwards et al., 2004; Turner et al., 2014; Narancic et al., 2017). Two key metrics of lake water balance modelled using water isotope data include the average isotope composition of lake source waters (δ_I), which can be related to the measured isotope composition of different water sources (Yi et al., 2008), and the ratio of evaporation to inflow ($E/I$) (Gibson et al., 1993). Sampling lake water for isotope analysis multiple times throughout the year provides data to assess the response of lake water balances to different hydrological processes, which can be related to meteorological conditions and compared to lake and watershed attributes. Recently, MacDonald et al. (2017) compared the $E/I$ and δ_I of thermokarst lakes from six regions in northern North America and found a wide range of water balances that were influenced by local meteorological conditions, permafrost extent, and vegetation characteristics. In some locations, such as the Alaskan Coastal Plain, $E/I$ ratios were mostly < 0.2, whereas lakes in the Hudson Bay Lowlands of northeastern Manitoba typically possessed $E/I$ ratios > 0.5, with some lakes trending towards desiccation.

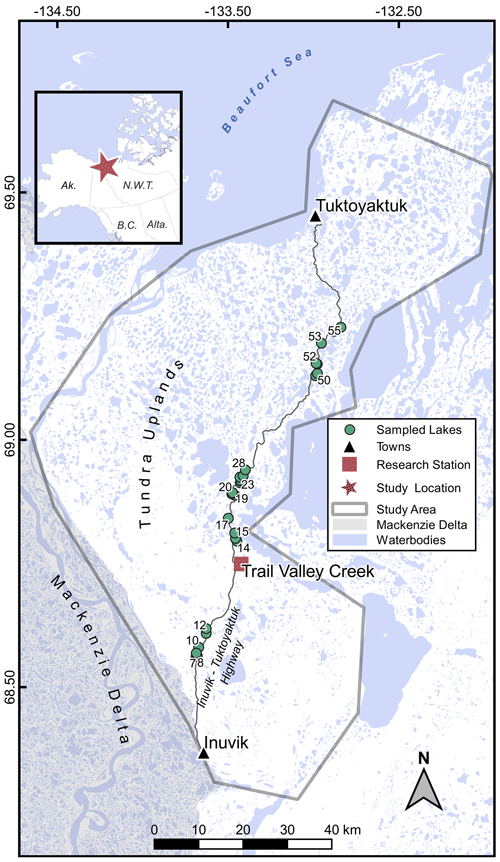
Figure 1 Study area showing the locations of the thermokarst lakes where water samples for isotope analysis were obtained. The study location relative to northwestern North America is shown in the inset map. Not all lakes are labelled on the map, but lakes are numbered sequentially from south to north.

This study aims to evaluate how meteorological conditions, hydrological processes, and lake and watershed attributes influence the δ_I and $E/I$ of lakes located in the tundra uplands east of the Mackenzie Delta in the Northwest Territories, Canada (Fig. 1). A previous study in this region showed that only 5 %–53 % of pre-snowmelt lake water is replaced by freshet on average, because snowmelt bypass leads to minimal mixing between freshet and pre-snowmelt lake water (Wilcox et al., 2022a). Snowmelt bypass occurs when less dense (∼ 0 ^∘C) freshet runoff flows underneath lake ice and passes through a lake without mixing with and replacing the deeper and denser (< 4 ^∘C) lake water (Bergmann and Welch, 1985). With this study, we explore whether snowmelt bypass influences summertime lake water balances, given that thermokarst lakes in other regions are prone to desiccation when they retain little snowmelt (Bouchard et al., 2013). We also investigate how watershed characteristics that have been identified to influence lake water balance in other regions, such as the $\mathrm{WA}/\mathrm{LA}$, influence lake water balances in our study area. We then use the relationship found between the average $E/I$ and watershed characteristics to predict the average $E/I$ for lakes in the region and assess their vulnerability to climate change.

2 Study area

The thermokarst lakes in this study are located in the tundra uplands east of the Mackenzie Delta in the northwest region of the Northwest Territories, Canada (Fig. 1). The landscape is comprised of rolling hills and has been shaped by the thaw of ice-rich permafrost, evidenced by the thousands of thermokarst lakes in the region (Rampton, 1988; Burn and Kokelj, 2009). Hillslopes are well drained by the network of peat channels that facilitate subsurface flow between mineral earth hummocks (Quinton and Marsh, 1998), whereas flatter areas are typically drained by high-centred ice-wedge polygons (Burn and Kokelj, 2009). Vegetation consists of tall-shrub (> 1 m), low-shrub (∼ 0.5 m), and shrub-free land cover types containing lichen, moss, and tussocks (Lantz et al., 2010; Grünberg et al., 2020).

Table 1 Lake and watershed attributes and isotope-derived hydrological indicators for all lakes.

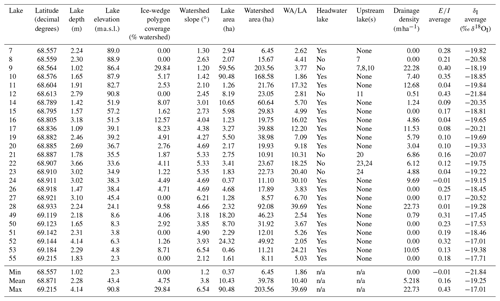
n/a stands for not applicable.

We selected 25 lakes that span a range of watershed sizes (6.45–203.56 ha) and lake surface areas (0.37–90.48 ha), among other characteristics, along a ∼ 70 km stretch of the Inuvik–Tuktoyaktuk Highway (Fig. 1, Table 1). Nineteen of the lakes are headwater lakes and the other six lakes are downstream of other sampled lakes (Table 1). All lakes have a defined outlet channel, and many lakes have defined channelized inflows from their watersheds in the form of small ephemeral streams or ice-wedge polygon troughs.

3 Methods

3.1 Lake water and precipitation sampling and analysis of isotope data

Water samples from the 25 thermokarst lakes were collected on 5 d (1 May, 15 June, 26 July, 2 August, and 3 September) during 2018 for water isotope analysis. Samples were collected on 1 May via a hole augured through the ice in the centre of each lake to capture the pre-snowmelt lake water balance conditions. The 1 May samples also represent the hydrological status of lakes during the freeze-up period of 2017, as virtually no hydrological activity occurs during the winter months due to the complete freezing of the soil and lake surface. Because 1 May water samples were influenced by fractionation that occurred during lake ice formation, the isotope compositions were corrected to represent the isotope composition of the lake before lake ice formation took place (Wilcox et al., 2022a). Lake water samples were corrected for ice fractionation by estimating the fraction of lake water that had been frozen and the corresponding amount of isotopic depletion of lake water that would have occurred assuming the lake was a closed system, following Ferrick et al. (2002). The 15 June was chosen as it marked the first day of the ice-free season for most lakes and was intended to capture the influence of snowmelt bypass; however, the southernmost lakes (lakes 7–12) became ice-free on 7 June, and some of the northernmost lakes (lakes 49–55) became ice-free on 17 June or 18 June. More information about ice correction and the response of lakes to snowmelt bypass is provided by Wilcox et al. (2022a). Next, samples were obtained on 26 July to capture the effects of evaporation and rainfall in the early ice-free season as well as before a large, forecasted rainfall event. Samples were then collected on 2 August to capture the influence of a weeklong rainy period following the sampling date on 26 July. Samples were lastly taken on 3 September to assess the lake water balance response to the relatively rainy and cool August weather prior to freeze-up. The four respective time periods between the five sampling dates are identified as “P1” (1 May to 15 June), “P2” (15 June to 26 July), “P3” (26 July to 2 August), and “P4” (2 August to 3 September).

From 15 June onward, water samples were collected at the shoreline of each lake where water was freely circulating. Samples of end-of-winter snow and ice-free season rainfall were obtained to determine the average isotope composition of rain (δ_R) and snow (δ_S). Snow samples (n = 11) were collected from the region in late April by taking a vertical core of the end-of-winter snowpack using a tube, completely melting the snow in a sealed plastic bag, and then filling a sampling bottle with the melted snow. Rainfall (n = 13) was collected between May and September in Inuvik using a clean high-density polyethylene container, which was then transferred into a sample bottle shortly after precipitation ceased. All samples were stored in 30 mL high-density polyethylene bottles. A Los Gatos Research (LGR) liquid water isotope analyser (model T-LWIA-45-EP) was used to measure the ratio of ${}^{\mathrm{18}}\mathrm{O}{/}^{\mathrm{16}}\mathrm{O}$ and ${}^{\mathrm{2}}\mathrm{H}{/}^{\mathrm{1}}\mathrm{H}$ in each sample at the Environmental Isotope Laboratory at the University of Waterloo (UW-EIL). Each isotope measurement consisted of eight injections of roughly 1000 nL sample volume, with the first two injections being discarded and the remaining six injections averaged to produce the measurement value. All samples were pre-filtered to 0.45 µm into 12 mm × 32 mm septum vials. Every fifth sample was measured a second time to determine the analytical uncertainties, which were ± 0.1 ‰ for δ¹⁸O and ± 0.6 ‰ for δ²H, calculated as 2 standard deviations from the difference between the duplicate samples. Isotope compositions are expressed in standard δ-notation:

$$\begin{array}{}\text{(1)}& {\mathit{\delta }}_{\text{sample}}={\displaystyle \frac{R_{\text{sample}}}{R_{\text{VSMOW}}}}-\mathrm{1},\end{array}$$

where R represents the ratio of ${}^{\mathrm{18}}\mathrm{O}{/}^{\mathrm{16}}\mathrm{O}$ or ${}^{\mathrm{2}}\mathrm{H}{/}^{\mathrm{1}}\mathrm{H}$, and VSMOW represents Vienna Mean Standard Ocean Water. Isotope values are normalized for Standard Light Antarctic Precipitation to δ¹⁸O = −55.5 ‰ and δ²H = −428 ‰ (Coplen, 1996). VSMOW and Vienna Standard Light Antarctic Precipitation (VSLAP) standards provided by LGR (which are calibrated using International Atomic Energy Agency, IAEA, standards) were employed to calibrate the instrument initially, and VSMOW and VSLAP standards were analyzed intermittently throughout the sample run to confirm the accuracy of the instrument.

3.2 Isotope framework, δ_I and $E/I$

The isotope data were initially described and interpreted with respect to an “isotope framework” that consists of two fundamental linear relationships that form when isotope data are plotted with δ¹⁸O on the x axis and δ²H on the y axis (“δ¹⁸O–δ²H space”). Globally, there is a strong linear correlation between δ¹⁸O and δ²H in meteoric water, with isotope compositions of precipitation plotting close to the Global Meteoric Water Line (GMWL, δ²H = 8.0 ⋅ δ¹⁸O + 10; Craig, 1961). However, the slope and intercept of a meteoric water line can vary for precipitation collected locally. The local meteoric water line (LMWL) represents the expected isotope composition of precipitation in a region. We estimated the LMWL for Inuvik using a linear regression through rainfall and snowfall isotope compositions. The average isotope compositions of rainfall (δ_R) and snowfall (δ_S) were calculated by averaging the isotope composition of all the rainfall and snowfall samples that we collected, respectively, with δ_P representing the average of δ_S and δ_R. The LMWL equation that we derived was δ²H = 7.1 ⋅ δ¹⁸O − 10, which is similar to the LMWL derived by Fritz et al. (2022), who used precipitation samples collected between 2015 and 2018 in Inuvik and estimated the Inuvik LMWL to be δ²H = 7.4 ⋅ δ¹⁸O − 6.7. Both of these LMWLs compare closely with the LMWL derived from the Global Network of Isotopes in Precipitation (GNIP) data set, which is comprised of precipitation samples in Inuvik between 1986 and 1989 and gives an LMWL of δ²H = 7.3 ⋅ δ¹⁸O − 3.6 (IAEA/WMO, 2023). We considered using the LMWL, δ_S, δ_P, and δ_R values produced by Fritz et al. (2022); however, we decided to use the LMWL that we developed because it more closely represented the input waters during the study period, and the δ_S, δ_P and δ_R values derived by Fritz et al. (2022) were close to the values that we obtained.

Evaporated waterbodies tend to plot along a local evaporation line (LEL), which can be defined independent of measured lake water isotope compositions. Using this approach and for the case of a lake fed by waters of mean annual isotope composition of precipitation, the LEL was anchored at δ_P and at the maximum isotopic enrichment that can be achieved for a given set of environmental conditions (δ^∗), which is dependent on air temperature, relative humidity, and the isotope composition of atmospheric moisture in the region (Gonfiantini, 1986). Along the LEL, a useful reference point exists at which the amount of evaporation that a waterbody is experiencing is equal to the amount of water input, defined as δ_SSL (steady-state lake water isotope composition of a terminal basin; Yi et al., 2008). When lake water isotope compositions are plotted in δ¹⁸O–δ²H space, they typically plot near the LEL, with more evaporated lakes plotting closer to δ^∗ and less evaporated lakes plotting closer to δ_P. Lakes preferentially sourced by rainfall will tend to plot above the LEL, whereas lakes preferentially influenced by snowmelt will tend to plot below the LEL, owing to the normally distinctive isotope composition of rainfall and snowmelt (Tondu et al., 2013).

Isotope compositions of the lakes were used to estimate the average isotope composition of source water (δ_I, or δ¹⁸O_I when referring to just δ¹⁸O). We followed the coupled isotope tracer method introduced by Yi et al. (2008) which has been applied in a variety of northern locations (Turner et al., 2014; MacDonald et al., 2017; Remmer et al., 2020). Calculating δ_I using the approach of Yi et al. (2008) involves generating a lake-specific evaporation line for each lake water isotope composition. This approach assumes that all lakes tend towards δ^∗ as they evaporate, and the lake-specific evaporation line is defined as the line that intersects the lake water isotope composition and δ^∗ in δ¹⁸O–δ²H space. δ_I is then calculated as the point of intersection between a lake-specific evaporation line and the LMWL.

We used these δ_I values to calculate the ratio of evaporation to inflow ($E/I$):

$$\begin{array}{}\text{(2)}& E/I={\displaystyle \frac{{\mathit{\delta }}_{\mathrm{I}}-{\mathit{\delta }}_{\mathrm{L}}}{{\mathit{\delta }}_{\mathrm{E}}-{\mathit{\delta }}_{\mathrm{L}}}},\end{array}$$

where δ_L is the isotope composition of the lake water and where δ_E is the isotope composition of evaporated vapour from the lake (Gonfiantini, 1986). More detailed information about the calculation of the isotope framework components, δ_I, and $E/I$ is provided in Appendix A.

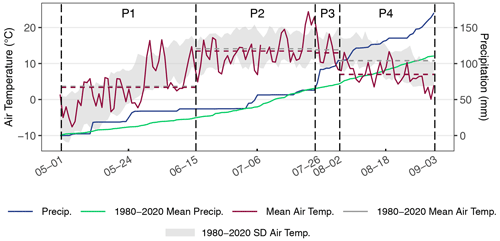
Figure 2 Air temperature and cumulative precipitation during the sampling period and the 1980–2020 mean, as recorded at Inuvik (WMO ID: 71364) (Fig. 1). Meteorological data were retrieved from Environment and Climate Change Canada (2019). The 5 respective days on which water samples were taken from lakes are shown by the vertical dashed lines. The respective periods between the sampling dates are labelled P1, P2, P3, and P4. Mean daily air temperature for 2018 and 1980–2020 for each period is indicated by the horizontal dashed lines.

3.3 Meteorological conditions and lake and watershed attributes

The end-of-winter snowpack at Trail Valley Creek contained 141 mm of snow water equivalent, similar to the 1991–2019 mean of 147 mm (Marsh et al., 2019). Air temperature at Inuvik was within 1 ^∘C of the long-term mean during P1, P2, and P3, but P4 was 3.8 ^∘C cooler than the long-term mean (Fig. 2). P1 and P2 experienced a total rainfall amount of 72.9 mm, close to the long-term mean of 66.0 mm for this period, while P3 and P4 experienced 107.3 mm of rainfall, more than double the long-term mean of 45.0 mm for this period (Fig. 2).

Multiple lake and watershed attributes for each lake were quantified for comparison with δ_I and $E/I$. Lake-specific properties included lake surface area, depth, latitude, and elevation, while watershed-specific properties included watershed surface area, mean hillslope angle, drainage density, vegetation cover, and ice-wedge polygon coverage (Table 1). Within each watershed, the areas of ice-wedge polygons were identified visually from satellite imagery and digitized manually. Drainage density was calculated as the length of all flow paths with a contributing area greater than 5000 m² and then divided by the total area of the watershed. A threshold of 5000 m² was chosen as this was roughly the threshold when water tracks became visible in optical satellite images. Vegetation height in each watershed was quantified using the remote sensing vegetation height product produced by Bartsch et al. (2020), which provides vegetation height at a 20 m spatial resolution with a root-mean-square error (RMSE) of 45 cm in vegetation height. All spatial analysis was carried out using ArcMap 10.7.1 (Esri, 2019).

To evaluate whether lake and watershed properties were correlated with lake water balance metrics derived from water isotope data, linear regressions between lake and watershed properties and $E/I$ and δ_I were tested. Only correlations where p < 0.01 were considered significant. The distribution of each variable was plotted on a histogram, and data were mathematically transformed if the distribution was non-uniform. Statistical analysis was performed using R 4.1.0 (R Core Team, 2021).

A correlation was identified between the $\mathrm{WA}/\mathrm{LA}$ and average $E/I$ (R² = 0.82), and we used this relationship to predict the average $E/I$ for lakes in the region with areas > 0.25 ha (n = 7454; Fig. 1). Watershed area was estimated, including the 25 lakes sampled for isotope composition, by applying the D8 water routing algorithm (O'Callaghan and Mark, 1984) to the 2 m resolution digital elevation model ArcticDEM (PGC, 2018). The $\mathrm{WA}/\mathrm{LA}$ ratio was calculated for each lake by dividing the total watershed area by the total area of the lake(s) in the watershed. In rare cases, watersheds were not delineated accurately and part of the watershed was clipped to the lake boundary due to slight offsets between the lake layer and ArcticDEM. We rejected all watersheds where $\mathrm{WA}/\mathrm{LA}$ < 1.5, as all watersheds that we inspected which met this criteria were improperly delineated due to the offset error described. After rejecting all watersheds where $\mathrm{WA}/\mathrm{LA}$ < 1.5, a total of 7340 watersheds remained.

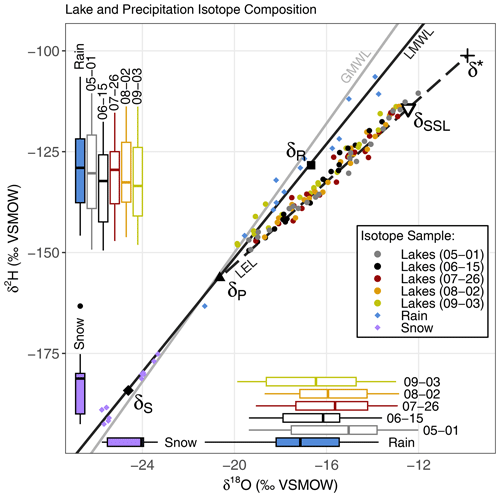
Figure 3 Isotope values for all lake and precipitation samples, with their respective ranges along each axis illustrated by box plots, plotted in δ¹⁸O–δ²H space, as deviations (in ‰) from Vienna Standard Mean Ocean Water (VSMOW). The local meteoric water line (LMWL, solid black line, δ²H = 7.1 ⋅ δ¹⁸O − 10.0) is calculated as a regression through snow samples collected throughout the study region and rain samples collected from Inuvik in 2018 (n=24). The average isotope composition of end-of-winter snow samples (δ_S), rainfall samples (δ_R), and the average of δ_S and δ_R (δ_P) are labelled along the LMWL. The local evaporation line (LEL, dashed dark grey line), the global meteoric water line (GMWL, solid light grey line), the maximum isotopic enrichment possible for a waterbody (δ^∗), and the point at which evaporation is equal to inflow ($E/I$ = 1, δ_SSL) are added for reference.

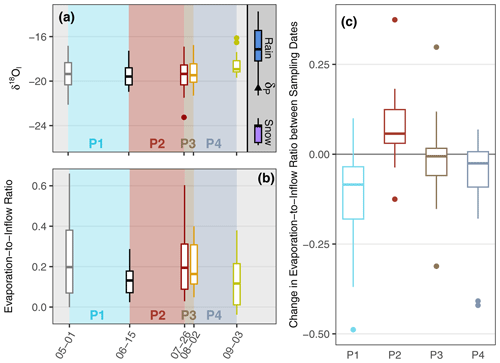
Figure 4 (a) The distribution of δ¹⁸O_I for each sampling date (in month–day format on the x axis) with the rain and snow isotope compositions for reference. (b) The distribution of $E/I$ values at all lakes across the five sampling dates. (c) The lake-specific change in the $E/I$ between the sampling dates was calculated as $\mathrm{\Delta }[E/I]$ = $[E/I{]}_{t_{\mathrm{2}}}^{\text{Ln}}-[E/I{]}_{t_{\mathrm{1}}}^{\text{Ln}}$, where Ln represents a specific lake and t represents a sampling date.

Table 2 Significant correlations between δ¹⁸O_I, $E/I$, and explanatory variables. In cases where there are multiple explanatory variables, the p values for each respective explanatory variable are listed. The adjusted R² was used in order to control for the tendency of R² to increase as explanatory variables are added to a model (Yin and Fan, 2001). The adjusted R² was calculated as $R_{\text{adj}}^{\mathrm{2}}$ = $\mathrm{1}-(\mathrm{1}-R^{\mathrm{2}})\cdot \left(\right(n-\mathrm{1})/(n-m-\mathrm{1}\left)\right)$, where n is the sample size and m is the number of explanatory variables. p values > 0.05 are italicized.

4 Results

4.1 Seasonal evolution of lake water balances

In general, we observed distinct shifts in lake water isotope composition, δ¹⁸O_I, and $E/I$ between sampling dates. Shifts in the $E/I$ between sampling dates were often more pronounced than shifts in δ¹⁸O_I. During P1 (1 May to 15 June), δ¹⁸O decreased from a median of −15.04 ‰ (−17.53 ‰ to −13.81 ‰ interquartile range, IQR) to −16.15 ‰ (−17.89 ‰ to −15.43 ‰ IQR) and δ²H values decreased from −130.35 ‰ (−139.08 ‰ to −120.88 ‰ IQR) to −132.27 ‰ (−142.41 ‰ to −125.77 ‰ IQR) (Fig. 3). At the same time, the range of δ¹⁸O_I values decreased and the median decreased slightly from −19.36 ‰ (−20.33 ‰ to −18.34 ‰ IQR) to −19.59 ‰ (−20.34 ‰ to −18.81 ‰ IQR) (Fig. 4a). The median (and range) of $E/I$ values also decreased during P1 from 0.20 (0.07 to 0.38 IQR) to 0.13 (0.07 to 0.18 IQR) (Fig. 4b). The median change in the $E/I$ was −0.08 (Fig. 4c). The reduction in $E/I$ values that occurred during P1 was larger than in any other period (Fig. 4c).

During P2 (15 June to 26 July), lake water isotope values increased slightly. The median δ¹⁸O increased from −16.15 ‰ (−17.89 ‰ to −15.43 ‰ IQR) to −15.63 ‰ (−17.33 ‰ to −14.22 ‰ IQR) and the median δ²H increased from −132.27 ‰ (−142.41 ‰ to −125.77 ‰ IQR) to −129.50 ‰ (−137.90 ‰ to −124.99 ‰ IQR) (Fig. 3). During P2, δ¹⁸O_I increased slightly from −19.59 ‰ (−20.34 ‰ to −18.81 ‰ IQR) to −19.35 ‰ (−20.34 ‰ to −18.55 ‰ IQR) (Fig. 4a). The median $E/I$ ratio increased from 0.13 (0.07 to 0.18 IQR) to 0.19 (0.09 to 0.31 IQR) (Fig. 4b). The median increase in the $E/I$ was 0.06 (0.03 to 0.12 IQR), although three lakes experienced a decrease in the $E/I$ (Fig. 4c).

Lake water isotope values decreased marginally during P3 (26 July to 2 August). Median δ¹⁸O decreased from −15.63 ‰ (−17.33 ‰ to −14.22 ‰ IQR) to −15.94 ‰ (−17.16 ‰ to −14.24 ‰ IQR) and median δ²H decreased from −129.50 ‰ (−137.90 ‰ to −124.99 ‰ IQR) to −132.60 ‰ (−137.51 ‰ to −122.68 ‰ IQR) (Fig. 3). The $E/I$ and δ¹⁸O_I values also shifted minimally during P3. Median δ¹⁸O_I decreased from −19.35 ‰ (−20.33 ‰ to −18.55 ‰ IQR) to −19.47 ‰ (−20.10 ‰ to −18.45 ‰ IQR) (Fig. 4b). The median change in the $E/I$ was −0.01 (−0.06 to 0.02 IQR), with a near-equal number of lakes experiencing an increase or decrease in the $E/I$ (Fig. 4c).

During P4 (2 August to 3 September), median δ¹⁸O values decreased from −15.94 ‰ (−17.16 ‰ to −14.24 ‰ IQR) to −16.55 ‰ (−18.65 ‰ to −15.00 ‰ IQR) and δ²H values decreased from −132.60 ‰ (−137.51 ‰ to −122.68 ‰ IQR) to −133.49 ‰ (−140.94 ‰ to −123.94 ‰ IQR) (Fig. 3). On 3 September, some lakes plotted close to the LMWL, indicating that their waters had experienced negligible amounts of evaporation (Fig. 3). The median δ¹⁸O_I values increased from −19.47 ‰ (−20.10 ‰ to −18.45 ‰ IQR) to −18.94 ‰ (−19.18 ‰ to −18.14 ‰ IQR) and the range of values narrowed and became more similar to rain (Fig. 4a). Median $E/I$ values returned to values similar to those on 15 June by the end of P4, decreasing to a median of 0.11 (0.00 to 0.21 IQR) (Fig. 4b). Two-thirds of the lakes experienced a decrease in the $E/I$, and the median change in the $E/I$ was −0.03 (−0.09 to 0.01 IQR) (Fig. 4c).

4.2 Correlation analysis between lake and watershed attributes and lake water balance metrics

Variability among lakes with respect to the average $E/I$ and δ¹⁸O_I was partially explained by statistically significant relationships with lake and watershed properties. The average $E/I$ was negatively correlated with the $\mathrm{WA}/\mathrm{LA}$ (p < 0.0001; Table 2, Fig. 5a) and average watershed slope (p = 0.0085; Table 2) and was positively correlated with the log of lake surface area (p < 0.0001; Table 2). Thus, lakes that had higher $E/I$ values tended to have a relatively smaller watershed size, a flatter watershed, and be larger in surface area. When these three variables are combined into a linear model, only the $\mathrm{WA}/\mathrm{LA}$ remained a significant predictor of the average $E/I$ (p = 0.0002), whereas lake area (p = 0.1949) and average watershed slope (p = 0.8472) became insignificant effects (Table 2). Both lake surface area and average watershed slope were correlated with the $\mathrm{WA}/\mathrm{LA}$ (Table 2). For the relationship between the average $E/I$ and $\mathrm{WA}/\mathrm{LA}$, the majority of downstream lakes were outliers, having higher than typical $E/I$ ratios for a given $\mathrm{WA}/\mathrm{LA}$ as they inherited evaporated waters from upstream waterbodies (Fig. 5a).

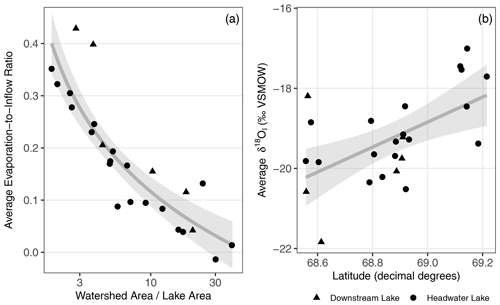
Figure 5 (a) Relationship between the average evaporation-to-inflow ratio ($E/I$) and ratio of watershed area to lake area ($\mathrm{WA}/\mathrm{LA}$) for sampled lakes. The grey line represents a line of best fit between the $\mathrm{WA}/\mathrm{LA}$ and the average $E/I$ ratio, such that y=log(x), with the 95 % confidence interval shown in grey shading (R² = 0.74, p < 0.0001). Note the logarithmic x axis. (b) The relationship between latitude and δ_I. The grey line represents a linear line of best fit between δ_I and latitude, with the 95 % confidence interval shown in grey shading (R² = 0.30, p = 0.0027).

Average δ¹⁸O_I was only correlated with two attributes: lake elevation (p = 0.0029) and latitude (p = 0.0027) (Table 2). Lakes at lower elevations and higher latitudes tended to have higher δ¹⁸O_I values (Fig. 5b). Lake elevation and latitude are also nearly perfectly correlated (R² = 0.97; Table 2), with lake elevation decreasing as latitude increases.

5 Discussion

5.1 Influence of meteorological conditions on lake water balances

Water isotope measurements from five discrete time points provide context for characterizing the seasonal evolution of thermokarst lake water balances as a series of phases in relation to meteorological conditions and influential hydrological processes (Fig. 6). A previous study at many of the same lakes by Wilcox et al. (2022a) observed the presence of snowmelt bypass (Henriksen and Wright, 1977; Hendrey et al., 1980; Bergmann and Welch, 1985) during the freshet phase (P1; Fig. 6). Initial snowmelt runoff flowing into lakes did not mix with water underneath lake ice because the ∼ 0 ^∘C snowmelt runoff was less dense than the deeper, warmer waters beneath the lake ice, causing it to flow into and out of lakes without mixing with lake water. This resulted in a much smaller reduction in the $E/I$ than would have occurred if freshet runoff was able to mix with the entire lake water column. While snowmelt bypass does limit the recharge of lake waters during the freshet phase, the sheer volume of snowmelt runoff and the lack of evaporation due to lake ice cover appear to compensate for the impact of snowmelt bypass and result in a greater reduction in the $E/I$ than any other phase (Fig. 4c).

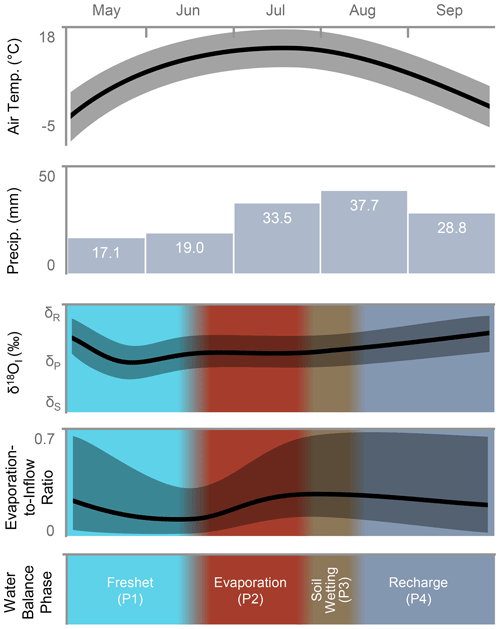
Figure 6 A simplified conceptual diagram comparing meteorological conditions and the response of the δ¹⁸O_I and $E/I$ used to designate water balance phases. Air temperature and precipitation data represent average values from 1980 to 2020 (Environment and Climate Change Canada, 2019). Shaded areas around the δ¹⁸O_I and $E/I$ lines represent the potential variability caused by lake and watershed attributes or meteorological conditions.

During the freshet phase, δ¹⁸O_I shifted towards the value of δ_P and not towards δ_S, even though minimal rainfall fell during the period (Fig. 2) and snowmelt runoff was flowing into lakes. Wilcox et al. (2022a) determined that the soil had begun to thaw by the time snowmelt runoff could mix with lake waters and, thus, allowed snowmelt runoff to mix with soil water from the previous year before flowing into lakes. This resulted in a post-snowmelt δ¹⁸O_I that was a mixture of snow-sourced and rain-sourced water (Fig. 4a). As only a small amount of snow-sourced water was incorporated into lakes during the freshet phase, the δ¹⁸O_I of lakes remained primarily rain-sourced throughout the entire study period (Fig. 4a).

The evaporation phase (P2; Fig. 6) was characterized by minimal change in δ¹⁸O_I (Fig. 4a) and rising $E/I$ ratios at nearly all lakes (Fig. 4c), caused by the relatively dry and warm conditions that are typical of this region. Previous water balance studies conducted in this region also found that lake evaporation rates were higher as a result of substantial incoming solar radiation in June and July, compared with August and September, and when inflow is minimal due to low precipitation (Marsh and Bigras, 1988; Pohl et al., 2009).

During the brief soil wetting phase (P3; Fig. 6), there was minimal change in the δ¹⁸O_I (Fig. 4a) and $E/I$ (Fig. 4b) despite the 41.2 mm of rainfall, which represented 25 % of the rainfall during the study period. This evidence suggests that little runoff was generated by this event and that rainfall which fell directly on lakes had only a minor effect on lake water balances. We hypothesize that dry conditions preceding the rainfall event allowed soils to absorb the rainfall without becoming saturated enough to generate much lateral flow. The lack of runoff in response to this rainfall event is expected given that antecedent soil moisture conditions have been observed to greatly influence the efficiency of runoff generation from rainfall events in areas underlain by continuous permafrost (Roulet and Woo, 1988; Kane et al., 1998; Favaro and Lamoureux, 2014; Stuefer et al., 2017). As the first half of the summer is typically drier than the second half (Fig. 6), soils generally experience drying throughout the first half of the summer before becoming rewetted.

The recharge phase (P4; Fig. 6) was defined by the δ¹⁸O_I of lakes becoming more similar to rainfall (Fig. 4a) and the $E/I$ ratios decreasing to values similar to the beginning of the freshet phase (Fig. 4b). The recharge phase of 2018 experienced temperatures that were 3.8 ^∘C lower than average and 66.1 mm of precipitation, exceeding the long-term mean of 37.2 mm (Fig. 2). Given the lower air temperatures, it is likely that evaporation rates also decreased and contributed to the decrease in $E/I$. As the meteorological conditions were wetter and cooler than the long-term means, we expect the water balance conditions of the recharge phase captured in 2018 to be more representative of a later sampling date during a more normal climate year (e.g., late September). The $E/I$ ratios on 1 May were greater than 3 September, suggesting that lakes received less inflow during the recharge phase in 2017 than in 2018 (Fig. 4b).

Findings from previous studies of thermokarst lakes in this region imply that the four phases of lake water balance that we observed are typical of this region. The four phases of seasonal water balance evolution that we identified (freshet, evaporation, soil wetting, and recharge) roughly follow the pattern of seasonal changes in lake surface area observed by Cooley et al. (2019), who analyzed near-weekly satellite imagery of a large region which encompassed the lakes that we studied. Cooley et al. (2019) observed initial decreases in total lake surface area during the evaporation phase, followed by stabilizing or increasing trends in lake surface area by the end of August. Additionally, Pohl et al. (2009) modelled the water balance for a single lake in our study region across a 30-year period and identified that the maximum lake level was most likely to occur in early June or late August–early September, corresponding to the start of the evaporation phase and the end of the recharge phase.

In comparison to the five thermokarst lake regions examined in a synthesis of isotope data by MacDonald et al. (2017), the relatively low $E/I$ ratios and rainfall-like δ¹⁸O_I values found at our study lakes compare most closely to lakes in the Alaskan Coastal Plain (ACP), where the majority of lakes also have an $E/I$ < 0.25 and a δ¹⁸O_I similar to rain. This region is cooler during the summer and has a shorter ice-free season (Arp et al., 2015) than our study region, but it receives less precipitation and is more lake-rich (MacDonald et al., 2017), suggesting lakes likely have smaller watersheds than in our study region. The cooler and shorter summers in the ACP, which decrease evaporation, may be offset by smaller watersheds and less precipitation, which decrease inflow, leading to similar $E/I$ values to those for our study region. Our lakes differed from the more nearby Old Crow Flats (OCF), where most lakes have an $E/I$ between 0.25 and 0.75 but have a smaller $\mathrm{WA}/\mathrm{LA}$ of ∼ 3, whereas the average $\mathrm{WA}/\mathrm{LA}$ of lakes that we sampled was 9.5 (Table 1). The OCF differs from our study region in that it is situated in a post-glacial lake bed underlain by fine-grained glaciolacustrine sediments (Hughes, 1972), resulting in a relatively flat landscape with a poorer ability to convey runoff in comparison with our study region, where rolling hills are well drained by networks of peat channels with high hydraulic conductivity (Quinton and Marsh, 1998). These differences between the OCF and our study region may explain the greater $E/I$ values at the former; however, our study year was cooler and wetter than average, which may also have contributed to the comparatively low $E/I$ ratios.

5.2 Effects of lake and watershed attributes on $E/I$

While shifts in the $E/I$ over time can be attributed to changing meteorological conditions and hydrological processes, differences in the $E/I$ among lakes can be further explained by lake and watershed attributes. Most of the variability in the average $E/I$ among lakes can be explained by the $\mathrm{WA}/\mathrm{LA}$ (R² = 0.74; Fig. 5a), as lakes with a smaller $\mathrm{WA}/\mathrm{LA}$ likely receive less inflow and have greater $E/I$ ratios as a result. A similar inverse relationship between the $E/I$ ratios and $\mathrm{WA}/\mathrm{LA}$ has also been observed in OCF (Turner et al., 2014) and the taiga-shield of the Northwest Territories (Gibson and Edwards, 2002). Four of the six downstream lakes that we sampled had anomalously high $E/I$ ratios compared with their $\mathrm{WA}/\mathrm{LA}$ (Fig. 5a). Downstream lakes receive evaporated inflow from their upstream lakes, which is then evaporated further in the downstream lake, producing an enhanced $E/I$ ratio. When downstream lakes are removed from the regression between $E/I$ and $\mathrm{WA}/\mathrm{LA}$, the R² improves from 0.74 to 0.82.

We estimated the $E/I$ for lakes in the study area using the strong relationship between the average $E/I$ and $\mathrm{WA}/\mathrm{LA}$. This was done by delineating the watersheds of lakes larger than 0.25 ha in the study area (Fig. 1) and applying the fitted regression between $\log \left(\mathrm{WA}/\mathrm{LA}\right)$ and the average $E/I$ for the headwater lakes that we sampled:

$$\begin{array}{}\text{(3)}& \text{average }E/I=-\mathrm{0.10867}\cdot \log \left(\mathrm{WA}/\mathrm{LA}\right)+\mathrm{0.37007}.\end{array}$$

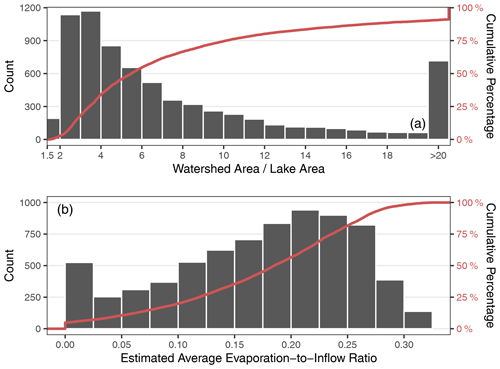
Figure 7 Distribution of (a)  the ratio of watershed area to lake area ($\mathrm{WA}/\mathrm{LA}$) and (b) evaporation to inflow ($E/I$) for 7340 lakes and their watersheds in the study area. Average $E/I$ is estimated using the relationship with the $\mathrm{WA}/\mathrm{LA}$ of headwater lakes. Note that the leftmost bin in panel (a) is only half the width of other bins, reflecting the rejection of all $\mathrm{WA}/\mathrm{LA}$ < 1.5 that we applied when filtering the data.

The resulting histogram of the average $E/I$ (Fig. 7b) is primarily skewed towards larger values, because the $\mathrm{WA}/\mathrm{LA}$ is skewed towards smaller values (Fig. 7a). An average $E/I$ between 0.2 and 0.225 is most common for lakes, indicating that the lakes are dominated by inflow. At $\mathrm{WA}/\mathrm{LA}$ > 30, the estimated $E/I$ becomes 0; as a result, 7 % of lakes are predicted to have an average $E/I$ of 0 (Fig. 7b). None of the lakes appear to be approaching desiccation.

We note that this distribution of $E/I$ values is dependent on the timing of our water sampling, the meteorological conditions during the study period, and the properties of the lakes that we selected. For example, the median lake depth of 34 lakes sampled in this region by Pienitz et al. (1997) was 3.0 m, similar to the lakes that we measured (Table 1); however, some lakes sampled by Pienitz et al. (1997) were up to 18.5 m in depth. The relationship that we derived between $\mathrm{WA}/\mathrm{LA}$ and $E/I$ is likely weaker for deeper lakes than sampled in our study, as lake surface area becomes less representative of lake volume when a wider range of lake depths are included. In that case, calculating the ratio of lake volume to watershed area could be a better predictor of $E/I$ ratios.

We hypothesize that the hydrological response of lakes in this region to climate change will be strongly influenced by their $\mathrm{WA}/\mathrm{LA}$. Recent predictions of future Arctic precipitation indicate greater rainfall, greater snowfall, and more annual precipitation overall (Brown and Mote, 2009; Bintanja and Andry, 2017; Bintanja et al., 2020); in the OCF, increased rainfall is already reducing lake $E/I$ ratios (MacDonald et al., 2021). Under wetter conditions, we would expect that $E/I$ ratios would decrease for all lakes and that the threshold where average $E/I$ = 0 would also decrease. The logarithmic nature of the relationship between the $\mathrm{WA}/\mathrm{LA}$ and $E/I$ indicates that the average $E/I$ is more sensitive to changes in inflow as the $\mathrm{WA}/\mathrm{LA}$ decreases. Therefore, we expect that lakes with a smaller $\mathrm{WA}/\mathrm{LA}$ would experience greater reductions in the average $E/I$ under a wetter future climate. We also hypothesize that lakes with a larger $\mathrm{WA}/\mathrm{LA}$ could be more vulnerable to rapid lake drainage because they receive more inflow and likely experience greater fluctuations in lake level as a result; rapid drainage is typically triggered when extremely high water levels lead to the rapid thermomechanical erosion of a new lake outlet (Mackay, 1988; Brewer et al., 1993; Turner et al., 2010).

Alternatively, climate change may lead to a drier future for lakes, as ice-free periods lengthen, higher air temperatures increase evaporation, and permafrost thaw leads to landscape drying (Walvoord and Kurylyk, 2016; Koch et al., 2022; Webb and Liljedahl, 2023). A combination of such conditions has already caused lake contraction in western Greenland (Finger Higgens et al., 2019). If drier conditions prevail, given the logarithmic nature of the relationship between the $\mathrm{WA}/\mathrm{LA}$ and average $E/I$, we expect that lakes with a smaller $\mathrm{WA}/\mathrm{LA}$ will experience greater increases in the average $E/I$. If future climate change causes sufficiently dry conditions to bring about lake desiccation, a large number of lakes in the study area could potentially be affected, given that the distribution of the $\mathrm{WA}/\mathrm{LA}$ in the region is skewed towards smaller $\mathrm{WA}/\mathrm{LA}$ values, with many lakes possessing a $\mathrm{WA}/\mathrm{LA}$ < 4 (Fig. 7a). The “drier future” scenario may not necessarily lead to lake desiccation, given that all $E/I$ ratios that we estimated were < 1; however, the portion of precipitation converted into runoff can be halved during dry periods when compared with wetter periods (Stuefer et al., 2017), further reducing runoff to lakes.

Future studies could build on our hypothesis that the $\mathrm{WA}/\mathrm{LA}$ will mediate the response of lakes to climate change by comparing past changes in lake surface area, via remote sensing and paleohydrological analyses, with the $\mathrm{WA}/\mathrm{LA}$. During drier periods, we would expect that lakes with a smaller $\mathrm{WA}/\mathrm{LA}$ would experience greater reductions in lake surface area than lakes with a larger $\mathrm{WA}/\mathrm{LA}$. Previous studies from this region have already found that lakes' surface area changes in response to seasonal (Cooley et al., 2019) and multi-year (Plug et al., 2008) shifts in precipitation, indicating that changes to lake water balances can be observed by tracking changes in water surface area.

6 Conclusions

Water isotope-derived metrics were used to derive distinct seasonal phases of lake water balances for 25 thermokarst lakes in the tundra uplands east of the Mackenzie Delta (Northwest Territories, Canada). The freshet phase saw lakes experience a reduction in the $E/I$ and a shift in δ_I values towards δ_P, as a mixture of soil water and snowmelt-sourced freshet entered lakes and evaporation was minimal due to lake ice cover. Following this period was the evaporation phase, during which minimal precipitation and warm and sunny conditions led to increasing $E/I$ ratios and no change in δ_I. Then, a brief and intense period of rainfall led to minimal response in the $E/I$ and δ_I at lakes, as dry soils absorbed most of the precipitation during the soil wetting phase. In the final stages of summer during the recharge phase, air temperatures declined and precipitation was unseasonably high, causing reductions in the $E/I$ and a shift in δ_I towards δ_R as lakes received increased runoff from their watersheds and evaporation rates were reduced.

Comparison of water isotope-derived lake water balance components with lake and watershed attributes shows that the $\mathrm{WA}/\mathrm{LA}$ explains the majority of variability in the $E/I$ among lakes. The strong relationship between the average $E/I$ and $\mathrm{WA}/\mathrm{LA}$ allowed us to predict the average $E/I$ for 7340 lakes in the study region. The predicted average $E/I$ values were low compared with other regions of thermokarst lakes, only reaching 0.33, indicating that lakes are not currently close to being at risk of desiccation. We hypothesize that lakes with a larger $\mathrm{WA}/\mathrm{LA}$ will be more prone to rapid drainage if future conditions are wetter.

Few studies have directly investigated the influence of the $\mathrm{WA}/\mathrm{LA}$ on $E/I$ (Gibson and Edwards, 2002; Turner et al., 2014); however, given the strong relationship that we found, the $\mathrm{WA}/\mathrm{LA}$ could serve as a useful metric in other permafrost environments for characterizing thermokarst lake water balances and predicting the vulnerability of lakes to climate change. The non-uniform response of lake surface area to past climate change (Smith et al., 2005; Plug et al., 2008; Arp et al., 2011; Jones et al., 2011; Andresen and Lougheed, 2015) may also be explained by the $\mathrm{WA}/\mathrm{LA}$; future studies could investigate whether lakes with a smaller $\mathrm{WA}/\mathrm{LA}$ are more likely to decrease in surface area than lakes with a larger $\mathrm{WA}/\mathrm{LA}$. Further associations between the $\mathrm{WA}/\mathrm{LA}$ and biogeochemical properties of lakes may also exist, as the $E/I$ has been linked to the biogeochemistry of a wide range of lakes, from tropical to tundra environments (Kosten et al., 2009).

Appendix A: Isotope framework

The calculation of the point of maximum evaporative isotopic enrichment, or the isotope composition of lake at the point of desiccation (δ^∗), was carried out as follows (Gonfiantini, 1986):

$$\begin{array}{}\text{(A1)}& {\mathit{\delta }}^{\ast }={\displaystyle \frac{h\cdot {\mathit{\delta }}_{\mathrm{As}}+{\mathit{\epsilon }}_{\mathrm{k}}+({\mathit{\epsilon }}^{\ast }/{\mathit{\alpha }}^{\ast })}{h-{\mathit{\epsilon }}_{\mathrm{k}}-({\mathit{\epsilon }}^{\ast }/{\mathit{\alpha }}^{\ast })}}.\end{array}$$

Here, α^∗ is the fractionation factor between the liquid and vapour phase of water, and ε^∗ and ε_k are the respective equilibrium and kinetic separation terms, with ε^∗ serving as a convenient expression of α^∗, where ${\mathit{\epsilon }}^{\ast }={\mathit{\alpha }}^{\ast }-\mathrm{1}$. The term h represents the relative humidity for the ice-free season (see below). Equilibrium fractionation (α^∗) was calculated following equations from Horita and Wesolowski (1994):

$$\begin{array}{}\text{(A2)}& \begin{array}{rl}\mathrm{1000}\ln \cdot {\mathit{\alpha }}^{\ast }& =-\mathrm{7.685}+\mathrm{6.7123}\cdot {\displaystyle \frac{{\mathrm{10}}^{\mathrm{3}}}{T}}-\mathrm{1.6664}\cdot {\displaystyle \frac{{\mathrm{10}}^{\mathrm{6}}}{T^{\mathrm{2}}}}\\ & +\mathrm{0.35041}\cdot {\displaystyle \frac{{\mathrm{10}}^{\mathrm{9}}}{T^{\mathrm{3}}}}\end{array}\end{array}$$

for δ¹⁸O, and

$$\begin{array}{}\text{(A3)}& \begin{array}{rl}\mathrm{1000}\ln \cdot {\mathit{\alpha }}^{\ast }& =\mathrm{1158.8}\cdot {\displaystyle \frac{T^{\mathrm{3}}}{{\mathrm{10}}^{\mathrm{9}}}}-\mathrm{1620.1}\cdot {\displaystyle \frac{T^{\mathrm{2}}}{{\mathrm{10}}^{\mathrm{6}}}}+\mathrm{794.84}\\ & \cdot {\displaystyle \frac{T}{{\mathrm{10}}^{\mathrm{3}}}}-\mathrm{161.04}+\mathrm{2.9992}\cdot {\displaystyle \frac{{\mathrm{10}}^{\mathrm{9}}}{T^{\mathrm{3}}}}\end{array}\end{array}$$

for δ²H. Here, T represents the temperature of the interface (K) (see below). The kinetic separation term ε_k was calculated as follows:

$$\begin{array}{}\text{(A4)}& {\mathit{\epsilon }}_{\mathrm{k}}=x\cdot (\mathrm{1}-h),\end{array}$$

where x=0.0142 for δ¹⁸O and x=0.0125 for δ²H (Gonfiantini, 1986). δ_As represents the isotope composition of atmospheric vapour, which we assume is in equilibrium with the isotope composition of summertime precipitation (δ_Ps; Gibson and Edwards, 2002). We can therefore estimate δ_As as follows:

$$\begin{array}{}\text{(A5)}& {\mathit{\delta }}_{\mathrm{As}}=\left({\mathit{\delta }}_{Ps}-{\mathit{\epsilon }}^{\ast }/{\mathit{\alpha }}^{\ast }\right).\end{array}$$

The reference point of when $E/I$ = 1 (δ_SSL) was calculated using

$$\begin{array}{}\text{(A6)}& {\mathit{\delta }}_{\mathrm{SSL}}=\left({\mathit{\alpha }}^{\ast }\cdot {\mathit{\delta }}_{\mathrm{P}}\cdot (\mathrm{1}-h+{\mathit{\epsilon }}_{\mathrm{k}})\right)+{\mathit{\alpha }}^{\ast }\cdot h\cdot {\mathit{\delta }}_{\mathrm{As}}+{\mathit{\alpha }}^{\ast }\cdot {\mathit{\epsilon }}_{\mathrm{k}}+{\mathit{\epsilon }}^{\ast },\end{array}$$

where δ_P represents average precipitation (Gonfiantini, 1986).

Data for air temperature and relative humidity were collected at Trail Valley Creek (TVC) near the centre of the study area. The time period used for the average air temperature and relative humidity spans from when lakes became ice-free (15 June 2018) until the last day of sampling (3 September 2018) to match the time span between the first and last sampling dates. For a few dates, air temperature was not recorded by the TVC meteorological station maintained by the Meteorological Service of Canada, and air temperature from another meteorological station at TVC was used instead.

The isotope composition of the lake-specific input water (δ_I) was calculated following Yi et al. (2008), where δ_I is estimated as the intersection of the LMWL and the lake-specific LEL, defined as the line between the measured isotope composition of the lake (δ_L) and δ_E, which is the isotope composition of vapour evaporating from the lake. δ_E was calculated following Gonfiantini (1986):

$$\begin{array}{}\text{(A7)}& {\mathit{\delta }}_{\mathrm{E}}={\displaystyle \frac{\left({\mathit{\delta }}_{\mathrm{L}}-{\mathit{\epsilon }}^{\ast }\right)/\left({\mathit{\alpha }}^{\ast }-h\cdot {\mathit{\delta }}_{\mathrm{As}}-{\mathit{\epsilon }}_{\mathrm{k}}\right)}{\mathrm{1}-h+{\mathit{\epsilon }}_{\mathrm{k}}}}.\end{array}$$

δ_I, δ_E, and δ_L were then used to calculate the ratio of evaporation to inflow ($E/I$) as described by Yi et al. (2008) and others as

$$\begin{array}{}\text{(A8)}& {\displaystyle \frac{E}{I}}={\displaystyle \frac{{\mathit{\delta }}_{\mathrm{I}}-{\mathit{\delta }}_{\mathrm{L}}}{{\mathit{\delta }}_{\mathrm{E}}-{\mathit{\delta }}_{\mathrm{L}}}}\end{array}$$

assuming that lakes are well mixed and in hydrological and isotopic steady state.

Table A1 List of variables used in isotope framework and their values.