Phenophase-based comparison of field observations to satellite-based actual evaporation estimates of a natural woodland: miombo woodland, southern Africa

The trend and magnitude of actual evaporation across the phenophases of miombo woodlands are unknown. This is because estimating evaporation in African woodland ecosystems continues to be a challenge, as flux observation towers are scant if not completely lacking in most ecosystems. Furthermore, significant phenophase-based discrepancies in both trend and magnitude exist among the satellite-based evaporation estimates (i.e. Global Land Evaporation Amsterdam Model (GLEAM), moderate resolution imaging spectroradiometer (MODIS), operational simplified surface energy balance (SSEBop), and water productivity through open-access remotely sensed derived data (WaPOR)), making it difficult to ascertain which of the estimates are close to field conditions. Despite the many limitations with estimation of evaporation in woodlands, the development and application of the distributed temperature system (DTS) is providing deepened insights and improved accuracy in woodland energy partitioning for evaporation assessment. In this study, the Bowen ratio distributed temperature sensing (BR-DTS) approach is used to partition available energy and estimate actual evaporation across three canopy phenophases of the miombo woodland, covering the entire 2021 dry season (May–October) and early rain season (November–December) at a representative site in Mpika in Zambia, southern Africa. To complement the field experiment, four satellite-based evaporation estimates are compared to the field observations. Our results show that actual evaporation of the miombo woodland appears to follow the trend of the net radiation, with the lowest values observed during the phenophase with the lowest net radiation in the cool dry season and the highest values during the phenophase with peak net radiation in the early rainy season. It appears the continued transpiration during the driest period in the dormant phenophase (with lowest canopy cover and photosynthetic activities) may be influenced by the species-dependent adapted physiological attributes such as access to moisture in deep soils (i.e. due to deep rooting), plant water storage, and the simultaneous leaf fall and leaf flush among miombo plants. Of the four satellite-based evaporation estimates, only the WaPOR has a similar trend to the field observations across the three phenophases. However, all four satellite-based estimates underestimate the actual evaporation during the dormant and green-up phenophases. Large coefficients of variation in actual evaporation estimates among the satellite-based estimates exist in the dormant and green-up phenophases and are indicative of the difficulty in estimating actual evaporation in these phenophases. The differences between field observations and satellite-based evaporation estimates can be attributed to the model structure, processes, and inputs.

1 Introduction

Global terrestrial evaporation is about 60 % of the total incoming precipitation (Miralles et al., 2011a; van der Ent et al., 2014). Evaporation in Africa, Asia, and South America accounts for 78  % of this terrestrial evaporation (Miralles et al., 2011a). A general paucity of evaporation flux observation towers exists across the vast spectrum of ecosystems. As a consequence, in most cases several satellite-based evaporation estimates (e.g. Global Land Evaporation Amsterdam Model (GLEAM), moderate resolution imaging spectroradiometer (MODIS), operational simplified surface energy balance (SSEBop) are used in hydrological modelling and water resources management without validation with field observations from the African ecosystems. In the face of climate change, accurate information on evaporation dynamics in major ecosystems, like the miombo woodland in southern Africa, is important in the management of scarce water resources. Some studies have been conducted to validate satellite-based evaporation estimates in Africa (e.g. Blatchford et al., 2020; Dile et al., 2020; Weerasinghe et al., 2020; Ramoelo et al., 2015). However, none of these studies used field observations based on the miombo woodland evaporation. In southern Africa, the miombo woodland is the largest dry forest formation (Fuller, 1999; Frost, 1996) and the characteristic vegetation cover for many river basins, including the Zambezi Basin. The miombo woodland has unique phenology (Chidumayo, 2001; Fuller, 1999; Frost, 1996) and plant–water interactions that are different from other ecosystems in Africa (Tian et al., 2018; Vinya et al., 2018). For instance, Fuller (1996) conducted an assessment of miombo canopy phenology, i.e. leaf display and canopy closure, in the Luangwa Basin in Zambia. The plots for the assessment included the mopane woodland and the miombo woodland. Both wet miombo (i.e. plateau miombo in Mpika) and dry miombo (i.e. valley areas) in the Luangwa Basin were assessed. The assessment involved field estimates of the normalised vegetation index (NDVI) for leaf display, and the upward pointing photographs were used for canopy closure observations. The results showed the plateau miombo with the lowest seasonality in the tree layer with mean range of 40 %–60 % closure over one season. The canopy closure values among the miombo plots ranged between a minimum of 2 % for the scrub miombo to a maximum of 70 % for the plateau miombo. For the plateau miombo, compared to other miombo plots (i.e. scrub and valley miombo), it was observed that there is net zero change in the increase in the canopy closure due to simultaneous leaf fall and leaf flush in the dry season before the commencement of the rains. The leaf fall, leaf flush, and the accompanying change in leaf colour occur during what is normally termed the transition period in the dry season (May–October) (Fuller, 1999; Frost, 1996; White, 1983). The leaf fall and leaf flush are species dependent, occurring at different times for each species in the dry season. The flushing of new leaves, weeks to months or more, before commencement of seasonal rainfall is a unique feature of the miombo woodland (Frost, 1996; White 1983). Depending on rainfall received in the preceding rain season, the leaf fall and leaf flush processes may start early in the cool dry season (i.e. in case of low rainfall received) or late (in case of high rainfall received) and may extend into November in the early rainy season (i.e. in the case of high rainfall received) (Fuller, 1999; Frost, 1996; White, 1983). The new young flushed leaves have high leaf water content of about 66 % which declines to around 51 % as the leaves harden until they are shed in the next season. The osmotic pressure in the flushed leaves in the dry season increases as the leaves harden but declines after the onset of the rains reaching minimum levels in February (Ernst and Walker, 1973). Most miombo species are broad leaved with capacity to intercept more radiation than other vegetation types such as the mopane species (Fuller, 1999). Wet miombo woodland canopies intercept between 18 %–20 % of incoming rainfall annually (i.e. Alexandre, 1977). Most miombo species are deep rooting, beyond 5 m, with access to deep soil moisture (Savory, 1963). The moisture in miombo woodland soils increases with depth (Chidumayo, 1994; Jeffers and Boaler, 1966; Savory, 1963). Miombo species also have a plant water storage mechanism (i.e. Vinya et al., 2018; Ernst and Walker, 1973) that helps to buffer dry season water limitations. The highlighted unique phenological attributes of the miombo species suggests that the miombo woodland gives evaporation feedback incomparable to other ecosystems. The evaporation dynamics of the miombo woodland and its relationship with the above highlighted phenological characteristics have not been studied. However, given the need for assessing the limited water resources in the ecosystem, there is a clear need for a detailed understanding of the phenophase-based evaporation of the miombo woodland. Yet, estimating evaporation over natural vegetation such as the miombo woodland in southern Africa remains a challenge. Limitations can be found in all available conventional approaches, such as the eddy covariance (EC) system (Foken et al., 2012; Jarmain et al., 2009; Savage et al., 1997), lysimeters (Sutanto et al., 2012; Teuling, 2018), scintillometry (Dzikiti et al., 2014; Jarmain et al., 2009), and the conventional Bowen ratio (Everson, 2001; Savage et al., 1997; Bowen, 1926). For instance, inability to account for energy fluxes near the observation tower causes energy closure problems in the EC systems. Site heterogeneities introduce horizontal and vertical advective terms that are impossible to resolve by single point flux tower measurements (Liu et al., 2006) . Furthermore, if the optical path is obscured, such as in wet conditions, the EC's optical open-path sensors do not work properly, and if the open-path analyser is wet, the evaporation which occurs shortly after a rainfall event is not observed (Coenders-Gerrits et al., 2020; Hirschi et al., 2017). In the case of the two vertical sensor-based Bowen ratios, each sensor has its own errors which are propagated to the Bowen ratio. Additionally, it is difficult to ensure that the two sensors are correctly aligned with each other, which results in incorrect Bowen ratio estimates (Angus and Watts, 1984; Spittlehouse and Black, 1980). Jarmain et al. (2009) assessed and reported on various conventional methods for estimating evaporation in different land surfaces in South Africa. However, recent advances in the distributed temperature sensing system have expanded possibilities for improved accuracy in energy partitioning and the application of the Bowen ratio for evaporation flux assessment in woodlands (Euser et al., 2014; Schilperoort et al., 2018, 2020). In contrast to the conventional Bowen ratio approach, the distributed temperature sensing Bowen ratio technique (BR-DTS) makes use of several vertical high-resolution temperature measurements made with a single fibre optic cable. This eliminates the need for the conventional configuration with two individual sensors at different locations and the associated errors with this type of set-up. One section of the fibre optic cable measures the air temperature profile, while a second section, covered in a constantly wetted cloth, measures the wet bulb temperature profile. The vapour pressure profile can be derived through the psychrometer principle. The DTS technique enables that wet and dry bulb temperature measurements can cover the entire vertical profile through a woodland stand: above the canopy, within the canopy, and under the canopy. This is conducted simultaneously along a single fibre optic cable, thereby facilitating a deepened understanding of the energy partitioning in a woodland (Schilperoort et al., 2018, 2020; Euser et al., 2014). Coenders-Gerrits et al. (2020) have suggested that the DTS technique offers opportunities to assess forest energy storage components that are not normally captured when using conventional approaches. The BR-DTS approach provides an avenue for enhanced understanding and increased accuracy in the estimation of forest evaporation. This is notwithstanding the challenges associated with the BR-DTS approach such as the requirement for sufficient ventilation and constant wetting of the fibre optic cable. Despite the highlighted advantages of the BR-DTS approach, its major limitation is that it is a point measurement. Furthermore, compared to the EC method, the BR-DTS approach tends to minimally overestimate diurnal latent heat flux (LE) by a mean difference of 18.7 W m⁻² (Schilperoort et al., 2018). For the miombo woodland, the need for field-based actual evaporation estimates is highlighted by the discrepancies in satellite-based evaporation estimates (Zimba et al., 2023). Due to a lack of field-based observations of actual evaporation of the miombo woodland, the satellite-based evaporation estimate(s) that are close to field conditions are unknown. Therefore, this study is focused on providing an independent estimation of actual evaporation of the wet miombo woodland that can be used to validate satellite-based evaporation estimates. In this study, field observations were compared to four commonly used free satellite-based actual evaporation estimates: GLEAM (Martens et al., 2017; Miralles et al., 2011b), MODIS (Mu et al., 2011), SSEBop (Senay et al., 2013), and water productivity through open-access remotely sensed derived data (WaPOR) (FAO, 2018). The satellite-based estimates were selected because they can be obtained free of cost, have comparatively high spatial–temporal resolution, have good spatial coverage (i.e. global in the case of GLEAM, MODIS, and SSEBop, and continental in the case of WaPOR), and are ready-to-use products with no further processing required. Hence, the focus of our study was on characterising the actual evaporation of the miombo woodland using the BR-DTS approach and comparing the field observations to the satellite-based evaporation estimates. Consequently, objectives of this study were to estimate the actual evaporation of the wet miombo woodland across different canopy/leaf phenophases to help understand the flux trend and magnitude in the ecosystem, and compare free satellite-based evaporation estimates to the field-based estimates at point scale across the different canopy/leaf phenophases of the wet miombo woodland.

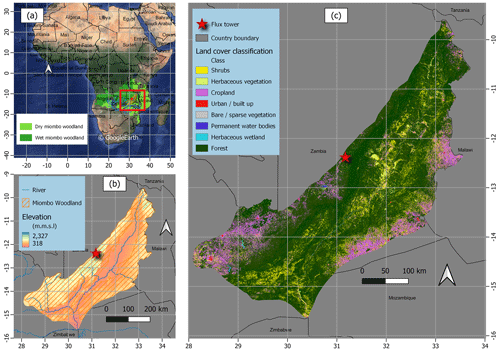
Figure 1 Location and extent of the miombo woodland in Africa (a), elevation characterisation in the Luangwa Basin and at the study site in Mpika (b), and land cover classification of the Luangwa Basin (c). The ASTER digital elevation model was used to depict elevation, while the 2019 Copernicus land cover for Africa was used for land cover characterisation.

2 Materials and methods

2.1 Study site

The study was centred on a miombo woodland at the Nsanzala and Mutinondo conservancy areas (lat: −12.38^∘ S, long: 31.17^∘ E) in the Mpika District, northern Zambia in southern Africa (Fig. 1). Zambia was selected because it is considered to have the largest diversity in miombo woodland species composition (Frost, 1996; White, 1983). The site in Mpika was chosen because it represents a large area of undisturbed miombo woodland with high heterogeneity in species typical of miombo woodland. The site is also situated in the largest miombo ecosystem component of the wetter central Zambezian miombo (Olson et al., 2001; White, 1983), in the north-western part of the Luangwa Basin (Fig. 1). At the study site, species identification and counts within a 250 m by 250 m sample plot showed that over 95 % of the dominant miombo species is semi-deciduous and include the following: Brachystegia floribunda, Brachystegia longifolia, Brachystegia boehmii, Brachystegia speciformis, Jubenerdia paninculata, Uapaca kirkiana, Pericopsis angolensis, Bauhinia petersenia, and Uapaca sansibarica. These are typical miombo species, especially the Brachystegia floribunda, found in the wetter Zambezian miombo woodland (Fuller, 1999; White, 1983). The typical characteristics of the miombo species at the site are that they shed off leaves (leaf fall) and also leaf flush during what is termed as the transition period in the dry season (May–October). Frost (1996) indicated that, based on the amounts of rainfall received in the preceding rain season, the leaf fall and leaf flush processes may start early (i.e. in case of low rainfall received) or late (in case of high rainfall received) and may extend up to November (i.e. in the case of high rainfall received). Elevation ranges between 318 m and 2327 m a.s.l. (above sea level) (Fig. 1b). The study site has a mean annual rainfall of 1200 mm yr⁻¹ and mean annual temperature of 26 ^∘C. Rainfall is a result of the movement of the intertropical convergence zone (ITCZ) over Zambia. The rainfall period is between October and April, while the dry season is between May and October (Hachigonta and Reason, 2006; Chidumayo, 2001).The woodland at the study site is undisturbed by anthropogenic activities due to the site being a conservancy. The major activities in the area are controlled cattle ranching and tourism.

Controlled burns at the study site are normally conducted in August when the dambos (wetlands) are dry, and these are mainly conducted in the dambo grassland for livestock grazing purposes. The non-burning of the study site ensured the evaporation observations were not influenced by fire activity, especially burning of the canopy leaves.

Figure 2 Characterisation of canopy phenophases of the miombo woodland in relation to seasonality at the study site. Photographs show the changes in the canopy cover on selected days across phenophases for the year 2021.

2.2 Study approach

Characterisation of phenophases at the study site

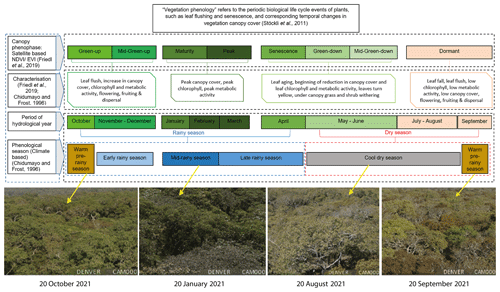
This study compared estimates of actual evaporation by the BR-DTS method with the Penman–Monteith reference evaporation (Allen et al., 1998) and to four satellite-based evaporation estimates at point scale in the miombo woodland. The observations were conducted for the period May to December 2021. The study period facilitated assessment of evaporation during the dry season and early rainy season across three different phenophases of the miombo woodland. The phenology, LAI, and NDVI data were obtained from https://modis.ornl.gov/globalsubset/ (last access: 20 February 2023) and https://app.climateengine.org/climateEngine (last access: 20 February 2023) (Myneni et al., 2021; Friedl et al., 2019, 2022; Gray et al., 2019; ORNL DAAC, 2018; Vermote and Wolfe, 2015; Zimba et al., 2020) and the climate (rainfall and temperature) and soil moisture-based classification by Chidumayo and Frost (1996). Satellite-based classification uses the changes in canopy greenness to characterise the canopy phenophases (Friedl et al., 2019; Gray et al., 2019). In this study, the collection 6 MODIS land cover dynamics (MCD12Q2) product (Gray et al., 2019; Friedl et al., 2019; Zhang et al., 2003) was used to identify the satellite-based phenophases. For the year 2021, eight phenophases were identified using the satellite-based data MCD12Q2 (Fig. 2), NDVI, leaf area index (LAI), and photographs from a digital camera (Denver WCT-8010) installed on the flux tower at the study site (see Fig. 9 in Sect. 3.6). For the climate and soil moisture-based classification, Chidumayo and Frost (1996) observed five phenological seasons: warm pre-rainy season, early rainy season, mid-rainy season, late rainy season, and the cool dry season (Fig. 2). Within these phenological seasons, the phenology of miombo species transition through various stages, i.e. from leaf fall/leaf flush, growth of stems, flowering to mortality of seed (Chidumayo and Frost, 1996). The satellite-based phenophases can be identified within the climate-based phenological seasons (Fig. 2). Based on the period for this study, May–December, five satellite-based phenophases were identified within three climate-based phenological seasons (Fig. 2). The identified phenophases based on satellite data were the green-down, mid-green-down, dormant, green-up, and the mid-green-up (Fig. 2). For ease of analysis, some satellite-based phenophases were merged based on the dominant activity.

For instance, the green-down and mid-green-down were merged together into one green-down phenophase, while the green-up and mid-green-up were merged into one green-up phenophase. The established satellite-based phenophases green-down (may-June), dormant (July–September), and green-up (October–December) were in the cool dry, warm pre-rainy, and early rainy phenological seasons (Fig. 2). The detailed characterisation of the phenology of the miombo woodland, particularly in Zambia, can be found in Chidumayo (2001), Fuller (1999), Chidumayo and Frost (1996), and Fuller and Prince (1996).

2.3 Estimating potential evaporation

The Penman–Monteith (PM) equation (i.e. Eq. 6 in Allen et al., 1998) was used to estimate reference evaporation (E_o) from which potential evaporation for the miombo woodland was calculated using Eq. (1). All required inputs for the PM equation were obtained at the study site. To obtain potential evaporation for the miombo woodland, the crop coefficient (K_c) value of 0.8 was used. The K_c value used was obtained from literature (Hunink et al., 2015). The K_c value was estimated based on the miombo woodland in Mahele, Tanzania. The K_c value for the Mahele region in Tanzania was utilised because it is situated in the wet miombo region receiving rainfall of about 1000 mm yr⁻¹, with similar seasonality as the study site in Mpika, Zambia, in which rainfall starts in late October and ends in early May (Hunink et al., 2015). Furthermore, despite its vast expanse, there is unexpectedly little variation in miombo woodland species diversity (Timberlake et al., 2010). In this study, the same K_c value was applied for the dry and the rainy season.

$$\begin{array}{}\text{(1)}& E_{\mathrm{c}\left(\mathrm{PM}\right)}=K_{\mathrm{c}}\cdot E_{\mathrm{o}}\end{array}$$

2.4 Conventional Bowen ratio energy balance method

The Bowen ratio is the proportion of the sensible (H) to the latent heat flux (LE) of a surface. In simple form, the Bowen ratio can be determined by multiplying the psychrometric constant by the ratio of the temperature and vapour pressure gradients as expressed in Eq. (2):

$$\begin{array}{}\text{(2)}& \mathit{\beta }\approx \mathit{\gamma }\cdot \mathrm{\Delta }{T}_{\mathrm{a}}/\mathrm{\Delta }{e}_{\mathrm{a}},\end{array}$$

where γ is the psychrometric constant (kPa K⁻¹) (Eq. 3), ΔT_a is the difference in temperature (K) between two heights, and Δe_a is the difference in the actual vapour pressure (kPa) between the same two heights. The psychrometric constant is obtained using the relationship between air pressure and ventilation of the psychrometer as given by Allen et al. (1998) in Eq. (3):

$$\begin{array}{}\text{(3)}& \mathit{\gamma }=\mathrm{0.0665}\times {\mathrm{10}}^{\mathrm{3}}\cdot P,\end{array}$$

where P is the atmospheric air pressure (kPa).

Despite the simplicity of the approach, the energy balance Bowen ratio method needs to meet several conditions in its application for results to be reliable. For instance, the two levels at which the temperature and vapour pressure are measured must be within the boundary layer of the air flow, which has adjusted to that particular land surface. The measurement site therefore requires extensive fetch in the upwind direction for the airflow over the land surface, in this case, the woodland canopy. A fetch of at least 100 times the maximum height of measurement is typically suggested for such measurements (Angus and Watts, 1984).

2.5 BR-DTS energy balance approach

The BR-DTS method measures air temperature gradients directly, and the vapour pressure gradients are estimated via the wet bulb temperatures using Eq. (4):

$$\begin{array}{}\text{(4)}& e_{{\mathrm{a}}_{\left(T_{\mathrm{a}}\right)}}=e_{{\mathrm{s}}_{\left(T_{\mathrm{w}}\right)}}-\mathit{\gamma }\left(T_{\mathrm{a}}-T_{\mathrm{w}}\right),\end{array}$$

where $e_{{\mathrm{a}}_{\left(T_{\mathrm{a}}\right)}}$ is the actual vapour pressure, $e_{{\mathrm{s}}_{\left(T_{\mathrm{w}}\right)}}$ is the saturated vapour pressure, γ is the psychrometric constant, and T_a and T_w are the dry bulb and wet bulb temperature. Details on this calculation can be found in Schilperoort et al. (2018). In contrast to the conventional Bowen ratio energy balance, where only the temperature and vapour pressure at two heights are used, the BR-DTS method uses all measuring points between two heights. All dry and wet bulb temperatures within this segment are used to determine the gradients according to a natural logarithmic of the height (Eqs. 5 and 6):

$$\begin{array}{}\text{(5)}& {\displaystyle }& {\displaystyle }{T}_{{\mathrm{a}}_{\mathrm{fit}}}=a\cdot \ln \left(z\right)+b\text{(6)}& {\displaystyle }& {\displaystyle }{e}_{{\mathrm{a}}_{\mathrm{fit}}}=c\cdot \ln \left(z\right)+d.\end{array}$$

The fitted DTS temperature and actual vapour pressure at 11 m (bottom) and 15.5 m (top) heights above the forest canopy were used to estimate the Bowen ratio following Eqs. (7)–(9):

$$\begin{array}{}\text{(7)}& \mathit{\beta }=\mathit{\gamma }\cdot {\displaystyle \frac{T_{\mathrm{a}\cdot \mathrm{fit}}}{\mathrm{\Delta }z}}/{\displaystyle \frac{\mathrm{\Delta }{e}_{\mathrm{a}\cdot \mathrm{fit}}}{\mathrm{\Delta }z}},\end{array}$$

in which

$$\begin{array}{}\text{(8)}& \begin{array}{rl}\mathrm{\Delta }{T}_{\mathrm{a}\cdot \mathrm{fit}}/& \mathrm{\Delta }z=T_{\mathrm{a}\cdot \mathrm{fit}}(z=\mathrm{top})-T_{\mathrm{a}\cdot \mathrm{fit}}(z=\mathrm{bottom})/\\ & (z=\mathrm{top}-z=\mathrm{bottom})+\mathrm{\Gamma }\left(z\right)\end{array}\end{array}$$

and

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{\mathrm{\Delta }{e}_{\mathrm{a}\cdot \mathrm{fit}}}{\mathrm{\Delta }z}}={\displaystyle \frac{e_{\mathrm{a}\cdot \mathrm{fit}}(z=\mathrm{top})-e_{\mathrm{a}\cdot \mathrm{fit}}(z=\mathrm{bottom})}{z=\mathrm{top}-z=\mathrm{bottom}}},\end{array}$$

where ΔT_a⋅fit is the difference in air temperature (K) of the fitted curve between the bottom and top of the height range used for the Bowen ratio, Δe_a⋅fit is the difference in actual vapour pressure (kPa) of the fitted curve over the same height as in temperature, Δz is the difference in height (m) between the two points, and Γ is the adiabatic lapse rate (normally around 0.01 km⁻¹). During dry and unsaturated conditions, very small temperature and vapour pressure gradients could result in errors in the Bowen ratio estimates. The use of the lapse rate is recommended in such circumstances (Schilperoort et al.,2018; Barr et al., 1994). In this study the lapse rate was applied throughout the study period following Schilperoort et al. (2018). Before fitting, the raw DTS data were calibrated following the approach by des Tombe et al. (2020) using freely available open source Python code (des Tombe et al., 2022).

2.6 DTS data quality control

The quality control process followed the demonstration by Schilperoort et al. (2018) as shown in Eqs. (10) and (11). Only diurnal temperature and actual vapour pressure data (i.e. obtained between 06:00 and 18:00 CAT were considered). This is because nighttime actual evaporation was not estimated, as it was assumed to be negligible. The correlation coefficient of determination (r²) values for fitted vapour pressure were used for quality control. The fitted actual vapour pressure with r² values below 0.2 and Bowen ratio values approaching −1.1 and −0.9 were removed from the data, and gaps were filled by the regression method. The coefficients (r²) for dry and wet bulb temperature were not considered because the high uncertainty in temperature is propagated in vapour pressure.

$$\begin{array}{}\text{(10)}& {\displaystyle }& {\displaystyle }\mathrm{Flag}\mathrm{1}:r_{e_{\mathrm{a}},z}^{\mathrm{2}}>\mathrm{0.20},\text{(11)}& {\displaystyle }& {\displaystyle }\mathrm{Flag}\mathrm{2}:\mathit{\beta }<-\mathrm{1.1}\mathrm{or}\mathit{\beta }>-\mathrm{0.9}\end{array}$$

Table 1 Characteristics of satellite evaporation products used in this study.

2.7 Actual evaporation estimation

Several studies (i.e. Buttar et al., 2018; Euser et al., 2014; Xing et al., 2008; Spittlehouse and Black, 1980) demonstrated the use of the Bowen ratio in combination with the energy balance to assess the latent heat flux. In combination with other energy terms, the Bowen ratio energy balance estimate of evaporation (E_β) can be performed using Eq. (12):

$$\begin{array}{}\text{(12)}& E_{\mathit{\beta }}=\left(R_{\mathrm{n}}-M-G_{\mathrm{s}}\right)/L(\mathrm{1}+\mathit{\beta }),\end{array}$$

where R_n is the net radiation flux (W m⁻²), L is the latent heat of vaporisation of water (2.45 MJ kg⁻¹), G_s is the ground heat flux (W m⁻²), and the M is the change in energy storage in the system canopy storage (W m⁻²). The ground heat flux in this study was estimated from the net radiation at hourly intervals. For the Penman–Monteith model (Allen et al., 1998), the ground heat flux for hourly (G_hr) or shorter periods for reference/growing crop can be estimated from net radiation (R_n) using Eq. (13) during daylight and Eq. (14) during nighttime periods. However, the G_s for woodlands is different from that of grass or growing crop. Some studies in different woodlands found G_s to be between 5 %–24 % of R_n (i.e. Ma et al., 2017; Van Der Meulen and Klaassen, 1996; McCaughey, 1982). With reference to observed G_s in different woodlands, this study selected 10 % of Rn for hourly daytime G_s. The 10 % was selected because the wet miombo woodland at the study site, at any period of the year, has about 70 % canopy closure (Fuller, 1999; Frost, 1996). Furthermore, during the dry season (May–October), topsoil (0–30 cm) moisture was not expected to vary significantly.

$$\begin{array}{}\text{(13)}& {\displaystyle }& {\displaystyle }{G}_{\mathrm{hr}}=\mathrm{0.1}{R}_{\mathrm{n}}\text{(14)}& {\displaystyle }& {\displaystyle }{G}_{\mathrm{hr}}=\mathrm{0.5}{R}_{\mathrm{n}}\end{array}$$

We follow Schilperoort et al. (2018) in their observation that the change in canopy storage (M) can be ignored. The E_β was estimated at hourly intervals and then summed up into daily and 10 d values.

2.8 Comparison of satellite-based evaporation estimates to field observations

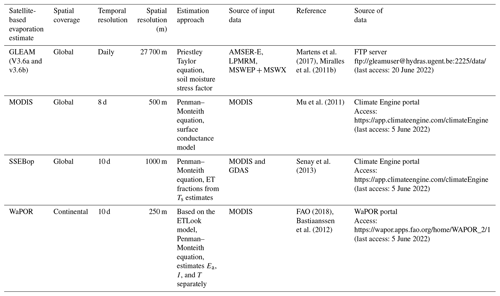
For comparison to satellite-based evaporation estimates, field actual evaporation estimates were aggregated into 10 d and monthly data sets to align with the satellite-based evaporation estimates temporal scales. The native spatial resolutions (Table 1) of the satellite-based evaporation estimates were used because these products are mostly applied or used in their native resolution configuration. All satellite-based estimates used in this study can be obtained free of cost and are readily available. In Africa, financial constraints are a resource limitation. Therefore, to access free-of-cost satellite evaporation products is a significant advantage. Furthermore, in the context of this study, sufficient historical data were available and all products are continuously being processed which assures, to a large extent, future availability of data for continued monitoring. Except for the WaPOR, which had a continental spatial extent, the rest of the satellite-based evaporation estimates had global spatial extent. However, all four products adequately covered the extent of the miombo woodland, which was the focus of this study. All four satellite-based estimates were accessed online from different platforms as indicated in Table 1. Details of the methods for each satellite-based evaporation estimate can be found in the specific documents cited in Table 1.

Figure 3 Schematic drawing (not to scale) of the field set-up of the observation tower at the study site in Mpika, Zambia.

2.9 Statistical analysis

The field observations and satellite-based evaporation estimates were compared using the Kendall and Pearson correlation coefficients, correlation coefficients of determination (R²) (Eq. 15), root mean square error (RMSE) (Eq. 16), and the mean bias error (MBE) (Eq. 17). These are some of the commonly used techniques for comparing pairs of variables and assessing performance of hydrological models (Helsel et al., 2020). The coefficient of determination measures the strength of relationship between the observed with the modelled values. The relationship between variables is strongest as the R² value approaches one. The RMSE quantifies the deviation of the predicted values from the observed values. The model predictions are more accurate as the RMSE value approaches zero. The mean bias error is the measure of the extent to which modelled values deviate from observed values and indicates whether there is under- or overestimation. The smaller the mean bias error value, the less the deviation of the predicted values from the observed values (Helsel et al., 2020). A negative value indicates underestimation, while a positive value indicates overestimation.

$$\begin{array}{}\text{(15)}& R^{\mathrm{2}}=\mathrm{1}-{\displaystyle \frac{\sum _i{\left(O_i-P_i\right)}^{\mathrm{2}}}{\sum _i{\left(O_i-\stackrel{\mathrm{‾}}{O}\right)}^{\mathrm{2}}}}\end{array}$$

$$\begin{array}{}\text{(16)}& {\displaystyle }& {\displaystyle }\mathrm{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n{\left(p_i-o_i\right)}^{\mathrm{2}}}\text{(17)}& {\displaystyle }& {\displaystyle }\mathrm{MBE}={\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n\left(p_i-o_i\right),\end{array}$$

where O_i is the flux tower observed evaporation, $\stackrel{\mathrm{‾}}{O}$ is the mean of the observed evaporation, P_i is the modelled evaporation, and n is the number of observations.

Figure 4 Optic fibre cable wrapped in the wet cloth (a) for collecting the wet bulb temperature, and (b) optic fibre cable not wrapped in cloth for estimating the dry bulb temperature on the observation tower at Mpika site, Zambia. Under canopy view without screens.

2.10 Flux observation tower set-up

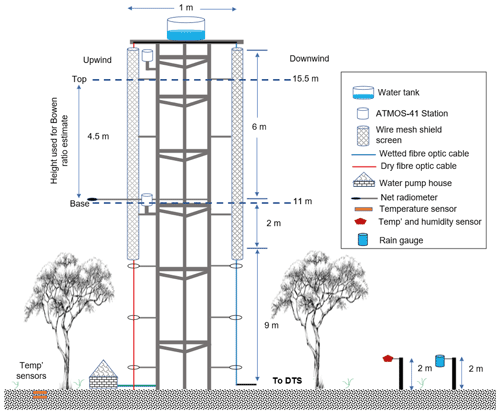
Temperature was measured using a single 3 mm 1 km long white jacket duplex single-tube fibre optic cable connected to the DTS machine. The cable's ends were spliced together to loop the signal back, making a double-ended configuration. Double-ended configuration is explained in van de Giesen et al. (2012). The DTS machine used is the Silixa XT-DTS (Silixa Ltd., 2016) with sensing capabilities as shown in Table A1 in the Appendix. A calibration bath was set up in which 10 m of the fibre cable from the DTS was placed in water together with 2×2 PT-100 probes for the entire period of the measurements. The DTS was set to take temperature measurements at a 5 min interval. The fibre optic cable was firmly secured on a 17.25 m vertical tower (illustrated in Figs. 3 and 4) following the techniques demonstrated by Euser et al. (2014) and Schilperoort et al. (2018). One section of the fibre cable (blue line in Fig. 3) from the DTS machine was wrapped in cotton cloth (Fig. 4a) starting at the base up to the top of the tower and was always kept wet for estimation of what is known as wet bulb temperature. Separated by a 1 m gap, the other section of the fibre cable (red cable in Fig. 3) was not wrapped (Fig. 4b) in a cotton cloth and was designated to measure the air temperature. The cloth on the designated wet cable was kept constantly wet by the water that was pumped to the 65 L tank placed at the top of the tower. The water flow from the water tank to the fibre cable was regulated (roughly 20 L d⁻¹) to ensure a smooth and constant wetting of the cotton cloth. As recommended by Euser et al. (2014), the wet cable was placed on the downwind side, while the dry cable was placed on the upwind side of the tower. The type of cables arrangement prevented water from the wetted cotton cloth for the wet cable from splashing onto the dry cable. This set-up of cables ensured that the dry bulb temperature measurements were not affected. Furthermore, a gap of 1 m also contributed to ensuring that the dry cable was not affected by the water from the wetted cotton cloth. Following the recommendation by Schilperoort et al. (2018), both the wet and dry cables were shielded from direct sunlight by 8 m long two-layered wire mesh screens placed above the canopy (Fig. 3).

A portion of data, within 2 m of the top of the tower, were not included in the assessment because they were assumed to influence the wet cloth/wet cable temperature, as the water from the tank above the tower was at a temperature slightly higher than the air temperature. The 2 m length was considered a sufficient length for the temperature of the water from the tank to be uniform with the environment and suitable for measurement of wet bulb temperature. For this study, the tower height was 17.25 m, and the fetch was beyond 1.7 km. The fetch covered an area with more than 20 km of uninterrupted miombo woodland with typical sporadic small seasonal wet grasslands (Fig. A1b). Furthermore, Spittlehouse and Black (1980) showed that greater accuracy in the Bowen ratio measurements could be attained by increasing the separation between and interchanging the psychrometers. In this study, it was ensured that more than 4 m separation was between the two levels at which the temperature and actual vapour pressure were selected above the canopy. To obtain the net radiation (R_n, W m⁻²), the NR Lite 2 net radiometer (Kipp & Zonen CNR4) was installed at about 2 m above the canopy (that is, 11 m from the ground) (Fig. 3). The net radiation was logged at an hourly interval using the Campbell CR10X data logger. With reference to estimates in other ecosystems (i.e. Ma et al., 2017; Van Der Meulen and Klaassen, 1996; McCaughey, 1982), an hourly ground heat flux (G_o, W m⁻²) was estimated at 10 % of the hourly net radiation. The soil moisture was obtained using two HOBOnet ECH2O™ EC-5 soil moisture sensors placed at 5 and 30 cm in the soil sub-surface. The Onset HOBO S-THB-M002 smart sensors were used to measure under-canopy air temperature and relative humidity at 2 m above the ground and logged at a 5 min interval. Using the Onset HOBO RG2-M rain gauge rainfall was measured at the flux tower site 2 m above ground and away from tree canopies (Fig. 3). The rain gauge was logged at a 5 min interval. The air temperature and actual vapour pressure to compare with the DTS measurements were obtained using METER Group Em60G ATMOS-41 all-in-one weather station sensors. The ATMOS-41 sensors meet standards for the World Meteorological Organization (WMO). The accuracy of the ATMOS-41 is ±0.6 ^∘C for air temperature at below 40 ^∘C and ±3 % for relative humidity. Details on the capabilities of the ATMOS-41 sensors can be found in the manual (Meter Group AG, 2020). Characteristics of selected ATMOS-41 sensors are given in Table A2 in the Appendix. Two ATMOS 41 stations were used, placed at 2 m above the canopy (11 m from the ground) and at 8 m above the canopy (16.5 m from the ground) (Fig. 3). The ATMOS-41 station sensors were logged at a 5 min interval, the same as the DTS. The collected field data (Zimba et al., 2022a, b) are available on the 4TU.ResearchData platform.

3 Results and discussion

3.1 Evaporation flux foot print/fetch analysis

An analysis of the evaporation flux foot print was performed using the wind rose (Fig. A1). The wind rose was used to obtain the most frequent and consistent wind direction to help determine which part of the study site had the greatest influence on the evaporation flux. The wind was predominantly coming from the eastern direction with wind speed ranging between 2–6 m s⁻¹. The use of the wind direction guided the selection of pixels of satellite-based evaporation estimates for comparison with BR-DTS evaporation estimates E_a(DTS). Using the identified predominant wind direction, the fetch/flux footprint equal to 100 times the height (17.25 m) of the observation tower was designed. Thus, the fetch/flux footprint was designed to cover a 1.725 km by 1.725 km area (approximately 2 km by 2 km grid).

3.2 DTS data quality control

The DTS measurements were conducted from 1 May to 25 December 2021. Following the quality control processes by Schilperoort et al. (2018), DTS data for 7 d (two in June, two in August, two in September, and one in October) did not pass the quality test. These data were collected on the days when challenges of keeping the entire wet fibre cable cloth constantly wet were experienced. The data were removed and gaps filled by the linear regression method. Due to challenges with power supply for the DTS machine, 6 d in December (26–31) were not available for analysis.

3.3 Comparison of DTS-based estimates with the ATMOS-41 estimates

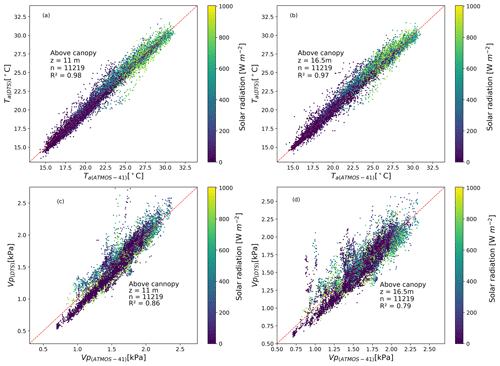
DTS estimates of air temperature and actual vapour pressure were compared with the ATMOS41 estimates at 11 and 16.5 m heights above the forest canopy on the tower (Fig. 3). At height 16.5 m, the DTS-based estimates and the ATMOS-41-based estimates showed relatively lower correlation (R²=0.97 and 0.79 for air temperature and actual vapour pressure respectively). However, at 11 m the correlation coefficients (R²=0.98; 0.86 for air temperature and actual vapour pressure respectively) were relatively higher (Fig. 5a–d). The lower correlation coefficients at 16.5 m may be explained by the installation of the ATMOS-41 weather stations above the forest canopy that exposed the temperature sensors to direct sunlight in early morning and late afternoon. This influenced the temperature measurements and resulted in deviations in ATMOS-41 air temperature for the two periods. Additionally, the water from the tank on the tower did not always reach the wet bulb temperature at the 16.5 m height, resulting in the overestimation of the DTS-based actual vapour pressure. Overall, the DTS and ATMOS-41-based estimates, at both heights, showed good agreement, sufficient for this study. The accuracy properties of the ATMOS-41 are shown in Table A2 in the Appendix.

Figure 5 Comparison of DTS temperature (T_a(DTS)) and actual vapour (VP_(DTS)) measurements with the ATMOS-41 (T_a(ATMOS-41) and VP_(ATMOS-41)) measurements at 11 and 16.5 m above the forest canopy.

3.4 Meteorological conditions

The wind direction was mainly between the north-east and south-east direction (approx. 50–110^∘) (Fig. A1). Wind speed (u) ranged between 0.7–8 m s⁻¹ with relatively higher speeds observed in the dry season between July and September during the dormant phenophase (Figs. 5 and 6). Minimum and maximum net radiation (R_N) were observed during the dry season and wet season respectively. The drop in air temperature (T_a) and relative humidity (RH) coincided with reduced soil moisture (SM) in the dormant phenophase in the dry season (Fig. 6). T_a ranged between 7–32 ^∘C. Relative humidity negatively co-varied with T_a and R_N.

Figure 6 Daily diurnal meteorological conditions at the Mpika study site in the Luangwa Basin for the period May 2021–December 2021. Shaded area for variables is the standard deviation. Shaded area for May–June is the canopy green-down phenophase, July–September is the dormant phenophase, and October–December is the green-up phenophase.

Using the DTS-based Bowen ratio (BR-DTS), available energy was partitioned into sensible (H) and latent heat (LE) fluxes (Figs. 6 and A2). The H and LE co-varied with latent heat predominantly exceeding sensible heat across phenophases. On days with precipitation (P), the H and LE appeared to be equally partitioned.

3.5 Canopy phenophase-based Bowen ratio and evaporation trend

During the green-down phenophase, the Bowen ratio was highest, while air temperature was lowest in a relatively lower net radiation and vapour pressure environment. During the dormant and green-up phenophases, the Bowen ratio was lowest, while the temperature was highest in relatively higher net radiation and lower relative humidity conditions (Figs. 6, 7, and A2). The green-down phenophase (i.e. May–June) showed the lowest air temperature and net radiation (Figs. 6 and 7) and exhibited the highest mean diurnal Bowen ratio (BR) (i.e. diurnal mean of BR ≈ 1.3), indicative of the energy being largely expended as sensible heat compared to the dormant (i.e. diurnal mean of BR ≈ 0.27) and green-up (i.e. diurnal mean of BR ≈ 0.35) phenophases with raised air temperature and net radiation when the energy was mainly expended as latent heat (i.e. diurnal mean of BR < 0.4) (Figs. 6 and 7). Alternating energy partitioning was detected across the phenophases as can be seen through the mean Bowen ratio and sensible and latent heat fluxes (Figs. 6 and 7). Diurnal energy partitioning interchange, across the three phenophases, occurred round 06:00 and 18:00 LT (Fig. 7). The study site is situated in a warmer miombo region (Timberlake et al., 2010). The observed alternating energy partitioning (i.e. Bowen ratio) pattern is similar to what has been observed in warm ecosystems and climates (i.e. Cho et al., 2012) such as the miombo ecosystem. Consequently, the diurnal evaporation pattern at the study site is dependent on daily energy partitioning, increasing with net radiation and air temperature (Figs. 6 and 7).

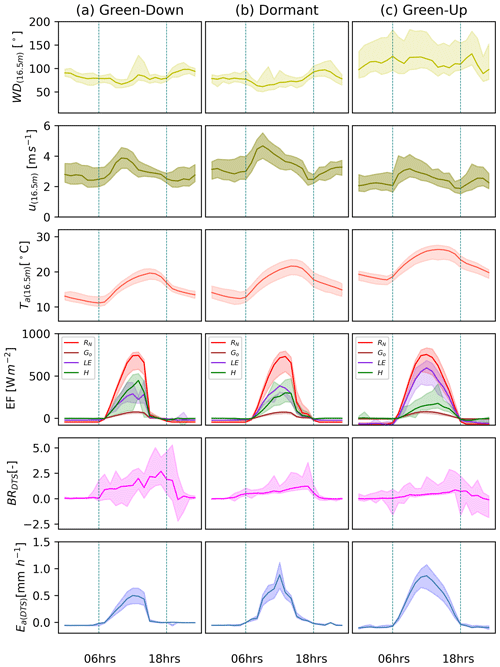
Figure 7 (a) Green-down, (b) dormant, and (c) green-up canopy phenophase-based hourly averages of wind direction (WD), wind speed (u), energy flux (EF) – net radiation (R_N), ground heat flux (G_o), latent heat flux (LE), and sensible heat flux (H) – Bowen ratio (BR_DTS), and actual evaporation (E_a(DTS)). Shaded area is the standard deviation.

3.6 Comparison of potential evaporation and actual evaporation

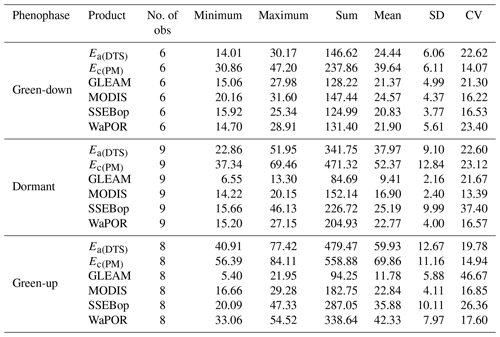
E_a(DTS) was estimated at diurnal (06:00–18:00 LT) hourly interval and then summed up into daily and dekadal (10 d) estimates. Overall, daily E_c(PM) was higher than E_a(DTS) by an average of 17 % (Fig. 8a). However, under low temperature conditions (i.e. June–July), on some days, the E_a(DTS) was higher than the E_c(PM) (Fig. 8a). In higher air temperature and low canopy cover (i.e. in the dormant phenophase August and September), E_c(PM) was higher than E_a(DTS). The soil water limitations and changes in leaf colour (Figs. 9 and A3) may have resulted in significantly higher E_c(PM) compared to E_a(DTS). The E_a(DTS) and E_c(PM) showed similar behaviour (i.e. trend and magnitude) across canopy phenophases with strong correlation (r=0.95) at dekadal scale (Fig. 8b and Table A4). For both E_a(DTS) and E_c(PM), significant variations (i.e. coefficients of variations and standard deviations) in evaporation estimates were observed in the green-up phenophases (i.e. October–December) (Fig. 8b, Table A3).

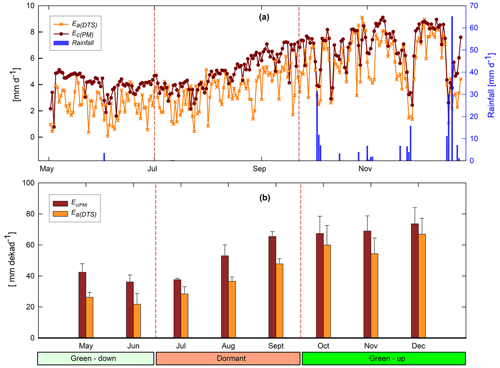
Figure 8 (a) May–December 2021 daily (06:00–18:00 LT) estimates of evaporation E_a(DTS) using the BR-DTS and E_c(PM) using the PM. (b) Comparison of dekadal evaporation estimates between E_a(DTS) estimates and E_c(PM) (E_c=K_cE_o). The E_a(DTS) and E_c(PM) show good agreement in both dry and rainy seasons and across canopy phenophases. Overall, at dekadal scale, the E_c(PM) is relatively higher than E_a(DTS) (b). Phenophases classification: May–June is the green-down phenophase, July–September is the dormant phenophase, and October–December is the green-up phenophase.

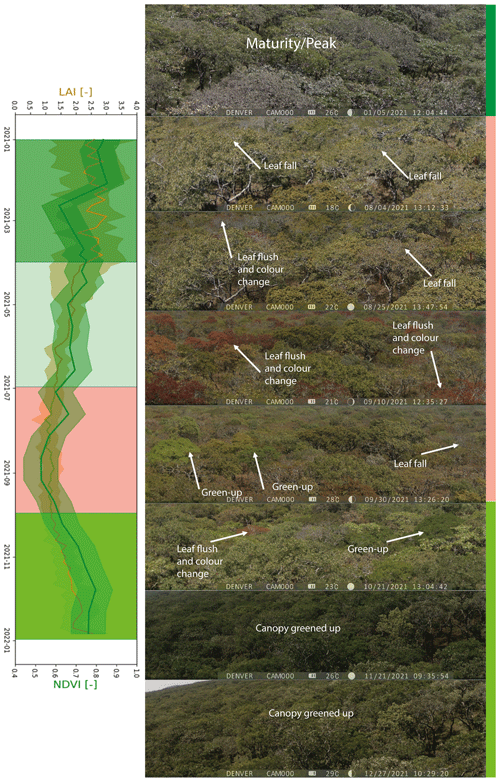
Figure 9 Selected aerial view images of the upwind direction (east direction) above the canopy from the flux tower across phenophases from January–December 2021. Shaded boxes are the phenophases: peak/maturity (January–March), senescence/green-down (April–June), dormant (July–September), and green-up (October–December). The satellite-based NDVI and LAI appear to agree with the changes in the canopy cover. Shading in variables LAI and NDVI is the minimum and maximum values.

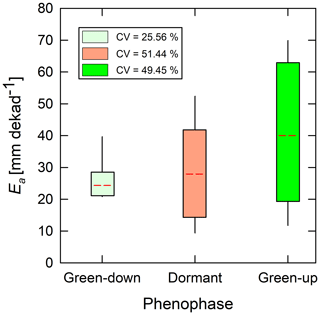
The high coefficients of variations in the magnitude of actual evaporation in the dormant and green-up phenophases could have been caused by changes in both meteorological conditions and forest canopy cover characteristics such as leaf fall, leaf flush, and leaf colour (i.e. Figs. 6 and 9). The E_a(DTS) appeared to follow the trend of available energy (i.e. net radiation, air temperature) (i.e. Kendall's tau (τ) from 0.09 to 0.6) instead of the changes in forest canopy cover (i.e. Kendall's tau (τ) from 0.09 to 0.2) (Figs. 6 and 10). For instance, the lowest E_a(DTS) was observed during the lowest net radiation and air temperature in June, while the highest E_a(DTS) was observed during the period with highest net radiation in the green-up phenophase. In the dormant phenophase, the E_a(DTS) increased as NDVI reduced ($\mathit{\tau }=-\mathrm{0.22}$). The upward trend in the dormant E_a(DTS) even when forest canopy cover (i.e. NDVI) reduced may have been caused by the access to deep soil moisture and vegetative water storage (Tian et al., 2018; Vinya et al., 2018) by plants that had either not started the leaf fall or those that already acquired new leaves and had greened-up (Fig. 9). The leaf fall and leaf colour transitions (i.e. Figs. 9 and A3) in some wet miombo species, at any given time, across the three phenophases, is compensated by the leaf flush and greening-up process in other species, which ensures that about 70 % evaporative surface (i.e. canopy closure) (Fuller, 1999; Frost, 1996 and Fig. 9) is available at any period of the year. The canopy cover percentage increases as the phenophases transition from dormant to the peak phenophase (i.e. Figs. 9 and A3). Zimba et al. (2020) showed that August/September and not June had the highest plant water stress (i.e. lowest normalised difference infrared index (NDII); Sriwongsitanon et al., 2016). June showed the lowest net radiation and air temperature (Fig. 6). However, E_a(DTS) for August/September was higher than that for June. This E_a(DTS) trend and magnitude of actual evaporation demonstrates available energy, coupled with adapted physiological processes, as the possible main driver (s) of the evaporation of the miombo woodland during the dormant phenophase (in the cool dry season and warm pre-rainy season).

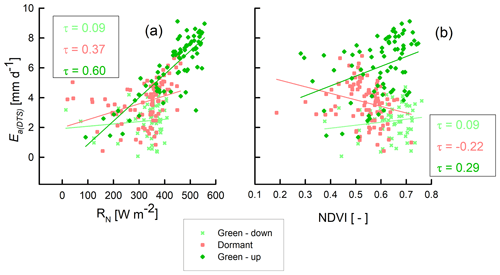
Figure 10 Kendall correlation of E_a(DTS) with R_N and NDVI in the green-down, dormant, and green-up phenophases of the miombo woodland at Mpika site, Zambia.

In the green-up phenophase, E_a(DTS) increased with increase in net radiation and NDVI (τ=0.60 and 0.29 respectively) (Fig. 10). The highest net radiation and air temperature were observed in the green-up phenophase (Fig. 6). The NDII values (i.e. vegetation water content) started to rise in September (Zimba et al., 2020). The increase in the E_a(DTS) from July was sustained through October to December (green-up phenophase) (Fig. 8), before the commencement of stable rains. The NDII trend (Zimba et al., 2020) in the green-up phenophase may have been as a result of the increased canopy cover as proxied by the LAI and NDVI (Fig. 9) facilitated by the plants' access to deep soil moisture/ground water after the leaf flush. The E_a(DTS) green-up phenophase trend could have been caused by increased canopy cover, access to deep soil moisture, and high available energy. The marginal drop of E_a(DTS), in November, at the start of the rain season, could be attributed to the drop in net radiation and air temperature (Fig. 6) influenced by cloud cover and rainfall activity (Fig. 8a). During increased rainfall activity, atmospheric water demand may have been lowered as relative humidity increased while net radiation reduced (Fig. 6). The same explanation holds for the E_a(DTS) estimates in December.

3.7 Comparison of satellite-based evaporation estimates to field observations

3.7.1 Comparison of temporal trend and magnitude

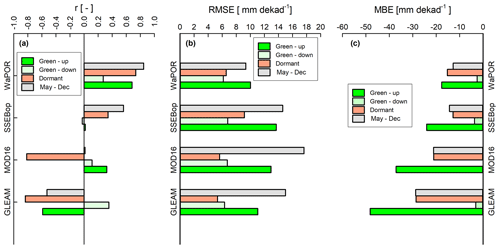
Among the four satellite-based evaporation estimates, only the WaPOR showed similar trend to field observations across the three phenophases from May to December with strong correlation coefficients (r=0.85 and 0.83 with E_a(DTS) and E_c(PM) respectively) (Fig. 11 and Table A4). This was followed by SSEBop (r=0.51 and 0.58 with E_a(DTS) and E_c(PM) respectively), while MODIS showed the weakest correlation (r=0.01 and −0.01 with E_a(DTS) and E_c(PM) respectively).

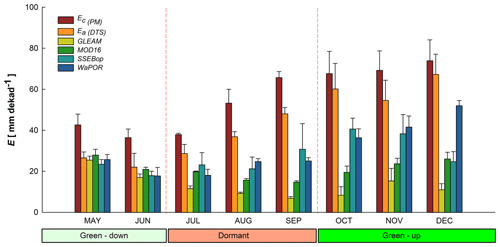
Figure 11 Bar graphs with standard deviation error bars comparing decadal averages of E_a(DTS) and E_c(PM) with satellite-based evaporation estimates from May–December 2021. The WaPOR shows a similar trend to both E_a(DTS) and E_c(PM).

In contrast, GLEAM showed a negative correlation with both E_a(DTS) and E_c(PM) observations ($r=-\mathrm{0.53}$ and −0.48 with E_a(DTS) and E_c(PM) respectively) (Fig. 11 and Table A4). With the exception of WaPOR, diversion from observed E_a(DTS) and E_c(PM) began in July at the commencement of the rise in air temperature and net radiation, increased wind speed, and the beginning of the dormant phenophase (i.e. typified by leaf fall, leaf flush, and leaf colour change activities (Figs. 6, 9, and 11). Surprisingly, GLEAM appeared to substantially underestimate actual evaporation during the dormant and green-up phenophases (in the cool dry season and warm pre-rainy season) (Figs. 2 and 11).

3.7.2 Phenophase-based cumulative estimates and coefficients of variations of estimates

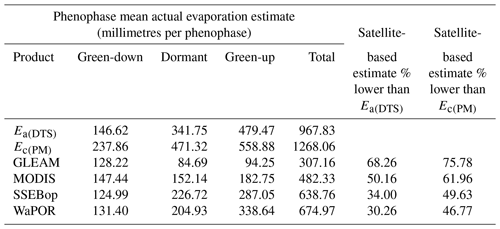
Between 1 May to 20 December 2021, observed actual evaporation E_a(DTS) was about 24 % lower than the estimated potential evaporation E_C(PM) (Table 2). The largest difference (approximately 130 mm) between E_C(PM) and E_a(DTS) was in the water-limited dormant phenophase in the dry season proper.

Table 2 Comparison of the 2021 monthly cumulative evaporation at Mpika miombo woodland site.

Over the same period, cumulative average GLEAM actual evaporation was about 76 % lower than potential evaporation and 68 % lower than E_a(DTS). MODIS was about 62 % lower than potential evaporation and 50 % lower than actual evaporation E_a(DTS). The SSEBop was about 50 % lower than potential evaporation and 34 % lower than actual evaporation E_a(DTS). WaPOR was about 46 % lower than potential evaporation and 30 % lower than actual evaporation E_a(DTS) (Table 2). The green-down phenophase showed the least differences between satellite-based evaporation estimates and field observations (Table 2). Overall, the four satellite-based estimates underestimated actual evaporation across the forest canopy phenophases (Fig. 11 and Table 2). However, in the green-down all four satellite-based estimates showed similar behaviour (i.e. trend and magnitude) with the E_a(DTS) (Fig. 11 and Table 2). The green-down phenophase showed the lowest coefficient of variation among the four satellite-based evaporation estimates (Fig. 12). The low coefficient of variation coupled with the low underestimation in the green-down phenophase showed that satellite-based estimates are closer to miombo woodland actual evaporation in conditions of high forest canopy cover and high soil moisture content in the sub-surface. The dormant and green-up phenophases showed large underestimation and large coefficients of variation among the satellite-based estimates (Table 2 and Fig. 12). The underestimation during the green-up phenophase may be caused by the difficulty of modelling interception, especially in October and November at the beginning of the rainy season. The significant variations in dormant phenophase actual evaporation estimates showed that satellite-based evaporation estimates have difficulty estimating evaporation of the miombo woodland in conditions with low canopy cover (with associated changes in leaf display characteristics), both high and low available energy, and low soil moisture content in the upper layers of the soil. If canopy transpiration is not coupled with access to deep soil moisture beyond 250 cm, as is the case with GLEAM (as explained in Sect. 4.1), satellite-based estimates are likely to underestimate actual evaporation in the dormant phenophase of the miombo woodland.

Figure 12 Box plots showing variations in satellite-based evaporation estimates at dekadal scale across phenophases. Dotted red line is the mean for each phenophase. Coefficients of variation (CV) of satellite-based evaporation estimates were largest during the dormant and green-up phenophases.

3.7.3 Performance statistics of satellite-based estimates with reference to BR-DTS estimates

Overall, for the 8-month period, the WaPOR showed the lowest underestimation (i.e. MBE) and had the highest correlation coefficient and lowest RMSE. The WaPOR was followed by the SSEBop and then MODIS. The GLEAM showed the lowest estimates, highest RMSE, and largest MBE. Only the WaPOR consistently showed positive correlation (r) with field observations across the three phenophases (Fig. 13a). The underestimations were mainly associated with the dormant and green-up phenophase (Fig. 11), as can be seen from the uncertainty RMSE and MBE values (Fig. 13b and c). Therefore, for satellite-based estimates, it appears the dormant and green-up phenophases are the most difficult to assess. The SSEBop and WaPOR estimates appeared closer to dry season miombo woodland actual evaporation than the MODIS and GLEAM. The behaviour, in terms of trend and magnitude, of satellite-based evaporation estimates in relation to field observations of the miombo woodland actual evaporation may be attributed to individual satellite product characteristics.

Figure 13 (a) Statistics of the correlation of E_a(DTS) with satellite-based estimates, and (b, c) statistics of uncertainty in satellite-based evaporation estimates with reference to E_a(DTS) for each phenophase and for the entire study period May–December 2021.

4 Potential causes of the discrepancies between E_a(DTS) and satellite-based estimates

4.1 Global Land Evaporation Amsterdam Model (GLEAM)

GLEAM has four modules that are used to obtain actual evaporation. The modules include the potential evaporation, rainfall interception, and soil and stress modules. The potential evaporation module uses the Priestly and Taylor equation and is driven by observed surface meteorology. The interception module is based on the Gash analytical model and is driven by observed precipitation. The soil module is a multi-layer model driven by observed precipitation and satellite surface soil moisture. The stress module is based on semi-empirical relation to root zone soil moisture and the vegetation optical depth (VOD) (Martens et al., 2017; Miralles et al., 2011b). GLEAM's green-down phenophase behaviour was similar to both field observations and other satellite-based evaporation estimates. However, GLEAM's behaviour, in low soil moisture and low forest canopy cover dormant phenophase, was different, both in terms of trend and magnitude. This showed GLEAM's sensitivity to changes in the sub-surface moisture dynamics. GLEAM soil module only takes into account 250 cm of the sub-surface soil moisture that is linked to observed precipitation. GLEAM drainage algorithm does not take into account horizontal and upward moisture fluxes beyond 250 cm depth. This implies that GLEAM is fully based on net precipitation, thereby not taking into account the groundwater fluxes that are not related to precipitation. At the study site, and the miombo woodland in general, the green-down and dormant phenophases occur in the dry season. The soil moisture (i.e. at 30 cm) begins to decline in March at the end of the rain season but stays relatively unchanged throughout the dry season (Fig. 6). However, the moisture residue at 30 cm subsurface is higher during the green-down phenophase as compared to the dormant and start of the green-up phenophases (Fig. 6 and Chidumayo, 2001). Studies (e.g. Gumbo et al., 2018; Tian et al., 2018; Vinya et al., 2018; Guan et al., 2014; Frost, 1996; Savory, 1963) showed that miombo species have vegetative water storage mechanisms and a deep (beyond 5 m depth in some species) and extensive lateral rooting system providing accessing to ground water resources. This explains the behaviour of field observations which showed a rise in evaporation during the dormant and green-up phenophases in the dry season. The rise in GLEAM actual evaporation in October could be attributed to the interception, due to rainfall activity, and the sporadic rise in soil moisture in October (Fig. 6). This validates GLEAM's dependence on net precipitation for actual evaporation assessment. In increased solar radiation and canopy cover (i.e. leaf area index – LAI) conditions, i.e. in October at the study site, a small amount of precipitation is likely to result in high interception and only begins to reduce as precipitation increases. This shows that the GLEAM interception module, aided by the use of good quality rainfall product, i.e. multi-source weighted-ensemble precipitation (MSWEP), is responsive in the miombo woodland. The overall driving factor of GLEAM's actual evaporation estimates, with reference to the E_a(DTS) in this study, might be the accuracy of the vegetation fraction product used in GLEAM, in this case the global vegetation continuous fields product (MOD44B). Since the evaporative flux components (i.e. interception loss, soil evaporation and transpiration, and potential evaporation estimates) are all based on the vegetation fraction cover, the accuracy of the vegetation fraction product is a key factor in the overall accuracy (in relation to the miombo ecosystem) of the estimated actual evaporation for each land cover. The GLEAM is based on four land cover classifications that include bare soil, low vegetation (i.e. grass), tall vegetation (i.e. trees), and open water (i.e. lakes). Misclassification of the land cover type will have a cascaded effect on several components of the model, including the interception loss estimation and the multiplicative stress factor which influences the estimation of the various evaporation components in the model. Additionally, the coarse spatial resolution (Table 1) could have contributed to the magnitude of GLEAM actual evaporation estimates as shown in Sect. 4.5 of this study. It is also possible that the Priestley–Taylor equation used in GLEAM underestimates evaporation for the miombo woodland in the cool dry season and warm pre-rainy season. This is because the other satellite-based evaporation estimates which use the Penman–Monteith equation (Table 1) appear to underestimate less compared to GLEAM during these two periods.

4.2 Moderate resolution imaging spectroradiometer (MODIS)

The MODIS evaporation algorithm is based on the Penman–Monteith equation (Monteith, 1965). The model computes actual evaporation as a summation of plant evaporation (canopy interception and transpiration) and soil evaporation utilising both remote sensing and meteorological inputs (Mu et al., 2011). In the green-down phenophase, MODIS showed similar behaviour, in terms of trend and magnitude, with E_a(DTS). However, in the dormant phenophase, MODIS had a different trend from E_a(DTS) and underestimated actual evaporation. In the green-up phenophase MODIS showed a trend similar to E_a(DTS) but underestimated evaporation. Potential evaporation (E_c(PM)) and actual evaporation (E_a(DTS)) showed lowest evaporation estimates in June (Figs. 8 and 11). In contrast, the MODIS showed September with the lowest estimates of actual evaporation (Fig. 11). This was a 2-month delay. During the dormant phenophase (i.e. dry season proper), miombo woodland actual evaporation is through the transpiration process. At Mpika's miombo woodland site, Zimba et al. (2020) showed lowest LAI and NDVI values in August and September respectively. The MODIS actual evaporation trend agreed with the vegetation indices, LAI, and NDVI. However, net radiation and air temperature started to increase in July (Fig. 6). At the Mpika miombo woodland, Zimba et al. (2020) showed a long-term average, 2009–2020, NDVI of about 0.5 in July. The July NDVI value was indicative of the presence of green healthy vegetation. Furthermore, the normalised difference infrared index (NDII) indicated that lowest soil moisture and maximum plant water stress was reached in August/September (i.e. Sriwongsitanon et al., 2016; Zimba et al., 2020). Additionally, miombo species dry season plant water interactions have been sufficiently highlighted (e.g.. Gumbo et al., 2018; Tian et al., 2018; Vinya et al., 2018; Frost, 1996; Savory, 1963). Therefore, the start in increase in air temperature and net radiation (indicative of available energy) in July is before the plants are highly water stressed and might be the correct start in rise in actual evaporation as depicted by E_a(DTS), SSEBop, and WaPOR. Consequently, if the MODIS energy balance module is not well adjusted for the miombo woodland, it may be the reason for downward dormant phenophase trend of evaporation estimates. The key MODIS component during the dormant and early green-up phenophase is the plant transpiration module driven by land cover/LAI, net radiation, air pressure, air temperature, and relative humidity. The canopy/stomata conductance thresholds are the link between the highlighted drivers and the assessed plant transpiration. The MODIS energy balance module and canopy conductance may not be appropriately configured for the miombo ecosystem. This could explain why the MODIS trend and magnitude of actual evaporation estimates differed from field observations. Furthermore, for the MODIS, the use of the relative humidity and vapour pressure difference as proxies for soil moisture maybe a source of uncertainty in estimating transpiration (Novick et al., 2016). Direct integration of soil moisture into the MODIS algorithm appeared to improve the accuracy of actual evaporation estimates (Brust et al., 2021). Additionally, daily MODIS evaporation is a summation of both day and night evaporation. E_a(DTS) was estimated at the hourly scale between 06:00 and 18:00 LT. Actual evaporation (E_a(DTS)) values for daytime only (about 12 h) were different from 24 h averages for MODIS.

4.3 Operational simplified surface energy balance (SSEBop)

The SSEBop is based on the energy balance, distinguishing between hot and cold pixels to estimate evaporation. The SSEBop actual evaporation is calculated using an evaporation fraction that is based on the hot/dry and cold limiting conditions. To obtain actual evaporation, the evaporation fraction is multiplied with the crop coefficient (K_c) and potential evaporation (E_o) (Senay et al., 2013). The SSEBop appeared to have a similar behaviour, both trend and magnitude, with E_a(DTS) during the green-down phenophase, but these differed during the dormant and green-up phenophases in August and December. The SSEBop is sensitive to solar radiation/temperature, and thus effectively responded to the changes in these variables (i.e. net radiation and air temperature) as they started to rise in July. The marginal drop in evaporation in August could be due to the leaf shedding processes that exposed the dry leaf and grass covered forest floor to more interaction with radiation resulting in increased temperature. The increased soil surface temperature was interpreted by SSEBop as non-evaporative surface. Furthermore, the drop in the SSEBop actual evaporation in August could have been caused by the relatively (i.e. compared to the MODIS and the WaPOR) coarser spatial resolution (i.e. 1 km), the heterogeneity in the leaf fall and leaf flush trend, and the bush burns that normally occur during this period (Gumbo et al., 2018; Frost, 1996). Additionally, the energy balance-based SSEBop does not explicitly consider soil moisture dependency and assumes that the variations in satellite-based land surface temperature and vegetation indices such as the NDVI account for the soil moisture (Senay et al., 2013). The challenge with the use of the proxies for soil moisture in surface energy balance models is that these are unable to fully account for changes in other factors that may influence sensible heat fluxes (Gokmen et al., 2012). To improve on the accuracy of estimation of water and energy fluxes in regions with recurrent plant water stress, i.e. miombo woodland, Gokmen et al. (2012) suggested that the soil moisture be integrated in the surface energy balance models. The SSEBop underestimation of actual evaporation in December could be attributed to two factors: cloud cover and the uncertainties associated with estimating land surface temperature (LST) in hot humid conditions (Dash et al., 2002). There is increased cloud cover and rainfall activity in December that affects the quality of the satellite LST product. The SSEBop is based on clear sky net radiation balance principle (Senay et al., 2013). Zimba et al. (2020) indicated that the quality pass for the satellite-based MODIS LST product at the study site was below 80 % during the rainy season (i.e. December). With reference to the E_a(DTS), the underestimation by the SSEBop could be attributed to several factors, including the quality of the satellite LST product used and the overpass time of the MODIS satellite over the study site. The SSEBop daily evaporation estimates includes the night time. E_a(DTS) estimates were between 06:00 and 18:00 LT. The differences in the time intervals results in different daily actual evaporation averages contributing to the observed discrepancy. This is even more important when the 10:00 and 13:00 CAT PM overpass time for MODIS terra and aqua is considered. The overpass time affects the minimum and maximum LST estimation which influences estimated SSEBop actual evaporation.

4.4 Water productivity through open-access remotely sensed derived data (WaPOR)

The WaPOR is the only one of the four satellite-based evaporation estimates which showed similar trend with E_a(DTS) across phenophases and had very strong correlation (r=0.85) (Fig. 11 and Table A4). However, WaPOR substantially underestimated actual evaporation in the dormant and green-up phenophases. WaPOR is based on satellite estimates from the modified Penman–Monteith (P–M) ETLook model which has been adapted to remote sensing inputs (Blatchford et al., 2020; FAO, 2018). The actual evaporation is estimated based on seven data components which include precipitation, surface albedo, solar radiation, NDVI, soil moisture stress, land cover, and weather data. The WaPOR actual evaporation is a summation of interception, soil evaporation, and canopy transpiration. In the WaPOR transpiration is coupled via the root zone soil moisture content, while soil evaporation is coupled via the topsoil moisture content. The net radiation is split into soil and canopy net radiation. This implies that increase in LAI exponentially reduces available soil net radiation and increases canopy net radiation. The LAI is derived from the NDVI. The WaPOR estimates canopy resistance and establishes the coupled response of soil moisture and LAI on transpiration. The land cover data are used to generate vegetation-type-dependent stomata conductance thresholds. In the WaPOR, the classes in the land cover data are used to estimate soil and canopy roughness, while the NDVI is used to account for seasonal variations during the growing season (Blatchford et al., 2020). In estimating the soil and canopy aerodynamic resistance, the WaPOR includes buoyance turbulence using the Monin–Obukhovi similarity theory. The accuracy of the land cover product used influences the thresholds for stomata conductance and other land cover type-related components of the model. The use of relatively high spatial resolution Copernicus land cover product in the WaPOR, which has high forest classification accuracy, contributes to its ability to capture the vegetation type, which coupled with appropriate parameterisation of the stomata conductance and other vegetation related variables, appeared to correctly model the trend of the actual evaporation of the miombo woodland. Unlike GLEAM, the WaPOR is not a product of a full net precipitation-based model. The ETLook model takes into account the vegetation type interaction with the sub-soil moisture content. The soil moisture stress module appeared to correctly model the miombo species interactions with soil moisture across the three phenophases. Most importantly, WaPOR correctly characterised actual evaporation trends in the dormant phenophase, which the other three satellite-based estimates did not. Both E_a(DTS) and WaPOR are dependent on correctly partitioning available energy into sensible and latent heat fluxes. Therefore, the WaPOR energy balance module correctly partitioned energy fluxes in the miombo woodland across the three phenophases. The various inputs and processes in the WaPOR, as described above, may explain why it showed the same trend as the field observation and had lower underestimation of actual evaporation. Just like in GLEAM, MODIS, and SSEBop, the underestimation by WaPOR could have been partly due to the differences in the daily time intervals for the estimation of actual evaporation and the quality of the net radiation product used in the model. The WaPOR is estimated over a 24 h (day) period, while E_a(DTS) was estimated between 06:00 and 18:00 LT.

4.5 Possible causes of the E_a(DTS) overestimation

It appeared that the spatial resolution of satellite-based estimates was of influence, as the underestimation was clearly observable, with reference to each satellite-based evaporation estimate's spatial scale. The correlation coefficient of −0.87 (Fig. 14) implies that the finer the spatial resolution, the higher the actual evaporation estimates. Therefore, the finer the spatial resolution, the lower the underestimation (Fig. 12 and Table 2). This indicates that at finer spatial resolutions, higher than the WaPOR's 250 m, the underestimation of actual evaporation is likely to be reduced. However, the results are statistically insignificant, since the p value > 0.05 and SSEBop's higher estimates than the MODIS may suggest that other factors other than the spatial resolution were of greater influence on the estimated evaporation.

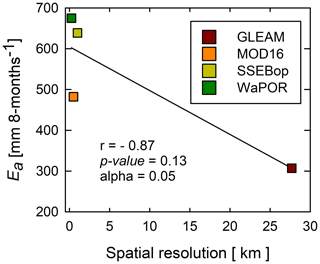
Figure 14 Point scale-based correlation of spatial resolution with actual evaporation of satellite-based estimates.

Furthermore, the ground heat flux (G_o) used in the E_a(DTS) estimates was taken as 10 % of the diurnal net radiation-based estimates found in other forests (i.e. Ma et al., 2017; Van Der Meulen and Klaassen, 1996; McCaughey, 1982). The miombo woodland phenology is different from other ecosystems. It is possible that the G_o was underestimated, and may have contributed to the higher E_a(DTS), as compared to the satellite-based evaporation estimates of the GLEAM, MODIS, SSEBop, and WaPOR. Another source of overestimation by the E_a(DTS) could be the overestimation of the latent heat flux (LE) due to difficulties in flux tower instrumentation. Diurnal high temperature in the dry season (i.e. the dormant and green-up phenophases), coupled with the challenge of the constant wetting of the fibre cable for attaining wet bulb temperature, could have resulted in overestimation of the actual vapour pressure and consequently underestimated the Bowen ratio. Underestimating the Bowen ratio could have resulted in overestimating diurnal latent heat flux, therefore overestimating the diurnal hourly actual evaporation. This suggestion agrees with the observation by Schilperoort et al. (2018) which showed that, compared to the EC approach, the BR-DTS method slightly overestimated diurnal LE by a mean difference of 18.7 W m⁻². However, using the water balance approach, Zimba et al. (2023) showed that satellite-based estimates generally underestimated actual evaporation in the largely miombo woodland-covered Luangwa Basin. Therefore, the outcome of this study's comparison of point-based field observations with satellite-based estimates, agreed with the larger picture at the Luangwa Basin scale. Consequently, the trend and magnitude of satellite-based evaporation estimates, across various miombo strata, are likely to be the same as what this current study has observed. Nevertheless, to consolidate the observations of this study, further studies, such as this one, are needed in the different miombo woodland stratifications in Africa.

5 Conclusions and recommendations

The study characterised evaporation across three forest canopy phenophases of the miombo woodland at point scale using the BR-DTS approach. Consequently, four satellite-based evaporation estimates were compared to the field observations. Major conclusions from our study are that despite the dry season challenge with consistently wetting the fibre optic cable, the BR-DTS approach can be used to successfully estimate actual evaporation across different canopy phenophases of the miombo woodland. The actual evaporation trends appeared to be rather more closely associated with the available energy for evaporation than the changes in the characteristic canopy cover dynamics during the three phenophases. This is because across the three phenophases analysed, actual evaporation had higher correlation with the net radiation trend than the changes in canopy cover (proxied by the NDVI). The actual evaporation estimates in the three phenophases are likely to be more representative of the evaporation of the miombo woodland plants. For instance, the total NDVI/LAI during the dormant and green-up phenophases in the cool dry season and warm pre-rainy season can largely be attributed to miombo plants. This is because in the three phenophases, the non-deep rooting understory and field layer components such as grasses and shrubs normally dry out. However, for a comprehensive analysis, it is important that evaporation for the period with the highest LAI and NDVI (January–March) is assessed. Coupling the canopy transpiration with the root zone storage taking into account the vertical upward (beyond 2.5 m) and horizontal soil moisture flux is likely to improve satellite-based dry season actual evaporation estimates of the miombo woodland. This is because during the dry season, i.e. dormant phenophase in the cool dry and warm pre-rainy seasons, field-based actual evaporation estimates were higher than satellite-based evaporation estimates. The trend and magnitude of the actual evaporation of the miombo woodland in the dry season is linked to the developed dry season water stress buffering mechanism, i.e. leaf fall, leaf flush, plant water storage ,and deep rooting access to deep soil moisture including ground water. Phenology plays a role in satellite-based actual evaporation estimates of the miombo woodland. This is evidenced by the phenophase-dependent variations (i.e. coefficients of variation) in satellite-based evaporation estimates. Some phenophases (i.e. dormant and green-up) had higher coefficients of variation in actual evaporation estimates compared to the green-down phenophase. Compared to field observations (E_a(DTS)), all satellite-based evaporation estimates underestimated actual evaporation. However, this result could have been influenced by the E_a(DTS) assessment time intervals, errors in flux tower instrumentation, spatial resolution of satellite-based estimates, and the ground heat flux used in the E_a(DTS) estimates. Consequently, of the four satellite products considered in this study, only the WaPOR showed the same trend as field observations of the actual evaporation of the miombo woodland across the three phenophases. The WaPOR also showed the least underestimation. For the wet miombo woodland, as was represented by this study site, and limited to the four satellite-based estimates assessed, the WaPOR represents a better choice for use across the assessed miombo phenophases. With inference based on the WaPOR, it appears that satellite-based estimates made at a scale that takes into account the local variations in the input variables might give better results. There is need for observations, such as found in the current study, to be conducted in the drier miombo landscapes and to compare the results. This is because this study was conducted in the wet miombo woodland; therefore, it is possible that the phenological response to changes in hydrological regimes in the drier miombo woodland will differ from the observations at the Mpika site.

Appendix A

Table A1 Sensing capabilities of the Silixa XT-DTS used in the study.

Table A2 Selected ATMOS 41 sensor specifications.

Table A3 Descriptive statistics of evaporation products at phenophase scale.

Table A4 Pearson r correlation coefficient of the comparison of evaporation products.

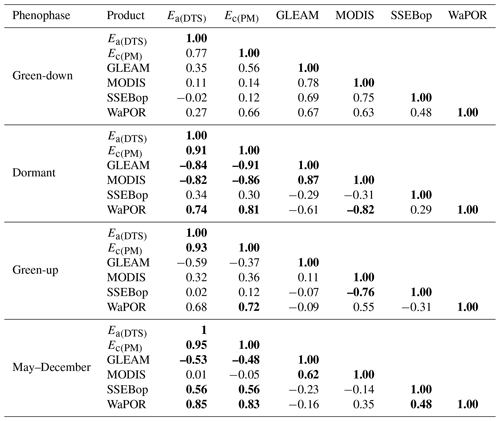
Values in bold are different from 0 with a significance level α=0.05.

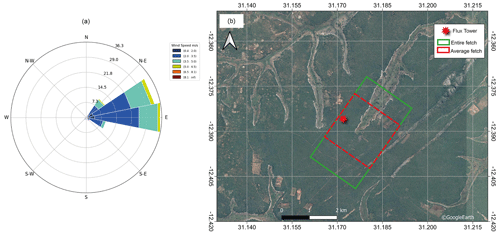
Figure A1 Analysis of the wind direction and wind speed using the wind rose (a), and the extent of the fetch for the DTS observations (b) based on the wind rose results.

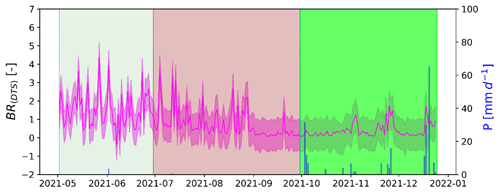
Figure A2 Estimated daily diurnal (06:00–18:00 LT) Bowen ratio for May to December 2021 at the Mpika miombo woodland study site. The shaded area for Bowen ratio is the standard deviation. The shaded area for dates is the phenophase (senescence/green-down: May–June, dormant: July–September, green-up: October–December).

Figure A3 Photographs of the top of the woodland canopy at Mpika site showing changes in canopy leaf cover in the dormant and green-up phenophases.