the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Prediction of the absolute hydraulic conductivity function from soil water retention data
Andre Peters
Tobias L. Hohenbrink
Sascha C. Iden
Martinus Th. van Genuchten
Wolfgang Durner
For modeling flow and transport processes in the soil–plant–atmosphere system, knowledge of the unsaturated hydraulic properties in functional form is mandatory. While much data are available for the water retention function, the hydraulic conductivity function often needs to be predicted. The classical approach is to predict the relative conductivity from the retention function and scale it with the measured saturated conductivity, Ks. In this paper we highlight the shortcomings of this approach, namely, that measured Ks values are often highly uncertain and biased, resulting in poor predictions of the unsaturated conductivity function.
We propose to reformulate the unsaturated hydraulic conductivity function by replacing the soil-specific Ks as a scaling factor with a generally applicable effective saturated tortuosity parameter τs and predicting total conductivity using only the water retention curve. Using four different unimodal expressions for the water retention curve, a soil-independent general value for τs was derived by fitting the new formulation to 12 data sets containing the relevant information. τs was found to be approximately 0.1.
Testing of the new prediction scheme with independent data showed a mean error between the fully predicted conductivity functions and measured data of less than half an order of magnitude. The new scheme can be used when insufficient or no conductivity data are available. The model also helps to predict the saturated conductivity of the soil matrix alone and thus to distinguish between the macropore conductivity and the soil matrix conductivity.
- Article
(2273 KB) - Full-text XML
-
Supplement
(1876 KB) - BibTeX
- EndNote
Accurate representations of the soil hydraulic properties (SHPs) in functional form are essential for simulations of water, energy, and solute transport in the vadose zone. Classical models for the soil water retention curve (WRC) (e.g., van Genuchten, 1980; Kosugi, 1996) and the related hydraulic conductivity curve (HCC) derived using pore-bundle concepts (e.g., Burdine, 1953; Mualem, 1976a) account for water storage and flow in completely filled capillaries but neglect adsorption of water and water flow in films and corners. We will refer to the latter processes as “non-capillary” as opposed to “capillary” in the remainder of this article. In this paper, the term “non-capillary” is used only for water held by adsorption, although water in very large pores (i.e., larger than 0.3 mm in diameter; Jarvis, 2007) is also not held by capillary forces. The non-capillary parts of the WRC and HCC become dominant when soils become dry (Iden et al., 2021a, b). Therefore, improved models of the SHPs have been proposed that extend models that were established for the wet range towards the dry range (e.g., Tuller and Or, 2001; Peters and Durner, 2008a, Lebeau and Konrad, 2010; Zhang, 2011; Peters, 2013). In the very dry range, liquid flow ceases, and vapor flow becomes the dominant transport process. Isothermal diffusion of water vapor can be expressed in terms of an equivalent hydraulic conductivity and incorporated into an effective conductivity function (Peters, 2013). The total hydraulic conductivity can then be expressed as the sum of three components:
where h [m] is the suction (i.e., the absolute value of the matric head or pressure head); K [m s−1] is the total hydraulic conductivity; and Kc, Knc, and Kv [m s−1] are the hydraulic conductivity components for capillary and non-capillary flow of liquid water and water vapor diffusion in the soil gas phase, respectively. Under isothermal conditions, the function Kv(h) can be predicted easily from the temperature-dependent diffusion coefficient of water vapor in air and the WRC (Saito, 2006; Peters and Durner, 2010). Recently, Peters et al. (2021) combined the mechanistic models of Lebeau and Konrad (2010) and Tokunaga (2009) with the conceptual model of Peters (2013) to obtain a simple prediction scheme for the absolute non-capillary conductivity function Knc(h).
Several models have been proposed to estimate the capillary conductivity function Kc(h) from conceptualizations of the pore space involving tortuous and interconnected pore bundles, most of which go back to the seminal studies by Burdine (1953) and Childs and Collis-George (1950) (CCG). Today, the capillary bundle model of Mualem (1976a), who refined the assumptions of the CCG model, is most frequently used (see Assouline and Or, 2013, for a critical review of this and similar models). The pore-size distribution of a porous medium is derived from the WRC, while the HCC is predicted using Poiseuille's law and some assumptions about the connectivity and tortuosity of the pore network. Attempts to predict the absolute capillary conductivity based on these theories (e.g., Millington and Quirk, 1961; Kunze et al., 1968) were not very satisfying because of large deviations with measured conductivities. However, the general shape of the HCC could be described well. Therefore, the models used in practice today predict a relative hydraulic conductivity function Krc(h) and scale it by fitting the function to one or more measured conductivity points. Most commonly, the measured saturated conductivity is used for this purpose. A comprehensive overview of these models is given by Mualem (1986). More recently, concepts to predict the saturated hydraulic conductivity Ks [m s−1] from the WRC were derived by Guarracino (2007), who used a fractal approach, and Mishra and Parker (1990) and Nasta et al. (2013), who used capillary bundle models to estimate Ks as a function of the WRC.
When predicting the hydraulic conductivity using a relative conductivity function that needs to be scaled by matching it to measured data, one faces three types of problems. First and most obviously, if no conductivity data are available for matching, scaling the relative conductivity is not possible. This is frequently the case. Second, if only measurements of Ks are available, the unsaturated conductivity estimates will be greatly affected by the dominant influence of structural pores on the variability of Ks. Thirdly, even if unsaturated conductivity data are available, the conductivity function near saturation may not be represented well. The latter two problems are outlined below.
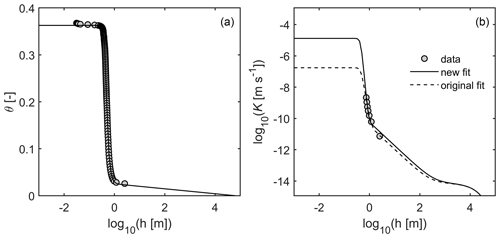
The problem of scaling Krc(h) by Ks stems from the influence of soil structure on the hydraulic conductivity at or near saturation. For more than 50 years, Ks has been known to vary over many orders of magnitude, even at the same site with a rather homogeneous texture (Nielsen et al., 1973; Kutílek and Nielsen, 1994, p. 249). If soil structure is not properly reflected in the WRC near full saturation, scaling Krc(h) with a measured Ks can lead to severe overestimation of conductivity in the medium moisture range (Durner, 1992, 1994; Schaap and Leij, 2000). We exemplarily illustrate this problem in Fig. 1, top, for a sandy soil. The average difference between data and model in the unsaturated region in this example is about 1 order of magnitude.
A better choice is therefore to use unsaturated conductivity data to scale the relative conductivity curve, as already proposed by Nielsen et al. (1960). However, such data are often not available, especially if the measurements were made in the past when more recent techniques such as the simplified evaporation method (SEM) (Schindler, 1980; Peters and Durner, 2008b, Peters et al., 2015) were not available. Moreover, the SEM typically yields information only in a limited suction range, typically between h≈0.6 to h≈8 m, because of the limited measurement range of tensiometers and the fact that the highest measurable conductivity by SEM is of the same order of magnitude as the evaporation rate (i.e., between 10−8 and 10−7 m s−1 depending on the laboratory conditions). This is particularly problematic with coarse materials for which the conductivity close to saturation is many orders of magnitude larger. We illustrate this problem in Fig. 1, bottom, which shows data for a well-graded sand, together with the fitted water retention and hydraulic functions. Whereas the match between model and the available data appears almost perfect, the conductivity curve near saturation is unreliable, and the model-predicted saturated conductivity of m s−1 (or 1.5 cm d−1) is at least 2 orders of magnitude too low for such a soil.
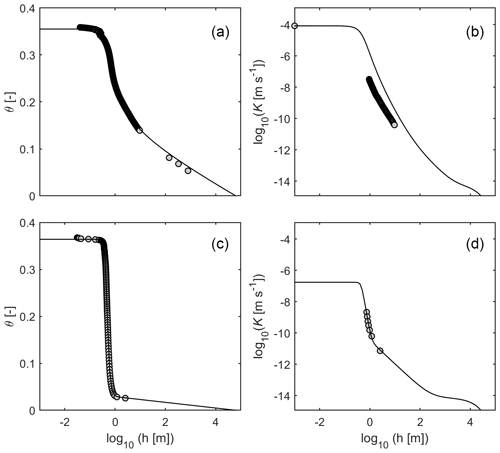
Figure 1Example of conductivity predictions for two soils as obtained by scaling the capillary conductivity with measured conductivity data. Plots on the left side show fitted retention functions; plots on the right side show the corresponding predicted conductivity functions. (a, b) K prediction by matching the relative K function to the saturated conductivity, Ks. (c, d) K prediction by matching the relative K function to unsaturated conductivity data, obtained using the simplified evaporation method. The retention functions and corresponding predicted hydraulic conductivity functions were parameterized using the Peters–Durner–Iden model system with the basic van Genuchten saturation function (Peters et al., 2021), as described in Appendix A. Data source: Peters et al. (2019).
The objective of this study was to develop a model which predicts the absolute capillary conductivity function Kc(h) in Eq. (1) from the WRC and thus to circumvent a need for scaling of the relative hydraulic conductivity function Krc(h) with measured conductivity data. The paper is organized as follows. First, we recall the basic model concept to characterize the capillary and non-capillary pore water components of the hydraulic conductivity in a soil. This is followed by a brief review of the essentials of conductivity estimation using pore-bundle models, which is required to understand our approach. We then develop a model to predict Kc(h) from the WRC. The combination of this model with previously developed models for predicting the complete Knc(h) and Kv(h) yields a soil hydraulic conductivity function that is predicted from the WRC and covers the dry (vapor-dominated), the dry to medium wet (film-dominated), and the medium wet to wet (capillary-dominated) ranges. We apply the obtained scheme using four different parametrizations of the WRC and discuss the accuracy of the conductivity estimates.
The unsaturated hydraulic conductivity function covering wet and dry conditions can be expressed by summing up a capillary component, a film flow component, and a contribution of isothermal vapor diffusion, as given by Eq. (1). This conceptualization is reflected in the PDI model system (Peters, 2013, 2014; Iden and Durner, 2014), where water retention and the liquid hydraulic conductivity are parameterized as sums of capillary and non-capillary components in a relatively simple, yet consistent, manner. Under isothermal conditions, the function Kv(h) can be predicted from the WRC (Saito, 2006; Peters and Durner, 2010). Using the mechanistic models of Lebeau and Konrad (2010) and Tokunaga (2009), the absolute non-capillary conductivity function Knc(h) can also be predicted from the WRC (Peters et al., 2021). But still, the capillary part of the conductivity function of the PDI model system needs to be scaled by matching measured conductivity data. In this contribution, we extend the conductivity predictions further towards capillary pores, which will lead to an absolute prediction of all terms in Eq. (1), without the need for any measured conductivity data. Our concept is based on classic concepts of the pore bundle models. To provide a clear understanding of our approach, we first outline below the PDI model concepts since the PDI parameterization differentiates between the capillary, non-capillary, and vapor-flow components of the SHPs.
2.1 Parametrizing capillary and non-capillary pore water components in the PDI model
The PDI model system (Peters, 2013, 2014; Iden and Durner, 2014) describes in a relatively simple, yet consistent, manner the water retention and liquid hydraulic conductivity in terms of sums of capillary and non-capillary components. The WRC is formulated as a superposition of a capillary saturation function Sc [–] and a non-capillary saturation function Snc [–] (Iden and Durner, 2014):
in which the first term considers water stored in saturated capillaries, and the second term considers water stored in adsorbed films and pore corners. θ [m3 m−3] is the total water content, and θs [m3 m−3] and θr [m3 m−3] are the saturated and maximum adsorbed water contents, respectively. To meet the physical requirement that the capillary saturation function reaches zero at oven dryness, a basic saturation function Γ(h) is scaled by the following (Iden and Durner, 2014):
with h0 [m] being the suction head at oven dryness, which can be set to 104.8 m (Schneider and Goss, 2012). Γ(h) can be any unimodal or multimodal saturation function, such as the unimodal functions used by van Genuchten (1980), Kosugi (1996), or Fredlund and Xing (1994), or their bimodal counterparts or combinations (Durner, 1994; Romano et al., 2011).
The total effective hydraulic conductivity function in the PDI model system is given by Eq. (1). It accounts for liquid water flow in completely filled capillary pores, liquid flow in partly filled pores such as in films on grain surfaces and in pore edges, and the isothermal vapor conductivity. Again, any capillary conductivity model (e.g., Burdine, 1953; Mualem, 1976a) can be used in the PDI system, as outlined by Peters (2013), Peters and Durner (2015), and Weber et al. (2019).
In the original version, both the capillary and non-capillary parts of the conductivity function needed to be scaled by matching the conductivity function to measured conductivity data. Recently, Peters et al. (2021) improved the model by integrating an absolute prediction of the non-capillary liquid conductivity Knc(h) as based on the WRC. This decreased the number of model parameters to the same number as for traditional models, which do not consider non-capillary storage and conductivity. Nevertheless, a scaling factor Ksc was required for the capillary conductivity component in Eq. (1):
Since Ksc is orders of magnitude higher than the non-capillary and vapor conductivity components, Ksc can be interpreted as being equal to the total saturated conductivity. A detailed description of the PDI model system is given in Appendix A1.
2.2 Relative conductivity predictions using capillary bundle models
Capillary bundle models use information about the effective pore-size distribution of a porous medium as contained in the WRC. Generally, the Hagen–Poiseuille law is applied to a bundle of capillaries with a size distribution that is consistent with the pore-size distribution of the medium along with some assumptions about pore connectivity and tortuosity to arrive at a mathematical description of the HCC. The water flux in a single capillary under unit-gradient conditions, Qc1 [m3 s−1], can be described with the law of Hagen–Poiseuille:
where ρ [kg m−3] is the fluid density, g [m s−2] is gravitational acceleration, η [N s m−2] is dynamic viscosity, and r [m] is the radius of the capillary, which is assumed to have a circular cross-section. Relating Qc1 to the cross-sectional area of the capillary yields the flux density or simply the hydraulic conductivity [m s−1] assuming unit gradient conditions:
If the porous medium is regarded as a bundle of parallel capillaries of different sizes, the hydraulic conductivity can be described as the sum of the unit-gradient fluxes of the single water-filled capillaries, divided by the sum of their cross-sectional areas, and corrected with the macroscopic capillary water content, θc [m3 m−3]. The latter is necessary because air-filled pores and the soil matrix do not contribute to the macroscopic conductivity. This yields then the following (Flühler and Roth, 2004):
where rm [m] is the maximum radius of the water-filled pores, and fk(r) is the pore-radius distribution. The pore-radius distribution is related to the pore-volume distribution fp(r), reflecting volumetric fractions by , which leads to
Since (the capillary water content), this simplifies to
Applying the Young–Laplace relation , in which σ [N m−2] is the surface tension between the fluid and gas phases and h [m] the suction, leads to the following expression for a bundle of parallel capillaries:
where is the dummy variable of integration.
Several factors distinguish a porous medium from a bundle of parallel tubes. They can be accounted for mostly by implementing a tortuosity–connectivity correction. The tortuosity describes the effect of the path length of a single water molecule, lp [m], being longer than a straight line l [m]. The factor of path extension is then given by [–]. This causes both a reduction in the local conductivity and the local hydraulic gradient (Bear, 1972), leading to lower effective hydraulic conductivity by a tortuosity factor [–]:
Note that deviations from flow in straight capillary bundles are not only affected by tortuosity in the strict sense but also by additional effects which will be discussed in Sect. 2.3 within the context of model development. Furthermore, the tortuosity factor is not a constant but a function of the capillary water content since the path length increases with decreasing water contents. Lumping the physical parameters of Eq. (10) into [m3 s−1] and considering the tortuosity correction τ(θc) leads to
Values of the physical constants used in this study are summarized in Table 1. In SI units, m3 s−1 at 20 ∘C.
Equation (12) is similar to the formulation by Nasta et al. (2013), who used the same approach to predict the saturated conductivity from the WRC of Brooks and Corey (1964). They optimized for this purpose the value of τ at saturation by fitting their model to measured Ks data from the GRIZZLY database (Haverkamp et al., 1997). As mentioned in the Introduction, Eq. (12) has proven to be insufficient to describe the unsaturated conductivity function K(h). Burdine (1953) for this reason normalized the expression by the corresponding integral over all capillary pores, which leads to the following relative conductivity function:
in which τs=τ(θs). Since the degree of capillary saturation, Sc, is given by , and hence
with the relative tortuosity factor . Note that the solution is similar for the classic (“non-PDI”) scheme, for which effective saturation is defined as . In this case we obtain . Burdine (1953) suggested that the tortuosity ( is inversely related to the capillary saturation, leading to and hence
In a more sophisticated approach, Mualem (1976a) followed the cut-and-random-rejoin model approach of Childs and Collis-George (1950) (CCG) and refined the model using the assumption that the length of a pore is directly proportional to its radius. Normalizing his integral expression by the corresponding integral over all capillary pores and considering a saturation-dependent tortuosity correction , the expression for the capillary conductivity function became (Mualem, 1976a)
with λ [–] as the tortuosity and connectivity factor. Applying his model to a variety of data, Mualem found empirically that λ≈ 0.5.
2.3 Absolute hydraulic conductivity prediction
For the reasons stated in the Introduction, it is preferable to predict the absolute capillary conductivity function Kc(h) from the WRC rather than calculating the relative function Krc(h) and scaling it with measured conductivity data. In this paper, we use the Mualem (1976a) model to derive the shape of the capillary conductivity function. Our concept keeps the dependency of the relative tortuosity factor on saturation in the original formulation of Mualem (1976a); that is, , which becomes unity at full saturation. However, instead of following Mualem's original concept of first normalizing the prediction integral and then scaling it with measured conductivity values, we predict the absolute Kc(h) from the WRC by introducing an absolute tortuosity coefficient, τ(Sc), which is given by the product of a relative and a saturated tortuosity coefficient τs:
By inserting this tortuosity expression into Eq. (12), by using Mualem's integral (occurring in Eq. 16), and by applying the substitution , we obtain the following equation for the capillary conductivity function:
Expressing the Mualem integral by , where F is the solution of the indefinite integral (Peters, 2014), leads to
In this model, τs is a new factor which scales the capillary conductivity function. We hypothesize that τs varies only moderately among different textures and that a universal value can be determined from experimental data. If τs is known and λ is set to Mualem's suggested value of 0.5, all three components of the HCC given by Eq. (1) can be calculated based on the WRC without the need for measured conductivity values.
The parameter Ks (in the classic “Non-PDI” scheme neglecting non-capillary processes) or Ksc (within the PDI system) of Eq. (16) is related to τs of Eq. (19) by
where is the PDI formulation of the denominator in Eq. (16) (Peters, 2014).
The hydraulic tortuosity of saturated porous materials has long been investigated using a variety of experimental and theoretical approaches. The earliest description of hydraulic tortuosity was introduced by Carman (1937), who modified the Kozeny (1927) equation for the saturated permeability. Using experimental data, Carman found that for a wide range of porosities. However, many found later that the saturated tortuosity is variable and depends on porosity and texture. We refer to Ghanbarian et al. (2013) for an overview of theoretical and experimental studies about this relationship. Most of the derived values for τs are between approximately 0.7 and 0.2.
Importantly, current schemes for the tortuosity generally only account for pathway elongation due to tortuous flow paths according to Eq. (11). In real soils, however, the deviation from flow in straight capillary bundles is not only affected by tortuosity in the strict sense but also by other soil-related factors such as the surface roughness of pore walls, non-circular capillaries, and dead-end pores. Additionally, not only the geometry of the pore space may differ from the ideal case but also such fluid properties as surface tension and viscosity likely will be different from those of pure free water. Finally, capillary bundle models will not represent the pore distribution and connectivity in an ideal way. Therefore, we seek in this contribution an empirical value of τs that lumps all these effects. The hypothesis that τs varies only moderately among different textures will be tested by fitting predicted K functions to test data. In doing so, conductivity data at or very close to saturation are not considered in the fitting, since the actual saturated tortuosity depends strongly on the nature of macropores (e.g., inter-aggregate space, wormholes, decayed plant roots). Therefore, we use the term “saturated tortuosity coefficient”, τs, for a (virtual) porous system without structural pores.
2.4 Connecting the capillary conductivity function with different WRC parametrizations
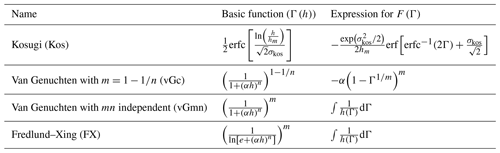
Dependent on the selected WRC parametrization, F in Eq. (19) can be expressed in closed form or must be calculated numerically. For this study, we used four unimodal models to describe the WRC and correspondingly to predict K(h). All four models are used within the PDI system. The basic capillary saturation functions are given by the function of Kosugi (1996), the van Genuchten functions (van Genuchten, 1980) with the usual constraint () and also in unconstrained form (m independent from n), and the Fredlund and Xing (1994) saturation function. The latter is the function given in the last row of Table 2. The models are referred to as Kos-PDI, vGc-PDI, vGmn-PDI, and FX-PDI. The saturation functions and the solutions for the integral F are given in Table 2. For the Kos and vGc saturation functions, F is given in analytical form. For the unconstrained vGmn and FX saturation functions, F needs to be evaluated using numerical integration. We chose these four functions as they are the most commonly used functions in the field of soil hydrology and geotechnics.
Although the derivation of Kc(h) is presented here for the PDI model, we note that the model concept is not limited to PDI-type soil hydraulic functions and that closed-form expressions can also be derived easily for “classical” models that use a residual water content and neglect the non-capillary components. For those cases, the expression for the integral F(Γ0) is zero. For the original van Genuchten–Mualem model with constraint , one obtains, for example,
where Se is the effective saturation function (, or simply
Table 2Summary of the basic water retention functions used in the PDI scheme (see Appendix A1) as well as the analytical solutions for F (Eq. 19) as given in Peters (2014). The parameters α, n, m, σkos, and hm are shape parameters, and e is the Euler number. In the case of FX and vGmn, no analytical solution for the integral in Eq. (19) is known, and F must be evaluated numerically.
3.1 Soil hydraulic models
The water retention and unsaturated hydraulic conductivity functions were described using the PDI model system with four different unimodal basis functions for capillary water (Table 2), combined with the Mualem (1976a) capillary bundle model to predict the shape of the capillary conductivity function, Kc(h). This function is given by Eq. (19) and included in the total conductivity function given by Eq. (1). The relative tortuosity parameter λ was set to 0.5 following Mualem (1976a), m3 s−1 (Sect. 2.2, Table 1), and τs is the new unknown tortuosity parameter. Knc and Kv were predicted from the WRC (Peters et al., 2021; see Appendix A1).
For soils with a wide pore-size distribution, Mualem's model (as all capillary bundle models) in combination with water retention models that gradually approach saturation can produce a non-physical sharp decrease in the hydraulic conductivity near saturation (e.g., Vogel et al., 2000; Ippisch et al., 2006). Madi et al. (2018) developed a mathematical criterion to test individual WRC parameterizations for physical plausibility. To avoid this model artifact, we used the “hclip approach” of Iden at al. (2015) in all cases. The hclip approach limits the pore size in the conductivity prediction integral to a maximum value, which is equivalent to a minimum suction, hcrit. According to Jarvis (2007), we use hcrit= 0.06 m, corresponding to an equivalent diameter of 0.5 mm (see also Sect. 2.4).
3.2 Estimating the saturated tortuosity coefficient, τs
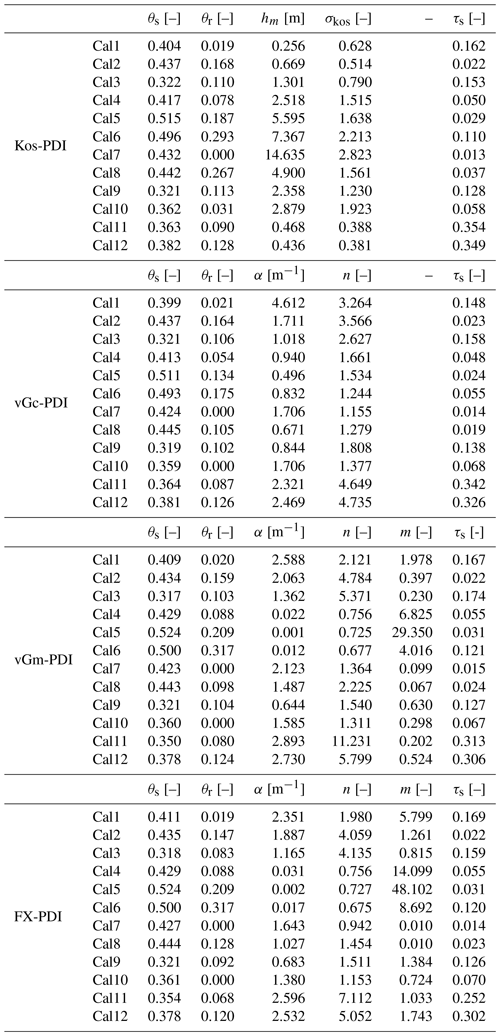
To obtain an estimate for τs, reliable data for the WRC and in particular for the HCC in the wet range (but not at saturation) are needed. We used six data sets used by Peters (2013) and six additional data sets from Sarkar et al. (2019), which fulfill the abovementioned requirements. Soil textures varied from pure sand to loamy clay, representing a wide variety of different soils. Details about the soils are given in the original literature and are summarized in Table 3. For each of the four PDI combinations with the capillary saturation functions given in Table 2, we determined a value for τs by fitting them to the 12 data sets and estimating the WRC parameters and τs. The median values of the estimated τs values were used in the corresponding prediction models.
3.3 Validation of the absolute K predictions
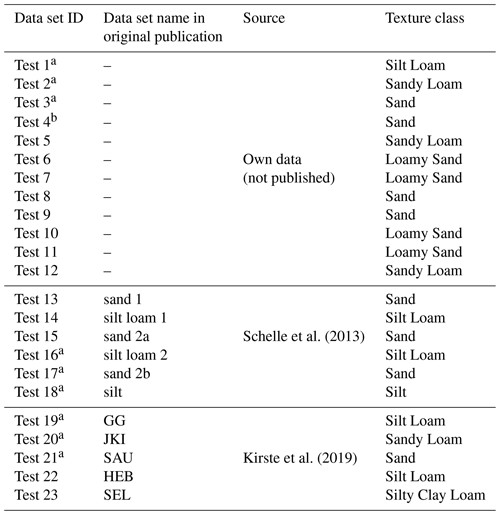
To test the predictions of K(h) from the WRC, we selected data sets that cover a relatively wide moisture range and could be described well using unimodal WRCs. We used 23 data sets, which were obtained at Technische Universität Braunschweig, Germany. The data comprised again a broad range of textural classes. Some of them stemmed from soil columns taken at the same sites at which the soil columns of Sarkar et al. (2019) were taken (locations JKI, GG, and SAU). However, we used independent data from different soil samples taken in different years. All data sets except one (Test 4) are from undisturbed samples. Details about the validation data are given in Table 4.
Table 3Calibration data sets used for estimating water retention curves and the saturated tortuosity coefficient τs.

3.4 Parameter estimation and diagnostics
The models were fitted to the data by minimizing the sum of weighted squared residuals between modeled and measured data (Peters, 2013):
where θi and θmod,i are the measured and modeled water contents, Ki and are measured and modeled hydraulic conductivities, nθ and nK are the respective number of data points, wθ=10 000 and wK=16 are weights for the two data groups (Peters, 2011), and b is the vector of unknown model parameters. The shuffled-complex-evolution algorithm SCE-UA (Duan et al., 1992) was used to minimize the objective function given by Eq. (23). In the case of estimating the general value of τs, the parameter vector contained all adjustable parameters of the water retention function plus τs. In the case of the hydraulic conductivity predictions, wK was set to 0, and the estimated parameter vector contained only the WRC parameters. The performance of the different approaches was compared in terms of the root-mean-square error (RMSE) for the WRC and the HCC (common log of K(h)), respectively. Model comparisons were based on the Akaike information criterion, AICc, corrected for small sample sizes (Hurvich and Tsai, 1989).
4.1 Empirical estimate of the saturated tortuosity coefficient τs
Figure 2 illustrates, using 4 of the 12 calibration data sets described in Table 3, the fitted water retention and conductivity functions for the four basic hydraulic models listed in Table 2. A full overview on all calibration data sets and the fitted models is given in the Supplement. All estimated parameters are given in Table A1. In general, all four models are well suited to describe the data. Actually, the models can be hardly distinguished on the plots since they lie largely on top of each other. Figure 3 shows the corresponding distributions of RMSEθ and RMSElogK, which allow one to better differentiate the fitting performance. Results confirm the visual impression from Fig. 2 that all four models fit similarly, with a slightly better performance of the models having six free parameters (i.e., FX-PDI and vGmn-PDI) as compared to those with five free parameters (vGc-PDI and Kos-PDI). We note that fitting the K functions of Peters et al. (2021), using Ks instead of τs as an adjustable parameter and leaving all other settings identical, would lead here exactly to the same results.
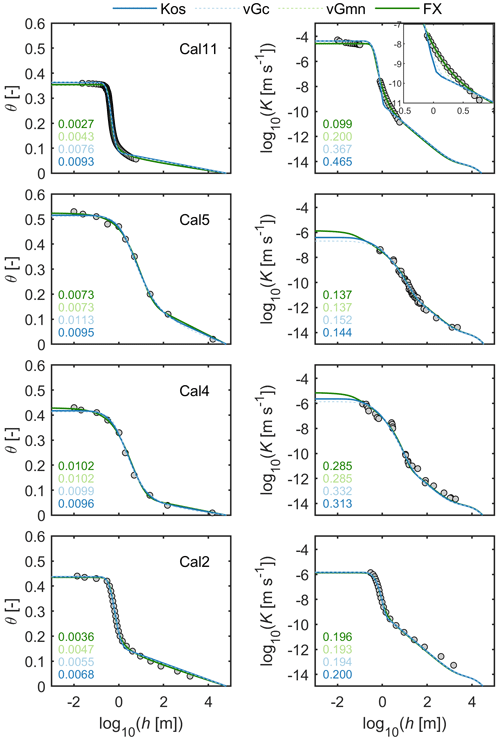
Figure 2Plots of 4 of the 12 calibration data sets and the fitted water retention and conductivity functions used to calibrate the saturated tortuosity coefficient τs in Eq. (19). Parameter λ was set to a value of 0.5 according to Mualem (1976a). Parameter τs and the retention parameters were allowed to vary. Numbers in the subplots indicate RMSEθ and RMSElogK values for the various model combinations.
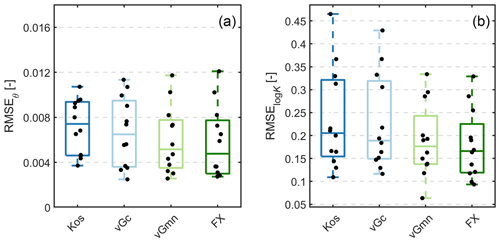
Figure 3Distributions of RMSEθ and RMSElogK of the fitted retention and conductivity models for the 12 data sets. Black dots indicate single realizations.
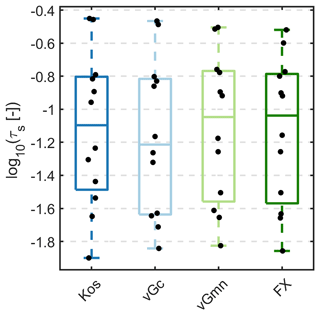
The distributions of the resulting values for τs for the four models are shown in Fig. 4. The median values for τs were 0.062 for the constrained van Genuchten function (vGc), 0.084 for the Kosugi function (Kos), and 0.094 and 0.095 for the unconstrained van Genuchten (vGmn) and Fredlund–Xing (FX) functions, respectively. It appears noteworthy that the two best-fitting WRC models yield almost identical estimates of τs. The range of τs for the 12 data sets spanned less than 1.5 orders of magnitude. We interpret this as an indication that the hypothesis of relatively moderate overall variability in τs may be justified. When fitting the classic PDI scheme (with Ks as a fitting parameter) to these data, which do not include measured conductivity data at saturation, the estimated Ks values varied by more than 3 orders of magnitude. In natural soils, the measured Ks values can vary even more due to the dominance of (texture-independent) structural pores and macropores on Ks (e.g., Usowicz and Lipiec, 2021).
4.2 Tests of the absolute conductivity predictions
By using median values of τs for the different models (0.084, 0.062, 0.094, and 0.095 for Kos-PDI, vGc-PDI, vGmn-PDI, and FX-PDI, respectively; Fig. 4), we predicted the hydraulic conductivity functions from the water retention functions for 23 test data sets. In Fig. 5, we show the resulting distributions of RMSEθ (fitted) and RMSElogK (predicted). Since measured conductivities were available primarily within the range where the capillary conductivity component dominates, RMSElogK can be interpreted as an approximate error of the capillary conductivity prediction. The medians of RMSElogK for the Kos-PDI and vGc-PDI models were 0.71 and 0.67, respectively. Combinations with the more flexible retention models yielded median RMSElogK values of 0.49 for vGmn-PDI and 0.40 for FX-PDI. To test whether conductivity predictions were biased, we calculated also the mean error (Fig. 6). For the FX-PDI model, the median was close to zero, indicating an unbiased conductivity prediction, whereas the other models tended to underestimate the conductivity data.
Figure 7 shows fitted WRCs and predicted HCCs along with the measured conductivity data. Due to space limitations, only a subset of six randomly selected cases is shown for the FX-PDI combination. The WRC fits and HCC predictions for all 23 test soils and all four models are listed in the Supplement.
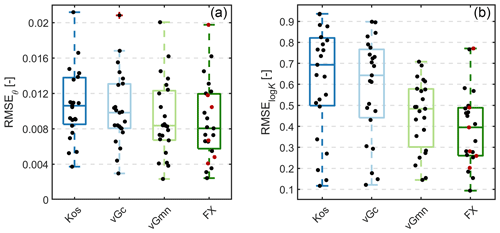
Figure 5RMSEθ and RMSElogK for prediction of the absolute conductivity from the soil water retention function of 23 test data sets. Black dots indicate the validation data sets; red dots indicate the data sets used to estimate a general value of the saturated tortuosity coefficient τs. The red cross indicates an outlier, defined by the MATLAB® default settings as 1.5 times the interquartile range away from the top or bottom of the box (https://de.mathworks.com/help/matlab/ref/boxchart.html, last access: 13 April 2023).
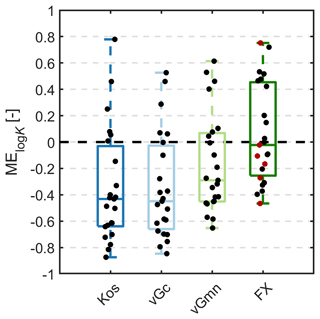
Figure 6Mean errors of the predicted absolute conductivity based on the soil water retention function for 23 test data sets. Black dots indicate all 23 validation data sets; red dots indicate data sets shown in Fig. 7.
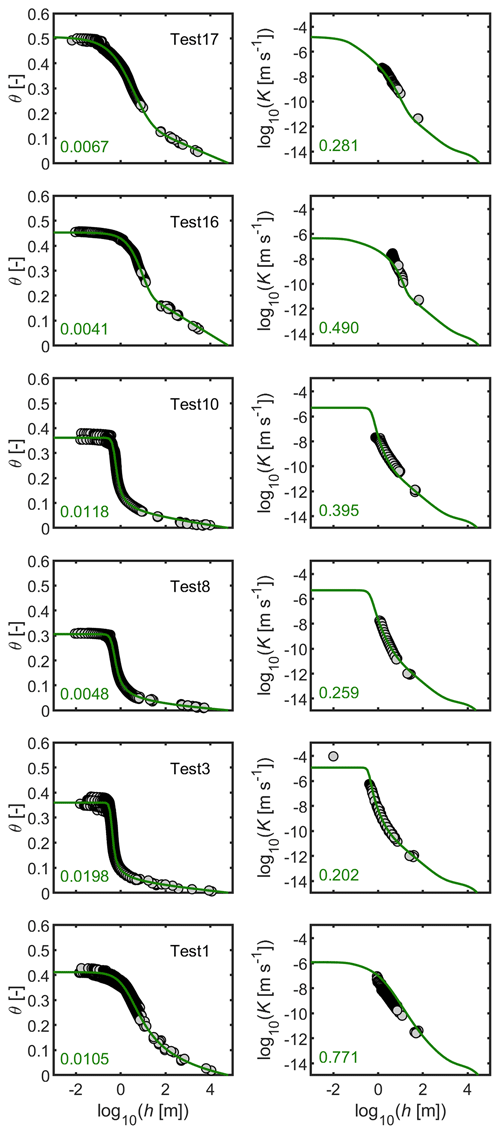
Figure 7Measured data (dots), fitted retention functions (a, c) and predicted conductivity functions (b, d). Shown are for six randomly selected soils out of 23 validation data sets. Numbers in the subplots indicate RMSEθ and RMSElogK values Note that the conductivity curves are not fits to the data.
4.3 Improved estimation of K functions when K data are available
Several authors (e.g., Schaap and Leij, 2000; Peters et al., 2011) have stressed that the tortuosity parameter λ might differ greatly from the value suggested by Mualem (1976a), since the change in tortuosity with respect to capillary saturation can obviously be different for different soils. The new scheme is valuable not only for cases where no or insufficient information about the conductivity is available. It is also useful when data are available for the unsaturated hydraulic conductivity but are missing in the wet range. This is the case, for example, with the commonly used evaporation method (Schindler, 1980; Peters and Durner, 2008b; Peters et al., 2015). Then, there is often high uncertainty in the wet moisture range; thus, an unrealistic conductivity extrapolation might result (see Fig. 1, bottom). In such cases, λ might be estimated, and only τs might be fixed. We illustrate this in Fig. 8 for the data set shown in Fig. 1 (bottom). Again, the vGmn-PDI retention model is used, but instead of Eq. (16), we now use Eq. (18) with τs=0.094. Now, the model is well able to be fitted to the data, and the hydraulic conductivity close to saturation is more reasonably predicted as in Fig. 1: predicted conductivity at saturation is m s−1 (or 1.5 cm d−1) for the original and m s−1 (or 112 cm d−1) for the new scheme. Note that the new scheme has one less adjustable parameter.
4.4 Considerations of the hydraulic conductivity at saturation
Because the saturated hydraulic conductivity is relatively easy to measure, many determine Ks experimentally. As emphasized earlier, the use of Ks for scaling the relative hydraulic conductivity function should be avoided as much as possible. Still, Ks provides valuable information for the hydraulic behavior of soils at and close to saturation, which cannot be derived from the WRC. Within the context of modeling macropore flow, Nimmo (2021) identified a need for approaches to determine the properties of the matrix only while excluding the remainder of the porous medium. Predictions of a capillary conductivity function may help to fill this research gap.
Our approach predicts the capillary hydraulic conductivity in the matrix domain up to a minimum suction. Following Jarvis (2007), we may choose for this a suction of about 0.06 m (pore diameter approximately 0.5 mm) up to which the macropore conductivity can be neglected. Accordingly, we call the conductivity at hcrit = 0.06 m the “saturated matrix conductivity” (Ks,matrix). Knowledge of Ks,matrix could substantially improve the parameterization of simulation models that explicitly distinguish between matrix and macropore flow (e.g., Reck et al., 2018; van Schaik et al., 2010).
The shape of the conductivity function in the macropore-affected range cannot be predicted using capillary bundle models (Durner, 1994). Thus, it is preferable to cover the region between Ks,matrix and the measured Ks using some interpolation function such as proposed by Schaap and van Genuchten (2006). Using the abovementioned value of 0.06 m for hcrit as a starting point for the interpolation and assuming that the saturated conductivity (Ks) is reached at a pore diameter of 5 mm (i.e., at hs= 0.006 m), we can formalize the interpolation as
As an example, we illustrate the interpolation with a simple smooth cosine interpolation function, with the log of the suction in the argument (Fig. 9). Mathematically, this interpolation is expressed as
with the transformed variables y=log (K) and x=log(h) and consideration of the corresponding subscripts. We note that the real course of the K(h) function in this moisture region probably will be different; hence, other interpolation schemes could be used. Still, any interpolation will probably improve the performance of numerical models if such conditions close to full saturation are encountered.
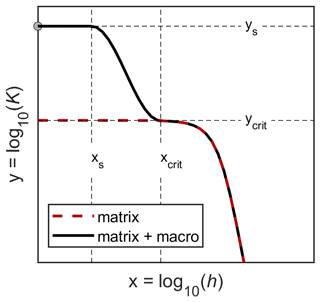
Figure 9Interpolation scheme between the predicted capillary conductivity (red dashed line) and the measured value of Ks (gray dot).
Figure 10 shows the practical application of the above interpolation scheme for the data given in Fig. 1 (top). The PDI water retention function was fitted to the retention data, while K(h) was predicted from the WRC from dryness to h= 0.06 m. From h=0.06 m to h=0.006 m, the smooth interpolation scheme (Eq. 24) was applied. With this scheme, we obtained a description of hydraulic conductivity from oven dryness to full saturation.
The unsaturated hydraulic conductivity of soils is still the most difficult hydraulic property to directly measure. The availability of commercial systems that allow one to determine SHPs using the simplified evaporation method has improved the situation somewhat; still, available conductivity data generally are restricted to a relatively limited soil moisture range so that predictive models for the hydraulic conductivity curve continue to play a critical role. To date, such predictions mostly use pore-bundle models that require measured conductivity data to scale the predicted curves. However, the HCC outside the range for which measured data are available is highly uncertain. In this contribution we presented a prediction scheme for the hydraulic conductivity covering the moisture range from very dry conditions to almost full saturation. The PDI modeling framework predicts three components of the conductivity, namely, vapor, non-capillary, and capillary liquid conductivity as absolute values from the water retention function.
Pore-bundle models do not in themselves account for important characteristics such as path elongation due to tortuosity, surface roughness of pore walls, non-circular capillaries, dead-end pores, physical properties of the liquid phase, etc. These effects can be accounted for with a parameter that is called tortuosity coefficient. We divide this parameter into two factors: a saturated tortuosity factor and a relative tortuosity function that takes the dependence of tortuosity on water content into account. The saturated tortuosity factor is shown to vary little among different soils, and we have determined a universal value empirically from data. The new scheme using a saturated tortuosity factor with an assigned universal value can be used to predict the hydraulic conductivity curve from the water retention curve when insufficient or no conductivity data are available.
The proposed general prediction scheme was tested by combining it with four parametric water retention models. Of these, the PDI model with the Fredlund and Xing (1994) basic saturation function and the model of van Genuchten with independent parameters m and n as basic function performed best. The identified value for the saturated tortuosity coefficient τs was 0.095. From a practical point of view, τs may simply be set to 0.1. The prediction accuracy with the new model was tested using a set of 23 soils for which measured K values were available. For the best-performing model FX-PDI, the predictions matched the measured data on average with a RMSElogK of about 0.4, without a bias between the predicted functions and measured data.
The conductivity estimation using our approach involves the conductivity of the soil matrix only and as such excludes the effects of the soil structure. The scheme is applicable only if retention data are available, and it opens new possibilities to use existing retention data collections (e.g., Gupta et al., 2022). The approach will also be helpful for situations where a measured value of the saturated conductivity Ks is available and where soil structure plays a role (which is the rule for most topsoils). In such cases, the predicted HCC can be combined with an interpolation towards Ks to obtain a well-estimated conductivity function over the full moisture range. Differentiating between structural and textural effects enables a physically more consistent use of measured SHP information.
In the cases where measured unsaturated conductivity data are available (such as from the simplified evaporation method), the proposed model with fixed τs can be fitted by adjusting a soil-specific relative tortuosity coefficient. This leads to a more reliable description of the conductivity function in the wet range, where no data are available, relative to current model approaches. Our new scheme can therefore improve the fitting of SHP models to measurements and can be implemented easily in the standard optimization software packages.
A1 The PDI model system
A1.1 PDI water retention function
The capillary saturation function Sc [–] and a non-capillary saturation function Snc [–] may be superimposed in the following form (Iden and Durner, 2014):
in which the first right-hand term holds for water stored in capillaries, and the second term holds for water stored in adsorbed water films and pore corners. θ [m3 m−3] is the total water content, h [m] is the suction head, and θs [m3 m−3] and θr [m3 m−3] are the saturated and maximum adsorbed water contents, respectively. To meet the physical requirement that the capillary saturation function reaches zero at oven dryness, a basic saturation function Γ(h) is scaled by (Iden and Durner, 2014)
with h0 [m] being the suction head at oven dryness, which can be set to 104.8 m following Schneider and Goss (2012). Γ(h) can be any unimodal or multimodal saturation function such as the unimodal functions of van Genuchten (1980) and Kosugi (1996) or their bimodal versions (Durner, 1994; Romano et al., 2011).
The saturation function for non-capillary water is given by a smoothed piecewise linear function (Iden and Durner, 2014), which is here given in the notation of Peters et al. (2021):
in which the parameter ha [m] reflects the suction head where non-capillary water reaches its saturation (fixed in our study to the suction at which capillary saturation reaches 0.75). We note that in earlier publications, we set for the constrained van Genuchten function. For the vGmn and the FX models, however, α−1 may be very high although the capillary saturation decreases already at low suctions. Setting would lead in such cases to unrealistic retention functions with Snc being close to unity, whereas Sc is already close to zero. The calculation scheme for ha as a quantile of Sc is given in Appendix A2. The parameter h0 in Eq. (A3) is the suction head where the water content reaches zero, which reflects the suction at oven-dry conditions. Snc(h) increases linearly from zero at oven dryness to its maximum value of 1.0 at ha, and it then remains constant towards saturation. In order to ensure a continuously differentiable water capacity function, Snc(h) must be smoothed around ha, which is achieved by the smoothing parameter b [–] (Iden and Durner, 2014), given here by
where bo=0.1 ln (10), and .
A1.2 PDI hydraulic conductivity
The PDI hydraulic conductivity model is expressed as (Peters et al., 2021)
where Kr,c [–] is the relative conductivity for the capillary component, Ks,c [m s−1] is the saturated conductivity for the capillary components, and Knc and Kv [m s−1] are the non-capillary and isothermal vapor conductivities, respectively. Knc is given by (Peters et al., 2021)
in which c is used to account for several physical and geometrical constants and being either a free fitting parameter to scale Knc or m s−1. Parameter θm [–] is the water content at h=103 m. We refer to Saito et al. (2006) or Peters (2013) for details regarding the formulation of Kv as a function of the invoked WRC. Note that the capillary liquid conductivity is formulated as a relative conductivity, which has to be scaled with a measured value, whereas the non-capillary conductivity and the isothermal vapor conductivity are formulated as absolute conductivities.
The relative conductivity for water flow in capillaries is in this paper described using the pore bundle model of Mualem (1976a), which reads in the PDI notation (Peters, 2014) as
where λ [–] is the tortuosity and connectivity parameter, and X is a dummy variable of integration.
A2 Calculation of ha as a function of the Sc quantile
Peters (2013) proposed two methods to define the critical tension ha (m) for the non-capillary saturation function Snc (–). He decided to set for van Genuchten's model and ha=hm for Kosugi's model (1996). His second option was to define ha as a quantile of the capillary saturation function, while suggesting the value of 0.5 as a potential choice. For completeness, we repeat here the relevant equations.
The capillary saturation function of van Genuchten is given by
Recall that this function ensures a saturation of zero at the suction corresponding to oven dryness, h0 (L). Iden and Durner (2014) proposed to scale Eq. (A8) using the function
where According to Peters (2013), we define the suction ha as
where β [–] represents the chosen quantile of Sc. Combining Eqs. (A8)–(A10) and solving for ha yields
in which the constant γ is defined as
Applying the same approach to the capillary saturation function of Kosugi (1996), i.e.,
yields
Thirdly, for the capillary saturation of Fredlund and Xing (1994), given as
we obtain
The 12 data sets used in this paper for model calibration are collected from the published literature and are available as follows. Cal 1 to Cal 3: Mualem (1976b); Cal 4 and Cal 6 (originally published in Pachepsky et al., 1984): Tuller and Or (2001); Cal 5: (originally published in Pachepsky et al., 1984): Zhang (2010); Cal 7 to Cal 12: Sarkar et al. (2019). The test data sets Test 1 to Test 23 can be obtained from the corresponding author upon request.
The supplement related to this article is available online at: https://doi.org/10.5194/hess-27-1565-2023-supplement.
Conceptualization: AP; model implementation and analysis: AP and TLH; draft preparation and discussions: AP, TLH, SCI, MTvG and WD; All authors read and approved the final paper.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This study was supported by the Deutsche Forschungsgemeinschaft (DFG grant PE 1912/4-1). We thank Gerrit de Rooij and John Nimmo as reviewers for their constructive comments, as well as Erwin Zehe for handling the manuscript.
This research has been supported by the Deutsche Forschungsgemeinschaft (grant no. PE 1912/4-1).
This open-access publication was funded by Technische Universität Braunschweig.
This paper was edited by Erwin Zehe and reviewed by John R. Nimmo and Gerrit H. de Rooij.
Assouline, S. and Or, D.: Conceptual and parametric representation of soil hydraulic properties: A review, Vadose Zone J., 12, 1–20, https://doi.org/10.2136/vzj2013.07.0121, 2013.
Bear, J.: Dynamics of Fluids in Porous Media, Elsevier, New York, ISBN 0486131807, 1972.
Brooks, R. H. and Corey, A. T.: Hydraulic properties of porous media. Hydrology Paper No. 3. Civil Engineering Department, Colorado State University, Fort Collins, CO, https://hess.copernicus.org/articles/27/385/2023/hess-27-385-2023.pdf (last access: 14 April 2023), 1964.
Burdine, N.: Relative permeability calculations from pore size distribution data, J. Petrol. Technol., 5, 71–78, 1953.
Carman, P. C.: Fluid flow through granular beds, Transactions, Institution of Chemical Engineers, London, 15, 150–166, 1937.
Childs, E. C. and Collis-George, N.: The permeability of porous materials, Proc. R. Soc. Lon. Ser.-A, 201, 392–405, 1950.
Duan, Q., Sorooshian, S., and Gupta, V.: Effective and efficient global optimization for conceptual rainfall-runoff models, Water Resour. Res., 28, 1015–1031, 1992.
Durner, W.: Predicting the unsaturated hydraulic conductivity using multi-porosity water retention curves, in: Proceedings of the International Workshop, Indirect Methods for Estimating the Hydraulic Properties of Unsaturated Soils, edited by: Van Genuchten, M. Th., Leij, F. J., and Lund, L. J., Univ. of California, Riverside, 185–202, 1992.
Durner, W.: Hydraulic conductivity estimation for soils with heterogeneous pore structure, Water Resour. Res., 30, 211–222, https://doi.org/10.1029/93WR02676, 1994.
Flühler, H. and Roth, K.: Physik der ungesättigten Zone. Lecture notes, Institute of Terrestrial Ecology, Swiss Federal Institute of Technology Zurich, Switzerland, 2004.
Fredlund, D. G. and Xing, A. Q.: Equations for the soil-water characteristic curve, Can. Geotech. J., 31, 521–532, https://doi.org/10.1139/t94-061, 1994.
Ghanbarian, B., Hunt, A. G., Ewing, R. P., and Sahimi, M.: Tortuosity in porous media: a critical review, Soil Sci. Soc. Am. J., 77, 1461–1477, 2013.
Guarracino, L.: Estimation of saturated hydraulic conductivity Ks from the van Genuchten shape parameter α, Water Resour. Res., 43, W11502, https://doi.org/10.1029/2006WR005766, 2007.
Gupta, S., Papritz, A., Lehmann, P., Hengl, T., Bonetti, S., and Or, D.: Global Soil Hydraulic Properties dataset based on legacy site observations and robust parameterization, Scientific Data, 9, 1–15, 2022.
Haverkamp, R., Zammit, C., Boubkraoui, F., Rajkai, K., Arrue, J. L., and Heckmann, N.: GRIZZLY, Grenoble soil catalogue: Soil survey of field data and description of particle-size, soil water retention and hydraulic conductivity functions, Lab. d'Etude des Transferts en Hydrol. et en Environ., Grenoble, France, 1997.
Hurvich, C. and Tsai, C.: Regression and time series model selection in small samples, Biometrika, 76, 297–307, https://doi.org/10.1093/biomet/76.2.297, 1989.
Iden, S. and Durner, W.: Comment on “Simple consistent models for water retention and hydraulic conductivity in the complete moisture range” by A. Peters, Water Resour. Res., 50, 7530–7534, https://doi.org/10.1002/2014WR015937, 2014.
Iden, S. C., Peters, A., and Durner, W.: Improving prediction of hydraulic conductivity by constraining capillary bundle models to a maximum pore size, Adv. Water Resour., 85, 86–92, 2015.
Iden, S. C., Blöcher, J., Diamantopoulos, E., and Durner, W.: Capillary, film, and vapor flow in transient bare soil evaporation (1): Identifiability analysis of hydraulic conductivity in the medium to dry moisture range, Water Resour. Res., 57, e2020WR028513, https://doi.org/10.1029/2020WR028513, 2021a.
Iden, S. C., Diamantopoulos, E., and Durner, W.: Capillary, film, and vapor flow in transient bare soil evaporation (1): Experimental identification of hydraulic conductivity in the medium to dry moisture range, Water Resour. Res., 57, e2020WR028514, https://doi.org/10.1029/2020WR028514, 2021b.
Ippisch, O., Vogel, H.-J., and Bastian, P.: Validity limits for the van Genuchten–Mualem model and implications for parameter estimation and numerical simulation, Adv. Water Resour., 29, 1780–1789, 2006.
Jarvis, N. J.: A review of non-equilibrium water flow and solute transport in soil macropores: Principles, controlling factors and consequences for water quality, Eur. J. Soil. Sci., 58, 523–546, 2007.
Kirste, B., Iden, S. C., and Durner, W.: Determination of the soil water retention curve around the wilting point: Optimized protocol for the dewpoint method, Soil Sci. Soc. Am. J., 83, 288–299, 2019.
Kosugi, K.: Lognormal distribution model for unsaturated soil hydraulic properties, Water Resour. Res., 32, 2697–2703, 1996.
Kozeny, J.: Über kapillare Leitung des Wassers im Boden, Sitzungsberichte Wiener Akademie, 136, 271–306, 1927.
Kunze, R. J., Uehara, G., and Graham, K.: Factors important in the calculation of hydraulic conductivity, Soil Sci. Soc. Am. J., 32, 760–765, 1968.
Kutílek, M. and Nielsen, D. R.: Soil hydrology: texbook for students of soil science, agriculture, forestry, geoecology, hydrology, geomorphology and other related disciplines, Catena Verlag, ISBN 9783923381265, 1994.
Lebeau, M. and Konrad, J.-M.: A new capillary and thin film flow model for predicting the hydraulic conductivity of unsaturated porous media, Water Resour. Res., 46, W12554, https://doi.org/10.1029/2010WR009092, 2010.
Madi, R., de Rooij, G. H., Mielenz, H., and Mai, J.: Parametric soil water retention models: a critical evaluation of expressions for the full moisture range, Hydrol. Earth Syst. Sci., 22, 1193–1219, https://doi.org/10.5194/hess-22-1193-2018, 2018.
Millington, R. J. and Quirk, J. P.: Permeability of porous solids, T. Faraday Soc., 57, 1200–1207, 1961.
Mishra, S. and Parker, J. C.: On the relation between saturated conductivity and capillary retention characteristics, Groundwater, 28, 775–777, 1990.
Mualem, Y.: A new model for predicting the hydraulic conductivity of unsaturated porous media, Water Resour. Res., 12, 513–522, 1976a.
Mualem, Y.: A catalog of the hydraulic properties of unsaturated soils (Tech. Rep), Technion – Israel Institute of Technology, 1976b.
Mualem, Y.: Hydraulic conductivity of unsaturated soils: Prediction and formulas, Methods of Soil Analysis: Part 1 Physical and Mineralogical Methods, 5, 799–822, https://doi.org/10.2136/sssabookser5.1.2ed.c31, 1986.
Nasta, P., Vrugt, J. A., and Romano, N.: Prediction of the saturated hydraulic conductivity from Brooks and Corey's water retention parameters, Water Resour. Res., 49, 2918–2925, 2013.
Nielsen, D. R., Kirkham, D., and Perrier, E. R.: Soil capillary conductivity: Comparison of measured and calculated values, Soil Sci. Soc. Am. J., 24, 157–160, 1960.
Nielson, D. R., Biggar, J. W., and Erh, K. T.: Spatial variability of field-measured soil-water properties, Hilgardia, 42, 215–259, 1973.
Nimmo, J. R.: The processes of preferential flow in the unsaturated zone, Soil Sci. Soc. Am. J., 85, 1–27, 2021.
Pachepsky, Y., Scherbakov, R., Varallyay, G., and Rajkai, K.: On obtaining soil hydraulic conductivity curves from water retention curves, Pochvovedenie, 10, 60–72, 1984 (in Russian).
Peters, A.: Simple consistent models for water retention and hydraulic conductivity in the complete moisture range, Water Resour. Res., 49, 6765–6780, https://doi.org/10.1002/wrcr.20548, 2013.
Peters, A.: Reply to comment by S. Iden and W. Durner on “Simple consistent models for water retention and hydraulic conductivity in the complete moisture range”, Water Resour. Res., 50, 7535–7539, https://doi.org/10.1002/2014WR016107, 2014.
Peters, A. and Durner, W.: A simple model for describing hydraulic conductivity in unsaturated porous media accounting for film and capillary flow, Water Resour. Res., 44,W11417, https://doi.org/10.1029/2008WR007136, 2008a.
Peters, A. and Durner, W.: Simplified evaporation method for determining soil hydraulic properties, J. Hydrol., 356, 147–162, https://doi.org/10.1016/j.jhydrol.2008.04.016, 2008b.
Peters, A. and Durner, W.: Reply to comment by N. Shokri and D. Or on “A simple model for describing hydraulic conductivity in unsaturated porous media accounting for film and capillary flow”, Water Resour. Res., 46, W06802, https://doi.org/10.1029/2010WR009181, 2010.
Peters, A. and Durner, W.: SHYPFIT 2.0 User's Manual. Research Report. Institut für Ökologie, Technische Universität Berlin, Germany, 2015.
Peters, A., Durner, W., and Wessolek, G.: Consistent parameter constraints for soil hydraulic functions, Adv. Water Resour., 34, 1352–1365, 2011.
Peters, A., Iden, S. C., and Durner, W.: Revisiting the simplified evaporation method: Identification of hydraulic functions considering vapor, film and corner flow, J. Hydrol., 527, 531–542, https://doi.org/10.1016/j.jhydrol.2015.05.020, 2015.
Peters, A., Iden, S. C., and Durner, W.: Local Solute Sinks and Sources Cause Erroneous Dispersion Fluxes in Transport Simulations with the Convection–Dispersion Equation, Vadose Zone J., 18, 190064, https://doi.org/10.2136/vzj2019.06.0064, 2019.
Peters, A., Hohenbrink, T. L., Iden, S. C., and Durner, W.: A simple model to predict hydraulic conductivity in medium to dry soil from the water retention curve, Water Resour. Res., 57, e2020WR029211, https://doi.org/10.1029/2020WR029211, 2021.
Reck, A., Jackisch, C., Hohenbrink, T. L., Schröder, B., Zangerlé, A., and van Schaik, L.: Impact of Temporal Macropore Dynamics on Infiltration: Field Experiments and Model Simulations, Vadose Zone J., 17, 170147, https://doi.org/10.2136/vzj2017.08.0147, 2018.
Romano, N., Nasta, P., Severino, G., and Hopmans, J. W.: Using Bimodal Lognormal Functions to Describe Soil Hydraulic Properties, Soil Sci. Soc. Am. J., 75, 468–480, https://doi.org/10.2136/sssaj2010.0084, 2011.
Saito, H., Šimůnek, J., and Mohanty, B. P.: Numerical analysis of coupled water, vapor, and heat transport in the vadose zone, Vadose Zone J., 5, 784–800, 2006.
Sarkar, S., Germer, K., Maity, R., and Durner, W.: Measuring near-saturated hydraulic conductivity of soils by quasi unit-gradient percolation – 2. Application of the methodology, J. Plant Nutr. Soil Sc., 182, 535–540, https://doi.org/10.1002/jpln.201800383, 2019.
Schaap, M. G. and Leij, F. J.: Improved prediction of unsaturated hydraulic conductivity with the Mualem-van Genuchten model, Soil Sci. Soc. Am. J., 64, 843–851, 2000.
Schaap, M. G. and Van Genuchten, M. Th.: A modified Mualem–van Genuchten formulation for improved description of the hydraulic conductivity near saturation, Vadose Zone J., 5, 27–34, 2006.
Schelle, H., Heise, L., Jänicke, K., and Durner, W.: Water retention characteristics of soils over the whole moisture range: A comparison of laboratory methods, Eur. J. Soil. Sci., 64, 814–821, 2013.
Schindler, U.: Ein Schnellverfahren zur Messung der Wasserleitfähigkeit im teilgesättigten Boden an Stechzylinderproben, Arch. Acker-u. Pflanzenbau u. Bodenkd. Berlin, 24, 1–7, 1980.
Schneider, M. and Goss, K.-U.: Prediction of the water sorption isotherm in air dry soils, Geoderma, 170, 64–69, https://doi.org/10.1016/j.geoderma.2011.10.008, 2012.
Tuller, M. and Or, D.: Hydraulic conductivity of variably saturated porous media: Film and corner flow in angular pore space, Water Resour. Res., 37, 1257–1276, https://doi.org/10.1029/2000WR900328, 2001.
Tokunaga, T. K.: Hydraulic properties of adsorbed water films in unsaturated porous media, Water Resour. Res., 45, W06415, https://doi.org/10.1029/2009WR007734, 2009.
Usowicz, B. and Lipiec, J.: Spatial variability of saturated hydraulic conductivity and its links with other soil properties at the regional scale, Sci. Rep., 11, 1–12, 2021.
van Genuchten, M. Th.: A closed-form equation for predicting the hydraulic conductivity of unsaturated soils, Soil Sci. Soc. Am. J., 44, 892–898, 1980.
van Schaik, L., Hendriks, R. F. A., and Jvan Dam, J.: Parameterization of macropore flow using dye-tracer infiltration patterns in the SWAP model, Vadose Zone J., 9, 95–106, https://doi.org/10.2136/vzj2009.0031, 2010.
Vogel, T., Van Genuchten, M. T., and Cislerova, M.: Effect of the shape of the soil hydraulic functions near saturation on variably-saturated flow predictions, Adv. Water Resour., 24, 133–144, 2000.
Weber, T. K., Durner, W., Streck, T., and Diamantopoulos, E.: A modular framework for modeling unsaturated soil hydraulic properties over the full moisture range, Water Resour. Res., 55, 4994–5011, 2019.
Zhang, Z. F.: Soil water retention and relative permeability for conditions from oven-dry to full saturation, Vadose Zone J., 10, 1299–1308, https://doi.org/10.2136/vzj2011.0019, 2011.