Diel streamflow cycles suggest more sensitive snowmelt-driven streamflow to climate change than land surface modeling does

Climate warming will cause mountain snowpacks to melt earlier, reducing summer streamflow and threatening water supplies and ecosystems. Quantifying how sensitive streamflow timing is to climate change and where it is most sensitive remain key questions. Physically based hydrological models are often used for this purpose; however, they have embedded assumptions that translate into uncertain hydrological projections that need to be quantified and constrained to provide reliable inferences. The purpose of this study is to evaluate differences in projected end-of-century changes to streamflow timing between a new empirical model based on diel (daily) streamflow cycles and regional land surface simulations across the mountainous western USA. We develop an observational technique for detecting streamflow responses to snowmelt using diel cycles of incoming solar radiation and streamflow to detect when snowmelt occurs. We measure the date of the 20th percentile of snowmelt days (DOS₂₀) across 31 western USA watersheds affected by snow, as a proxy for the beginning of snowmelt-initiated streamflow. Historic DOS₂₀ varies from mid-January to late May among our sites, with warmer basins having earlier snowmelt-mediated streamflow. Mean annual DOS₂₀ strongly correlates with the dates of 25 % and 50 % annual streamflow volume (DOQ₂₅ and DOQ₅₀, both R²=0.85), suggesting that a 1 d earlier DOS₂₀ corresponds with a 1 d earlier DOQ₂₅ and 0.7 d earlier DOQ₅₀. Empirical projections of future DOS₂₀ based on a stepwise multiple linear regression across sites and years under the RCP8.5 scenario for the late 21st century show that DOS₂₀ will occur on average 11±4 d earlier per 1 ^∘C of warming. However, DOS₂₀ in colder watersheds (mean November–February air temperature, $T_{\mathrm{NDJF}}<-\mathrm{8}$ ^∘C) is on average 70 % more sensitive to climate change than in warmer watersheds (T_NDJF>0 ^∘C). Moreover, empirical projections of DOQ₂₅ and DOQ₅₀ based on DOS₂₀ are about four and two times more sensitive to climate change, respectively, than those simulated by a state-of-the-art land surface model (NoahMP-WRF) under the same scenario. Given the importance of changes in streamflow timing for water resources, and the significant discrepancies found in projected streamflow sensitivity, snowmelt detection methods such as DOS₂₀ based on diel streamflow cycles may help to constrain model parameters, improve hydrological predictions, and inform process understanding.

1 Introduction

Earlier streamflow caused by earlier snowmelt is of great concern in a changing climate (Barnett et al., 2005; Harpold and Brooks, 2018; Musselman et al., 2017; Stewart et al., 2004, 2005). Earlier winter and spring streamflow volume comes at the expense of later summer streamflow in regions like the western United States (USA; Hidalgo et al., 2009; McCabe and Clark, 2005; Regonda et al., 2005; Stewart et al., 2004, 2005) and challenges reservoir operations (Barnett et al., 2005; Immerzeel et al., 2020; Viviroli et al., 2011). Furthermore, ecosystems may evaporate more water as reductions in albedo increase energy inputs (Meira Neto et al., 2020; Gordon et al., 2022), decreasing runoff from upland forested watersheds (Foster et al., 2016; Jepsen et al., 2018; Milly and Dunne, 2020). More than 50 % of mountainous watersheds play essential roles in supporting downstream systems (Viviroli et al., 2007), and snowpack changes are likely to increase lowland agriculture water stress (Immerzeel et al., 2020). However, it remains difficult to predict how much streamflow timing and amount will shift in future climates (Gordon et al., 2022) due to altered snow accumulation patterns (Mote et al., 2018) and melt rates (Musselman et al., 2017) and shifts from snowfall to rainfall (Klos et al., 2014).

Physically based hydrological models are typically used to predict how snow accumulation and melt will interact with the critical zone (CZ) to affect short-term flooding and seasonal water supply (Kopp et al., 2018; Wood and Lettenmaier, 2006). In mountainous regions like the western USA, models need to accurately simulate snow processes across watersheds with varying snowpack conditions (Serreze et al., 1999) and then transport and store that water in the CZ with varying subsurface properties (Brooks et al., 2015). More precipitation falling as rain instead of snow will result in streamflow dynamics that more closely mirror the amount and timing of rainfall. Precipitation phase (rainfall versus snowfall) is mediated by basin elevation and hypsometry (Jennings et al., 2018; Wayand et al., 2015), which also influences precipitation amounts (Houze, 2012), with higher elevations and steeper watersheds typically having higher precipitation and snowfall. Solar radiation is the primary energy source for snowmelt in snow-dominated montane watersheds (Cline, 1997; Marks and Dozier, 1992). Conversely, cloudiness lowers solar radiation and melt rates (Sumargo and Cayan, 2018). Shallower snowpacks have less cold content and begin to melt earlier when solar radiation is lower (Harpold et al., 2012; Harpold and Brooks, 2018; Musselman et al., 2017), which shifts streamflow earlier (Clow, 2010). Storage and drainage of water in the CZ control the sensitivity of streamflow to earlier rain or meltwater inputs. For example, snowmelt-mediated spring streamflow timing is more sensitive to climate change in watersheds with rapid subsurface drainage than in landscapes with deep groundwater reservoirs that drain slowly (Safeeq et al., 2013). In contrast, slow-draining watersheds have greater sensitivity to snowmelt-mediated summer streamflow volume from climate change (Tague and Grant, 2009). The complexity of these storage relationships is exemplified by isotopic evidence showing that the fraction of streamflow that is young water (less than 3 months old) is smaller in steeper watersheds (Jasechko et al., 2016), suggesting that physically modeling interactions between CZ water storage and changing hydrometeorology will be challenging in mountainous areas. In a recent data-driven review, Gordon et al. (2022) proposed a predictive framework composed of three testable and interrelated mechanisms to infer changes to snowmelt-driven streamflow response under warming. Such mechanisms are associated with snow season energy and mass exchanges and the intensity of snow season liquid water input and the synchrony of energy and water availability, and their analysis highlights the complexities in predicting future streamflow in regions where multiple mechanisms interact.

Hydrologists typically apply the following two types of modeling tools to predict streamflow: empirical models and more mechanistically oriented models (conceptual or physically based land surface models). Empirical models assume that long-term and often site-to-site statistical relationships among predictor variables (e.g., precipitation and air temperature) and water fluxes (e.g., evapotranspiration and streamflow) can be used to understand and model their likely changes over time or space. Empirical models used to predict changes over time (sometimes referred to as space-for-time substitutions) have been used to predict responses to climate change in fields such as hydrology (Goulden and Bales, 2014; Jepsen et al., 2018; Sivapalan et al., 2011), biodiversity (Blois et al., 2013), and tree growth (Klesse et al., 2020). Such models use retrospective information from different places (space), typically spanning wide range of conditions (e.g., climate gradients), to predict future changes over time. For example, observed characteristics from warm regions maybe used to infer future changes in cold regions due to global warming. A limitation of this approach is that it neglects non-correlated (or independent) changes in spatially variable factors (Jepsen et al., 2018). For example, heterogeneous patterns of warming, variations in precipitation and vegetation, or changes that occur at different temporal scales (e.g., development of soil properties over hundreds to thousands of years versus shifts from rain to snow over hours) are implicitly neglected in such empirical frameworks.

Conversely, physically based models embed state-of-the-art physical understanding of hydrological processes. These models typically require some degree of calibration or validation to observations (e.g., daily streamflow) to improve and assess their predictive skill. The current generation of regional weather models using the Weather Research and Forecasting model (WRF; Skamarock et al., 2008) coupled to the Noah-Multiple Parameterization land surface model (Noah-MP; Niu et al., 2011), which we refer as NoahMP-WRF, has shown promising results for modeling atmospheric and snow processes in the contiguous USA (He et al., 2019; Liu et al., 2017; Musselman et al., 2017; Scaff et al., 2020). For example, snow simulations have been used to quantify mountain snowmelt and streamflow response to climate change (Musselman et al., 2017, 2018). These simulations use a pseudo global warming approach, which perturbs the historical climate with a climate change signal from an ensemble of global climate models (GCMs); using this perturbation avoids systemic biases in the GCMs and avoids issues related to their interannual variability (Liu et al., 2017). Comparisons between land surface models and empirically based predictions of future streamflow are rare but valuable (Jepsen et al., 2018) and could help to diagnose modeling deficiencies and improve predictions.

New observations of streamflow generation during snowmelt could be key to improving current hydrological models. Determining whether streamflow response was produced by rainfall or snowmelt is an important but difficult task (Weiler et al., 2018). Few simple, low-cost observational tools are available to separate rainfall-driven from snowmelt-driven contributions to streamflow or to separate this year's snowmelt from the previous years' melt and storage. One method that can be straightforwardly applied to existing long-term observations is based on coupled diel cycles in solar radiation, snowmelt, and streamflow (Kirchner et al., 2020; Lundquist and Cayan, 2002). Diel (24 h) cycles in streamflow and shallow groundwater levels can result from daily cycles in snow-/ice melt and evapotranspiration, which are both ultimately driven by solar radiation inputs (Kirchner et al., 2020). This mechanistic response has been used to study watershed properties like kinematic wave celerity (Kirchner et al., 2020), the impact of snowpack variability on streamflow timing (Lundquist and Dettinger, 2005), groundwater fluctuations (Loheide and Lundquist, 2009), and transitions from snowmelt to evapotranspiration-dominated streamflow fluctuations (Kirchner et al., 2020; Mutzner et al., 2015; Woelber et al., 2018). More recently, Kirchner et al. (2020) combined local observations and remote sensing to show that streamflow diel response was tightly controlled by the timing of snowpack disappearance. However, it remains unknown whether information embedded in the diel streamflow response following snowmelt events can be used to inform streamflow predictions under climate change and whether such projections are consistent with current state-of-the-art hydrological modeling. The purpose of this research is to evaluate whether land surface hydrology model simulations and a new diel streamflow-based empirical model yield similar projected end-of-century changes in streamflow volume timing across mountainous western USA headwater watersheds. To this aim, we extend the diel cycle index approach of Kirchner et al. (2020) using diel streamflow observations to detect days when streamflow is coupled to snowmelt inputs (i.e., a snowmelt-dominated streamflow event) and investigate their contributions to historical variability in streamflow volume timing. We then compare empirical diel streamflow-based projections by the end of the century under a RCP8.5 pseudo global warming scenario against predictions from a state-of-the-art land surface model (under the same climate scenario) across 31 mountainous watersheds in the western USA to answer the following questions:

1. Do historical diel streamflow cycles indicate earlier snowmelt in warmer watersheds and years, and can we use diel observations of snowmelt to predict the timing of streamflow volume?

2. In which watersheds is the timing of snowmelt the most sensitive to climate change, as projected by an empirical diel streamflow-based model?

3. Do historical streamflow volume timings and future empirical diel streamflow-based projections diverge from commonly used, state-of-the-art land surface models?

A list with the abbreviations used in this study is presented in Table 1.

Table 1 List of abbreviations.

2 Methods

2.1 Study domain and data

We studied 31 mountainous watersheds in the western USA (Table 2), spanning snow fractions from 0.27 to 0.78 (Fig. A3a), aridity index values from 0.22 to 2.86 (Addor et al., 2017), and soil depths from 0.27 to 2.52 m (Addor et al., 2017; Pelletier et al., 2016; Table 2). These watersheds are part of the CAMELS (Catchments Attributes and MEteorology for Large-sample Studies) dataset (Addor et al., 2017; Newman et al., 2015), which provides daily streamflow and meteorological forcing, among other observed and simulated hydrometeorological variables at the watershed scale. These watersheds were chosen because their streamflows are unregulated, they have relatively small drainage areas (<250 km²), and they are at relatively high elevations (>1000 m a.s.l. – above sea level). This last criterion was introduced to focus on watersheds with snowmelt-driven streamflow regimes. The names, locations, elevations, slopes, drainage areas, and other key characteristics of the 31 watersheds are presented in Table 2.

Table 2 List of the 31 watersheds from the CAMELS dataset included in this study. Data are from Addor et al. (2017). Note: USGS is the United States Geological Survey.

The data used in this analysis include hourly streamflow, incoming shortwave radiation, mean daily relative humidity, air temperature, and precipitation. Hourly streamflow was obtained from the U.S. Geological Survey (USGS). Hourly incoming shortwave radiation is from phase 2 of the National Land Data Assimilation System (NLDAS-2; Xia et al., 2012) at the nearest grid point to the watershed outlet. Mean daily relative humidity, air temperature, and precipitation at the watershed scale are from CAMELS, based on the Daymet dataset (https://daymet.ornl.gov/, last access: 20 June 2022), which in turn is interpolated from existing ground observations. Available hourly streamflow records vary significantly across watersheds, extending back to 1986 for some sites. Figure A1a shows the number of years that have more than 70 %, 80 %, and 90 % of days with hourly records for the period between 1 December and 1 August. Based on this preliminary analysis, we selected water years with more than 80 % of days with hourly streamflow records. This threshold for data availability results in most watersheds having more than 5 years to analyze (except for site ID 10 and 30 with 4 years).

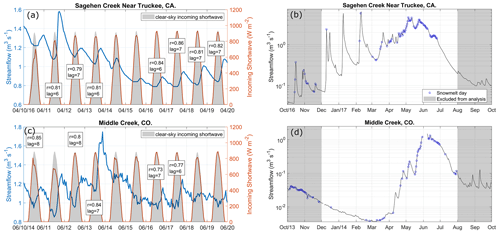
Figure 1 Examples of the diel cycle analysis applied to two watersheds located in (a, b) California (WY2016) and (c, d) Colorado (WY2014). Panels (a) and (c) show hourly solar radiation (orange) and streamflow (blue). The first statistically significant (p<0.01) lagged Spearman correlation (r>0.6) between streamflow and solar radiation is shown in a text box for clear-sky days only (>80 % of clear-sky solar radiation). Panels (b) and (d) show the solar radiation-driven snowmelt days (blue circles) on top of the annual hydrograph (semi-log scale) for the period of analysis (white background; December to July).

2.2 Snowmelt and streamflow diel coupling

To identify days when solar radiation-driven snowmelt is coupled to the streamflow response, hereafter called snowmelt days for simplicity, we calculated the correlation between hourly values of solar radiation and lagged streamflow (Fig. 1). A snowmelt day is defined as a day in which the Spearman correlation between hourly solar radiation and lagged streamflow is statistically significant (p value ≤ 0.01) and exceeds a given cutoff. Due to the lagged diel streamflow response after snowmelt, we lagged diel streamflow from solar radiation between 6 and 18 h, computed the correlation of all combinations, and kept those statistically significant correlations that were above a predefined correlation cutoff. Although having both a correlation cutoff and a statistical significance criterion may be redundant, we used both to guarantee significant correlations above different correlation cutoffs. We tried several correlation cutoffs (r>0.5, 0.6, 0.7, 0.8, and 0.9; see Fig. 1 for r>0.6) to assess their effects on the detection algorithm (Fig. A2). The preliminary lag window of 6 to 18 h was used to avoid confounding snowmelt signals with evapotranspiration (ET)-induced streamflow diel responses (Kirchner et al., 2020; Mutzner et al., 2015; Woelber et al., 2018). ET-induced streamflow diel response can positively correlate with solar radiation with lags below 6 h, due to the previous day's ET, and above 18 h, due to the next day's ET diurnal signal (Kirchner et al., 2020). However, this preliminary lag window may incorrectly select days with a rainfall-induced streamflow diel response or rain-on-snow events. To minimize this, we further restricted the lags that could be selected based on optimum lags from snowmelt days with clear skies. Clear-sky days were defined as days with solar radiation greater than 80 % of the clear-sky solar radiation value (gray areas in left panels on Fig. 1). This lag window was defined on a monthly and watershed basis and was calculated as the lags between the 10th and 90th percentile of clear-sky days with Spearman correlations above 0.8. This second filter also helped to avoid the incorrect selection of ET-induced streamflow diel response, as it minimized the chance of selecting 18 h lags that can be associated with ET. Despite efforts to select only snowmelt-driven streamflow diel responses, this methodology does not guarantee that rainfall-driven streamflow diel changes with lags within our lag window will always be excluded. Excluding such cases would require hourly precipitation observations, which are unavailable at some of our study watersheds. However, we believe that any such cases will minimally affect the results of our analysis.

To better assess the potential impact that rainfall may have on our proposed diel analysis, particularly on the effect of rain-on-snow events, we analyzed which days classified as snowmelt days also had rainfall. We assessed daily rainfall using the daily precipitation time series from CAMELS based on the Daymet product for each watershed. A false detection rate metric was computed for each watershed, in which every day classified as a snowmelt day with daily precipitation above 5 mm and a mean daily air temperature above 2 ^∘C was assumed to be misclassified (Fig. 2). A false detection rate of 100 % means that all snowmelt days were misclassified and 0 % means that no days had significant rainfall. On average, the false detection rate was estimated at 7 %, with a standard deviation of 5 %, and only watershed ID 24 and 31 (located in WA and OR, respectively) exceeded 15 %, with 21 % and 29 %, respectively. This suggests that the effect of potential rainfall-induced diel streamflow cycles (including rain-on-snow events) in most watersheds is low (except for watershed ID 24 and 31), supporting further analysis. We also assessed the mean cross-site false detection rate for precipitation thresholds of 1 and 10 mm and found reasonable values of 12 % and 3 %, respectively. However, we believe that 1 mm is not a reasonable threshold, as a 1 mm rainfall event would be unlikely to produce a distinguishable diel streamflow signal and could represent error/noise in the Daymet product.

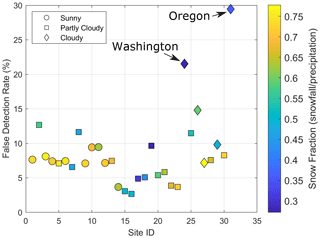
Figure 2 Percentage of days that were classified as having snowmelt following the diel streamflow cycle analysis that also had daily precipitation above 5 mm and a mean daily air temperature above 2 ^∘C. Symbols are associated with the mean annual percentage of snowmelt days under clear-sky conditions. Sunny sites (circles) have >90 %, clear-sky snowmelt days, partly cloudy sites (squares) have between 70 % and 90 %, and cloudy sites (diamonds) have <70 % clear-sky snowmelt days. Clear-sky snowmelt days are defined as those with more than 80 % of the potential clear-sky solar radiation.

2.3 The empirical diel streamflow-based model

We defined the day when the 20th percentile of the snowmelt days (as defined in Sect. 2.2) occurs (DOS₂₀) as a new metric to characterize the seasonality of early snowmelt for each water year and watershed. However, other metrics such as the 5th, 10th, and 30th percentiles (presented in the Appendix) were also investigated to assess the impact of this choice on the analysis. We chose this metric because we expected it to be associated with the timing of streamflow volume, and the choice of slightly earlier or later snowmelt day metrics (e.g., DOS₁₀ or DOS₃₀) would not substantially change our results. We fitted a stepwise multiple linear regression model (MLR; p value < 0.01; Eq. 1) to reconstruct historical DOS₂₀ across all watersheds and years (Fig. 7) using four climate variables as predictors, i.e., total precipitation, air temperature, relative humidity, and solar radiation, as follows:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\mathrm{DOS}}_{\mathrm{20}}& ={\mathit{\beta }}_{\mathrm{1}}{x}_{\mathrm{1}}+{\mathit{\beta }}_{\mathrm{2}}{x}_{\mathrm{2}}+{\mathit{\beta }}_{\mathrm{3}}{x}_{\mathrm{3}}+{\mathit{\beta }}_{\mathrm{4}}{x}_{\mathrm{4}}+{\mathit{\beta }}_{\mathrm{5}}{x}_{\mathrm{1}}{x}_{\mathrm{2}}+{\mathit{\beta }}_{\mathrm{6}}{x}_{\mathrm{1}}{x}_{\mathrm{3}}\\ & +{\mathit{\beta }}_{\mathrm{7}}{x}_{\mathrm{1}}{x}_{\mathrm{4}}+{\mathit{\beta }}_{\mathrm{8}}{x}_{\mathrm{2}}{x}_{\mathrm{3}}+{\mathit{\beta }}_{\mathrm{9}}{x}_{\mathrm{2}}{x}_{\mathrm{4}}+{\mathit{\beta }}_{\mathrm{10}}{x}_{\mathrm{3}}{x}_{\mathrm{4}},\end{array}\end{array}$$

where x₁ is cumulative air temperature (i.e., degree day; ^∘ C), x₂ is cumulative precipitation (mm), x₃ is mean relative humidity (%), x₄ is mean solar radiation (W m⁻²), and the β_i are regression coefficients. Mean annual climate variables were calculated for the period between 1 November and DOS₂₀ (i.e., between late fall and the metric representing the date of early snowmelt events). As a result, DOS₂₀ is present in both sides of Eq. (1); therefore, the stepwise MLR requires an iterative solution when used in a predictive mode (i.e., for the climate change analysis when DOS₂₀ is unknown). The MLR model is the basis of our empirical diel streamflow-based model which is used to assess changes in DOS₂₀ due to climate change (i.e., changes in x₁, x₂, x₃, and x₄ in Eq. 1). We verified the stepwise MLR assumptions, namely linear relationships between each predictor and DOS₂₀, normally distributed residuals, homoscedasticity, and the absence of strong multicollinearity (as suggested by a variance inflation factor < 3). We also tested other metrics related to the timing of early snowmelt events. These included the first snowmelt day, the first three consecutive snowmelt events, and the 5th, 10th, and 30th percentiles of snowmelt days (DOS₅, DOS₁₀, and DOS₃₀, respectively). All metrics were also computed using each of the different Spearman correlation cutoffs (Tables A1–A5), but the main analysis presented here focuses on DOS₂₀ based on snowmelt days calculated with hourly Spearman correlations > 0.8.

We predict changes to DOS₂₀ based on the stepwise MLR model and end-of-the-century mean climate change forcing from NoahMP-WRF (Liu et al., 2017). NoahMP-WRF was run under a high-emission scenario (RCP8.5), using the pseudo global warming approach for the end of the century. Overall, it projects a warmer (4–5.2 ^∘C), wetter (0 %–20 % increase in precipitation) climate (Figs. A4 and A5). These mean annual changes in climate were applied to the predictors in the stepwise MLR model to predict changes in DOS₂₀. As previously mentioned, predictors used in the stepwise MLR were calculated for the period between 1 November and DOS₂₀; therefore, as we do not know the value of DOS₂₀ in the future, an iterative solution is required to solve for DOS₂₀ in Eq. (1). We find a numerical solution, using a 2 d convergence threshold between iterations, so that |DOS20_i+1–DOS20${}_i|\le \mathrm{2}$ d, where i is the number of the iteration.

2.4 Streamflow volume timing from a land surface model

Historical NoahMP-WRF simulations include the period 2001–2013 over the contiguous USA at 4 km spatial resolution and the period 2071–2100 under pseudo global warming (Liu et al., 2017). NoahMP-WRF simulations include an improved Noah configuration, which aims to better represent the snow physics. These improvements include the following (Liu et al., 2017): the rain–snow transition is based on a microphysics partitioning approach as opposed to a subjective temperature-based approach, patchy snowpack are allowed in the calculation of the surface energy balance, the heat transport from rainfall to the ground is included, and the snow depletion curve is vegetation dependent. These improvements allow for a better representation of the surface energy balance and the simulation of snow accumulation and melt processes. We used daily watershed-scale outputs of surface and subsurface runoff from historical and future NoahMP-WRF simulations to estimate the date of 25 % and 50 % of annual streamflow volume (DOQ₂₅ and DOQ₅₀, respectively). Given the range of the watershed drainage areas (4–236 km²; Table 2), watersheds covering several grid cells use the total surface and subsurface runoff for their corresponding grid cells. Small watersheds are represented by only the single nearest NoahMP-WRF grid cell. The way NoahMP-WRF is implemented within WRF lacks a streamflow routing scheme such as the one in WRF-Hydro (Gochis et al., 2020); therefore, we used the sum of surface and subsurface runoff to estimate DOQ₂₅ and DOQ₅₀. We also repeated the analysis using surface runoff only, leading to similar results (Fig. A7). Given the relatively coarse NoahMP-WRF spatial resolution (4 km) compared to the watershed drainage areas (4–236 km²), we assume that mean streamflow timing metrics are not significantly affected by the lack of streamflow routing.

3 Results

3.1 Empirical relationships between DOS₂₀, climate, and streamflow

Mean annual DOS₂₀ (the date of the 20th percentile of snowmelt days) has a strong regional variability that is reasonably captured by a negative linear correlation (R²=0.48) with the mean winter air temperature (November to February; T_NDJF) in watersheds with $T_{\mathrm{NDJF}}<-\mathrm{3}$ ^∘C, whereas warmer watersheds do not follow the same pattern (Figs. 3a and 4a). Warmer sites ($T_{\mathrm{NDJF}}>-\mathrm{3}$ ^∘C) have a more variable mean DOS₂₀, ranging from mid-January to early May, whereas the coldest sites ($T_{\mathrm{NDJF}}<-\mathrm{8}$ ^∘C) have a later and less variable DOS₂₀ around mid- to late May. On average, the regression suggests that a 1 ^∘C warming of results in 7.2 d earlier DOS₂₀. A relationship between later DOS₂₀ and colder T_NDJF is also found in the year-to-year variations at most watersheds (21 out of 31; Fig. 3b). A strong negative linear relationship was found between the date of the 25 % of the annual streamflow volume (DOQ₂₅) and T_NDJF (Fig. 3c). Warmer watersheds (T_NDJF>0 ^∘C) generate streamflow earlier (DOQ₂₅ between mid-December and early March) compared to the coldest watersheds ($T_{\mathrm{NDJF}}<-\mathrm{8}$ ^∘C) where DOQ₂₅ is between early and late May (Fig. 3c). On average, the cross-site regression shows that each 1 ^∘C warmer T_NDJF produces a 13 d earlier DOQ₂₅. For most watersheds (25 out of 31), interannual regressions show a similar pattern, with warmer years having earlier DOQ₂₅; however, these interannual regressions have shallower slopes than the cross-site relationships (Fig. 3b and d). Previous work by Stewart et al. (2005) also related seasonal meteorological patterns with the spring onset and streamflow timing and found similar relationships (e.g., warmer watersheds have earlier spring onset and streamflow timing). However, the definition of the spring onset was based on the cumulative hydrograph (the day when the cumulative departure from the mean streamflow was the minimum), as opposed to our more mechanistic diel streamflow analysis. Other definitions for spring onset based on streamflow, snow pillows, and air temperature are presented by Lundquist et al. (2004).

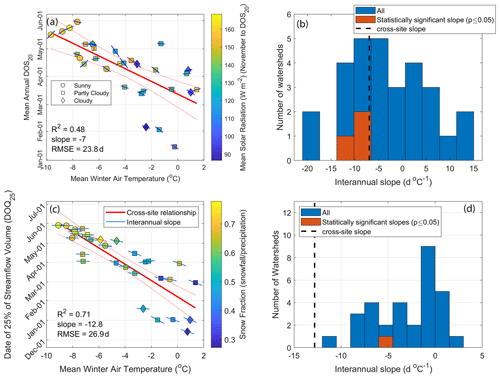
Figure 3 Panels (a) and (c) show cross-site relationships between mean winter air temperature (November to February) and DOS₂₀ and the date of 25 % of the annual streamflow volume (DOQ₂₅), respectively. Slopes of individual sites' interannual relationships are shown as the lines on top of each symbol, where statistically significant (p value ≤ 0.05) slopes are red. Non-significant interannual slopes are presented to show the overall tendency in their spatial distribution. Symbols are associated with the mean annual percentage of snowmelt days under clear-sky conditions. Sunny sites (circles) have >90 % clear-sky snowmelt days, partly cloudy sites (squares) have between 70 % and 90 %, and cloudy sites (diamonds) have <70 % clear-sky snowmelt days. Clear-sky snowmelt days are defined as those with more than 80 % of the potential clear-sky solar radiation. Panels (b) and (d) show histograms of interannual slopes (for all watersheds and those with statistically significant relationships), and the cross-site relationships are presented in their respective left panel.

Figure 4 Spatial variability in watershed-level interannual slopes for (a) DOS₂₀ versus winter air temperature and (b) DOQ₂₅ versus winter air temperature. Watersheds with statistically significant relationships are highlighted in symbols with thicker edges and are associated with those presented in Fig. 3. Symbols are associated with the mean annual percentage of snowmelt days under clear-sky conditions. Sunny sites (circles) have >90 % clear-sky snowmelt days, partly cloudy sites (squares) have between 70 % and 90 %, and cloudy sites (diamonds) have <70 % clear-sky snowmelt days. Clear-sky snowmelt days are defined as those with more than 80 % of the potential clear-sky solar radiation.

Strong correlations between DOS₂₀ and both DOQ₂₅ and DOQ₅₀ (the date of 50 % of the annual streamflow volume; R²=0.85; Fig. 5a and c) suggest connections between the timing of snowmelt and streamflow generation across watersheds and years. On average, sites that melt earlier are associated with earlier DOQ₂₅ (Fig. 5a) and a lower ratio of snowfall to total precipitation (snow fraction < 0.5). The relationship between DOS₂₀ and DOQ₂₅ closely follows the 1:1 line (Fig. 5a), although three sites in Washington and Oregon (site ID 24, 25, and 31; see Table 2 and Fig. 6a) deviate substantially from this pattern, perhaps because they receive relatively little of their precipitation as snow. Similar watershed-level relationships using interannual variability in DOQ₂₅ were found for most watersheds, with statistically significant slopes varying between 0.4 and 2.5 d d⁻¹ (Fig. 5b). DOS₂₀ also predicts DOQ₅₀ well, with 10 d earlier snowmelt producing 7 d earlier DOQ₅₀ on average (Fig. 5c) and similar watershed-level interannual relationships (Fig. 5d). The same three relatively rainy watersheds have DOQ₅₀ prior to the DOS₂₀ (Figs. 5c and 6b), suggesting that early snowmelt timing is not an important predictor of DOQ₅₀ in such places.

Figure 5 (a) The day when the 20th percentile of snowmelt days occurs (DOS₂₀), compared to the date of the 25 % of the annual streamflow volume (DOQ₂₅). (c) DOS₂₀ against the date of 50 % of the annual streamflow volume (DOQ₅₀). Dashed lines in panels (a) and (c) are 1:1 lines, and the slopes of the sites' interannual relationships are shown as the lines on top of each symbol, with statistically significant (p value ≤ 0.05) slopes shown in red. Site ID 24, 25, and 31, indicated by dashed circles, fall far from the linear regression and are not included in its calculation. Symbols indicate the mean annual percentage of clear-sky snowmelt days, where sunny sites (circles) have >90 % clear-sky snowmelt days, partly cloudy sites (squares) have between 70 % and 90 %, and cloudy sites (diamonds) have <70 %; clear-sky snowmelt days are defined as those with more than 80 % of the potential clear-sky solar radiation. Panels (b) and (d) show histograms of interannual slopes (for all watersheds and those with statistically significant relationships), and the cross-site relationships are presented in their respective left panels.

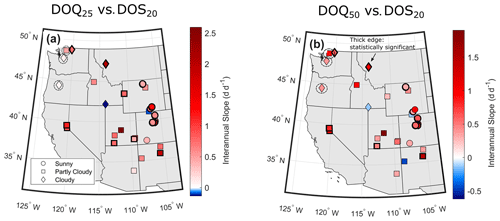
Figure 6 Spatial variability in the watershed-level interannual slopes for (a) DOQ₂₅ versus DOS₂₀ and (b) DOQ₅₀ versus DOS₂₀. Watersheds with statistically significant relationships are highlighted in symbols with thicker edges and are associated with those presented in Fig. 5. Watersheds that fall far from the linear regression presented in Fig. 5 are surrounded by a circle with a dashed line. Symbols are associated with the mean annual percentage of snowmelt days under clear-sky conditions. Sunny sites (circles) have >90 % clear-sky snowmelt days, partly cloudy sites (squares) have between 70 % and 90 %, and cloudy sites (diamonds) have <70 %. Clear-sky snowmelt days are defined as those with more than 80 % of the potential clear-sky solar radiation.

3.2 Diel streamflow-based sensitivity of snowmelt timing (DOS₂₀) to climate change

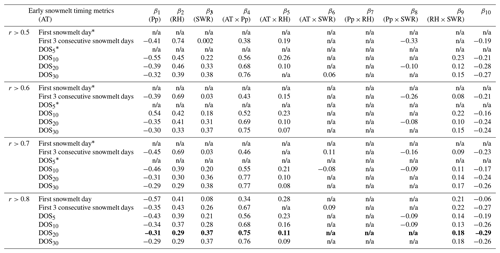
We fitted a stepwise MLR with four climate variables (air temperature, precipitation, relative humidity, and solar radiation) to predict the diel streamflow-based DOS₂₀ metric across watersheds and years. A total of 333 watershed–year combinations of DOS₂₀ and climate variables were used to train the stepwise MLR model. The watershed–year relationship between observed and MLR predictions has a relatively high R² of 0.83, a root mean square error (RMSE) of 17.5 d, and normally distributed residuals (p<0.01) off the 1:1 line and centered at 0, with a standard deviation of 17.3 d (Fig. 7a). The relationship between observations and MLR predictions of inter-watershed mean annual DOS₂₀ (Fig. 7b) is also strong (R²=0.83 and RMSE = 13.2 d) and follows the 1:1 line. Similarly, when we look at interannual values, represented by the lines overlapping the circles in Fig. 7b, we find a good agreement with most slopes close to 1:1 (see the inset in Fig. 7b). This analysis demonstrates that the MLR model can reasonably represent both the mean annual DOS₂₀ values at each watershed and their interannual variability. Table A4 shows the standardized beta coefficients that indicate the importance of each climate variable in the stepwise MLR. For the 0.8 correlation cutoff, we found that incoming shortwave radiation has the greatest importance (β=0.75), followed by relative humidity (β=0.37) and air temperature ($\mathit{\beta }=-\mathrm{0.31}$).

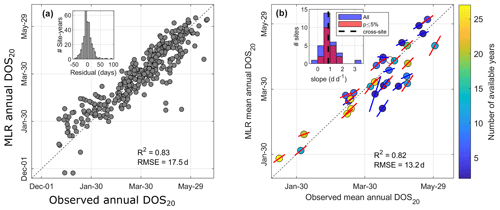
Figure 7 (a) Scatterplot showing the fit of the stepwise multiple linear regression (MLR) model to the observed DOS₂₀ across all sites and years. Panel (b) shows the same stepwise MLR model applied at the mean annual watershed level across all watersheds. Interannual variability represented by the slope of the linear relationship is shown as a line overlapping each circle (i.e., watershed); red and blue lines indicate statistically significant (p≤0.05) and insignificant slopes, respectively.

Empirical diel streamflow-based projections under climate change show earlier mean annual DOS₂₀ in all watersheds (i.e., earlier snowmelt initiation), with significant variability from site to site (Fig. 8a). Most watersheds show significant end-of-century changes in DOS₂₀, ranging from up to 3 months earlier in cold sites where, historically, snowmelt under clear-sky conditions dominates (circles in Fig. 8a) to as little as 20 d earlier in warm sites under historically cloudier conditions. The cross-site average change in DOS₂₀ is 55.3 d, with a standard deviation of 21.8 d. In many watersheds, the mean projection of DOS₂₀ under climate change is within the historically observed variability in DOS₂₀ (Fig. 8a). The empirical model predicts that, on average, colder watersheds ($T_{\mathrm{NDJF}}\le -\mathrm{8}$ ^∘C) are about 70 % more sensitive to climate change (13.7±4.6 d ^∘C⁻¹) than warmer watersheds (T_NDJF>0 ^∘C) (8.1±6.2 d ^∘C⁻¹), as represented by the change in the DOS₂₀ per degree of warming (Fig. 8b). Site ID 24 (South Fork Tolt River, WA) shows almost no change in its DOS₂₀, which can be attributed to its weaker climate change signal compared to the other watersheds (about +4 ^∘C, 5 % precipitation increase and virtually no change in humidity and solar radiation; Fig. A4). The diel streamflow-based analysis suggests an average sensitivity of DOS₂₀ to a climate change of 11.1±4.2 d ^∘C⁻¹ across all watersheds.

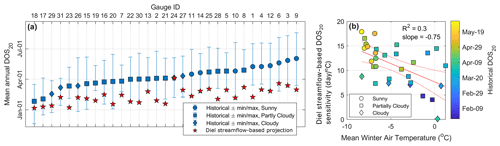
Figure 8 (a) Historical DOS₂₀ from the diel analysis and projected changes in DOS₂₀ using the empirical diel streamflow-based projections under the RCP8.5 pseudo global warming climate for the end of the 21st century. Watersheds are sorted from earlier (left) to later (right) historical DOS₂₀. Symbols associated with future projections (stars) are not classified by sunny, partly cloudy, or cloudy conditions, as we make no inference about the cloudiness condition of snowmelt days under the climate change scenario. Blue symbols in panel (a) represent the mean annual percentage of clear-sky snowmelt days, where sunny sites (circles) have >90 % clear-sky snowmelt days, partly cloudy sites (squares) have between 70 % and 90 %, and cloudy sites (diamonds) have <70 %. Clear-sky snowmelt days are defined as those with more than 80 % of the potential clear-sky solar radiation. (b) Relationship between mean winter air temperature and the sensitivity of DOS₂₀ to climate change, as projected by the empirical diel streamflow-based model.

3.3 Sensitivity of streamflow timing to climate change: empirical diel streamflow-based model versus NoahMP-WRF

We compared historical and empirical diel streamflow-based projections for DOQ₂₅ and DOQ₅₀ with those from NoahMP-WRF. Empirical streamflow timing sensitivity projections for DOS₂₀ under climate change were derived from the linear regressions presented in Fig. 5a and c (DOQ₂₅ and DOQ₅₀ versus DOS₂₀) with projected changes in DOS₂₀ using the MLR under climate change. Empirical projections for DOQ₂₅ range from early January to late May (red symbols; Fig. 9a), advancing between 20 and 100 d under RCP8.5 (x axis; Fig. 9c). The DOQ₅₀ is projected to advance between roughly 15 and 65 d (x axis; Fig. 9d), ranging from mid-February to late May (red symbols; Fig. 9b). The historical DOQ₂₅ is underestimated by NoahMP-WRF (blue symbols; Fig. 9a), with a mean DOQ₂₅ in mid-February, whereas historical DOQ₂₅ is in early April (50 d mean difference). Projected changes to DOQ₂₅ by NoahMP-WRF under pseudo global warming range between early January to mid-March (mean in early February; Fig. 9a), averaging −15 d (ΔDOQ₂₅; Fig. 9c), whereas empirical diel streamflow-based projections range between early January and late March (mean in mid-February; Fig. 9a), averaging about −60 d (ΔDOQ₂₅; Fig. 9c). These results indicate that empirical diel streamflow-based projections of DOQ₂₅ are about 4 times more sensitive to climate change than those from NoahMP-WRF. Historical DOQ₅₀ is reasonably well represented by NoahMP-WRF under the current climate (blue symbols; Fig. 9b) with a mean difference against observations of 7 d; however, future changes of about −20 d are projected, which are roughly half of the −40 d predicted by the empirical streamflow-based projections (ΔDOQ₅₀; Fig. 9d). Empirical diel streamflow-based projections of DOQ₅₀ range between mid-February and early April, whereas NoahMP-WRF projections range between mid-March and mid-May, suggesting later estimates of streamflow volume by the land surface model. Watersheds with the largest disagreement between the empirical model and NoahMP-WRF projections for streamflow volume timing are those where DOS₂₀ is the most sensitive to warming (represented by the orange and yellow symbols in Fig. 9c and d). These watersheds are characterized by historical cold winter temperatures ($T_{\mathrm{NDJF}}<-\mathrm{6}$ ^∘C), with snowmelt occurring mostly under sunny conditions (circle symbols) in the Rocky Mountains.

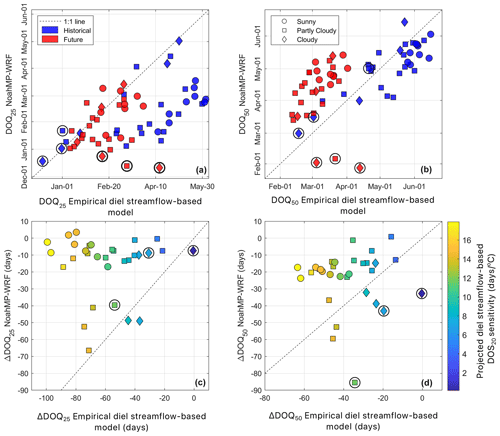
Figure 9 Changes to DOQ₂₅ and DOQ₅₀ due to climate change under a RCP8.5 pseudo global warming climate scenario by the end of the century. Panels (a) and (b) compare historical against projected values between NoahMP-WRF and the empirical diel streamflow-based model. Panels (c) and (d) compare the projected change in streamflow timing (future minus historical) between NoahMP-WRF and the empirical diel streamflow-based model, colored by the sensitivity of DOS₂₀ to climate change as projected by the empirical diel streamflow-based model (Fig. 8b). Symbols surrounded by black circles indicate sites that were excluded from the regression analysis in Fig. 5 (rainier site ID 24, 25, and 31). Symbols represent the historical mean annual percentage of clear-sky snowmelt days, where sunny sites (circles) have >90 % clear-sky snowmelt days, partly cloudy sites (squares) have between 70 % and 90 %, and cloudy sites (diamonds) have <70 %; clear-sky snowmelt days are defined as those with more than 80 % of the potential clear-sky solar radiation. We make no inference about the cloudiness condition of snowmelt days under the RCP8.5 climate scenario; however, red symbols (upper panels) follow the same symbology for easier interpretation.

4 Discussion

The new DOS₂₀ metric based on the diel streamflow analysis quantifies the timing of early snowmelt events and suggests that shifts towards earlier snowmelt will generate larger shifts toward earlier streamflow in colder, sunnier watersheds than in warmer, cloudier watersheds where snowmelt is more interspersed with rain. Despite the intuitive connections between snowmelt and streamflow, empirically linking changes in earlier snowmelt rates (Harpold and Brooks, 2018; Musselman et al., 2017) with changes in streamflow amount (Barnhart et al., 2016) and timing (Stewart et al., 2004) has been challenging (Weiler et al., 2018). This study represents of the first empirical analysis of streamflow-induced snowmelt change across a regional climate gradient not relying only on streamflow volume. Understanding these connections is challenging due to the representative scales at which snow (point scale) and streamflow (watershed-scale) are typically measured and analyzed. For example, evidence of snowmelt at Snow Telemetry (SNOTEL) sites in the USA has shown more intermittent snowmelt events at sites with higher humidity, and future modeling suggests lower-humidity sites will experience slower, earlier snowmelt (Harpold and Brooks, 2018; Musselman et al., 2017). However, the cascading effects of earlier and slower snowmelt on streamflow amount and timing remain relatively unexplored (e.g. Berghuijs et al., 2014) and are potentially affected by surface and subsurface hydrological connectivity, vegetation water use, and other processes that are not easily measured or parameterized. Our diel streamflow analysis has limitations in places dominated by rainfall, as evidenced by higher false detections in areas with low snow fractions (Fig. 2) and by the small (or nonexistent) interannual correlation between DOS₂₀ and the metrics DOQ₂₅ and DOQ₅₀ (Fig. 5a and c) in those places. Conversely, the colder and sunnier watersheds, primarily in the intermountain region, have strong interannual correlations between DOS₂₀ and DOQ₂₅ (Figs. 5a and 6a), reflecting the importance of snowmelt (instead of rain) in controlling streamflow volume timing.

Because the diel streamflow analysis does not require the many assumptions that are embedded in physically based models, it is an independent tool that can be used to verify historical streamflow simulations from subdaily resolved hydrological models. For example, land surface models could be benchmarked against observed snowmelt days based on the diel streamflow analysis or metrics like DOS₂₀ to better represent processes associated with snowmelt-driven streamflow generation. The diel streamflow analysis is also easier to implement than detailed process-based models because it only requires observed hourly streamflow data and solar radiation. If measured solar radiation is not available, it can be reliably represented by land surface models like NLDAS-2 (Luo et al., 2003) that assimilate field observations and remotely sensed radiation (including the effects of clouds) into an atmospheric modeling framework. In our analysis, we tested the sensitivity of some modeling decisions, such as the correlation cutoff between hourly solar radiation and streamflow used to detect snowmelt days and metrics for snowmelt timing and found similar sensitivities of DOS₂₀ to climate change across different correlation cutoffs and snowmelt timing percentiles (Table A5). Metrics like the first snowmelt day or the first 3 consecutive snowmelt days showed less consistent results (Table A5), likely due to individual early or midwinter melt events that do not necessarily represent the seasonal watershed behavior. The diel streamflow analysis has the following four main limitations that need to be examined in future work: (1) it requires a steep enough stage–discharge relationship so that daily streamflow cycles can be detected across the flow regime, (2) it focuses on snowmelt driven by solar radiation (and energy fluxes synchronized with it), (3) it is sensitive to assumptions about the lag time between solar radiation and streamflow, and (4) it is sensitive to assumptions about evapotranspiration losses. A steep stage–discharge relationship, in which small changes in discharge are associated with large changes in stage, is ideal to observe small diel streamflow changes with sufficient precision. The second limitation originates from the assumption that the majority of snowmelt is correlated with solar radiation, which is supported by the dominant role of solar radiation in process-based studies of maritime and continental snowpacks (Cline, 1997; Jepsen et al., 2012; Marks and Dozier, 1992). Because our method allows the lag time between solar radiation and streamflow to vary within a predefined window, we expect it to capture the effects of other important energy fluxes, such as sensible heat, that often lag the diel patterns of solar radiation by several hours (Ohmura, 2001). Rain-on-snow events are particularly challenging to detect with our analysis, as days with a lower percentage of incoming shortwave radiation (<80 % of clear sky) are filtered out to avoid issues with potential rainfall-dominated diel signals. It may also misclassify rainfall-driven diel streamflow cycles, although we checked for rainfall-induced cycles and found that these accounted for only a small fraction (7 % on average; Fig. 2) of our inferred snowmelt days. The relationships between streamflow timing (i.e., DOS₂₀, DOQ₂₅, and DOQ₅₀) and meteorological drivers in rainier sites showed cross-site and interannual relationships that are consistent with those in colder, more snow-dominated places (except for watershed ID 24, 25, and 31; e.g., Fig. 3a and c). The third limitation is that the spatiotemporal variability in snowpack, surface and subsurface storage, and evapotranspiration will change the magnitude and lag time of the diel streamflow response (Kirchner et al., 2020; Lundquist and Cayan, 2002; Lundquist and Dettinger, 2005), which we address by allowing variable watershed- and month-specific time lags. However, lag times greater than 24 h, which are associated with large watersheds or large subsurface storage, will make this method impossible to apply. The method may also miss early snowmelt-driven diel cycles in watersheds with dry soils, as the diel signal will be buffered by the subsurface storage capacity before generating a measurable streamflow response. Our empirical diel streamflow-based model implicitly assumes that other variables not included in the analysis vary together with the predictive variables (climate) and neglects watersheds' physical (e.g., soil storage) and biological (e.g., vegetation) properties that do not necessarily covary with climate. The fourth limitation is that evapotranspiration losses must be small relative to snowmelt inputs, which is necessary because the effect of evapotranspiration is out of phase with the effect of snowmelt (Kirchner et al., 2020). Evapotranspiration effects are minimized by focusing on early snowmelt periods, when evapotranspiration losses are small (Bowling et al., 2018; Cooper et al., 2020; Winchell et al., 2016).

Hydrological modeling in land surface models attempts to physically represent snowpack storage, snowmelt, subsurface storage, and its release to the streamflow, which is challenged by uncertain forcing data and simplified and uncertain model parameters. For example, snowmelt modeling in complex terrain is challenged by steep climate gradients and by the lack of adequate forcing data (precipitation, temperature, wind, etc.). Characterizing precipitation phase and timing in steep watersheds remains challenging in rain-to-snow transition zones (Harpold et al., 2017; Jennings et al., 2018; Wayand et al., 2015), which will presumably increase in extent in the future (Klos et al., 2014). Complex terrain affects radiation fluxes, which are hard to estimate at kilometer spatial scales (Müller and Scherer, 2005) used in most land surface models. Most of our study sites are forest covered, which exerts a strong control on the snowpack mass and energy balance (Lundquist et al., 2013; Pomeroy et al., 1998; Safa et al., 2021) with spatially heterogeneous effects on snow accumulation and melt that remain challenging to model (Broxton et al., 2015; Krogh et al., 2020). The presence of preferential flow paths through the snowpack impacts the timing of melt release (Leroux and Pomeroy, 2017) and is not typically included in hydrological models. Once snowmelt is released from the snowpack, simulating (and validating) what fraction flows as subsurface and surface runoff remains difficult. Decades of tracer studies (e.g., Godsey et al., 2010; Kirchner, 2003) have shown that streamflow during and after hydrologic events (i.e., snowmelt or rainfall events) is typically old water that has been stored in the watershed for months to years. Land surface models like NoahMP-WRF lack realistic groundwater stores to represent old water and lack hillslope and near-stream processes (Fan et al., 2019). For example, previous work at Sagehen Creek (site ID 23) suggests that streamflow remains ∼80 % groundwater even during the snowmelt freshet (Urióstegui et al., 2017), despite a strong snowmelt diel response caused by pressure changes induced by infiltrating snowmelt. Innovative observations that give new physical insights, like the diel streamflow analysis, could bring new information to modeling beyond what is possible with typical daily discharge resolution (Kirchner, 2006).

The diel-based analysis of snowmelt-driven streamflow to changing climate gives unique insights over previous efforts using daily and seasonal streamflow volumes (Berghuijs et al., 2014; Stewart et al., 2005) and retrospective hydrological modeling (Barnhart et al., 2016). Empirical projections of DOS₂₀ under the pseudo global warming scenario (Fig. 8b) show that colder, drier, and sunnier sites (typical of the Rocky Mountains) are about twice as sensitive to warming as warmer, more humid, and cloudier sites (typical of the Pacific Northwest). Humid and warmer sites have lower snow fractions (<0.5; more rainfall effects) and, thus, a smaller snowmelt signal in the diel streamflow observations. In contrast, Harpold and Brooks (2018) showed that winter ablation at SNOTEL sites in humid places, like the Pacific Northwest, are more sensitive to warming than less humid places, like the southwestern USA. However, Kirchner et al. (2020) showed general agreement between SNOTEL snowmelt response and the snowmelt-induced diel streamflow signal at the warm Sagehen Creek watershed (site ID 23). The sensitivity of the early snowmelt timing metric (DOS₂₀) to climate change is a function of changes in precipitation phase (rainfall versus snowfall), snowpack ablation (changes in the patterns of melt and sublimation), and hydrological partitioning to streamflow versus evaporative loss. Due to the empirical basis of our analysis, these sensitivities are not easy to disentangle, but the diel analysis is a new source of information that could help in that effort. The reliability of the empirical diel streamflow-based projections partially depends on whether climate projections are within or outside the range of observed climate conditions across the large climatic gradient found in the western USA. Under the pseudo global warming scenario, cold, sunny watersheds like those in the Rocky Mountains (site ID 9 and 10) will shift toward more humid, warmer conditions (Fig. A6), like those observed in Southern Idaho (site ID 29) and the northern Sierra Nevada (site ID 23). In contrast, the pseudo global warming scenarios for places like the Pacific Northwest, particularly those involving changes in atmospheric humidity above 5 g m⁻³ (Fig. A4), have not been observed in the historical record and therefore are more uncertain. Determining reasonable conditions to apply empirical models that use observed differences in sites to predict future changes (often called space-for-time models), like the presented diel streamflow analysis, has been posed as one of the 23 unsolved problems in hydrology (Blöschl et al., 2019).

The sensitivity of historical snowmelt-mediated streamflow volume timing (DOQ₂₅ and DOQ₅₀) to climate change differs substantially between the empirical diel streamflow-based approach and a land surface model, raising questions about current state-of-the-art projections of early season streamflow timing from NoahMP-WRF, particularly in cold watersheds (Fig. 9c and d). The observed data used in the diel streamflow-based approach have larger and more variable streamflow timing responses to climate change (10–17 d ^∘C⁻¹) in cold, dry, sunny places that are representative of small, high-elevation Rocky Mountain watersheds (Fig. 8b). The historical diel streamflow analysis suggests that NoahMP-WRF may be systematically underpredicting the sensitivity of streamflow volume timing to earlier snowmelt-induced streamflow in colder and sunnier places (Fig. 9c) that are most likely to have increased temperature and increased cloudiness in the future. The same mean annual future climate scenarios were applied to both approaches; however, important differences in the streamflow timing response were found between NoahMP-WRF and diel streamflow-based projections (Fig. 9c and d). NoahMP-WRF underpredicts historical DOQ₂₅ (Fig. 9a) across most sites, whereas DOQ₅₀ is much better represented. It is worth noting that when DOQ₂₅ simulated by NoahMP-WRF is calculated using surface runoff alone (Fig. A7a), rather than subsurface plus surface runoff, it performs better against observed DOQ₂₅. However, NoahMP-WRF projected sensitivity in streamflow timing to climate change remains significantly lower than predictions based on the diel-streamflow analysis (Fig. A7c). We used these simulations in the analysis because Noah-MP underlies the U.S. National Water Model, and thus, its relevance to policy and research is high. There are many differences in the way that NoahMP-WRF and the empirical diel streamflow-based approach function. NoahMP-WRF can track the hourly covariance in precipitation, temperature, and humidity to estimate precipitation partitioning between rain and snow. It is also able to represent hourly radiative and turbulent energy at the snowpack, and the cold content needed to predict snowmelt. Its physical hydrology is also advanced and able to consider antecedent conditions and allow evapotranspiration losses that also modulate streamflow. Despite the advantages of land surface models like NoahMP-WRF in constraining processes for future projections, the simplicity of diel streamflow-based analysis also provides several advantages. One of the main advantages is that it is derived from observations, and thus, it is well constrained by the observed spatial and temporal variability of snowmelt across watersheds and years (Fig. 7b). Also, it does not assume anything about the complex spatial distribution of snowpacks and precipitation or subsurface properties, which are major constraints to physically based models (Baroni et al., 2010; Christiaens and Feyen, 2001; Wilby et al., 2002). While the empirical diel streamflow-based model is not a replacement for land surface models like NoahMP-WRF, partly because the underlying streamflow datasets are not available everywhere, there is added value in including new benchmarks like the proposed DOS₂₀ to further constrain modeling decisions and improve model fidelity required for reliable and accurate hydrological predictions.

5 Conclusions

Water management in the western USA requires accurate predictions of how both short-term climate variability and long-term climate change will alter snowmelt and streamflow. Differences in predictions of snowmelt-induced streamflow between empirical diel streamflow-based projections and a land surface model (NoahMP-WRF) raise important questions about the sensitivity of streamflow timing to climate change, particularly in cold regions, and its impact on water planning. Significant differences exist in the way diel streamflow-based and land surface models predict changes to snowmelt and streamflow timing, with both approaches having strengths and weaknesses; however, the land surface model misrepresents historical patterns in streamflow response that are more accurately estimated by the empirical model. We show that DOS₂₀ is a strong predictor of the early season hydrograph response, particularly in cold, sunny areas where the NoahMP-WRF streamflow timing simulations lack sensitivity to climate change. Rigorously validating future model predictions is impossible, but snowmelt and streamflow timing, inferred from diel streamflow cycles, could be used to refine land surface models and better determine the risk to valuable snow water resources (Barnett et al., 2005; Sturm et al., 2017; Viviroli et al., 2007), particularly in cold regions. Our novel approach can complement the benchmarking or calibration of physically based hydrological models beyond typical benchmarking against daily streamflow or snow accumulation metrics. For example, the snowmelt timing metric DOS₂₀ based on diel streamflow observations could be used to test how well land surface models, running at subdaily scales and fine spatial resolution, can reproduce the historical snowmelt regime across watersheds and years. As land surface models move towards real application for water management (Kopp et al., 2018), the hydrology community must seek ways to test and improve them using widely available datasets if we are to meet the grand water management challenges posed by climate change in mountainous regions.

Appendix A

Figure A1 (a) Number of available years with less than 30 %, 20 %, and 10 % gaps in days with hourly streamflow records between 1 December and 1 August. Gauge ID is as presented in Table 2. Numbers of years at site ID 13 are the same for all thresholds (overlapping symbols). (b) Sensitivity of the mean annual number of detected snowmelt days to different Spearman correlation cutoffs (0.5, 0.6, 0.7, and 0.9) between hourly solar radiation and streamflow. Error bar represents the standard deviation.

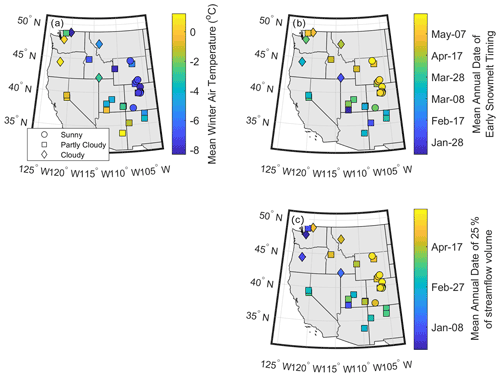
Figure A2 (a) CAMELS mean winter (November to February) air temperature, (b) mean annual DOS20, and (c) mean annual DOQ25. Symbols (circle, square, and diamond) represent the mean annual percentage of clear-sky snowmelt days, where sunny sites have >90 % clear-sky snowmelt days, partly cloudy have between 70 % and 90 %, and cloudy have <70 %; clear-sky snowmelt days are defined as those with more than 80 % of the potential clear-sky solar radiation.

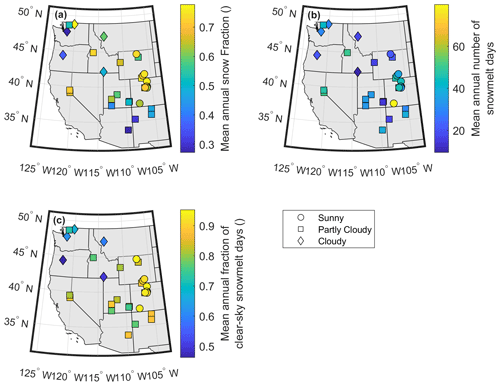
Figure A3 (a) CAMELS mean annual snow fraction (snowfall$/$precipitation), (b) mean annual number of snowmelt days between 1 December and 1 August (calculated as the days with a correlation between hourly solar radiation and lagged streamflow greater than 0.8), and (c) mean annual fraction of clear-sky snowmelt days, calculated as the number of snowmelt days with clear-sky conditions as a fraction of total snowmelt days. A clear-sky snowmelt day is defined as having more than 80 % of the potential clear-sky solar radiation. Symbols (circle, square, and diamond) represent the mean annual percentage of clear-sky snowmelt days, where sunny sites have >90 % clear-sky snowmelt days, partly cloudy have between 70 % and 90 %, and cloudy have <70.

Figure A4 Historic winter climate variability for each predictor used in the stepwise MLR model (Eq. 1) for the period between November and DOS₂₀ in blue. (a) Precipitation, (b) air temperature, (c) absolute humidity, and (d) solar radiation. In red are the perturbed mean climate variables under the RCP8.5 pseudo global warming scenario by the end of the century. This analysis suggests that most of the climate change signal from NoahMP-WRF pseudo global warming is within the observed climate variability, except for air temperature and atmospheric humidity in some watersheds. Blue symbols (circle, square, and diamond) associated with historical values represent the mean annual percentage of clear-sky snowmelt days, where sunny sites have >90 % clear-sky snowmelt days, partly cloudy have between 70 % and 90 %, and cloudy have <70 %; clear-sky snowmelt days are defined as those with more than 80 % of the potential clear-sky solar radiation. We make no inference about the cloudiness condition of snowmelt days under the RCP8.5 pseudo global warming scenario, and thus, we use a five-point star (in red) for the future scenario.

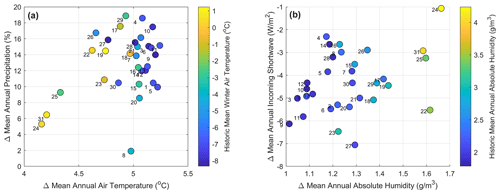
Figure A5 Mean annual climate changes projected by WRF under a RCP8.5 pseudo global warming scenario by the end of the century. Panel (a) shows changes in precipitation against air temperature. Panel (b) shows incoming shortwave against absolute humidity. Numbers represent the gauge IDs as presented in Table 2.

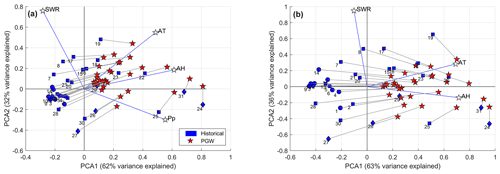
Figure A6 (a) Principal component analysis for historical precipitation (Pp), air temperature (AT), absolute humidity (AH) and shortwave radiation (SWR) at each watershed and the changes associated with the pseudo global warming as simulated by WRF. Panel (b) shows the same analysis but excluding precipitation from the analysis. Blue symbols (circle, square, and diamond) associated with historical values represent the mean annual percentage of clear-sky snowmelt days, where sunny sites have >90 % clear-sky snowmelt days, partly cloudy have between 70 % and 90 %, and cloudy have <70 %; clear-sky snowmelt days are defined as those with more than 80 % of the potential clear-sky solar radiation. We make no inference about the cloudiness condition during snowmelt days under the RCP8.5 pseudo global warming scenario, and thus, we use a five-point star (in red) for the future scenario. Numbers next to blue symbols represent the gauge IDs as presented in Table 2.

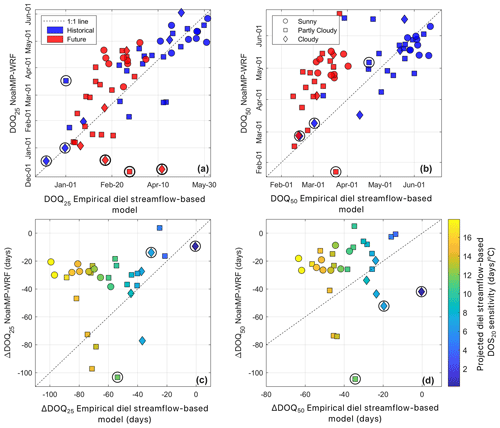
Figure A7 Same as Fig. 9 but using streamflow timing metrics from NoahMP-WRF for a RCP8.5 pseudo global warming scenario, calculated using surface runoff only instead of using surface plus subsurface runoff (as in Fig. 6). Note the improved fit in historical DOQ₂₅; however, this analysis yields very similar results to those in Fig. 6, with NoahMP-WRF streamflow simulations being much less sensitive to climate change than the empirical diel streamflow-based model suggests. Panels (a) and (b) compare historical against projected values between NoahMP-WRF and the empirical diel streamflow-based model. Panels (c) and (d) compare the projected change (future minus historical) between NoahMP-WRF and the diel streamflow-based model, colored by the sensitivity of DOS₂₀ to climate change as projected by the empirical diel streamflow-based model (Fig. 5b). Symbols surrounded by black circles indicate sites that were excluded from the regression analysis in Fig. 3 (rainier site ID 24, 25, and 31). Symbols (circle, square, and diamond) represent the historical mean annual percentage of clear-sky snowmelt days, where sunny sites have >90 % clear-sky snowmelt days, partly cloudy have between 70 % and 90 %, and cloudy have <70 %; clear-sky snowmelt days are defined as those with more than 80 % of the potential clear-sky solar radiation. We make no inference about the cloudiness condition of snowmelt days under the RCP8.5 pseudo global warming climate scenario; however, red symbols (upper panels) follow the same symbology for easier interpretation.

Table A1 Coefficient of determination (R²) and slope (in parentheses; day/day) of the linear regression between different early snowmelt timing metrics and DOQ₂₅ and DOQ₅₀, as presented in Fig. 5, for different correlation cutoffs (r) between hourly solar radiation and streamflow. DOS_xx represent the date when the xxth percentile of snowmelt days occurs. Site ID 24, 35, and 31 are excluded from the linear relationship. Bolded numbers are those used in the result and discussion sections.

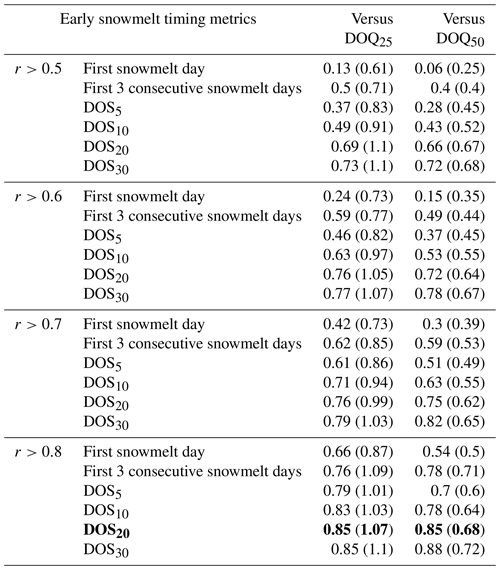
Table A2 Root mean square error (RMSE) and coefficient of determination (R²; in parentheses) associated with several stepwise multiple linear regressions (similar to the one in Eq. 1) using different early snowmelt timing metrics (e.g., Eq. 1 uses DOS₂₀) and correlation cutoffs (r) between hourly solar radiation and streamflow used to define snowmelt days. DOS_xx represents the date when the xxth percentile of snowmelt days occurs. Bolded numbers are associated with the stepwise MLR in Eq. (1), which is also shown in Fig. 7a.

Table A3 Coefficient of determination (R²) for the site-averaged stepwise multiple linear regression, analogous to that presented in Fig. 7b, for different modeling decisions (correlation cutoff between hourly solar radiation and streamflow, r, and early snowmelt days metrics). DOS_xx represents the date when the xxth percentile of snowmelt days occurs. The bolded number is associated with the stepwise MLR in Eq. (1) using DOS₂₀.

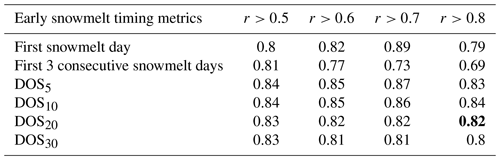
Table A4 Standardized beta coefficients for the stepwise MLR associated with the different correlation cutoffs (r) between hourly solar radiation and streamflow and different early snowmelt metrics. These stepwise MLR models follow the same structure as that of Eq. (1); however, in this case, predictors were standardized to estimate their relative importance. Note: AT – air temperature; Pp – precipitation; RH – relative humidity; SWR – incoming shortwave radiation. DOS_xx represent the date when the xxth percentile of snowmelt days occurs. The asterisk^* indicates rows that do not meet all the MLR assumptions. Bolded numbers are associated with the modeling decisions used in the result and discussion sections.

Note: n/a stands for not applicable.

Table A5 Coefficient of determination (R²) and slope (in parentheses; d ^∘C⁻¹) of the linear regression between the empirical diel streamflow-based model sensitivity to warming and sites' mean winter air temperature as presented in Fig. 8b, for different early snowmelt day metrics and correlation cutoffs (r) between hourly solar radiation and streamflow. DOS_xx represent the date when the xxth percentile of snowmelt days occurs. Bolded numbers are associated with the modeling decisions used in the result and discussion sections.