Ensemble streamflow forecasting over a cascade reservoir catchment with integrated hydrometeorological modeling and machine learning

A popular way to forecast streamflow is to use bias-corrected meteorological forecasts to drive a calibrated hydrological model, but these hydrometeorological approaches suffer from deficiencies over small catchments due to uncertainty in meteorological forecasts and errors from hydrological models, especially over catchments that are regulated by dams and reservoirs. For a cascade reservoir catchment, the discharge from the upstream reservoir contributes to an important part of the streamflow over the downstream areas, which makes it tremendously hard to explore the added value of meteorological forecasts. Here, we integrate meteorological forecasts, land surface hydrological model simulations and machine learning to forecast hourly streamflow over the Yantan catchment, where the streamflow is influenced by both the upstream reservoir water release and the rainfall–runoff processes within the catchment. Evaluation of the hourly streamflow hindcasts during the rainy seasons of 2013–2017 shows that the hydrometeorological ensemble forecast approach reduces probabilistic and deterministic forecast errors by 6 % compared with the traditional ensemble streamflow prediction (ESP) approach during the first 7 d. The deterministic forecast error can be further reduced by 6 % in the first 72 h when combining the hydrometeorological forecasts with the long short-term memory (LSTM) deep learning method. However, the forecast skill for LSTM using only historical observations drops sharply after the first 24 h. This study implies the potential of improving flood forecasts over a cascade reservoir catchment by integrating meteorological forecasts, hydrological modeling and machine learning.

1 Introduction

Floods are the most destructive events among natural disasters, causing huge amounts of damage to human society. Reservoirs are constructed to regulate river flows and have significantly reduced flood risks and damage (Ji et al., 2020). However, the number and intensity of extreme precipitation events are increasing in many areas as global warming continues, thereby amplifying the potential for flood hazards (Hao et al., 2013; Shao et al., 2016; Wei et al., 2018; Yuan et al., 2018a; Wang et al., 2019). Thus, accurate streamflow forecasts are needed to provide guidelines for reservoir operations (Robertson and Wang, 2013).

A common approach to streamflow forecasting is to use hydrological models; the first attempt at this kind streamflow forecasting can be traced back to the 1850s and involved simple regression-type approaches to predict discharge from observed precipitation (Mulvaney, 1851). Since then, model concepts have been further augmented by designing new data networks, addressing the heterogeneity of hydrological processes, capturing the nonlinear characteristics of hydrologic system and parameterizing models (Hornberger and Boyer, 1995; Kirchner, 2006). With advancements in computer technology and high-resolution observation, a well-parameterized hydrological model can now simulate streamflow with high accuracy (Kollet et al., 2010; Ye et al., 2014; Graaf et al., 2015; Yuan et al., 2018b).

Streamflow simulations from hydrological models heavily rely on meteorological forcing inputs, especially precipitation, which can be measured at in situ gauges or retrieved from satellites and radars. However, for medium-range (2–15 d ahead) streamflow forecasts, precipitation forecasts are needed (Hopson and Webster, 2010). To improve the forecasts, ensemble techniques that can give a deterministic estimate as well as the estimate's uncertainty have become popular. Ensemble weather forecasting can be traced back to 1963 (Lorenz, 1963). Later, Leith (1974) transferred a deterministic forecast into an ensemble using the Monte Carlo method in order to describe the atmospheric uncertainty. In the 1990s, ensemble forecasting was developed into an integral part of numerical weather prediction that showed higher skill than the deterministic forecast, even with higher model resolution (Toth et al., 2001). Due to the rapid development of this technique, ensemble weather forecasting and climate predictions are applied to hydrological forecasting studies by combining them with hydrological models (Jasper et al., 2002; Balint et al., 2006; Jaun et al., 2008; Xu et al., 2015; Yuan et al., 2016; Zhu et al., 2019). Provided with an ensemble of streamflow forecasts and their forecast variability, a reservoir can maintain a reliable utility from natural streamflow better than that provided with a deterministic streamflow forecast only (Zhao et al., 2011). However, the streamflow prediction skill depends on whether the precipitation forecasts introduced into the hydrological model are skillful (Alfieri et al., 2013). When assessing the skill of this hydrometeorological forecasting approach, a benchmark is needed. Using ensembles of historical climatology data (Day, 1985) as meteorological forecast inputs, which is known as ensemble streamflow prediction (ESP), is often selected as the benchmark approach. Evaluations of hydrological forecasts have indicated that forecast skill has a close relationship with the catchment size, geographical location and resolution (Alfieri et al., 2013; Pappenberger et al., 2015); thus, there is a necessity to compare these forecasts with the ESP in order to establish the skill of the hydrometeorological forecasting approach.

Although physically based hydrological models are widely used, it is still hard to apply a hyper-resolution distributed model to streamflow forecasting due to its demand for observation data, its complex model structures, and the computational resource requirements for calibration and application (Wood et al., 2011; Kratzert et al., 2018; Yaseen et al., 2018). In cascade reservoir systems, there are two sources of streamflow: the rainfall within the interval basin and the upstream reservoir discharge. While the rainfall–runoff relationship is well studied, it is challenging to reproduce the reservoir operating rules in a physical model (Gao et al., 2010; Zhang et al., 2016; Dang et al., 2020).

Machine learning methods can recognize patterns hidden in input data and can simulate or predict streamflow without explicit descriptions of the underlying physical processes (Kisi, 2007; Adnan et al., 2019). Neural networks are suitable for streamflow forecasting among machine learning models, and some of them can even outperform physically based hydrological models. For example, Humphrey et al. (2016) showed that their combined Bayesian artificial neural network (ANN) with the modèle du Génie Rural à 4 paramètres Journalier (GR4J) approach outperforms the GR4J model with respect to monthly streamflow forecasting. Kratzert et al. (2019) showed that an approach based on the long short-term memory (LSTM) technique outperforms a well-calibrated Sacramento Soil Moisture Accounting Model (SAC-SMA). Yang et al. (2020) used a geomorphology-based hydrological model (GBHM) combined with a traditional ANN model to simulate daily streamflow, which can provide enough physical evidence and can run with less observation data. Although neural network models are criticized with little physical evidence (Abrahart et al., 2012), their potential in hydrological forecasting is yet to be explored.

In this study, we combine machine learning with a hydrometeorological approach for hourly streamflow forecasting over a cascade reservoir catchment located in southwestern China. We use the meteorological hindcast data from the European Centre for Medium-Range Weather Forecasts (ECMWF) model that participated in the THORPEX (THe Observing-system Research and Predictability EXperiment) Interactive Grand Global Ensemble (TIGGE) project to drive a newly developed high-resolution land surface model, named “CSSPv2” (Conjunctive Surface-Subsurface Process, version 2; Yuan et al., 2018b), to provide runoff and streamflow forecasts, and we corrected the forecasts using the LSTM model. We aim to improve flood forecasting over the cascade reservoir catchment by integrating meteorological forecasts, hydrological modeling and machine learning. So we strive to (1) calibrate the hydrological model, (2) bias correct the meteorological forecasts, (3) evaluate the streamflow forecast skill and (4) test the combined physical–statistical approach.

2 Study area, data, model and method

2.1 Study area

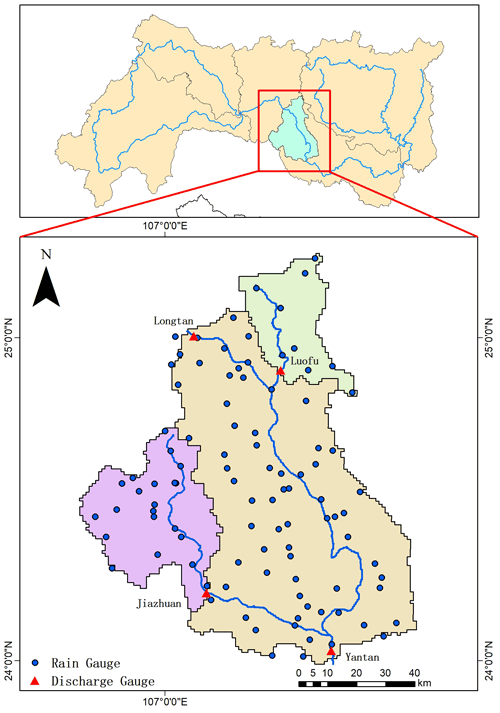
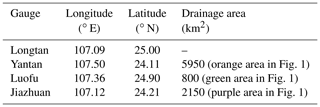
The Yantan Hydropower Station is in the middle reaches of the Hongshui River in Dahua Yao Autonomous County, Guangxi Province. This station is the fifth level in the 10-level development of the Hongshuihe hydropower base in the Nanpanjiang River, connected with the upstream Longtan Hydropower Station and the downstream Dahua Hydropower Station. The drainage area between the Longtan Hydropower Station and Yantan Hydropower Station is 8900 km². The annual mean streamflow at the Yantan hydrological gauge is 55.5 ×10⁹ m³. The river passes through a karst mountain area, with a narrow valley, steep slope and scattered cultivated land, and the average slope is 0.036 %. Figure 1 shows the locations of four hydrological gauges, with detailed information listed in Table 1.

Figure 1 Locations of discharge gauges and rain gauges over the Yantan Basin.

Table 1 Information on hydrological gauges.

2.2 Data and method

2.2.1 Hydrometeorological observations

There are 97 meteorological observation stations within the catchment (Fig. 1). Here, observed hourly 2 m temperature, 10 m wind speed, relative humidity, accumulated precipitation and surface pressure data were interpolated onto a 5 km gridded observation dataset using the inverse distance weight method. The hourly surface downward solar radiation data from the China Meteorological Administration Land Data Assimilation System (CLDAS) were also interpolated onto a 5 km dataset using the bilinear interpolation method. The hourly surface downward thermal radiation was estimated by specific humidity, pressure and temperature. This dataset was used to drive the CSSPv2 land surface hydrological model.

The monthly runoff for each 5 km grid was estimated by disaggregating control streamflow station observations with the ratio of observed grid monthly precipitation and catchment mean precipitation. The gridded runoff was used to calibrate the CSSPv2 model at each grid (Yuan et al., 2016). The calibrated runoff parameters can be used to better represent the heterogeneity of the rainfall–runoff processes and make precise runoff simulations.

2.2.2 Ensemble meteorological hindcast data and ESP hindcasts

The TIGGE dataset consists of ensemble forecast data from 10 global numerical weather prediction centers starting from October 2006; the dataset has been made available for scientific research via data archive portals at ECMWF and the China Meteorological Administration (CMA). TIGGE has become the focal point for a range of research projects, including research on ensemble forecasting, predictability and the development of products to improve the prediction of severe weather (Bougeault et al., 2010). In this paper, TIGGE data from April to September during 2013–2017 from ECMWF were used as meteorological hindcast data. The 3-hourly meteorological hindcasts for a 7 d lead time from 51 ensemble members (including a control forecast) were interpolated to a 5 km resolution via bilinear interpolation. The forecast precipitation and temperature were corrected to match the observational means in order to remove the biases.

The ESP was accomplished by applying historical meteorological forcings (Day, 1985). In this paper, the meteorological forcings from the same date as the forecast start date to the next 9 d of each year (excluding the target year) were selected as the ESP forcings. Take 1 April 2013​​​​​​​ as an example, the 7 d observation periods starting from 1 to 10 April (i.e., 1–7 April, 2–8 April, …, 10–16 April) in the years 2014, 2015, 2016 and 2017 were selected as the forecast ensemble forcings of the issue date (1 April), resulting in a total of 40 ensemble members. The detailed information on the raw datasets is given in Table 2.

Table 2 Information on hydrological datasets. (Please note that dates are given in the following format in this table: yyyy/mm/dd.)

2.2.3 CSSPv2 streamflow hindcasts

The physical hydrological model used in this paper is the Conjunctive Surface-Subsurface Process model, version 2 (CSSPv2; Yuan et al., 2018b). The CSSPv2 model is a distributed, grid-based land surface hydrological model that was developed from the Common Land Model (Dai et al., 2003, 2004), but it has better representations of lateral surface and subsurface hydrological processes and their interactions. The routing model used here employs the kinetic wave equation as a covariance function, which is solved via a Newton algorithm. A main reason for adopting this covariance function is that it suits basins with mountainous terrain. The CSSPv2 model was successfully used to perform a high-resolution (3 km) land surface simulation over the Sanjiangyuan region, which is the headwater of major Chinese rivers (Ji and Yuan, 2018). In this paper, we calibrated the CSSPv2 model against monthly estimated runoff to simulate the natural hydrological processes using the shuffled complex evolution (SCE-UA) approach (Duan et al., 1994). The calibrated parameters include the maximum velocity of baseflow, the variable infiltration curve parameter, the fraction of maximum soil moisture where nonlinear baseflow occurs and the fraction of maximum velocity of baseflow where nonlinear baseflow begins. The hourly observed streamflow at the Yantan hydrological gauge was used to manually calibrate the CSSPv2 routing model, including the slope, river density, roughness, width and depth. The observed streamflow values at the Longtan hydrological gauge were added into the corresponding grid to provide upstream streamflow information. We used a high-resolution elevation database (hereafter referred to as DEM90) for sub-grid parameterization and then calculated the initial values of these river channel parameters. We first extracted the slope angle and the natural river flow path from DEM90 and then identified the accurate river network using a drainage area threshold of 0.18 km². River density and bed slope values for each 5 km grid were calculated as follows​​​​​​​:

$$\begin{array}{}\text{(1)}& {\displaystyle }\mathrm{rivden}=\sum l/A,\text{(2)}& {\displaystyle }\mathrm{bedslp}=\mathrm{mean}\left(\tan \right(\mathit{\beta }\left)\right),\end{array}$$

where rivden is the river density (km/km²), bedslp is the river channel bed slope (unitless), A is the area of a 5 km grid (km²), ∑l is the total river channel length (m) within the grid and β is the slope angle (radian) for each river segment located in the grid.

Other river channel parameters were estimated using empirical formulas (Getirana et al., 2012; Luo et al., 2017) as follows:

$$\begin{array}{}\text{(3)}& {\displaystyle }W=\mathrm{1.956}\times A_{\mathrm{acc}}^{\mathrm{0.413}},\text{(4)}& {\displaystyle }H=\mathrm{0.245}\times A_{\mathrm{acc}}^{\mathrm{0.342}},\text{(5)}& {\displaystyle }n=\mathrm{0.03}+\left(\mathrm{0.05}-\mathrm{0.03}\right){\displaystyle \frac{H_{\max }-H}{H_{\max }-H_{\min }}},\end{array}$$

where W, H and n are river width (m), depth (m) and roughness (unitless) for each 5 km grid; A_acc is the upstream drainage area (km²); and H_max and H_min refer to the maximum and minimum values of river depth calculated by Eq. (4).

Using a trial-and-error procedure, we calibrated these river channel parameters to match the simulated streamflow with observed hourly records at the Yantan hydrological gauge. The simulation results were evaluated by calculating the Nash–Sutcliffe efficiency (NSE) with corresponding observation data. The descriptions of the calibrated parameters and their ranges are given in Table 3.

Table 3 Descriptions of calibrated parameters.

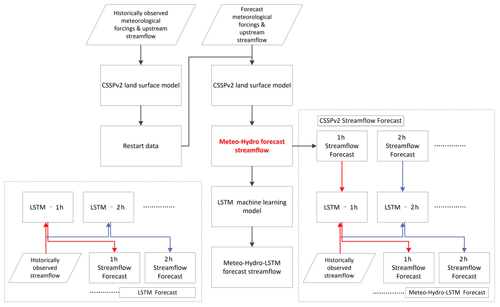
After calibration, we drove the CSSPv2 model using 5 km regridded and bias-corrected TIGGE-ECMWF forecast forcing during 2013–2017 to provide a set of 7 d hindcasts. Streamflow hindcasts from both the ESP and the hydrometeorlogical approach (TIGGE-ECMWF/CSSPv2, where CSSPv2 was driven by TIGGE-ECMWF) were corrected by matching monthly mean streamflow observations to remove the biases, and the hindcast experiments were termed “ESP-Hydro” and “Meteo-Hydro” (Table 4). Figure 2 shows the procession of the CSSPv2 hindcasts: the calibrated CSSPv2 model was first driven with the observation dataset to generate initial hydrological conditions (e.g., soil moisture and surface water) for each forecast issue date, and the CSSPv2 model was then driven with forecast data (TIGGE-ECMWF or ESP) at every forecast issue date with the generated initial conditions to perform a 7 d hindcast.

Table 4 Experimental design in this study.

Figure 2 A diagram for the integrated hydrometeorological and machine learning streamflow prediction.

2.2.4 LSTM streamflow forecast

Long short-term memory (LSTM) is a type of recurrent neural network model that learns from sequential data. The input of the LSTM model includes the forecast interval streamflow at the specified forecast step obtained from TIGGE-ECMWF/CSSPv2, historical upstream streamflow observations and historical streamflow observations at the Yantan hydrological gauge. The network was trained on sequences of April to September data from 2013 to 2017, with six historical streamflow observations and one forecast interval streamflow to predict the total streamflow at each forecast time step (Fig. 2). The LSTM was calibrated using a cross validation method by leaving the target year out.

Before calibration, all input and output variables were normalized as follows:

$$\begin{array}{}\text{(6)}& q_{\mathrm{0}}={\displaystyle \frac{(q-q_{\min })}{(q_{\max }-q_{\min })}},\end{array}$$

where q₀, q, q_max and q_min are the normalized variable, the input variable, and the maximum and minimum of the sequence of the variable, respectively. The hindcast experiment was termed “Meteo-Hydro-LSTM” (Table 2). In addition, we also tried an LSTM streamflow forecasting approach that only used 6 h historical streamflow data as inputs; this experiment was termed “LSTM” (Table 2). The process of LSTM is similar to Meteo-Hydro-LSTM but without the forecast interval streamflow, which is also shown in Fig. 2.

2.3 Evaluation method

The root-mean-squared error (RMSE) was used to evaluate the deterministic forecast, i.e., the ensemble means of 51 (ECMWF) or 40 (ESP) forecast members. To evaluate probabilistic forecasts, the continuous ranked probability score (CRPS) was calculated as follows:

$$\begin{array}{}\text{(7)}& \mathrm{CRPS}={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}[F\left(y\right)-F_o(y){]}^{\mathrm{2}},\end{array}$$

where

$$\begin{array}{}\text{(8)}& F_o\left(y\right)=\left\{\begin{array}{l}\mathrm{0},y<\text{observed value}\\ \mathrm{1},y\ge \text{observed value}\end{array}\right.\end{array}$$

is a cumulative probability step function that jumps from zero to one at the point where the forecast variable y equals the observation, and F(y) is a cumulative probability distribution curve formed by the forecast ensembles. The CRPS has a negative orientation (smaller values are better), and it rewards the concentration of probability around the step function located at the observed value (Wilks et al., 2005). The skill score for deterministic forecast was calculated as

$$\begin{array}{}\text{(9)}& {\mathrm{SS}}_{\mathrm{RMSE}}={\displaystyle \frac{\mathrm{RMSE}-{\mathrm{RMSE}}_{\mathrm{ref}}}{\mathrm{0}-{\mathrm{RMSE}}_{\mathrm{ref}}}}=\mathrm{1}-{\displaystyle \frac{\mathrm{RMSE}}{{\mathrm{RMSE}}_{\mathrm{ref}}}}.\end{array}$$

The skill score for a probabilistic forecast (CRPSS) could be calculated similarly to the SS_RMSE.

3 Results

3.1 Evaluation of CSSP calibration

The employed CSSPv2 model is a fully distributed hydrological model, and the streamflow is calculated through a process of converting gridded rainfall into runoff and a process of runoff routing. Figure 3 shows the runoff calibration results by calculating the NSE of monthly runoff simulations compared with observed gridded monthly runoff. After calibrating the CSSPv2 runoff model, the NSE of all grids are above zero, which indicates that the runoff simulation results in all grids are more reliable than the climatology method. In addition, grids distributed in the downstream region have better NSE than the upstream grids. The NSE values of the grids in the southern part are greater than 0.5, which accounts for two-thirds of the interval basin area. Higher NSE values in the upstream part of Jiazhuan station (Fig. 1) are due to the more humid climate (not shown), as hydrological models usually have better performance over wetter areas. For the downstream areas with less precipitation, the higher NSE values are related to the higher percentage of sand in the soil (not shown). Under the same meteorological conditions, there is higher hydraulic conductivity with higher sand content (Wang et al., 2016), and it yields less runoff under infiltration excess, which is more suitable for the saturation-excess-based runoff generation for the CSSPv2 model (Yuan et al., 2018b).

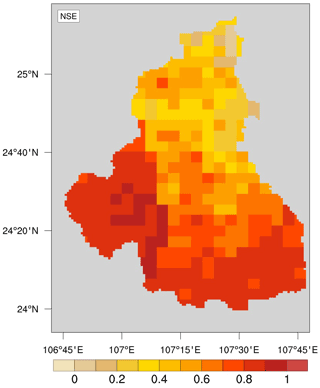
Figure 3 Nash–Sutcliffe efficiency coefficients for the calibrated grid runoff simulation from CSSPv2.

Figures 4 and 5 show the results after the calibration of the routing model, where CSSPv2 is driven by observed meteorological forcings to provide streamflow simulations and compared against observed streamflow at the Yantan hydrological gauge. Figure 4 shows the daily and monthly streamflow simulation results. The monthly result (Fig. 4f) shows that the simulated streamflow closely follows the observed streamflow, and the NSE is 0.96. The daily streamflow simulations during flood seasons (Fig. 4a–e) also show good performance, and the NSE is 0.92. During June and July in 2014, 2015 and 2017, the CSSPv2 model underestimated the daily streamflow with a maximum of 1104 m³/s and an average of 334 m³/s (Fig. 4b, c, e). In 2013 and 2016, the difference between the observed and simulated streamflow is relatively small, and the average difference is 96 m³/s (Fig. 4a, d).

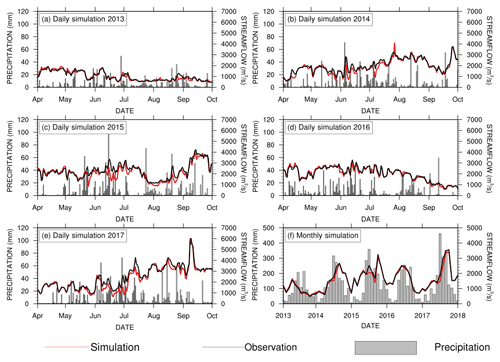
Figure 4 Evaluation of streamflow simulations at the Yantan hydrological gauge. The black and red lines are the observed and simulated streamflow. Panels (a)–(e) show daily streamflow, and panel (f) shows monthly streamflow. The gray bars represent daily (or monthly) precipitation.

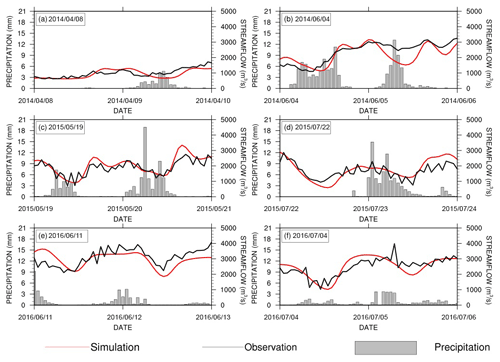
Figure 5 The same as Fig. 4 but for the evaluation of hourly streamflow simulations at the Yantan hydrological gauge. (Please note that dates are given in the following format in this figure: yyyy/mm/dd.)

Figure 5 shows the hourly streamflow simulation results for a few flood events. Figure 5a shows that the CSSPv2 model can accurately simulate the streamflow response to a rainfall event after a dry period. Figure 5b–d show that the CSSPv2 model overpredicted water loss during the recession period for instantaneous heavy rainfall events. Figure 5e–f show that the simulated streamflow has a larger fluctuation than the observations for continuous rainfall events. The simulated streamflow is also smoother than the observations. Nevertheless, the NSE for the hourly streamflow simulation is 0.61, which suggests that CSSPv2 has acceptable performance on an hourly timescale.

3.2 Bias correction of the TIGGE-ECMWF meteorological forecasts

The resolution of TIGGE-ECMWF grid data is 0.25^∘, so the data were interpolated onto a 5 km grid to drive the CSSPv2 model. We calculated the annual average precipitation and temperature for both the observations and TIGGE-ECMWF and then performed a bias correction by adding back the difference (for precipitation) or multiplying back the ratio (for temperature) to match the observations' averages. Figure 6 shows the correlation coefficient and RMSE of TIGGE-ECMWF precipitation and temperature forecasts compared against the observations, either before or after bias correction. The 51-ensemble mean shows better performance for precipitation and temperature (the red dashed lines) than the best ensemble members (the green dashed lines), with an average RMSE reduction of 3.66 mm/d and an average correlation increase of 0.04 for precipitation as well as an average RMSE reduction of 0.1 K and an average correlation increase of 0.03 for temperature. After bias correction, the 51-ensemble means still perform better than best ensemble members. Compared with the ensemble mean results before bias correction, the RMSE decreased by 0.23 mm/d for the bias-corrected precipitation and decreased by 1 K for the bias-corrected surface air temperature. For the bias-corrected ensemble mean results, the average RMSE and correlation are 14.6 mm/d and 0.44 for precipitation, and they are 1.25 K and 0.87 for surface air temperature.

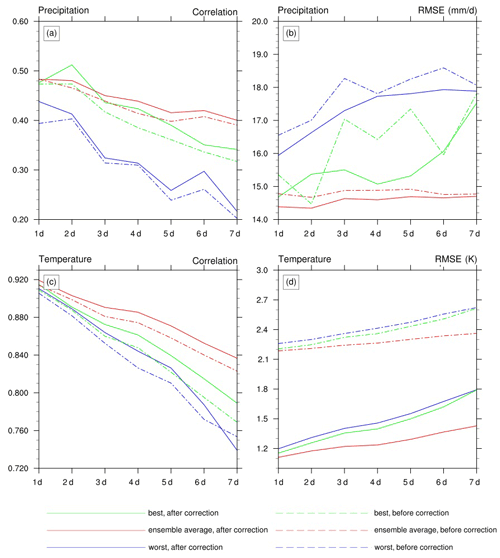
Figure 6 Evaluation of precipitation and temperature hindcasts from TIGGE-ECMWF. The red and blue lines represent the best and worst results among the 51 TIGGE-ECMWF ensemble members, respectively, and the green lines represent the results for the ensemble means of 51 members. Solid and dashed lines represent the results after and before bias corrections, respectively.

3.3 Comparison between the ESP-Hydro and Meteo-Hydro streamflow forecasts

Figure 7 presents the variations in RMSE and CRPS for the ESP-Hydro and Meteo-Hydro hourly streamflow forecasts at the Yantan hydrological gauge. For the probabilistic forecast, Fig. 7a shows that the CRPS for the Meteo-Hydro streamflow forecast ranges from 165 to 225 m³/s, while the CRPS for the ESP-Hydro streamflow forecast ranges from 170 to 230 m³/s. The Meteo-Hydro approach performs better than ESP-Hydro, with a lower CRPS at all lead times and an average 6 % improvement in the CRPSS (Fig. 7c). For the deterministic forecast, Fig. 7b shows that the RMSE for the Meteo-Hydro streamflow forecast ranges from 250 to 350 m³/s, while the RMSE for the ESP-Hydro streamflow forecast ranges from 250 to 390 m³/s. The Meteo-Hydro approach also performs better than ESP-Hydro with a lower RMSE at all lead times, especially after 3 d, with the average reduction in the RMSE reaching 6 % (Fig. 7d).

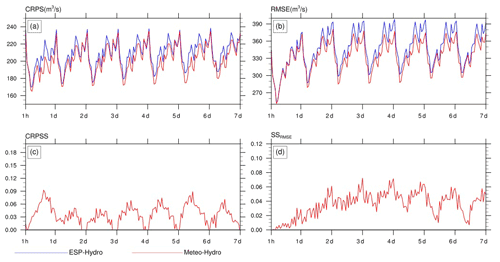
Figure 7 (a) The continuous ranked probability score (CRPS) and (b) root-mean-squared error (RMSE) for the daily streamflow ensemble forecasts at the Yantan hydrological gauge. Panels (c) and (d) show the skill score in terms of the CRPS and RMSE for Meteo-Hydro, where ESP-Hydro is used as the reference forecast.

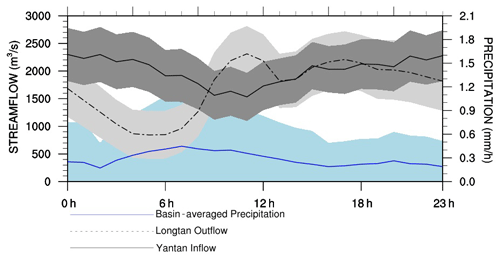
Figure 7 also shows that the forecast skill of both metrics have a similar diurnal cycle, where the RMSE and CRPS reach their peaks at around 00:00 UTC and drop to their lows at 06:00 UTC. Figure 8 shows the diurnal cycle of the variables employed in the model, namely observed catchment mean rainfall and observed streamflow at the Yantan and Longtan hydrological gauges, to explain the diurnal cycle of the ESP-Hydro and Meteo-Hydro forecasting skill. These three input variables show different diurnal patterns: the observed rainfall starts to rise at 00:00 UTC and reaches its maximum at 06:00 UTC; the observed streamflow at the Yantan hydrological gauge drops to its minimum at 12:00 UTC and rises to its maximum at 00:00 UTC; and the streamflow from upstream of the Longtan hydrological gauge starts to drop at 00:00 UTC and reaches its minimum at 06:00 UTC. After comparing these diurnal cycles with the cycle of forecast skill, it is found that the forecast skill decreases when the upstream Longtan outflow starts to decrease and the precipitation starts to increase. When the upstream Longtan outflow increases and the precipitation starts to decrease (after 06:00 UTC), the forecast skill rises.

Figure 8 Diurnal cycle of Longtan outflow (m³/s; dashed black line), Yantan inflow (m³/s; solid black line) and basin-averaged precipitation (mm/h; blue line) as well as their ranges. The time shown in this figure is universal time.

3.4 The Meteo-Hydro-LSTM streamflow forecast

Machine learning methods can recognize patterns hidden in input data and can simulate or predict streamflow without explicit descriptions of the underlying physical processes. Figure 9 shows the RMSE of the Meteo-Hydro-LSTM streamflow forecast using the ensemble mean hydrological forecast as described in the section above and using the past 6 h observed streamflow of the Yantan hydrological gauge as input. Compared with the Meteo-Hydro and ESP-Hydro approach, applying the LSTM model can further decrease the RMSE within the first 72 h. The RMSE of the Meteo-Hydro-LSTM approach ranges from 205 to 363 m³/s during these 3 days, suggesting an average 6 % improvement compared with the Meteo-Hydro approach.

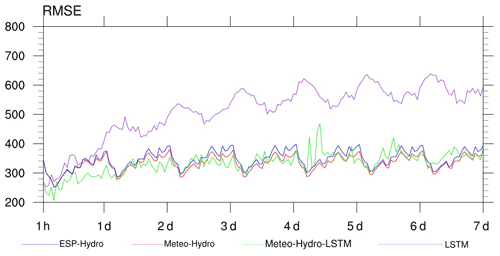
Figure 9 The RMSE (m³/s) for the hourly streamflow hindcasts from four forecasting approaches. The green line represents the Meteo-Hydro-LSTM forecast, the red line represents the Meteo-Hydro forecast, the blue line represent the ESP-Hydro forecast and the purple line represents the LSTM forecast based on historical streamflow observations alone.

Figure 9 also shows the RMSE of the LSTM streamflow forecast using only the past 6 h observed streamflow of the Yantan hydrological gauge as input. Without using the physical model forecast, the RMSE is improved only when the lead time is less than 1 d. Moreover, the performance of LSTM is far worse than the Meteo-Hydro streamflow forecast when the lead time is more than 2 d.

Figure 10 presents several examples of streamflow forecasts using the Meteo-Hydro-LSTM and Meteo-Hydro approaches to show the forecast improvements in detail. The Meteo-Hydro-LSTM approach reduced the flood peak value and the water loss during flood recession period compared with the Meteo-Hydro streamflow forecast approach, which improves the streamflow prediction for most cases (Fig. 10b–f). However, when the upstream reservoir's flood operation is triggered by continuous heavy rain, Meteo-Hydro may underpredict the streamflow. As the LSTM model further decreases the streamflow, the Meteo-Hydro-LSTM method can end up worsening the streamflow forecast, which means that the machine learning method may not always improve the forecasts (Fig. 10a).

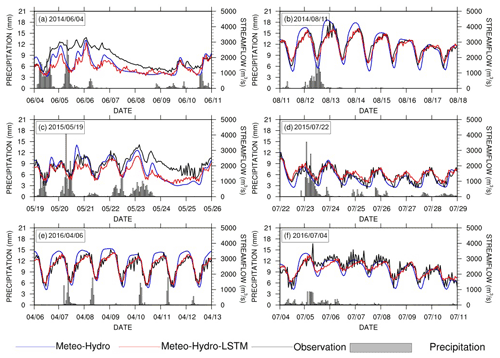
Figure 10 Evaluation of the forecast approaches for a few flooding events. The black lines are observed streamflow from the Yantan hydrological gauge, the blue lines are the Meteo-Hydro ensemble mean streamflow forecast and the red lines are the Meteo-Hydro-LSTM forecast streamflow using the Meteo-Hydro ensemble mean forecast with LSTM. The gray bars represent hourly precipitation averaged over the basin. (Please note that dates are given in the following format in this figure: mm/dd.)

4 Conclusions

In this study, we developed and evaluated a streamflow forecasting framework by coupling meteorological forecasts with a land surface hydrological model (CSSPv2) and a machine learning method (LSTM) over a cascade reservoir catchment using hindcast data from 2013 to 2017. The monthly observed runoff was used to calibrate the runoff generation module of the CSSPv2 model grid by grid, and the hourly observed streamflow at the Yantan hydrological gauge was used to calibrate the routing module of the CSSPv2 model. The bias-corrected TIGGE-ECMWF ensemble forecasts were then used to drive the CSSPv2 for streamflow forecasts, and the LSTM model was used to correct the streamflow forecasts, resulting in an integrated meteorological–hydrological–machine learning forecast framework.

With automatic offline calibration of the CSSPv2 model, the NSE values are 0.96, 0.92 and 0.61 for streamflow simulations at the Yantan hydrological gauge at monthly, daily and hourly timescales, respectively. The bias-corrected ensemble mean TIGGE-ECMWF forcings, which perform the best among all ensemble members, show average respective RMSE and correlation values of 14.6 mm/d and 0.44 for precipitation forecasts and 1.3 K and 0.87 for surface air temperature forecasts. By comparing these results with the hourly observed streamflow, it is found that the integrated hydrometeorological forecast approach (Meteo-Hydro) increases the probabilistic and deterministic forecast skill against the initial condition-based approach (ESP-Hydro) by 6 %.

Adding the LSTM model to the hydrometeorological forecast (Meteo-Hydro-LSTM) can further reduce the forecast error. Within the first 72 h, LSTM can improve the forecast skill by a maximum of 25 % and an average of 6 %. However, if we do not use the streamflow predicted by Meteo-Hydro, the error from the LSTM increases rapidly after 24 h, and the historical-data-based LSTM method performs worse than the Meteo-Hydro method. Most cascade reservoirs cannot currently forecast streamflow beyond 6 h, and the integrated Meteo-Hydro-LSTM approach has the potential to improve the forecasts at long lead times. This study mainly focused on exploring the added value of meteorology–hydrology coupled forecast and LSTM forecasts in a non-closed catchment; therefore, the forecast uncertainty from upstream outflow was ignored by using the observed outflow. In the future, it is planned to include the upstream outflow forecast; however, this will be very challenging, as it requires the development of an upstream hydrometeorological forecast capability as well as reservoir regulation forecasts. Artificial intelligence (AI) techniques are expected to complement the physical model for reservoir regulation forecasts.