the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Theoretical and empirical evidence against the Budyko catchment trajectory conjecture
David A. Kaplan
Harald Klammler
James W. Jawitz
The Budyko framework posits that a catchment's long-term mean evapotranspiration (ET) is primarily governed by the availabilities of water and energy, represented by long-term mean precipitation (P) and potential evapotranspiration (PET), respectively. This assertion is supported by the distinctive clustering pattern that catchments take in Budyko space. Several semi-empirical, nonparametric curves have been shown to generally represent this clustering pattern but cannot explain deviations from the central tendency. Parametric Budyko equations attempt to generalize the nonparametric framework, through the introduction of a catchment-specific parameter (n or w). Prevailing interpretations of Budyko curves suggest that the explicit functional forms represent trajectories through Budyko space for individual catchments undergoing changes in the aridity index, , while the n and w values represent catchment biophysical features; however, neither of these interpretations arise from the derivation of the Budyko equations. In this study, we reexamine, reinterpret, and test these two key assumptions of the current Budyko framework both theoretically and empirically. In our theoretical test, we use a biophysical model for ET to demonstrate that n and w values can change without invoking changes in landscape biophysical features and that catchments are not required to follow Budyko curve trajectories. Our empirical test uses data from 728 reference catchments in the United Kingdom (UK) and United States (US) to illustrate that catchments rarely follow Budyko curve trajectories and that n and w are not transferable between catchments or across time for individual catchments. This nontransferability implies that n and w are proxy variables for , rendering the parametric Budyko equations underdetermined and lacking predictive ability. Finally, we show that the parametric Budyko equations are nonunique, suggesting their physical interpretations are unfounded. Overall, we conclude that, while the shape of Budyko curves generally captures the global behavior of multiple catchments, their specific functional forms are arbitrary and not reflective of the dynamic behavior of individual catchments.
- Article
(3432 KB) - Full-text XML
-
Supplement
(601 KB) - BibTeX
- EndNote
The Budyko framework represents a catchment's long-term mean evapotranspiration (ET) as a function of the aridity index (ϕ), which is defined as the ratio of mean precipitation depth (P) to mean potential evapotranspiration (PET). Current understanding of the Budyko framework is the result of hydrological research over more than a century. The approach has seen a resurgence within catchment hydrology in recent years, partially due to its simplicity, analytical elegance, and potential for studying and predicting landscape precipitation partitioning under changing climate and land use (C. Wang et al., 2016; Mianabadi et al., 2020). Early investigators proposed equations for semi-empirical curves to describe the aggregate behavior of ET as a function of P and PET for large numbers of catchments (Schreiber, 1904; Ol'Dekop, 1911; Budyko, 1974). Since then, efforts to extend the utility of the Budyko framework have both retained and emphasized the concept of explicit curves (i.e., specific mathematical relationships), leading to the development of parametric Budyko equations. The parameters of these equations are typically referred to as “catchment-specific parameters” and are generally interpreted as representing the influence of all catchment biophysical features, other than P and PET, on ET (C. Wang et al., 2016). This interpretation has motivated profound efforts to understand the relationship between biophysical features and catchment-specific parameters (Yang et al., 2007, 2009, 2016; Donohue et al., 2012; Shao et al., 2012; Li et al., 2013; S. Li et al., 2020; T. Li et al., 2020; Xu et al., 2013; Cong et al., 2015; Zhang et al., 2018, 2019b; Abatzoglou and Ficklin, 2017; Xing et al., 2018a; Zhao et al., 2020; Ning et al., 2019, 2020a, b; Bai et al., 2019). Numerous studies have also focused on determining the sensitivity of precipitation partitioning to climatic and/or land use changes (Roderick and Farquhar, 2011; Wang and Hejazi, 2011; Yang and Yang, 2011; W. Wang et al., 2016; Zhou et al., 2016; Shen et al., 2017; Zhang et al., 2016, 2020; Yeh and Tsao, 2020; Sinha et al., 2020; Ning et al., 2020b; Liu et al., 2020; Li et al., 2018, 2019; H. Li et al., 2020; Z. Li et al., 2020a; J. Liu et al., 2019a; Yang et al., 2018; Xing et al., 2018b; Xiangyu et al., 2020) as well as on deriving causal attribution to changes in this partitioning (Wang and Hejazi, 2011; Xing et al., 2018b; Jaramillo et al., 2018; Mo et al., 2018; Sun et al., 2014; Jiang et al., 2015; Liang et al., 2015; Huang et al., 2016; Zhang et al., 2019a, 2020; Yeh and Tsao, 2020; Xiangyu et al., 2020; Song et al., 2020; Sinha et al., 2020; H. Li et al., 2020; Z. Li et al., 2020b; Deng et al., 2020; Young et al., 2019; Xin et al., 2019; Wang et al., 2018, 2019; Lv et al., 2019; N. Liu et al., 2019; Lee and Yeh, 2019; Kazemi et al., 2019; G. He et al., 2019; Y. He et al., 2019b; Xu et al., 2014).
Despite this widespread application, several doubts have been raised about the robustness of the assumptions and interpretations that underpin this vast and growing literature, particularly with respect to the parametric Budyko equations. For example, Gentine et al. (2012) suggested that the aggregate Budyko curve behavior already reflects the interdependence among vegetation, soil, and climate; therefore, they proposed that the inclusion of the catchment-specific parameter into the Budyko framework is unnecessary. However, this interpretation was partially based on catchment data with limited scatter in Budyko space. Additionally, Greve et al. (2015) highlighted that the catchment-specific parameter has no a priori physical meaning, cannot be estimated for ungauged catchments, and its specific dependence on biophysical features can vary substantially between catchments. Furthermore, Padrón et al. (2017) undertook a comprehensive overview of the wide variety of biophysical features proposed to control the catchment-specific parameter, finding that most proposed features did not actually correlate with the parameter and the types of features that were correlated varied substantially between climatic regions. Finally, Sposito (2017a, b) suggested that the interpretation of the catchment-specific parameter as representing biophysical features does not arise from physical reasoning; thus, identified statistical relationships between the parameter and biophysical features may be spurious and premature.
Given the recent resurgence of the Budyko framework and its importance to catchment hydrology, we build upon these previous critical observations, presenting a retrospective review of the framework's assumptions and development, with the overarching goals of harmonizing historical and current interpretations as well as understanding their implications. Specifically, we critically reinterpret two key and interrelated assumptions of the current framework: (1) the concept that explicit curves represent trajectories of individual catchments through climate space, and (2) the parametric forms of the Budyko equation themselves. We contend that many current interpretations of these assumptions are unsupported by the underlying framework, potentially leading researchers to spurious conclusions about catchment hydrology. However, we stress that the aim of this reinterpretation is not to discard the voluminous efforts put forth using current interpretations of the Budyko framework but rather to recontextualize the conclusions obtained from them. Additionally, we emphasize that the Budyko framework based on the curve-like clustering pattern observed across multiple catchments is a powerful and useful concept when used appropriately and within the proper context.
We first reexamine interpretations of Budyko curves that ascribe physical meaning to the functional form of the curve, thus implying that explicit curves govern catchment evapotranspiration (e.g., C. Wang et al., 2016; Wang and Hejazi, 2011; Jiang et al., 2015; Liang et al., 2015; Jaramillo et al., 2018; Zhang et al., 2004, 2018). This concept is typically articulated through the suggestion that an individual catchment undergoing only changes in the aridity index will follow an explicit Budyko curve trajectory (“the catchment trajectory conjecture”). However, we note that it is mathematically impossible for the aridity index to vary independently of other climate variables that impact PET or P, meaning that the catchment trajectory conjecture, as typically stated, is ill posed and untestable. Given the stated conjecture's mathematical impossibility, in practice, it is generalized implicitly (or unintentionally) to a well-posed and testable form, which suggests that individual catchments with stable basin characteristics that undergo changes in the aridity index will follow an explicit Budyko curve trajectory. Here, we examine the support for the well-posed conjecture and test it, the results of which suggest that specific functional forms of Budyko curves do not have intrinsic physical meaning but are instead semi-empirical conceptual tools that describe the general aggregate behavior of multiple catchments – but do not predict the specific behavior of individual catchments.
Second, we revisit the parametric Budyko equations that are currently interpreted by most authors to represent more generalized forms of the nonparametric Budyko equations (Budyko, 1974), and which can thus be used to separate the effects of changes in the average climate (i.e., changes in the aridity index ϕ) on ET from the effects of all other biophysical features (Wang and Hejazi, 2011; Xing et al., 2018b; Jaramillo et al., 2018; Mo et al., 2018; Sun et al., 2014; Jiang et al., 2015; Liang et al., 2015; Huang et al., 2016; Zhang et al., 2019a, 2020; Yeh and Tsao, 2020; Xiangyu et al., 2020; Song et al., 2020; Sinha et al., 2020; H. Li et al., 2020; Z. Li et al., 2020a; Deng et al., 2020; Young et al., 2019; Xin et al., 2019; Wang et al., 2019; Lv et al., 2019; N. Liu et al., 2019; Lee and Yeh, 2019; Kazemi et al., 2019; G. He et al., 2019; Y. He et al., 2019a, b; Wang et al., 2018; Xu et al., 2014). We argue and demonstrate herein that the two widely accepted parametric Budyko equations (i.e., those derived in Zhang et al., 2004 and Yang et al., 2008) are nonunique, meaning they are only two of many possible single-parameter Budyko equations. Importantly, under the catchment trajectory conjecture, the various versions of the parametric Budyko equations are contradictory, which casts doubt on their current interpretations.
Additionally, while the catchment-specific parameters in the parametric Budyko equations are typically regarded as empirical, “effective” parameters analogous to, for example, Manning's roughness coefficient in open channel flow or hydraulic conductivity in groundwater flow, we demonstrate that this is not the case, as their values are not transferable between catchments or across time for individual catchments. For an empirical parameter to be transferable, the specific functional form of the mathematical relationship in which it is contained must be empirically valid. In such cases (e.g., Manning's formula and Darcy's Law), the validated functional form contains information about the physics of its respective system, allowing for the empirical parameter to be consistently and independently related to physical properties of the system (e.g., channel surface roughness for Manning's roughness coefficient and soil pore size for hydraulic conductivity). In these cases, the effective empirical parameters can be estimated a priori, allowing their respective empirical relationships to be used for making quantitative predictions under future conditions (e.g., different hydraulic gradients). We test the empirical validity of the parametric Budyko equations, with results suggesting that the catchment-specific parameter is nontransferable. Thus, the value of the catchment-specific parameter cannot be determined without first obtaining estimates of P, PET, and (most importantly) ET, effectively rendering it a proxy variable for that has no additional physical meaning and precluding the use of the parametric Budyko equations in predictive pursuits.
Our reinterpretation is demonstrated theoretically using a stochastic soil moisture model (Porporato et al., 2004) as well as empirically using data from 728 reference catchments in the United Kingdom (UK) and United States (US). To provide context for these analyses, we first provide a brief background of the Budyko framework, describe its current dominant interpretations in the literature, and recall Budyko's own interpretation of explicit curves.
2.1 Overview of the Budyko hypothesis and equations
In its foundation, the Budyko framework is an expression of the water balance for a catchment. Over long time periods, it is reasonable to assume that positive and negative short-term changes in catchment storage average to negligibly small values (ΔS≈0) with respect to the cumulative long-term volumes involved in the water balance. Thus, with ΔS=0, the long-term average precipitation, P, is partitioned into either evapotranspiration, ET, or discharge, Q, from the catchment, yielding
Budyko (1974), among others (e.g., Ol'Dekop, 1911; Thornthwaite, 1948), recognized that available water (i.e., P) and energy (i.e., PET) are the primary drivers of long-term average catchment evapotranspiration; therefore, it has been suggested that ET is a function of P and PET:
Several explicit functional forms of f0 have been proposed based on their ability to match the central tendency of observed ET for multiple catchments across a wide range of climates (Ol'Dekop, 1911; Schreiber, 1904; Bagrov, 1953), with Budyko (1974) putting forth the following expression:
However, Eq. (3) and other forms of Eq. (2) are unable to explain differences in ET or the evaporative ratio between catchments with identical P and PET or aridity indices, respectively.
Given this limitation, the original Budyko hypothesis has been modified in an attempt to explain deviations of individual catchments from the explicit Budyko curves by invoking a function that is implicit in ET (Yang et al., 2008):
where for a given P and PET, there may be more than one value of ET that satisfies Eq. (4). Using the hypothesized relationship given by Eq. (4) and applying constraints for purely water- and energy-limited conditions, it is possible to analytically derive explicit forms of f1. It has been shown that there are at least two possible analytical solutions to Eq. (4). The functional form of the first of these solutions was proposed prior (Turc, 1953; Choudhury, 1999; Mezentsev, 1955) to its formal derivation from Eq. (4) by Yang et al. (2008) and is given by
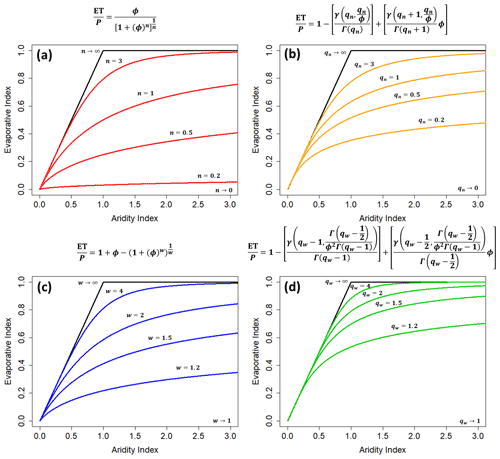
where n is a parameter specific to each catchment. With slightly different assumptions about the structure and boundary conditions of f1, a different parametric form of the Budyko equation can also be derived (Fu, 1981; Zhang et al., 2004):
where w is also a catchment-specific parameter. This equation was also proposed prior to its formal derivation (Tixeront, 1964; Berkaloff and Tixeront, 1958). Equations (5) and (6) express the evaporative index as a function of the aridity index ; however, equivalent forms for both equations exist that express the R Index (Yao, 1974) as a function of the humidity index (Hulme et al., 1992). We refer to all of these expressions as the “parametric Budyko equations”.
Equation (4) has been interpreted as indirectly capturing unknown catchment-specific factors impacting ET, other than P and PET. The catchment-specific parameters in Eqs. (5) and (6) (n or w) arise in part due to the implicit nature of Eq. (4). Two catchments that experience the same P and PET but have a different n or w will have different ET. Higher values of n and w correspond to a higher fraction of P becoming ET, with ET approaching PET in energy-limited systems and ET approaching P in water-limited systems (i.e., as n or w approaches ∞). The lower limits of n and w are 0 and 1, respectively. Mathematically, the value of the catchment-specific parameter describes a family of curves in Budyko space.
2.2 Current interpretations of explicit Budyko curves and the parametric framework
Most current interpretations of the functional forms of Budyko curves explicitly acknowledge their semi-empirical nature; however, many studies simultaneously ascribe specific physical meaning to the mathematical expressions. This interpretation suggests that the curves represent trajectories within Budyko space that a catchment will follow if its aridity index changes, which supposedly allows one to make predictions about ET under different climates (e.g., Roderick and Farquhar, 2011; Wang and Hejazi, 2011; Yang and Yang, 2011; W. Wang et al., 2016; Zhou et al., 2016; Shen et al., 2017; Zhang et al., 2016; Milly et al., 2018). Critically, this interpretation extends the concept of an explicit curve from its representation of an emergent global behavior of multiple catchments to the behavior of individual catchments, implying that the mathematical expressions describing Budyko curves represent fundamental catchment hydrological processes associated with the aridity index. The specific details of these catchment processes are considered to be unknown, but their integrated effects are represented in the functional form of the explicit curves.
Current interpretations of the catchment-specific parameter follow from the application of explicit curves to individual catchment behavior. Generally, these interpretations can be grouped into four distinct viewpoints. (1) The catchment-specific parameter is an effective empirical parameter related to biophysical features, and it is possible to discern and understand that relationship (e.g., C. Wang et al., 2016). (2) The parameter is related to biophysical features, but it may not be possible to determine an explicit relationship; therefore, it should be treated probabilistically (Gudmundsson et al., 2016; Greve et al., 2015; Singh and Kumar, 2015). (3) The catchment-specific parameter and parametric forms of the Budyko equation contradict the Budyko hypothesis (Sposito, 2017a, b; Gentine et al., 2012). (4) The parameter is an arbitrary empirical constant that is generated as a part of the solution to Eq. (4), but it has no a priori physical meaning (Greve et al., 2015; Sposito, 2017b; Daly et al., 2019a). In particular, the idea that the catchment-specific parameter is an effective empirical parameter related to biophysical features (i.e., interpretation 1) has been widely embraced by the catchment hydrology community, which has identified and grouped relevant biophysical features into three categories (Donohue et al., 2012; Harman and Troch, 2014): (1) climate variability, (2) catchment physical processes, and (3) vegetation structure and function. While it is generally well acknowledged that certain climatic variables (e.g., precipitation variability or the fraction of precipitation falling as snow) can influence the catchment-specific parameter (e.g., Roderick and Farquhar, 2011; Berghuijs and Woods, 2016), in practice, many studies effectively neglect this, instead focusing primarily on the role of landscape features or vegetation functioning (C. Wang et al., 2016; Zhang et al., 2004, 2018; Yang et al., 2008, 2016; Greve et al., 2015; Xu et al., 2013; Donohue et al., 2012; Knighton et al., 2020; Gao et al., 2020; Chen et al., 2020; Wu et al., 2019; Qiu et al., 2019; J. Liu et al., 2019b; Liu et al., 2020; Guo et al., 2019).
The widely held interpretations of explicit curves representing individual catchment behavior and the catchment-specific parameter representing biophysical/landscape features has led to the development of methods to determine the sensitivity of precipitation partitioning to climate and/or landscape changes for individual catchments (Roderick and Farquhar, 2011; Wang and Hejazi, 2011; Yang and Yang, 2011; W. Wang et al., 2016; Zhou et al., 2016; Shen et al., 2017; Yeh and Tsao, 2020; Zhang et al., 2016, 2020; Sinha et al., 2020; Ning et al., 2020b; J. Liu et al., 2019a; Liu et al., 2020; Li et al., 2018, 2019; Z. Li et al., 2020b; H. Li et al., 2020; Yang et al., 2018; Xing et al., 2018b; Xiangyu et al., 2020) and multiple methods for decomposing anthropogenic and climatic impacts on precipitation partitioning (Wang and Hejazi, 2011; Xing et al., 2018b; Jaramillo et al., 2018; Mo et al., 2018; Sun et al., 2014; Jiang et al., 2015; Liang et al., 2015; Huang et al., 2016; Zhang et al., 2020; Yeh and Tsao, 2020; Xiangyu et al., 2020; Song et al., 2020; Sinha et al., 2020; Z. Li et al., 2020a; H. Li et al., 2020a; Deng et al., 2020; Zhang et al., 2019a; Young et al., 2019; Xin et al., 2019; Wang et al., 2019; Lv et al., 2019; N. Liu et al., 2019; Lee and Yeh, 2019; Kazemi et al., 2019; Y. He et al., 2019a, b; G. He et al., 2019; Wang et al., 2018; Xu et al., 2014). Additionally, these interpretations have led numerous studies to pursue predictive relationships for the catchment-specific parameter based on various biophysical features (Table S1 in the Supplemental Information) (Yang et al., 2007; Donohue et al., 2012; Yang et al., 2009; Shao et al., 2012; Li et al., 2013; Xu et al., 2013; Cong et al., 2015; Yang et al., 2016; Zhang et al., 2018; Abatzoglou and Ficklin, 2017; Xing et al., 2018a; Zhao et al., 2020; Ning et al., 2020b; Ning et al., 2020a; T. Li et al., 2020; S. Li et al., 2020; Zhang et al., 2019b; Ning et al., 2019; Bai et al., 2019; Ning et al., 2017). However, these relationships are all statistical or derived from curve fitting, which makes it difficult to develop a mechanistic understanding of causal relationships between the catchment-specific parameter and relevant biophysical features. Additionally, interpretations of these relationships implicitly assume that the functional forms of either Eqs. (5) or (6) represent a physically meaningful relationship between the aridity and evaporative indices, which has not been empirically validated as previously noted by Berghuijs et al. (2020). An explicit derivation of n or w in terms of biophysical features would substantially improve our understanding of the catchment-specific parameter, as has been noted many times (Zhang et al., 2004, 2018; Yang et al., 2008; Donohue et al., 2012; Xu et al., 2013; Greve et al., 2015; C. Wang et al., 2016). Reaver et al. (2020) fulfilled this literature-identified need by analytically inverting both forms of the parametric Budyko equations, i.e., Eq. (5) and (6), resulting in expressions for n and w only in terms of P, PET, and ET. These expressions allow for n and w to be explicitly expressed in terms of biophysical features through the dependence of P, PET, and ET on those same features.
2.3 Budyko's interpretation of explicit curves
It is useful to recall that Budyko (1974) considered explicit curves to be semi-empirical. While the physical basis for explicit curves is dictated by the conservation of mass and energy (i.e., the curves could never cross the water and energy limits in Budyko space) and the fact that the curves must approach the energy and water limits for increasing humidity (i.e., ϕ→0) and aridity (i.e., ϕ→∞), respectively, their empirical nature comes from the choice of functional form as they transition between the energy and water limits. Any functional form that satisfies the previous two conditions and provides a “good” fit to observed data could thus be a reasonable choice. Indeed, Budyko's own explicit formulation (Eq. 3) was simply the geometric mean of the Schreiber and Ol'Dekop formulae, which provided a slightly better fit to observed data (Budyko, 1974). These interpretations are suggested by Budyko's own words (Budyko, 1974, p. 325–326):
“The choice of one or another interpolation function for the transition from the first of these conditions to the second is not very important, since, over most of the range of variation in the parameters of the relationship equation, the appropriate relation deviates little from one or the other boundary condition.”.
From this interpretation, it is clear that the explicit curves resulting from the original Budyko hypothesis, while constrained at their limits by fundamental physical laws, are empirical in nature and not derived from catchment hydrologic processes. It should also be noted that the explicit curve relationships were developed to describe the general behavior of multiple catchments over a wide range of aridity indices. This gives the nonparametric Budyko curves (e.g., Eq. 3) some predictive power, albeit in a probabilistic sense. Any given individual catchment would, on average, be expected to fall close to the explicit curves but, in principle, could fall anywhere in Budyko space. Therefore, predictions of ET using the original Budyko curves have a quantifiable uncertainty associated with them. Budyko and Zubenok (1961) showed that this mean error was approximately 10 %, which has been confirmed more recently (Gentine et al., 2012).
Given this background, it is important to recognize the difference between applying a semi-empirical curve to describe the general behavior of aggregated catchments and using a similar curve to represent the trajectory of an individual catchment undergoing changes in aridity. The original Budyko curve emerges from the ensemble characteristics of many catchments across a range of aridity indices. Suggesting that Budyko curve behavior applies to the trajectories of individual catchments may be a reasonable conjecture, but it requires either theoretical justification or empirical validation, both of which are currently lacking. In the following sections (Sect. 3.1.1, 3.1.2), we describe our methods for testing this assumption using both theoretical models and empirical data.
3.1 Reinterpreting explicit Budyko curves
3.1.1 Theoretically testing for Budyko curve trajectories
To test the catchment trajectory conjecture, we employed the biophysical stochastic soil moisture model of Porporato et al. (2004). This model, being physically based, has been used to lend support to Budyko curves and in developing relationships between n or w and catchment biophysical features (e.g., Donohue et al., 2012; Zhang et al., 2018; Cong et al., 2015). Porporato et al. (2004) developed a model of the equilibrium probability distribution of the “effective” relative soil moisture under stationary stochastic precipitation in the form of a marked Poisson process, from which ET can also be calculated. It is important to note that this model accounts for the temporal dependence of precipitation but assumes constant potential evaporation. While this limits some of the specific conclusions that can be drawn from the model, it is adequate for testing the Budyko curve catchment trajectory conjecture, as the conjecture cannot be valid generally if it is not valid for catchments with time-invariant potential evapotranspiration.
We first write the model of Porporato et al. (2004) in a form that can be plotted in Budyko space:
where is the mean of effective relative soil moisture ; s is the relative soil moisture; sW is the relative soil moisture at wilting point; sI is the well-watered condition threshold relative soil moisture falling between saturation (i.e., s=1) and relative soil field capacity; ρ is the soil porosity; Zr is the effective rooting depth; α and λ are the mean precipitation depth and event frequency for marked Poisson process precipitation, respectively; and γ( , ) is the lower incomplete gamma function. The seven parameters (sW, sI, ρ, Zr, α, λ, and PET), can be rewritten in terms of three effective parameters, defined as , , and . This simplifies the expression of Eq. (7) to
which we refer to as the “Porporato model” hereafter. The four parameters that correspond to landscape properties (sW, sI, ρ, and Zr) are combined into a single effective parameter, Z0, which represents maximum soil water storage available for evapotranspiration, while the three parameters corresponding to the climate (α, λ, and PET) reduce to two effective parameters, ψ and η, defined above. The ratio of ψ to η is the aridity index, . Equation (8) could be further simplified into only two effective parameters (Porporato et al., 2004; Harman et al., 2011; Doulatyari et al., 2015), although doing so reduces the conceptual clarity provided by Z0, ψ, and η, which explicitly distinguish climate and landscape parameters.
We tested the catchment trajectory conjecture by varying the model climatic parameters while holding the landscape parameter constant. If the resulting trajectories are not Budyko curves, the conjecture should be rejected. Notably, there are five qualitatively distinct ways that ψ and η can be varied to produce trajectories in Budyko space, giving five test cases of the catchment trajectory conjecture: (1) varying ψ alone, which we denote “variable storm size”; (2) varying η alone, which we denote “variable storm frequency”; (3) varying ψ less than η, which we denote “storm-frequency-dominated aridity” (Trenberth, 2011; Fischer et al., 2014); (4) varying ψ more than η, which we denote “storm-size-dominated aridity” (Fischer et al., 2014); and (5) varying ψ equal to η, which we denote “variable precipitation flashiness”. All of these test cases can be expressed through a functional relationship between the two variables, η=ψc, with c=0 for the variable storm size test case, c→∞ for the variable storm frequency test case, c=2 for the storm-frequency-dominated aridity test case, for the storm-size-dominated aridity test case, and c=1 for the variable precipitation flashiness test case. In all test cases, we set Z0=2 m.
The effective climate and landscape parameters in the Porporato model appear exclusively in ratios, such that only the relative magnitude between parameters is important. Moreover, the same trajectories can be made from infinite parameter combinations. For our test cases, we chose parameter values to maintain illustrative simplicity and to produce visually informative trajectories not restricted to a small portion of Budyko space.
3.2 Empirically testing for Budyko curve trajectories
Our empirical test of the catchment trajectory conjecture involves tracking the actual trajectories of reference catchments in Budyko space over time and quantifying whether they follow Budyko curves. Reference catchments are defined based on long-term stability of land use. Therefore, any changes to precipitation partitioning over time in reference catchments must be attributed to climatic factors, and the catchment trajectory conjecture predicts that their expected trajectories through Budyko space must be Budyko curves (i.e., those described by Eqs. 5 or 6). This prediction can be tested by comparing actual Budyko space trajectories of reference catchments computed from empirical observations against the expectation from the catchment trajectory conjecture. If the observed reference catchment trajectories are distinct from the expected Budyko curve trajectories, the conjecture should be rejected.
For a given reference catchment, estimates of P and PET were obtained from daily records of precipitation and potential evapotranspiration, while estimates of ET were calculated from the catchment water balance, , which assumes that impacts from storage dynamics are negligible (ΔS≈0). As P, PET and ET represent temporal averages, and we were also interested in temporal trajectories of those magnitudes, we computed time series of moving averages for each of the three variables, similar to the method employed by van der Velde et al. (2014). The temporal averaging window for which ΔS≈0 is typically unknown; however it has been shown to exhibit a threshold behavior (i.e., above a certain averaging window size, ΔS is consistently negligible) (Han et al., 2020). The threshold averaging window size can vary between catchments, but approximately 71 % of global catchments reach the threshold with an averaging window of 10 years, and 94 % of catchments reach the threshold with an averaging window of 30 years (Han et al., 2020). To address the uncertainty in the threshold averaging window size, we computed different “realizations” of the actual trajectories in terms of and for each catchment for all possible integer-year averaging windows in annual steps from 1 year to the full length of record. The “conjectured” Budyko curve of Eq. (5) was fitted by adjusting the value of n using the full length of record in each catchment.
The conjecture was tested for each reference catchment by comparing all realizations of actual trajectories to the conjectured Budyko curve trajectory using the nonparametric sign test (Holander and Wolfe, 1973). This is a distribution-free test for consistent over- or underestimation between paired observations (see also Sect. S2). If the catchment trajectory conjecture is correct, then the frequency at which actual and expected Budyko space trajectories are found to be statistically indistinguishable will be higher than what is expected due to random chance (see also Sect. S2). Moreover, we calculated the maximum deviations of the actual trajectories (using the 10-year averaging window) from the expected Budyko curve trajectory for all reference catchments. These values represent the largest magnitudes of climate-induced changes in precipitation partitioning that would be misinterpreted as land-use-induced changes when subscribing to the catchment trajectory conjecture. Finally, we estimated the magnitude of the largest errors in the evaporative index that occurred when using the well-established nonparametric Budyko curve instead of the parametric form. This was done by calculating the maximum deviations between Eq. (3) and the actual trajectories (10-year averaging window) for all reference catchments.
Our empirical tests were based on 728 UK and US reference catchments identified from well-accepted peer-reviewed datasets. These datasets were produced using standardized methodologies with well-documented quality control standards. The 68 UK catchments (Fig. S1a) were from the Catchment Attributes and MEteorology for Large-sample Studies for Great Britain (CAMELS-GB) dataset (Coxon et al., 2020a), which also had membership in the UK Benchmark Network (UKBN2) dataset (Harrigan et al., 2018) and had the highest data-quality metric (a benchmark score of 6). UKBN2 reference catchments have been identified as “near-natural” and are intended to be used for the investigation of climate-driven changes in river flow. The CAMELS-GB dataset contains daily time series of discharge, precipitation, and potential evapotranspiration for each catchment with contiguous record lengths of between 12 and 45 years. The 660 US reference catchments (Fig. S1b) were from the original CAMELS dataset (Addor et al., 2017; Newman et al., 2015). All catchments in the CAMELS dataset are considered reference catchments, with minimal land use changes or disturbances and minimal human water withdrawals (Newman et al., 2015). Daily times series of discharge, precipitation, maximum temperature, and minimum temperature with contiguous lengths between 20 and 35 years were available for each US reference catchment. Daily potential evapotranspiration time series were computed from the daily Tmax and Tmin values using the Hargreaves potential evaporation equation (Hargreaves and Allen, 2003; Lu et al., 2005; Allen et al., 1998), although we note that our empirical test methodology is insensitive to the specific choice of potential evapotranspiration method (see Sect. S2.6).
The aridity indices of the 728 UK and US reference catchments span from 0.13 to 5.93 (300 are arid, ϕ>1, and 428 are humid, ϕ<1) and, thus, provide excellent coverage of Budyko space. Additionally, the reference catchments span a wide range of climates, capturing 4 of the 5 main Köppen–Geiger climate classification groups (arid, warm temperate, boreal, and polar) and 16 of the 31 subclassifications (hot desert, cold desert, hot semiarid, cold semiarid, humid subtropical, temperate oceanic, subpolar oceanic, hot-summer Mediterranean, warm-summer Mediterranean, cold-summer Mediterranean, hot-summer humid continental, warm-summer humid continental, subarctic, Mediterranean-influenced warm-summer humid continental, Mediterranean-influenced subarctic climate, and tundra) (Kottek et al., 2006; Rubel et al., 2017; McCurley Pisarello and Jawitz, 2020). With this broad and inclusive range of climatic conditions, robust and general conclusions about the Budyko framework and catchment trajectory conjecture can be drawn from this set of reference catchments.
3.3 Reinterpreting the parametric Budyko framework
3.3.1 Catchment-specific parameters as proxy variables for the evaporative index
To understand the limitations of the catchment-specific parameters within the parametric Budyko framework, it is illuminating to first review their origin. In the derivations of both forms of the parametric Budyko equations (Eqs. 5 and 6), n and w arise as arbitrary constants from mathematical necessity rather than being introduced in relation to any physically relevant quantities (Zhang et al., 2004; Yang et al., 2008). Specifically, they arise as “separation constants” that are used when solving partial differential equations by the method of separation of variables. Therefore, the most basic interpretation of the catchment-specific parameter is that it is an arbitrary constant required for the solutions of Eq. (4) to satisfy the boundary conditions (i.e., the water and energy balances) while allowing catchments to have different values of ET for a given P and PET. This is contrary to the prevailing interpretation of the catchment-specific parameter as an empirical effective parameter related to biophysical features (Sects. 1, 2.2). The association of the catchment-specific parameter to biophysical features seems to have first arisen as conjecture that was subsequently bolstered by statistical and curve-fitting relationships (Table S1), rather than being motivated by specific physical processes.
Empirical relationships with effective parameters are common and useful in hydrology (e.g., Manning's formula and Darcy's Law). The usefulness of such relationships comes from their transferability either between similar physical systems or within the same system at different times. For example, Darcy's Law states that under certain constraints (i.e., small flow velocities and laminar flow) the flux of water through a porous medium will change linearly with changes in the hydraulic gradient. As long as the flow velocities within the given medium remain small, the slope of the relationship between the hydraulic gradient and flux (i.e., the hydraulic conductivity) will remain constant, meaning its value is transferable across time for that porous medium system. The linear gradient–flux relationship holds for a wide range of different porous media, which allows the slope of the relationship to be independently related to physical properties of the various systems (e.g., pore size distributions, Wang et al., 2017). Therefore, the hydraulic conductivity can be estimated a priori from information independent of the hydraulic gradient and flux, and its value can be consistently transferred between systems with similar properties (i.e., those with similar porous media). For the parametric Budyko equations to be useful empirical relationships analogous to Darcy's Law, the functional forms of Eqs. (5) and (6) must be empirically valid. Specifically, the formulae must be shown to describe how a catchment's evaporative index changes for a given change in the aridity index (i.e., the catchment trajectory conjecture would need to be shown to be valid).
We test the empirical validity of the parametric Budyko framework and the transferability of the catchment-specific parameter with our empirical test of the catchment trajectory conjecture using the 728 UK and US reference catchments (Sect. 3.1.2). This analysis tests the hypothesis that catchments' evaporative indices follow parametric Budyko curves through Budyko space when undergoing changes in the aridity indices. Our test of the transferability of the parametric Budyko curves is directly analogous to testing the linear gradient–flux relationship for Darcy's Law.
3.3.2 Nonuniqueness of the parametric Budyko equations
Equations (5) and (6) are the most widely accepted and frequently used single-parameter Budyko equations. The following properties of these equations are used either as foundational constraints in their derivation or to justify their validity in describing Budyko space: (1) they describe a family of concave down, nonintersecting curves; (2) these curves satisfy conservation of mass and energy; (3) every point within Budyko space belongs to only one curve (i.e., the uniqueness requirement); (4) the values and first derivatives of all curves approach 0 and 1, respectively, in the humid limit (i.e., ϕ→0); (5) the values and first derivatives of all curves are 1 and 0, respectively, in the arid limit (i.e., ϕ→∞); (6) the curves asymptotically approach the energy and water limits as the parameter approaches infinity; and (7) the curves asymptotically approach 0 as the parameter approaches its lower bound. Many previously proposed single-parameter equations violate at least one of these properties (e.g., Zhang et al., 2001, violates property 2; Wang and Tang, 2014, violates property 3; and Milly, 1993, violates property 5). However, any other single-parameter equation that has these properties is as equally valid as Eqs. (5) and (6). In this sense, neither Eqs. (5) and (6) nor any other possible single-parameter Budyko equation has a particular claim of being the “correct” equation for representing Budyko space.
Commonly held interpretations about the parametric Budyko equations, such as the catchment trajectory conjecture, explicitly or implicitly ascribe physical meaning to the specific mathematical functions (e.g., Eqs. 5 and 6) that describe single-parameter curves (e.g., individual catchment trajectories). However, different (but valid) single-parameter Budyko curves described by nonequivalent functions will produce contradictory results when used in hydrological applications (e.g., causal attributions and sensitivity analyses). Such results suggest that the physical interpretations attributed to specific functional expressions of Budyko curves are unfounded.
To illustrate the contradictory nature of the parametric Budyko equations, we compare behaviors of Eqs. (5) and (6) to those of two new relationships that also conform to all of the properties of Eqs. (5) and (6) and have analogous parameters:
and
where qn and qw are the catchment-specific parameters and Γ() is the gamma function. The parameter qn is analogous to n of Eq. (5), taking values ranging between 0 and ∞, and qw is analogous to w in Eq. (6), taking values ranging between 1 and ∞ (Eqs. 9 and 10 are developed fully in Sect. S3).
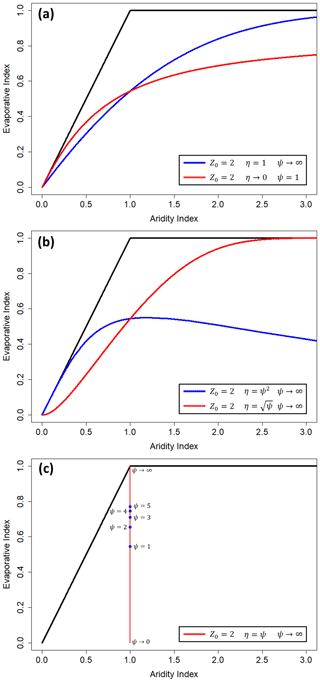
Figure 1Resulting trajectories of the theoretical test of the Budyko curve conjecture plotted in Budyko space. The energy and water limits of Budyko space are given as solid black lines. (a) Trajectories for test case 1, variable storm size (blue), and test case 2, variable storm frequency (red). (b) Trajectories for test case 3, storm-frequency-dominated aridity (blue), and test case 4, storm-size-dominated aridity (red). (c) Trajectory for test case 5, variable precipitation flashiness (red), with locations corresponding to specific values of ψ (blue).
4.1 Reinterpreting explicit Budyko curves
4.1.1 Theoretically testing for Budyko curve trajectories
The theoretical test of the catchment trajectory conjecture for cases 1 (variable storm size) and 2 (variable storm frequency) generally resemble Budyko curves in that they are monotonically increasing, concave down, and approach the energy and water limits as ϕ approaches 0 and ∞, respectively (Fig. 1a). While the trajectories of these two cases appear “Budyko-like”, they have nonidentical shapes (i.e., they follow two distinct paths), contrary to what would be expected from the catchment trajectory conjecture. For test cases 3 (storm-frequency-dominated aridity) and 4 (storm-size-dominated aridity), neither theoretical catchment trajectory can be described as a Budyko-like curve (Fig. 1b). When using the relationship η=ψ2 (storm-frequency-dominated aridity), the trajectory is not even monotonically increasing and actually moves away from the water limit with increasing aridity. The main conclusion of this theoretical test is that a catchment undergoing changes in the aridity index does not have to follow a Budyko curve, contrary to the catchment trajectory conjecture.
The Budyko space trajectory for test case 5 (variable precipitation flashiness) is a vertical line at ϕ=1, with as ψ→0 and as ψ→∞ (Fig. 1c), which is clearly not a Budyko-like curve. Additionally, this trajectory shows that the catchment-specific parameter is not independent of climate and that changes in climate alone (i.e., changing only ψ and η in the Porporato model) can result in arbitrary values of the catchment-specific parameters. The main conclusion to be taken from this test is that the catchment-specific parameter can be highly dependent on climate. While this climate dependency is acknowledged in many current interpretations of n and w (Sect. 2.2), it is contrary to how the catchment-specific parameter is typically used in practice, namely as purely representative of landscape features alone. In combination, our five theoretical tests illustrate that catchments undergoing changes in climate alone can follow Budyko-like curves but are not required to do so.
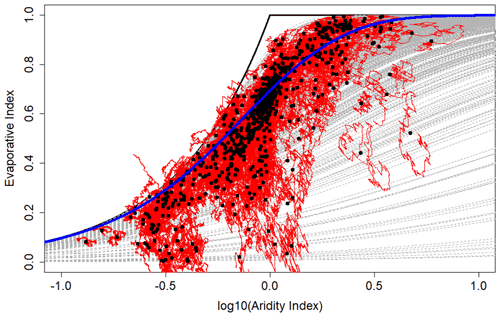
Figure 2Semi-log plot of the Budyko space locations (black dots) of the 728 UK and US reference catchments and their corresponding expected Budyko curves (Eq. 5, gray dashed curves) and 10-year average actual trajectory realizations (red solid curves). The global behavior of the catchments and their actual trajectories generally agree with the nonparametric Budyko curve (Eq. 3, blue solid curve) but not with the expected parametric Budyko curves.
4.1.2 Empirically testing for Budyko curve trajectories
The empirical test of the Budyko curve catchment trajectory conjecture evaluated whether real-world reference catchments not subjected to significant land use change actually follow Budyko curve trajectories over time. The catchments investigated span a wide range of aridity indices, climate zones, latitudes, longitudes, and vegetation types, and the global behavior of their long-term mean water balances is in agreement with the nonparametric Budyko curve (Fig. 2). However, individual catchments do not generally follow parametric Budyko curve trajectories (Figs. 2, 3a), implying significant errors in the prediction of precipitation partitioning sensitivity based on the catchment trajectory conjecture (Fig. 3b). In addition to the theoretical test of the conjecture (Sects. 3.1.1, 4.1.1), the qualitative and quantitative results of this empirical test provide further evidence against the conjecture.
The data for the 728 UK and US reference catchments are shown in Budyko space with their corresponding expected and actual Budyko curve trajectories in Fig. 2. The data generally cluster in a manner reflective of the well-known nonparametric Budyko curve behavior (blue solid curve). Additionally, the aggregate behavior of the actual trajectories (red solid curves) also generally follows the nonparametric Budyko curve. However, there are significant discrepancies between the shape of the overall ensemble cloud of catchments and their actual trajectories versus the corresponding conjectured trajectories (gray dashed curves) for most individual catchments. Many of the curves that would be expected based on the catchment trajectory conjecture span regions of “unpopulated” Budyko space where actual catchments are rarely observed.

Figure 3Comparison of actual catchment trajectories with their corresponding expected Budyko curves (Eq. 5) suggested by the catchment trajectory conjecture. (a) Example catchments with statistically distinguishable (red solid curves) and indistinguishable (blue solid curves) actual (10-year average) and expected trajectories (black dashed curves). Catchments and p values from the nonparametric sign test, in order of increasing evaporative index: Bull Lake Creek, Wind River Reservation, WY, US, USGS Station 06224000, ; River Lune, Killington, Cumbria, UK, NRFA Station 72005, ; River Dee, Woodend, Aberdeenshire, UK, NRFA Station 12001, ; Shell Creek, Bighorn National Forest, WY, US, USGS Station 06278300, p∼0; River Ithon, Disserth, Powys, UK, NRFA Station 55016, ; River Fal, Tregony, Cornwall, UK, NRFA Station 48003, p∼0.28; Kiamichi River, Big Cedar, OK, US, USGS Station 07335700, ; West Clear Creek, Camp Verde, AZ, US, USGS Station 09505800, p∼0.061; Little Withlacoochee River, Rerdell, FL, US, USGS Station 02312200, . (b) Histogram of the maximum absolute relative error in the evaporative index between the 10-year average actual trajectory realizations and expected trajectories for all 728 reference catchments, truncated to 225 %. Values for the nine example catchments from panel (a) are indicated with arrows colored in correspondence with their statistical distinguishability. The overall mean of the distribution (26 %) is given as a vertical black dashed line.
Nonparametric sign tests showed that none of the reference catchments consistently followed the Budyko curves that would be expected based on the catchment trajectory conjecture (i.e., for multiple realizations of actual trajectories using different averaging window sizes). From the total of 24 501 actual trajectory realizations, 23 231 (95 %) were found to have consistent differences (p < 0.05) from their expected trajectories (i.e., they did not follow Budyko curves), whereas only 1270 (5 %) were found to be statistically indistinguishable (p > 0.05). We note that the 5 % of actual trajectory realizations for which Budyko curve trajectories could not be rejected is consistent with the expected 5 % that would be accepted due to random chance at a significance level of 95 %.
Figure 3a gives examples of actual trajectory realizations (10-year average) that are statistically distinguishable (red curves) and indistinguishable (blue curves) from their expected trajectories (black dotted curves). The maximum deviation between the actual evaporative index (10-year average) and those determined from expected trajectories shown in Fig. 3a is 0.14, corresponding to an absolute relative error of 212 %. Figure 3b gives a histogram of the maximum absolute relative errors in the evaporative index between the 10-year average actual trajectory realizations and expected trajectories for all 728 reference catchments, truncated to a maximum value of 225 %. The locations of the errors associated with the example trajectories in Fig. 3a are given by arrows in Fig. 3b, with their colors (red or blue) corresponding to the trajectory's statistical distinguishability. The full range of evaporative index errors spanned from 0.4 % to 1991 %, with a mean of 26 %. The mean error closely agrees with the value (27.9 %) found by Berghuijs and Woods (2016) in a comparable test of the catchment trajectory conjecture using Eq. (6) and 420 catchments from the MOPEX (Model Parameter Estimation Project) dataset (Schaake et al., 2006). Importantly, the average relative error for the parametric Budyko framework (26 %) is actually larger than that for Eq. (3) (23 %), which suggests that the nonparametric Budyko curve is in better agreement with the global behavior of catchments than the ensemble of parametric curves specifically fit to the individual catchments.
From these results, we can conclude that individual catchments do not generally or consistently follow Budyko curve trajectories as posited by the catchment trajectory conjecture. As such, the use of this conjecture in hydrological analyses (e.g., precipitation partitioning sensitivity and causal attribution to anthropogenic and climatic impacts) will likely introduce significant errors and may lead to spurious conclusions.
4.2 Reinterpreting the parametric Budyko framework
4.3 Catchment-specific parameters as proxy variables for the evaporative index
The results of our empirical test of the Budyko curve catchment trajectory conjecture (Sects. 3.1.2, 4.1.2) strongly suggest that the parametric Budyko equations do not describe the long-term evaporative behavior of individual catchments (i.e., they are not empirically valid). This further suggests that their specific functional forms are not physically meaningful, and the catchment-specific parameter cannot be independently related to physical properties. Thus, n and w are not transferrable either between catchments or between different time points in a single catchment. Without empirical tethers to physical reality, the functional forms of Eqs. (5) and (6) do not carry information independent of P, PET, and ET, leaving the parametric Budyko equations underdetermined and establishing that the catchment-specific parameter and are proxies for each other.
Due to this nontransferability and proxy relationship, it is not possible to solve for n or w without first obtaining , making it impossible to obtain the value of n and w for a catchment a priori. When P and PET are known, the values of n or w and are inextricably intertwined because they can only be “measured” by inverting Eqs. (5) and (6) using the same evaporative fluxes that are to be eventually estimated. This reliance makes their use in predictive pursuits purely circular. Thus, the parametric Budyko equations are underdetermined, as each equation will always contain two unknowns (i.e., and either n or w). This means that for any given ϕ, there are infinite valid combinations of the catchment-specific parameter and (Sect. S4, Fig. S2).
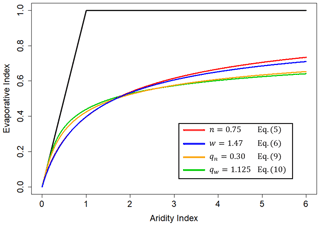
Figure 5Illustration of the contradiction between different versions of the four parametric Budyko equations. Constant parameter trajectories, defined by each of the four parametric equations, cross one another. This means that if a catchment has a constant parameter trajectory in one formulation, the parameter must change for the other formulations.
The inability to estimate n and w without has also been noted previously in the literature (e.g., Zhang et al., 2004; Greve et al., 2015). This fact is made even more evident by examining the processes used to develop the proposed n and w relationships summarized in Table S1. In every case, is first estimated empirically from discharge and precipitation data or from a biophysical model prior to being used to calculate a value for n or w, which is subsequently used to develop the statistical curve-fitting relationships. The apparent dependence of the catchment-specific parameter on biophysical features is, thus, directly derived from the dependence of on those same features (Reaver et al., 2020). In all of these cases, transforming to n or w adds no new information given our empirical finding that Eqs. (5) and (6) do not represent trajectories of individual catchments (Sect. 4.1.2). For the relationships in Table S1, the parametric Budyko equations essentially act as (unnecessary) coordinate transformations from Budyko space, with coordinates , to “Budyko curve space”, with coordinates or . Practically, n and w could be eliminated from each of these studies by fitting the proposed models to the estimated values of directly, bypassing the parametric Budyko framework altogether. The resulting models would likely be easier to interpret, as they would relate catchment biophysical features to a real quantity, either or ET, rather than to an ambiguous parameter. In short, using the parametric Budyko equations to estimate ET from P and PET always requires one to first estimate ET; the same is true for estimating changes in ET from changes in P and PET. This severely limits the practical applicability of the parametric Budyko framework.
In principle, with an appropriate interpretation of the catchment-specific parameter, use of the parametric Budyko framework in landscape hydrology is benign, if unnecessary. However, in practice, even with an appropriate interpretation of n and w, the use of Eqs. (5) and (6) in a hydrological analysis will likely have deleterious effects on both the quantitative values of results and their interpretations. The reason for this is that the catchment-specific parameter is a poor proxy variable for , as it maps the finite space of (i.e., 0 to 1) to the infinite spaces of n (i.e., 0 to ∞) and w (i.e., 1 to ∞). Therefore, as a catchment approaches the water and energy limits in Budyko space, infinitesimal changes in result in infinitely large changes in the catchment-specific parameter, allowing for small numerical errors to be dramatically amplified and further confounding relationships based on these transformations (e.g., the relationships in Table S1).
While the acknowledgment of the proxy nature of the catchment-specific parameter and casts doubt on the specific conclusions of previous parametric Budyko-based research, we note that both the intent and much of the effort of many such studies can be preserved. For example, studies that related n or w to catchment biophysical features using various analytical tools could employ the same methods to relate ET or to biophysical features directly. Doing so would preserve most of the analyses of such studies (i.e., near-identical methods) as well as their intent (i.e., understanding the relationship between ET and catchment biophysical features).
4.3.1 Nonuniqueness of the parametric Budyko equations
If the family of curves described by parametric Budyko equations are interpreted as trajectories for catchments undergoing changes in aridity, then each possible parametric Budyko equation contradicts all others, as each gives specific but nonequivalent functional forms for the trajectories. Even Eqs. (5) and (6), which are generally regarded as essentially interchangeable when using the approximate relationship, (Yang et al., 2008; Andréassian and Sari, 2019), give nonequivalent trajectories, particularly for small values of the catchment-specific parameter. The contradiction between Eqs. (5) and (6) alone should cast doubt on current commonly held interpretations of parametric Budyko equations, particularly regarding the physical meaning of explicit curves and the provenance and meaning of the catchment-specific parameter. However, our introduction of Eqs. (9) and (10) further illustrates the irreconcilable contradictions between competing parametric Budyko equations.
The parametric Budyko equations described by Eqs. (5), (6), (9), and (10) represent four equally valid families of curves (Fig. 4) in that they are all monotonically increasing, concave down, and approach the energy and water limits as ϕ approaches 0 and ∞, respectively. Curves with constant parameters from each of the four parametric Budyko formulations generally cross and diverge as the aridity index changes (Fig. 5). Traveling along a trajectory with a constant catchment-specific parameter (i.e., n, w, qn, or qw) in one formulation of the parametric Budyko equations means the parameters of the other three formulations must continuously change. Thus, Eqs. (5), (6), (9), and (10) directly contradict each other.
Of the previously proposed parametric Budyko equations, Eqs. (5) and (6) have been the most widely used (e.g., Donohue et al., 2012; Yang et al., 2007, 2009, 2016; Shao et al., 2012; Li et al., 2013; T. Li et al., 2020; S. Li et al., 2020; Xu et al., 2013; Cong et al., 2015; Zhang et al., 2018, 2019b; Abatzoglou and Ficklin, 2017; Xing et al., 2018a; Zhao et al., 2020; Ning et al., 2019, 2020a, b; Bai et al., 2019). Any of these studies could have justifiably used Eqs. (9) or (10) instead, as there is not an objective reason to choose any one over the others. However, each equation would lead to substantially different and potentially contradictory results. For example, methods for predicting the sensitivity of precipitation partitioning to changes in the aridity index or the catchment-specific parameter (Sect. 2.2) rely on the specified shape of the Budyko curve. The use of Eq. (5) to compute sensitivities would produce substantially different results compared with those produced from Eq. (10). Additionally, methods for attributing changes in precipitation partitioning to anthropogenic and climatic changes (Sect. 2.2) will produce contradictory conclusions when using one parametric Budyko formulation compared with using another.
It is important to note that Eqs. (5), (6), (9), and (10) are not the only potential parametric Budyko equations. In fact, the Porporato model (Eq. 8) can be manipulated into a single-parameter Budyko equation (e.g., Harman et al., 2011; Daly et al., 2019b). There are likely many more, all equally valid, versions with even starker differences in the shapes of the curves (leading to even larger discrepancies between formulations if the current interpretations of explicit Budyko curves and parametric Budyko equations are maintained). This “equifinality” and nonuniqueness of the parametric Budyko equations is incompatible with the overwhelming current interpretation of the parametric framework and lends support to our contention that the parametric Budyko formulations are better understood as arbitrary coordinate transformations between alternative representations of Budyko space.
The original Budyko hypothesis given in Eq. (2) and the resulting nonparametric curve (e.g., Eq. 3) provide an overarching framework for understanding catchment hydrology in terms of energy and water balances. As the development of the Budyko framework advanced over the past century, early conceptual tools, such as explicit functional curves, gained considerable influence, resulting in interpretations that are not actually supported by the framework and which may lead to spurious conclusions. In this study, we have revisited, summarized, and critically evaluated these interpretations, leading to a reinterpretation of explicit Budyko curves and the parametric Budyko equations.
It is apparent from the literature that the prevailing interpretation of explicit Budyko curves ascribes undue physical meaning to the explicit mathematical expression describing the curve. By returning to Budyko's own interpretation of explicit curves, we saw that earlier conceptual frameworks considered the specific choice of functional form to be arbitrary as long as the curves suggested conservation of energy and mass in the humid and arid limits and provided a good representation of the global behavior of multiple catchments across a range of aridity conditions. We reinforce that the general global Budyko curve behavior observed across multiple catchments is a valid, well-documented, and physically driven phenomenon. However, the attribution of physical meaning to the specific functional forms of curves, as well as explicitly interpreting them as trajectories for catchments undergoing changes in aridity, is an unsupported conjecture. Our tests of this conjecture showed, both theoretically and empirically, that conceptualizing Budyko curves as trajectories is unjustified. Therefore, as an alternative to using explicit Budyko curves to understand catchment trajectories, we reiterate the long-standing suggestion (e.g., Eagleson, 1978; Milly, 1994; Daly and Porporato, 2006; Rodriguez-Iturbe et al., 1999; Feng et al., 2015, etc.) that process-based evapotranspiration models should be used. Additionally, to be a valid representation of catchment evapotranspiration, process-based models need to able to reproduce the empirically established, nonparametric Budyko curve behavior when applied to multiple catchments across a range of climates. Thus, the general Budyko curve behavior can serve as a global constraint (i.e., calibration or validation) in the application of such models (e.g., Greve et al. 2020). Furthermore, while the parametric Budyko framework lacks predictive power, the nonparametric framework allows for probabilistic predictions of ET and Q as well as changes in ET and Q for ungauged basins. Within these contexts, the nonparametric Budyko framework is a tremendously useful conceptualization.
A literature review suggests that most current interpretations view the parametric Budyko equations as more general and versatile forms of the nonparametric Budyko equations. We illustrated that the parametric Budyko equations are underdetermined, lack predictive power, and are nonunique, merely serving as a coordinate transformation between Budyko space and Budyko curve space. Coupled to current interpretations of the parametric equations is the idea that the catchment-specific parameter is a lumped quantity that represents the influence of catchment biophysical features on , with many studies, in practice, treating it as only representing landscape features. We tested the climate independence of the catchment-specific parameter theoretically and demonstrated that its value can change due to climate alone. Given the underdetermined nature of the parametric Budyko equations, the catchment-specific parameter is best understood as an arbitrary constant that is effectively a proxy variable for . The collective results from our analyses suggest that current commonly held interpretations of Budyko curve trajectories and the parametric Budyko equations are unsupported. We propose that the catchment hydrology community look critically at the well-accepted but unjustified interpretations that are the current commonly held standard.
In closing, we recommend that improved understanding of ET should emerge from fundamental physical and biological controls, utilizing the empirically validated global Budyko curve behavior as a constraint, rather than ascribing undue meaning to arbitrary functional forms or ambiguous parameters. As with any empirical relationship, extrapolating the use of the Budyko curve beyond the regime for which is was developed is unjustified without additional evidence. By doing so we risk drawing spurious conclusions about the hydrologic functioning of landscapes. Empirical relationships, such as the Budyko curve, emerge from the underlying physics within a given context, but those relationships are susceptible to losing their physical foundations outside of that context.
The data used in this paper can be obtained from the following locations: the CAMELS-GB database (https://doi.org/10.5285/8344e4f3-d2ea-44f5-8afa-86d2987543a9, Coxon et al., 2020b); the UKBN2 database (https://nrfa.ceh.ac.uk/benchmark-network, Harrigan et al., 2018) and (http://nrfa.ceh.ac.uk/sites/default/files/UKBN_Station_List_vUKBN2.0_1.xlsx, Harrigan et al., 2018); and the CAMELS database (https://doi.org/10.5065/D6MW2F4D, Newman et al., 2014).
The supplement related to this article is available online at: https://doi.org/10.5194/hess-26-1507-2022-supplement.
NGFR conceived the study, compiled the data, performed the analyses, and drafted the paper. All authors contributed in the methodological design, interpretation of results, and paper preparation.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Nathan G. F. Reaver received support from a University of Florida graduate fellowship.
This paper was edited by Luis Samaniego and reviewed by two anonymous referees.
Abatzoglou, J. T. and Ficklin, D. L.: Climatic and physiographic controls of spatial variability in surface water balance over the contiguous United States using the Budyko relationship, Water Resour. Res., 53, 7630–7643, 2017.
Addor, N., Newman, A. J., Mizukami, N., and Clark, M. P.: The CAMELS data set: catchment attributes and meteorology for large-sample studies, Hydrol. Earth Syst. Sci., 21, 5293–5313, https://doi.org/10.5194/hess-21-5293-2017, 2017.
Allen, R. G., Pereira, L. S., Raes, D., and Smith, M.: Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56, Fao, Rome, 300, D05109, ISBN 92-5-104219-5, 1998.
Andréassian, V. and Sari, T.: Technical Note: On the puzzling similarity of two water balance formulas – Turc–Mezentsev vs. Tixeront–Fu, Hydrol. Earth Syst. Sci., 23, 2339–2350, https://doi.org/10.5194/hess-23-2339-2019, 2019.
Bagrov, N.: O srednem mnogoletnem isparenii s poverchnosti susi (Über den vieljährigen Durchschnittswert der Verdunstung von der Oberfläche des Festlands), Meteorog. i Gridrolog, 10, 20–25, 1953.
Bai, P., Liu, X., Zhang, D., and Liu, C.: Estimation of the Budyko model parameter for small basins in China, Hydrol. Process., 34, 125–138, https://doi.org/10.1002/hyp.13577, 2019.
Berghuijs, W. R. and Woods, R. A.: Correspondence: Space-time asymmetry undermines water yield assessment, Nat. Commun., 7, 11603, https://doi.org/10.1038/ncomms11603, 2016.
Berghuijs, W. R., Gnann, S. J., and Woods, R. A.: Unanswered questions on the Budyko framework, Hydrol. Process., 34, 5699–5703, https://doi.org/10.1002/hyp.13958, 2020.
Berkaloff, E. and Tixeront, J.: Notice de la carte du ruissellement annuel moyen en Tunisie, Etudes Hydraulique et Hydrologie, Série I, Fascicule, vol. 7, p. 11, 1958.
Budyko, M. and Zubenok, L.: The determination of evaporation from the land surface, Izv. Akad. Nauk SSSR Ser. Geogr, 6, 3–17, 1961.
Chen, H., Huo, Z., Zhang, L., and White, I.: New perspective about application of extended Budyko formula in arid irrigation district with shallow groundwater, J. Hydrol., 582, 124496, https://doi.org/10.1016/j.jhydrol.2019.124496, 2020.
Choudhury, B.: Evaluation of an empirical equation for annual evaporation using field observations and results from a biophysical model, J. Hydrol., 216, 99–110, 1999.
Cong, Z., Zhang, X., Li, D., Yang, H., and Yang, D.: Understanding hydrological trends by combining the Budyko hypothesis and a stochastic soil moisture model, Hydrol. Sci. J., 60, 145–155, https://doi.org/10.1080/02626667.2013.866710, 2015.
Coxon, G., Addor, N., Bloomfield, J. P., Freer, J., Fry, M., Hannaford, J., Howden, N. J. K., Lane, R., Lewis, M., Robinson, E. L., Wagener, T., and Woods, R.: CAMELS-GB: hydrometeorological time series and landscape attributes for 671 catchments in Great Britain, Earth Syst. Sci. Data, 12, 2459–2483, https://doi.org/10.5194/essd-12-2459-2020, 2020.
Coxon, G., Addor, N., Bloomfield, J. P., Freer, J., Fry, M., Hannaford, J., Howden, N. J. K., Lane, R., Lewis, M. Robinson, E. L., Wagener, T., and Woods, R.: Catchment attributes and hydro-meteorological timeseries for 671 catchments across Great Britain (CAMELS-GB), NERC Environmental Information Data Centre, [data set], https://doi.org/10.5285/8344e4f3-d2ea-44f5-8afa-86d2987543a9, 2020b.
Daly, E. and Porporato, A.: Impact of hydroclimatic fluctuations on the soil water balance, Water Resour. Res., 42, W06401, https://doi.org/10.1029/2005wr004606, 2006.
Daly, E., Calabrese, S., Yin, J., and Porporato, A.: Linking parametric and water-balance models of the Budyko and Turc spaces, Adv. Water Res., 134, 103435, https://doi.org/10.1016/j.advwatres.2019.103435, 2019a.
Daly, E., Calabrese, S., Yin, J., and Porporato, A.: Hydrological Spaces of Long-Term Catchment Water Balance, Water Resour. Res., 55, 10747–10764, https://doi.org/10.1029/2019wr025952, 2019b.
Deng, W., Song, J., Sun, H., Cheng, D., Zhang, X., Liu, J., Kong, F., Wang, H., and Khan, A. J.: Isolating of climate and land surface contribution to basin runoff variability: A case study from the Weihe River Basin, China, Ecol. Eng., 153, 105904, https://doi.org/10.1016/j.ecoleng.2020.105904, 2020.
Donohue, R. J., Roderick, M. L., and McVicar, T. R.: Roots, storms and soil pores: Incorporating key ecohydrological processes into Budyko's hydrological model, J. Hydrol., 436, 35–50, https://doi.org/10.1016/j.jhydrol.2012.02.033, 2012.
Doulatyari, B., Betterle, A., Basso, S., Biswal, B., Schirmer, M., and Botter, G.: Predicting streamflow distributions and flow duration curves from landscape and climate, Adv. Water Res., 83, 285–298, https://doi.org/10.1016/j.advwatres.2015.06.013, 2015.
Eagleson, P.: Climate, soil and vegetation. 1 Introduction to water balance dynamics, Water Resour. Res., 14, 705–712, 1978.
Feng, X., Porporato, A., and Rodriguez-Iturbe, I.: Stochastic soil water balance under seasonal climates, Proc. Math. Phys. Eng. Sci., 471, 20140623, https://doi.org/10.1098/rspa.2014.0623, 2015.
Fischer, E. M., Sedláček, J., Hawkins, E., and Knutti, R.: Models agree on forced response pattern of precipitation and temperature extremes, Geophys. Res. Lett., 41, 8554–8562, 10.1002/2014gl062018, 2014.
Fu, B.: On the calculation of the evaporation from land surface, Sci. Atmos. Sin., 5, 23–31, 1981.
Gao, F., Wang, H., and Liu, C.: Long-term assessment of groundwater resources carrying capacity using GRACE data and Budyko model, J. Hydrol., 588, 125042, https://doi.org/10.1016/j.jhydrol.2020.125042, 2020.
Gentine, P., D'Odorico, P., Lintner, B. R., Sivandran, G., and Salvucci, G.: Interdependence of climate, soil, and vegetation as constrained by the Budyko curve, Geophys. Res. Lett., 39, L19404, https://doi.org/10.1029/2012gl053492, 2012.
Greve, P., Gudmundsson, L., Orlowsky, B., and Seneviratne, S. I.: Introducing a probabilistic Budyko framework, Geophys. Res. Lett., 42, 2261-2269, https://doi.org/10.1002/2015gl063449, 2015.
Greve, P., Burek, P., and Wada, Y.: Using the Budyko Framework for Calibrating a Global Hydrological Model, Water Resour. Res., 56, e2019WR026280, https://doi.org/10.1029/2019wr026280, 2020.
Gudmundsson, L., Greve, P., and Seneviratne, S. I.: The sensitivity of water availability to changes in the aridity index and other factors – a probabilistic analysis in the Budyko-space, Geophys. Res. Lett., 43, 6985–6994, https://doi.org/10.1002/2016gl069763, 2016.
Guo, A., Chang, J., Wang, Y., Huang, Q., Guo, Z., and Li, Y.: Uncertainty analysis of water availability assessment through the Budyko framework, J. Hydrol., 576, 396–407, https://doi.org/10.1016/j.jhydrol.2019.06.033, 2019.
Han, J., Yang, Y., Roderick, M. L., McVicar, T. R., Yang, D., Zhang, S., and Beck, H. E.: Assessing the Steady-State Assumption in Water Balance Calculation Across Global Catchments, Water Resour. Res., 56, e2020WR027392, https://doi.org/10.1029/2020wr027392, 2020.
Hargreaves, G. H. and Allen, R. G.: History and evaluation of Hargreaves evapotranspiration equation, J. Irrig. Drain. E., 129, 53–63, 2003.
Harman, C. and Troch, P. A.: What makes Darwinian hydrology “Darwinian”? Asking a different kind of question about landscapes, Hydrol. Earth Syst. Sci., 18, 417–433, https://doi.org/10.5194/hess-18-417-2014, 2014.
Harman, C. J., Rao, P. S. C., Basu, N. B., McGrath, G. S., Kumar, P., and Sivapalan, M.: Climate, soil, and vegetation controls on the temporal variability of vadose zone transport, Water Resour. Res., 47, W00J13, https://doi.org/10.1029/2010wr010194, 2011.
Harrigan, S., Hannaford, J., Muchan, K., and Marsh, T. J.: Designation and trend analysis of the updated UK Benchmark Network of river flow stations: the UKBN2 dataset, Hydrol. Res., 49, 552–567, https://doi.org/10.2166/nh.2017.058, 2018 (data available at: https://nrfa.ceh.ac.uk/benchmark-network, http://nrfa.ceh.ac.uk/sites/default/files/UKBN_Station_List_vUKBN2.0_1.xlsx, last access: 28 September 2020).
He, G., Zhao, Y., Wang, J., Gao, X., He, F., Li, H., Zhai, J., Wang, Q., and Zhu, Y.: Attribution analysis based on Budyko hypothesis for land evapotranspiration change in the Loess Plateau, China, J. Arid Land, 11, 939–953, https://doi.org/10.1007/s40333-019-0107-5, 2019.
He, Y., Jiang, X., Wang, N., Zhang, S., Ning, T., Zhao, Y., and Hu, Y.: Changes in mountainous runoff in three inland river basins in the arid Hexi Corridor, China, and its influencing factors, Sustain. Cities Soc., 50, 101703, https://doi.org/10.1016/j.scs.2019.101703, 2019a.
He, Y., Qiu, H., Song, J., Zhao, Y., Zhang, L., Hu, S., and Hu, Y.: Quantitative contribution of climate change and human activities to runoff changes in the Bahe River watershed of the Qinling Mountains, China, Sustain. Cities Soc., 51, 101729, https://doi.org/10.1016/j.scs.2019.101729, 2019b.
Holander, M. and Wolfe, D. A.: Nonparametric statistical methods, New York, John Wiley and Sons, Inc., 503 pp., 1973.
Huang, S., Chang, J., Huang, Q., Chen, Y., and Leng, G.: Quantifying the Relative Contribution of Climate and Human Impacts on Runoff Change Based on the Budyko Hypothesis and SVM Model, Water Resour. Manage., 30, 2377–2390, https://doi.org/10.1007/s11269-016-1286-x, 2016.
Hulme, M., Marsh, R., and Jones, P. D.: Global changes in a humidity index between 1931-60 and 1961-90, Clim. Res., 2, 1–22, https://doi.org/10.3354/cr002001, 1992.
Jaramillo, F., Cory, N., Arheimer, B., Laudon, H., van der Velde, Y., Hasper, T. B., Teutschbein, C., and Uddling, J.: Dominant effect of increasing forest biomass on evapotranspiration: interpretations of movement in Budyko space, Hydrol. Earth Syst. Sci., 22, 567–580, https://doi.org/10.5194/hess-22-567-2018, 2018.
Jiang, C., Xiong, L., Wang, D., Liu, P., Guo, S., and Xu, C.-Y.: Separating the impacts of climate change and human activities on runoff using the Budyko-type equations with time-varying parameters, J. Hydrol., 522, 326–338, https://doi.org/10.1016/j.jhydrol.2014.12.060, 2015.
Kazemi, H., Sarukkalige, R., and Badrzadeh, H.: Evaluation of streamflow changes due to climate variation and human activities using the Budyko approach, Environ. Earth Sci., 78, 713, https://doi.org/10.1007/s12665-019-8735-9, 2019.
Knighton, J., Singh, K., and Evaristo, J.: Understanding Catchment-Scale Forest Root Water Uptake Strategies Across the Continental United States Through Inverse Ecohydrological Modeling, Geophys. Res. Lett., 47, e2019GL085937, https://doi.org/10.1029/2019gl085937, 2020.
Kottek, M., Grieser, J., Beck, C., Rudolf, B., and Rubel, F.: World Map of the Köppen-Geiger climate classification updated, Meteorol. Z., 15, 259–263, https://doi.org/10.1127/0941-2948/2006/0130, 2006.
Lee, C.-H. and Yeh, H.-F.: Impact of Climate Change and Human Activities on Streamflow Variations Based on the Budyko Framework, Water, 11, 2001, https://doi.org/10.3390/w11102001, 2019.
Li, C., Wang, L., Wanrui, W., Qi, J., Linshan, Y., Zhang, Y., Lei, W., Cui, X., and Wang, P.: An analytical approach to separate climate and human contributions to basin streamflow variability, J. Hydrol., 559, 30–42, https://doi.org/10.1016/j.jhydrol.2018.02.019, 2018.
Li, D., Pan, M., Cong, Z., Zhang, L., and Wood, E.: Vegetation control on water and energy balance within the Budyko framework, Water Resour. Res., 49, 969–976, https://doi.org/10.1002/wrcr.20107, 2013.
Li, H., Shi, C., Zhang, Y., Ning, T., Sun, P., Liu, X., Ma, X., Liu, W., and Collins, A. L.: Using the Budyko hypothesis for detecting and attributing changes in runoff to climate and vegetation change in the soft sandstone area of the middle Yellow River basin, China, Sci. Total Environ., 703, 135588, https://doi.org/10.1016/j.scitotenv.2019.135588, 2020.
Li, S., Zhang, L., Du, Y., Zhuang, Y., and Yan, C.: Anthropogenic impacts on streamflow-compensated climate change effect in the Hanjiang River basin, China, J. Hydrol. Eng., 25, p.04019058, https://doi.org/10.1061/(asce)he.1943-5584.0001876, 2020.
Li, T., Xia, J., She, D., Cheng, L., Zou, L., and Liu, B.: Quantifying the Impacts of Climate Change and Vegetation Variation on Actual Evapotranspiration Based on the Budyko Hypothesis in North and South Panjiang Basin, China, Water, 12, 508, https://doi.org/10.3390/w12020508, 2020.
Li, Y., Liu, C., Yu, W., Tian, D., and Bai, P.: Response of streamflow to environmental changes: A Budyko-type analysis based on 144 river basins over China, Sci. Total Environ., 664, 824–833, https://doi.org/10.1016/j.scitotenv.2019.02.011, 2019.
Li, Z., Huang, S., Liu, D., Leng, G., Zhou, S., and Huang, Q.: Assessing the effects of climate change and human activities on runoff variations from a seasonal perspective, Stoch. Env. Res. Risk A., 34, 575–592, https://doi.org/10.1007/s00477-020-01785-1, 2020a.
Li, Z., Li, Q., Wang, J., Feng, Y., and Shao, Q.: Impacts of projected climate change on runoff in upper reach of Heihe River basin using climate elasticity method and GCMs, Sci. Total Environ., 716, 137072, https://doi.org/10.1016/j.scitotenv.2020.137072, 2020b.
Liang, W., Bai, D., Wang, F., Fu, B., Yan, J., Wang, S., Yang, Y., Long, D., and Feng, M.: Quantifying the impacts of climate change and ecological restoration on streamflow changes based on a Budyko hydrological model in China's Loess Plateau, Water Resour. Res., 51, 6500–6519, 2015.
Liu, J., Chen, J., Xu, J., Lin, Y., Yuan, Z., and Zhou, M.: Attribution of Runoff Variation in the Headwaters of the Yangtze River Based on the Budyko Hypothesis, Int. J. Environ. Res. Public Health, 16, https://doi.org/10.3390/ijerph16142506, 2019a.
Liu, J., Xu, S., Han, X., Chen, X., and He, R.: A Multi-Dimensional Hydro-Climatic Similarity and Classification Framework Based on Budyko Theory for Continental-Scale Applications in China, Water, 11, 319, https://doi.org/10.3390/w11020319, 2019b.
Liu, N., Harper, R. J., Smettem, K. R. J., Dell, B., and Liu, S.: Responses of streamflow to vegetation and climate change in southwestern Australia, J. Hydrol., 572, 761–770, https://doi.org/10.1016/j.jhydrol.2019.03.005, 2019.
Liu, Z., Cheng, L., Zhou, G., Chen, X., Lin, K., Zhang, W., Chen, X., and Zhou, P.: Global Response of Evapotranspiration Ratio to Climate Conditions and Watershed Characteristics in a Changing Environment, J. Geophys. Res.-Atmos., 125, e2020JD032371, https://doi.org/10.1029/2020jd032371, 2020.
Lu, J., Sun, G., McNulty, S. G., and Amatya, D. M.: A comparison of six potential evapotranspiration methods for regional use in the southeastern United States, J. Am. Water Resour. Assoc., 41, 621–633, 2005.
Lv, X., Zuo, Z., Ni, Y., Sun, J., and Wang, H.: The effects of climate and catchment characteristic change on streamflow in a typical tributary of the Yellow River, Sci. Rep., 9, 14535, https://doi.org/10.1038/s41598-019-51115-x, 2019.
McCurley Pisarello, K. L. and Jawitz, J. W.: Coherence of global hydroclimate classification systems, Hydrol. Earth Syst. Sci., 25, 6173–6183, https://doi.org/10.5194/hess-25-6173-2021, 2021.
Mezentsev, V.: More on the calculation of average total evaporation, Meteorol. Gidrol, 5, 24–26, 1955.
Mianabadi, A., Davary, K., Pourreza-Bilondi, M., and Coenders-Gerrits, A. M. J.: Budyko framework; towards non-steady state conditions, J. Hydrol., 588, 125089, https://doi.org/10.1016/j.jhydrol.2020.125089, 2020.
Milly, P.: Climate, soil water storage, and the average annual water balance, Water Resour. Res., 30, 2143–2156, 1994.
Milly, P. C. D.: An analytic solution of the stochastic storage problem applicable to soil water, Water Resour. Res., 29, 3755–3758, https://doi.org/10.1029/93WR01934, 1993.
Milly, P. C. D., Kam, J., and Dunne, K. A.: On the Sensitivity of Annual Streamflow to Air Temperature, Water Resour. Res., 54, 2624–2641, https://doi.org/10.1002/2017WR021970, 2018.
Mo, S., Li, Z., Gou, K., Qin, L., and Shen, B.: Quantifying the Effects of Climate Variability and Direct Human Activities on the Change in Mean Annual Runoff for the Bahe River (Northwest China), J. Coast. Res., 341, 81–89, https://doi.org/10.2112/jcoastres-d-16-00159.1, 2018.
Newman, A. J., Clark, M. P., Sampson, K., Wood, A., Hay, L. E., Bock, A., Viger, R. J., Blodgett, D., Brekke, L., Arnold, J. R., Hopson, T., and Duan, Q.: Development of a large-sample watershed-scale hydrometeorological data set for the contiguous USA: data set characteristics and assessment of regional variability in hydrologic model performance, Hydrol. Earth Syst. Sci., 19, 209–223, https://doi.org/10.5194/hess-19-209-2015, 2015.
Newman, A., Sampson, K., Clark, M. P., Bock, A., Viger, R. J., Blodgett, D.: A large-sample watershed-scale hydrometeorological dataset for the contiguous USA, Boulder, CO, UCAR/NCAR [data set], https://doi.org/10.5065/D6MW2F4D, 2014.
Ning, T., Li, Z., and Liu, W.: Vegetation dynamics and climate seasonality jointly control the interannual catchment water balance in the Loess Plateau under the Budyko framework, Hydrol. Earth Syst. Sci., 21, 1515–1526, https://doi.org/10.5194/hess-21-1515-2017, 2017.
Ning, T., Zhou, S., Chang, F., Shen, H., Li, Z., and Liu, W.: Interaction of vegetation, climate and topography on evapotranspiration modelling at different time scales within the Budyko framework, Agr. Forest Meteorol., 275, 59–68, https://doi.org/10.1016/j.agrformet.2019.05.001, 2019.
Ning, T., Li, Z., Feng, Q., Chen, W., and Li, Z.: Effects of forest cover change on catchment evapotranspiration variation in China, Hydrol. Process., 34, 2219-2228, 10.1002/hyp.13719, 2020a.
Ning, T., Liu, W., Li, Z., and Feng, Q.: Modelling and attributing evapotranspiration changes on China's Loess Plateau with Budyko framework considering vegetation dynamics and climate seasonality, Stoch. Env. Res. Risk A., 34, 1217–1230, https://doi.org/10.1007/s00477-020-01813-0 2020b.
Ol'Dekop, E.:Evaporation from the surface of river basins (Bcgapeyie c] godepxyocnb pexysx], acceqyod]), Collection of the Works of Students of the Meteorological Observatory. University of Tartu-Jurjew-Dorpat, Tartu, Estonia,, 4, p. 209., 1911.
Padrón, R. S., Gudmundsson, L., Greve, P., and Seneviratne, S. I.: Large-Scale Controls of the Surface Water Balance Over Land: Insights From a Systematic Review and Meta-Analysis, Water Resour. Res., 53, 9659-9678, 10.1002/2017wr021215, 2017.
Porporato, A., Daly, E., and Rodriguez-Iturbe, I.: Soil water balance and ecosystem response to climate change, Am. Nat., 164, 625–632, 2004.
Qiu, H., Niu, J., and Phanikumar, M. S.: Quantifying the space – time variability of water balance components in an agricultural basin using a process-based hydrologic model and the Budyko framework, Sci. Total Environ., 676, 176–189, https://doi.org/10.1016/j.scitotenv.2019.04.147, 2019.
Reaver, N. G. F., Kaplan, D. A., Klammler, H., and Jawitz, J. W.: Technical Note: Analytical Inversion of the Parametric Budyko Equations, Hydrol. Earth Syst. Sci. Discuss. [preprint], https://doi.org/10.5194/hess-2020-585, 2020.
Roderick, M. L. and Farquhar, G. D.: A simple framework for relating variations in runoff to variations in climatic conditions and catchment properties, Water Resour. Res., 47, W00G07, https://doi.org/10.1029/2010wr009826, 2011.
Rodriguez-Iturbe, I., Porporato, A., Ridolfi, L., Isham, V., and Coxi, D.: Probabilistic modelling of water balance at a point: the role of climate, soil and vegetation, P. Roy. Soc. A-Math. Phy., 455, 3789–3805, 1999.
Rubel, F., Brugger, K., Haslinger, K., and Auer, I.: The climate of the European Alps: Shift of very high resolution Köppen-Geiger climate zones 1800–2100, Meteorol. Z., 26, 115–125, https://doi.org/10.1127/metz/2016/0816, 2017.
Schaake, J., Cong, S., and Duan, Q.: The US MOPEX data set, IAHS Publ., 307, 9, https://www.osti.gov/servlets/purl/899413, 2006.
Schreiber, P.: Über die Beziehungen zwischen dem Niederschlag und der Wasserführung der Flüsse in Mitteleuropa, Meteorol. Z., 21, 441–452, 1904.
Shao, Q., Traylen, A., and Zhang, L.: Nonparametric method for estimating the effects of climatic and catchment characteristics on mean annual evapotranspiration, Water Resour. Res., 48, W03517, https://doi.org/10.1029/2010wr009610, 2012.
Shen, Q., Cong, Z., and Lei, H.: Evaluating the impact of climate and underlying surface change on runoff within the Budyko framework: A study across 224 catchments in China, J. Hydrol., 554, 251–262, https://doi.org/10.1016/j.jhydrol.2017.09.023, 2017.
Singh, R. and Kumar, R.: Vulnerability of water availability in India due to climate change: A bottom-up probabilistic Budyko analysis, Geophys. Res. Lett., 42, 9799–9807, 10.1002/2015gl066363, 2015.
Sinha, J., Das, J., Jha, S., and Goyal, M. K.: Analysing model disparity in diagnosing the climatic and human stresses on runoff variability over India, J. Hydrol., 581, 124407, https://doi.org/10.1016/j.jhydrol.2019.124407, 2020.
Song, X., Sun, W., Zhang, Y., Song, S., Li, J., and Gao, Y.: Using hydrological modelling and data-driven approaches to quantify mining activities impacts on centennial streamflow, J. Hydrol., 585, 124764, https://doi.org/10.1016/j.jhydrol.2020.124764, 2020.
Sposito, G.: Incorporating the Vadose Zone into the Budyko Framework, Water, 9, 698, https://doi.org/10.3390/w9090698, 2017a.
Sposito, G.: Understanding the Budyko Equation, Water, 9, 236, https://doi.org/10.3390/w9040236, 2017b.
Sun, Y., Tian, F., Yang, L., and Hu, H.: Exploring the spatial variability of contributions from climate variation and change in catchment properties to streamflow decrease in a mesoscale basin by three different methods, J. Hydrol., 508, 170–180, https://doi.org/10.1016/j.jhydrol.2013.11.004, 2014.
Thornthwaite, C. W.: An approach toward a rational classification of climate, Geogr. Rev., 38, 55–94, 1948.
Tixeront, J.: Prévision des apports des cours d'eau, Symposium sur les Eau de surface, Assemblée générale de l'IUGG, Berkeley, 118–126, 1964.
Trenberth, K. E.: Changes in precipitation with climate change, Clim. Res., 47, 123–138, https://doi.org/10.3354/cr00953, 2011.
Turc, L.: Le bilan d'eau des sols: relations entre les précipitations, l'évaporation et l'écoulement, 491–595, 1953.
van der Velde, Y., Vercauteren, N., Jaramillo, F., Dekker, S. C., Destouni, G., and Lyon, S. W.: Exploring hydroclimatic change disparity via the Budyko framework, Hydrol. Process., 28, 4110–4118, https://doi.org/10.1002/hyp.9949, 2014.
Wang, C., Wang, S., Fu, B., and Zhang, L.: Advances in hydrological modelling with the Budyko framework: A review, Prog. Phys. Geogr., 40, 409–430, https://doi.org/10.1177/0309133315620997, 2016.
Wang, D. and Hejazi, M.: Quantifying the relative contribution of the climate and direct human impacts on mean annual streamflow in the contiguous United States, Water Resour. Res., 47, W00J12, https://doi.org/10.1029/2010wr010283, 2011.
Wang, D. and Tang, Y.: A one-parameter Budyko model for water balance captures emergent behavior in darwinian hydrologic models, Geophys. Res. Lett., 41, 4569–4577, https://doi.org/10.1002/2014gl060509, 2014.
Wang, F., Duan, K., Fu, S., Gou, F., Liang, W., Yan, J., and Zhang, W.: Partitioning climate and human contributions to changes in mean annual streamflow based on the Budyko complementary relationship in the Loess Plateau, China, Sci. Total Environ., 665, 579–590, https://doi.org/10.1016/j.scitotenv.2019.01.386, 2019.
Wang, J.-P., François, B., and Lambert, P.: Equations for hydraulic conductivity estimation from particle size distribution: A dimensional analysis, Water Resour. Res., 53, 8127–8134, https://doi.org/10.1002/2017wr020888, 2017.
Wang, T., Yang, H., Yang, D., Qin, Y., and Wang, Y.: Quantifying the streamflow response to frozen ground degradation in the source region of the Yellow River within the Budyko framework, J. Hydrol., 558, 301–313, https://doi.org/10.1016/j.jhydrol.2018.01.050, 2018.
Wang, W., Zou, S., Shao, Q., Xing, W., Chen, X., Jiao, X., Luo, Y., Yong, B., and Yu, Z.: The analytical derivation of multiple elasticities of runoff to climate change and catchment characteristics alteration, J. Hydrol., 541, 1042–1056, https://doi.org/10.1016/j.jhydrol.2016.08.014, 2016.
Wu, C., Yeh, P. J. F., Wu, H., Hu, B. X., and Huang, G.: Global Analysis of the Role of Terrestrial Water Storage in the Evapotranspiration Estimated from the Budyko Framework at Annual to Monthly Time Scales, J. Hydrometeorol., 20, 2003–2021, https://doi.org/10.1175/jhm-d-19-0065.1, 2019.
Xiangyu, Z., Chao, Z., and Jinyan, Y.: Quantitative Analysis of Impact of Climate Variability and Human Activities on Water Resources Change in Suzhou City, IOP Conference Series: Earth and Environmental Science, https://doi.org/10.1088/1755-1315/435/1/012015, 012015, 2020.
Xin, Z., Li, Y., Zhang, L., Ding, W., Ye, L., Wu, J., and Zhang, C.: Quantifying the relative contribution of climate and human impacts on seasonal streamflow, J. Hydrol., 574, 936–945, https://doi.org/10.1016/j.jhydrol.2019.04.095, 2019.
Xing, W., Wang, W., Shao, Q., and Yong, B.: Identification of dominant interactions between climatic seasonality, catchment characteristics and agricultural activities on Budyko-type equation parameter estimation, J. Hydrol., 556, 585–599, https://doi.org/10.1016/j.jhydrol.2017.11.048, 2018a.
Xing, W., Wang, W., Zou, S., and Deng, C.: Projection of future runoff change using climate elasticity method derived from Budyko framework in major basins across China, Global Planet. Change, 162, 120–135, https://doi.org/10.1016/j.gloplacha.2018.01.006, 2018b.
Xu, X., Liu, W., Scanlon, B. R., Zhang, L., and Pan, M.: Local and global factors controlling water-energy balances within the Budyko framework, Geophys. Res. Lett., 40, 6123–6129, https://doi.org/10.1002/2013gl058324, 2013.
Xu, X., Yang, D., Yang, H., and Lei, H.: Attribution analysis based on the Budyko hypothesis for detecting the dominant cause of runoff decline in Haihe basin, J. Hydrol., 510, 530–540, https://doi.org/10.1016/j.jhydrol.2013.12.052, 2014.
Yang, D., Sun, F., Liu, Z., Cong, Z., Ni, G., and Lei, Z.: Analyzing spatial and temporal variability of annual water-energy balance in nonhumid regions of China using the Budyko hypothesis, Water Resour. Res., 43, W04426, https://doi.org/10.1029/2006wr005224, 2007.
Yang, D., Shao, W., Yeh, P. J. F., Yang, H., Kanae, S., and Oki, T.: Impact of vegetation coverage on regional water balance in the nonhumid regions of China, Water Resour. Res., 45, W00A14, https://doi.org/10.1029/2008wr006948, 2009.
Yang, H., Yang, D., Lei, Z., and Sun, F.: New analytical derivation of the mean annual water-energy balance equation, Water Resour. Res., 44, W03410, https://doi.org/10.1029/2007wr006135, 2008.
Yang, H. and Yang, D.: Derivation of climate elasticity of runoff to assess the effects of climate change on annual runoff, Water Resour. Res., 47, W07526, https://doi.org/10.1029/2010wr009287, 2011.
Yang, Y., Donohue, R. J., and McVicar, T. R.: Global estimation of effective plant rooting depth: Implications for hydrological modeling, Water Resour. Res., 52, 8260–8276, https://doi.org/10.1002/2016wr019392, 2016.
Yang, Y., Zhang, S., McVicar, T. R., Beck, H. E., Zhang, Y., and Liu, B.: Disconnection between trends of atmospheric drying and continental runoff, Water Resour. Res., 54, 4700–4713, https://doi.org/10.1029/2018wr022593, 2018.
Yao, A. Y. M.: Agricultural potential estimated from the ratio of actual to potential evapotranspiration, Agr. Meteorol., 13, 405–417, https://doi.org/10.1016/0002-1571(74)90081-8, 1974.
Yeh, H.-F. and Tsao, J.: Hydrological Response to Natural and Anthropogenic Factors in Southern Taiwan, Sustainability, 12, https://doi.org/10.3390/su12051981, 2020.
Young, D., Zegre, N., Edwards, P., and Fernandez, R.: Assessing streamflow sensitivity of forested headwater catchments to disturbance and climate change in the central Appalachian Mountains region, USA, Sci. Total Environ., 694, 133382, https://doi.org/10.1016/j.scitotenv.2019.07.188, 2019.
Zhang, K., Ruben, G. B., Li, X., Li, Z., Yu, Z., Xia, J., and Dong, Z.: A comprehensive assessment framework for quantifying climatic and anthropogenic contributions to streamflow changes: A case study in a typical semi-arid North China basin, Environ. Modell. Softw., 128, 104704, https://doi.org/10.1016/j.envsoft.2020.104704, 2020.
Zhang, L., Dawes, W., and Walker, G.: Response of mean annual evapotranspiration to vegetation changes at catchment scale, Water Resour. Res., 37, 701–708, 2001.
Zhang, L., Hickel, K., Dawes, W. R., Chiew, F. H. S., Western, A. W., and Briggs, P. R.: A rational function approach for estimating mean annual evapotranspiration, Water Resour. Res., 40, W02502, https://doi.org/10.1029/2003wr002710, 2004.
Zhang, S., Yang, H., Yang, D., and Jayawardena, A.: Quantifying the effect of vegetation change on the regional water balance within the Budyko framework, Geophys. Res. Lett., 43, 1140–1148, 2016.
Zhang, S., Yang, Y., McVicar, T. R., and Yang, D.: An Analytical Solution for the Impact of Vegetation Changes on Hydrological Partitioning Within the Budyko Framework, Water Resour. Res., 54, 519–537, https://doi.org/10.1002/2017WR022028, 2018.
Zhang, X., Dong, Q., Cheng, L., and Xia, J.: A Budyko-based framework for quantifying the impacts of aridity index and other factors on annual runoff, J. Hydrol., 579, 124224, https://doi.org/10.1016/j.jhydrol.2019.124224, 2019a.
Zhang, X., Dong, Q., Costa, V., and Wang, X.: A hierarchical Bayesian model for decomposing the impacts of human activities and climate change on water resources in China, Sci. Total Environ., 665, 836–847, 10.1016/j.scitotenv.2019.02.189, 2019b.
Zhao, J., Huang, S., Huang, Q., Leng, G., Wang, H., and Li, P.: Watershed water-energy balance dynamics and their association with diverse influencing factors at multiple time scales, Sci. Total Environ., 711, 135189, https://doi.org/10.1016/j.scitotenv.2019.135189, 2020.
Zhou, S., Yu, B., Huang, Y., and Wang, G.: The complementary relationship and generation of the Budyko functions, Geophys. Res. Lett., 42, 1781–1790, https://doi.org/10.1002/2015gl063511, 2015.
Zhou, S., Yu, B., Zhang, L., Huang, Y., Pan, M., and Wang, G.: A new method to partition climate and catchment effect on the mean annual runoff based on the Budyko complementary relationship, Water Resour. Res., 52, 7163–7177, https://doi.org/10.1002/2016wr019046, 2016.