An inverse dielectric mixing model at 50 MHz that considers soil organic carbon

The prevalent soil moisture probe algorithms are based on a polynomial function that does not account for the variability in soil organic matter. Users are expected to choose a model before application: either a model for mineral soil or a model for organic soil. Both approaches inevitably suffer from limitations with respect to estimating the volumetric soil water content in soils with a wide range of organic matter content. In this study, we propose a new algorithm based on the idea that the amount of soil organic matter (SOM) is related to major uncertainties in the in situ soil moisture data obtained using soil probe instruments. To test this theory, we derived a multiphase inversion algorithm from a physically based dielectric mixing model capable of using the SOM amount, performed a selection process from the multiphase model outcomes, and tested whether this new approach improves the accuracy of soil moisture (SM) data probes. The validation of the proposed new soil probe algorithm was performed using both gravimetric and dielectric data from the Soil Moisture Active Passive Validation Experiment in 2012 (SMAPVEX12). The new algorithm is more accurate than the previous soil-probe algorithm, resulting in a slightly improved correlation (0.824 to 0.848), 12 % lower root mean square error (RMSE; 0.0824 to 0.0727 cm³ cm⁻³), and 95 % less bias (−0.0042 to 0.0001 cm³ cm⁻³). These results suggest that applying the new dielectric mixing model together with global SOM estimates will result in more reliable soil moisture reference data for weather and climate models and satellite validation.

1 Introduction

Soil moisture (SM) plays a critical role in weather and climate by affecting atmospheric variables via latent and sensible heat exchange. For example, near-surface air temperature can be affected by the evapotranspiration of surface and root zone soil moisture. Therefore, its correlation with the near-surface temperature is usually considered an effective indicator of the coupling strength between the land surface and the atmosphere (Seneviratne et al., 2006; Koster et al., 2009; Seneviratne et al., 2010; Jaeger and Seneviratne, 2011; Seneviratne et al., 2013; Hirschi et al., 2014; Whan et al., 2015). In particular, soil moisture anomalies in a dry regime have been reported as the main cause of strong land–atmosphere coupling, which can trigger drought and heat waves (Fischer et al., 2007; Zampieri et al., 2009; Guillod et al., 2015; Hauser et al., 2016; Hirschi et al., 2011; Miralles et al., 2011; Taylor et al., 2012; Mueller and Seneviratne, 2012; Seo et al., 2019). Soil moisture also influences precipitation formation and storm tracks by coupling with the atmosphere (Koster et al., 2004; Taylor et al., 2012; Guillod et al., 2015; Santanello et al., 2018, 2019; Zhang et al., 2019). Consequently, inaccurate SM information in the land-surface model hinders accurate predictions of extreme climate and weather because of unrealistic land–atmosphere interactions that result from uncertainties in air temperature, moisture, dynamics, cloud formation, and precipitation.

High-quality in situ soil moisture data are an important reference for evaluating climate models (Yuan and Quiring, 2017; Zhuo et al., 2019) and remote-sensed SM data (Entekhabi et al., 2010; Kerr et al., 2010). However, it is not practically possible to perform in situ SM measurements with high spatial and temporal coverage. Soil moisture networks based on cosmic ray neutron probes might be more manageable for long-term operation; however, this approach and associated networks are not established, globally, as a dielectric-based approach. A practical alternative is to employ a portable soil probe that is calibrated using locally measured soil moisture. In particular, portable dielectric sensors make use of the relationship between the dielectric constant and volumetric soil water content. However, such retrieval of the volumetric soil water content from dielectric measurements does not account for soil organic matter (SOM) and saturation conditions. A few studies have reported the relationship between the dielectric constant and the volumetric soil water content in organic soils (Topp et al., 1980; Roth et al., 1992; Bircher et al., 2012). However, the calibration functions derived from these studies have limitations for global-scale applications because they were developed using only a few specific sites and/or are applicable only for the sites with a limited range of organic matter content. For the purpose of a global soil moisture probe observing system, using an inversion method of the existing physical dielectric mixing model can be a great alternative approach to incorporate the variability of organic matter into the probe algorithm beyond the current empirical probe models.

With this background, this work provides a pathway for a physical model to consider soil organic matter. We developed an inverse dielectric mixing model for mineral soil derived from Park et al. (2019, 2017) to obtain more accurate volumetric soil moisture estimates from the dielectric constant. The proposed model reflects the damping effect and simulates the supersaturation of soil moisture over soil porosity (when soil moisture occupied more than the porosity of dry compacted soil in the unit volume, causing lightweight clay swelling or starting the existence of standing water or starting surface runoff due to the precipitation accumulation over the soil surface more quickly than infiltration), so that we can capture the standing water and surface runoff during flood events, which has not been studied in other prevalent dielectric mixing models.

The most recent high-resolution SOM map (Hengl et al., 2014; Batjes, 2016) is only available as a static variable for the land model; therefore, the realism of the parameterization for surface runoff, infiltration, evapotranspiration, and soil respiration is limited. Therefore, it would be important to obtain a spatially and temporally varying SOC map from satellite measurements. SMAP has the potential to provide an unprecedented and unique benefit to solve various challenges in deriving such maps regardless of the relatively coarse resolution of the Soil Moisture Active Passive (SMAP) radiometer measurements for the following three reasons: (1) microwaves can detect SOC underneath vegetation, which other shorter-wave sensors cannot perceive, (2) the temporally varying OC evolution obtained even from a low-resolution satellite image will be helpful in various modeling and observation studies, and (3) the limitation of the low-resolution issue can be overcome by recent downscaling approaches, such as machine-learning methods, that can utilize a synergy with other ground, spaceborne, and satellite data. Consequently, the other aim of this study is to provide a foundation for global SOM estimation using observations from a satellite, such as SMAP, by developing a dielectric mixing model based on accurate in situ SOM and gravimetric soil moisture.

The remainder of this paper is organized as follows: Sect. 2 introduces the inversion approach of the dielectric mixing model to estimate soil moisture from organic-rich mineral soil using the probe. The data used in this study are described in Sect. 3. In Sect. 4, we evaluate the results using the soil moisture measured during SMAPVEX12. Finally, a summary and discussion for further applications are provided in Sect. 5.

2 Method

The dielectric constant indicates a polarizability of materials at a certain wavelength. The dipole structure of water molecules is highly sensitive to a microwave electric field with a very high dielectric constant (approximately 80). On the other hand, the dielectric constant of mineral soil at microwave electric fields is rarely reacting, having only low values from 3 to 5. Therefore, an instrument which can measure the effective dielectric constant of a soil medium such as a Stevens HydraProbe can provide an accurate estimate of water amount within soil (Jackson et al., 1982; Schmugge, 1983; Stafford, 1988). Also, from space, microwave satellites such as SMAP (Soil Moisture Active Passive) (Entekhabi et al., 2010), SMOS (Soil Moisture and Ocean Salinity) (Wigneron et al., 2007), and AMSR-E (Advanced Microwave Scanning Radiometer for EOS) can effectively estimate soil moisture from the measured brightness temperature by relating the effective dielectric constant of the land surface.

For the application of portable soil moisture probes, the in situ soil moisture data are provided based on the empirical relationship between the measured dielectric constant and the volumetric soil moisture (Seyfried and Murdock, 2004; Bell et al., 2013) using the following equation:

$$\begin{array}{}\text{(1)}& w=\mathrm{0.0838}\sqrt{{\mathit{\epsilon }}_{\mathrm{obs}}}-\mathrm{0.0846},\end{array}$$

where ε_obs is the real part of the dielectric constant measured with the soil probe and w is the estimation of the volumetric soil moisture (cm³ cm⁻³). As apparent in Eq. (1), the dependence of ε_obs on SOM was not considered in the estimation of w.

To consider the SOM, we first derive Eqs. (2)–(4), based on Park et al. (2019).

If the observed real part of the dielectric constant measured with the soil probe is smaller than the real part of the dielectric constant at the wilting point, ε_obs<ε_wp, we obtain the following.

For w<w_wp,

$$\begin{array}{}\text{(2)}& w=a\left(\left({\mathit{\epsilon }}_{\mathrm{obs}}-\mathrm{1}\right)H^{-\mathrm{1}}+\mathrm{1}\right)+b,\end{array}$$

where

$$\begin{array}{c}{\displaystyle }a=\mathrm{1}/\left({\mathit{\epsilon }}_{\mathrm{bound}}-{\mathit{\epsilon }}_{\mathrm{air}}\right),\\ {\displaystyle }b=-{\displaystyle \frac{\left(\mathrm{1}-p\right){\mathit{\epsilon }}_{\mathrm{soil}}+p{\mathit{\epsilon }}_{\mathrm{air}}}{{\mathit{\epsilon }}_{\mathrm{bound}}-{\mathit{\epsilon }}_{\mathrm{air}}}},\end{array}$$

where H is the damping factor (0.8), ε_bound is the dielectric constant for bound water, ε_free is the dielectric constant for free water, and ε_air is the dielectric constant for air (Eq. 1).

If the observed real part of the dielectric constant measured with the soil probe is larger than the real part of the dielectric constant at the wilting point and still smaller than the saturation point, ${\mathit{\epsilon }}_{\mathrm{wp}}<{\mathit{\epsilon }}_{\mathrm{obs}}<{\mathit{\epsilon }}_{\mathrm{p}}$, we get the following.

For $w_{\mathrm{wp}}<w<p$,

$$\begin{array}{}\text{(3)}& w={\displaystyle \frac{-b+\sqrt{b^{\mathrm{2}}-\mathrm{4}a\left(c-\left({\mathit{\epsilon }}_{\mathrm{obs}}-\mathrm{1}\right)H^{-\mathrm{1}}-\mathrm{1}\right)}}{\mathrm{2}a}},\end{array}$$

where

$$\begin{array}{c}{\displaystyle }a={\displaystyle \frac{{\mathit{\epsilon }}_{\mathrm{free}}-{\mathit{\epsilon }}_{\mathrm{bound}}}{p-w_{\mathrm{wp}}}},\\ {\displaystyle }b={\displaystyle \frac{p{\mathit{\epsilon }}_{\mathrm{bound}}-w_{\mathrm{wp}}{\mathit{\epsilon }}_{\mathrm{free}}}{p-w_{\mathrm{wp}}}}-{\mathit{\epsilon }}_{\mathrm{air}},\\ {\displaystyle }c=\left(\mathrm{1}-p\right){\mathit{\epsilon }}_{\mathrm{soil}}+p{\mathit{\epsilon }}_{\mathrm{air}}.\end{array}$$

Finally, for ε_obs>ε_p, we get the following.

For p<w,

$$\begin{array}{}\text{(4)}& w=a\left(\left({\mathit{\epsilon }}_{\mathrm{obs}}-\mathrm{1}\right)H^{-\mathrm{1}}+\mathrm{1}\right)+b,\end{array}$$

where

$$\begin{array}{c}{\displaystyle }a={\displaystyle \frac{\mathrm{1}}{{\mathit{\epsilon }}_{\mathrm{free}}-{\mathit{\epsilon }}_{\mathrm{soil}}}},\\ {\displaystyle }b=-{\displaystyle \frac{{\mathit{\epsilon }}_{\mathrm{soil}}}{{\mathit{\epsilon }}_{\mathrm{free}}-{\mathit{\epsilon }}_{\mathrm{soil}}}}.\end{array}$$

According to Debye relaxation, the dielectric constant of free water at less than 2 GHz frequency has a constant value of approximately 80. However, in the field measurements (Curtis et al., 1995; Ishida, 2000; Mironov et al., 2013; Fal et al., 2016), it is found that in clay-rich soil, the real part of the dielectric constant increases at lower frequencies, which occurs by the clay–ion-complex interaction (Kelleners et al., 2005). Therefore, in this study for 50 MHz, the clay content and the real part of the dielectric constant at 1.4 GHz are empirically considered in the dielectric constant not only for free, but also for bound water (Eqs. 5, 6).

$$\begin{array}{}\text{(5)}& {\displaystyle }{\mathit{\epsilon }}_{\mathrm{free}}={\mathit{\epsilon }}_{{\mathrm{free}}_{\mathrm{1.4}\mathrm{GHz}}}+\mathrm{65}\cdot v_{\mathrm{clay}}\text{(6)}& {\displaystyle }{\mathit{\epsilon }}_{\mathrm{bound}}={\mathit{\epsilon }}_{{\mathrm{bound}}_{\mathrm{1.4}\mathrm{GHz}}}+\mathrm{5}\cdot v_{\mathrm{clay}}\end{array}$$

Also, we proposed the formulation of the dielectric constant for the dried organic-rich mineral soil at 50 MHz, as shown in Eq. (7).

$$\begin{array}{}\text{(7)}& \begin{array}{rl}{\mathit{\epsilon }}_{\mathrm{soil}}& =\left({\mathit{\epsilon }}_{\mathrm{clay}}\cdot v_{\mathrm{clay}}+{\mathit{\epsilon }}_{\mathrm{sand}}\cdot v_{\mathrm{sand}}+{\mathit{\epsilon }}_{\mathrm{silt}}\cdot v_{\mathrm{silt}}\right)\\ & \cdot \left(\mathrm{1}-v_{\mathrm{SOM}}\right)+{\mathit{\epsilon }}_{\mathrm{SOM}}\cdot v_{\mathrm{SOM}},\end{array}\end{array}$$

where ε_{free 1.4 GHz} and ε_{bound 1.4 GHz} are the dielectric constants for free and bound water at 1.4 GHz, respectively, and v_clay, v_silt, and v_sand are the volumetric ratios (cm³ cm⁻³) for clay, silt, and sand, respectively.

The bulk density for organic soils can be computed with pure mineral and organic matter densities (Federer et al., 1993) or be expressed with their total volume and mass of these components (Liu et al., 2013; Jin et al., 2017). By relating these two formulas, we can derive the following volumetric ratio of organic matter (v_SOM, cm³ cm⁻³) (see Appendix A for more details):

$$\begin{array}{}\text{(8)}& v_{\mathrm{SOM}}={\left(\left({\displaystyle \frac{\mathrm{1}}{\mathrm{SOM}}}-\mathrm{1}\right){\displaystyle \frac{{\text{BD}}_{\mathrm{SOM}}}{{\text{BD}}_{\mathrm{MI}}}}+\mathrm{1}\right)}^{-\mathrm{1}},\end{array}$$

where

$$\begin{array}{}\text{(9)}& {\displaystyle }\mathrm{SOM}\left[\mathrm{kg}{\mathrm{kg}}^{-\mathrm{1}}\right]=f_{\mathrm{oc}}\cdot {\displaystyle \frac{\mathrm{OC}\left[\mathrm{g}{\mathrm{kg}}^{-\mathrm{1}}\right]}{\mathrm{1000}}},\text{(10)}& {\displaystyle }\text{BD}=\mathrm{0.071}+\mathrm{1.322}\cdot \exp \left(-\mathrm{0.0071}\cdot \mathrm{OC}\right).\end{array}$$

SOM is expressed as organic carbon (OC) in the majority of global soil maps (Hugelius et al., 2013; Hengl et al., 2014, 2017; Harmonized world soil database, 2020) as well as in the published units in the SMAPVEX 12 study (Manns and Berg, 2014). Organic carbon is the major component of SOM, and in order to convert OC to SOM, the conversion factor (f_oc) of 1.8 was used in Eq. (9). The conventional OC-to-SOM conversion factor was proposed to be 1.724 by Waksman and Stevens (1930) and Stenberg et al. (2010). However, it has been reported that the OC-to-SOM conversion factor can vary from 1.25 to 2.5, and the conventional value of 1.724 tends to overestimate the OC, as reported by Pribyl (2010). Instead of 1.724, 1.8 is a more appropriate value for a wide range of OC, as supported by various studies (Broadbent, 1953; Ranney, 1969; Manns and Berg, 2014). Therefore, in this study, we applied 1.8 for the conversion factor f_oc in Eq. (9). If a further effort in mapping conversion factors on the global scale is made in a future study, the probe sensor algorithm might benefit in the improvement of its accuracy for soil moisture estimation in organic and peat soils.

By applying Eq. (10) (Hossain et al., 2015), BD_MI (bulk density of “pure” mineral matter) and BD_SOM (bulk density of “pure” organic matter) in Eq. (8) are computed as 1.393 g cm⁻³ with 0 % OC (0 g OC per 1 kg soil) and 0.097 g cm⁻³ with 56 % OC (560 g OC per 1 kg soil) converted from 100 % SOM with the conversion factor 1.8 by Eq. (9), respectively.

In a previous study, Eq. (11) was proposed as the wilting point, which is a function of SOM (kg kg⁻¹), with the slope parameter of SOM modified from 0.786 to 0.6 (Park et al., 2019). In our study the porosity is suggested as a power law function according to the SOM variable, as shown in Eq. (12) (please see the result of simulations in all SOM and clay regions in Fig. B1 in Appendix B).

$$\begin{array}{}\text{(11)}& {\displaystyle }{w}_{\mathrm{wp}}=\mathrm{0.02982}+\mathrm{0.089}\cdot v_{\mathrm{clay}}+\mathrm{0.65}\cdot \text{SOM}\text{(12)}& {\displaystyle }p=\mathrm{0.194}+\mathrm{0.26}\cdot v_{\mathrm{clay}}+\mathrm{0.5}\cdot {\mathrm{SOM}}^{\mathrm{0.5}}\end{array}$$

By applying Eqs. (11) and (12), which require Eq. (8), Eqs. (2)–(4) can be used to compose the inverse dielectric mixing model for the IDO. A detailed description of the parameters used in the algorithm is provided in Table 1. Previous studies (Saxton et al., 1986; Vereecken et al., 1989; Schaap et al., 1998, 2001; Chadburn et al., 2015) showed that greater SOM values increase the wilting point and porosity as proposed in Eqs. (11)–(12). If the wilting point and porosity in dense peat moss, which has very low bulk density, largely differ according to the type of organic matter, the relationship between the amount of total organic matter and those parameters might be more complex. Such a complex relationship should be considered by including detailed classification of SOM as sapric, hemic, and fibric based on a previous study (Verry et al., 2011).

Table 1 Required physical properties to inverse the dielectric mixing model.

The IDO model is composed of bound, mixed, and free water models, as shown in Fig. 1a–c, respectively. The dielectric constant at the wilting point or porosity should be calculated first and then compared with the measured data in order to determine which model should be used among Eqs. (2), (3), or (4) for soil moisture estimation from the measured dielectric constant. The results of this selection for soil moisture estimation from the measured dielectric constant are displayed as shown as red dots in Fig. 1d.

The difference in the soil moisture estimation from the observed dielectric constant based on the Seyfried and IDO models is presented in Fig. 1e. The IDO model provides larger SM values with high SOM input (purple curve) and lower SM values in low SOM input (orange curve) compared with the Seyfried model (black dotted curve). The factory setting (default probe algorithm) reflects the average SOM effect empirically in the generalized model. Even with medium-range SOM (red curve), a relatively small but more complex difference between the two approaches can be revealed in the SM estimation: lower SM estimation in wet soil and higher SM estimation in dry soil than the probe estimated (black dotted).

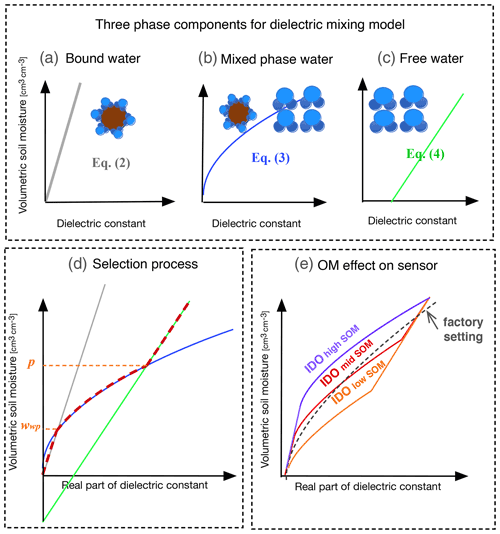
Figure 1 Single phase relationship between (a) dielectric constant and bound water, (b) bound and free water mixture, (c) free water, (d) soil moisture estimated among those models, and (e) comparison with the polynomial-based soil probe sensor algorithm proposed by Seyfried (Seyfried and Murdock, 2004) and for IDO.

3 Data

First, it was necessary to determine whether including the organic matter parameter in the dielectric mixing model improves the accuracy of soil moisture estimation from the probed dielectric constant. Thus, we compared the results with the SM measured using the gravimetric method during SMAPVEX12. The SMAPVEX12 field campaign took place in 2012 (southwest of Winnipeg, Manitoba, Canada), and the SMAP SM retrieval algorithms were calibrated and validated before the launch of the SMAP satellite in 2015 (McNairn et al., 2015). During this field campaign, intensive data of the L-band brightness temperature and total radar backscatter cross section (Tsang and Li, 1999; Entekhabi et al., 2010; Kim et al., 2014) were collected using airborne sensors. The land surface type, crop type, crop water content, and soil texture (clay and sand contents) were evaluated during the experiment. Soil sampling included numerous measurements of the real part of the dielectric constant: these measurements were obtained using soil probes obtained from 16 sampling locations on 50 different agricultural fields (McNairn et al., 2015). The dielectric data were obtained approximately every 2 d between 6 June and 17 July 2012. The sampling depth of the probe is approximately 5.7 cm and is representative of the soil layer relevant to the brightness temperature emission depth detectable by SMOS and SMAP (Schmugge, 1983; Jackson et al., 1997). In addition to the dielectric observations, a gravimetric soil sample was obtained from each sampling field during the sampling dates. The gravimetric samples were obtained from a sampling core with dimensions of 4.7 cm diameter × 4.6 cm depth (Manns and Berg, 2014); the volumetric water content from these samples was also used for the development of calibration equations for the dielectric probes (Rowlandson et al., 2013). For comparison with our new model, we used probe measurements (real dielectric constant) as the input and volumetric soil moisture data as references (Rowlandson et al., 2013), which were simultaneously archived with microwave brightness temperature measured from NASA's airborne L-band active–passive PALS instrument. The ancillary information for this function (soil texture information) was provided by Bullock et al. (2014). At the SMAPVEX12 validation sites (Fig. 2a), the volumetric clay and sand mixing ratios for Eqs. (5), (6), (7), (11), and (12) are from the Agriculture and Agri-Food Canada (AAFC) Soil Landscapes of Canada (Government of Canada, 2011). The OC information was sampled from the SoilGrid250m database (Hengl et al., 2017, 2014; Poggio et al., 2021) and compared with the field estimates of the OC put forth by Manns and Berg (2014). The field samples of the OC were processed by grinding oven-dried soil samples and igniting and burning off organic mass at 375 ^∘C. The SOM was determined from the weight difference between before and after igniting the soil samples and divided by 1.8 (Ball, 1964; Manns and Berg, 2014; Wang et al., 2011) to convert SOM to OC.

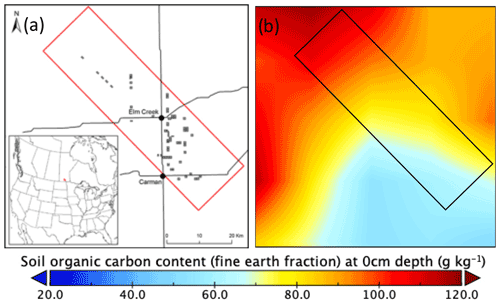
Figure 2 (a) SMAPVEX12 validation sites (adapted from Rowlandson et al., 2013) and (b) calculated distribution of soil organic matter in Canada based on the SoilGrid250m database.

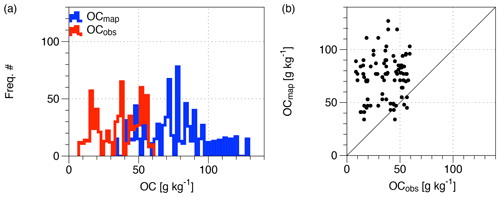
There are significant range differences among the global soil organic carbon maps (Zhu et al., 2019), such as the HWSD (Harmonized World Soil Database, 2020), SoilGrid250m (Hengl et al., 2014, 2017), WISE30sec (Batjes, 2016), and Northern Circumpolar Soil Carbon Database (NCSCD; Hugelius et al., 2013). Therefore, the reliability of the global soil organic maps used for local soil moisture estimation using soil probes is still unknown. To investigate the potential limitation of global OC maps (hereafter called the OC_map experiment), we performed a comparison of OC measurements obtained from each SMAPVEX12 site (Manns and Berg, 2014) with those retrieved from the SoilGrid205 map. As shown in Fig. 3a, there is an offset between both datasets of ∼50 g kg⁻¹. The estimated OC from the map was greater and showed a wider OC range compared with the measured OC at the SMAPVEX12 sites (Fig. 3b). This means that the SoilGrid250m (Hengl et al., 2017) estimates are, on average, more than 100 % higher than the measured data. Thus, a potential limitation of the SoilGrid250m map exists not only in the spatial pattern, but also in the overall magnitude (74.4 g kg⁻¹ on average). In this study, we used OC from SoilGrid250m (without any scaling factor) for the OC_map experiment.

We investigated the OC accuracy using one type of OC input into the new soil probe algorithm (Eqs. 2–4) by performing two experiments: (1) OC entered using a SoilGrid250m map (OC_map experiment; blue in Fig. 3) and (2) SMAPVEX12 of the OC in situ of SMAPVEX12 (red in Fig. 3).

Figure 3 Comparison between organic carbon (OC) observation from SMAPVEX12 (red) and data sampled from the highly resolved SoilGrid250m map (Hengl et al., 2017) (blue) (a) in histogram and (b) in scatter plot.

4 Calibration of portable soil moisture sensors

The development of the calibration models is necessary for further campaigns or further extension of the global soil moisture network based on a portable soil moisture sensor. For example, calibration models (Rowlandson et al., 2013) were proposed by deriving the parameters A, B, and C of the quadratic function between the effective dielectric constant and soil moisture for each SMAPVEX12 station.

$$\begin{array}{}\text{(13)}& {\mathit{\epsilon }}_{\mathrm{obs}}=A{w}^{\mathrm{2}}+Bw+C\end{array}$$

At each site a unique set of A, B, and C was obtained to estimate w (volumetric soil moisture) from the measured dielectric constant ε. It is important to verify whether these empirical models are transferable to other field sites based on physical interpretation. Therefore, we compared them with those derived from the dielectric mixing model, as shown in Table 2. The weighting function describing the attenuation of signal on probe and satellite sensor can be an exponential form basically following the Beer–Lambert law, where infinite attenuation of the electric field is allowed but is negligible for the deeper sampling depth. On the other hand, a quadratic form can be considered the weighting function based on the assumption of a linearly decreasing refractive index scheme (Wilheit, 1978), so that the emission can be assumed to be zero from the deeper sampling depth. In this study, as shown in Table 2, we assumed the Beer–Lambert law to consider the attenuation effect by applying the damping factor 0.8 applicable for both probe and satellite remote sensing. More detailed derivation associated with the damping factor can be found in the previous study (Park et al., 2017).

Table 2 A, B, and C parameters of the relationship between the effective dielectric constant and soil moisture adapted from Park et al. (2017) with damping factor H (0.8); dielectric constant for free (ε_free), bound water (ε_bound), and soil mineral, including organic matter (ε_soil).

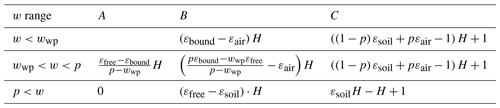
We observed that when the wilting point and porosity increased with increasing OC (according to Eqs. 11–12), A and B increased and decreased, respectively, as shown in Fig. 4. The results of this matching (Fig. 4) showed that A and B used in the quadratic function computed for SMAPVEX12 can be parameterized with soil texture, wilting point, porosity, and the bound and free water dielectric constants. Additionally, the C parameter indicates the effective dielectric constant of the mixture of dry organic matter (approximately 1.2; Savin et al., 2020) and solid mineral soil (3–5); ideally, the C parameter value should decrease with an increase in OC. Notably, the clay content was also positively correlated with an increase in OC in SMAPVEX12. Therefore, owing to the simultaneous increase in clay content, which is characterized by a high dielectric constant, the sensitivity of the C parameter to OC variation (decreasing pattern in C) is nullified, as shown in Fig. 4c. Furthermore, because C perfectly represents the dielectric constant of dry soil, it should be greater than 1, which is the real part of the dielectric constant of a vacuum. Based on this physical constraint, the previous C (gray points in Fig. 4) is unrealistically low (less than that of the vacuum state) in the higher SOM range. The minimum C is (1−p)ε_soil among three w ranges (Eq. 4), because the following order is always true, [$(\mathrm{1}-p){\mathit{\epsilon }}_{\mathrm{soil}}<(\mathrm{1}-p){\mathit{\epsilon }}_{\mathrm{soil}}+p<{\mathit{\epsilon }}_{\mathrm{soil}}$], and it is larger than 2, as shown in Fig. 4c. This shows that the proposed IDO computes a more realistic value of the dielectric constant for organic-rich mineral soil.

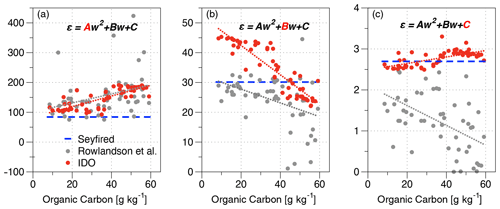
Figure 4 Relationship between soil organic carbon measurements (x axis) and calibration parameters (A, B, and C) (y axis) relating between measured dielectric constant (ε) and volumetric soil moisture (w): (blue dash lines) A, B, and C, which are not sensitive to OC measurements (Seyfried approach); (gray dots) A, B, and C, which are empirically obtained (Rowlandson et al., 2013); (red dots) A, B, and C, which are physically simulated by the proposed IDO, which applies the wilting point and porosity as functions of sand and clay volumetric mixing ratios as well as soil organic carbon with the damping factor applied.

5 Results

This study aimed to mitigate a significant discrepancy found between volumetric soil moisture estimated by soil probe sensor (considered a ground truth for the validation of land surface modeling and remote sensing) and the gravimetric soil moisture. Therefore, in this section, the new approach proposed in Sect. 2 investigated whether the accuracy of the new sensor algorithm can be improved compared with the existing probe algorithm. Firstly, looking at Fig. 5a, the current issue in the probe SM estimates was well displayed in terms of the matching pattern of the gravimetric soil moisture with the measured dielectric constant. It showed that the existing probe soil moisture (red dots in Fig. 5a) could not follow both features that appeared in the measurements (the significant scattering degree and the distinct varying patterns under dry and wet conditions). This is a fundamental limitation of the traditional polynomial function, the Seyfried model, as well as a two-mode system (mineral or organic (peat) soil), as proposed by Topp et al. (1980) or Roth et al. (1992).

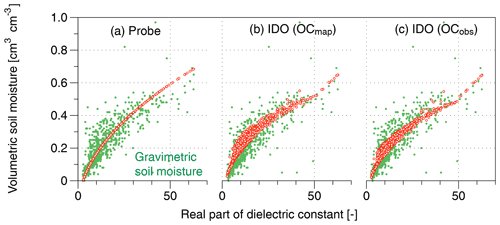
Figure 5 Scatter plot between probe measurements of the real part of the dielectric constant (x axis) and volumetric soil moisture (y axis) measured by the gravimetric method (green dots in a–c), Seyfried model (red dots in a), the IDO with SOM taken from SoilGrid250m (Hengl et al., 2017) (red dots in b), and the IDO using OC measured during SMAPVEX12 (Manns and Berg, 2014) (red dots in c).

On the other hand, the IDO, with soil organic carbon considered, allowed us to compute SM with a similar scattering pattern comparable with that measured by the gravimetric method. It means that soil organic carbon is a critical factor in the application of the soil moisture sensors from portable to satellite based. With regards to the shape appearing in the scattering pattern, the IDO captured the distinctively curved edge in the low- and high-end points close to the values of 12 and 50, respectively, on the x axis for the real part of the dielectric constant. The only difference between (b) and (c) in Fig. 5 is OC input, originating from SoilGrid250m or in situ obtained during SMAPVEX12, respectively, with the same input of clay and sand mixing ratio from SMAPVEX 12. This pattern is probably related to the transition moments from bound to mixed (a to b in Fig. 1) and from mixed to free water states (b to c in Fig. 1), which is very interesting evidence indicating that soil probes can detect critical soil parameters such as wilting point and soil porosity based on the accumulated dielectric measurements of certain sites.

Even though the shape of SM scattering estimated from the measured dielectric data (x axis) became similar to the one appearing in the gravimetric soil moisture, it is also required to investigate whether the actual improvement in the SM accuracy has been achieved via the point-by-point comparison with the gravimetric data. This analysis was illustrated in the Q–Q plot in Fig. 6. It showed that the scattered uncertainty shown in Fig. 6a of the current soil probe algorithm can be reduced by the IDO approach as in panels (b) and (c). The scatter error shown in Fig. 6a slightly converged to a 1:1 line when the IDO adapted the OC map as input (Fig. 6b) and further improved with a narrower scattered error pattern with OC in situ (Fig. 6c). This result further showed that the OC variability with the proposed model can mitigate the uncertainty in SM estimation of the current dielectric-based soil moisture sensor network.

Figure 6 Performance of soil moisture probe algorithms in terms of scattering degree to the gravimetric measurements (x axis): soil moisture estimates (y axis) using (a) a third-order polynomial approach (Seyfried and Murdock, 2004; Bell et al., 2013), (b) the proposed IDO with the variational soil organic matter (SOM) sampled from the SoilGrid250m map (Hengl et al., 2017), and (c) the same algorithm but with SOM measured from SMAPVEX12 (Manns and Berg, 2014).

In Fig. 7, we investigated more characteristics of SM uncertainty: how the biases of SM estimated by the conventional probe algorithm are related to the in situ OC and whether they can be mitigated by the proposed algorithm with the OC measurements. Figure 7a shows that both negative and positive biases are affected by the IDO. Figure 7b, obtained by spreading out the histogram according to the degree of SOM, provides an in-depth analysis of how these biases are distributed according to the measured SOM. This shows that the negative bias in the high SOM range was reduced because the polynomial function of the conventional probe algorithm presented in Fig. 1e tends to overestimate the SM in the cases of lower SOM and underestimate the SM in the cases of higher SOM (as compared with the proposed multiphase model).

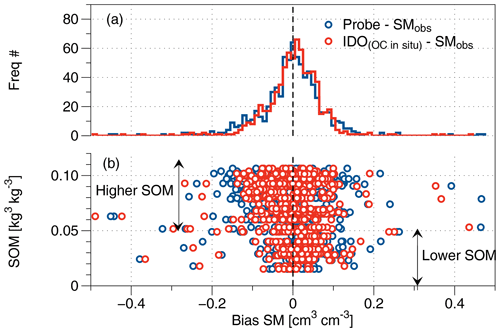
Figure 7 (a) Histogram of soil moisture (SM) bias and (b) its scatter relationship according to SOM converted from in situ organic carbon (OC).

The importance of accurate and highly resolved organic carbon data in soil moisture estimation from portable soil sensors is highly evident from the statistical validation presented in Table 3. The results confirmed that the IDO performs better than the traditional probe algorithm based on a third-order polynomial function, especially with the OC measured in the SMAPVEX12 field campaign (with a maintained spatial variability): RMSE = 0.0727 cm³ cm⁻³, correlation of 0.848, and bias of 0.0001 cm³ cm⁻³.

Table 3 Validation of soil moisture obtained from Probe (Probe SM), organic-rich mineral soil based on the SoilGrid250m organic carbon map (IDOmap), and SMAPVEX12 OC in situ observation (IDO_obs).

The results in this section demonstrated that the wilting point and porosity which emerged in pairing the gravimetric soil moisture and the dielectric measurements could also be detected by the new model. Also, it is proven that the volumetric soil moisture could be estimated from the sensor more accurately in terms of bias, RMSE, and correlation analysis. It means that our approach can provide a more accurate soil moisture probe algorithm than that currently used in various soil moisture networks, such as the USCRN (US Surface Climate Observing Reference Networks) and SMAPVEX field campaigns. In the boreal forest and Alaska tundra region with abundant SOM, our study can deliver a significant effect on the validation and conclusion of the previous studies in land surface modeling and microwave satellite remote sensing, which used the probe soil moisture as reference data.

6 Summary and discussion

In this study, we proposed an inverse dielectric mixing model for a 50 MHz soil sensor for agricultural organic-rich mineral soil. The 50 MHz sensor is a prevalent frequency band for soil moisture probes. Cosh et al. (2021) found that in North America soil sensors using this waveband occupied 40 % of the soil moisture networks (10 of 25, including USCRN) and 53 % of sensors (1021 of 1923 locations). Therefore, the proposed algorithm has the potential to contribute significantly to the accuracy of the soil moisture estimates derived from current in situ soil moisture measurements. Furthermore, since the SMAPVEX also used 50 MHz sensors, it is anticipated that the accuracy of the calibration and validation of the SMAP-related soil moisture algorithms will be increased. The proposed model is composed of three nonlinear functions that are mathematically capable of describing the physical behavior, including the effect of the organic matter content. In this model, we proposed a physical mixing approach of organic matter in dry soil and improved the wilting point and saturation point. This derivation can also be applied to other bands for capacitance sensors (5 TE (70 MHz), wet (20 MHz), time-domain reflectometry (TDR) (TDR100/200 (1450 MHz), SoilVUE-10 (1450 MHz), and satellite sensors SMAP (L-band), and SMOS (L-band) (AMSR-E (JAXA) X/C, Sentinel-1 (ESA) – C). It is also noticed that the applied organic matter carbon data sampled from SMAPVEX12 sites (36 g kg⁻¹) were half those of the OC map (74 g kg⁻¹). The validation results demonstrated a higher performance of the new model. Regardless of the small amount of OC, its effect improved the performance of the SM estimation, which was demonstrated via the IDO proposed in this study. We compared the obtained soil moisture retrievals with improved RMSE (13 % ↓), slightly stronger correlation (3 % ↑), and lower bias (90 % ↓) using the new model and gravimetric soil moisture data. However, the coverage of the simulated pattern over the measured points was still smaller. Therefore, we sought out a potential further improvement based on the additional experiment designed with SOM varying within the proposed model. The simulation based on the conventional polynomial function (red curve in Fig. 8a) could not reduce the innate uncertainties, and the IDO proposed in this study could resolve this issue. However, the red dots simulated with the IDO (Fig. 8b) covered over the measured green dots insufficiently. Therefore, in order to activate this weak pattern, we performed the experiments to impose a more dynamic OC estimate to investigate whether greater or less SOM can cover a similar boundary of the measured distribution through the IDO model. The results showed that the piecewise pattern of SM simulated with the proposed approach covered well the measured pattern with imposing lower (1 %) to higher (30 %) SOM.

Figure 8 Investigation of the similarity of the scatter pattern between the measured dielectric constant and the soil moisture: (a) obtained from the gravimetric measurements and (b) experimentally simulated with extreme SOM from 0 % to 30 %.

Because the SOM is translated from OC with a conversion factor (1.8) in this study, the improvement might not have been sufficient. A realistic estimation of the conversion factor (f_oc) in Eq. (10) varying from 1.25 up to 2.5 might be a possible solution for this. In addition, the IDO is a model able to replace the calibration factors A, B, and C of Eq. (13) with the soil properties presented in Table 2. Overall, the proposed more physics-based IDO can replace the current soil probe sensor algorithm, which does not incorporate the importance of organic matter variability.

A significant improvement could not be shown, probably for two reasons: the instrumental error in measuring OC from the soil sample or the constant OC-to-SOM conversion factor (1.8 for all soil samples). In addition, uncertainty can be suspected from other sources, such as clay or sand contents or soil salinity (assumed to be 0 % in this study) used in the IDO. These effects on the dielectric measurements and their uncertainties probably served as the limitation of further improvement by the IDO. Therefore, for the potential users to apply our approach, note the following range of SOM applied: our study was validated in 1 %–15 % and performed the sensitivity experiment in 1 %–30 % SOM.

Nevertheless, the results regarding the adaptation of in situ OC in our study demonstrated that the accuracy of the SOM input for the IDO is critical for the accuracy of SM estimation from the probe sensor.

In previous studies (Topp et al., 1980; Roth et al., 1992; Bircher et al., 2016), in the organic mode or the peat soil, the dielectric constant and soil moisture relationship is calibrated to be able to simulate the dielectric constant lower than mineral soil with a given soil moisture. These results are consistent with our study, which showed a decreasing dielectric constant value in higher SOM by increasing the bound water fraction due to a higher wilting point (wp). Therefore, if we have more information about the dielectric constant of perfectly dried peat soil and a more accurate model for the wilting point and porosity of this soil, our model will be able to cover soils from mineral to peat regions to obtain more accurate global soil moisture. In addition, if we improve this model toward a frequency-dependent model in a future study, the existing and future probe measurements obtained in various frequencies will be able to contribute more extensively to the calibration and validation of satellites and models.

Appendix A

Based on the computation of the bulk density for organic soils, the volumetric mixing ratio of soil organic matter can be derived as shown in Eqs. (A1)–(A7).

$$\begin{array}{}\text{(A1)}& {\displaystyle }\begin{array}{rl}{\text{BD}}_{\mathrm{soil}}& ={\displaystyle \frac{M_{\mathrm{MI}}+M_{\mathrm{SOM}}}{V_{\mathrm{MI}}+V_{\mathrm{SOM}}}}\\ & ={\displaystyle \frac{{\text{BD}}_{\mathrm{MI}}\times {\text{BD}}_{\mathrm{SOM}}}{\left(\mathrm{1}-\text{SOM}\right)\times {\text{BD}}_{\mathrm{SOM}}+\text{SOM}\times {\text{BD}}_{\mathrm{MI}}}},\end{array}\text{(A2)}& {\displaystyle }\begin{array}{rl}& {\displaystyle \frac{V_{\mathrm{SOM}}}{V_{\mathrm{MI}}+V_{\mathrm{SOM}}}}{\displaystyle \frac{M_{\mathrm{MI}}+M_{\mathrm{SOM}}}{V_{\mathrm{SOM}}}}\\ & ={\displaystyle \frac{{\text{BD}}_{\mathrm{MI}}\times {\text{BD}}_{\mathrm{SOM}}}{\left(\mathrm{1}-\text{SOM}\right)\times {\text{BD}}_{\mathrm{SOM}}+\text{SOM}\times {\text{BD}}_{\mathrm{MI}}}},\end{array}\text{(A3)}& {\displaystyle }\begin{array}{rl}{\mathit{\upsilon }}_{\mathrm{SOM}}& ={\displaystyle \frac{V_{\mathrm{SOM}}}{M_{\mathrm{MI}}+M_{\mathrm{SOM}}}}\\ & \times {\displaystyle \frac{{\text{BD}}_{\mathrm{MI}}\times {\text{BD}}_{\mathrm{SOM}}}{\left(\mathrm{1}-\text{SOM}\right)\times {\text{BD}}_{\mathrm{SOM}}+\text{SOM}\times {\text{BD}}_{\mathrm{MI}}}},\end{array}\text{(A4)}& {\displaystyle }\begin{array}{rl}{\mathit{\upsilon }}_{\mathrm{SOM}}& ={\displaystyle \frac{M_{\mathrm{SOM}}}{M_{\mathrm{MI}}+M_{\mathrm{SOM}}}}{\displaystyle \frac{V_{\mathrm{SOM}}}{M_{\mathrm{SOM}}}}\\ & \times {\displaystyle \frac{{\text{BD}}_{\mathrm{MI}}\times {\text{BD}}_{\mathrm{SOM}}}{\left(\mathrm{1}-\text{SOM}\right)\times {\text{BD}}_{\mathrm{SOM}}+\text{SOM}\times {\text{BD}}_{\mathrm{MI}}}},\end{array}\text{(A5)}& {\displaystyle }\begin{array}{rl}{\mathit{\upsilon }}_{\mathrm{SOM}}& ={\displaystyle \frac{\text{SOM}}{{\text{BD}}_{\mathrm{SOM}}}}\\ & \times {\displaystyle \frac{{\text{BD}}_{\mathrm{MI}}\times {\text{BD}}_{\mathrm{SOM}}}{\left(\mathrm{1}-\text{SOM}\right)\times {\text{BD}}_{\mathrm{SOM}}+\text{SOM}\times {\text{BD}}_{\mathrm{MI}}}},\end{array}\text{(A6)}& {\displaystyle }{\mathit{\upsilon }}_{\mathrm{SOM}}={\displaystyle \frac{{\text{BD}}_{\mathrm{MI}}}{\frac{\left(\mathrm{1}-\text{SOM}\right)}{\text{SOM}}\times {\text{BD}}_{\mathrm{SOM}}+{\text{BD}}_{\mathrm{MI}}}}\text{(A7)}& {\displaystyle }{\mathit{\upsilon }}_{\mathrm{SOM}}={\displaystyle \frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{\text{SOM}}-\mathrm{1}\right)\times \frac{{\text{BD}}_{\mathrm{SOM}}}{{\text{BD}}_{\mathrm{MI}}}+\mathrm{1}}},\end{array}$$

where M_MI (kg) and M_SOM (kg) are mass of mineral and soil organic matter, V_MI (cm³) and V_SOM (cm³) are volume of mineral soil and soil organic matter, υ_SOM (cm³ cm⁻³) and SOM (kg kg⁻¹) are volume and mass mixing ratio, and BD_MI (kg cm⁻³) and BD_SOM (kg cm⁻³) are bulk density of mineral and organic matters, respectively.

Appendix B

Figure B1 Simulations of wilting point, Eq. (11) improved from Park et al. (2019), and porosity, Eq. (12), proposed in this study, which are functions of soil organic matter in extreme case (a) volumetric clay mixing ratio 100 % and (b) 0 % of the total mineral within soil.