the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Technical note: PMR – a proxy metric to assess hydrological model robustness in a changing climate
Paul Royer-Gaspard
Vazken Andréassian
Guillaume Thirel
The ability of hydrological models to perform in climatic conditions different from those encountered in calibration is crucial to ensure a reliable assessment of the impact of climate change on river regimes and water availability. However, most evaluation studies based on the differential split-sample test (DSST) endorsed the consensus that rainfall–runoff models lack climatic robustness. Models applied under climatologically different conditions typically exhibit substantial errors in streamflow volumes. In this technical note, we propose a new performance metric to evaluate model robustness without applying the DSST, and it can be performed with a single hydrological model calibration. The proxy for model robustness (PMR) is based on the systematic computation of model error on sliding sub-periods of the whole streamflow time series. We demonstrate that the PMR metric shows patterns similar to those obtained with the DSST for a conceptual model on a set of 377 French catchments. An analysis of the sensitivity to the length of the sub-periods shows that this length influences the values of the PMR and its equivalency with DSST biases. We recommend a range of a few years for the choice of sub-period lengths, although this should be context dependent. Our work makes it possible to evaluate the temporal transferability of any hydrological model, including uncalibrated models, at a very low computational cost.
- Article
(2204 KB) - Full-text XML
- BibTeX
- EndNote
In the context of climate change, quantifying the performance of the models used for assessing the impact of a changing climate is essential for informing model selection and estimating uncertainty. Assessing the impact of a changing climate typically involves a modelling chain ranging from general circulation models to impact models such as catchment hydrological models (Clark et al., 2016). It is now acknowledged that the contribution of hydrological model uncertainty to the total uncertainty of projections may be significant and should be addressed along with other sources of uncertainty (e.g. Hagemann et al., 2013; Schewe et al., 2014; Vidal et al., 2016; Melsen et al., 2018). A key issue in the reduction of hydrological model uncertainty is the assessment of robustness to climatic changes, i.e. their ability to perform in climatic conditions that differ from those encountered in calibration.
Advocating that hydrological models needed to be tested under conditions that would “represent a situation similar to which the data are to be generated”, Klemeš (1986) suggested a series of tests to evaluate the robustness of hydrological models. Among these testing procedures, the most popular scheme to assess model robustness to varying climatic conditions is the differential split-sample test (DSST). The DSST consists in a calibration–evaluation exercise in two periods of the available time series chosen to be as climatically different as possible. Variants of the DSST have also been proposed for specific purposes, such as the generalized split-sample test (Coron et al., 2012), which consists in a systematic calibration–evaluation experiment on every pair of independent periods that one can possibly define. However, these variants all rely on the same principles as the DSST (e.g. Dakhlaoui et al., 2019).
Many studies report poor model simulations resulting from the application of the DSST in various modelling contexts (e.g. Thirel et al., 2015). Among the deficiencies observed in the tested models, a common feature is their tendency to produce biased streamflow simulations in evaluation conditions (e.g. Vaze et al., 2010; Merz et al., 2011; Broderick et al., 2016; Dakhlaoui et al., 2017; Mathevet et al., 2020). Although changes in catchment temperature and/or precipitation are usually associated with volume errors, these errors vary across the tested models and catchments (e.g. Vaze et al., 2010; Broderick et al., 2016; Dakhlaoui et al., 2017). The dire need to improve hydrological models is widely recognized and is considered as being one of the 23 unsolved problems in modern hydrology (Blöschl et al., 2019, UPH no. 19). However, to improve models, we first need a good diagnostic method, and the design of alternatives to the DSST for the evaluation of model robustness could contribute to these advancements.
The first shortcoming of the DSST is its limited application regarding a particular category of hydrological models. Indeed, Refsgaard et al. (2014) pointed out that split-sample procedures cannot be applied to models that are not calibrated. The evaluation of such models is usually performed by testing their spatial transferability with data from proxy sites. It is therefore difficult to compare the robustness of highly complex hydrological models to simpler models such as the ones typically tested in the aforementioned DSST studies. A further limitation is the necessity for determining a set of climatic variables to inform the definition of different calibration and evaluation periods. This is, of course, highly relevant in contexts where the direction of future changes is unambiguously predicted. In other situations, however, the robustness assessment would benefit from evaluating the model on a wider spectrum of hydro-climatic changes. Variants of the DSST, such as the generalized split-sample test, may circumvent this problem, but at a high computational cost that not all modellers can afford (Coron et al., 2012).
This technical note presents and assesses a way of quantifying model robustness as a mathematical performance criterion computed without splitting time series into calibration and evaluation periods. This criterion is conceived to be a proxy for model robustness (PMR), i.e. to reproduce the hydrological model average error as obtained by applying the DSST. It is based on the computation of interannual model bias derived from graphical considerations in the work of Coron et al. (2014). In order to be reliable, the PMR must indicate typical model biases as obtained in DSST on independent evaluation periods. It should also help to identify catchments where a model lacks robustness. We summarize the important aspects that we discuss, in the following, with two research questions:
-
Does the PMR faithfully relate to model robustness as assessed in DSST experiments?
-
How do computation choices (e.g. sub-period length and sub-period weight) affect the results obtained when applying the PMR?
It is worth noting that hydrological model robustness is here considered especially through the prism of model bias. Given that the biased simulations are one the most common outcomes of the previous works about model robustness, we considered that model bias was an adequate metric as a first approach. Of course, model robustness relates to the stability of model performance in general and, thus, to every possible metric assessing model skills. Hence, the PMR as presented here should be considered as a satisfactory proxy for model robustness as estimated using the DSST rather that the proxy for model robustness.
The first question will be addressed by comparing the metric with model bias, as determined by in the DSST for a conceptual model across a large set of French catchments. The underpinning mathematical choices will be discussed in a sensitivity analysis comparing the metric and the results obtained by applying the DSST. The description of the PMR is given in Sect. 2. The hydrological model and the data are presented in Sect. 3. The reliability of the metric is assessed in Sect. 4, and the opportunities the metric offers for model evaluation, as well as some inherent computation choices, are discussed in Sect. 5 and in Appendix B.
2.1 Building the moving bias curve
Hydrological model robustness to climate change lies in the model's ability to perform well under different climatic conditions without parameters being recalibrated to match the changes in the precipitation–streamflow relationship. Performance is deemed robust if it is minimally sensitive to the characteristics of the calibration and evaluation periods. For instance, if a model calibrated during wet years and validated during dry years exhibits similar validation bias than the same model calibrated during dry years and validated during wet years, then it would be deemed robust to changes in climate. A robust model should, thus, simulate streamflow volumes for any type of climatic condition experienced by a catchment with a stable bias (of course, the lower the bias, the better). For example, if these two model configurations both had a percent bias of 20 %, then the model is robust to changes in climate, even if not particularly accurate. If one model configuration had a percent bias of 20 % in the validation period and one of −20 %, then the model is not robust – it exhibits strong sensitivity to climate conditions. It should be noted that a model may lack robustness while providing accurate (i.e. unbiased) estimations of average streamflow volumes on a long period of time.
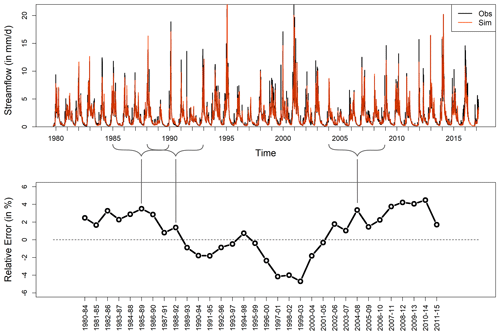
Figure 1Construction of the moving bias curve. The top panel shows daily simulated (orange line) and observed (black line) streamflow. The bottom panel shows moving bias curve expressed as the relative error (in percent); each point of the curve corresponds to a 5-year sub-period of the time series (as exemplified by the brackets).
Coron et al. (2014) suggested a simple way to visualize model robustness by computing the bias of a model simulation on sliding sub-periods of the available time series (Fig. 1). The curve of model bias on the moving sub-periods, named here the moving bias curve, indicates the temporal evolution of model volumetric errors. Since a robust model should perform similarly well whatever the considered sub-period, the flatter the moving bias curve, the more robust a model. Coron et al. (2014) showed that hydrological models would typically not have the ability to flatten their associated moving bias curve. The authors indeed calibrated model parameters on each sub-period of the data and plotted all the produced moving bias curves on the same graph. One of the main conclusions of their study was that the obtained moving bias curves were all almost parallel, and that calibration conditions had a greater influence on the vertical positioning of the curves rather than their shape. This observation was true for models of different complexities across the small set of catchments used in that study. The phenomenon described by Coron et al. (2014) is illustrated in Fig. 2.

Figure 2Moving bias curves of a hydrological model on the Steir river at Guengat (J4313010; in France) for three different calibration periods. The filled dot of the blue (respectively, red) curves indicates the 1984–1988 (respectively, 1999–2003) calibration period of the model. The crosses indicate the evaluation bias for 1999–2003 of the 1984–1988 calibration and the evaluation bias for 1984–1988 of the 1999–2003 calibration. The grey moving bias curve is obtained by calibrating the model on the total period. The grey area corresponds to a proxy for model robustness, as suggested in Sect. 2.2.
The moving bias curve obtained with the model calibrated on the blue sub-period (1984–1988; the coldest sub-period of the time series) is almost parallel to the moving bias curve derived from the calibration on the total period. The y axis shift corresponds to a model bias on the calibration sub-period almost equal to zero. Calibrating the model on another sub-period (1999–2003; the warmest sub-period of the time series; in red) yields a different shift of the moving bias curve, which corresponds to a null model bias on the red calibration sub-period. With the shape of the curve being almost identical, whatever the calibration period in the illustrated case, it offers an interesting perspective on model robustness. The flatness of the curve is indeed almost independent of the period used for model calibration.
Whether they are perfectly parallel or not, depending on the modelling context (model, catchment, data, etc.), the moving bias curves appear to be a relevant tool for analysing model robustness. Before performing calibration–evaluation tests, assessing the flatness of the moving bias curve obtained by calibrating a model as well as possible (i.e. with all available data) could be seen as a first estimate for model robustness. We, thus, propose a simple mathematical expression to calculate this flatness, which will be referred to as the PMR in the following. Please note that the PMR is bias derived and could thus be named PMRbias, opening the door to other types of PMR based on alternative metrics. This issue will be further discussed in Sect. 5.3.
2.2 Computation of the proxy for model robustness
The PMR is based on the computation of the average absolute difference between the actual moving bias curve computed on k-year-long sub-periods and the average bias of the model, normalized by the average observed streamflow (Eq. 1). It thus corresponds to the normalized area between the moving bias curve and the average bias of the model.
and are the respective averages of the observed and of the simulated streamflows on the total period. and are the respective averages of the observed and of the simulated streamflows on the k-year-long sub-period whose index is i. N is the number of sub-periods that can be defined with a k-year moving window ( when there are no gaps in the data, with n being the number of years in the record).
As explained in the Sect. 2.1, the idea behind the PMR is that the robustness of the model is linked to the variability in model performance in time. By computing the difference between the moving bias curve and model average bias, the metric track changes in model bias across time around its mean value. It should be noted that, if the evaluated model is unbiased, as is the case on Fig. 2 for the grey moving bias curve (model calibrated on the whole data set), then the PMR reduces to the absolute integral of the moving bias curve around y=0. Although the terms in the sum are computed in absolute terms, this does not mean that changes in sign in model bias (for example, from 20 % to −20 %) are not accounted for. Indeed, we should recall here that the PMR computes the deviations of model bias from model average bias; thus, any variations in model bias contribute to the PMR, regardless of whether the actual biases on the sub-periods are negative or positive.
In order to compare the PMR with model biases in DSST, we included values multiplied by 2 in the computation of the PMR, in order to compensate for the smoothing effect of comparing model biases on sub-periods to the average model bias (see, for example, the gaps between the red and blue moving bias curves in Fig. 2 compared to the accounted deviations from the grey moving bias curve). A normalization by the average observed streamflow instead of the average streamflow of each sub-period was proposed in order to reduce the weight of very dry years. It also avoids dealing with zeros in the denominator in intermittent catchments. This choice is further discussed in Appendix B.
In the following, the sub-period length has been set to k=5 years. The choice of the sub-period length in the computation of the PMR is discussed in Sect. 4.3.
3.1 Data set
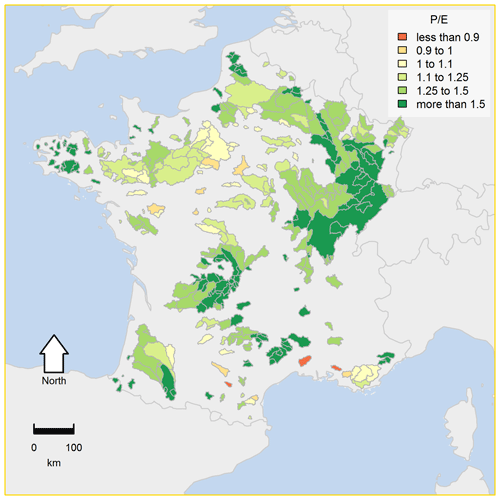
The observed hydro-climatic data for the set of 377 French catchments used in this study (Fig. 3) come from the Hydro-SAFRAN daily data set (Delaigue et al., 2020). The selected French catchments cover a variety of physical and hydroclimatic characteristics and were selected as human activities have little impact on streamflow, and they have limited solid precipitation (<10 % of the total precipitation, on average). Western France is characterized by an oceanic climate with no marked wet and dry seasons. The climate of the eastern part of the country is more continental, with a larger annual temperature range. Southeastern France has a Mediterranean climate, with humid springs and autumns and dry summers. The yearly average precipitation of the catchments ranges from 662 to almost 1926 mm, while the average temperatures vary from 8 to 14.4 ∘C. Daily streamflow measurements at the outlet of the catchments were retrieved from Banque HYDRO (http://www.data.eaufrance.fr/, last access: 21 January 2019; Leleu et al., 2014). Daily meteorological data were supplied by the SAFRAN atmospheric reanalysis (Vidal et al., 2010) aggregated at catchment scale. We used the temperature- and radiation-based formula proposed by Oudin et al. (2005) to compute potential evaporation. In every catchment, streamflow observations cover at least 20 hydrological years (40 years on average). In France, a hydrological year lasts from October to the following September.
3.2 Hydrological model
The tests were performed with GR4J (Perrin et al., 2003), a daily lumped hydrological model. The model is parsimonious (four parameters to calibrate, with two reservoirs and two unit hydrographs) and has been widely used in research studies focusing on hydrological model robustness (e.g. Coron et al., 2014; Broderick et al., 2016; Fowler et al., 2016). The two-parameter CemaNeige degree-day snow module (Valéry et al., 2014) was used to account for solid precipitation. The parameters of the snow module were fixed to median values as recommended by Valéry et al. (2014) for catchments with a limited impact of snow. The GR4J and CemaNeige models are used with the airGR R package (Coron et al., 2017, 2018).
The parameters of the hydrological models were calibrated by optimizing the Kling–Gupta efficiency (KGE; Gupta et al., 2009) computed on the square root of streamflow in order to limit error heteroscedasticity (i.e. dependency of model error variance on streamflow value). The optimization algorithm is a simple procedure consisting in a prior global screening on a gross predefined grid, followed by a descent local search from the best parameter set of the grid. The procedure has been successfully used in multiple studies involving GR4J (e.g. Mathevet, 2005; Coron et al., 2014).
3.3 DSST experiments
DSST experiments consist in selecting contrasting periods (according to some hydrologically relevant indicator) and performing a calibration–evaluation experiment. Our DSST experiments are based on three hydroclimatic variables. The procedure consists in dividing the time series into sub-periods of L consecutive years and selecting six sub-periods from these. The following sub-periods of the DSST are chosen:
-
the driest and the wettest in terms of precipitation
-
the warmest and the coldest in terms of temperature
-
the least and the most productive in terms of runoff ratio (computed as the ratio of mean observed streamflow to mean precipitation).
The model parameters are then calibrated on each sub-period and transferred to the sub-period of the opposite climate. The process is summarized in Table 1.
Table 1Summary of the different setups of the DSST. , and , respectively, stand for average observed streamflow, precipitation and temperature computed on the sub-periods.
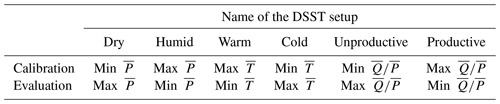
The runoff ratio was preferred to the humidity index since the latter is highly correlated to average precipitation in France and would, therefore, be redundant with DSST experiments based on precipitation. Since runoff ratio is computed from average streamflow, it cannot be used for predictive purposes of model biases in future climate conditions. However, it estimates how catchments respond to precipitation forcings. Its use in the DSST may, thus, indicate how well a model is able to represent variations in catchment response to climatic conditions.
The sub-period length for the DSST experiments has been fixed at L=5 years so as to match the length of the sub-period involved in the computation of the PMR. The length of sub-periods used in the computation of the PMR is discussed in Sect. 5. The length of the sub-periods used for the DSST are discussed in Sect. 4.3. We remind the reader that the PMR is computed from model simulations obtained by calibrating the model on the whole time series, while the DSST results are obtained through calibration evaluation on sub-periods of the time series. It should also be mentioned that model biases obtained in DSST were calculated with respect to model bias in calibration so that they address the stability of bias and, thus, could be compared to PMR values, as follows:
The index a indicates the calibration period (i.e. the dry period when validating on the humid period, etc.). Please note that, in the case of GR4J, biases in calibration are usually very close to zero because the model is calibrated by optimizing the KGE, which explicitly targets model bias, and because GR4J has the ability to correct water balance with the free parameters governing inter-catchment groundwater exchange. Therefore, the term on the right of the subtraction sign is negligible in practice. It should also be noted that, since the PMR is positive by definition, model biases were computed in absolute values. A straightforward drawback is that it prevents the interpretation of the sign of model errors. Therefore, it has been analysed in the different DSST setups in Appendix A. In the following, the model bias obtained in DSST will systematically be calculated in absolute terms, unless clearly stated.
The next section presents a comparison between the PMR and the model biases obtained in DSST. A prior analysis is devoted to comparing scales of variation in the PMR and DSST absolute biases. The ability of the PMR to predict model biases in DSST is then investigated. Finally, the last results show the influence of the length of sub-periods on which model errors are computed on the PMR values and on its predictive ability.
4.1 Comparison of the distributions of PMR values and DSST bias
The PMR is designed to quantify the average bias that would be obtained from DSSTs of the model. The bias obtained for GR4J for each type of DSST setup is plotted in Fig. 4. Compared to absolute biases obtained in the different DSST setups, PMR values have the same order of magnitude as biases in precipitation- or temperature-based experiments. However, the distribution of PMR values exhibits less spread than DSST biases. In the case of DSSTs designed on changes in runoff ratio, model biases are larger than PMR values. The PMR thus seems to relate rather well to model biases observed in typical differential calibration–validation experiments (see Appendix A for more details about DSST results). In summary, one can say that the results presented in Fig. 4 simply indicate that, on average, PMR is the same order of magnitude as the model bias in DSST.
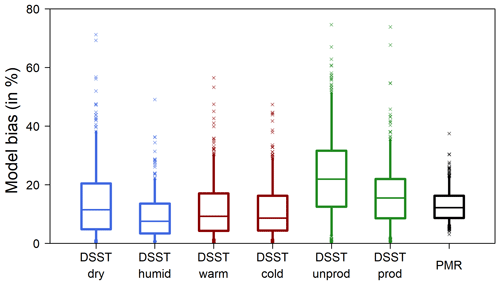
Figure 4Distribution over the catchment set of the absolute value of model bias in DSST for each type of setup compared to PMR values. The box plots represent the 5, 25, 50, 75 and 95 quantiles, and the crosses denote the outliers. Blue, red and green box plots are, respectively, associated to the DSST setups based on precipitation, temperature and runoff ratio.
4.2 Assessment of the predictive ability of the PMR for model robustness
To further investigate the link between the PMR and model robustness as measured by the DSST, we plotted the average model bias across the DSST setups for each catchment against PMR values (Fig. 5). The reader is reminded that model bias is calculated in absolute values, and thus, there are no compensations between the averaged six model biases for each catchment. This comparison was made in order to assess the ability of the PMR to assess the variations in model robustness across the catchment set. Figure 5 shows an acceptable correlation between the two indicators. Overall, the PMR seems to be a satisfactory approximation for model robustness, even if the PMR values underestimate model bias in the worst catchments (and, thus, somewhat overestimate model robustness). The predictive power of the PMR for model bias is further confirmed in Table 2 by the fair correlation values, especially when the model bias obtained in the DSST is averaged. DSST setups based on runoff ratio also relate better with the PMR. This indicates that the PMR has a high potential to help identify catchments where the model struggles in particularly adverse transferability conditions. The fact that the higher correlation is obtained by averaging model biases in the DSST can be explained by the fact that the PMR is designed to be an average of model biases and is, thus, more representative of an average of model errors on a few sub-periods rather than model bias on a single sub-period.
Moreover, although model biases in the DSST based on runoff ratio and PMR values have quite different spreads, the good correlation between model biases in the DSST based on runoff ratio and PMR values indicates that the PMR could be particularly useful for comparing model robustness in relative terms rather than in absolute terms. Since it seems meaningful to compare PMR values reached by the model in these conditions where model errors vary drastically from one catchment to another, it is likely that the PMR could be used to relatively compare different models or different model configurations showing various behaviours. Therefore, the PMR appears to be a reliable estimator of model robustness, even if it exhibits tighter variations across the catchment set and, thus, underestimates typical biases encountered in catchments where the hydrological model is less robust. It should be noted that we did not find any particular differences in topographic or climatic properties between catchments where PMR values and DSST biases closely match and catchments where they do not.

Figure 5Catchment-wise PMR values against catchment-wise DSST absolute bias (one point per catchment) on average (left) and for each DSST setup (right). The red line corresponds to the fitted linear model relating DSST absolute bias to PMR.
Table 2Pearson's correlation between the PMR and model biases obtained in DSST across the catchment set.

Even if the PMR, as defined in Eq. (1), provides satisfactory results and allows a reliable assessment of model robustness without performing a DSST, the metric could have been computed in different ways. The chosen length of sub-periods or the mathematical expression of model bias are possibly important factors influencing the behaviour of the metric. In the following, we conducted a sensitivity analysis with the objective of identifying a way to compute the PMR that best matches the bias that would be obtained by applying a DSST procedure. Therefore, we strived to define the metric so that it corresponds as closely as possible to errors on streamflow volumes typically made by the model in adverse simulation conditions.
4.3 Influence of sub-period length on the sensitivity and on the reliability of the PMR
We tested the sensitivity of the metric values to the length of sub-periods used for its computation in Fig. 6. The PMR metric values decrease when the sub-period length used in the computation increases; model interannual errors on streamflow volumes tend to compensate when the PMR is computed on longer sub-periods. Therefore, the sub-period length should preferably not be too long in order to avoid loss of information about model bias across the years. This statement is corroborated by the slight decrease in metric variability when sub-period length increases (standard deviation of the metric on the catchment set decreases from 7 % to 5 %), which suggests that differences in model robustness across the catchment set are less clear when sub-periods are too long.
To be useful and reliable, it is necessary to verify that the metric relates well to model biases in the DSST, whatever the length of the sub-periods. Figure 7 displays the evolution of the average correlation between PMR values and the DSST biases for various sub-period lengths used for the DSST (horizontal axis) and for the computation of the PMR (vertical axis). The heat map clearly shows that shorter sub-periods for the computation of the PMR generally relate better to shorter calibration periods in the DSST experiments. Conversely, longer sub-periods for the computation of the PMR relate better to longer calibration periods in the DSST experiments. This result is not surprising given that the PMR computed on n-year sub-periods represents the average model bias as computed on n years and, therefore, should show similar patterns to model biases computed in DSST experiments involving n-year periods.
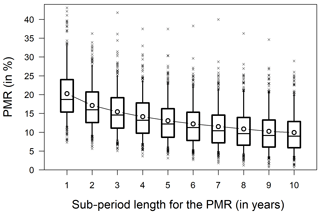
Figure 6Distribution of PMR values on our catchment set for different sub-periods lengths from 1 to 10 years. The model is calibrated on the whole time series. Black circles indicate the average PMR value.
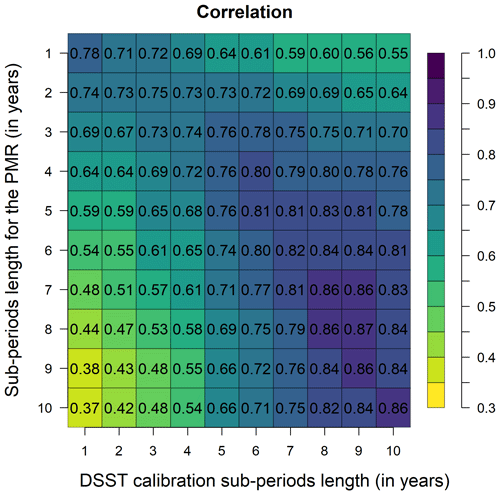
Figure 7Pearson's correlation between the PMR computed on varying sub-period lengths (vertical axis) and the average DSST biases obtained on varying sub-period lengths for calibration and evaluation (horizontal axis).
However, some sub-period lengths for the PMR computation exhibit a high correlation with a wider range of DSST setups. By computing row-wise averages in the matrix, we observed that PMR computations based on 3- to 5-year sub-periods reach an average correlation of 0.73 with DSST biases across the range of sub-period lengths. In comparison, the correlation coefficient of PMR values computed on 1-year sub-periods is, on average, 0.65. Therefore, defining sub-periods with lengths between 3 and 5 years may be the most suitable choice to ensure PMR representativeness across a wide spectrum of possible DSST experiments.
5.1 The choice of an adequate sub-period length for the PMR
Overall, the choice of the best sub-period length for the computation of the PMR must satisfy the following two conditions: (i) be small enough to limit loss of information about model robustness and (ii) maximize correlation scores with DSST biases in order to ensure its consistency. The first condition relates to the sensitivity of the PMR to the model's actual robustness, while the second condition relates to the reliability of the PMR in different DSST setups for the evaluation of model robustness. We would suggest that the interpretability of the moving bias curve associated with the PMR accounts for a third condition for the choice of the sub-period length. In order to be interpreted easily, the curve should be smooth enough to clearly distinguish periods during which a model overestimates or underestimates observed streamflow and, thus, involve long enough sub-periods. Of course, for cases where only PMR values were to be used without any analyses of the moving bias curves, this issue is incidental.
Under the conditions of our experiment, we found that lengths between 2 and 5 years were relevant to fulfil the second requirement. The sensitivity requirement would lead to computing the PMR on 2-year sub-periods; however, we acknowledge from our experience with moving bias curves that such sub-periods are too short for quick visual analyses. Therefore, we consider 3–5 years to be an adequate length for the computation of the PMR.
However, it should be pointed out that these results are likely to be context dependent and may have been different for other models. For these reasons, the aim of the study was more the demonstration that it is possible to assess hydrological model robustness to climatic changes without performing a DSST, rather than demonstrating that the PMR is perfectly reliable and that it should substitute split-sample tests. Moreover, the length of the sub-periods involved in the computation of the PMR should also reflect the particular needs of each model evaluation study. One could imagine that it may be chosen according to the temporal variability or periodicity of some climate indices (e.g. the North Atlantic Oscillation index).
5.2 Predicting model bias in DSST from the moving bias curve
Although the PMR shows in average a good ability to predict model biases on average, it also exhibits a poorer match with model bias in each DSST experiment. Since the PMR is designed to estimate the average deviation of model biases, this outcome was expected. A further argument against the PMR is that its value is necessarily positive and, thus, does not shows whether a model is overestimating or underestimating streamflow if climatic conditions change.
It should be recalled that the PMR is meant as a synthetic metric to embrace model robustness and has been designed to avoid choosing an arbitrary period to perform a split-sample test or an arbitrary climate variable to perform a DSST. In the research field of hydrological model robustness, scientists are usually interested in evaluating and improving the general skills of their models, and they try to avoid skewing their results by accidentally selecting testing conditions that are too favourable or too unfavourable. However, when it comes to addressing more specific questions, metrics such as the PMR may be uninformative. We, thus, suggest additional metrics, derived from the moving bias curve (see Fig. 2), to overcome the issues mentioned above.
Given two sub-periods of different climate conditions, a and b, we define the specific proxy for model robustness (denoted as sPMR) as follows:
The sPMR(a,b) is simply the difference between the model error on sub-period a and the model error on sub-period b, relative to the average streamflow on the whole time series. It can be computed from a from a single model simulation and, thus, be applied to models calibrated on the whole data set or to uncalibrated models. The sPMR can be either positive or negative and is supposed to assess model bias, as it would be obtained from a DSST for a model calibrated on sub-period a and evaluated on sub-period b. Notice that . The comparison between the sPMR and model biases obtained in DSST (without absolute values from Eq. 2) are shown on Fig. 8.
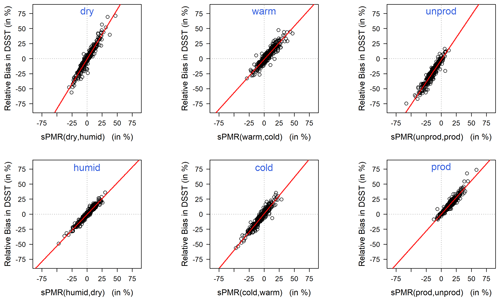
Figure 8Catchment-wise sPMR values against catchment-wise DSST relative bias (one point per catchment) for each DSST setup. The red line corresponds to the fitted linear model relating DSST relative bias to sPMR for each DSST setup.
Our results show a very good fit between model biases in DSST and the sPMR metric, indicating a good potential to be used as a substitute for the DSST for models on which it cannot be applied. In the case of GR4J, the similarity between sPMR and biases in DSST indicate that the information about model bias in extrapolation can be retrieved from a single calibration on the whole period. In other words, it indicates a strong parallelism between the moving bias curves (Fig. 2), whatever the calibration period, for periods at least longer than 5 years, confirming the results of Coron et al. (2014).
5.3 Generalization of the PMR for the evaluation of hydrological models
In this study, our approach of hydrological models robustness was focused on their ability to estimate annual or interannual water volumes. However, motivations for extrapolating streamflow with hydrological models are manifold and are not limited to annual resource assessments. In this regard, a strength of the traditional DSST is that the choice of the performance metrics for model evaluation is unlimited, whereas the PMR is simply a metric. It is, yet, worth noting that the PMR is based on a simple idea, namely that model robustness is associated to the stability of model performance in time and under a variety of climatic conditions. Hence, it is possible to extend this principle to other performance metrics, focusing on other aspects than the simple annual volumes. One could therefore imagine computing Nash–Sutcliffe efficiency (NSE; Nash and Sutcliffe, 1970) or KGE on multiple sub-periods of the data and assessing its variability. However, interpreting the stability of such metrics is not straightforward because they are both non-linear and highly sensitive to error heteroscedasticity. In addition, an interesting feature of the PMR, as it is presented in this study, is that it gives a rough estimate of what model bias could be in a generic split-sample test experiment and is, thus, easy to interpret. This feature is due to the structure of model bias, which is both linear and centred around zero. Therefore, any metric respecting these requirements would have the same property as the PMR.
Adapting the PMR framework to specific modelling issues could be done in various ways. A possibility would, for example, be to compute model bias on a portion of streamflow data above (respectively, below) a given threshold. This procedure has been applied by Royer-Gaspard (2021) to assess the robustness of GR4J for the simulation of different ranges of the streamflow (low, intermediate and high flows). Another option would be to compute model bias on streamflow components, such as baseflow and storm flow, derived from hydrograph separation techniques, to obtain insights of the models' ability to represent their interannual variations. Some authors have already applied common performance metrics on such streamflow components (e.g. Samuel et al., 2012). Eventually, streamflow transformations may be usefully applied as well to derive alternative PMR focusing on weighted parts of the streamflow (e.g. with exponent functions).
Traditional methods to assess the robustness of hydrological models to changes in climatic conditions rely on calibration–evaluation exercises, preferably performed on climatically different periods of a time series. Although the DSST or its variants represent the most appropriate procedure one can imagine in terms of model-robustness evaluation, they cannot be used on models that need to be calibrated on all the available data or to uncalibrated models. Furthermore, the DSST is based on the selection of hydro-climatic variables whose change is supposed to place the model in unfavourable conditions to perform but whose actual link with robustness is strongly context dependent.
In this technical note, we propose a performance metric able to evaluate model robustness from a single model calibrated on the entire period of record. The so-called PMR, thus, does not need multiple calibrations of the model on sub-periods of the time series and can be used for any kind of hydrological model. The PMR is constructed as an indicator of the flatness of the moving bias curve, which is a graphical representation of the temporal evolution of model bias across sliding sub-periods of the data.
The reliability of the PMR was compared with the results obtained by applying different DSST setups on GR4J, a typical conceptual model, on a data set of 377 French catchments. We tested the predictive ability of the metric to estimate model bias obtained by transferring model parameters from calibration periods to climatically opposite evaluation periods, for six types of hydro-climatic changes (changes in both directions of average precipitation, average temperature and average runoff ratio).
Our results show that PMR relates well to absolute model biases in the DSST, especially when these biases derived from the six DSST setups are averaged. Although the metric values do not vary much across the catchment set, this sensitivity can be enhanced by reducing the length of the sub-periods on which the PMR is computed. An analysis of the correlation between the PMR and model biases in the DSST for different sub-period lengths pinpointed that the reliability of PMR was better when the metric was computed on sub-periods with lengths between 2 and 5 years. Ultimately, the need to find a balance between metric sensitivity and reliability led us to recommend computing the PMR on 3- to 5-year sub-periods for GR4J.
Our results should encourage hydrological modellers to include the PMR as part of their panoply of evaluation metrics to judge their models. The metric addressing models transferability within the context of observed climate variability can be useful in model robustness assessments. In the context of climate change impact assessments, though, it should be recalled that demonstrating model robustness in the historical period is a necessary yet insufficient requirement to validate model robustness in future conditions outside the range of past observations. Still, being relevant for any kind of hydrological model, it may be used to inform model selection for such simulations. Of course, it appears difficult to define acceptability thresholds for the PMR a model should pass to be used in extrapolation, since it would be catchment and objective dependent. However, one could imagine adapting a standardized PMR by comparing PMR values with a benchmark model, as is done for NSE (for example, a simple yearly Budyko model). Further work should also examine the potential of PMR to be incorporated as a hydrological signature in multi-objective calibration procedures essentially to constrain model parameters governing slow temporal changes in catchment response.
Model biases in the DSST have been calculated in an absolute way in the Sect. 4 so that they could be compared with PMR values. This resulted in a loss of information about the sign of model errors. In this section, it is shown how the sign of these errors relates to the different DSST experiments. The biases obtained for GR4J for each of the six types of DSST setup are plotted in Fig. A1 without taking their absolute values.
Model bias follows different patterns, depending on the climatic variable used to define the calibration and evaluation periods of the DSST. While the distribution of model errors seems comparatively even for periods characterized by different average precipitation, transferring model parameters between periods with different runoff ratios clearly triggers opposite model bias, whether the transfer is performed in one way or in another. For most catchments, GR4J indeed underestimates streamflow volumes when runoff ratio increases and, conversely, overestimates streamflow volumes when runoff ratio decreases. DSSTs based on temperature yield situations in between, since median model bias is slightly negative (respectively, positive) when calibrated on warmer (respectively, colder) periods. When calculated in absolute terms, model bias was larger in DSSTs based on runoff ratio than for experiments based on temperature and precipitation (Fig. A1). Therefore, robustness issues for the model appear to be caused less by changes in climatic changes than by modification of the catchment response to precipitation. This result is in line with the conclusion of Saft et al. (2016), who tested a number of hydrological models in southeastern Australia during prolonged droughts. The authors observed that many of these models would produce biased simulations of streamflow during the drought if, and only if, the catchments had experienced shifts in the rainfall–runoff relationship from pre-drought to drought conditions. Our results extend this statement for GR4J to situations where the runoff ratio increases and shows opposite model biases, depending on the sign of the change.
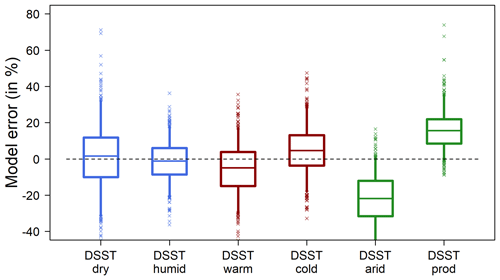
Figure A1Distribution of model biases in DSST for each type of setup. The box plots represent the 5, 25, 50, 75 and 95 quantiles, and the little crosses denote the outliers. Blue, red and green box plots are, respectively, associated to DSST setups based on precipitation, temperature and runoff ratio.
The mathematical expression of the PMR also results from a choice that needs to be discussed. For example, Coron et al. (2014) proposed computing the flatness of the moving bias curve as the standard deviation of model bias on the sub-periods.
We discussed the mathematical form chosen for the PMR by comparing the metrics defined in Eqs. (1) and (B1). Figure B1 shows the differences between the metrics in Pearson's correlation with model biases obtained in the DSST performed on 5-year periods. The length of the sub-periods used in the PMR varies from 1 to 10 years. It appears that short sub-periods confer greater benefit to the reliability of the PMR (Eq. 1), whereas longer sub-periods benefit the alternative PMR (Eq. B1). Choosing a 5-year sub-period for the computation of the PMR does not, on average, favour either the one or the other formulation of the metric. As mentioned previously, we sought to formulate the PMR so that it maximizes the correlation with DSST biases while enhancing the sensitivity of the metric. For this reason, better agreement for the PMR, as formulated in Eq. (1), with DSST biases obtained for shorter sub-periods, where the PMR is most sensitive to model robustness, makes it more suitable. Therefore, the PMR computed as the sum of absolute average model error on 5-year sub-periods is best suited to evaluating model robustness.
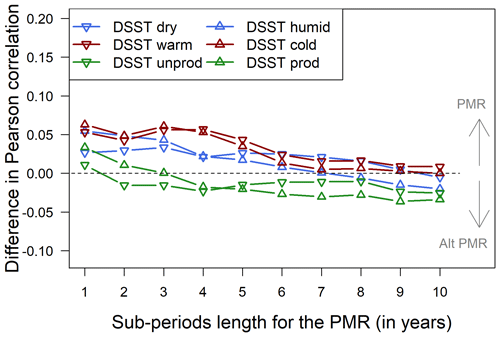
Figure B1Differences between the correlations of PMR and alternative PMR with DSST biases (performed on 6-year calibration and evaluation periods), depending on the DSST experiment and on the length of the sub-periods used for the computation of the PMR. Values above zero indicate better agreement between PMR and DSST results compared to alternative PMR, and vice versa.
In addition, we note that the alternative PMR corresponds better overall to DSST experiments based on runoff ratio, which, we remind the reader, yielded the larger model biases. The fact that model biases are squared in the computation of the alternative PMR enhances the weight of sub-periods where the model simulations are the worst and, thus, potentially where the observed runoff ratio differs the most from the average. It is possible that calculating the error differences in absolute terms rather than squared makes the metric less dependent on years when the model is drastically worse or on years with large measurement errors.
Furthermore, the PMR, as defined in Eq. (1), may have other advantages compared to Eq. (B1). The fact that model error on each sub-period is normalized by the average observed streamflow during the total period instead of the average observed streamflow during the sub-period may put less emphasis on very dry years when observed streamflow is close to zero. Model bias on such dry years can be undesirably large; thus, the PMR, as defined in Eq. (1), could be a better option for arid catchments. This also makes it possible to compute the PMR in catchments where rivers might eventually cease to flow for long periods of time without any further adjustments to the data. In addition, the interpretation of the PMR is perceived as being more straightforward in Eq. (1) than in Eq. (B1) as model error is simply compared to the observed streamflow averaged on the whole time series rather than to a quantity that varies across the sub-periods.
The GR4J model is freely available in the airGR R package. The code for calculating the PMR can be made available upon request.
Streamflow data were provided by the French database Banque HYDRO and are available at http://www.data.eaufrance.fr/ (SCHAPI, 2021). Meteorological data were provided by Météo-France and must be requested from this institute.
PRG designed the study, made the technical development and conducted the analysis. PRG also wrote and revised the paper. PRG, VA and GT discussed the design and results and contributed to the final version of the paper.
The authors declare that they have no competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Gaëlle Tallec and Charles Perrin, for their careful review prior to article submission. Ludovic Oudin, Laurent Coron, Éric Martin and Nathalie de Noblet-Ducoudré are gratefully acknowledged, for their advice on the doctoral research of the first author. Météo-France and SCHAPI are acknowledged, for providing climatic and streamflow data, respectively. We thank Isabella Athanassiou, for her cautious proofreading and help in making the English easier to read. The authors gratefully acknowledge the reviews by James Craig and by another anonymous reviewer.
This work has been funded by the project AQUACLEW, which is part of ERA4CS, an ERA-NET project initiated by JPI Climate, and funded by FORMAS (SE), DLR (DE), BMWFW (AT), IFD (DK), MINECO (ES) and ANR (FR), with co-funding by the European Commission (grant no. 690462).
This paper was edited by Genevieve Ali and reviewed by James Craig and one anonymous referee.
Blöschl, G., Bierkens, M. F. P., Chambel, A., et al.: Twenty-three unsolved problems in hydrology (UPH) – a community perspective, Hydrolog. Sci. J., 64, 1141–1158, https://doi.org/10.1080/02626667.2019.1620507, 2019. a
Broderick, C., Matthews, T., Wilby, R. L., Bastola, S., and Murphy, C.: Transferability of hydrological models and ensemble averaging methods between contrasting climatic periods, Water Resour. Res., 52, 8343–8373, https://doi.org/10.1002/2016wr018850, 2016. a, b, c
Clark, M. P., Wilby, R. L., Gutmann, E. D., Vano, J. A., Gangopadhyay, S., Wood, A. W., Fowler, H. J., Prudhomme, C., Arnold, J. R., and Brekke, L. D.: Characterizing uncertainty of the hydrologic impacts of climate change, Curr. Clim. Change Rep., 2, 55–64, https://doi.org/10.1007/s40641-016-0034-x, 2016. a
Coron, L., Andréassian, V., Perrin, C., Lerat, J., Vaze, J., Bourqui, M., and Hendrickx, F.: Crash testing hydrological models in contrasted climate conditions: An experiment on 216 Australian catchments, Water Resour. Res., 48, W05552, https://doi.org/10.1029/2011wr011721, 2012. a, b
Coron, L., Andréassian, V., Perrin, C., Bourqui, M., and Hendrickx, F.: On the lack of robustness of hydrologic models regarding water balance simulation: a diagnostic approach applied to three models of increasing complexity on 20 mountainous catchments, Hydrol. Earth Syst. Sci., 18, 727–746, https://doi.org/10.5194/hess-18-727-2014, 2014. a, b, c, d, e, f, g, h
Coron, L., Thirel, G., Delaigue, O., Perrin, C., and Andréassian, V.: The suite of lumped GR hydrological models in an R package, Environ. Model. Softw., 94, 166–171, https://doi.org/10.1016/j.envsoft.2017.05.002, 2017. a
Coron, L., Perrin, C., Delaigue, O., Thirel, G., and Michel, C.: airGR: Suite of GR Hydrological Models for Precipitation-Runoff Modelling, R package version 1.0.12.3.2, available at: https://webgr.inrae.fr/en/airGR/, last access: 28 August 2018. a
Dakhlaoui, H., Ruelland, D., Tramblay, Y., and Bargaoui, Z.: Evaluating the robustness of conceptual rainfall-runoff models under climate variability in northern Tunisia, J. Hydrol., 550, 201–217, https://doi.org/10.1016/j.jhydrol.2017.04.032, 2017. a, b
Dakhlaoui, H., Ruelland, D., and Tramblay, Y.: A bootstrap-based differential split-sample test to assess the transferability of conceptual rainfall-runoff models under past and future climate variability, J. Hydrol., 575, 470–486, https://doi.org/10.1016/j.jhydrol.2019.05.056, 2019. a
Delaigue, O., Génot, B., Lebecherel, L., Brigode, P., and Bourgin, P. Y.: Database of watershed-scale hydroclimatic observations in France, Université Paris-Saclay, INRAE, HYCAR Research Unit, Hydrology group, Antony, [data set], available at: https://webgr.inrae.fr/base-de-donnees/, last access: 31 July 2020. a
Fowler, K. J. A., Peel, M. C., Western, A. W., Zhang, L., and Peterson, T. J.: Simulating runoff under changing climatic conditions: Revisiting an apparent deficiency of conceptual rainfall–runoff models, Water Resour. Res., 52, 1820–1846, https://doi.org/10.1002/2015wr018068, 2016. a
Gupta, H. V., Kling, H., Yilmaz, K. K., and Martinez, G. F.: Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling, J. Hydrol., 377, 80–91, https://doi.org/10.1016/j.jhydrol.2009.08.003, 2009. a
Hagemann, S., Chen, C., Clark, D. B., Folwell, S., Gosling, S. N., Haddeland, I., Hanasaki, N., Heinke, J., Ludwig, F., Voss, F., and Wiltshire, A. J.: Climate change impact on available water resources obtained using multiple global climate and hydrology models, Earth Syst. Dynam., 4, 129–144, https://doi.org/10.5194/esd-4-129-2013, 2013. a
Klemeš, V.: Operational testing of hydrological simulation models, Hydrolog. Sci. J., 31, 13–24, https://doi.org/10.1080/02626668609491024, 1986. a
Leleu, I., Tonnelier, I., Puechberty, R., Gouin, P., Viquendi, I., Cobos, L., Foray, A., Baillon, M., and Ndima, P.-O.: La refonte du système d'information national pour la gestion et la mise à disposition des données hydrométriques, Houille Blanche, 1, 25–32, https://doi.org/10.1051/lhb/2014004, 2014. a
Mathevet, T.: Quels modèles pluie-débit globaux au pas de temps horaire? Développements empiriques et comparaison de modèles sur un large échantillon de bassins versants, PhD, ENGREF Paris, available at: https://hal.inrae.fr/tel-02587642 (last access: 27 April 2020), 2005. a
Mathevet, T., Gupta, H., Perrin, C., Andréassian, V., and Le Moine, N.: Assessing the performance and robustness of two conceptual rainfall-runoff models on a worldwide sample of watersheds, J. Hydrol., 124698, https://doi.org/10.1016/j.jhydrol.2020.124698, 2020. a
Melsen, L. A., Addor, N., Mizukami, N., Newman, A. J., Torfs, P. J. J. F., Clark, M. P., Uijlenhoet, R., and Teuling, A. J.: Mapping (dis)agreement in hydrologic projections, Hydrol. Earth Syst. Sci., 22, 1775–1791, https://doi.org/10.5194/hess-22-1775-2018, 2018. a
Merz, R., Parajka, J., and Blöschl, G.: Time stability of catchment model parameters: Implications for climate impact analyses, Water Resour. Res., 47, W02531, https://doi.org/10.1029/2010wr009505, 2011. a
Nash, J. E. and Sutcliffe, J. V.: River flow forecasting through conceptual models part I – A discussion of principles, J. Hydrol., 10, 282–290, https://doi.org/10.1016/0022-1694(70)90255-6, 1970. a
Oudin, L., Hervieu, F., Michel, C., Perrin, C., Andréassian, V., Anctil, F., and Loumagne, C.: Which potential evapotranspiration input for a lumped rainfall–runoff model?: Part 2 – Towards a simple and efficient potential evapotranspiration model for rainfall–runoff modelling, J. Hydrol., 303, 290–306, https://doi.org/10.1016/j.jhydrol.2004.08.026, 2005. a
Perrin, C., Michel, C., and Andréassian, V.: Improvement of a parsimonious model for streamflow simulation, J. Hydrol., 279, 275–289, https://doi.org/10.1016/s0022-1694(03)00225-7, 2003. a
Refsgaard, J. C., Madsen, H., Andréassian, V., Arnbjerg-Nielsen, K., Davidson, T. A., Drews, M., Hamilton, D. P., Jeppesen, E., Kjellström, E., Olesen, J. E., Sonnenborg, T. O., Trolle, D., Willems, P., and Christensen, J. H.: A framework for testing the ability of models to project climate change and its impacts, Climatic Change, 122, 271–282, https://doi.org/10.1007/s10584-013-0990-2, 2014. a
Royer-Gaspard, P.: De la robustesse des modèles hydrologiques face à des conditions climatiques variables, PhD, Sorbonne Université, Paris, available at: https://webgr.inrae.fr/wp-content/uploads/2021/08/thesis_Royer-GaspardPaul_FR.pdf, last access: 1 October 2021. a
Saft, M., Peel, M. C., Western, A. W., Perraud, J.-M., and Zhang, L.: Bias in streamflow projections due to climate-induced shifts in catchment response, Geophys. Res. Lett., 43, 1574–1581, https://doi.org/10.1002/2015gl067326, 2016. a
Samuel, J., Coulibaly, P., and Metcalfe, R. A.: Identification of rainfall–runoff model for improved baseflow estimation in ungauged basins, Hydrol. Process., 26, 356–366, https://doi.org/10.1002/hyp.8133, 2012. a
SCHAPI: Banque HYDRO, available at: http://www.data.eaufrance.fr/ (last access: 21 January 2019), 2021. a
Schewe, J., Heinke, J., Gerten, D., Haddeland, I., Arnell, N. W., Clark, D. B., Dankers, R., Eisner, S., Fekete, B. M., Colón-González, F. J., Gosling, S. N., Kim, H., Liu, X., Masaki, Y., Portmann, F. T., Satoh, Y., Stacke, T., Tang, Q., Wada, Y., Wisser, D., Albrecht, T., Frieler, K., Piontek, F., Warszawski, L., and Kabat, P.: Multimodel assessment of water scarcity under climate change, P. Natl. Acad. Sci. USA, 11, 3245–3250, https://doi.org/10.1073/pnas.1222460110, 2014. a
Thirel, G., Andréassian, V., Perrin, C., Audouy, J.-N., Berthet, L., Edwards, P., Folton, N. Furusho, C., Kuentz, A., Lerat, J., Lindström, G., Martin, E., Mathevet, T., Merz, R., Parajka, J., Ruelland, D., and Vaze, J.: Hydrology under change: an evaluation protocol to investigate how hydrological models deal with changing catchments, Hydrolog. Sci. J., 60, 1184–1199, https://doi.org/10.1080/02626667.2014.967248, 2015. a
Valéry, A., Andréassian, V., and Perrin, C.: “As simple as possible but not simpler”: What is useful in a temperature-based snow-accounting routine? Part 2 – Sensitivity analysis of the Cemaneige snow accounting routine on 380 catchments, J. Hydrol., 517, 1176–1187, https://doi.org/10.1016/j.jhydrol.2014.04.058, 2014. a, b
Vaze, J., Post, D. A., Chiew, F. H. S., Perraud, J.-M., Viney, N. R., and Teng, J.: Climate non-stationarity–validity of calibrated rainfall–runoff models for use in climate change studies, J. Hydrol., 394, 447–457, https://doi.org/10.1016/j.jhydrol.2010.09.018, 2010. a, b
Vidal, J.-P., Martin, E., Franchistéguy, L., Baillon, M., and Soubeyroux, J.-M.: A 50-year high-resolution atmospheric reanalysis over France with the Safran system, Int. J. Climatol., 30, 1627–1644, https://doi.org/10.1002/joc.2003, 2010. a
Vidal, J.-P., Hingray, B., Magand, C., Sauquet, E., and Ducharne, A.: Hierarchy of climate and hydrological uncertainties in transient low-flow projections, Hydrol. Earth Syst. Sci., 20, 3651–3672, https://doi.org/10.5194/hess-20-3651-2016, 2016. a
- Abstract
- Introduction
- Description of the proxy for model robustness
- Material and methods
- Results: reliability of the proxy for model robustness to indicate model robustness
- Discussion
- Conclusions
- Appendix A: Characterization of model bias across DSST setups
- Appendix B: The choice of an adequate mathematical expression
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Description of the proxy for model robustness
- Material and methods
- Results: reliability of the proxy for model robustness to indicate model robustness
- Discussion
- Conclusions
- Appendix A: Characterization of model bias across DSST setups
- Appendix B: The choice of an adequate mathematical expression
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References