A global algorithm for identifying changing streamflow regimes: application to Canadian natural streams (1966–2010)

Climate change affects natural streamflow regimes globally. To assess alterations in streamflow regimes, typically temporal variations in one or a few streamflow characteristics are taken into account. This approach, however, cannot see simultaneous changes in multiple streamflow characteristics, does not utilize all the available information contained in a streamflow hydrograph, and cannot describe how and to what extent streamflow regimes evolve from one to another. To address these gaps, we conceptualize streamflow regimes as intersecting spectrums that are formed by multiple streamflow characteristics. Accordingly, the changes in a streamflow regime should be diagnosed through gradual, yet continuous changes in an ensemble of streamflow characteristics. To incorporate these key considerations, we propose a generic algorithm to first classify streams into a finite set of intersecting fuzzy clusters. Accordingly, by analyzing how the degrees of membership to each cluster change in a given stream, we quantify shifts from one regime to another. We apply this approach to the data, obtained from 105 natural Canadian streams, during the period of 1966 to 2010. We show that natural streamflow in Canada can be categorized into six regime types, with clear hydrological and geographical distinctions. Analyses of trends in membership values show that alterations in natural streamflow regimes vary among different regions. Having said that, we show that in more than 80 % of considered streams, there is a dominant regime shift that can be attributed to simultaneous changes in streamflow characteristics, some of which have remained previously unknown. Our study not only introduces a new globally relevant algorithm for identifying changing streamflow regimes but also provides a fresh look at streamflow alterations in Canada, highlighting complex and multifaceted impacts of climate change on streamflow regimes in cold regions.

1 Introduction

Natural characteristics of streamflow are critical to ecosystem livelihood and human settlements around river systems (Poff et al., 2010; Nazemi and Wheater, 2014; Hassanzadeh et al., 2017). Historically, humans have considered the seasonality, variability, and magnitude of natural streamflow as key factors for determining potentials for socio-economic developments (Knouft and Ficklin, 2017). Streamflow characteristics are diverse and can contain different information. While some streamflow characteristics determine potentials for agriculture and energy production (Hamududu and Killingtveit, 2012; Amir Jabbari and Nazemi, 2019; Nazemi et al., 2020), some others act as proxies for the consequences of devastating disasters such as floods or droughts (Arheimer and Lindström, 2015; Burn and Whitfield, 2016; Zandmoghaddam et al., 2019).

A set of streamflow characteristics, collectively defining the overall flow behaviour in a river reach, is called the streamflow regime (Poff et al., 1997). Traditionally, streamflow regimes have been considered stationary in time (Milly et al., 2008). However, the looming effects of climate change along with human interventions through land and water management have raised fundamental questions regarding the stationarity of streamflow regimes during the current “Anthropocene” (Arnell and Gosling, 2013; Nazemi and Wheater, 2015a, b). Even in undisturbed streams, recent literature is full of evidence indicating major alterations induced by heightened climate variability and change (Barnett et al., 2005; Stahl et al., 2010; Rood et al., 2016; Hodgkins et al., 2017; Dierauer et al., 2018). As a result, assessing how streamflow regimes are changing as a result of alterations in natural and anthropogenic drivers is currently one of the imminent questions in the field of hydrology.

Despite the extensive body of knowledge already gathered around assessing the effects of climate change on altering streamflow regimes, there is still room for methodological developments. Most importantly, among many potential flow characteristics that can constitute and describe a streamflow regime, often only a few are taken into account (Whitfield and Cannon, 2000; Hall et al., 2014; Vormoor et al., 2015). This is a limitation because climate change impacts are often manifested in the entire streamflow hydrograph and not only around a unique set of streamflow characteristics (Olden and Poff, 2003). This is particularly the case in cold regions as at the watershed scale, multiple processes contribute to the streamflow generation, each behaving differently in response to climate variability and change (Whitfield and Pomeroy, 2016). As a result, alterations in streamflow regimes are not only significant (e.g., Déry and Wood, 2005; MacDonald et al., 2018; Islam et al., 2019; Champagne et al., 2020), but they are also complex due to compound impacts of changes in temperature, shifts in forms and magnitude of precipitation, and alterations in snow and ice accumulation and melt (DeBeer et al., 2016; Hatami et al., 2018; Rottler et al., 2020). At this stage of development, it is not yet possible to systematically quantify streamflow regimes and their alterations to one another using a large set of simultaneously changing streamflow characteristics (Burn et al., 2016; Burn and Whitfield, 2018).

Here, we propose a new methodology to address this challenge. First, by considering more streamflow characteristics, the distinctions between regime types and their alterations become more fuzzy and relative. Accordingly, in line with some recent suggestions in the literature (see, for example, Ternynck et al., 2016; Burn and Whitfield, 2017; Knoben et al., 2018; Brunner et al., 2018, 2019; Aksamit and Whitfield, 2019; Jehn et al., 2020), we conceptualize streamflow regimes as continuous spectrums rather than distinct states. This conceptualization requires a methodology that can formally deal with subjectivity in the definition of streamflow regimes. For this purpose, we use elements of fuzzy set theory (see Zadeh, 1965; Nazemi et al., 2002) to provide a methodological basis to classify streamflow regimes as intersecting clusters. We then measure the gradual departure from one fuzzy cluster to others using significant monotonic trends in membership degrees and use this information as an indicator for a regime shift in a given stream. Accordingly, we highlight how such regime shifts are attributed to changes in streamflow characteristics using a formal dependence analysis.

We apply this algorithm in Canada, where the rate of warming is twice the global average (Bush and Lemmen, 2019), and changes in streamflow characteristics are significant in time and space (e.g., Buttle et al., 2016; O'Neil et al., 2017; Dierauer et al., 2020). By considering more than 100 natural streams, we provide – for the first time – a homogeneous, pan-Canadian view on recent alterations in natural streamflow regimes. The remainder of this paper is as the following: sect. 2 describes our three-step methodology related to (i) clustering regime types, (ii) detecting regime changes, and (iii) attributing regime changes to alterations in streamflow characteristics. Section 3 introduces our case study and the data. The results and discussions are presented in Sects. 4 and 5. Finally, Sect. 6 concludes our work and provides some further remarks.

2 Methodology

2.1 Rationale and proposed algorithm

From both conceptual and computational perspectives, quantifying changes in streamflow regimes is not a trivial task due to the relativity in the definition of streamflow regime and how a change can be identified. On the one hand, the flow regime at a given stream is defined by a large number of streamflow characteristics, some of which have conflicting trends in time and space. On the other hand, the flow regime is often identified based on similarity/dissimilarity of characteristics in a set of benchmarking streams with known regimes. Accordingly, regime shifts are not only defined based on alterations in streamflow characteristics relative to the past but also with respect to relative changes as regards other streams with known regime types. This creates a complex mathematical problem due to the “curse of dimensionality” (see, for example, Trunk, 1979), meaning that the complexity of the problem increases exponentially by increasing the number of streams and/or streamflow characteristics with which the streamflow regime is defined. To solve this problem, the general tendency in the literature is to reduce the dimensionality of the problem through the use of methodologies, such as multidimensional scaling, empirical orthogonal functions, and principal component analysis (e.g., Maurer et al., 2004; Johnston and Shmagin, 2008). Despite methodological differences, all these approaches try to provide a parsimonious representation of a hyperdimensional space by creating a much simpler space that can preserve the sample variability in the original domain (Guetter and Georgakakos, 1993). Although these methodologies are able to substantially reduce the dimensionality and give valuable insights into changes in hyperdimensional data sets, the results are hard to interpret, particularly when attribution to some physical characteristics are concerned (Matalas and Reiher, 1967; Overland and Preisendorfer, 1982; Hannachi et al., 2009, and references therein). In the case of quantifying changes in streamflow regimes, this limitation translates into an inability to attribute the formation and transition in regime types directly to a set of specific streamflow characteristics.

Here, we aim at addressing this problem through a new methodology that does not rely on dimension reduction; rather, it tries to embrace the inherent high dimensionality of the problem. Below we suggest an integrated approach to (1) classify natural streamflow regimes into a set of interpolating regime types, (2) diagnose the gradual evolution in regime types and their shifts in time, and (3) attribute changes in streamflow regimes to alterations in streamflow characteristics. Figure 1 shows the proposed procedure. We use MATLAB^® programming platform for the implementation of this procedure.

Figure 1 The workflow of the proposed three-step algorithm for classifying streamflow regime, diagnosing shift in streamflow regime, and attributing the regime shift to the changes in streamflow characteristics.

Our approach is built upon two fundamental considerations. First, we acknowledge that streamflow regimes are constituted by several streamflow characteristics, and therefore changes in streamflow regimes are manifested through changes in a large ensemble of streamflow characteristics. Second, we recognize that there are soft as opposed to hard distinctions between streamflow regimes, and regime shifts occur gradually rather than abruptly. We select a large set of streamflow characteristics – or features – to collectively characterize the streamflow regime. We then use the fuzzy c-means algorithm (FCM) to classify streams into a set of overlapping regime types during a common initial data period. We accordingly quantify changes in degrees of association to each regime type during the entire data period using a moving trend analysis. By monitoring the co-occurrence of divergent trends in membership values, the transitions of regime types to one another can be identified. Finally, we monitor the co-evolution of regime shifts with the alterations in streamflow characteristics through a formal dependency analysis.

2.2 Feature selection

Indicators of hydrologic alterations (IHAs; Richter et al., 1996) are commonly applied as features to characterize changes in natural streamflow regimes (e.g., Wang et al., 2018). Different sets of IHAs can be considered to constitute streamflow regimes. Here we consider 15 IHAs, including annual mean flow, monthly mean flows, and timings of the annual low and high flows that together can represent the shape of the annual hydrograph. At each stream, we use the mean (first moment) and variance (second moment) of these 15 indicators during a multi-year timeframe to come up with 30 features that together can capture the shape of the expected annual hydrograph and the variability around it. Table 1 shows the name and notation of the features used, where $x_{j=\mathrm{1}:\mathrm{15}}$ and $y_{j=\mathrm{1}:\mathrm{15}}$ denote the mean and the variance of the 15 considered IHAs.

Table 1 The thirty streamflow features used for clustering natural streamflow regime in Canada.

2.3 Fuzzy c-means clustering

Clustering is the process of arranging data into a finite set of classes so that members in the same class have similar characteristics. Various statistical methodologies are used for clustering in hydrology (see Tarasova et al., 2019; Brunner et al., 2020), often to non-overlapping (i.e., hard) classes (Olden et al., 2012). Recent theoretical developments have alternatively considered a set of overlapping (i.e., soft) classes, in particular in the form of fuzzy clusters (e.g., Knoben et al., 2018; Wolfe et al., 2019). The association to each fuzzy cluster can be quantified using a degree of membership (see Bezdek, 1981; Sikorska et al., 2015). The process of clustering streamflow regime using FCM can be summarized as the following: assume that streamflow data from N hydrometric gauges during a common timeframe w with the length of l years are available. For each stream, the first and second moments of n IHAs (here n=15), i.e., $\mathbf{X}=\left[x_{ij}\right]\mathbf{Y}=\left[y_{ij}\right];$ $i\in \left\{\mathrm{1},\mathrm{\dots },N\right\}$, $j\in \left\{\mathrm{1},\mathrm{\dots },n\right\}$, can be extracted during the initial timeframe w. Before going forward, extracted features are normalized to avoid scale mismatches:

$$\begin{array}{}\text{(1a)}& {\displaystyle }{\stackrel{\mathrm{‾}}{x}}_{i,j}={\displaystyle \frac{x_{i,j}-\mathbf{min}\mathit{\left\{}{x}_{i=\mathrm{1}:N,j}\mathit{\right\}}}{\mathbf{max}\mathit{\left\{}{x}_{i=\mathrm{1}:N,j}\mathit{\right\}}-\mathbf{min}\mathit{\left\{}{x}_{i=\mathrm{1}:N,j}\mathit{\right\}}}}\forall j\in \left\{\mathrm{1},\mathrm{\dots },n\right\},\text{(1b)}& {\displaystyle }{\stackrel{\mathrm{‾}}{y}}_{i,j}={\displaystyle \frac{y_{i,j}-\mathbf{min}\mathit{\left\{}{y}_{i=\mathrm{1}:N,j}\mathit{\right\}}}{\mathbf{max}\mathit{\left\{}{y}_{i=\mathrm{1}:N,j}\mathit{\right\}}-\mathbf{min}\mathit{\left\{}{y}_{i=\mathrm{1}:N,j}\mathit{\right\}}}}\forall j\in \left\{\mathrm{1},\mathrm{\dots },n\right\},\end{array}$$

where $\stackrel{\mathrm{‾}}{\mathbf{X}}=\left[{\stackrel{\mathrm{‾}}{x}}_{ij}\right]$ and $\stackrel{\mathrm{‾}}{\mathbf{Y}}=\left[{\stackrel{\mathrm{‾}}{y}}_{ij}\right]$ are the matrices of normalized streamflow features (NSFs). FCM partitions the N streams into C fuzzy clusters such that the sum of distances for all streams $i\in \left\{\mathrm{1},\mathrm{\dots },N\right\}$ between NSFs and cluster centroids is minimized. This is often formulated through an iterative optimization procedure aiming at finding the cluster centroid by minimizing the generalized least-squared error function as the objective of optimization (Bezdek, 1981).

$$\begin{array}{}\text{(2a)}& \begin{array}{rl}\mathbf{J}\left(\mathbf{U},\mathbf{V}\mathrm{|}\stackrel{\mathrm{‾}}{\mathbf{X}},\stackrel{\mathrm{‾}}{\mathbf{Y}}\right)& =\sum _{c=\mathrm{1}}^C\cdot \sum _{i=\mathrm{1}}^N{\left(u_{i,c}\right)}^{\mathrm{2}}\\ & \cdot {\mathbf{d}}^{\mathrm{2}}\left(\left[{\stackrel{\mathrm{‾}}{x}}_{i,j=\mathrm{1}:n}{\stackrel{\mathrm{‾}}{y}}_{i,j=\mathrm{1}:n}\right],v_{c,m=\mathrm{1}:\mathrm{2}n}\right)\end{array}\end{array}$$

This objective function is subject to the following two constraints:

$$\begin{array}{}\text{(2b)}& {\displaystyle }\sum _{c=\mathrm{1}}^C{u}_{i,c}=\mathrm{1}\forall i\in \left\{\mathrm{1},\mathrm{\dots },N\right\},\text{(2c)}& {\displaystyle }\mathrm{0}<\sum _{i=\mathrm{1}}^N{u}_{i,c}<N\forall c\in \left\{\mathrm{1},\mathrm{\dots },C\right\},\end{array}$$

where $\mathbf{V}=v_{c=\mathrm{1}:C,m=\mathrm{1}:\mathrm{2}n}=\left[{\stackrel{\mathrm{‾}}{x^{\ast }}}_{c,j=\mathrm{1}:n},{\stackrel{\mathrm{‾}}{y^{\ast }}}_{c,j=\mathrm{1}:n}\right]=\left[{\stackrel{\mathrm{‾}}{x^{\ast }}}_{c,\mathrm{1}}\mathrm{\dots }{\stackrel{\mathrm{‾}}{x^{\ast }}}_{c,n}{\stackrel{\mathrm{‾}}{y^{\ast }}}_{c,\mathrm{1}}\mathrm{\dots }{\stackrel{\mathrm{‾}}{y^{\ast }}}_{c,n}\right]\in R^{\mathrm{2}n}$ is the matrix of cluster centroids (i.e., regime types); the matrix of $\mathbf{U}=\left[u_{i,c}\right];i\in \left\{\mathrm{1},\mathrm{\dots },N\right\}c\in \left\{\mathrm{1},\mathrm{\dots },C\right\}$ is the matrix of memberships; and ${\mathbf{d}}^{\mathrm{2}}\left([{\stackrel{\mathrm{‾}}{x}}_{i,j=\mathrm{1}:n},{\stackrel{\mathrm{‾}}{y}}_{i,j=\mathrm{1}:n}],v_{c,m=\mathrm{1}:\mathrm{2}n}\right)$ is the matrix of squared Euclidian distances between NSFs of stream i and a cluster's centroid c. The fuzzy membership matrix can be accordingly calculated as follows:

$$\begin{array}{}\text{(3)}& \begin{array}{rl}& u_{i,c}={\displaystyle \frac{\left(\frac{\mathrm{1}}{{\mathbf{d}}^{\mathrm{2}}\left(\left[{\stackrel{\mathrm{‾}}{x}}_{i,j=\mathrm{1}:n}{\stackrel{\mathrm{‾}}{y}}_{i,j=\mathrm{1}:n}\right],v_{c,m=\mathrm{1}:\mathrm{2}n}\right)}\right)}{\sum _{c=\mathrm{1}}^C\left(\frac{\mathrm{1}}{{\mathbf{d}}^{\mathrm{2}}\left(\left[{\stackrel{\mathrm{‾}}{x}}_{i,j=\mathrm{1}:n}{\stackrel{\mathrm{‾}}{y}}_{i,j=\mathrm{1}:n}\right],v_{c,m=\mathrm{1}:\mathrm{2}n}\right)}\right)}};\\ & i\in \left\{\mathrm{1},\mathrm{\dots },N\right\},c\in \left\{\mathrm{1},\mathrm{\dots },C\right\}.\end{array}\end{array}$$

The number of clusters C (here regime types) can be chosen as a priori or empirically using validity indices (Srinivas et al., 2008). Here, we implement three validity indices of the Xie–Beni index (V_XB; Xie and Beni, 1991), partition index (V_SC; Bensaid et al., 1996), and separation index (V_S; Fukuyama and Sugeno, 1989). These indices are based on two criteria, namely compactness and separation. The compactness characterizes how close members to each cluster are, whereas the separation measures how distinct two clusters are. A good clustering result should have both small intra-cluster compactness and large inter-cluster separation. The Xie–Beni validity index is the ratio of compactness to the separation, quantified by the average of the fuzzy variation in NSFs from a cluster's centroid to the minimum squared distance between cluster centroids. Note that ${\sum }_{i=\mathrm{1}}^N{\left(u_{i,c}\right)}^{\mathrm{2}}{\mathbf{d}}^{\mathrm{2}}\left(\left[{\stackrel{\mathrm{‾}}{x}}_{i,j=\mathrm{1}:n},{\stackrel{\mathrm{‾}}{y}}_{i,j=\mathrm{1}:n}\right],v_{c,m=\mathrm{1}:\mathrm{2}n}\right)$ is the compactness of fuzzy cluster c, and separation of fuzzy clusters is quantified by the minimum squared Euclidean distance between cluster centroids.

$$\begin{array}{}\text{(4)}& V_{\mathrm{XB}}={\displaystyle \frac{{\sum }_{c=\mathrm{1}}^C{\sum }_{i=\mathrm{1}}^N{\left(u_{i,c}\right)}^{\mathrm{2}}{\mathbf{d}}^{\mathrm{2}}\left(\left[{\stackrel{\mathrm{‾}}{x}}_{i,j=\mathrm{1}:n},{\stackrel{\mathrm{‾}}{y}}_{i,j=\mathrm{1}:n}\right],v_{c,m=\mathrm{1}:\mathrm{2}n}\right)}{N\times \underset{c,l\ne c}{min}\left({\mathbf{d}}^{\mathrm{2}}\left(v_{l,m=\mathrm{1}:\mathrm{2}n},v_{c,m=\mathrm{1}:\mathrm{2}n}\right)\right)}}\end{array}$$

Partition index is quantified by the sum of individual fuzzy cluster variations (i.e., the compactness of fuzzy clusters) to the sum of the distances from cluster centroids (i.e., the separation of fuzzy clusters). This ratio is further normalized by fuzzy cardinality weight γ_c, defined by ${\mathit{\gamma }}_c={\sum }_{i=\mathrm{1}}^N{u}_{i,c}$, to avoid the bias made by cluster sizes.

$$\begin{array}{}\text{(5)}& V_{\mathrm{SC}}={\sum }_{c=\mathrm{1}}^C\left\{{\displaystyle \frac{{\sum }_{i=\mathrm{1}}^N{\left(u_{i,c}\right)}^{\mathrm{2}}{\mathbf{d}}^{\mathrm{2}}\left(\left[{\stackrel{\mathrm{‾}}{x}}_{i,j=\mathrm{1}:n},{\stackrel{\mathrm{‾}}{y}}_{i,j=\mathrm{1}:n}\right],v_{c,m=\mathrm{1}:\mathrm{2}n}\right)}{{\mathit{\gamma }}_c\times {\sum }_{l=\mathrm{1}}^c{\mathbf{d}}^{\mathrm{2}}\left(v_{l,m=\mathrm{1}:\mathrm{2}n},v_{c,m=\mathrm{1}:\mathrm{2}n}\right)}}\right\}\end{array}$$

The separation index, also known as Fukuyama and Sugeno index, is defined based on the difference between the compactness and the separation of fuzzy clusters:

$$\begin{array}{}\text{(6)}& \begin{array}{rl}{V}_{\mathrm{S}}& =\left\{{\sum }_{c=\mathrm{1}}^C{\sum }_{i=\mathrm{1}}^N{u}_{i,c}^{\mathrm{2}}.{\mathbf{d}}^{\mathrm{2}}\left([{\stackrel{\mathrm{‾}}{x}}_{i,j=\mathrm{1}:n},{\stackrel{\mathrm{‾}}{y}}_{i,j=\mathrm{1}:n}],v_{c,m=\mathrm{1}:\mathrm{2}n}\right)\right\}\\ & -\left\{{\sum }_{c=\mathrm{1}}^C{\sum }_{i=\mathrm{1}}^N{u}_{i,c}^{\mathrm{2}}.{\mathbf{d}}^{\mathrm{2}}\left([v_{c,m=\mathrm{1}:\mathrm{2}n},\stackrel{\mathrm{‾}}{v}\right)\right\},\end{array}\end{array}$$

in which $\stackrel{\mathrm{‾}}{v}={\sum }_{c=\mathrm{1}}^C{v}_i/c$. We identify the optimal number of clusters using the elbow method (see Satopaa et al., 2011; Kuentz et al., 2017), which involves finding the maximum number of clusters, beyond which slopes of improvement in validity indices flatten significantly, and adding a new cluster does not justify the increased complexity.

2.4 Detection of change in streamflow regimes

Clustering natural streams into c regime types takes place during a baseline timeframe (i.e., the first initial years with the length of l years), in which the optimal number of clusters, cluster centroids, and initial membership degrees to each regime type are identified. For each stream, the timeframe can be moved year-by-year, and the membership values can be recalculated for the new window using Eq. (3). Figure 2 exemplifies this process in a hypothetical case. This results in C time series of membership degrees at each stream, showing how the association to each regime type evolves in time – see Jaramillo and Nazemi (2018). In order to quantify the gradual change in membership degrees, the Mann–Kendall trend test with the Sen's slope is applied (Mann, 1945; Sen, 1968; Kendall, 1975). As the sum of memberships in each timeframe is 1 (see Eq. 2b), a positive trend in memberships to one cluster should coincide with a negative trend in the membership of at least one other cluster. At each stream, this transition can be identified by significant negative dependencies between membership degrees.

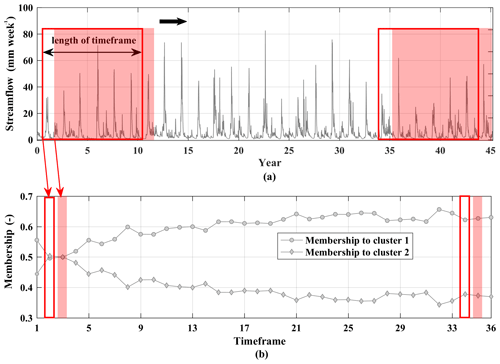
Figure 2 A schematic view to the procedure of identifying the evolution in membership values using a moving window: (a) a decadal timeframe slides over the streamflow time series year-by-year, and (b) membership degrees are recalculated at each decadal timeframe to systematically determine the changes in association to each regime type determined in the beginning of the data period.

Given the pair of clusters p and q in the stream i, the rate of shift from p to q can be quantified using Eq. (7), where u_i,p(w) and u_i,q(w) are membership degrees to clusters p and q in stream i during the timeframe w, $w\in \left\{\mathrm{1},\mathrm{\dots },r\right\}$, r is the number of moving timeframes needed to cover the whole data period year-by-year, E(u_i,p) and E(u_i,q) are the expected memberships, and $S_{i,(p,q)}$ is the slope of the best-fitted line.

$$\begin{array}{}\text{(7)}& S_{i,\left(p,q\right)}=\left|{\displaystyle \frac{\sum _{w=\mathrm{1}}^m\left(u_{i,q}\left(w\right)-\mathbf{E}\left(u_{i,q}\right)\right)\left(u_{i,p}\left(w\right)-\mathbf{E}\left(u_{i,p}\right)\right)}{\sum _{w=\mathrm{1}}^m{\left(u_{i,q}\left(w\right)-\mathbf{E}\left(u_{i,q}\right)\right)}^{\mathrm{2}}}}\right|\end{array}$$

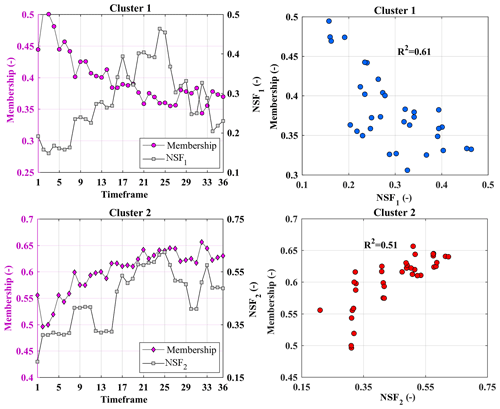
Figure 3 The procedure of attributing changes in membership degrees to changes in streamflow characteristics. The left column shows the co-evolution of membership degrees and normalized streamflow features (i.e., NSF₁ and NSF₂). The right column measures the correspondence between changes in membership degrees and normalized streamflow features through percentage of described variance quantified using R². Red and blue dots show the positive and negative dependencies, respectively.

2.5 Attribution of change in streamflow regime to alterations in streamflow characteristics

Here, the existence of significant dependence between membership values and streamflow features is taken as the basis for attribution. Accordingly, we use Kendall's tau (Genest and Favre, 2007; Nazemi and Elshorbagy, 2012) to detect the co-occurrence between changes in memberships and changes in NSFs. Figure 3 shows the procedure of attribution. Left panels show the changes in membership degrees of two hypothetical clusters (purple lines), along with the corresponding changes in two NSFs (grey lines). Right panels show the scatter plots of membership degrees vs. the NSFs. We identify the significance and the direction of dependence using Kendall's tau coefficient. To measure the linear association between changes in streamflow features x_i,j and membership values u_i,c, the coefficient of determination (R²; see Legates and McCabe, 1999) is used. R² varies between [0, 1] and determines how much of the variability in the degrees of membership can be described by the variability in a given streamflow characteristic. The greater the R² is, the stronger the association between changes in degrees of membership and the streamflow characteristics is. The coefficient of determination can be calculated as follows:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}& R^{\mathrm{2}}\left(u_{i,c},x_{i,j}\right)={\displaystyle \frac{{\left\{\sum _{w=\mathrm{1}}^r\left(u_{i,c}-\mathbf{E}\left(u_{i,c}\right)\right)\left(x_{i,j}-\mathbf{E}\left(x_{i,j}\right)\right)\right\}}^{\mathrm{2}}}{\sum _{w=\mathrm{1}}^r{\left(u_{i,c}-\mathbf{E}\left(u_{i,c}\right)\right)}^{\mathrm{2}}\sum _{w=\mathrm{1}}^r{\left(x_{i,j}-\mathbf{E}\left(x_{i,j}\right)\right)}^{\mathrm{2}}}}\\ & \forall i\in \left\{\mathrm{1},\mathrm{\dots },N\right\}.\end{array}\end{array}$$

By the simultaneous use of Kendall's tau and R², we try to facilitate quantitative communication of the impact of changes in a specific streamflow characteristic on the transition from one regime type to another. By using Kendall's tau, we identify the sign and significance of dependencies between changes in membership degrees and streamflow characteristics using a non-parametric approach that can handle nonlinearity in the form of association. Using R², we quantify how much of the variability in the membership degrees can be described by the variability in the changes in streamflow characteristics. This is to provide a comprehendible measure of association between the two quantities. As R² is a linear-based measure, we repeat the experiment by replacing the R² with squared Kendall's tau and discuss the uncertainty in our attribution. The key advantage of our proposed algorithm is in providing a workflow in which the detection of a change in streamflow regime is directly attributed to changes in streamflow characteristics. Figure 4 shows this integration using a hypothetical example. Figure 4a demonstrates a multifaceted change in the shape of the annual hydrograph in a given stream during two separate periods, shown with grey and pink envelopes. The black and red lines are expected annual hydrographs for each envelope (i.e., the mean of annual streamflow hydrographs over the timeframe). Any shift between flow regimes is described by at least a pair of membership time series with opposite trends. The strength of the link is measured using R². Figure 4b shows the rates of shifts and the attribution to changes in streamflow characteristics. The thickness of links is proportional to rates of shift and/or R² values.

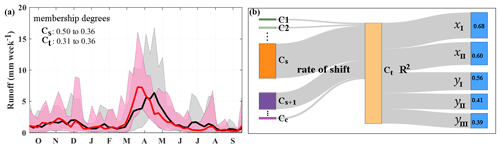
Figure 4 An example for transitions between regime types along with attribution of change to streamflow characteristics. Panel (a) shows annual hydrographs in two separate periods using grey and pink envelopes. Panel (b) shows the dominant shift in the flow regime by maximum rate of shift and attributes this shift to changes in significantly dependent streamflow characteristics. The dominant shift is visualized by the thickest grey envelope. The strength of the association between regime shift and significantly dependent streamflow characteristics are measured and communicated by R².

3 Case study and data

With a total drainage area equivalent to 6 % of the global land area, Canadian rivers support important socio-economic activities such as agriculture and hydropower production. River systems in Canada can be divided into four major ocean-drained basins, namely Pacific, Atlantic, Arctic, and Hudson Bay that can be further divided into a number of sub-basins (Pearse et al., 1985; Natural Resources Canada, 2007). The Pacific basin, the smallest among all, spreads along the west coast from the US border to Yukon and drains around 1 million km². The main sub-basins in the Pacific include Fraser, Yukon, Columbia, and the Seaboard. In the east coast, the Atlantic basin drains a total area of 1.6 million km² and includes important water bodies such as the Great Lakes. The basin includes three sub-basins, namely the St. Lawrence River, Seaboard, and the Saint John-St. Croix. Towards the north, the Arctic basin drains over 3.5 million km² of northern lands and includes some of Canada's largest lakes other than the Great Lakes such as the Slave, Athabasca, and Great Bear lakes. The Mackenzie, Peace–Athabasca, and Seaboard are the main sub-basins in the Arctic basin. With an area of 3.8 million km², Hudson Bay is the largest drainage basin in Canada, covering five provinces from Alberta in the west to Québec in the east. The basin includes four major sub-basins, namely Western and Northern Hudson Bay, Nelson, Northern Ontario, and Northern Québec. Nelson, Saskatchewan, and Churchill rivers are the major river systems in Hudson Bay.

Natural streamflow regimes in Canada have undergone drastic changes in recent years which are expected to increase under future climate change conditions (Woo et al., 2008). Observed and projected changes in streamflow regimes are not only between different regions (Kang et al., 2016; Islam et al., 2019), but they also occur within the same ecological and/or hydrological regions (Whitfield, 2001; Whitfield et al., 2020). For instance, there are significant differences among forms of change in streamflow regimes between the northern and southern Pacific (Kang et al., 2016; Brahney et al., 2017). Similarly, glacier-fed rivers in northern Canada show increases in summer runoff (Fleming and Clarke, 2003), whereas other rivers show a tendency toward decreasing summer runoff (Fleming and Clarke, 2003; Janowicz, 2008, 2011). To diagnose simultaneous changes in natural streamflow regimes across Canada, we use the data from the Reference Hydrometric Basin Network (RHBN; Water Survey of Canada, 2017, http://www.wsc.ec.gc.ca/, last access: August 2020). RHBN includes 782 Canadian hydrometric stations that measure streamflow at unregulated tributaries and are particularly suitable to address climate change impacts on natural streamflow regimes (Brimley et al., 1999; Harvey et al., 1999). In the period of 1903 to 2015, we search for the largest subset of hydrologically unconnected stations with the longest continuous daily record during a common period and less than a month worth of missing data in a typical year. This results in selecting 105 streamflow stations during the water years of 1966 to 2010 (1 October 1965 to 30 September 2010).

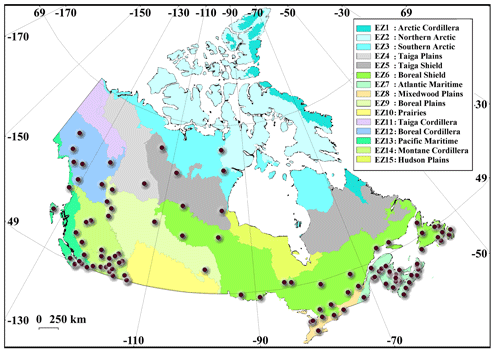
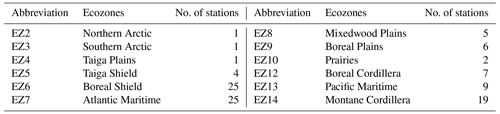
Although drainage basins are often used as the spatial unit in which alteration in streamflow regimes is investigated, there are substantial differences within a drainage basin in terms of climate, topography, vegetation, geology, and land use. This results into multiple forms of hydrological responses within one drainage basin. In contrast to drainage basins, terrestrial ecozones are identified based on similarity in climate and land characteristics, and therefore, they can be more representative of different hydrological responses (Whitfield, 2001). In brief, an ecozone is a patch of land with distinct climatic, ecologic, and aquatic characteristics (see Wiken, 1986; Marshall et al., 1999; Wong et al., 2017). Canada includes 15 ecozones. Starting from the north, the Arctic Cordillera (EZ1), covering 2 % of Canada's landmass, contains the only major mountainous region in Canada other than the Rockies. The Northern Arctic (EZ2) is equivalent to 14 % of Canada's landmass and covers Arctic islands (Coops et al., 2008). The Southern Arctic (EZ3) includes the northern mainland, covering 8 % of Canada. The Taiga Plains (EZ4) extends mainly on the western side of the Northwest Territories, covers 6 % of Canada's landmass, and includes a large number of wetlands. Taiga Shield (EZ5), with a large number of lakes, covers 13 % of Canada's landmass in the south of the southern Arctic (Marshall et al., 1999). The Boreal Shield (EZ6) is Canada's largest ecozone covering 18 % of the country's landmass, extending from northern Saskatchewan toward the south into Ontario and Québec and then northward toward eastern Newfoundland (Rowe and Sheard, 1981). The Atlantic Maritime (EZ7) includes the Appalachian mountain region, covering 2 % of Canada and extending from the mouth of the St. Lawrence River and Bay of Fundy to coastlines of New Brunswick, Nova Scotia, and Prince Edward Island. The Mixedwood Plains (EZ8) is the most southerly ecozone, covering 2 % of Canada, but includes the country's most populated regions in Ontario and Québec. The Boreal Plains (EZ9) covers 7 % of Canada's landmass in western Canada, from British Columbia to the southeastern corner of Manitoba in the south of the Boreal Shield (Ireson et al., 2015). The Prairies (EZ10) extend from south-central Alberta to southeastern Manitoba, covering 5 % of Canada's landmass and the majority of Canada's agricultural lands (Nazemi et al., 2017). The Taiga Cordillera (EZ11) includes 3 % of Canada with the least amount of Canada's forest and lies along the northern portion of the Rocky Mountains (Power and Gillis, 2006). The Boreal Cordillera (EZ12) covers 5 % of Canada from northern British Columbia to the southern Yukon, with mountainous uplands and forested lowlands. The Pacific Maritime (EZ13) mainly includes the coastal mountains of British Columbia and lands adjacent to the Pacific coast, having the warmest and wettest climate in the country, in an area around 2 % of Canada (Wiken, 1986). The Montane Cordillera (EZ14), with the most diverse climate in Canada, includes 5 % of Canada in mountainous areas of southern British Columbia and southwestern Alberta and provides headwater flow to some important river systems such as Fraser, Saskatchewan, and Athabasca (Marshall et al., 1999). Finally, Hudson Plains (EZ15) includes 4 % of Canada in the southern part of Hudson Bay with a large number of wetlands. Table 2 summarizes the selected stations within each ecozone.

Table 2 List of Canadian ecozones with at least one RHBN station in this study, along with their abbreviations and the number of RHBN stations considered within each ecozone.

Tables S1 to S4 in the Supplement introduce these stations across the four drainage basins in Canada. Figure 5 shows the distribution of the selected stations across the 15 ecozones. As is clear, the density of selected stations varies greatly among ecozones. The highest numbers of stations are within Atlantic Maritime, Boreal Shield, and Montane Cordillera, while the southern and northern Arctic, as well as Taiga Plains, include only one; and there is no station in the Arctic Cordillera, Taiga Cordillera, and Hudson Plains. At the basin/sub-basin scale, the selected stations cover all 14 main Canadian sub-basins – see Table S5 and Fig. S1 in the Supplement.

Figure 5 The distribution of the selected 105 RHBN streamflow stations within the Canadian ecozones.

4 Results

We apply the framework proposed in Sect. 2 to the selected RHBN streams. At each stream, we first convert the daily discharge data into runoff depth in millimetres per week and calculate the thirty streamflow features introduced in Table 1. We then consider a multi-year timeframe for clustering and assigning initial membership values. The length of this timeframe should be chosen in a way that (1) provides a notion for streamflow regime and (2) provides enough timeframes to assess evolution in membership values. As the aim is to address temporal changes in the streamflow regime, the baseline timeframe is considered at the beginning of the streamflow time series. Here, we present our result based on considering decadal timeframes and the period of 1966 to 1975 as the baseline. We address and discuss the sensitivity of our results to these assumptions in Sect. 5.

4.1 Identifying natural streamflow regimes in Canada

We attempt to find the optimal number of clusters empirically from the pool of $c=\mathit{\{}\mathrm{2},\mathrm{3},\mathrm{\dots },\mathrm{10}\mathit{\}}$, using the three validity indices introduced in Sect. 2.3. Figure S2 in the Supplement shows the result of this investigation, indicating the optimal number of clusters as c=6, in which decreasing slopes of the three validity indices flatten. To provide a sense of these streamflow regimes and their changes in time, we visualize the shapes of annual streamflow hydrographs in the archetype streams during the baseline and the last decadal timeframe (i.e., 1966 to 1975 vs. 2001 to 2010) in Fig. S3 in the Supplement. Archetype streams are those streams that have the highest association with the identified regime types and can represent the characteristics of a given regime better than other members of the cluster. Table 3 introduces these six regimes along with their notation and archetype streams. We name clusters based on two key characteristics, i.e., the form of hydrologic response (i.e., fast vs. slow response) and the timing of the annual peak flow (i.e., cold-season, freshet, and warm-season peaks). The form of hydrologic response can be proxied by variability in the annual streamflow hydrograph. The greater the variability in the annual streamflow hydrograph is, the faster the hydrologic response is.

Table 3 Six identified regime clusters along with their labelled regime type and archetype stream.

Figure 6 shows a synoptic look at the distribution of streams belonging to each flow regime during the initial baseline timeframe. In each panel, the red star represents the archetype stream, and streams with membership values of 0.1 and larger are shown with circles. The larger the size of a circle is, the greater the degree of membership to each cluster is. As Fig. 5 shows, the six clusters are geographically identifiable and resemble some of the already-known regime types across the country (see Whitfield, 2001; Bawden et al., 2015; Burn and Whitfield, 2016; Bush and Lemmen, 2019).

The “slow-response/warm-season peak” regime, i.e., cluster C1, includes streams with strong seasonality, high discharge in summer, and smaller variability in annual streamflow hydrograph compared to cluster C2, i.e., the “fast-response/warm-season peak” regime. Cluster C1 is characterized by a gradual rise after spring snowmelt, prolonged peak discharge throughout summer, gradual recession during fall, and low runoff in winter (Déry et al., 2009). Streams belonging to C1 spread mostly in northwestern Canada and are either glacial-fed or lake-dominated streams, in which the hydrologic responses are delayed due to the slow rate of glacial retreats and/or storage effects of large in-stream lakes. The Kazan River releasing into Baker Lake in Nunavut is the archetype stream for this regime type. C2 is very similar to C1, however with greater variability in annual streamflow hydrographs. The streams belonging to this stream type are mainly concentrated in western Canada, particularly in the Montane Cordillera (46 % of streams), and include streams that are fed mainly through snow and glacial melts (Eaton and Moore, 2010; Moore et al., 2012; Schnorbus et al., 2014). There are, however, streams belonging to C2 that are located in the Boreal Shield (23 % of streams), where the streamflow generation is governed by other processes such as fill-and-spill in which segments of a basin have to be filled above their capacity before spillage (Spence and Phillips, 2015). The Clearwater River near Clearwater in southern Alberta is the representative stream for this regime type.

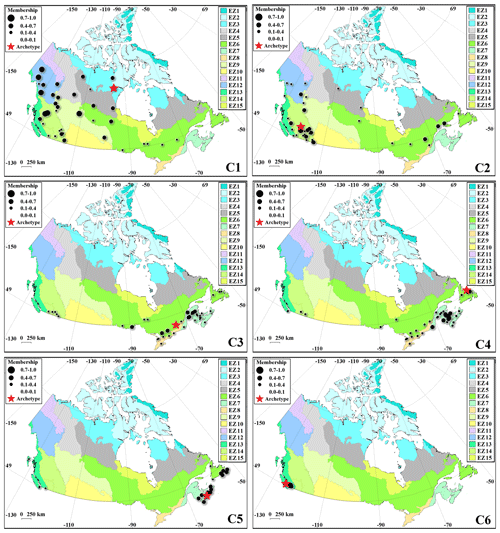
Figure 6 The distribution of the identified regime types across Canadian ecozones during the baseline l timeframe of 1966 to 1975. Each stream is represented by a circle with a radius proportional to a membership degree quantifying the association to a given regime type. Only RHBN stations with degrees of membership of 0.1 or larger are shown in each panel. The red stars are the archetype stations related to each regime type.

The cluster C3, i.e., the “slow-response/freshet peak” regime, includes streams in which the annual streamflow volume is mainly contributed by a short high-flow period during spring snowmelt, sharp recession in summer, yet relatively smaller variations in the shape of hydrograph compared to the cluster C4, i.e., “fast-response/freshet peak” regime. Nearly 45 % of the streams with this regime type are located in Atlantic Maritime. The rest are distributed in the Boreal Shield (28 %), Mixedwood Plains (15 %), and Montane Cordillera (12 %). The Matawin River originating from lake Matawin in Québec is the archetype for the C3 regime. The streams belonging to C4 are also dominated by spring snowmelt but showing more variation in the shape of annual hydrographs compared to the C3 regime. Streams belonging to the C4 regime often have two distinct peaks, one in spring induced by snowmelt and one in fall due to high precipitation, and from that sense, they largely resemble nival–pluvial streams (Hock et al., 2005). Almost all streams belonging to the C4 regime are located in eastern Canada (50 % in Atlantic Maritime, 26 % in the Boreal Shield, 16 % in Mixedwood Plains). Gander River at Partridgeberry Hill in Newfoundland is the archetype for this regime.

The cluster C5, i.e., “slow-response/cold-season peak” regime, comprises streams with weak seasonality and slightly more discharge in fall and winter. The annual flow for streams belonging to this regime is more influenced by rainfall around late fall, followed by a slight increase in discharge due to snowmelt; therefore, they resemble a hybrid pluvial–nival regime (Kang et al., 2016). The concentration of streams belonging to this regime is again in eastern Canada (48 % in Atlantic Maritime; 33 % in the Boreal Shield), with a few streams being in the Pacific Maritime. Beaver Bank River in Nova Scotia is the representative stream for this regime type. Finally, the cluster C6, i.e., “fast-response/cold season peak regime, is similar to the C5 regime and exhibits a weak seasonality but with a greater variation in shapes of annual hydrographs. The runoff in streams belonging to this regime is dominated by heavy precipitation, especially during winter, and lower runoff during summer, resembling the pluvial regime (Wade et al., 2001; Whitfield, 2001). Streams belonging to this regime are only concentrated in the Pacific. The Sproat River near Alberni is the archetype stream of the C6 cluster.

4.2 Detection of changing streamflow regimes

To understand temporal shifts in streamflow regimes throughout selected RHBN streams, we calculate the decadal membership values as shown in Fig. 2. We accordingly apply the Mann–Kendall trend test with the Sen's Slope on the time series of decadal memberships. The detailed results including the membership time series for all streams and corresponding trend analyses are shown in Figs. S4 and S5 in the Supplement over major drainage basins/sub-basins and the terrestrial ecozones in Canada, respectively. Figure 7 summarizes our findings over the 15 Canadian ecozones. The colour (blue vs. red) and the size (large vs. small) of triangles show decreasing vs. increasing trends, as well as significant vs. insignificant trends at p value ≤0.05. Although inconsistent patterns of change are observed in the Boreal and Montane cordilleras, particularly between the southern and northern regions, there are clear downward trends in the member of regime C1 in the Taiga Shield and Boreal Shield. Upward trends are observed in membership values of C2 in the Boreal Cordillera and Taiga Shield, while downward trends are seen in the member of C2 in southern and eastern parts of the Montane Cordillera and Boreal Shield. The C3 regime shows intensification in the Montane Cordillera and Boreal Shield. It also intensifies in southern parts of Atlantic Maritime but weakens in northern regions. The pattern of change in C4 is very similar to C3 but with fewer significant downward trends in northern parts of Atlantic Maritime. Considering the C5 regime, streams mainly show decreasing trends in the Appalachian region including the eastern Boreal Shield and southern parts of Atlantic Maritime. Mixed patterns of change in membership degree are observed in the Pacific Maritime for both C5 and C6 regimes.

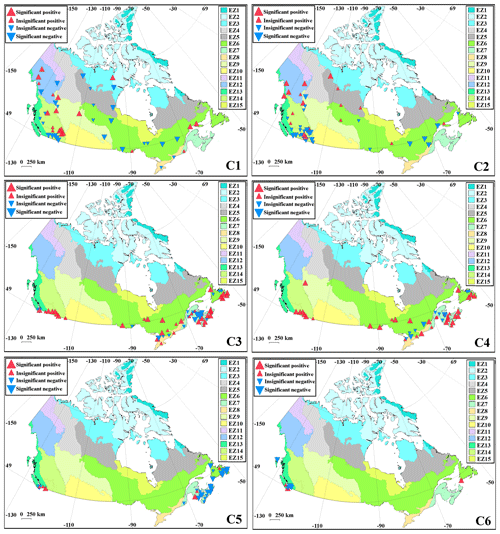
Figure 7 Trends in decadal memberships, quantifying the change in association of the 105 selected RHBN streams to the six regime types during 1966 to 2010.

The nature of regime shifts at each stream can be investigated by quantifying the rate of relative shift between opposing significant trends. Figure S6 in the Supplement summarizes the results. Overall, the dominant modes of transition at the ecozone scale are from C1 to C2 in the northern ecozones (EZ5 and EZ12), from C2 to C1 and from C2 to C3 in the western ecozones (EZ9 and EZ14), from C2 to C3 at the two stations located in the Prairies, from C1 to C3 in the eastern ecozones (EZ6, EZ8, and EZ15), and from C5 to C4 in the Appalachian region (EZ7 and eastern part of EZ6). The variability between the regime shifts inside each ecozone can be described by elevation. To better synthesize our findings in Canada and highlight dominant regime shifts and their geographic extent across the country, Fig. 8 shows Sankey diagrams demonstrating the initial regime types in the considered streams. Streams are grouped by the ecozones on the left side of each panel and transform to one particular target regime type (right side of each panel). The six natural regime types are distinguished by colour codes, and stations within each ecozone are sorted from the lowest to the highest elevation from top to the bottom. The width of each arrow is proportional to the rates of shift, calculated using Eq. (7). The highest rate of a shift in each stream and/or ecozone can be considered as the dominant regime shift.

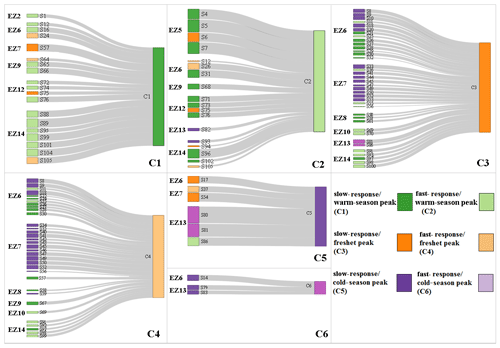
Figure 8 Sankey diagrams showing transitions in Canadian natural streamflow regimes described across ecozones from 1966 to 2010. Each panel presents the transformation from five potential regime types to one particular target regime. Streams in the left side are grouped according to ecozones and are sorted from the lowest to highest elevations from the top to the bottom. Colours show the six regime types. The widths of arrows are proportional to the rate of shift.

Some important findings can be made from Fig. 8. While regime shifts are varied, there are some dominant regime shifts that are frequently observed across different ecozones. For example, frequent shifts are observed from C2 to C1, as well as C1 to C2, that are quite strong across the Montane Cordillera and Taiga Shield, respectively. Second, it is possible that the streamflow regime in a given ecozone shifts from one regime to two or more regime types. For instance, streamflow in Atlantic Maritime shifts from C5 to C3 and C4. Also, it is possible to have opposing regime shifts in a given ecozone. As an example, the flow regime varies from C5 to C6 and vice versa across Pacific Maritime. Such variabilities in regime shift can be partially explained by latitude. More generally, it is possible to shift from two or more regime types into one or more regime types across a particular ecozone. For example, streams with C1 and C5 regimes are shifting to C3 and C4 across the Boreal Shield. Such variabilities within an ecozone can be described in many cases by elevation. In the Boreal Shield, for example, elevation controls the constitution of the initial streamflow regime from C5 in lowlands to C1 in highlands. Finally, the most frequent regime shifts are not necessarily the strongest ones. For instance, the streamflow regime shifts across six ecozones toward C3 and C4, but the rates of the shift are not strong when compared with the shift between C6 to C5 that happens in limited streams in Pacific Maritime, but quite strong.

4.3 Identifying forms of transformation in streamflow regimes

The procedure presented in Sect. 2.5 attributes regime shifts to changes in streamflow characteristics using dependence analysis. Figure 9 summarizes the results of attribution for the 105 RHBN stations. Streams are shown in rows, grouped in each ecozone, and ordered from low to high elevations from the top to the bottom. For each stream, there are three groups of cells, with 15, 15, and 2 cells from left to right. The first two groups of cells are related to the values of mean (i.e., x₁ to x₁₅) and variance (i.e., y₁ to y₁₅) of the 15 considered IHAs. In these two groups of cells, shades of blue and red show negative and positive dependencies between a given pair of streamflow characteristic and membership degree, respectively. Note that we only identify those streamflow characteristics that have significant dependencies with variations in membership degrees based on Kendall's tau (p value ≤0.05) Colour saturations show the values for the coefficient of determination, quantifying the fraction of variability in membership degrees that are described by the variability in streamflow characteristics. The last two cells are related to the dominant regime shift in each stream from one initial regime (left hand cell) to an altered regime (right hand cell). The colour scheme, defining the regime types, is shown in the legend. The analyses over basin and sub-basin scales are presented in Figs. S7 and S8 in the Supplement.

The most important observation is the fact that in more than 80 % the considered natural streams, there are some identifiable regime shifts that are significantly dependent on the changes in the streamflow characteristics. Some dominant regime shifts are frequent within an ecozone, while some are less frequent and may depend on latitude and/or elevation. In the only considered stream in the Northern Arctic Ecozone, the shift from the C2 to the C1 regime is attributed to the earlier and more variable timing of the annual low flow, as well as the increasing June flow. An opposing shift is observed in Taiga Shield, i.e., from C1 to C2, which can be attributed to the earlier and more variable timing of annual high flow, as well as the increasing seasonal flow in fall. The regime shift from C5 to C4 in the lowlands of the Boreal Shield is attributed to the decreasing mean of and variance in annual flow particularly in August. In the highland of this ecozone, however, the dominant regime shift is from C1 to C3 and can be attributed to the decreasing monthly flow in August and September, as well as more variability in the timing of the annual low flow. In Atlantic Maritime, particularly across lowlands, decreasing mean of and variation in the flow in August along with decreasing monthly flow in June and July, as well as decreasing mean annual and seasonal flow in the fall, lead to a shift from C5 to C4.

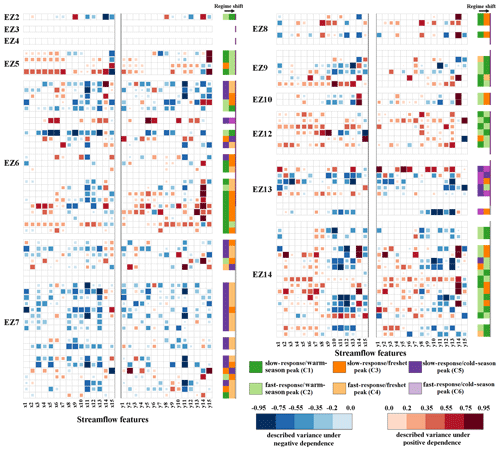
Figure 9 Dominant regime shifts across 105 RHBN streams in Canada attributed to the first and second moments of the 15 IHAs considered. Shades of red and blue show the positive and negative dependencies between changes in streamflow features and degrees of membership. Colour saturations are proportional to the values of the coefficient of determination. The dominant regime shift at each stream is identified by the colour scheme described in the legend. Streams are grouped in ecozones and ordered from low (top) to high (bottom) elevations.

In Mixedwood Plains, the shift from C1 to C3 is attributed mainly to the earlier and more variable timing of annual low flow. In the lowlands of Boreal Plains, the increasing variation in April's flow and decreasing annual and summer flows contribute to the shift from C2 to C1. Streams in the highlands of Boreal Plains, however, shift from C1 to C2 due to the increasing annual and summer flows, along with the later and more variable timing of low flows. In the Prairies, in the two considered streams, the shift from C2 to C3 is attributed to the delayed and more variable timing of low flows and decreasing summer flows. In the Boreal Cordillera, more variable annual flow and increasing mean of and variation in May flow correspond to the shift from C1 to C2. Opposing shifts from C2 to C1, however, are mainly attributed to the increasing monthly flows in February, March, April, and May. The most pronounced shift in Pacific Maritime is from C5 to C6, which mainly corresponds to increasing mean of and variation in October flow, as well as increasing annual flows. The most pronounced shift in the Montane Cordillera is from C2 to C1 for the streams in the northern part, attributed to decreasing mean of and variability in July flow and increasing monthly flow in April and May. Streams in southern parts, however, shift from C2 to C3, attributed mainly to increasing monthly flow in February, March, and April, more variability in the timing of the low flow, and decreasing September flow.

5 Discussion

The application of the proposed methodology in Canada identifies six distinct natural regimes across the country, address their change in time and space, attribute dominant regime shifts to changes in a range of streamflow characteristics at each stream, and accordingly upscale the findings from individual streams to ecozones. Having said that, still there are some unanswered questions. First, it is still unclear how robust our proposed algorithm is particularly in light of the assumptions made with respect to the length of the timeframes and/or selecting the baseline period. Second, it is obvious that our selected streams are only a sample of available RHBN stations across Canada, and it is still unclear how our findings can be extended to out-of-sample streams. Finally, there is a large body of literature reporting shifts in streamflow regimes across different regions in Canada due to changes in temperature patterns, magnitude and form of precipitation, and snowmelt and snow accumulation, as well as glacier retreat and permafrost degradation. Accordingly, it is crucial to frame and position our findings with respect to earlier studies. These three tasks are pursued in this section.

5.1 Addressing uncertainty

The results presented in Sect. 4 are based on decadal timeframes and the selection of the first decadal timeframe as the baseline period. Here we relax these two assumptions and monitor alterations in our findings. First, we repeat the clustering algorithm over all possible decadal timeframes throughout the study period and recalculate the cluster centers. This experiment addresses the sensitivity of our clustering algorithms to the choice of baseline period. Second, we repeat the approach implemented in Sect. 4 again with 15- and 20-year timeframes and address how cluster centers, as well as our specific findings, would be altered by increasing the length of timeframe. We do not consider timeframes less than decadal length due to the insufficiency of numbers of data points for trend analysis. We also do not consider timeframes larger than 20 years to allow there to be at least two fully independent timeframes during the study period with a gap of a few years. Figure 10 summarizes our findings in terms of the sensitivity of our clustering results with respect to the two assumptions made. Panel (a) shows the cluster centers when different decadal baselines are considered. Coloured dots show the centers of clusters related to all possible decadal timeframes except the period of 1966 to 1975. The centers of clusters are scaled into two dimensions using multidimensional scaling (MDS; Cox and Cox, 2008), in which the distance between the dots represents the approximate dissimilarity of centers of clusters. Dimensions 1 and 2 delineate the space in which the original data are mapped. Black crosses show the centers of the first decadal timeframe mapped using MDS. Colours identify regime types. The result clearly shows that despite changing the baseline timeframe, the distinctions between cluster centers are maintained, and the position of centers does not substantially change by changing the baseline period. Panel (b) shows the results of our sensitivity analysis with respect to changing the length of timeframe. Again, there are not notable changes in the cluster centers. These two findings highlight the robustness of our clustering analysis.

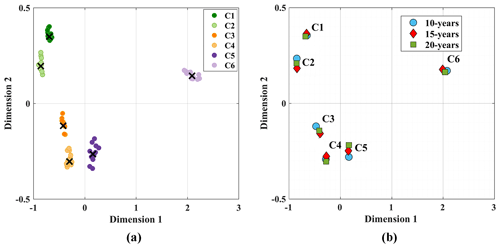
Figure 10 The sensitivity of the cluster centers to (a) the choice of decadal timeframe for clustering and (b) the length of the timeframe used for analysis. In panel (a) dots show the two-dimensional scaling of the cluster centers in which distances between dots represent dissimilarities between cluster centers. Black crosses show the centers identified by choosing the first decadal timeframe. Panel (b) shows the two-dimensional scaling of the cluster centers considering 10-, 15-, and 20-year timeframes.

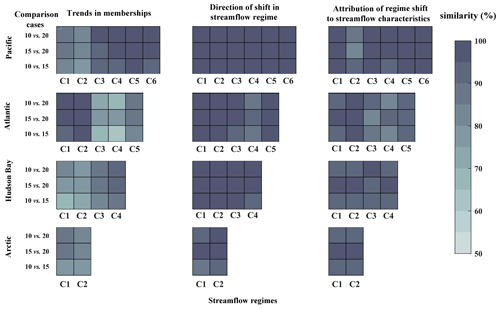
We also look at possible differences in the direction of trends in membership degrees, dominant regime shifts, and the attribution to streamflow features at the basin scale if the length of timeframes are changed. Figure 11 (left column) intercompares the results obtained by 10-, 15-, and 20-year timeframes in terms of percentages of similarities in the direction of trends during 1966 to 2010 at each basin. In brief, there is at least 80 % agreement between the results obtained in the Pacific and the Arctic basins. There are more discrepancies in the direction of trends in the Atlantic and Hudson Bay basins. This is particularly the case for the C1 regime in Hudson Bay and for the C3 and C4 regimes in the Atlantic, for which the results are less consistent among different timeframes; yet, in the worst-case scenario (i.e., the C4 regime in Atlantic), there is still more than 60 % agreement between the results of trend analysis obtained by 10-, 15-, and 20-year timeframes.

Dominant regime shifts are also performed with 15- and 20-year timeframes and are intercompared with corresponding results obtained by decadal timeframes. Our analysis shows that results obtained by 15- and 20-year timeframes are in agreement with the results obtained using decadal timeframes. Even for the case with the largest discrepancy (i.e., C4 regime in the Atlantic), there is 86 % agreement in terms of the direction of shift in streamflow regimes, obtained by 10- and 20-year timeframes. In terms of attribution of regime shifts to changes in streamflow characteristics, again the results obtained by different lengths are in large agreement in at least 80 % of streams.

Finally to investigate the sensitivity of attribution to the choice of measure, we substitute R² with squared Kendall's tau and repeat the experiment. The result of this experiment is summarized in Fig. S9 in the Supplement. Comparing Fig. S9 with Fig. 9 shows that in general the selected streamflow characteristics are similar with no remarkable changes in the degrees of attribution that influence our general findings. The most sensitive ecozones to the choice of measure of association are EZ5 and EZ14, demonstrating the greater values of association measured by the squared Kendall's tau. This is due to the higher degree of nonlinearity between regime shifts and alterations in streamflow characteristics in these ecozones.

Figure 11 Similarities (in percentage) between the results obtained by 10-, 15-, and 20-year timeframes related to trends in membership values, direction of shift in streamflow regimes, and attribution to streamflow characteristics in the four major Canadian basins.

5.2 Validation in out-of-sample streams

One important question remaining unanswered is how the six regime types identified can be extended into out-of-sample streams. Here we investigate this in the Prairies ecozone, a region with importance for global food security. Natural streams in the Prairies have been relatively overlooked in the literature (Whitfield et al., 2020) because often the streams do not have continuous streamflow records partially due to the fact that many streams are seasonal. In addition, the majority of annual streamflow volume is contributed from mountainous headwaters outside of the Prairies, and the fact is that at many basins a large proportion of the land does not normally contribute to the streamflow (Spence et al., 2010; Shook et al., 2015; Mekonnen et al., 2015). In addition, only two stations in the Prairies meet our data criteria in Sect. 3. Here, we reduce the length of data and investigate for new streams that satisfy our data criteria during 1976 to 2010. This has resulted in the selection of nine new stations – see Fig. 12 for the location of these stations (P1 to P9). The detailed information about these stations are provided in Table S6 in the Supplement. Here we investigate how these new stations fit into previously identified regime types, check the trends in the membership degrees, and identify dominant regime shifts in these streams. We compare our findings for the nine new stations with the two previously selected stations in the Prairie region, namely, Waterton River near Waterton Park (S69; 05AD003) and Belly River near Mountain View (S70; 05AD005) during the common period of 1976 to 2010 for which the nine new stations are selected. The right panel shows the analysis of trends in anomalies of decadal memberships, in which stations are ordered from the east to west from the top to the bottom. The analysis of trends in membership degrees shows mainly decreasing trends for C1 and C2 regimes and increasing trends for C5 and C6 regimes. Regarding C3 and C4 regimes, mainly upward trends are observed in the east, whereas downward trends are observed in the west. These findings are in line with our results in S69 and S70. The two columns at the right side of right panel are related to the dominant regime shift in each stream. The legend identifies the six identified regime types. Although the regime shifts are vibrant, the dominant regime shift observed is from C2 to C5, which is the same in S69 and S70 during the period of 1976 to 2010.

5.3 Summary of findings and positioning against earlier studies

Although to the best of our knowledge our work is the first study in which a systematic algorithm is used to provide a temporally homogeneous view on recent changes in pan-Canadian streamflow regime, the literature of Canadian hydrology is rich in terms of documenting changes in streamflow characteristics across the country. Thanks to the pioneering work of so many hydrologists before us, including the late iconic northern hydrologist, Richard Janowicz, to whom this paper is dedicated. Here we attempt to position our results with respect to earlier studies. Table 4 summarizes our findings in terms of dominant regime shifts and associated changes in streamflow characteristics at the sub-basin scale.

Table 4 Positioning our findings with respect to earlier studies across major Canadian basins and sub-basins.

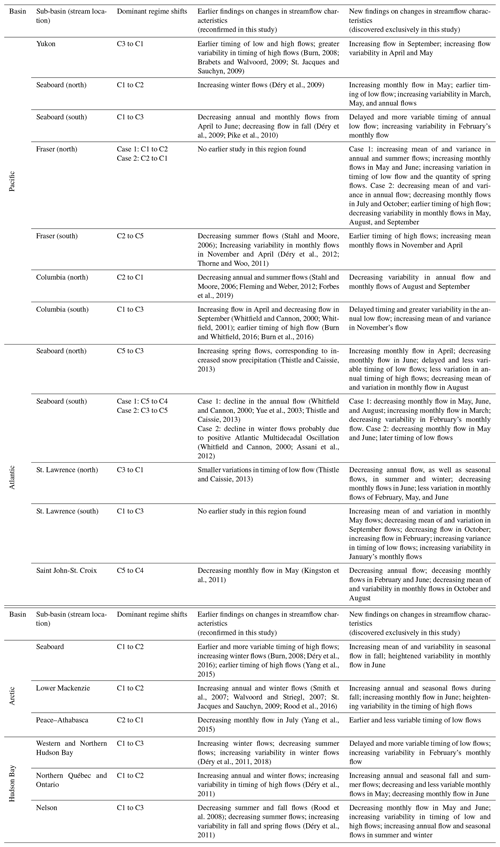
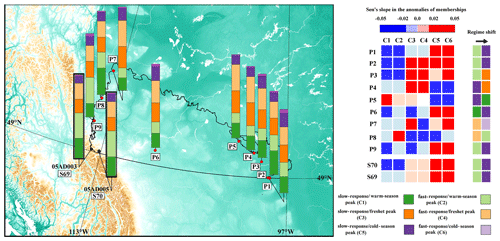
Figure 12 Validation of the proposed algorithm in nine out-of-sample streams during 1976 to 2010 in the Canadian Prairies. The colour bars in the left map show the degrees of membership to each cluster. The right panel shows the trends in the degree of membership in the six clusters at the 11 stations considered. Positive and negative trends are shown with red and blue colours, respectively. Sharp colours show significant cases. The out-of-sample stations S1 to S9 are sorted from east to west from the top to the bottom.

Table 4 makes a clear distinction between the earlier findings and those exclusively found in our study. Even though earlier studies have different data periods and may include streams that are not within the RHBN streams, our study reconfirms previous findings and also discovers new changes in streamflow characteristics that have remained previously overlooked. Our study clearly shows that changes in variability in monthly, seasonal, and annual flows can be important drivers of shifts in streamflow regimes across the majority of sub-basins in Canada. This is another line of evidence for the complex and multifaceted nature of change in streamflow regimes and the need for a simultaneous look at alterations in both expected values and variability in streamflow characteristics to diagnose changes in natural streamflow regimes.

6 Concluding remarks and outlook

This study presents an attempt toward providing a globally relevant algorithm for identifying changing streamflow regimes. The proposed approach is based on two fundamental considerations. First, a streamflow regime is collectively formed by a large number of streamflow characteristics. Second, streamflow types are rather in the form of spectrums, not clear-cut states; if regime shifts are caused by climate change, the transition from one regime type to another should be gradual rather than abrupt. To accommodate these two considerations, we suggest representing streamflow regime types as intersecting fuzzy sets in such a way that the belongingness of each stream to each regime type can be quantified by a membership function. Accordingly, monitoring the trends in membership values in time and space can provide a basis to identify the regime shift from one type to another. We consider the existence of a significant trend in membership values as evidence for the regime shift. In addition, analyzing the covariance of membership values with streamflow characteristics can provide a basis to attribute regime shifts to alterations in certain streamflow characteristics in time and/or space. A significant dependence between a given regime shift and simultaneous alterations in streamflow characteristics highlights attribution, which can be communicated by R².

To apply this algorithm, we consider 45 years of daily data from 105 RHBN streamflow gauges across Canada to provide a comprehensive and temporally homogeneous look at forms and extents of change in natural streamflow regime in Canada, from coast to coast to coast. Our results show that streamflow regimes in Canada can be categorized into six distinct regime types with clear physical and geographical interpretations. Analyses of trends in membership values show that alterations in natural streamflow regimes are vibrant and can be different across different regions. Overall, in more than 80 % of the considered streams there is a dominant regime shift that can be attributed to changes in streamflow characteristics. At the ecozone scale, the dominant regime shifts are from C1 to C2 in the northern ecozones (EZ5 and EZ12), from C2 to C1 and from C2 to C3 in the western ecozones (EZ9 and EZ14), from C2 to C3 at the two stations located in the Prairies, from C1 to C3 in the eastern ecozones (EZ6, EZ8, and EZ15), and from C5 to C4 in the Appalachian region (EZ7 and eastern part of EZ6). The variability between the regime shifts inside each ecozone can be described by elevation and/or latitude. At the basin scale, dominant modes of transition are from C3 to C1 in the northern Pacific and from C1 to C3 in the southern Pacific, between the C4 and C5 regimes, as well as C3 and C5, in the Atlantic, between C1 and C2 in the Arctic, and between the C1 and C3, as well as C2 and C3, regimes in Hudson Bay. The details of change in streamflow regime, however, are subject to a spatial variability within each drainage basin. In the Atlantic and Pacific regions, there are clear divides between dominant regime shifts in northern and southern regions. For instance, In the Pacific, the association to C1 is increasing in Yukon and northern parts of the Columbia and Fraser sub-basins, but it is significantly decreasing in the southern regions. This can be due to different manifestations of climate change, which are more apparent as temperature increases in the north and growing ratios of rain over precipitation in the south, shifting the streamflow more toward rain-dominated regimes (Fleming and Clarke, 2003). This reconfirms the important role of latitude in driving the streamflow response to climate change.

The proposed framework provides an opportunity to identify the changing streamflow regimes and attributes such changes to a large set of streamflow characteristics. This approach, however, does not explore the attribution of the shifts in streamflow regimes to the changes in temperature pattern, form and magnitude of precipitation, snowmelt, glacial retreat, and permafrost degradation. These can be potential areas for future research. We hope our study triggers more attention to the multifaceted nature of change in streamflow regimes in Canada and the rest of the world during the current Anthropocene.