the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Information-based uncertainty decomposition in dual-channel microwave remote sensing of soil moisture
Stephen P. Good
The National Aeronautics and Space Administration (NASA) Soil Moisture Active-Passive (SMAP) mission characterizes global spatiotemporal patterns in surface soil moisture using dual L-band microwave retrievals of horizontal (TBh) and vertical (TBv) polarized microwave brightness temperatures through a modeled mechanistic relationship between vegetation opacity, surface scattering albedo, and soil effective temperature (Teff). Although this model has been validated against in situ soil moisture, there is a lack of systematic characterization of where and why SMAP estimates deviate from the in situ observations. Here, we assess how the information content of in situ soil moisture observations from the US Climate Reference Network contrasts with (1) the information contained within raw SMAP observations (i.e., “informational random uncertainty”) derived from TBh, TBv, and Teff themselves and with (2) the information contained in SMAP's dual-channel algorithm (DCA) soil moisture estimates (i.e., “informational model uncertainty”) derived from the model's inherent structure and parameterizations. The results show that, on average, 80 % of the information in the in situ soil moisture is unexplained by SMAP DCA soil moisture estimates. Loss of information in the DCA modeling process contributes 35 % of the unexplained information, while the remainder is induced by a lack of additional explanatory power within TBh, TBv, and Teff. Overall, retrieval quality of SMAP DCA soil moisture, denoted as the Pearson correlation coefficient between SMAP DCA soil moisture and in situ soil moisture, is negatively correlated with the informational uncertainties, with slight differences across different land covers. The informational model uncertainty (Pearson correlation of −0.59) was found to be more influential than the informational random uncertainty (Pearson correlation of −0.34), suggesting that the poor performance of SMAP DCA at some locations is driven by model parameterization and/or structure and not underlying satellite measurements of TBh and TBv. A decomposition of mutual information between TBh, TBv, and DCA soil moisture shows that on average 58 % of information provided by TBh and TBv to DCA estimates is redundant. The amount of information redundantly and synergistically provided by TBh and TBv was found to be closely related (Pearson correlations of 0.79 and −0.82, respectively) to the retrieval quality of SMAP DCA. TBh and TBv tend to contribute large redundant information to DCA estimates under surfaces or conditions where DCA makes better retrievals. This study provides a baseline approach that can also be applied to evaluate other remote sensing models and understand informational loss as satellite retrievals are translated to end-user products.
- Article
(4164 KB) - Full-text XML
-
Supplement
(121 KB) - BibTeX
- EndNote
Accurate information on soil moisture is of great importance for understanding various biophysical processes in hydrology, agronomy, and ecosystem sciences (Bassiouni et al., 2020; Uber et al., 2018). The poor spatial representativeness of in situ soil moisture sensors, combined with their labor-intensive installation and maintenance, impedes the application of these sensors to understand large-scale ecosystem phenomena (Babaeian et al., 2019; Petropoulos et al., 2015). Spaceborne passive microwave remote sensing has been developed as a reliable method to estimate surface soil moisture at large scales (Wigneron et al., 2017). It leverages the large discrepancies in dielectric properties between liquid water and dry soil that result in a high dependency of soil dielectric constants on soil moisture (Njoku and Entekhabi, 1996). Various microwave frequencies have been available to date, amongst which the L-band microwave frequencies were found to be desirable for soil moisture estimations because they can sense soil moisture at a relatively deeper layer (∼5 cm) and can provide greater vegetation penetration power (Mohanty et al., 2017). Though microwave remote sensing has been investigated for decades, significant uncertainties still exist in both microwave radiometry and in the algorithms used to translate microwave observations to soil moisture estimates (Gruber et al., 2020).
Passive L-band remote sensing soil moisture estimation uses a radiometer to measure surface emission intensity, which is proportional to the brightness temperature (Wang and Qu, 2009). The brightness temperature is linked to soil moisture and vegetation opacity through the “tau-omeg” emission model and parameterized by soil and vegetation functions (Jackson et al., 1982; Mo et al., 1982). The “tau-omega” model rationale has been adopted by the National Aeronautics and Space Administration (NASA) Soil Moisture Active-Passive (SMAP) mission, which is one of the Earth observation missions dedicated to estimating soil moisture at L-band microwave frequency (Entekhabi et al., 2010). The SMAP mission implemented two primary algorithms: (1) the single-channel algorithm (SCA) that uses one polarized brightness temperature as the primary input to retrieve soil moisture and (2) the dual-channel algorithm (DCA) that retrieves soil moisture and vegetation opacity simultaneously by taking the polarized brightness temperature information in the both horizontal and vertical directions (O'Neill et.al., 2020a). There is strong interest in the DCA approach because of its independent estimation of vegetation opacity in lieu of the specified vegetation climatology employed by the SCA (O'Neill et.al., 2020a). Other L-band-focused satellite mission such as Soil Moisture and Ocean Salinity (SMOS) retrieves both soil moisture and vegetation optical depth by using numerous brightness measurements for different incidence angles (Kerr et al., 2012). Additionally, it has been suggested that using a time-integrated vegetation opacity, as is employed in the multi-temporal dual-channel algorithm (MT-DCA) for instance (Konings et al., 2016), improves the estimates of soil and vegetation state. These contrasting approaches, as well as other studies on SMAP's temporal polarized ratio algorithm (TPRA) (Gao et al., 2020) and regularized dual-channel algorithm (RDCA) (Chaubell et al., 2020), suggested there is still uncertainty about how SMAP observations of horizontal and vertical brightness temperature can best be translated into estimates of surface properties. Although SMAP can provide spatially explicit soil moisture estimates that have been shown to be useful for understanding a set of ecohydrological problems (Dadap et al., 2019; Feldman et al., 2018), the soil moisture retrievals are still subject to a significant amount of uncertainty due to the imperfection of the model and the forcing datasets. It is also important to consider how the amount of duplicate information carried within a set of observations limits the number of independent parameters to be inferred (Konings et al., 2015). Therefore, it is critical to diagnose and quantify the causality of the uncertainty caused by the SMAP algorithm to improve the soil moisture and vegetation opacity retrieval quality.
SMAP soil moisture products have been extensively validated against well-calibrated in situ soil moisture using unbiased root mean square error (ubRMSE), bias, RMSE Pearson correlation coefficients, and the triple collocation method at “core” and “sparse” validation sites (Chan et al., 2016; Chen et al., 2017; Colliander et al., 2017; Zhang et al., 2019). These validation investigations found that SMAP met the required accuracy target (ubRMSE, 0.04 m3 m−3) on average, while there exist some locations where the performance of SMAP did not meet the expected performance. All these validation studies were focused on finding the general uncertainty of SMAP (which is the deviation of SMAP soil moisture from the in situ or reference soil moisture) and cannot diagnose and differentiate where the uncertainty arises. Indeed, the causality of uncertainty of SMAP soil moisture may arise from two aspects: (1) the uncertainty due to the inaccuracies from forcing the datasets and (2) the uncertainty due to poor model structure and parameterizations. In addition, the assessment metrics used in these evaluation studies are either heavily dependent on in situ soil moisture or additional reference datasets, which does not allow for SMAP to be validated in some remote and inaccessible areas.
The challenges faced by previous SMAP evaluation investigations can be resolved by leveraging two information quantities: (1) Shannon's entropy (Shannon, 1948), which is the amount of information required to fully describe a random variable, and (2) mutual information (Cover and Thomas, 2005), which represents the amount of information of knowing one variable given the knowledge of another or a set of random variables (Gong et al., 2013) first leveraged against these information quantities to partition overall uncertainty in the hydrological modeling process into two categories: (1) random uncertainty that arises by incompleteness of an exploratory variable and/or inherent stochasticity of forcing datasets and (2) model uncertainty that is contributed by poor model parameterization or formulation. The random uncertainty is not resolvable for the given system, as it is only related to the probability distributions of the forcing data itself, while the model uncertainty is reducible by a better model parameterization.
Given that both horizontal and vertical polarized brightness temperatures are measured by SMAP, it is unclear how each polarization contributes information to the overall performance of the DCA. Recent research on partial information decomposition has provided tremendous opportunities for understanding the nuanced interactions among different variables and model structure. Initially proposed by Williams and Beer (2010) and further advanced by Goodwell and Kumar (2017), this approach has been used to understand environmental processes that link two source variables with a target variable by partitioning multivariate mutual information into unique, redundant, and synergistic components. The unique information represents the amount of information shared with the target variable from each individual source variable separately (Finn and Lizier, 2018). Synergistic information is the information provided to the target, while both source variables act jointly (Kunert-Graf et al., 2020). Redundant information is the overlapping information that both source variables redundantly provide to a target (Wibral et al., 2017). Information partitioning brings new insight by unambiguously characterizing the interdependencies between source variables and a target variable without any underlying assumption (Goodwell et al., 2018).
The overall objective of this study is to demonstrate that by assessing how information flows through satellite algorithms from raw retrievals to end-user products, we can illuminate areas where improvements can be made and diagnose instances where algorithm estimates are expected to be uncertain. In this study, we focus on (1) quantifying the random uncertainty and model uncertainty in SMAP's DCA and understand how these uncertainties are related to DCA retrieval quality and (2) exploring how the partial information components between SMAP DCA soil moisture and horizontally polarized and vertically polarized brightness temperature can be used to indicate overall DCA soil moisture retrieval performance.
2.1 In situ soil moisture
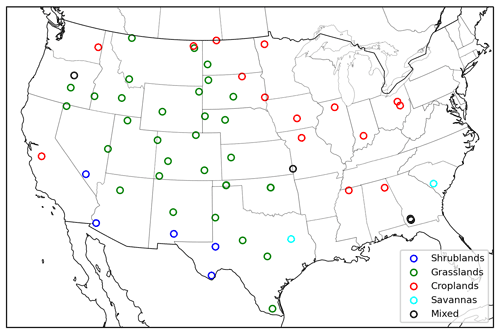
The US Climate Reference Network (USCRN) is a systematic and sustained network that is operated and maintained by the National Oceanic and Atmospheric Administration (NOAA) to support climate-impact research with continuous high-quality field-observed soil moisture, soil temperature, and wind speed at different temporal scales (Diamond et al., 2013). The USCRN provides soil moisture observations at five different standard depths (5, 10, 20, 50, and 100 cm) in 114 locations of the contiguous US (CONUS) (Bell et al., 2013). These in situ datasets have been used for a wide variety of research, such as drought evaluation and satellite soil moisture validation (Bell et al., 2015; Leeper et al., 2017). The hourly soil moisture (beta version product) datasets at a depth of 5 cm were collected from 58 (15 croplands, 32 grasslands, 5 shrublands, 2 savannas, 4 mixed) selected USCRN stations (Fig. 1 and Table S1 in the Supplement) based on the availability of in situ soil moisture datasets and the data quality of SMAP pixels in the study period of 31 March 2015 to 10 December 2020.
2.2 SMAP Level-2 datasets
In this study, we acquired the water-body-corrected horizontally polarized brightness temperature (TBh), vertically polarized brightness temperature (TBv), soil effective temperature (Teff), DCA soil moisture, and fraction of land cover at each selected USCRN station from the SMAP Level-2 Radiometer Half-Orbit 36 km EASE-Grid Soil moisture, version 7 data product (O'Neill et al., 2020b) in the same period as the USCRN soil moisture at every station. The extracted data series were filtered by the internal quality flags of TBh (“tb_qual_flag_h”), TBv (“tb_qual_flag_v”), and DCA (“retrieval_qual_flag_option3”) as provided in SMAP data files. We retain data points at a particular SMAP observation time when they all simultaneously pass quality control and fall within their corresponding valid ranges (e.g., 0 ∼330 K for TBh and TBv, 253.15–313.15 K for Teff, >0.02 m3 m−3 for DCA soil moisture) as specified in the SMAP documentation (Chan, 2020). On average, the number of data points across all the sites is 1090, with a minimum of 225 and a maximum of 1651. DCA retrieves soil moisture based on the “tau-omega” model (Jackson et al., 1982; Mo et al., 1982), which is a well-known radiative transfer-based soil moisture retrieval algorithm in the passive microwave soil moisture community. It requires the brightness temperatures as the main inputs and soil effective temperature as an ancillary input and is parameterized based on overlaying vegetation and soil surface information (Njoku and Entekhabi, 1996). The DCA iteratively feeds the “tau-omega” model with initial guesses of soil moisture and vegetation optical depth. The retrieved soil moisture is assumed to be close to the real value when the estimated brightness temperatures are similar to the satellite-observed brightness temperature (Konings et al., 2017; O'Neill et al., 2020a). Compared to the SCAs, the DCA uses a different polarization mixing factor function and different values of vegetation single scattering albedo (O'Neill et al., 2020a).
The SMAP fraction of the land-cover data field provides the fraction of the top three dominant land covers that were classified by the International Geosphere–Biosphere Programme (IGBP) ecosystem surface classification scheme at each pixel (Chan, 2020). The IGBP classified land surface into water, evergreen needleleaf forest, evergreen broadleaf forest, deciduous needleleaf forest, deciduous broadleaf forest, mixed forest, closed shrublands, open shrublands, woody savannas, savannas, grasslands, permanent wetlands, croplands, urban and built-up, croplands/natural vegetation mosaics, snow and ice, and barren (Seitzinger et al., 2015). In this study, the land cover of the study site was classified as the most dominant land cover if the fraction of the most dominant land cover was greater than 50 %. Otherwise, the land cover of the study site is classified as the “mixed” land cover. Furthermore, the study sites that are dominated by woody savanna were classified as savannas, by closed/open shrublands that were classified as shrublands, and by cropland/natural vegetation mosaics that were classified as croplands. Sites meeting specified data requirements and their associated land-cover classification are shown in Fig. 1. Additionally, the 500 m leaf area index (LAI) of each site was obtained from NASA's Moderate Resolution Imaging Spectrometer (MODIS) mission (Myneni et al., 2015; ORNL DAAC, 2018) and averaged in time. Within each site the mean and standard deviation of LAI of all pixels within each SMAP pixel were calculated as a measure of vegetation biomass and variability.
2.3 Information-based uncertainty partitioning
The fundamental quantity of information theory is Shannon's entropy (Shannon, 1948), which represents the amount of information required to fully describe a random variable (Cover and Thomas, 2005). Shannon's entropy is the basic building block of computing mutual information and the informational uncertainties. The entropy of a single random variable is defined as
where p(x) is the probability mass function of random variable X. The estimation of p(x) often involves discretizing the values of X into a set of bins, and then the p(x) of a specific bin is computed by dividing the total number of data points within a specific bin by the total of number of data points of X. The number of bins in this study is estimated by the Freedman–Diaconis binning method (Freedman and Diaconis, 1981). The entropy calculated by Eq. (1) is in unit of bits.
A previous study has indicated that this method (Eq. 1) may underestimate the true entropy (Paninski, 2003). Therefore, we leveraged the simple Miller–Madow-corrected entropy estimator (Zhang and Grabchak, 2013), and we also normalized the entropy to remove the bias that may cause the heterogeneity in length of available datasets across all stations. We acknowledge that there exist several entropy estimation methods. However, we select the Miller–Madow correction based on its simplicity and effectiveness. The corrected and normalized entropy is then expressed as
where HCN(X) is the Miller–Madow corrected and normalized entropy of random variable X (hereafter entropy), H(X) is the uncorrected entropy from Eq. (1), n is the number of data points of X, and K is the number of non-zero probabilities (bins containing more than one data point) based on the fixed binned method (Freedman and Diaconis, 1981). In this study, all entropies of single random variables in the later equations (i.e., HCN(TBh), HCN(TBv), HCN(in situ), etc.) are computed using the combination of Eqs. (1) and (2) with the replacement of p(•) by their individual probability mass functions.
The joint entropy (Cover and Thomas, 2005) is a critical intermediate information quantity to calculate these informational uncertainties. It represents the amount of information required to describe a set of random variables. The joint entropy for two random variables is defined as
where p(x,y) is the joint probability mass function associated with X and Y that is estimated by the same method mentioned above. The same normalization and correction method of Eq. (2) is applied to joint entropy of Eq. (3). The entropy after the correction and normalization is formulated as
where HCN(X,Y) is the corrected and normalized joint entropy of a random variable associated with {X,Y}, H(X,Y) is the uncorrected and unnormalized entropy from Eq. (3), n is the number of data points that were used to calculate the normalized joint entropy (hereafter joint entropy), and K is the number of non-zero joint probabilities based on the Freeman and Diaconis method (Freedman and Diaconis, 1981). All the joint entropies that are associated with two or more random variables in the later equations (i.e., HCN(in situ,DCA), , , in situ, etc.) are computed using the combination of Eqs. (3) and (4) with the replacement of p(•) by their joint probability mass functions, respectively.
Generally, modeling efforts are focused on capturing the information of a random variable of interest via other explanatory variables through some physically or empirically based models. However, most of the models, being constructed of natural processes, are not perfect, and the model outputs are often not capable of capturing the exact relationship between the available input variables and the variable of interest (Gong et al., 2013). There exists a maximum achievable performance of a model that describes the variable of interest the best for a particular system given the available datasets (Gong et al., 2013), yet the detailed structure of this model is often unknown. Mutual information (Cover and Thomas, 2005), for instance I(A;B), is a measure of the amount information due to the knowledge of knowing either random variable A or B in the function . Mutual information between model inputs and in situ observations of model output (hereafter in situ observations) can be used as a useful and effective measure of the best-achievable performance model because it links the model inputs and in situ observations only through the joint and marginal probability mass functions that do not involve any a priori model assumptions (Gong et al., 2013).
The mutual information can be defined based on entropy and joint entropy (Cover and Thomas, 2005). The mutual information between TBh and DCA and the mutual information between TBv and DCA are computed as
and
The mutual information between in situ and DCA soil moisture is computed as
The mutual information between DCA and in situ soil moisture is calculated as
The mutual information between TBh, TBv, Teff, and in situ soil moisture is computed as
We adopted the information uncertainty analysis by Gong et al. (2013) and applied it to SMAP DCA. For a given system in which the input and output are linked via mathematical functions, the mutual information between model output and in situ observation can never exceed the entropy of the in situ observations. Conceptually, the entropies of model output and in situ observations can be considered two circles (of equal or unequal sizes), and the mutual information between model output and in situ observation can be viewed as the overlapping area of these two circles (Uda, 2020). Therefore, the maximum mutual information shared between model output and in situ is the minimum of the entropy of model output and in situ observations, i.e., . Intuitively, the overlapping area of two circles cannot be larger than that of the smaller circle. Because we are focused on representing the observed soil condition, the information gap between in situ observations, HCN(in situ), and the mutual information shared between in situ observations and model output, I(DCA,in situ), is defined as informational total uncertainty (ITot). This quantity describes how much of the information within in situ observations, as measured by HCN(in situ), is not captured by the estimator, as measured by I(DCA,in situ). The mutual information between the in situ observations and the available explanatory variables is also always smaller than the entropy of in situ observations. This information gap, defined as informational random uncertainty (IRnd), is caused by the existence of inherent data uncertainty of the explanatory variables and a lack of complete explanatory variables to fully capture the information in the in situ observations (Gong et al., 2013). Furthermore, the mutual information between model inputs and in situ observations should equal the mutual information between in situ observations and model output if the model hypothesis completely captures the true relationship between model inputs and in situ observations. However, it is commonly stated that “All models are wrong” (Box, 1976), and model assumptions typically cannot fully express the true relationship between the explanatory variables and in situ observations. Hence, the mutual information between model output and in situ observation is expected to be smaller than the mutual information between model inputs and in situ observations (Gong et al., 2013). This information gap, defined as informational model uncertainty (IMod), is induced by poor model assumption, formulations, and/or inappropriate model parameterizations. Therefore, the informational total uncertainty (ITot) is the sum of the informational random uncertainty and informational model uncertainty come naturally given the explicit definition of these informational uncertainties.
In this study, the explanatory variables of DCA are TBh, TBv, and Teff. The in situ observation and model output are in situ USCRN soil moisture and DCA soil moisture, respectively. Leveraging Eqs. (7) and (9), the DCA informational random uncertainty (IRnd), DCA informational model uncertainty (IMod), and DCA total informational uncertainty (ITot) calculated are calculated as
and
2.4 Partial information decomposition
The distinct informational contributions of TBh and TBv to the DCA soil moisture are assessed through a decomposition of the mutual information. This method partitions multivariate mutual information to unique, redundant, and synergistic components (Williams and Beer, 2010). The decomposed information components on the DCA model inputs and outputs are expected to indicative of informational flow as model inputs are translated to end-user products, and these components may have potential for evaluating model performance. The partial information decomposition of can be expressed as
where Uh and Uv are unique information of TBh and TBv shared with DCA, respectively. S and R are the synergistic information and redundant information that TBh and TBv shared with DCA estimates, respectively. All the decomposed components are non-negative real values (Williams and Beer, 2010).
The mutual information between TBh and DCA and mutual information between TBv and DCA are formulated as
and
In this approach, Uh, Uv, S, and R are unknowns in the systems of Eqs. (13)–(15). Goodwell and Kumar (2017) showed that the R can be formulated as
where
and
The interaction information (II) is TBh, TBv, and DCA and can be computed as
It is important to note that we used the point-based in situ soil moisture as the ground truth in this analysis. Due to coarse spatial resolution of SMAP products, we acknowledge that in situ soil moisture may not be able to represent the spatially averaged soil moisture well. Although the nominal sensing depth of L-band SMAP soil moisture is 5 cm, the penetration depth was found to be even shallower in wetter regions (Shellito et al., 2016). In fact, the L-band sensing depth was found to be as little as ∼1 cm (Jackson et al., 2012) and was found to vary with surface soil moisture conditions (Escorihuela et al., 2010; Raju et al., 1995). The heterogeneity in each pixel relative to the in situ observations together with the sensing depth disparity may influence the results of this study and can bias the estimation of informational uncertainties. We also acknowledge the existence of upscaling methods for matching the in situ soil moisture to a satellite footprint (Crow et al., 2012). However, most of upscaling methods are achieved with the assistance of additional reference soil moisture datasets. This process introduces additional pieces of information into the DCA system, making the separation of the uncertainty induced by the upscaling algorithm or additional dataset from other informational uncertainties much harder. Additionally, we used the hourly in situ data to best match the SMAP DCA soil moisture retrievals in time (within an hour). Based on current technologies, it is difficult to find a reference dataset with high frequency in the time domain and good spatial coverage. Here we consider the informational uncertainty caused by the spatial mismatch and sensing depth mismatch between in situ and DCA soil moisture to be part of the informational random uncertainty (IRnd) because the DCA is essentially a mathematical function and does not inherently require the inputs to be at a specific resolution. The spatial resolution is often the inherent attribute of the data. The reader should also keep these in mind while interpreting and adopting the results in this study.
3.1 Information quantities and system informational uncertainties
The estimated entropies across all the study sites are shown in Fig. 2, while the mutual information quantities are shown in Fig. 3. The brightness temperature entropies, HCN(TBh) and HCN(TBv), generally follow the same pattern across sites, with both having an average value of 0.37. Although the patterns of HCN(TBh) and HCN(TBv) are similar, the HCN(TBh) is slightly more variable than HCN(TBv), with the coefficients of variation (CVs) being 0.053 and 0.046, respectively. HCN(Teff) shares the same average with HCN(TBh) and HCN(TBv), whereas the pattern of HCN(Teff) is quite different (Fig. 2). On average, the HCN(in situ) is 0.35, while HCN(DCA) is 0.38. In general, HCN(DCA) follows the pattern of HCN(in situ), with the CV of HCN(DCA) (0.064) being smaller than the CV of HCN(in situ) (0.081).
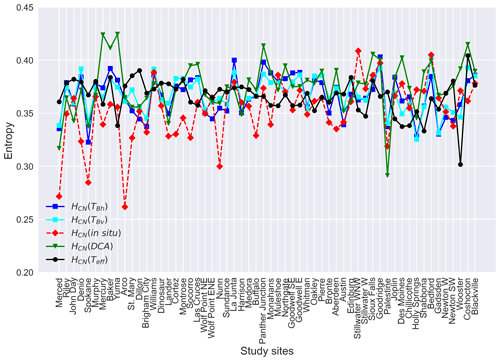
Figure 2Entropies of horizontally polarized brightness temperature (TBh), vertically polarized brightness temperature (TBv), in situ soil moisture, DCA soil moisture, and soil effective temperature (Teff) across the study sites. The sites are ordered by longitude (west to east).
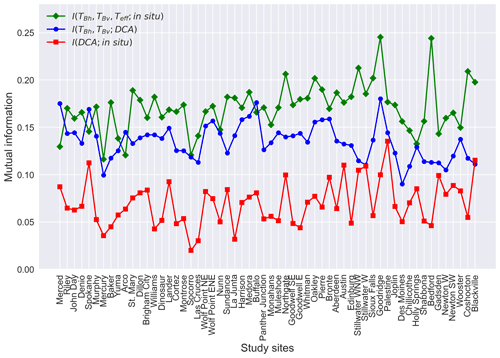
Figure 3Mutual information between horizontally polarized brightness temperature (TBh), vertically polarized brightness temperature (TBv), soil effective temperature (Teff), and in situ soil moisture; mutual information between horizontally polarized brightness temperature (TBh), vertically polarized brightness temperature (TBv), and DCA soil moisture; mutual information between DCA soil moisture and in situ soil moisture. See Fig. 2 caption for site ordering.
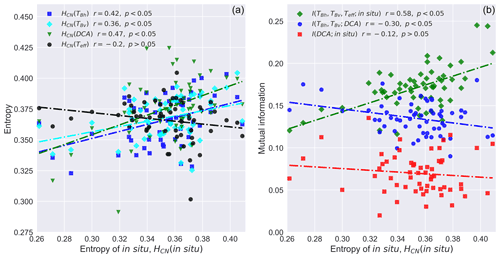
Figure 4Entropy of in situ soil moisture against the entropies of DCA soil moisture, horizontally polarized brightness temperature (TBh), vertically polarized brightness temperature (TBv), and soil effective temperature (Teff) (a) and mutual information quantities (b).
As shown in Fig. 4a, the entropies of the retrieved brightness temperatures and DCA model output, HCN(TBh), HCN(TBv), and HCN(DCA), are significantly correlated with the entropy of in situ observations, HCN(in situ), while no significant correlation is found between HCN(in situ) and HCN(Teff). The HCN(DCA) has the strongest correlation strength with HCN(in situ) compared with other entropy quantities (Fig. 4a). As expected, the mutual information quantities (Fig. 3) are shown to be generally smaller than the entropy quantities (Fig. 2). On average, is 0.14, while I(DCA;insitu) and are 0.07 and 0.17 (Fig. 3), respectively. and are significantly correlated (0.58 and −0.30) with HCN(in situ), while no significant correlation is found for I(DCA;in situ) and HCN(in situ) (Fig. 4b).
Table 1The number of informational uncertainties in percentage. The values in the table are the average of each land cover. The values in “Overall” are the averages of all the sites. The “Lumped” field is computed using all available datasets.
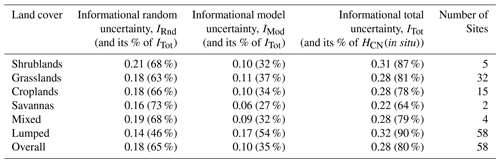
It is noticeable that there exists a large information gap between HCN(in situ) in Fig. 2 and and and I(DCA;in situ) in Fig. 3. These information gaps confirm the existence of informational random uncertainty (IRnd) and informational model uncertainty (IMod) in the SMAP DCA system. When calculating informational quantities on a site-by-site basis and then averaging, the SMAP DCA explains 20 % of the HCN(in situ), leaving 80 % of the HCN(in situ) that is unexplained (Table 1) as informational total uncertainty (ITot); 35 % of the ITot is caused by IMod, while the rest is induced by IRnd. The information uncertainties vary slightly across different land covers. On average across sites, the SMAP DCA system is capable of capturing more information of HCN(in situ) at croplands and savannas (Table 1). Shrublands have the largest absolute IRnd (0.21) than other land covers, while savannas have the largest proportion of IRnd to ITot (Table 1). IMod in absolute value is greater in shrublands, grasslands, and croplands, with grasslands having the largest proportion of IMod to ITot (Table 1). When lumping all the datasets together and recalculating informational quantities, we observe that SMAP DCA captures 10 % of the information in the in situ soil moisture and the proportion of IMod to ITot is larger.

Figure 5SMAP informational total uncertainty (a), SMAP informational model uncertainty (b), and SMAP informational random uncertainty (c) against Pearson correlation between in situ soil moisture and DCA soil moisture.
The relationship between different informational uncertainties and the Pearson correlation coefficients between in situ soil moisture and SMAP DCA soil moisture, a commonly adopted relative model evaluation metric in SMAP studies (Chan et al., 2016; Colliander et al., 2017), was evaluated. The ITot, IMod, and IRnd are shown to be related to how well the SMAP DCA soil moisture is correlated with in situ soil moisture (Fig. 5a–c). ITot is found to be negatively correlated (, Fig. 5a) with the Pearson correlation between in situ soil moisture and SMAP DCA soil moisture. Similarly, IMod and IRnd are also shown to be negatively (−0.59 and −0.34, respectively) related to the Pearson correlation between in situ soil moisture and SMAP DCA soil moisture, with IMod being more influential than IRnd (Fig. 5b and c). These negative relationships are consistent with general expectations since SMAP tends to capture more information about the in situ soil moisture (i.e., lower ITot, IMod, and IRnd) when it retrieves high-quality datasets (higher correlation between in situ soil moisture and SMAP DCA soil moisture).
3.2 Partial information decomposition of DCA
The partial information decompositions were assessed on a site basis and are shown in Fig. 6. The fractional contribution of each component to that site's mutual information between brightness temperatures and DCA estimates, , was also calculated and is given in Table 2. Generally, the majority of is redundantly (R) shared by TBh and TBv, which is about 0.08 (58 % of ) on average (Table 2). The mean values of unique information of TBh(Uh) and synergistic information (S) of TBh and TBv are 0.024 (18 % of ) and 0.018 (14 % of ), respectively (Table 2). Compared to other decomposed information components, Uv is the smallest, with its mean being 0.013 (10 % of ). Savannas have the highest absolute and fraction of R (0.101, 78 % of ) (Table 2). In general, the DCA system is mainly dominated by R, as indicated by both site-wise decomposition and when lumping all datasets together (45 % of ), and S is consistently the lowest (Table 2).
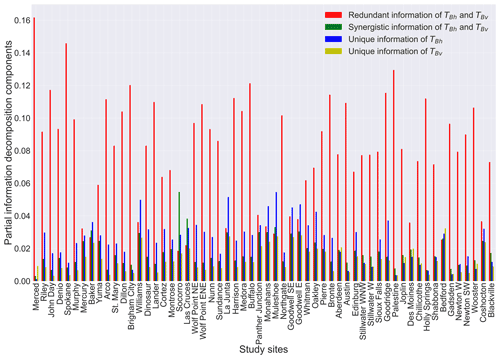
Figure 6Partial information decomposition components between horizontally (TBh) and vertically (TBv) polarized brightness temperature and DCA soil moisture. See Fig. 2 caption for site ordering.
Table 2The partial information decomposition components. The values in the table are the average of each land cover. The values in “Overall” are the average of all the sites. The “Lumped” field is computed using all available datasets.

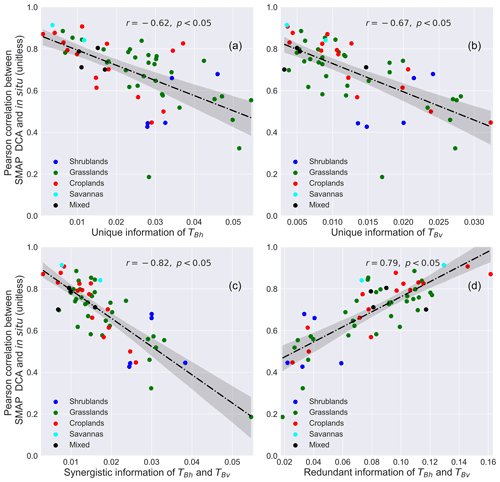
Figure 7Partial information decomposition components between horizontally (TBh) and vertically (TBv) polarized brightness temperature against Pearson correlation coefficient between in situ and DCA soil moisture.
Through this analysis, it is shown in Fig. 7 that there are strong relationships between SMAP DCA retrieval quality and decomposed information components. In general, the correlation strength between DCA and in situ soil moisture is higher when Uh, Uv, and S are low and R is high. This is demonstrated by a significant correlation of these components with the Pearson correlation between in situ and DCA soil moisture. The negative relationship between increasing S and decreasing DCA quantity is the strongest of the decomposed components, though the positive relationship between increasing R and decreasing DCA is of a similar correlation strength. This indicates that R or S contains useful information about DCA soil moisture quality.
4.1 DCA informational uncertainties
The first objective of this study is to leverage information theory to quantitatively decompose the informational total uncertainty into informational random uncertainty and informational model uncertainty in the DCA as an approach to understand where retrieval uncertainties arise. This information theory approach can provide new insight into SMAP modeling diagnosis. It offers an opportunity to partition the total informational uncertainty in the DCA into the uncertainty due to the input datasets and the uncertainty due to model structure and model parameterizations. This partition process cannot be achieved by leveraging the common DCA assessment metrics (Chan et al., 2016) (e.g., Pearson correlation, ubRMSE) that only involve the DCA soil moisture and in situ soil moisture.
The DCA model structure is inherently a hypothesis that relates the input datasets to soil moisture based on prior physical knowledge. The DCA is thus a procedure of processing the input dataset into estimates of soil moisture. Thus, models, even those that perform the best, can only reduce the available information in its inputs and are not capable of adding new information about the “true” soil moisture. Hence, there is no possibility of building a model that is better than the one with the best-achievable performance of the input data themselves (yet even achieving this theoretical limit is nearly impossible) (Gong et al., 2013). If, however, more freedom of available datasets to incorporate is given, it is possible to build models that outperform the best-achievable model performance by adding new explanatory variables, which may lead to a family of models that have completely different model structures. Based on Table 1, we find that the DCA has more informational uncertainty in shrublands than grasslands and croplands. This might be due to stronger variability in vegetation for shrublands, while grasslands and croplands tend to be more uniform and homogeneous. It is worth noting that these findings are based on averaging our studied sites within different land-cover categories, and results may be different while comparing two specific sites from different land covers. In addition, we find that the proportion of informational uncertainty increases as the data are lumped together relative to averaging these statistics calculated on a site-by-site basis (Table 1). Treating all the surfaces together as a whole does not reduce the informational total uncertainty because the lumping process contains both “high-quality” and “low-quality” (as assessed by the Pearson correlation between in situ and DCA soil moisture) datasets. The uncertainties in these datasets may accumulate while lumping them together and result in an increase in total informational uncertainty.
The fraction that informational random uncertainty contributes to the informational total uncertainty is quite significant (65 % on average) in this study. The informational random uncertainty in the system may arise from the inherent error due to calibration of TBh and TBv (Al-Yaari et al., 2017), the mismatch in the scale of observations, and the presence of water bodies (Ye et al., 2015). If poorly calibrated, the soil moisture estimations can be exacerbated due to the error propagation that hinders the correct information from being expressed. Furthermore, SMAP attempts Teff to capture both soil and canopy temperature because the differences between canopy and soil temperature are minimized in the morning and afternoon orbits. The Teff is computed based on a model that uses the information from the average soil temperature of the first layer and second layer of a land surface model for SMAP soil moisture retrievals (O'Neill et al., 2020a). The modeling processes may produce an erroneous Teff dataset and hence contribute the informational random uncertainty of DCA. Therefore, a better and robust calibration strategy of TBh and TBv for the presence of water bodies and a comprehensive assessment of Teff may be needed to reduce some of the information random uncertainty.
Informational model uncertainty contributes a non-negligible portion to the informational total uncertainty (35 % on average). This model uncertainty may arise from poor model parameterizations, which may vary with site soil moisture dynamics (HCN(in situ)). As shown in Fig. 4b, the increases as the in situ soil moisture is more dynamic, as reflected by high values of HCN(TBh) and HCN(TBv). The raw observations (TBv, TBh, and Teff) provide more available information to the system, whereas such information is not properly captured by the algorithm, as reflected by low correlation strength between HCN(in situ) and I(DCA;in situ). Therefore, it is more likely to observe large information model uncertainty where the soil moisture is more dynamic, which may cause a low efficiency of DCA to correctly transmit the available information. It is known that DCA is parameterized with a set of surface and vegetation parameters such as vegetation single scattering albedo (ω) and surface height standard deviation (s). These parameter values are land cover dependent and are derived from past studies as well as prior experience and some information discussions with experts, all of which could be biased and inaccurate (O'Neill et al., 2020a). These parameter values are also not differentiated by land-cover microwave polarization directions and were assumed to be constant in time. It is possible that these parameters (such as ω) vary in time (Konings et al., 2017) and shift during senescence or harvesting seasons. It is observed that the proportion of the informational model uncertainty is slightly smaller in shrublands (Table 1) (here we do not include savannas in the discussion since this land cover only has two sites), while these proportions are larger in croplands and grasslands (Table 1). This might be because the model parameterizations are more reasonable in shrublands than other land covers. In addition, croplands and grasslands may have seasonal harvesting and therefore may be more subject to changes in these values, while shrublands may not. Additionally, when averaging informational values site by site, the informational random uncertainty is a larger fraction of the total uncertainty, whereas when all data are lumped together, the informational model uncertainty is a larger fraction (Table 1). DCA parameters are different with respect to each land cover, and the biases induced by these parameters at each site may accumulate through the system, resulting in a dominance in informational model uncertainty over informational random uncertainty when all sites are lumped together.
To summarize, this is the first attempt at leveraging a mutual information approach to analyze the uncertainty components in microwave remote sensing models. The results of this study can be further used as guidance in assessing an SMAP algorithm and can quantitatively identify where information is lost in the process of SMAP soil moisture modeling. More broadly, this study, though focused on SMAP, can be transferred and extended to analyze other remote sensing algorithms. Over many decades, a lot of effort, resources, and time have been devoted to the launch of numerous satellite missions to retrieve the key environmental variables such as evapotranspiration and vegetation biomass (Dubayah et al., 2020; Hulley et al., 2017). Performing such an analysis on these retrieval algorithms is expected to be beneficial in understanding the informational flow in these algorithms and may provide insights to further improve the data retrieval accuracy as well as make maximum use of data collected at greater expense.
4.2 Model evaluation from another perspective
The second objective of this study was to demonstrate that the partitioned information components contain useful information about DCA model performance that does not depend on in situ soil moisture and other ancillary datasets. We find a strong linear relationship between redundant (R) and synergistic (S) information of the polarized brightness temperatures and Pearson correlation between DCA and in situ soil moisture. In general, it is more likely to observe higher R and lower S (and Uh and Uv) in the less woody land covers such as croplands and grasslands, where the range of brightness temperature may possibly be greater. These information components were found to be marginally correlated with factors such as vegetation density (the Pearson correlations of average LAI with R, S, Uh, and Uv are 0.23, −0.38, −0.54, and −0.19, respectively) and vegetation heterogeneity (the Pearson correlations of LAI standard deviations with R, S, Uh, and Uv are 0.22, −0.39, −0.53, and −0.22, respectively). Additionally, these informational components were also found to be correlated with the mutual information shared between brightness temperatures and DCA estimates (the Pearson correlations of with R, S, Uh, and Uv are 0.6, −0.27, 0.22, and −0.16, respectively), the informational total uncertainty (the Pearson correlations of ITot with R, S, Uh, and Uv are −0.75, 0.62, 0.55, and 0.68, respectively), informational random uncertainty (the Pearson correlations of IRnd with R, S, Uh, and Uv are −0.41, 0.30, 0.05, and 0.15, respectively), and informational model uncertainty (the Pearson correlations of IMod with R, S, Uh, and Uv are −0.62, 0.55, 0.66, and 0.74, respectively). This indicates that these informational components in the DCA system are not only physically driven by both vegetation density and heterogeneity, but also other factors, such as how an algorithm processes the information from TBh and TBv to produce the DCA outputs. It is more likely to observe higher R and lower S in locations where vegetation is denser and more heterogeneous, yet the correlations of these variables with model quality (0.47 for mean LAI and 0.42 for the standard deviation of LAI) are weaker than the correlations found between R and S and model quality shown in Fig. 7. The R and S metrics in this study can thus not only integrate information about how the surface vegetation density and heterogeneity influence the algorithm performance, but also provide insight into how effectively the DCA uses the information from TBh and TBv.
Compared with other ancillary and in situ independent metrics such as correlation strength between a Pearson correlation of TBh with TBv and the Pearson correlation between in situ and DCA soil moisture (0.67), the correlation strengths of S and R with Pearson correlations of in situ and DCA soil moisture are closer (0.79 and −0.82 for R and S). This suggests that the complex nonlinear relationship between TBh and TBv with DCA soil moisture is better captured by R and S as compared to the direct correlation between the two brightness temperatures themselves. Given the strength of this relationship, the R and S hold the potential to be used as a DCA evaluation metric that does not depend on in situ measurement and an ancillary dataset. It is also useful for SMAP DCA soil moisture users to have a rough estimation of how high the quality (as characterized by the correlation strength between DCA and in situ) of the obtained DCA soil moisture is without actually knowing the in situ soil moisture. However, this depends on specific user requirements for data quality. In general, the DCA soil moisture tends to be high in terms of retrieval quality (∼0.75 in Pearson correlation) when the R is greater than 0.1 or S is smaller than 0.015. It is important to note that the decomposed information components are dependent on the DCA parameterizations (e.g., ω, h) that may influence how the TBh and TBv are probabilistically linked with the DCA and hence may alter the partitioned information components.
4.3 Approach limitations
While we expect that this approach can be generalized to analyze other remote sensing models, it may be difficult to compute the joint probability density functions for models with high-dimensional inputs. Difficulty in determining the joint probability density functions hinders the estimation of high-dimensional joint entropy and mutual information components, and these are still open questions in the field of information theory. Although there exist serval data dimension reduction techniques, these dimension reduction techniques are mostly based on some assumptions (Xu et al., 2019). In practice, most of the systems with high-dimension inputs tend to be complex. Therefore, there is a strong risk of introducing additional uncertainty if one chooses an inappropriate technique.
It is important to understand that the SMAP DCA system retrieves soil moisture with the help of vegetation water content climatology derived from the MODIS NDVI data stream. This is specified as a set value for each location and day of year combination and is used to estimate the unknown vegetation optical depth (O'Neill et al., 2020a). The reader should keep in mind that this study considers such data as a dynamic time-varying parameter, and it is not treated as a data input in this study. Adding NDVI as a data input would result in being larger than or equal to in the calculation of IRnd, and therefore IRnd would decrease. Since ITot only considers DCA output and in situ data, it is not altered by adding dynamic parameters, and IMod would therefore increase. Thus, consideration of additional dynamic parameters in this informational assessment would serve to shift uncertainties from those attributed to the input data themselves to uncertainties attributed to the model structure and parameterizations.
This study was conducted only at locations where in situ soil moisture is readily available. It could be an interesting topic to explore whether, and how, information-based uncertainty analysis can be applied in the locations without in situ soil moisture measurements. We would expect the informational uncertainty analysis to provide the estimates of random and model uncertainties. The best performance we can expect from this current uncertainty analysis is to use all the available datasets we have, yet we believe that uncertainty estimations of this approach should be stabilized given adequate representative locations and data records.
This study differentiates and quantifies the uncertainty sources in the SMAP DCA using information theory. We found that on average DCA soil moisture explains 20 % of the information in the in situ soil moisture, leaving 80 % unexplained. Among the unexplained information, 65 % is informational random uncertainty that is caused by the inherent stochasticity of the explanatory variables of SMAP DCA and a lack of additional explanatory variables in the system, while the rest of the informational uncertainty is caused by inappropriateness of the assumption of DCA model structure and parameterizations. We show that informational random uncertainty contributes a larger proportion of the informational total uncertainty across different land covers. However, the informational model uncertainty contributes more to total uncertainty when lumping all the datasets together. The performance of SMAP DCA is negatively correlated with all the information uncertainties, with the informational model uncertainty being more reflective of overall SMAP DCA retrieval quality than the informational random uncertainty.
The decomposition of the mutual information has shown that all decomposed components are significantly related to the Pearson correlation between in situ and DCA soil moisture, with the redundant and synergistic information being the strongest. Good DCA model performance (as measured by the Pearson correlation between in situ and DCA soil moisture) is more likely to be found in locations where the redundant information of brightness temperatures shared with DCA soil moisture is high and is more dominant relative to other components. The informational uncertainty decomposition analysis opens a new window for SMAP algorithm uncertainty diagnosis. SMAP DCA users may examine the R and S components to have an approximate estimation of the soil moisture data quality obtained when no in situ soil moisture is readily available.
The code regarding the SMAP dataset time series, mutual information, and partial information decomposition calculation can obtained from https://doi.org/10.5281/zenodo.5508246 (Li, 2021).
SMAP L2 Radiometer Half-Orbit 36 km EASE-Grid Soil Moisture, version 7, is acquired from US National Snow and Ice Data Center (https://doi.org/10.5067/F1TZ0CBN1F5N, O'Neill et al., 2020b). The in situ soil moisture is accessible through U.S. Climate Reference Network (https://www.ncdc.noaa.gov/crn/qcdatasets.html, NOAA, 2021; Bell et al., 2013; Diamond et al., 2013). The leaf area index dataset can be accessed through the Oak Ridge National Laboratory Distributed Active Archive Center (https://doi.org/10.5067/MODIS/MCD15A3H.006, Myneni et al., 2015).
The supplement related to this article is available online at: https://doi.org/10.5194/hess-25-5029-2021-supplement.
BL and SPG designed this study; BL wrote the manuscript; SPG co-wrote and revised the manuscript.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This project was supported by the National Aeronautics and Space Administration (NASA) under grant NNX16AN13G.
This research has been supported by the National Aeronautics and Space Administration (grant no. NNX16AN13G).
This paper was edited by Roger Moussa and reviewed by Nemesio Rodriguez-Fernandez and two anonymous referees.
Al-Yaari, A., Wigneron, J.-P., Kerr, Y., Rodriguez-Fernandez, N., O'Neill, P. E., Jackson, T. J., De Lannoy, G. J. M., Al Bitar, A., Mialon, A., Richaume, P., Walker, J. P., Mahmoodi, A., and Yueh, S.: Evaluating soil moisture retrievals from ESA's SMOS and NASA's SMAP brightness temperature datasets, Remote Sens. Environ., 193, 257–273, https://doi.org/10.1016/j.rse.2017.03.010, 2017.
Babaeian, E., Sadeghi, M., Jones, S. B., Montzka, C., Vereecken, H., and Tuller, M.: Ground, Proximal, and Satellite Remote Sensing of Soil Moisture, Rev. Geophys., 57, 530–616, https://doi.org/10.1029/2018RG000618, 2019.
Bassiouni, M., Good, S. P., Still, C. J., and Higgins, C. W.: Plant Water Uptake Thresholds Inferred From Satellite Soil Moisture, Geophys. Res. Lett., 47, e2020GL087077, https://doi.org/10.1029/2020GL087077, 2020.
Bell, J. E., Palecki, M. A., Baker, C. B., Collins, W. G., Lawrimore, J. H., Leeper, R. D., Hall, M. E., Kochendorfer, J., Meyers, T. P., Wilson, T., and Diamond, H. J.: U.S. Climate Reference Network Soil Moisture and Temperature Observations, J. Hydrometeorol., 14, 977–988, https://doi.org/10.1175/JHM-D-12-0146.1, 2013.
Bell, J. E., Leeper, R. D., Palecki, M. A., Coopersmith, E., Wilson, T., Bilotta, R., and Embler, S.: Evaluation of the 2012 Drought with a Newly Established National Soil Monitoring Network, Vadose Zone J., 14, vzj2015.02.0023, https://doi.org/10.2136/vzj2015.02.0023, 2015.
Box, G. E. P.: Science and Statistics, J. Am. Stat. Assoc., 71, 791–799, https://doi.org/10.1080/01621459.1976.10480949, 1976.
Chan, S.: Soil Moisture Active Passive (SMAP) Level 2 Passive Soil Moisture Product Specification Document, Jet Propuls. Lab. Inst. Technol., Pasadena, USA, JPL D-72547 (Version 7.0), 63, 2020.
Chan, S. K., Bindlish, R., O'Neill, P. E., Njoku, E., Jackson, T., Colliander, A., Chen, F., Burgin, M., Dunbar, S., Piepmeier, J., Yueh, S., Entekhabi, D., Cosh, M. H., Caldwell, T., Walker, J., Wu, X., Berg, A., Rowlandson, T., Pacheco, A., McNairn, H., Thibeault, M., Martinez-Fernandez, J., Gonzalez-Zamora, A., Seyfried, M., Bosch, D., Starks, P., Goodrich, D., Prueger, J., Palecki, M., Small, E. E., Zreda, M., Calvet, J.-C., Crow, W. T., and Kerr, Y.: Assessment of the SMAP Passive Soil Moisture Product, IEEE T. Geosci. Remote, 54, 4994–5007, https://doi.org/10.1109/TGRS.2016.2561938, 2016.
Chaubell, M. J., Yueh, S. H., Scott Dunbar, R., Colliander, A., Chen, F., Chan, S. K., Entekhabi, D., Bindlish, R., O'Neill, P. E., Asanuma, J., Berg, A. A., Bosch, D. D., Caldwell, T., Cosh, M. H., Collins, C. H., Martinez-Fernandez, J., Seyfried, M., Starks, P. J., Su, Z., Thibeault, M., and Walker, J.: Improved SMAP Dual-Channel Algorithm for the Retrieval of Soil Moisture, IEEE T. Geosci. Remote, 58, 3894–3905, https://doi.org/10.1109/TGRS.2019.2959239, 2020.
Chen, F., Crow, W. T., Colliander, A., Cosh, M. H., Jackson, T. J., Bindlish, R., Reichle, R. H., Chan, S. K., Bosch, D. D., Starks, P. J., Goodrich, D. C., and Seyfried, M. S.: Application of Triple Collocation in Ground-Based Validation of Soil Moisture Active/Passive (SMAP) Level 2 Data Products, IEEE J. Sel. Top. Appl., 10, 489–502, https://doi.org/10.1109/JSTARS.2016.2569998, 2017.
Colliander, A., Jackson, T. J., Bindlish, R., Chan, S., Das, N., Kim, S. B., Cosh, M. H., Dunbar, R. S., Dang, L., Pashaian, L., Asanuma, J., Aida, K., Berg, A., Rowlandson, T., Bosch, D., Caldwell, T., Caylor, K., Goodrich, D., al Jassar, H., Lopez-Baeza, E., Martínez-Fernández, J., González-Zamora, A., Livingston, S., McNairn, H., Pacheco, A., Moghaddam, M., Montzka, C., Notarnicola, C., Niedrist, G., Pellarin, T., Prueger, J., Pulliainen, J., Rautiainen, K., Ramos, J., Seyfried, M., Starks, P., Su, Z., Zeng, Y., van der Velde, R., Thibeault, M., Dorigo, W., Vreugdenhil, M., Walker, J. P., Wu, X., Monerris, A., O'Neill, P. E., Entekhabi, D., Njoku, E. G., and Yueh, S.: Validation of SMAP surface soil moisture products with core validation sites, Remote Sens. Environ., 191, 215–231, https://doi.org/10.1016/j.rse.2017.01.021, 2017.
Cover, T. M. and Thomas, J. A.: Elements of Information Theory, Wiley, Hoboken, NJ, 2005.
Crow, W. T., Berg, A. A., Cosh, M. H., Loew, A., Mohanty, B. P., Panciera, R., de Rosnay, P., Ryu, D., and Walker, J. P.: Upscaling sparse ground-based soil moisture observations for the validation of coarse-resolution satellite soil moisture products, Rev. Geophys., 50, RG2002, https://doi.org/10.1029/2011RG000372, 2012.
Dadap, N. C., Cobb, A. R., Hoyt, A. M., Harvey, C. F., and Konings, A. G.: Satellite soil moisture observations predict burned area in Southeast Asian peatlands, Environ. Res. Lett., 14, 094014, https://doi.org/10.1088/1748-9326/ab3891, 2019.
Diamond, H. J., Karl, T. R., Palecki, M. A., Baker, C. B., Bell, J. E., Leeper, R. D., Easterling, D. R., Lawrimore, J. H., Meyers, T. P., Helfert, M. R., Goodge, G., and Thorne, P. W.: U.S. Climate Reference Network after One Decade of Operations: Status and Assessment, B. Am. Meteorol. Soc., 94, 485–498, https://doi.org/10.1175/BAMS-D-12-00170.1, 2013.
Dubayah, R., Blair, J. B., Goetz, S., Fatoyinbo, L., Hansen, M., Healey, S., Hofton, M., Hurtt, G., Kellner, J., Luthcke, S., Armston, J., Tang, H., Duncanson, L., Hancock, S., Jantz, P., Marselis, S., Patterson, P. L., Qi, W., and Silva, C.: The Global Ecosystem Dynamics Investigation: High-resolution laser ranging of the Earth's forests and topography, Science of Remote Sensing, 1, 100002, https://doi.org/10.1016/j.srs.2020.100002, 2020.
Entekhabi, D., Njoku, E. G., O'Neill, P. E., Kellogg, K. H., Crow, W. T., Edelstein, W. N., Entin, J. K., Goodman, S. D., Jackson, T. J., Johnson, J., Kimball, J., Piepmeier, J. R., Koster, R. D., Martin, N., McDonald, K. C., Moghaddam, M., Moran, S., Reichle, R., Shi, J. C., Spencer, M. W., Thurman, S. W., Tsang, L., and Van Zyl, J.: The Soil Moisture Active Passive (SMAP) Mission, Proc. IEEE, 98(5), 704–716, https://doi.org/10.1109/JPROC.2010.2043918, 2010.
Escorihuela, M. J., Chanzy, A., Wigneron, J. P., and Kerr, Y. H.: Effective soil moisture sampling depth of L-band radiometry: A case study, Remote Sens. Environ., 114, 995–1001, https://doi.org/10.1016/j.rse.2009.12.011, 2010.
Feldman, A. F., Short Gianotti, D. J., Konings, A. G., McColl, K. A., Akbar, R., Salvucci, G. D., and Entekhabi, D.: Moisture pulse-reserve in the soil-plant continuum observed across biomes, Nat. Plants, 4, 1026–1033, https://doi.org/10.1038/s41477-018-0304-9, 2018.
Finn, C. and Lizier, J.: Pointwise Partial Information Decomposition Using the Specificity and Ambiguity Lattices, Entropy, 20, 297, https://doi.org/10.3390/e20040297, 2018.
Freedman, D. and Diaconis, P.: On the histogram as a density estimator: L2 theory, Z. Wahrscheinlichkeit., 57, 453–476, https://doi.org/10.1007/BF01025868, 1981.
Gao, L., Sadeghi, M., Ebtehaj, A., and Wigneron, J.-P.: A temporal polarization ratio algorithm for calibration-free retrieval of soil moisture at L-band, Remote Sens. Environ., 249, 112019, https://doi.org/10.1016/j.rse.2020.112019, 2020.
Gong, W., Gupta, H. V., Yang, D., Sricharan, K., and Hero, A. O.: Estimating epistemic and aleatory uncertainties during hydrologic modeling: An information theoretic approach, Water Resour. Res., 49, 2253–2273, https://doi.org/10.1002/wrcr.20161, 2013.
Goodwell, A. E. and Kumar, P.: Temporal information partitioning: Characterizing synergy, uniqueness, and redundancy in interacting environmental variables, Water Resour. Res., 53, 5920–5942, https://doi.org/10.1002/2016WR020216, 2017.
Goodwell, A. E., Kumar, P., Fellows, A. W., and Flerchinger, G. N.: Dynamic process connectivity explains ecohydrologic responses to rainfall pulses and drought, P. Natl. Acad. Sci. USA, 115, E8604–E8613, https://doi.org/10.1073/pnas.1800236115, 2018.
Gruber, A., De Lannoy, G., Albergel, C., Al-Yaari, A., Brocca, L., Calvet, J.-C., Colliander, A., Cosh, M., Crow, W., Dorigo, W., Draper, C., Hirschi, M., Kerr, Y., Konings, A., Lahoz, W., McColl, K., Montzka, C., Muñoz-Sabater, J., Peng, J., Reichle, R., Richaume, P., Rüdiger, C., Scanlon, T., van der Schalie, R., Wigneron, J.-P., and Wagner, W.: Validation practices for satellite soil moisture retrievals: What are (the) errors?, Remote Sens. Environ., 244, 111806, https://doi.org/10.1016/j.rse.2020.111806, 2020.
Hulley, G., Hook, S., Fisher, J., and Lee, C.: ECOSTRESS, A NASA Earth-Ventures Instrument for studying links between the water cycle and plant health over the diurnal cycle, 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), 5494–5496, IEEE, 23–28 July 2017, Fort Worth, TX, USA, 2017.
Jackson, T. J., Schmugge, T. J., and Wang, J. R.: Passive microwave sensing of soil moisture under vegetation canopies, Water Resour. Res., 18, 1137–1142, https://doi.org/10.1029/WR018i004p01137, 1982.
Jackson, T. J., Bindlish, R., Cosh, M. H., Zhao, T., Starks, P. J., Bosch, D. D., Seyfried, M., Moran, M. S., Goodrich, D. C., Kerr, Y. H., and Leroux, D.: Validation of Soil Moisture and Ocean Salinity (SMOS) Soil Moisture Over Watershed Networks in the U.S., IEEE T. Geosci. Remote, 50, 1530–1543, https://doi.org/10.1109/TGRS.2011.2168533, 2012.
Kerr, Y. H., Waldteufel, P., Richaume, P., Wigneron, J. P., Ferrazzoli, P., Mahmoodi, A., Al Bitar, A., Cabot, F., Gruhier, C., Juglea, S. E., Leroux, D., Mialon, A., and Delwart, S.: The SMOS Soil Moisture Retrieval Algorithm, IEEE T. Geosci. Remote, 50, 1384–1403, https://doi.org/10.1109/TGRS.2012.2184548, 2012.
Konings, A. G., McColl, K. A., Piles, M., and Entekhabi, D.: How Many Parameters Can Be Maximally Estimated From a Set of Measurements?, IEEE Geosci. Remote S., 12, 1081–1085, https://doi.org/10.1109/LGRS.2014.2381641, 2015.
Konings, A. G., Piles, M., Rötzer, K., McColl, K. A., Chan, S. K., and Entekhabi, D.: Vegetation optical depth and scattering albedo retrieval using time series of dual-polarized L-band radiometer observations, Remote Sens. Environ., 172, 178–189, https://doi.org/10.1016/j.rse.2015.11.009, 2016.
Konings, A. G., Piles, M., Das, N., and Entekhabi, D.: L-band vegetation optical depth and effective scattering albedo estimation from SMAP, Remote Sens. Environ., 198, 460–470, https://doi.org/10.1016/j.rse.2017.06.037, 2017.
Kunert-Graf, J., Sakhanenko, N., and Galas, D.: Partial Information Decomposition and the Information Delta: A Geometric Unification Disentangling Non-Pairwise Information, Entropy, 22, 1333, https://doi.org/10.3390/e22121333, 2020.
Leeper, R. D., Bell, J. E., Vines, C., and Palecki, M.: An Evaluation of the North American Regional Reanalysis Simulated Soil Moisture Conditions during the 2011–13 Drought Period, J. Hydrometeorol., 18, 515–527, https://doi.org/10.1175/JHM-D-16-0132.1, 2017.
Li, B.: Information-based uncertainty decomposition of remote sensing of soil moisture, https://doi.org/10.5281/zenodo.5508246, 2021.
Mo, T., Choudhury, B. J., Schmugge, T. J., Wang, J. R., and Jackson, T. J.: A model for microwave emission from vegetation-covered fields, J. Geophys. Res., 87, 11229, https://doi.org/10.1029/JC087iC13p11229, 1982.
Mohanty, B. P., Cosh, M. H., Lakshmi, V., and Montzka, C.: Soil Moisture Remote Sensing: State-of-the-Science, Vadose Zone J., 16, vzj2016.10.0105, https://doi.org/10.2136/vzj2016.10.0105, 2017.
Myneni, R., Knyazikhin, Y., and Park, T.: MCD15A3H MODIS/Terra+Aqua Leaf Area Index/FPAR 4-day L4 Global 500 m SIN Grid V006 [Data set], NASA EOSDIS Land Processes DAAC, https://doi.org/10.5067/MODIS/MCD15A3H.006, 2015.
NOAA: In situ soil moisture, available at: https://www.ncdc.noaa.gov/crn/qcdatasets.html, last access: July 2021.
Njoku, E. G. and Entekhabi, D.: Passive microwave remote sensing of soil moisture, J. Hydrol., 184, 101–129, https://doi.org/10.1016/0022-1694(95)02970-2, 1996.
O'Neill, P., Bindlish, R., Chan, S., Njoku, E., and Jackson, T.: Algorithm theoretical basis document: Level 2 & 3 soil moisture (passive) data products (revision F), Jet Propulsion Laboratory California Insititude of Technology, Pasadena, USA, JPL D-66480, 2020a.
O'Neill, P. E., Chan, S., Njoku, E. G., Jackson, T., Bindlish, R., and Chaubell, J.: SMAP L2 Radiometer Half-Orbit 36 km EASE-Grid Soil Moisture, Version 7, Boulder, Colorado, USA, NASA National Snow and Ice Data Center Distributed Active Archive Center, available at https://doi.org/10.5067/F1TZ0CBN1F5N, 2020b.
ORNL DAAC: MODIS and VIIRS Land Products Global Subsetting and Visualization Tool, ORNL DAAC, Oak Ridge, Tennessee, USA, https://doi.org/10.3334/ORNLDAAC/1379, 2018.
Paninski, L.: Estimation of Entropy and Mutual Information, Neural Comput., 15, 1191–1253, https://doi.org/10.1162/089976603321780272, 2003.
Petropoulos, G. P., Ireland, G., and Barrett, B.: Surface soil moisture retrievals from remote sensing: Current status, products & future trends, Phys. Chem. Earth, 83–84, 36–56, https://doi.org/10.1016/j.pce.2015.02.009, 2015.
Raju, S., Chanzy, A., Wigneron, J.-P., Calvet, J.-C., Kerr, Y., and Laguerre, L.: Soil moisture and temperature profile effects on microwave emission at low frequencies, Remote Sens. Environ., 54, 85–97, https://doi.org/10.1016/0034-4257(95)00133-L, 1995.
Seitzinger, S. P., Gaffney, O., Brasseur, G., Broadgate, W., Ciais, P., Claussen, M., Erisman, J. W., Kiefer, T., Lancelot, C., Monks, P. S., Smyth, K., Syvitski, J., and Uematsu, M.: International Geosphere–Biosphere Programme and Earth system science: Three decades of co-evolution, Anthropocene, 12, 3–16, https://doi.org/10.1016/j.ancene.2016.01.001, 2015.
Shannon, C. E.: A Mathematical Theory of Communication, AT&T Tech. J., 27, 379–423, https://doi.org/10.1002/j.1538-7305.1948.tb01338.x, 1948.
Shellito, P. J., Small, E. E., Colliander, A., Bindlish, R., Cosh, M. H., Berg, A. A., Bosch, D. D., Caldwell, T. G., Goodrich, D. C., McNairn, H., Prueger, J. H., Starks, P. J., van der Velde, R., and Walker, J. P.: SMAP soil moisture drying more rapid than observed in situ following rainfall events, Geophys. Res. Lett., 43, 8068–8075, https://doi.org/10.1002/2016GL069946, 2016.
Uber, M., Vandervaere, J.-P., Zin, I., Braud, I., Heistermann, M., Legoût, C., Molinié, G., and Nord, G.: How does initial soil moisture influence the hydrological response? A case study from southern France, Hydrol. Earth Syst. Sci., 22, 6127–6146, https://doi.org/10.5194/hess-22-6127-2018, 2018.
Uda, S.: Application of information theory in systems biology, Biophys. Rev., 12, 377–384, https://doi.org/10.1007/s12551-020-00665-w, 2020.
Wang, L. and Qu, J. J.: Satellite remote sensing applications for surface soil moisture monitoring: A review, Front. Earth Sci. China, 3, 237–247, https://doi.org/10.1007/s11707-009-0023-7, 2009.
Wibral, M., Priesemann, V., Kay, J. W., Lizier, J. T., and Phillips, W. A.: Partial information decomposition as a unified approach to the specification of neural goal functions, Brain Cognition, 112, 25–38, https://doi.org/10.1016/j.bandc.2015.09.004, 2017.
Wigneron, J.-P., Jackson, T. J., O'Neill, P., De Lannoy, G., de Rosnay, P., Walker, J. P., Ferrazzoli, P., Mironov, V., Bircher, S., Grant, J. P., Kurum, M., Schwank, M., Munoz-Sabater, J., Das, N., Royer, A., Al-Yaari, A., Al Bitar, A., Fernandez-Moran, R., Lawrence, H., Mialon, A., Parrens, M., Richaume, P., Delwart, S., and Kerr, Y.: Modelling the passive microwave signature from land surfaces: A review of recent results and application to the L-band SMOS & SMAP soil moisture retrieval algorithms, Remote Sens. Environ., 192, 238–262, https://doi.org/10.1016/j.rse.2017.01.024, 2017.
Williams, P. L. and Beer, R. D.: Nonnegative Decomposition of Multivariate Information, available at: http://arxiv.org/abs/1004.2515 (last access: 10 December 2020), 2010.
Xu, X., Liang, T., Zhu, J., Zheng, D., and Sun, T.: Review of classical dimensionality reduction and sample selection methods for large-scale data processing, Neurocomputing, 328, 5–15, https://doi.org/10.1016/j.neucom.2018.02.100, 2019.
Ye, N., Walker, J. P., Guerschman, J., Ryu, D., and Gurney, R. J.: Standing water effect on soil moisture retrieval from L-band passive microwave observations, Remote Sens. Environ., 169, 232–242, https://doi.org/10.1016/j.rse.2015.08.013, 2015.
Zhang, R., Kim, S., and Sharma, A.: A comprehensive validation of the SMAP Enhanced Level-3 Soil Moisture product using ground measurements over varied climates and landscapes, Remote Sens. Environ., 223, 82–94, https://doi.org/10.1016/j.rse.2019.01.015, 2019.
Zhang, Z. and Grabchak, M.: Bias Adjustment for a Nonparametric Entropy Estimator, Entropy, 15, 1999–2011, https://doi.org/10.3390/e15061999, 2013.