the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Satellite soil moisture data assimilation for improved operational continental water balance prediction
Luigi J. Renzullo
Robert C. Pipunic
Julien Lerat
Wendy Sharples
Chantal Donnelly
A simple and effective two-step data assimilation framework was developed to improve soil moisture representation in an operational large-scale water balance model. The first step is a Kalman-filter-type sequential state updating process that exploits temporal covariance statistics between modelled and satellite-derived soil moisture to produce analysed estimates. The second step is to use analysed surface moisture estimates to impart mass conservation constraints (mass redistribution) on related states and fluxes of the model using tangent linear modelling theory in a post-analysis adjustment after the state updating at each time step. In this study, we assimilate satellite soil moisture retrievals from both Soil Moisture Active Passive (SMAP) and Soil Moisture and Ocean Salinity (SMOS) missions simultaneously into the Australian Water Resources Assessment Landscape model (AWRA-L) using the proposed framework and evaluate its impact on the model's accuracy against in situ observations across water balance components. We show that the correlation between simulated surface soil moisture and in situ observation increases from 0.54 (open loop) to 0.77 (data assimilation). Furthermore, indirect verification of root-zone soil moisture using remotely sensed Enhanced Vegetation Index (EVI) time series across cropland areas results in significant improvements from 0.52 to 0.64 in correlation. The improvements gained from data assimilation can persist for more than 1 week in surface soil moisture estimates and 1 month in root-zone soil moisture estimates, thus demonstrating the efficacy of this data assimilation framework.
- Article
(11068 KB) - Full-text XML
- BibTeX
- EndNote
Accurate estimation of soil moisture is fundamental to monitoring and forecasting water availability and land surface conditions under extreme events such as droughts, heatwaves and floods (Ines et al., 2013; Sheffield and Wood, 2007; Tian et al., 2019b). The spatial pattern of soil moisture can vary significantly due to the heterogeneous spatial distribution of rainfall and variability in soil properties, land cover type and topography. Due to this large spatial variability, the utility of ground-based, point-scale measurements is limited in estimating soil water availability at continental scale. Soil moisture estimates from land surface models are adversely affected by the uncertainties of atmospheric forcing, model dynamics and model parameterization. Remotely sensed data can provide spatially and temporally varying constraints on the modelling of biophysical landscape variables that are often superior to those achieved by a single static set of model parameters. Data assimilation merges models and observations in a way that takes advantage of their respective strength (e.g. uncertainty, coverage), resulting in improved accuracy, coverage and ultimately forecasting capability.
The assimilation of satellite soil moisture (SSM) into land surface and hydrology models has been repeatedly demonstrated to improve model representation of soil water dynamics, evapotranspiration and streamflow (De Lannoy and Reichle, 2016; Draper et al., 2012; Kumar et al., 2009; Li et al., 2012; Pipunic et al., 2008; Reichle and Koster, 2005; Renzullo et al., 2014; Tian et al., 2017, 2019a; Crow and Yilmaz, 2014; Alvarez-Garreton et al., 2015; Crow and Ryu, 2009; Baldwin et al., 2017; Patil and Ramsankaran, 2017; Wanders et al., 2014b; Peters-Lidard et al., 2011; Su et al., 2014). Accurate knowledge of initial soil moisture states gained from data assimilation contributes significantly to the skill of flood forecasting, drought monitoring and weather forecasts (Bolten et al., 2009; Carrera et al., 2019; Wanders et al., 2014b; Yan et al., 2018; Alvarez-Garreton et al., 2015). Wanders et al. (2014a) found that the assimilation of remotely sensed soil moisture in combination with discharge observation can improve the quality of the operational flood alerts, both in terms of timing and in the exact height of the flood peak.
Methods of assimilation are many and varied; however commonalities exist between them. These commonalities are such that, for any time step, the time-integrated first guess (the forecast) of soil moisture states is adjusted by an amount determined by the difference between observed and modelled soil moisture (the innovation), which is weighted by the respective error variances of modelled and observed quantities (the gain), to generate revised soil moisture states (the analysis). At the end of this process, the revised model soil moisture states are out of balance with the other stores and fluxes, until the model integrates forward to the next time step, whereupon water balance discontinuity is progressively removed through model physics. Soil moisture is the linchpin between atmospheric fluxes, surface water and groundwater hydrology; thus it is important that any changes in modelled state variables are not detrimental to other components of the water balance. However, the assimilation of remotely sensed soil moisture or total water storage data may lead to undesired impacts on groundwater or evapotranspiration simulations due to the mass imbalance or random error covariances (Girotto et al., 2017; Tangdamrongsub et al., 2020; Tian et al., 2017). Studies considering mass conservation in data assimilation often require extra data sources such as evapotranspiration and runoff as constraints or without considering the fluxes (Li et al., 2012; Pan and Wood, 2006).
From an operational water balance perspective, it is important that the method of data assimilation (i) be computationally efficient for routine, automated simulation over the whole model domain; (ii) be robust to data gaps; and (iii) make lasting positive improvements to future predictions of soil water stores and fluxes. An additional constraint is that if a data assimilation method is applied to an existing operational system, then it ought to require minimal modification to the system framework and be as least disruptive as possible to the model performance. Currently, there are few operational continental water balance modelling systems that provide near-real-time soil moisture estimates that have been constrained through the assimilation of satellite observations, and mainly at a relatively coarse resolution. Some recent examples include surface soil wetness observations from the Advanced Scatterometer (ASCAT) active radar system, on the meteorological operational satellite (MetOp), being assimilated into the Unified Model (Davies et al., 2005) through nudging to provide soil moisture analysis at 40 km globally (Dharssi et al., 2011). Additionally, ASCAT data are used in the ECMWF (European Centre for Medium-Range Weather Forecasts) Land Data Assimilation System through a simplified extended Kalman filter approach (De Rosnay et al., 2013) to provide near-real-time surface soil moisture and root-zone soil moisture at 25 km resolution globally. SMOS (Soil Moisture and Ocean Salinity) brightness temperatures have been assimilated in ECMWF's global NWP (numerical weather prediction) system through the Surface Data Assimilation System, based on the extended Kalman filter, to produce soil moisture reanalysis at 40 km resolution (Muñoz-Sabater, 2015). Level-2 radiometer soil moisture retrievals from the SMAP mission (Entekhabi et al., 2010) have been assimilated into the real-time instance of the NASA Land Information System (LIS) over the conterminous United States (CONUS) to produce hourly outputs at 0.03∘ resolution using the ensemble Kalman filter (Blankenship et al., 2018). However, unlike the aforementioned systems where data assimilation is inherent in the system design, many operational water balance models, or catchment hydrology models, are calibrated to observations a priori. Including data assimilation as an afterthought restrains the flexibility of the system, thereby limiting the complexity of the data assimilation scheme for operational use.
In this study, we develop a simple, computationally efficient and effective data assimilation framework with mass conservation for incorporating satellite soil moisture products into an existing operational national water balance model. We demonstrate the application of the method to the Australian Water Resources Assessment Landscape model (AWRA-L), which provides daily water balance estimates at ∼5 km resolution across Australia, with the assimilation of satellite soil moisture from both SMOS and SMAP. The proposed data assimilation framework is a two-step process that requires minimal modification of the existing operational system. The first step is the sequential state updating, with weightings between models and observations derived from the triple collocation (TC) approach (Chen et al., 2018; Crow and Van den Berg, 2010; Crow and Ryu, 2009; Crow and Yilmaz, 2014; Yilmaz and Crow, 2014; Su et al., 2014). The second step is to impart mass conservation constraints on related states and fluxes such as root-zone soil water storage, evapotranspiration and streamflow, thus improving the accuracy of the water balance post assimilation. Accurate initial water balance conditions are of critical importance in the forecasting of water availability and land surface water dynamics. However, few studies quantify how long the impacts of data assimilation persist in the model system's memory. To explore the impacts of data assimilation on model predictions, we quantified the persistence of the correction to key model components with respect to open-loop simulations, to illustrate the potential gains from data assimilation in improving water balance forecasts.
2.1 Australian water resources assessment modelling system
The Australian Water Resources Assessment Landscape (AWRA-L) model (Van Dijk, 2010) underpins the annual national water resource assessments and water use accounts for Australia (Frost et al., 2018; Vogel et al., 2021). The operational implementation of the AWRA-L by the Australian Bureau of Meteorology provides daily 0.05∘ (approximately 5 km) national gridded water balance estimates. The outputs from the operational AWRA-L have been widely used in various agricultural applications and natural resources risk assessment and planning, including commodity forecasting, irrigation scheduling, flood and drought risk analysis, as well as flood forecasting (Frost et al., 2018; Hafeez et al., 2015; Nguyen et al., 2019; Van Dijk et al., 2013; Van Dijk and Renzullo, 2011). The version of the AWRA-L model used in the study was obtained from the Community Modelling system (AWRA-CMS) and is freely available from https://github.com/awracms/awra_cms (last access: 1 September 2020).
AWRA-L is a one-dimensional grid-based model that simulates water balance for each grid cell across the modelling domain by distributing rainfall influx into plant-accessible water, soil moisture and groundwater stores and computing outflux such as evapotranspiration, runoff and deep drainage. The soil water column is partitioned into three layers (surface: 0–10 cm, shallow: 10–100 cm, and deep: 1–6 m) and simulated separately for two hydrological response units, i.e. deep-rooted (trees) and shallow-rooted (grass) vegetation. The water storage for the surface-layer soil is termed S0, while Ss is used for the shallow layer and Sd for the deeper layer. In addition to the modelling of soil columns, the model includes a surface water and a groundwater storage that are simulated at each grid cell and conceptualized as a small unimpaired catchment. In this study, we used forcing inputs from the AWAP (Australian Water Availability Project) gridded climate data, including daily precipitation, air temperature and solar exposure (Jones et al., 2009) and interpolated site-based wind speed (McVicar et al., 2008). It is acknowledged that the accuracy of the model estimates is limited in regions with insufficient coverage in the ground-based observation network (e.g. rain gauges), which is the raw source of AWAP-gridded data used to force the model. This is limited to very remote and mostly uninhabited arid regions in Australia.
2.2 Satellite soil moisture (SSM)
To maximize daily spatial coverage, we used two satellite soil moisture products derived from passive L-band systems: the Soil Moisture Active Passive (SMAP) product from NASA (Entekhabi et al., 2010) and the product from the European Space Agency's (ESA's) Soil Moisture and Ocean Salinity (SMOS) mission (Kerr et al., 2001). The SMAP product is the level-2 enhanced radiometer half-orbit 9 km EASE grid soil moisture (Chan et al., 2018). The SMOS product is the level-2 soil moisture product on a ∼25 km grid (Rahmoune et al., 2013). Both SMAP and SMOS produce volumetric soil moisture estimates (in m3 m−3) of approximately the upper 5 cm of soil. Available swath data for each product covering Australia were collated for each 24 h period, approximating the AWRA-CMS operational time steps and resampled to a regular 0.05∘ grid across the modelling domain using bilinear interpolation from 2015 to 2019. The volumetric soil moisture retrievals from both SMAP and SMOS were converted into water storage units (mm) to be consistent in units and soil depths with model estimates, using mean and variance matching to remove the systematic bias. Figure 1 shows an example of daily composites of SMAP (Fig. 1a) and SMOS (Fig. 1b) soil moisture retrievals in model units compared to AWRA-L estimates of S0 (Fig. 1c). For regions with sparse rain-gauge coverage such as central Western Australia (Fig. 1c), AWRA-L modelled S0 persists as zeros or very low values for the experiment period, reflecting a deficiency in the gauge-based analysis of daily rainfall used to drive model simulations. The result of mean and variance matching in these gauge-sparse areas will flatten the variability of SSM time series to zero when using values of the modelled S0 for these areas directly. To resolve this problem and fully leverage the information available in the SSM products to fill the gaps in modelled outputs across the continent, we derived a set of coefficients for the mean and variance matching over the gauge sparse regions by sampling modelled and SSM data from cells surrounding the gaps. Specifically, we fitted a linear model between the maximum SSM values through time and the coefficients for mean and variance matching for each cell in neighbouring region. We applied the derived linear relationship to estimate the corresponding “slope” and “intercept” from the maximum SSM values in the rainfall gaps. This provided a transformation of the SSM into water storage units (mm) and ensures the assimilation can effectively influence the spatial pattern of soil moisture over the sparsely gauged regions.
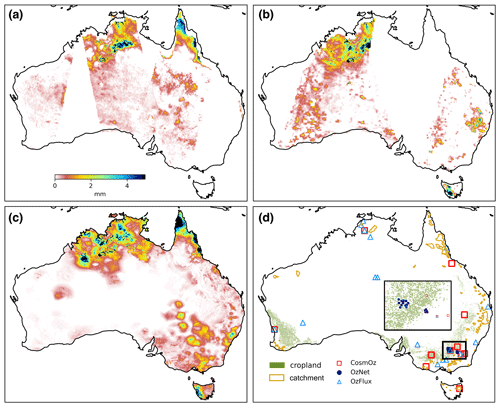
Figure 1Satellite soil moisture retrievals in model unit (mm) for (a) SMAP and (b) SMOS compared to (c) AWRA-L estimates of surface soil water storage for 1 January 2019. (d) Locations of in situ soil moisture monitoring networks (CosmOz, OzNet and OzFlux), catchments for streamflow validation and grid cells classified as cropland. The rectangular inset map provides a zoomed-in view of the OzNet network region in south-eastern Australia.
2.3 Validation data
2.3.1 In situ measurements
Evaluation of the modelled soil water storages was made against measurements from three soil moisture monitoring networks in Australia from 2016 to 2018, namely OzNet (Smith et al., 2012), CosmOz (Hawdon et al., 2014) and OzFlux (Fig. 1d). AWRA-L model estimates of water storage in surface soil layers were compared against in situ measurements from the top 10 cm of soil across all three networks. The depths of in situ measurements of root-zone moisture varied across networks from 0–30 cm to 0–1 m. As such, AWRA-L soil water storages over the root zone were constructed by combining surface- and shallow-layer soil water storage in the appropriate proportions to be consistent with in situ measurement depth. OzFlux sites are also used for the evaluation of AWRA-L evapotranspiration estimates, which were calculated from accumulated latent heat flux measurements at each location. In total, there are 45 sites for soil moisture validation and 14 sites for evapotranspiration validation. Streamflow observations for 110 catchments across Australia have been used in the validation based on the quality and data availability (Fig. 1d).
2.3.2 Vegetation index
In water-limited regions like Australia, shallow-rooted vegetation normally responds quickly to soil water availability, typically within a month. Consistency between root-zone soil water storage and vegetation greenness may be considered an indirect independent verification of the simulation of root-zone soil water dynamics (Tian et al., 2019a, b). The 0.05∘ monthly Enhanced Vegetation Index (EVI) from Moderate Resolution Imaging Spectroradiometer (MODIS, MYD13C2 v6; Didan, 2021) was used to evaluate estimates of monthly root-zone soil water storage (the sum of water storage in surface layer (S0) and shallow layer (Ss) within the AWRA-L soil column) over cropland regions of the continent. The EVI is used here to characterize vegetation dynamics since it is less sensitive to atmospheric effects and canopy background noise and has a greater dynamic range (i.e. less likely to saturate) in areas of dense vegetation compared to the Normalized Difference Vegetation Index (NDVI). The choice of root-zone soil water storage at 0–1 m depth is due to the average rooting depths varying from 30–80 cm over the cropland areas in Australia (Donohue et al., 2012; Figueroa-Bustos et al., 2018; Incerti and O'Leary, 1990). The 250 m land cover classification map from Geoscience Australia (Lymburner et al., 2015) was resampled to 0.05∘ over the model domain and used in the identification of cropland areas.
3.1 Triple-collocation-based error characteristics
Triple collocation (TC) was developed as a method of quantifying error characteristics in geophysical variables when the true error structure is elusive. It was first applied to near-surface wind data (Stoffelen, 1998) and later extensively applied to soil moisture (Chen et al., 2018; Crow and Yilmaz, 2014; Dorigo et al., 2017; McColl et al., 2014; Scipal et al., 2008; Yilmaz and Crow, 2014; Zwieback et al., 2013; Crow and Van den Berg, 2010; Su et al., 2014) and rainfall (Alemohammad et al., 2015; Massari et al., 2017). The assumption of this approach is that three independent data sets of the same geophysical variable can be used to infer the error variances in each. Here we use TC as a way of inferring error variances from our three independent estimates of surface soil moisture, AWRA-L S0, SMAP and SMOS from 2015 to 2019. These three collocated measurements were assumed to be linearly related to the true value with additive random errors. To ensure the errors from the three independent sources were unbiased relative to each other, SMAP and SMOS soil moisture retrievals were rescaled to the reference model estimates (AWRA-L S0) using temporal mean and variance matching. McColl et al. (2014) show that the error variances (σ2) of each data set can be calculated from the temporal variance and covariance between data sets respectively as
where x, y and z denote AWRA-L, SMAP and SMOS soil moisture estimates respectively, and Q denotes temporal variance and covariance between the data sets. These estimates of error variance are used in the determination of the weighting of each data source in the data assimilation (Sect. 3.2).
3.2 Sequential state updating
The data assimilation method used here is a time-sequential updating of model state(s) given observations of relevant model variables (Reichle, 2008). There are two key modelling components in data assimilation: the dynamics operator, which describes the time integration of the system states and fluxes, which in this study is the AWRA-CMS; and the observation operator, which provides the mathematical mapping from state to observation space. The role of the observation operator is to perform a mapping between observation and state space, as often observations are not directly comparable to model states.
The common state updating equation for sequential data assimilation is written as
which says that the best estimate of model state, known as analysis (), is equal to the first guess or forecast () plus a weighted difference between observations, yt, and the model equivalent to the observation, , for that time step. In this study, the AWRA-L model soil water storage in S0 for shallow-rooted vegetation and deep-rooted vegetation at the surface layer is updated directly through the sequential data assimilation. Satellite surface soil moisture (SSM) products from both SMOS and SMAP are used as the observations to update the model simulation. The observation operator H here is the aggregation of soil water storage estimates in the top-soil layer for two land cover types, i.e. shallow-rooted vegetation and deep-rooted vegetation. When both SMAP and SMOS observations are available, Eq. (2) can be written as a weighted linear combination of model estimates () and satellite observations (: SMAP observations, : SMOS observations) as
The gain factor, K, contains the error variances (σ2) for both model estimates and observations and can be written as
where x, y and z denote the AWRA-L, SMAP and SMOS soil moisture retrievals respectively. If only one satellite observation is available for a time step, the gain factor is calculated using the error variance from the corresponding observation. If neither SMAP nor SMOS are available, the analysis remains the same as the model forecast. Observation error variance is often estimated through field campaigns (Draper et al., 2009; Panciera et al., 2013), but these rarely represent the spatial and temporal variability of errors in gridded satellite products. Alternatively, data providers often specify error estimates, but their magnitude can be overly optimistic. Here, we applied the triple collocation approach (Sect. 3.1) to characterize the temporal error variances of the model estimates and the two satellite observations for each grid cell across Australia. The analysis receives a higher contribution from observations with smaller error variance (Eq. 2). Given the relatively short time series (small number) of observations, however, a single set of error variances is calculated for all time. This results in spatially varying but temporally static error variances (and thus gain weights) for each of the three sources (Fig. 2). We acknowledge the limitations of assuming a temporally constant error variances, and future refinements to the assimilation method will consider introducing seasonally varying error variances.
3.3 Analysis increment redistribution (AIR)
The assimilation of satellite soil moisture temporarily violates mass conservation in the model through the analysis update. The difference between the analysis, , and the forecast, (known as the analysis increment), represents an amount of water that has been added or subtracted from the system that was not present at the start of model integration for the given time step. In this study, we use the concept of tangent linear modelling (Errico, 1997; Giering, 2000) to redistribute the analysis increment of surface soil water storage, S0, to all the relevant model states and fluxes as a way of maintaining mass (i.e. water) balance within each model time step. This adjustment is applied after the sequential state updating as the second step in the assimilation framework, which we refer to as analysis increment redistribution (AIR).
The adjoint and tangent linear models were originally used in variational data assimilation (Bouttier and Courtier, 2002) and have been used to estimate the sensitivity of model outputs with respect to input (Errico, 1997). If we assume the input perturbation here is the analysis increment after the data assimilation (i.e. from Eq. 2), then the change in other model outputs due to the change in inputs can be determined through tangent linear modelling. Assuming model variable b is related to the state variable x, the relationship between them can be simply described as
where M denotes the model operator. The change in output variable Δb at time step t due to the input change Δx can be determined by
In this study, we applied the tangent linear modelling approach to correct the model forecast of soil water storage for shallow-layer (Ss) and deep-layer soil water storage (Sd), evapotranspiration (Etot) and total streamflow (Qtot) after the state updating of surface soil moisture (S0) at each time step. Note that this process ensures that the correction is affecting all model states in proportion to their sensitivity against changes in the S0. All the model equations regarding the mass redistribution were derived using model equations (Frost et al., 2018; Van Dijk, 2010) and can be found in Appendix A.
4.1 Impact on surface soil water storage estimates
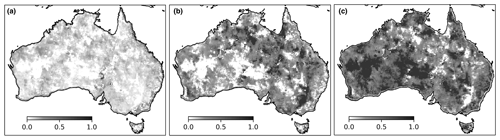
Error variances were derived using TC for AWRA-L model estimates and the SSM products and showed that SMAP soil moisture had smaller error variance than SMOS and the model estimates for the majority of the grid cells over the continent. This is consistent with other studies that have shown SMAP provides the best-performing satellite soil moisture product over the majority of applicable global land pixels (Chen et al., 2018). Figure 2 shows the relative weightings (derived from the TC error variances) of model estimates, SMOS and SMAP soil moisture in the data assimilation. The analysed surface soil water storage estimates (S0) receive a greater contribution from SSM products, in particular SMAP observations, compared to model simulations (Fig. 2). Figure 3 gives an example of the temporal change in modelled S0 estimates before and after the assimilation for 2017. The temporal dynamics of S0 estimates after the assimilation has been highly adjusted towards SSM retrievals and in consistency with in situ measurements.
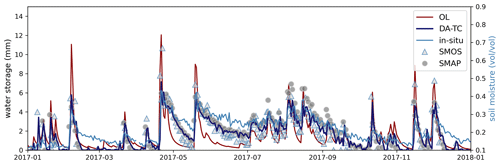
Figure 3Time series of AWRA-L surface soil water storage estimates from open loop (OL) compared to estimates after data assimilation (DA-TC) of SMAP and SMOS soil moisture retrievals at CosmOz monitoring site: Bennets (35.826∘ E, 143.004∘ S). Note that the in situ soil moisture values are in volumetric units.
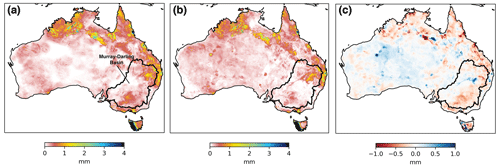
Figure 4Comparison of average daily surface soil water storage estimates (S0) for December 2019 from (a) model open loop (OL), (b) joint assimilation of SMAP and SMOS with triple collocation (DA-TC) and (c) average change between daily estimates from DA-TC and OL.
AWRA-L model simulations are driven by gauge-based rainfall analyses. As such the model has difficulty in adequately simulating soil moisture patterns over regions lacking in rain gauge coverage, such as Western Australia and central Australia (Fig. 1c). Water storage simulations over these regions default to zero; thus very little or no weight was given to the AWRA-L estimates in these regions (Fig. 2a). Figure 4 shows different spatial patterns of daily average S0 estimates for December 2019 from model open loop (OL) without data assimilation and with data assimilation through TC-derived weighting (DA-TC). Data assimilation has the effect of adding moisture to AWRA-L S0 simulations over most gauge-sparse areas, as shown in Fig. 4c. Analysed AWRA-L simulations of S0 are dominated by the satellite SSM data as a result of TC weighting in the region, which largely eliminates the erroneous artefacts associated with deficient rainfall data forcing. Reduced water storage in the surface layer of the soil column was found over the south-east of Australia, particularly within the Murray–Darling Basin. This suggests that AWRA-L OL simulations underestimated the severity of the drought experienced in the region in December 2019. The analysis increments of AWRA-L S0(xa−xf) were compared with the difference between in situ rainfall observations from OzFlux network, POzFlux, and AWAP rainfall forcing, PAWAP (Fig. 5). The increasing S0 simulations align with missing or underestimated rainfall events in the AWAP rainfall forcing ( and vice versa (Fig. 5). This supports the hypothesis that data assimilation correctly distributes water into the system and mitigates the impact of uncertainty in rainfall forcing.

Figure 5Analysis increments of AWRA-L surface soil water storage () in comparison with the difference between in situ rainfall observations and rainfall forcing from AWAP used in AWRA-L modelling (POzFlux−PAWAP) for (a) Yanco site (34.989∘ E, 146.291∘ S) and (b) Wombat Forest (37.422∘ E, 144.094∘ S).
4.2 Impact on root-zone soil water storage and fluxes estimates
If the analysis increment redistribution (AIR) is not applied, the soil water storage in the surface layer (S0) is the only state variable directly updated with SSM (DA-TC). Other variables such as root-zone soil water storage, evapotranspiration and streamflow are adjusted with model integration to the next time step using the analysed S0 as the surface layer initial condition. Therefore, the observed changes in those variables following DA-TC (Fig. 6, centre column) are relatively small when compared to model open-loop estimates (Fig. 6, left column). For example, the OL soil water storage of shallow-layer (Ss) estimates in those gauge-sparse regions of Australia remain zero or very low due to the AWAP rainfall forcing. The predictions of Ss receive a relatively small contribution from the analysed S0 since the analysis increment of S0 is small compared to the field capacity of Ss.
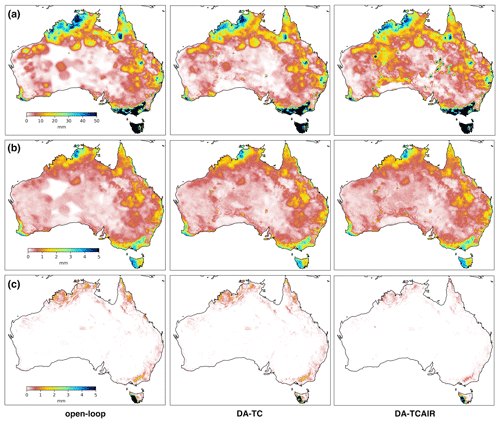
Figure 6Averaged estimates of (a) shallow-layer (10–100 cm) soil water storage (Ss), (b) evapotranspiration (Etot) and (c) total streamflow (Qtot) for December 2019 from model open loop, data assimilation (DA-TC) and after the analysis increment redistribution (DA-TCAIR).
One known issue of sequential state updating is the temporary break of water balance at each time step until the next model integration. The proposed AIR approach (Sect. 3.2) adjusts variables coupled with surface soil moisture after the state updating at each time step. A significant difference in the spatial patterns of Ss, Etot and Qtot after the mass redistribution (DA-TCAIR) can be seen in Fig. 6 (right column) compared to model open loop or forecasts after only S0 updating. The changes in estimates of Ss and Etot over coastal regions are relatively small due to more accurate rainfall forcing data with the dense network of rain gauges. Finally, the Qtot estimates after AIR are lower than the DA-TC and OL. This reduction in streamflow over south-eastern Australia and northern Australia is consistent with the reduced surface soil moisture in those regions (Fig. 4c).
4.3 Quantitative evaluation
Estimates of surface soil moisture, root-zone soil moisture, evapotranspiration and streamflow after data assimilation (DA-TC) and data assimilation with mass redistribution (DA-TCAIR) were compared with time series of in situ observations. We compared the model outputs after DA-TC and DA-TCAIR separately to investigate the benefits of maintaining mass balance in data assimilation. Pearson's correlation coefficients were computed from time series of model estimates and observations between January 2016 and December 2018 for each site. The distribution of correlation coefficients for OL, DA-TC and DA-TCAIR is displayed as boxplots in Fig. 7. Consistent, significant improvement in modelled surface layer soil water storage estimates (S0) was observed across all sites (Fig. 7a), with the single exception of an OzFlux site located in a tropical rainforest, where microwave SSM retrievals are known to be typically poor (Njoku and Entekhabi, 1996). TC-based assimilation (DA-TC) increases the correlation between in situ surface SM measurements from 0.47 to 0.72 on average for CosmOz sites, 0.54 to 0.69 for OzFlux sites and 0.56 to 0.77 for OzNet sites compared to OL. This is a significant improvement in AWRA-L simulations of surface soil moisture dynamics, with an increase in correlation of 0.23 on average across all in situ sites.
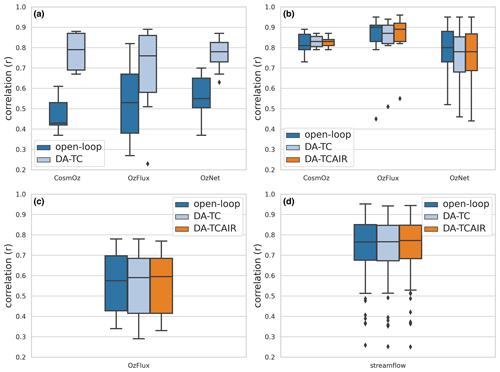
Figure 7Distribution of correlation statistics of AWRA-L water balance estimates against in situ measurements of (a) surface soil moisture, (b) root-zone soil moisture, (c) evapotranspiration and (d) streamflow.
Overall subtle improvements were observed across the AWRA-L estimates of root-zone soil water storage, evapotranspiration and streamflow after the assimilation (DA-TC) (Fig. 7b–d). This level of improvement is not surprising since those variables were not directly updated through DA-TC and are only influenced through the integration of the model to the next time step. Degradation was found in root-zone soil moisture estimation for a few OzFlux and OzNet monitoring sites. This is likely due to the break of water balance in the assimilation, since the estimates followed by the second step of AIR (DA-TCAIR) slightly increase the correlation with in situ observations compared to model open loop and the estimates after assimilation without mass redistribution (DA-TC). Moreover, the model estimates of root-zone soil moisture from model OL are in good agreement with in situ observations, with an average correlation above 0.8 (Fig. 7b), which leaves little room for improvement.
Although the corrections of other water balance estimates from the analysis increment redistribution are relatively small compared to direct state updating, they are improvements nevertheless. Slight improvements were found similarly in streamflow estimates after the AIR (Fig. 7d). Figure 8 shows an example of the OL estimates of streamflow, the analysed streamflow after the application of AIR and the streamflow observations, Qtot obs. Also displayed is the streamflow analysis increments, i.e. , for each time step. The negative streamflow analysis increment (Fig. 8) indicates that water is removed from the surface water store after the assimilation of SSM and application of AIR, which appears to compensate for the overall overestimate of OL simulations, in this example. Although the change in streamflow due to the soil moisture data assimilation is small compared to the disparity between model and observed streamflow, the adjustment in the direction towards observations highlights the importance of accurate antecedent soil moisture conditions in the simulation of runoff response. The joint assimilation of gauge-measured streamflow and satellite soil moisture retrievals into AWRA-L is expected to improve the streamflow simulation.
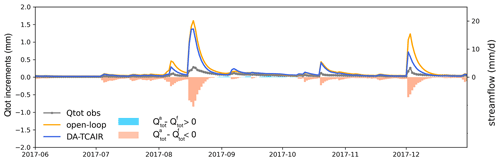
Figure 8Changes in streamflow Qtot estimates after the analysis increment redistribution (DA-TCAIR) for a catchment in south-eastern Australia (centre coordinates: 36.63∘ E, 147.43∘ S) compared to in situ streamflow observations (Qtot obs) and model open loop.
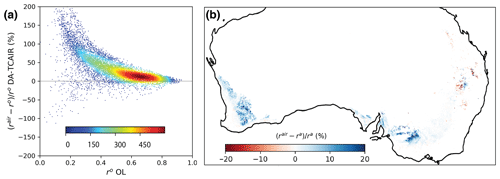
A limited number of root-zone soil moisture monitoring sites as well as the large spatial disparity between the point-scale in situ measurements and modelling resolution (∼5 km grid cell) represent substantial limitations for wide-area evaluation of root-zone soil moisture estimates. An indirect verification of AWRA-L simulations of root-zone soil moisture was based on a comparison against satellite-derived EVI. This provided an independent, albeit indirect, way of evaluating the impact of data assimilation over larger areas. We calculated the correlation between time series of monthly average AWRA-L root-zone soil moisture estimates from OL, DA-TC and DA-TCAIR against EVI for cropland across Australia from 2015 to 2018. Cropland cover type was selected based on the rooting depths of the dominant grass species and wheat varieties in the area that have been shown to have rooting depths spanning at least half the combined soil depths (0–1 m) of the surface- and shallow-layer soil water storage in AWRA-L. Figure 9a shows the relative change in correlation between root-zone soil water storage simulations from DA-TCAIR and those from model OL against EVI data for cropland areas of Australia. Significant improvements were found after the data assimilation and mass redistribution for the vast majority of model grid cells (Fig. 9a). The averaged correlation with EVI is 0.64 from DA-TCAIR compared to 0.52 for model open loop. The root-zone soil water storage estimates after the mass redistribution are significantly improved over the cropland in Western Australia and southern Australia, with more than 20 % increase in correlation comparing to DA-TC without mass redistribution (Fig. 9b). This demonstrates that enforcing mass balances as part of the soil moisture data assimilation at each time step is essential to improving the simulation of root-zone soil water balance. Limited differences between DA-TC and DA-TCAIR were found over cropland regions over south-eastern Australia, likely due to the overall good performance of AWRA-L OL root-zone soil moisture estimates in those areas (Fig. 7b). The improved consistency with EVI after data assimilation highlights the potential of improving agricultural planning with more accurate information of root-zone soil water availability.
4.4 Implications for water balance forecasting
To quantify how long improvements in model state last in AWRA-L simulations, we used OL and DA-TCAIR estimates between 1 March 2018 and 28 February 2019. The model states for each day over this 1-year period served as initial conditions for 100 d AWRA-L simulations, from which we calculated the number of days it took for the simulation from the analysed DA-TCAIR states to converge to within ±5 % of those from OL. Results showed that data assimilation can impact model states and fluxes for weeks and sometimes up to 2–3 months (Fig. 10). The impacts of data assimilation can persist in simulated S0 for as long as a week over coastal regions and longer in central Western Australia and northern Australia, with up to a month persistence in winter and spring (Fig. 10a). There is less impact on S0 simulations during wet season (summer–autumn) in northern Australia since the S0 can saturate rapidly due to the heavy rainfall. Overall, the longest persistence is found in winter, with a continental average of 13 d; the shortest is 6 d on average in autumn and summer. The memory of initial conditions in simulations of Ss can persist even longer due to the slower response to rainfall variability and higher field capacity (Fig. 10b). Summer persistence for Ss is the least, with a continental average of 30 d; in winter this increased to 45 d.
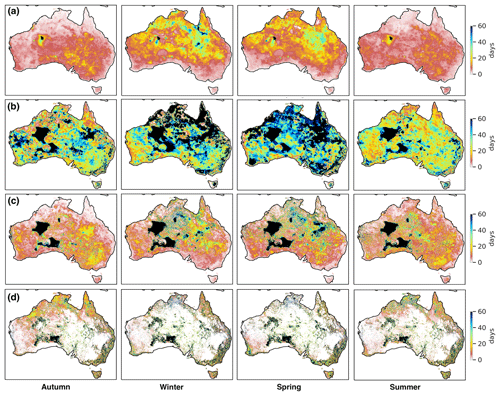
Figure 10Quantified impacts of data assimilation on forecasting AWRA-L state variables using the initial condition from DA-TCAIR: average time period that the impact of data assimilation can persist in autumn (March–May 2018), winter (June–August 2018), spring (September–November 2018) and summer (December 2018–February 2019) on (a) upper layer soil water storage S0, (b) lower layer soil water storage Ss, (c) total evapotranspiration Etot and (d) total runoff Qtot.
On average, the impact of antecedent soil moisture conditions on evapotranspiration simulations can persist for 1 week over coastal areas but for up to months in central Western Australia (Fig. 10c). The continental average varies from 13 to 20 d for each season. The areas with the longest persistence are those areas with artefacts of zero rainfall in the forcing. This demonstrates that improvements in AWRA-L estimates after SSM assimilation over regions with sparse rain-gauge coverage can persist in the system for more than 2 months. The impact on runoff varies from 1 week to 3 months over the continent (Fig. 10d). The majority of areas impacted for more than 2 months are in locations of low rainfall and runoff. However, in areas of heavy runoff, e.g. north-eastern Australia, there is between 1–2 weeks of persistence.
In this study, we assimilated SMAP and SMOS data into an operational AWRA-L water balance modelling system through a simple sequential state updating approach, with weightings derived using triple collocation approach (DA-TC), followed by a post-adjustment for mass redistribution (DA-TCAIR). Previous data assimilation studies using the AWRA-L model opted for ensemble-based methods (Renzullo et al., 2014; Shokri et al., 2019; Tian et al., 2017, 2019a, b). Ensemble-based methods rely on a priori knowledge of uncertainty in forcing data and model error variances to derive spatially and temporally varying gain matrices at each time step. However ensembles often require post hoc correction such as state inflation (Anderson et al., 2009) to achieve optimal performance and many members (>10) comprised of multiple model runs to infer statistically meaningful error variances, which can be computationally costly. In contrast, the proposed DA-TC and DA-TCAIR framework is simple, effective and computationally efficient and requires minimal modification in the current operational system. The gain factor in the proposed assimilation framework is temporally constant but spatially varying. It is derived from the temporal covariances between modelled and satellite-derived soil moisture for each grid cell across the domain through the widely used triple collocation (TC) method (Chen et al., 2018; Crow and Van den Berg, 2010; Crow and Yilmaz, 2014; Yilmaz and Crow, 2014; Su et al., 2014). The significant improvements in AWRA-L model surface soil moisture estimation demonstrates the efficiency of the proposed assimilation approach (Fig. 7a). A temporally varying gain factor is considered for future improvement to the approach once a longer time series of SMAP data is available.
Pan and Wood (2006) used mass redistribution in a two-step constrained Kalman filter that required error covariances derived from evapotranspiration and runoff observations. However, these observations are often not available for continental-scale studies. Li et al. (2012) redistribute the mass imbalance within soil layers during the assimilation but without the updates of fluxes. Our proposed method based on tangent linear modelling redistributes the mass change across all the states and fluxes related to surface soil moisture states without the need for extra observations. The analysis increment redistribution (AIR) method conserves the mass balance, thereby improving water balance estimates (Fig. 7); in particular it can improve the root-zone soil moisture estimates over croplands (Fig. 9). Although the improvements are limited, the streamflow estimates from the AIR are predominantly a better match to observations (Fig. 8). Model physics limits the strength of coupling between an analysed state and resulting fluxes (Kumar et al., 2009; Walker et al., 2001). Thus, a small level of improvement in performance in AWRA-L streamflow in response to soil moisture state updating is not unexpected due to a weak coupling between the states and fluxes. Calibration of model parameters using satellite and in situ observations may lead to further improvements.
Many studies have demonstrated the assimilation of satellite soil moisture can improve model forecasts due to the correction for initial soil moisture conditions (Crow and Ryu, 2009; Pauwels et al., 2001; Scipal et al., 2008). Getirana et al. (2020a, b) found that using initial conditions derived from the assimilation of GRACE (Gravity Recovery and Climate Experiment) total water storage observations can improve the seasonal streamflow and groundwater forecast due to the long memory of groundwater and soil moisture. However, few studies quantify how long the impacts of data assimilation can persist in the model system's memory for different states. In this study, we found that the impact of different initial conditions of root-zone soil water storage has a long memory in the system, exceeding 2 months (Fig. 10b). The constraints on the simulations of surface soil moisture, evapotranspiration and streamflow can persist 1–2 weeks due to the high temporal variability. This highlights the potential gains from data assimilation for agricultural planning and flood forecasting, as a result of improved short-term water balance forecasts.
In this study, we proposed a simple and robust framework for assimilating SMAP and SMOS soil moisture products into the operational Australian Water Resources Assessment modelling system. The method involves the sequential (daily) updating of the model's surface soil water storage with satellite soil moisture observations using weights determined through triple collocation (DA-TC). Furthermore, we proposed an additional component to the data assimilation, whereby the analysis increment of the upper layer soil water storage is propagated into relevant model states and fluxes as a way of maintaining mass balance (DA-TCAIR). Evaluation against in situ measurements showed that simulations of surface soil moisture dynamics is improved significantly after TC data assimilation, with an average increase of 0.23 correlation units compared with open-loop simulations. An evaluation of the root-zone soil moisture, evapotranspiration and streamflow estimates showed that the TC-AIR appeared to provide marginal, yet positive, improvement over the TC data assimilation method alone. However, in an indirect verification of modelled root-zone soil moisture against satellite-derived EVI, DA-TCAIR was seen to provide significant improvement over the TC method alone. This demonstrates that by enforcing mass balances as part of the SSM data assimilation each time step, AWRA-L can better represent soil water dynamics such that it has greater consistency with the observed vegetation response.
The assimilation of satellite soil moisture estimates together with the mass redistribution reduces the uncertainties in model estimates resulting mainly from uncertain forcing and model physics and provides temporally and spatially varying constraints on model water balance estimates. For example, the assimilation resolves the gaps in rainfall forcing over Western Australia and central Australia. We demonstrate that the impacts of data assimilation can persist in the model system for more than a week for surface soil water storage and more than a month for root-zone soil water storage. This highlights the importance of accurate initial hydrological states for improving forecast skill over longer lead times. Hence, an operational water balance modelling system, with satellite data assimilation, has strong potential to add value for assessing and predicting water availability for a range of decision makers across industries and sectors.
For a complete understanding and description of the AWRA-L model equations, please refer to Frost et al. (2018). Here we only present those parts of the model equation related to S0.
The analysis increments after the data assimilation can be calculated as
where denotes the analysed upper layer soil water storage, and denotes the forecast, or initial estimate. The change in S0 affects the drainage to the lower layer soil water storage (D0) and interflow draining laterally from the upper layer (). The corresponding change in drainage to lower layer soil water storage from the increment ΔS0 is calculated as
where and Smax are model parameters representing the saturated hydraulic conductivity and maximum storage of the upper soil layer, respectively. The proportion of overall top layer drainage that is lateral drainage (β0) is given as
where β and kβ are the slope radians and scaling factor, and kζ is a scaling factor for the ratio of saturated hydraulic conductivity. The revised lower layer soil water storage is then determined as
The change in Ss will lead to the change in the shallow soil water storage (Ds) and lateral interflow (). The soil water storage in the lower layer is thus updated as
Similarly, the groundwater storage Sg will be adjusted with the increment of deep soil layer drainage.
The total runoff () should be updated as
where kr is a routing delay factor.
The surface water storage Sr should be updated accordingly as
The total evapotranspiration change (ΔEtot) caused by the changes in S0 and Ss can be updated as follows:
where Es is the evaporation flux from the surface soil store (S0), and Et is the total actual plant transpiration. The term δEs is given as
where is relative soil evaporation, and fsat is the fraction of the grid cell that is saturated, and
The term δEt is from the changes in root water uptake from shallow and deep soil layers as
with
where and are the maximum root water uptake from the shallow soil store and from the deep soil store. and are the water-limiting relative water content from the shallow and deep soil layer.
Finally,
where is the scaling factor corresponding to unlimited soil water supply, with
where wz is the relative soil wetness of layer z, i.e. either 0, s or d.
The Australian Water Resources Assessment (AWRA) Community Modelling System (Frost et al., 2018) code is freely available for download (https://github.com/awracms/awra_cms, last access: 1 September 2021) (AWRA-CMS, 2021). The SMAP product used here is the level-2 enhanced radiometer half-orbit 9 km EASE-grid soil moisture from the US National Snow and Ice Data Center (https://doi.org/10.5067/Q8J8E3A89923) (O'Neill et al., 2020). The SMOS level-2 soil moisture product is available from ESA's SMOS online dissemination service (https://smos-diss.eo.esa.int/oads/access/, last access: 1 September 2019) (ESA, 2019). The MYD13C2 EVI data are accessible through the Land Processes Distributed Active Archive Centre (https://doi.org/10.5067/MODIS/MYD13C2.061) (Didan, 2021). The National Dynamic Land Cover Dataset of Australia is available from Geoscience Australia (http://pid.geoscience.gov.au/dataset/ga/83868, last access: 1 August 2020) (Lymburner et al., 2015).
ST developed and led the implementation of the method in AWRA-CMS. ST led the writing of the manuscript and graphics creation. LR co-wrote the project plan and co-developed the method. LR guided the application and evaluation. LR contributed to manuscript writing. RP facilitated sharing of data feeds, coordinated the transition of method to operational implementation and edited and reviewed the manuscript. JL guided the selection of streamflow observation and reviewed the manuscript. WS guided the modification to AWRA-CMS and reviewed the manuscript. CD co-wrote the project plan and reviewed the manuscript.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We would like to thank Stuart Baron-Hay from the Bureau of Meteorology for his help with implementation of the AWRA-CMS. This research was undertaken with the assistance of resources and services from the National Computational Infrastructure (NCI), which is supported by the Australian Government through the National Collaborative Research Infrastructure Strategy.
This research has been supported by a collaborative research agreement between the Australian Bureau of Meteorology and Australian National University (grant no. 35130).
This paper was edited by Patricia Saco and reviewed by three anonymous referees.
Alemohammad, S. H., McColl, K. A., Konings, A. G., Entekhabi, D., and Stoffelen, A.: Characterization of precipitation product errors across the United States using multiplicative triple collocation, Hydrol. Earth Syst. Sci., 19, 3489–3503, https://doi.org/10.5194/hess-19-3489-2015, 2015.
Alvarez-Garreton, C., Ryu, D., Western, A. W., Su, C. H., Crow, W. T., Robertson, D. E., and Leahy, C.: Improving operational flood ensemble prediction by the assimilation of satellite soil moisture: comparison between lumped and semi-distributed schemes, Hydrol. Earth Syst. Sci., 19, 1659–1676, https://doi.org/10.5194/hess-19-1659-2015, 2015.
Anderson, J., Hoar, T., Raeder, K., Liu, H., Collins, N., Torn, R., and Avellano, A.: The data assimilation research testbed: A community facility, B. Am. Meteorol. Soc., 90, 1283–1296, 2009.
AWRA-CMS – The Australian Water Resources Assessment: Community Modelling System (Frost et al. 2018), Github [code], availalbe at: https://github.com/awracms/awra_cms, last access: 1 September 2021.
Baldwin, D., Manfreda, S., Keller, K., and Smithwick, E.: Predicting root zone soil moisture with soil properties and satellite near-surface moisture data across the conterminous United States, J. Hydrol., 546, 393–404, 2017.
Blankenship, C. B., Case, J. L., Crosson, W. L., and Zavodsky, B. T.: Correction of forcing-related spatial artifacts in a land surface model by satellite soil moisture data assimilation, IEEE Geosci. Remote Sens. Lett., 15, 498–502, 2018.
Bolten, J. D., Crow, W. T., Zhan, X., Jackson, T. J., and Reynolds, C. A.: Evaluating the utility of remotely sensed soil moisture retrievals for operational agricultural drought monitoring, IEEE J.-Stars, 3, 57–66, 2009.
Bouttier, F. and Courtier, P.: Data assimilation concepts and methods March 1999, in: Meteorological training course lecture series 718, ECMWF, 59 pp., available at: https://www.ecmwf.int/node/16928 (last access: 24 August 2021), 2002.
Carrera, M. L., Bilodeau, B., Bélair, S., Abrahamowicz, M., Russell, A., and Wang, X.: Assimilation of passive L-band microwave brightness temperatures in the Canadian land data assimilation system: Impacts on short-range warm season numerical weather prediction, J. Hydrometeorol., 20, 1053–1079, 2019.
Chan, S. K., Bindlish, R., O'Neill, P., Jackson, T., Njoku, E., Dunbar, S., Chaubell, J., Piepmeier, J., Yueh, S., Entekhabi, D., Colliander, A., Chen, F., Cosh, M. H., Caldwell, T., Walker, J., Berg, A., McNairn, H., Thibeault, M., Martinez-Fernandez, J., Uldall, F., Seyfried, M., Bosch, D., Starks, P., Collins, C. H., Prueger, J., van der Velde, R., Asanuma, J., Palecki, M., Small, E. E., Zreda, M., Calvet, J., Crow, W. T., and Kerr, Y.: Development and assessment of the SMAP enhanced passive soil moisture product, Remote Sens. Environ., 204, 931–941, https://doi.org/10.1016/j.rse.2017.08.025, 2018.
Chen, F., Crow, W. T., Bindlish, R., Colliander, A., Burgin, M. S., Asanuma, J., and Aida, K.: Global-scale evaluation of SMAP, SMOS and ASCAT soil moisture products using triple collocation, Remote Sens. Environ., 214, 1–13, 2018.
Crow, W. and Van den Berg, M.: An improved approach for estimating observation and model error parameters in soil moisture data assimilation, Water Resour. Res., 46, W12519, https://doi.org/10.1029/2010WR009402, 2010.
Crow, W. T. and Ryu, D.: A new data assimilation approach for improving runoff prediction using remotely-sensed soil moisture retrievals, Hydrol. Earth Syst. Sci., 13, 1–16, https://doi.org/10.5194/hess-13-1-2009, 2009.
Crow, W. T. and Yilmaz, M. T.: The auto-tuned land data assimilation system (ATLAS), Water Resour. Res., 50, 371–385, 2014.
Davies, T., Cullen, M. J. P., Malcolm, A. J., Mawson, M. H., Staniforth, A., White, A. A., and Wood, N.: A new dynamical core for the Met Office's global and regional modelling of the atmosphere, Q. J. Roy. Meteorol. Soc., 131, 1759–1782, https://doi.org/10.1256/qj.04.101, 2005.
De Lannoy, G. J. and Reichle, R. H.: Global assimilation of multiangle and multipolarization SMOS brightness temperature observations into the GEOS-5 catchment land surface model for soil moisture estimation, J. Hydrometeorol., 17, 669–691, 2016.
De Rosnay, P., Drusch, M., Vasiljevic, D., Balsamo, G., Albergel, C., and Isaksen, L.: A simplified Extended Kalman Filter for the global operational soil moisture analysis at ECMWF, Q. J. Roy. Meteorol. Soc., 139, 1199–1213, https://doi.org/10.1002/qj.2023, 2013.
Dharssi, I., Bovis, K. J., Macpherson, B., and Jones, C. P.: Operational assimilation of ASCAT surface soil wetness at the Met Office, Hydrol. Earth Syst. Sci., 15, 2729–2746, https://doi.org/10.5194/hess-15-2729-2011, 2011.
Didan, K.: MODIS/Aqua Vegetation Indices Monthly L3 Global 0.05Deg CMG V061, [data set], NASA EOSDIS Land Processes DAAC, https://doi.org/10.5067/MODIS/MYD13C2.061, 2021.
Donohue, R. J., Roderick, M. L., and McVicar, T. R.: Roots, storms and soil pores: Incorporating key ecohydrological processes into Budyko's hydrological model, J. Hydrol., 436, 35–50, 2012.
Dorigo, W., Wagner, W., Albergel, C., Albrecht, F., Balsamo, G., Brocca, L., Chung, D., Ertl, M., Forkel, M., and Gruber, A.: ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions, Remote Sens. Environ., 203, 185–215, 2017.
Draper, C. S., Walker, J. P., Steinle, P. J., De Jeu, R. A., and Holmes, T. R.: An evaluation of AMSR-E derived soil moisture over Australia, Remote Sens. Environ., 113, 703–710, 2009.
Draper, C. S., Reichle, R. H., De Lannoy, G. J. M., and Liu, Q.: Assimilation of passive and active microwave soil moisture retrievals, Geophys. Res. Lett., 39, L04401, https://doi.org/10.1029/2011gl050655, 2012.
Entekhabi, D., Njoku, E. G., O'Neill, P. E., Kellogg, K. H., Crow, W. T., Edelstein, W. N., Entin, J. K., Goodman, S. D., Jackson, T. J., Johnson, J., Kimball, J., Piepmeier, J. R., Koster, R. D., Martin, N., McDonald, K. C., Moghaddam, M., Moran, S., Reichle, R., Shi, J. C., Spencer, M. W., Thurman, S. W., Tsang, L., and Van Zyl, J.: The Soil Moisture Active Passive (SMAP) Mission, Proc. IEEE, 98, 704–716, https://doi.org/10.1109/Jproc.2010.2043918, 2010.
Errico, R. M.: What is an adjoint model?, B. Am. Meteorol. Soc., 78, 2577–2592, 1997.
ESA: SMOS, available at: https://smos-diss.eo.esa.int/oads/access/, last access: 1 September 2019.
Figueroa-Bustos, V., Palta, J. A., Chen, Y., and Siddique, K. H.: Characterization of root and shoot traits in wheat cultivars with putative differences in root system size, Agronomy, 8, 109, https://doi.org/10.3390/agronomy8070109, 2018.
Frost, A., Ramchurn, A., and Smith, A.: The australian landscape water balance model (awra-l v6), Technical Report, technical description of the australian water resources assessment landscape model version 6, Bureau of Meteorology, Melbourne, 2018.
Getirana, A., Jung, H. C., Arsenault, K., Shukla, S., Kumar, S., Peters-Lidard, C., Maigari, I., and Mamane, B.: Satellite Gravimetry Improves Seasonal Streamflow Forecast Initialization in Africa, Water Resour. Res., 56, e2019WR026259, https://doi.org/10.1029/2019WR026259, 2020a.
Getirana, A., Rodell, M., Kumar, S., Beaudoing, H. K., Arsenault, K., Zaitchik, B., Save, H., and Bettadpur, S.: GRACE Improves Seasonal Groundwater Forecast Initialization over the United States, J. Hydrometeorol., 21, 59–71, https://doi.org/10.1175/Jhm-D-19-0096.1, 2020b.
Giering, R.: Tangent linear and adjoint biogeochemical models, Geophys. Monogr., 114, 33–48, 2000.
Girotto, M., De Lannoy, G. J., Reichle, R. H., Rodell, M., Draper, C., Bhanja, S. N., and Mukherjee, A.: Benefits and pitfalls of GRACE data assimilation: A case study of terrestrial water storage depletion in India, Geophys. Res. Lett., 44, 4107–4115, 2017.
Hafeez, F., Frost, A., Vaze, J., Dutta, D., Smith, A., and Elmahdi, A.: A new integrated continental hydrological simulation system, Water J. Aust. Water Assoc., 42, 75–82, 2015.
Hawdon, A., McJannet, D., and Wallace, J.: Calibration and correction procedures for cosmic-ray neutron soil moisture probes located across Australia, Water Resour. Res., 50, 5029–5043, https://doi.org/10.1002/2013wr015138, 2014.
Incerti, M. and O'Leary, G.: Rooting depth of wheat in the Victorian Mallee, Aust. J. Exp. Agricult., 30, 817–824, 1990.
Ines, A. V. M., Das, N. N., Hansen, J. W., and Njoku, E. G.: Assimilation of remotely sensed soil moisture and vegetation with a crop simulation model for maize yield prediction, Remote Sens. Environ., 138, 149–164, https://doi.org/10.1016/j.rse.2013.07.018, 2013.
Jones, D. A., Wang, W., and Fawcett, R.: High-quality spatial climate data-sets for Australia, Aust. Meteorol. Ocean, 58, 233, https://doi.org/10.22499/2.5804.003, 2009.
Kerr, Y. H., Waldteufel, P., Wigneron, J. P., Martinuzzi, J. M., Font, J., and Berger, M.: Soil moisture retrieval from space: The Soil Moisture and Ocean Salinity (SMOS) mission, IEEE T. Geosci. Remote, 39, 1729–1735, https://doi.org/10.1109/36.942551, 2001.
Kumar, S. V., Reichle, R. H., Koster, R. D., Crow, W. T., and Peters-Lidard, C. D.: Role of Subsurface Physics in the Assimilation of Surface Soil Moisture Observations, J. Hydrometeorol., 10, 1534–1547, https://doi.org/10.1175/2009jhm1134.1, 2009.
Li, B., Toll, D., Zhan, X., and Cosgrove, B.: Improving estimated soil moisture fields through assimilation of AMSR-E soil moisture retrievals with an ensemble Kalman filter and a mass conservation constraint, Hydrol. Earth Syst. Sci., 16, 105–119, https://doi.org/10.5194/hess-16-105-2012, 2012.
Lymburner, L., Tan, P., McIntyre, A., Thankappan, M., and Sixsmith, J.: Dynamic Land Cover Dataset Version 2.1 [data set], Geoscience Australia, Canberra, available at: http://pid.geoscience.gov.au/dataset/ga/83868 (last access: 1 August 2020), 2015.
Massari, C., Crow, W., and Brocca, L.: An assessment of the performance of global rainfall estimates without ground-based observations, Hydrol. Earth Syst. Sci., 21, 4347–4361, https://doi.org/10.5194/hess-21-4347-2017, 2017.
McColl, K. A., Vogelzang, J., Konings, A. G., Entekhabi, D., Piles, M., and Stoffelen, A.: Extended triple collocation: Estimating errors and correlation coefficients with respect to an unknown target, Geophys. Res. Lett., 41, 6229–6236, 2014.
McVicar, T. R., Van Niel, T. G., Li, L. T., Roderick, M. L., Rayner, D. P., Ricciardulli, L., and Donohue, R. J.: Wind speed climatology and trends for Australia, 1975–2006: Capturing the stilling phenomenon and comparison with near-surface reanalysis output, Geophys. Res. Lett., 35, L20403, https://doi.org/10.1029/2008GL035627, 2008.
Muñoz-Sabater, J.: Incorporation of passive microwave brightness temperatures in the ECMWF soil moisture analysis, Remote Sens., 7, 5758–5784, 2015.
Nguyen, H., Wheeler, M. C., Otkin, J. A., Cowan, T., Frost, A., and Stone, R.: Using the evaporative stress index to monitor flash drought in Australia, Environ. Res. Lett., 14, 064016, https://doi.org/10.1088/1748-9326/ab2103, 2019.
Njoku, E. G. and Entekhabi, D.: Passive microwave remote sensing of soil moisture, J. Hydrol., 184, 101–129, https://doi.org/10.1016/0022-1694(95)02970-2, 1996.
O'Neill, P. E., Chan, S., Njoku, E. G., Jackson, T., Bindlish, R., and Chaubell, J.: SMAP Enhanced L2 Radiometer Half-Orbit 9 km EASE-Grid Soil Moisture, Version 4, [data set], NASA National Snow and Ice Data Center Distributed Active Archive Center, Boulder, Colorado USA, https://doi.org/10.5067/Q8J8E3A89923, 2020.
Pan, M. and Wood, E. F.: Data assimilation for estimating the terrestrial water budget using a constrained ensemble Kalman filter, J. Hydrometeorol., 7, 534–547, https://doi.org/10.1175/Jhm495.1, 2006.
Panciera, R., Walker, J. P., Jackson, T. J., Gray, D. A., Tanase, M. A., Ryu, D., Monerris, A., Yardley, H., Rüdiger, C., and Wu, X.: The soil moisture active passive experiments (SMAPEx): Toward soil moisture retrieval from the SMAP mission, IEEE T. Geosci. Remote, 52, 490–507, 2013.
Patil, A. and Ramsankaran, R.: Improving streamflow simulations and forecasting performance of SWAT model by assimilating remotely sensed soil moisture observations, J. Hydrol., 555, 683–696, 2017.
Pauwels, V. R. N., Hoeben, R., Verhoest, N. E. C., and De Troch, F. P.: The importance of the spatial patterns of remotely sensed soil moisture in the improvement of discharge predictions for small-scale basins through data assimilation, J. Hydrol., 251, 88–102, https://doi.org/10.1016/S0022-1694(01)00440-1, 2001.
Peters-Lidard, C. D., Kumar, S. V., Mocko, D. M., and Tian, Y.: Estimating evapotranspiration with land data assimilation systems, Hydrol. Process., 25, 3979–3992, 2011.
Pipunic, R. C., Walker, J. P., and Western, A.: Assimilation of remotely sensed data for improved latent and sensible heat flux prediction: A comparative synthetic study, Remote Sens. Environ., 112, 1295–1305, https://doi.org/10.1016/j.rse.2007.02.038, 2008.
Rahmoune, R., Ferrazzoli, P., Kerr, Y. H., and Richaume, P.: SMOS Level 2 Retrieval Algorithm Over Forests: Description and Generation of Global Maps, IEEE J.-Stars, 6, 1430–1439, https://doi.org/10.1109/Jstars.2013.2256339, 2013.
Reichle, R. H.: Data assimilation methods in the Earth sciences, Adv. Water Resour., 31, 1411–1418, 2008.
Reichle, R. H. and Koster, R. D.: Global assimilation of satellite surface soil moisture retrievals into the NASA Catchment land surface model, Geophys. Res. Lett., 32, L02404, https://doi.org/10.1029/2004gl021700, 2005.
Renzullo, L. J., van Dijk, A. I. J. M., Perraud, J. M., Collins, D., Henderson, B., Jin, H., Smith, A. B., and McJannet, D. L.: Continental satellite soil moisture data assimilation improves root-zone moisture analysis for water resources assessment, J. Hydrol., 519, 2747–2762, https://doi.org/10.1016/j.jhydrol.2014.08.008, 2014.
Scipal, K., Holmes, T., De Jeu, R., Naeimi, V., and Wagner, W.: A possible solution for the problem of estimating the error structure of global soil moisture data sets, Geophys. Res. Lett., 35, L24403, https://doi.org/10.1029/2008GL035599, 2008.
Sheffield, J. and Wood, E. F.: Characteristics of global and regional drought, 1950–2000: Analysis of soil moisture data from off-line simulation of the terrestrial hydrologic cycle, J. Geophys. Res.-Atmos., 112, D17115, https://doi.org/10.1029/2006jd008288, 2007.
Shokri, A., Walker, J. P., van Dijk, A. I., and Pauwels, V. R.: On the use of adaptive ensemble Kalman filtering to mitigate error misspecifications in GRACE data assimilation, Water Resour. Res., 55, 7622–7637, 2019.
Smith, A. B., Walker, J. P., Western, A. W., Young, R. I., Ellett, K. M., Pipunic, R. C., Grayson, R. B., Siriwardena, L., Chiew, F. H. S., and Richter, H.: The Murrumbidgee soil moisture monitoring network data set, Water Resour. Res., 48, W07701, https://doi.org/10.1029/2012wr011976, 2012.
Stoffelen, A.: Toward the true near-surface wind speed: Error modeling and calibration using triple collocation, J. Geophys. Res.-Oceans, 103, 7755–7766, 1998.
Su, C. H., Ryu, D., Crow, W. T., and Western, A. W.: Beyond triple collocation: Applications to soil moisture monitoring, J. Geophys. Res.-Atmos., 119, 6419–6439, 2014.
Tangdamrongsub, N., Han, S.-C., Yeo, I.-Y., Dong, J., Steele-Dunne, S. C., Willgoose, G., and Walker, J. P.: Multivariate data assimilation of GRACE, SMOS, SMAP measurements for improved regional soil moisture and groundwater storage estimates, Adv. Water Resour., 135, 103477, https://doi.org/10.1016/j.advwatres.2019.103477, 2020.
Tian, S., Tregoning, P., Renzullo, L. J., van Dijk, A. I. J. M., Walker, J. P., Pauwels, V. R. N., and Allgeyer, S.: Improved water balance component estimates through joint assimilation of GRACE water storage and SMOS soil moisture retrievals, Water Resour. Res., 53, 1820–1840, https://doi.org/10.1002/2016wr019641, 2017.
Tian, S., Renzullo, L. J., van Dijk, A. I. J. M., Tregoning, P., and Walker, J. P.: Global joint assimilation of GRACE and SMOS for improved estimation of root-zone soil moisture and vegetation response, Hydrol. Earth Syst. Sci., 23, 1067–1081, https://doi.org/10.5194/hess-23-1067-2019, 2019a.
Tian, S., Van Dijk, A. I. J. M., Tregoning, P., and Renzullo, L. J.: Forecasting dryland vegetation condition months in advance through satellite data assimilation, Nat. Commun., 10, 469, https://doi.org/10.1038/s41467-019-08403-x, 2019b.
Van Dijk, A. I., Peña-Arancibia, J. L., Wood, E. F., Sheffield, J., and Beck, H. E.: Global analysis of seasonal streamflow predictability using an ensemble prediction system and observations from 6192 small catchments worldwide, Water Resour. Res., 49, 2729–2746, 2013.
Van Dijk, A. I. J. M.: AWRA Technical Report 3, Landscape Model (version 0.5) Technical Description, WIRADA, CSIRO Water for a Healthy Country Flagship, Canberra, 2010.
Van Dijk, A. I. J. M. and Renzullo, L. J.: Water resource monitoring systems and the role of satellite observations, Hydrol. Earth Syst. Sci., 15, 39–55, https://doi.org/10.5194/hess-15-39-2011, 2011.
Vogel, E., Lerat, J., Pipunic, R., Frost, A. J., Donnelly, C., Griffiths, M., Hudson, D., and Loh, S.: Seasonal ensemble forecasts for soil moisture, evapotranspiration and runoff across Australia, J. Hydrol., 601, 126620, https://doi.org/10.1016/j.jhydrol.2021.126620, 2021.
Walker, J. P., Willgoose, G. R., and Kalma, J. D.: One-dimensional soil moisture profile retrieval by assimilation of near-surface measurements: A simplified soil moisture model and field application, J. Hydrometeorol., 2, 356–373, 2001.
Wanders, N., Karssenberg, D., de Roo, A., de Jong, S. M., and Bierkens, M. F. P.: The suitability of remotely sensed soil moisture for improving operational flood forecasting, Hydrol. Earth Syst. Sci., 18, 2343–2357, https://doi.org/10.5194/hess-18-2343-2014, 2014a.
Wanders, N., Karssenberg, D., de Roo, A., de Jong, S. M., and Bierkens, M. F. P.: The suitability of remotely sensed soil moisture for improving operational flood forecasting, Hydrol. Earth Syst. Sci., 18, 2343–2357, https://doi.org/10.5194/hess-18-2343-2014, 2014b.
Yan, H., Zarekarizi, M., and Moradkhani, H.: Toward improving drought monitoring using the remotely sensed soil moisture assimilation: A parallel particle filtering framework, Remote Sens. Environ., 216, 456–471, 2018.
Yilmaz, M. T. and Crow, W. T.: Evaluation of assumptions in soil moisture triple collocation analysis, J. Hydrometeorol., 15, 1293–1302, 2014.
Zwieback, S., Dorigo, W., and Wagner, W.: Estimation of the temporal autocorrelation structure by the collocation technique with an emphasis on soil moisture studies, Hydrolog. Sci. J., 58, 1729–1747, 2013.