A two-stage blending approach for merging multiple satellite precipitation estimates and rain gauge observations: an experiment in the northeastern Tibetan Plateau

Substantial biases exist in satellite precipitation estimates (SPEs) over complex terrain regions, and it has always been a challenge to quantify and correct such biases. The combination of multiple SPEs and rain gauge observations would be beneficial to improve the gridded precipitation estimates. In this study, a two-stage blending (TSB) approach is proposed, which firstly reduces the systematic errors of the original SPEs based on a Bayesian correction model and then merges the bias-corrected SPEs with a Bayesian weighting model. In the first stage, the gauge-based observations are assumed to be a generalized regression function of the SPEs and terrain feature. In the second stage, the relative weights of the bias-corrected SPEs are calculated based on the associated performances with ground references. The proposed TSB method has the ability to extract benefits from the bias-corrected SPEs in terms of higher performance and mitigate negative impacts from the ones with lower quality. In addition, Bayesian analysis is applied in the two phases by specifying the prior distributions on model parameters, which enables the posterior ensembles associated with their predictive uncertainties to be produced. The performance of the proposed TSB method is evaluated with independent validation data in the warm season of 2010–2014 in the northeastern Tibetan Plateau. Results show that the blended SPE is greatly improved compared to the original SPEs, even in heavy rainfall events. This study can be expanded as a data fusion framework in the development of high-quality precipitation products in any region of interest.

1 Introduction

High-quality precipitation data are fundamental to the understanding of regional and global hydrological processes. However, it is still difficult to acquire accurate precipitation information in the mountainous regions, e.g., the Tibetan Plateau (TP), due to limited ground sensors (Ma et al., 2015). Satellite sensors can provide precipitation estimates at a large scale (Hou et al., 2014), but performances of available satellite products vary among different retrieval methods and climate areas (Yong et al., 2015; Prat and Nelson, 2015; Ma et al., 2016). Thus, it is suggested to incorporate precipitation estimates from multiple sources into a fusion procedure with full consideration of the strength of individual members and associated uncertainty.

Precipitation data fusion was initially reported by merging radar–gauge rainfall in the mid-1980s (Krajewski, 1987). The Global Precipitation Climatology Project (GPCP) was an earlier attempt for satellite–gauge data fusion, which adopted a mean bias correction method and an inverse-error-variance weighting approach to develop a monthly, 0.25^∘ global precipitation dataset (Huffman et al., 1997). Another popular dataset, the Climate Prediction Center Merged Analysis of Precipitation (CMAP), included global monthly precipitation with a 2.5^∘ × 2.5^∘spatial resolution for a 17-year period by merging gauges, satellites, and reanalysis data using the maximum likelihood estimation method (Xie and Arkin, 1997). Since then, several blending approaches have been developed to generate gridded rainfall products with higher quality by merging gauge, radar, and satellite observations (e.g., Li et al., 2015; Beck et al., 2017; Xie and Xiong, 2011; Yang et al., 2017; Baez-Villanueva et al., 2020). Overall, these fusion methods follow a general concept by eliminating biases in satellite and radar-based data and then merging the bias-corrected satellite and radar estimates with point-wise gauge observations. However, these efforts might be insufficient for quantifying the predicted data uncertainty. Some blended estimates are also partially polluted by the poorly performing individuals (Tang et al., 2018).

This paper develops a new data fusion method that enhances the quantitative modeling of individual error structures, prevents potential negative impacts from lower quality members, and enables an explicit description of a model's predictive uncertainty. In addition, a Bayesian concept for accurate rainfall estimation is proposed based on these assumptions. The Bayesian analysis has the advantage of a statistical post-processing idea that could yield a predictive distribution with quantitative uncertainty (Renard, 2011; Shrestha et al., 2015). For example, a Bayesian kriging approach, which assumes a Gaussian process of precipitation at any location and considers the elevation a covariate, is developed for merging monthly satellite and gauge precipitation data (Verdin et al., 2015). A dynamic Bayesian model averaging (BMA) method, which shows better skill scores than the existing one-outlier-removed (OOR) method, is applied for satellite precipitation data fusion across the TP (Ma et al., 2018; Shen et al., 2014). Given the challenges of quantifying precipitation biases in regions with complex terrain (Derin et al., 2019), continuous efforts are required to extract the potential merit of Bayesian analysis for this critical issue.

In this study, a two-stage blending (TSB) approach is proposed for merging multiple satellite precipitation estimates (SPEs) and ground observations. The experiment is performed in the warm season (from May to September) during 2010–2014 in the northeastern TP (NETP), where a relatively denser network of rain gauges is available compared to other regions of the TP. The TSB method is expected to help with the exploration of multi-source/scale precipitation data fusion in regions with complex terrain.

The remainder of this paper is organized below: Sect. 2 describes the experiment including the study region and precipitation data. Section 3 details the methodology, including the TSB approach, and two existing fusion methods (i.e., BMA and OOR). Results and discussions are presented in Sects. 4 and 5, respectively. The primary findings are summarized in Sect. 6.

2 Study area and data

The study domain is located in the upper Yellow River basin of the NETP (Fig. 1). As shown in the 90 m digital elevation data, the altitude ranges from 785 m in the northeast to 6252 m in the southeast. The total annual precipitation is around 500 mm, and the annual mean temperature is 0.7 ^∘C (Cuo et al., 2013). To avoid snowfall contamination in the gauge observation in the cold season, satellite and ground precipitation data from the warm season (May to September) of 2010 to 2014 are collected for the case study.

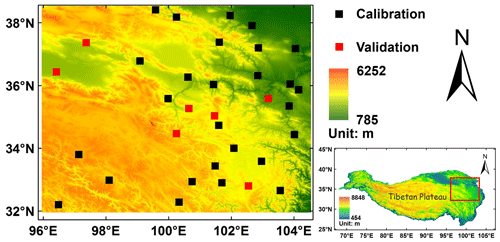
Figure 1 Spatial map of the topography and GR network used in the study, where 27 black cells are used for model calibration and 7 red cells are for model verification.

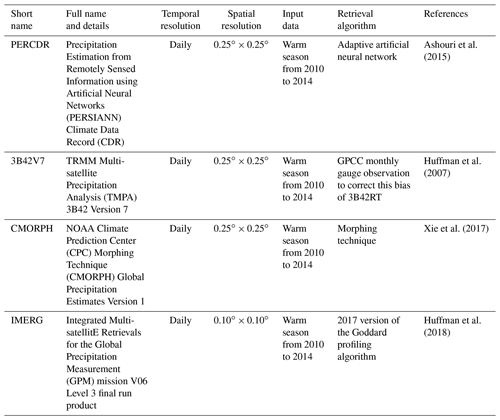
Four mainstream SPEs are used, including Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks – Climate Data Record (PERSIANN-CDR) (Ashouri et al., 2015), Tropical Rainfall Measuring Mission (TRMM) Multi-satellite Precipitation Analysis (TMPA) 3B42 version 7 (3B42V7) (Huffman et al., 2007), National Oceanic and Atmospheric Administration (NOAA) Climate Prediction Center (CPC) Morphing Technique Global Precipitation Analyses Version 1 (CMORPH) (Xie et al., 2017), and the Integrated Multi-satellitE Retrievals for the Global Precipitation Measurement (GPM) mission V06 Level 3 final run product (IMERG) (Huffman et al., 2018). Basic information on the SPEs is shown in Table 1. The IMERG has a 0.10^∘ × 0.10^∘ resolution, and other SPEs have a spatial resolution of 0.25^∘ × 0.25^∘. To eliminate the scale difference in the fusion process, IMERG is resampled from 0.10 to 0.25^∘ using the nearest neighbor interpolation method in advance.

Table 1 Basic information of the original SPEs used in this study.

The China Gauge-based Daily Precipitation Analysis (CGDPA) is used as ground precipitation source. It is developed based on a rain gauge network of 2400 gauge stations in mainland China using a climatology-based optimal interpolation and topographic correction algorithm (Shen and Xiong, 2016). The 34 grid cells with the gauge sites in the regions of interest are assumed as ground references (GRs), and all of the grid cells are independent from the Global Precipitation Climatology Center (GPCC) stations, which are used for bias correction of the TRMM/GPM-era data (e.g., 3B42V7 and IMERG) and CMORPH (Huffman et al., 2007; Hou et al., 2014; Xie et al., 2017; Joyce et al., 2004).

Figure 2 The diagram of the proposed TSB algorithm.

3 Methodology

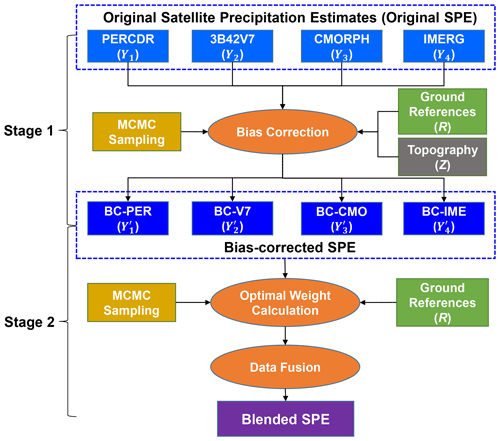
3.1 TSB

The diagram of the TSB method is shown in Fig. 2. Stage 1 is designed to reduce the bias of the original SPEs based on the GRs at the training sites with a Bayesian correction (BC) procedure. In Stage 2, a Bayesian weighting (BW) model is used to merge the bias-corrected SPEs.

3.1.1 Bias correction

(a) Model structure

Let R(st) denote near-surface precipitation at the GR cell s and the tth day. The original SPEs and bias-corrected SPEs of PERCDR, 3B42V7, CMORPH, and IMERG at the GR cell s and the tth day are defined as (Y₁(s,t), Y₂(s,t), …, Y_p(s,t) and ($Y_{\mathrm{1}}^{\prime }(s,t)$, $Y_{\mathrm{2}}^{\prime }(s,t)$, …, $Y_p^{\prime }(s,t)$), respectively. For simplification purposes, and without losing generality, these data at a particular GR cell and day will be denoted by R, (Y₁–Y₄), and ($Y_{\mathrm{1}}^{\prime }$–$Y_{\mathrm{4}}^{\prime }$), while for all GR cells and days, they will be denoted in bold R, (Y₁–Y₄), and (${\mathbf{Y}}_{\mathrm{1}}^{\prime }$–${\mathbf{Y}}_{\mathrm{4}}^{\prime }$).

In Stage 1, we perform a conditional modeling of GRs on each SPE, i.e., the probabilistic distribution f(R) to improve the accuracy of the original SPEs. Given that an appropriate assumption of f(R) is necessary, the goodness-of-fit of the lognormal, Gaussian, and gamma distribution for the GRs is examined graphically by using a probability–probability (PP) plot at the training sets (Fig. 3). It is found that the usage of a gamma distribution is more reliable as the associated PP plot is closer to the diagonal line than the others. For each satellite product, the gamma distribution is parameterized as follows:

$$\begin{array}{}\text{(1)}& R\sim \mathrm{\Gamma }\left({\mathit{\alpha }}_i,{\displaystyle \frac{{\mathit{\alpha }}_i}{{\mathit{\mu }}_i}}\right),\end{array}$$

where i is the number of satellite products, and α_i, μ_i, and $\frac{{\mathit{\alpha }}_i}{{\mathit{\mu }}_i}$ are the shape, mean, and rate parameters of the gamma distribution, respectively. Let the ith SPE Y_i and the associated terrain feature Z be covariates related to the GRs; the mean μ_i in Eq. (1) can be described with generalized linear regression of covariates Y_i and Z, which is written as follows:

$$\begin{array}{}\text{(2)}& \log \left({\mathit{\mu }}_i\right)={\mathit{\delta }}_i+{\mathit{\beta }}_i\cdot \log \left(Y_i\right)+{\mathit{\gamma }}_i\cdot Z,\end{array}$$

where Z, ranging from 0 to 1, is the normalized elevation feature of each site. θ_i={α_i, δ_i, β_i, γ_i} (i=1, …, 4) is summarized as a parameter set and will be estimated in the Bayesian framework. In the following, Z will be denoted as the collection of the normalized elevation feature for all training data.

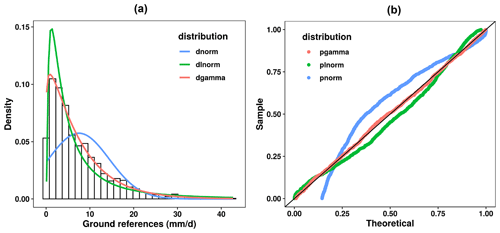
Figure 3 (a) The histogram density plot and (b) the corresponding probability–probability plot of GRs at the training grids in the warm season of 2014 in the NETP, where the red, blue, and green lines shows the fitted gamma, lognormal, and Gaussian distribution, respectively.

According to Bayes' theorem, the posterior probability density function (PDF) of parameter set θ_i is expressed as

$$\begin{array}{}\text{(3)}& f\left({\mathit{\theta }}_i\mathrm{|}R,Y_i,Z\right)\propto f\left(R\mathrm{|}{\mathit{\theta }}_i,Y_i,Z\right)f\left({\mathit{\theta }}_i\right),\end{array}$$

where f(θ_i) is the prior distribution and implies parameter information other than GR and SPE data, and f(R|θ_i, Y_i, Z) is the likelihood function that defines the conditional probability of GRs on the SPE and elevation. The priors of f(θ_i) are initialized as a Cauchy distribution, with α_i in terms of its location at zero and scale as ${\mathit{\sigma }}_{{\mathit{\alpha }}_i}$ in Eq. (4), and Gaussian distribution, with δ_iβ_iγ_i in terms of its mean at zero and standard deviation (SD) at ${\mathit{\sigma }}_{{\mathit{\delta }}_i}{\mathit{\sigma }}_{{\mathit{\beta }}_i}{\mathit{\sigma }}_{{\mathit{\gamma }}_i}$ in Eqs. (5)–(7), respectively.

$$\begin{array}{}\text{(4)}& {\displaystyle }& {\displaystyle }{\mathit{\alpha }}_i\sim \mathrm{Cauchy}\left(\mathrm{0},{\mathit{\sigma }}_{{\mathit{\alpha }}_i}\right)\text{(5)}& {\displaystyle }& {\displaystyle }{\mathit{\delta }}_i\sim \mathrm{Normal}\left(\mathrm{0},{\mathit{\sigma }}_{{\mathit{\delta }}_i}\right)\text{(6)}& {\displaystyle }& {\displaystyle }{\mathit{\beta }}_i\sim \mathrm{Normal}\left(\mathrm{0},{\mathit{\sigma }}_{{\mathit{\beta }}_i}\right)\text{(7)}& {\displaystyle }& {\displaystyle }{\mathit{\gamma }}_i\sim \mathrm{Normal}\left(\mathrm{0},{\mathit{\sigma }}_{{\mathit{\gamma }}_i}\right)\end{array}$$

Given that the assumption of the weakly informative priors ensures the Bayesian inference in an appropriate range (Ma et al., 2020b), the hyperpriors of ${\mathit{\sigma }}_{{\mathit{\alpha }}_i}$, ${\mathit{\sigma }}_{{\mathit{\delta }}_i}{\mathit{\sigma }}_{{\mathit{\beta }}_i}$, and ${\mathit{\sigma }}_{{\mathit{\gamma }}_i}$ are specified as 2, 10, 10, and 10, respectively.

(b) Parameter estimation

The estimation of the posterior distribution f(θ_i|R, Y_i, Z) in Eq. (3) becomes difficult as its dimension grows with the number of parameters (Renard, 2011; Ma and Chandrasekar, 2020). Robertson et al. (2013) obtained the maximum a posteriori (MAP) solution for model parameters using a stepwise method. Here, the Markov chain Monte Carlo (MCMC) technique with its sampling algorithm as the No-U-Turn Sampler (NUTS) variant of Hamiltonian Monte Carlo in the Stan program is performed to address this issue (Gelman et al., 2013). The sampling records of model parameters are obtained based on the training data in the warm season of 2014 in the NETP. Since we only have four parameters in this model, the MCMC converges very quickly. Thus, we run a chain of length 2000, removing the first 1000 iterations as the warm-up period and retaining the second 1000 iterations. The parameter samples of these 1000 iterations are the samples of the posterior distribution f(θ_i|R, Y_i, Z).

(c) Bayesian inference

Based on the posterior distribution of parameter set θ_i of each SPE, calculating the bias-corrected SPE R^* at new site is of interest. It can be quantitatively simulated from its posterior distribution in Eq. (8) using the associated SPE $Y_i^{*}$, normalized elevation $Z_i^{*}$, and training data R, Y_iZ:

$$\begin{array}{}\text{(8)}& f\left(R^{*}\mathrm{|}{Y}_i^{*},Z_i^{*},R,Y_i,Z\right)=\int f\left(R^{*},{\mathit{\theta }}_i\mathrm{|}{Y}_i^{*},Z_i^{*},R,Y_i,Z\right)\mathrm{d}{\mathit{\theta }}_i.\end{array}$$

Following the rule of joint probabilistic distributions, the right term inside the integral of Eq. (8) can be written as

$$\begin{array}{}\text{(9)}& \begin{array}{rl}f\left(R^{*},{\mathit{\theta }}_i\mathrm{|}{Y}_i^{*},Z_i^{*},R,Y_i,Z\right)=& f\left(R^{*}\mathrm{|}{Y}_i^{*},Z_i^{*},R,Y_i,Z,{\mathit{\theta }}_i\right)\\ & f\left({\mathit{\theta }}_i\mathrm{|}{Y}_i^{*},Z_i^{*},R,Y_{i}Z\right).\end{array}\end{array}$$

Given that the new bias-corrected SPE R^* is independent from the training data, the first term of the right side in Eq. (9) is transformed as

$$\begin{array}{}\text{(10)}& f\left(R^{*}\mathrm{|}{Y}_i^{*},Z_i^{*},R,Y_i,Z,{\mathit{\theta }}_i\right)=f\left(R^{*}\mathrm{|}{Y}_i^{*},Z_i^{*},{\mathit{\theta }}_i\right).\end{array}$$

Since the parameters θ_i are only dependent upon the training data RY_i, Z, the second term of the right side in Eq. (9) is expressed as

$$\begin{array}{}\text{(11)}& f\left({\mathit{\theta }}_i\mathrm{|}{Y}_i^{*},Z_i^{*},R,Y_i,Z\right)=f\left({\mathit{\theta }}_i\mathrm{|}R,Y_i,Z\right).\end{array}$$

Therefore, the predictive PDF of R^* in Eq. (8) is written below:

$$\begin{array}{}\text{(12)}& \begin{array}{rl}f\left(R^{*}\mathrm{|}{Y}_i^{*},Z_i^{*},R,Y_i,Z\right)=& \int f\left(R^{*}\mathrm{|}{Y}_i^{*},Z_i^{*},{\mathit{\theta }}_i\right)\\ & f\left({\mathit{\theta }}_i\mathrm{|}R,Y_i,Z\right)\mathrm{d}{\mathit{\theta }}_i.\end{array}\end{array}$$

Since there is no general way to calculate the associated integral in Eq. (12), the prediction is performed using the MCMC iterated samplings (Renard, 2011). As for each SPE, a numerical algorithm is suggested below, where n_sim stands for the replicate of the post-convergence MCMC samples and is set as 1000 in the case study. Thus, the predicted samples for R^* in Eq. (12) are iterated ($k=\mathrm{1}:n_{\mathrm{sim}}$) as follows:

1. For the ith satellite product, randomly select a parameter sample θ_i={α_i, δ_i, β_i, γ_i} from the MCMC samples.

2. Generate a value $R_k^{*}$ from a Γ(α_i, $\frac{{\mathit{\alpha }}_i}{{\mathit{\mu }}_i^{*}})$, where $\log \left({\mathit{\mu }}_i^{*}\right)={\mathit{\delta }}_i+{\mathit{\beta }}_i\cdot Y_i^{*}+{\mathit{\gamma }}_i\cdot Z^{*}$.

Repeating step 1 and 2 n_sim times, the samples $R_k^{*}$ ($k=\mathrm{1}:n_{\mathrm{sim}}$) are regarded as the realizations of the distribution of the bias-corrected SPE associated with the satellite estimation $Y_i^{*}$ and normalized elevation Z^*. The mean value of the samples $R_k^{*}$, denoted by $Y_i^{\prime }$, is regarded as the bias-corrected SPE, and the associated credible intervals (e.g., 2.5 % and 97.5 % quantiles) are used for predictive uncertainty.

3.1.2 Data merging

Ideally, the blended SPE (B) should be close to GRs, i.e., R. Given the gamma distribution of GRs in Step 1, the blended SPE can be parameterized below:

$$\begin{array}{}\text{(13)}& B\sim \mathrm{\Gamma }\left({\mathit{\alpha }}_B,{\displaystyle \frac{{\mathit{\alpha }}_B}{{\mathit{\mu }}_B}}\right),\end{array}$$

where α_B, μ_B, and $\frac{{\mathit{\alpha }}_B}{{\mathit{\mu }}_B}$ are the shape, mean, and rate parameters, respectively. In this step, the bias-corrected SPEs of four satellites are merged with weight parameters w_i (i=1, …, 4), and ε is the residual error. The data fusion of bias-corrected SPEs specified in the log scale is defined as follows:

$$\begin{array}{}\text{(14)}& {\displaystyle }& {\displaystyle }\log \left({\mathit{\mu }}_B\right)=\sum _{i=\mathrm{1}}^{\mathrm{4}}\log \left(Y_i^{\prime }\right)\cdot w_i+\mathit{\epsilon }\text{(15)}& {\displaystyle }& {\displaystyle }\sum _{i=\mathrm{1}}^{\mathrm{4}}{w}_i=\mathrm{1}\text{(16)}& {\displaystyle }& {\displaystyle }\mathit{\epsilon }\sim \mathrm{Normal}\left(\mathrm{0},{\mathit{\sigma }}_{\mathit{\epsilon }}\right).\end{array}$$

Thereby, all parameters including α_B, w_i, (i=1, 2, … 4) and σ_ε can be estimated from the GRs and bias-corrected SPEs at the training sites. The estimation process in a Bayesian framework is similar to that described in Stage 1. After all parameters are estimated, as similar to the Bayesian inference in Stage 1, the blended SPE at any site and time can be derived with the bias-corrected SPEs and corresponding weights using the MCMC iterations.

3.2 Comparison model

3.2.1 BMA

The BMA method is a statistical algorithm that merges predictive ensembles based on the individual SPE at the training period in regions of interest. Here, the BMA result refers to the ensemble SPE. Based on the law of total probability, the conditional probability of the BMA data on the individual SPEs is expressed as

$$\begin{array}{}\text{(17)}& f\left(\mathrm{BMA}\mathrm{|}{Y}_{\mathrm{1}},\mathrm{\dots },Y_p\right)=\sum _{i=\mathrm{1}}^{p}f\left(\mathrm{BMA}\mathrm{|}{Y}_i\right)\cdot w_i,\end{array}$$

where f(BMA|Y_i) is the predictive PDF given by the individual SPE Y_i, and w_i is the corresponding weight. The log-likelihood function l is applied to calculate the BMA parameter set ϑ, which is written as

$$\begin{array}{}\text{(18)}& l\left(\mathit{\vartheta }\right)=\log \left(\sum _{i=\mathrm{1}}^p{w}_i\times f\left(\mathrm{BMA}\mathrm{|}{Y}_i\right)\right).\end{array}$$

It is assumed that f(BMA|Y_i) follows a Gaussian distribution with its parameters as θ_i, and BMA is ideally close to GRs at any site and time. Equation (18) is written as

$$\begin{array}{}\text{(19)}& l\left(\mathit{\vartheta }\right)=\log \left(\sum _{i=\mathrm{1}}^p{w}_i\times g\left(\mathrm{GR}\mathrm{|}{\mathit{\theta }}_i\right)\right),\end{array}$$

where g(⋅) stands for Gaussian distribution, and ϑ={w_i, θ_i, i=1, …, p}. The optimal BMA parameters ϑ are calculated by maximizing the log-likelihood function using the expectation–maximization algorithm. Before executing the BMA method, both GR and SPE data are preprocessed using the Box–Cox transformation to ensure that f(BMA|Y_i) (i=1, …, 4) is close to Gaussian distribution. As the BMA weights, w_i, i=1, …, 4 are obtained, the BMA data are calculated by weighted sum of the original SPEs at any site and time. More details of the BMA method can be found in Ma et al. (2018).

3.2.2 OOR

The OOR method is defined as the arithmetic mean of the individual SPEs by removing the feature with the largest offset. It is written as

$$\begin{array}{}\text{(20)}& \mathrm{OOR}={\displaystyle \frac{\mathrm{1}}{p-\mathrm{1}}}\sum _{i=\mathrm{1}}^{p-\mathrm{1}}{Y}_i,\end{array}$$

where Y_i is the individual SPE, and p is the number of SPEs. The original SPE with the largest offset among the satellite products is removed, and the average of the remaining SPE is regarded as the OOR result.

3.3 Error analysis

To assess the performance of the proposed TSB method, several statistical error indices including the root mean square error (RMSE), normalized mean absolute error (NMAE), and the Pearson's correlation coefficient (CC) are used in this study. The specific formulas of these metrics can be found below:

$$\begin{array}{}\text{(21)}& {\displaystyle }& {\displaystyle }\mathrm{RMSE}=\sqrt{<(\mathrm{Sim}-\mathrm{Obs}{)}^{\mathrm{2}}>}\text{(22)}& {\displaystyle }& {\displaystyle }\mathrm{NMAE}={\displaystyle \frac{<\mathrm{|}\mathrm{Sim}-\mathrm{Obs}\mathrm{|}>}{<\mathrm{Obs}>}}\times \mathrm{100}\mathit{\%}\text{(23)}& {\displaystyle }& {\displaystyle }\mathrm{CC}={\displaystyle \frac{\sum \left[\right(\mathrm{Sim}-<\mathrm{Sim}>\left)\right(\mathrm{Obs}-<\mathrm{Obs}>\left)\right]}{\sqrt{\sum (\mathrm{Sim}-<\mathrm{Sim}>{)}^{\mathrm{2}}}\sqrt{\sum (\mathrm{Obs}-<\mathrm{Obs}>{)}^{\mathrm{2}}}}},\end{array}$$

where “Sim” and “Obs” stand for the simulated and observed data, respectively; the angle brackets stand for the sample average.

4 Results

In the experiment, model parameters are calibrated on the daily precipitation of warm season in 2014, where GR data at the 27 black grids in Fig. 1 are randomly selected for training the model. The model validation is performed under two scenarios: Scenario 1 will validate the model in space based on the data of the same period in validation stations (i.e., the seven red grids in Fig. 1), and Scenario 2 will validate the model in time based on the data of warm season from 2010 to 2013 at the same 27 black grids in Fig. 1. In addition, we consider a 10-fold cross-validation in space by randomly selecting 7 sites for model validation and the data of the remaining 27 sites as the training set. The performance of the TSB approach is further compared with BMA and OOR in the two scenarios.

4.1 Parameter estimates

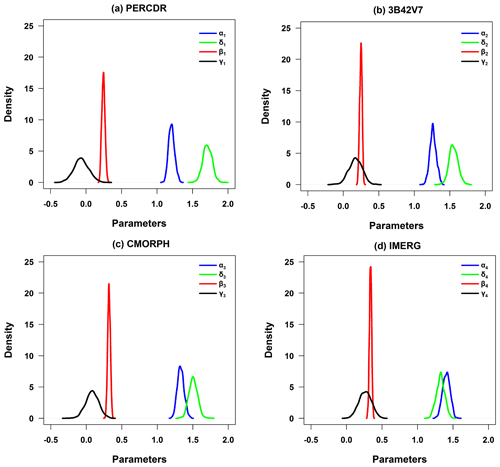
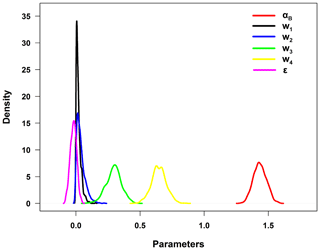
Figures 4 and 5 show the posterior distribution curves of the posterior parameters in Stage 1 and 2, respectively. As for each parameter in the bias-corrected process, the individual SPEs including PERCDR, 3B42V7, CMORPH, and IMERG show a similar pattern (Fig. 4a to d). This shows that the bias structures of the original SPEs have similar characteristics. For all SPEs, the distribution mass of parameter β_i is completely on the right side of zero, which implies that a systematic bias exists for all satellite products. When looking at the effects of elevation, the posterior distribution of parameter γ_i for PERCDR, 3B42V7, and CMORPH (Fig. 4a–c) has a value zero in the middle range of the distribution, which implies that elevation may have little impact on these three satellite products, while for IMERG in Fig. 4d, the distribution mass of parameter γ_i is mostly on the right side of zero, which implies a clear effect of elevation on this satellite product. In the data fusion step (Fig. 5), IMERG has the highest weight and PERCDR has the lowest weight among the four bias-corrected SPEs. Moreover, 3B42V7 and PERCDR have a similar contribution in the blended result. Basically, Bayesian analysis is able to simulate the parameter uncertainty in contrast to traditional statistical methods.

Figure 4 The PDF curves of posterior parameter sets with regard to (a) PERCDR, (b) 3B42V7, (c) CMORPH, and (d) IMERG in the bias correction process of Stage 1.

Figure 5 The PDF curves of posterior parameter sets in the data fusion process of Stage 2.

4.2 Model validation under two scenarios

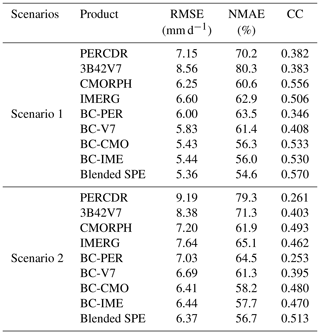
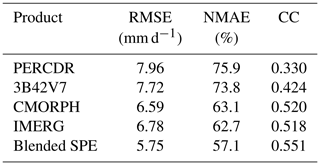
Table 2 presents the summary of the statistical error indices including RMSE, NMAE, and CC of the original (i.e., PERCDR, 3B42V7, CMORPH and IMERG), bias-corrected (i.e., BC-PER, BC-V7, BC-CMO, and BC-IME), and blended SPE under two scenarios in the NETP. Subsection 4.2.1 and 4.2.2 show the performance of the model validation under Scenario 1 and 2, respectively.

Table 2 Summary of statistical error indices (i.e., RMSE, NMAE, and CC) of the original, bias-corrected, and blended SPEs in two scenarios in the NETP.

4.2.1 Scenario 1

The original SPEs show large biases, with the RMSE, NMAE, and CC indices ranging from 6.25–8.56 mm d⁻¹, 60.6 %–80.3 %, and 0.382–0.556, respectively. 3B42V7 has the worst skill, with the highest RMSE of 8.56 mm d⁻¹, the highest NMAE of 80.3 %, and the second lowest CC of 0.383. CMORPH shows the best performance, with the lowest RMSE of 6.25 mm d⁻¹, the lowest NMAE of 60.6 %, and the highest CC of 0.556, which presents its superiority compared with the other original SPEs in the NETP. Based on the BC model, all the bias-corrected SPEs have better agreement with GRs compared with the original SPEs. Their RMSE scores range from 5.43 to 6 mm d⁻¹ and decrease by 13 %–31.8 %, and their NMAE scores vary from 56.0 % to 63.5 %, and decline by 7.1 % to 23.5 %, respectively. Meanwhile, their CC values range from 0.346 to 0.533 after bias correction. With the BW model, the blended SPE is closer to GRs in terms of RMSE, NMAE, and CC at 5.36 mm h⁻¹, 54.6 %, and 0.57, respectively, compared with both the original and bias-corrected SPEs. The RMSE and NMAE values of the blended SPE decrease by 14.3 %–37.4 % and 10 %–32 %, respectively, and the CC value increases by 2.4 %–49.2 %, accordingly, compared to the original SPEs. In addition, the RMSE, NMAE, and CC of the blended SPE increase by 1.4 %–10.8 %, 2.5 %–14.1 %, and 6.8 %–64.8 %, respectively, compared with the bias-corrected SPEs. This proves that the blended SPE exhibits higher quality after Stage 2, due to the ensemble contribution of the bias-corrected SPEs. The relative weight of BC-PER, BC-V7, BC-CMO, and BC-IME is 0.02, 0.038, 0.295, and 0.647, respectively. The BC-IME and BC-PER have the highest and lowest weights, respectively, and the BC-V7 and BC-CMO rank between BC-IME and BC-PER (Fig. 6a). As for the original SPEs, it is found that there is an overestimation when the rainfall is less than 7.6 mm d⁻¹ and an underestimation when the rainfall is more than 7.6 mm d⁻¹. Based on the proposed TSB approach, the blended SPE is closer towards the GRs (Fig. 6b and c). Meanwhile, BC-PER seems to be clearly different from the other bias-corrected SPEs, and up to this point in the study has shown little value for it to be kept in consideration in the merging process. However, it is worth noting that PERCDR can in fact be informative on a case-by-case basis.

Figure 6 (a) The box-and-whisker plots of relative weights for the bias-corrected SPEs, (b) the scatter plots between GRs and the original SPEs, and (c) the PDF of daily rainfall for the GRs and original and blended SPEs with various rain intensities in Scenario 1 in the NETP.

4.2.2 Scenario 2

The proposed TSB approach is also validated in Scenario 2, where the blended SPE shows better performance in terms of its RMSE, NMAE, and CC at 6.37 mm h⁻¹, 56.7 %, and 0.513, respectively, compared with both the original and bias-corrected SPEs. It shows that the original SPEs including PERCDR, 3B42V7, CMORPH, and IMERG have high RMSE and NMAE scores in terms of 7.20–9.19 mm h⁻¹ and 61.9 %–79.3 %, respectively, and low CC values in terms of 0.261–0.493. After the bias correction, the four satellite products have increased their performance, with lower error indices than the original SPEs. The RMSE indices of the bias-corrected SPEs vary from 6.41 to 7.03 mm h⁻¹, and the corresponding NMAE and CC indices are from 57.7 % to 64.5 % and from 0.253 to 0.48, respectively. Based on the data fusion process, the error indices of the blended SPE including RMSE, NMAE, and CC are 6.37 mm h⁻¹, 56.7 %, and 0.513, respectively. It is found that the RMSE and NMAE values of the blended SPE decreased by 11.5 %–30.7 % and 8.4 %–28.5 %, respectively, and the CC value increases by 4.1 %–96.6 % compared with the original SPEs.

As learned from the two validated scenarios, it is proven that the TSB approach has the potential to improve the satellite rainfall accuracy, and it has the ability to extract benefits from SPEs in terms of higher performances and mitigate poor impacts from the ones with lower quality.

4.3 Cross-validation

Figures 7 and 8 show the statistics of evaluation scores of RMSE, NMAE, and CC for the original SPEs and blended estimates at the validation grids, with 10 random tests of the gauge locations in the warm season of 2014. For each test, seven grid sites are randomly selected from the 34 grid cells and used for model verification, and the remaining 27 grid sites are used for training the model.

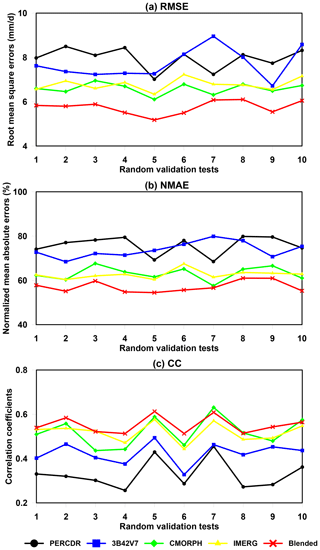
Figure 7 Statistical error indices of the original and blended SPEs for 10 random verified tests in the warm season of 2014 in the NETP: (a) RMSE, (b) NMAE, and (c) CC.

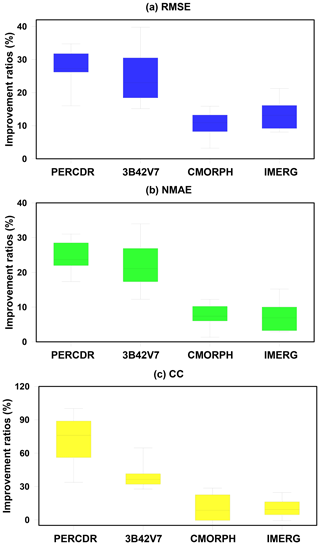
Figure 8 The box-and-whisker plots of improvement ratios of statistics for the blended SPE compared with the original SPEs, including PERCDR, 3B42V7, CMORPH, and IMERG for 10 random verified tests in the warm season of 2014 in the NETP: (a) RMSE, (b) NMAE, and (c) CC.

As for the blended SPE, it achieves similar scores at the validation grids among the 10-fold random samples. The blended SPE shows better skill compared with the original SPEs for each test in terms of RMSE, NMAE, and CC (Fig. 7). Statistically, the mean values of RMSE, NMAE, and CC for the blended SPE are 5.75 mm h⁻¹, 57.1 %, and 0.551, respectively (Table 3). The averaged improvement ratios of RMSE for the blended SPE are 27.6 %, 25 %, 10.6 %, and 13 % compared to the PERCDR, 3B42V7, CMORPH and IMERG, respectively, and a similar performance is seen for NMAE, with average improvement ratios of 24.5 %, 22.3 %, 7.8 %, and 7.3 %, respectively (Table 4). In summary, the 10-fold cross-validation further verified that the blended SPE has a higher accuracy of gridded precipitation than the original satellite products.

Table 3 Summary of the mean values of RMSE, NMAE, and CC for the original and blended SPEs for 10 random verified tests in the warm season of 2014 in the NETP.

Table 4 Mean improvement ratios of statistical error indices of the blended SPE, in terms of RMSE, NMAE, and CC compared with the original SPES for 10 random verified tests in the warm season of 2014 in the NETP.

4.4 Model comparison with BMA and OOR

To assess the performance of the proposed TSB approach, it is beneficial to compare the TSB result with the existing fusion approach. In this study, the BMA approach makes use of four original satellite data and the corresponding GR data at the 27 black grids shown in Fig. 1 in the warm season of 2014 to estimate the optimal BMA weights. In Scenario 1, the BMA data are calculated based on the BMA weights and the original SPEs from the seven red grids in the warm season of 2014, and the OOR data are calculated based on the OOR method using the original SPE data from the seven red grids in the warm season of 2014. In Scenario 2, the BMA data are calculated based on the BMA weights and the original SPEs from the 27 black grids in the warm season from 2010 to 2013, and the OOR result is calculated based on the OOR method and the original SPE data from the 27 black grids in the warm season from 2010 to 2013. Herein, we compare the blended SPE with both the BMA and OOR predictions in two scenarios, and their statistical error summary is shown in Table 5.

Table 5 Summary of statistical error indices (i.e., RMSE, NMAE, and CC) for three fusion methods (i.e., OOR, BMA, and TSB) in the two scenarios in the NETP.

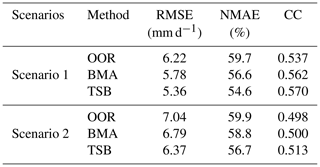
In Scenario 1, the TSB method achieves better skill scores, with RMSE, NMAE, and CC values of 5.36 mm d⁻¹, 54.6 %, and 0.57, respectively, as compared with the BMA and OOR approaches. In addition, OOR shows the worst performance in terms of RMSE, NMAE, and CC at 6.22 mm d⁻¹, 59.7 %, and 0.537, respectively. BMA shows better skill than OOR but worse skill than TSB, in terms of the RMSE, NMAE, and CC values at 5.78 mm d⁻¹, 56.6 %, and 0.562, respectively. In Scenario 2, a similar performance is found for the TSB approach, which has a lower RMSE (6.37 mm d⁻¹) and NMAE (56.7 %) and higher CC (0.513) than both the OOR and BMA results. Basically, as compared with the two existing fusion algorithms (BMA and OOR) in the two validated scenarios, it is confirmed that the TSB method has the advantage of combining the original SPEs and reducing the bias of the satellite precipitation retrievals. It is noted that the daily precipitation estimates follow a gamma distribution (Eq. 1) in this study. In future work it would be interesting to examine whether the gamma distribution can be used in the BMA algorithm without converting it to a Gaussian distribution.

Figure 9 (a) Spatial pattern of gauge-based measurements during a heavy rainfall case of 22 September 2014 in the NETP, where the site IDs 56171, 56173, and 56067 report the top three daily rainfall amounts of 32.3, 30.9, and 28.7 mm, respectively. (b) The corresponding box-and-whisker plots of relative weights of the bias-corrected SPEs in the data fusion process.

4.5 Model performance on a heavy rainfall case

Local recycling plays a premier role in the moisture sources of rainfall extremes in the NETP (Ma et al., 2020a). The 22 September 2014 event was a storm that represents the local heavy rainfall pattern in the warm season. Considering that accurate precipitation estimates for extreme weather are very important for flood hazard mitigation, we investigate the utility of the proposed TSB approach for this event to quantify its performance in an extreme rainfall case (Fig. 9a). The relative weights of BC-PER, BC-V7, BC-CMO, and BC-IME for the blended SPE are 0.264, 0.14, 0.191, and 0.405, respectively, for this event (Fig. 9b). It is found that the IMERG data have the biggest contribution, and the 3B42V7 and CMORPH data have a nearly similar contribution in the blended SPE.

Table 6 Summary of statistical error indices (i.e., RMSE, NMAE, and CC) for the original and blended SPEs during a heavy rainfall event of 22 September 2014 in the NETP.

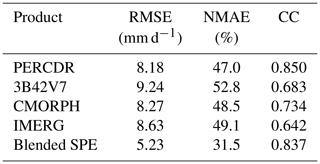
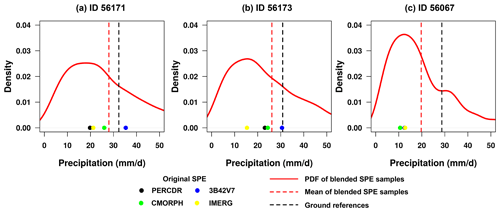
Figure 10 The PDF curves of blended SPE samples and the corresponding mean value at three gauge-based grids for a heavy rainfall case on 22 September 2014: (a) ID 56171, (b) ID 56173, and (c) ID 56067. The original SPEs and GRs at each pixel are also indicated in each panel.

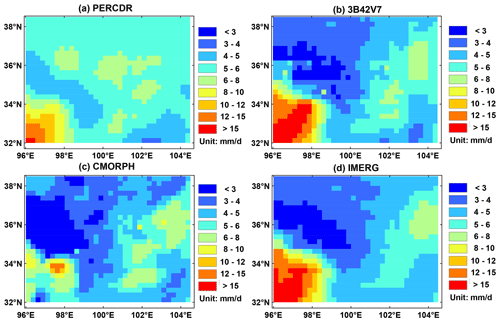
Figure 11 Spatial patterns of the daily mean precipitation in terms of the original SPEs in the warm season of 2010 to 2014 in the NETP: (a) PERCDR, (b) 3B42V7, (c) CMORPH, and (d) IMERG.

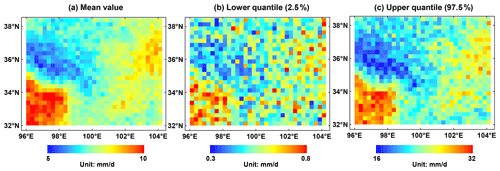
Figure 12 Spatial patterns of the blended SPE in terms of (a) mean, (b) lower quantile (2.5 %), and (c) upper quantile (97.5 %) of daily mean precipitation in the warm season of 2010 to 2014 in the NETP.

Table 6 reports the evaluation statistics reflecting the blended performance for this case. It shows that the RMSE, NMAE, and CC values of the original SPEs range from 8.18–9.24 mm d⁻¹, 47 %–52.8 %, and 0.642–0.85, respectively. Compared to the original SPEs, the blended SPE has a lower RMSE of 5.23 mm d⁻¹, lower NMAE of 31.5 %, and higher CC of 0.837, respectively. The RMSE and NMAE values of the blended SPE decrease by 36.1 %–43.4 % and 33 %–40.3 %, respectively. The performance of the TSB approach is further explored at three gauge cells (i.e., IDs 56171, 56173, 56067), with the top three daily rainfall records on 22 September 2014. Figure 10 shows the PDF curves of blended samples at the three sites in this case. It demonstrates that the blended SPE has the advantage in quantifying the predictive uncertainty on rainfall extremes at each site. For example, at ID 56171, the rainfall estimates that are derived from the original SPEs are 19.8 mm (PERCDR), 35.3 mm (3B42V7), 26 mm (CMORPH), and 21.2 mm (IMERG), respectively. 3B42V7 shows an overestimation, while PERCDR, CMORPH, and IMERG underperform the daily rainfall at the corresponding pixel (Fig. 10a). Based on the proposed TSB approach, the mean value of the merging estimates is 28 mm d⁻¹. At IDs 56173 and 56067, the mean values of the blended SPE are 26.2 and 19.7 mm d⁻¹, respectively, and they are close to GRs with daily amounts of 30.9 and 28.7 mm, respectively (Fig. 10b and c). Overall, these analyses reveal that the TSB algorithm could not only quantify its predictive uncertainty, but also improve the daily rainfall amount, even under heavy rainfall conditions.

4.6 Model application in a spatial domain

It is important to explore the Bayesian ensembles at unknown sites in the domain. As learned from Fig. 11, it seems that each of the original SPEs can capture the spatial pattern of daily mean precipitation in the warm season but might fail in the representation of the precipitation amount, partly because of the satellite retrieval bias in complex terrain and limited GR network. Thus, the TSB method is further applied in the region of interest to demonstrate its performance for daily precipitation in the warm season of 2010–2014 in the NETP. It is found that the blended SPE shows high precipitation in the southwest and low precipitation in the northwest, as well as moderate precipitation in the eastern region. In addition, as compared with the original SPEs, higher values disappear from the spatial map except in the southwest corner for the blended SPE. The possible reason is that daily mean rainfall is the highest in the southwest corner for most SPEs, and larger value exists after the TSB approach. Meanwhile, the predictive Bayesian uncertainties including lower (2.5 %) and upper (97.5 %) quantiles are displayed from Fig. 12b to c to illustrate the blending variation in this application.

5 Discussion

In spite of the superior performance of the TSB algorithm, some issues still need to be considered in practical applications, detailed in the following.

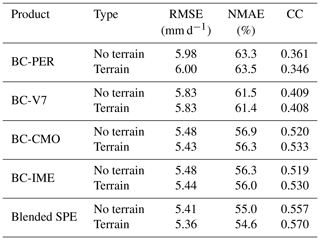
Because of limited knowledge on the influences of complex terrain and local climate on the rainfall patterns in the study area, the elevation feature is considered in the first stage. Table 7 quantifies the impact of the elevation covariate on the bias-corrected and blended SPE performances in Scenario 1 in the warm season of 2014 in the NETP. It is found that the inclusion of the elevation feature provides slightly better skill compared with the results without terrain information in this experiment. Considering that deep convective systems occurring near the mountainous area have an effect on the precipitation cloud (Houze, 2012), more attempts are required to improve the orographic precipitation in the TP in future.

Table 7 Summary of statistical error indices (i.e., RMSE, NMAE, and CC) for bias-corrected and blended SPEs with and without consideration of terrain feature as a covariate in the TSB method in Scenario 1 in the NETP.

The data fusion application is based on four mainstream SPEs, and BC-IME and BC-PER show the best and worst performances among the bias-corrected SPEs in Stage 1. It raises a question as to why the first stage of bias correction is not simply applied and then the best-performing bias-corrected SPE selected as the final product. To address this issue, we investigate the statistical error differences among the BC-IME and blended SPE before and after the removal of BC-PER for 10-fold cross validation in the warm season of 2014 in the NETP (Fig. 13). It is beneficial to involve the Stage 2 in the TSB method because the blended SPE performs better skill than the best-performed bias-corrected SPE (i.e., BC-IME) in Stage 1. The primary reason is that the BW model is designed to integrate various types of bias-corrected SPE, which is limited in the BC model. In addition, both the blended SPEs with and without the consideration of PERCDR show similar performances of the RMSE, NMAE, and CC indices (Fig. 13). It implies that the TSB approach has the advantage of not being impacted by the poor-quality individuals (e.g., BC-PER), partly because the BW model can reallocate the contribution of the bias-corrected SPEs based on their corresponding bias characteristics.

Figure 13 Statistical error indices (i.e., RMSE, NMAE, and CC) of the best-performing bias-corrected SPE (i.e., BC-IME, black) and blended SPE before (red) and after (blue) removing the worst-performing BC-PER, for 10 random verified tests in the warm season of 2014 in the NETP.

In addition, as calculating the blended result at any new sites, the model parameters derived from the training grid sites are assumed to be applicable in the whole domain. Since we have a relatively dense GR network in the survey region, the current assumption is acceptable according to the performance of the blended SPE. It is helpful to give some guidelines on how many training sites are needed to apply the TSB approach in a region with complex terrain and limited GRs. The sensitivity analysis of the number of training grid cells on the performance of blended SPE at the validation grids is explored in Fig. 14. As the number of training sites is increasing, there is a decreasing trend for the RMSE and NMAE values but a slight increasing trend for the CC value. It seems that the performance of the blended SPE becomes similar as the number of training sites increases to 21. We admit that more information from the ground observations would be more beneficial for the blended gridded product in the region of interest. It is noted that, if extended to the TP or global scale, the extension of model parameters and training sites should be carefully considered. For instance, there are few gauges installed in the western and central TP (Ma et al., 2015); it might be a potential risk to directly apply this fusion algorithm to these regions.

Figure 14 Statistical error indices (i.e., RMSE, NMAE, and CC) of the blended SPE at the validation grid locations in terms of a different number of training sites in the warm season of 2014 in the NETP.

The aim of this study is not to model rainfall processes in a target domain but to propose an idea to extract valuable information from available SPEs and provide more reliable gridded precipitation in the high–cold region with complex terrain. Considering its spatiotemporal differences and the existence of many zero-value records, rainfall is extremely difficult to observe and predict (Yong et al., 2015; Bartsotas et al., 2018). With regard to the probability of rainfall occurrence, a zero-inflated model, which is coherent with the empirical distribution of rainfall amount, is expected to improve the proposed TSB algorithm. Also, hourly or even instantaneous precipitation intensity is extremely vital for flood prediction, which should be specifically designed when extending this fusion framework in the next step.

6 Summary and prospects

This study proposes a TSB algorithm for multi-SPE data fusion. A preliminary experiment is conducted in the NETP using four mainstream SPEs (i.e., PERCDR, 3B42V7, CMORPH, and IMERG) to demonstrate the performance of this TSB approach. Primary conclusions are summarized below:

1. This TSB algorithm has two stages and involves the BC and BW models. It is found that this blended method is capable of involving a group of original SPEs. Meanwhile, it provides a convenient way to quantify the fusion performance and the associated uncertainty.

2. The experiment shows that the blended SPE has better skill scores compared to the original SPEs in the two validated scenarios. The 10-fold cross validation in Scenario 1 further confirms the superiority of the TSB algorithm. In addition, it is found that the TSB method outperforms another two existing fusion methods (i.e., BMA and OOR) in the two scenarios. The performance of this fusion method is also demonstrated for a heavy rainfall event in the region of interest.

3. The application proves that this algorithm can allocate the contribution of individual SPEs to the blended result because it is capable of ingesting useful information from uneven individuals and alleviating potential negative impacts from the poorly performing members.

Overall, this work provides an opportunity for merging SPEs in the high–cold region with complex terrain. The evaluation analysis of this TSB method for extended regions (e.g., TP) in terms of higher temporal resolution (e.g., hourly) will be performed in a future study.