Attribution of growing season evapotranspiration variability considering snowmelt and vegetation changes in the arid alpine basins

Previous studies have successfully applied variance decomposition frameworks based on the Budyko equations to determine the relative contribution of variability in precipitation, potential evapotranspiration (E₀), and total water storage changes (ΔS) to evapotranspiration variance (${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$) on different timescales; however, the effects of snowmelt (Q_m) and vegetation (M) changes have not been incorporated into this framework in snow-dependent basins. Taking the arid alpine basins in the Qilian Mountains in northwest China as the study area, we extended the Budyko framework to decompose the growing season ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$ into the temporal variance and covariance of rainfall (R), E₀, ΔS,Q_m, and M. The results indicate that the incorporation of Q_m could improve the performance of the Budyko framework on a monthly scale; ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$ was primarily controlled by the R variance with a mean contribution of 63 %, followed by the coupled R and M (24.3 %) and then the coupled R and E₀ (14.1 %). The effects of M variance or Q_m variance cannot be ignored because they contribute 4.3 % and 1.8 % of ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$, respectively. By contrast, the interaction of some coupled factors adversely affected ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$, and the out-of-phase seasonality between R and Q_m had the largest effect (−7.6 %). Our methodology and these findings are helpful for quantitatively assessing and understanding hydrological responses to climate and vegetation changes in snow-dependent regions on a finer timescale.

1 Introduction

Actual evapotranspiration (ET) drives energy and water exchanges among the hydrosphere, atmosphere, and biosphere (Wang et al., 2007). The temporal variability in ET is thus the combined effect of multiple factors interacting across the soil–vegetation–atmosphere interface (Katul et al., 2012; Xu and Singh, 2005). Investigating the mechanism behind ET variability is also fundamental for understanding hydrological processes. The basin-scale ET variability has been widely investigated with the Budyko framework (Budyko, 1961, 1974); however, most studies are conducted on long-term or inter-annual scales and cannot interpret the short-term ET variability (e.g. monthly scales).

Short-term ET and runoff (Q_r) variance have been investigated recently for their dominant driving factors (Feng et al., 2020; Liu et al., 2019; Wu et al., 2017; Ye et al., 2016; Zeng and Cai, 2015, 2016; Zhang et al., 2016a); to this end, an overall framework was presented by Zeng and Cai (2015) and Liu et al. (2019). Zeng and Cai (2015) decomposed the intra-annual ET variance into the variance and covariance of precipitation (P), potential evapotranspiration (E₀), and water storage change (ΔS) under the Budyko framework based on the work of Koster and Suarez (1999). Subsequently, Liu et al. (2019) proposed a new framework to identify the driving factors of global Q_r variance by considering the temporal variance of P, E₀, ΔS, and other factors such as the climate seasonality, land cover, and human impact. Although the proposed framework performs well for the ET variance decomposition, further research is necessary for considering additional driving factors and for studying regions with unique hydrological processes.

The impact of vegetation change should first be fully considered when studying the variability of ET. Vegetation change significantly affects the hydrological cycle through rainfall interception, evapotranspiration, and infiltration (Rodriguez-Iturbe, 2000; Zhang et al., 2016b). Higher vegetation coverage increases ET and reduces the ratio of Q_r to P (Feng et al., 2016). However, most of the existing studies on ET variance decomposition either ignored the effects of vegetation change or did not quantify its contributions. Vegetation change is closely related to the Budyko controlling parameters, and several empirical relationships have been successfully developed on long-term and inter-annual scales (Li et al., 2013; Liu et al., 2018; Ning et al., 2020; Xu et al., 2013; Yang et al., 2009). However, the relationship between vegetation and its controlling parameters on a finer timescale has received less attention. As such, it is important to quantitatively investigate the contribution of vegetation change to ET variability on a finer timescale.

Second, the short-term water balance equation was the foundation of decomposing ET or Q_r variance. Its general form can be expressed as

$$\begin{array}{}\text{(1)}& P=\mathrm{ET}+Q_{\mathrm{r}}+\mathrm{\Delta }S,\end{array}$$

where P, including liquid (rainfall) and solid (snowfall) precipitation, is the total water source of the hydrological cycle. But this equation is unsuitable for regions where the land surface hydrology is highly dependent on the winter mountain snowpack and spring snowmelt runoff. It has been reported that annual Q_r originating from snowmelt accounts for 20 %–70 % of the total runoff, including the western United States (Huning and AghaKouchak, 2018), coastal areas of Europe (Barnett et al., 2005), western China (Li et al., 2019b), northwest India (Maurya et al., 2018), south of the Hindu Kush (Ragettli et al., 2015), and high-mountain Asia (Qin et al., 2020). In these regions, the mountain snowpack serves as a natural reservoir that stores cold-season P to meet the warm-season water demand (Qin et al., 2020; Stewart, 2009). Thus, the water balance equation should be modified to consider the impacts of snowmelt on runoff on a short-term timescale:

$$\begin{array}{}\text{(2)}& R+Q_{\mathrm{m}}=\mathrm{ET}+Q_{\mathrm{r}}+\mathrm{\Delta }S,\end{array}$$

where R is the rainfall and Q_m is the snowmelt runoff. Many observations and modelling experiments have found that due to global warming, increasing temperatures would induce earlier runoff in the spring or winter and reduce the flows in summer and autumn (Barnett et al., 2005; Godsey et al., 2014; Stewart et al., 2005; Zhang et al., 2015). Therefore, the role of snowmelt change on ET variability in snow-dependent basins on a finer timescale should be studied.

The overall objective of this study was to decompose the ET variance into the temporal variability of multiple factors considering vegetation and snowmelt change. The six cold alpine basins in the Qilian Mountains of northwest China were taken as an example study area. Specifically, we aimed to: (1) determine the dominant driving factor controlling the ET variance, (2) investigate the roles of vegetation and snowmelt change in the variance, and (3) understand the interactions among the controlling factors in ET variance. The proposed method will help quantify the hydrological response to changes in snowmelt and vegetation in snowmelt-dependent regions, and our results will prove to be insightful for water resource management in other similar regions worldwide.

2 Materials

2.1 Study area

Six sub-basins located in the upper reaches of the Heihe, Shiyang, and Shule rivers in the Qilian Mountains were chosen as the study area (Fig. 1). They are important inland rivers in the dry region of northwest China. The runoff generated from the upper reaches contributes to nearly 70 % of the water resources of the entire basin and thus plays an important role in supporting agriculture, industry development, and ecosystem maintenance in the middle and downstream rivers (Cong et al., 2017; Wang et al., 2010a). Snowmelt and in-mountain-generated rainfall make up the water supply system for the upper basins (Matin and Bourque, 2015), and the annual average P exceeds 450 mm in this region. At higher altitudes, as much as 600–700 mm of P can be observed (Yang et al., 2017). Nearly 70 % of the total rainfall concentrates between June and September, while only 19 % of the total rainfall occurs from March to June. Snowmelt runoff is an important water source (Li et al., 2012, 2018, 2016); in the spring, 70 % of the runoff is supplied by snowmelt water (Wang and Li, 2001). Characterised by a continental alpine semi-humid climate, alpine desert glaciers, alpine meadows, forests, and upland meadows are the predominant vegetation distribution patterns (Deng et al., 2013). Furthermore, this region has experienced substantial vegetation changes and resultant hydrological changes in recent decades (Bourque and Mir, 2012; Du et al., 2019; Ma et al., 2008).

Figure 1 The six basins in China's northern Qilian Mountains. The Digital elevation data, at 30 m resolution, were provided by the Geospatial Data Cloud site, Computer Network Information Center, Chinese Academy of Sciences.

2.2 Data

Daily climate data were collected for 25 stations distributed in and around the Qilian Mountains from the China Meteorological Administration. They comprised rainfall, air temperature, sunshine hours, and relative humidity and were used to calculate the monthly E₀ using the Priestley and Taylor (1972) equation.

The monthly runoff at the Dangchengwan, Changmabu, Zhamashike, Qilian, Yingluoxia, and Shagousi hydrological stations were obtained for 2001–2014 from the Bureau of Hydrology and Water Resources, Gansu Province. The sum of the monthly soil moisture and plant canopy surface water with a resolution of $\mathrm{0.25}{}^{\circ }\times \mathrm{0.25}{}^{\circ }$ from the Global Land Data Assimilation System (GLDAS) Noah model was used to estimate the total water storage. The monthly ΔS was calculated as the water storage difference between two neighbouring months. Eight-day composites of the MODIS MOD10A2 Version 6 snow cover product from the MODIS TERRA satellite were used to produce the monthly snow cover area (SCA) of each basin. The SCA data were used to drive the snowmelt runoff model.

A monthly normalised difference vegetation index (NDVI) at a spatial resolution of 1 km from the MODIS MOD13A3.006 product was used to assess the vegetation coverage (M), which can be calculated from the method of Yang et al. (2009):

$$\begin{array}{}\text{(3)}& M={\displaystyle \frac{\mathrm{NDVI}-{\mathrm{NDVI}}_{\min }}{{\mathrm{NDVI}}_{\max }-{\mathrm{NDVI}}_{\min }}},\end{array}$$

where NDVI_max and NDVI_min are the NDVI values of dense forest (0.80) and bare soil (0.05).

ET from the “ground truth of land surface evapotranspiration at regional scale in the Heihe River Basin (2012–2016) ET_map Version 1.0” (hereafter “ET_map”) dataset, was used to validate the reliability of our estimated ET. This dataset was published by National Tibetan Plateau Data Center. It was upscaled from 36 eddy covariance flux tower sites (65 site years) to the regional scale with five machine learning algorithms and then applied to estimate ET for each grid cell (1 km × 1 km) across the Heihe River Basin each day from May to September over the period 2012–2016. It has been evaluated to have high accuracy (Xu et al., 2018). Basins 3, 4, and 5 in our study belong to the headwater sub-basins of Heihe River, and our monthly ET from May to September during 2012–2014 was thus compared with ET_map.

3 Methods

3.1 The Budyko framework at monthly scales

Probing the ET variability in the growing season can provide basic scientific reference points for agricultural activities and water resource planning and management (Li et al., 2015; Wagle and Kakani, 2014). Thus, we focus on the growing season ET variability on a monthly scale in this study.

Among the mathematical forms of the Budyko framework, this study employed the function proposed by Choudhury (1999) and Yang et al. (2008) to assess the basin water balance for good performance (Zhou et al., 2015):

$$\begin{array}{}\text{(4)}& \mathrm{ET}={\displaystyle \frac{P_e\times E_{\mathrm{0}}}{(P_e^n+E_{\mathrm{0}}^n{)}^{\mathrm{1}/n}}},\end{array}$$

where n is the controlling parameter of the Choudhury–Yang equation. P_e is the total available water supply for ET. In previous studies, P_e included P and ΔS ($P_e=P-\mathrm{\Delta }S$) on a finer timescale (Liu et al., 2019; Zeng and Cai, 2015; Zhang et al., 2016a), but snowmelt runoff should also be considered in the snow-dependent basins. Thus, P_e can be defined as

$$\begin{array}{}\text{(5)}& P_e=R+Q_{\mathrm{m}}-\mathrm{\Delta }S.\end{array}$$

Equation (4) can thus be redefined as follows:

$$\begin{array}{}\text{(6)}& {\mathrm{ET}}_i={\displaystyle \frac{(R_i+Q_{m_i}-\mathrm{\Delta }{S}_i)\times E_{{\mathrm{0}}_i}}{\left(\right(R_i+Q_{m_i}-\mathrm{\Delta }{S}_i{)}^{n_i}+E_{{\mathrm{0}}_i}^{n_i}{)}^{\mathrm{1}/n_i}}},\end{array}$$

where i indicates each month of the growing season (April to September). After estimating the monthly ET of the growing season using Eq (2), the values of n for each month can be obtained via Eq. (6).

3.2 Estimating the equivalent of snowmelt runoff

With the developed relationship between snowmelt and air temperature (Hock, 2003), the degree-day model simplifies the complex processes and performs well, so it is widely used in snowmelt estimation (Griessinger et al., 2016; Rice et al., 2011; Semadeni-Davies, 1997; Wang et al., 2010a). This study estimated the monthly Q_m using the degree-day model following the Wang et al. (2015) procedure. Specifically, the water equivalent of snowmelt (W, mm) during the period m can be calculated as

$$\begin{array}{}\text{(7)}& {\sum }_{i=\mathrm{1}}^m{W}_i=\mathrm{DDF}{\sum }_{i=\mathrm{1}}^m{T}_i^{+},\end{array}$$

where DDF denotes the degree-day factor (mm/day ⋅ ^∘C) and T⁺ is the sum of the positive air temperatures of each month. After obtaining W, the monthly Q_m of each elevation zone can be expressed as

$$\begin{array}{}\text{(8)}& {\sum }_{i=\mathrm{1}}^m{Q}_{\mathrm{m}i}={\sum }_{i=\mathrm{1}}^m{W}_i{\mathrm{SCA}}_i,\end{array}$$

where SCA_iis the snow cover area of each elevation zone.

According to Gao et al. (2011), the DDF values of Basins 1–6 were set to 3.4, 3.4, 4.0, 4.0, 4.0, and 1.7 mm/day ⋅ ^∘C, respectively. The six basins were divided into seven elevation zones with elevation differences of 500 m. The sum of Q_m in each elevation zone could be considered as the total Q_m of each basin. Previous studies have found that the major snow melting period is from March to July in this area (Wang and Li, 2005; Wu et al., 2015); furthermore, the MODIS snow product also showed that the SCA decreased significantly at the end of July. Thus, the snowmelt runoff from April to July for the growing season was estimated in this study.

3.3 Relationship between the Budyko controlling parameter and vegetation change

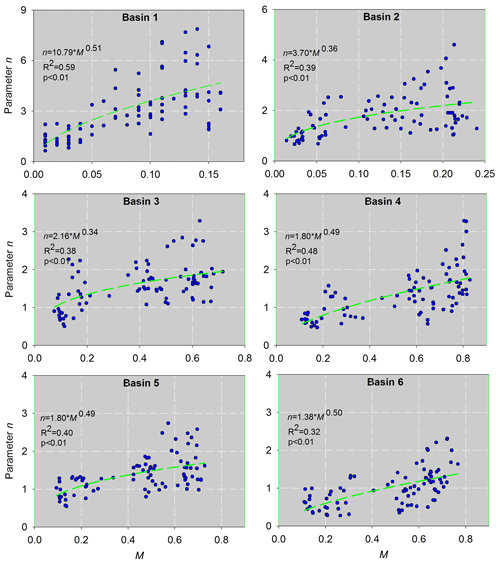
The relationships between the monthly parameters n and M for each basin in the growing season for 2001–2014 are presented in Fig. 2. It can be seen that parameter n was significantly positively related to M in all six basins (p<0.05), which means that ET increased with increasing vegetation conditions under the given climate conditions.

In Eq. (6), when n→0, ET→0, which means M should have the following limiting conditions: if ET→0, T→0 (transpiration), and thus M→0. Considering the relationship shown in Fig. 2 and the above limiting conditions, the general form of parameter n can be expressed by power function followed previous studies (Liu et al., 2018; Ning et al., 2017; Yang et al., 2007):

$$\begin{array}{}\text{(9)}& n=\mathrm{a}\times M^{\mathrm{b}},\end{array}$$

where a and b are constants, and their specific values for each basin are fitted in Fig. 2.

Figure 2 Relationships between the parameter n and the vegetation coverage for each basin on a monthly scale.

3.4 ET variance decomposition

Liu et al. (2019) proposed a framework to identify the driving factors behind the temporal variance of Q_r by combining the unbiased sample variance of Q_r with the total differentiation of Q_r changes. Here, we extended this method by considering the effects of changes in snowmelt runoff and vegetation coverage on ET variance.

By combining Eq. (6) with (9), Eq. (6) can be simplified as ET≈f(R_i, Q_mi, ΔS_i, E_0i, M_i). Thus, the total differentiation of ET changes can be expressed as

$$\begin{array}{}\text{(10)}& \begin{array}{rl}{\mathrm{dET}}_i& ={\displaystyle \frac{\partial f}{\partial R}}\mathrm{d}{R}_i+{\displaystyle \frac{\partial f}{\partial Q_{\mathrm{m}}}}\mathrm{d}{Q}_{{\mathrm{m}}_i}+{\displaystyle \frac{\partial f}{\partial \mathrm{\Delta }S}}\mathrm{d}\mathrm{\Delta }{S}_i\\ & +{\displaystyle \frac{\partial f}{\partial E_{\mathrm{0}}}}\mathrm{d}{E}_{{\mathrm{0}}_i}+{\displaystyle \frac{\partial f}{\partial M}}\mathrm{d}{M}_i+\mathit{\tau },\end{array}\end{array}$$

where τ is the error. $\frac{\partial f}{\partial R}$, $\frac{\partial f}{\partial Q_{\mathrm{m}}}$, $\frac{\partial f}{\partial \mathrm{\Delta }S}$, $\frac{\partial f}{\partial E_{\mathrm{0}}}$, and $\frac{\partial f}{\partial M}$ are the partial differential coefficients of ET to R, Q_m, ΔS,E₀ and M, respectively, which can be calculated as

$$\begin{array}{}\text{(11a)}& {\displaystyle \frac{\partial \mathrm{ET}}{\partial R}}={\displaystyle \frac{\partial \mathrm{ET}}{\partial Q_{\mathrm{m}}}}=-{\displaystyle \frac{\partial \mathrm{ET}}{\partial \mathrm{\Delta }S}}={\displaystyle \frac{\mathrm{ET}}{P_e}}\times \left({\displaystyle \frac{E_{\mathrm{0}}^n}{P_e^n+E_{\mathrm{0}}^n}}\right),\text{(11b)}& {\displaystyle \frac{\partial \mathrm{ET}}{\partial E_{\mathrm{0}}}}={\displaystyle \frac{\mathrm{ET}}{E_{\mathrm{0}}}}\times \left({\displaystyle \frac{P_e^n}{P_e^n+E_{\mathrm{0}}^n}}\right),\text{(11c)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\partial \mathrm{ET}}{\partial M}}& ={\displaystyle \frac{\mathrm{ET}}{n}}\left({\displaystyle \frac{\ln (P_e^n+E_{\mathrm{0}}^n)}{n}}-{\displaystyle \frac{P_e^{n}lnP+E_{\mathrm{0}}^{n}ln{E}_{\mathrm{0}}}{P_e^n+E_{\mathrm{0}}^n}}\right)\\ & \times \mathrm{a}\times \mathrm{b}\times M^{\mathrm{b}-\mathrm{1}}.\end{array}\end{array}$$

The first-order approximation of ET changes in Eq. (10) can be expressed as

$$\begin{array}{}\text{(12)}& \mathrm{\Delta }{\mathrm{ET}}_i\approx {\mathit{\epsilon }}_{\mathrm{1}}\mathrm{\Delta }{R}_i+{\mathit{\epsilon }}_{\mathrm{2}}\mathrm{\Delta }{Q}_{{\mathrm{m}}_i}+{\mathit{\epsilon }}_{\mathrm{3}}\mathrm{\Delta }{S}_i+{\mathit{\epsilon }}_{\mathrm{4}}\mathrm{\Delta }{E}_{{\mathrm{0}}_i}+{\mathit{\epsilon }}_{\mathrm{5}}\mathrm{\Delta }{M}_i,\end{array}$$

where ${\mathit{\epsilon }}_{\mathrm{1}}=\frac{\partial \mathrm{ET}}{\partial R}$; ${\mathit{\epsilon }}_{\mathrm{2}}=\frac{\partial \mathrm{ET}}{\partial Q_{\mathrm{m}}}$; ${\mathit{\epsilon }}_{\mathrm{3}}=\frac{\partial \mathrm{ET}}{\partial \mathrm{\Delta }S}$; ${\mathit{\epsilon }}_{\mathrm{4}}=\frac{\partial \mathrm{ET}}{\partial E_{\mathrm{0}}}$; ${\mathit{\epsilon }}_{\mathrm{5}}=\frac{\partial \mathrm{ET}}{\partial M}$.

In this study, the temporal variance of ET reflects the fluctuation of monthly ET in the growing season for years, which can be quantified by the unbiased sample variance (${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$):

$$\begin{array}{}\text{(13)}& \begin{array}{rl}{\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}& ={\displaystyle \frac{\mathrm{1}}{N-\mathrm{1}}}{\sum }_{i=\mathrm{1}}^N({\mathrm{ET}}_i-\stackrel{\mathrm{‾}}{\mathrm{ET}}{)}^{\mathrm{2}}\\ & ={\displaystyle \frac{\mathrm{1}}{N-\mathrm{1}}}{\sum }_{i=\mathrm{1}}^N(\mathrm{\Delta }{\mathrm{ET}}_i{)}^{\mathrm{2}},\end{array}\end{array}$$

where $\stackrel{\mathrm{‾}}{\mathrm{ET}}$ is the long-term monthly mean of ET. N is the sample size and equals 84 in this study (6 months/year ×14 years=84 months). i is used to index time series of month from 1 to N. ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$ indicates how far a set of monthly ET in growing season is spread out from their average value. The larger the ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$, the larger the fluctuation of ET, and vice versa.

Combining Eq. (12) with (13), ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$ can be decomposed as the contribution from different variance and covariance sources:

$$\begin{array}{}\text{(14)}& \begin{array}{rl}& {\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}=\\ & {\sum }_{i=\mathrm{1}}^N({\mathit{\epsilon }}_{\mathrm{1}}\mathrm{\Delta }{R}_i+{\mathit{\epsilon }}_{\mathrm{2}}\mathrm{\Delta }{Q}_{{\mathrm{m}}_i}+{\mathit{\epsilon }}_{\mathrm{3}}\mathrm{\Delta }{S}_i+{\mathit{\epsilon }}_{\mathrm{4}}\mathrm{\Delta }{E}_{{\mathrm{0}}_i}+{\mathit{\epsilon }}_{\mathrm{5}}\mathrm{\Delta }{M}_i{)}^{\mathrm{2}}.\end{array}\end{array}$$

Expanding Eq. (14), ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$ can be further rewritten as

$$\begin{array}{}\text{(15)}& \begin{array}{rl}{\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}& ={\mathit{\epsilon }}_{\mathrm{1}}^{\mathrm{2}}{\mathit{\sigma }}_R^{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{2}}^{\mathrm{2}}{\mathit{\sigma }}_{Q_{\mathrm{m}}}^{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{3}}^{\mathrm{2}}{\mathit{\sigma }}_{\mathrm{\Delta }S}^{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{4}}^{\mathrm{2}}{\mathit{\sigma }}_{E_{\mathrm{0}}}^{\mathrm{2}}+{\mathit{\epsilon }}_{\mathrm{5}}^{\mathrm{2}}{\mathit{\sigma }}_M^{\mathrm{2}}\\ & +\mathrm{2}{\mathit{\epsilon }}_{\mathrm{1}}{\mathit{\epsilon }}_{\mathrm{2}}\mathrm{cov}\left(R,Q_{\mathrm{m}}\right)+\mathrm{2}{\mathit{\epsilon }}_{\mathrm{1}}{\mathit{\epsilon }}_{\mathrm{3}}\mathrm{cov}\left(R,\mathrm{\Delta }S\right)\\ & +\mathrm{2}{\mathit{\epsilon }}_{\mathrm{1}}{\mathit{\epsilon }}_{\mathrm{4}}\mathrm{cov}\left(R,E_{\mathrm{0}}\right)+\mathrm{2}{\mathit{\epsilon }}_{\mathrm{1}}{\mathit{\epsilon }}_{\mathrm{5}}\mathrm{cov}\left(R,M\right)\\ & +\mathrm{2}{\mathit{\epsilon }}_{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{3}}\mathrm{cov}\left(Q_{\mathrm{m}},\mathrm{\Delta }S\right)+\mathrm{2}{\mathit{\epsilon }}_{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{4}}\mathrm{cov}\left(Q_{\mathrm{m}},E_{\mathrm{0}}\right)\\ & +\mathrm{2}{\mathit{\epsilon }}_{\mathrm{2}}{\mathit{\epsilon }}_{\mathrm{5}}\mathrm{cov}\left(Q_{\mathrm{m}},M\right)+\mathrm{2}{\mathit{\epsilon }}_{\mathrm{3}}{\mathit{\epsilon }}_{\mathrm{4}}\mathrm{cov}\left(E_{\mathrm{0}},\mathrm{\Delta }S\right)\\ & +\mathrm{2}{\mathit{\epsilon }}_{\mathrm{3}}{\mathit{\epsilon }}_{\mathrm{5}}\mathrm{cov}\left(M,\mathrm{\Delta }S\right)+\mathrm{2}{\mathit{\epsilon }}_{\mathrm{4}}{\mathit{\epsilon }}_{\mathrm{5}}\mathrm{cov}\left(E_{\mathrm{0}},M\right),\end{array}\end{array}$$

where σ represents the standard deviation, and cov represents the covariance. Eq. (15) can be further simplified as

$$\begin{array}{}\text{(16)}& \begin{array}{rl}{\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}& =F\left(R\right)+F\left(Q_{\mathrm{m}}\right)+F\left(\mathrm{\Delta }S\right)+F\left(E_{\mathrm{0}}\right)+F\left(M\right)\\ & +F\left(R\mathit{\_}{Q}_{\mathrm{m}}\right)+F\left(R\mathit{\_}\mathrm{\Delta }S\right)+F\left(R\mathit{\_}{E}_{\mathrm{0}}\right)+F\left(R\mathit{\_}M\right)\\ & +F\left(Q_{\mathrm{m}}\mathit{\_}\mathrm{\Delta }S\right)+F\left(Q_{\mathrm{m}}\mathit{\_}{E}_{\mathrm{0}}\right)+F\left(Q_{\mathrm{m}}\mathit{\_}M\right)\\ & +F\left(\mathrm{\Delta }S\mathit{\_}{E}_{\mathrm{0}}\right)+F\left(\mathrm{\Delta }S\mathit{\_}M\right)+F\left(E_{\mathrm{0}}\mathit{\_}M\right),\end{array}\end{array}$$

where F is the individual contributions of each factor; each two factors linked by an underscore represents the interaction effects between them.

By separating out Eq. (16), the relative contribution of each factor (C(X)) to ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$ can be calculated as

$$\begin{array}{}\text{(17)}& C\left(X\right)={\displaystyle \frac{F\left(X\right)}{{\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}}}\times \mathrm{100}\mathit{\%},\end{array}$$

where X represents the 15 components in Eq. (16).

4 Results and discussion

4.1 The effects of monthly storage change and snowmelt runoff in the Budyko framework

The Budyko framework is usually used for analyses of long-term average catchment water balance; however, it was employed for the interpretation of the monthly variability of the water balance in this study. Thus, it's necessary to validate the feasibility of Budyko equation for monthly variability. Furthermore, the impact of ΔS on the representation of Budyko framework on a finer timescale has been assessed by several studies (Chen et al., 2013; Du et al., 2016; Liu et al., 2019; Zeng and Cai, 2015). However, the impact of Q_m and its combined effects with ΔS in snowmelt-dependent basins are mostly ignored. Therefore, we present the water balance in the monthly scale of six basins in the Budyko's framework with three different computations of aridity index ($\mathit{\varphi }=E_{\mathrm{0}}/P_e$) or ET ratio (ET $/$ P_e) in Fig. 3. In Fig. 3a, $\mathrm{ET}=R-Q_{\mathrm{r}}$ when R is considered as water supply, i.e. P_e=R. The points of monthly ET ratio and aridity index in April and May were well below Budyko curves in six basins; the monthly ET ratio was even negative in several years, which means the local rains are not the only sources of ET in this area, especially in spring. In Fig. 3b, $\mathrm{ET}=R-\mathrm{\Delta }S-Q_{\mathrm{r}}$ with $P_e=R-\mathrm{\Delta }S$. Compared with Fig. 3a, the outliers in April and May were improved to a certain extent but negative points still existed, suggesting that except for R, ΔS also play a significant role in maintaining spring ET, but the variability of ET cannot be completely explained by these two variables. In Fig. 3c, $\mathrm{ET}=R-\mathrm{\Delta }S+Q_{\mathrm{m}}-Q_{\mathrm{r}}$ with $P_e=R-\mathrm{\Delta }S+Q_{\mathrm{m}}$. Compared to the points in Fig. 3a, b, all points focused on Budyko's curves more closely in each basin when $P_e=R+Q_{\mathrm{m}}-\mathrm{\Delta }S$. From this comparison, it can be concluded that the Budyko framework is applicable to the monthly scale in snowmelt-dependent basins if the water supply is described accurately by considering ΔS and Q_m.

Figure 3 Plots for the aridity index vs. evapotranspiration index scaled by the available water supply for monthly series in the growing season. The total water availability is (a) R, (b) R−ΔS, and (c) $R+Q_{\mathrm{m}}-\mathrm{\Delta }S$. The n value for each Budyko curve is fitted by long-term averaged monthly data.

4.2 Variations in the growing season water balance

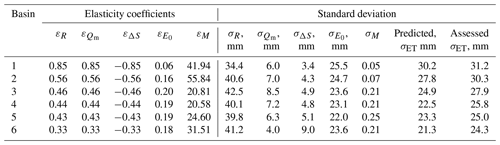
The mean and standard deviation (σ) for each item in the growing season water balance in the six basins are summarised in Tables 1 and 2. The proportion of ΔS in the water balance was small, with a mean value of 1.2 mm; however, its intra-annual fluctuation was relatively large, with a σ_ΔS of 5.3 mm, and σ_ΔS was even as high as 9.0 mm in Basin 6. Compared to ΔS, Q_m represented a larger proportion of the water balance with a mean of 8.5±6.5 mm, indicating its important role in the basin water supply. For this region, the water supply of ET was not only R but also included Q_m and ΔS. Consequently, the mean monthly ET generally approached R (55.8±27.4 mm) or higher values in Basin 1.

Table 1 Averaged monthly hydrometeorological characteristics and vegetation coverage in the growing season (2001–2014).

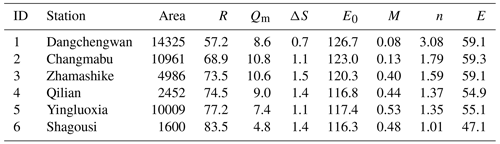
Table 2 The elasticity coefficients of ET for five variables and the standard deviation of each variable for the six basins.

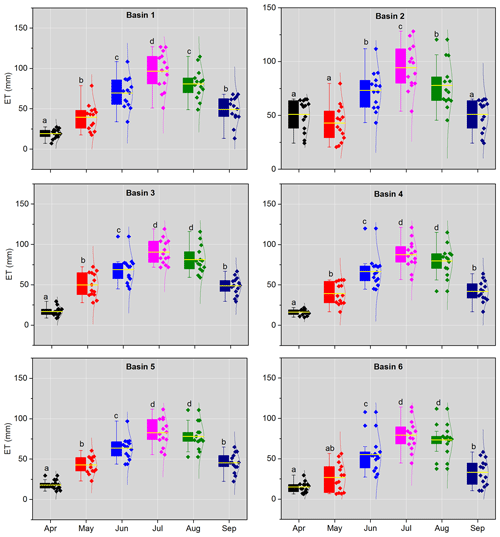
The change patterns of the monthly R, ΔS, Q_m, and ET during the growing season are presented in Figs. 4 and S1–S3 in the Supplement. R exhibited a regular unimodal trend, with a maximum value occurring in July. The maximum Q_m appeared in May, which is a result that is in agreement with previous studies in this region (Wang and Qin, 2017; Zhang et al., 2016c). The peak of ΔS lagged that of Q_m for 1 month in Basins 1–4 and 3 months in Basins 5–6, indicating a recharge of soil water by snowmelt. Yang et al. (2015) also detected the time differences between ΔS and Q_m and found that ΔS had a time lag of 3–4 months more than did Q_m in the Tarim River Basin, another arid alpine basin in northwestern China with hydroclimatic conditions similar to those of the study region. Further, the abundant R in July should contribute to more available water for ΔS; however, the ΔS in July was relatively small. This can be partially explained by the higher water consumption, i.e. the ET in July. In a manner similar to the change pattern of R, ET exhibited a unimodal trend, suggesting the crucial role of R.

Figure 4 Variations in the monthly ET for each basin during 2001–2014. A distribution curve is shown to the right side of each box plot, and the data points are represented by diamonds. Different letters indicate significant differences at p<0.05.

4.3 Controlling factors of the ET variance

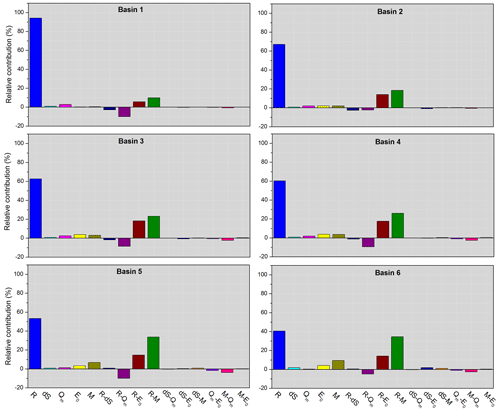
The contributions of R, E₀,Q_m, ΔS,and M to ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$ for each basin are shown in Fig. 5. The results showed that the variance of these five factors could explain ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$, with the total contribution rates ranging from 56.5 % (Basin 6) to 98.6 % (Basin 1). With the decreasing ϕ from Basin 1 to Basin 6, C(R) showed an increasing trend, ranging from 40.6 % to 94.2 %; conversely, C(E₀) exhibited a decreasing trend, ranging from 0.2 % to 4.1 %. This result indicated that R played a key role in ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$ in this region. Similarly, Zhang et al. (2016a) found that C(P) increased rapidly with increasing ϕ, whereas C(E₀) decreased rapidly based on 282 basins in China. Our results are also consistent with previous conclusions that changes in ET or Q_r are dominated by changes in water conditions rather than by energy conditions in dry regions (Berghuijs et al., 2017; Yang et al., 2006; Zeng and Cai, 2016; Zhang et al., 2016a).

The M variance had the second largest contribution to ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$ with a mean C(M) value of 4.3 % for the six basins. Specifically, C(M) showed an increasing trend from 0.5 % to 9.5 % with the decreasing ϕ, implying that the contribution of vegetation change to ET variance was larger in relatively humid basin. It can be explained that transpiration is more sensitive to vegetation change and thus the higher vegetation coverage could increase the proportion of transpiration to ET in humid regions (Niu et al., 2019; Zhang et al., 2020). The Budyko hypothesis stated that a change in ET is controlled by a change in available energy when water supply is not a limiting factor under humid conditions (Budyko, 1974; Yang et al., 2006). The increasing M results in the reallocation of available energy between the canopy and soil. Specifically, more energy is consumed by the canopy and thus increases transpiration. Further, previous studies have found that ET differs greatly among species, because of the difference in canopy roughness, the timing of physiological functioning, water holding capacity of the soil, and rooting depth of the vegetation (Baldocchi et al., 2004; Bruemmer et al., 2012). Generally, forests had larger ET than grasslands (Ma et al., 2020; Zha et al., 2010). The fraction of forest area is relatively high and thus lead to the higher contributions to ET for the whole basin in the humid region. For example, Wei et al. (2018) showed that the global average variation in the annual Q_r due to the vegetation cover change was 30.7±22.5 % in forest-dominated regions on long-term scales, which was higher than our results because of their higher forest cover.

The contribution of the Q_m variance ranked third with a mean value of 1.8 %. Similar as C(R), C(Q_m) showed a downward trend with the decreasing ϕ, ranging from 2.9 % to 0.4 %. The larger C(Q_m) can be explained by the larger variance in Q_m in Basins 2–4 (σ values in Table 2). However, the Q_m in Basin 1 was only 8.6 mm, and C(Q_m) was the largest in all six sub-basins (2.9 %). It can be explained that the contribution of each variable to ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$ was not only the product of the partial differential coefficients, but also relied on its variance value according to Eq. (14). Specifically, the partial differential coefficients of 0.1 for a variable means that a 10 % change in that variable may result in a change in ET by 1 %, which can only reflect the theoretical contribution of each variable. By multiplying the variance value, the actual contribution of each variable could be obtained. The ${\mathit{\epsilon }}_{Q_{\mathrm{m}}}$value was the largest in Basin 1 and thus led to the largest C(Q_m). In addition, shifts in the snowmelt period can also partially explain the positive contribution of the Q_m variance. Like many snow-dominated regions of the world (Barnett et al., 2005), climate warming shifted the timing of snowmelt earlier in the spring in the Qilian Mountains (Li et al., 2012). Earlier snowmelt due to a warmer atmosphere resulted in increased soil moisture and a greater proportion of Q_m to ET (Barnhart et al., 2016; Bosson et al., 2012).

Previous studies have considered that most precipitation changes are transferred to water storage (Wang and Hejazi, 2011); thus, ΔS has distinct impacts on the intra-annual ET or Q_r variance in arid regions (Ye et al., 2016; Zeng and Cai, 2016; Zhang et al., 2016a). However, the study region under investigation has a small C(ΔS) with a mean value of 1.02 %, which is likely to be caused by the vegetation conditions and timescale. First, the six basins have higher vegetation coverage compared to other arid basins; consequently, plant transpiration and rainfall interception consume most of the water supply and reduce the transformation of rainfall to water storage. This is consistent with previous studies that showed that the fractional contribution of transpiration to ET would increase with increasing woody cover (Villegas et al., 2010; Wang et al., 2010b). Second, the large contribution of ΔS to the intra-annual ET or Q_r variance in arid regions is mostly detected at monthly scales. The smaller ΔS in the non-growing season will increase the annual value of σ_ΔS. However, this study focused on the growing season with a smaller σ_ΔS, which consequently led to a lower C(ΔS).

4.4 Interaction effects between controlling factors on the ET variance

The interaction effect of two factors on the ET variance was represented by their covariance coefficients using Eqs. (15) and (16) (Fig. 5). Among the 10 groups of interaction effects, the coupled R and M had the largest contribution to the ET variance, with a mean value of 24.3 %. The positive covariance of R and M indicated that M changes in-phase with R (i.e. R occurred in the growing season), thus increasing the ET variance. C(R_M) showed an increasing trend from 9.9 % to 34.6 % with decreasing ϕ. With different water conditions, the types and proportions of the main ecosystems varied across basins. In particular, the forest cover showed an increasing trend with decreasing ϕ, which partially explained the spatial variations in C(R_M). Previous studies concluded that the differences in physiological and phenological characteristics of ecosystem types are likely to modulate the response of the ecosystem ET to climate variability (Bruemmer et al., 2012; Falge et al., 2002; Li et al., 2019a). For example, Yuan et al. (2010) found that at the beginning of the growing season a significantly higher ET was observed in evergreen needleleaf forests; however, during the middle term of the growing season (June–August), the ET was largest in deciduous broadleaf forests in a typical Alaskan basin.

As an indicator of climate seasonality, the covariance of R and E₀ indicates matching conditions between the water and energy supplies, such as the phase difference between the storm season and warm season. A positive cov(R, E₀) suggests an in-phase R change with E₀ and consequently increases the ET variance. In this study, following C(R_M), the coupled R and E₀ had a large impact on the ET variance with a mean contribution of 14.1 %. With a typical temperate continental climate, the study area has in-phase water and energy conditions; however, its ET is limited by the water supply in spite of the abundant energy supply (Yang et al., 2006). The vegetation receives the largest water supply in the growing season and can vary its biomass seasonally in order to adapt to the R seasonality (Potter et al., 2005; Ye et al., 2016). Consequently, the impact of climate variability on ET variance was mainly reflected by the R seasonality in the study area.

In comparison, the interacting effects between R and Q_m, M and Q_m, R and ΔS, and Q_m and E₀ contributed negatively to the ET variance. Among them, the effect of the coupled R and Q_m was largest with a C(R_Q_m) of −7.6 %. This may suggest that Q_m changes were out of phase with R. Specifically, the major snow melting period was from March to May, when snowmelt water accounts for ∼70 % of the water supply; however, ∼65 % of the annual R occurred in the summer (June–August) (Li et al., 2019a). Overall, Q_m sustains the ET in the spring, but R supports the ET in the summer.

Figure 5 Contribution to the ET variance in the growing season from each component in Eq. (15).

4.5 Uncertainties

Uncertainties from different sources may result in errors for this study. First, this study estimated ΔS and Q_m with the GLDAS Noah land surface model and the degree-day model, respectively. Although the GLDAS_ΔS has been widely used in hydrological studies, it ignores the change in deep groundwater (Nie et al., 2016; Syed et al., 2008; Zhang et al., 2016a), which may lead to errors in ET estimation based on water balance equation. But previous studies showed that the groundwater change in our study area is relatively small and can thus be ignored. For example, Du et al. (2016) used the abcd model to quantitatively determine monthly variations of water balance for the sub-basins of Heihe River (including Basins 3–5 in our study) and found that the soil water storage change have obvious effects on the monthly water balance, whilst the impact of monthly groundwater storage change is negligible. Furthermore, it has been found that any change in climate conditions and underlying basin characteristics will affect the contributions of heat balance components and cause temporal variations of DDF (Kuusisto, 1980; Ohmura, 2001). But previous studies indicated that there is no significant seasonal change in DDF in western China (Zhang et al., 2006); as such, it is acceptable to estimate snowmelt runoff using fixed DDF values in this study. In comparison, the contribution of snow meltwater to runoff (F_s) was 12.9 % in Basin 2 during 1971-2015 using the Spatial Processes in Hydrology model (Li et al., 2019), while F_s was 25 % in Basin 3 from 2001 to 2012 based on geomorphology-based ecohydrological model (Li et al., 2018), <10 % in Basin 6 during 1961–2006 using the snowmelt runoff model (SRM) model (Gao et al., 2011). Our results indicated that the F_s in Basins 2, 3, and 6 were 14.8 %, 24.5 %, and 6.7 %, respectively, which were close to those from different models. Finally, the uncertainties of ΔS and Q_m may lead to errors in ET estimation by the water balance equation. To validate the reliability of our estimated ET, the comparison with ET_map from May to September during 2012–2014 was conducted (Fig. S4 in the Supplement). The results showed that our estimated ET fitted well with ET_map and basically fell around the 1:1 line, indicating ET estimated using water balance equation by considering the items of ΔS and Q_m is acceptable. However, it cannot be ignored that our estimated ET was generally lower than ET_map. The error of rainfall spatial interpolation may explain the underestimation of ET. Most meteorological stations are located at low elevations or in river valleys, but some stations are distributed in high elevations in the Qilian Mountains (Fig. 1). It has been found that rainfall in mountainous regions is generally larger than that in plain regions (Qiang et al., 2015). Even if the topography effect was considered for interpolation, it still resulted in bias in areal rainfall. The best method to improve the quality of spatial rainfall estimation is to increase the density of the monitoring network. However, this process is limited by harsh environment and funds (Buytaert et al., 2006). The error of rainfall will be transferred to contribution quantification of ET variance by underestimating the rainfall contribution while overestimating the Q_m and ΔS contribution.

Second, previous studies concluded that three main factors could be responsible for the variability of n, including underlying physical conditions (such as soil and topography characteristics) (Milly, 1994; Yang et al., 2009), climate seasonality (such as the temporal variability of rainfall and mismatch between water and energy) (Ning et al., 2017; Potter et al., 2005), and vegetation dynamics (Donohue et al., 2007; Zhang et al., 2001). On the short timescale, the changes in soil and topography are negligible and its impact on the variability of n can be ignored. Consequently, the factors that should be considered are climate seasonality and vegetation dynamics. When parameterising n, this study considered M but ignored climate seasonality since the covariance item between R and E₀, i.e. ε₁ε₄cov(R, E₀) in Eq. (15), can represent climate seasonality. In addition, human influence represented by parameter n on the water balance cannot be ignored, which requires further investigation.

5 Conclusions

Recently, several studies have applied a variance decomposition framework based on the Budyko equation to elucidate the dominant driving factors of the ET variance at annual and intra-annual scales by decomposing the intra-annual ET variance into the variance and covariance of P, E₀, and ΔS. Vegetation changes can greatly affect the ET variability but their effects on the ET variance on finer timescales was not quantified by this decomposed method. Further, in snow-dependent regions, the snowpack stores precipitation in winter and releases water in spring; thus, Q_m plays an important role in the hydrological cycle. Therefore, it is also necessary to consider the role of the Q_m changes on the ET variability.

In this study, six arid alpine basins in the Qilian Mountains of northwest China were chosen as examples. The monthly Q_m during 2001–2014 was estimated using the degree-day model, and the growing season ET was calculated using the water balance equation ($\mathrm{ET}=R+Q_s-Q_{\mathrm{r}}-\mathrm{\Delta }S$). The controlling parameter n of the Choudhury–Yang equation was found to be closely correlated with M, as estimated by NDVI data. Thus, by combining the Choudhury–Yang equation with the semi-empirical formula between n and M, the growing season ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$ is decomposed into the temporal variance and covariance of R, E₀, ΔS,Q_m, and M. The main results showed that considering Q_m and ΔS in the water balance equation can improve the performance of the Budyko framework in snow-dependent basins on a monthly scale; ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$ was primarily enhanced by the R variance, followed by the coupled R and M and then the coupled R and E₀. The enhancing effects of the variance in M and Q_m cannot be ignored; however, the interactions between R and Q_m, M and Q_m, R and ΔS, and Q_m and E₀ dampened ${\mathit{\sigma }}_{\mathrm{ET}}^{\mathrm{2}}$. As a simple and effective method, our extended ET variance decomposition method has the potential to be widely used to assess the hydrological responses to changes in the climate and vegetation in snow-dependent regions at finer timescales.