Reconstruction of the 1941 GLOF process chain at Lake Palcacocha (Cordillera Blanca, Peru)

The Cordillera Blanca in Peru has been the scene of rapid deglaciation for many decades. One of numerous lakes formed in the front of the retreating glaciers is the moraine-dammed Lake Palcacocha, which drained suddenly due to an unknown cause in 1941. The resulting Glacial Lake Outburst Flood (GLOF) led to dam failure and complete drainage of Lake Jircacocha downstream, and to major destruction and thousands of fatalities in the city of Huaráz at a distance of 23 km. We chose an integrated approach to revisit the 1941 event in terms of topographic reconstruction and numerical back-calculation with the GIS-based open-source mass flow/process chain simulation framework r.avaflow, which builds on an enhanced version of the Pudasaini (2012) two-phase flow model. Thereby we consider four scenarios: (A) and (AX) breach of the moraine dam of Lake Palcacocha due to retrogressive erosion, assuming two different fluid characteristics; (B) failure of the moraine dam caused by the impact of a landslide on the lake; and (C) geomechanical failure and collapse of the moraine dam. The simulations largely yield empirically adequate results with physically plausible parameters, taking the documentation of the 1941 event and previous calculations of future scenarios as reference. Most simulation scenarios indicate travel times between 36 and 70 min to reach Huaráz, accompanied with peak discharges above 10 000 m³ s⁻¹. The results of the scenarios indicate that the most likely initiation mechanism would be retrogressive erosion, possibly triggered by a minor impact wave and/or facilitated by a weak stability condition of the moraine dam. However, the involvement of Lake Jircacocha disguises part of the signal of process initiation farther downstream. Predictive simulations of possible future events have to be based on a larger set of back-calculated GLOF process chains, taking into account the expected parameter uncertainties and appropriate strategies to deal with critical threshold effects.

1 Introduction

Glacial retreat in high-mountain areas often leads, after some lag time (Harrison et al., 2018), to the formation of proglacial lakes, which are impounded by moraine dams or bedrock swells. Such lakes may drain suddenly, releasing a large amount of water which may result in complex and potentially catastrophic process chains downstream. Glacial lakes and outburst floods (GLOFs) have been subject of numerous studies covering many mountain regions all around the globe (Hewitt, 1982; Haeberli, 1983; Richardson and Reynolds, 2000; Huggel et al., 2003; Breien et al., 2008; Hewitt and Liu, 2010; Bolch et al., 2011; Mergili and Schneider, 2011; Mergili et al., 2013; Clague and O'Connor, 2014; Emmer et al., 2015, 2016; Sattar et al., 2019a, b; Turzewski et al., 2019).

The Cordillera Blanca (Peru) represents the most glacierized mountain chain of the tropics. Glacial lakes and GLOFs are particularly common there (Carey, 2005). A total of 882 high-mountain lakes were identified by Emmer et al. (2016). Some of these lakes are susceptible to GLOFs (Vilímek et al., 2005; Emmer and Vilímek, 2013, 2014; ANA, 2014; Iturrizaga, 2014). A total of 28 geomorphologically effective GLOFs originating from moraine-dammed lakes have been documented (Emmer, 2017). Most recently, GLOFs were recorded at Lake Safuna Alta (2002 – the trigger was a rock avalanche into the lake; Hubbard et al., 2005), at Lake Palcacocha (2003 – landslide-induced overtopping of the dam; Vilímek et al., 2005), and at Lake 513 (2010 – triggered by an ice avalanche; Carey et al., 2012). Lake Artizón Alto was hit by a landslide from a moraine in 2012, which resulted in cascading effects involving three more lakes and entrainment of a considerable amount of debris in the Artizón Valley and, farther downstream, the Santa Cruz Valley (Mergili et al., 2018a). A pronounced peak in the frequency of high-magnitude GLOFs, however, was already observed in the 1940s and 1950s, when lakes of notable size had formed behind steep terminal moraine walls. The most prominent and well-documented GLOF in this period occurred on 13 December 1941, when Lake Palcacocha in the Quilcay Catchment drained suddenly, leading to a process chain that resulted in at least 1600 fatalities and major destruction in the town of Huaráz 23 km downstream (Broggi, 1942; Oppenheim, 1946; Concha, 1952; Wegner, 2014).

In the Cordillera Blanca, the local population is highly vulnerable to high-mountain process chains, often induced by GLOFs (Carey, 2005; Hofflinger et al., 2019). In order to mitigate this threat, tens of lakes in the Cordillera Blanca have been remediated through technical measures such as open cuts, artificial dams, or tunnels during the last decades (Oppenheim, 1946; Zapata, 1978; Portocarrero, 1984, 2014; Carey, 2005; Emmer et al., 2018). Most notably, lowering the lake level of Laguna 513 through a system of tunnels in the 1990s has probably prevented a disaster downstream when a rock-ice avalanche impacted that lake in 2010 (Reynolds, 1998; Reynolds et al., 1998; Schneider et al., 2014). However, the management of GLOF risk is a difficult task (Carey et al., 2014). Anticipation of the impact area and magnitude of GLOF cascades – and, as a consequence, also hazard mapping and the design of technical remediation measures – relies to a large extent on the application of computational mass flow models (GAPHAZ, 2017). Important progress was made since the mid-20th century: various models were developed, and have more recently been implemented in simulation software tools (Voellmy, 1955; Savage and Hutter, 1989; Iverson, 1997; Takahashi et al., 1992; Pitman and Le, 2005; McDougall and Hungr, 2004; Pudasaini and Hutter, 2007; Chisolm and McKinney, 2018). Most of these approaches represent single-phase mixture models. Tools like RAMMS (Christen et al., 2010) or FLO-2D were used for the simulation of GLOFs (Mergili et al., 2011). Schneider et al. (2014), Worni et al. (2014), and Somos-Valenzuela et al. (2016) have sequentially coupled two or more tools for simulating landslide–GLOF cascades. However, single-phase models do not describe the interactions between the solid and the fluid phase, or dynamic landslide–lake interactions, in an appropriate way, so that workarounds are necessary (Gabl et al., 2015). Worni et al. (2014) called for integrated approaches. They would have to build on two- or even three-phase models considering not only water, debris, and ice separately, but also the interactions between the phases and the flow transformations. Pudasaini (2012) introduced a general two-phase flow model considering mixtures of solid particles and viscous fluid which has been used for the simulation of computer-generated examples of sub-aqueous landslides and particle transport (Kafle et al., 2016, 2019) as well as GLOFs (Kattel et al., 2016).

The recently introduced open-source GIS simulation framework r.avaflow (Mergili et al., 2017) applies an extended version of the approach of Pudasaini (2012). It was used to back-calculate the 2012 Santa Cruz process chain involving four lakes (Mergili et al., 2018a), and the 1962 and 1970 Huascarán landslides (Mergili et al., 2018b), both in the Cordillera Blanca. These studies identified the capability of that tool to appropriately simulate the transformations at the boundary of individual processes, where one process transforms to the next, as one of the major challenges. Open issues include the proper understanding of wave generation as a response to landslides impacting high-mountain lakes and, as a consequence, the quantification of essential parameters such as the volume of overtopping water and the discharge (Westoby et al., 2014). Further, uncertainties in the model parameters and the initial conditions accumulate at process boundaries (Schaub et al., 2016), and threshold effects are expected to result in strongly non-linear responses of the model error (Mergili et al., 2018a, b). In high-energy mass flows, the physical characteristics of the processes involved are not always understood at the required level of detail (Mergili et al., 2018b).

On the one hand, flow models and simulation tools can help us to better understand some of the key mechanisms of high-mountain process chains. On the other hand, well documented case studies are important to gain a better understanding on which questions can be tackled with simulation tools, and which questions cannot be answered without further research. In the present work, we explore this field of uncertainty by applying the r.avaflow computational tool to the 1941 Lake Palcacocha GLOF process chain. Thereby, based on the simulation of different scenarios, we investigate on the following research questions:

1. What is the most likely release mechanism of initiating the process chain of the 1941 GLOF of Lake Palcacocha?

2. Are we able to back-calculate this process chain in an empirically adequate way with physically plausible model parameters? Mergili et al. (2018b) reported a trade-off between these two criteria for the simulation of the 1970 Huascarán landslide.

3. What are the major challenges in achieving successful (empirically adequate and physically plausible) simulations?

4. What can we learn with regard to forward calculations of possible future events?

In Sect. 2 we depict the local conditions and the documentation of the event. After having introduced the computational framework r.avaflow (Sect. 3), we describe in detail the simulation input (Sect. 4) and our findings (Sect. 5). We discuss the results (Sect. 6) and finally summarize the key points of the research (Sect. 7).

2 Lake Palcacocha

2.1 Quilcay catchment and Cojup Valley

Lake Palcacocha is part of a proglacial system in the headwaters of the Cojup Valley in the Cordillera Blanca, Peru (Fig. 1). This system was – and is still – shaped by the glaciers originating from the southwestern slopes of Nevado Palcaraju (6264 m a.s.l.) and Nevado Pucaranra (6156 m a.s.l.). A prominent horseshoe-shaped ridge of lateral and terminal moraines marks the extent of the glacier during the first peak of the Little Ice Age, dated using lichenometry to the 17th century (Emmer, 2017). With glacier retreat, the depression behind the moraine ridge was filled with a lake, named Lake Palcacocha. A photograph taken by Hans Kinzl in 1939 (Kinzl and Schneider, 1950) indicates a lake level of 4610 m a.s.l., allowing surficial outflow (Fig. 2a). Using this photograph, Vilímek et al. (2005) estimated a lake volume between 9 and 11 million m³ at that time, whereas an unpublished estimate of the Autoridad Nacional del Agua (ANA) arrived at approx. 13.1 million m³. It is assumed that the situation was essentially the same at the time of the 1941 GLOF (Sect. 2.2).

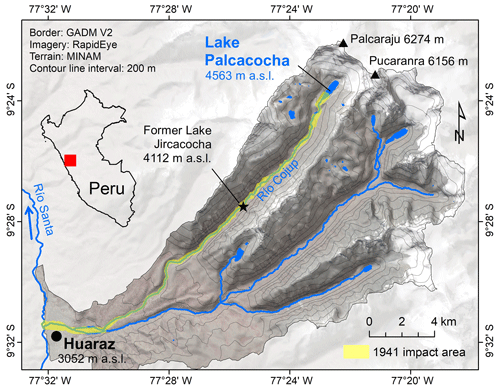
Figure 1 Location and main geographic features of the Quilcay catchment with Lake Palcacocha and the former Lake Jircacocha.

Figure 2 The Quilcay catchment from Lake Palcacocha down to Huaráz. (a) Lake Palcacocha in 1939, two years prior to the 1941 event. (b) The site of former Lake Jircacocha with the breached landslide dam and the former lake level. (c) Breached moraine dam and 1941 GLOF deposits, seen from downstream. (d) Left lateral moraine of Lake Palcacocha with landslide area of 2003. (e) Panoramic view of Lake Palcacocha, with the breach in the moraine dam and the modern lake impounded by a smaller terminal moraine and two artificial dams. (f) Panoramic view of Huaráz with city centre and approximate impact area of the 1941 event. Note that a small part of the lowermost portion of the impact area is hidden behind a hillslope. Photos: (a) Hans Kinzl, 1939 (Kinzl and Schneider, 1950); (b) Martin Mergili, July 2017; (c) Gisela Eberhard, July 2018; (d) and (f) Martin Mergili, July 2017.

The Cojup Valley is part of the Quilcay catchment, draining towards southwest to the city of Huaráz, capital of the department of Ancash located at 3090 m a.s.l. at the outlet to the Río Santa Valley (Callejon de Huaylas). Huaráz had a population of <20 000 at that time (Frey et al., 2018). The distance between Lake Palcacocha and Huaráz is approx. 23 km, whereas the vertical drop is approx. 1500 m. The Cojup Valley forms a glacially shaped high-mountain valley in its upper part whilst cutting through the promontory of the Cordillera Blanca in its lower part. Downstream from Lake Palcacocha by about 8 km (15 km upstream of Huaráz), the landslide-dammed Lake Jircacocha (4.8 million m³; Vilímek et al., 2005) existed until 1941 (Andres et al., 2018). The remnants of this lake are still clearly visible in the landscape in 2017, mainly through the change in vegetation and the presence of fine lake sediments (Fig. 2b). Table 1 summarizes the major characteristics of Lake Palcacocha and Lake Jircacocha before the 1941 GLOF.

Table 1 Characteristics of Lake Palcacocha (1941 and 2016) and Lake Jircacocha (1941), and changes due to the 1941 GLOF. Topographic reconstruction according to field observations and historic photographs. Additional information from Vilímek et al. (2005) and ANA (2016).

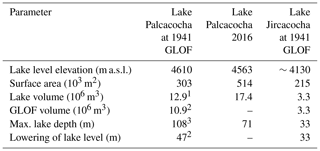
¹ Reference values differ among sources: according to Vilímek et al. (2005), the volume of Lake Palcacocha in 1941 was 9–11 million m³, whereas a reconstruction of ANA resulted in 13.1 million m³. In contrast, Vilímek et al. (2005) estimate a pre-failure volume of 4.8 million m³ for Lake Jircacocha, whereas, according to ANA, the volume was only 3.0 million m³. ² Computed from the difference between the pre-1941 lake level and the modern lake level (before mitigation) of 4563 m. A reconstruction of ANA in 1948 resulted in a residual lake volume of approx. 100 000 m³ and a residual depth of 17 m, both much smaller than values derived through the reconstruction in the present work. One of the reasons for this discrepancy might be the change of the glacier in the period 1941–1948. ³ This value is highly uncertain and might represent an overestimation: the maximum depth of the lake strongly depends on the exact position of the glacier terminus, which was most likely located in an area of increasing lake depth in 1941.

Figure 3 Situation in 1948, seven years after the 1941 event. (a) Residual Lake Palcacocha, and traces of the 1941 event. (b) Huaráz with the impact area of the 1941 event. Imagery source: Servicio Aerofotogramétrico Nacional, Peru.

2.2 1941 multi-lake outburst flood from Lake Palcacocha

On 13 December 1941 part of the city of Huaráz was destroyed by a catastrophic GLOF-induced debris and mud flow, with thousands of fatalities. Portocarrero (1984) gives an estimate of 4000 deaths, Wegner (2014) an estimate of 1800; but this type of information has to be interpreted with care (Evans et al., 2009). The disaster was the result of a multi-lake outburst flood in the upper part of the Cojup Valley. A sudden breach of the dam and the drainage of Lake Palcacocha (Fig. 2c and e) led to a mass flow proceeding down the valley. Part of the eroded dam material, mostly coarse material, blocks, and boulders, was deposited directly downstream from the moraine dam, forming an outwash fan typical for moraine dam failures (Fig. 2c), whereas additional solid material forming the catastrophic mass flow was most likely eroded further along the flow path (both lateral and basal erosion were observed; Wegner, 2014). The impact of the flow on Lake Jircacocha led to overtopping and erosion of the landslide dam down to its base, leading to the complete and permanent disappearance of this lake. The associated uptake of the additional water and debris increased the energy of the flow, and massive erosion occurred in the steeper downstream part of the valley, near the city of Huaráz. Reports by the local communities indicate that the valley was deepened substantially, so that the traffic between villages was interrupted. According to Somos-Valenzuela et al. (2016), the valley bottom was lowered by as much as 50 m in some parts.

The impact area of the 1941 multi-GLOF and the condition of Lake Palcacocha after the event are well documented through aerial imagery acquired in 1948 (Fig. 3). The image of Hans Kinzl acquired in 1939 (Fig. 2a) is the only record of the status before the event. Additional information is available through eyewitness reports (Wegner, 2014). However, as Lake Palcacocha is located in a remote, uninhabited area, no direct estimates of travel times or associated flow velocities are available. Also the trigger of the sudden drainage of Lake Palcacocha remains unclear. Two mechanisms appear most likely: (i) retrogressive erosion, possibly triggered by an impact wave related to calving or an ice avalanche, resulting in overtopping of the dam (however, Vilímek et al., 2005 state that there are no indicators for such an impact), or (ii) internal erosion of the dam through piping, leading to the failure.

2.3 Lake evolution since 1941

As shown on the aerial images from 1948, Lake Palcacocha was drastically reduced to a small remnant proglacial pond, impounded by a basal moraine ridge within the former lake area, at a water level of 4563 m a.s.l., 47 m lower than before the 1941 event (Fig. 3a). However, glacial retreat during the following decades led to an increase in the lake area and volume (Vilímek et al., 2005). After reinforcement of the dam and the construction of artificial drainage in the early 1970s, a lake volume of 514 800 m³ was derived from bathymetric measurements (Ojeda, 1974). In 1974, two artificial dams and a permanent drainage channel were installed, stabilizing the lake level with a freeboard of 7 m to the dam crest (Portocarrero, 2014). By 2003, the volume had increased to 3.69 million m³ (Zapata et al., 2003). In the same year, a landslide from the left lateral moraine caused a minor flood wave in the Cojup Valley (Fig. 2d). In 2016, the lake volume had increased to 17.40 million m³ due to continued deglaciation (ANA, 2016). The potential of further growth is limited since, as of 2017, Lake Palcacocha is only connected to a small regenerating glacier. Further, the lake level is lowered artificially, using a set of siphons (it decreased by 3 m between December 2016 and July 2017). Table 1 summarizes the major characteristics of Lake Palcacocha in 2016. The overall situation in July 2017 is illustrated in Fig. 2c.

2.4 Previous simulations of possible future GLOF process chains

Due to its history, recent growth, and catchment characteristics, Lake Palcacocha is considered hazardous for the downstream communities, including the city of Huaráz (Fig. 2e). Whilst Vilímek et al. (2005) point out that the lake volume would not allow an event comparable to 1941, by 2016 the lake volume had become much larger than the volume before 1941 (ANA, 2016). Even though the lower potential of dam erosion (Somos-Valenzuela et al., 2016) and the non-existence of Lake Jircacocha make a 1941-magnitude event appear unlikely, the steep glacierized mountain walls in the back of the lake may produce ice or rock-ice avalanches leading to impact waves, dam overtopping, erosion, and subsequent mass flows. Investigations by Klimeš et al. (2016) of the steep lateral moraines surrounding the lake indicate that failures and slides from moraines are possible at several sites but do not have the potential to create a major overtopping wave, partly due to the elongated shape of the lake. Rivas et al. (2015) elaborated on the possible effects of moraine-failure-induced impact waves. Recently, Somos-Valenzuela et al. (2016) used a combination of simulation approaches to assess the possible impact of process chains triggered by ice avalanching into Lake Palcacocha on Huaráz. They considered three scenarios of ice avalanches detaching from the slope of Palcaraju (0.5, 1.0, and 3.0 million m³) in order to create flood intensity maps and to indicate travel times of the mass flow to various points of interest. For the large scenario, the mass flow would reach the uppermost part of the city of Huaráz after approx. 1 h 20 min, for the other scenarios this time would increase to 2 h 50 min (medium scenario) and 8 h 40 min (small scenario). For the large scenario in particular, a high level of hazard is identified for a considerable zone near the Quilcay River, whereas zones of medium or low hazard become more abundant with the medium and small scenarios, or with the assumption of a lowered lake level (Somos-Valenzuela et al., 2016). In addition, Chisolm and McKinney (2018) analysed the dynamics impulse waves generated by avalanches using FLOW-3D. A similar modelling approach was applied by Frey et al. (2018) to derive a map of GLOF hazards for the Quilcay catchment. For Lake Palcacocha the same ice avalanche scenarios as applied by Somos-Valenzuela et al. (2016) were employed, with correspondingly comparable results in the Cojup Valley and for the city of Huaráz.

3 The r.avaflow computational tool

r.avaflow is an open-source tool for simulating the dynamics of complex mass flows in mountain areas. It employs a two-phase model including solid particles and viscous fluid, making it different to most other mass flow simulation tools which build on one-phase mixture models. r.avaflow considers the interactions between the phases as well as erosion and entrainment of material from the basal surface. Consequently, it is well-suited for the simulation of complex, cascading flow-type landslide processes. The r.avaflow framework is introduced in detail by Mergili et al. (2017), and only those aspects relevant for the present work are explained here.

The Pudasaini (2012) two-phase flow model is used for propagating mass flows from at least one defined release area through a digital terrain model (DTM). Flow dynamics is computed through depth-averaged equations describing the conservation of mass and momentum for both solid and fluid. The solid stress is computed on the basis of the Mohr–Coulomb plasticity, whereas the fluid is treated with a solid-volume-fraction-gradient-enhanced non-Newtonian viscous stress. Virtual mass due to the relative motion and acceleration as well as generalized viscous drag accounts for the strong transfer of momentum between the phases. Buoyancy is also considered. The momentum transfer results in the simultaneous deformation, separation, and mixing of the phases (Mergili et al., 2018a). Pudasaini (2012) gives a full description of the set of equations.

Certain enhancements are included, compared to the original model: for example, drag and virtual mass are computed according to extended analytical functions constructed by Pudasaini (2019a, b). Additional (complementary) functionalities include surface control, diffusion control, and basal entrainment (Mergili et al., 2017, 2018a, 2019). A conceptual model is used for entrainment: thereby, the empirically derived entrainment coefficient C_E is multiplied with the flow kinetic energy:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}& q_{\mathrm{E},\mathrm{s}}=C_{\mathrm{E}}\left|T_{\mathrm{s}}+T_{\mathrm{f}}\right|{\mathit{\alpha }}_{\mathrm{s},\mathrm{E}},\\ & q_{\mathrm{E},\mathrm{f}}=C_{\mathrm{E}}\left|T_{\mathrm{s}}+T_{\mathrm{f}}\right|\left(\mathrm{1}-{\mathit{\alpha }}_{\mathrm{s},\mathrm{E}}\right).\end{array}\end{array}$$

q_E,s and q_E,f (m s⁻¹) are the solid and fluid entrainment rates, T_s and T_f (J) are the solid and fluid kinetic energies, and α_s,E is the solid fraction of the entrainable material (Mergili et al., 2019). Flow heights and momenta as well as the change of elevation of the basal surface are updated at each time step (Mergili et al., 2017).

Any desired combination of solid and fluid release and entrainable heights can be defined. The main results are raster maps of the evolution of solid and fluid flow heights, velocities, and entrained heights in time. Pressures and kinetic energies are derived from the flow heights and velocities. Output hydrographs can be generated as an additional option (Mergili et al., 2018a). Spatial discretization works on the basis of GIS raster cells: the flow propagates between neighbouring cells during each time step. The Total Variation Diminishing Non-Oscillatory Central Differencing (TVD-NOC) scheme (Nessyahu and Tadmor, 1990; Tai et al., 2002; Wang et al., 2004) is employed for solving the model equations. This approach builds on a staggered grid, in which the system is shifted half the cell size during each step in time (Mergili et al., 2018b).

r.avaflow operates as a raster module of the open-source software GRASS GIS 7 (GRASS Development Team, 2019), employing the programming languages Python and C as well as the R software (R Core Team, 2019). More details about r.avaflow are provided by Mergili et al. (2017).

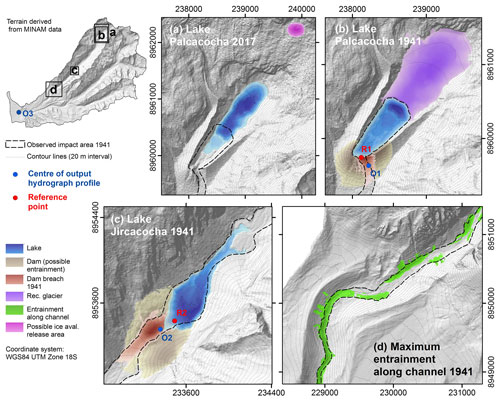
Figure 4 Reconstruction of lakes and topography. (a) Lake Palcacocha in 2017. (b) Lake Palcacocha before the 1941 event. (c) Lake Jircacocha before the 1941 event. (d) Part of the promontory section of the Cojup Valley, with lowering of the valley bottom by up to 50 m. The possible rock avalanche release area is shown in (a) for clarity but is applied to the 1941 situation.

4 Simulation input

The simulations build on the topography, represented by a DTM, and on particular sets of initial conditions and model parameters. For the DTM, we use a 5 m resolution digital elevation model (DEM) provided by the Peruvian Ministry of Environment, MINAM (Horizons, 2013). It was deduced from recent stereo aerial photographs and airborne lidar. The DEM is processed in order to derive a DTM representing the situation before the 1941 event. Therefore, we neglect the possible error introduced by the effects of vegetation or buildings and focus on the effects of the lakes and of erosion (Fig. 4):

1. For the area of Lake Palcacocha the elevation of the lake surface is replaced by a DTM of the lake bathymetry derived from ANA (2016). Possible sedimentation since that time is neglected. The photograph taken by Hans Kinzl in 1939 (Fig. 2a) is used to reconstruct the moraine dam before the breach, and the glacier at the same time. As an exact positioning of the glacier terminus is not possible purely based on the photo, the position is optimized towards a lake volume of approx. 13 million m³, following the estimate of ANA. It is further assumed that there was surficial drainage of Lake Palcacocha as suggested by Fig. 2a, i.e. the lowest part of the moraine crest is set equal to the former lake level of 4610 m a.s.l. (Fig. 4b).

2. For Lake Jircacocha, surficial overflow is also assumed (a situation that is observed for most of the recent landslide-dammed lakes in the Cordillera Blanca). On this basis the landslide dam before its breach is reconstructed, guided by topographic and geometric considerations. The lowest point of the dam crest is set to 4130 m a.s.l. (Fig. 4c).

3. Erosional features along the flow channel are assumed to largely relate to the 1941 event. These features are filled accordingly (see Table 2 for the filled volumes). In particular, the flow channel in the lower part of the valley, reportedly deepened by up to 50 m in the 1941 event (Vilímek et al., 2005), was filled in order to represent the situation before the event in a plausible way (Fig. 4d).

All lakes are considered as fluid release volumes in r.avaflow. The initial level of Lake Palcacocha in 1941 is set to 4610 m a.s.l., whereas the level of Lake Jircacocha is set to 4129 m a.s.l. The frontal part of the moraine dam impounding Lake Palcacocha and the landslide dam impounding Lake Jircacocha are considered as entrainable volumes. Further, those areas filled up along the flow path (Fig. 4d) are considered entrainable, mainly following Vilímek et al. (2005). However, as it is assumed that part of the material was removed through secondary processes or afterwards, only 75 % of the added material are allowed to be entrained. All entrained material is considered 80 % solid and 20 % fluid per volume.

Table 2 Reference information used for back-calculation of the 1941 process chain.

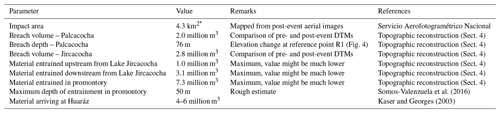
^* This includes the surface of Lake Palcacocha.

The reconstructed lake, breach, and entrainable volumes are shown in Tables 1 and 2. The glacier terminus in 1941 was located in an area where the lake depth increases by several tens of metres, so that small inaccuracies in the position of the glacier tongue may result in large inaccuracies in the volume, so that some uncertainty has to be accepted.

As the trigger of the sudden drainage of Lake Palcacocha is not clear, we consider four scenarios, based on the situation before the event as shown in the photo taken by Hans Kinzl; experiences from other documented GLOF events in the Cordillera Blanca (Schneider et al., 2014; Mergili et al., 2018a); considerations by Vilímek et al. (2005), Portocarrero (2014), and Somos-Valenzuela et al. (2016); and geotechnical considerations:

• A: retrogressive erosion, possibly induced by minor or moderate overtopping. This scenario is related to a possible minor impact wave, caused for example by calving of ice from the glacier front, an increased lake level due to meteorological reasons, or a combination of these factors. In the simulation, the process chain is started by cutting an initial breach into the dam in order to initiate overtopping and erosion. The fluid phase is considered as pure water.

• AX: similar to Scenario A, but with the second phase considered a mixture of fine mud and water. For this purpose, density is increased to 1100 instead of 1000 kg m⁻³, and a yield strength of 5 Pa is introduced (Domnik et al., 2013; Pudasaini and Mergili, 2019; Table 3). For simplicity, we still refer to this mixture as a fluid. Such changed phase characteristics may be related to the input of fine sediment into the lake water (e.g. caused by a landslide from the lateral moraine as triggering event) but are mainly considered here in order to highlight the effects of uncertainties in the definition and parameterization of the two-phase mixture flow.

• B: retrogressive erosion, induced by violent overtopping. This scenario is related to a large impact wave caused by a major rock–ice avalanche or ice avalanche rushing into the lake. In the simulation, the process chain is initiated through a hypothetic landslide of 3 million m³ of 75 % solid and 25 % fluid material, following the large scenario of Somos-Valenzuela et al. (2016) in terms of volume and release area. In order to be consistent with Scenario A, fluid is considered as pure water.

• C: internal erosion-induced failure of the moraine dam. Here, the process chain is induced by the collapse of the entire reconstructed breach volume (Fig. 4b). In the simulation, this is done by considering this part of the moraine not as entrainable volume, but as release volume (80 % solid, 20 % fluid, whereby fluid is again considered as pure water).

Failure of the dam of Lake Jircacocha is assumed to have occurred through overtopping and retrogressive erosion, induced by the increased lake level and a minor impact wave from the flood upstream. No further assumptions of the initial conditions are required in this case.

Table 3 Key model parameters applied to the simulations in the present work. Where three values are given, the first value applies to the glacier, the second value to the remaining area upstream of the dam of Lake Jircacocha, and the third value to the area downstream of the dam of Lake Jircacocha.

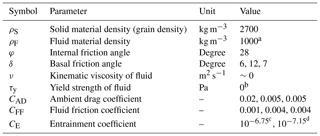
^a The fluid material density is set to 1100 kg m⁻³ in Scenario AX. ^b The yield strength of the fluid phase is set to 5 Pa in Scenario AX. ^c This value applies to the dam of Lake Palcacocha. ^d This value applies to all other areas.

The model parameter values are selected in accordance with experiences gained from previous simulations with r.avaflow for other study areas and are summarized in Table 3. Three parameters mainly characterizing the flow friction (basal friction of solid δ, ambient drag coefficient C_AD, and fluid friction coefficient C_FF) and the entrainment coefficient C_E are optimized in a spatially differentiated way to maximize the empirical adequacy of the simulations in terms of estimates of impact areas, erosion depths, and flow and breach volumes. As no travel times or velocities are documented for the 1941 event, we use the values given by Somos-Valenzuela et al. (2016) as a rough reference. Varying those four parameters while keeping the others constant helps us to capture variability while minimizing the degrees of freedom, remaining aware of possible equifinality issues (Beven, 1996; Beven and Freer, 2001).

A particularly uncertain parameter is the empirical entrainment coefficient C_E (Eq. 1). In order to optimize C_E, we consider (i) successful prediction of the reconstructed breach volumes and (ii) correspondence of peak discharge with published empirical equations on the relation between peak discharge and both lake volume and dam height (Walder and O'Connor, 1997). Table 4 summarizes these equations for moraine dams (applied to Lake Palcacocha) and landslide dams (applied to Lake Jircacocha), and the values obtained for the regression and the envelope, using the volumes of both lakes. We note that Table 4 reveals very large differences – roughly 1 order of magnitude – between regression and envelope. In case of the breach of the moraine dam of Lake Palcacocha, we consider an extreme event due to the steep, poorly consolidated, and maybe soaked moraine, with a peak discharge close to the envelope (approx. 15 000 m³ s⁻¹). For Lake Jircacocha, in contrast, the envelope values of peak discharge do not appear realistic. However, due to the high rate of water inflow from above, a value well above the regression line still appears plausible, even though the usefulness of the empirical laws for this type of lake drainage can be questioned. The value of C_E optimized for the dam of Lake Jircacocha is also used for entrainment along the flow path.

Table 4 Empirical relationships for the peak discharge in case of breach of moraine and landslide dams (Walder and O'Connor, 1997), and the peak discharges estimated for Lake Palcacocha and Lake Jircacocha. q_p = peak discharge (m³ s⁻¹), V = total volume of water passing through the breach (m³); D = drop of lake level (m); REG = regression; ENV = envelope. The values of V and D for the two lakes are summarized in Table 1. See also Rivas et al. (2015).

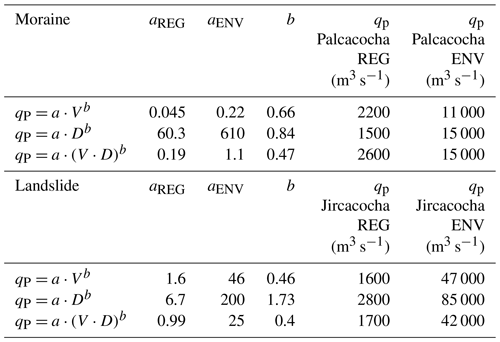
All of the computational experiments are run with 10 m spatial resolution. Only flow heights ≥25 cm are considered for visualization and evaluation. We now describe one representative simulation result for each of the considered scenarios, thereby spanning the most plausible and empirically adequate field of simulations.

Figure 5 Hydrographs of moraine dam failure of Lake Palcacocha (a, d), landslide dam failure of Lake Jircacocha (b, e), and the flow entering the urban area of Huaráz (c, f) for scenarios A and AX. Note that, for clarity, fluid flow heights and discharges are plotted in the negative direction.

5 r.avaflow simulation results

5.1 Scenario A – event induced by overtopping; fluid without yield strength

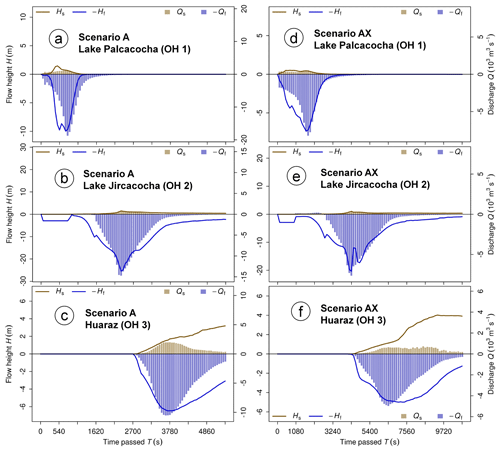
Outflow from Lake Palcacocha starts immediately, leading to (1) lowering of the lake level and (2) retrogressive erosion of the moraine dam. The bell-shaped fluid discharge curve at the hydrograph profile O1 (Fig. 4) reaches its peak of 18 700 m³ s⁻¹ after approx. 780 s and then decreases to a small residual (Fig. 5a). Channel incision happens quickly – 53 m of lowering of the terrain at the reference point R1 occurs within the first 1200 s, whereas the lowering at the end of the simulation is 60 m (Fig. 6a). This number represents an underestimation, compared to the reference value of 76 m (Table 2). The lake level decreases by 42 m, whereby 36.5 m of the decrease occurs within the first 1200 s. The slight underestimation, compared to the reference value of 47 m of lake level decrease, is most likely a consequence of uncertainties in the topographic reconstruction. A total amount of 1.5 million m³ is eroded from the moraine dam of Lake Palcacocha, corresponding to an underestimation of 22 %, compared to the reconstructed breach volume. Underestimations mainly occur at both sides of the lateral parts of the eroded channel near the moraine crest – an area where additional post-event erosion can be expected, so that the patterns and degree of underestimation appear plausible (Fig. 7a). In contrast, some overestimation of erosion occurs in the inner part of the dam. For numerical reasons, some minor erosion is also simulated away from the eroded channel. The iterative optimization procedure results in an entrainment coefficient $C_{\mathrm{E}}={\mathrm{10}}^{-\mathrm{6.75}}$.

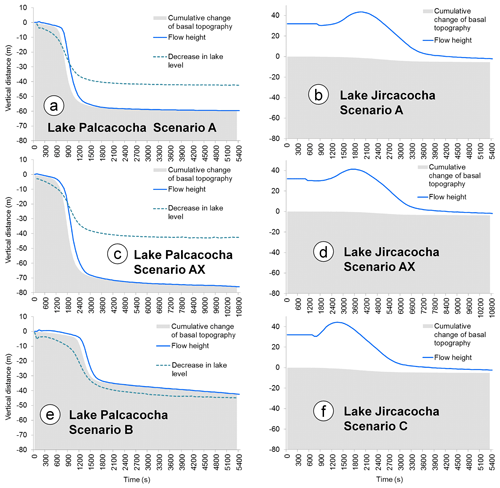
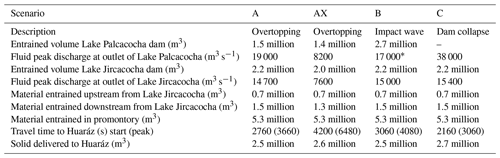
Figure 6 Evolution of flow height and basal topography at the outlets of Lake Palcacocha (reference point R1 in Fig. 4b), and Lake Jircacocha (reference point R2 in Fig. 4c). The reference points are placed in a way to best represent the evolution of the breach in the dam for Lake Palcacocha, and the evolution of the impact wave for Lake Jircacocha. Additionally, the evolution of the lake level is shown for Lake Palcacocha. Note that the result for Scenario B is only displayed for Lake Palcacocha (e), whereas the result for Scenario C is only illustrated for Lake Jircacocha (f). The vertical distance displayed on the y axis refers to the terrain height or the lake level at the start of the simulation, respectively, whereby the flow height is imposed onto the topography. In Scenario B, the initial impact wave at the dam of Lake Palcacocha is only poorly represented due to the low temporal resolution of the simulation, and due to blurring by numerical effects (e).

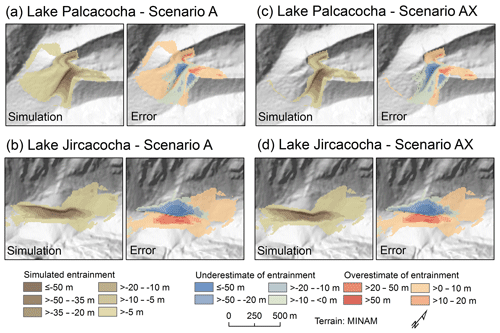
Figure 7 Simulated versus reconstructed entrainment patterns for scenarios A and AX. The total entrained height and the difference between simulated and reconstructed entrainment (error) are shown. (a) Lake Palcacocha, Scenario A. (b) Lake Jircacocha, Scenario A. (c) Lake Palcacocha, Scenario AX. (d) Lake Jircacocha, Scenario AX.

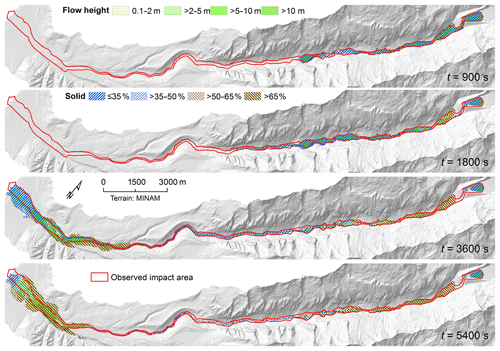
The deposit of much of the solid material eroded from the moraine dam directly downstream from Lake Palcacocha, as observed in the field (Fig. 2c), is reasonably well reproduced by this simulation, so that the flow proceeding down-valley is dominated by the fluid phase (Fig. 8). It reaches Lake Jircacocha after t=840 s (Fig. 5b). As the inflow occurs smoothly, there is no impact wave in the strict sense, but it is rather the steadily rising water level (see Fig. 6b for the evolution of the water level at the reference point R2) inducing overtopping and erosion of the dam. This only starts gradually after some lag time, at approx. t=1200 s. The discharge curve at the profile O2 (Fig. 4) reaches its pronounced peak of 750 m³ s⁻¹ solid and 14 700 m³ s⁻¹ fluid material at t=2340 s and then tails off slowly.

Figure 8 Evolution of the flow in space and time (Scenario A).

In the case of Lake Jircacocha, the simulated breach is clearly shifted south, compared to the observed breach. With the optimized value of the entrainment coefficient $C_{\mathrm{E}}={\mathrm{10}}^{-\mathrm{7.15}}$, the breach volume is underestimated by 24 %, compared to the reconstruction (Fig. 7b). Also, here, this intentionally introduced discrepancy accounts for some post-event erosion. However, we note that volumes are uncertain as the reconstruction of the dam of Lake Jircacocha – in contrast to Lake Palcacocha – is a rough estimation due to lacking reference data.

Due to erosion of the dam of Lake Jircacocha, and also erosion of the valley bottom and slopes, the solid fraction of the flow increases considerably downstream. Much of the solid material, however, is deposited in the lateral parts of the flow channel, so that the flow arriving at Huaráz is fluid-dominated again (Fig. 8). The front enters the alluvial fan of Huaráz at t=2760 s, whereas the broad peak of 10 500 m³ s⁻¹ of fluid and 2000 m³ s⁻¹ of solid material (solid fraction of 16 %) is reached in the period between 3600 and 3780 s (Figs. 4 and 5c). Discharge decreases steadily afterwards. A total of 2.5 million m³ of solid and 14.0 million m³ of fluid material passes the hydrograph profile O3 until t=5400 s. Referring only to the solid, this is less material than reported by Kaser and Georges (2003). However, (i) there is still some material coming after, and (ii) pore volume has to be added to the solid volume, so that the order of magnitude of material delivered to Huaráz corresponds to the documentation in a better way. Still, the solid ratio of the hydrograph might represent an underestimation.

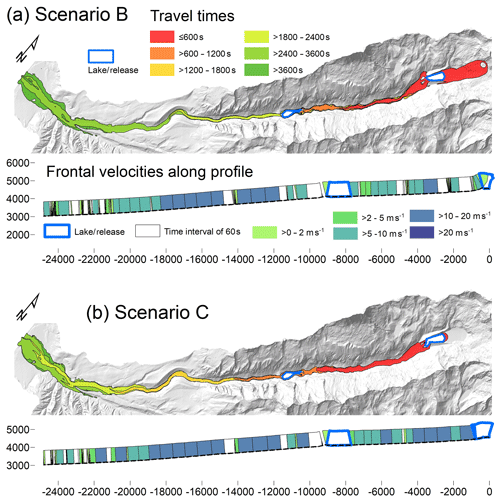
As prescribed by the parameter optimization, the volumes entrained along the channel are of the same order of magnitude, but lower than the reconstructed volumes summarized in Table 2: 0.7 million m³ of material is entrained upstream, 1.5 million m³ is entrained downstream of Lake Jircacocha, and 5.3 million m³ is entrained in the promontory. Figure 9a summarizes the travel times and the flow velocities of the entire process chain. Frontal velocities mostly vary between 5 and 20 m s⁻¹, with the higher values in the steeper part below Lake Jircacocha. The low and undefined velocities directly downstream of Lake Jircacocha reflect the time lag of substantial overtopping. The key numbers in terms of times, discharges, and volumes are summarized in Table 5.

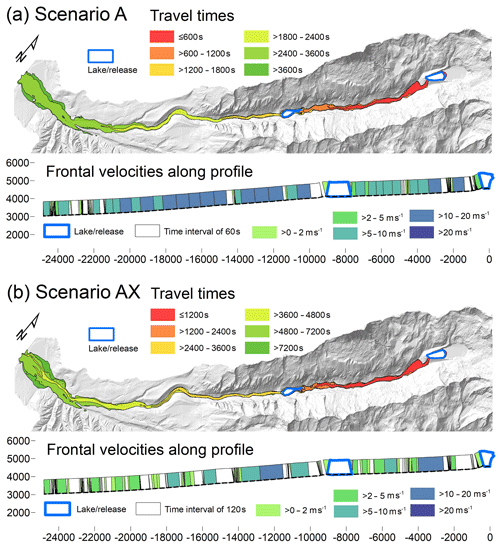
Figure 9 Travel times and frontal velocities for scenarios (a) A and (b) AX. Void fields in the profile graph refer to areas without clearly defined flow front.

Table 5 Summary of the key results obtained with the computational experiments A–C. Refer to Tables 1 and 2 for the volumes involved, and to Table 4 for empirically expected peak discharges. Note that all entrained volumes are composed of 80 % of solid and 20 % of fluid material in terms of volume.

^* Peak of initial overtopping as response to the impact wave: 7000 m³ s⁻¹.

5.2 Scenario AX – event induced by overtopping; fluid with yield strength

Adding a yield strength of τ_y=5 Pa to the characteristics of the fluid substantially changes the temporal rather than the spatial evolution of the process cascade. As the fluid now behaves as fine mud instead of water and is more resistant to motion, velocities are lower, travel times are much longer, and the entrained volumes are smaller than in Scenario A (Fig. 9b; Table 5). The peak discharge at the outlet of Lake Palcacocha is reached at t=1800 s. Fluid peak discharge of 8200 m³ s⁻¹ is less than half the value yielded in Scenario A (Fig. 5d). The volume of material eroded from the dam is only slightly smaller than in Scenario A (1.4 versus 1.5 million m³). The numerically induced false positives with regard to erosion observed in Scenario A are not observed in Scenario AX, as the resistance to oscillations in the lake is higher with the added yield strength (Fig. 7c). Still, the major patterns of erosion and entrainment are the same. Interestingly, erosion is deeper in Scenario AX, reaching 76 m at the end of the simulation (Fig. 6c) and therefore the base of the entrainable material (Table 2). This is most likely a consequence of the spatially more concentrated flow and therefore higher erosion rates along the centre of the breach channel, with less lateral spreading than in Scenario A.

Consequently, Lake Jircacocha is also reached later than in Scenario A (Fig. 6d), and the peak discharge at its outlet is delayed (t=4320 s) and lower (7600 m³ s⁻¹ of fluid and 320 m³ s⁻¹ of solid material) (Fig. 5e). A total of 2.0 million m³ of material is entrained from the dam of Lake Jircacocha, with similar spatial patterns to those in Scenario A (Fig. 7d). Huaráz is reached after t=4200 s, and the peak discharge of 5000 m³ s⁻¹ of fluid and 640 m³ s⁻¹ of solid material at O3 occurs after t=6480 s (Fig. 5f). This corresponds to a solid ratio of 11 %. Interpretation of the solid ratio requires care here as the fluid is defined as fine mud, so that the water content is much lower than the remaining 89 %. The volumes entrained along the flow channel are similar in magnitude to those obtained in the simulation of Scenario A (Table 5).

5.3 Scenario B – event induced by impact wave

Scenario B is based on the assumption of an impact wave from a 3 million m³ landslide. However, due to the relatively gently sloped glacier tongue heading into Lake Palcacocha at the time of the 1941 event (Figs. 2a and 4b), only a small fraction of the initial landslide volume reaches the lake, and impact velocities and energies are reduced, compared to a direct impact from the steep slope. Approx. 1 million m³ of the landslide have entered the lake by t=120 s, an amount which only slightly increases thereafter. Most of the landslide deposits on the glacier surface. Caused by the impact wave, discharge at the outlet of Lake Palcacocha (O1) sets in at t=95 s and, due to overtopping of the impact wave, immediately reaches a relatively moderate first peak of 7000 m³ s⁻¹ of fluid discharge. The main peak of 16 900 m³ s⁻¹ of fluid and 2000 m³ s⁻¹ of solid discharge occurs at t=1200 s due do the erosion of the breach channel. Afterwards, discharge decreases relatively quickly to a low base level (Fig. 10a). The optimized value of $C_{\mathrm{E}}={\mathrm{10}}^{-\mathrm{6.75}}$ is used also for this scenario. The depth of erosion along the main path of the breach channel is clearly less than in Scenario A (Fig. 6e). However, Table 5 shows a higher volume of eroded dam material than the other scenarios. These two contradicting patterns are explained by Fig. 11a: the overtopping due to the impact wave initiates erosion of not only the main breach, but also of a secondary breach farther north. Consequently, discharge is split among the two breaches and therefore less concentrated, explaining the lower erosion at the main channel despite a larger total amount of eroded material. The secondary drainage channel can also be deduced from observations (Fig. 3a) but has probably played a less important role than suggested by this simulation.

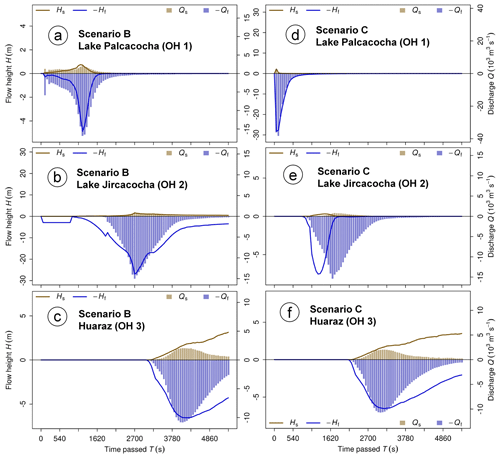
Figure 10 Hydrographs of moraine dam failure of Lake Palcacocha (a, d), landslide dam failure of Lake Jircacocha (b, e), and the flow entering the urban area of Huaráz (c, f) for scenarios B and C. Note that, for clarity, fluid flow heights and discharges are plotted in negative direction.

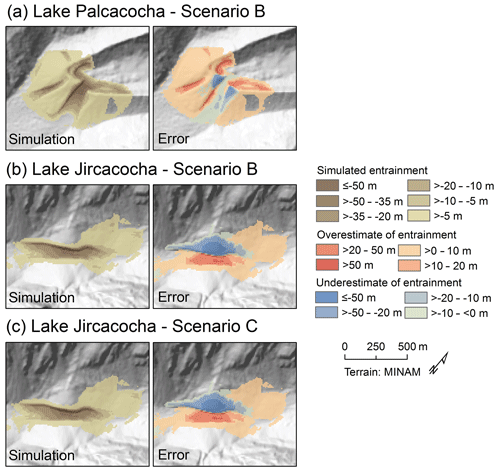
Figure 11 Simulated versus reconstructed entrainment patterns for scenarios B and C. The total entrained height and the difference between simulated and reconstructed entrainment (error) are shown. (a) Lake Palcacocha, Scenario B. (b) Lake Jircacocha, Scenario B. (c) Lake Jircacocha, Scenario C.

The downstream results of Scenario B largely correspond to the results of Scenario A, with some delay partly related to the time from the initial landslide to the overtopping of the impact wave. Discharge at the outlet of Lake Jircacocha peaks at t=2700 s (Fig. 10b), and the alluvial fan of Huaráz is reached after 3060 s (Fig. 10c). The peak discharges at O2 and O3 are similar to those obtained in Scenario A. The erosion patterns at the dam of Lake Jircacocha (again, $C_{\mathrm{E}}={\mathrm{10}}^{-\mathrm{7.15}}$) very much resemble those yielded with scenarios A and AX (Fig. 11b), and so does the volume of entrained dam material (2.2 million m³). The same is true for the 2.5 million m³ of solid and 13.9 million m³ of fluid material entering the area of Huaráz until t=5400 s, according to this simulation.

Also in this scenario, the volumes entrained along the flow channel are very similar to those obtained in the simulation of Scenario A. The travel times and frontal velocities – resembling the patterns obtained in Scenario A, with the exception of the delay – are shown in Fig. 12a, whereas Table 5 summarizes the key numbers in terms of times, volumes, and discharges.

Figure 12 Travel times and frontal velocities for scenarios (a) B and (b) C. Note that the legend of (a) also applies to (b). Void fields in the profile graph refer to areas without clearly defined flow front.

5.4 Scenario C – event induced by dam collapse

In Scenario C, we assume that the breached part of the moraine dam collapses, and the collapsed mass mixes with the water from the suddenly draining lake and flows downstream. The more sudden and powerful release, compared to the two other scenarios, leads to higher frontal velocities and shorter travel times (Fig. 12b; Table 5).

In contrast to the other scenarios, impact downstream starts earlier, as more material is released at once, instead of steadily increasing retrogressive erosion and lowering of the lake level. The fluid discharge at O1 peaks at almost 40 000 m³ s⁻¹ (Fig. 10d) rapidly after release. Consequently, Lake Jircacocha is reached already after 720 s, and the impact wave in the lake evolves more quickly than in all the other scenarios considered (Fig. 6f). The lake drains with a peak discharge of 15 400 m³ s⁻¹ of fluid and 830 m³ s⁻¹ of solid material after 1680–1740 s (Fig. 10e). In contrast to the more rapid evolution of the process chain, discharge magnitudes are largely comparable to those obtained with the other scenarios. The same is true for the hydrograph profile O3: the flow reaches the alluvial fan of Huaráz after t=2160 s, with a peak discharge slightly exceeding 10 000 m³ s⁻¹ of fluid and 2000 m³ s⁻¹ of solid material between t=2940 and 3240 s. A total of 2.7 million m³ of solid and 14.6 million m³ of fluid material enter the area of Huaráz until t=5400 s, which is slightly more than in the other scenarios, indicating the more powerful dynamics of the flow (Table 5). The fraction of solid material arriving at Huaráz remains low, with 16 % solid at peak discharge and 15 % in total. Again, the volumes entrained along the flow channel are very similar to those obtained with the simulations of the other scenarios (Table 5).

6 Discussion

6.1 Possible trigger of the GLOF process chain

In contrast to other GLOF process chains in the Cordillera Blanca, such as the 2010 event at Laguna 513 (Schneider et al., 2014), which was clearly triggered by an ice-rock avalanche into the lake, there is disagreement upon the trigger of the 1941 multi-lake outburst flood in the Quilcay catchment. Whereas, according to contemporary reports, there is no evidence of a landslide (for example, ice avalanche) impact on the lake (Vilímek et al., 2005; Wegner, 2014), and dam rupture would have been triggered by internal erosion, some authors postulate at least a small impact starting the process chain (Portocarrero, 2014; Somos-Valenzuela et al., 2016).

Each of the three assumed initiation mechanisms of the 1941 event, represented by scenarios A/AX, B, and C, yields results which are plausible in principle. We consider a combination of all three mechanisms a likely cause of this extreme process chain. Overtopping of the moraine dam, possibly related to a minor impact wave, leads to the best correspondence of the model results with the observation, documentation, and reconstruction. In particular, the signs of minor erosion of the moraine dam north of the main breach (Fig. 3a) support this conclusion: a major impact wave, resulting in violent overtopping of the entire frontal part of the moraine dam, would supposedly also have led to more pronounced erosion in that area, as to some extent predicted by Scenario B. There is also no evidence for strong landslide–glacier interactions (massive entrainment of ice or even detachment of the glacier tongue), which would be likely scenarios in the case of a very large landslide. Anyway, the observations do not allow for substantial conclusions on the volume of a hypothetic triggering landslide: as suggested by Scenario B, even a large landslide from the slopes of Palcaraju or Pucaranra could have been partly alleviated on the rather gently sloped glacier tongue between the likely release area and Lake Palcacocha.

The minor erosional feature north of the main breach was already visible in the photo of Kinzl (Fig. 2a), possibly indicating an earlier, small GLOF. It remains unclear whether it was reactivated in 1941. Such a reactivation could only be directly explained by an impact wave, but not by retrogressive erosion only (A/AX) or internal failure of the dam (C) – so, more research is needed here. The source area of a possible impacting landslide could have been the slopes of Palcaraju or Pucaranra (Fig. 1), or the calving glacier front (Fig. 2a). Attempts to quantify the most likely release volume and material composition would be considered speculative due to the remaining difficulties in adequately simulating landslide–lake and possibly landslide–glacier–lake interactions (Westoby et al., 2014). Further research is necessary in this direction. In any case, a poor stability condition of the dam (factor of safety ∼1) could have facilitated the major retrogressive erosion of the main breach. A better understanding of the hydro-mechanical load applied by a possible overtopping wave and the mechanical strength of the moraine dam could help to resolve this issue.

The downstream patterns of the flow are largely similar for each of scenarios A, AX, B, and C, with the exception of travel times and velocities. Interaction with Lake Jircacocha disguises much of the signal of process initiation. Lag times between the impact of the flow front on Lake Jircacocha and the onset of substantial overtopping and erosion are approx. 10 in in scenarios A and B, and less than 3 min in Scenario C. This clearly reflects the slow and steady onset of those flows generated through retrogressive erosion. The moderate initial overtopping in Scenario B seems to be alleviated before reaching Lake Jircacocha. Sudden mechanical failure of the dam (Scenario C), in contrast, leads to a more sudden evolution of the flow, with more immediate downstream consequences.

6.2 Parameter uncertainties

We have tried to back-calculate the 1941 event in a way reasonably corresponding to the observation, documentation, and reconstruction, and building on physically plausible parameter sets. Earlier work on the Huascarán landslides of 1962 and 1970 has demonstrated that empirically adequate back-calculations are not necessarily plausible with regard to parameterization (Mergili et al., 2018b). This issue may be connected to equifinality issues (Beven, 1996; Beven and Freer, 2001), and in the case of the very extreme and complex Huascarán 1970 event, by the inability of the flow model and its numerical solution to adequately reproduce some of the process components (Mergili et al., 2018b). In the present work, however, reasonable levels of empirical adequacy and physical plausibility are achieved. Open questions remain with regard to the spatial differentiation of the basal friction angle required to obtain adequate results (Table 3): lower values of δ downstream from the dam of Lake Jircacocha are necessary to ensure that a certain fraction of solid passes the hydrograph profile O3 and reaches Huaráz. Still, solid fractions at O3 appear rather low in all simulations. A better understanding of the interplay between friction, drag, virtual mass, entrainment, deposition, and phase separation could help to resolve this issue (Pudasaini and Fischer, 2016a, b; Pudasaini, 2019a, b).

The empirically adequate reproduction of the documented spatial patterns is only one part of the story (Mergili et al., 2018a). The dynamic flow characteristics (velocities, travel times, hydrographs) are commonly much less well documented, particularly for events in remote areas which happened a long time ago. Therefore, direct references for evaluating the empirical adequacy of the dimension of time in the simulation results are lacking. However, travel times play a crucial role related to the planning and design of (early) warning systems and risk reduction measures (Hofflinger et al., 2019). Comparison of the results of scenarios A and AX (Fig. 9) reveals almost doubling travel times when adding a yield stress to the fluid fraction. In both scenarios, the travel times to Huaráz are of the same order of magnitude as the travel times simulated by Somos-Valenzuela et al. (2016) and therefore considered plausible, so that it is hard to decide which is the more adequate assumption. Even though the strategy of using the results of earlier simulations as reference may increase the robustness of model results, it might also reproduce errors and inaccuracies of earlier simulation attempts, and thereby confirm wrong results.

The large amount of more or less pure lake water would point towards Scenario A, whereas intense mixing and entrainment of fine material would favour Scenario AX. More work is necessary in this direction, also considering possible phase transformations (Pudasaini and Krautblatter, 2014). At the same time, the optimization and evaluation of the simulated discharges remains a challenge. Here we rely on empirical relationships gained from the analysis of comparable events (Walder and O'Connor, 1997).

6.3 Implications for predictive simulations

Considering what was said above, the findings from the back-calculation of the 1941 event can help us to better understand and constrain possible mechanisms of this extreme process chain. In principle, such an understanding can be transferred to present hazardous situations in order to inform the design of technical remediation measures. Earlier, measures were implemented not only at Lake Palcacocha (Portocarrero, 2014), but also at various other lakes such as Laguna 513: a tunnelling scheme implemented in the 1990s strongly reduced the impacts of the 2010 GLOF process chain (Reynolds, 1998; Reynolds et al., 1998; Schneider et al., 2014).

However, the findings of this study should only be applied for forward simulations in the same area or other areas with utmost care. The initial conditions and model parameters are not necessarily valid for events of different characteristics and magnitudes (Mergili et al., 2018b). In the case of Lake Palcacocha, the situation has changed substantially since 1941: the lake level is much lower and the volume larger, and the lake is directly connected to the steep glacierized slopes, so that the impact of a hypothetic landslide could be very different now. Also, the current lake is dammed by a different moraine than the pre-1941 lake, with a very different dam geometry (Somos-Valenzuela et al., 2016). In general, the mechanisms of the landslide impact into the lake, which were not the focus of the present study, would require more detailed investigations. Ideally, such work would be based on a three-phase model (Pudasaini and Mergili, 2019; considering ice as a separate phase) and consider knowledge and experience gained from comparable, well-documented events. A possible candidate for such an event would be the 2010 event at Laguna 513, which was back-calculated by Schneider et al. (2014). In general, it remains a challenge to reliably predict the outcomes of given future scenarios. The magnitude of the 1941 event was amplified by the interaction with Lake Jircacocha, whereas the 2012 GLOF process chain in the Santa Cruz Valley (Mergili et al., 2018a) alleviated due to the interaction with Lake Jatuncocha, comparable in size. While it seems clear that the result of such an interaction depends on event magnitude, topography, and the dam characteristics of the impacted lake, Mergili et al. (2018a, b) have demonstrated the high sensitivity of the behaviour of the simulated flow to the friction parameters, but also to the material involved (release mass, entrainment). A larger number of back-calculated process chains will be necessary to derive guiding parameter sets which could facilitate predictive simulations, and so will an appropriate consideration of model uncertainties and possible threshold effects (Mergili et al., 2018b). Earlier studies, considering the 2010 event at Laguna 513 (Schneider et al., 2014) and three future scenarios for Lake Palcacocha (Somos-Valenzuela et al., 2016) have followed a different strategy, using model cascades instead of integrated simulations, so that a comparison with studies based on r.avaflow is only possible to a limited extent.

Another remaining issue is the lateral spreading of the flow on the fan of Huaráz, which is overestimated in all four simulations (Figs. 8, 9, and 12): the most likely reason for this is the insufficient representation of fine-scale structures such as buildings or walls in the DEM, which would serve as obstacles confining the flow in lateral direction.

7 Conclusions

We have performed back-calculations of the documented 1941 GLOF process chain involving Lake Palcacocha and Lake Jircacocha in the Quilcay catchment in the Cordillera Blanca, Peru. The key messages of this work are summarized as follows:

• Retrogressive erosion, possibly caused by a minor impact wave, appears to be the most likely release mechanism of the process chain, facilitated by a geotechnically poorly stable dam with a low width-to-height ratio. This type of failure – a combination of the idealized scenarios considered in this work – can be inferred from observations, and appears most plausible with regard to the simulation results. The identification of the triggering process remains difficult, also because the subsequent interaction with Lake Jircacocha disguises part of the respective signature downstream.

• The correspondence between simulation results and observations is reasonable, and the model parameter values used are physically plausible. However, considerable uncertainties remain with regard to peaks and shapes of the discharge hydrographs, and to the quantification of flow velocities and travel times. Adding a yield strength to the fluid phase (Scenario AX) completely changes the temporal, but not the spatial evolution of the flow. Still, travel times remain of the same order of magnitude as those derived by Somos-Valenzuela et al. (2016) for possible future events.

• Transfer of the findings to forward simulations in the same area or elsewhere remains a challenge due to differences in the initial conditions, uncertainties of the reference data, equifinality issues, and the effects of process magnitude (Mergili et al., 2018b).