the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Hydrological signatures describing the translation of climate seasonality into streamflow seasonality
Sebastian J. Gnann
Nicholas J. K. Howden
Ross A. Woods
Seasonality is ubiquitous in nature, and it is closely linked to water quality, ecology, hydrological extremes, and water resources management. Hydrological signatures aim at extracting information about certain aspects of hydrological behaviour. Commonly used seasonal hydro-climatological signatures consider climate or streamflow seasonality, but they do not consider how climate seasonality translates into streamflow seasonality. In order to analyse the translation of seasonal climate input (precipitation minus potential evapotranspiration) into seasonal catchment output (streamflow), we represent the two time series by their seasonal (annual) Fourier mode, i.e. by sine waves. A catchment alters the input sine wave by reducing its amplitude and by shifting its phase. We propose to use these quantities, the amplitude ratio and the phase shift, as seasonal hydrological signatures. We present analytical solutions describing the response of linear reservoirs to periodic forcing to interpret the seasonal signatures in terms of configurations of linear reservoirs. Using data from the UK and the US, we show that the seasonal signatures exhibit hydrologically interpretable patterns and that they are a function of both climate and catchment attributes. Wet, rather impermeable catchments hardly attenuate the seasonal climate input. Drier catchments, especially if underlain by a productive aquifer, strongly attenuate the input sine wave leading to phase shifts up to several months. As an example application, we test whether two commonly used hydrological models (Identification of unit Hydrographs and Component flows from Rainfall, Evaporation and Streamflow – IHACRES; modèle du Génie Rural à 4 paramètres Journalier – GR4J) can reproduce the observed ranges of seasonal signatures in the UK. The results show that the seasonal signatures have the potential to be useful for catchment classification, predictions in ungauged catchments, and model building and evaluation. The use of potential evapotranspiration in the input restricts the applicability of the signatures to energy-limited (humid) catchments.
- Article
(4568 KB) - Full-text XML
-
Supplement
(824 KB) - BibTeX
- EndNote
The annual course of the Earth around the Sun leads to seasonal cycles in climate in many places. Seasonal patterns in precipitation, evapotranspiration, and snowfall, as well as the characteristics of the catchment a stream drains, often result in a distinct seasonal streamflow regime (Cayan et al., 1993; Regonda et al., 2005; Berghuijs et al., 2014). The seasonal flow regime is closely linked to water chemistry and water quality (DeWalle et al., 1997; Vega et al., 1998). Streamflow seasonality plays a crucial role for biological systems and ecosystems (Colwell, 1974; Poff et al., 1997; Poff and Zimmerman, 2010). Low flows are typically seasonal, and droughts – albeit a more general phenomenon than low flows – often occur during the low-flow season and thus are to some degree predictable (Smakhtin, 2001; Peters et al., 2003). From a more applied point of view, the seasonal streamflow regime is crucial for water resources management, agriculture, and hydropower generation (Weingartner et al., 2013; Laaha et al., 2013; Svensson, 2016; Harrigan et al., 2018b). This is reflected in the increased application and development of seasonal forecasting methods (Shi et al., 2008; Svensson, 2016; Harrigan et al., 2018b). In summary, for many applications the mean seasonal regime is of high importance and thus deserves attention.
In this work we focus on the average seasonal hydrological response of snow-free catchments. We do not focus, for instance, on the seasonality of events (e.g. storms), noting, however, that the seasonal water balance can have an impact at event scales (Berghuijs et al., 2014). In snow-free areas, the seasonality of the flow regime is primarily driven by the incoming forcing, that is, the seasonality of precipitation (water) and potential evapotranspiration (energy). Given a certain forcing, the flow regime of a catchment is determined by a catchment's form and function, that is, by how much water can infiltrate, how much water can be stored, and how slowly that water is being released. Since groundwater recharge and thus groundwater discharge are often very seasonal (Jasechko et al., 2014), many hydrogeological studies focus on seasonality, or more specifically, on how seasonal recharge is propagated through an aquifer system (Townley, 1995; Erskine and Papaioannou, 1997; Peters et al., 2003; Obergfell et al., 2019). Slowly responding, groundwater-dominated catchments closely resemble the aquifer system feeding the stream. Understanding the seasonal streamflow regime is therefore particularly important for understanding slow (groundwater-driven) dynamics in catchments.
Different aspects of hydrological behaviour, such as streamflow seasonality, can be quantified by summarising metrics now mostly called hydrological signatures (McMillan et al., 2017). The use of such summarising metrics is not new, and they have been used extensively in ecohydrological studies (e.g. Clausen and Biggs, 2000; Olden and Poff, 2003) and hydrological studies (e.g. Jothityangkoon et al., 2001; Farmer et al., 2003). Hydrological signatures offer a way to quantify hydrologic similarity. This makes them useful for catchment classification (Wagener et al., 2007; Sawicz et al., 2011), for hydrological process exploration (McMillan et al., 2014), and for predictions in ungauged basins (Yadav et al., 2007; Hrachowitz et al., 2013; Westerberg et al., 2016). Hydrological signatures can also be used to guide diagnostic model evaluation (Gupta et al., 2008; Peel and Blöschl, 2011; Euser et al., 2013; Hrachowitz et al., 2014; Shafii and Tolson, 2015), as they offer a potentially more meaningful and fit-for-purpose alternative to the typically used statistical metrics such as the Nash–Sutcliffe efficiency (NSE; Nash and Sutcliffe, 1970) or the Kling–Gupta efficiency (KGE; Gupta et al., 2009).
There are many hydrological signatures, and we therefore need guidelines for signature selection (McMillan et al., 2017; Addor et al., 2018). Some of these guidelines refer to more technical aspects: the uncertainty in a signature should not be larger within a catchment than between catchments (identifiability); a signature should be insensitive to the data sources (robustness); and a signature should be comparable across (heterogeneous) catchments (consistency; McMillan et al., 2017). When using combinations of signatures, the different signatures should also contain different information, i.e. they should not be redundant (Olden and Poff, 2003; Addor et al., 2018). From a more hydrological perspective, a signature should be meaningful at the relevant scale (representativeness), and a signature should relate to and increase our knowledge of hydrological function (discriminatory power; McMillan et al., 2017). Since (hydro-)climatic signatures such as the mean flow are already well understood, we should try to explain and use signatures that tell us more about catchment functioning (Addor et al., 2018), such as signatures that relate climate input to catchment output.
There are a multitude of hydrological signatures focusing on seasonality. Climate seasonality is accounted for by (hydro-)climatic signatures such as the (co-)seasonality of precipitation and potential evapotranspiration (Milly, 1994; Knoben et al., 2018). Streamflow seasonality can be characterised by the Pardé coefficients (Weingartner et al., 2013) or the regime curve, which is related to the slow-flow component of the flow duration curve (FDC; Yokoo and Sivapalan, 2011). Seasonal signatures related to streamflow timing are the half flow date and the half flow interval (Court, 1962) and the date of each annual 1 d maximum (or minimum; Richter et al., 1996). Seasonal streamflow signatures focusing on low flows are for example the seasonality index, which measures the mean day of low-flow occurrence and the intensity of seasonality, or the seasonality histogram, which shows the occurrence of low flows in each month (Laaha and Blöschl, 2006). Colwell's predictability is another measure describing periodic signals (Colwell, 1974), mostly used in ecological studies. It consists of constancy (how variable the intra-annual flow regime is) and contingency (how persistent the inter-annual flow regime is). All of these signatures describe (parts of) the seasonality of either climate or streamflow, yet none of them look at how climate seasonality translates into streamflow seasonality. As the transformation of climate input into streamflow is, after all, what we are trying to understand, investigating the seasonal aspect of that seems worthwhile. Relating streamflow to climate input also removes the arbitrariness of picking a start date (e.g. by defining a water year), which is a limitation of many signatures that relate flows to a date (e.g. the half flow date).
In this work, we propose the use of hydrological signatures based on how catchments attenuate the seasonal climate input (forcing). We approximate the input signal to a catchment (the forcing) by precipitation minus potential evapotranspiration and the output signal from a catchment by streamflow. We quantify the seasonal component of both signals by fitting sine waves to them; i.e. we extract their (annual) Fourier modes. As the period is fixed (1 year), the incoming sine wave and the outgoing sine wave differ only in their amplitude, their phase, and their mean. As the mean is rather a measure of the annual water balance, we are primarily interested in amplitude and phase. The differences in amplitude and phase are used as signatures describing the steady-state response of a catchment to periodic forcing. This idea is similar to the approach of Peters et al. (2003) who investigated drought propagation through groundwater using sinusoidal recharge and to the approach of Obergfell et al. (2019) who used the seasonal behaviour as an additional signature in recharge estimation. The approach is also similar to approaches in transit time modelling (e.g. McGuire and McDonnell, 2006; Kirchner, 2016). Instead of focusing on the velocity of water particles, we, however, focus on the hydraulic response to periodic forcing, that is the celerity of the input “wave” of hydraulic potential (Harman, 2019). The proposed signatures are essentially also spectral domain signatures (Montanari and Toth, 2007), focusing only on a certain meaningful period – the annual period.
While there are other methods that quantify input–output relations, we propose the use of the seasonal signatures for several reasons. The seasonal signatures can be related to conceptual linear reservoirs (this will be outlined in Sect. 2); i.e. they can be interpreted in terms of simple conceptual model structures and parameter values (the reservoir time constants or response times). This gives them some hydrological interpretability (cf. discriminatory power; McMillan et al., 2017). Furthermore, by quantifying the delay between seasonal climate input and catchment output, we obtain a timescale that focuses on seasonal and thus rather slow dynamics. This might make it a valuable addition to methods focusing on event scales (e.g. recession analysis) and to other slow-flow signatures such as the baseflow index (BFI) or the flow duration curve and parts thereof (e.g. Q95), which focus on volumes and frequencies, respectively. Lastly, the signatures do not require any parameters; they can be estimated directly from precipitation, potential evapotranspiration, and streamflow data, which makes it straightforward to apply them to large samples of catchments.
In the following, we will first define the seasonal signatures, and we will present analytical solutions describing the response of linear reservoirs to periodic forcing (Sect. 2). Second, we will calculate the seasonal signatures for a range of catchments in the UK and in the US (Sect. 4; the data sources are presented in Sect. 3). We will explore how they relate to hydro-climatic forcing and catchment form, and we will interpret the underlying hydrological processes as well as limitations of the approach (Sect. 5). Finally, we will present an example application in which we test whether two commonly used hydrological models (Identification of unit Hydrographs and Component flows from Rainfall, Evaporation and Streamflow – IHACRES; modèle du Génie Rural à 4 paramètres Journalier – GR4J) can reproduce the observed ranges of seasonal signatures in the UK. This modelling experiment aims at exploring whether the signatures can be used as an additional source of information in model evaluation (Sect. 5.4).
2.1 Extracting seasonal components from time series
2.1.1 Quantification of periodic components
To analyse the periodic components (Fourier modes) of time series, we first need to quantify these components. While we could investigate the whole frequency spectrum of our time series and see how this is altered by a catchment (Montanari and Toth, 2007), we will focus on a period T of 1 year. The annual period has a clear physical meaning, as it is the period the Earth moves in its orbit around the Sun, which is directly linked to the energy input to the Earth system. Furthermore, the annual mode is the strongest mode in the vast majority of catchments investigated here (see Sect. S2.2 in the Supplement for further details). The input to a catchment, the forcing F, is approximated by precipitation P minus potential evapotranspiration Ep (). We use Ep to avoid the need for a model or additional data which would be needed to obtain actual evapotranspiration Ea. This might be particularly problematic in water-limited catchments, where actual evapotranspiration is much smaller than potential evapotranspiration, and in catchments where precipitation and potential evapotranspiration are out of phase. We will discuss that in Sect. 5. The seasonal component of the forcing Fsin is given by (Milly, 1994).
where is the mean, δF is the ratio between the amplitude and the mean (the dimensionless amplitude), and ϕF is the phase (with respect to a reference date) of the seasonal forcing component. The output from a catchment is approximated by streamflow Q. The seasonal component of streamflow Qsin is given by
where is the mean, δQ is the ratio between the amplitude and the mean, and ϕQ is the phase (with respect to the same reference date) of the seasonal streamflow component.
Since we know the period T of interest, we need to quantify the mean, the amplitude, and the phase of the periodic components. There are different methods to fit a sine curve of a certain period to data, i.e. to extract Fourier modes. We have compared two sine curve fitting methods, namely multiple linear regression and a method that makes use of the cross covariance of two sine waves. Both methods lead to virtually the same results. A description and a comparison of the methods is shown in Sect. S2.1. For the rest of the analysis, we will use results obtained by means of multiple linear regression (details on the fitting method can be found in Sect. S2.1.1).
2.1.2 Calculation of seasonal signatures
Once we have extracted the seasonal components from our time series (precipitation minus potential evapotranspiration, streamflow), we can quantify how the outgoing sine wave Qsin has been altered by the catchment by comparing it to the incoming sine wave Fsin. We define two metrics, the amplitude ratio and the phase shift, which together we call seasonal signatures. The amplitude ratio A is the ratio between the seasonal streamflow amplitude and the seasonal forcing amplitude .
Given a closed long-term water balance, the amplitude ratio should theoretically always be between 0 and unity; that is, the streamflow amplitude cannot be larger than the forcing amplitude. The phase shift ϕ is the difference between the phase of the seasonal streamflow component ϕQ and the phase of the seasonal forcing component ϕF.
The phase shift should theoretically always be positive (the input should lead the output) and smaller than 1 year.
2.2 Linear reservoir theory
The derivations presented here all rely on the assumption of a linear time-invariant system (see e.g. Dooge, 1973, for an overview of linear systems theory). This implies that forcings of different wavelengths are not influencing each other. This is invalid for most real systems, yet the assumption of linearity is still widely made, as it can yield useful insights.
A linear reservoir is described by
where Q (mm d−1) is the outflow from the reservoir, S is storage (mm), and τ (d) is a time constant describing how fast (slow) the reservoir responds. Conservation of mass requires
where Qin is the inflow to the reservoir.
2.2.1 Periodic forcing of a linear reservoir
If we approximate the seasonal input to a linear reservoir by a sine wave of period T (e.g. 1 year), we can combine Eqs. (1), (5), and (6) to obtain
We might neglect the (initial) phase if we choose a starting time t that is aligned with the seasonal forcing component (ϕF=0). It can be shown that the steady-state response of a linear reservoir to a sinusoidal input signal is a damped and phase-shifted version of the input signal (see Sect. S1.1 for a more detailed derivation; or Eriksson, 1971; Peters et al., 2003).
where A is the amplitude ratio and ϕ is the phase shift induced by a single linear reservoir.
We can rewrite Eq. (8) as follows:
In a steady-state mass-conserving system, the mean of the output should equal the mean of the input. If the means obtained from data are different, either the forcing term is inaccurate (e.g. due to differences between actual and potential evapotranspiration) or the streamflow term is inaccurate (e.g. due to other losses or gains). The product of input amplitude and amplitude ratio equals the output amplitude ().
From Eqs. (9) and (10), we can see that the amplitude ratio and the phase shift are given by A and arccos(A), respectively. Since A is fully defined by the ratio between τ and T and T is usually known (e.g. 1 year), we can theoretically use A to determine the time constant τ of the reservoir. This requires the identification of both the seasonal components of the input and output signal of that period (see Sect. 2.1) and assumes the system to behave as a single linear reservoir. In theory, we could also apply the theory to periods other than 1 year, but for the reasons stated above we only investigate the annual period.
The amplitude ratio A and the phase shift arccos(A) can be plotted against each other for various values of τ as shown in Fig. 1. This results in a characteristic curve which captures the response of all single linear reservoirs. Different time constants τ (as proportions of the period; here 1 year) lead to different positions on the curve. For very fast reservoirs, the phase shift is close to 0 d, and the amplitude ratio is close to unity (that is, the signal is not attenuated at all). For very slow reservoirs, the signal is phase shifted up to 91 days, and the amplitude ratio approaches 0. The maximum phase shift of about 91 days corresponds to a quarter of a period (90∘). Mathematically, this can be explained by Eq. (10), as the arccosine of a quantity between 0 and unity (such as A) ranges between 0 and 90∘.
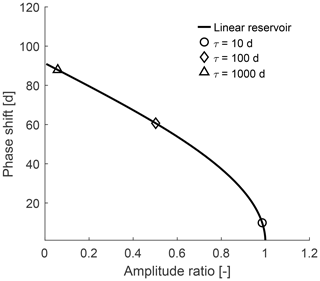
Figure 1Amplitude ratio against phase shift for a single linear reservoir for varying time constants τ. Three example time constants are indicated by the symbols.
Note the similarity of Fig. 1 to Fig. 3c in Kirchner (2016), which shows the relationship between amplitude ratio and phase shift for gamma-distributed catchment transit time distributions. An exponential transit time distribution (a special case of the gamma distribution) corresponds to a linear reservoir describing the velocity of particles. Similarly, a linear reservoir describing the impulse response (the linear reservoir from Eq. 5), i.e. the celerity of the incoming wave of hydraulic potential, corresponds to an exponential response time distribution or an exponential unit hydrograph (cf. Eriksson, 1971; Dooge, 1973).
2.2.2 Combinations of linear reservoirs
Linear systems (Dooge, 1973) have the advantage that it is relatively straightforward to add more components, that is, reservoirs. It is quite common to have serial and/or parallel combinations in rainfall–runoff models. In theory, we can find analytical solutions for the amplitude ratio and phase shift for all combinations of linear reservoirs (cf. the transfer function approach of Young, 1998, who identifies combinations of reservoirs that best fit the data in an inductive way). There are two basic arrangements, a serial arrangement of reservoirs and a parallel arrangement of reservoirs.
2.2.3 Linear reservoirs in series
Linear reservoirs in series can be conceptualised as follows. Every outflow is the inflow to the next reservoir. Hence, if the ith reservoir has a time constant τi, the amplitude ratios Ai are multiplied, and the phase shifts ϕi are added (see Sect. S1.2 for a more detailed derivation).
Figure 2 shows the amplitude ratio plotted against the phase shift similar to Fig. 1, but now for two linear reservoirs it includes two linear reservoirs in series. The different lines are examples with fixed time constants of the first reservoir. They all start from the black line (from the points marked by the symbols in Fig. 1), the characteristic curve for a single linear reservoir, which is the lower limit. Then, as the time constant of the second reservoirs increases, the lines “move” left and upwards, which corresponds to a decrease in amplitude ratio and an increase in phase shift. For example, the red line (τ1=10 d) starts out with a phase shift of about 10 d and ends at a phase shift of about 101 d, which is an increase of about 91 d, the maximum phase shift of the second reservoir. The lines cross each other as we allow τ2 to be larger than τ1. This implies that sometimes a faster reservoir is followed by a slower one, and sometimes a slower reservoir is followed by a faster one. The grey shaded area contains all possible combinations for two reservoirs in series. The lower limit is a single linear reservoir. The upper limit corresponds to two reservoirs with the same time constant (a two-reservoir Nash cascade), which equals a gamma distribution with a shape parameter equal to 2 (Nash, 1957).
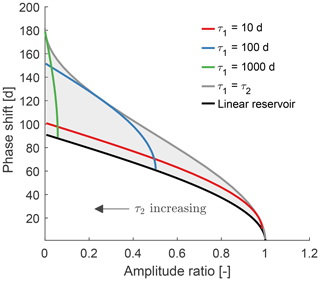
Figure 2Amplitude ratio against phase shift for two linear reservoirs in series. Each line corresponds to a fixed time constant for the first reservoir (τ1), while the time constant of the second reservoir varies ( d; it is increasing from right to left). The black line indicates a single linear reservoir (the lower boundary). The grey line indicates the upper boundary where τ1=τ2. The shaded area contains all possible combinations of amplitude ratio and phase shift for two linear reservoirs in series.

Figure 3Amplitude ratio against phase shift for two linear reservoirs in parallel. (a) Each line has a fixed time constant for the first reservoir (τ1), while the time constant of the second reservoir varies ( d; it is increasing from right to left). The fraction p going into the second reservoir is 0.3. (b) Same as (a) with p=0.6. (c) Same as (a) with p=0.9. (d) Each line has a fixed time constant for the first reservoir (τ1=1 d) and for the second reservoir (τ2). The fraction p going into the second reservoir is varied (it is increasing from right to left). The shaded area contains all the possible combinations of amplitude ratio and phase shift for two linear reservoirs in parallel.
2.2.4 Linear reservoirs in parallel
Linear reservoirs in parallel result in a “mixture” of the outflows from each reservoir. The resulting flow is a combination of sine waves of the same period, weighted by the fraction pi going into each reservoir. For the sake of simplicity, we only consider two reservoirs in parallel. We denote the fraction going into the second reservoir by p, and therefore the fraction going into the first reservoir is 1−p. Thinking of the second reservoir as the slow one, p might be compared to the idea of the baseflow index, the volumetric ratio between baseflow and total streamflow (Institute of Hydrology, 1980). For two reservoirs in parallel we get (see Sect. S1.3 for a more detailed derivation)
Figure 3 shows the amplitude ratio plotted against the phase shift similar to Fig. 1, but now for two linear reservoirs it includes two linear reservoirs in parallel. We show multiple plots to highlight the three degrees of freedom: the two reservoir time constants and the fraction going into each reservoir. The latter is highlighted in Fig. 3d, but it is also visible in Fig. 3a-c. The grey shaded area contains all the possible combinations for two reservoirs in parallel. The upper limit is a single linear reservoir. The lower limit is effectively given by the x and the y axis.
As an example, Fig. 3a can be explained as follows: τ1 is always 1 d, the fraction p going into the second reservoir is 0.3, and τ2 starts with a value of 10 d and then increases. So at first, both reservoirs are rather fast, and we get a high amplitude ratio and a small phase shift for the combined sine wave (see Eqs. 14 and 15). Then, the second reservoirs gets slower, leading to a decrease in amplitude ratio and an increase in phase shift. As the second reservoirs gets slower and slower, it will contribute less and less to the overall sine wave. For very high values of τ2 (e.g. 10 000 d), the sine wave coming out of the second reservoir is almost a straight line, so the combined sine wave primarily consists of the sine wave coming out of the first reservoir. Since only a fraction of of the total input has gone into the first reservoir, the amplitude of the combined sine wave is approximately 0.7 times the input amplitude with a very small phase shift, as the first reservoir hardly attenuates the signal.
2.3 Seasonal signatures as a diagnostic tool for evaluating hydrological models
We use two conceptual rainfall–runoff models and we test whether the seasonal signatures can be used as a diagnostic tool to assess model performance (Gupta et al., 2008). In particular, we test whether the models are capable of reproducing the range of observed signatures without calibrating them to streamflow data (cf. Vogel and Sankarasubramanian, 2003). This modelling experiment is intended to test whether the proposed signatures have the potential to be a useful additional source of information in model building and evaluation. We do not intend (or suggest) that the presented evaluation approach can replace existing model evaluation methods. We limit the analysis to 2 models and 40 catchments to keep the computational demand manageable. We also limit the model evaluation to catchments in the UK, as the seasonal signatures are unreliable in arid catchments (see Sect. 5). The subset of catchments is described in Sects. 3 and S3.1.
The first model is the IHACRES model. It is conceptually relatively similar to the considerations in Sect. 2. It has a soil moisture store (non-linear deficit store) and two parallel linear stores for fast flow and for slow flow (Croke and Jakeman, 2004). It has been used in many modelling studies in Australia (Post and Jakeman, 1999) and also in the UK (Sefton and Howarth, 1998). The second model is the GR4J model. It also has a parallel flow structure, but the internal parametrisation is different. It contains more non-linearities, and it has fixed internal parameters. Additionally, it has a groundwater exchange parameter aimed at representing inter-catchment groundwater flows. It has been used in many modelling studies in France (Perrin et al., 2003), in the UK (Smith et al., 2019; Harrigan et al., 2018b), and in the US (Oudin et al., 2018). We use the implementations of the two models in the Modular Assessment of Rainfall-Runoff Models Toolbox (MARRMoT) v1.2 (Knoben et al., 2019a), a MATLAB toolbox containing many hydrological models aimed at model comparison studies. The pure delay function in the MARRMoT implementation of IHACRES is set to 0, making it (conceptually, not necessarily numerically) equal to the version used by Croke and Jakeman (2004). In our modelling experiment, IHACRES has therefore six parameters, and GR4J has four parameters. Detailed information on the parameter ranges and on model warm-up periods can be found in Sect. S3.
To test which ranges of seasonal signatures the two models can reproduce, we run a Monte Carlo sampling experiment. We sample parameter sets for both models using Latin hypercube sampling, an efficient sampling method (Cheng and Druzdzel, 2000) that assumes uniform prior parameter distributions. With the parameter sets obtained, we run both models for each of the 40 catchments; i.e. we use the same parameter sets for each catchment. To test for robustness, we sample an increasing number of parameter sets (20 000 parameter sets are considered sufficient; see Sect. S3.2 for more information). We then use the modelled streamflow time series to calculate three hydrological signatures per parameter set: the two seasonal signatures presented here and the baseflow index. The resulting modelled signatures are compared to observed signatures and explored in a rather general way, as we want to examine what the models can do without actually calibrating them to streamflow data (cf. Vogel and Sankarasubramanian, 2003). That is, we are not interested in finding the “best” parameter set but in whether a certain model (given certain parameter ranges) is generally capable of reproducing the signatures we observe.
3.1 Data sources
We use catchment data from the UK and the US. The data for the UK are obtained from different sources. Daily streamflow data, catchment characteristics, and catchment boundaries are obtained from the National River Flow Archive (NRFA; National River Flow Archive, 2019); precipitation data are from the UK Centre for Ecology & Hydrology's gridded estimates of daily and monthly areal rainfall for the UK (CEH-GEAR; Tanguy et al., 2016); and potential evapotranspiration data are from the climate hydrology and ecology research support system potential evapotranspiration dataset for Great Britain (CHESS-PE; Robinson et al., 2016). For the model evaluation we select catchments that are part of the UK Benchmark Network (UKBN; Harrigan et al., 2018a), which describes catchments in the UK that are near-natural. The subset of catchments is chosen to be representative of the UK; details are shown in Sect. S3.1. The data for the US are obtained from the Catchment Attributes and Meteorology for Large-sample Studies (CAMELS) dataset (Newman et al., 2015; Addor et al., 2017a). CAMELS includes daily precipitation, potential evapotranspiration (we use Daily Surface Weather and Climatological Summaries forcing data; Daymet) and streamflow data as well as a wide range of catchment attributes for 671 catchments in the contiguous US. We trim the daily data to contain only full water years (starting 1 October), and we analyse data from 1989 to 2009. We also remove catchments with missing records during that time period. While we need to pick a start date for the analysis, this date does not influence the results (e.g. using 1 January as the starting date would result in the same phase shift).
3.2 Hydrological signatures and catchment attributes
We calculate different hydrological signatures, and we use different catchment attributes, all summarised in Table 1. The climate indices from Knoben et al. (2018) are based on monthly averages, and they need to be interpreted as follows. A moisture index Im of 1 indicates the most humid (energy-limited) catchments; a moisture index of −1 indicates the most arid (water-limited) catchments. A moisture index seasonality Im,r of 0 indicates catchments where the climate stays constant throughout the year; a moisture index seasonality of 2 indicates catchments where the climate switches between fully arid and fully humid within the year.
Institute of Hydrology (1980)Knoben et al. (2018)Knoben et al. (2018)Knoben et al. (2018)National River Flow Archive (2019)National River Flow Archive (2019)Addor et al. (2017a)Table 1Hydrological signatures and catchment attributes used in this study.
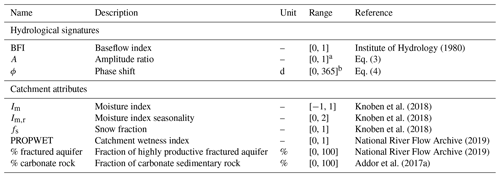
a Should in theory be smaller than unity. b Should theoretically always be positive and in practice be smaller than 1 year. Further discussions on the possible ranges of the seasonal signatures can be found in the text. PROPWET: PROPortion of time soils are WET.
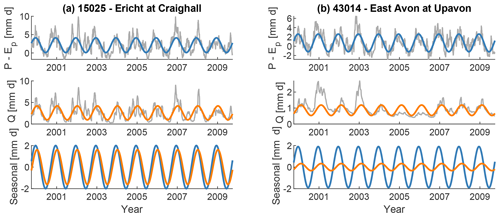
Figure 4Climate input (P−Ep; blue) and catchment output (Q; orange) for two example catchments in the UK and their respective seasonal components. The time series are smoothed using a 30 d moving mean. The Ericht is a rather responsive catchment (BFI = 0.47), while the East Avon has a large baseflow component (BFI = 0.89). Note that for the bottom plots (“Seasonal”) the mean values of the sine curves are set to 0.
4.1 Extracting seasonal components from time series
First, we extract seasonal components from P−Ep (forcing) and Q (streamflow) for all catchments. The resulting sine wave parameters are then used to calculate the amplitude ratios (Eq. 3) and phase shifts (Eq. 4), respectively. Figure 4 shows P−Ep and Q for two catchments alongside their seasonal (sinusoidal) components. Both catchments experience a similar forcing, but their response is very different. The Ericht at Craighall, a rather responsive catchment, shows a seasonal streamflow component that is very similar to the seasonal forcing component. In contrast, the East Avon at Upavon, a groundwater-dominated catchment, shows a strongly attenuated seasonal streamflow component. For our seasonal signatures this would mean (a) that the responsive catchment has a high amplitude ratio (i.e. the streamflow amplitude is almost as large as the forcing amplitude, while the groundwater-dominated catchment has a low amplitude ratio) and (b) that the responsive catchment has a small phase shift (i.e. it responds quickly to the seasonal forcing, while the groundwater-dominated catchment has a large phase shift).
4.2 Seasonal signatures of observed catchment data
To visualise the seasonal signatures, we plot the amplitude ratios and phase shifts in a similar way as in Figs. 1–3. This is shown in Fig. 5a for all UK catchments. These include catchments with human influences, such as groundwater abstractions, man-made reservoirs, or water transfers. The overall pattern in Fig. 5a is very similar to the pattern using benchmark catchments alone (grey dots). We therefore use all of the catchments, noting that a few catchments might be unsuitable for individual analyses.
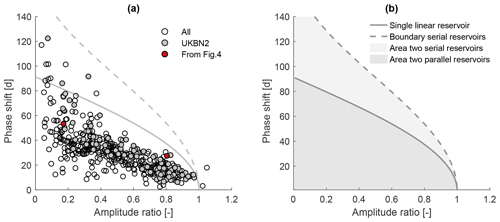
Figure 5(a) Amplitude ratio against phase shift for UK catchments. Grey dots indicate benchmark catchments, and red dots indicate the two catchments shown in Fig. 4. The grey solid line indicates a single linear reservoir, and the grey dashed line indicates the outer envelope for two reservoirs in parallel. Note that both axes are limited (two catchments are not shown). (b) Theoretical areas and limits for a single linear reservoir, two reservoirs in series, and two reservoirs in parallel.
Figure 5a shows that most of the catchments fall below the solid grey line, which indicates the type of response that could be simulated by a single linear reservoir (see Fig. 5b). The area below the solid line can be simulated by two reservoirs in parallel. This would be the most parsimonious way to reproduce the observed behaviour if we decide to construct our model using linear reservoirs only. A few catchments plot above the solid line. For these catchments, the most parsimonious way to reproduce the pair of observed amplitude ratio and phase shift would therefore be two reservoirs in series. Very few catchments have an amplitude ratio larger than unity. While this could be caused by various errors in the data, it is likely due to erroneous catchment areas and/or the presence of inter-catchment groundwater flows or water transfers. If a catchment receives more net rainfall than the surface catchment area suggests (runoff ratio > 1), the amplitude in the output signal (streamflow) can be larger than the amplitude in the (erroneous) input signal.
4.3 Relationship between seasonal signatures and catchment attributes – UK
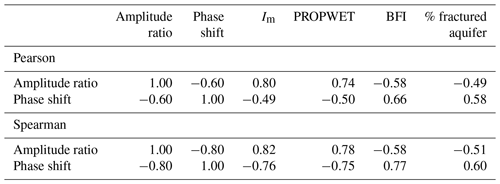
Figure 6 shows pairs of amplitude ratios and phase shifts, coloured according to different hydrological signatures and catchment attributes, respectively (explained in Table 1). Corresponding correlation coefficients can be found in Table 2. Figure 6a shows a clear pattern between the moisture index and the seasonal signatures. Generally, the less humid the catchments are, the lower the amplitude ratio is, and the larger the phase shift is. In other words, drier catchments attenuate the incoming forcing signal more strongly. This might partly be because we use potential evapotranspiration as our forcing. Lower actual evapotranspiration than potential evapotranspiration leads to a decreased input amplitude and thus to a higher amplitude ratio. Most of the very humid catchments plot close together, and the relationship between amplitude ratio and phase shift seems to be almost linear. Less humid catchments (note that in the UK none of the catchments are actually water-limited at the annual scale) show a larger spread, especially regarding the phase shift. Figure 6b shows a very similar pattern between the catchment wetness index and the seasonal signatures. Wetter catchments exhibit higher amplitude ratios and lower phase shifts, and vice versa. The catchment wetness index is strongly correlated with the moisture index (Spearman rank correlation of 0.94). Figure 6c shows a clear pattern between the baseflow index and the seasonal signatures. In contrast to the moisture index, where the stratification mostly follows the x axis (amplitude ratio), the stratification mostly follows the y axis (phase shift). Catchments with high BFIs exhibit low amplitude ratios and large phase shifts, and vice versa. Finally, in Fig. 6d we can see that catchments underlain by highly productive fractured aquifers exhibit (with a few exceptions) low amplitude ratios and large phase shifts.
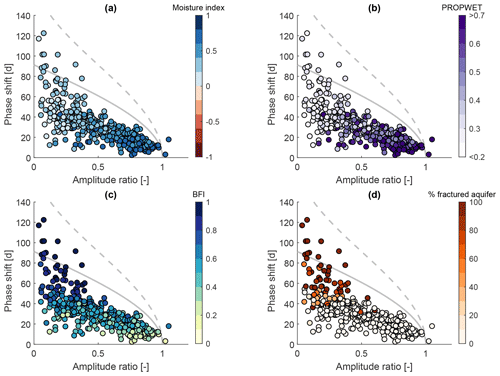
Figure 6Amplitude ratio against phase shift for UK catchments. The grey solid line indicates a single linear reservoir, and the grey dashed line indicates the outer envelope for two reservoirs in parallel. Colours indicate (a) the moisture index, (b) the catchment wetness index, (c) the baseflow index, and (d) the fraction of highly productive fractured aquifer. Note that both axes are limited (two catchments are not shown).
4.4 Relationship between seasonal signatures and catchment attributes – US
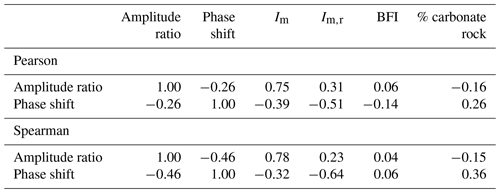
Figure 7 shows pairs of amplitude ratios and phase shifts for the US, coloured according to different hydrological signatures and catchment attributes, respectively (explained in Table 1). Corresponding correlation coefficients can be found in Table 3. Catchments with a significant snow fraction (fs>0.001) are removed, as snow presents another hydrological process which is not the focus of this study. Generally, snow adds another storage process, and this is reflected in large phase shifts observed in snowy catchments (see Sect. S2.3 for more information). The non-snowy catchments in the US show a similar trend to the catchments in the UK. Yet generally, the amplitude ratios are lower, and the phase shifts are larger compared to the UK (note that the y axes in Fig. 7 differ in their range from the y axes in Fig. 6). Humid catchments tend to have higher amplitude ratios and smaller phase shifts (Fig. 7a). Climate seasonality, indicated by the moisture index seasonality (see Fig. 7b), also influences the seasonal signatures. Catchments with a larger moisture index seasonality, i.e. a more variable monthly moisture index over the year, tend to have smaller phase shifts. The BFI (Fig. 7c) does not show such a clear pattern as for the UK catchments (Fig. 6c). Similarly, subsurface properties such as the fraction of carbonate sedimentary rock (Fig. 7d; and other attributes not shown here) only show a weak relationship with the seasonal signatures. Catchments with larger fractions of carbonate sedimentary rocks tend to have lower amplitude ratios and larger phase shifts. The overall pattern, however, is rather scattered. Contrary to the UK, some of the catchments in the US plot outside the area that can be modelled by either two reservoirs in series or in parallel, and some catchments have phase shifts larger than 182 d, the approximate limit for two reservoirs in series. These catchments are very arid and the low moisture seasonality index indicates that most of the precipitation in these catchments falls when potential evapotranspiration is highest, i.e. in summer.
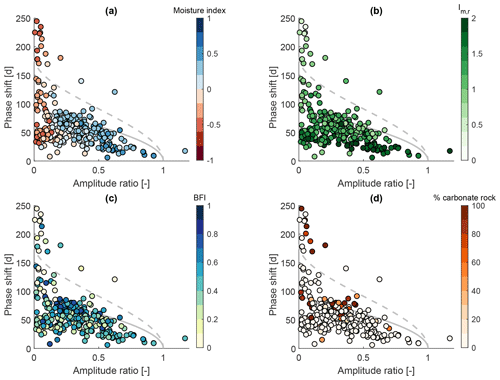
Figure 7Amplitude ratio against phase shift for CAMELS catchments. Catchments with a snow fraction (fs>0.001) are removed from the analysis. The grey solid line indicates a single linear reservoir, and the grey dashed line indicates the outer envelope for two reservoirs in parallel. Colours indicate (a) the moisture index, (b) the moisture index seasonality, (c) the baseflow index, and (d) the fraction of carbonate sedimentary rock. Note that both axes are limited (12 catchments are not shown) and that the range of the phase shift axis is different from Fig. 6.
4.5 Seasonal signatures as a diagnostic tool for evaluating hydrological models
In a similar fashion as for the observed catchment data, we now investigate the model runs using IHACRES and GR4J. Fig. 8 shows the resulting amplitude ratios and phase shifts for all model runs, that is for 20 000 parameter sets using data from a subset of 40 catchments in the UK. These plots show which combinations of seasonal signatures (and BFI) can be obtained with each model, given the forcing of 40 different catchments covering most of the hydro-climatic variability of the UK and given the parameter ranges chosen. They hence show the “signature space” of a model in the dimensions given by amplitude ratio and phase shift (and BFI).
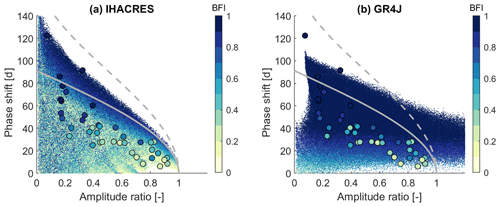
Figure 8Amplitude ratio against phase shift for 40 catchments in the UK using 20 000 parameter sets each for (a) IHACRES and (b) GR4J. The large dots show the observed signatures of the 40 catchments used for the modelling experiment. Colours indicate the BFI. Note that both axes are limited.
IHACRES (Fig. 8a) shows a pattern that covers the area that can be modelled by two reservoirs in parallel and a large fraction of the area that can be modelled by two reservoirs in series (see Figs. 2 and 3). The BFI spans the whole range from 0 to 1. IHACRES can reproduce the observed amplitude ratios and phase shifts, although one catchment sits just at the boundary of the point cloud. GR4J (Fig. 8b) covers a different signature space. The phase shift never exceeds 105 d, the amplitude ratio often exceeds unity, and the BFI tends to be high. GR4J can reproduce most of the observed amplitude ratios and phase shifts, except for catchments with very large phase shifts. Furthermore, it struggles to simultaneously reproduce the observed phase shifts and BFIs. Both models sometimes yield phase shifts that are close to 1 year (not shown here), which are effectively negative phase shifts. A negative phase shift implies that the periodic component of Q leads the periodic component of P−Ep. This can happen if actual evapotranspiration Ea differs considerably from potential evapotranspiration Ep, and hence most of the input seasonality stems from P (and not Ep). This can be observed in a few catchments in the US (not shown here). It is only observed once in the UK (in a catchment with a man-made reservoir, not shown here), and therefore we do not investigate these model runs further.
Figure 9 shows distributions (“one-dimensional signatures spaces”) for three hydrological signatures for the 40 catchments investigated here. These plots tell us which signature values a model tends to produce (given a certain sampling scheme), the ranges of signatures a model can reproduce (given the parameter ranges chosen), and how (much) a signature varies with varying forcing.
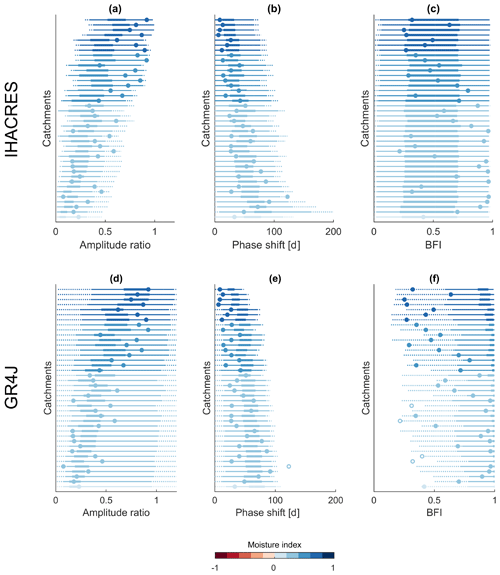
Figure 9Distributions of different hydrological signatures resulting from the modelling experiment. Each line stands for one of the 40 catchments, and the colours indicate the corresponding moisture index. The distributions of the modelled signatures are indicated by box-whisker-type plots. The thick line spans from the 25th to the 75th percentile. The thin line spans from the 1st (75th) to the 25th (99th) percentile. The dotted line indicates values below (above) the 1st (99th) percentile. The circles indicate the observed signature values, while filled circles indicate that the observed signature is inside the modelled signature space and vice versa. Panels (a), (b), and (c) show results for IHACRES. Panels (d), (e), and (f) show results for GR4J. Model runs with amplitude ratios lower than 0.01, amplitude ratios larger than 1.2, or phase shifts larger than 200 d have been removed.
Figure 9 displays similar information as Fig. 8, yet it does not consider interactions between the three signatures. IHACRES can produce amplitude ratios from 0 to 1 and phase shifts up to 182 d (which is the limit for two reservoirs in series) and larger. GR4J can produce amplitude ratios that clearly exceed 1 and cannot model phase shifts larger than 105 d (given the parameter ranges chosen). For both models, more arid forcing leads to lower amplitude ratios and larger phase shifts, and vice versa. For the BFI (Fig. 9c and f) we can see that IHACRES covers the whole possible space (0 to 1) relatively evenly. GR4J tends to produce very high BFIs for almost every parameter set. BFIs smaller than 0.5 are possible with GR4J, but these are rather rare (or unlikely).
5.1 Representation of seasonal components by sine waves and limitations of the approach
A sine wave is a simple way of describing the seasonality of a signal. The results suggest that for most of the catchments investigated here, this approach is reasonable and efficient. Figure 4 shows that the average seasonal pattern is captured by the fitted sine waves. Differences between years cannot be captured by our approach, as we fit a single sine wave to describe the average seasonal behaviour. To robustly capture the average seasonal behaviour, we need relatively long time series. Comparing results from two different 10-year periods shows that the signatures are robust for the majority of catchments; i.e. their values do not differ substantially from one time period to the other (details are shown in Sect. S2.1.3).
The UK catchments and most of the US catchments exhibit a relatively strong unimodal (climate) seasonality (see e.g. Knoben et al., 2018). In other climates with a less distinct seasonal pattern, or with two seasons per year (Knoben et al., 2019b), our approach will not work. Semi-arid and arid catchments also tend to have a less smooth seasonal input, as water availability is more fragmented (Peters et al., 2003). Water-limited catchments can show a strong difference between potential evapotranspiration and actual evapotranspiration, which limits the applicability of our approach (we will discuss that later in more detail). We exclude catchments where precipitation is falling as snow. While snowy catchments are typically also strongly seasonal (Schaefli, 2016), this seasonality is mostly a climate phenomenon. It is rather related to temperature seasonality and not to the response of a catchment to periodic forcing.
5.2 A perceptual model of the seasonal response of catchments in the UK
The results, in particular Figs. 5 and 6 and Table 2, show clear patterns in the seasonal signatures. We can see that the seasonal response in the UK can be simulated by either two reservoirs in series or two reservoirs in parallel. This does not mean that there are no other configurations of more reservoirs leading to the same pairs of amplitude ratio and phase shift. Rather, two reservoirs in series and in parallel, respectively, are the most parsimonious reservoir configuration to reproduce the observed seasonal behaviour. Of course, two reservoirs in parallel and two reservoirs in series, respectively, might be seen as “special cases” of a soil reservoir followed by a fast and a slow reservoir, i.e. a three-reservoir arrangement. Furthermore, there might be concepts other than reservoirs which can explain the observed behaviour. Still, the observed patterns, both where the catchments plot for amplitude ratio vs. phase shift (Fig. 5) and how the catchment attributes relate to that (Fig. 6), suggest that the seasonal signatures are indeed a window into catchment functioning (Berghuijs et al., 2014) and thus have discriminatory power (McMillan et al., 2017; Addor et al., 2018).
Figure 6a and b shows how climate aridity and catchment wetness influence amplitude ratio and phase shift. The observation that more humid catchments respond more quickly to forcing (Fig. 6a and b) concurs with our understanding of these catchments. Wetter and therefore more saturated catchments partition the incoming water mostly into fast flow. The hydrograph closely resembles the forcing, which can also be seen in Fig. 4 for the responsive Ericht. The drier the catchments become, the more water is able to infiltrate, and subsurface properties become more important. This might explain why the spread becomes larger for less humid and hence less saturated catchments. In less humid catchments, actual evapotranspiration is more likely to deviate from potential evapotranspiration. This might be another reason for the greater attenuation in drier catchments, as the actual input (P−Ea) is lower than the theoretical one we compare to (P−Ep). In the UK the assumption that Ea=Ep seems reasonable (see Sect. S2.4 for further information). In more arid regions, such as parts of the US (see Sect. 5.3), this assumption is invalid.
The variability among UK catchments that cannot be explained by catchment wetness can mostly be explained by subsurface properties and the associated response time of a catchment. Catchments with high BFIs and thus large baseflow components show lower amplitude ratios and larger phase shifts, that is a more damped and lagged response (Peters et al., 2003). This can also be seen in Fig. 4 for the groundwater-dominated East Avon River. The relationship between BFI and the seasonal signatures (Fig. 6c) is not surprising, yet since the relationship is not unique, the seasonal signatures add another piece of information. In particular, the phase shift adds a timescale, which quantifies how long – on average – the seasonal input is delayed to become the seasonal output. While the phase shift is only a few days for the most responsive catchments, in the slowest catchments the seasonal signal is shifted up to 4 months. Since the BFI is rather a consequence of a catchment's hydrological behaviour (as are the seasonal signatures) than an attribute of a catchment, the BFI cannot be seen as a cause for the observed patterns in the seasonal signatures. It cannot be used, for example, as a predictor in ungauged catchments. A qualitative attribute that could theoretically be available in ungauged catchments, the fraction of highly productive fractured aquifer, reinforces the influence of the subsurface (Fig. 6d). Except for a few catchments, catchments underlain by such an aquifer exhibit very large phase shifts. In fact, all the catchments above the single reservoir line are underlain by highly productive aquifers. In these catchments, mostly underlain by Chalk, almost all the incoming water infiltrates into the aquifer, and the fast-flow component often is negligible. This might explain why they do not behave like reservoirs in parallel but rather like reservoirs in series, e.g. a soil reservoir (recharge) and a very slow groundwater reservoir. The few catchments which are underlain by highly productive aquifers, but do not exhibit large phase shifts, are typically overlain by rather impermeable drift, which stops water from infiltrating into the aquifer below.
Many models frequently used (and some of them developed) in the UK have a parallel flow structure, and catchments are usually conceptualised as having a fast and a slow component. While parametrisations and model structures vary between models, an overall parallel flow structure following a soil moisture module can be found in the probability distributed model (PDM; Moore, 2007), the TOPography-based hydrological MODEL (TOPMODEL) modelling concept (consisting of two fast flow responses; Beven and Kirkby, 1979), the IHACRES model (Croke and Jakeman, 2004), the GR4J model (Perrin et al., 2003), and many others. These or similar models have been applied to many catchments in the UK by various authors (e.g. Smith et al., 2019; Lane et al., 2019; Coxon et al., 2019). The seasonal signatures suggest that for most of the catchments, particularly if they are not underlain by a highly productive aquifer, a parallel model structure is a reasonable choice (at least for reproducing the response to seasonal forcing). For some groundwater-dominated catchments, however, the fast-flow component seems to be rather unimportant. Many of these catchments, typically catchments underlain by Chalk, could only be poorly modelled in national-scale modelling studies (Smith et al., 2019; Lane et al., 2019; Coxon et al., 2019). While this might partly be due to water balance problems (inter-catchment groundwater flows), it might also be due to an inadequate model structure or inadequate parameter ranges. The most parsimonious reservoir configuration for explaining the seasonal behaviour of these catchments (phase shifts > 91 d) would be two reservoirs in series, e.g. a soil or unsaturated zone reservoir transforming the incoming forcing into recharge and a (linear) groundwater reservoir. At least one of these reservoirs would need to be very slow to obtain such large phase shifts (cf. Fig. 2). For these groundwater-dominated catchments, a serial structure as it is also used in simple lumped groundwater models (e.g. Peters et al., 2003; Obergfell et al., 2019) seems to be a reasonable choice (at least for reproducing the response to seasonal forcing). As mentioned before, two reservoirs in parallel and two reservoirs in series, respectively, might be seen as “special cases” of a soil reservoir followed by a fast and a slow reservoir. For example, some of the catchments underlain by a highly productive aquifer fall in the area that can be simulated by two reservoirs in parallel (see Fig. 6d). Their large phase shifts and their proximity to the “single reservoir line” suggest, however, that the slow-flow component is of particular importance and that large time constants (>100 d) are required to model their behaviour.
In summary, the first control on the attenuation of the seasonal signal in the UK is the partitioning between fast flow and slow flow. More saturated catchments partition more rainfall into fast flow and hence lead to a higher amplitude ratio and to a smaller phase shift. The second control are catchment subsurface properties, which determine the available storage and how slowly water leaves the system. The slower the catchment responds, the larger the phase shift is, and the lower the amplitude ratio is. The Chalk catchments in the UK might be seen as an extreme case where almost all the water infiltrates, and hence the response time of a single slow reservoir (or perhaps two reservoirs in series) is the main control on the propagation of a periodic signal. On the other end of the spectrum, there are fully saturated, very responsive catchments mostly along the west coast of the UK, which behave almost like a single fast reservoir. Using conceptual reservoirs is only one way to interpret the seasonal signatures. It is useful as many hydrological models are built in that way. There might be, however, other possible ways of interpretation which we do not consider here.
5.3 A hydro-meteorologically more diverse set of catchments – the contiguous US
From Fig. 7 and Table 3 it can be seen that for CAMELS catchments (US) the climate indices explain most of the variability in the seasonal response. Again, more humid catchments tend to create more fast flow, and hence they have high amplitude ratios and small phase shifts. Catchments with a larger moisture index seasonality tend to have smaller phase shifts. In these catchments precipitation and potential evapotranspiration are mostly out of phase. Therefore, precipitation falls in more humid months, which might lead to a more flashy response. That means that both precipitation falling on wetter catchments and precipitation falling in wetter months will be less attenuated. The influence of catchment form is much less pronounced than in the climatically more homogeneous UK. Continental or global studies tend to identify climate as the dominant hydrological driving force (van Dijk, 2010; Beck et al., 2015), yet regional studies often show that other attributes such as geology are important (for baseflow, see e.g. Longobardi and Villani, 2008; Bloomfield et al., 2009). Our findings highlight anew that generalising from a global to a regional scale, or from a regional to a global scale, is not straightforward. Such scaling should ideally be done in a process-based way, or by analysing sub-climates, as the dominance of climate might mask the influence of other factors at large scales. We can also see that the attribute “fraction of highly productive fractured aquifers” (Fig. 6d), which is a hydrogeological classification available for the UK, shows a much clearer pattern than any soil or geology attributes in the US (see e.g. Fig. 7d which shows the fraction of carbonate sedimentary rock; the same is true if we use e.g. soil permeability for the UK). This might partly be due to the more heterogeneous US climate which masks the influence of subsurface properties to some degree. But it might also indicate that the soil or geology data used do not contain the hydrologically relevant soil or geology information. The hydrogeological classification based on expert judgement available for the UK, even though it is only categorical, might be more representative of the actual hydro(geo-)logical processes at the scale of interest. We therefore cannot conclude that in the US catchment form does not play a role. We can merely say that the catchment attributes used do not show clear patterns at the continental scale.
Some of the rather arid catchments in the US plot outside the area that can be modelled by two reservoirs in series or in parallel (Fig. 7). This either indicates that we would need another reservoir in series to model the observed phase shift (three reservoirs in series would result in a maximum phase shift of approximately 273 d), that (linear) reservoirs are not a good description of the hydrological processes, or that the proposed signatures are unreliable for these arid catchments. Since in water-limited catchments, actual evapotranspiration is typically much smaller than potential evapotranspiration, the input signal we use is very likely a poor proxy for the actual input signal. In very arid catchments (; dark red dots in Fig. 7a), particularly with the low moisture seasonality index (Fig. 7b), the results should therefore be interpreted with care. It is unclear to what extent these large phase shifts are the result of a poorly approximated input signal or actual catchment function. This compromises the consistency (McMillan et al., 2017) of the seasonal signatures and makes them most suitable for energy-limited catchments. A way to overcome this limitation would be the use of modelled or measured actual evapotranspiration as input data. As this would require another modelling step or additional data, we leave this for future work (see Sect. S2.4 for further information).
5.4 Can two common hydrological models reproduce the observed seasonal signatures?
The ensemble of IHACRES simulations covers the observed range of amplitude ratios and phase shifts, although one catchment sits just at the boundary of the point cloud (Figs. 8a and 9a–c). The BFI pattern also roughly resembles the observed pattern (Fig. 6c). Catchments with low BFIs tend to have high amplitude ratios and small phase shifts, and vice versa. To explain the signature space of IHACRES, it is useful to recall the structure of the model. IHACRES consists of a soil moisture deficit store, followed by two parallel linear reservoirs. It thus approximately features the two examples introduced in Sect. 2, namely two reservoirs in series or in parallel.
If one of the parallel reservoirs in IHACRES receives very little water (due to an extremely high or low fraction p going into the slow reservoir), the whole system acts like two reservoirs in series. The only difference is that the first reservoir is not a single linear reservoir. It is a non-linear deficit store and thus different from the idealised linear reservoir. This might explain why the upper boundary looks similar to the grey dashed line indicating two linear reservoirs in series, yet it does not look exactly the same. We did explore how non-linear reservoirs behave in terms of amplitude ratio and phase shift, and they seem to behave similar to linear reservoirs (see Sect. S1.4). Another reason for IHACRES not covering the whole area might be the parameter ranges (see Sect. S3 for details). The parameter ranges used are intended to be wide, yet especially the fast reservoir (in order to be indeed fast) is limited to 10 d, which limits the theoretical space to be smaller than shown in Fig. 2.
If the soil moisture reservoir transmits water relatively quickly without much attenuation, the whole system acts like two reservoirs in parallel. In summary, IHACRES is very similar to the idealised arrangement we introduced in Sect. 2, and this can be seen in the model output. It is therefore likely that IHACRES is capable of reproducing the observed seasonal signatures for catchments in the UK (Fig. 6) and for most of the catchments in the US (Fig. 7). Whether IHACRES can reproduce the seasonal signatures, other hydrological signatures and achieve satisfactory statistical performance metrics simultaneously is to be explored and beyond the scope of this paper.
The ensemble of GR4J simulations covers most of the amplitude ratios and phase shifts observed in the UK (Figs. 8b and 9d–f). Many of the model runs lead to amplitude ratios higher than unity, which is caused by the groundwater exchange parameter, which allows the model to import water in addition to incoming P. While this is possible (and can in fact be observed; e.g. in Fig. 6c the blue dot outside the grey boundaries is a catchment with water transfer from a neighbouring catchment), it is observed very rarely in the catchments investigated. Furthermore, a non-zero groundwater exchange parameter should ideally be associated with actual water inputs or outputs (e.g. inter-catchment groundwater flows), and these inputs or outputs are usually unknown. It is worth noting that many model runs that lead to signature values at the boundaries of the signature space (e.g. low BFIs or large phase shifts) are associated with large (positive or negative) values for the groundwater exchange parameter (not shown here). This might further reduce the “realistic” signature space, as, for example, obtaining a low amplitude ratio by removing water might be seen as “the right answer for the wrong reason”. No model run leads to a phase shift larger than about 105 d. GR4J also has a soil moisture store followed by two parallel routing stores; i.e. the overall model structure is similar to IHACRES. The stores are, however, not linear reservoirs. In addition to that, GR4J has fixed internal parameter values, such as the fraction of water going through the slow routing store, which is set to 0.9. This might explain why the BFI tends to be very high, as it can be seen from Fig. 9f. Despite the tendency towards large BFIs, GR4J cannot produce phase shifts larger than about 105 d given the parameter ranges used here. This might be due to a range of the flow delay parameter which is too narrow (maximum 15 d). So, to model both the phase shift and the BFI correctly, we might require a more flexible splitting between fast and slow routing and a means to produce larger phase shifts (e.g. via a wider range for the flow delay parameter).
Figure 9 also shows how the seasonal signatures (and the BFI) vary with different inputs (forcing). For both models, more humid catchments lead to higher amplitude ratios and smaller phase shifts, and vice versa. This trend, not necessarily the values themselves, agrees with the observed behaviour shown in Figs. 6a and 7a.
This analysis is necessarily incomplete for (at least) two reasons. First, we only looked at 40 catchments in the UK to limit the computational demand. Therefore, the conclusions are not necessarily transferable to catchments outside the UK. More arid catchments (e.g. in the US) might show a different behaviour (e.g. the catchments showing phase shifts larger than 182 d; see Fig. 7). Second, the sampling scheme (Latin hypercube sampling) explores only a subspace of the actual parameter values (both because of the parameter ranges and because of the finite amount of parameter sets). We also made an a priori decision of how to sample by choosing Latin hypercube sampling in the first place. This is inevitably subjective, and other sampling schemes might lead to different results. This might especially affect the distributions of the modelled signatures shown in Fig. 9. Wider parameter ranges might change the ranges of the resulting signature spaces. As we use rather wide ranges based on recent literature (see Sect. S3 for details), our results should (at least) be representative of current modelling practice. This kind of analysis and the seasonal signatures can therefore help to select (or not select) models a priori, without calibrating them to streamflow data (cf. Vogel and Sankarasubramanian, 2003). This might be particular helpful for large sample studies where often a certain model structure is chosen a priori, even if it might be inadequate for the catchment sample investigated (Addor and Melsen, 2019).
We have tested seasonal hydrological signatures aimed at representing how climate seasonality is translated into streamflow seasonality, both approximated by sine waves. The damping (the amplitude ratio) and the phase shift of the incoming sine wave have been used to quantify how catchments respond to seasonal forcing. The presented signatures follow the guidelines of McMillan et al. (2017). The signatures are identifiable, robust, and consistent (see Sect. S2.1 for further information). They are representative and have discriminatory power as they exhibit explicable, hydrologically interpretable patterns, particularly for energy-limited catchments (Figs. 6 and 7). They can be related to conceptual model structures (arrangements of linear reservoirs; Fig. 5), and the model evaluation (Fig. 8) has shown that we can indeed observe this theoretical behaviour in model outputs. As we use precipitation minus potential evapotranspiration as a proxy for the input to a catchment, the seasonal signatures are unreliable for water-limited catchments. To use the seasonal signatures in water-limited catchments, we would need to estimate actual evapotranspiration. The current approach is therefore only suitable for energy-limited, non-snowy catchments with a distinct unimodal seasonality, such as catchments in the UK.
We have found that the propagation of the seasonal input through a catchment depends both on climate and catchment form. Climate aridity and seasonality, and corresponding annual and seasonal catchment wetness, drive the partitioning of the incoming forcing into fast flow and slow flow. Catchment form, such as subsurface properties, influences how strongly the seasonal input gets attenuated. This is particularly visible in the UK, where the hydrogeological classification available (fraction of highly productive aquifer) can explain the very slow response of some catchments. The seemingly more dominant (and less clear) role of climate in the US highlights that scaling from a regional to a continental (or global) scale is not straightforward and requires thoughtful, ideally process-based, approaches. Or in the words of Turner (1989), “conclusions or inferences regarding landscape patterns and processes must be drawn with an acute awareness of scale”. Nonetheless, the clear link to climate and aquifer characteristics in the UK suggests that the signatures might be useful for catchment classification and for predictions in ungauged catchments, as long as potential evapotranspiration is an adequate proxy for actual evapotranspiration.
The model evaluation has shown that the signatures have the potential to be used as a diagnostic tool. GR4J could not reproduce the observed combinations of phase shift and BFI, pointing towards structural deficiencies of the model for certain catchments. As the seasonal signatures are relatable to conceptual model structures (arrangements of reservoirs), we could – given sufficient data – also build models based on inference from observed values of the signatures and not just test existing model structures. This could be done in a stepwise fashion, starting with the seasonal timescale and then adding more complexity if needed (Jothityangkoon et al., 2001; Farmer et al., 2003; McMillan et al., 2011). It would be a step towards model structure identification based on hydrological reasoning, i.e. getting the right answers for the right reasons (Kirchner, 2006). If we decide on a certain model structure (e.g. two reservoirs in series), we can then use the presented theory to estimate time constants of the reservoirs (the parameters). This could be used as an additional constraint in the calibration process. If the time constants obtained from the seasonal signatures differ from time constants obtained by other means, e.g. by calibrating the model using a metric such as KGE, this might be indicative of limitations of typical modelling approaches (Fowler et al., 2018). It might be that the slower annual signal is exciting different parts of the catchments than events (individual peaks or recessions) do, which we typically calibrate to.
The idea of exploring a model's signature space (following the approach of Vogel and Sankarasubramanian, 2003) perhaps deserves more attention. It allows for exploring models systematically, and it can reveal whether a model can simulate the ranges of hydrological signatures we obtain by analysing catchment data. Similar to sensitivity analysis, it allows us to explore and to better understand how a model works, which parameters are important for which signature, and what output behaviour a model can generate in general – without (and before) calibration. While we limited this analysis to a few signatures, in future studies we should focus on testing whether a model can simultaneously reproduce multiple signatures focusing on different aspects of the hydrological system (Euser et al., 2013; Hrachowitz et al., 2014).
A repository with MATLAB code used for the analysis and the resulting data is available from https://github.com/SebastianGnann/Seasonal_signatures_paper_public (last access: 31 January 2020). Colours are based on http://colorbrewer2.org/#type=sequential&scheme=BuGn&n=3 (last access: 31 January 2020) by Cynthia A. Brewer of Pennsylvania State University. MARRMoT is available from https://doi.org/10.5281/zenodo.3552961 (Knoben, 2019). The CAMELS dataset is available from https://doi.org/10.5065/D6G73C3Q (Addor et al., 2017b). Information about the UK Benchmark Network can be obtained from https://nrfa.ceh.ac.uk/benchmark-network (last access: 31 January 2020). Streamflow data and catchments attributes are available from https://nrfa.ceh.ac.uk (last access: 31 January 2020). CEH-GEAR precipitation data are available from https://doi.org/10.5285/33604ea0-c238-4488-813d-0ad9ab7c51ca (Tanguy et al., 2016). CHESS-PE potential evapotranspiration data are available from https://doi.org/10.5285/8baf805d-39ce-4dac-b224-c926ada353b7 (Robinson et al., 2016).
The supplement related to this article is available online at: https://doi.org/10.5194/hess-24-561-2020-supplement.
SJG, NJKH, and RAW conceptualised the research project. SJG performed the formal analysis. SJG prepared the paper with contributions from all co-authors.
The authors declare that they have no conflict of interest.
Parts of this work were carried out using the computational facilities of the Advanced Computing Research Centre of the University of Bristol (http://www.bris.ac.uk/acrc/) (last access: 31 January 2020). Thanks to Wouter Knoben for help with MARRMoT, helpful discussions, and helpful comments on an earlier version of this paper. Thanks to Gemma Coxon for assisting with the data. We also thank the editor and three anonymous reviewers for their helpful feedback.
This work is funded as part of the Water Informatics Science and Engineering Centre for Doctoral Training (WISE CDT) under a grant from the Engineering and Physical Sciences Research Council (EPSRC; grant no. EP/L016214/1).
This paper was edited by Martijn Westhoff and reviewed by two anonymous referees.
Addor, N. and Melsen, L. A.: Legacy, rather than adequacy, drives the selection of hydrological models, Water Resour. Res., 55, 378–390, https://doi.org/10.1029/2018WR022958, 2019. a
Addor, N., Newman, A. J., Mizukami, N., and Clark, M. P.: The CAMELS data set: catchment attributes and meteorology for large-sample studies, Hydrol. Earth Syst. Sci., 21, 5293–5313, https://doi.org/10.5194/hess-21-5293-2017, 2017a. a, b
Addor, N., Newman, A., Mizukami, M., and Clark, M. P.: Catchment attributes for large-sample studies, UCAR/NCAR, Boulder, CO, https://doi.org/10.5065/D6G73C3Q, 2017b. a
Addor, N., Nearing, G., Prieto, C., Newman, A. J., Le Vine, N., and Clark, M. P.: A ranking of hydrological signatures based on their predictability in space, Water Resour. Res., 54, 8792–8812, https://doi.org/10.1029/2018WR022606, 2018. a, b, c, d
Beck, H. E., de Roo, A., and van Dijk, A. I. J. M.: Global maps of streamflow characteristics based on observations from several thousand catchments, J. Hydrometeorol., 16, 1478–1501, https://doi.org/10.1175/JHM-D-14-0155.1, 2015. a
Berghuijs, W. R., Sivapalan, M., Woods, R. A., and Savenije, H. H. G.: Patterns of similarity of seasonal water balances: A window into streamflow variability over a range of time scales, Water Resour. Res., 50, 5638–5661, https://doi.org/10.1002/2014WR015692, 2014. a, b, c
Beven, K. J. and Kirkby, M. J.: A physically based, variable contributing area model of basin hydrology, Hydrolog. Sci. Bull., 24, 43–69, https://doi.org/10.1080/02626667909491834, 1979. a
Bloomfield, J. P., Allen, D. J., and Griffiths, K. J.: Examining geological controls on baseflow index (BFI) using regression analysis: An illustration from the Thames Basin, UK, J. Hydrol., 373, 164–176, https://doi.org/10.1016/j.jhydrol.2009.04.025, 2009. a
Cayan, D. R., Riddle, L. G., and Aguado, E.: The influence of precipitation and temperature on seasonal streamflow in California, Water Resour. Res., 29, 1127–1140, https://doi.org/10.1029/92WR02802, 1993. a
Cheng, J. and Druzdzel, M.: Latin hypercube sampling in Bayesian networks, in: Proceedings of the Thirteenth International Florida Artificial Intelligence Research Symposium Conference, 287–292, available at: http://www.aaai.org/Papers/FLAIRS/2000/FLAIRS00-054.pdf (last access: 31 January 2020), 2000. a
Clausen, B. and Biggs, B.: Flow variables for ecological studies in temperate streams: groupings based on covariance, J. Hydrol., 237, 184–197, https://doi.org/10.1016/S0022-1694(00)00306-1, 2000. a
Colwell, R. K.: Predictability, constancy, and contingency of periodic phenomena, Ecology, 55, 1148–1153, https://doi.org/10.2307/1940366, 1974. a, b
Court, A.: Measures of streamflow timing, J. Geophys. Res., 67, 4335–4339, https://doi.org/10.1029/JZ067i011p04335, 1962. a
Coxon, G., Freer, J., Lane, R., Dunne, T., Knoben, W. J. M., Howden, N. J. K., Quinn, N., Wagener, T., and Woods, R.: DECIPHeR v1: Dynamic fluxEs and ConnectIvity for Predictions of HydRology, Geosci. Model Dev., 12, 2285–2306, https://doi.org/10.5194/gmd-12-2285-2019, 2019. a, b
Croke, B. F. and Jakeman, A. J.: A catchment moisture deficit module for the IHACRES rainfall-runoff model, Environ. Model. Softw., 19, 1–5, https://doi.org/10.1016/j.envsoft.2003.09.001, 2004. a, b, c
DeWalle, D. R., Edwards, P. J., Swistock, B. ., Aravena, R., and Drimmie, R. J.: Seasonal isotope hydrology of three Appalachian forest catchments, Hydrol. Process., 11, 1895–1906, https://doi.org/10.1002/(SICI)1099-1085(199712)11:15<1895::AID-HYP538>3.0.CO;2-%23, 1997. a
Dooge, J.: Linear theory of hydrologic systems, 1468, Agricultural Research Service, Technical Bulletin No. 1468, US Department of Agriculture, 1973. a, b, c
Eriksson, E.: Compartment models and reservoir theory, Annu. Rev. Ecol. System., 2, 67–84, https://doi.org/10.1146/annurev.es.02.110171.000435, 1971. a, b
Erskine, A. and Papaioannou, A.: The use of aquifer response rate in the assessment of groundwater resources, J. Hydrol., 202, 373–391, https://doi.org/10.1016/S0022-1694(97)00058-9, 1997. a
Euser, T., Winsemius, H. C., Hrachowitz, M., Fenicia, F., Uhlenbrook, S., and Savenije, H. H. G.: A framework to assess the realism of model structures using hydrological signatures, Hydrol. Earth Syst. Sci., 17, 1893–1912, https://doi.org/10.5194/hess-17-1893-2013, 2013. a, b
Farmer, D., Sivapalan, M., and Jothityangkoon, C.: Climate, soil, and vegetation controls upon the variability of water balance in temperate and semiarid landscapes: Downward approach to water balance analysis, Water Resour. Res., 39, 1–21, https://doi.org/10.1029/2001WR000328, 2003. a, b
Fowler, K., Coxon, G., Freer, J., Peel, M., Wagener, T., Western, A., Woods, R. A., and Zhang, L.: Simulating runoff under changing climatic conditions: a framework for model improvement, Water Resour. Res., 54, 9812–9832, https://doi.org/10.1029/2018WR023989, 2018. a
Gupta, H. V., Wagener, T., and Liu, Y.: Reconciling theory with observations: elements of a diagnostic approach to model evaluation, Hydrol. Process., 22, 3802–3813, https://doi.org/10.1002/hyp.6989, 2008. a, b
Gupta, H. V., Kling, H., Yilmaz, K. K., and Martinez, G. F.: Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling, J. Hydrol., 377, 80–91, https://doi.org/10.1016/j.jhydrol.2009.08.003, 2009. a
Harman, C. J.: Age-ranked storage-discharge relations – a unified description of spatially-lumped flow and water age in hydrologic systems, Water Resour. Res., 55, 7143–7165, https://doi.org/10.1029/2017WR022304, 2019. a
Harrigan, S., Hannaford, J., Muchan, K., and Marsh, T. J.: Designation and trend analysis of the updated UK Benchmark Network of river flow stations: the UKBN2 dataset, Hydrol. Res., 49, 552–567, https://doi.org/10.2166/nh.2017.058, 2018a. a
Harrigan, S., Prudhomme, C., Parry, S., Smith, K., and Tanguy, M.: Benchmarking ensemble streamflow prediction skill in the UK, Hydrol. Earth Syst. Sci., 22, 2023–2039, https://doi.org/10.5194/hess-22-2023-2018, 2018b. a, b, c
Hrachowitz, M., Savenije, H., Blöschl, G., McDonnell, J., Sivapalan, M., Pomeroy, J., Arheimer, B., Blume, T., Clark, M., Ehret, U., Fenicia, F., Freer, J., Gelfan, A., Gupta, H., Hughes, D., Hut, R., Montanari, A., Pande, S., Tetzlaff, D., Troch, P., Uhlenbrook, S., Wagener, T., Winsemius, H., Woods, R., Zehe, E., and Cudennec, C.: A decade of Predictions in Ungauged Basins (PUB) – a review, Hydrolog. Sci. J., 58, 1198–1255, https://doi.org/10.1080/02626667.2013.803183, 2013. a
Hrachowitz, M., Fovet, O., Ruiz, L., Euser, T., Gharari, S., Nijzink, R., Freer, J., Savenije, H. H. G., and Gascuel-Odoux, C.: Process consistency in models: The importance of system signatures, expert knowledge, and process complexity, Water Resour. Res., 50, 7445–7469, https://doi.org/10.1002/2014WR015484, 2014. a, b
Institute of Hydrology: Low Flow Studies Report No. 1: Research Report, Institute of Hydrology Research Report 1, 1980. a, b
Jasechko, S., Birks, S. J., Gleeson, T., Wada, Y., Fawcett, P. J., Sharp, Z. D., McDonnell, J. J., and Welker, J. M.: The pronounced seasonality of global groundwater recharge, Water Resour. Res., 50, 8845–8867, https://doi.org/10.1002/2014WR015809, 2014. a
Jothityangkoon, C., Sivapalan, M., and Farmer, D.: Process controls of water balance variability in a large semi-arid catchment: downward approach to hydrological model development, J. Hydrol., 254, 174–198, https://doi.org/10.1016/S0022-1694(01)00496-6, 2001. a, b
Kirchner, J. W.: Getting the right answers for the right reasons: Linking measurements, analyses, and models to advance the science of hydrology, Water Resour. Res., 42, 1–5, https://doi.org/10.1029/2005WR004362, 2006. a
Kirchner, J. W.: Aggregation in environmental systems – Part 1: Seasonal tracer cycles quantify young water fractions, but not mean transit times, in spatially heterogeneous catchments, Hydrol. Earth Syst. Sci., 20, 279–297, https://doi.org/10.5194/hess-20-279-2016, 2016. a, b
Knoben, W. J. M.: wknoben/MARRMoT: MARRMoT_v1.3 (Version v1.3), Zenodo, https://doi.org/10.5281/zenodo.3552961, 2019. a
Knoben, W. J. M., Woods, R. A., and Freer, J. E.: A quantitative hydrological climate classification evaluated with independent streamflow data, Water Resour. Res., 54, 5088–5109, https://doi.org/10.1029/2018WR022913, 2018. a, b, c, d, e, f
Knoben, W. J. M., Freer, J. E., Fowler, K. J. A., Peel, M. C., and Woods, R. A.: Modular Assessment of Rainfall–Runoff Models Toolbox (MARRMoT) v1.2: an open-source, extendable framework providing implementations of 46 conceptual hydrologic models as continuous state-space formulations, Geosci. Model Dev., 12, 2463–2480, https://doi.org/10.5194/gmd-12-2463-2019, 2019a. a
Knoben, W. J. M., Woods, R. A., and Freer, J. E.: Global bimodal precipitation seasonality: A systematic overview, Int. J. Climatol., 39, 558–567, https://doi.org/10.1002/joc.5786, 2019b. a
Laaha, G. and Blöschl, G.: Seasonality indices for regionalizing low flows, Hydrol. Process., 20, 3851–3878, https://doi.org/10.1002/hyp.6161, 2006. a
Laaha, G., Demuth, S., Hisdal, H., Kroll, C. N., van Lanen, H. A. J., Nester, T., Rogger, M., Sauquet, E., Tallaksen, L. M., Woods, R. A., and Young, A.: Prediction of low flows in ungauged basins, in: Runoff Prediction in Ungauged Basins, edited by: Blöschl, G., Sivapalan, M., Wagener, T., Viglione, A., and Savenije, H., Cambridge University Press, Cambridge, 163–188, https://doi.org/10.1017/CBO9781139235761.011, 2013. a
Lane, R. A., Coxon, G., Freer, J. E., Wagener, T., Johnes, P. J., Bloomfield, J. P., Greene, S., Macleod, C. J. A., and Reaney, S. M.: Benchmarking the predictive capability of hydrological models for river flow and flood peak predictions across over 1000 catchments in Great Britain, Hydrol. Earth Syst. Sci., 23, 4011–4032, https://doi.org/10.5194/hess-23-4011-2019, 2019. a, b
Longobardi, A. and Villani, P.: Baseflow index regionalization analysis in a Mediterranean area and data scarcity context: Role of the catchment permeability index, J. Hydrol., 355, 63–75, https://doi.org/10.1016/j.jhydrol.2008.03.011, 2008. a
McGuire, K. J. and McDonnell, J. J.: A review and evaluation of catchment transit time modeling, J. Hydrol., 330, 543–563, https://doi.org/10.1016/j.jhydrol.2006.04.020, 2006. a
McMillan, H. K., Clark, M. P., Bowden, W. B., Duncan, M., and Woods, R. A.: Hydrological field data from a modeller's perspective: Part 1. Diagnostic tests for model structure, Hydrol. Process., 25, 511–522, https://doi.org/10.1002/hyp.7841, 2011. a
McMillan, H. K., Gueguen, M., Grimon, E., Woods, R. A., Clark, M. P., and Rupp, D. E.: Spatial variability of hydrological processes and model structure diagnostics in a 50 km2 catchment, Hydrol. Process., 28, 4896–4913, https://doi.org/10.1002/hyp.9988, 2014. a
McMillan, H. K., Westerberg, I., and Branger, F.: Five guidelines for selecting hydrological signatures, Hydrol. Process., 31, 4757–4761, https://doi.org/10.1002/hyp.11300, 2017. a, b, c, d, e, f, g, h
Milly, P. C. D.: Climate, soil water storage, and the average annual water balance, Water Resour. Res., 30, 2143–2156, https://doi.org/10.1029/94WR00586, 1994. a, b
Montanari, A. and Toth, E.: Calibration of hydrological models in the spectral domain: An opportunity for scarcely gauged basins?, Water Resour. Res., 43, 1–10, https://doi.org/10.1029/2006WR005184, 2007. a, b
Moore, R. J.: The PDM rainfall-runoff model, Hydrol. Earth Syst. Sci., 11, 483–499, https://doi.org/10.5194/hess-11-483-2007, 2007. a
Nash, J.: The form of the instantaneous unit hydrograph, Int. Assoc. Scient. Hydrol., 3, 114–121, 1957. a
Nash, J. and Sutcliffe, J.: River flow forecasting through conceptual models part I – A discussion of principles, J. Hydrol., 10, 282–290, https://doi.org/10.1016/0022-1694(70)90255-6, 1970. a
National River Flow Archive: NERC CEH, Wallingford, available at: https://nrfa.ceh.ac.uk (last access: 31 January 2020), 2019. a, b, c
Newman, A. J., Clark, M. P., Sampson, K., Wood, A., Hay, L. E., Bock, A., Viger, R. J., Blodgett, D., Brekke, L., Arnold, J. R., Hopson, T., and Duan, Q.: Development of a large-sample watershed-scale hydrometeorological data set for the contiguous USA: data set characteristics and assessment of regional variability in hydrologic model performance, Hydrol. Earth Syst. Sci., 19, 209–223, https://doi.org/10.5194/hess-19-209-2015, 2015. a
Obergfell, C., Bakker, M., and Maas, K.: Estimation of average diffuse aquifer recharge using time series modeling of groundwater heads, Water Resour. Res., 55, 2194–2210, https://doi.org/10.1029/2018WR024235, 2019. a, b, c
Olden, J. D. and Poff, N. L.: Redundancy and the choice of hydrologic indices for characterizing streamflow regimes, River Res. Appl., 19, 101–121, https://doi.org/10.1002/rra.700, 2003. a, b
Oudin, L., Salavati, B., Furusho-Percot, C., Ribstein, P., and Saadi, M.: Hydrological impacts of urbanization at the catchment scale, J. Hydrol., 559, 774–786, https://doi.org/10.1016/j.jhydrol.2018.02.064, 2018. a
Peel, M. C. and Blöschl, G.: Hydrological modelling in a changing world, Prog. Phys. Geogr., 35, 249–261, https://doi.org/10.1177/0309133311402550, 2011. a
Perrin, C., Michel, C., and Andréassian, V.: Improvement of a parsimonious model for streamflow simulation, J. Hydrol., 279, 275–289, https://doi.org/10.1016/S0022-1694(03)00225-7, 2003. a, b
Peters, E., Torfs, P. J., van Lanen, H. A., and Bier, G.: Propagation of drought through groundwater – A new approach using linear reservoir theory, Hydrol. Process., 17, 3023–3040, https://doi.org/10.1002/hyp.1274, 2003. a, b, c, d, e, f, g
Poff, N. L. and Zimmerman, J. K. H.: Ecological responses to altered flow regimes: a literature review to inform the science and management of environmental flows, Freshwater Biol., 55, 194–205, https://doi.org/10.1111/j.1365-2427.2009.02272.x, 2010. a
Poff, N. L., Allan, J. D., Bain, M. B., Karr, J. R., Prestegaard, K. L., Richter, B. D., Sparks, R. E., and Stromberg, J. C.: The Natural Flow Regime, BioScience, 47, 769–784, https://doi.org/10.2307/1313099, 1997. a
Post, D. A. and Jakeman, A. J.: Predicting the daily streamflow of ungauged catchments in S.E. Australia by regionalising the parameters of a lumped conceptual rainfall-runoff model, Ecol. Model., 123, 91–104, https://doi.org/10.1016/S0304-3800(99)00125-8, 1999. a
Regonda, S. K., Rajagopalan, B., Clark, M., and Pitlick, J.: Seasonal cycle shifts in hydroclimatology over the western United States, J. Climate, 18, 372–384, https://doi.org/10.1175/JCLI-3272.1, 2005. a
Richter, B. D., Baumgartner, J. V., Powell, J., and Braun, D. P.: A method for assessing hydrologic alteration within ecosystems, Conserv. Biol., 10, 1163–1174, https://doi.org/10.1046/j.1523-1739.1996.10041163.x, 1996. a
Robinson, E. L., Blyth, E., Clark, D. B., Comyn-Platt, E., Finch, J., and Rudd, A. C.: Climate hydrology and ecology research support system potential evapotranspiration dataset for Great Britain (1961–2015) [CHESS-PE], NERC Environmental Information Data Centre, https://doi.org/10.5285/8baf805d-39ce-4dac-b224-c926ada353b7, 2016. a, b
Sawicz, K., Wagener, T., Sivapalan, M., Troch, P. A., and Carrillo, G.: Catchment classification: Empirical analysis of hydrologic similarity based on catchment function in the eastern USA, Hydrol. Earth Syst. Sci., 15, 2895–2911, https://doi.org/10.5194/hess-15-2895-2011, 2011. a
Schaefli, B.: Snow hydrology signatures for model identification within a limits-of-acceptability approach, Hydrol. Process., 30, 4019–4035, https://doi.org/10.1002/hyp.10972, 2016. a
Sefton, C. and Howarth, S.: Relationships between dynamic response characteristics and physical descriptors of catchments in England and Wales, J. Hydrol., 211, 1–16, https://doi.org/10.1016/S0022-1694(98)00163-2, 1998. a
Shafii, M. and Tolson, B. A.: Optimizing hydrological consistency by incorporating hydrological signatures into model calibration objectives, Water Resour. Res., 51, 3796–3814, https://doi.org/10.1002/2014WR016520, 2015. a
Shi, X., Wood, A. W., and Lettenmaier, D. P.: How essential is hydrologic model calibration to seasonal streamflow forecasting?, J. Hydrometeorol., 9, 1350–1363, https://doi.org/10.1175/2008JHM1001.1, 2008. a
Smakhtin, V.: Low flow hydrology: a review, J. Hydrol., 240, 147–186, https://doi.org/10.1016/S0022-1694(00)00340-1, 2001. a
Smith, K. A., Barker, L. J., Tanguy, M., Parry, S., Harrigan, S., Legg, T. P., Prudhomme, C., and Hannaford, J.: A multi-objective ensemble approach to hydrological modelling in the UK: an application to historic drought reconstruction, Hydrol. Earth Syst. Sci., 23, 3247–3268, https://doi.org/10.5194/hess-23-3247-2019, 2019. a, b, c
Svensson, C.: Seasonal river flow forecasts for the United Kingdom using persistence and historical analogues, Hydrolog. Sci. J., 61, 19–35, https://doi.org/10.1080/02626667.2014.992788, 2016. a, b
Tanguy, M., Dixon, H., Prosdocimi, I., Morris, D. G., and Keller, V. D. J.: Gridded estimates of daily and monthly areal rainfall for the United Kingdom (1890–2015) [CEH-GEAR], NERC Environmental Information Data Centre, https://doi.org/10.5285/33604ea0-c238-4488-813d-0ad9ab7c51ca, 2016. a, b
Townley, L. R.: The response of aquifers to periodic forcing, Adv. Water Resour., 18, 125–146, https://doi.org/10.1016/0309-1708(95)00008-7, 1995. a
Turner, M. G.: Landscape ecology: the effect of pattern on process, Annu. Rev. Ecol. System., 20, 171–197, https://doi.org/10.1146/annurev.es.20.110189.001131, 1989. a
van Dijk, A. I. J. M.: Climate and terrain factors explaining streamflow response and recession in Australian catchments, Hydrol. Earth Syst. Sci., 14, 159–169, https://doi.org/10.5194/hess-14-159-2010, 2010. a
Vega, M., Pardo, R., Barrado, E., and Debán, L.: Assessment of seasonal and polluting effects on the quality of river water by exploratory data analysis, Water Res., 32, 3581–3592, https://doi.org/10.1016/S0043-1354(98)00138-9, 1998. a
Vogel, R. M. and Sankarasubramanian, A.: Validation of a watershed model without calibration, Water Resour. Res., 39, 1–9, https://doi.org/10.1029/2002WR001940, 2003. a, b, c, d
Wagener, T., Sivapalan, M., Troch, P., and Woods, R.: Catchment classification and hydrologic similarity, Geogr. Compass, 1, 901–931, https://doi.org/10.1111/j.1749-8198.2007.00039.x, 2007. a
Weingartner, R., Blöschl, G., Hannah, D. M., Marks, D. G., Parajka, J., Pearson, C. S., Rogger, M., Salinas, J. L., Sauquet, E., Srikanthan, R., Thompson, S. E., and Viglione, A.: Prediction of seasonal runoff in ungauged basins, in: Runoff Prediction in Ungauged Basins, edited by: Blöschl, G., Sivapalan, M., Wagener, T., Viglione, A., and Savenije, H., Cambridge University Press, Cambridge, 102–134, https://doi.org/10.1017/CBO9781139235761.009, 2013. a, b
Westerberg, I. K., Wagener, T., Coxon, G., McMillan, H. K., Castellarin, A., Montanari, A., and Freer, J.: Uncertainty in hydrological signatures for gauged and ungauged catchments, Water Resour. Res., 52, 1847–1865, https://doi.org/10.1002/2015WR017635, 2016. a
Yadav, M., Wagener, T., and Gupta, H. V.: Regionalization of constraints on expected watershed response behavior for improved predictions in ungauged basins, Adv. Water Resour., 30, 1756–1774, https://doi.org/10.1016/j.advwatres.2007.01.005, 2007. a
Yokoo, Y. and Sivapalan, M.: Towards reconstruction of the flow duration curve: Development of a conceptual framework with a physical basis, Hydrol. Earth Syst. Sci., 15, 2805–2819, https://doi.org/10.5194/hess-15-2805-2011, 2011. a
Young, P.: Data-based mechanistic modelling of environmental, ecological, economic and engineering systems, Environ. Model. Softw., 13, 105–122, https://doi.org/10.1016/S1364-8152(98)00011-5, 1998. a