the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The role of household adaptation measures in reducing vulnerability to flooding: a coupled agent-based and flood modelling approach
Yared Abayneh Abebe
Amineh Ghorbani
Igor Nikolic
Natasa Manojlovic
Angelika Gruhn
Zoran Vojinovic
Flood adaptation measures implemented at the household level play an important role in reducing communities' vulnerability. The aim of this study is to enhance the current modelling practices of human–flood interaction to draw new insights for flood risk management (FRM) policy design. The paper presents a coupled agent-based and flood model for the case of Hamburg, Germany, to explore how individual adaptation behaviour is influenced by flood event scenarios, economic incentives and shared and individual strategies. Simulation results show that a unique trajectory of adaptation measures and flood damages emerges from different flood event series. Another finding is that providing subsidies increases the number of coping households in the long run. Households' social network also has a strong influence on their coping behaviour. The paper also highlights the role of simple measures such as adapted furnishings, which do not incur any monetary cost, in reducing households' vulnerability and preventing millions of euros of contents damages. Generally, we demonstrate that coupled agent-based and flood models can potentially be used as decision support tools to examine the role of household adaptation measures in flood risk management. Although the findings of the paper are case-specific, the improved modelling approach shows the potential to be applied in testing policy levers and strategies considering heterogeneous individual behaviours.
- Article
(8619 KB) - Full-text XML
- BibTeX
- EndNote
One of the goals of flood risk management (FRM) is the evaluation of strategies, policies and measures to foster flood risk reduction and promote continuous improvement in flood preparedness and recovery practices (IPCC, 2014). As flood risk is a function of flood hazard and communities' exposure and vulnerability, one way of reducing flood risk is by reducing the vulnerability at the household level. Focusing on the physical and economic aspects, measures to reduce vulnerability include elevating houses, retrofitting, dry or wet flood proofing, insurance and subsidies. These measures either prevent flooding or minimise the impact. While measures such as subsidies are offered by authorities or aid groups, the decision to implement most adaptation measures is made at the household level.
Household adaptation behaviour is affected by many factors such as flood risk perception, experience with flooding, socio-economic and geographic factors, reliance on public protection and competency to carry out adaptation measures (Bubeck et al., 2012). The current literature mainly makes use of empirical research to draw insights into the role of household adaptation behaviour in reducing flood risk (for example, Botzen et al., 2019; Grahn and Jaldell, 2019; Grothmann and Reusswig, 2006; Poussin et al., 2014; Schlef et al., 2018). Nevertheless, modelling efforts that bring behavioural and physical attributes together can further enrich these insights and add even more knowledge by incorporating the complex reality surrounding human–flood interactions.
One of the research gaps in the current literature that presents models to study household flood adaptation behaviour (for example, Erdlenbruch and Bonté, 2018; Haer et al., 2016) is that flood events are not included in the simulation models. These studies define flood experience as an agent attribute that is set initially and stays the same throughout the simulations. A household that was not flooded in past events may get flooded in the future and may re-evaluate previous adaptation decisions, which in turn necessitates that flood events are included in the modelling. The second gap is that the effects of an economic incentive on the adaptation behaviour of individuals have not been addressed in the models. Such an analysis would provide an understanding of how much incentives contribute to flood risk reduction.
This study aims to enhance the current modelling practices of human–flood interaction to address the shortcomings of the current literature and draw new insights for FRM policy design. To achieve this aim, we build a coupled agent-based and flood model that comprehensively includes both human and flood attributes in a holistic manner (Vojinovic, 2015). Agent-based models (ABMs) are computational models in which autonomous and heterogeneous agents (for example, households) interact with each other and their environment (Railsback and Grimm, 2012), exploring the behaviour of agents in a system. The coupled ABM–flood model builds on empirical and modelling insights in the literature (i) by presenting an integrated simulation model instead of only agent-based models and (ii) by testing the effects of economic incentives and institutional configurations that have not yet been studied in the context of household flood adaptation behaviour. We use the protection motivation theory (PMT; Rogers, 1983) to investigate household-level decision-making in adopting mitigation measures against flood threats.
More specifically, this paper extends two studies presented in Birkholz (2014) and Abebe et al. (2019b). Birkholz qualitatively explored PMT to study household flood preparedness behaviour in the German city of Hamburg. Birkholz collected information on local communities' flood risk perceptions and flood preparedness using semi-structured interviews. The current study uses the qualitative study as a base to conceptualise and further explore the household flood preparedness behaviour in Hamburg using an ABM. Abebe et al. (2019b) employ the coupled flood-agent-institution modelling (CLAIM) framework developed in Abebe et al. (2019a) to conceptualise the agent–flood interaction by decomposing the system into five components – agents, institutions, urban environment, physical processes and external factors. Their main focus was to study the implications of formal rules as institutions. In contrast, the current study mainly investigates the effect of informal institutions in the form of shared strategies applying the CLAIM framework. Additionally, the study examines individual strategies that affect households' adaptation behaviour.
The remainder of the paper is structured as follows: Sect. 2 describes the study area. Section 3 provides a brief description of PMT and explains how it is conceptualised for the study area. Section 4 discussed how CLAIM is used to decompose the system, the ABM and flood model setups, model evaluations and experimental setups. Section 5 presents the results of the modelling exercises, followed by a discussion of the implications of the study findings and conclusions in Sect. 6.
We develop a coupled ABM–flood model that uses PMT as a tool to model households' flood vulnerability reduction behaviour for the FRM case of Wilhelmsburg, a quarter of Hamburg, Germany. The Wilhelmsburg quarter is built on a river island formed by the branching river Elbe, as shown in Fig. 1. Most areas in Wilhelmsburg are just above sea level. Thus, a flood defence ring of dykes and flood walls protects the quarter. In 1962, a hurricane-induced storm surge (5.70 m above sea level) overtopped and breached the dykes, and more than 200 people lost their lives and properties were damaged due to coastal flooding in Wilhelmsburg (Munich RE, 2012). As a result, the authorities heightened and reinforced the coastal defence system. According to the Munich RE report, after 1962, eight storm surges of levels higher than 5.70 m occurred (most between 1990 and 1999), but none of the events caused any damage as coastal protection had been improved.
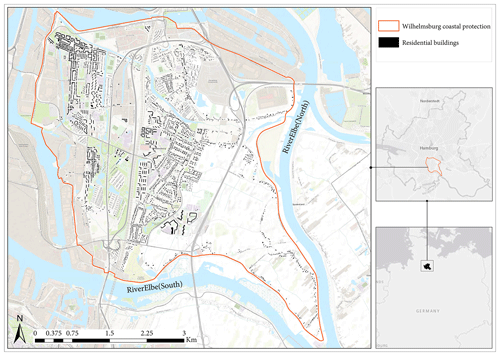
Figure 1A map of the study area of Wilhelmsburg. The red polygon shows Wilhelmsburg's coastal protection ring of dykes and walls. The study focuses on residential housing within the protected area. The buildings shown in the map are only those that are part of the model conceptualisation. The inset maps on the right show a map of Germany (bottom) and of Hamburg (top). (source: the base map is an ESRI topographic map.)
Those events reminded residents of the potential risks of coastal flooding while, at the same time, increasing their reliance on the dyke protection system. The reliance on public protection is promoted by the authorities, who do not encourage the implementation of individual flood risk reduction measures, referring to the strength of the dyke system. On the other hand, the authorities disseminate warning and evacuation strategies to the public, acknowledging that there could be a flood in future. There is a probability that a storm surge bigger than the design period of the coastal defence may occur in the future, and climate change and sea level rise may even intensify the event. Hence, protecting houses from flooding should not necessarily be the responsibility of the authorities. Households should also have a protection motivation that leads to implementing measures to reduce flood risk.
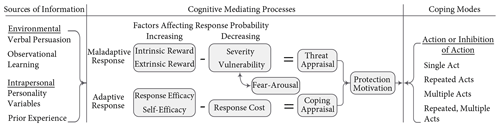
As shown in Fig. 2, PMT has three parts – sources of information, cognitive mediating processes and coping modes (Rogers, 1983). The “sources of information” can be environmental, such as seeing what happens to others, and intrapersonal, such as experience of a similar threat. Triggered by the information, the “cognitive mediation process” includes the threat and coping appraisals. The “threat appraisal” evaluates the severity of and the vulnerability to the threat against the intrinsic and extrinsic positive reinforcers. The “coping appraisal” evaluates the effectiveness of an adaptation measure to mitigate or reduce the risk, the ability to implement the measure and the associated cost of implementing the measure. If the threat and coping appraisals are high, households develop a “protection motivation” that leads to action. The “coping modes” can be a “single act”, “repeated acts”, “multiple acts” or “repeated, multiple acts”.
Originally developed in the health domain (Rogers, 1983), PMT has been extended and applied in diverse domains that involve a threat for which individuals can carry out an available effective recommended response (Floyd et al., 2000). For example, in FRM studies, Poussin et al. (2014) extended the PMT by adding five factors – flood experience, risk attitudes, FRM policies, social networks and social norms and socio-economic factors – that directly determine the protection motivation of households. Two studies applied PMT in ABMs to test the effectiveness of flood risk communication strategies and the influence of the social network on the adoption of protective measures to reduce households' vulnerability to flooding (Erdlenbruch and Bonté, 2018; Haer et al., 2016). They compute the odds ratio and probability of implementation to model household decisions on flood preparedness. One of the conclusions of the studies is that communication policies should have information regarding both the flood threat and coping methods to increase the adaptation rate.
Conceptualising the protection motivation theory for Wilhelmsburg
In the present work, we have modified the original PMT (Rogers, 1983) to use it in FRM and ABM contexts for the specific case of Wilhelmsburg. In the original theory, the sources of information initiate both the threat appraisal and coping appraisal processes. However, in the current study, the sources of information influence the threat appraisal only. We assume that if there is a threat and need to implement a coping measure, the agents know the type of measure they implement based on their house categories (see Table 1).
In the threat appraisal, the “maladaptive response” is the current behaviour of not implementing household-level flood vulnerability reduction measures. In the case of Wilhelmsburg, the maladaptive response is affected by flood experience, reliance on public protection (i.e. the dyke system), climate change perception and the source of information.
The flood experience refers to any experience of households being directly affected by flooding or witnessing flooding that affected others in Wilhelmsburg.
The reliance on public protection is related to the flood experience. Residents of Wilhelmsburg who have not experienced flooding have a high reliance on the dyke system. The fact of seeing the dykes on a daily basis gives residents a sense of protection and causes them to underestimate the flood threat. The reliance on public protection is also associated with the trust the residents have in the authorities when it comes to FRM. However, as some informants who experienced the 1962 flood described, the reliance on the dyke system drops if flooding occurs in the future (Birkholz, 2014).
We include agents' climate change perception as a factor as some residents of Wilhelmsburg described that sea level rise might increase the occurrence of flooding in future. The effects of climate change create some discomfort and stress, and hence, it is seen as a source of concern. Besides, Germans, in general, are concerned about climate change, whereby 86 % are “extremely to somewhat worried” (NatCen Social Research, 2017).
The source of information is an important factor that shapes residents' perception of flood risk. The municipal and state authorities have a firm belief that the dyke system is the primary flood protection measure and that there is no need to implement individual measures to protect properties. However, these authorities communicate evacuation strategies in the case that the dykes fail or are overtopped by a storm surge. On the other hand, other sources such as experts from the Technical University of Hamburg-Harburg organised flood risk awareness workshops presenting the flood risk in Wilhelmsburg and different adaptation measures that individuals could implement. Media also has a role in creating concern by showing flooding and its impacts in other German cities and even other countries.
In the coping appraisal, the “adaptive response” is developing a protection motivation behaviour to implement flood vulnerability reduction measure. The factors that affect the response probability in this conceptualisation are personal flood experience, house ownership, household income, subsidies from the state and social networks.
Personal flood experience refers to a direct flood experience in which an agent's house was flooded before. It is a major factor that drives the adaptive response (Bubeck et al., 2012). The factor is used as a proxy for behaviours in the case of near-miss flood events as agents tend to make riskier decisions if they escape damage while others are flooded (Tonn and Guikema, 2017).
We include house ownership as a factor, though it has a small to medium effect on the adaptive response (Bubeck et al., 2012). However, this factor is also used as a proxy for tenancy, which is an important factor since tenants tend not to implement measures. Hence, house ownership in this context specifies whether an owner or a tenant occupies a house at a given time.
Household income has a significant influence on the adaptive response, especially when agents implement measures that bring structural changes or adjustments to buildings such as flood proofing and installing utility systems at higher ground (Bubeck et al., 2013). Hence, this factor affects only those households that intend to implement structural measures.
Subsidies are any financial help the authorities may provide to encourage implementation of individual adaptation measures. Currently, the authorities do not provide subsidies as they only invest in public protection. But, the assumption is that if a future low-probability storm surge overtops or overflows the dyke system and flooding occurs, the authorities may take responsibility for the damage to properties, given their assurance that people are safe and do not need to implement individual measures. As subsidies are financial support, we conceptualise this factor similarly to the household income affecting household agents that implement structural measures.
The social network factor represents agents' relatives, friends or neighbours who have implemented any adaptation measure. Bubeck et al. (2013) showed that residents conform to the protection mitigation behaviour of others in their social network.
The state subsidy and the household income are proxy measures for the “financial response cost” of implementing the measures. In terms of other costs, such as time and effort, we assume that the agents have no limitation. The assumptions related to response efficacy are that agents implement the adaptation measure specified in the shared strategy based on the type of houses they own and that the measure is assumed to be effective in reducing flood damage. However, it does not necessarily imply that the measure is the best possible. Similarly, the assumption related to self-efficacy is that either agents need to hire technicians that are capable of successfully implementing the measures or they are capable of implementing the measures by themselves. Appendix A lists the assumptions made in conceptualising and developing the model.
Lastly, “protection motivation” is an intention to implement coping responses (Rogers, 1983), which may not necessarily lead to actual behaviour (Grothmann and Reusswig, 2006). In our conceptualisation, agents may delay the implementation of measures after they positively appraise coping. Agents may also change their behaviour through time and abandon temporary measures, affecting their protection motivation.
We use the CLAIM framework (Abebe et al., 2019a) to decompose and structure the FRM case of Wilhelmsburg as CLAIM provides the means to explicitly conceptualise household behaviour and decision-making, households' interaction among themselves and with floods and institutions that shape household behaviour. CLAIM has five components: (i) agents are entities that represent an individual or composite actors/stakeholders in a model; (ii) institutions are the rules, norms and strategies defined by actors to organise their actions, interactions and decision-making (Crawford and Ostrom, 1995); (iii) the urban environment is where agents live and floods occur and is the component that connects the human and flood subsystems; (iv) physical processes are hydrologic and hydrodynamic components related to floods; (v) external factors are elements that affect the “local” agent–flood interactions but are not affected by the direct actions and interactions of agents in the local settings. Agents and institutions are part of the human subsystem and are modelled using ABMs, whereas the physical processes are part of the flood subsystem and are modelled using hydrodynamic models. As the urban environment links the two subsystems, features of this component can be conceptualised in either of the subsystems. Similarly, external factors may affect both subsystems and, hence, can be part of either subsystem. The conceptualisations of the CLAIM components are discussed in the following two subsections.
The primary source of data for the conceptualisation is the doctoral dissertation by Birkholz (2014). Birkholz applied semi-structured, in-depth interviews with residents, academic and grey literature reviews and personal observation of the study area. Appendix B provides an elaboration on the link between Birkholz (2014) and the current study. In addition, we use local expert knowledge of the study area to develop the conceptual model.
4.1 Agent-based model setup
We will describe the FRM case of Wilhelmsburg using the agent, urban environment, and institution components of the CLAIM framework.
Agents. We identified two types of agents – the household and the
authority agents.
-
The household agents are representative of the residents of Wilhelmsburg. These agents live in residential houses. The actions they pursue include appraising the threat and coping, implementing adaptation measure and assessing direct damage. The agent attributes related to threat appraisal are flood experience, reliance on public protection, perception of climate change and the source of information about flooding. The attributes related to coping appraisal are direct flood experience, house ownership and household income. If agents decide to implement an adaptation measure, they know which measure to implement based on the institutions identified. The conceptualisation excludes businesses, industries, farmlands and other auxiliary buildings due to a lack of data.
-
The authority agent represents the relevant municipal and state authorities that have the mandate to manage flood risk in Wilhelmsburg. This agent does not have a spatial representation in the ABM. The only action of this agent is to provide subsidies to household agents based on the policy lever defined in the experimental setup of the ABM. We model subsidies in a more abstract sense in that if agents receive a subsidy, they implement an adaptation measure, assuming that agents are satisfied with the amount they receive.
Urban environment. The Wilhelmsburg quarter that is surrounded by the ring of dykes and walls defines the urban environment (see Fig. 1). The household and authority agents live and interact in this environment. In our conceptualisation, we focus only on household behaviour to protect their houses. Therefore, the only physical artefacts explicitly included in the conceptual model are residential houses, which spatially represent the household agents in the ABM. Their geographical location is represented by the use of polygon features, as illustrated in Fig. 1. These polygons are used to compute the area of the houses. Houses also have types, which are classified based on “the type of building, occupancy of the ground floor and the type of facing of the building.” (Ujeyl and Rose, 2015, p. 1540006-6). This study includes 31 types of houses, which we group into five categories: single-family houses, bungalows, IBA buildings, garden houses and apartment/high-rise buildings. Appendix C provides a complete list of the 31 types of houses.
If a house is flooded, the potential building and contents damages of the
house are computed in monetary terms based on the house type. A raster file
represents the urban environment, and if floods occur, agents obtain
information about flood depth at their house from the environment. The
adaptation measures that households may implement do not have physical
representations in the model, though their impact is implicitly evaluated if
a house is exposed to flooding.
Institutions. In Wilhelmsburg, there is a common understanding that it is the responsibility of the authorities to protect the people. There is no institution, formal or informal, that influences household behaviour to reduce vulnerability. As a result, we will test hypothetical shared strategies that may have some effect on household agents' flood risk. The conceptual model consists of five institutions of which one is related to the authority agent providing subsidies to household agents, and the rest are related to households implementing vulnerability reduction measures depending on the house categories.
Institutions in CLAIM are coded using the ADICO grammar, which refers to the five elements that institutional statements might contain: “Attributes”, “Deontic”, “aIm”, “Condition” and “Or else” (Crawford and Ostrom, 1995). Table 1 shows the five institutional statements that influence the implementation of individual flood risk reduction measures. When an agent is permitted to do an action (deontic “may”) with no explicit sanction (no “or else”) for failing to do the action, the statement is referred to as a “norm”. In this case, the last institutional statement related to the subsidies is conceptualised as a norm. The authority agent may give subsidies, but it is not obliged to do so and faces no sanction if it decides not to provide subsidies. When the deontic and “or else” components are absent from an ADICO statement, the statement is referred to as a “shared strategy”. Therefore, the first four statements in Table 1 are shared strategies as there are no sanctions for non-compliance with the statements (no “or else” component), and there is no deontic component. When a shared strategy drives a system, agents do what the majority in that system does. As a result, a household implements a measure when the majority of households implement the adaptation measure. However, the household also has the option not to implement the measure without incurring any punishment.
In our conceptualisation, households implement a specific primary measure or a secondary measure (stated in the “aim” component) based on the category of a house they occupy (stated in the “condition” component). Considering primary measures, as most single-family houses in Wilhelmsburg have two or three floors, household agents that live in such houses install utilities such as heating, energy, gas and water supply installations in higher floors. Household agents that live in bungalows and IBA buildings implement flood-adapted interior fittings such as walls and floors made of waterproof building materials. Agents that live in garden houses and apartment/high-rise buildings implement flood barriers. The barriers implemented by garden houses are sandbags and water-tight windows and door sealing, while the latter implement flood protection walls. Household agents that have already implemented a primary measure may also implement a secondary measure. This measure is adapted furnishings, which includes moving furniture and electrical appliances to higher floors. As most bungalows and garden houses are single-storey housings, they do not implement adapted furnishings.
Installing utilities in higher floors and flood-adapted interior fittings
are permanent measures that alter the structure of the house, and we assume
that once they are implemented, they will not be abandoned. Therefore, in
PMT terminology, implementing these measures is a “single act” coping mode. In contrast, flood
barriers and adapted furnishings are temporary measures which agents must
decide whether to implement every time, just before a flood event.
Therefore, implementing these measures is a “repeated act” coping mode. Implementing both primary and
secondary measures is a “repeated, multiple act” coping mode.
External factors. There is no external institution conceptualised in this model. Although there is a European Union Floods Directive that requires member states such as Germany to take measures to reduce flood risk, it does not specify the type of measure implemented. In Wilhelmsburg, the authorities invest primarily in the dyke system; hence the implications of the Floods Directive for individual adaptation measures are not relevant in this study.
Dynamics of the agent-based model
The model implementation flow chart shown in Fig. 3 lays out the actions agents perform at every time step. First, household agents assess if they perceive flood as a threat. If they do, they appraise coping that leads to protection motivation behaviour. Second, if there is the intention to implement a measure, they implement the adaptation measure specified in the institutional table. Lastly, if there is a flood event at a given time step, the house layer is overlaid with a flood map corresponding to the event. Households check the flood depth at their property and assess the building and contents damages. Agents' attributes are updated if the actions change their states. This process is performed until the end of the simulation time. We will describe below how the actions – threat appraisal, coping appraisal, adaptation measure implementation, damages assessment and the abandoning of measures – are evaluated in the model.
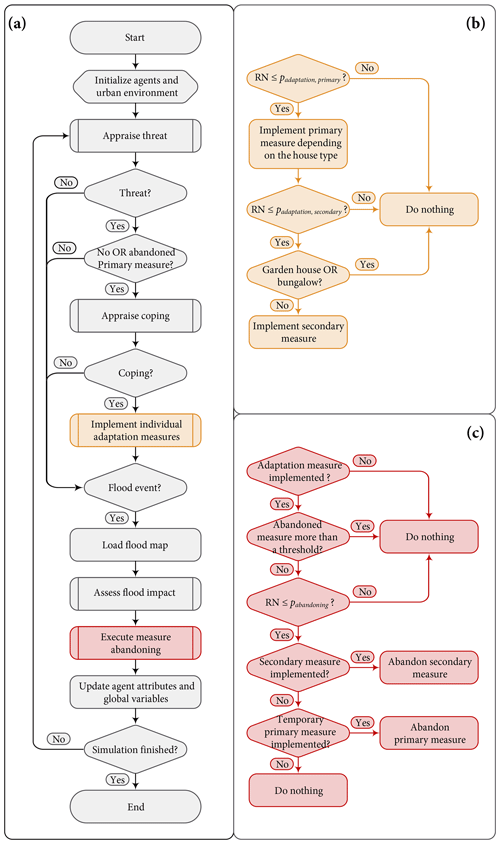
Figure 3CLAIM model implementation flow chart for the FRM case of Wilhelmsburg. Panel (a) shows the general flow chart, and (b) shows how implementing individual adaptation measures is modelled in the ABM, while (c) shows how the abandoning of measures is modelled. The rest of the actions shown in sub-process shapes in (a) (shapes with double-struck vertical edges) are shown in figures below. In (b) and (c), RN is a random number, padaptation, primary and padaptation, secondary are the probabilities of adapting primary and secondary measures, respectively, and pabandoning is the probability of abandoning a primary or a secondary measure.
4.1.1 Action 1: threat appraisal
In the ABM, the factors that affect household agents perception of flood threat in Wilhelmsburg are their flood experience (FE), their reliance on public protection (R), mainly the ring of dykes, their perception of future climate change (CC) and their source of information (SoI). Household agents update the four factors every time step based on the following criteria.
FE is related to whether an agent lives in Wilhelmsburg when a flood event happens, and it has a binary value of yes and no. The value of FE changes only after a flood event as given in Eq. (1). We assume that the flood experience does not fade over time.
R has a value of low, medium and high. It is dependent on FE and whether an agent has direct flood experience (see Eq. 2). The medium value reflects the uncertain position of agents towards the dyke system if they witness flooding in Wilhelmsburg. The value of R does not change unless there is a flood event and agents are flooded. This attribute is initialised based on the agent's FE status.
CC has a value of yes, no and uncertain. The CC value of every agent is generated randomly from a uniform distribution, as shown in Eq. (3). The value of this attribute may change over the simulation period. Assuming that agents may update their CC attribute at least once every YCC years, there is a probability of 1∕YCC at every time step of updating the attribute using Eq. (3).
We broadly categorise SoI as information from authorities, which informs agents that the dykes will protect everyone and there is no flood threat, and information from other sources, which informs agents that there can be a flood threat and agents need to prepare. SoI is assigned to agents randomly. Similar to the CC attribute, there is a probability of 1∕YSoI of updating the SoI attribute, assuming that agents may update this attribute at least once every YSoI years.
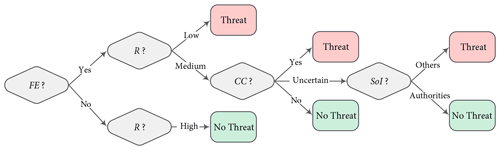
The flood threat is a function of the four factors, and agents assess their perception of flooding as a threat using a rule-based decision tree (see Fig. 4). If an agent has no experience of flooding, their reliance on public protection is high, and they perceive no threat of flooding regardless of the other factors. On the other hand, if an agent has low reliance on the dyke system, they perceive flooding as a threat regardless of the other factors. In the case that an agent's reliance on public protection is intermediate, their perception of climate change determines the threat appraisal. A concern regarding future impacts of climate change results in a perception of the flood threat, while no concern leads to no perception of the flood threat. If an agent is uncertain about climate change impacts, their source of information determines the threat appraisal. As some of the attributes of agents may change over time, all agents appraise the threat at every time step.
4.1.2 Action 2: coping appraisal
Coping behaviour is initiated depending on agents' belief in their ability to implement a measure, agents' expectation that the measure removes the threat or improves the situation and the perceived costs of implementation. In our model, coping appraisal is influenced by agents' direct flood experience, i.e. if they have had personal flood experience (PFE), house ownership (HO), household income (HI), state/government subsidy (SS) and the number of measures within an agent's social network (SN).
-
PFE has a value of yes or no based on agents' direct flood experience. This attribute is initialised as no for all agents. The value of PFE changes only when an agent's house is flooded after an event as given in Eq. (4).
-
HO has a value of own or rented. Initially, agents are randomly assigned to one of the values. Then, we assume that the house ownership of a percentage of the household agents changes randomly, at every time step.
-
HI has a value of low or high. Similar to the house ownership, we assume that the income of a percentage of the household agents changes randomly, at every time step. It should be noted that this factor affects the agents that implement permanent adaptation measures of installing utilities in higher storeys and flood-adapted interior fittings, which are classified as structural measures (see Bubeck et al., 2013, p. 1330).
-
SS has a value of yes or no. This variable is related to the last institution mentioned in Table 1. In the ABM setup, it is used as a policy lever to test the effect of subsidies on the implementation of structural adaptation measures.
-
SN has a value of low or high. As shown in Eq. (5), this factor depends on the number of agents that implement a specific type of adaptation measure for a given house category. If the number is greater than a threshold, agents who occupy that same house category will have a high SN value. Otherwise, SN is low.
where NAmeasureType is the number of agents that implement a specific type of measure depending on the category of house they occupy.
Coping is a function of the five factors, and agents appraise their coping using a rule-based decision tree illustrated in Fig. 5. For households that implement a structural measure, the full decision tree is evaluated, while for those that implement non-structural measures (i.e. temporary measures), the dashed shapes and lines are not assessed. If household agents have direct flood experience, the conditions that cause no intention to cope and implement a structural measure are if they occupy a rented house and (i) they have high income but have low SN, (ii) they have low income and received no subsidy or (iii) they have low income and received a subsidy but have low SN. If agents live in their own house, the only condition that causes no intention to cope is if they have low income, received no subsidy and have low SN. In all the other cases, agents' coping appraisal results in the intention to cope. If agents do not have direct flood experience, the only case in which they develop a coping behaviour is when the agents own the house they occupy and (i) they have high income and have high SN or (ii) they have low income, have received a subsidy and have high SN. In the rest of the cases, household agents do not develop coping behaviour.
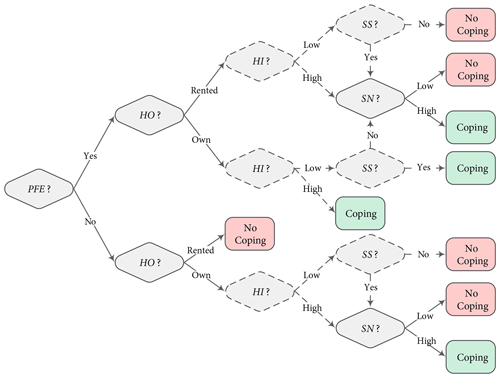
Figure 5Decision tree for the coping appraisal. The dashed shapes and lines are related to the income and subsidy factors, and they are executed only when households implement structural measures.
In the case of household agents that implement temporary measures, if the agents have direct flood experience, the only condition that causes no intention to cope is if they occupy a rented house and have low SN. If agents do not have direct flood experience, the conditions that causes no intention to cope are as follows: (i) if they occupy a rented house and (ii) if they own the house but have low SN. In the rest of the cases, household agents develop coping behaviour.
An important aspect regarding the SN factor in our conceptualisation is that its value is the same for all households who live in houses of the same category. That means, for example, if the value of SN is high for a certain house category, all households who occupy houses of that category will follow the same behaviour. But, as shared strategies drive the system in this case, households have the option not to develop that behaviour, though most follow the crowd. To reflect this property of shared strategies, we introduce a shared strategy parameter (SSP) that works in tandem with the SN. The SSP is a kind of threshold that defines the percentage of household agents that follow the shared strategy. For example, if an agent's SN factor is high, they develop a coping behaviour when a randomly drawn number from a uniform distribution is less than or equal to a predefined value of SSP.
4.1.3 Action 3: household adaptation measure implementation
Following Erdlenbruch and Bonté (2018), we introduce a delay parameter that affects measures implementation. The delay parameter represents the average number of years agents take to transform a protection motivation behaviour into an action, which is implementing a primary measure. The probability that a motivated individual will adapt in a given year is computed as . We also introduce a secondary measure parameter that determines whether agents implement secondary measures. This parameter is set as a threshold value defined by the modeller's estimation. As shown in Fig. 3b, agents only consider implementing secondary measures if they implement primary measures. The assumption is that these agents have already appraised coping positively, and they may have a protection motivation to implement a secondary measure. As stated earlier, only multi-storey house categories implement secondary measures.
4.1.4 Action 4: damages assessment
The impacts of a flood event can be estimated by the direct and indirect damages of flooding to tangible and intangible assets. In this study, we measure the flood impact based on the potential direct damages which are caused by the physical contact of floodwater with residential houses. We estimate the building and contents damages using depth–damage curves developed for the 31 types of houses in Wilhelmsburg, as discussed in Ujeyl and Rose (2015). The building damages are related to replacement and clean-up costs, whereas the contents damages are related to replacement costs of fixed and dismountable furnishings. Fig. 6 shows the depth–damage curves for the different house types.
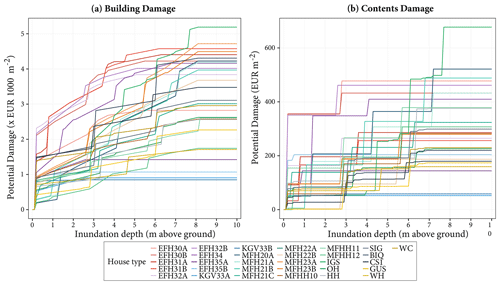
Figure 6Depth–damage curves for building (a) and contents (b) of 31 house types in Wilhelmsburg. A description of the house type codes is given in Appendix C.
If household agents implement adaptation measures, the building and contents damages of their house reduce. Based on empirical research (Kreibich and Thieken, 2009; Poussin et al., 2015), we compute the damages reduced as a percentage reduction of the ones presented in Fig. 6. Installing utilities in higher storeys reduces the building damage by 36 % while it has no impact on the contents damage reduction. Implementing flood-adapted interior fittings reduces both types of damage by 53 %. Implementing adapted furnishings reduces the contents damages by 77 %, while it has no impact on the building damage reduction. In the case of flood barriers, implementing sandbags, water-tight windows and door sealing only reduces the building damage by 29 %, whereas implementing flood protection walls reduces the flood depth by a maximum of 1 m.
4.1.5 Action 5: abandoning measures
We also introduce an adaptation duration parameter factor that affects the abandoning of measures, following Erdlenbruch and Bonté (2018). The adaptation duration parameter represents the average number of consecutive years a household agent implements an adaptation measure. It is used to estimate the probability that an agent abandons the measure in a given year. The likelihood that a motivated individual abandons a measure in a given year is computed as . This parameter only affects agents that implement temporary measures. The minimum adaptation duration would be 1 year. As shown in Fig. 3c, we limit the frequency of abandoning a measure by an agent using the abandoning frequency threshold. The assumption is that agents will not abandon a measure any more if they abandon and implement it a certain number of times specified in the threshold. If an agent has implemented a secondary measure, the first option to abandon is that measure. Otherwise, the agent abandons the temporary primary measure. In the latter case, the agent appraises coping once again.
Once the conceptual model is developed, we convert it to a programmed model using the Java-based Repast Simphony modelling environment (North et al., 2013). The ABM software developed in this study, together with the ODD protocol (Grimm et al., 2010) that describes the model, is available at https://github.com/yaredo77/Coupled_ABM-Flood_Model_Hamburg (last access: 3 June 2020).
4.2 Flood model setup
Hydrologic and hydrodynamic processes. Located in the Elbe estuary,
the main physical hazard that poses a risk on Wilhelmsburg is storm surges
from the North Sea. If the surge is high or strong enough to overtop,
overflow or breach the dykes, a coastal flood occurs. The study only
considers surge-induced coastal flooding due to dyke overtopping and
overflows.
Urban environment. The dyke system is implicitly included in the hydrodynamic processes to set up the boundary conditions of overflow and overtopping discharge that causes coastal flooding. The conceptualisation does not include any other infrastructure.
The flood model in this study is based on extreme storm surge scenarios and two-dimensional (2D) hydrodynamic models explained in Naulin et al. (2012) and Ujeyl and Rose (2015). The storm surge is composed of wind surge, local tides and a possible external surge due to cyclones. The extreme storm surge events are computed by considering the highest observed occurrence of each component. The three storm surge events – Event A, Event B and Event C – used in this study have a peak water level of 8.00, 7.25 and 8.64 m, respectively (Naulin et al., 2012). Numerical 2D hydrodynamic models are used to calculate water levels and wave stages around the dyke ring. In turn, these data are used to compute the overflow and wave overtopping discharges for the three scenarios.
To assess the flood hazard from the three scenario events, flood models that simulate coastal flooding are implemented. The model is developed using the MIKE21 unstructured grid modelling software (DHI, 2017). The 2D model domain defines the computational mesh and bathymetry, the latter of which is based on a digital terrain model (see Fig. 7). The surface resistance is expressed using a space-dependent Manning number that is based on the current land use categories. The time-dependent overflow and overtopping discharges over the dykes described above are used as boundary conditions. The output of the hydrodynamic model relevant for the current study is the inundation map showing the maximum flood depth in Wilhelmsburg. This is because the main factor that significantly contributes to building and contents damages is the flood depth (Kreibich and Thieken, 2009). Further, as houses are represented by polygon features (see Fig. 1), the flood depth for a specific house is the maximum of the depths extracted for each vertex of the polygon that defines the house.
4.3 Coupled model factors and setup
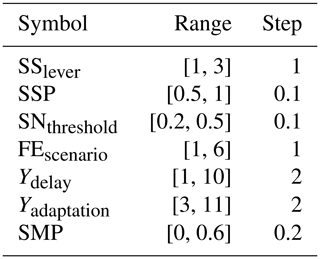
The input factors of the coupled ABM–flood model are presented in Table 2. The input factors are grouped into two. The first group includes the initial conditions and parameters that are regarded as control variables. Varying these factors is not of interest for the study; and hence, they are not included in the model experimentation. That said, a sensitivity analysis (SA) is carried out on these factors to assess which of them contribute more to the uncertainty of the model output. A detailed discussion of the SA we carried out is given in Appendix E. The second group comprises factors that are used to set up model experimentation and to evaluate the effect of household adaptation measures in FRM. In this group, the first three factors are related to the shared strategies defined in Table 1, while the last three are related to individual strategies. The flood event scenario is a randomly generated storm surge event series (see Fig. 8). The percentage base values in Table 2 are respective to the total number of agents.
Table 2List of model input factors and their base values.
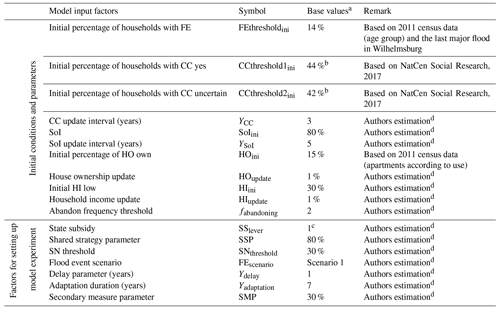
a The percentage base values are respective to the total number of agents. b The sum of the two CC thresholds should not exceed 100 %. If the sum is less than 100 %, the remaining is the percentage of agents who do not perceive CC as a source of threat. cSSlever=1 refers to no subsidy. d These estimations are based on authors' expertise and knowledge of the study area.
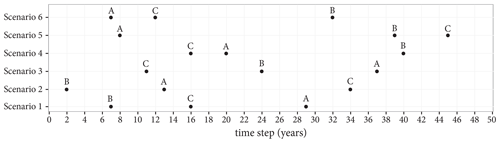
Figure 8Scenarios of flood event series. A, B and C represent flood events of storm surge with peak water levels of 8.00, 7.25 and 8.64 m, respectively.
Due to the lack of available data, most of the factors are parameterised based on our expert estimations. Some, however, are based on literature or census data. For example, since the last major flood occurred in 1962 and only 14 % of Wilhelmsburg's residents are older than the age of 65 (according to the 2011 census1), the FE attribute of 86 % of the agents is randomly initialised as no. The climate-change-related thresholds (see also Eq. 3) are based on a study on country-level concern about climate change in which 44 % Germans are “very or extremely worried”, 42 % are “somewhat worried” and the remaining 14 % are “not at all or not very worried, or do not think climate change is happening” (NatCen Social Research, 2017). However, the study does not directly relate climate change with flooding. According to the 2011 census, in Wilhelmsburg, the share of apartments occupied by the owners was 15 %, while apartments rented for a residential purpose were 82 %. The remaining 3 % were vacant. Based on that, in the ABM model, we randomly initialise 15 % of the households as owners of the houses they occupy while the remaining 85 % as renters, assuming that the 3 % vacant apartments can potentially be rented. Finally, since income is considered sensitive information, the data are not readily available. Hence, we randomly initialise 30 % of the agents as low-income households and the rest as high-income.
The response factors we use to measure the model outcome are the cumulative number of household agents that positively appraised coping (copingyes), that positively appraised coping due to the social network element (copingyes, SN), that implemented primary measures (PMimplemented), that abandoned primary measures (PMabandoned), that implemented secondary measures (SMimplemented) and that abandoned secondary measures (SMabandoned). In terms of damage, we focus on the building and contents damages mitigated rather than the total damage to highlight the benefits of household adaptation measures.
4.4 Model verification and validation
As mentioned in Sect. 4.2, the flood model we utilise in this study was developed and reported in a previous publication. Hence, we take the calibration and validation of the flood model at face value. Regarding the ABM, we carried out model verification by evaluating the relationship between agents' actions and expected response factors. For example, when agents implement measures, the system-level number of secondary measures implemented cannot be higher than the primary measures implemented. Or, in coping appraisal, with an increase in the number of agents with high income, we expect a system-level increase in the number of coping agents. However, the average number of agents that implement permanent measures should not be influenced as there is no relationship between income and permanent measures' implementation as specified in the conceptual model.
Regarding the model validation, we validated the conceptual model using expert and local knowledge of the study area. Currently, there is no practice of implementing household adaptation measures in Wilhelmsburg. The study is looking into the potential future direction of reducing vulnerability using a “what if” approach. Thus, due to the modelling approach performed, undertaking classical validation is not possible. Given the limitations, the practical purpose of the ABM is to showcase the benefits of household adaptation measures so that authorities and communities in Wilhelmsburg may consider implementing such measures to mitigate potential damages. Moreover, the model serves the purpose of advancing scientific understanding and modelling of socio-hydrologic systems, particularly human–flood interactions.
4.5 Experimental setup
To evaluate the effect of the shared strategies listed in Table 1 and individual strategies such as delaying the implementation of measures, implementing secondary measures and abandoning measures, we set up simulations by varying the values of selected input factors as presented in Table 3. The subsidy levers 1, 2 and 3 represent no subsidy, subsidy only for flooded household agents and subsidy for all agents that consider flood as a threat, respectively. Considering the computational cost of simulations, we evaluate six flood event scenarios. The event series of the scenarios are randomly generated and shown in Fig. 8. In these batch of simulations, all the other input factors are set to their base values, as stated in Table 2.
Table 3Input factors for model experimentation and their value ranges. Some factors' values are converted from percentages to decimals.
The simulation period of the ABM is 50 time steps, each of which represents a year. The number of household agents is 7859. Every simulation of parameter combinations is replicated 3000 times. Hence, for the SA and policy-related experiments, simulation outputs are computed as averages of 3000 simulations per input factor setting. A detailed description of estimating the simulation replication is provided in Appendix D. All simulations in this study are performed using the SURFsara high-performance computing cloud facility (https://userinfo.surfsara.nl/systems/hpc-cloud, last access: 3 June 2020).
5.1 Effects of flood event scenarios
We have tested six different flood event scenarios, and the adaptation behaviours of agents are shown in Fig. 9. The plots show that each scenario results in a unique trajectory of adaptation measures. However, Scenarios 1, 3, 4 and 6 have similar curves of PMimplemented, while Scenarios 1 and 4 appear to overlap. The two curves appear to overlap because the effect of the first event in Scenario 1 (Event B) is very small, and the second and biggest flood event (Event C) of Scenario 1, which happens at the same time as that of Scenario 4, dictates the number of measures implemented. Irrespective of the subsidy lever, the four scenarios have a similar number of PMimplemented at the end of the simulation period. In these scenarios, the biggest event (Event C) occurs first or second. As this event is big enough to flood every agent's house directly, most agents tend to develop protection motivation behaviour earlier. On the other hand, Scenarios 2 and 5 display a lower number of the response factor, which improves with a subsidy. In these scenarios, Event C occurs last; and hence, the PMimplemented rises rapidly after time step =35. Furthermore, there are no major increases in the number of houses that implemented primary measures after the first flood events in the cases of Scenarios 1 and 2, i.e. after time step =7 and time step =2, respectively. The reason is that the first flood event in both scenarios (Event B) is a small event, and it only affects a few houses. Hence, its effect on the number of primary measures is minimal (but not zero). The curves appear flat, but there are minor increases in the slope of the curves after the time steps mentioned.
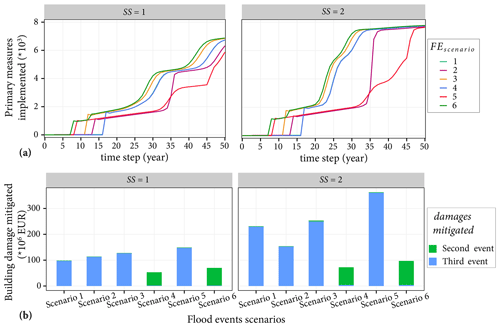
Figure 9Effects of six flood event scenarios on the adaptation behaviour of agents and the associated impact. Panel (a) shows the cumulative number of primary measures implemented. In both plots, the curves for Scenario 1 and Scenario 4 appear to overlap. Panel (b) shows the potential building damage mitigated due to the primary measures implemented. In both (a) and (b), the left and right panels show the simulation results without subsidies and with subsidies for flooded agents, respectively.
In terms of building damage mitigated, the scenarios with the two big events (C and A) occurring first and second and within a short time interval display the least damage mitigated (see Fig. 9b, Scenarios 4 and 6). These are considered to be the worst cases of the six scenarios as agents did not have a coping behaviour before the first big event, and most agents did not yet develop coping behaviour when the second big event occurred after 5 years. Only 21 % and 14 % of the agents implemented a measure in the cases of Scenarios 4 and 6, respectively, without subsidy. In contrast, in the case of Scenario 5, agents gradually develop coping behaviour after a first big event. By the time the second big event occurred after 37 years, about 45 % and 70 % of the agents already implemented a primary adaptation measure to flooded houses without subsidy and with a subsidy, respectively. Scenario 5 can be considered to be the best scenario in which household agents have time to adapt and significantly reduce the potential damage that may occur in the future.
The main lesson from the results of the scenario exercise is that agents should be prepared or adapt quickly after an event to mitigate considerable potential damages. Big events may occur within a short time interval, and households should be prepared to mitigate associated damages. It should be noted that in Fig. 9b there is no mitigated damage in the first event as we assumed that no mitigation measure was implemented initially.
5.2 Impacts of subsidies and shared strategies
The effects of the institutions are analysed in two categories. The first ones are the impacts of subsidies, and the second effects are that of the social network and shared strategy parameters.
5.2.1 Impacts of subsidies
The cumulative number of implemented primary measures plotted in Fig. 10 shows that providing subsidies increases the protection motivation behaviour of agents irrespective of the flood event scenario. For example, in the case of Scenario 1 flood event series, the building damage mitigated increases by about 130 % when a subsidy is provided to agents (see Fig. 9b). However, giving subsidies either only to flooded agents or to all agents does not have a difference in the coping responses of agents. That is depicted by the overlapping curves of SS =2 and SS =3 in Fig. 10. The result can be justified by the fact that (i) the subsidies only affect agents that implement permanent measures and (ii) when a big flood event happens, it floods most of the agents, essentially levelling the number of agents impacted by SS =2 and SS =3.
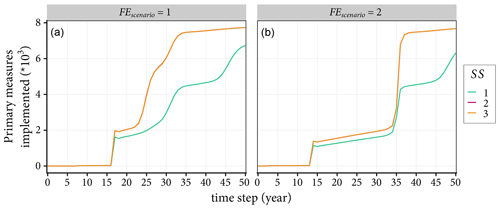
Figure 10Impacts of subsidy on the adaptation behaviour of agents. The subsidy levers 1, 2 and 3 represent no subsidy, subsidy only for flooded household agents and subsidy for all agents that consider floods to be a threat, respectively. Panels (a) and (b) show simulation results with flood events scenarios of 1 and 2, respectively.
5.2.2 Impacts of social network and shared strategy parameters
Figure 11 shows that an increase in the value of the social network parameter reduces the number of agents that develop a coping behaviour. As the SN parameter is associated with the proportion of coping agents within a house category, a higher SN requires a majority of agents in a given house category to have developed a coping behaviour to start influencing other agents. For example, when SN =0.5, no agent is influenced by their social network as the criterion that at least 50 % of the agents in the same house category should have already implemented a measure to influence others has never been satisfied. On the other hand, when SN =0.2, about 75 % of the agents that developed a coping behaviour after time step =20 are influenced by their social network. Figure 11 also shows that the shared strategy parameter does not have a significant effect on the number of agents that develop a coping behaviour (for example, see the solid lines cluster together). This means that when the SN criteria are satisfied, most agents tend to follow the crowd.
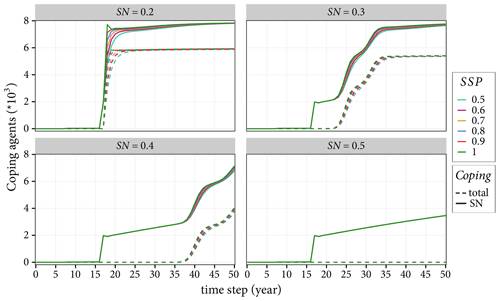
Figure 11Impacts of the social network and shared strategy parameter factors on the adaptation behaviour of agents. The solid lines show the total number of coping agents, while the dashed lines show the agents that develop a coping behaviour influenced by their social network.
In practical terms, this result shows that if agents need to wait to see many others implement measures to be influenced, most likely, they will not develop a motivation protection behaviour. Hence, aspects such as stronger community togetherness in which a few neighbours can influence others can increase the possibility of implementing adaptation measures.
5.3 Impacts of individual strategies
In this section, we will analyse the effects of three factors that characterise individual strategies: the delay parameter, adaptation duration parameter and secondary measure parameter.
5.3.1 Impacts of the delay parameter
As shown in Fig. 12, the percentage of agents that transform the coping behaviour to action decreases as the value of the delay parameter increases. When DP =1, all agents that developed coping behaviour implement adaptation measures at the same time step. However, when DP =9 (i.e. when the probability that a coping agent will implement a measure in a given year is 1∕9), the number of agents that implement measures is 75 % of the number that develop a coping behaviour by the end of the simulation period.
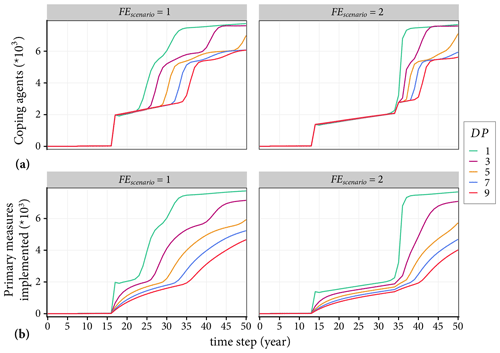
Figure 12Impacts of the delay parameter on the adaptation behaviour of agents. Panel (a) shows the coping behaviour of agents, and (b) shows the cumulative number of agents that converted their coping behaviour to action, i.e. implement primary adaptation measures. Simulations that generated the results are set with SS =2. The left and right panels show simulation results with Scenarios 1 and 2, respectively.
Furthermore, both the number of coping agents and agents that implemented measures decreases with an increase in DP value. For example, when FEscenario=2 and the value of DP increases from 1 to 9, the numbers of coping agents and agents that implemented a primary measure drop by about 27 % and 48 %, respectively, at time step =50. This also has a knock-on effect on the implementation of a secondary measure, which reduces by about 50 %. Based on the outputs of the simulations, the delayed implementation of measures reduces the potential building and contents damages that could have been mitigated by EUR 36.3 million and EUR 8.7 million, respectively.
The main reason for the lower number of measures implemented with the increase in the value of the delay parameter is the decision of agents to delay the implementation. However, that also contributes to lowering the number of agents influenced by their social network. In practical terms, this means that authorities should support households who tend to develop protection motivation behaviour so that they will implement adaptation measures promptly.
5.3.2 Impacts of the adaptation duration parameter
We evaluate the impacts of the adaptation duration using the number of agents that implemented and abandoned primary and secondary measures. The simulation results in Fig. 13a show that the adaptation duration parameter has a minor impact on the number of primary and secondary measures implemented, regardless of the subsidy lever. For example, the largest percentage difference between the highest and lowest PMimplemented is exhibited around time step =30, which accounts about 28 %. One reason for the minor impact of Yadaptation on PMimplemented could be that the parameter only affects agents that implement temporary primary measures, which is about half of the total number of agents. Another one could be that an increase in PMimplemented also increases the number of agents that potentially abandon the measure. This is reflected in Fig. 13b in which the peaks of PMabandoned correspond to the steepest slope of the curve displaying PMimplemented.
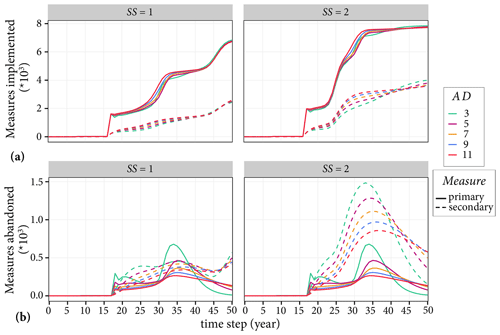
Figure 13Impacts of the adaptation duration on the adaptation behaviour of agents. Panel (a) shows the primary and secondary measures that are implemented, and (b) shows the primary and secondary measures that are abandoned. The left and right panels show simulation results without subsidies and with subsidies for flooded agents, respectively.
Figure 13b also shows that more agents abandon measures when the value of Yadaptation decreases. But then the number of measures that are abandoned decreases as agents reach the fixed number of times they could abandon measures, which is specified by the fabandoning parameter. In addition, the figure illustrates that, in general, SMabandoned is larger than PMabandoned through the simulation period. This can be explained by the model conceptualisation, whereby agents first abandon secondary measures provided that they consider implementing them.
The practical lesson from the simulation results is that if agents tend to implement temporary measures, there should be a mechanism that encourages them to continue implementing the measures in future. For example, authorities may create and raise public awareness of how to seal windows and doors and the availability of sandbags. This should be done regularly and especially just before the event occurs as the measures can be implemented within a short period.
5.3.3 Impacts of the secondary measure parameter
Finally, we analyse the impacts of the secondary measure parameter (SMP) on the number of agents that implemented secondary measures. Since the secondary measure conceptualised in the model is adapted furnishings, the effects of SMP are evaluated based on the contents damages mitigated.
Figure 14a shows that the cumulative number of agents that implemented secondary measure increases as the parameter value increases. But, the rate of increase in SMimplemented is marginal especially for SMP≥0.4, in both cases of subsidy levers. When flooded agents receive a subsidy, SMimplemented increases by about 1000 agents compared to the policy lever with no subsidy. Although the subsidy does not directly affect the implementation of secondary measures, it increases the implementation of primary measures, which in turn, increases SMimplemented. The only exception is when SMP =0; in that case, no agents implement secondary measures despite the subsidy lever.
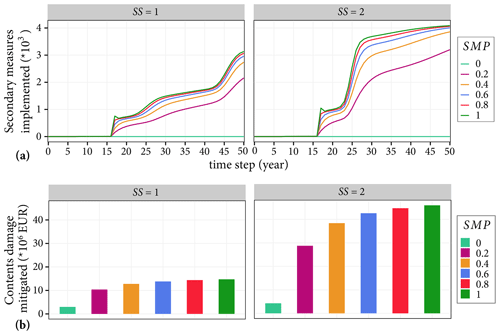
Figure 14Impacts of the secondary measure parameter on the adaptation behaviour of agents. Panel (a) shows the cumulative number of secondary measures implemented, and (b) shows the potential contents damages mitigated. The left and right panels show simulation results without subsidies and with subsidies for flooded agents, respectively.
Similarly, Fig. 14b shows that the contents damages mitigated increases marginally with the increase in the SMP value. The damages mitigated when SMP =0 is because some agents implemented flood-adapted interior fittings, which are classified as primary measures, and these measures mitigate both building and contents damages. When there is a subsidy, the contents damages mitigated increases by about 3-fold for each of the SMP values, except SMP =0, compared to the policy lever with no subsidy.
The marginal increases in the SMimplemented and the contents damages mitigated together with the increase in the values of SMP is because not all agents could implement secondary measures. As discussed in the model conceptualisation, agents that live in bungalows and garden houses do not implement adapted furnishings since those house categories are single-storey houses. In general, based on our simulation outputs, implementing only a secondary measure could mitigate more than EUR 40 million. Hence, decision makers should encourage households to consider implementing such simple measures that could be done at no monetary cost provided that there is space to keep contents safe.
The study aims to improve the current modelling practices of human–flood interaction and draw new insights for FRM policy design. Below, we discuss our modelling contributions and how they lead to policy insights.
We have incorporated occurrences of flood events to examine how these influence household agents' adaptation behaviour. In our study, we examined six flood event scenarios, each comprising three coastal flood events occurring within a 50-year simulation period. Simulation results show that a unique trajectory of adaptation measures and flood damages emerge from each flood event series. The interval between the occurrences of two big events is an important factor in defining households' adaptation behaviour. If a big event occurs first, it can serve as a wake-up call for future coping behaviours. However, that comes with a substantial amount of building and contents damages. Households and authorities in Wilhelmsburg should avoid maladaptive practices (in PMT terms) such as avoidance and denial of possible future flooding and implement measures to mitigate potential damages.
We have analysed the effects of a subsidy on the adaptation behaviour of individuals. We tested three subsidy levers: no subsidy, subsidy only for flooded household agents and subsidy for all agents that consider flood as a threat. Based on the simulation results, the last two levers have similar outcomes in terms of coping behaviours. It may depend on the flood event series, but providing subsidies increases the number of coping households in the long run. Hence authorities in Wilhelmsburg may consider providing subsidies to motivate households that implement permanent measures.
We have formulated the implementation of adaptation measures as informal institutions in the form of shared strategies that are influenced by social networks. Simulation results reveal that a “wait and see” approach, such as high social network parameter settings, does not help to increase the number of coping households. There should be an approach in which a small group of trusted community members or public figures may influence others in their community.
We have also analysed the effect of individual strategies on household adaptation behaviour. The strategies are delaying the implementation of measures, decisions on the adaptation durations of temporary measures and implementing secondary measures. Simulation results show that delaying measures' implementation reduces millions of euros that could have been mitigated. On the other hand, the overall impact of longer adaptation duration by some households could be cancelled out by the decision to abandon measures by others. It is essential to raise awareness continuously so that households do not forget about or abandon implementing temporary measures. The role of simple measures such as adapted furnishings, which do not incur any monetary cost, should also be highlighted as these measures could contribute to reducing millions of euros of contents damages.
In conclusion, the paper presented a coupled agent-based (ABM) and flood model developed to evaluate the adaptation behaviour and decision-making of households to implement vulnerability reduction measures in the Wilhelmsburg quarter of Hamburg, Germany. We have employed the coupled flood-agent-institution modelling (CLAIM) framework to conceptualise the agent–flood interaction in the coupled model and the protection motivation theory (PMT) to study household flood preparedness behaviour. The model conceptualisation has benefitted from the qualitative exploration of PMT carried out in the same study area. Adding local knowledge of flood risk management (FRM) issues and using other data sources, we extended the previous work by developing a simulation model that could support decision-making. Furthermore, the study has extended other prior works (Abebe et al., 2019b; Erdlenbruch and Bonté, 2018; Haer et al., 2016) to study human–flood interaction better and to gain new policy insights. With all the extensions, we have demonstrated that coupled ABM and flood models, together with a behavioural model, can potentially be used as decision support tools to examine the role of household adaptation measures in FRM. Although the focus of the paper is the case of Wilhelmsburg, the improved modelling approach can be applied to any case to test policy levers and strategies considering heterogeneous individual behaviours.
It is worth mentioning that the results and analysis of the model outputs are subject to the limitations of the model conceptualisations. The threat and coping appraisals are modelled using rule-based decision trees. These trees are simplified ones that show linear and deterministic decision-making process by individuals. Although abstraction is an essential aspect of modelling, we acknowledge that actual decisions regarding protection motivation behaviour can be more complex. Despite the stochastic elements in the model that could have provided unexpected results, the linear and deterministic nature of the decision trees may contribute to expected findings, especially the general trend.
Additionally, we defined the configuration of the decision trees (i.e. the importance of the factors that affect the threat and coping appraisal of individuals) based on previous empirical research that has been conducted in other study areas. However, some other factors could have been more important in a different study area. Hence, testing different decision-tree configurations would account for the uncertainties in the model conceptualisation. The trees could also have feedback loops in which the outcomes of agents' threat and coping appraisals could influence back the attributes that result in the appraisals. Future research may use intelligent decision-making models such as Bayesian networks, as in Abdulkareem et al. (2018). In the flood model, considering dyke breaches and other flood events and flood event series could be relevant modelling exercises.
The model conceptualisation and the results would also benefit from further refinement to provide more accurate insights into policy design. For example, more representative datasets are needed to reduce the input factors' uncertainty as indicated by the sensitivity analysis (see Appendix E). In our model conceptualisation, households implement specific measures based on the category of a house they occupy, as defined in the shared strategies. These are expert-based hypothetical strategies that could have been defined otherwise. We defined the institutions as shared strategies to give agents an option of whether to develop a protection motivation behaviour or not. In the study area, there are no formal institutions that oblige households to implement any adaptation measure. Hence, we assumed introducing institutions as shared strategies would be a reasonable starting point for the study area. Thus, the modelling exercises and their outcomes should be seen as an effort (i) to advance the use of coupled ABM–flood models in FRM and (ii) to provoke communities and decision makers in Wilhelmsburg to investigate the role of household adaptation measures in mitigating potential damages further. Furthermore, it is important to note that while the existing work addressed household measures, the same approach can also be applied to a range of different measures and contexts such as local and regional measures, nature-based solutions, traditional “grey infrastructure” and the role of media in agents' behaviour, some of which we intend to address in our future work.
Finally, the research presented can be enhanced by analysing model uncertainty. One may conceptualise the ABM differently, and investigating the impact of the different model conceptualisation is essential to communicate the uncertainty in model results. The research objective could also be extended by including other types of agents such as businesses and industries and other response factors such as indirect damages (e.g. lost revenues due to business interruptions) to provide a broader view of the role of individual adaptation measures.
To structure and conceptualise the Wilhelmsburg flood risk management case and develop the agent-based model, we have made the following assumptions. The reasons for making these assumptions are model simplification (i.e. to develop a less complicated model) and lack of data.
-
Household agents are spatially represented by the houses they live in; hence, they are static.
-
There is a one-to-one relationship between household agents and houses (i.e. a household owns only one house and vice versa).
-
Houses are represented by polygon features such that each polygon represents one household agent. In the case of multi-storey buildings, the agent represents the household(s) living on the ground floor.
-
When apartments and high-rise buildings are represented by one single polygon feature, the whole building is considered one house representing one household agent.
-
A maximum of one flood event occurs per time step.
-
Only three flood event scenarios are considered. All the scenarios simulate dyke overtopping and have very low exceedance probability. Dyke breaches are not considered in the conceptualisation.
-
When there is a flood, the flood depth of a house is extracted from the flood maps as the maximum of the flood depths read at the vertices of the polygon feature that represent the house.
-
A house is considered to be flooded if the flood depth is greater than 10 cm, assuming that all houses have a floor elevation of at least 10 cm.
-
Damage assessment does not include aspects such as damages to other assets (e.g. cars), indirect damage (e.g. business interruptions), risk to life and structural collapse of buildings.
-
Damage is only assessed based on the flood water level. The effect of floodwater velocity, duration and contamination level is not included in the damage assessment.
-
Both building and content damages are assessed per building type. The damages of all houses of the same building type are calculated using the depth–damage curves for that building type.
-
The sources of information do not initiate the coping appraisal process as in the original PMT study as agents know the kind of measure they implement.
-
If a house has already appraised coping and implemented a measure, they do not appraise coping again, unless they abandon the measure, assuming that they do not implement another primary measure.
-
Adaptation measures are sufficient to reduce flood damage in all flood events (perceived efficacy of measures).
-
Agents are capable of successfully implementing adaptation measures (perceived self-efficacy).
-
The effect of flood barriers such as flood protection walls and sandbags on the flood hydraulics is not accounted for.
-
Agents only implement a maximum of one primary and one secondary measure at a given time step.
-
Agents do not implement temporary adaptation measures (i.e. flood barriers) at any time step, but deciding to implement the measures entails they only deploy them when there is a flood.
-
If agents abandon measures, they only abandon non-permanent measures such as flood barriers.
-
In the case of non-permanent measures, if a household agent decides to implement a measure, the decision is valid, at least for a year.
-
If a household agent abandons a measure, it abandons it for at least a year.
-
Household agents do not implement the same primary measure twice unless they abandon it.
-
The adaptation duration specified in a simulation is the same for all temporary measures.
Considering that model conceptualisation in the current article is greatly informed by the data collected and the analysis in the doctoral dissertation by Birkholz (2014), in this appendix, we will elaborate on the links between the two studies.
Birkholz utilised three data collection methods: semi-structured, in-depth interviews as a primary data source, data from academic and grey literature and data obtained through personal observations of the study area as secondary data sources. The primary data collection was conducted through a snowball sampling strategy, in which interviewed informants provided contacts of other potential informants, and opportunist interviews. The informants were residents and workers in the Wilhelmsburg quarter. The total number of informants was 28. We consider this is a small number of informants to represent the residents of the study area statistically. Hence, we use the results of the dissertation to inform the conceptual model rather than to set up agents' attributes. Informing the conceptual model mainly refers to identifying factors that affect the threat and coping appraisals of households.
Birkholz found out that most of the informants did not experience the 1962 flood in Wilhelmsburg. As a result, flood experience was considered to be an important factor that affects agents' threat appraisals. The environmental source of information identified by Birkholz includes verbal persuasion such as passing on of information concerning the threat of flooding or the history of flood. Senior members of the community are the primary sources of such information. However, most receivers of the information, especially younger individuals, are not that interested in the topic. Hence, we do not include this kind of source of information in our model conceptualisation. Another source of information is organisational interactions, which involve the interactions between residents and organisations such as the local authorities, called “Behörde”. The Behörde distributes pamphlets that describe flood warning and evacuation routes. Since the focus of our article is on measures that reduce household vulnerability to flooding, operational level information (i.e. warning and evacuation) is not included in our model conceptualisation.
On the other hand, informants gave the impression that they did not need to prepare to implement measures because the Behörde is prepared, for example, by raising dykes. Some informants even mentioned that they felt the Behörde conveyed messages that the dykes are high enough, and residents do not need to do anything (in terms of individual adaptation measures). Considering that finding and our knowledge of the study area, we include in our model conceptualisation that household agents will not appraise threat if their source of information is the authority agent. In relation to that, we conceptualised the reliance on public protection to be a key factor that affects household agents' threat appraisal. Birkholz associated the factor with informants' sources of safety and sources of trust from the dykes and the authorities. We believe that the sources of safety from the dykes exist as long as the dykes are not overtopped or breached. Hence, we associate the reliance on the dykes with the flood experiences of household agents. Birkholz also found out that impacts of climate change were concerns among the informants. Hence, we include the climate change perception factor as a factor that determines the threat appraisal.
Regarding coping appraisal, Birkholz found out that informants had undertaken very little. That is mainly because most of the informants did not have flood experience. Birkholz elicited coping appraisal by introducing a hypothetical storm surge that breached the dykes protecting Wilhelmsburg. During the interview, informants were asked how they would respond to such a flood event. Since the responses of informants were not related to implementing individual adaptation measures that could mitigate or reduce flood risk, we avoid basing our conceptualisation (of coping appraisal) on the findings of the dissertation. Instead, we use other empirical studies, as described in Sect. 3.
| EFH30A – Single-family house, thermal insulation composite system | |
| EFH30B – Single-family house, cavity wall with insulation | |
| EFH31A – Single-family house, plastered brickwork, ground level: raised ground floor | |
| EFH31B – Single-family house, plastered brickwork, basement | |
| EFH32A – Single-family house, plastered brickwork | |
| EFH32B – Single-family house, faced brickwork | |
| EFH34 – Single-family house, plastered brickwork, basement: apartment | |
| EFH35A – Bungalow, plastered brickwork | |
| EFH35B – Bungalow, wooden construction | |
| KGV33A – Garden/summer house, plastered brickwork | |
| KGV33B – Garden/summer house, wooden construction | |
| MFH20A – Apartment building, basement: waterproof concrete tanking | |
| MFH21A – Apartment building, plastered brickwork, ground level: apartments | |
| MFH21B – Apartment building, faced brickwork, ground level: apartments | |
| MFH21C – Apartment building, faced reinforced concrete, ground level: apartments | |
| MFH22A – Apartment building, faced brickwork, ground level: business | |
| MFH22B – Apartment building, faced brickwork, ground level: business (same as MFH22A) | |
| MFH23A – Apartment building, plastered brickwork, ground level: apartments | |
| MFH23B – Apartment building, faced brickwork, ground level: apartments | |
| MFHH10 – High-rise building, dry construction, ground level: general use | |
| MFHH11 – High-rise building, reinforced concrete, ground level: general use | |
| MFHH12 – High-rise building, dry construction, ground level with garages | |
| IGS – Hybrid house – IGS centre | |
| OH – Hybrid house – open house | |
| HH – Hybrid house | |
| SIG – Phase change material – smart is green | |
| BIQ – Smart material house – BIQ | |
| CS1 – Smart price house | |
| GUS – Smart price house – Grundbau und Siedler (do-it-yourself builders) | |
| WH – Wälderhaus | |
| WC – Wood cube |
ABMs are often stochastic. For example, agent behaviours are determined based on random values generated from pseudo-random numbers, which produces results that show variability even for the same input factor setting (Bruch and Atwell, 2015; Lorscheid et al., 2012; Nikolic et al., 2013, p. 110–111). Hence, reliable ABM outputs are obtained by running simulations multiple times. To determine the number of simulation runs, we apply the experimental error variance analysis suggested by Lorscheid et al. (2012). The coefficient of variation (cv) is used to measure the variability in the model output. Starting from a relatively low number of runs, the cv of the model output is calculated by increasing the number of runs iteratively for the same factor settings. The number of runs is fixed when the cv stabilises or the difference between the cv values of iterations falls below a criterion. This experiment is done for selected input factor settings to cross-check whether output variations stabilise around the same number of runs irrespective of the factor setting. We evaluate the cv values for the six response factors.
Table D1Coefficient of variations (cv) of response factors per iterations. The bold font shows the number of runs in which the cv values of all the response factors are stable for a difference criterion of 0.001.
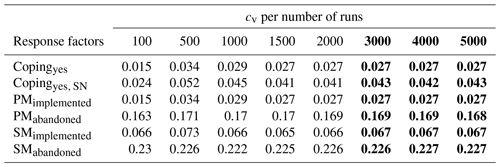
We iteratively run simulations starting from 100 to 5000 and compute the cv values of six response factors for each iteration, for several input factor settings. As an example, Table D-1 shows the cv values for the factor setting in which all the input factors have the base values. Selecting a difference criterion of 0.001, the minimum sample size in which the cv values start to stabilise is 3000. As the cv values do not change while increasing the number of runs, we fix the number of runs to be 3000. For the SA and policy-related experiments, simulation outputs are computed as averages of 3000 simulations per input factor setting.
As in any model, the ABM developed in this study is subject to uncertainties. Regarding input factors uncertainty, the initial conditions and parameters mentioned in Table 2 are either based on our expert estimations or based on available coarse datasets such as the 2011 national census in Germany. Hence, a sensitivity analysis (SA) is carried out to allocate the model output uncertainty to the model input uncertainty. The SA method adopted in this study is the elementary effect (EE) method, also called the Morris method (Morris, 1991). The method is effective in identifying the important input factors with a relatively small number of sample points (Saltelli et al., 2008, p. 109). Saltelli et al. (2008) explained that “the method is convenient when the number of factors is large [and] the model execution time is such that the computational cost of more sophisticated techniques is excessive” (p. 127). We employ this method because of the high computational cost related to the large number of simulation repetitions estimated (see Appendix D).
Table E1Input factors considered in the sensitivity analysis, their distributions and value ranges. Factors specified in percentages are converted to decimals.
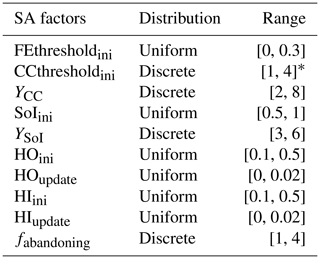
∗ The CCthresholdini values for “yes” and “uncertain” are 0.35, 0.4, 0.45 and 0.5 for the discrete values of 1, 2, 3 and 4, respectively.
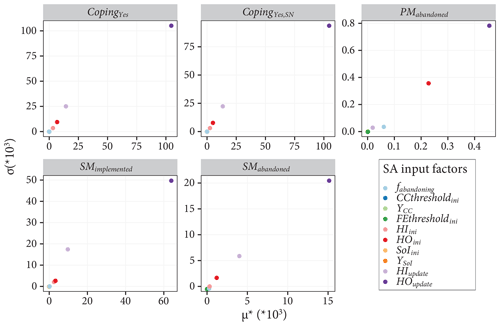
Figure E1Scatter plots displaying the Morris sensitivity measures μ∗ and σ for five of the response factors. Points representing the least important factors may not be visible as they overlap close to the (0, 0) coordinate.
The EE method is a specialised one-at-a-time SA design that removes the dependence on a single sample point by introducing ranges of variations for the inputs and averaging local measures. The sensitivity measures proposed by Morris are the mean (μ) and standard deviation (σ) of the set of EEs, which are incremental ratios, of each input factor. In a revised Morris method, Campolongo et al. (2007) proposed an additional sensitivity measure, μ∗, which is the estimate of the mean of the distribution of the absolute values of the EEs. The sampling strategy to estimate the sensitivity measures is building r EE trajectories of (k+1) points for each k factor, resulting in a total of r(k+1) sample points. Following Saltelli et al. (2008, p. 119), we choose r to be 10, and each model input is divided into four levels within the input value range. In this study, the input factors selected for the SA are the initial conditions and parameters (as specified in Table 2). Therefore, the computational cost of the SA is . In Table E1, we list these factors, their distributions and value ranges. In the SA, the other input factors presented in Table 2 are set to their base values.
The SA is carried out on the 10 input factors, and the outputs quantify five response factors evaluated at time step =50. Figure E1 shows the Morris sensitivity measures μ∗ and σ plotted against each other for five response factors. As Ydelay=1 in all the simulations, the response factors copingyes and PMimplemented have exactly the same value. Hence, only the former response factor is displayed in the figure. The results show that the most important factor by far is HOupdate, though its value varies only between zero and 2 % of the total number of agents. The base value of this factor, representing the change in house ownership, is estimated by the authors of this paper. It is also modelled in such a way that randomly selected household agents may change house ownership state every time step. Considering the influence of HOupdate on the model output (given the current model conceptualisation), it would be essential to acquire reliable data and better model representation of the factor to reduce the model output uncertainties.
The next influential factors are HIupdate, HOini and HIini. The base values of the household income-related factors are also based on our estimations as there is no publicly available record due to the sensitive nature of income data. Similarly, obtaining a better dataset would help to reduce the output uncertainty. The initial house ownership variable is based on census data, but agents' house ownership is assigned randomly as there are no available data regarding its spatial distribution. The fabandoning factor is influential in the case of primary measures being abandoned as it sets a limit on the number of times an agent can abandon a measure. Better data would also reduce this factor's allocation to the model output uncertainty. All the other factors are non-influential as points representing these factors overlap around the (0, 0) coordinate.
The agent-based model code is available at https://github.com/yaredo77/Coupled_ABM-Flood_Model_Hamburg, last access: 3 June 2020; Abebe, 2020.
YAA, AGh and IN developed the study. YAA, AGh, IN, NM and AGr developed the conceptual model. YAA developed the model code and performed the simulations. YAA prepared the original draft of the manuscript, with further reviewing and editing by all co-authors. ZV organised funding acquisition.
The authors declare that they have no conflict of interest.
The research leading to these results has received funding from the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement no. 603663 for the research project PEARL (Preparing for Extreme And Rare events in coastaL regions) and from the European Union's Horizon 2020 Research and Innovation Programme under grant agreement no. 776866 for the research project RECONECT. The study reflects only the authors' views and the European Union is not liable for any use that may be made of the information contained herein. We thank SURFsara (https://www.surf.nl/en, last access: 3 June 2020) for providing the high-performance computing (HPC) cloud resources that we used to run all the simulations.
This research has been supported by the European Commission (PEARL (grant no. 603663)) and the European Commission (RECONECT (grant no. 776866)).
This paper was edited by Nadia Ursino and reviewed by two anonymous referees.
Abdulkareem, S. A., Augustijn, E.-W., Mustafa, Y. T., and Filatova, T.: Intelligent judgements over health risks in a spatial agent-based model, Int. J. Health Geogr., 17, 8, https://doi.org/10.1186/s12942-018-0128-x, 2018.
Abebe, Y. A., Ghorbani, A., Nikolic, I., Vojinovic, Z., and Sanchez, A.: A coupled flood-agent-institution modelling (CLAIM) framework for urban flood risk management, Environ. Modell. Softw., 111, 483–492, https://doi.org/10.1016/j.envsoft.2018.10.015, 2019a.
Abebe, Y. A., Ghorbani, A., Nikolic, I., Vojinovic, Z., and Sanchez, A.: Flood risk management in Sint Maarten – A coupled agent-based and flood modelling method, J. Environ. Manag., 248, 109317, https://doi.org/10.1016/j.jenvman.2019.109317, 2019b.
Abebe, Y. A.: Coupled ABM-Flood Model Hamburg, GitHub, available at: https://github.com/yaredo77/Coupled_ABM-Flood_Model_Hamburg, last access: 3 June 2020.
Birkholz, S. A.: The prospect of flooding and the motivation to prepare in contrasting urban communities: A qualitative exploration of Protection Motivation Theory, Cranfield University, Cranfield, UK, available at: http://dspace.lib.cranfield.ac.uk/handle/1826/9329 (last access: 11 July 2019), 2014.
Botzen, W. J. W., Kunreuther, H., Czajkowski, J., and de Moel, H.: Adoption of Individual Flood Damage Mitigation Measures in New York City: An Extension of Protection Motivation Theory, Risk Anal., 39, 2143–2159, https://doi.org/10.1111/risa.13318, 2019.
Bruch, E. and Atwell, J.: Agent-based Models in Empirical Social Research, Sociol. Method. Res., 44, 186–221, https://doi.org/10.1177/0049124113506405, 2015.
Bubeck, P., Botzen, W. J. W., and Aerts, J. C. J. H.: A Review of Risk Perceptions and Other Factors that Influence Flood Mitigation Behavior, Risk Anal., 32, 1481–1495, https://doi.org/10.1111/j.1539-6924.2011.01783.x, 2012.
Bubeck, P., Botzen, W. J. W., Kreibich, H. and Aerts, J. C. J. H.: Detailed insights into the influence of flood-coping appraisals on mitigation behaviour, Global Environ. Chang., 23, 1327–1338, https://doi.org/10.1016/j.gloenvcha.2013.05.009, 2013.
Campolongo, F., Cariboni, J., and Saltelli, A.: An effective screening design for sensitivity analysis of large models, Environ. Modell. Softw., 22, 1509–1518, https://doi.org/10.1016/j.envsoft.2006.10.004, 2007.
Crawford, S. E. S. and Ostrom, E.: A Grammar of Institutions, Am. Polit. Sci. Rev., 89, 582–600, https://doi.org/10.2307/2082975, 1995.
DHI: MIKE21 Flow Model FM: Hydrodynamic Module User Guide, MIKE Powered by DHI, Hørsholm, Denmark, available at: https://manuals.mikepoweredbydhi.help/2017/Coast_and_Sea/MIKE_FM_HD_2D.pdf (last access: 12 November 2020), 2017.
Erdlenbruch, K. and Bonté, B.: Simulating the dynamics of individual adaptation to floods, Environ. Sci. Policy, 84, 134–148, https://doi.org/10.1016/j.envsci.2018.03.005, 2018.
Floyd, D. L., Prentice-Dunn, S., and Rogers, R. W.: A Meta-Analysis of Research on Protection Motivation Theory, J. Appl. Soc. Psychol., 30, 407–429, https://doi.org/10.1111/j.1559-1816.2000.tb02323.x, 2000.
Grahn, T. and Jaldell, H.: Households (un)willingness to perform private flood risk reduction – Results from a Swedish survey, Safety Sci., 116, 127–136, https://doi.org/10.1016/j.ssci.2019.03.011, 2019.
Grimm, V., Berger, U., DeAngelis, D. L., Polhill, J. G., Giske, J., and Railsback, S. F.: The ODD protocol: A review and first update, Ecol. Model., 221, 2760–2768, https://doi.org/10.1016/j.ecolmodel.2010.08.019, 2010.
Grothmann, T. and Reusswig, F.: People at Risk of Flooding: Why Some Residents Take Precautionary Action While Others Do Not, Nat. Hazards, 38, 101–120, https://doi.org/10.1007/s11069-005-8604-6, 2006.
Haer, T., Botzen, W. J. W., and Aerts, J. C. J. H.: The effectiveness of flood risk communication strategies and the influence of social networks – Insights from an agent-based model, Environ. Sci. Policy, 60, 44–52, https://doi.org/10.1016/j.envsci.2016.03.006, 2016.
IPCC: Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Barros, V. R., Field, C. B., Dokken, D. J., Mastrandrea, M. D., Mach,K. J., Bilir, T. E., Chatterjee, M., Ebi, K. L., Estrada, Y. O., Genova, R. C., Girma, B., Kissel, E. S., Levy, A. N., MacCracken, S., Mastrandrea, P. R., and White, L. L., Cambridge University Press, Cambridge, UK and New York, NY, USA, 2014.
Kreibich, H. and Thieken, A. H.: Coping with floods in the city of Dresden, Germany, Nat. Hazards, 51, 423–436, https://doi.org/10.1007/s11069-007-9200-8, 2009.
Lorscheid, I., Heine, B.-O., and Meyer, M.: Opening the `black box' of simulations: increased transparency and effective communication through the systematic design of experiments, Comput. Math. Organ. Theory, 18, 22–62, https://doi.org/10.1007/s10588-011-9097-3, 2012.
Morris, M. D.: Factorial Sampling Plans for Preliminary Computational Experiments, Technometrics, 33, 161–174, https://doi.org/10.2307/1269043, 1991.
Munich RE: 50th Anniversary of the North Sea Flood of Hamburg, Press Dossier, Munich RE, 2012.
NatCen Social Research: Climate concern and pessimism: Examining public attitudes across Europe, NatCen Social Research, London, UK, available at: http://www.natcen.ac.uk/media/1513272/ESS-Climate-Change-report-FINAL.pdf (last access: 21 November 2019), 2017.
Naulin, M., Kortenhaus, A., and Oumeraci, H.: Reliability analysis and breach modelling of sea/estuary dikes and coastal dunes in an integrated risk analysis, Coast. Eng. Proc., 33, 61, https://doi.org/10.9753/icce.v33.management.61, 2012.
Nikolic, I., van Dam, K. H., and Kasmire, J.: Practice, in Agent-Based Modelling of Socio-Technical Systems, edited by: van Dam. K. H., Nikolic, I., and Lukszo, Z., pp. 73–137, Springer, Dordrecht, The Netherlands, 2013.
North, M. J., Collier, N. T., Ozik, J., Tatara, E. R., Macal, C. M., Bragen, M., and Sydelko, P.: Complex adaptive systems modeling with Repast Simphony, Complex Adapt. Syst. Model., 1, 3, https://doi.org/10.1186/2194-3206-1-3, 2013.
Poussin, J. K., Botzen, W. J. W., and Aerts, J. C. J. H.: Factors of influence on flood damage mitigation behaviour by households, Environ. Sci. Policy, 40, 69–77, https://doi.org/10.1016/j.envsci.2014.01.013, 2014.
Poussin, J. K., Wouter Botzen, W. J., and Aerts, J. C. J. H.: Effectiveness of flood damage mitigation measures: Empirical evidence from French flood disasters, Global Environ. Chang., 31, 74–84, https://doi.org/10.1016/j.gloenvcha.2014.12.007, 2015.
Railsback, S. F. and Grimm, V.: Agent-Based and Individual-Based Modeling: A Practical Introduction, Princeton University Press, Princeton, New Jersey, USA, available at: http://www.jstor.org/stable/j.ctt7sns7 (last access: 9 October 2017), 2012.
Rogers, R. W.: Cognitive and physiological process in fear appeals and attitudes changer: A revised theory of protection motivation, in: Social psychophysiology: A sourcebook, edited by: Cacioppo J. T. and Petty, R. E., pp. 153–176, Guilford Press, New York, NY, USA, available at: https://www.scienceopen.com/document?vid=a182a645-fc12-4d21-9e22-15c96a792275 (last access: 1 July 2019), 1983.
Saltelli, A., Ratto, M., Andres, T., Campolongo, F., Cariboni, J., Gatelli, D., Saisana, M., and Tarantola, S.: Global Sensitivity Analysis: The Primer, John Wiley & Sons, Chichester, England, 2008.
Schlef, K. E., Kaboré, L., Karambiri, H., Yang, Y. C. E., and Brown, C. M.: Relating perceptions of flood risk and coping ability to mitigation behavior in West Africa: Case study of Burkina Faso, Environ. Sci. Policy, 89, 254–265, https://doi.org/10.1016/j.envsci.2018.07.013, 2018.
Tonn, G. L. and Guikema, S. D.: An Agent-Based Model of Evolving Community Flood Risk, Risk Anal., 38, 1258–1278, https://doi.org/10.1111/risa.12939, 2017.
Ujeyl, G. and Rose, J.: Estimating Direct and Indirect Damages from Storm Surges: The Case of Hamburg–Wilhelmsburg, Coast. Eng. J., 57, 1540006-1–1540006-26, https://doi.org/10.1142/S0578563415400069, 2015.
Vojinovic, Z.: Flood Risk: The Holistic Perspective–From Integrated to Interactive Planning for Flood Resilience, IWA Publishing, London, UK, 2015.
Interactive maps for Hamburg for the 2011 census can be found at https://www.statistik-nord.de/fileadmin/maps/zensus2011_hh/index.html, last access: 3 June 2020
- Abstract
- Introduction
- Study area
- Protection motivation theory
- CLAIM decomposition and model setup
- Results
- Discussion and conclusion
- Appendix A: List of assumptions made to build the coupled ABM–flood model
- Appendix B: Elaboration on the link between Birkholz (2014) and the current study
- Appendix C: List of house types in Wilhelmsburg
- Appendix D: Estimating simulation repetition
- Appendix E: Sensitivity analysis
- Code availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Study area
- Protection motivation theory
- CLAIM decomposition and model setup
- Results
- Discussion and conclusion
- Appendix A: List of assumptions made to build the coupled ABM–flood model
- Appendix B: Elaboration on the link between Birkholz (2014) and the current study
- Appendix C: List of house types in Wilhelmsburg
- Appendix D: Estimating simulation repetition
- Appendix E: Sensitivity analysis
- Code availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References