The influence of assimilating leaf area index in a land surface model on global water fluxes and storages

Vegetation plays a fundamental role not only in the energy and carbon cycles but also in the global water balance by controlling surface evapotranspiration (ET). Thus, accurately estimating vegetation-related variables has the potential to improve our understanding and estimation of the dynamic interactions between the water, energy, and carbon cycles. This study aims to assess the extent to which a land surface model (LSM) can be optimized through the assimilation of leaf area index (LAI) observations at the global scale. Two observing system simulation experiments (OSSEs) are performed to evaluate the efficiency of assimilating LAI into an LSM through an ensemble Kalman filter (EnKF) to estimate LAI, ET, canopy-interception evaporation (CIE), canopy water storage (CWS), surface soil moisture (SSM), and terrestrial water storage (TWS). Results show that the LAI data assimilation framework not only effectively reduces errors in LAI model simulations but also improves all the modeled water flux and storage variables considered in this study (ET, CIE, CWS, SSM, and TWS), even when the forcing precipitation is strongly positively biased (extremely wet conditions). However, it tends to worsen some of the modeled water-related variables (SSM and TWS) when the forcing precipitation is affected by a dry bias. This is attributed to the fact that the amount of water in the LSM is conservative, and the LAI assimilation introduces more vegetation, which requires more water than what is available within the soil.

1 Introduction

Terrestrial vegetation plays a vital role in the global water cycle, as it controls the surface evapotranspiration (ET) and the state of the carbon cycle. As shown in past literature, a strong relationship exists among vegetation, precipitation, and soil moisture (Di et al., 1994; Farrar et al., 1994; Richard and Poccard, 1998; Adegoke and Carleton, 2002). Nevertheless, the role that vegetation and its dynamics play in the water cycle (for instance in the variability of precipitation) is extremely complex (Wang and Eltahir, 2000; Wang et al., 2011). Over the past 50 years, these land surface processes and feedbacks have been examined through numerical modeling experiments (Foley et al., 1996; Kim and Wang, 2007; Druel et al., 2019). In early generation land surface models (LSMs), the development stage of vegetation was prescribed by regularly updating vegetation variables, based on fixed lookup tables to simplify the model computation (Foley et al., 1996). This approach uses constant vegetation indices, e.g., the leaf area index (LAI), while in reality the growth of vegetation continuously changes in response to weather and climate conditions. To overcome this deficiency, new generation LSMs are coupled with dynamic vegetation modules that comprehensively simulate several biogeochemical processes (Woodward and Lomas, 2004; Gibelin et al., 2006; Fisher et al., 2018) and that are able to capture more detailed variations in plant productivity than traditional methods (Kucharik et al., 2000; Arora, 2002; Krinner et al., 2005).

The LAI can also be estimated through observations from satellite sensors, such as the Moderate Resolution Imaging Spectroradiometer (MODIS, Pagano and Durham, 1993; Justice et al., 2002), the Système Probatoire d'Observation de la Terre VEGETATION (SPOT-VGT, Baret et al., 2007), and the National Oceanic and Atmospheric Administration (NOAA) Advanced Very High Resolution Radiometer (AVHRR, Cracknell, 1997). LAI products retrieved from different satellite missions and sensors provide spatially and temporally varying LAI fields on a routine basis at regional and global scales, including the MODIS LAI (Myneni et al., 2002), the Global Land Surface Satellite (GLASS) LAI (Xiao et al., 2013), and the GLOBMAP LAI dataset (Liu et al., 2012), among others. Satellite-derived LAI products have been found to be affected by uncertainties due to the limitation of retrieval algorithms and vegetation type sampling issues (Cohen and Justice, 1999; Privette et al., 2002; Tian et al., 2002; Morisette et al., 2002).

A method to combine the inherently incorrect estimates from satellite observations and model simulations is data assimilation (DA). One of the most common DA systems – the ensemble Kalman filter (EnKF; Evensen, 2003) – dynamically updates the model error covariance information by producing an ensemble of model predictions, which are individual model realizations perturbed by the assumed model error (Reichle et al., 2007). The ensemble approach is widely used in hydrology because of its flexibility with respect to the type of model error (Crow and Wood, 2003) and is well suited to the nonlinear nature of land surface processes (Reichle et al., 2002a, b; Andreadis and Lettenmaier, 2006; Durand and Margulis, 2008; Kumar et al., 2008; Pan and Wood, 2006; Pauwels and De Lannoy, 2006; Zhou et al., 2006). However, the use of an EnKF for the assimilation of LAI in LSMs has not been thoroughly investigated in the past. Pauwels et al. (2007) proposed an observing system simulation experiment (OSSE) to evaluate the performance of assimilating LAI in a hydrology–crop growth model with an EnKF algorithm. Other studies have also tested simplified 1D-Var and extended Kalman filter methods for LAI assimilation (e.g., Sabater et al., 2008; Barbu et al., 2011; Fairbairn et al., 2017). Recently, Kumar et al. (2019) assimilated GLASS LAI in a land surface model with an EnKF across the continental US. Some water budget variables were improved through the assimilation procedure, particularly in agricultural areas where the assimilation added harvesting information to the model. Ling et al. (2019) assimilated global LAI information with an ensemble adjust Kalman filter (EAKF) algorithm and found that the assimilation is more effective during the growing season. LAI assimilation also had a positive impact on gross primary production (GPP) and ET in low-latitude regions.

Nevertheless, most of the aforementioned studies mainly focused on the impact of LAI assimilation on the simulated LAI or vegetation biomass. Only a few studies discussed the influences of LAI assimilation on the estimation of water variables such as soil moisture or streamflow (Pauwels et al., 2007; Sabater et al., 2008) and most of them focused on limited regions. Most recently, Albergel et al. (2017) conducted a study on a much larger domain – Europe and the Mediterranean Basin – and showed improvement in soil moisture at various depths thanks to LAI assimilation.

This work leverages upon these studies but aims to assess the extent to which a land surface model, especially the simulation of water-related variables, can be optimized through the assimilation of LAI observations at the global scale. As this study serves as a feasibility test to quantify the impact of LAI assimilation on water cycle variables, an OSSE is chosen to investigate the model's behavior. This guarantees that reference variables (often referred to as the “truth”), which are synthetically produced, are available to quantify the performance of the proposed framework. Specifically, two OSSEs that apply an EnKF algorithm to the Noah LSM with multi-parameterization options (Noah-MP, Niu et al., 2011; Yang et al., 2011) are performed to evaluate the efficiency of assimilating LAI observations for estimating ET, canopy-interception evaporation (CIE), canopy water storage (CWS), surface soil moisture (SSM), and terrestrial water storage (TWS).

2 Methods and materials

2.1 Land surface model (Noah-MP)

The Noah-MP 3.6 LSM (Niu et al., 2011; Yang et al., 2011) is adopted in this study. Noah-MP contains a separate vegetation canopy defined by a canopy top and bottom, crown radius, and leaves with defined dimensions, orientation, density, and radiometric properties (Niu et al., 2011). Multiple options are available for surface water infiltration, runoff, and groundwater transfer and storage, including water table depth to an unconfined aquifer (Niu et al., 2007), dynamic vegetation, canopy resistance, and frozen soil physics. Specifically, the prognostic vegetation growth combines a Ball–Berry photosynthesis-based stomatal resistance (Ball et al., 1987) with a dynamic vegetation model (Dickinson et al., 1998). The dynamic vegetation model calculates the carbon storage in various parts of the vegetation (leaf, stem, wood, and root) and the soil carbon pools.

The Noah-MP 3.6 LSM has been implemented into the National Aeronautics and Space Administration (NASA) Land Information System (LIS; Peters-Lidard et al., 2007; Kumar et al., 2006). LIS is a software that provides an interagency test bed for land surface modeling and data assimilation which allows customized systems to be built, assembled, and reconfigured easily, using shared plugins and standard interfaces. All of the experiments in this study are set up through LIS. The Modern-Era Retrospective analysis for Research and Applications Version 2 (MERRA-2; Gelaro et al., 2017) dataset serves as the meteorological forcings of Noah-MP. MERRA-2 is the latest atmospheric reanalysis produced by the NASA Global Modeling and Assimilation Office (GMAO) and includes updates from the Goddard Earth Observing System (GEOS). The meteorological variables selected from MERRA-2 include surface pressure, surface air temperature, surface specific humidity, incident radiations, wind speed, and precipitation rate.

Five model output variables that describe terrestrial water fluxes and storages are investigated in this work: ET, which is defined as the sum of evaporation and the plant transpiration (kg m⁻² s⁻¹); CIE, which is defined as the evaporation of the canopy-intercepted water (kg m⁻² s⁻¹); CWS, which is defined as the amount of canopy-intercepted water in both the liquid and ice phases (kg m⁻²); SSM, which is defined as the water content in the top 10 cm of the soil column (m³ m⁻³); and TWS, which is defined as the sum of all water storage on the land surface and in the subsurface (mm).

2.2 Experimental design

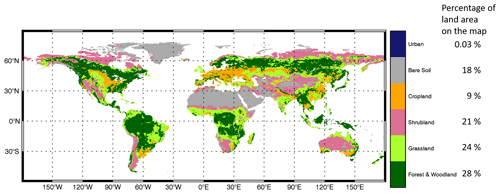
An OSSE is designed to understand the efficiency of assimilating LAI within Noah-MP version 3.6 using a one-dimensional EnKF algorithm (Reichle et al., 2010), when the precipitation forcing data are strongly biased. As it is the major driving force of the hydrological cycle, the quality of input precipitation is critical for the accuracy of land surface model outputs. However, global precipitation datasets are far from being perfect and are often affected by large regional biases. For example, the MERRA-2 precipitation dataset shows a widespread relative bias greater than 100 % in South Asia (Ghatak et al., 2018). Although an EnKF is optimal only under the assumption of unbiasedness (which is not met in the proposed experimental setup), here we want to investigate the extent to which the EnKF LAI assimilation (even if suboptimal) can improve water storages and fluxes under two extreme conditions, i.e., a very dry and a very wet precipitation bias, knowing that such biases are very plausible in the real world and are often unknown (and therefore difficult to remove). The proposed framework is evaluated through a global experiment (Antarctica excluded) at the $\mathrm{0.625}{}^{\circ }\times \mathrm{0.5}{}^{\circ }$ spatial resolution of the MERRA-2 forcing dataset (Fig. 1).

Figure 1 Study domain and land cover types (Hansen et al., 2000).

Figure 2 Schematic diagram of the OSSE design.

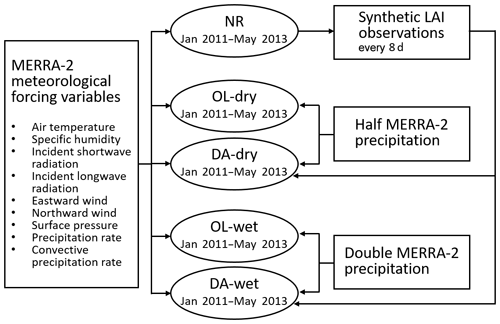
Figure 2 shows a schematic diagram of the experiments. First, the Noah-MP model is spun up for a 10-year period (2001–2010) to ensure a physically realistic state of equilibrium. Second, the model is run for a 29-month period (January 2011–May 2013) to conduct the nature run (NR) with the same configuration as the spin-up run. By definition, an OSSE is a controlled experiment that does not assimilate any real observation. Instead, it treats all of the model outputs from the NR as the “true” condition (denoted as the “synthetic truth”). The “true” LAI (i.e., the LAI output from NR) is then perturbed via a simple additive error model to produce the synthetic observations to be assimilated into the DA runs. The spin-up run and the NR are forced by the original MERRA-2 precipitation data. Third, two open loop (OL) runs (no DA) are conducted for the same 29-month period under two conditions: (i) “extremely dry” (the model is forced by halving the MERRA-2 precipitation data; OL-dry), and (ii) “extremely wet” (the model is forced by doubling the MERRA-2 precipitation; OL-wet). The biased forcing precipitation data in OL mimic typical precipitation biases in current precipitation reanalysis and satellite products (e.g., Ghatak et al., 2018; Yoon et al., 2019).

The two DA runs are then conducted under the two same conditions (DA-dry and DA-wet) using a one-dimensional EnKF assimilation algorithm, which is a built-in DA method in LIS. The EnKF DA algorithm is suitable for nonlinear and intermittent land surface processes (Reichle et al., 2002a, b). Details of the algorithm can be found in numerous previous studies (Reichle et al., 2010; De Lannoy et al., 2012; Liu et al., 2015; Kumar et al., 2019a).

The model ensemble is generated by perturbing a set of meteorological forcing. To select the optimal ensemble size, a sensitivity test is performed for ensemble sizes spanning from 2 to 24 members (not shown here). The number of ensemble members has a strong impact on the model results at small sizes, while the model performance tends to become steady when more than 20 ensemble members are considered. Thus, all the DA simulations are run for 20 members.

The synthetic LAI observations are obtained from the NR and assimilated into the DA system every 8 d. The synthetic LAI observation has the same temporal resolution as the MODIS LAI product but with full coverage over the study domain. In real case studies, satellite LAI products contain a substantial amount of missing data, mainly due to the cloud obscuration gaps. Based on the vegetation type in the model, the leaf mass fields are also updated. Random perturbations of MERRA-2 meteorological forcings and synthetic LAI observations are applied to create an ensemble of land surface conditions that represent the uncertainties in the LSM.

Similar to previous work (Kumar et al., 2014, 2019a, b), the MERRA-2 forcing inputs such as shortwave and longwave radiation and precipitation are perturbed hourly. Multiplicative perturbations are applied to the shortwave radiation and precipitation with a mean of 1 and standard deviations of 0.3 and 0.5, respectively. The longwave radiation is perturbed via an additive perturbation with a standard deviation of 50 W m⁻². The perturbations of the three meteorological forcing variables also include cross correlations: the cross correlation between shortwave radiation and precipitation is −0.8, the cross correlation between longwave radiation and precipitation is 0.5; and the cross correlation between shortwave and longwave radiations is −0.5. The synthetic LAI observations are perturbed via an additive model with a standard deviation of 0.1.

2.3 Evaluation and error metrics

Output variables from the OL and DA runs are evaluated against the “truth” from the NR at daily, monthly, and seasonal temporal scales. Besides LAI, five more water fluxes and storages are evaluated in the results section: ET, CIE, CWS, SSM, and TWS.

The initial condition for the OL and DA runs is generated by a spin-up run that uses the original MERRA-2 precipitation as input. However, the OL and DA runs are forced by either doubled or halved precipitation, which is not consistent with the spin-up run, and the model needs some time to stabilize. Therefore, the first 5-month model outputs are eliminated from the evaluation to avoid the model systematic instability at the beginning of the OL and DA simulations; hence, the evaluation only focused on model outputs from 1 June 2011 to 31 May 2013. Results are discussed using maps and time series of global averaged values and anomalies. Each of the anomaly time series is computed relative to the mean of its respective model run. Moreover, two error metrics are employed to quantify the difference between OL (and DA) with respect to the reference variables (from the NR). The first error metric is the normalized and centered root mean square error (NCRMSE), which is defined as follows:

$$\begin{array}{}\text{(1)}& E={\displaystyle \frac{{\left\{\frac{\mathrm{1}}{N}{\sum }_{i=\mathrm{1}}^N{\left[\left(X_i-\mathrm{mean}\left(X\right)\right)-\left(O_i-\mathrm{mean}\left(O\right)\right)\right]}^{\mathrm{2}}\right\}}^{\frac{\mathrm{1}}{\mathrm{2}}}}{\mathrm{mean}\left(O\right)}},\end{array}$$

where E is the NCRMSE, O is the NR output variable, and X is the output variable from the OL runs or DA runs. N is the total number of X values, and i represents the index of each X value. Second, to investigate the improvement (or degradation) due to the DA of LAI observations, we adopt the normalized information contribution (NIC, similar to the NIC in Kumar et al., 2016) index based on the NCRMSE and defined as follows:

$$\begin{array}{}\text{(2)}& C={\displaystyle \frac{E_{\mathrm{DA}}-E_{\mathrm{OL}}}{\mathrm{0}-E_{\mathrm{OL}}}},\end{array}$$

where C represents the NIC index, and E is the NCRMSE for OL or DA runs. An NIC equal to 1 means that DA realizes the maximum possible improvement over the OL; an NIC equal to zero means that DA and OL show the same performance skills; and a negative NIC indicates a model degradation through DA.

3 Results and discussion

3.1 LAI

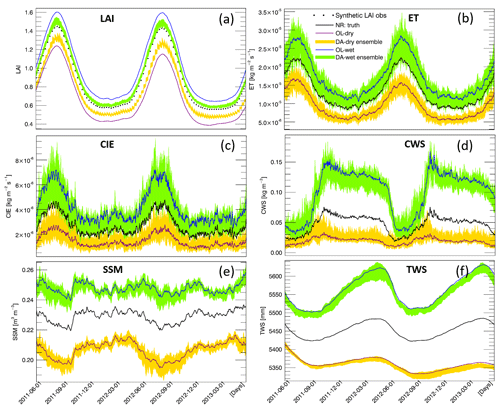
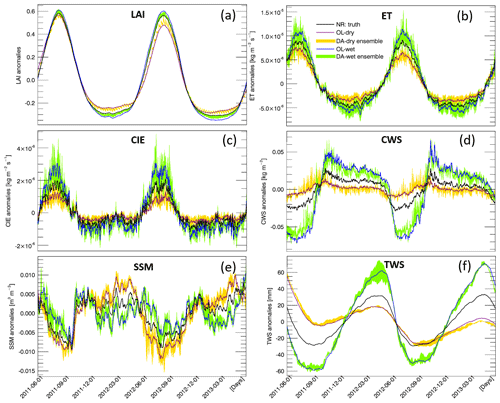
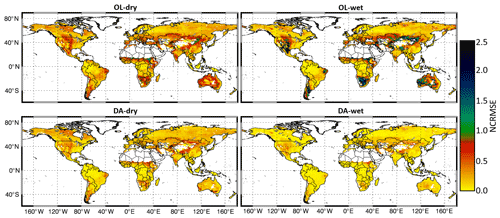
Figures 3a and 4a show time series of the global averaged LAI values and the corresponding anomalies, respectively. As expected, LAI values are largely impacted by the extreme precipitation conditions. The wet condition introduces more vegetation, whereas the dry condition limits the vegetation growth throughout the 2-year period. The DA procedure effectively corrects the LAI errors caused by the biased precipitation input. The seasonality of LAI anomalies is evident, showing larger variations in DJF (December–January–February) and JJA (June–July–August) than during the transition periods (MAM, March–April–May, and SON, September–October–November). The OL-wet condition simulation shows larger LAI anomalies than the NR reference, whereas the OL-dry condition has smaller LAI anomalies than NR. The LAI anomalies obtained from DA runs under both wet and dry conditions are closer to the reference anomalies than the corresponding OL runs. In general, DA performs better in the wet condition experiment than in the dry case. Moreover, the DA runs show lower NCRMSE values than the corresponding OL runs across the globe (Fig. 5a), especially over shrubland and grassland (refer to Fig. 1 for land covers).

Figure 3 Global averaged daily values of LAI and five water variables (1 June 2011–31 May 2013).

Figure 4 Global averaged daily anomalies of LAI and five water variables (1 June 2011–31 May 2013).

Figure 5 Maps of the LAI NCRMSE for the OL and DA runs.

In order to illustrate how LAI assimilation performs for different seasons, Figs. 6a and 7a show monthly averages of NCRMSE for LAI across the Northern and Southern hemispheres, respectively. In the Northern Hemisphere (Fig. 6a), the NCRMSE time series follow clear seasonal patterns. First, the NCRMSE is higher in DJF and MAM and is lower in JJA and SON for both extreme precipitation conditions. The highest NCRMSE values are in March and April, and the lowest values are in July, August, and September. The differences in the NCRMSE between OL and the corresponding DA runs tend to be much larger in MAM than in any other seasons, which means that LAI assimilation is more effective during the vegetation growth period. Moreover, the NCRMSE is constantly higher in the dry condition runs than in the wet runs, which is due to the fact that the growth of vegetation is sensitive to the lack of water. Differences between wet and dry conditions are much smaller in JJA than in other seasons. In JJA, leaves in the Northern Hemisphere are fully developed and the plants can use stomatal closure to preserve water under water-limited conditions (the dry condition). Thus, the NCRMSE of the dry condition becomes smaller and does not show much difference from the wet condition. The Southern Hemisphere (Fig. 7a), which does not have a strong climate seasonality, shows more modest seasonal NCRMSE patterns than the Northern Hemisphere regions. In general, the NCRMSE values in the Southern Hemisphere are smaller than those in the Northern Hemisphere all year around. Specifically, NCRMSE values in the Southern Hemisphere are slightly higher in October, November, and December, when the differences between the OL and DA runs are also larger.

Figure 6 Monthly averaged NCRMSE for LAI and five water variables over the Northern Hemisphere.

Figure 7 Same as in Fig. 6 but for the Southern Hemisphere.

3.2 Water fluxes and storages

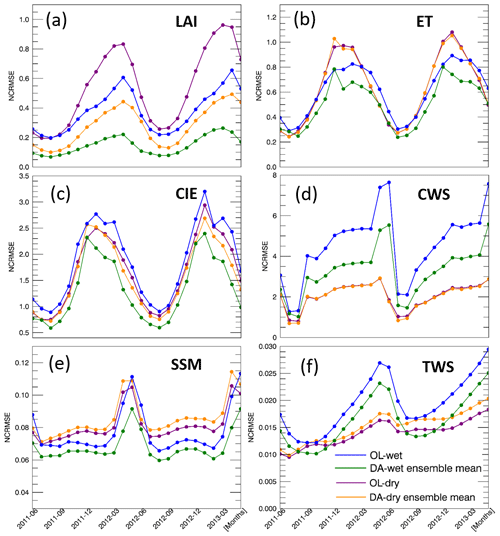
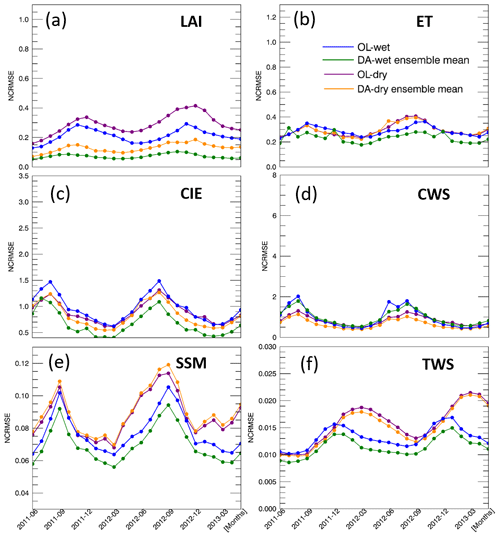
As mentioned in Sect. 2.3, we focus on five water-related variables from the Noah-MP output to evaluate the impact of LAI assimilation on simulating the water cycle (ET, CIE, CWS, SSM, and TWS). Daily time series of global averaged values and corresponding anomalies of the five water variables are shown in Figs. 3b–f and 4b–f, respectively. The model shows good simulation performance with respect to the seasonality of all of the water fluxes/storages considered here. The OL runs reveal that global average values of all five variables are impacted by the highly biased precipitation conditions. The variations of anomalies for ET, CIE, CWS, and TWS tend to be amplified by the wet condition and tend to be dampened by the dry condition. On the contrary, the anomalies of the SSM become larger under dry conditions and become smaller under wet conditions, which is probably due to the limited soil water capacity. The surface soil is more likely to become saturated under wet conditions when the precipitation doubles the original amount, but the SSM cannot become larger once the soil is saturated, even if there is more precipitation added to the system. Thus, the range of the SSM anomalies in the wet experiment is limited and narrower than in the dry experiment. The green and yellow shaded areas in Figs. 3 and 4 represent the ensemble of the DA runs. The anomaly ensembles of the five water variables show slight improvements through DA when precipitation is severely positively biased (wet condition). However, none of these variables show improvement when the precipitation is severely negatively biased (dry condition) – the anomalies either have no change through the LAI DA (ET, CIE, and CWS) or worsen the OL-dry run (SSM and TWS).

To further investigate the efficiency of assimilating LAI in Noah-MP, time series of monthly NCRMSE averages are shown in Figs. 6b–f and 7b–f for all five water variables. The five variables can be divided into two main groups based on their performances: ET, CIE, and CWS, and SSM and TWS. For the wet bias experiment, DA improves the NCRMSE for all variables. However, LAI assimilation is not able to correct the model when the input precipitation is negatively biased (dry condition). A dry precipitation bias means that the system (erroneously) has less water than in reality (NR in the synthetic experiment). As no water is otherwise added to the system, LAI DA cannot fully correct water-related model states (such as soil moisture). The NCRMSE values of DA runs are either the same as in the OL runs (ET, CIE, and CWS) or worse (SSM and TWS). Specifically, ET, CIE, and CWS have larger NCRMSE values in the Northern Hemisphere and much smaller NCRMSE values in the Southern Hemisphere, but SSM and TWS do not show large differences between the Northern and Southern hemispheres. Moreover, ET, CIE, and CWS in the Northern Hemisphere follow a seasonal pattern: NCRMSE values are lower in the warm season (JJA) and higher in the colder season (DJF and March). In the Southern Hemisphere, the three variables also have relative higher NCRMSE values in the colder season (JJA). On the contrary, SSM and TWS show a different seasonal pattern with larger NCRMSE values in the warmer season (April, May, and June) over the Northern Hemisphere. In the Southern Hemisphere, TWS also has larger NCRMSE values in the warmer season (October to April), but the SSM shows higher NCRMSE values in the colder season (similar to the ET, CIE, and CWS group).

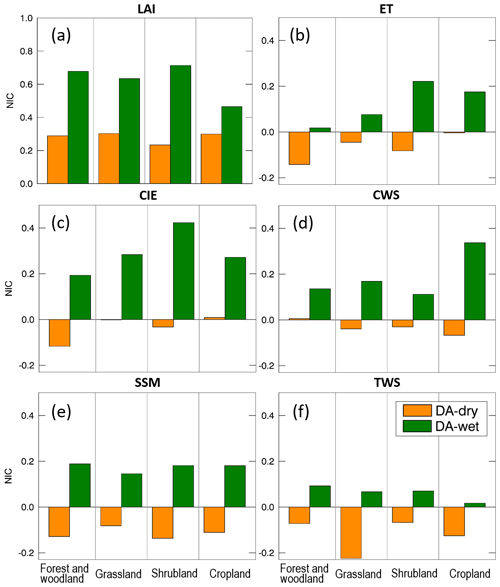
The improvements in the model water fluxes and storages through LAI DA are also quantified by the NIC index (defined in Eq. 2). Figure 8 presents comparisons among NIC indices for each water variable analyzed in this study across areas with four different land cover types: forest and woodland, grassland, shrubland, and cropland. In general, LAI DA improves the NIC indices with positively biased input precipitation (DA-wet) but worsens the NIC when negatively biased input precipitation (DA-dry) is considered. Specifically, in the wet condition experiment, ET, CIE, and CWS have higher variability over areas with different land cover types, whereas SSM and TWS have similar NIC values across different land covers. Shrubland and cropland tend to perform better under wet conditions except for TWS. Under dry conditions, the NIC values of ET, CIE, and TWS have higher variability than those of CWS and SSM. SSM and TWS show very low NIC values in the dry condition for almost all land covers. Overall, the NIC values of ET, CIE, and CWS are better than those of SSM and TWS for all land cover types, although the NIC values of ET and CIE over forest and woodland perform very poorly.

Figure 8 The NIC for different variables and different land cover types for the two DA runs.

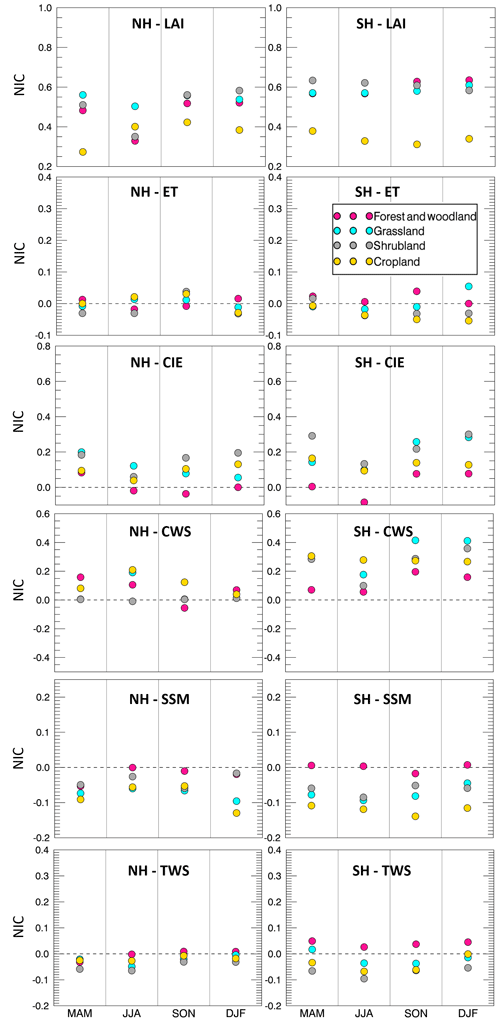
Therefore, the effectiveness of LAI DA varies across the Northern and Southern hemispheres, different land cover types, and different input precipitation biases. To further investigate the influence of LAI assimilation, Figs. 8 and 9 present NIC values for each hemisphere, each season, and each of the input precipitation conditions – wet and dry, respectively. For the wet case (Fig. 9), the NIC is positive in most cases, which means that the five water variables benefit from the LAI assimilation in all seasons and in both hemispheres. The only exception is CWS which has negative NIC values in the Southern Hemisphere over grassland (in MAM) and over forest and woodland (in all seasons). In fact, the forest and woodland land cover regions tends to show the least improvement through the LAI assimilation among all land cover types. This is probably because forests and woodlands have a large water-holding capacity; thus, the change in the water amount caused by LAI DA is not enough to improve the water-related variables. In other words, forest and woodland regions tend to have lower sensitivity in response to the change in precipitation conditions because of their large rooting depth. On the contrary, cropland is very sensitive to precipitation, and it benefits the most from the assimilation of LAI for most of the variables. Moreover, the NIC values of ET, CIE, and CWS tend to be smaller than the NIC values of SSM and TWS. There is no clear seasonality in the NIC values, although they have a weak tendency to be lower in warm seasons.

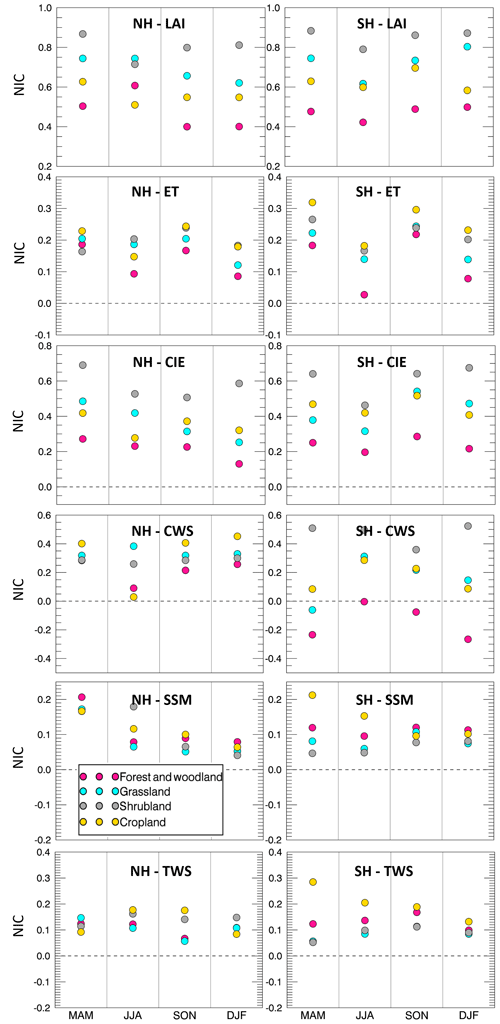
Figure 9 The NIC of five water variables under wet precipitation conditions over Northern and Southern hemispheres (NH and SH, respectively) during the different seasons (MAM, JJA, SON, and DJF).

Figure 10 Same as in Fig. 9 but for the dry precipitation experiment.

For the dry condition case (Fig. 10), the NIC values are much lower than in the wet bias case. Nearly half of the NIC values for the five water-related variables are negative, meaning that DA degrades the OL estimates. Nevertheless, the forest and woodland regions tend to perform better than other land covers under dry conditions for SSM and TWS. This is due to the large soil reservoir of forests and woodlands, which keeps the model water storage more stable when the input precipitation is affected by large negative biases.

3.3 Discussion

As a key factor in land surface processes, precipitation greatly affects surface water fluxes and states and, consequently, affects vegetation development. Furthermore, changes in vegetation also have considerable impact on the surface water condition. Section 3.1 and 3.2 quantified changes in five water variables (ET, CIE, CWS, SSM, and TWS) due to the LAI assimilation in Noah-MP. Among the five variables, CIE and CWS are directly related to LAI, while the relationships between LAI and ET, SSM, and TWS are more complex (and indirect) and involve several other factors. For example, ET counts the water losses via both vegetation and soil; SSM is impacted by factors such as precipitation, temperature, and soil characteristics; and TWS considers all of the water storage in the land surface and subsurface, including CWS and SSM.

The performance of the proposed LAI assimilation largely varies depending on the modeled variable, land cover type, errors in the model input (e.g., wet or dry bias in the forcing precipitation), and season. This is due to the complex relationships between vegetation and land water condition. Specifically, results from this study indicate that assimilating LAI in Noah-MP improves the model estimates of water fluxes and storages under positively biased precipitation input but does not benefit most of the selected water variables when the precipitation input is characterized by a negative bias.

In the dry condition runs, Noah-MP is fed by only half of the original MERRA-2 precipitation used in the NR. Considering that the amount of water in Noah-MP is conservative (as it is based on a water balance equation), the model has no additional water source in the system, even though the LAI assimilation pushes the model towards more vegetation (which should result in more water). As a matter of fact, introducing more vegetation in the system results in more ET and more root water uptake from the soil, which is most likely the cause of the poor performance of most water fluxes and storages in the DA-dry experiment.

Conversely, the LAI assimilation is found to improve the original OL runs when the input precipitation is positively biased. This is because LAI assimilation is able to help constrain the partitioning of model water storage when there is abundant water in the system, thereby improving the performance of water-related variables. In summary, although the EnKF is run in a suboptimal mode here (not satisfying the unbiasedness assumption), the assimilation of LAI is shown to have a positive impact on multiple variables and in several regions of the world.

Overall the improvement of water variables through LAI assimilation is not remarkable enough to compensate for the model degradation caused by the biased precipitation forcing data. Previous studies (Pauwels et al., 2007; Sabater et al., 2008; Barbu et al., 2011; Fairbairn et al., 2017; Albergel et al., 2017) have tested the performance of the joint assimilation of LAI and soil moisture over regional domains and have shown promising results. However, no experiments have been performed at the global scale. Future work could investigate a multivariate data assimilation system that concurrently merges both LAI and soil moisture (or TWS) observations globally.

4 Conclusions

This study evaluates the efficiency of assimilating vegetation information (i.e., LAI synthetic observations) within a land surface model (Noah-MP 3.6) when the precipitation forcing data are strongly biased (either positively or negatively). Two OSSEs that use an EnKF algorithm for LAI assimilation are performed at a global scale for the period from June 2011 to May 2013. The experiments use MERRA-2 as meteorological forcing data. The OL and DA runs are evaluated against a synthetic “truth” from a nature run, in which the MERRA-2 precipitation is neither perturbed nor biased. The performance of the proposed framework is evaluated for several model output variables, including LAI estimates and five water-related variables (ET, CIE, CWS, SSM, and TWS).

Overall, the EnKF LAI assimilation procedure effectively reduces the LAI error under positively (wet case) and negatively (dry case) biased precipitation conditions. For the five selected water flux or storage variables, LAI DA improves the model estimates when the model input precipitation is positively biased, but it tends to worsen the OL estimates for some of those variables when the input precipitation is negatively biased. Specifically, SSM and TWS estimates are degraded in the DA-dry run with respect to the OL-dry run, whereas ET, CIE, and CWS do not present large changes when LAI is assimilated in the dry bias run. The poor performance of LAI DA under dry condition is mainly attributed to the fact that the amount of water in Noah-MP is conservative. The LAI assimilation in the dry condition experiment introduces more vegetation, which requires more water in the system to replenish the soil water supply. However, the model has no additional source of water, as the input precipitation is negatively biased.

Although a blind bias case (e.g., unknown biases in the precipitation forcing dataset) is presented here in which the EnKF is run in a suboptimal mode, the assimilation of LAI observations is proven useful to improve several model output variables. Future research should focus on alternative DA methods, such as updating other related model states while assimilating LAI observations, perturbing the model initial condition and model parameters, and/or assimilating actual satellite-based LAI observations (e.g., MODIS, GLASS) at the global scale to verify the efficiency of the proposed vegetation DA framework. This may be particularly useful in agricultural areas, where the vegetation conditions are largely impacted by cropping schedules (Kumar et al., 2019b). Moreover, future work could investigate multivariate DA techniques that combine the assimilation of several variables (such as LAI, soil moisture, and TWS) at the global scale.