Beyond Perrault's experiments: repeatability, didactics and complexity

The naturalistic and philosophical studies conducted in the second half of the 17th century were crucial both for the birth of modern hydrological science and modern epistemology. Thanks to quantitative observations and to the new experiment-based scientific approach, the Sun was about to be fully recognized as the engine of the hydrological cycle. In this context of great vitality and rapid cultural changes, Pierre Perrault published his classical opus De l'origine des fontaines (On the origin of springs) in 1674. The opus presents a discussion on the origin of springs and contains the report of a set of experiments of water flow through a soil column, which may be considered the first of modern hydrology.

In assessing the importance of Perrault's opus, we will discuss his epistemological relevance by looking at the novelty of his approach, at the repeatability of the experiments, at the intriguing didactic aspects for the modern teaching of hydrology and at his attitude in facing the complexity of hydrological processes.

Perrault places himself in the context of a novel experimental epistemology. On the basis of our analyses he seems to be aware that the processes involved in the hydrological cycle and in soil hydrology are hardly reproducible by means of a controlled laboratory model. This circumstance put the modern scientific approach to a severe test at its very beginning. It is suggested that some of Perrault's epistemological and methodological reflections are precursors of the modern epistemology of complexity. Thus even if Perrault's conclusions followed an ancient opinion, his work is not only seminal for hydrology, but also helps to enlighten some features of the scientific revolution of the 17th century.

1 Introduction

By the second half of the 17th century, hydrology was at a crucial passage of its evolution, because scientists were about to fully recognize the Sun as the engine of the hydrological cycle. The debate on what the engine of the hydrological cycle was, whether it was the Sun or the Earth, is ancient and dates back to Aristotle. He in fact assumed that, whereas little rivers and small springs could be supplied by subsurface reservoirs, the amount of water flowing in big rivers was too great to be stored in any reservoir and, thus, it could not derive entirely from precipitation. Therefore he concluded that big rivers must be supplied by a continuous evaporation and condensation process, acting within the Earth as a result of an unknown underground source of heat (Aristotle and Lee, 1952, Book 1). By this assertion, Aristotle openly disagreed with previous Presocratic philosophers who had already given a substantially correct view of the hydrological cycle (Brutsaert, 2005, p. 560, and following). The discussion on the relative importance of the two engines characterized the scientific debate until the 17th century and beyond (see Biswas, 1970; Duffy, 2017, for an overview), when quantitative observations and a new experiment-based scientific approach proved that precipitation is adequate to account for all the water flowing in rivers.

Pierre Perrault (1611–1680) was one of the first, if not the first, to uphold such an idea. In his opus De l'origine des fontaines (On the origin of springs; Fig. 1), Perrault devised methods of measurement, performed experiments and collected many observations both to assess the water balance at the basin scale and to understand the water movement in the upper soil layers (Perrault, 1674, 1678; Perrault and LaRoque, 1967; Perrault, 1986). Perrault seemed to be aware that his measurements of the water balance were quite crude and were affected by some inaccuracies (see Sect. 7). However, these errors compensated for each other, so that his assessment of the water balance turned out to be quite correct (Gascuel-Odoux, 2000). A few years later, Perrault's fellow countryman Mariotte (1686) refined and improved his method and offered the first rigorous basin-scale measurement in the history of hydrology. In fact, Perrault paved the way for the effective comprehension of the water cycle, although he himself did not understand it correctly. Indeed even if he showed with his experiments that precipitation might provide much more water than necessary to supply springs and rivers, he still decided to subscribe to Aristotle's position.

Figure 1 Front matter of Perrault's opus De l'origine des fontaines (Perrault, 1674, credits: Bayerische Staatsbibliothek München, Rar. 4600, sheet 7, urn:nbn:de:bvb:12-bsb10862482-0).

Figure 2 Front matter of Schott's opus Anatomia physico–hydrostatica fontium ac fluminum (Schott, 1663, credits: Bayerische Staatsbibliothek München, Phys.sp. 604 b, sheet 11, urn:nbn:de:bvb:12-bsb10134736-2).

Despite these limits, Perrault's contribution to hydrology has been remarkable, as already illustrated in the seminal article by Raymond L. Nace, published in 1974, on the occasion of the Tercentenary of Scientific Hydrology (Nace, 1974). The Origine contains a number of significant insights into various hydrological matters, such as the ideas of bank and floodplain storage and return flow (even if he had no name for these processes). He also proposed several accurate observations on soil, weather and climate, not to speak of his astute reflections on phenomena like evaporation, condensation and infiltration (for more detailed discussions of single issues see Nace, 1974). However, the most important aspect of Perrault's contribution is that he “brought to Hydrology a new frame of mind” (Nace, 1974).

The aim of this paper is to clarify the new frame of mind, which made hydrology possible as a science. Indeed, hydrology needed two steps in order to become a modern science: they were the concept of scientific experiment and the assessment of the quantitative evaluation of the water cycle. Perrault took both these steps. His work therefore allows an understanding of how the birth of modern hydrological science was strictly linked to the scientific revolution of the 17th century (referred to as the Scientific Revolution hereafter). In fact, Perrault paved the way to scientific hydrology because he had a new, critical attitude towards tradition, also shared with scientist–philosophers like Descartes and Pascal (Tixeront, 1974).

For this purpose, we will reconstruct the cultural and intellectual context in which Perrault operated, highlighting the similarities between his position and that of the major scientists and philosophers of the age (Sect. 2). Afterwards, we will focus more specifically on Perrault's book, adopting a comparative method of analysis, to show the novelty of his approach to hydrological matters compared to his contemporary Gaspar Schott (Sect. 3). Then, we will analyse Perrault's experiments in depth and present today's repetition of them, on the basis of the reports contained in his book, thus stressing the importance of the notion of repeatability (Sect. 4 and 5). In the following section we will enhance the didactical aspects of Perrault's experiments, which can be used to illustrate the general aspects of the scientific practice and the specific problems connected with soil hydrology (Sect. 6). In the conclusion, we will go into more detail about Perrault's epistemological assumptions, contained in his Letter to Mr. Huygens, by showing interesting correspondences between Perrault's anti-dogmatic and problematizing approach, and some issues arising from the modern paradigm of complexity in hydrology (Sect. 7 and Conclusion).

2 Perrault's cultural and scientific context

Perrault's seminal opus may be framed in the context of the querelle des anciens et des modernes (controversy between the ancients and the moderns), a spirited debate that took place in France during the second half of the 17th century and had profound resonances all over Europe (Fumaroli, 2001). Although the controversy emerged in a literary milieu, it rapidly spread in the scientific field and became entwined with the debates of the nascent Scientific Revolution. Pierre Perrault was a cultured man of noble origin and he played a role in the controversy, as well as his brothers, who were prominent figures in various fields of politics and culture (Nace, 1974). For instance Perrault's brother Charles, a renowned poet of the age, was the author of four volumes that focused on the question of whether the primacy in art and knowledge should lie with the ancients or with the moderns (Perrault, 1697).

The epistemological meaning of this dispute was immediately evident for the intellectuals of the age: at stake there was the correct way of achieving the truth. Whereas the supporters of the ancients defended the pre-eminence of the old principle of authority, the moderns put forward the idea that knowledge must be grounded only on reason and experience. The querelle can thus be seen as the way French intellectuals of the âge d'or dealt with the deep cultural transformations of their time. The comparison between modern knowledge and skills and those inherited from antiquity represented for them an effort to become aware of the historical and intellectual break-up they were living in. Like his brother Charles, Pierre Perrault sided with the moderns in his research field and applied the new experimental method to the problems of hydrology for the first time. Therefore, it is not surprising to find in his writings a strong reflection of the spirit of the Scientific Revolution and a thorough awareness of its achievements. He appears fully conscious of the difference between his own approach and that of his predecessors and considers the experiments as the primal source of scientific knowledge:

I know all too well that it is to experiments that we owe the finest knowledge we now have concerning the things of nature which had been unknown to Antiquity; and I base myself only on such principles. (Perrault and LaRoque, 1967, p. 11)

In the introductory Avertissement (Warning) of the Origine, Perrault explains his method and circumscribes the field of his enquiry. He states that he will not present “great reasonings of Physics”. Rather, he will speak “with a simplicity which can appeal to the most ordinary brains” (Perrault and LaRoque, 1967, p. 9). In so doing, the author immediately distances himself from the Aristotelian approach, according to which natural science was a “logical deductive structure derived from uncontestable basic statements or premises” (Applebaum, 2000, p. 341). Perrault is not interested in discussing the primal causes of natural phenomena and the principles of physics. He focuses only on the specific issue of the hydrological cycle, providing sensate experiences to support his opinion: “my intention has been to speak only of that which is obviously perceived by the senses” (Perrault and LaRoque, 1967, p. 10). Such a declaration of intent is in line with the incipit of René Descartes' seminal opus, the Discours de la méthode (Discourse on the method), a text that aimed to divulge the correct approach in “conducting one's reason and seeking truth in sciences”, as stated in the title (Descartes, 1637; Descartes and Maclean, 2006). Descartes plainly rejects the traditional centrality of classical studies and, therefore, the authority of past philosophers. On the contrary, he claims that “good sense is the most evenly distributed thing in the world” and that science is in principle accessible to anyone, provided that one proceeds step by step, “for it is not enough to possess a good mind; the most important thing is to apply it correctly” (Descartes and Maclean, 2006, p. 5). According to Descartes, the method should not start from general principles derived from philosophical heritage:

As for the other disciplines, in so far as they borrow their principles from philosophy, I concluded that nothing solid could have been built on such shaky foundations. (Descartes and Maclean, 2006, p. 10)

On the contrary, the path of science can only consist of an analytically ordered succession of experiences, each one supported by the constant check of reason. Thus, in this new perspective, reason does not dictate abstract principles; rather it plays an ordering and regulative role. At the same time, reason and experience are not opposite, for the latter provides the indispensable “matter” to any reasoning (Descartes and Maclean, 2006, p. 20).

A similar centrality of experience can be found also in Pascal's Préface pour un traité du vide (Preface to the treatise on vacuum, written in 1651), which is another relevant reference to understand Perrault's position (Pascal, 1954, 1910). Here, the French philosopher and scientist states that whereas authority is essential with regard to literary and historical issues, it is useless in the domain of matters that fall under our senses, such as the investigation of nature. In a few pages Pascal establishes the basis for the separation between humanistic and scientific attitudes, which still persists nowadays, yet with important differences (Preti, 2018). In fact, Pascal's separation between the so-called “two cultures” (Snow, 1998) is an argument against those academicians who wished to submit science to the dogmatic authority of metaphysics and theology. According to the author, the investigation of nature is characterized by “freedom”, as it is based on experience, whereas “dogmatism” is typical of literary, philosophical and theological studies. This position paved the way to the overcoming of Aristotelianism: as long as experience plays a crucial role, the philosopher's word could not be authoritative in the knowledge of nature. In his Avertissement Perrault shares this posture towards the past authors without falling into arrogance, as he claims that

It is not an extraordinary thing to examine the ideas of any author, it is permitted to the least disciples to ask the most renowned Philosophers, in the very school where they have most credit, the reasons for the propositions that they have advanced. (Perrault and LaRoque, 1967, p. 10)

Beyond the consonance of the epistemological attitude, it is also noteworthy that Pascal's role in the development of scientific hydrology was not merely speculative. He knew the work of Galilei and Torricelli, which shaped modern mechanics and hydraulics, and he tried in many different ways to reproduce the experiment performed in 1644 by Torricelli, to measure the atmospheric pressure (Tixeront, 1974; Applebaum, 2000). Pascal's measurements and observations were important examples for comparison in the implementation of Perrault's experiments. Although Perrault criticizes some of Pascal's assertions on specific issues (Perrault and LaRoque, 1967, p. 150), the epistemological perspective and the method that underpins his work refers to Pascal's Préface. On this basis, we can claim that Perrault is permeated with the critical attitude that should characterize a modern scientist. In his critique of both ancient (e.g. Aristotle) and modern scholars (e.g. Nicolas Papin) he makes use of concepts drawn from the works of Bacon and Galilei, Descartes and Pascal. Thus the driving forces in the passage towards quantitative hydrology are the overturning of the primacy of auctoritas and the centrality of experiments as a primal source of knowledge.

3 Comparison between Schott's and Perrault's opus

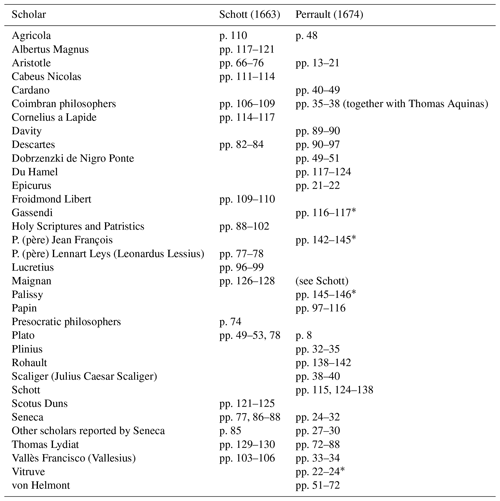
The depth of the paradigmatic novelty fostered by Perrault with his opus may be recognized by comparing the Origine with another opus, the Anatomia physico–hydrostatica fontium ac fluminum (Physical–hydrostatic anatomy of springs and rivers; Fig. 2), published only one decade before by the Jesuit Gaspar Schott (Schott, 1663). The Origine was written in French to be accessible to a broader audience, whereas the Anatomia was written in Latin. In his opus, Schott carefully reviews and discusses the opinions of ancient and modern authors about the origin of springs and rivers (see Table 1). Finally he states his own conjecture, according to which (a) the sea is the origin of most of the springs, and (b) the water rises from the sea mostly due to the greater altitude of the sea, with respect to the mountains. A comparison between the form and structure of the two texts reveals further important differences, despite the short lapse of time which separates them.

Schott (1663)Perrault (1674)

Table 1 List of previous scholars referred to by Schott (1663) and by Perrault (1674).

^* Authors referred to as Opinion Commune by Perrault.

The Anatomia appears to be an opiniones (opinions) book, deeply rooted in the ancient humanistic and dialectical approach and far from the modern scientific method. It is noteworthy that Schott felt it necessary to focus on histories of ancient springs, drawn by classic literary sources, in which mythological and imaginary witnesses are mixed together with historical and geographical accounts (Schott, 1663, pp. 12–63). In Schott's frame of mind, the purpose of scientific description does not conflict with the recreational intent of literature, and the stories handed down by the ancients still represent for him the point of departure for intellectual investigation. Therefore it seems that he does not take into account the distinction between humanistic and scientific discourse proposed by Pascal. In contrast, Perrault does not take any consideration in the mythological and literary tradition about springs, showing a deep awareness of the above-mentioned separation between the “two cultures”. However, both authors provide an extensive and detailed discussion of past scholars' opinions about the origin and nature of springs and rivers. Here the difference between Schott and Perrault lies (a) in the way of discussing texts and (b) in the choice of the authors which are cited (or not) by them (see again Table 1). It can be assessed in general terms that Schott's text does not present a clear demarcation between the exposition and the critique. In addition, his critiques often appear to be grounded on philosophical considerations and also on the appeal to authority arguments. In particular, he dedicates a detailed examination to the Holy Scriptures, which are also regarded as being reliable as a scientific treatise (Schott, 1663, pp. 88–102).

By contrast, Perrault's opus provides, for each author discussed, a clear separation between exposition and critique and, most importantly, he motivates his objections on the basis of the experimental results which are presented in the “Second Part” of the work. He does not consider the Holy Scriptures as a pertinent source in the context of his work. This choice represents another indication of his critical attitude towards the principle of authority. Furthermore, Perrault discusses a set of authors that he defines as supporters of the Opinion Commune (common opinion) (Perrault, 1674, p. 150 ff.). These authors are Vitruvius, Bernard Palissy, Paul Gassendi and père Jean François. It is noteworthy that Vitruvius' capital opus De Architectura (On architecture) was translated into French by Perrault's brother Claude, one of the major architects of the time, in 1673 (Vitruvius and Perrault, 1673). All these authors share an interest in the practical application of hydrological knowledge, and all of them are absent from Schott's treatise, apart from a cursory reference to Vitruvius in chap. XVI of Book IV (Schott, 1663, pp. 269–271). This discrepancy reveals the different epistemological positions held by the two authors. Schott still considers his work as an essentially intellectual activity and as definitely distant from the practical problems of technical application. On the other hand, Perrault regards hydrology as strictly connected with the sphere of technique and engineering.

It is in our opinion no coincidence that Schott did not refer to Palissy's work. Indeed Bernard Palissy was not a scholar, but a ceramic artist. His strong commitment to technical investigation is reflected also in the Discours admirable (The admirable discourses), where he imagines a polemical dialogue between the personifications of Theory and Practice (Palissy, 1580; Palissy and LaRoque, 1957). The triumph of the latter signifies the superiority of the “vulgar methods” over the scholastic and speculative approach of the traditional philosophy of nature. Although Perrault argues against Palissy and the common opinion, he agrees with him that practice could teach more than books about nature. However, Palissy's approach still reflects a Renaissance idea of experience, related to craft work, in which an artist craftsman subjectively learns from his experience and on the basis of his own sensibility. By contrast, the Scientific Revolution broke the tie between art and knowledge of nature, the latter deriving from a series of ordered experiences whose objectivity is guaranteed by the repeatability of measurements. Perrault does not only affirm the superiority of experience over authority, but he also performs an experiment and, most importantly, provides an experimental report whose accuracy fits the standards of modern scientific practice. Differently from Palissy, Perrault felt the necessity of submitting concrete and checkable results in order to support his thesis.

The crucial difference with Schott's opus lies, indeed, in the fact that Perrault supports his theses with the report of an experimental activity. In fact, the reference to experience is not absent in the Anatomia but Schott did not perform any experiment first-hand, and his exposition does not have the characteristics of experimental report. In his book, he mentions some observations recently made by Maignan (1653) about the capability of water to rise within a soil column:

Fill, with dry sand, a glass pipe opened on both sides, then cover the lower mouth with a cloth so that the sand cannot pour out; and dip the covered mouth into water only to the depth of a transverse finger: you will observe that water rises a little and all the sand is wetted, up to the height of three palms above the surface of the water [which is] in a vessel. (Schott, 1663, p. 254, our translation)

Schott's description is a faithful and complete report of Maignan's experiments. Perrault took a cue from this description to design his own experiments, but there are important differences between the approaches of the authors. First, it is worth noting that Maignan does not refer to the experiment in chap. 17, which is devoted to water-related issues (De aqua), but rather in chap. 14, which is devoted to a classical Aristotelian topic, that is heaviness and lightness of natural bodies (De corpore naturali gravi et levi). Second, although Schott and Maignan provide these few approximate measures, their perspective is focused on the qualitative behaviour of the water within the sand. Third, the form of their argumentation is still shaped by the model of the scholastic dialectical disputation between conflicting opinions. Even when elements derived from experience are introduced, their remarks are casual and not crucial in order to address the controversies. On the other hand, Perrault designs experiments precisely in order to support his hypotheses and he places the report of the experiments at a turning point of the book, after which the conclusions are thoroughly and quantitatively discussed. With this approach he places himself in the perspective of a novel epistemology which reflects the major aspects of the Scientific Revolution. The exclusion from the discourse of mythical, literary and religious elements, and the attention to practical and technical applications are combined with a quantitative evaluation of the phenomena. All this makes the design of critical experiments possible, i.e. of experiences which can invalidate hypotheses and which can be repeated.

4 Perrault's experiments

After discussing previous authors' opinions (Perrault, 1674, pp. 8–146), Perrault enunciates his idea (Perrault, 1674, pp. 148-150; Fig. 3). According to him water cannot easily infiltrate, flow through the soil and reach great depths, but it is retained in the superficial layers and directly contributes to evaporation and marginally to refilling the surface springs. He contrasts his theses to the aforementioned common opinion (Perrault, 1674, pp. 150–152), according to which water could penetrate the soil until it reaches a layer of terre grasse (translated as “fatty earth” in Perrault and LaRoque, 1967, p. 75) or rocks. This impervious layer would laterally deflect its pathway until it reaches the surface, so as to form a spring. Perrault disputes this view on the basis of two major objections. First, he calls into question the fact that water could actually penetrate the soil to greater depths. Second, he doubts that it could spontaneously outcrop (Perrault, 1678, pp. 153–154). To prove the validity of his objections, Pierre Perrault designed and implemented an experimental activity, the report of which can be found in the subsequent pages (Perrault, 1674, pp. 154–160). He concluded that the water alone has no tendency to deeply penetrate the soil nor to spontaneously outcrop to form springs, thus corroborating his theses (Perrault, 1674, p. 160ff.). These issues were also discussed a few years later by Mariotte, who recognized the importance of the macropores in water percolation, and by Perrault's brother, Charles. In fact in 1690 Charles performed an experiment, together with Philippe de la Hire, during which they buried a clay vessel at a certain depth and connected it with a lead pipe to a cellar, in order to verify the water capability to percolate through the soil (Philip et al., 1989).

Figure 3 Statement of Perrault's opinion (Perrault, 1674, p. 148, credits: Bayerische Staatsbibliothek München, Rar. 4600, sheet 174, urn:nbn:de:bvb:12-bsb10862482-0).

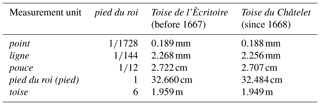
The remaining part of the Origine contains a general discussion of the hydrological cycle, in which Perrault shows some evidence for the fact that about one-sixth of precipitation is sufficient to provide rivers with flowing water (Perrault, 1674, p. 204ff.). Finally he admits that small springs could be affected by precipitation and snow melting, but he points out that the general circulation of water in soil is necessarily supported by a process of evaporation and condensation within the Earth. This model is in line with that described by Descartes and substantially goes back to the Aristotelian solution (see the Introduction for details). Before presenting the repetitions of his experiments, in the following we will briefly summarize what is reported by Perrault. The measurements given by Perrault are converted into the International System according to the Toise de Châtelet system, which entered into force in 1668 (Blamont, 2001; see Table 2).

Table 2 Measurement systems used in 17th-century France (Blamont, 2001).

On p. 154 of the Origine, Perrault (1674) introduces the experimental activity he performed to clarify the two doubts previously mentioned. We reproduce here his note in the English translation:

Before beginning the discussion of these two difficulties, I wish to describe here an experiment I have made, which may shed a little light on what we have to say. (Perrault and LaRoque, 1967, p. 78)

His experience is effectively grouped into four experiments that he performed with a lead pipe, which was filled with various soils and in various imbibition conditions.

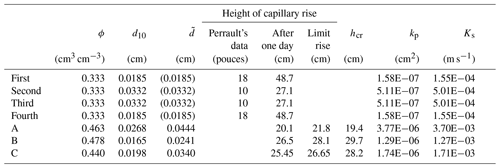
During the first experiment Perrault took a lead pipe, 65 cm long and with a diameter of 4.5 cm. He closed it on one side with a cloth and filled it with river sand, sieved with a coarse sieve. He held the pipe vertically and dipped it into a wide water-filled vessel, leaving it in this position for one day. After 24 h, as he reported, he found that the water rose within the soil up to 48.7 cm. At this point it is not clear how he performed this observation, as elsewhere (at the end of the description of the first experiment) he reports that in order to appreciate how the soil was wetted, he needed to shake the pipe to let the soil slide out. Maybe he reports here a measurement that he performed at the end of the experiment, or he extracted the sand, made the measurement and then filled the pipe again to proceed with new measurements. As a first conclusion he reports that he was surprised at such a rise of the water within the column. Then he wanted to check whether a spring could spontaneously outcrop above the water surface. He therefore made a hole about 5.4 cm above the water surface, with a diameter between 1.6 and 1.8 cm. He added a 5.4 cm long spout that sloped toward the vessel, without touching the water surface. In order to restore the medium continuity between the inside and the outside of the pipe, the spout was covered with grey paper, to show any possible wetting, and with a thin layer of sand. He commented that in the case a spring had onset, then perpetual motion would have been established. On the contrary he only observed that the sand and the paper were wetted, without producing any drop of water. It is worth noting that this case was already recognized by Schott (1663) in his Fig. XI (see Fig. 4 in this paper). According to it a spring might start only if the extreme end of the spout (a cloth, in Schott's example) was below the water surface in the vessel. Afterwards Perrault suspended the pipe over an empty vessel in order to check whether the soil allowed some water to drain, but also in this case no water was collected in half a day's time. Then he added a certain amount of water twice (the amount of water is not specified). The day after the first imbibition he collected three-quarters of the added water, and the day after the second one he collected all the added water. Finally he wanted to evaluate the water content of the soil and shook the pipe in order to let the soil slide out. He thus recognized that the lower part of the soil was thoroughly wetted as “very wet mortar” (Perrault and LaRoque, 1967, p. 79). The second experiment was a repetition of the first with three different soils (details are reported in Table 3). Perrault reports that he made the same observations, yet with different heights of rise (10 pouces≃27.1 cm for the sand with gravel and for the sieved sandstone, and 18 pouces≃48.7 cm for the crumbled loam). Perrault's measurements are reported in Table 4 together with those collected during our repetitions.

Table 3 Perrault's description of the soils used during the first and second experiment.

Table 4 Height of capillary rise and characterization of Perrault's soils (first, second, third, fourth) and of the soils used for the repetitions of the first experiment (A, B, C). ϕ: porosity; d₁₀: characteristic diameter for the Polubarinova-Kochina's relationship; $\stackrel{\mathrm{̃}}{d}$: characteristic diameter for Kozeny and Carman's relationship; h_cr: Polubarinova-Kochina's capillary rise; k_p: Kozeny and Carman's intrinsic permeability; K_s: Kozeny and Carman's hydraulic conductivity at saturation. Perrault's soils are described in Table 3.

Figure 4 Figure XI from Schott's opus Anatomia physico–hydrostatica fontium ac fluminum (Schott, 1663, credits: Bayerische Staatsbibliothek München, Phys.sp. 604 b, sheet 355, urn:nbn:de:bvb:12-bsb10134736-2).

Perrault performed a third experiment to check whether the rainfall water could reach a layer of impervious soil or rock, where it could stop and rise to form a spring. In order to do so, he took the pipe and filled it with dry and sieved loam, compacting it with a rod. He suspended the pipe over an empty vessel and poured many times the amount of water contained in a glass vial, which was filled up to the spout, and which had the same volume as a medium ball of the jeu de paulme (today jeu de paume, palm game; Perrault and LaRoque, 1967, p. 80). The practice of measuring liquid volumes with reference to the balls of the jeu de paulme was quite common in 17th- and 18th-century France. Yet it was not possible to find a reference for the actual dimension of a medium ball of the jeu de paulme in Perrault's era. Therefore in order to repeat the experiment its volume was deduced from the notes reported by Perrault in the description of the third experiment. In fact he slowly poured the water on the soil 3 times without recovering any water at the bottom. Afterwards he added a fourth vial and recovered one-third of its volume. Then the flux stopped for at least 18 h. He added two more vials and collected all their volume. He waited three days and added a seventh vial and collected three-quarters of the volume (he observed that the surface of the soil was drier than before, because some water evaporated). Afterwards he added an eighth one and collected all the added volume. Then he extracted the soil from the pipe and observed that only the lowest 48.7 cm was very wet, so he concluded (a) that the soil may leak the water only if it is thoroughly wetted before, and (b) that in order to do so three plus one-half vials are required. Their volume correspond to the third part of the volume of the wet soil. Even if there is a little incongruence between the data (after the first imbibition three plus two-thirds vials were stored in the soil), this information is valuable because it allows conjecture that the volume of Perrault's vial was about 74 cm³ (Barontini et al., 2013).

In the fourth reported experiment, Perrault aimed at testing whether salty water, rising by capillarity within the soil, maintained its salt content or if it left it in the sand. As in fact spring water is commonly fresh, this was considered a key aspect in understanding the circulation of water within the Earth. Perrault's report is not detailed in this case, but he only notes that, after the water rose in the sand column up to 48.7 cm, the sand was salty both at the top and at the bottom. He guessed that, if the sand at the top was less salty than that at the bottom, it probably meant that the soil was less wet at the top than at the bottom.

About two pages (Perrault, 1674, p. 160–162) are devoted to summarizing the conclusions that Perrault made after the experiments. It is worth noting that the first conclusion starts from the experiment, to give a general epistemological comment on the tendency of the authors to obtain general conclusions from limited observations:

First I know that Magnanus' opinion [Maignan's opinion] is not acceptable, and that it is based on a fact which is only half true: upon which I note in passing that what I have said elsewhere is really correct, that most of those who make experiments on discoveries of which they wish to pass as the Authors, will look at them only in the aspect that serves their ends, as did Magnanus who only wanted to prove the absorption of water by the Earth. (Perrault and LaRoque, 1967, p. 80)

The other conclusions directly refer to the experiment. They may be summarized by saying that once a soil is wet, it tends to retain water and not to give it back, and this is true also when the soil is so wetted that it becomes permeable to water. In that case in fact, as soon as the water addition stops, the percolation rapidly diminishes and in the end the soil still retains the amount it needed to become permeable. Perrault then comes back to the discussion of the two difficulties he found regarding the common opinion (Perrault, 1674, pp. 162–183) and concludes that

After what I have just observed concerning the two difficulties which I have found in the common opinion, I think it must be agreed that the penetration of the Earth by rain water cannot be achieved according to this opinion; and the rains to which it attributes the origin of springs not being enough to produce them, and still less to cause them to flow continually, it is proper to reject this view. (Perrault and LaRoque, 1967, p. 89)

5 Repetition of Perrault's experiments

The great detail of Perrault's experimental report left us with two questions: (a) Are Perrault's experiments really qualitatively and quantitatively repeatable in the laboratory? (b) Is it possible, on the basis of Perrault's data, to infer what the hydrological properties of his soils could be? The questions were addressed both in the laboratory (Berta and Barontini, 2020) and with numerical simulations (Barontini et al., 2013). Some aspects of the numerical simulations will be mentioned in the next section. Here the main laboratory procedures and results will be summarized. The experimental details and data are fully reported by Berta and Barontini (2020).

A polycarbonate pipe of 4.5 cm in diameter, cut to a length of 65 cm, mimicked Perrault's lead pipe. A punched metal plate and a cloth of nonwoven fabric were used to hold the soil and to drain the water when the column was held in a vertical position (Fig. 5). Three quarry sands, commonly used in building works, were chosen to repeat the experiments. In the following the soils will be referred to as A, B and C, according to the order in which they were used for the repetitions. The grain size distribution curves were determined by dry sieving, since the fine soil component was negligible. The soils were classified as coarse-to-medium sand (A, C) and medium-to-fine sand (B). The soils were poorly graded, with a uniformity coefficient $U=d_{\mathrm{60}}/d_{\mathrm{10}}$ of about 2.1 for A and B, and about 2.2 for C (d₆₀ and d₁₀ are the equivalent diameters which retain 40 % and 90 % of the soil weight, respectively). The hydraulic conductivity at soil saturation K_s was difficult to estimate by means of the laboratory falling-head permeameter, because expected values were greater then 10⁻⁵ m s⁻¹. It was therefore estimated by means of Kozeny and Carman's equation (see Eq. A1 in the Appendix). The soil-water retention relationships were measured by means of Richards' pressure plates for pressure values $\mathrm{\Psi }\le -\mathrm{10}\mathrm{kPa}$ (Richards and Fireman, 1943), and by means of a hydrostatic method for $-\mathrm{3}\mathrm{kPa}\le \mathrm{\Psi }\le -\mathrm{1}\mathrm{kPa}$. The couples (w,Ψ), where w is the gravimetric water content, were interpolated by means of Brooks and Corey's retention curve (Eq. A5) and van Genuchten's retention curve (Eq. A6), both with or without the usual constraints (Eq. A7) on m and n. An example of the obtained soil-water retention relationships is represented in Fig. 6 for the medium-to-fine sand (soil B). Values at $\mathrm{\Psi }=-\mathrm{3}\mathrm{kPa}$ were too sparse and were not used for the regressions.

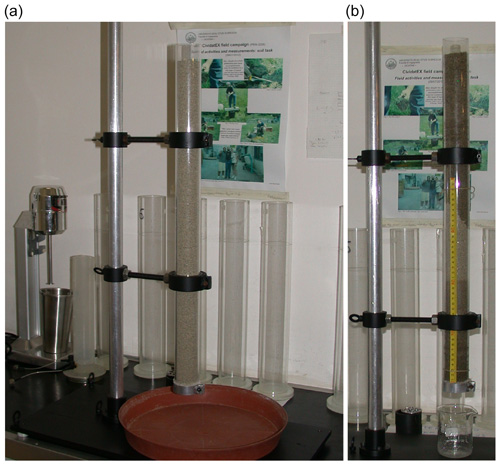
Figure 5 Laboratory setup of the soil column (a) and the soil column during the second part of the first experiment, when the top and the bottom imbibition fronts meet (b).

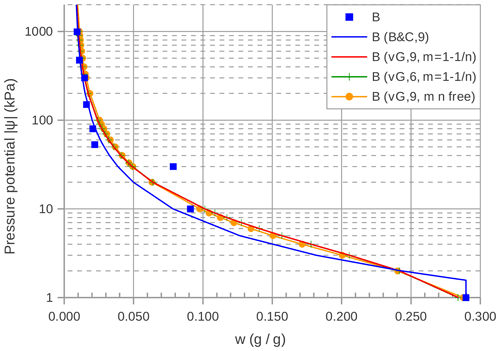
Figure 6 Experimental and interpolated soil-water retention relationships of one of the sandy soils used to repeat Perrault's experiments. B: soil identification; □: experimental data; B&C: Brooks and Corey's curve; vG: van Genuchten's curve; 6 and 9 are the number of experimental points which were used to interpolate the analytical curves.

In Fig. 7 and in Tables 4 and 5 the results of the repetitions of the first experiment are reported. The unitary amount of water poured on the soils was in this case 74 cm³ for all the soils, as determined by Barontini et al. (2013). All the soils showed a qualitative and (to some extent) a quantitative agreement, both during the spontaneous imbibition from the bottom, and during the forced imbibition from the top. In Table 4 the capillary rises, measured after one day, and the upper limit values of the capillary rises are compared both with data reported by Perrault and with the capillary rise h_cr (cm) determined by Polubarinova-Kochina's relationship (Polubarinova-Kochina, 1962):

$$\begin{array}{}\text{(1)}& h_{\mathrm{cr}}={\displaystyle \frac{\mathrm{0.45}}{d_{\mathrm{10}}}}{\displaystyle \frac{\mathrm{1}-\mathit{\varphi }}{\mathit{\varphi }}}.\end{array}$$

In Eq. (1) ϕ is the soil porosity. The good agreement between the measured capillary rise and h_cr allows us to infer that Perrault's soils almost reached their asymptotic capillary rise. Thus, accounting for a porosity ϕ= one-third (because Perrault estimated the amount of water in the soil as one-third of the wetted soil volume) it is possible to estimate the competent characteristic diameter d₁₀ (values are reported in Table 4).

Table 5 Imbibition and percolation volumes measured during the first experiment. Data are reported as the number of vials, in order to make a comparison with Perrault's data. The unitary volume of a vial was estimated to be equal to 74 cm³ for all the soils, according to Barontini et al. (2013).

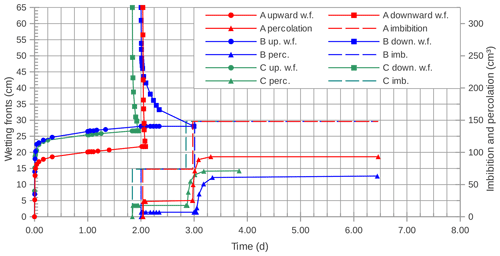
Figure 7 Measures of the position of the water fronts and of the imbibition and percolation volumes collected during the three repetitions of the first experiment. The unitary volume of a vial was estimated to be equal to 74 cm³ for all the soils, according to Barontini et al. (2013). A, B, C: soil identification; ◦: upward moving water front; □: downward moving water front; △: percolation volume; dashed line: imbibition volume.

Characterizing the hydraulic conductivity at soil saturation is less immediate because the information given by Perrault about the percolation times is incomplete. If we consider that (at least) some of Perrault's soils were sieved, in order to remove the coarse fraction, we hypothesize that the characteristic diameter d₁₀, determined by Polubarinova-Kochina's equation (Eq. 1), is an approximation of the equivalent diameter $\stackrel{\mathrm{̃}}{d}$ (Eq. A3) needed to determine K_s by Kozeny and Carman's equation (Eq. A1). Comparing d₁₀ and $\stackrel{\mathrm{̃}}{d}$ as determined for soils A, B and C (Table 4) this conjecture may be considered realistic.

Another interesting comparison between Perrault's experiments and their repetition was done with regard to the amount of water that was added and that percolated. The imbibition and percolation volumes are represented in Table 5. Values are expressed as the number of vials and in this case the volume of a vial was assumed to be equal to 74 cm³. Data are qualitatively in agreement, and although they differ numerically, it emerges that Perrault's data are complete and quantitatively comparable. The same data are presented in Figs. 8 and 9 and in Table 6 for the third experiment. It is worth recalling that in this case the volume of 1 vial was chosen with reference to the capability of the soil to retain water. In fact in his conclusions regarding the experimental activity, Perrault stressed his point of view about the proneness of a soil to allow water to drain. Here he considered that drainage may happen when the soil is wetted with an amount of water which corresponds to one-third of the wetted volume of soil at equilibrium. In the conclusions in fact he states

that in order to wet earth and make it ready for penetration as much water as one third the height and thickness of the earth is necessary. (Perrault and LaRoque, 1967, p. 81)

He stated that this amount of water corresponded, in the investigated case, to three plus one-half vials. Yet the amount of three plus two-thirds vials seems more correct on the basis of Perrault's data. Therefore we estimated the unitary volume V_i of a reference vial, for each soil, by dividing the volume of water stored at equilibrium V_w by three plus two-thirds. The determined unitary volumes are V_i = 31.3, 50.5 and 41.0 cm³ for the soils A, B and C, respectively. Also in this case we observe a good qualitative correspondence between Perrault's experiments and the repetitions, but what is important to stress is the fact that data provided by Perrault allow us to make a robust quantitative comparison.

Table 6 Imbibition and percolation volumes measured during the third experiment. Data are reported as the number of vials, in order to make a comparison with Perrault's data. The unitary volume V_i of a vial was estimated to be equal to V_i= 31.3, 50.5 and 41.0 cm³ for soil A, B and C, respectively, according to the procedure described in Sect. 5.

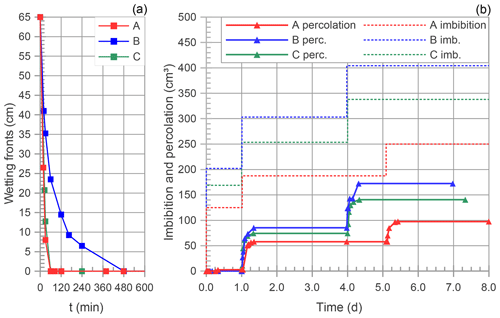
Figure 8 Measures collected during the three repetitions of the third experiment: depth of the imbibition fronts (a) and volumes of imbibition and percolation (b). The unitary volume V_i of a vial was estimated to be equal to V_i= 31.3, 50.5 and 41.0 cm³ for soil A, B and C, respectively, according to the procedure described in Sect. 5. A, B, C: soil identification; □: downward moving water front; △: percolation volume; dashed line: imbibition volume.

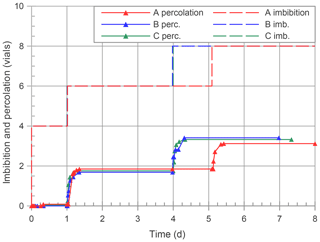
Figure 9 Imbibition and percolation volumes during the three repetitions of the third experiment expressed as the number of vials. The unitary volume V_i of a vial was estimated to be equal to V_i= 31.3, 50.5 and 41.0 cm³ for soil A, B and C, respectively, according to the procedure described in Sect. 5. A, B, C: soil identification; △: percolation volume; dashed line: imbibition volume.

With regard to the repeatability of Perrault's experiments we may therefore conclude that they are almost completely repeatable, in a qualitative sense. If we assume that a quantitative repetition should not be intended to obtain the same results obtained by Perrault, but to define results which may be compared with Perrault's results on a quantitative basis, we may say that Perrault's experiments are also quantitatively repeatable. In fact, the detail with which Perrault describes his experimental activity allows us (a) to clearly identify most of the quantities that he measured, (b) to make realistic conjectures for the quantities about which the Origine is not precise (i.e. the unitary amount of water added with one vial) and (c) to recognize the lack of information (i.e. the time between the beginning of imbibition, the beginning of drainage and the end of drainage). In the next section some conclusions will also be made with regard to the second question posed at the beginning of this section.

6 Didactics of Perrault's experiments

Perrault's opus and experiments can be used in several didactic ways, meeting the objectives of at least the first three elements of the Dublin descriptors, i.e. knowledge and understanding, applying knowledge and understanding, and making judgements (Bologna Working Group on Qualifications Frameworks, 2005). As a general preliminary aspect, comparing the Origine and the different published models of the hydrological cycle induces the students to reflect on the long scientific path, which was taken to move from initial observations and conjectures to the modern description. It also stimulates an exercise of analysis of current understanding (which may be regarded as our modern Opinion Commune) and the exploration of alternative descriptions.

Focusing with more detail on soil hydrology, Perrault's experiments offer a wide range of didactic cases, useful to teach and exemplify many aspects of the subject. As an application of this idea, the experiment was used as an underlying cross-theme of a recently published didactic book (Barontini, 2017). In fact the description given by Perrault of the first and second experiment offers the opportunity to teach the hydrostatics of the soil water, above a groundwater table and above a capillary barrier, and to present capillary fringe and soil-water retention curves. The lack of flow through the soil, as reported in the third experiment, is related to the action of the capillary barrier exerted by the cloth at the bottom of the soil column. It stresses the importance of locally reaching the soil saturation at the soil bottom, before percolation starts, so as to have the continuity of the generalized piezometric potential $\mathrm{\Phi }=\mathrm{\Psi }+z$ (Ψ being the pressure potential and z the elevation). This issue is directly related to Perrault's observation regarding the capability of soil to retain water and the difficulties of infiltrated precipitation to percolate. The field capacity is here defined as the amount of water stored by the soil in practically hydrostatic conditions (see e.g. Romano and Santini, 2002). This definition evidences the dependence of field capacity on soil layering. It may be increased by the presence of coarse layers in the subsoil, which act as capillary barriers. During the experiment, the soil column was suspended and the soil had greater field capacity than if it were in the field, so Perrault was induced to think that precipitation faces great difficulties in percolating toward deep soil layers. During the discussions with students, it might be didactically effective to have them reflect on what would have happened if the length of the soil column was varied, in order to allow understanding of the importance of soil depth and layering on field capacity. The fourth experiment, even if minimally described, also allows the introduction of the hydrostatics of an unsaturated soil with solutes.

The experiments also illustrate the effect of a great variety of boundary conditions. These include the condition of known pressure potential (bottom boundary of the first experiment), of null flux (top boundary of the first experiment) and of seepage (bottom boundary of the third experiment). The condition of known flux at the top boundary does not clearly emerge from the report, because Perrault unfortunately does not say how long the imbibition lasted during the third experiment. This, together with the other incomplete or omitted data, gives the students an opportunity to recognize the completeness or lack of information. Moreover, trying to interpret and understand ancient observations with modern conceptual frameworks makes it challenging to test and apply their new knowledge.

Finally students may face the second question previously introduced, regarding the capability of inferring the hydrological properties of Perrault's soils, on the basis of the data reported. In the previous section the problem of the conductivity at soil saturation was introduced. Now we will focus on the soil-water retention relationships.

If Perrault's soils are regarded to as Δ soils (i.e. soils with a step-wise soil-water retention relationship), the height of capillary rise h_cr also defines the soil-water retention relationship as

$$\begin{array}{}\text{(2)}& \left\{\begin{array}{ll}s=\mathrm{1}& -h_{\mathrm{cr}}\le \mathrm{\Psi }\le \mathrm{0}\\ s=\mathrm{0}& \mathrm{\Psi }<-h_{\mathrm{cr}}\end{array}\right..\end{array}$$

In Eq. (2) s is the effective soil saturation as introduced by Eq. (A4). A delta-shaped soil-water retention relationship may be considered a first approximation of the hydrological characteristics of Perrault's soils, but other soil-water retention curves are compatible with the information provided by Perrault. As an example which is effective for the soil of the first experiment, the hypothesis is introduced that the height of capillary rise of 48.7 cm, observed by Perrault, is between the scale factor Ψ₁ and the inflexion point Ψ_f of van Genuchten's soil-water retention relationship (see Eqs. A6 and A8 for the explanation of the symbols; Barontini et al., 2013). Therefore, one can fix either ϕ< one-third and Ψ₁=48.7 cm, or ϕ< one-third and Ψ_f=48.7 cm. The remaining parameters of the soil-water retention relationships are determined, provided that at equilibrium the volume of water stored in the soil V_w is

$$\begin{array}{}\text{(3)}& V_{\mathrm{w}}=A\underset{\mathrm{0}}{\overset{\mathrm{65}\mathrm{cm}}{\int }}\mathit{\theta }\left(x\right)\mathrm{d}x\equiv \mathrm{3.5}\cdot \mathrm{74}{\mathrm{cm}}^{\mathrm{3}}.\end{array}$$

In Eq. (3) θ is the volumetric soil-water content. An analogous hypothesis may be introduced with respect to Brooks and Corey's bubbling pressure Ψ_b (Barontini, 2017), and in both cases the soil will approximate a Δ soil at increasing n or λ, and consequently at increasing the porosity ϕ. The Δ soil will therefore be the limit case for ϕ= one-third.

In any case both these hypotheses, according to Perrault's epistemological approach, should now be tested with the soils used for the repetitions of Perrault's experiments. The results are reported in Fig. 10, in which the observed capillary rises are plotted together with Polubarinova-Kochina h_cr and with the estimated values of Ψ_b, Ψ₁ and Ψ_f. The hypotheses are not rigorously satisfied, but the capillary rises are comparable with Ψ_b, Ψ₁ and Ψ_f, and this indicates that to some extent the hypotheses may lead to a realistic approximation of Perrault's soil constitutive laws. The results might be better, if the experimental soil-water retention curves were measured with more detail near saturation. Yet what is important for teaching purposes at this point is that the comparison between the hypotheses and the experimental evidence induces the students to critically analyse their modus operandi, and to understand what the strong constraints of the epistemological approach based on the experimental practice are.

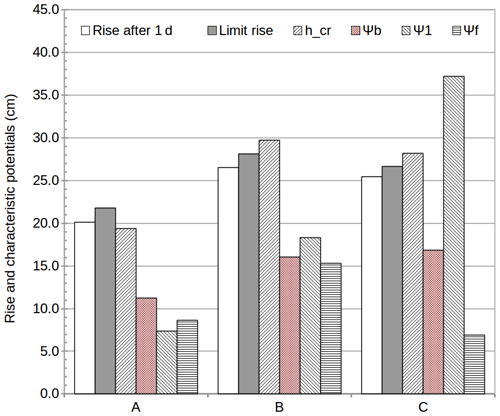
Figure 10 Comparison between the measured height of capillary rise after 1 d, the limit height of capillary rise, the height of capillary rise h_cr estimated by means of the Polubarinova-Kochina formula, and the absolute values of the characteristic potentials Ψ_b, Ψ₁ and Ψ_f for the three soils used to repeat Perrault's experiments.

With regard to the second question posed at the beginning of Sect. 5, we may therefore conclude that (a) it is not possible to define a set of hydrological properties which completely describes one of Perrault's soils, but (b) it is possible to make a set of reasonable hypotheses, which allow a range of realistic values to be defined for the hydrological properties of the described soils.

7 Perrault and the complexity

Perrault's discussion to confute the Opinion Commune (Perrault, 1674, pp. 162–183) is conducted, both by using philosophical conjecture, and by claiming the importance of his experimental activity:

What the earth drinks, this Philosopher [Seneca] says, is little … but I add to this reasoning experiments made daily on this penetration of the earth, (Perrault and LaRoque, 1967, p. 81)

and above all by showing a great attention to field phenomena:

To understand this [the second difficulty with the common opinion] completely, one must picture and discuss in detail, how the penetration of the Earth according to the common opinion can be accomplished. The water that falls on the Earth begins by wetting the parts of the earth or sand nearest to it; then it wets other, more distant parts, then others, always going downward, and wetting the Earth in all its parts one after the other. (Perrault and LaRoque, 1967, p. 86)

This attention permeates all the following pages and makes him move his focus from the laboratory to nature.

Here Perrault, according with his refusal of the principle of authority, challenges his perspective with Aristotle's famous assertion, according to which the total mass flowing from springs or in rivers during one year would be greater than the entire Earth's mass:

The name of its Author, the number of rivers on the Earth and the length of a year, are things that strike the imagination so strongly that it is hard not to be won over to such a likely idea, and such a hard one to argue about. But without being amazed, let us try to consider this objection, and without distrusting our strength overmuch, let us try to find a solution for it. (Perrault and LaRoque, 1967, p. 90)

Discussing Aristotle's statement, Perrault concludes that the total amount of water flowing in the rivers is great, but much less than Aristotle says. In order to reinforce his conjectures, Perrault recognizes the necessity to collect measurements so as to argue more effectively against those who do not agree on the fact that the precipitation volume is greater than the runoff volume:

but as these reasons bear only on the destruction of the opposing opinion, some attempt must be made to give other reasons that might support the one that I maintain and show that rain waters are enough to cause the flow of springs and rivers for a whole year. … I shall try nevertheless by making rough estimates of the volume of rains and of that of the flow of rivers, to give some basis for judgement on the opinion that I uphold, and to arrive at such judgement. (Perrault and LaRoque, 1967, p. 95)

As a first step he clearly establishes the methods of measurement he will employ in his observations:

It is necessary above all to reach an agreement on ways of measuring these two kinds of water. (Perrault and LaRoque, 1967, p. 95)

Then he reports the results of his measurements of the precipitation and runoff made between 1668 and 1671 in the Seine catchment, thus concluding that

only about one-sixth part of the rain and snow water that falls, is therefore needed to cause this river to flow continually for one year. (Perrault and LaRoque, 1967, p. 97)

What is the value given by Perrault to this conclusion? He seems to be aware that the measurements are imprecise and not complete, but in this context, rather than providing exact results, he aims at showing a research path that will lead to the birth of modern hydrology:

I know very well that this deduction has no certainty: but who could give one that would be certain? Nevertheless whatever this one may be, I believe it is more satisfactory than a simple negative like Aristotle's and that of those who maintain, without knowing why, that it does not rain enough to supply the flow of rivers. However that may be, until someone makes more exact observations, by which he proves the contrary of what I have advanced, I shall hold to my view, and be content with the feeble light shed by the observations I have made, being unable to have a stronger one. (Perrault and LaRoque, 1967, p. 97)

The estimation of the water balance led Perrault to recognize that precipitation provides enough water to guarantee the flow in rivers, so he should have admitted that both rivers and springs are caused by rainfall and snowfall. Yet Perrault takes his experiment as a milestone, and he rejects the possibility that precipitation may percolate so deeply that it reaches the impermeable layer and becomes the source of both the groundwater table and the springs. Therefore, in order to explain the origin of springs, with particular reference to the mountain springs, Perrault surprisingly comes back to the undemonstrated theses traditionally rooted within Aristotle's conjectures:

Since I have found the material of springs of the best quality possible, I mean fresh water in plenty, passed through and purified by pure and clean sands and that it remains for me only to raise it to the mouths of springs, I no longer have any difficulty, all Philosophy, ancient and modern, is with me, and is in agreement that that can be done easily and naturally. (Perrault and LaRoque, 1967, p. 108)

After briefly recalling the main theses on this subject as reported by some philosophers, among which there is Aristotle, Seneca, Lydiat and Descartes, Perrault assumes that

all have remained in agreement about this rising of water or of aqueous vapors to the top of mountains; and this consensus, although based on different principles, is a fairly good sign of the truth of this fact. (Perrault and LaRoque, 1967, p. 109)

The fact that Perrault explains the hydrological cycle by going back to the ancient tradition enlightens some intricate features of the Scientific Revolution, which did not proceed straightforwardly, but which was characterized by alternative phases of advancement and uncertainty. Nevertheless, with his attitude of moving from the laboratory to the field, his research based on common methods of measurement, his acceptance of quantitative observations until they are not falsified by other researchers, Perrault demonstrates the spirit of the Scientific Revolution. Moreover he seems to anticipate some themes which are characteristic of the modern epistemology of complexity. We should probably admit that, already in the 17th century, some scientists realized that the nascent paradigm of classical physics, that focused on the perfect repeatability of an experiment, was inadequate to deal with some natural phenomena. Therefore, the birth of modern hydrology reflected not only the emergence of the scientific method, but also a supplementary epistemological reflection on the limits of laboratory experiments, thus going beyond the common image of the Scientific Revolution.

Apart from what is reflected in the Origine, is it possible to find evidence of this supplementary epistemological reflection in Perrault's opus? Perrault's Cartesian appeal to simplicity, practice and common sense appears to clash with epistemological awareness. However, in the Lettre à Mr. Hu[y]guens au sujet des experiences (Letter to Mr. Huygens about experiments, written in 1672 and published as an appendix of the Origine two years later) Perrault demonstrates that he had deeply reflected on the limits of the scientific method (Perrault and LaRoque, 1967, pp. 146–157). In this letter to the great Dutch physicist, Perrault defends two hypotheses which are wrong. Nonetheless, he presents arguments which are not devoid of interest from the epistemological point of view. Huygens warmly (and correctly) invites him to refute the old idea of horror vacui as an explanation for the functioning of pumps and he also advises him to discard attraction and repulsion as valid physical concepts. Perrault answers with claims which raise some questions for the nascent scientific method, as they call into question the risks of a blind faith in the experimental results. The core of Perrault's thesis can be briefly sketched as follows: a deep awareness of the limits of experience is essential to a thoroughly scientific approach, and the result of a single experiment must never lead scientists to undue generalizations of their theses. Hereafter, we resume the main arguments he puts forward to support this claim.

First, according to Perrault, a scientist must never declare himself satisfied with the results of an experiment before he has reached a full agreement between experience and judgement:

For whatever experiments can be performed, one cannot stop there, if judgement and the senses all together do not agree about them: the senses are often mistaken when they act alone, and the judgement is often deceived also sometimes unless the senses set it right. (Perrault and LaRoque, 1967, p. 147)

Senses alone are necessary but not sufficient in order to obtain effective knowledge, and the same applies for judgement. Therefore, it is wrong to consider any experiment definitive, insofar as it leaves open the possibility of both different interpretation and further experience. The second argument concerns the concepts of cause and effect: according to Perrault, in Nature no effect is produced by a single cause, but rather every effect is the consequence of a multiplicity of causes. He also introduces the distinction between internal causes (which are intrinsic to the dynamic of the phenomena) and external causes (which play an accidental role in the determination of the effect):

It is certain that in Nature, no effect is produced by a single cause, and that on the contrary there is none without several causes, some of which are particular to the things on which the effects are produced, and the others are alien to them and come from the outside, and nevertheless take part in the production of their effects. (Perrault and LaRoque, 1967, p. 147)

The third argument calls into question what Perrault calls the “machines”, i.e. all the instruments which are used to measure the phenomena and to assemble the experimental model. While he considers the question of measurement as absolutely crucial for the success of the experiment, Perrault warns that the discrepancy of proportions between a laboratory model and a real natural process could compromise the generalization of experimental results:

It appears that proportion is absolutely necessary in machines to make them yield the effects desired; and it is likewise obvious that general conclusions cannot be drawn from many experiments that are made, and that all that may be learned from them is merely that what they show us, can be done with the machines, the instruments and the materials which we have used; and at the same time to make us fear that in making them with other machines and of other proportions, or with other instruments, other materials and in other circumstances, they might have other results. (Perrault and LaRoque, 1967, p. 149)

Lastly, Perrault recalls that nobody can exclude further explanations of old problems, given the progress of both human mind and technical application, which will probably make new interpretations and experimental models available:

… if these experiments have caused us to doubt so many things about which we were, so it seemed, very sure, they should cause us to doubt even more many things which we now believe are very certain and cause us to fear that some day posterity will give us the same treatment, and laugh at our Philosophy just as we laugh at that of Antiquity. (Perrault and LaRoque, 1967, p. 151)

Perrault's thesis about the horror vacui has been proved to be wrong, but the questions he raises are noteworthy from many points of view. Above all, in the letter there are neither direct references to his experiments reported in the Origine nor to the basin hydrology. However, the letter was written in 1672, just after the three years in which he was collecting data about the water balance of the Seine river, and it was probably written during the composition of the book. If we consider these circumstances, it might be realistic to think that the hydrological studies of the Origine and the epistemological remarks of the letter deeply influenced each other.

What can be inferred by Perrault's remarks? As for the first argument, it is a classical topos of the Scientific Revolution, and thus it does not depart from the 17th century's paradigm. On the contrary, Perrault's emphasis on the multiplicity of causes may be connected to his studies to understand the hydrological cycle. It is important to stress that, according to Perrault, the multiplicity of causes does not represent an objection, but rather a stimulus for scientific enquiry. Furthermore, there is no contradiction between the epistemology of the letter and the scientific practice of the Origine. Indeed in the forethought of the Origine, which is dedicated to Huygens, Perrault states that

What I have said in my letter to Mr. Hu[y]guens, which is at the end of this book, is not to criticize the experiments, as has been said by a few who had already seen this letter: but only to say that there is no certainty to be drawn from the general conclusion of certain experiments, and on that basis to attribute to certain things certain effects rather than to others, and to exclude from them all other causes, known or unknown. (Perrault and LaRoque, 1967, p. 11)

Perrault's awareness of the problem of proportions in the design of the laboratory model is remarkable: he is in fact posing a problem that will be faced a couple of centuries later with the theory of hydraulic and mechanical models, based on dimensional analysis.

More generally, despite his undeniable faith in scientific progress, Perrault is significantly conscious of the risks involved in an acritical and dogmatic acceptance of experimental results. Not only he is aware that scientific results are strictly connected to the opportunities offered by technical progress, but he also admits the possibility of new interpretations of the achieved results. He therefore shows an understanding of science as an indefinitely open and perfectible field of knowledge. Although we can consider him as one of the founders of scientific soil hydrology and one of the progenitors of a modern scientific spirit, Perrault did not consider the experiment as an oracle. On the contrary, he clearly saw the risk of underestimating the complexity of the phenomena and the influence of the instruments on the object of observation. Far from being a naïve empiricist, he rejects the blind faith in experimental results as well as the old appeal to authority. To summarize, the Lettre is not only proof of the individual guile and lucidity of the author, it also demonstrates that the birth of quantitative hydrology implied a deep epistemological reflection on the limits of experiments and laboratory models.

8 Conclusions

Perrault framed his main opus, the Origine, in a novel epistemological approach. This approach embraced the new experimental and Galilean method, rooted in quantitative measurements, integrated with the traditional method, based on qualitative observations and on the discussion of conjectures. In the critical section of his opus he presents, in a few pages, a set of four experiments. With these experiments he intended to test two main difficulties he found in the modern understanding of the hydrological cycle, which at that time was about to be accepted. The difficulties were (a) whether the water may spontaneously rise in the soil and form springs, and (b) whether it may easily percolate through the soil to reach an impervious layer, where a groundwater table will form and the water level will rise to form springs.

The experiments are precisely described and most of the measurements are detailed, so that we are able both to repeat them in the laboratory and to recognize incomplete data and missing information. Perrault's idea was therefore not only to test his conjecture, but also to make his experiments repeatable, and in this sense we may regard them as probably the first modern hydrological experiments. Yet two of his observations misled his interpretation of the hydrological cycle: at first he tried to create a spring above what would have been the groundwater table, then he did not recognize the importance of the capillary barrier in confining the water percolation, and in reducing the consequent recharge of the groundwater. The repetition of the experiments and the discussion about their interpretation provide interesting cases. These are useful in allowing hydrology students to learn about the fundamental aspects of epistemology, and to understand the modern theoretical framework of soil hydrology.

Perrault's misinterpretation of the hydrological cycle also opens up a discussion about some attractive epistemological issues. As a result of his experiments, Perrault goes back to accept the undemonstrated theory, rooted in Aristotelian thought, according to which the hydrological cycle is mainly the effect of an evaporation and condensation process that takes place in the centre of the Earth. This was despite his demonstration for the Seine basin that precipitation greatly exceeded his estimate of river flow. This provides some evidence that the Scientific Revolution was not a straightforward line, but, as a great cultural movement, was articulated in alternative phases of advancement and uncertainty. Then, the problems posed by soil hydrology, even at an early stage, appear irreducible to the classical paradigm of the Scientific Revolution. Even if the experiments designed by Perrault have proven to be repeatable, an in-depth analysis of them shows that the questions posed on the hydrological cycle could not be tested by means of a controlled laboratory model.

Perrault's scientific practice, which was many–sided, confronted him with complex issues, such as the hydrological cycle and the catchment water balance. This objective complexity seems to be reflected in his letter to Huyguens which, although often disregarded, contains remarkable ideas anticipating a modern epistemology. Perrault should therefore be considered not only as an amateur scientist, but also as a refined scholar who worked at a turning point within the developing epistemology of the Scientific Revolution, being aware of its uncertainties and conflicts. In one of his essays, the novelist and literary critic Italo Calvino gave several definitions of what in his opinion is a classic. Among these, the sixth one is “A classic is a book which has never exhausted all it has to say to its readers” (Calvino, 1991, p. 5). In conclusion we may state that Perrault's Origine attractively meets this definition, and many years after its first appearance it still provides intriguing stimuli and suggestions.

Appendix A: Relationships used to characterize soil hydrological properties

A1 Hydraulic conductivity at soil saturation

The hydraulic conductivity K_s at soil saturation was estimated by means of Kozeny and Carman's relationship:

$$\begin{array}{}\text{(A1)}& K_{\mathrm{s}}={\displaystyle \frac{\mathit{\gamma }}{\mathit{\mu }}}{\displaystyle \frac{{\stackrel{\mathrm{̃}}{d}}^{\mathrm{2}}}{\mathrm{180}}}{\displaystyle \frac{{\mathit{\varphi }}^{\mathrm{3}}}{\mathrm{1}-{\mathit{\varphi }}^{\mathrm{2}}}},\end{array}$$

in which γ [M L T⁻² L⁻³] is the water unitary weight, μ [M L⁻¹ T⁻¹] is the dynamic water viscosity, and the term

$$\begin{array}{}\text{(A2)}& k_{\mathrm{p}}={\displaystyle \frac{{\stackrel{\mathrm{̃}}{d}}^{\mathrm{2}}}{\mathrm{180}}}{\displaystyle \frac{{\mathit{\varphi }}^{\mathrm{3}}}{\mathrm{1}-{\mathit{\varphi }}^{\mathrm{2}}}}\end{array}$$

is the intrinsic permeability k_p [L²]. In Eq. (A2) $\stackrel{\mathrm{̃}}{d}$ [L] is a characteristic grain diameter of the soil and ϕ [L³ L⁻³] is the soil porosity. Knowing the grain size distribution curve of the soil, the characteristic diameter $\stackrel{\mathrm{̃}}{d}$ was estimated by means of the weighed harmonic average of the grain size distribution curve diameters d_i:

$$\begin{array}{}\text{(A3)}& \stackrel{\mathrm{̃}}{d}={\displaystyle \frac{\mathrm{1}}{{\sum }_i\left(W_{i+\mathrm{1}}-W_i\right)\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{d_{i+\mathrm{1}}}+\frac{\mathrm{1}}{d_i}\right)}},\end{array}$$

where the weights W_i [M M⁻¹] are the fraction of the soil passing through the sieve with diameter d_i. Therefore $W_{i+\mathrm{1}}-W_i$ is the soil fraction retained by the sieve $d_i<d_{i+\mathrm{1}}$ and ${\sum }_i\left(W_{i+\mathrm{1}}-W_i\right)=\mathrm{1}$.

A2 Soil-water retention relationships

The effective soil saturation s is firstly introduced as

$$\begin{array}{}\text{(A4)}& s={\displaystyle \frac{\mathit{\theta }-{\mathit{\theta }}_{\mathrm{r}}}{{\mathit{\varphi }}_{\mathrm{e}}}},\end{array}$$

in which θ [L³ L⁻³] is the volumetric soil-water content, θ_r [L³ L⁻³] is the residual (volumetric) soil water content, and ${\mathit{\varphi }}_{\mathrm{e}}={\mathit{\theta }}_{\mathrm{s}}-{\mathit{\theta }}_{\mathrm{r}}$ [L³ L⁻³] is the effective porosity, being θ_s [L³ L⁻³] the (volumetric) water content at soil saturation.

Soil-water retention relationships were represented in the forms proposed by Brooks and Corey (1964) and by van Genuchten (1980). Brooks and Corey's relationship is

$$\begin{array}{}\text{(A5)}& s=\left\{\begin{array}{ll}{\left(\frac{\mathrm{\Psi }}{{\mathrm{\Psi }}_{\mathrm{b}}}\right)}^{-\mathit{\lambda }}& \mathrm{\Psi }\le {\mathrm{\Psi }}_{\mathrm{b}}\\ \mathrm{1}& {\mathrm{\Psi }}_{\mathrm{b}}<\mathrm{\Psi }\le \mathrm{0}\end{array}\right.,\end{array}$$

where s is the effective soil saturation; Ψ [M L T⁻² L⁻²] is the soil-water pressure, which may also be expressed in potential form (i.e. with the length dimension, L); Ψ_b is the bubbling pressure (with the same dimension as Ψ), i.e. the minimum value of the pressure potential for which the gaseous phase is discontinuous; and λ is the pore-size distribution index. Generally the greater the value of λ, the greater the soil-grain uniformity is.

Van Genuchten's relationship is

$$\begin{array}{}\text{(A6)}& s={\displaystyle \frac{\mathrm{1}}{{\left[\mathrm{1}+{\left(\frac{\mathrm{\Psi }}{{\mathrm{\Psi }}_{\mathrm{1}}}\right)}^n\right]}^m}},\end{array}$$

where s is again the effective soil saturation, Ψ is the soil-water pressure or pressure potential, Ψ₁ is a scaling factor (with the same dimension as Ψ), and n and m are shape coefficients. According to van Genuchten (1980), in order to analytically integrate Mualem's predictive form for the conductivity of the unsaturated soil, the shape coefficients are constrained by the following relationship:

$$\begin{array}{}\text{(A7)}& m=\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{n}}.\end{array}$$

If m and n are not constrained, the soil-water retention curve (A6) has an inflexion point Ψ_f at

$$\begin{array}{}\text{(A8)}& {\displaystyle \frac{{\mathrm{\Psi }}_{\mathrm{f}}}{{\mathrm{\Psi }}_{\mathrm{1}}}}=\sqrt[n]{{\displaystyle \frac{n-\mathrm{1}}{mn+\mathrm{1}}}}.\end{array}$$

If Eq. (A7) holds, the relationship (Eq. A8) takes the following form:

$$\begin{array}{}\text{(A9)}& {\displaystyle \frac{{\mathrm{\Psi }}_{\mathrm{f}}}{{\mathrm{\Psi }}_{\mathrm{1}}}}=\sqrt[n]{{\displaystyle \frac{n-\mathrm{1}}{n}}}\equiv m^{\frac{\mathrm{1}}{n}}.\end{array}$$