the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Surface water and groundwater: unifying conceptualization and quantification of the two “water worlds”
Brian Berkowitz
While both surface water and groundwater hydrological systems exhibit structural, hydraulic, and chemical heterogeneity and signatures of self-organization, modelling approaches between these two “water world” communities generally remain separate and distinct. To begin to unify these water worlds, we recognize that preferential flows, in a general sense, are a manifestation of self-organization; they hinder perfect mixing within a system, due to a more “energy-efficient” and hence faster throughput of water and matter. We develop this general notion by detailing the role of preferential flow for residence times and chemical transport, as well as for energy conversions and energy dissipation associated with flows of water and mass. Our principal focus is on the role of heterogeneity and preferential flow and transport of water and chemical species. We propose, essentially, that related conceptualizations and quantitative characterizations can be unified in terms of a theory that connects these two water worlds in a dynamic framework. We discuss key features of fluid flow and chemical transport dynamics in these two systems – surface water and groundwater – and then focus on chemical transport, merging treatment of many of these dynamics in a proposed quantitative framework. We then discuss aspects of a unified treatment of surface water and groundwater systems in terms of energy and mass flows, and close with a reflection on complementary manifestations of self-organization in spatial patterns and temporal dynamic behaviour.
- Article
(8343 KB) - Full-text XML
- BibTeX
- EndNote
While surface and subsurface flow and transport of water and chemicals are strongly interrelated, the catchment hydrology (“surface water”) and groundwater communities are split into two “water worlds”. The communities even separate terminology, writing “surface water” as two words but “groundwater” as one word!
At a very general level, it is well recognized that both catchment systems and groundwater systems exhibit enormous structural and functional heterogeneity, which are for example manifested through the emergence of preferential flow and space–time distributions of water, chemicals, sediments, and colloids, and energy across all scales and within or across compartments (soil, aquifers, surface rills and river networks, full catchment systems, and vegetation). Dooge (1986) was among the first hydrologists who distinguished between different types of heterogeneity – namely, between stochastic and organized or structured variability – and reflected upon how these forms affect the predictability of hydrological dynamics. He concluded that most hydrological systems fall into Weinberg's (1975) category of organized complexity – meaning that they are too heterogeneous to allow pure deterministic handling but exhibit too much organization to enable pure statistical treatment.
A common way to define the spatial organization of a physical system is through its distance from the maximum-entropy state (Kondepudi and Prigogine, 1998; Kleidon, 2012). Isolated systems, which do not exchange energy, mass, or entropy with their environment, evolve due to the second law of thermodynamics into a perfectly mixed “dead state” called thermodynamic equilibrium. In such cases, entropy is maximized and Gibbs free energy is minimized, because all gradients have been dissipated by irreversible processes. Hydrological systems are, however, open systems, as they exchange mass (water, chemicals, sediments, colloids), energy, and entropy across their system boundaries with their environment. Hydrological systems may hence persist in a state far from thermodynamic equilibrium. They may even evolve to states of a lower entropy, and thus stronger spatial organization, for instance through the steepening of gradients, in topography for example, or in the emergence of structured variability of system characteristics or network-like structures. Such a development is referred to as “self-organization” (Haken, 1983) because local-scale dissipative interactions, which are irreversible and produce entropy, lead to ordered states or dynamic behaviour at the (macro-)scale of the entire system. Self-organization requires free energy transfer into the system to perform the necessary physical work, self-reinforcement through a positive feedback to assure “growth” of the organized structure or patterns in space, and the export of the entropy which is produced within the local interactions to the environment (Kleidon, 2012).

Figure 1Hillslope-scale rill networks developed during an overland flow event at the Dornbirner Ach in Austria (left panel; we gratefully acknowledge the copyright holder © Ulrike Scherer, KIT) and the South Fork of Walker Creek in California (right panel; we gratefully acknowledge the copyright holder © James Kirchner, ETH Zürich).
Manifestations of self-organization in catchment systems are manifold. The most obvious one is the persistence of smooth topographic gradients (Reinhardt and Ellis, 2015; Kleidon et al., 2012), which reflect the interplay of tectonic uplift and the amount of work water and biota have performed to weather and erode solid materials, to form soils and create flow paths. Although these processes are dissipative and produce entropy, they nevertheless leave signatures of self-organization in catchment systems. These are expressed, for instance, through the soil catena – a largely deterministic arrangement of soil types along the topographic gradient of hillslopes (Milne, 1936; Zehe et al., 2014) – and even more strongly through the formation of rill and river networks (Fig. 1) at the hillslope and catchment scales (Howard, 1990; Paik and Kumar, 2010; Kleidon et al., 2013). These networks form because flow in rills is, in comparison to sheet flow, associated with a larger hydraulic radius, which implies less frictional energy dissipation per unit volume of flow. This causes higher flow rates, which in turn may erode more sediment. As a result, these networks commonly increase the efficiency in transporting water, chemicals, sediments and energy through hydrological systems, which also results in increased kinetic energy transport through the network and across system boundaries.
In contrast, the term self-organization is rarely applied to groundwater systems, except in the context of positive or negative feedbacks during processes of precipitation and dissolution (e.g. Worthington and Ford, 2009). We argue, though, that the subsurface, too, displays some characteristics of (partial) self-organization. This is manifested, in particular, through ubiquitous, spatially correlated, anisotropic patterns of aquifer structural and hydraulic properties, particularly in non-Gaussian systems (Bardossy, 2006), as these have a much smaller entropy compared to spatially uncorrelated patterns. The emergence and persistence of preferential pathways even in homogeneous sand packs (e.g. Hoffman et al., 1996; Oswald et al., 1997; Levy and Berkowitz, 2003) is a striking example of formation of a self-organized pattern of “smooth fluid pressure gradients”.
Our general recognition is that hydrological systems exhibit – below and above ground – both (structural, hydraulic, and chemical) heterogeneity and signatures of (self-)organization. We propose that all kinds of preferential flow paths and flow networks veining the land surface and the subsurface are prime examples of spatial organization (Bejan et al., 2008; Rodriguez-Iturbe and Rinaldo, 2001) because they exhibit, independently of their genesis, similar topological characteristics. Our starting point to unify both water worlds is the recognition that any form of preferential flow is a manifestation of self-organization, because it hinders perfect mixing within a system and implies a more “energy-efficient” and hence faster throughput of water and matter (Rodriguez-Iturbe et al., 1999; Zehe et al., 2010; Kleidon et al., 2013). This general notion can be elaborated further by detailing the role of preferential flow for the transport of mass and chemical species, and related fingerprints in travel distances or travel times, as well as for energy conversion and energy dissipation associated with flows of water.
In terms of models, hydrological modelling (and hydrological theory) attempts to predict how processes described by equations evolve in and interact with a structured heterogeneous domain (i.e. hydrological landscape). However, our key argument that both systems are subject to similar manifestations of self-organization does not imply proposed use of a single model. Rather, we argue that similar conceptualizations and methods of quantification – whether related to preferential flow paths, dynamics and patterning of chemical transport and reactivity, or characterization in terms of energy dissipation and entropy production, for example – can and should be applied to both catchment and groundwater systems, to the benefit of both research communities. The main focus of this contribution is on the role of heterogeneity and preferential flow and transport of water and chemical species. At a general level, we show that preferential flow causes deviations from the maximum-entropy state, though these deviations have different manifestations depending on whether we observe solute transport in space or in time. Based on this insight, we propose, essentially, that related conceptualizations and quantitative characterizations can be unified in terms of a theory that is applicable in catchment and groundwater systems and thus connects these two water worlds.
We first discuss key features of fluid flow and chemical transport dynamics in these two systems – catchments (including surface water) and groundwater – using the (often distinct) terminology of each of these water world research communities. We outline the particular questions, methods, limitations, and uncertainties in each “world” (Sect. 2). We then focus on chemical transport, merging treatment of many of these dynamics in a proposed quantitative framework, providing specific examples (Sect. 3). More specifically, Sect. 3 first defines specific conceptual and quantitative tools and, within this context, introduces a continuous time random walk (CTRW) modelling framework with a clear connection to microscale physics and to the well-known advection–dispersion equation. Section 3 then offers new insights, in terms of contrasting power law and inverse gamma distributions – used in the groundwater literature to describe different travel time distributions that control long tailing in breakthrough curves – as well as gamma distributions used more often in the surface water (catchment system) literature. This analysis is a basis for suggesting how surface water systems (catchment response to chemical transport) can be treated within the CTRW framework. Final conclusions and perspectives appear in Sect. 4. Throughout, we attempt to offer an innovative synthesis of concepts and methods from the generally disparate surface water (catchment hydrology) and groundwater research communities. Each community has developed sophisticated modelling and measurement capabilities – which have led to significant scientific advances over the last two decades – that could benefit the other community and help address outstanding, unsolved problems.
Before proceeding, we emphasize that our use of the term “two water worlds” throughout this paper is intended to highlight the disparate catchment and groundwater communities, and is not used in the specific context of mobile–immobile water in the root zone (McDonnell, 2014), as discussed at the end of Sect. 3.1.
2.1 Governing laws of fluid flow, the momentum balance, and energy dissipation
In both water worlds, a major focus is on travel distances, as well as travel times (residence times) of water, as they provide the main link between water quantity and quality (Hrachowitz et al., 2016). Catchment hydrology also deals with extremes, i.e. floods and droughts, as well as land surface–atmosphere feedbacks, fluvial geomorphology, and eco-hydrology.
From the outset, we recognize that predictions of water dynamics in catchment and aquifer systems require joint treatment of their mass, momentum, and energy balances. Catchment science and modelling has, traditionally, a strong focus on catchment mass and (in part) energy balances, as evaporation and transpiration release energy in the form of latent heat to the atmosphere. The momentum balance is treated in an implicit conceptualized manner, as detailed below. Predictions of fluid flow in groundwater systems rely on the joint treatment of the mass and the stationary momentum balances using Darcy's law, while the energy balance appears at first sight to be of low importance.
Chemical transport and travel times through hydrological systems are, however, strongly related to both the momentum and the energy balances, because they jointly control the spectrum of fluid velocities and the direction of streamlines. The governing equations that characterize water flow velocities along the land surface and in groundwater systems are simplifications of the Navier–Stokes equations (Eq. 1), which describe the momentum balance of the fluid as an interplay of driving forces and hindering frictional forces:
where v (m s−1) is the fluid velocity vector, g (m s−2) the gravitation acceleration vector, ρ (kg m−3) the water density, and η the dynamic viscosity (kg m−1 s−1) of the fluid.
2.1.1 Surface water flow and Manning's law
Overland and channel flow are driven by surface topography, or more precisely, by gravitational potential energy differences. But only minute amounts of these energy differences are converted into kinetic energy of the flow (Loritz et al., 2019), while the rest is dissipated. Surface water flow velocity is often characterized by Manning's law (Eq. 2), a steady-state, one-dimensional approximation of the Navier–Stokes equation that neglects inertial acceleration for the case of turbulent shear stress and thus turbulent energy dissipation. Fluid velocity grows proportionally to the square root of the driving hydraulic head gradient; the latter corresponds to the potential energy of a unit mass of water:
where vsurface (m s−1) is the overland flow velocity vector, R (m) the hydraulic radius defined as the ratio of the wetted cross section Awet (m2) to the wetted perimeter Uwet (m), n is Manning's roughness (m), z (m) is topographical elevation, h (m) is depth of the flow, and Φ (m) is the total hydraulic head.
Moreover, as friction occurs mainly at the contact line between the fluid and the solid, the hydraulic radius R (m) can be used to scale the ratio between driving gravity force and the hindering frictional dissipative force. Kleidon et al. (2013) classified this as a “weak form” of dissipative interaction between fluid and solid. In this context, they showed that overland flow in rills implies, due to the larger hydraulic radius, a smaller dissipative loss per unit volume and thus a higher energy efficiency compared to sheet flow. Along the same line, they showed that flow in a smaller number of wider channels is more efficient than flow in a higher number of narrower channels. Both effects, flow in rills and channelling, lead to a higher fluid velocity, and thus a higher power (kinetic energy flux) through the network. Note that a 10 % faster fluid velocity implies 30 % more power as the latter grows with the cube of the fluid velocity.
2.1.2 Subsurface flow and Darcy's law
Flow through subsurface porous media, on the other hand, is driven by the gradient in total hydraulic head, reflecting differences in gravitational potential, matric potential, and pressure potential energies as described in the respective forms of Darcy's law (Eq. 3). The latter is also a steady-state, one-dimensional approximation of the Navier–Stokes equation neglecting the inertial terms. However, in this case flow is essentially laminar and dissipative frictional losses in the porous medium are so much larger than in open surface flow that kinetic energy can be neglected. When solving Darcy's law (Eq. 3, first line) for the interstitial travel velocities and defining the flow resistance as inverse hydraulic conductivity, one obtains a form of Darcy's law (Eq. 3, second line) which is similar to Manning's law (Eq. 2). The main difference arises from the different dependencies on the hydraulic head gradient, reflecting the turbulent and laminar flow regimes, respectively:
where qvadose and qgw (m s−1) are water flux vectors (filter velocities) in the partially saturated and saturated zones, respectively, vvadose and vgw (m s−1) are the respective interstitial travel velocities, θ and θs are the soil water content (–) and the porosity (–), k(θ) and ks (m s−1) are the partially saturated and saturated hydraulic conductivity, ψ (m) and H (m) denote the capillary pressure and pressure potentials, and Φvadose and Φgw are total hydraulic heads in the partially saturated and saturated zones.
The strikingly high dissipative nature of porous media flow becomes obvious when recalling that the driving matric potential gradients in the vadose zone are often orders of magnitude larger than 1 m m−1. This implies a capillary acceleration term much larger than Earth's gravitational acceleration g (m s−2), yet fluid velocities in the porous matrix are several orders of magnitude smaller than in surface water systems. However, the generally much slower fluid velocity in groundwater systems does not impose a slow hydraulic response time during rainstorms; on the contrary, aquifers may release – almost instantaneously – “older”, pre-event water into a catchment outlet stream. This apparent paradox – often referred to as the “old–new water paradox” (Kirchner, 2003) – is explained by propagation of pressure waves. Shear or compression waves (or waves in general) transport momentum and energy through continua without an associated transport of mass or particles (Everett, 2013; Goldstein, 2013), and group velocity (or “celerity”) is many orders of magnitude larger than the fluid velocity in aquifer systems (McDonnell and Beven, 2014). Today, it is known that depending on landscape setting, antecedent wetness conditions, and the dominant runoff mechanisms, pre-event water fractions in storm runoff can vary from near zero to more than 60 % of storm water, having an isotopic signature different from that of rainfall (Sklash and Farvolden, 1979; Sklash et al., 1996; Blume et al., 2008).
2.1.3 Preferred flow paths as maximum power structures and non-Fickian transport
Flow velocity within subsurface preferential pathways (macropores, pipes, fractures) is known to be much faster than matrix flow (Beven and Germann, 1982, 2013). This is caused not only by the vanishing capillary forces, but also, largely, by the strong reduction in frictional dissipation in macropores compared to flow in the porous matrix. Viscous dissipation in preferential pathways occurs, similar to open channel flow, mainly at the contact line between fluid and solid, i.e. the wetted perimeter of the macropore, which implies – similar to the case of rill and river networks – a larger hydraulic radius and thus a much more energy-efficient flow (Zehe et al., 2010). Darcy's law is hence inappropriate to characterize preferential flow (Germann, 2018). Clearly, rapid localized flow and transport in preferential pathways hinders the transition from imperfectly mixed stochastic advective transport in the near field to well-mixed advective–dispersive transport in the far field. Predictions of solute plumes and travel times in the near field are thus challenging as this requires detailed knowledge of the velocity field, while transport at the well-mixed Fickian limit depends on the average fluid velocity and the dispersion coefficient (Simmons, 1982; Sposito et al., 1986; Bodin, 2015).
Although the revisited laws, interactions, and phenomena are well known, we suggest that an energy-centred point of view yields a unifying perspective to explain why macropore, rill, and river networks are the preferred (preferential) pathways for water flow on land and below. One might hence expect that water flows along the path of maximum power (Howard, 1990; Kleidon et al., 2013), which is the product of the flow velocity times the driving potential difference. The paths of maximum power correspond in the case of constant friction to the path of steepest descent in hydraulic head, while in the case of a constant gradient, it corresponds to the path of minimum flow resistance (Zehe et al., 2010). From the discussion above, we further conclude that catchment hydrology and groundwater hydrology are inseparable. We can separate neither a river from its catchment and its subsurface nor an aquifer from the land surface and the catchment. Both streamflow response to rainfall and groundwater are composed of “waters of different ages”, reflecting the ranges of overland flow, subsurface storm flow, and base-flow contributions with their specific velocities, usually non-Fickian travel time distributions, and chemical signatures.
In the following, we elaborate briefly on the specific model paradigms in catchment and groundwater hydrology with an emphasis on preferential pathways for fluid flow and chemical transport, and on the resulting ubiquitous, anomalous early and late arrivals of chemicals to measurement outlets.
2.2 Catchment hydrology from the water balance to solute transport
2.2.1 The catchment concept and the duality in water balance modelling
Catchment hydrology developed largely as an engineering discipline around traditional tasks of designing and operating reservoirs, flood risk assessment, and water resources management (Sivapalan, 2018). Although the catchment concept is elementary to these tasks, we think it worthwhile to reflect briefly on it here. The watershed boundary delimits a control volume where the streamlines are expected to converge into the river network, and hence ideally the entire set of surface and subsurface runoff components feeds the stream. We can thus characterize the water balance of an ideally closed catchment control volume based on observations of rainfall input and streamflow response (with uncertainty). Even more importantly, the catchment water balance can be solved without an explicit treatment of the momentum balance, because flow lines end up in the stream.
This is a twofold blessing. First, hydrological models can be benchmarked against integral water balance observations. We posit that this unique property of catchments is the reason why integral conceptual hydrological models, which largely ignore the momentum balance, allow successful predictions of streamflow to the catchment outlet (Sivapalan, 2018). As conceptual models directly address processes at the system level without accounting for sub-scale mechanistic reasons, their application is often referred to as “top-down” modelling. The other end of the model spectrum consists of physics-based, spatially distributed models, originally proposed by the blueprint of Freeze and Harlan (1969), which follow a “bottom-up” mechanistic paradigm. These models are thus also referred to as reductionist models. While the pros and cons of top-down conceptual models and bottom-up physics-based models have been discussed extensively, we agree with Hrachowitz and Clark (2017) that they offer complementary merits, as detailed below. As an aside, it is interesting to reflect why conceptual models due not exist in the field of, for example, meteorology. We suggest that this is because atmospheric flows are not governed by organized structures acting similarly to catchments, which implies that the amount of air mass flowing from one location to another cannot be predicted without knowing the flow lines.
2.2.2 Top-down modelling of the catchment water balance
Top-down conceptual hydrological models simulate water storage, redistribution, and release within the catchment system through a combination of non-linear and linear reservoirs, characterized by effective state variables and effective parameters and effective fluxes (Savenije and Hrachowitz, 2017). Due to their mathematical simplicity, conceptual models are straightforward to code. With the advent of combinatorial optimization methods for automated parameter search, and fast computers (Duan et al., 1992; Bárdossy and Singh, 2008; Vrugt and Ter Braak, 2011), these models also became, at first sight, straightforward to apply. Automated, random parameter search led, however, to the discovery of the well-known equifinality problem – namely, that several model structures or parameter sets may reproduce the target data in an acceptable manner (Beven and Binley, 1992), within the calibration and validation period, but these models and parameter sets yield uncertain future predictions (e.g. Wagener and Wheater, 2006). Equifinality and related parameter uncertainty arises from the ill-posed nature of inverse parameter estimation and from parameter interactions in the equations. While the first problem can be tackled using multi-objective and multi-response calibration (e.g. Mertens et al., 2004; Ebel and Loague, 2006; Fenicia et al., 2007), the latter is inherent to the model equations regardless of whether they are conceptual (as shown by Bárdossy, 2007, for the Nash cascade) or physically based (as shown by Klaus and Zehe, 2010, and Zehe et al., 2014, for example).
A well-known shortcoming of conceptual models is that their key parameters cannot be measured directly. This motivated numerous parameter regionalization efforts (He et al., 2011a) to relate conceptual parameters to measurable catchment characteristics, typically broadly available data on soils (including texture), land use, and topography. As a consequence, such functions have been derived successfully, for example, to relate parameters of the soil moisture accounting scheme to soil type and land use (as shown by, for example, Hundecha and Bardossy, 2004; Samaniego and Bardossy, 2006; He et al., 2011b; and Singh et al., 2016) or parameters of the soil moisture accounting of the mHm (Samaniego et al., 2010) to soil textural data. As these relations are landscape-specific, they require a new calibration when moving to new target areas. This is of course possible if high quality discharge data are available. Yet, due to the incompatibility between the corresponding measurement and observations scales, these regionalization functions are not straightforwardly explained using physical reasoning. This is true even if soil moisture accounting from soil physics is used, e.g. the Brooks and Corey (1964) soil water retention curve, as in the case of the mHm model.
A number of early efforts to meaningfully define hydrological response units for regional modelling of hydrological landscapes were reported by Knudsen et al. (1986), Flügel (1995), and Winter (2001), for example. Savenije (2010) and Fencia et al. (2011) significantly improved the link between conceptual models and landscape structure in their flexible model framework. The key idea is to subdivide the landscape into different functional units (plateaus, hillslopes, wetlands, rivers), and to represent each of them by a specific combination of conceptual model components to mimic their dominant runoff generation processes. Landscapes with different dominant runoff generation mechanisms are represented through an appropriate combination of these conceptual “building blocks” (Fenicia et al., 2014; Gao et al., 2014; Wrede et al., 2015) using suitable topographical signatures such as “height above next drainage” (Gharari et al., 2011) to estimate their areal share. This is a clear advantage that facilitates model calibration and reduction of predictive uncertainty.
The strength of integral conceptual models is their ability to provide parsimonious and reliable predictions of streamflow Q (m3 s−1) directly at the catchment outlet. However, it is nevertheless not straightforward to apply these models for predictions of transport of tracers, and more generally chemical species through the catchment into a stream, as elaborated in the following.
2.2.3 Integral approaches to solute transport modelling in catchment hydrology
Predictions of solute transport require information about the spectrum of fluid velocities and travel distances across the various flow paths into the stream (we can usually neglect the travel time within the river network due to the much higher fluid velocities, as argued in Sect. 3.1). Such information can generally be inferred from breakthrough curves of tracers that enter and leave the system through well-defined boundaries, as shown for instance by the early work of Simmons (1982) and Jury and Sposito (1986), using transfer functions to model solute transport through soil columns. The transfer function approach is based on the theory of linear systems. This implies that the outflow concentration (volumetric flux-averaged concentration) Cout (kg m−3) at time t is, in the case of steady-state water flow, the convolution of the solute input time series Cin with the system function G (Green's function):
The transfer function is the system response to a delta function input. Note that Eq. (4) should in general be formulated for the input and output mass flows, which correspond to the input–output concentration multiplied by the input–output volumetric water flows. It is important to note in this context that the average travel time through the system can be calculated from the water flow and length of flow path, as the average travel velocity corresponds to the flow divided by the wetted cross section of the soil column (see Eq. 3). The latter implies that travel time distributions through partially saturated soils are transient and hence constrained by the input time (Jury and Sposito, 1986; Sposito et al., 1986). The well-known fact that the flow velocity field changes continuously with changing soil water content explains why transfer function approaches have been largely put aside in soil physics and solute transport modelling in the partially saturated zone.
In the case of catchments, simulated runoff from conceptual hydrological models cannot, unfortunately, be used to constrain the average transport velocity. This is simply because conceptual models provide, by definition, no information about the wetted cross of the flow path through the catchment, and the latter determines essentially the average fluid velocity v from simulated total runoff Q. The fact that the simple equation Q=vtransportAwet has an infinite solution space, if Awet is unknown, is also a major source of equifinality. This was shown by Klaus and Zehe (2010) and Wienhöfer and Zehe (2014), using a physically based hydrological model to investigate the role of vertical lateral preferential flow paths of hillslope rainfall–runoff response. These authors found that several network configurations matched the observed flow response equally well: some configurations consisted of a small number of larger macropores of higher conductance, while others consisted of a higher number of less conductive macropores. Overall, these configurations yielded the same volumetric water flow, but they performed rather differently with respect to the simulation of solute transport. An even larger challenge for transport modelling through catchments arises from the fact that the distribution of flow path lengths is even more difficult to constrain, compared to a soil column.
Despite these challenges, the tracer hydrology community made considerable progress in understanding catchment transit time distributions and predicting isotope or tracer concentrations in streamflow (Harman, 2015). Initially, stable isotopologues of the water molecule and other tracers gained attention as they allow a separation of the storm hydrograph into pre-event and event water fractions using stable end member mixing (Bonell et al., 1990; Sklash et al., 1996). Today isotopes of the water molecules and water chemistry data are used as a continuous source of information to infer travel time distributions of water through catchments (McGlynn et al., 2002; McGlynn and Seibert, 2003; Weiler et al., 2003; Klaus et al., 2013). Early attempts to predict tracer concentrations in the stream relied on the same kind of transfer functions as outlined in Eq. (4) for soil columns. Hence, they naturally faced the same problems of state and thus time-dependent travel time distributions (Hrachowitz et al., 2013; Klaus et al., 2015; Rodriguez et al., 2018). More recent approaches rely on age-ranked storage as a “state” variable in combination with storage selection (SAS) functions for streamflow and evapotranspiration to infer their respective travel time distributions (Harmann, 2015; Rinaldo et al., 2015). Aged ranked storage needs to be inferred from solving the master equation, i.e. the catchment water balance for each time and each age. This can be done by using either conceptually modelled or observed discharge and evapotranspiration, and it requires a proper selection of the functional form of the SAS functions and optionally their time-dependent weights (Rodriguez and Klaus, 2019). Related studies rely on a single gamma distribution or several gamma distributions (Hrachowitz et al., 2010; Klaus et al., 2015; Rodriguez and Klaus, 2019); others used the beta distribution (van der Velde et al., 2012) or piece-wise linear distributions (Hrachowitz et al., 2013, 2015).
Here we propose that the CTRW framework from the groundwater “world” has much to offer to catchment travel time modelling (as detailed in Sect. 3). We show that, in particular, the inverse gamma distribution may offer a useful alternative that offers the asset of a clear connection to microscale physics and the well-known advection–dispersion equation, which is used in bottom-up modelling (Sect. 2.2.4). In this context, it is interesting to recall that catchments were modelled as time-invariant linear systems for a considerable time, since the unit hydrograph was introduced by Sherman (1932). While the effect of precipitation was calculated using runoff coefficients, the streamflow response was simulated by convoluting effective precipitation with the system function, i.e. the unit hydrograph. The “Nash” cascade of linear reservoirs was a popular means to describe the unit hydrograph in a parametric form, and it is well known that the latter is mathematically equivalent to a gamma distribution (Nash, 1957). As streamflow response of the catchment is affected largely by surface and subsurface preferential pathways, which cause non-Fickian transport, one might hence wonder whether a gamma distribution function is an ideal choice to represent the fingerprint of preferential flow.
2.2.4 Bottom-up modelling of the catchment water balance
The blueprint of a physically based hydrology, introduced by Freeze and Harlan (1969), has found manifold implementations. Physically based models like MikeShe (Refsgaard and Storm, 1995) or CATHY (Camporese et al., 2010) typically rely on the Darcy–Richards equation for soil water dynamics (Eq. 3), the Penman–Monteith equation for soil–vegetation–atmosphere exchange processes, and the Manning's equation for estimating overland and streamflow velocities (Eq. 2).
Each of these approaches is naturally subject to limitations, reflecting our yet imperfect understanding, and suffers from the limited transferability of their related parameters from idealized, homogeneous laboratory conditions to heterogeneous and spatially organized natural systems (Grayson et al., 1992; Gupta et al., 2012). In this context, the Darcy–Richards model has received by far the strongest criticism (Beven and Germann, 2013), simply because the underlying assumption regarding the dominance of capillarity-controlled diffusive flow, under local equilibrium conditions, is largely inappropriate when accounting for preferential flow. The Darcy model is hence incomplete when accounting for infiltration (Germann, 2018) and preferential flow, and several approaches have been proposed to close this gap. These range from (a) the early idea of stochastic convection assuming no mixing at all (Simmons, 1982), to (b) dual-permeability conceptualizations relying on overlapping, exchanging continua (Šimunek et al., 2003), to (c) spatially explicit representations of macropores as connected flow paths (Vogel et al., 2006; Sander and Gerke, 2009; Zehe et al., 2010; Wienhöfer and Zehe, 2014; Loritz et al., 2017), and to (d) pore-network models based on mathematical morphology (Vogel and Roth, 2001). An alternative approach to dealing with preferential flow and transport employs Lagrangian models such as SAMP (Ewen, 1996a, b), MIPs (Davies and Beven, 2012; Davies et al., 2013), and LAST (Zehe and Jackisch, 2016; Jackisch and Zehe, 2018; Sternagel et al., 2019).
Reductionist models are, despite the challenge to represent preferential flow and transport, indispensable tools for scientific learning. They particularly allow the exploration of how distributed patterns and their spatial organization jointly control distributed state dynamics and integral behaviour of hydrological systems (Zehe and Blöschl, 2004). Related studies include the investigation of (a) how changes in agricultural practices affect the streamflow generation in a catchment (Pérez et al., 2011), (b) the role of bedrock topography for runoff generation (Hopp and McDonnell, 2009) at the Panola hillslope and the Colpach catchment (Loritz et al., 2017), and (c) the role of vertical and lateral preferential flow networks on subsurface water flow and solute transport at the hillslope scale (Bishop et al., 2015; Wienhöfer and Zehe; 2014; Klaus and Zehe, 2011, 2010), including the issue of equifinality. Setting up a physically based model, however, requires an enormous amount of highly resolved spatial data, particularly on subsurface characteristics. Such data sets are rare, and the “hunger” for data in such models risks a much higher structural model uncertainty. On the other hand, these models also offer greater opportunities for constraining their structure using multiple data orthogonal to discharge (Ebel and Loague, 2006; Wienhöfer and Zehe, 2014).
Another asset of reductionist models is their thermodynamic consistency, which implies that energy conversions related to flow and storage dynamics of water in the catchment systems are straightforward to calculate (Zehe et al., 2014). This offers the opportunity to test the feasibility of thermodynamic optimality as constraint for parameter inference (Zehe et al., 2013); the latter is rather challenging when using conceptual models (Westhoff and Zehe, 2013; Westhoff et al., 2016). More recent applications demonstrated, in line with this asset, new ways to simplify distributed models without lumping, which allowed the successful simulation of the water balance of a 19 km2 large catchment using a single effective hillslope model (Loritz et al., 2017). The key to this was to respect energy conservation during the aggregation procedure, specifically through derivation of an effective topography that conserved the average distribution of potential energy along the average flow path length to the stream, and through a macro-scale effective soil water retention curve that conserved the relation between the average soil water content and matric potential energy using a set point-scale retention experiments (Jackisch, 2015; Zehe et al., 2019).
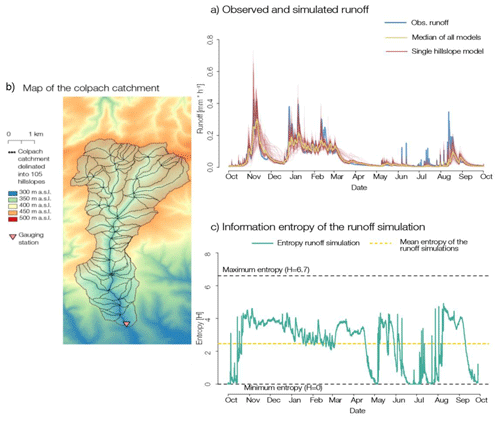
Figure 2(a) Observed and simulated runoff of the Colpach catchment. The red lines correspond to individual hillslope models and the yellow line to the area-weighted median of all hillslopes. (b) Map of the Colpach catchment and the 105 different hillslopes. (c) Shannon entropy in turquoise for the runoff simulations as well as the corresponding mean. © Ralf Loritz, KIT; from Loritz et al. (2018).
Along similar lines, Loritz et al. (2018) showed that simulations using a fully distributed set-up of the same Colpach catchment using 105 different hillslopes yielded strongly redundant contributions of streamflow (Fig. 2). The Shannon entropy (Shannon, 1948, defined in Eq. 6 in Sect. 2.4) was used to quantify the diversity in simulated runoff of the hillslope ensemble at each time step. They found that although the entropy of the ensemble was rather dynamic in time, it never reached the maximum value. Note that an entropy maximum implies that hillslopes contribute in a unique fashion, while a value of zero implies that all hillslopes yield a similar runoff response. They further showed that the fully distributed model, consisting of 105 hillslopes, can be compressed to a model using 6 hillslopes with distinctly different runoff responses, without a loss in simulation performance. Based on these findings, they concluded that spatial organization leads to the emergence of functional similarity at the hillslope scale, as proposed by Zehe et al. (2014). This in turn explains why conceptual models can be reasonably applied, as most of the spatial heterogeneity in the catchment seems to be irrelevant for runoff production. However, this is not the case when it comes to the transport of chemicals, as elaborated in the next section.
In accord with Hrachowitz and Clark (2017), we conclude that top-down and bottom-up models indeed have complementary merits. Moreover, we propose that the applicability of conceptual models at larger scales arises from the fact that spatial organization leads in conjunction with the strongly dissipative nature of hydrological process to the emergence of simplicity at larger scales (Savenije and Hrachowitz, 2017; Loritz et al., 2018).
2.3 Distributed solute transport modelling – the key role of the critical zone
Reductionist physically based models are straightforward to couple with the advection–dispersion equation (compare Eq. 11 in Sect. 3) or particle-tracking schemes to simulate transport of tracers and reactive compounds through the critical zone into groundwater or along the surface and through the subsurface into the stream.
The soil–vegetation–atmosphere–transfer system (SVAT system), or in more recent terms, the “critical” zone, is the mediator between the atmosphere and the two water worlds. This tiny compartment controls the splitting of rainfall into overland flow and infiltration, and the interplay among soil water storage, root water uptake, and groundwater recharge. Soil water and soil air contents control CO2 emissions of forest soils, denitrification, and related trace gas emissions into the atmosphere (Koehler et al., 2010, 2012), as well as biogeochemical transformations of chemical species.
Partly saturated soils may, depending on their initial state and structure, respond with preferential flow and transport of contaminants and nutrients through the most biologically active topsoil buffer (Flury et al., 1994, 1995; Flury, 1996; McGrath et al., 2008, 2010; Klaus et al., 2014). Rapid transport operates within strongly localized preferential pathways such as root channels, cracks, and worm burrows or within connected inter-aggregate pore networks which “bypass” the soil matrix continuum (e.g. Beven and Germann, 1982, 2013; Blume et al., 2009; Wienhöfer et al., 2009). The well-known fingerprint of preferential flow is a “fingered” flow pattern, which is often visualized through dye staining or two-dimensional concentration patterns in vertical soil profiles (Fig. 3). These reveal imperfectly mixed conditions in the near field, which implies that the spatial concentration pattern deviates from the well-mixed Fickian limit over a relatively long time. The latter corresponds in the case of a delta input to a Gaussian distribution of travel distances at a fixed time, where the centre of mass travels with the average transport velocity while the spreading of the concentration grows linearly with time proportionally to the macrodispersion coefficient (Simmons, 1982; Bodin, 2015). Note that according to Trefry et al. (2003) this Gaussian travel distance corresponds to a state of maximum entropy. Preferential flow hence implies a deviation from this well-mixed maximum-entropy state, which cannot be predicted with the advection–dispersion equation (e.g. Roth and Hammel, 1996). A recent study (Sternagel et al., 2019) revealed that even double-domain models such as Hydrus 1D may fail to match the flow fingers and/or long-term concentration tails in tracer profiles. Frequently, the partially saturated region of the subsurface is simply too thin to allow perfectly mixed Gaussian travel distances to be established; hence non-Fickian transport in the critical zone is today regarded as being the rule rather than the exception.

Figure 3Finger flow pattern revealed from standardized dye staining experiments for a transport time of 1 d; images were generously provided by Flury et al. (1994, 1995; © American Geophysical Union 1994, 1995) for Switzerland, Blume et al. (2009, © Theresa Blume) for Chile, Wienhöfer et al. (2009, © Jan Wienhöfer, KIT) for Austria, and Zehe and Flühler (2001, © Erwin Zehe, KIT) and van Schaik et al. (2014, © John Wiley & Sons, Ltd. 2013) for the German Weiherbach.
Because preferential transport leads to strongly localized accumulation of water and chemical species, preferential pathways are potential biogeochemical hotspots. This is particularly the case for biopores such as worm burrows and root channels. Worm burrows provide a high amount of organic carbon and worms “catalyse” microbiological activity due to their enzymatic activity (Bundt et al., 2001; Binet et al., 2006; Bolduan and Zehe, 2006; van Schaik et al., 2014). Similarly, plant roots provide litter and exude carbon substrates to facilitate nutrient uptake. Intense runoff and preferential flow events optionally connect these isolated “hot spots” to lateral subsurface flow paths such as a tile drain network or a pipe network along the bedrock interface and thereby establish “hydrological connectivity” (Tromp-van Meerveld and McDonnell, 2006; Lehmann et al., 2007; Faulkner, 2008). The onset of hydrological connectivity comprises again a “hot moment” as upslope areas and, potentially, the entire catchment start “feeding” the stream with water, nutrients, and contaminants (Wilcke et al., 2001; Goller et al., 2006).
The critical zone, furthermore, crucially controls the Bowen ratio (the partitioning of net radiation energy into sensible and latent heat), and soil water available to plants is a key controlling factor. The residual soil water content is not available for plants, as it is generally stored in fine pores subject to very high capillary forces. Isotopic tracers have been fundamental to unravelling water flow paths in soils, using dual plots (Benettin et al., 2018; Sprenger et al., 2018), and to distinguishing soil water that is recycled to the atmosphere and released as streamflow (Brooks et al., 2010; McDonnell, 2014).
Further to the above points, it is noted that laboratory and numerical studies of multiple cycles of infiltration and drainage of water and chemicals into a porous medium demonstrate clearly the establishment of stable “old” water clusters or pockets, and even a “memory effect” (Kapetas et al., 2014), which remain even with multiple cycles of “new” water infiltration (Gouet-Kaplan and Berkowitz, 2011). These pore-scale studies are in qualitative (and semi-quantitative) agreement with studies at the field scale, which show similar retention behaviour of bromide (introduced during the first infiltration cycle) after multiple infiltration–drainage cycles (Turton et al., 1995; Collins et al., 2000). As a consequence, when each cycle of infiltration contains water with a different chemical signature, stable pockets of water can be established with highly varying chemical composition. We hence emphasize that mobile and immobile waters sustaining evaporation and streamflow – and the chemical species they contain – exist at a continuum of scales from the pore to the field level. Thus, rather than attempting to delineate pockets of less and more mobile water at each scale – separating these pockets at the pore, the column, the metre, the 10 m, and the field and catchment scales – we instead suggest recognizing and delineating an “overall effect” of separation between “old” (immobile) and “new” (mobile) waters at a given “effective” scale of interest, which integrates over all such old and new waters. As we discuss in detail at the end of Sect. 3.1 and thereafter, we argue that it is a more effective approach to consider chemical transport as following distributions of travel distances and residence times, which can then be characterized by various (often power law) probability density functions (PDFs).
2.4 Groundwater systems
As noted in Sect. 1, analysis of groundwater systems has developed largely independently of the investigation of catchment systems, although it, too, developed originally as a large deterministic engineering discipline around the traditional task of water supply for domestic and agricultural use. It was only in the 1980s that “stochastic” (probabilistic and statistical) techniques began to be implemented extensively, to account for the many uncertainties associated with aquifer structure and hydraulic properties that control the flow of groundwater. In parallel, significant interest in (and concern with) water quality and environmental contamination in groundwater systems only entered the research community's consciousness in the 1980s, although some pioneering laboratory experiments and field measurements were initiated from the late 1950s.
It is worth noting, too, that the methods and models applied in groundwater research developed independently and separately from research on catchment systems (Sect. 1). The only partial connection or “integrator” has traditionally been with aquifer connections to the vadose zone (or critical zone, discussed in Sect. 2.3). Another connection between surface water and groundwater systems, though not generally recognized as such, has been analysis of water flow, and to a lesser extent chemical species transport, in the hyporheic zone. The hyporheic zone can be defined as the region of sediment and subsurface porous domain below and adjacent to a streambed, which enables mixing of shallow groundwater and surface water (e.g. Haggerty et al., 2002).
To quantify chemical transport, landmark laboratory experiments (e.g. Aronofsky and Heller, 1957; Scheidegger, 1959) measured the breakthrough of conservative (non-reactive) chemical tracers through columns of sand. These measurements underpinned theoretical developments, also based on concepts of Fickian diffusion, which led to consideration of the classical advection–dispersion equation. Since that time, the advection–dispersion equation – and variants of it – have been used extensively to quantify chemical transport in porous media. However, as thoroughly discussed in Berkowitz et al. (2006), solutions of the advection–dispersion equation have repeatedly demonstrated an inability to properly match the results of extensive series of laboratory experiments, field measurements, and numerical simulations. These findings naturally lead to the conclusion that the conceptual picture underlying the advection–dispersion equation framework is insufficient; as detailed in Sect. 2.2, the soil physics community arrived at a similar conclusion. Stochastic variants of the advection–dispersion equation and the implementation of multiple-continua, advection–dispersion equation formulations (including mobile–immobile models) have been used to provide insights into factors that affect chemical transport – particularly given uncertain knowledge of detailed structural and hydraulic aquifer properties – but they have been largely unable to capture measured behaviour of chemical transport. This observation is largely in line with what we reported for the critical zone.
The first key is to recognize that heterogeneities are present at all scales in groundwater systems, from sub-millimetre pore scales to the scale of an entire aquifer. Indeed, use of the term “heterogeneities” refers to varying distributions of structural properties (e.g. porosity, presence of fractures, and other lithological features), hydraulic properties (e.g. hydraulic conductivity), and – in the case of chemical transport (a general term used here and throughout to denote migration of chemical and/or microbial components) – variations in the biogeochemical properties of the porous domain medium. The second key is to recognize that these variations in distributions, at all scales, deny the possibility of obtaining complete knowledge of the aquifer domain in which fluids and chemical species are transported. A third key, when considering chemical transport (and transport of stable water molecule isotopes), is to recognize that chemical species are subject to several critical transport mechanisms and controls, in addition to advection, that do not affect flow of water – molecular diffusion, dispersion, and reaction (sorption, complexation, transformation) – so that chemical migration through an aquifer is influenced strongly by aquifer heterogeneities and initial or boundary conditions. Extensive analysis of high-resolution experimental measurements and numerical simulations of transport demonstrate that small-scale heterogeneities can significantly affect large-scale behaviour, and that small-scale fluctuations in chemical concentrations do not simply average out and become insignificant at large scales.
As discussed in the preceding sections, preferential pathways are ubiquitous and affect both water and chemical species, resulting from system heterogeneity. To be more specific, (local) hydraulic conductivities vary in space over orders of magnitudes, even within distances of centimetres to metres, and these variations ultimately control patterns of fluid and chemical movement. The resulting patterns of movement in these systems involve highly ramified preferential pathways for water movement and chemical migration. To illustrate these points, consider the hydraulic conductivity (K) and preferential pathway maps shown in Fig. 4a; see Edery et al. (2014) for full details.
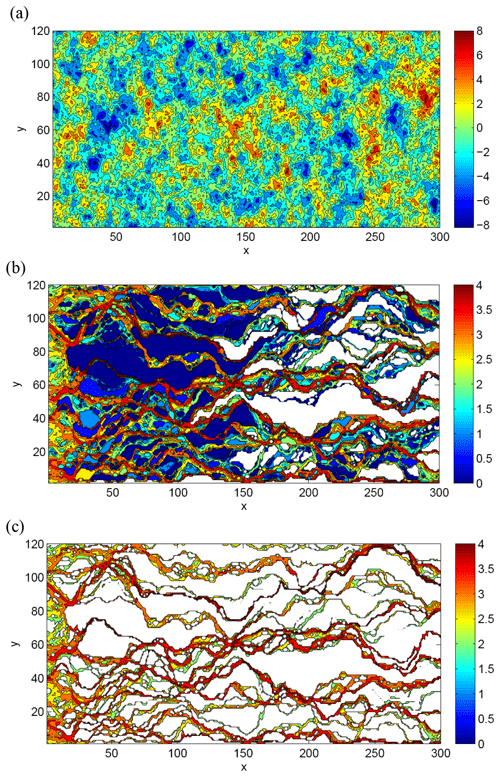
Figure 4(a) Spatial map showing a sample hydraulic conductivity (K) field generated statistically (right side bar shows scale of ln (K)). (b) Spatial map showing particle paths through the domain, for overall hydraulic gradient (water flow) from left to right. “Particles” representing dissolving chemical species are injected along the left vertical boundary and followed through the domain. White regions indicate where no particles “visit” (interrogate) the domain. Blue regions have only a small number of particle visitations. Red regions have significant particle visitations. Note that the colour bar is in log10 number of particles. (c) Spatial map showing preferential particle paths, defined as paths through cells (underlying subdivisions in the domain, each with a different K value as shown in panel a above) that each contain a “visitation” of a minimum of 0.1 % of the total number of particles in the domain. Note that the colour bar is in log10 number of particles (after Edery et al., 2014; © with permission from the American Geophysical Union 2014).
Figure 4a shows a numerically generated, two-dimensional domain measuring 300×120 discretized grid cells of uniform size (0.2 units). The K field shown here was generated as a random realization of a statistically homogeneous, isotropic, Gaussian ln (K) field, with ln (K) variance of σ2=5. Fluid flow through this domain was solved at the Darcy level by assuming constant head boundary conditions on the left and right boundaries, and no-flow horizontal boundaries; the hydraulic head values determined throughout the domain were then converted to local velocities, and thus streamlines. Conservative chemical transport was determined using a standard Lagrangian particle-tracking method, with 105 particles representing the dissolved chemical species. Particles advanced by advection along the streamlines and molecular diffusion (enabling movement between streamlines), to generate breakthrough curves (concentration vs. time) at various distances throughout the domain. Figure 4b shows particle pathways through the domain, wherein the number of particles visiting each cell is represented by colours. The emergence of distinct, limited particle preferential pathways from inlet boundary to outlet boundary is striking. Notably, too, there are significant regions that remain free of particles (the white regions in Fig. 4b), and preferential pathways are confined and converge between low conductivity areas. Even more striking is the set of even sparser preferential pathways shown in Fig. 4c: here, only cells which were visited by at least 0.1 % of all injected particles are shown. In other words, 99.9 % of all chemical species migrating through the domain shown in Fig. 4a advance through a limited number and spatial extent of preferential pathways. It is significant, too, that the preferential pathways comprise a combination of higher conductivity cells in the paths, but also some low conductivity cells, as also reported in Bianchi et al. (2011); see Sect. 3.1 for further discussion of this behaviour.
Thus, it is clear that the groundwater systems incorporate regions of water – distributed throughout the domain – that may have very different chemical signatures, even in close proximity to each other. Moreover, these regions can be relatively stable over time, modified only by the extent of chemical diffusion into and out of the “immobile” regions.
In accordance with our definition of spatial organization in Sect. 1, we propose the use of Shannon entropy H (bits) to quantify the degree of spatial organization in the flow pattern in Fig. 4c. To this end, we define the discrete probability density distribution to find a particle in a grid element, Δyi, at the inlet (x=0) and at the outlet (x=300) of the flow domain, based on the numbers of particles that entered and left the domain through the corresponding grid cells divided the total number of particles that entered and left the domain Nin∕Nout, as follows:
where are probabilities that particle entered and left the domain at Δyi, are the numbers of particles that entered and left the domain at Δyi. Using these probability distributions, we calculate the respective Shannon entropy values as follows:
The Shannon entropy of the uniform input distribution, with 6.9 bits, corresponds to an entropy maximum. Preferential flow reduced this to H=3.58 bits at the outlet, which reflects a release of chemicals that is much more organized in space. Note that a well-mixed advective–dispersive pattern would maximize the entropy at the outlet, as the concentration would be constant along the y coordinate. Considering now arrival times of chemical species at the domain outlet boundary, Fig. 5 shows the relative concentration (C∕Co) vs. time – breakthrough curves – for three degrees of domain heterogeneity (ln (K) variance). (The well-mixed case would maximize the entropy at the outlet, corresponding to a CTRW fit with β=2 in Fig. 5.) It is evident that the chemical transport in this domain displays “non-Fickian” (or “anomalous”) transport, in the sense that late-term (long tail) arrivals are registered at the measurement plane. Furthermore, Fickian-based advection–dispersion equation models clearly fail to quantify such behaviour (Fig. 5). However, Fig. 5 shows solutions – based on the CTRW framework – that do effectively describe the chemical transport. The CTRW framework and governing transport equations are detailed in Sect. 3.3.
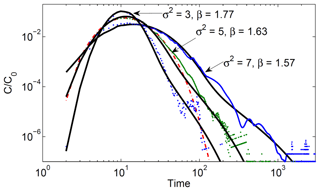
Figure 5Breakthrough curves (points) for three ln (K) variances (σ2=3, 5, 7; 100 realizations each), at the domain outlet (x=300 length units), and corresponding CTRW fits (curves). Also shown is a fit of the advection–dispersion equation (dashed–dotted curve), for σ2=5. See Sect. 3.3 for further discussion and explanation of β. All values are in consistent, arbitrary length and time units (after Edery et al., 2014; © with permission from the American Geophysical Union 2014).
3.1 Conceptual pictures, travel times, and mixtures of water with different chemical signatures
Clearly, any quantitative model of fluid flow and chemical transport in a catchment must first define a conceptual picture. In the context of the discussion in Sects. 2 and 3 that led us to this point, we require a picture that accounts naturally for overland and interacting subsurface flow and transport, recognizing the ubiquity of preferential pathways and broad (and often different) distributions of fluid and chemical travel times. Moreover, any such conceptual picture also requires definition of the available measurement benchmark against which a quantitative model can be compared. In the case of catchments, a common measurement is that of chemical arrival times at a downstream sampling point in a catchment stream that drains and exits the catchment. Thus, the dynamics of fluid flow and chemical transport in a fully three-dimensional (or simplified two-dimensional overland) catchment are often represented by measurements in an effective, spatially averaged one-dimensional system. (Of course, higher resolution, multidimensional (in space) measurements, if available, should also be considered in a quantitative model)
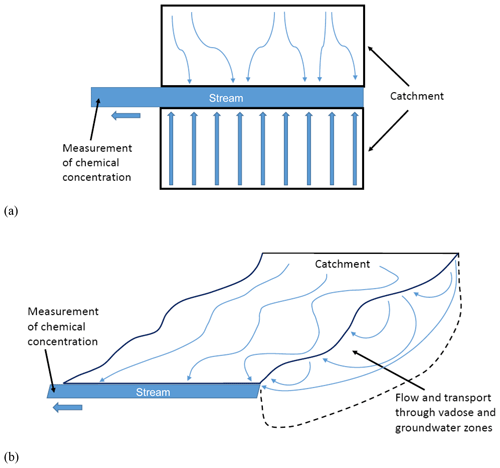
Figure 6Conceptual pictures of water flow and chemical transport in catchments under a pulse of rainfall over the entire catchment. Each curved arrow (or idealized straight arrow) indicates a different path, each of which embodies different travel times through the system until reaching the stream. Note that each preferential pathway carrying water and chemical species may be purely overland or include interactions and advance within soil layers (partially saturated, or vadose, zone) and saturated groundwater systems. (a) Schematic showing idealized 2D catchment area. Arrows through two rectangular regions of catchment indicate a range of preferential pathways carrying water and chemical species. (b) Schematic showing idealized 3D catchment area, under a pulse of rainfall over the entire catchment.
Figure 6a and b show, schematically, 2D and 3D conceptualizations of preferential pathways, with associated varying travel times through the catchment, for both fluid flow and chemical transport. We stress here – and as discussed below in Sect. 3.3 – that the larger-scale, effective (or “characteristic”, or average) fluid velocities and chemical species transport velocities need not be identical. For example, using a conceptual mixing model, Hrachowitz et al. (2015) showed that chloride transport can be slower than water transport. In fact, these two velocities are rarely the same, as a consequence of the ubiquity of preferential pathways for water and migrating chemical species in any surface water and/or soil–aquifer domain. Because of these pathways, regions of higher and lower hydraulic conductivity (fluid and chemical mobility) – and thus the entire system – interrogated by water and chemical species differ. While both water molecules and chemical species are subject to diffusive and dispersive transport mechanisms, in addition to advection, these effects are clearly identifiable for chemical species, while they are undistinguishable for individual water molecules. Thus the effects of diffusion and dispersion on “bulk water” transport, e.g. into and out of low conductivity zones, are invisible and irrelevant, while chemical species retained in these same zones can have a major impact on the overall (and “average”, centre of mass) advance of a chemical plume. These effects are also visible and relevant for isotopes of the water molecule, as deuterium and tritium are subject to self-diffusion in water. The latter implies that isotope concentrations between old and new water pockets in the subsurface might mix diffusively, even when there is no physical mixing between these waters. Hence, the relation between water age and its isotopic decomposition is not straightforward.
The conceptual picture discussed here is our basis for arguing that we should expect to find distributions of travel times and mixtures of water with different chemical signatures at all scales. Moreover, these considerations align well with our reflections in Sect. 2 and key studies in catchment hydrology, which clearly recognize the occurrence of wide distributions of water and chemical travel times, and long-term chemical persistence in water catchment storage (e.g. Niemi, 1977; Botter et al., 2010, 2011; Hrachowitz et al., 2010; McDonnell and Beven, 2014; Kirchner, 2016).
As pointed out in Sect. 2, several studies in recent years have specifically reported the presence of water bodies (or pockets, or regions, depending on scale), with different chemical compositions and isotopic signatures, that are in close proximity or even “overlapping” (in some sense). Some authors use the term “two water worlds” – immobile and mobile – in this context (e.g. McDonnell, 2014) to describe the different sources of water returned to the atmosphere by vegetation transpiration and released to streams; we stress again that our use of the term in this paper highlights the different catchment hydrology and groundwater communities and associated research tools. In light of the discussion in Sect. 2, we stress here that the conceptual picture to explain spatially and temporally varying chemical compositions (in subsurface, soil, sediment, and aquifer systems), and associated uptake by vegetation, is subtle. We question the conceptualization of two (or more) separate, fully compartmentalized mobile and immobile regions of water and chemicals. We argue that mobile and immobile regions are more appropriately considered as overlapping continua or ensemble or effective averages, as those are found at all scales from pores to hundreds of metres (e.g. Turton et al., 1995; Collins et al., 2000; Gouet-Kaplan and Berkowitz, 2011; recall Sect. 2.3). With the occurrence of mixtures of travel times and waters having different chemical signatures at all scales, we argue that it is preferable to think in terms of time, such that there is a range of overlapping temporal (transition time) distributions that each contribute to the overall, large-scale fluid flow and chemical transport. This leads naturally to the CTRW framework.
3.2 Space vs. time: the travel time perspective of transport
It is critical to point out that in the figures shown above in Sect. 2.3 and 2.4, the residence times of water and chemicals are the key factors that determine transport behaviour. This leads to the CTRW framework, which operates more (or at least equally) in terms of time than in terms of space (see Sect. 3.2). To introduce CTRW, in the context of the pathway of “self-organization” shown in Fig. 5c, we demonstrate the importance of thinking in terms of time rather than space. Consider the simple example of driving a distance of 100 km; we consider a scenario in which we travel 50 km at 1 km h−1, and then 50 km at 99 km h−1. The average speed of travel, in terms of space (distance), is determined as follows: given that we travelled 50 km at each of two speeds, the average speed is km h−1. Thus, with this calculation, the total time to travel 100 km “should” be 2 h. However, the actual time taken to travel this distance – 50 km at 1 km h−1, and then 50 km at 99 km h−1 – is 50.5 h. In other words, traditional (but incorrect) conceptual spatial thinking highlights the erroneous effects of focusing only on spatial heterogeneity and quantification based only on spatial characteristics.
In a similar analogy, it is sometimes faster to pass through a bottleneck region (e.g. drive for a short time through a very narrow and slow road) to ultimately reach a fast highway, rather than to travel at medium speed along a road for an entire journey.
Another aspect related to misplaced emphasis on spatial heterogeneities is also noted here. Referring again to the preferential pathways shown in Fig. 4c, it is seen that these pathways actually contain some low hydraulic conductivity (K) regions as well. This can be explained most easily, conceptually, in terms of one-dimensional pathways. Consider a number of high and low K cells in series, [3 3 3 3 3] vs. [6 6 1 6 6], where the effective or average K is given by the harmonic mean. While a [3 3 3 3 3] series may appear to enable a greater volumetric flow rate than a [6 6 1 6 6] series, due to the “bottleneck” low K value in the centre, both series in fact have the same harmonic mean (=3) and conduct fluid equally well.
A similar argument can be applied to analysis of land topography and surface water flow. The “high-resistance” (in principle, but not necessarily), localized small “humps of roughness elements” and surface tension effects – analogous to the low K cells given in the previous paragraph – can be overcome, to allow development of preferential pathways that do not always follow the path of steepest descent in terms of surface topography. There are thus small bypassing effects. Moreover, there is flow and transport from land surface into the subsurface (e.g. hyporheic zone), which also “bypasses” localized small “humps” in the land surface and allows fluid connection and communication further downstream (along a pathway). As a consequence, we argue that it is misleading to place undue focus on the high-resistance (or surface “hump”) bottlenecks; rather, it should be recognized that entire “high K” or “potential” regions for flow are often unsampled or barely sampled by flowing water and chemicals, at least over moderate timescales.
To further expand on the link between spatial and temporal heterogeneity, we point out that the key is to think in space–time and complementary manifestations of heterogeneity of preferential flow. We already showed that a heterogeneous preferential flow pattern implies that chemical species leave the system at distinct locations, which implies a strong reduction in Shannon entropy, as shown in Sect. 2.4 for the example of Edery et al. (2014). When observed at a fixed outlet, these heterogeneous flow patterns translate into signatures of the breakthrough curve. Again, this can be quantified through the corresponding deviations from a Fickian breakthrough curve, which is the maximum-entropy travel time distribution, reflecting well-mixed advective–dispersive transport (Tefry et al., 2003). The overall key messages of Sect. 3 are that (a) CTRW is consistent with the advection–dispersion equation and advances beyond it, particularly in terms of capturing dispersion and tailing effects, and (b) the power law exponent is related to porous media characteristics as well as the flow conditions, although this relation is not unique. Nevertheless, the opportunity arises to at least partly constrain spatial signatures of the subsurface from temporal ones with uncertainty. This non-uniqueness is another manifestation of the inherent equifinality problem when reviewing model concepts in catchment science in Sect. 2.1.
In the next section, we adopt a temporal framework to introduce continuous time random (CTRW) theory, which is the basis of our proposed means to unify quantification of groundwater and surface water transport dynamics.
3.3 Continuous time random walks: theory
Preferential flow leads to non-Fickian (or “anomalous”) travel time distributions, characterized by rapid breakthrough and/or long tailing of chemical species through heterogeneous domains. The CTRW framework is well suited to deal with this in a manner that is consistent with microscale physics, and it steps beyond the advection–dispersion equation approach. This might also offer opportunities to understand SAS from a bottom-up perspective, as age-ranked storage relates to the integral of the travel time distribution across all ages.
Detailed descriptions of CTRW can be found in Berkowitz et al. (2006, 2016), for example. Here, we present only a brief outline of the essential elements. The CTRW framework is based on direct incorporation of the distribution of flow field fluctuations and thus of the fluctuations in concentrations of transported chemicals. As such, the CTRW is a non-local-time approach that can quantify chemical transport over a range of length (and time) scales, and address other processes such as chemical reactions.
From a microscale of view, “particles”, representing dissolved chemical species, are used to treat chemical transport; each particle undergoes spatio-temporal transitions – “transitions (or steps) in a random walk” – that encompass both displacement due to structural heterogeneity and the time taken to make each particle movement. Unlike other approaches, the formulation focuses on retaining the full distribution of transition times. Thus, CTRW defines a probability density function (PDF), ψ(s,t), of a random walk that couples the spatial displacement s and time t of the transition. As shown in Dentz et al. (2008), it is convenient and generally applicable (but not obligatory) to use the decoupled form , where ψ(t) is the probability rate for a transition time t between sites, and p(s) is the probability distribution of the length of the transitions. We stress here that the particle transition time distribution represents the PDF of times for any given particle transition over the distance s, while the travel time distribution – also called a “first passage time distribution” – discussed above and below is the PDF of arrival times (an “overall response”) through a catchment, soil column, or aquifer at a measurement point or plane. A breakthrough curve, representing the concentration of all particles arriving at a control or measurement point (or plane) over time, can then be determined by calculating the average travel (first passage) times of all particles exiting the boundary of the flow domain. Thus, the transition time distribution – however chosen – is the PDF underlying the resulting solution (which can be characterized in terms of the breakthrough curve, as well as travel time, or first passage time, distribution, as well as in terms of spatial profiles and moments) of the governing transport equation; see Sect. 3.4 for further discussion. (Note that, regarding first passage time distributions and breakthrough curves, a subtlety must be kept in mind, namely, that the breakthrough curve is equal to the first passage time distribution if one measures it at an absorbing boundary; “exiting the flow domain” could be represented by an absorbing boundary. Otherwise, the flux-averaged concentration is obtained from the net flux across a boundary; see Simmons (1982) or the Appendix of Dentz et al. (2004). Nevertheless, the analytical expressions for the first passage time distribution and flux concentration are equal under certain boundary conditions.)
The defining transport equation is equivalent to a generalized master equation (GME), which is essentially a mass balance equation in space and time. Using a Taylor expansion, the GME can be transformed into the continuum version (ensemble-averaged system) of the CTRW, in the form of an integro-partial differential equation:
for the normalized concentration c(s,t), where M is a memory function, the transport velocity vψ and the generalized dispersion Dψ are defined in terms of the first and second moments of p(s), and the dyadic symbol : denotes a tensor product. In Laplace space, Eq. (1) becomes
where the memory function , is a characteristic time, with ∼ denoting Laplace space and u denoting the Laplace variable. Note that this continuum formulation contains a non-local-time convolution, in terms of the memory function.
In contrast to the classical advection–dispersion equation (see Eq. 11, below), the “transport velocity,” vψ, is in principle distinct from the “average fluid velocity,” v. This is because chemical transport is “clearly identifiable”, subject to diffusive and dispersive mechanisms (recall the discussion on Fig. 6), so that the effective, overall transport (i.e. a “characteristic” velocity) of chemical may be faster or slower than the average fluid velocity. We point out, moreover, that residence times are a key characterization, as they generally differ for water and chemical species. To illustrate, it is sufficient to recognize that the preferential flow paths themselves are generally stable when the overall hydraulic gradient changes (unless dealing with significant changes or turbulent flow), so that the residence time dictates the relative influence of diffusion and chemical movement into and out of less mobile zones, which ultimately affects breakthrough curves (Berkowitz and Scher, 2009).
It is critical to recognize that the occurrence of “rare events” – even a small proportion of chemical species migrating extremely slowly in some regions, and/or being repeatedly trapped and released from slow regions over a series of spatial transitions – are sufficient to lead to anomalous transport and extremely long “average” chemical transport times (Berkowitz et al., 2016). Thus, it is important to differentiate between “average” (recall Sect. 3.1) and “effective” transport of “most” particles. Indeed, we emphasize, too, that the effects of these “rare events” are deeply significant: they do not simply average out, but rather propagate to larger time and space scales.
With the decoupled form , the transition time distribution, ψ(t), is thus at heart of the CTRW framework, and its form determines the memory function; the role of p(s) on non-Fickian transport is relatively insignificant as long it has a compact (finite) range (Dentz et al., 2008). As discussed in detail (e.g. Berkowitz et al., 2006, 2016), it is expedient to define ψ(t) as a truncated power law (TPL), which enables an evolution to Fickian behaviour:
for , with the normalization constant
and with denoting the incomplete Gamma function (Abramowitz and Stegun, 1970). This functional form of ψ(t) has been particularly successful in interpreting a wide range of laboratory and field observations, as well as numerical simulations. We chose the characteristic time appearing in the memory function to be t1, which represents the onset of the power law region. The truncated power law form of ψ(t) behaves as a power law proportional to for transition times in the range ; ψ(t) decreases exponentially for transition times t>t2. Thus, the TPL enables quantification of non-Fickian transport, with a finite (sufficiently small) t2, and it facilitates (where appropriate) a longer-term, smooth evolution to Fickian transport. We note, too, that the CTRW framework also simplifies (e.g. Berkowitz et al., 2006, 2016) to specialized subsets of non-Fickian transport behaviour embodied within, for example, multirate mass transfer (Haggerty and Gorelick, 1995) and fractional derivative (Zhang et al., 2009) formulations.
It is important to recognize, too, that specification of a pure exponential form for ψ(t), namely , with mean 1∕λ, and/or choice of β>2, reduces the CTRW transport in Eq. (7) to the classical advection–dispersion equation, given in a general form as
where v(s) is the velocity field and D(s) is the dispersion tensor.
It is thus clear that the power law exponent β in ψ(t) characterizes the local disorder of the system and the degree of non-Fickian transport as an integral, temporal fingerprint in the breakthrough curves. This reflects the effect of a strongly localized preferential movement of chemical species on travel times (recall Fig. 4), caused by the pattern of local driving gradients and hydraulic conductivity. Because the particle movement is clearly organized in space, we suggest that this might be seen as self-organization: local disorder is manifested in deviation from advective–dispersive transport, which leads to non-local, organized dynamic behaviour in time at the system scale. This implies that the CTRW framework provides a means to quantify the integral, temporal fingerprint of spatially organized preferential flow through the power law exponent β and the related distance from a Gaussian travel time distribution.
The CTRW transport equation, in partial differential equation form, can be solved in Laplace space (Cortis and Berkowitz, 2005) as well as in real space (Ben-Zvi et al., 2019). One can also solve the transport equation by implementing various particle-tracking formulations. This was done, for example, to obtain the fits to the long-tailed breakthrough curve displayed in Fig. 6. Particle-tracking (PT) approaches offer an efficient numerical tool to treat a variety of chemical transport scenarios (for both conservative and reactive chemical species). They are particularly well suited to accounting for pore-scale to column-scale dynamics. “Particles” (representing chemical mass) advance by sampling transitions in space and time from the associated CTRW distributions. We emphasize that this PT approach can be employed to treat both advection–dispersion equation (Fickian, normal transport) and CTRW (non-Fickian, anomalous transport) formulations, via an appropriate choice of (exponential or power law, respectively) ψ(t).
The efficacy and relevance of the CTRW framework has been demonstrated extensively for subsurface chemical transport (Berkowitz et al., 2006, 2016; Berkowitz and Scher, 2009; and references therein), from pore to aquifer scales, on the basis of extensive numerical simulations, laboratory experiments, and field measurements. The formulation for chemical transport is general and robust over length scales ranging from pore to field, for different flow rates within the same domain, for chemically reactive species, and even for time-dependent velocity fields (Nissan et al., 2017).
To conclude this section and bridge to the discussion that follows in the next section, we point out here that the curved power law form can in some cases be a more useful representation than the truncated power law (TPL) (Eq. 9), as shown by Nissan and Berkowitz (2019). In this case, we write ψ(t) as a curved power law function (Chabrier, 2003):
where , is the normalization constant of the probability density function and Γ is the Gamma function. Here, t∗ (a characteristic time) controls the exponential increase, while β accounts for the power law region. It is important to note that this curved power law is an inverse gamma distribution, with shape parameter β and scale (or rate) parameter t∗. Note that unlike the TPL in Eq. (9), notwithstanding the exponential term in Eq. (12), there is no cut-off time that enables a transition to Fickian transport. These perspectives will be discussed in detail in Sect. 3.4.
3.4 Continuous time random walks: application to surface water systems
In the context of our discussion in Sects. 2 and 3.1, recognizing that dynamics of chemical transport in surface water and groundwater systems are at least phenomenologically and functionally or dynamically similar over enormous spatial and temporal scales, we argue there that simulations and analysis using the CTRW framework are also meaningful and applicable to quantifying the (anomalous) dynamics of chemical transport in surface water systems. In both surface water and groundwater systems, there is always “unresolved heterogeneity” (e.g. hydraulic conductivity, structure) at all scales. Fluid and chemical inputs range from being reasonably well defined to unknown (e.g. in terms of location and extent of a subsurface contamination leak, areal extent, and space–time heterogeneities of rainfall and related stable isotope concentrations), while outputs may also be reasonably well defined to unknown (e.g. arrival times of a chemical species to a monitoring point downstream, such as a stream gauge, near-surface spring, or tile drain outlet). As a consequence, efforts to delineate preferential flow paths and quantify chemical transport must be “adjusted” (or “be appropriate”) to the level of knowledge and spatial–temporal resolution.
More specifically, we note that the preferential pathways shown in Fig. 4b and c are (phenomenologically, at least) similar to those of surface water systems shown in Fig. 1, while the (temporal) breakthrough curves in Fig. 5 are similar to those determined at stream gauges and tile drain outlets. Clearly, in surface water systems, and throughout small, intermediate, and large scales, there are stable regions of “water pockets” (less mobile water) that can be distinguished by strongly varying chemical (ionic, isotopic) compositions. The presence of tributaries leading to rivers in catchments demonstrates clear channelling effects and the establishment of preferential pathways (Sect. 2).
Before discussing chemical transport and considering CTRW applications in the context of surface water systems, we emphasize – as described early in Sect. 3.3 – the interrelationship between transition time distributions, travel time distributions, and breakthrough curves. The transition time distribution, as used particularly in the context of particle-tracking and random walk model formulations, is the underlying (“building block”) characterization of chemical movement in the domain. In other words, the transition time distribution controls the nature of the overall transport. The travel time distribution is obtained as the normalized histogram of the travel times (which can be based on the transition time distribution) over all flow paths, or in other words, the travel time is the sum of the individual transition times and the distribution is obtained by sampling over all travel times. (Note that if one integrates the travel time distribution over all particles entering the system in space and in time, for a step input, one obtains the cumulative breakthrough curve, c vs. t. The relation between flux concentrations, pulse inputs, and breakthrough curves, relative to the first passage time distribution for a homogeneous medium, is discussed in Sect. 3.1 of Dentz and Berkowitz (2003).)
In the context of these three types of quantification of chemical movement, and in light of the consideration of Eqs. (3) and (6) and the analysis to follow below, we stress the fundamental importance of the underlying transition time distribution in quantifying chemical transport through an aquifer or catchment. Common formulations of the governing transport equation, particularly the advection–dispersion equation and many variants thereof, do not include an explicit accounting of the transition or travel time distributions. However, as seen from the discussion of Eq. (11), an underlying exponential transition time distribution in the CTRW transport equation leads to the advection–dispersion equation with a Gaussian breakthrough curve. In sharp contrast, in the case of a power law transition time distribution that scales as , such as given in Eqs. (9) and (12), the resulting breakthrough curve for a point or pulse input also scales as , as a direct consequence of the generalized central limit theorem (e.g. Dentz and Berkowitz, 2003, Eqs. 73 and 82). For a step input, the scaling is t−β, because it can be obtained from the point by integration in time.
CTRW has also been applied in some partially saturated soil–water systems, which further strengthens the connection of CTRW to surface water systems; as discussed in Sects. 2 and 3.1 (Fig. 4a, b), surface water flow and associated chemical transport are not purely overland processes, but involve coupled interactions with the partially saturated (vadose) zone (Sect. 2.3) and groundwater zone (Sect. 2.4).
Indeed, CTRW methods (and subsets) have already been applied in some sense, at least qualitatively, to interpret anomalous transport in various surface water system scenarios. For example, Boano et al. (2007) used CTRW to quantify chemical transport in a stream, accounting for fluid–chemical interactions with the underlying sediment (i.e. the hyporheic zone). Other studies have recorded power law and related multirate rate mass transfer dynamics for chemical transport in stream and catchment systems (e.g. Haggerty et al., 2002; Gooseff et al., 2003). These authors note, in particular, that the hyporheic zone exhibits an enormous range of timescales over which chemical exchange can occur, with significant amounts of chemical species being retained over extremely long times.
However, while full application of CTRW to catchment-scale surface water systems has not been reported to date, there are additional strong indications that it is applicable. We point out two key aspects to support this claim, from the catchment hydrology literature. As discussed in Sect. 2.2.3, previous studies used a gamma distribution to parameterize travel time distributions (e.g. Hrachowitz et al., 2010), while more recent studies use a single gamma distribution or several gamma distributions to characterize storage selection functions of streamflow and evaporation. The gamma distribution, used particularly in connection with arrival times of stable isotopes at a catchment outlet (river outlet, measurement control plane) – i.e. as a travel time distribution – has been applied to describe the superposition of different functions to account for time dependence (e.g. Hrachowitz et al., 2010). Related directly to this point, too, are unit hydrograph analyses that were used in the past to describe runoff concentration and flood routing, through a Nash cascade, which is essentially a gamma distribution, as also discussed in Sect. 2.2.3. We now focus on this aspect in detail.
The gamma distribution is given by
where , or, equivalently (and for comparison to Eq. 12),
where . The gamma distribution describes processes for which the waiting times between Poisson distributed events are important.
In light of Sect. 2, and the discussion of transition and travel time distributions in Sect. 3.3 and above, we consider what underlying transition time distribution leads to a gamma distributed travel time. Given that a sum of gamma distributed random variables can also be gamma distributed, the choice of a gamma distribution for both transition and travel time distributions is convenient.
Indeed, in terms of transition time distributions, let us compare the gamma distribution in the form of Eq. (14) to the inverse gamma distribution as shown in Eq. (12). Aside from the normalization coefficients, the inverse gamma and gamma distributions shown in Eqs. (12) and (14) differ in two fundamental ways – the power law (exponent of t) terms, vs. , and the exponential terms, vs. , respectively. We stress again, as explained in Sect. 3.2, that the inverse gamma distribution is a power law distribution (without an exponential cut-off time to allow transition to Fickian transport), and thus one form of transition time distribution ψ(t) in the CTRW formulation.
We plot in Fig. 7a the truncated power law, curved power law (inverse gamma) and gamma (transition time) distributions, P(t), for the specific parameters β=1.5, t1=1, t2=103, and . We plot in log–log scale to emphasize the long-term portion of the transition time distribution. Figure 7b shows the same curves plotted on a linear scale, to contrast the fact that linear plots (noting the short timescale on the x axis) do not illustrate the long-term contributions, which can have a critical effect on the overall transport behaviour. Clearly, from Fig. 7b, the gamma distribution does not include the possibility of long times; it has an exponential cut-off to Gaussian behaviour at times larger than t∗, as the exponential term dominates the power law term when . However, note that the power law is rather than . The inverse gamma distribution, on the other hand, does not display an exponential cut-off but has the same power law scaling as the TPL.
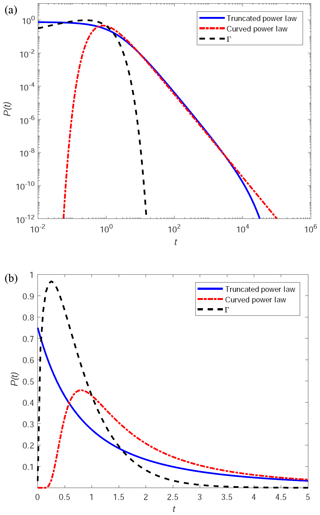
Figure 7Truncated power law, curved power law (inverse gamma distribution) and gamma distribution, for the specific parameters: β=1.5, t1=1, t2=103, . (a) Log–log scale to emphasize the long-term tailing behaviour. (b) Linear scale.
We thus conclude (recall also the conceptual picture and discussion in Sect. 3.1) that although there is no universally “right” or “wrong” choice, the gamma (transition time) distribution does not generally appear as a suitable “candidate” to quantify chemical transport in surface water systems, notwithstanding its empirical use in the literature. We suggest that the CTRW framework (Sect. 3.3) rests on a more physically justified conceptual picture and corresponding coherent and robust mathematical formulation; other such frameworks and transition time distributions can of course also be considered, if justified physically. The choice of a truncated power law or inverse gamma (transition time) distribution is largely a function of scale. The inverse gamma distribution may better suit pore-scale (microscale) domains, where the peak of the function is important, and where ergodicity is not relevant (the cut-off is not needed). Using the truncated power law is “more” general and better suits a variety of larger-scale problems.
We now consider a specific example that demonstrates the relevance and applicability of the CTRW framework for chemical transport in surface water systems, keeping the above arguments in mind. Referring to the 2D case shown in Fig. 6a, we consider the effective (travel time distribution) response, h(t), to a rainfall pulse containing a chemical species over the entire area of a catchment. Every point over this area may be considered a source of chemical species (“tracer”). A stream running through the catchment acts as a line sink (collector) for the tracer. This catchment picture can be idealized as two rectangles straddling this stream sink (Fig. 6a). Measurements of tracer arrivals at a control point downstream of this stream (known as an “absorbing boundary”) yield a tracer arrival “counting rate” that is a breakthrough curve.
The first-passage time distribution F(ls,t) defines the travel time distribution from a (pulse) source at the origin l to the point ls. Then the chemical tracer or species concentration at position ls and time t, cs(ls,t) is given by
where cR(l,t) is the chemical input from rainfall at a position l in a catchment of area Ω. Referring then to Fig. 6a, because we sample chemical arrivals downstream, we can consider the sampling position as an “instantaneous” integration of all chemical species or tracer arrivals from the catchment pathways along the entire length of the stream. Travel time within the stream can generally be assumed to be negligible, relative to the catchment travel times, as stream velocities are generally much faster than combined overland or subsurface flows. We thus determine the total chemical flux into the stream by integrating over all chemical inputs in the catchment that reach the stream; this defines overall first-passage time distributions at the downstream measurement point. Assuming that all of the sampling positions in ls are small regions compared to Ω, then . For uniform rainfall distribution over Ω, we have , and we can hence define for the effective, overall response (travel time distribution)
Long-term measurements of chloride tracer concentrations cR(t) in the rainfall over a catchment area in Plynlimon, Wales, were compared to the time series of the chloride tracer concentration cs(t) in the catchment of the Hafren stream (Kirchner et al., 2000). These authors related the input and output concentrations through the convolution integral
Using a spectral analysis, Kirchner et al. (2000) concluded that overall chloride transport in the catchment scaled as , with m≈0.5, over a time period from 0.01 to 10 years. They reported similar scaling in North American and Scandinavian field sites with m≈ 0.4–0.65.
Kirchner et al. (2000) continued their analysis by noting (i) that an exponential travel time distribution (which is implicit in the advection–dispersion equation; see discussion above Eq. 11) does not match the data, and (ii) that conceptualization of the entire catchment as a single flow path, and use of the advection–dispersion equation to describe travel times, do not correctly match even the basic character of the chloride concentration arrivals. The authors concluded that catchment travel time distributions should be quantified as an approximate power law distribution, to correctly account for long-term chemical retention and release in catchments, and defined h(t) as a gamma distribution (recall Eq. 14). It should be recognized that the choice of a gamma distribution is empirical, and other functions can generate similar behaviour in the spectral (Laplace or Fourier) domain. Significantly, the slope identified by Kirchner et al. (2000) reflects high frequencies, i.e. short timescales; several decades of tracer data to validate the power spectrum at low frequencies were not available.
Scher et al. (2002) reanalysed this catchment system behaviour with the CTRW framework, arguing that subsurface flow and transport are dominant factors controlling the overall chemical species arrival to the stream outlet measurement point. Based on Eqs. (15) and (16), they first (re)examined the solution of the one-dimensional advection–dispersion equation; they confirmed that the temporal dependence of h(t) does not represent the field measurements (similar to Kirchner et al., 2000). Significantly, though, they employed a pure power law form of the transition time distribution, , and developed Eqs. (15) and (16) – based on the seminal analysis of Scher and Montroll (1975) – to obtain
The turnover time t∗ between these two slopes arises naturally as an outcome of chemical transport in the system embodied in Eq. (16). The smaller times represent chemical inputs following along fastest flow paths to the sampling point; for , all chemical inputs over the entire catchment area are contributing particles to the sampling point, as accounted for in Eq. (17). In this latter case, the power law represents the overall particle movement in the domain, but especially the effects of the slow particles (longer transition times and influence of less mobile zones) and the longer travel distances.
In the context of the Hafren stream system, the turnover time t∗ was estimated as about 10 years (Scher et al., 2002), in agreement with the findings and measurement range of Kirchner et al. (2000), with β=0.5. Figure 8 shows a representative plot of Eq. (18) for this system. As noted in Scher et al. (2002), measurements have not yet been analysed to confirm the turnover to the longer-term scaling behaviour, which is indicative of extremely long retention times. Note that high-resolution measurements of low concentration levels in water are generally required to analyse these longer-term tails. The key recognition here is that while the effective catchment response may potentially, initially (i.e, at relatively short times), be represented by a type of gamma distribution (i.e. a power law , ignoring the exponential cut-off) at sufficiently small times (<10 years in the case of the Hafren catchment) – and this is embodied in the CTRW framework as seen in Eq. (18) – full (CTRW framework) power law behaviour (i.e. ) over longer times should also be incorporated to describe expected long-term catchment retention behaviour. An evolution to Fickian transport, via an exponential cut-off after very long times, can also be included (if relevant). To conclude, while direct, quantitative application of CTRW to analysis of chemical transport at the catchment scale remains to be done, it appears – on the basis of the conceptual pictures, extensive application to subsurface systems, and direct similarities to catchment systems, as well as the robust and general nature of the CTRW formulation – to be a highly promising avenue for future research.
4.1 Preferential flow and non-Fickian travel times: the spatial and the temporal manifestation of organized complexity
Based on Sects. 2 and 3, we can state that (a) preferential flow and related non-Fickian transport is an omnipresent, unifying element between both water worlds, and (b) the CTRW framework can effectively quantify and predict non-Fickian transport of water and chemicals species in a manner that connects to and clearly steps beyond the advection–dispersion paradigm. In this section, we link these insights to our central proposition that preferential flow is a prime manifestation of how a local-scale heterogeneous flow process causes a macro-scale organized flow pattern in space. The key is to acknowledge that organization manifests also through organized dynamic behaviour in time, which occurs through non-Fickian travel time distributions of water and chemical species. Note that the degree of organization in space manifests in the deviation of spatial patterns of system characteristics or fluid flow from the maximum-entropy pattern. The latter corresponds, in the case that the mean value is known, to a uniform distribution of system characteristics and/or a uniform flow pattern. Along the same lines, we propose that the degree of organization in dynamic behaviour in time manifests through the deviation of the breakthrough curve from the case of a well-mixed Gaussian system, which is quantified within the CTRW framework based on the power law exponent. A power law exponent ≥2 corresponds well to a mixed travel time distribution. The latter reflects a spatial concentration equal to a Gaussian, which maximizes entropy when the mean and the variance are known (Trefry et al., 2003).
In terms of how power law transition distributions are linked to the formation, evolution, and function of preferential flow paths in surface water systems, and how and if they can be expected to improve the representation thereof in models, we first emphasize that power law transition time distributions are linked to the function of preferential flow paths, but not to their formation and evolution. It is clear and well known that preferential flow implies non-Fickian residence times or travel distance. But what has not been recognized is that the fingerprint of preferential flow in the overall travel time distribution can be captured by a (truncated) power law for the transition time distribution, and through the related exponent we can quantify the deviation from the well-mixed Fickian case. As discussed in Sect. 2.4, the findings of Edery et al. (2014) suggest a further connection between the characteristics of an aquifer and the power law exponent in breakthrough curves. This implies that the fitted parameters are a macro-scale fingerprint of spatial media characteristics that determine the temporal arrival of chemical species. While we do not expect that this relation is unique, it does imply that “fitted” parameters have a physical meaning that can be used to constrain characteristics of the domain (i.e. the hydrological landscape mentioned above) in a spatially distributed model.
We argue that this should also hold for other complex media characteristics that relate to their spatial organization, such as the correlation length or topology of preferential flow paths. We therefore suggest that these insights offer opportunities to relate signatures of spatial organization in flow patterns to signatures of temporal organization in breakthrough curves. For both perspectives, we can quantify organization using information entropy, as we showed in Sect. 2.4. These arguments might also offer, ultimately, opportunities to test whether hydrological systems and their preferential flow networks co-evolve towards more energy-efficient drainage, which can also be quantified (Kleidon et al., 2013; Zehe et al., 2019; Savenije and Hrachowitz, 2017). We leave a more detailed reflection on this for future studies.
4.2 Overall conclusions and perspectives
In an effort to integrate and unify conceptualization and quantitative modelling of the two water worlds – surface water and groundwater systems – we recognize preferential fluid flows as a unifying element and consider them as a manifestation of self-organization. Preferential flows hinder perfect mixing within a system, due to a more “energy-efficient” and hence faster throughput of water, which affects residence times of water, matter, and chemical species in hydrological systems across all scales. While our main focus here is on the role of preferential flow for residence times and chemical transport, we relate our proposed unifying concept to the role of preferential flow in energy conversions and energy dissipation associated with flows of water and mass.
Essentially, we have proposed that related conceptualizations on the role of heterogeneity and preferential fluid flow for chemical species transport, and its quantitative characterization, can be unified in terms of a theory, based on the CTRW framework, that connects these two water worlds in a dynamic framework. We emphasize the occurrence of power law behaviour that characterize travel times of chemical species and highlight the critical role played by system heterogeneity and chemical species residence times, which are distinct from travel times of water. In particular, we compare and contrast specific power law distributions and argue that the closely related inverse gamma and algebraic power law distributions are more appropriate than the oft-used gamma distribution to quantify chemical species transport.
Moreover, we identify deviations from well-mixed Gaussian transport as a manifestation of self-organized dynamic behaviour in time, and the power law exponent as a suitable means to measure the strength of this deviation. Along a complementary line, we propose that self-organization in space is immanent primarily through strongly localized preferential flow through rill and river networks at the land surface. We relate the degree of spatial organization to the deviation of the flow pattern from spatially homogeneous flow, which is a state of maximum entropy. In this context, we reflect on the ongoing controversial discussion regarding whether or not self-organization in open hydrological systems leads to evolution to a more energy-efficient or even thermodynamic optimal system configuration. Finally, we propose that our concept of temporally organized travel times can help to test the possible emergence of thermodynamic optimality. Complementary to this idea, we suggest that an energetic perspective of chemical species transport may help to explain the organization of travel paths (Fig. 4), in the sense that contrary to common assumptions, preferential pathways often include “bottlenecks” of low hydraulic conductivity. A testable option could be that chemical species travel along the path of maximum power, with power being defined in this case as the flow of chemical energy (rather than the flow of kinetic energy) through the system.
Overall, we conclude that self-organization arises equally in surface water and groundwater systems, as local heterogeneity and disorder in fluid flow and chemical transport processes lead to ordered behaviour at the macro-scale. Naturally, the surface water community has developed a strong emphasis on the localized spatial fingerprints, because rills and rivers are clearly visible on land (Fig. 1), while the groundwater community has focused more naturally on non-local temporal fingerprints, as the flow paths are largely unobservable. But these are just two sides of the same conceptual coin of organized complexity (Dooge, 1986).
The data reviewed in this study are available from the respective source publications and authors.
The entire study was developed in close cooperation and nearly equal contribution of both authors. BB had the main idea to propose this unifying concept and provided the CTRW perspective, and EZ provided the energy and entropy perspective.
The authors declare that they have no conflict of interest.
The authors thank Markus Hrachowitz, Nicolas Rodriguez, Matthias Sprenger, and an anonymous referee for particularly constructive reviews of this work. Brian Berkowitz thanks Harvey Scher for in-depth discussions. Brian Berkowitz holds the Sam Zuckerberg Professorial Chair in Hydrology. Erwin Zehe gratefully acknowledges intellectual support by the “Catchments as Organized Systems” (CAOS) research unit. The authors acknowledge support by Deutsche Forschungsgemeinschaft and the Open Access Publishing Fund of Karlsruhe Institute of Technology (KIT).
This research has been supported by the Israel Water Authority (grant no 45015199895), the Israel Science Foundation (grant no. 485/16), and the German Research Foundation, DFG (grant nos. FOR 1598, ZE 533/11-1, ZE 533/12-1).
The article processing charges for this open-access
publication were covered by a Research
Centre of the Helmholtz Association.
This paper was edited by Hubert H. G. Savenije and reviewed by Markus Hrachowitz and one anonymous referee.
Abramowitz, M. and Stegun, I.: Handbook of Mathematical Functions, Dover, Mineola, NY, USA, 1970.
Aronofsky, J. S. and Heller, J. P.: A diffusion model to explain mixing of flowing miscible fluids in porous media, T. Am. I. Min. Met. Eng., 210, 345–349, 1957.
Bardossy, A.: Copula-based geostatistical models for groundwater quality parameters, Water Resour. Res., 42, W11416, https://doi.org/10.1029/2005wr004754, 2006.
Bárdossy, A.: Calibration of hydrological model parameters for ungauged catchments, Hydrol. Earth Syst. Sci., 11, 703–710, https://doi.org/10.5194/hess-11-703-2007, 2007.
Bárdossy, A. and Singh, S. K.: Robust estimation of hydrological model parameters, Hydrol. Earth Syst. Sci., 12, 1273–1283, https://doi.org/10.5194/hess-12-1273-2008, 2008.
Bejan, A., Lorente, S., and Lee, J.: Unifying constructal theory of tree roots, canopies and forests, J. Theor. Biol., 254, 529–540, https://doi.org/10.1016/j.jtbi.2008.06.026, 2008.
Benettin, P., Volkmann, T. H. M., von Freyberg, J., Frentress, J., Penna, D., Dawson, T. E., and Kirchner, J. W.: Effects of climatic seasonality on the isotopic composition of evaporating soil waters, Hydrol. Earth Syst. Sci., 22, 2881–2890, https://doi.org/10.5194/hess-22-2881-2018, 2018.
Ben-Zvi, R., Jiang, S., Scher, H., and Berkowitz, B.: Finite-Element Method solution of non-Fickian transport in porous media: The CTRW-FEM package, Groundwater, 57, 479–484, https://doi.org/10.1111/gwat.12813, 2019.
Berkowitz, B. and Scher, H.: Exploring the nature of non-Fickian transport in laboratory experiments, Adv. Water Resour., 32, 750–755, https://doi.org/10.1016/j.advwatres.2008.05.004, 2009.
Berkowitz, B., Cortis, A., Dentz, M., and Scher, H.: Modeling non-Fickian transport in geological formations as a continuous time random walk, Rev. Geophys., 44, RG2003, https://doi.org/10.1029/2005RG000178, 2006.
Berkowitz, B., Dror, I., Hansen, S. K., and Scher, H.: Measurements and models of reactive transport in geological media, Rev. Geophys., 54, 930–986, https://doi.org/10.1002/2016RG000524, 2016.
Beven, K. and Binley, A.: The future of distributed models: Model calibration and uncertainty prediction, Hydrol. Process., 6, 265–277, https://doi.org/10.1002/hyp.3360060305, 1992.
Beven, K. and Germann, P.: Macropores and water flow in soils, Water Resour. Res., 18, 1311–1325, https://doi.org/10.1029/WR018i005p01311, 1982.
Beven, K. and Germann, P.: Macropores and water flow in soils revisited, Water Resour. Res., 49, 3071–3092, https://doi.org/10.1002/wrcr.20156, 2013.
Bianchi, M., Zheng, C., Wilson, C., Tick, G. R., Liu, G., and Gorelick, S. M.: Spatial connectivity in a highly heterogeneous aquifer: From cores to preferential flow paths, Water Resour. Res., 47, W05524, https://doi.org/10.1029/2009WR008966, 2011.
Binet, F., Kersante, A., Munier-Lamy, C., Le Bayon, R. C., Belgy, M. J., and Shipitalo, M. J.: Lumbricid macrofauna alter atrazine mineralization and sorption in a silt loam soil, Soil Biol. Biochem., 38, 1255–1263, https://doi.org/10.1016/j.soilbio.2005.09.018, 2006.
Bishop, J. M., Callaghan, M. V., Cey, E. E., and Bentley, L. R.: Measurement and simulation of subsurface tracer migration to tile drains in low permeability, macroporous soil, Water Resour. Res., 51, 3956–3981, https://doi.org/10.1002/2014WR016310, 2015.
Blume, T., Zehe, E., and Bronstert, A.: Investigation of runoff generation in a pristine, poorly gauged catchment in the Chilean Andes ii: Qualitative and quantitative use of tracers at three spatial scales, Hydrol. Process., 22, 3676–3688, https://doi.org/10.1002/hyp.6970, 2008.
Blume, T., Zehe, E., and Bronstert, A.: Use of soil moisture dynamics and patterns at different spatio-temporal scales for the investigation of subsurface flow processes, Hydrol. Earth Syst. Sci., 13, 1215–1233, https://doi.org/10.5194/hess-13-1215-2009, 2009.
Boano, F., Packman, A. I., Cortis, A., Revelli, R., and Ridolfi, L.: A continuous time random walk approach to the stream transport of solutes, Water Resour. Res., 43, W10425, https://doi.org/10.1029/2007WR006062, 2007.
Bodin, J.: From analytical solutions of solute transport equations to multidimensional time-domain random walk (TDRW) algorithms, Water Resour. Res., 51, 1860–1871, https://doi.org/10.1002/2014WR015910, 2015.
Bolduan, R. and Zehe, E.: Degradation of isoproturon in earthworm macropores and subsoil matrix – a field study, J. Plant Nutr. Soil Sc., 169, 87–94, https://doi.org/10.1002/jpln.200521754, 2006.
Bonell, M., Pearce, A. J., and Stewart, M. K.: The identification of runoff-production mechanisms using environmental isotopes in a tussock grassland catchment, eastern otago, new-zealand, Hydrol. Process., 4, 15–34, https://doi.org/10.1002/hyp.3360040103, 1990.
Botter, G., Bertuzzo, E., and Rinaldo, A.: Transport in the hydrologic response: Travel time distributions, soil moisture dynamics, and the old water paradox, Water Resour. Res., 46, W03514, https://doi.org/10.1029/2009WR008371, 2010.
Botter, G., Bertuzzo, E., and Rinaldo, A.: Catchment residence and travel time distributions: The master equation, Geophys. Res. Lett., 38, L11403, https://doi.org/10.1029/2011GL047666, 2011.
Brooks, R. H. and Corey, A. T.: Hydraulic properties of porous media, Hydrology Paper, 3, 22–27, 1964.
Brooks, J. R., Barnard, H. R., Coulombe, R., and McDonnell, J. J.: Ecohydrologic separation of water between trees and streams in a Mediterranean climate, Nat. Geosci., 3, 100–104, https://doi.org/10.1038/ngeo722, 2010.
Bundt, M., Widmer, F., Pesaro, M., Zeyer, J., and Blaser, P.: Preferential flow paths: Biological “hot spots” in soils, Soil Biol. Biochem., 33, 729–738, https://doi.org/10.1016/S0038-0717(00)00218-2, 2001.
Camporese, M., Paniconi, C., Putti, M., and Orlandini, S.: Surface-subsurface flow modeling with path-based runoff routing, boundary condition-based coupling, and assimilation of multisource observation data, Water Resour. Res., 46, W0251210, https://doi.org/10.1029/2008WR007536, 2010.
Chabrier, G.: Galactic stellar and substellar initial mass function, Publ. Astron. Soc. Pac., 115, 763–795, https://doi.org/10.1086/376392, 2003.
Collins, R., Jenkins, A., and Harrow, M. A.: The contribution of old and new water to a storm hydrograph determined by tracer addition to a whole catchment, Hydrol. Processes, 14, 701–711, https://doi.org/10.1002/(SICI)1099-1085(200003)14:4<701::AID-HYP967>3.0.CO;2-2, 2000.
Cortis, A. and Berkowitz, B.: Computing “anomalous” contaminant transport in porous media: The CTRW MATLAB toolbox, Ground Water, 43, 947–950, https://doi.org/10.1111/j.1745-6584.2005.00045.x, 2005.
Davies, J. and Beven, K.: Comparison of a multiple interacting pathways model with a classical kinematic wave subsurface flow solution, Hydrolog. Sci. J., 57, 203–216, https://doi.org/10.1080/02626667.2011.645476, 2012.
Davies, J., Beven, K., Rodhe, A., Nyberg, L., and Bishop, K.: Integrated modeling of flow and residence times at the catchment scale with multiple interacting pathways, Water Resour. Res., 49, 4738–4750, https://doi.org/10.1002/wrcr.20377, 2013.
Dentz, M., and Berkowitz, B.: Transport behavior of a passive solute in continuous time random walks and multirate mass transfer, Water Resour. Res., 39, 1111, https://doi.org/10.1029/2001WR001163, 2003.
Dentz, M., Cortis, A., Scher, H., and Berkowitz, B.: Time behavior of solute transport in heterogeneous media: Transition from anomalous to normal transport, Adv. Water Resour., 27, 155–173, https://doi.org/10.1016/j.advwatres.2003.11.002, 2004.
Dentz, M., Scher, H., Holder, D., and Berkowitz, B.: Transport behaviour of coupled continuous-time random walks, Phys. Rev. E, 78, 41110, https://doi.org/10.1103/PhysRevE.78.041110, 2008.
Dooge, J. C. I.: Looking for hydrological laws, Water Resour. Res., 22, 46S–58S, https://doi.org/10.1029/WR022i09Sp0046S, 1986.
Duan, Q. Y., Sorooshian, S., and Gupta, H.V.: Effective and efficient global optimization for conceptual rainfall-runoff models, Water Resour. Res., 28, 1015–1031, https://doi.org/10.1029/91WR02985, 1992.
Ebel, B. A. and Loague, K.: Physics-based hydrologic-response simulation: Seeing through the fog of equifinality, Hydrol. Process., 20, 2887–2900, https://doi.org/10.1002/hyp.6388, 2006.
Edery, Y., Guadagnini, A., Scher, H., and Berkowitz, B.: Origins of anomalous transport in disordered media: Structural and dynamic controls, Water Resour. Res., 50, 1490–1505, https://doi.org/10.1002/2013WR015111, 2014.
Everett, M. E.: Near-Surface Applied Geophysics, Cambridge University Press, Cambridge, UK, 2013.
Ewen, J.: “Samp” model for water and solute movement in unsaturated porous media involving thermodynamic subsystems and moving packets 1. Theory, J. Hydrol., 182, 175–194, https://doi.org/10.1016/0022-1694(95)02925-7, 1996a.
Ewen, J.: “Samp” model for water and solute movement in unsaturated porous media involving thermodynamic subsystems and moving packets 2. Design and application, J. Hydrol., 182, 195–207, https://doi.org/10.1016/0022-1694(95)02926-5, 1996b.
Faulkner, H.: Connectivity as a crucial determinant of badland morphology and evolution, Geomorphology, 100, 91–103, https://doi.org/10.1016/j.geomorph.2007.04.039, 2008.
Fenicia, F., Savenije, H. H. G., Matgen, P., and Pfister, L.: A comparison of alternative multiobjective calibration strategies for hydrological modelling, Water Resour. Res., 43, W03434, https://doi.org/10.1029/2006WR005098, 2007.
Fenicia, F., Kavetski, D., and Savenije, H. H. G.: Elements of a flexible approach for conceptual hydrological modeling: 1. Motivation and theoretical development, Water Resour. Res., 47, W11510, https://doi.org/10.1029/2010wr010174, 2011.
Fenicia, F., Kavetski, D., Savenije, H. H. G., Clark, M. P., Schoups, G., Pfister, L., and Freer, J.: Catchment properties, function, and conceptual model representation: Is there a correspondence?, Hydrol. Process., 28, 2451–2467, https://doi.org/10.1002/hyp.9726, 2014.
Flügel, W. A.: Delineating hydrological response units by geographical information system analyses for regional hydrological modelling using PRMS/MMS in the drainage basin of the River Bröl, Germany, Hydrol. Process., 9, 423–436, https://doi.org/10.1002/hyp.3360090313, 1995.
Flury, M.: Experimental evidence of transport of pesticides through field soils – a review, J. Environ. Qual., 25, 25–45, https://doi.org/10.2134/jeq1996.00472425002500010005x, 1996.
Flury, M., Flühler, H., Leuenberger, J., and Jury, W. A.: Susceptibility of soils to preferential flow of water: A field study, Water Resour. Res., 30, 1945–1954, https://doi.org/10.1029/94WR00871, 1994.
Flury, M., Leuenberger, J., Studer, B., and Flühler, H.: Transport of anions and herbicides in a loamy and a sandy soil, Water Resour. Res., 31, 823–835, https://doi.org/10.1029/94WR02852, 1995.
Freeze, R. A. and Harlan, R. L.: Blueprint for a physically-based, digitally simulated hydrologic response model, J. Hydrol., 9, 237–258, https://doi.org/10.1016/0022-1694(69)90020-1, 1969.
Gao, H., Hrachowitz, M., Fenicia, F., Gharari, S., and Savenije, H. H. G.: Testing the realism of a topography-driven model (FLEX-Topo) in the nested catchments of the Upper Heihe, China, Hydrol. Earth Syst. Sci., 18, 1895–1915, https://doi.org/10.5194/hess-18-1895-2014, 2014.
Germann, P.: Preferential flow: Stokes approach to infiltration and drainage, Geographica Bernensia, G 88, 199 pp., https://doi.org/10.4480/GB2018.G88, 2018.
Gharari, S., Hrachowitz, M., Fenicia, F., and Savenije, H. H. G.: Hydrological landscape classification: investigating the performance of HAND based landscape classifications in a central European meso-scale catchment, Hydrol. Earth Syst. Sci., 15, 3275–3291, https://doi.org/10.5194/hess-15-3275-2011, 2011.
Goldstein, H.: Classical Mechanics, Pearson Education Limited, Harlow, UK, 2013.
Goller, R., Wilcke, W., Fleischbein, K., Valarezo, C., and Zech, W., Dissolved nitrogen, phosphorus, and sulfur forms in the ecosystem fluxes of a montane forest in Ecuador, Biogeochemistry, 77, 57–89, https://doi.org/10.1007/s10533-005-1061-1, 2006.
Gooseff, M. N., Wondzell, S. M., Haggerty, R., and Anderson, J.: Comparing transient storage modeling and residence time distribution (RTD) analysis in geomorphically varied reaches in the Lookout Creek basin, Oregon, USA, Adv. Water Resour., 26, 925–937, https://doi.org/10.1016/S0309-1708(03)00105-2, 2003.
Gouet-Kaplan, M. and Berkowitz, B.: Measurements of interactions between resident and infiltrating water in a lattice micromodel, Vadose Zone J., 10, 624–633, https://doi.org/10.2136/vzj2010.0103, 2011.
Grayson, R. B., Moore, I. D., and McMahon, T. A.: Physically based hydrologic modeling: 2. Is the concept realistic?. Water Resour. Res., 28, 2659–2666, https://doi.org/10.1029/92WR01259, 1992.
Gupta, H. V., Clark, M. P., Vrugt, J. A., Abramowitz, G., and Ye, M.: Towards a comprehensive assessment of model structural adequacy, Water Resour. Res., 48, 1–16, https://doi.org/10.1029/2011WR011044, 2012.
Haggerty, R. and Gorelick S. M.: Multiple rate mass transfer for modeling diffusion and surface reactions in media with pore-scale heterogeneity, Water Resour. Res., 31, 2383–2400, https://doi.org/10.1029/95WR10583, 1995.
Haggerty, R., Wondzell, S. M., and Johnson, M. A.: Power-law residence time distribution in the hyporheic zone of a 2nd-order mountain stream, Geophys. Res. Lett., 29, 18-1–18-4, https://doi.org/10.1029/2002GL014743, 2002.
Haken, H.: Synergetics: An introduction; nonequilibrium phase transitions and self-organization in physics, chemistry and biology, Springer Series in Synergetics, Springer Berlin, Germany, 355 pp., 1983.
Harman, C. J.: Time-variable transit time distributions and transport: Theory and application to storage-dependent transport of chloride in a watershed, Water Resour. Res., 51, 1–30, https://doi.org/10.1002/2014wr015707, 2015.
He, Y., Bárdossy, A., and Zehe, E.: A review of regionalisation for continuous streamflow simulation, Hydrol. Earth Syst. Sci., 15, 3539–3553, https://doi.org/10.5194/hess-15-3539-2011, 2011a.
He, Y., Bardossy, A., and Zehe, E.: A catchment classification scheme using local variance reduction method, J. Hydrol., 411, 140–154, https://doi.org/10.1016/j.jhydrol.2011.09.042, 2011b.
Hoffman, F., Ronen, D., and Pearl, Z.: Evaluation of flow characteristics of a sand column using magnetic resonance imaging, J. Contam. Hydrol., 22, 95–107, https://doi.org/10.1016/0169-7722(95)00079-8, 1996.
Hopp, L. and McDonnell, J. J.: Connectivity at the hillslope scale: Identifying interactions between storm size, bedrock permeability, slope angle and soil depth, J. Hydrol., 376, 378–391, https://doi.org/10.1016/j.jhydrol.2009.07.047, 2009.
Howard, A. D.: Theoretical model of optimal drainage networks, Water Resour. Res., 26, 2107–2117, https://doi.org/10.1029/WR026i009p02107, 1990.
Hrachowitz, M. and Clark, M. P.: HESS Opinions: The complementary merits of competing modelling philosophies in hydrology, Hydrol. Earth Syst. Sci., 21, 3953–3973, https://doi.org/10.5194/hess-21-3953-2017, 2017.
Hrachowitz, M., Soulsby, C., Tetzlaff, D., Malcolm, I. A., and Schoups, G.: Gamma distribution models for transit time estimation in catchments: Physical interpretation of parameters and implications for time-variant transit time assessment, Water Resour. Res., 46, W10536, https://doi.org/10.1029/2010WR009148, 2010.
Hrachowitz, M., Savenije, H., Bogaard, T. A., Tetzlaff, D., and Soulsby, C.: What can flux tracking teach us about water age distribution patterns and their temporal dynamics?, Hydrol. Earth Syst. Sci., 17, 533–564, https://doi.org/10.5194/hess-17-533-2013, 2013.
Hrachowitz, M., Fovet, O., Ruiz, L., and Savenije, H. H.: Transit time distributions, legacy contamination and variability in biogeochemical 1/f scaling: how are hydrological response dynamics linked to water quality at the catchment scale?, Hydrol. Process., 29, 5241–5256, 2015.
Hrachowitz, M., Benettin, P., van Breukelen, B. M., Fovet, O., Howden, N. J. K., Ruiz, L., van der Velde, Y., and Wade, A. J.: Transit times – the link between hydrology and water quality at the catchment scale, Wiley Interdisciplinary Reviews – Water, 3, 629–657, https://doi.org/10.1002/wat2.1155, 2016.
Hundecha, Y. and Bardossy, A.: Modeling of the effect of land use changes on the runoff generation of a river basin through parameter regionalization of a watershed model, J. Hydrol., 292, 281–295, https://doi.org/10.1016/j.jhydrol.2004.01.002, 2004.
Jackisch, C.: Linking structure and functioning of hydrological systems, PhD Thesis, Karlsruhe Institute of Technology, 171 pp., https://doi.org/10.5445/IR/1000051494, 2015.
Jackisch, C. and Zehe, E.: Ecohydrological particle model based on representative domains, Hydrol. Earth Syst. Sci., 22, 3639–3662, https://doi.org/10.5194/hess-22-3639-2018, 2018.
Jury, W. A. and Sposito, G.: A transfer function model of solute transport through soil: 1. Fundamental concepts, Water Resour. Res., 22, 243–247, 1986.
Kapetas, L., Dror, I., and Berkowitz, B.: Evidence of preferential path formation and path memory effect during successive infiltration and drainage cycles in uniform sand columns, J. Contam. Hydrol., 165, 1–10, https://doi.org/10.1016/j.jconhyd.2014.06.016, 2014.
Kirchner, J. W.: A double paradox in catchment hydrology and geochemistry, Hydrol. Process., 17, 871–874, https://doi.org/10.1002/hyp.5108, 2003.
Kirchner, J. W.: Aggregation in environmental systems – Part 1: Seasonal tracer cycles quantify young water fractions, but not mean transit times, in spatially heterogeneous catchments, Hydrol. Earth Syst. Sci., 20, 279–297, https://doi.org/10.5194/hess-20-279-2016, 2016.
Kirchner, J. W., Feng, X., and Neal, C.: Fractal stream chemistry and its implications for contaminant transport in catchments, Nature, 403, 524–527, https://doi.org/10.1038/35000537, 2000.
Klaus, J. and Zehe, E.: Modelling rapid flow response of a tile drained field site using a 2D-physically based model: Assessment of “equifinal” model setups, Hydrol. Process., 24, 1595–1609, https://doi.org/10.1002/hyp.7687, 2010.
Klaus, J. and Zehe, E.: A novel explicit approach to model bromide and pesticide transport in connected soil structures, Hydrol. Earth Syst. Sci., 15, 2127–2144, https://doi.org/10.5194/hess-15-2127-2011, 2011.
Klaus, J., Zehe, E., Elsner, M., Külls, C., and McDonnell, J. J.: Macropore flow of old water revisited: experimental insights from a tile-drained hillslope, Hydrol. Earth Syst. Sci., 17, 103–118, https://doi.org/10.5194/hess-17-103-2013, 2013.
Klaus, J., Zehe, E., Elsner, M., Palm, J., Schneider, D., Schroeder, B., Steinbeiss, S., van Schaik, L., and West, S.: Controls of event-based pesticide leaching in natural soils: A systematic study based on replicated field scale irrigation experiments, J. Hydrol., 512, 528–539, https://doi.org/10.1016/j.jhydrol.2014.03.020, 2014.
Klaus, J., Chun, K. P., McGuire, K. J., and McDonnell, J. J.: Temporal dynamics of catchment transit times from stable isotope data, Water Resour. Res., 51, 4208–4223, https://doi.org/10.1002/2014wr016247, 2015.
Kleidon, A.: How does the earth system generate and maintain thermodynamic disequilibrium and what does it imply for the future of the planet?, Philos. T. Roy. Soc. A, 370, 1012–1040, https://doi.org/10.1098/rsta.2011.0316, 2012.
Kleidon, A., Zehe, E., and Lin, H.: Thermodynamic limits of the critical zone and their relevance to hydropedology, in: Hydropedology: Synergistic Integration of Soil Science and Hydrology, Elsevier, Amsterdam, the Netherlands, 854 pp., p. 243, 2012.
Kleidon, A., Zehe, E., Ehret, U., and Scherer, U.: Thermodynamics, maximum power, and the dynamics of preferential river flow structures at the continental scale, Hydrol. Earth Syst. Sci., 17, 225–251, https://doi.org/10.5194/hess-17-225-2013, 2013.
Knudsen, J., Thomsen, A., and Refsgaard, J. C.: WATBAL, Hydrol. Res., 17, 347–362, doi.org/10.2166/nh.1986.0026, 1986.
Koehler, B., Zehe, E., Corre, M. D., and Veldkamp, E.: An inverse analysis reveals limitations of the soil-CO2 profile method to calculate CO2 production and efflux for well-structured soils, Biogeosciences, 7, 2311–2325, https://doi.org/10.5194/bg-7-2311-2010, 2010.
Koehler, B., Corre, M. D., Steger, K., Well, R., Zehe, E., Sueta, J. P., and Veldkamp, E.: An in-depth look into a tropical lowland forest soil: Nitrogen-addition effects on the contents of N2O, CO2 and CH4 and N2O isotopic signatures down to 2-m depth, Biogeochemistry, 111, 695–713, https://doi.org/10.1007/s10533-012-9711-6, 2012.
Kondepudi, D. and Prigogine, I.: Modern thermodynamics: From heat engines to dissipative structures, John Wiley, Chichester, UK, 1998.
Lehmann, P., Hinz, C., McGrath, G., Tromp-van Meerveld, H. J., and McDonnell, J. J.: Rainfall threshold for hillslope outflow: an emergent property of flow pathway connectivity, Hydrol. Earth Syst. Sci., 11, 1047–1063, https://doi.org/10.5194/hess-11-1047-2007, 2007.
Levy, M. and Berkowitz, B.: Measurement and analysis of non-Fickian dispersion in heterogeneous porous media, J. Contam. Hydrol., 64, 203–226, https://doi.org/10.1016/S0169-7722(02)00204-8, 2003.
Loritz, R., Hassler, S. K., Jackisch, C., Allroggen, N., van Schaik, L., Wienhöfer, J., and Zehe, E.: Picturing and modeling catchments by representative hillslopes, Hydrol. Earth Syst. Sci., 21, 1225–1249, https://doi.org/10.5194/hess-21-1225-2017, 2017.
Loritz, R., Gupta, H., Jackisch, C., Westhoff, M., Kleidon, A., Ehret, U., and Zehe, E.: On the dynamic nature of hydrological similarity, Hydrol. Earth Syst. Sci., 22, 3663–3684, https://doi.org/10.5194/hess-22-3663-2018, 2018.
Loritz, R., Kleidon, A., Jackisch, C., Westhoff, M., Ehret, U., Gupta, H., and Zehe, E.: A topographic index explaining hydrological similarity by accounting for the joint controls of runoff formation, Hydrol. Earth Syst. Sci., 23, 3807–3821, https://doi.org/10.5194/hess-23-3807-2019, 2019.
McDonnell, J. J.: The two water worlds hypothesis: Ecohydrological separation of water between streams and trees?, Wiley Interdisciplinary Reviews – Water, 1, 323–329, https://doi.org/10.1002/wat2.1027, 2014.
McDonnell, J. J. and Beven, K.: Debates-the future of hydrological sciences: A (common) path forward? A call to action aimed at understanding velocities, celerities and residence time distributions of the headwater hydrograph, Water Resour. Res., 50, 5342–5350, https://doi.org/10.1002/2013wr015141, 2014.
McGlynn, B. and Seibert, J.: Distributed assessment of contributing area and riparian buffering along stream networks, Water Resour. Res., 39, WR001521, https://doi.org/10.1029/2002WR001521, 2003.
McGlynn, B., McDonnell, J. J., Stewart, M., and Seibert, J.: On the relationships between catchment scale and streamwater mean residence time, Hydrol. Process., 17, 175–181, https://doi.org/10.1002/hyp.5085, 2002.
McGrath, G. S., Hinz, C., and Sivapalan, M.: Modelling the impact of within-storm variability of rainfall on the loading of solutes to preferential flow pathways, Eur. J. Soil Sci., 59, 24–33, https://doi.org/10.1111/j.1365-2389.2007.00987.x, 2008.
McGrath, G. S., Hinz, C., Sivapalan, M., Dressel, J., Puetz, T., and Vereecken, H.: Identifying a rainfall event threshold triggering herbicide leaching by preferential flow, Water Resour. Res., 46, W02513, https://doi.org/10.1029/2008wr007506, 2010.
Mertens, J., Madsen, H., Feyen, L., Jacques, D., and Feyen, J.: Including prior information in the estimation of effective soil parameters in unsaturated zone modelling, J. Hydrol., 294, 251–269, https://doi.org/10.1016/j.jhydrol.2004.02.011, 2004.
Milne, G.: Normal erosion as a factor in soil profile development, Nature, 138, 548–549, https://doi.org/10.1038/138548c0, 1936.
Nash, J. E.: The form of the instantaneous unit hydrograph, International Association of Hydrological Sciences, 45, 114–121, 1957.
Niemi, A. J.: Residence time distribution of variable flow processes, Int. J. Appl. Radiat. Is., 28, 855–860, https://doi.org/10.1016/0020-708X(77)90026-6, 1977.
Nissan, A. and Berkowitz, B.: Anomalous transport dependence on Péclet number, porous medium heterogeneity, and a temporally varying velocity field, Phys. Rev. E, 99, 033108, https://doi.org/10.1103/PhysRevE.99.033108, 2019.
Nissan, A., Dror, I., and Berkowitz, B.: Time-dependent velocity-field controls on anomalous chemical transport in porous media, Water Resour. Res., 53, 3760–3769, https://doi.org/10.1002/2016WR020143, 2017.
Oswald, S., Kinzelbach, W., Greiner, A., and Brix, G.: Observation of flow and transport processes in artificial porous media via magnetic resonance imaging in three dimensions, Geoderma, 80, 417–429, https://doi.org/10.1016/S0016-7061(97)00064-5, 1997.
Paik, K. and Kumar, P.: Optimality approaches to describe characteristic fluvial patterns on landscapes, Philos. T. Roy. Soc. B, 365, 1387–1395, https://doi.org/10.1098/rstb.2009.0303, 2010.
Pérez, A. J., Abrahao, R., Causape, J., Cirpka, O. A., and Burger, C. M.: Simulating the transition of a semi-arid rainfed catchment towards irrigation agriculture, J. Hydrol., 409, 663–681, https://doi.org/10.1016/j.jhydrol.2011.08.061, 2011.
Refsgaard, J. C. and Storm, B.: MikeShe, in: Computer models of watershed hydrology, edited by: Singh, V. P., Water Resources Publications, Highland Ranch, Colorado, USA, 809–846, 1995.
Reinhardt, L. and Ellis, M. A.: The emergence of topographic steady state in a perpetually dynamic self organised critical landscape, Water Resour. Res., 51, 4986–5003, https://doi.org/10.1002/2014WR016223, 2015.
Rinaldo, A., Benettin, P., Harman, C. J., Hrachowitz, M., McGuire, K. J., van der Velde, Y., Bertuzzo, E., and Botter, G.: Storage selection functions: A coherent framework for quantifying how catchments store and release water and solutes, Water Resour. Res., 51, 4840–4847, https://doi.org/10.1002/2015wr017273, 2015.
Rodriguez, N. B. and Klaus, J.: Catchment travel times from composite storage selection functions representing the superposition of streamflow generation processes, Water Resour. Res., 55, 9292–9314, https://doi.org/10.1029/2019wr024973, 2019.
Rodriguez, N. B., McGuire, K. J., and Klaus, J.: Time-varying storage-water age relationships in a catchment with a mediterranean climate, Water Resour. Res., 54, 3988–4008, https://doi.org/10.1029/2017wr021964, 2018.
Rodriguez-Iturbe, I. and Rinaldo, A.: Fractal river basins: Chance and self-organization, Cambridge Univ. Press, Cambridge UK, 2001.
Rodriguez-Iturbe, I., D'Odorico, P., Porporato, A., and Ridolfi, L.: On the spatial and temporal links between vegetation, climate, and soil moisture, Water Resour. Res., 35, 3709–3722, https://doi.org/10.1029/1999wr900255, 1999.
Roth, K. and Hammel, K.: Transport of conservative chemical through an unsaturated two-dimensional Miller-similar medium with steady state flow, Water Resour. Res., 32, 1653–1663, https://doi.org/10.1029/96WR00756, 1996.
Samaniego, L. and Bardossy, A.: Simulation of the impacts of land use/cover and climatic changes on the runoff characteristics at the mesoscale, Ecol. Model., 196, 45–61, https://doi.org/10.1016/j.ecolmodel.2006.01.005, 2006.
Samaniego, L., Kumar, R., and Attinger, S.: Multiscale parameter regionalization of a grid-based hydrologic model at the mesoscale, Water Resour. Res., 46, W05523, https://doi.org/10.1029/2008wr007327, 2010.
Sander, T. and Gerke, H. H.: Modelling field-data of preferential flow in paddy soil induced by earthworm burrows, J. Contam. Hydrol., 104, 126–136, https://doi.org/10.1016/j.jconhyd.2008.11.003, 2009.
Savenije, H. H. G.: HESS Opinions “Topography driven conceptual modelling (FLEX-Topo)”, Hydrol. Earth Syst. Sci., 14, 2681–2692, https://doi.org/10.5194/hess-14-2681-2010, 2010.
Savenije, H. H. G. and Hrachowitz, M.: HESS Opinions “Catchments as meta-organisms – a new blueprint for hydrological modelling”, Hydrol. Earth Syst. Sci., 21, 1107–1116, https://doi.org/10.5194/hess-21-1107-2017, 2017.
Scheidegger, A. E.: An evaluation of the accuracy of the diffusivity equation for describing miscible displacement in porous media, in: Proc. Theory Fluid Flow Porous Media 2nd Conf., 1959, Univ. Oklahoma, Norman, Oklahoma, USA, 101–116, 1959.
Scher, H. and Montroll, E. W.: Anomalous transit time dispersion in amorphous solids, Phys. Rev. B, 12, 2455–2477, https://doi.org/10.1103/PhysRevB.12.2455, 1975.
Scher, H., Margolin, G., Metzler, R., Klafter, J., and Berkowitz, B.: The dynamical foundation of fractal stream chemistry: The origin of extremely long retention times, Geophys. Res. Lett., 29, 1061, https://doi.org/10.1029/2001GL014123, 2002.
Shannon, C. E.: A mathematical theory of communication, Bell Syst. Tech. J., 27, 379–423, https://doi.org/10.1145/584091.584093, 1948.
Sherman, L. K.: Streamflow from rainfall by the unit hydrograph method, Eng. News-Rec., 180, 501–505, 1932.
Simmons, C. S.: A stochastic-convective transport representation of dispersion in one dimensional porous media systems, Water Resour. Res., 18, 1193–1214, https://doi.org/10.1029/WR018i004p01193, 1982.
Šimunek, J., Jarvis, N. J., van Genuchten, M. T., and Gardenas, A.: Review and comparison of models for describing non-equilibrium and preferential flow and transport in the vadose zone, J. Hydrol., 272, 14–35, https://doi.org/10.1016/S0022-1694(02)00252-4, 2003.
Singh, S. K., McMillan, H., Bardossy, A., and Fateh, C.: Nonparametric catchment clustering using the data depth function, Hydrolog. Sci. J., 61, 2649–2667, https://doi.org/10.1080/02626667.2016.1168927, 2016.
Sivapalan, M.: From engineering hydrology to Earth system science: milestones in the transformation of hydrologic science, Hydrol. Earth Syst. Sci., 22, 1665–1693, https://doi.org/10.5194/hess-22-1665-2018, 2018.
Sklash, M. G. and Farvolden, R. N.: The role of groundwater in storm runoff, J. Hydrol., 43, 45–65, https://doi.org/10.1016/0022-1694(79)90164-1, 1979.
Sklash, M. G., Beven, K. J., Gilman, K., and Darling, W. G.: Isotope studies of pipeflow at Plynlimon, Wales, UK, Hydrol. Process., 10, 921–944, https://doi.org/10.1002/(SICI)1099-1085(199607)10:7<921::AID-HYP347>3.0.CO;2-B, 1996.
Sposito, G., Jury, W. A., and Gupta, V. K.: Fundamental problems in the stochastic convection-dispersion model of solute transport in aquifers and field soils, Water Resour. Res., 22, 77–88, 1986.
Sprenger, M., Tetzlaff, D., Buttle, J., Laudon, H., Leistert, H., Mitchell, C. P. J., Snelgrove, J., Weiler, M., and Soulsby, C.: Measuring and modeling stable isotopes of mobile and bulk soil water, Vadose Zone J., 17, 1–18, https://doi.org/10.2136/vzj2017.08.0149, 2018.
Sternagel, A., Loritz, R., Wilcke, W., and Zehe, E.: Simulating preferential soil water flow and tracer transport using the Lagrangian Soil Water and Solute Transport Model, Hydrol. Earth Syst. Sci., 23, 4249–4267, https://doi.org/10.5194/hess-23-4249-2019, 2019.
Trefry, M. G., Ruan, F. P., and McLaughlin, D.: Numerical simulations of preasymptotic transport in heterogeneous porous media: Departures from the Gaussian limit, Water Resour. Res., 39, 1063, https://doi.org/10.1029/2001WR001101, 2003.
Tromp-van Meerveld, H. J. and McDonnell, J. J.: Threshold relations in subsurface stormflow: 2. The fill and spill hypothesis, Water Resour. Res., 42, W02411, https://doi.org/10.1029/2004wr003800, 2006.
Turton, D. J., Barnes, D. R., and de Jesus Navar, J.: Old and new water in subsurface flow from a forest soil block, J. Environ. Qual., 24, 139–146, https://doi.org/10.2134/jeq1995.00472425002400010020x, 1995.
van der Velde, Y., Torfs, P. J. J. F., van der Zee, S. E. A. T. M., and Uijlenhoet, R.: Quantifying catchment scale mixing and its effect on time varying travel time distributions. Water Resour. Res., 48, W06536, https://doi.org/10.1029/2011WR011310, 2012.
van Schaik, L., Palm, J., Klaus, J., Zehe, E., and Schröder, B.: Linking spatial earthworm distribution to macropore numbers and hydrological effectiveness, Ecohydrology, 7, 401–408, https://doi.org/10.1002/eco.1358, 2014.
Vogel, H. J. and Roth, K.: Quantitative morphology and network representation of soil pore structure, Adv. Water Resour., 24, 233–242, https://doi.org/10.1016/S0309-1708(00)00055-5, 2001.
Vogel, H.-J., Cousin, I., Ippisch, O., and Bastian, P.: The dominant role of structure for solute transport in soil: experimental evidence and modelling of structure and transport in a field experiment, Hydrol. Earth Syst. Sci., 10, 495–506, https://doi.org/10.5194/hess-10-495-2006, 2006.
Vrugt, J. A. and Ter Braak, C. J. F.: DREAM(D): an adaptive Markov Chain Monte Carlo simulation algorithm to solve discrete, noncontinuous, and combinatorial posterior parameter estimation problems, Hydrol. Earth Syst. Sci., 15, 3701–3713, https://doi.org/10.5194/hess-15-3701-2011, 2011.
Wagener, T. and Wheater, H. S.: Parameter estimation and regionalization for continuous rainfall-runoff models including uncertainty, J. Hydrol., 320, 132–154, 2006.
Weiler, M., McGlynn, B. L., McGuire, K. J., and McDonnell, J. J.: How does rainfall become runoff? A combined tracer and runoff transfer function approach, Water Resour. Res., 39, 1315, https://doi.org/10.1029/2003wr002331, 2003.
Weinberg, G. M.: An Introduction to General Systems Thinking, John Wiley & Sons, New York, USA, p. 279, 1975.
Westhoff, M., Zehe, E., Archambeau, P., and Dewals, B.: Does the Budyko curve reflect a maximum-power state of hydrological systems? A backward analysis, Hydrol. Earth Syst. Sci., 20, 479–486, https://doi.org/10.5194/hess-20-479-2016, 2016.
Westhoff, M. C. and Zehe, E.: Maximum entropy production: can it be used to constrain conceptual hydrological models?, Hydrol. Earth Syst. Sci., 17, 3141–3157, https://doi.org/10.5194/hess-17-3141-2013, 2013.
Wienhöfer, J. and Zehe, E.: Predicting subsurface stormflow response of a forested hillslope – the role of connected flow paths, Hydrol. Earth Syst. Sci., 18, 121–138, https://doi.org/10.5194/hess-18-121-2014, 2014.
Wienhöfer, J., Germer, K., Lindenmaier, F., Färber, A., and Zehe, E.: Applied tracers for the observation of subsurface stormflow at the hillslope scale, Hydrol. Earth Syst. Sci., 13, 1145–1161, https://doi.org/10.5194/hess-13-1145-2009, 2009.
Wilcke, W., Yasin, S., Valarezo, C., and Zech, W.: Change in water quality during the passage through a tropical montane rain forest in Ecuador, Biogeochemistry, 55, 45–72, https://doi.org/10.1023/A:1010631407270, 2001.
Winter, T. C.: The concept of hydrologic landscapes, J. Am. Water Resour. Assoc., 37, 335–349, https://doi.org/10.1111/j.1752-1688.2001.tb00973.x, 2001.
Worthington, S. R. H. and Ford D. C.: Self-organised permeability in carbonate aquifers, Groundwater, 47, 326–336, https://doi.org/10.1111/j.1745-6584.2009.00551.x, 2009.
Wrede, S., Fenicia, F., Martinez-Carreras, N., Juilleret, J., Hissler, C., Krein, A., Savenije, H. H. G., Uhlenbrook, S., Kavetski, D., and Pfister, L.: Towards more systematic perceptual model development: A case study using 3 Luxembourgish catchments, Hydrol. Process., 29, 2731–2750, https://doi.org/10.1002/hyp.10393, 2015.
Zehe, E. and Blöschl, G.: Predictability of hydrologic response at the plot and catchment scales: Role of initial conditions, Water Resour. Res., 40, W10202, https://doi.org/10.1029/2003wr002869, 2004.
Zehe, E. and Flühler, H.: Slope scale distribution of flow patterns in soil profiles, J. Hydrol., 247, 116–132, 2001.
Zehe, E. and Jackisch, C.: A Lagrangian model for soil water dynamics during rainfall-driven conditions, Hydrol. Earth Syst. Sci., 20, 3511–3526, https://doi.org/10.5194/hess-20-3511-2016, 2016.
Zehe, E., Blume, T., and Bloschl, G.: The principle of 'maximum energy dissipation': A novel thermodynamic perspective on rapid water flow in connected soil structures, Philos. T. Roy. Soc. B, 365, 1377–1386, https://doi.org/10.1098/rstb.2009.0308, 2010.
Zehe, E., Ehret, U., Blume, T., Kleidon, A., Scherer, U., and Westhoff, M.: A thermodynamic approach to link self-organization, preferential flow and rainfall–runoff behaviour, Hydrol. Earth Syst. Sci., 17, 4297–4322, https://doi.org/10.5194/hess-17-4297-2013, 2013.
Zehe, E., Ehret, U., Pfister, L., Blume, T., Schröder, B., Westhoff, M., Jackisch, C., Schymanski, S. J., Weiler, M., Schulz, K., Allroggen, N., Tronicke, J., van Schaik, L., Dietrich, P., Scherer, U., Eccard, J., Wulfmeyer, V., and Kleidon, A.: HESS Opinions: From response units to functional units: a thermodynamic reinterpretation of the HRU concept to link spatial organization and functioning of intermediate scale catchments, Hydrol. Earth Syst. Sci., 18, 4635–4655, https://doi.org/10.5194/hess-18-4635-2014, 2014.
Zehe, E., Loritz, R., Jackisch, C., Westhoff, M., Kleidon, A., Blume, T., Hassler, S. K., and Savenije, H. H.: Energy states of soil water – a thermodynamic perspective on soil water dynamics and storage-controlled streamflow generation in different landscapes, Hydrol. Earth Syst. Sci., 23, 971–987, https://doi.org/10.5194/hess-23-971-2019, 2019.
Zhang, Y., Benson, D. A., and Reeves, D. M.: Time and space nonlocalities underlying fractional-derivative models: Distinction and review of field applications, Adv. Water Resour., 32, 561–581, https://doi.org/10.1016/j.advwatres.2009.01.008, 2009.
blueprintfor a unified modelling framework to quantify chemical transport in both surface water and groundwater systems. There has been extensive debate over recent decades, particularly in the surface water literature, about how to explain and account for long travel times of chemical species that are distinct from water flow (rainfall-runoff) travel times. We suggest a powerful modelling framework known to be robust and effective from the field of groundwater hydrology.
blueprintfor a unified modelling framework to quantify chemical transport in both...