Dynamics of hydrological-model parameters: mechanisms, problems and solutions

It has been demonstrated that the application of time-varying hydrological-model parameters based on dynamic catchment behavior significantly improves the accuracy and robustness of conventional models. However, the fundamental problems for calibrating dynamic parameters still need to be addressed. In this study, five calibration schemes for dynamic parameters in hydrological models were designed to investigate the underlying causes of poor model performance. The five schemes were assessed with respect to the model performance in different flow phases, the transferability of the dynamic parameters to different time periods, the state variables and fluxes time series, and the response of the dynamic parameter set to the dynamic catchment characteristics. Furthermore, the potential reasons for the poor response of the dynamic parameter set to the catchment dynamics were investigated. The results showed that the underlying causes of poor model performance included time-invariant parameters, “compensation” among parameters, high dimensionality and abrupt shifts in the parameters. The recommended calibration scheme exhibited good performance and overcame these problems by characterizing the dynamic behavior of the catchments. The main reason for the poor response of the dynamic parameter set to the catchment dynamics may be the poor convergence performance of the parameters. In addition, the assessment results of the state variables and fluxes and the convergence performance of the parameters provided robust indications of the dominant response modes of the hydrological models in different sub-periods or catchments with distinguishing catchment characteristics.

1 Introduction

Hydrological modeling is an essential tool for understanding the hydrological processes of a catchment and forecasting streamflow (Liu et al., 2015, 2018; Turner et al., 2017; Delorit et al., 2017; Fenicia et al., 2014, 2018; Hublart et al., 2016; Höge et al., 2018; Sarrazin et al., 2016; Wi et al., 2015; Herman et al., 2013; Wagener et al., 2001, 2003; Madsen, 2000; Osuch et al., 2019; Zhang et al., 2019). Unfortunately, the paucity of progress in model development is partly due to structural inadequacy. For example, dynamic components in hydrological models are oversimplified due to a poor understanding of their physical mechanisms (Xiong et al., 2019; Deng et al., 2016, 2018; Dakhlaoui et al., 2017; Sarhadi et al., 2016; Pathiraja et al., 2016; Ouyang et al., 2016). Previous studies have demonstrated that the assumption of time-invariant parameters is usually inappropriate. The reasons are that a unique parameter set optimized by hydrological models only represents the average hydrological processes, which do not accurately represent the dynamic response modes of the catchments processes (Pathiraja et al., 2018; Fowler et al., 2018; Zhao et al., 2017; Kim and Han, 2017; Golmohammadi et al., 2017; Delorit et al., 2017; Chen et al., 2017). To investigate the problems caused by time-invariant parameters, a control scheme, i.e., scheme 1, is designed and assessed in this study. In this regard, the dynamics of the hydrological-model parameters may be a type of compensation for models that are missing key processes such as climate- and land-surface-related changes (Xiong et al., 2019; Deng et al., 2016, 2018; Wang et al., 2017b; Dakhlaoui et al., 2017; Sarhadi et al., 2016; Pathiraja et al., 2016; Ouyang et al., 2016; Todorovic and Plavsic, 2015).

However, a critical but often overlooked issue related to dynamic parameters is that there are linear or nonlinear correlations among hydrological-model parameters, also called the “compensation” between parameters (Wagener and Kollat, 2007). The compensation between parameters could even result in the dynamics of the individual parameters may not represent the time-varying properties of river catchments (Höge et al., 2018; Cibin et al., 2010; Bárdossy and Singh, 2008; Bárdossy, 2007; Huang, 2005; Wagener and Kollat, 2007). Hence, it has been conclusively demonstrated that the optimal parameters in hydrological models should not be considered as individual parameters but instead as parameter vector “teams” (Wagener and Kollat, 2007). In this research, the effects of the compensation between the parameters on the dynamics of hydrological-model parameters are investigated using a control scheme i.e., scheme 2.

In view of the compensation between parameters, the most common approach for assessing the dynamics of the hydrological-model parameters is that the calibration period is partitioned into different sub-periods based on the temporal dynamic catchment characteristics (Sarhadi et al., 2016; Merz et al., 2011; Lan et al., 2018; Xiong et al., 2019; Motavita et al., 2019; Deng et al., 2016, 2018; Dakhlaoui et al., 2017; Choi and Beven, 2007; Brigode et al., 2013; Kim et al., 2015; Kim and Han, 2017; Zhao et al., 2017; Pfannerstill et al., 2015; Me et al., 2015; Coron et al., 2014; Vormoor et al., 2018; Luo et al., 2012; Guse et al., 2016; Zhang et al., 2011, 2015; Ouyang et al., 2016). The parameter set in each sub-period is optimized to obtain the dynamic parameter team. Previous studies have demonstrated that sub-period calibration based on the dynamic catchment behavior accurately captures the temporal variations of the catchment characteristics, thereby compensating for structural inadequacy (Lan et al., 2018; Zhao et al., 2017; Kim and Han, 2017; Zhang et al., 2011; de Vos et al., 2010; Gupta et al., 2009; Choi and Beven, 2007; van Griensven et al., 2006; Freer et al., 2003). In the study of Choi and Beven (2007), the sub-periods were identified based on different hydrological characteristics using a clustering technique. The results showed that the model that considered the dynamic catchment characteristics exhibited good performance at the global level (i.e., overall calibration and validation periods). Merz et al. (2011) demonstrated that the parameters of the catchment model related to snow and soil moisture showed clear time trends for the climate indicators. Zhang et al. (2011) proposed a general multi-period calibration approach for improving the performance of hydrological models based on the fuzzy c-means clustering technique under time-varying climatic conditions. The results indicated that model simulations using parameters obtained from the multi-period calibration approach exhibited considerable improvements over those from the conventional single-period model. Brigode et al. (2013) demonstrated the dependence of the optimal parameter set on the climate characteristics of the calibration period. Lan et al. (2018) focused on the sub-period clustering or partition based on the climate–land-surface variations and relevant studies, such as the choice and pre-process of clustering indices in the light of various catchment characteristics and the clustering operation based on different clustering index systems. The results showed that the sub-annual calibration with the clustering preprocessing (CPP) framework exhibited significant improvements in overall performance.

Even though the sub-period calibration performed well for describing the dynamics of the hydrological-model parameters, some fundamental problems still need to be addressed because the analysis involves the hydrological model structure, global optimization, physical mechanisms of dynamic catchment characteristics, as well as complex relationships between the parameters, state variables and fluxes. For example, multiple parameter sets are optimized simultaneously in different sub-periods. Questions like which possible disaster would be brought by parameter optimization in a high-dimensional parameter space remain to be answered. This study aims to investigate the underlying causes of poor model performance in hydrological models with dynamic parameters via designing five calibration schemes and exploring the potential reasons for the poor response of the dynamic parameter set to the catchment dynamics are explored. In addition to schemes 1 and 2 described above, this study designed and assessed a control scheme, i.e., scheme 3, to investigate the problem of high dimensionality. Also, abrupt changes in the parameter set between two sub-periods may result in anomalous or incorrect values in the fluxes and state variables of the time series. Hence, control scheme 4 is designed to investigate potential problems caused by abrupt changes in the parameters. These control schemes are assessed as follows: (1) the model performance is assessed at very low, low, medium, high and very high phases of flow, and the transferability of the dynamic parameter set to different time periods is determined; (2) the state variable and flux time series and their changes between two consecutive sub-periods are evaluated; and (3) the response of the dynamic parameter set to the dynamic catchment characteristics is evaluated. The underlying causes for poor model performance when sub-period calibration is used are investigated, and an effective calibration scheme for dynamic hydrological-model parameters, scheme 5, is recommended as a solution. Furthermore, the underlying mechanism of the lack of a response of the dynamic parameter set to the dynamic catchment characteristics is investigated.

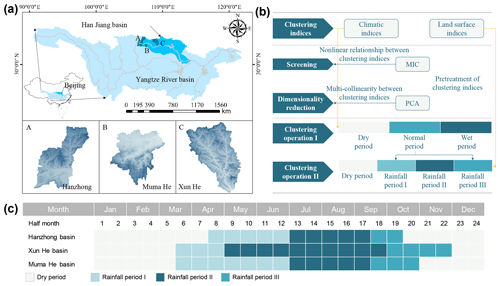
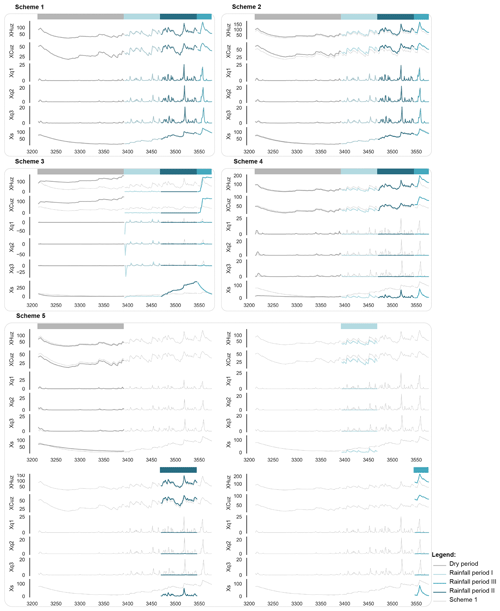
Figure 1 Study cases and data. (a) Locations of the study region, the Han Jiang and its three major tributaries considered in this study, i.e., the Hanzhong, Muma He and Xun He. (b) Flowchart of the sub-period partition using the CPP framework. (c) Heat map of sub-period partition. Note that the sub-periods include the dry period, rainfall period I, rainfall period II and rainfall period III. In the dry period, both the total amount and the variance values of all the precipitation series reach the minimum. In contrast, the total amount and the variance values of the precipitation series in rainfall period II (wettest period) reach the maximum, and the frequency of heavy rain is highest. In the two normal sub-annual periods (rainfall period I and rainfall period III), the climatic patterns are similar, but the streamflow volume is higher in rainfall period III than in rainfall period I. The reason is that higher antecedent soil moisture content contributed to the higher runoff in rainfall period III than in rainfall period I. More detailed descriptions of the clustering are described in Lan et al. (2018).

The paper is structured as follows. Section 2 presents the study cases and data, the partition methods, and the results of the sub-periods based on the dynamic catchment characteristics. Section 3 elaborates on the five calibration schemes for the dynamic parameters of the hydrological model and the assessment approaches. Section 4 presents the assessment results of the different schemes, the potential problems and the recommendation of an effective calibration scheme. Section 5 summarizes the underlying causes of poor model performance, followed by a discussion of the poor response of the dynamic parameters to the catchment dynamics. Section 6 summarizes the key conclusions of the study and outlines directions for future research.

2 Study cases and data

In this study, three sub-basins with different spatial scales in the Han Jiang basin, i.e., Hanzhong basin, Muma He basin and Xun He basin, were selected to demonstrate the proposed approach (Fig. 1a). Climatically, the Han Jiang basin is located in the monsoon region of the eastern Asia subtropical zone. The area is cold and dry in winter and warm and humid in summer (Lin et al., 2010), and there are seasonal changes in vegetation density and types (Fang et al., 2002). Subtropical vegetation affects temporal moisture conditions. Significant intra-annual changes in the climate and land surface conditions allow for exploring the seasonal dynamics of the hydrological processes. Therefore, the three basins are ideal locations for investigating the dynamics of hydrological-model parameters. Daily streamflow and climatic data from 1980 to 1990 were used. Nearly 73 % of the data samples (1980–1987) were used for calibration, and the remainder (1988–1990) was utilized to verify the model.

Figure 2 Calibration schemes. (a) Objectives of the schemes. (b) Schematic illustration of the five schemes. Note that in scheme 1, the parameters are time-invariant; in scheme 2, the dynamic of only the specific parameter is operated. The specific parameters in different sub-periods and the other fixed parameters are optimized simultaneously; in scheme 3, the parameter set is dynamized. The parameter sets in different sub-periods are optimized simultaneously; in scheme 4, only the data from the individual sub-periods are used for minimizing the objective function, while the model is run for the whole period. The parameter sets in different sub-periods are optimized. In the validation period, the parameter set between two consecutive sub-periods is updated accordingly. In scheme 5, the calibration is the same as in scheme 4. In the validation period, the simulated flow data from each separate sub-period are combined and compared with the observed flow.

The flowchart of the reasonable sub-period partition based on the dynamic catchment characteristics is shown in Fig. 1b. The data mining techniques were integrated to develop a CPP framework for sub-period partition to simulate dynamic behavior. The hydrological model was calibrated in each sub-period to achieve the dynamics of the parameter set, as illustrated in Fig. 1b. In the CPP, a set of climate–land-surface indices was provided and pre-processed using the maximal information coefficient (MIC) and principal components analysis (PCA). The climatic indices included total precipitation, maximum 1 d precipitation, maximum 5 d precipitation, moderate precipitation days, heavy precipitation days, total pan evaporation, maximum 1 d pan evaporation and minimum 1 d pan evaporation. The land surface indices included antecedent streamflow and runoff coefficient. Two clustering operations were performed based on the pre-processed climatic index system and land surface index system, respectively. The clustering results are shown in Fig. 1c. The results showed that the performance of the model with a CPP framework was significantly improved at high, middle and low streamflow. The transferability of the dynamic parameter set from the calibration to the validation period was also greatly improved.

It is worth emphasizing that the dynamic parameters during the validation period are set to the same as in the calibration period. The values are dependent on the calendar days. This is because our previous research (Lan et al., 2018) showed that the clustering results of the validation period are almost the same as the results of the calibration period. In that study, the hydrological model was calibrated in each sub-period to achieve the dynamics of the parameter set. The calendar year is clustered into four sub-annual periods based on hydrological similarities, and the clustering results were further verified by the hydrological data in the validation period. The reason is that the study area, i.e., the Han Jiang basin, is located in the monsoon region of the eastern Asia subtropical zone, and the seasonal variations of both climate conditions and vegetation density and types are more important than inter-annual variations (Fang et al., 2002).

Table 1 Definition of parameters, state variables and fluxes used in the HYMOD model (Wagener et al., 2001).

Note that the K_q parameter with the highest identifiability is chosen as the dynamic parameter in scheme 2.

3 Methodology

3.1 Calibration schemes

Five calibration schemes are designed and compared (see Fig. 2). The potential problems when dynamics of hydrological-model parameters are used include time-invariant parameters, compensation among parameters, the high dimensionality of the parameters and abrupt changes in the parameters; these factors are investigated, and a solution is recommended. For illustration purposes, the HYMOD (HYdrological MODel) model (Moore, 1985; Wagener et al., 2001; Vrugt et al., 2002; Yadav et al., 2007; de Vos et al., 2010; Pathiraja et al., 2018), which is a commonly used lumped rainfall–runoff model with five parameters, is utilized. It consists of a simple rainfall excess model based on the probability-distributed moisture store which characterizes the catchment storage as a Pareto distribution of buckets of varying depths as the soil moisture accounting component. It routes through three parallel tanks for quick flow and a tank for slow flow and required five adjustable parameters: H_UZ, B, α, K_q and K_s. XH_UZ and XC_UZ are state variables characterizing the upper soil moisture content; AE is actual evapotranspiration, which is calculated by linear correlations between the soil moisture state and the potential evapotranspiration; eff_P is effective precipitation; OV is excess precipitation to the routing module generated from the overflow of the soil moisture accounting component; see Moore (1985) for a detailed description of the soil moisture accounting model; $X_{q_{\mathrm{1}}}$, $X_{q_{\mathrm{2}}}$, $X_{q_{\mathrm{3}}}$ and X_s are the state variables of the individual tanks of the routing module; and Q_q and Q_s are the flow values generated from the quick- and slow-flow tanks, respectively. The definitions of the model parameters, state variable and fluxes are presented in Table 1. All schemes with the same set of shuffled complex evolution method were developed at the University of Arizona (SCE-UA). The SCE-UA algorithm is a subset of a global evolution algorithm (Duan et al., 1993; Hanne, 2000; Michalewicz and Schoenauer, 1996; Omran and Mahdavi, 2008; Storn and Price, 1997; Yiu-Wing and Yuping, 2001) which was used as an example of a global optimization algorithm in this study. More information is presented in Sect. S1 of the Supplement. The simulations have a warm-up period of 1 year in the calibration period and 3 months in the validation period. The objective function is defined as the combination of the Nash–Sutcliffe efficiency index (NSE) and the logarithmic transformation (LNSE) (Nash and Sutcliffe, 1970). The NSE is sensitive to the discharge dynamics, and the LNSE emphasizes the low flows because the log of the discharge is used (Nash and Sutcliffe, 1970; Guntner et al., 1999; Kiptala et al., 2014; Nijzink et al., 2016). It is expressed as

$$\begin{array}{}\text{(1)}& \mathrm{OF}=\mathrm{1}-\mathrm{0.5}\cdot (\mathrm{NSE}+\mathrm{LNSE}),\end{array}$$

where OF(0, ∞) is the objective function value. The closer the value of OF is to zero, the better the model performance is.

• Scheme 1. This scheme investigates the problem of time-invariant parameters. The parameters do not change during the entire calibration and validation periods.

• Scheme 2. This scheme investigates the compensation among the parameters. In the calibration period, a specific dynamic parameter and the other fixed parameters in different sub-periods are optimized simultaneously. For example, eight parameters, namely one specific parameter in the four sub-periods and another four fixed (i.e., temporally invariant) parameters, are optimized simultaneously during one run in HYMOD. The transition of the state variables and fluxes between two consecutive sub-periods is achieved by considering the last values of the former period as the initial values of the next period. In the validation period, the model is run using the inputs with the specific dynamic parameter and other fixed parameters. The transitions of parameters, state variables and fluxes between two consecutive sub-periods are handled the same as in the calibration period.

  The specific dynamic parameter is usually identified by whether it responds to the dynamic catchment characteristics. However, due to the complex correlations among the parameters and imperfect model structures (missing processes or oversimplified parameterizations in the model), the individual parameters may not represent their defined physical characteristics, such as temporal changes in soil, land cover and climate conditions. Hence, the parameter with the highest sensitivity was chosen as the dynamic parameter (Merz et al., 2011; Pfannerstill et al., 2014; Zhang et al., 2015; Deng et al., 2016, 2018; Guse et al., 2016; Ouyang et al., 2016; Xiong et al., 2019). In this study, the dynamic parameter K_q with the highest identifiability and the other fixed parameters are optimized. The chosen parameter is marked in Table 1.

• Scheme 3. This scheme investigates the high dimensionality of the parameters. In the calibration period, the parameter sets in different sub-periods are optimized simultaneously. For example, 20 parameters, namely 5 parameters of the hydrological model in 4 sub-periods, are optimized simultaneously in one run. The transition of the state variables and fluxes between two consecutive sub-periods is achieved by considering the last values of the former period as the initial values of the next period. In the validation period, the model is run using the dynamic parameter set. The transitions of the parameters, state variables and fluxes between two consecutive sub-periods are handled the same as in the calibration period.

• Scheme 4. This scheme investigates the abrupt changes in the parameters. In the calibration period, only the data from the individual sub-periods are used for minimizing the objective function, while the model is run for the whole period. For example, five parameters of the hydrological model in four sub-periods are optimized in four runs. The calibrated flow data from each sub-period are then combined and compared with the observed flow. In the validation period, the transitions of parameters, state variables and fluxes between two consecutive sub-periods are handled the same as in the validation period of scheme 3. In the validation period, the effects of the correlations and high dimensions of the parameters are excluded, and the influences caused by the abrupt changes in the parameters are investigated.

• Scheme 5. A solution is recommended to overcome the above problems that are caused by the time-invariant parameters, compensation among parameters, high dimensionality and abrupt shifts in the parameters. In the calibration period, the model run is the same as that of the calibration period of scheme 4. In the validation period, the simulated flow data from each sub-period are combined and compared with the observed flow.

The above description reveals that the model run in the calibration period is the same in scheme 4 and scheme 5. However, the model run in the validation period is actually different. In the validation period of scheme 4, the model runs one time using the dynamic parameter set. The parameter set between two consecutive sub-periods is switched. As a result, the transition of the state variables and fluxes between two consecutive sub-periods is abrupt and achieved by considering the last values of the former period as the initial values of the next period. In the validation period of scheme 5, the model runs N times (N is the number of the divided sub-periods), combining the simulated flow data in the sub-periods. The comparison between scheme 4 and scheme 5 is to investigate the effect of the abrupt shifts in the parameters on the model run with dynamic parameters.

3.2 Assessment

3.2.1 Assessment of model performance

The performance assessments of the calibration schemes include (1) an assessment of the performance in different phases of the streamflow and (2) an assessment of the transferability of the dynamic parameters to different time periods. Seven performance metrics are used to assess the performance for different parts of the hydrograph in the calibration and validation periods. The metrics are listed and defined in Table 2. The differences in these metrics between the calibration period and the validation period are used to assess the transferability of the optimized parameters. The transferability of the parameters to different time periods is considered a requirement for the successful validation of the model (Gharari et al., 2013; Klemeš, 1986).

Table 2 Definitions of the performance metrics.

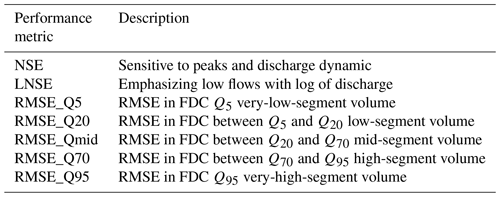
Note that the flow duration curve (FDC) is usually split into different segments to describe different flow characteristics of a catchment (Cheng et al., 2012; Coopersmith et al., 2012; Kim and Kaluarachchi, 2014; Pugliese et al., 2014; Pfannerstill et al., 2014). The RMSE with quadratic character is usually used to evaluate poor model performance due to the strong sensitivity to extreme positive and negative error values.

3.2.2 Assessment of the state variables and fluxes

The internal processes of the hydrological model run include the state variable and flux time series. The abrupt changes in the parameters between two consecutive sub-periods may result in changes in the state variables and fluxes, thereby affecting the simulation results. Hence, all the state variables and fluxes obtained from the different schemes are investigated, and the underlying physical mechanisms are discussed (Kim and Han, 2017).

3.2.3 Assessment of the dynamic parameter set

The response of the dynamic parameter sets to the dynamic catchment characteristics in all schemes is investigated for the two response modes of HYMOD, i.e., the soil moisture mode and routing mode. Furthermore, the underlying physical mechanisms based on dynamic catchment characteristics are analyzed.

4 Results

4.1 Model performance

For a concise model evaluation, the model performance is analyzed with multi-metric frameworks with appropriate performance metrics, including five-segment evaluation (5 FDC; flow duration curve with the root mean square error) (Pfannerstill et al., 2014), the Nash–Sutcliffe efficiency index (NSE) (Nash and Sutcliffe, 1970) and the logarithmic transformation. For the robustness of model evaluation, the transferability of the optimized parameters between the calibration period and the validation period is considered. The results of the assessment are shown in Fig. 3.

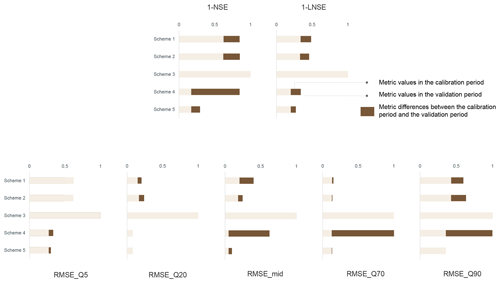
Figure 3 Model performance. Model performance of the five schemes in the Hanzhong basin; (1) the performance in different phases of the streamflow and (2) the transferability of dynamic parameters to different time periods.

The performance of scheme 2 is only slightly better than that of scheme 1, which indicates only a slight increase in the model performance. Scheme 3 has the worst model performance at the global level; i.e., all metrics are much higher than one in the calibration period and validation period. Scheme 4 has the highest overall model performance in the calibration period. For example, the NSE and LNSE are 45.3 % and 13.8 %, respectively; these values are considerably higher than the metrics of scheme 1. The other metrics also indicate that scheme 4 performs best in all flow phases in the calibration period. However, the model performance of scheme 4 in the validation period is only slightly better than that of scheme 1. Scheme 5 has the same model performance as scheme 4 in the calibration period. Nevertheless, the overall model performance of scheme 5 is significantly higher than that of the other schemes in the validation period. The transferability of the optimized parameters is analyzed in all schemes. Scheme 5 has the smallest differences, and scheme 4 has the largest differences in the metrics between the calibration period and validation period.

In summary, scheme 5 does not only have the highest overall performance under different flow conditions in the calibration period and validation period but also exhibits good transferability of the model parameters. Scheme 4 exhibits good performance in the calibration period but does not perform well in the validation period. Scheme 3 has extremely poor model performance at the global level. Scheme 2 does not have better performance than scheme 1. The evaluation results of the five schemes in the Muma He basin and Xun He basin are listed in Sect. S3. The results are similar to those of the Hanzhong basin and will be discussed in Sect. 5.1.

4.2 State variables and fluxes

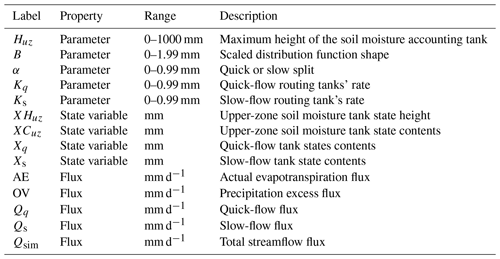
The assessment results of the state variables and fluxes are shown in Figs. 4 and 5. The variables of scheme 2 are similar to those of scheme 1. The model performance of scheme 2 is only slightly better than that of scheme 1. In scheme 3, there are some unexpected values of the state variables in the time series. In scheme 4, invalid values of the fluxes and state variables are found at the junction of sub-periods, where the parameter set exhibits abrupt changes. In scheme 5, (1) Q_s, XH_UZ and XC_UZ are lower in the dry period and higher in rainfall period II than those in scheme 1. The results indicate that the performance of the model run is better in the dry period and rainfall period II because the runoff is usually overestimated in the dry period (Pool et al., 2017; Wang et al., 2017a; Tongal and Booij, 2018; Xiong et al., 2018) and underestimated in the wettest period (Guo et al., 2018; Höge et al., 2018; Pande and Moayeri, 2018; Wang et al., 2018). It is observed that the state variable X_s and the flux Q_s have larger effects on simulating runoff than the quick-flow (Q_q and X_q) mode in rainfall period II. The reason is that most of the excess streamflow is diverted to the slow-flow routing, hence the fluxes and state variables present more representativeness of the slow-flow tank mode. (2) A comparison of the observations and simulations of the runoff in scheme 1 and scheme 5 indicates that both peak flows in rainfall period II are more accurately simulated by scheme 5. (3) Scheme 5 also exhibits superior performance in the two normal periods because the state variables provide a good representation of the physical mechanism. The state variables XH_UZ and XC_UZ are lower in rainfall period I and higher in rainfall period III than in scheme 1. The reason is that the antecedent soil moisture content in rainfall period III is higher than in rainfall period I (Lan et al., 2018). Consequently, the results are consistent with the results in Sect. 4.1. The dynamic parameters in scheme 5 provided a good representation of the dynamic catchment characteristics.

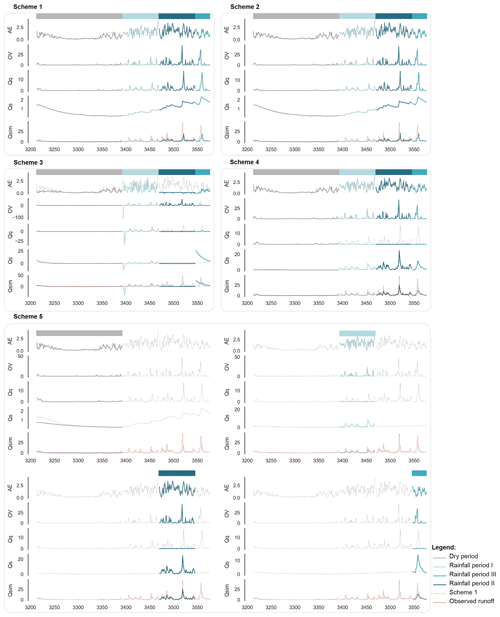
Figure 4 Results of the flux assessment. The fluxes (including AE, OV, Q_q, Q_s and Q_sim) for the five schemes in the reference year in the validation period in the Hanzhong basin. Note that the variables in different sub-periods are denoted by different colors (same colors as in Fig. 2a). The variables of scheme 0 are denoted by the thin grey lines in each box. The observed streamflow time series data are denoted as thin red lines. All fluxes and state variables in the calibration and validation periods are presented in Sect. S3.

Figure 5 Results of the state variable assessment. The state variables (including XH_UZ, XC_UZ, $X_{q_{\mathrm{1}}}$, $X_{q_{\mathrm{2}}}$, $X_{q_{\mathrm{3}}}$ and X_s) for the five schemes in the reference year in the validation period in the Hanzhong basin.

4.3 Dynamic parameter set

The dynamic parameter values optimized by the four sub-period calibration schemes in the Hanzhong basin are shown in Fig. 6. In scheme 2, the dynamic parameter K_q with the highest identifiability and the other fixed parameters are optimized. The result shows that the responses of the dynamic parameter K_q to the dynamic catchment characteristics are not clear. In scheme 3, the parameters H_UZ and B in the soil moisture mode of HYMOD (Moore, 1985; Vrugt et al., 2002) show no regular patterns in any of the schemes, and this is similar for α, K_q and K_s in the slow- and quick-flow routing mode. In short, the dynamic parameters do not show clear responses to the dynamic catchment characteristics in scheme 2 or scheme 3. In scheme 5, which is the same as scheme 4 in the calibration period, K_s accurately describes the model responses in the sub-periods for the different catchment characteristics. The value of K_s is lowest in the dry period and highest in the wettest period. However, the parameter K_q exhibits no significantly regular changes. The main reason is that most of the excess streamflow in the three rainfall periods is diverted to the slow-flow tank because the α values are close to zero. This means that the quick-flow tanks do not have an effect on the simulations. The parameter sets optimized by scheme 1 and scheme 5 in the Muma He basin and Xun He basin are listed in Sect. S3. The results are similar to those of the Hanzhong basin.

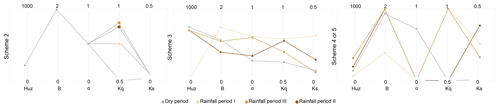
Figure 6 Results of the dynamic-parameter-set assessment. The dynamic parameter sets optimized by the four sub-period calibration schemes in the Hanzhong basin.

In summary, scheme 5 performs best for identifying the dominant parameters and their responses to the dynamic catchment characteristics. The dynamic features of the parameters also demonstrate the necessity for sub-period calibration. Furthermore, it is interesting that the state variables and fluxes describe the dynamic catchment behavior more robustly than the dynamic parameters. In light of this, the underlying causes for the poor response of the dynamic parameter set to the catchment dynamics are investigated.

5 Discussion

5.1 Underlying causes of poor model performance

The evaluation results of the five schemes are summarized to explore the possible reasons for poor model performance:

1. Time-invariant parameters. Scheme 1, with the time-invariant parameter set, averages the hydrological responses. As a result, scheme 1 resulted in poor simulation accuracy or weak transferability of the optimized parameters in different flow conditions. The results were consistent with Delorit et al. (2017), Fowler et al. (2018), and Xiong et al. (2019).

2. Compensation among parameters. In scheme 2, the individual parameters with high identifiability did show clear responses to the dynamic catchment characteristics. Bárdossy (2007) demonstrated that changes in one parameter may be compensated for by changes in other parameters due to their interdependence (Westra et al., 2014; Klotz et al., 2017; Wang et al., 2017b, 2018). Therefore, although a specific parameter is dynamic, the other parameters may counteract those changes, resulting in no overall change in the hydrological processes. Hence, the model performance in scheme 2 was relatively low.

3. High dimensionality of parameters. In scheme 3, it has a sound logic by continuously running the model with the dynamic parameter set like the real system. However, the results showed that all fluxes and state variables in the time series were anomalous, and the model exhibited extremely poor performance. It was demonstrated that parameter optimization in high-dimensional parameter space with correlated parameters resulted in the failure of the modeling run (Beven and Binley, 1992; Sivakumar, 2004; Bárdossy and Singh, 2008; Laloy and Vrugt, 2012).

4. Abrupt shifts in parameters. In scheme 4, the abrupt shifts in the parameter set between the sub-periods resulted in anomalous values in the fluxes and state variables in the time series, which results in the failure of the model in the validation period. Kim and Han (2017) also emphasized the negative effects of abrupt shifts in the parameter set on the model performance.

In summary, scheme 5 is recommended for dynamic hydrological-model parameters because it can capture the temporal variations of the dynamic catchment characteristics and overcome the underlying problems responsible for poor model performance. Although scheme 5 has a higher computational cost, this does not represent a large problem with current computing devices.

5.2 Underlying causes of the poor response of the dynamic parameters to the catchment dynamics

The dynamic parameter set was estimated using global optimization algorithms. However, if the convergence fails, the global optimum cannot be determined, and the optimal parameter values may be anomalous. In this case, the optimal results do not represent the hydrological processes in a catchment (Gomez, 2019; Weise, 2009). In order to investigate the underlying causes of the poor response of the dynamic parameters to the catchment dynamics, we assessed the convergence performance of the dynamic parameters and determined the ability of the parameters to respond to the catchment dynamics (Zecchin et al., 2012; Zheng et al., 2017; Azad and Optimization, 2019).

5.2.1 A tool for the convergence evaluation of the dynamic parameters

In order to overcome the limitation of traditional tools for evaluating the convergence behavior of global optimization algorithms for hydrological models, including the visualization of the high-dimensional parameter response surface, rough response surfaces with discontinuous derivatives, poor or inconsistent sensitivities of the response surface, non-convex mesh surfaces, and the dynamic convergence process in high-dimensional parameter spaces (Duan et al., 1992, 1994; Sorooshian et al., 1993; Cooper et al., 1997; Gupta et al., 1998; Vrugt et al., 2005; Weise, 2009; Zhang et al., 2009; Sun et al., 2012; Arora and Singh, 2013; Derrac et al., 2014; Piotrowski et al., 2017; Gomez, 2019), a simple and powerful approach is proposed, namely, Evaluate the Convergence Performance using Violin Plots (ECP-VP). This tool represents the potential features of the fitness landscapes (see Fig. 7) and provides a visualization of the convergence behavior in multi-parameter space. The strategy is as follows.

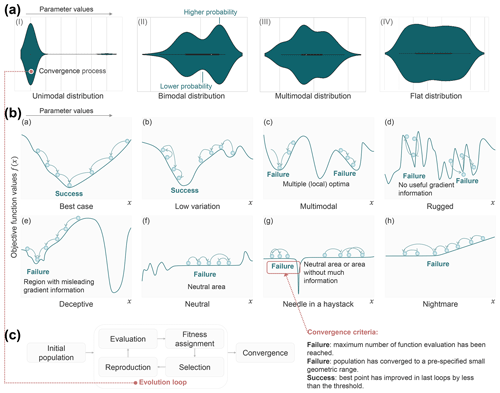
Figure 7 Evaluation of the ability of the dynamic parameters to respond to the catchment dynamics. (a) Evaluation of the convergence processes using violin plots (ECP-VP). The horizontal axis of the violin plot denotes the parameter values, and the vertical axis denotes the probability values. The probability distribution of elements of the search space is represented by the violin plots. (b) All possible properties of the fitness landscapes. (c)  The basic cycle of the global evolution algorithm. Initial population: create an initial population of random individual. Evaluation: compute the objective values of the solution candidates. Fitness assignment: use the objective values to determine the fitness values. Selection: select the fittest individuals for reproduction. Reproduction: create new individuals from the mating pool by crossover and mutation. Note that the fitness landscapes are a very powerful metaphor for visualizing the convergence processes in global optimization. Some intuitive sketches of fitness landscapes with possible properties are as follows. The horizontal axis denotes the parameter values, and the vertical axis denotes the objective function values. The direction of the arrow represents the direction of evolution. The possible properties include the following. (a) Best case: an optimization process is ideal for estimating the globally optimal parameters. (b) Low variation: an optimization process with low variation is fair for estimating the globally optimal parameters. (c) Premature convergence: an optimization process has prematurely converged to a local optimum if it is no longer able to explore other parts of the search space than the area currently being examined and there exists another region that contains a superior solution. (d) Ruggedness: if the objective function values are fluctuating, i.e., increasing or decreasing, it is difficult to determine the correct direction for the optimization process. In short, ruggedness is multimodality plus steep ascends and descends in the fitness landscape. (e) Deceptiveness: the gradient of the deceptive objective function values leads the optimizer away from the optima. (f) Neutrality: the outcome of the application of a search operation to an element of the search space is neutral if it yields no change in the objective function values. (g) Needle in a haystack: the optimum occurs as an isolated spike in a plane, representing the occurrences of extreme ruggedness combined with a general lack of information in the fitness landscape. (h) Nightmare: the optimum is difficult to achieve in an approximate plane. More details on the fitness landscapes and their properties can be found in Weise (2009).

The end of each evolution loop in the optimization process is regarded as a cut-off point. The parameter set with the best objective function value in each evolution loop is recorded in the “convergence process”.

Violin plots, which are an excellent tool to visualize the kernel density distribution of the data points (Hintze and Nelson, 1998; Piel et al., 2010), are used to configure the convergence process in the individual parameter spaces. The probability distributions of the violin plots are used to represent the possible properties of the fitness landscapes. The anatomy of the violin plot and the associated information can be found in Sect. S2. With an adequate parameter space and sufficient density of coverage, the four types of distributions of violin plots are matched to the property sketches of the fitness landscapes (Weinberger, 1990; Forrest, 1995; Harik et al., 1999; Gibbs et al., 2004; Arsenault et al., 2014; Maier et al., 2014).

A decrease in the performance of the convergence and the candidate mechanisms are interpreted as (I) an unimodal distribution: an ideal global convergence process is used to estimate the best solution. The unimodal distribution matches two types of fitness landscape sketches including the best case and low variation. These can also be interpreted as (II) a bimodal distribution: there are two main local optima and the distance to the two local convergence regions is far. It becomes more complicated for the optimization process to find the global optimum, and the premature convergence to a local optimum may occur (Duan et al., 1992, 1993, 1994; Weise, 2009; Sun et al., 2012; Derrac et al., 2014; Gomez, 2019). The bimodal distribution symbolizes the two types of fitness landscape sketches including the multimodal and deceptive types. These can also be interpreted as (III) a multimodal distribution: the response surface may be multimodal plus steep ascends and descends. This means that multiple local optima exist. With the maze of minor local optima, the calibration algorithm may fail to reach the global optimum. Because the minor optima may be found quite far from the global optimum, the search may terminate prematurely without finding an approximate solution (Dakhlaoui et al., 2017; Duan et al., 1992, 1993, 1994). The multimodal distribution matches the three types of fitness landscape sketches including the multimodal, rugged and deceptive types. These can also be interpreted as (IV) a flat distribution: this is similar to the multimodal distribution, and its surface may be noisy. The very poor sensitivity of the objective function to the parameter fluctuation causes weak convergence of the parameter (Duan et al., 1992, 1993, 1994; Dakhlaoui et al., 2017; Rahnamay Naeini et al., 2018; Vrugt and Beven, 2018). The flat distribution matches the three types of fitness landscape sketches, including the neutral, needle-in-a-haystack and nightmare types.

5.2.2 Convergence assessment

The convergence assessment results of scheme 1 and scheme 5 in the Hanzhong basin are shown in Fig. 8. In scheme 1, (1) the parameter B represents the bimodal distribution in the parameter space, indicating that the fitness landscape of B is unsteady or fluctuating (see Fig. 8a). It is inferred that the convergence processes of the parameter B may be affected by a prominent local optimum. The outcomes of the search operations may be arbitrary, which leads to a divergence away from the global optima. As a result, the convergence performance of B is poor. (2) Although H_UZ, α, K_q and K_s rapidly converge, and the range is small, the magnification (Fig. 8b) shows bimodal or multimodal distributions. The global optima cannot be determined in the H_UZ, α, K_q and K_s parameter space. As a consequence, the convergence of the parameters in scheme 1 is poor and the response of the parameters to the catchment behavior with a low level of confidence.

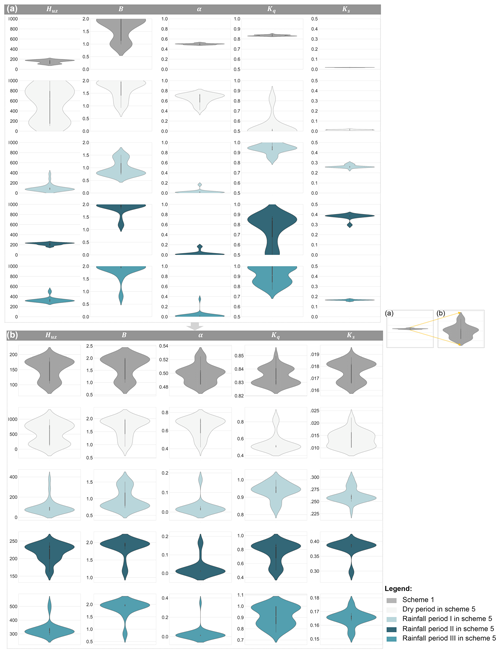
Figure 8 Convergence performance for scheme 1 and scheme 5 in the Hanzhong basin. (a) The convergence processes in the parameter spaces; (b) magnification of the convergence processes of the parameters.

In scheme 5, the four sub-periods are evaluated separately. (1) In the dry period, except for K_s, the distributions of the other parameters are oscillating in the entire feasible parameter space. Indeed, the magnification of parameter K_s (see Fig. 8b) shows a multimodal distribution. The result indicates that the convergence performance of the parameter set in the dry period is poor. Due to the weak relationship between precipitation and runoff in the dry period (Moore, 1985; Yadav et al., 2007; de Vos et al., 2010), most modules of the model in the dry period do not accurately characterize the behavior of the catchment. (2) In rainfall periods I–III, the parameters α and K_s with a unimodal distribution have the best convergence performance. The α values in the three rainfall periods are close to the minimum; hence the slow-flow tank controls the cascade routing component of the model. The α and K_s parameters, with high identicality and the best convergence performance, also demonstrate that the chosen model is most suitable for the streamflow simulation in the three rainfall periods. The main reason is that the HYMOD model is well suited for catchments dominated by “saturation excess overland flow” processes. Intense rainfall events contribute to saturation excess overland flow in rainfall periods (Herman et al., 2013; Sarrazin et al., 2016; Wang et al., 2017a; 2018). Moreover, the results also illustrate that the optimal α and K_q (or K_s) in the cascade routing component have higher reliability than the optimal H_UZ and B in the soil moisture component. In summary, the dynamic parameters α and K_q (or K_s) in scheme 5 have good convergence performance and accurately describe the response to the dynamic catchment characteristics. However, the parameters H_UZ and B, with poor convergence performance, exhibit a poor ability to describe the response to the dynamic catchment characteristics. Interestingly, the convergence performance results of the parameters for the dominant response modes in HYMOD are consistent with the results of the performance of the state variables and fluxes and the dynamic parameter set. The evaluation results of ECP-VP for scheme 1 and scheme 5 in the Muma He basin and Xun He basin are shown in Sect. S4. The results are similar to those of the Hanzhong basin.

The following results were observed: (1) the proposed ECP-VP tool accurately described the convergence behavior of the models in the individual parameter spaces, demonstrating the reliability of the optimized dynamic parameter values in responding dynamic catchment characteristics. The tool can be used to determine the reason for the potentially poor convergence performance. (2) The convergence performance can be used to identify the operation modes of hydrological models and provides valuable guidance for the improvement of hydrological models with different catchment characteristics. (3) The convergence performance of the parameters in one sub-period might be superior or inferior to those of other sub-periods. For example, the convergence performance of all parameters was worse in the dry period than in the three rainfall periods. Indeed, due to the complex correlations between the parameters in a parameter set, the convergence performance of an individual parameter may be significantly affected by the other parameters. For this reason, it is not recommended to use the convergence performance of individual parameters but rather the convergence performance of the parameter set. However, the application of this solution requires a significant amount of experiments, validation, analysis and discussion, and these points will be investigated in future studies.

6 Conclusions

We designed five calibration schemes for the dynamics of hydrological-model parameters to investigate the underlying causes of poor model performance. An assessment system was proposed to determine an appropriate calibration scheme. The potential reasons for the poor response of the dynamic parameter set to the catchment dynamics were discussed. The following conclusions were drawn:

1. The five schemes were systematically evaluated with respect to the model performance in different flow phases, the transferability of the dynamic parameters to different time periods, the state variable and flux time series, and the response of the dynamic parameter set to the dynamic catchment characteristics. The possible reasons for the poor model performance included (1) time-invariant parameters, (2) compensation among parameters, (3) high dimensionality of the parameters and (4) abrupt shifts of the parameters. Interestingly, the results also proved that changes in the state variables and fluxes time series provided a more robust description of the dynamic catchment characteristics than the dynamic parameters.

2. The proposed calibration (1) compensated for the deficiencies in the model structure, (2) provided high forecast accuracy for different flow phases, (3) exhibited good transferability of the model parameters between the calibration and validation periods, (4) improved the ability to identify the dominant parameters and their responses to the catchment processes, and (5) accurately characterized the dynamic behavior of the catchments.

3. The reasons for the poor response of the dynamic parameter to the catchment dynamics were determined by assessing the convergence performance of the dynamic parameters. The results indicated that the dynamic parameters with good convergence performance accurately described the response to the dynamic catchment characteristics, whereas parameters with a poor convergence performance had poor ability to describe the response to the dynamic catchment characteristics.

4. The assessment results of the state variables and fluxes and the convergence performance of the parameters provided robust indications of the dominant response modes of the hydrological models in different sub-periods or catchments with distinguishing catchment characteristics.