the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Multivariate stochastic bias corrections with optimal transport
Mathieu Vrac
Philippe Naveau
Pascal Yiou
Bias correction methods are used to calibrate climate model outputs with respect to observational records. The goal is to ensure that statistical features (such as means and variances) of climate simulations are coherent with observations. In this article, a multivariate stochastic bias correction method is developed based on optimal transport. Bias correction methods are usually defined as transfer functions between random variables. We show that such transfer functions induce a joint probability distribution between the biased random variable and its correction. The optimal transport theory allows us to construct a joint distribution that minimizes an energy spent in bias correction. This extends the classical univariate quantile mapping techniques in the multivariate case. We also propose a definition of non-stationary bias correction as a transfer of the model to the observational world, and we extend our method in this context. Those methodologies are first tested on an idealized chaotic system with three variables. In those controlled experiments, the correlations between variables appear almost perfectly corrected by our method, as opposed to a univariate correction. Our methodology is also tested on daily precipitation and temperatures over 12 locations in southern France. The correction of the inter-variable and inter-site structures of temperatures and precipitation appears in agreement with the multi-dimensional evolution of the model, hence satisfying our suggested definition of non-stationarity.
- Article
(2859 KB) - Full-text XML
-
Supplement
(756 KB) - BibTeX
- EndNote
Global climate models (GCMs) and regional climate models (RCMs) are used to study the climate system. However, their outputs often appear biased compared to observational references (e.g., Randall et al., 2007). For example, the temperature means can be shifted. Thus, removing this bias is often necessary to drive impact studies such as those based on crop or hydrological models (Chen et al., 2013). The main goal of bias correction (BC) is to match the statistical features of climate model outputs with observations (see, e.g., Ehret et al., 2012; Gudmundsson et al., 2012). The most used method is the quantile mapping (Panofsky and Brier, 1958; Wood et al., 2004; Déqué, 2007), which adjusts the quantiles of the variables of interest in the stationary case (Shrestha et al., 2014). The importance of the stationarity hypothesis has been discussed by a few studies (Christensen et al., 2008; Maraun, 2012; Nahar et al., 2017). Some extensions, like CDF-t (Cumulative Distribution Function transfer, Michelangeli et al., 2009), can take into account some of the non-stationarity in GCMs or RCMs.
Most of those methods are univariate, and do not take into account the spatial and inter-variable correlations, which may alter the quality of the corrections (e.g., Wilcke et al., 2013; Maraun, 2016). Maraun et al. (2017) have pointed out that correcting model output could induce biases of physical processes and that such procedures require an understanding of the nature of the biases. In particular it is crucial to investigate the way key climate variables co-vary.
This shortcoming has led to the recent development of multivariate techniques. As mentioned by Vrac (2018), two kinds of methods are currently available. The first type corrects separately each marginal and applies afterwards a correction of the dependence structure (e.g., Vrac and Friederichs, 2015; Vrac, 2018; Nahar et al., 2018; Cannon, 2018). The second kind performs recursive corrections: each variable is corrected conditionally on the previously already corrected variables (Bárdossy and Pegram, 2012; Dekens et al., 2017). These last methods have two main limitations. First, the correction depends on the ordering of the marginals. Second, each marginal is adjusted conditionally on previously corrected marginals, which reduces the number of data at each step. Furthermore, the variability of observations is generally greater than that of the climate models. To increase the variability, von Storch (1999), Wong et al. (2014) and Mao et al. (2015) suggested introducing a stochastic component into the bias correction procedure. In this paper, we develop a multivariate and stochastic bias correction method, different from the two categories presented, based on elements from optimal transport theory.
Optimal transport theory is a natural way to measure the dissimilarity between multivariate probability distributions (Villani, 2008; Muskulus and Verduyn-Lunel, 2011; Robin et al., 2017), especially in a multivariate case. For example, this has already been successfully applied in image processing to transfer colors between images (Rubner et al., 2000; Ferradans et al., 2013). Here, our goal is to apply optimal transport techniques to perform bias correction in estimating a particular joint law (called a transport plan) that links the probability distributions of a biased random variable and its correction. This joint law minimizes a cost function, representing the energy needed to transform a multivariate probability distribution to another. In this optimal transport context, any realization of the biased random variable induces a conditional law of the transport plan, associating the realization and its correction. As the corrections are randomly drawn from these conditional laws, the suggested method is stochastic by construction.
Moreover, Maraun et al. (2017) also stressed that BC methods do not correct the physical processes of the model, and errors can propagate into the corrections. However, one key aspect of the present work is to highlight that, in a climate change context (or more generally, in a framework where corrections are performed in conditions different from the calibration dataset), a proper BC method should provide changes – from calibration to projection periods – in agreement with the modeled data to be corrected. Knowing the quality of the raw modeled data (and of the underlying processes) is therefore an important a priori step. Nevertheless, this is beyond the scope of bias correction per se.
This paper is organized as follows. In Sect. 2, the developed theoretical framework to perform bias correction is presented. In particular, the classical definition of bias correction as transfer function is generalized with optimal transport theory. Two methods are presented: optimal transport correction (OTC, stationary case) and dynamical optimal transport correction (dOTC, non-stationary case). In Sect. 3, the proposed methodology is tested on an idealized non-stationary case based on chaotic attractors. In Sect. 4, a multivariate bias correction is performed on a regional climate model (RCM) simulation of temperatures and precipitation, in a cross-validation case. Section 5 provides conclusions and perspectives.
The general goal of this paper is the correction of a random variable, denoted X (e.g., a biased climate model output) with respect to a reference random variable, denoted Y. The random variables X and Y live in dimension d. If d=1, we denote them X and Y. The probability law of X (or Y) is denoted ℙX (or ℙY).
Following Piani et al. (2010), a bias correction method of X with respect to Y is a map , called a transfer function, such that the random variable 𝒯(X) (the correction) follows the same law as Y, i.e., ℙ𝒯(X)=ℙY. This definition covers most of the practical cases, but we can construct random variables where no deterministic transfer function exists, e.g., if X is constant and Y is not. Thus, beyond a multivariate transfer function, it is necessary to extend the definition of bias correction.
In the first part, we highlight our method of bias correction with a univariate example starting from quantile mapping. In the second part, the mathematical theory is explained. Finally, an extension of our method in a non-stationary context is presented.
2.1 From quantile mapping to optimal transport
We start with the construction of a quantile mapping method in the univariate case, i.e., with d=1. In this context, the biased and reference random variables are denoted X and Y, respectively. A transfer function 𝒯 between X and Y is constructed on the cumulative distribution functions (CDFs) of X and Y, defined by
A realization y of Y is the correction of a realization x of X if and only if FX(x)=FY(y). Under the assumption that FY is invertible, the correction y of x is given by
Thus the transfer function is written . This method is called quantile mapping. Indeed, the quantiles of X and Y are matched through the relation FX(x)=FY(y).
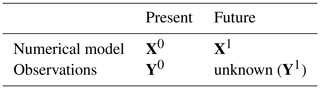
Figure 1Histogram of two Gaussian laws X and Y in blue and red. (a) The x axis indicates the edges of each bar. The black arrows indicate how the quantile mapping matches an element of X with its correction. (b) The x axis gives the center of each bar. The black arrows indicate the possibilities for how the probability of obtaining the value x1 for X can be distributed among the possible values yj of Y. The γ1j correspond to the number of realizations moved. These arrows can be generalized to each xi. (c) The x axis gives the center of each bar. The black arrows indicate the non-zero γij estimated by the OTC method. (d) Bivariate histogram of two Gaussian laws. The black arrows represent how the OTC method fits each xi with its correction. To facilitate readability, only 30 arrows are represented.
We illustrate the quantile mapping method with an example in Fig. 1a. In this example, the random variables X and Y are two Gaussian laws centered, respectively, on 0 and 10, with a standard deviation of 1. We cut ℝ into cells of length 1 and estimate the histograms. Fig. 1a shows the two histograms of X and Y in red and blue, respectively. The x axis gives the empirical quantiles of the edges of each cell. The black arrows indicate how the quantile mapping connects a cell of X to a cell of Y. For example, the realizations of X in the first blue cell are corrected and transferred to realizations in the first three red cells of Y.
The main point here is the following: in the univariate context, we can perform a bias correction with only the black arrows. A realization in a cell of X is corrected to a realization into a cell of Y connected by a black arrow. Because in a multivariate context the quantile mapping can not be used to estimate these arrows (CDFs are not invertible), our problem is the following: how to construct these black arrows in a multivariate context.
For this, let xi (yj) be the centers of each cell of the histogram of X (Y). Let pxi be the number of realizations of X in the interval xi, and let pyj be the number of realizations of Y in the interval yj. We represent all possible black arrows by a collection of coefficients γij. A γij value corresponds to the number of realizations in the cell xi that are transferred to realizations in the cell yj. We obtain the following two equalities:
representing how the cell xj is split into each cell yj; and
representing how cell yj received the realizations from each cell xi. We depict the γ1j coefficients in Fig. 1b. The black arrows represent the number of realizations γ1j that are transferred to each yj.
The problem is to calculate the coefficients γij. For each displacement γij, we can associate a cost, which is the square of the length of the displacement, . This choice comes from the optimal transport theory, and will be highlighted in the next section. To correct γij realizations, we have a cost of . We thus obtain a global cost associated with the γij coefficients:
Our bias correction method is defined by the γij coefficients minimizing the functional C. The γij obtained by minimizing C for our example are shown in Fig. 1c. Comparing with the quantile mapping in Fig. 1a, we can see that the obtained coefficients (the black arrows) are similar. Indeed, the coefficients induced by the quantile mapping are precisely those minimizing the functional C. Proofs of this statement can be found in Farchi et al. (2016, Appendix A) and Santambrogio (2015, chap. 2). In other words, even in the absence of CDF, a bias correction can be carried out by calculating the minimum of the function C.
The advantage of this approach is that the functional C can be written in the multivariate case by replacing by , where xi and yj are the center of multivariate cells, and the Euclidean norm. We illustrate in Fig. 1d how the displacements are carried out in the case of two bivariate Gaussian distributions. The black arrows again represent the non-zero coefficients estimated by the OTC method (we only represent 30 arrows).
In the next section we present the mathematical theory behind this example with probability measures of X and Y. If we normalize the number of realizations of X and Y in each bin by the total number of realizations of X and Y, we obtain pxi and pyj. Therefore, the transport can be written as a transport of a fraction of mass, instead of a transport of the number of realizations.
2.2 Bias correction as a joint distribution
In the multivariate context we assume the existence of a transfer function 𝒯 between X and Y. By construction, the random variables X and 𝒯(X) are dependent, and their associated joint law can be summarized by the function
The map κ connects the random variable X with its correction 𝒯(X) on the space ℝd×ℝd. Furthermore, the map κ induces a probability law on ℝd×ℝd, denoted ℙ𝒯, and given for all measurable sets by
The critical property here concerns the margins of ℙ𝒯: the first (second) margin of ℙ𝒯 is ℙX (ℙY). To understand why it is critical, let Γ(ℙX,ℙY) be the set of probability measures on ℝd×ℝd for which ℙX is the first margin and ℙY the second one. By definition, . Thus, any bias correction method defined by a transfer function is an element of Γ(ℙX,ℙY).
We argue that any probability distribution in Γ(ℙX,ℙY) induces a bias correction method. For , γ(x,y) can be interpreted as the probability that y is the correction of x. Formally, the Jirina theorem (see, e.g., Strook, 1995, chap. 5) states that there exists a collection of probability laws γx, x∈ℝd, such that γx are the conditional laws of Y given X. In other words, for γx(B) is the probability that the correction y∈B, given X=x. The correction of x is then sampled from the law γx. Thus, any defines a bias correction method, through the conditional laws γx. This highlights the stochastic part of this approach: all corrections are sampled from the laws γx, and the corrected values follow the law ℙY (by definition of a conditional law).
We note that the problem where X is constant is easily solved with this approach. The set Γ(ℙX,ℙY) is reduced to one element: the independent law δx×ℙY, where δx is the Dirac mass in x. Thus, γx=ℙY, and the correction of X is given by sampling each correction with the law ℙY.
We have defined a bias correction method as an element of Γ(ℙX,ℙY). However, this set can be very large. The goal of the next section is to present a criterion to select an element of Γ(ℙX,ℙY).
2.3 Selection of a joint law with optimal transport theory
To select a probability law , we propose using a cost function on this set. The minimum of this cost function corresponds to an optimal bias correction method. We propose minimizing the energy needed to transform a realization x of X to its correction y, i.e., minimizing , weighted by γ(x,y). Thus, the cost function C is given by
This cost function minimizes the square of the distance between x and its correction y. Our bias correction method is associated with the law γ that minimizes C. This cost function stems from optimal transport theory (Villani, 2008). The choice of the square in Eq. (1) guarantees the uniqueness of the solution. In the univariate case, it can be shown that the joint law defined by the quantile mapping minimizes the cost function C of Eq. (1). Proofs of this statement can be found in Farchi et al. (2016, Appendix A) and Santambrogio (2015, chap. 2).
Our next step is to explain how this minimization strategy can be extended in the multivariate case.
2.4 Multivariate bias correction with optimal transport selection: the stationary case
We assume that and are two independent and identically distributed (i.i.d.) samples of the random variables X and Y. A first step is to estimate the empirical distributions, and . We denote ci a collection of regularly spaced cells that partition ℝd and cover and . The center of each cell is also denoted ci. With this notation, and can be written as a sum of I and J Dirac masses:
The scalar pX,i (or pY,j) is the empirical weight around ci (or cj) and induced from the sampling of X (or Y). A natural estimator of can be written as
The coefficients γij are the probabilities to transform ci (i.e., a x∈ci) to cj (i.e., a y∈cj). They are unknown, and they have to obey the marginal properties:
Finally, the cost function defined in Eq. (1) can be approximated by
Finding γij, i.e., solving the problem defined by constraints of Eqs. (2)–(3) and minimization of Eq. (4), is called a linear programming problem. It can be solved (for example) by the network simplex algorithm (see, e.g., Bazaraa et al., 2009). We use the python implementation of Flamary and Courty (2017). To correct X, we have to follow the plan of γij. For a realization Xl of X, we take the cell ci that contains Xl. Following , ci is moved to cj with probability (applying Eq. (2), the sum over j is 1). To determine cj, we randomly draw it according to the conditional law . Finally, we draw uniformly y in cj. This methodology is summarized in Algorithm A1, and we refer to it as optimal transport correction (OTC).

Note that the traditional one-dimensional quantile mapping preserves the ordering of quantiles. In the multivariate case, this type of property can be viewed as the Monge–Mather (1991) shortening principle (see, e.g., Villani, 2008, chap. 8). The idea is that the extremes of a multivariate distribution are moved to extremes, the boundary to the boundary, the level lines to level lines, etc.
2.5 Non-stationary bias correction
Climate models offer a valuable tool to study future realistic climate trajectories. Climate model outputs of the present period need to be bias corrected with respect to current observations. Future climate simulations also need to be adjusted. However, no observation is available for the future and clear assumptions have to be made to correct simulations for future periods. Table 1 displays the basic framework of bias correction. Future unobserved data, say Y1, should be inferred from the current reference vector, Y0, and two numerical runs, one in the present, say X0, and one in the future, say X1. Period 0 is called the calibration period, and period 1 the projection period. In the univariate case, denoting Fi (Gi) the CDF of Xi (Yi), the CDF-t (CDF transform) method of Michelangeli et al. (2009) assumes that
Recombining Eq. (5), the CDF of Y1 is given by , and can be used to perform a quantile mapping correction. Here, the fundamental hypothesis means that the transfer functions to capture the temporal changes are identical in the model and observational worlds.
CDF-t learns the change between X0 and X1, and transfers it to Y0 to estimate Y1. In the multivariate case, following CDF-t, we want to learn the evolution (i.e., the change or the temporal evolution) between X0 and X1, and apply it to Y0. This generates Y1, and OTC can then be applied between X1 and Y1. Note also that the reverse hypothesis could be considered, meaning that the bias is learned, and transferred along the dynamic. In this case, the correction of example given in Sect. 3 does not correspond to the reference (not shown), so we rejected this assumption. Thus, our definition of non-stationary bias correction assumes a transfer of the evolution of the model to the observational world. Indeed, climate change is one of the main signals that we want to account for in the projected corrections. However, the change in the observations can be different, and therefore the resulting corrections can also be different from observations. Nevertheless, this methodology is justified because different simulations can have different evolutions; e.g., the four RCP scenarios provide four different simulations, giving four different corrections. This is also true for different climate models, which can show different changes. This information is therefore kept in the corrections.
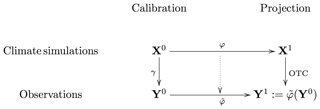
Using OTC, we define two optimal plans: the optimal plan γ, between X0 and Y0, and the optimal plan φ, between X0 and X1. The law γ is the bias between X0 and Y0, whereas φ is the evolution between X0 and X1. Our goal is to move φ along γ, defining a plan , to estimate Y1 as the evolution of Y0, i.e., . Then, we correct X1 with respect to , with the OTC method. This is summarized in Fig. 2.
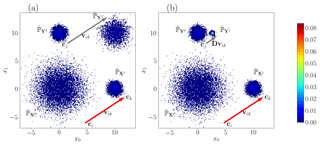
Figure 3Bivariate histogram with bin size equal to 0.1. In each panel we have a Gaussian law centered on (0,0) with covariance 4Id2 (), a Gaussian law centered on (10,0) with covariance 1∕4Id2 () and a Gaussian law centered on (0,10) with covariance 1∕4Id2 (). The red arrow is the local evolution between and . (a) The probability distribution is the correction with OTC-t and D=Id2. The grey arrow is the estimation of the evolution of . (b) The probability distribution is the correction with dOTC and D given by Eq. (6). The grey arrow is the estimation of the evolution of .
The estimation of is performed in three steps:
-
transformation of φ into a collection of vectors,
-
transferral of these vectors along γ and
-
adaptation of these vectors to Y0.
To illustrate our methodology, Fig. 3 shows an example where the random variables X0, X1 and Y0 follow a bivariate Gaussian law. They are, respectively, centered at (0,0), (10,0) and (0,10), with covariance matrices 4×Id2, Id2∕4 and Id2∕4 (the matrix Idd is the d-dimensional identity matrix). Without loss of generality, we write the empirical distribution of X0, X1 and Y0 as a sum of Dirac masses,

Figure 4Random variables generated by the Lorenz (1984) model, OTC, dOTC, quantile mapping and CDF-t. (a) Biased random variable X0 (red) and references Y0 (blue) for time period 0. (b) Biased random variable X0 (red) and correction Z0 with OTC (green). (c) Biased random variable X0 (red) and correction Q0 with quantile mapping (green). (d) Biased random variable X1 (red) and references Y1 (blue) for time period 1. (e) Biased random variable X1 (red) and correction Z1 with dOTC (green). (f) Biased random variable X1 (red) and correction Q1 with CDF-t (green).
-
Step 1. Transformation of φ. Using the OTC method, φ moves the bin ci of to the bin ck of . The vector represents the evolution from ci to ck (i.e., the local evolution between X0 and X1). The collection of vectors vik is an estimation of the process between X0 and X1. In Fig. 3, the red arrow is an example of vector vik.
-
Step 2. Transfer along γ. Using the OTC method, γ moves the bin ci of to the bin cj of . Thus, the estimation of could be defined by the vector vik applied to cj; i.e., a realization of Y1 is given by cj+vik. The grey arrow in Fig. 3a depicts this operation. But the vik can cross, and the correction is not coherent. This is due to normalizing issues and because the collection of vectors vik applied to Y0 does not define an optimal transport plan. The standard deviation decreases between X0 and X1, whereas it increases between Y0 and Y1 in our example. Furthermore, the quantiles are inverted in this example (low values are moved to high values). Consequently, we have to adapt the vectors vik to .
-
Step 3. Adaptation of vik. To solve this problem, we introduce a matrix factor D, which rescales the collection of vectors vik. In the univariate case, Bürger et al. (2011) proposed a factor , where σ is the standard deviation. The idea is to remove the scale of X0 and to replace it by the scale of Y0. Bárdossy and Pegram (2012) and Cannon (2016) proposed a multivariate equivalent that uses the Cholesky decomposition of the covariance matrix. Denoting Σ the covariance matrix, and Cho(Σ) its Cholesky decomposition, we multiply (in a matrix sense) vik by the following matrix:
The Cholesky decomposition only exists if Σ is symmetric and positive-definite. Some covariance matrices do not have this property, e.g., highly correlated random variables. In such a case, Σ must be slightly perturbed to be positive-definite (see, e.g., Higham, 1988; Knol and ten Berge, 1989). Furthermore, the Cholesky decomposition can be poorly estimated if the number of available data is too small compared to the dimension. Indeed, the inverse of a covariance matrix is highly biased. In this case, a pragmatic solution is to replace the matrix D by the diagonal matrix of the standard deviation, i.e., .
Finally, a realization of Y1 is given by . Figure 3b shows an estimation of Y1. Visually, the shape of Y1 appears coherent with the evolution between X0 and X1. The mean of Y1 is (2.53,10). The standard deviation between X0 and X1 is divided by 4. The mean shift between X0 and X1 is (10,0). This shift of 10 units is correctly taken into account in the rescaling of Y0 by the standard deviation (equal to 4) between X0 and X1:
The value of the covariance matrix of Y1 is . It is close to the expected value . The shift of 10 units of the model is not followed. It is interpreted as a correction of the bias into the evolution of the model. However, depending on the hypotheses desired by the user, the dOTC method can easily provide corrections whose mean evolutions and trends are in agreement with those given by the simulations to be corrected, like in the EDQM bias correction method (Li et al., 2010). The complete method of correction is summarized in Algorithm A2. We refer to it as dOTC (dynamical optimal transport correction).

We first propose evaluating OTC and dOTC on an idealized case.
3.1 Model and methodology
To evaluate our bias correction method, we construct an idealized biased case, based on the Lorenz (1984) model. This three-dimensional system is generated by the differential equations
The function ψ(t) is a linear forcing proposed by Drótos et al. (2015). Classically, ψ also contains a seasonal cycle (Lorenz, 1990), where the length of a “year” is fixed at t=73 time units. Here we integrate this equation for the following forcing between 0 and 7×73 (i.e., 7 “years” of integration):
The integration is performed with a Runge–Kutta (order 4) scheme with a time step of size 0.005. All trajectories of the Lorenz (1984) model converge on a unique subset of ℝ3 (called an attractor), and remain trapped on it. According to Drótos et al. (2015), the first 5 “years” correspond to the time required to trap the trajectories.
One realization of random variable Y0 (Y1) is year 6 (year 7). Each year contains elements. According to Eq. (8), the linear forcing is applied during year 7. The non-stationarity is induced by the change between the two time periods.
We introduce a bias by multiplying each point of the trajectories by a triangular matrix S, and add a vector m, i.e., . The addition changes the mean, whereas the multiplication alters the covariances. The matrix S is chosen empirically such that the covariance matrices of X0, X1, Y0 and Y1 differ. We fix
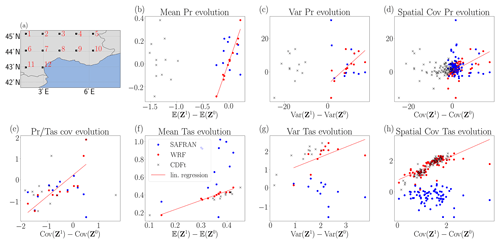
Figure 5(a) Map of the southeast of France. The 12 black squares are the locations where corrections are performed. (b–h) The x axis of the panels is the evolution of the correction with dOTC. The y axis of panels (b)–(h) is the evolution of WRF in red and the evolution of SAFRAN in blue. The red line is the linear regression between the evolution of correction and the evolution of WRF. The black cross markers are the scatterplots between the evolution of correction with CDF-t and evolution of WRF. (b) Evolution of mean precipitation, i.e., difference between the projection period and the calibration period. (c) Evolution of variance of precipitation. (d) Evolution of spatial covariance of precipitation. (e) Evolution of covariance between precipitation and temperatures. (f) Evolution of mean temperatures. (g) Evolution of variance of temperatures. (h) Evolution of spatial covariance of temperatures.
The random variables X and Y are plotted in Fig. 4a, d. The blue (red) curve of Fig. 4a is the trajectory of Y0 (X0). The mean is largely altered. We estimate the covariance matrices as
Similarly to Fig. 4a, d depicts in blue Y1 and in red X1. The forcing of Eq. (8) has changed the properties of the trajectories, and they became chaotic. It is worthwhile noticing that the dynamic of Y is comparable to the one of X. The covariance matrices are largely affected:
We estimate the empirical distributions , , and with a three-dimensional histogram. We cut a large cube around the trajectories into cells of size . Then we count the number of points in each cell.
Finally, we evaluate the quality of the correction by comparing the covariance matrices of Y0 and X0, and the covariance matrices of Y1 and X1.
3.2 Correction of the biased Lorenz (1984) model
We apply our method to correct X0 and X1. The random variable X0 is corrected with respect to Y0 and using the OTC method. The random variable X1 is corrected with respect to the estimation of Y1, coming from the dOTC method. The resulting random variables Z0 and Z1 are given in Fig. 4b, e. We show in Fig. 4c, f a univariate correction with quantile mapping for the period 0, generating the random variable Q0. The same is shown for CDFt, period 1 and the random variable Q1.
The correction Z0 is visually very similar to the reference in blue in Fig. 4a. The covariance matrix is almost perfectly reproduced:
The correction Z1 is depicted in green in Fig. 4d. It is visually hard to compare to Fig. 4b, but we recognize Y1. The covariance matrix is correctly rectified:
Finally, the cost of transformation, given by Eq. (1), of Z1 into Y1 is 93 % smaller than the cost between Y1 and X1; i.e., is more similar to than . Furthermore, if we replace the Cholesky matrix of dOTC by the matrix of standard deviation, the maximum difference between covariance matrices increases to 0.22, but the cost is 85 % smaller. Thus, using the standard deviation slightly degrades the correction. However, visually, it is very hard to distinguish the corrections with the Cholesky matrix or the standard deviation matrix. The figure corresponding to Fig. 4 with the standard deviation matrix is given in the Supplement.
By contrast, Q0 and Q1, depicted, respectively, in Fig. 4c, f, do not reproduce Y0 and Y1. Thus, the multivariate correction is largely better than the univariate correction. This is confirmed by the covariance matrices, which reproduce exactly the covariances of X0 and X1:
We have performed a tri-variate correction on a nonlinear system exhibiting non-standard probability measures (i.e., non-Gaussian, non-exponential). In the stationary case, the OTC method works almost perfectly. In the non-stationary case, the dOTC method produces a probability distribution closed to the expected result. We propose now to apply OTC and dOTC to climate model simulations.
4.1 Data
The dataset used as a reference for the bias correction (BC) is the Systeme d'Analyse Fournissant des Renseignements Atmospheriques a la Neige (SAFRAN, Vidal et al., 2010) reanalysis. SAFRAN is a hourly reanalysis over France between 1958 and present, with a horizontal resolution of 8 km × 8 km. Quintana-Seguí et al. (2008) claimed that the daily mean of the surface atmospheric temperature (tas) and precipitation (pr) presents no bias compared to observations from the climatological database of Météo-France. This justifies the use of SAFRAN as a reference.
We test our multivariate BC method on a simulation of the Weather Research and Forecast (WRF) atmospheric model (Skamarock et al., 2008) performed within the EURO-CORDEX initiative (Vautard et al., 2013; Jacob et al., 2014) with a 0.11∘ × 0.11∘ horizontal resolution. The boundaries of the simulation were forced by a historical simulation of the Institut Pierre-Simon Laplace (IPSL) coupled model (Marti et al., 2010; Dufresne et al., 2013). This EURO-CORDEX historical simulation will be called “WRF” in the following.
SAFRAN and WRF data are re-mapped onto the same grid, with a spatial resolution of 0.11∘ × 0.11∘ (i.e., ∼ 12 km × 12 km). The nearest neighbor interpolation is used. We only keep the land region comprised in 1.8–7.85∘ E × 41.8–45.2∘ N, i.e., covering the southeast of France. This region is characterized by a complex topography, which creates a strong spatial heterogeneity, especially for precipitation. For the present application, we extract 12 grid points regularly spaced (see Fig. 5a), with a one-to-one spatial correspondence between SAFRAN and WRF.
In both datasets, we will consider daily surface air temperatures and precipitation. The goal of this section is to correct the bias in tas and pr in the WRF data with respect to SAFRAN.
4.2 Cross-validation protocol
We focus on the daily timescale over the 1970–2000 period. We correct the warm season (May–September). The analysis and conclusions are available for the cold season, and the corresponding figure (i.e., Fig. 5) is given in the Supplement. We split that period into two sub-periods, 1970–1985 (2295 days) and 1985–2000 (2295 days), to perform a cross-validation. The SAFRAN (WRF) values over the first time period correspond to the random variable Y0 (X0), and are called the calibration period. The SAFRAN (WRF) values over the second time period correspond to Y1 (X1), and are called the projection period. SAFRAN during 1985–2000 (i.e., Y1) is assumed to be unknown, and is used for cross-validation.
We perform two bias corrections: univariate and 24-variate (12 grid points and 2 variables).
-
For univariate correction, quantile mapping is used for the calibration period, and CDF-t for the projection period.
-
For 24-variate correction, OTC is used for the calibration period, and dOTC for the projection period. The spatial structure and the dependence between the two variables are used. Due to the dimension, the Cholesky matrix is poorly estimated. We replace it by the matrix of standard deviation in the rescaling step.
We estimate the empirical distributions by computing histograms with bins of size 0.1 in each dimension. Furthermore, CDF-t and dOTC can shift close to 0 values to negative values for precipitation. Thus, negative precipitation values are replaced by 0 after correction. We test the quality of the correction by plotting the evolution of the mean, the standard deviation, and the spatial and inter-variable covariance, i.e., the difference between the projection and calibration periods. These indicators are summarized in Fig. 5. During the calibration period, the goal is that the probability distribution of correction of the WRF simulation will be the probability distribution of SAFRAN. By construction of OTC, the correction is almost perfect, and we focus on the projection period. In the projection period, the goal is that the evolution of corrections will be close to the evolution of the WRF simulation.
4.3 Evolution analysis
As we have seen in the previous section, the corrections of X1 and Y1 are identical only if the evolution of SAFRAN is identical to the evolution of WRF. To analyze the evolution of WRF, SAFRAN and the corrections, we compute the difference of statistical indicators between the projection and the calibration period at each grid point. The indicators are the mean (Fig. 5b, f), the variance (Fig. 5c, g), the covariance between pr and tas (Fig. 5e) and the spatial covariance for each variable (Fig. 5d, h).
Table 2r-value, p-value and standard error (SE) of linear regression between the evolution of correction and evolution of WRF.
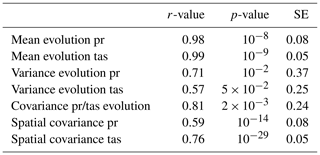
The x axis of Fig. 5a–h is the evolution of the correction (i.e., 𝔼(Z1)−𝔼(Z0),…). The y axis of Fig. 5a–h is the evolution of WRF in red (i.e., 𝔼(X1)−𝔼(X0),…), and the evolution of SAFRAN in blue (i.e., 𝔼(Y1)−𝔼(Y0),…). Furthermore, the red line is the linear regression between the evolution of the 24-variate correction and the evolution of WRF. The correlation (r-value), p-value and standard error of each linear regression are summarized in Table 2.
The linear regression between evolution of 24-variate correction and evolution of WRF (red line) shows a strong statistical link for all statistical indicators. The evolution of the mean is almost perfectly reproduced for the two variables (r-values is at least equal to 0.98, with a maximal p-value at 10−9). The evolution of variance of WRF is also reproduced, the linear regression being significant (maximal p-value is ).
The evolution of dependence structure is given by the evolution of spatial and inter-variables covariance. The minimal r-value for linear regression is equal to 0.59 with a maximal p-value equal to . This means that dOTC reproduces the evolution of WRF between calibration and projection period. Because the calibration period is perfectly corrected, the correction during projection period appears as the evolution of WRF, applied to SAFRAN.
A linear regression, the Spearman rank correlation between the evolution of SAFRAN, and the evolution of the correction with WRF do not show a significant statistical link (not shown). We conclude that the evolution of WRF is different of the evolution of SAFRAN. This indicates it is not possible to reproduce SAFRAN during projection period using dOTC and WRF. For example, WRF predicts an increase between 0.2 and 0.4 K of the mean temperature, whereas SAFRAN gives an increase between 0.2 and 1 K.
The correction with CDF-t appears to be satisfactory for the temperatures, and very similar to the correction with dOTC. But for the precipitation, the structure is not coherent with WRF or SAFRAN. This dissimilarity is due to the difference between the probability distribution of temperatures (quasi-Gaussian) and precipitations (exponential/Gamma laws).
We conclude that the evolution of the 24-variate correction with dOTC between calibration and projection periods is close to the evolution of WRF. Furthermore, the evolution of SAFRAN is very different from the evolution of WRF. In particular, this example illustrates how the classical cross-validation methodology does not differentiate the variations of SAFRAN and WRF, and that the correction can not be compared to the reference during the projection period.
We have developed a new method for multivariate bias correction, generalizing the quantile mapping in the multivariate case. To do so, we have developed a new theoretical framework to understand any bias correction (BC) method: any BC method is here characterized by a joint law between the biased dataset and the correction. This joint probability distribution is estimated based on optimal transport techniques, and the BC method is then referred to as optimal transport correction (OTC). A definition of non-stationary bias correction is also proposed: the evolution of the model is learned and transferred to the reference world. An extension of OTC called dynamical OTC (dOTC) has been developed to account for temporal non-stationarities.
OTC and dOTC methods have been tested on an idealized three-dimensional case based on Lorenz (1984) time-dependent attractors, which induced changes in the correlation between variables. The bias correction appeared to perform very well in those idealized experiments.
Then, 12 grid points of a WRF simulation have been corrected with respect to SAFRAN reanalyses for precipitation and temperature in Southern France. A 24-variate correction was performed. The correction in stationary context was almost perfect. In the non-stationary case, the evolutions of WRF and SAFRAN were different, and, as expected, the correction with dOTC differed from SAFRAN. However, the correction presented a multidimensional evolution similar to that of WRF. We can therefore conclude that the correction is consistent with the definition proposed for the non-stationary case.
This is consistent with the results of Maraun et al. (2017): the fundamental errors of a model are not corrected, but transferred to the world of observations. The dOTC method preserves the signal of climate change inferred from the model simulations. As suggested by Maraun and Widmann (2018), our cross-validation method does not compare the correction to the observations on the validation period, which can produce false positive or true negative due to internal variability of model or observations, but assesses whether the statistical evolution of the model is kept.
Furthermore, although the number of available data is very small compared to the dimensions (2295 days and 24 dimensions), the OTC and dOTC performed a correction without numerical problems, and, moreover, only in a few minutes on a personal computer.
The methods OTC and dOTC are able to correct the dependence structure (i.e., the joint law), and not only the inter-variable and spatial correlations. In particular, the copula function (which contains the information about dependence) is corrected. In addition, dOTC proposes a definition of non-stationarity, and explicitly gives what the correction corresponds to (the evolution of the model applied to observations). In the particular case of the temperatures/precipitation correction, compared to, e.g., Piani and Haerter (2012) and Räty et al. (2018), the correction is at least as good during the calibration period, although the comparison is not done over the projection period, because the indicators are different.
As a perspective of improvement of the method, we note that the optimal plan can only be used to correct data points that are already known. If a new data point is obtained, and alters the estimate of the probability density function, then the plan needs to be recomputed. However, such a situation is relatively rare in bias correction. Indeed, the corrections usually have to be performed on climate model simulations that cover many years and decades. This means that the whole time series are available at once and are not continuously updated. One possibility would be to “smooth” the optimal plan that, thus, could be applied to new points without recalculating the plan. Finally, a promising application of this method is the post-processing of operational forecasts. In such a case, the question of internal variability (Maraun et al., 2017) would not affect the bias correction procedure as climate dynamics is consistently represented between the model and observations.
OTC and dOTC are implemented in two packages: ARyga (R) and Apyga (python3). These packages are available at https://github.com/yrobink/Ayga.git (Robin, 2019). The example of Sect. 3 is given in Apyga. SAFRAN and EURO-CORDEX data are, respectively, available at: http://www.drias-climat.fr (last access: 29 January 2019) and https://www.euro-cordex.net (last access: 29 January 2019).
The supplement related to this article is available online at: https://doi.org/10.5194/hess-23-773-2019-supplement.
YR performed the analyses. The experiments were co-designed by YR and MV. All the authors contributed to writing the manuscript.
The authors declare that they have no conflict of interest.
This work was supported by ERC grant no. 338965-A2C2.
Edited by: Uwe Ehret
Reviewed by: Michael
Muskulus and one anonymous referee
Bárdossy, A. and Pegram, G.: Multiscale spatial recorrelation of RCM precipitation to produce unbiased climate change scenarios over large areas and small, Water Resour. Res., 48, W09502, https://doi.org/10.1029/2011WR011524, 2012. a, b
Bazaraa, M. S., Jarvis, J. J., and Sherali, H. D.: Linear Programming and Network Flows, 4th edn., John Wiley & Sons, 2009. a
Bürger, G., Schulla, J., and Werner, A. T.: Estimates of future flow, including extremes, of the Columbia River headwaters, Water Resour. Res., 47, W10520, https://doi.org/10.1029/2010WR009716, 2011. a
Cannon, A. J.: Multivariate Bias Correction of Climate Model Output: Matching Marginal Distributions and Intervariable Dependence Structure, J. Climate, 29, 7045–7064, https://doi.org/10.1175/JCLI-D-15-0679.1, 2016. a
Cannon, A. J.: Multivariate quantile mapping bias correction: an N-dimensional probability density function transform for climate model simulations of multiple variables, Clim. Dynam, 50, 31–49, https://doi.org/10.1007/s00382-017-3580-6, 2018. a
Chen, J., Brissette, F. P., Chaumont, D., and Braun, M.: Finding appropriate bias correction methods in downscaling precipitation for hydrologic impact studies over North America, Water Resour. Res., 49, 4187–4205, https://doi.org/10.1002/wrcr.20331, 2013. a
Christensen, J. H., Boberg, F., Christensen, O. B., and Lucas-Picher, P.: On the need for bias correction of regional climate change projections of temperature and precipitation, Geophys. Res. Lett., 35, L20709, https://doi.org/10.1029/2008GL035694, 2008. a
Dekens, L., Parey, S., Grandjacques, M., and Dacunha-Castelle, D.: Multivariate distribution correction of climate model outputs: A generalization of quantile mapping approaches, Environmetrics, 28, E2454, https://doi.org/10.1002/env.2454, 2017. a
Déqué, M.: Frequency of precipitation and temperature extremes over France in an anthropogenic scenario: Model results and statistical correction according to observed values, Global Planet. Change, 57, 16–26, https://doi.org/10.1016/j.gloplacha.2006.11.030, 2007. a
Drótos, G., Bódai, T., and Tél, T.: Probabilistic concepts in a changing climate: a snapshot attractor picture, J. Climate, 28, 3275–3288, https://doi.org/10.1175/JCLI-D-14-00459.1, 2015. a, b
Dufresne, J.-L., Foujols, M.-A., Denvil, S., Caubel, A., Marti, O., Aumont, O., Balkanski, Y., Bekki, S., Bellenger, H., Benshila, R., Bony, S., Bopp, L., Braconnot, P., Brockmann, P., Cadule, P., Cheruy, F., Codron, F., Cozic, A., Cugnet, D., de Noblet, N., Duvel, J.-P., Ethé, C., Fairhead, L., Fichefet, T., Flavoni, S., Friedlingstein, P., Grandpeix, J.-Y., Guez, L., Guilyardi, E., Hauglustaine, D., Hourdin, F., Idelkadi, A., Ghattas, J., Joussaume, S., Kageyama, M., Krinner, G., Labetoulle, S., Lahellec, A., Lefebvre, M.-P., Lefevre, F., Levy, C., Li, Z. X., Lloyd, J., Lott, F., Madec, G., Mancip, M., Marchand, M., Masson, S., Meurdesoif, Y., Mignot, J., Musat, I., Parouty, S., Polcher, J., Rio, C., Schulz, M., Swingedouw, D., Szopa, S., Talandier, C., Terray, P., Viovy, N., and Vuichard, N.: Climate change projections using the IPSL-CM5 Earth System Model: from CMIP3 to CMIP5, Clim. Dynam, 40, 2123–2165, https://doi.org/10.1007/s00382-012-1636-1, 2013. a
Ehret, U., Zehe, E., Wulfmeyer, V., Warrach-Sagi, K., and Liebert, J.: HESS Opinions “Should we apply bias correction to global and regional climate model data?”, Hydrol. Earth Syst. Sci., 16, 3391–3404, https://doi.org/10.5194/hess-16-3391-2012, 2012. a
Farchi, A., Bocquet, M., Roustan, Y., Mathieu, A., and Quérel, A.: Using the Wasserstein distance to compare fields of pollutants: application to the radionuclide atmospheric dispersion of the Fukushima-Daiichi accident, Tellus B, 68, 31682, https://doi.org/10.3402/tellusb.v68.31682, 2016. a, b
Ferradans, S., Papadakis, N., Rabin, J., Peyré, G., and Aujol, J.-F.: Regularized Discrete Optimal Transport, Springer Berlin Heidelberg, Berlin, Heidelberg, 428–439, https://doi.org/10.1007/978-3-642-38267-3_36, 2013. a
Flamary, R. and Courty, N.: POT Python Optimal Transport library, 2017. a
Gudmundsson, L., Bremnes, J. B., Haugen, J. E., and Engen-Skaugen, T.: Technical Note: Downscaling RCM precipitation to the station scale using statistical transformations – a comparison of methods, Hydrol. Earth Syst. Sci., 16, 3383–3390, https://doi.org/10.5194/hess-16-3383-2012, 2012. a
Higham, N. J.: Computing a nearest symmetric positive semidefinite matrix, Linear Algebra Appl., 103, 103–118, https://doi.org/10.1016/0024-3795(88)90223-6, 1988. a
Jacob, D., Petersen, J., Eggert, B., Alias, A., Christensen, O. B., Bouwer, L. M., Braun, A., Colette, A., Déqué, M., Georgievski, G., Georgopoulou, E., Gobiet, A., Menut, L., Nikulin, G., Haensler, A., Hempelmann, N., Jones, C., Keuler, K., Kovats, S., Kröner, N., Kotlarski, S., Kriegsmann, A., Martin, E., van Meijgaard, E., Moseley, C., Pfeifer, S., Preuschmann, S., Radermacher, C., Radtke, K., Rechid, D., Rounsevell, M., Samuelsson, P., Somot, S., Soussana, J.-F., Teichmann, C., Valentini, R., Vautard, R., Weber, B., and Yiou, P.: EURO-CORDEX: new high-resolution climate change projections for European impact research, Reg. Environ. Change, 14, 563–578, https://doi.org/10.1007/s10113-013-0499-2, 2014. a
Knol, D. L. and ten Berge, J. M. F.: Least-squares approximation of an improper correlation matrix by a proper one, Psychometrika, 54, 53–61, https://doi.org/10.1007/BF02294448, 1989. a
Li, H., Sheffield, J., and Wood, E. F.: Bias correction of monthly precipitation and temperature fields from Intergovernmental Panel on Climate Change AR4 models using equidistant quantile matching, J. Geophys. Res.-Atmos., 115, D10101, https://doi.org/10.1029/2009JD012882, 2010. a
Lorenz, E. N.: Irregularity: a fundamental property of the atmosphere, Tellus A, 36, 98–110, 1984. a, b, c, d
Lorenz, E. N.: Can chaos and intransitivity lead to interannual variability?, Tellus A, 42, 378–389, 1990. a
Mao, G., Vogl, S., Laux, P., Wagner, S., and Kunstmann, H.: Stochastic bias correction of dynamically downscaled precipitation fields for Germany through Copula-based integration of gridded observation data, Hydrol. Earth Syst. Sci., 19, 1787–1806, https://doi.org/10.5194/hess-19-1787-2015, 2015. a
Maraun, D.: Nonstationarities of regional climate model biases in European seasonal mean temperature and precipitation sums, Geophys. Res. Lett., 39, L06706, https://doi.org/10.1029/2012GL051210, 2012. a
Maraun, D.: Bias Correcting Climate Change Simulations – a Critical Review, Curr. Clim. Change Rep., 2, 211–220, https://doi.org/10.1007/s40641-016-0050-x, 2016. a
Maraun, D. and Widmann, M.: Cross-validation of bias-corrected climate simulations is misleading, Hydrol. Earth Syst. Sci., 22, 4867–4873, https://doi.org/10.5194/hess-22-4867-2018, 2018. a
Maraun, D., Shepherd, T. G., Widmann, M., Zappa, G., Walton, D., Gutiérrez, J., Hagemann, S., Richter, I., Soares, P. M. M., Hall, A., and Mearns, L. O.: Towards process-informed bias correction of climate change simulations, Nat. Clim. Change, 7, 764–773, 2017. a, b, c, d
Marti, O., Braconnot, P., Dufresne, J.-L., Bellier, J., Benshila, R., Bony, S., Brockmann, P., Cadule, P., Caubel, A., Codron, F., de Noblet, N., Denvil, S., Fairhead, L., Fichefet, T., Foujols, M.-A., Friedlingstein, P., Goosse, H., Grandpeix, J.-Y., Guilyardi, E., Hourdin, F., Idelkadi, A., Kageyama, M., Krinner, G., Lévy, C., Madec, G., Mignot, J., Musat, I., Swingedouw, D., and Talandier, C.: Key features of the IPSL ocean atmosphere model and its sensitivity to atmospheric resolution, Clim. Dynam, 34, 1–26, https://doi.org/10.1007/s00382-009-0640-6, 2010. a
Mather, J. N.: Action minimizing invariant measures for positive definite Lagrangian systems, Math. Z., 207, 169–207, https://doi.org/10.1007/BF02571383, 1991. a
Michelangeli, P.-A., Vrac, M., and Loukos, H.: Probabilistic downscaling approaches: Application to wind cumulative distribution functions, Geophys. Res. Lett., 36, L11708, https://doi.org/10.1029/2009GL038401, 2009. a, b
Muskulus, M. and Verduyn-Lunel, S.: Wasserstein distances in the analysis of time series and dynamical systems, Physica D, 240, 45–58, https://doi.org/10.1016/j.physd.2010.08.005, 2011. a
Nahar, J., Johnson, F., and Sharma, A.: Assessing the extent of non-stationary biases in GCMs, J. Hydrol., 549, 148–162, https://doi.org/10.1016/j.jhydrol.2017.03.045, 2017. a
Nahar, J., Johnson, F., and Sharma, A.: Addressing Spatial Dependence Bias in Climate Model Simulations: An Independent Component Analysis Approach, Water Resour. Res., 54, 827–841, https://doi.org/10.1002/2017WR021293, 2018. a
Panofsky, H. A. and Brier, G. W.: Some applications of statistics to meteorology, Mineral Industries Extension Services, College of Mineral Industries, Pennsylvania State University, 103 pp., 1958. a
Piani, C. and Haerter, J. O.: Two dimensional bias correction of temperature and precipitation copulas in climate models, Geophys. Res. Lett., 39, https://doi.org/10.1029/2012GL053839, 2012. a
Piani, C., Weedon, G., Best, M., Gomes, S., Viterbo, P., Hagemann, S., and Haerter, J.: Statistical bias correction of global simulated daily precipitation and temperature for the application of hydrological models, J. Hydrol., 395, 199–215, https://doi.org/10.1016/j.jhydrol.2010.10.024, 2010. a
Quintana-Seguí, P., Le Moigne, P., Durand, Y., Martin, E., Habets, F., Baillon, M., Canellas, C., Franchisteguy, L., and Morel, S.: Analysis of Near-Surface Atmospheric Variables: Validation of the SAFRAN Analysis over France, J. Appl. Meteorol. Clim., 47, 92–107, https://doi.org/10.1175/2007JAMC1636.1, 2008. a
Randall, D. A., Wood, R. A., Bony, S., Colman, R., Fichefet, T., Fyfe, J., Kattsov, V., Pitman, A., Shukla, J., Srinivasan, J., Stouffer, R. J., Sumi, A., and Taylor, K. E.: Climate models and their evaluation, in: Climate change 2007: The physical science basis. Contribution of Working Group I to the Fourth Assessment Report of the IPCC (FAR), Cambridge University Press, 589–662, 2007. a
Räty, O., Räisänen, J., Bosshard, T., and Donnelly, C.: Intercomparison of Univariate and Joint Bias Correction Methods in Changing Climate From a Hydrological Perspective, Climate, 6, 33 https://doi.org/10.3390/cli6020033, 2018. a
Robin, Y.: Ayga, Python and R bias correction library, available at: https://github.com/yrobink/Ayga.git, last access: 29 January 2019. a
Robin, Y., Yiou, P., and Naveau, P.: Detecting changes in forced climate attractors with Wasserstein distance, Nonlinear Proc. Geoph., 24, 393–405, 2017. a
Rubner, Y., Tomasi, C., and Guibas, L. J.: The Earth Mover's Distance as a Metric for Image Retrieval, Int. J. Comput. Vis., 40, 99–121, https://doi.org/10.1023/A:1026543900054, 2000. a
Santambrogio, F.: Optimal Transport for Applied Mathematicians, vol. 87, Birkhäuser Basel, 2015. a, b
Shrestha, R. R., Schnorbus, M. A., Werner, A. T., and Zwiers, F. W.: Evaluating Hydroclimatic Change Signals from Statistically and Dynamically Downscaled GCMs and Hydrologic Models, J. Hydrometeorol., 15, 844–860, https://doi.org/10.1175/JHM-D-13-030.1, 2014. a
Skamarock, W., Klemp, J. B., Dudhia, J., Gill, D. O., Barker, D., Duda, M. G., Huang, X., Wang, W., and Powers, J. G.: A Description of the Advanced Research WRF Version 3, in: NCAR Technical Note, NCAR/TN-475+STR, https://doi.org/10.5065/D68S4MVH, 2008. a
Strook, D. W.: Probability Theory, an Analytic View, J. Royal Stat. Soc. Series A, 158, 356–357, https://doi.org/10.2307/2983317, 1995. a
Vautard, R., Gobiet, A., Jacob, D., Belda, M., Colette, A., Déqué, M., Fernández, J., García-Díez, M., Goergen, K., Güttler, I., Halenka, T., Karacostas, T., Katragkou, E., Keuler, K., Kotlarski, S., Mayer, S., van Meijgaard, E., Nikulin, G., Patarčić, M., Scinocca, J., Sobolowski, S., Suklitsch, M., Teichmann, C., Warrach-Sagi, K., Wulfmeyer, V., and Yiou, P.: The simulation of European heat waves from an ensemble of regional climate models within the EURO-CORDEX project, Clim. Dynam, 41, 2555–2575, https://doi.org/10.1007/s00382-013-1714-z, 2013. a
Vidal, J.-P., Martin, E., Franchistéguy, L., Baillon, M., and Soubeyroux, J.-M.: A 50-year high-resolution atmospheric reanalysis over France with the Safran system, Int. J. Climatol., 30, 1627–1644, https://doi.org/10.1002/joc.2003, 2010. a
Villani, C.: Optimal Transport: Old and New, in: Grundlehren der mathematischen Wissenschaften, 1 edn., Springer Science & Business Media, 992 pp., 2008. a, b, c
von Storch, H.: On the Use of “Inflation” in Statistical Downscaling, J. Climate, 12, 3505–3506, https://doi.org/10.1175/1520-0442(1999)012<3505:OTUOII>2.0.CO;2, 1999. a
Vrac, M.: Multivariate bias adjustment of high-dimensional climate simulations: the Rank Resampling for Distributions and Dependences (R2D2) bias correction, Hydrol. Earth Syst. Sci., 22, 3175–3196, https://doi.org/10.5194/hess-22-3175-2018, 2018. a, b
Vrac, M. and Friederichs, P.: Multivariate–Intervariable, Spatial, and Temporal–Bias Correction, J. Climate, 28, 218–237, https://doi.org/10.1175/JCLI-D-14-00059.1, 2015. a
Wilcke, R. A. I., Mendlik, T., and Gobiet, A.: Multi-variable error correction of regional climate models, Clim. Change, 120, 871–887, https://doi.org/10.1007/s10584-013-0845-x, 2013. a
Wong, G., Maraun, D., Vrac, M., Widmann, M., Eden, J. M., and Kent, T.: Stochastic Model Output Statistics for Bias Correcting and Downscaling Precipitation Including Extremes, J. Climate, 27, 6940–6959, https://doi.org/10.1175/JCLI-D-13-00604.1, 2014. a
Wood, A. W., Leung, L. R., Sridhar, V., and Lettenmaier, D. P.: Hydrologic Implications of Dynamical and Statistical Approaches to Downscaling Climate Model Outputs, Clim. Change, 62, 189–216, https://doi.org/10.1023/B:CLIM.0000013685.99609.9e, 2004. a