the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A global Budyko model to partition evaporation into interception and transpiration
Ameneh Mianabadi
Miriam Coenders-Gerrits
Pooya Shirazi
Bijan Ghahraman
Amin Alizadeh
Evaporation is a crucial flux in the hydrological cycle and links the water and energy balance of a catchment. The Budyko framework is often used to provide a first-order estimate of evaporation, as it is a straightforward model with only rainfall and potential evaporation as required input. Many researchers have improved the Budyko framework by including more physics and catchment characteristics in the original equation. However, the parameterization of these improved Budyko models is not so straightforward, is data demanding, and requires local knowledge that is difficult to obtain at the global scale. In this paper we present an improvement of the previously presented Gerrits' model (“Analytical derivation of the Budyko curve based on rainfall characteristics and a simple evaporation model” in Gerrits et al., 2009 WRR), whereby total evaporation is calculated on the basis of simple interception and transpiration thresholds in combination with measurable parameters like rainfall dynamics and storage availability from remotely sensed data sources. While Gerrits' model was previously investigated for 10 catchments with different climate conditions and where some parameters were assumed to be constant, in this study we applied the model at the global scale and fed the model with remotely sensed input data. The output of the model has been compared to two complex land-surface models, STEAM and GLEAM, as well as the database of Landflux-EVAL. Our results show that total evaporation estimated by Gerrits' model is in good agreement with Landflux-EVAL, STEAM, and GLEAM. The results also show that Gerrits' model underestimates interception in comparison to STEAM and overestimates it in comparison to GLEAM, whereas the opposite is found for transpiration. Errors in interception can partly be explained by differences in the definition of interception that successively introduce errors in the calculation of transpiration. Relating to the Budyko framework, the model shows a reasonable performance for the estimation of total evaporation. The results also found a unimodal distribution of the transpiration to precipitation fraction (), indicating that both increasing and decreasing aridity will result in a decline in the fraction of transpired rainfall by plants for growth and metabolism.
- Article
(2405 KB) - Full-text XML
- BibTeX
- EndNote
Budyko curves are used as a first-order estimate of annual evaporation in terms of annual precipitation and potential evaporation. If the available energy is sufficient to evaporate the available moisture, annual evaporation can approach annual precipitation (water-limited situation). If the available energy is not sufficient, annual evaporation can approach potential evaporation (energy-limited situation). Using the water balance and the energy balance, and applying the definition of the aridity index and Bowen ratio, the Budyko framework can be described as (Arora, 2002)
with Ea annual evaporation (L T−1), Pa annual precipitation (L T−1), the evaporation ratio (–), and ∅ the aridity index, which is defined as the potential evaporation divided by annual precipitation (–). All Budyko curves, developed by different researchers (Table 1), have a similar pattern to Eq. (1).
The equations shown in Table 1 assume that the evaporation ratio is determined by climate only and do not take into account the effect of other controls on the water balance. Therefore, some researchers incorporated more physics into the Budyko framework. For example, Milly (1993, 1994) investigated the root zone storage as an essential secondary control on the water balance. Choudhury (1999) used net radiation and a calibration factor in the Budyko curves. Zhang et al. (2001, 2004) tried to add a plant-available water coefficient, Porporato et al. (2004) took into account the maximum storage capacity, Yang et al. (2006, 2008) incorporated a catchment parameter, and Donohue et al. (2007) tried to consider vegetation dynamics. The inclusion of these physics and catchment characteristics improved the performance of the Budyko curves locally; however, it made them less applicable for the global scale, since the parameterization is data demanding and requires local knowledge, which is not always available. Therefore, in this study, we aim to show that the Budyko framework can also be explained with a simple analytical model that is less dependent on local data that are difficult to obtain at the global scale. Accordingly, we use the reasoning of the model of Gerrits et al. (2009) (hereafter Gerrits' model) that recognizes the characteristic timescales of the different evaporation processes (i.e. interception at daily scale and transpiration at monthly scale). Despite the fact that Gerrits et al. (2009) aimed to develop an analytical model that is physically based and only uses measurable parameters, some of the required input values are not available at the global scale – e.g. carry-over parameter (A), interception storage capacity (Smax), and plant-available water (Su,max). Now with the current developments in remotely sensed data, new opportunities have arisen to overcome this data limitation. Therefore, in this study, we propose relations between the missing input parameters and remotely sensed data products, so Gerrits' model can be tested at the global scale.
One of the input parameters is soil moisture storage. Recently, many studies (e.g. Chen et al., 2013; Donohue et al., 2010; Istanbulluoglu et al., 2012; Milly and Dunne, 2002; Wang, 2012; Zhang et al., 2008) found that soil moisture storage change is a critical component in modelling the interannual water balance. Including soil water information in the Budyko framework was often difficult, because this information is not widely available. However, Gao et al. (2014) presented a new method where the available soil water (which is often linked to soil water capacity) is derived from time series of rainfall and potential evaporation, plus a long-term runoff coefficient. These input time series can be obtained locally (e.g. de Boer-Euser et al., 2016), but can also be derived from remotely sensed data as shown by Wang-Erlandsson et al. (2016), allowing us to apply the method at the global scale and incorporate it into Gerrits' model.
Next to using the method of Gao et al. (2014) to globally estimate the maximum soil water storage (Su,max), we also tested a method to derive the interception storage capacity (Smax) from remotely sensed data. These two parameters are required to make a first-order estimate of total evaporation and to partition this into interception evaporation and transpiration as well. The outcome is compared to more complex land–surface–atmosphere models. Furthermore, the model results will be related to the Budyko framework for a better understanding of the partitioning of evaporation into transpiration and interception.
Total evaporation (E) may be partitioned as follows (Shuttleworth, 1993):
in which Ei is interception evaporation, Et is transpiration, Eo is evaporation from water bodies, and Es is evaporation from the soil, all with dimension (L T−1). In this definition, interception is the amount of evaporation from any wet surface including canopy, understory, forest floor, and the top layer of the soil. Soil evaporation is defined as evaporation of the moisture in the soil that is connected to the root zone (de Groen and Savenije, 2006) and therefore is different from evaporation of the top layer of the soil (several millimetres of soil depth, which is here considered to be part of the interception evaporation). Hence interception evaporation is the fast feedback of moisture to the atmosphere within a day from the rainfall event and soil evaporation is evaporation from the non-superficial soil constrained by soil moisture storage in the root zone. Like Gerrits et al. (2009), we assume that evaporation from soil moisture is negligible (or can be combined with interception evaporation). Evaporation from water bodies is used for inland open water, where interception evaporation and transpiration is zero. As a result, Eq. (2) becomes
where Ei is direct feedback from short-term moisture storage on vegetation, ground, and top layer, and Et is evaporation from soil moisture storage in the root zone.
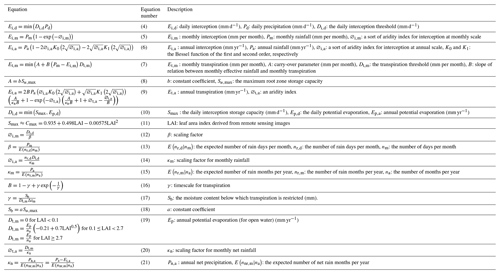
For modelling of evaporation, it is important to consider that interception and transpiration have different timescales (i.e. the stock divided by the evaporative flux) (Blyth and Harding, 2011). With a stock of a few millimetres and the evaporative flux of a few millimetres per day, interception has a timescale of the order of 1 d (Dolman and Gregory, 1992; Gerrits et al., 2007, 2009; Savenije, 2004; Scott et al., 1995). In the case of transpiration, the stock amounts to tens to hundreds of millimetres and the evaporative flux to a few millimetres per day (Baird and Wilby, 1999), resulting in a timescale of the order of month(s) (Gerrits et al., 2009). In Gerrits' model, it is successively assumed that interception and transpiration can be modelled as threshold processes at the daily and monthly timescales, respectively. Rainfall characteristics are successively used to temporally upscale from daily to monthly and from monthly to annual. A full description of the derivation and assumptions can be found in Gerrits et al. (2009). Here, we only summarize the relevant equations (Table 2) and not the complete derivation. Since we now test the model at the global scale, we do show how we estimated the required model parameters and the inputs used.
Table 2Summary of the interception and transpiration equations of Gerrits' model (Gerrits et al., 2009).
2.1 Interception
Gerrits' model considers evaporation from interception to be a threshold process at the daily timescale (Eq. 4, Table 2). Daily interception (Ei,d), then, is upscaled to monthly interception (Ei,m, Eq. 5, Table 2) by considering the frequency distribution of rainfall on a rain day (β parameter) and subsequently to annual interception (Ei,a, Eq. 6, Table 2) by considering the frequency distribution of rainfall in a rain month (κm parameter) (see de Groen and Savenije, 2006; Gerrits et al., 2009). A rain day is defined as a day with more than 0.1 mm d−1 of rain and a rain month is a month with more than 2 mm per month of rain.
While Gerrits et al. (2009) assumed a constant interception threshold ( mm d−1) for the studied locations, we here use a globally variable value based on the leaf area index (LAI) from remote sensing data. The interception threshold (Di,d) is a daily average during the year and is limited either by the daily interception storage capacity Smax (mm d−1) or by the daily potential evaporation (Eq. 9, Table 2) and is thus not seasonally variable. We can assume this because for most locations Smax is smaller than Ep,d even if we consider a daily varying potential evaporation. Additionally, Smax (based on LAI) could also be changed seasonally; however, many studies show that the storage capacity does not change significantly between the leafed and leafless periods (e.g. Leyton et al., 1967; Dolman, 1987; Rutter et al., 1975), especially once interception is defined in the broad sense that it includes all evaporation from the canopy, understory, forest floor, and the top layer of the soil: leaves that are dropped from the canopy retain their interception capacity as they are on the forest floor in the leafless period. Furthermore, Gerrits et al. (2010) showed with a Rutter-like model that interception is more sensitive to the rainfall pattern than to the storage capacity. This was confirmed by Miralles et al. (2010). Hence, in interception modelling, the value of the storage capacity is of minor concern, and its seasonality is incorporated into the temporal rainfall patterns.
The daily interception storage capacity should be seen as the maximum interception capacity within 1 d, including the (partly) emptying and filling of the storage between events per day, i.e. , where Cmax (L) is the interception storage capacity specific to a land cover type. If there is only one rain event per day (n=1 d−1) (Gerrits et al., 2010), Smax (L T−1) equals Cmax (L), as is often found in the literature. Despite proposing modifications for storms, which last more than 1 d (Pearce and Rowe, 1981), and multiple storms per rain day (Mulder, 1985), Miralles et al. (2010) and Pearce and Rowe (1981) both mentioned that accounting for n is rarely necessary. Pearce and Rowe (1981) mentioned that “In many climates, however, such adjustments will not be necessary, or small enough that they can be neglected”. In our interpretation, this is because the number of times the interception storage can be filled and completely emptied is limited once we assume a drying time of a couple of hours (e.g. 4), which is common (Wang-Erlandsson et al., 2014).
For n=1, the interception storage capacity can be estimated from Von Hoyningen-Huene (1981), which is obtained for a series of crops based on the LAI (de Jong and Jetten, 2007) (Eq. 10, Table 2). Since the storage capacity of the forest floor is not directly related to LAI, it could be said that the 0.935 mm in Eq. (10) is sort of the storage capacity of the forest floor. Since this equation was developed for crops, it is likely that it underestimates interception by forests with a denser understory and forest floor interception capacity.
2.2 Transpiration
Transpiration is considered to be a threshold process at the monthly timescale (Et,m (mm per month, Eq. 7, Table 2) and successively is upscaled to annual transpiration (Et,a (mm yr−1, Eq. 8, Table 2) by considering the frequency distribution of the net monthly rainfall () expressed with the parameter κn. To estimate the monthly and annual transpiration, two parameters A and B are required. A is the initial soil moisture or carry-over value (mm per month) and B is dimensionless and described as Eq. (15), where the dimensionless γ is obtained by Eq. (16).
Gerrits et al. (2009) assumed a constant carry-over value (A) and used A=0, 5, 15, and 20 mm per month, depending on the location, to determine annual transpiration. Moreover, they considered γ to be constant (γ=0.5). In the current study, we determined these two parameters based on the maximum root zone storage capacity (Su,max). In Eq. (17) Δtm equals 1 month and Sb is estimated by aSu,max (Eq. 18 in Table 2), where a is 0.5–0.8 (de Groen, 2002; Shuttleworth, 1993). In this study, we assumed a to be 0.5 as this value is commonly used for many crops (Allen et al., 1998). Furthermore, we assumed that the monthly carry-over A could be estimated by Eq. (18), and in this study, we assumed b=0.2, which gave the best global results for all land classes. In the sensitivity analysis both the sensitivity of a and b towards total evaporation will be investigated. To estimate A and γ, it is important to have a reliable database of Su,max. For this purpose, we used the global estimation of Su,max from Wang-Erlandsson et al. (2016). Su,max is derived by the mass balance method using satellite-based precipitation and evaporation (Wang-Erlandsson et al., 2016). Wang-Erlandsson et al. (2016) estimated the root zone storage capacity from the maximum soil moisture deficit, as the integral of the outgoing flux (i.e. evaporation which is the sum of transpiration, evaporation, interception, soil moisture evaporation, and open water evaporation) minus the incoming flux (i.e. precipitation and irrigation). In their study, the root zone storage capacity was defined as the total amount of water that plants can store to survive droughts. Note that this recent method (Gao et al., 2014) to estimate Su,max does not require soil information, but only uses climatic data. It is assumed that ecosystems adjust their storage capacity to climatic demands irrespective of the soil properties. Under wet conditions, Gao's method appeared to perform better than soil-based methods. For (semi-)arid climates the differences between this method and soil-based methods appear to be small (de Boer-Euser et al., 2016).
Furthermore, Gerrits et al. (2009) estimated the average monthly transpiration threshold (Dt,m) as (where na = number of months per year), which assumes that if there is little interception, plants can transpire at the same rate as a well-watered reference grass as calculated with the Penman–Monteith equation (University of East Anglia Climatic Research Unit, 2014). In reality, most plants encounter more resistance (crop resistance) than grass; hence, we used Eq. (17), Table 2 (Fredlund et al., 2012) to convert potential evaporation of reference grass (Ep) to potential transpiration of a certain crop depending on the LAI (i.e. the transpiration threshold Dt,m – millimetres per month). Furthermore, similarly to the daily interception threshold, we took a constant Dt,m, which can be problematic in energy-constrained areas. However, in those areas temperature and radiation often follow a sinusoidal pattern without complex double seasonality, as e.g. occurs in the ITCZ. This implies that the overestimation of Et,m in winter will be compensated (on the annual timescale) by the underestimation in summer time. By means of a sensitivity analysis the effect of a constant Dt,m will be investigated.
For precipitation, we used the AgMERRA product from the AgMIP climate forcing data set (Ruane et al., 2015), which has a daily timescale and a spatial resolution of 0.25∘ × 0.25∘. The spatial coverage of AgMERRA is global for the years 1980–2010. The AgMERRA product is available on the NASA Goddard Institute for Space Studies website (http://data.giss.nasa.gov/impacts/agmipcf/agmerra/, last access: 18 April 2015).
Potential evaporation data (calculated by the FAO–Penman–Monteith equation; Allen et al., 1998) were taken from the Center for Environmental Data Archival website (http://catalogue.ceda.ac.uk/uuid/4a6d071383976a5fb24b5b42e28cf28f, last access: 17 June 2015), produced by the Climatic Research Unit (CRU) at the University of East Anglia (University of East Anglia Climatic Research Unit, 2014). These data are at the monthly timescale over the period 1901–2013 and has a spatial resolution of 0.5∘ × 0.5∘. We used the data of 1980–2010 in consistency with the precipitation data set.
LAI data were obtained from Vegetation Remote Sensing & Climate Research (http://sites.bu.edu/cliveg/datacodes/, last access: 1 May 2015) (Zhu et al., 2013). The spatial resolution of the data sets is 1∕12∘, with 15 d composites (two per month) for the period July 1981 to December 2011.
The data of Su,max are prepared data by Wang-Erlandsson et al. (2016) and are based on the satellite-based precipitation and evaporation with 0.5∘ × 0.5∘ resolution over the period 2003–2013. They used the USGS Climate Hazards Group InfraRed Precipitation with Stations (CHIRPS) precipitation data at 0.05∘ (Funk et al., 2014) and the ensemble mean of three data sets of evaporation, including CSIRO MODIS Reflectance Scaling EvapoTranspiration (CMRSET) at 0.05∘ (Guerschman et al., 2009), the Operational Simplified Surface Energy Balance (SSEBop) at 30′′ (Senay et al., 2013), and MODIS evapotranspiration (MOD16) at 0.05∘ (Mu et al., 2011). They calculated potential evaporation using the Penman–Monteith equation (Monteith, 1965).
The model performance was evaluated by comparing our results at the global scale to global evaporation estimates from other studies. Most available products only provide total evaporation estimates and do not distinguish between interception and transpiration. Therefore, we chose to compare our interception and transpiration results to two land-surface models: the Global Land Evaporation Amsterdam Model (GLEAM) (v3.0a) database (Martens et al., 2017; Miralles et al., 2011a) and Simple Terrestrial Evaporation to Atmosphere Model (STEAM) (Wang-Erlandsson et al., 2014, 2016). GLEAM estimates different fluxes of evaporation, including transpiration, interception, bare soil evaporation, snow sublimation, and open water evaporation. STEAM, on the other hand, estimates the different components of evaporation, including transpiration, vegetation interception, floor interception, soil moisture evaporation, and open water evaporation. Thus for the comparison of interception, we used the sum of the canopy and floor interception and soil evaporation from STEAM and canopy interception and bare soil evaporation from GLEAM. Furthermore, STEAM includes an irrigation module (Wang-Erlandsson et al., 2014), while Miralles et al. (2011a) mentioned that they did not include irrigation in GLEAM, but the assimilation of the soil moisture from satellite data would account for it as soil moisture adjusted to seasonal dynamics of any region. The total evaporation was also compared to LandFlux-EVAL products (Mueller et al., 2013). The GLEAM database (https://www.gleam.eu/, last access: 25 January 2016) is available for 1980–2014 with a resolution of 0.25∘ × 0.25∘ and the STEAM model was performed for 2003–2013 with a resolution of 1.5∘ × 1.5∘. LandFlux-EVAL data (https://data.iac.ethz.ch/landflux/, last access: 22 January 2016) are available for 1989–2005. We compared Gerrits' model to other products based on the land cover to judge the performance of the model for different types of land cover. The global land cover map (Channan et al., 2014; Friedl et al., 2010) was obtained from http://glcf.umd.edu/data/lc/ (last access: 14 November 2016). We used root mean square error (RMSE) (Eq. 20), mean bias error (MBE) (Eq. 21), and relative error (RE) (Eq. 22) to evaluate the results.
In these equations, xiM is evaporation of the benchmark models to which Gerrits' model is compared for pixel i, xiG is evaporation from Gerrits' model for pixel i, is the average evaporation of Gerrits' model, is the average evaporation of the benchmark models, and n is the number of pixels of the evaporation map. Negative MBE and RE show Gerrits' model underestimates evaporation and vice versa. As the spatial resolution of the products is different, we regridded all the products to the coarsest resolution (1.5∘ × 1.5∘) for the comparison. Furthermore, the comparisons were shown for each land cover using the Taylor diagram (Taylor, 2001). A Taylor diagram can provide a concise statistical summary of how the models are comparable to the reference data (observation or given model) in terms of their correlation, RMSE, and the ratio of their variances. In this paper, the reference data are Gerrits' model. Since the different models for different land cover types have been used in this study, which have different numerical values, the results are normalized by the reference data. It should be noted that the standard deviation of the reference data is normalized by itself and, therefore, it is plotted at unit distance from the origin along the horizontal axis (Taylor, 2001). According to the Taylor diagram, when the points are close to reference data (“Ref” in Figs. 2, 4, and 6), it shows that the RMSE is less and the correlation is higher and, therefore, the models are in more reasonable agreement.
5.1 Total evaporation comparison
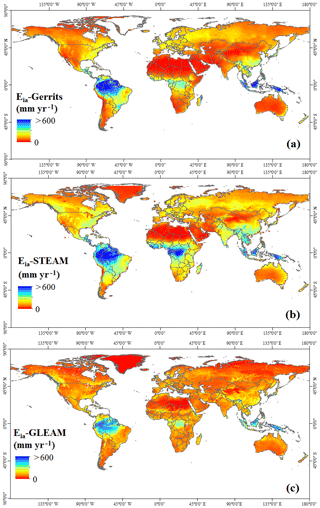
Figure 1 shows the mean annual evaporation from the data sets of Gerrits' model, Landflux-EVAL, STEAM, and GLEAM. In general, the spatial distribution of evaporation simulated by Gerrits' model is similar to that of the benchmark models. Figure 1a demonstrates that, as expected, the highest annual evaporation (sum of interception evaporation and transpiration) occurs in tropical evergreen broadleaf forests and that the lowest rate occurs in the barren and sparsely vegetated desert regions. Total evaporation varies between almost zero in arid regions to more than 1500 mm yr−1 in the tropics.
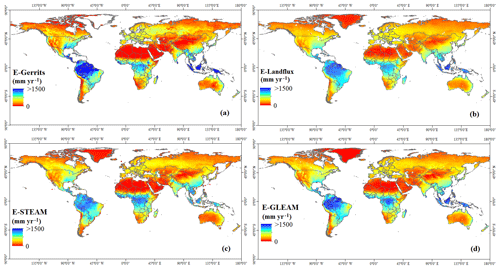
Figure 1Mean annual evaporation estimated by (a) Gerrits' model, (b) Landflux-EVAL (Mueller et al., 2013), (c) STEAM (Wang-Erlandsson et al., 2014, 2016), and (d) GLEAM (Martens et al., 2017; Miralles et al., 2011a).
As can be seen in Fig. 1, there also exist large differences between STEAM, GLEAM, and Landflux-EVAL. Different precipitation products used in the models are likely the reason for the differences. As found by Gerrits et al. (2009), the model sensitivity to the number of rain days and rain months especially for the higher rates of precipitation can be a probable reason for the poor performance of a model, especially for the forests with the highest amount of precipitation. In Sect. 5.5 we will elaborate on the sensitivity of these parameters on the global scale.
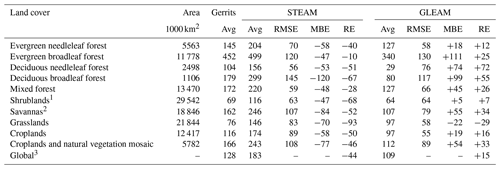
The contributions of mean annual evaporation per land cover type from Gerrits' model and other products, as well as RMSE, MBE, and RE, are shown in Table 3. Globally, mean annual evaporations estimated (for the overlapped pixels with 1.5∘ × 1.5∘ resolution) by Gerrits' model, Landflux-EVAL, STEAM, and GLEAM are 443, 469, 475, and 462 mm yr−1, respectively. Our results are comparable to those of Haddeland et al. (2011), where the simulated global terrestrial evaporation ranges between 415 and 586 mm yr−1 for the period 1985–1999. Generally, Gerrits' model overestimates evaporation for most land cover types in comparison to Landflux-EVAL and GLEAM and underestimates evaporation in comparison to STEAM (see also MBE and RE). Since the number of pixels covered by each land use is different, RMSE, MBE, and RE cannot be comparable between land cover types. RMSE, MBE, and RE for each land cover type show that, generally, Gerrits' model is in better agreement with Landflux and GLEAM than STEAM. The Taylor diagram for total evaporation, as estimated by Gerrits' model in comparison to Landflux-EVAL, STEAM, and GLEAM for all data (no. 1 in Fig. 2) and for each land cover type (no. 2 to no. 11 in Fig. 2), also indicates that Gerrits' model is in better agreement with Landflux-EVAL and GLEAM than the STEAM model, especially for evergreen broadleaf forest, shrublands, savannas, and croplands (see also Table 3).
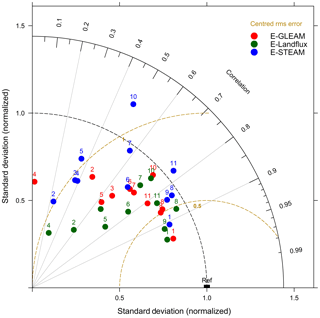
Figure 2Taylor diagram for mean annual evaporation estimated by Gerrits' model in comparison to Landflux-EVAL (green circles), STEAM (blue circles), and GLEAM (red circles) for all data (no. 1), evergreen needleleaf forest (no. 2), evergreen broadleaf forest (no. 3), deciduous needleleaf forest (no. 4), deciduous broadleaf forest (no. 5), mixed forest (no. 6), shrublands (no. 7), savannas (no. 8), grasslands (no. 9), croplands (no. 10), and croplands and natural vegetation mosaic (no. 11).
Table 3Comparison of mean annual evaporation estimated by Gerrits' model to Landflux-EVAL, STEAM, and GLEAM through average, RMSE, MBE, and RE per land cover type. Negative MBE and RE show Gerrits' model underestimates evaporation and vice versa. Average, RMSE, and MBE are in mm yr−1 and RE is in %.

1 Including open and closed shrublands. 2 Including woody savannas and savannas. 3 For overlapped pixels with 1.5∘ × 1.5∘ resolution.
5.2 Annual interception comparison
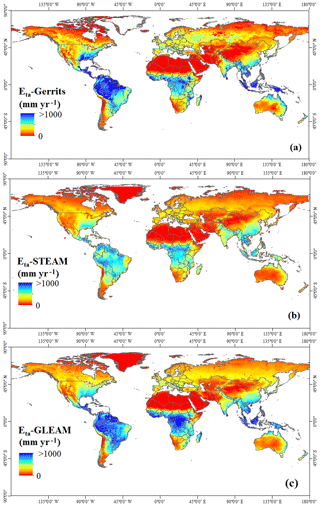
While Wang-Erlandsson et al. (2014, 2016) estimated canopy interception, floor interception, and soil evaporation separately, in the current study we assumed that these three components of evaporation can be lumped as interception evaporation. Figure 3 shows the mean annual evaporation from interception at the global scale as estimated by Gerrits' model, STEAM, and GLEAM. In this figure, interception from STEAM is calculated by the sum of canopy interception, floor interception, and soil evaporation. Furthermore, interception from GLEAM is calculated as the sum of canopy interception and bare soil evaporation (GLEAM does not estimate floor interception). In general, the spatial distribution of Gerrits' simulated interception is partly similar to that of STEAM and GLEAM. In the tropics, with high amounts of annual precipitation and high storage capacities due to the dense vegetation (evergreen broadleaf forests and savannas), annual interception shows the highest values. Table 4 shows the average interception, RMSE, MBE, and RE per land cover type. This table indicates that Gerrits' model underestimates interception in comparison to STEAM for all land cover types. Table 4 also shows that, in comparison to GLEAM, Gerrits' model overestimates interception for all land cover types, because in GLEAM floor interception has not been taken into account. Figure 4 also shows that Gerrits' model is in better agreement with STEAM (especially for grasslands and mixed forest) than GLEAM. The reason for an underestimated interception in comparison to STEAM could be the role of the understory. LAI does not account for understory; therefore, maybe Smax should be larger than modelled with Eq. (10). However, there are almost no data available to estimate the interception storage capacity of the forest floor at the global scale.
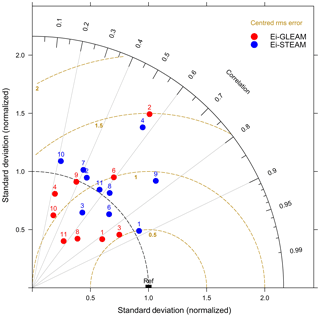
Figure 4Taylor diagram for mean annual interception estimated by Gerrits' model in comparison to STEAM (blue circles) and GLEAM (red circles) for all data (no. 1), evergreen needleleaf forest (no. 2), evergreen broadleaf forest (no. 3), deciduous needleleaf forest (no. 4), deciduous broadleaf forest (no. 5), mixed forest (no. 6), shrublands (no. 7), savannas (no. 8), grasslands (no. 9), croplands (no. 10), and croplands and natural vegetation mosaic (no. 11).
Table 4Comparison of interception estimated by Gerrits' model to STEAM and GLEAM through average, RMSE, MBE, and RE per land cover type. Negative MBE and RE show Gerrits' model underestimates evaporation and vice versa. Average, RMSE, and MBE are in mm yr−1 and RE is in %.
1 Including open and closed shrublands. 2 Including woody savannas and savannas. 3 For overlapped pixels with 1.5∘ × 1.5∘ resolution.
5.3 Annual transpiration comparison
Figure 5 illustrates the mean annual transpiration as estimated by Gerrits' model, STEAM, and GLEAM. The spatial distribution is similar to the results of STEAM and GLEAM. Mean annual transpiration varies between 0 mm yr−1 for arid areas in the north of Africa (Sahara) and more than 1000 mm yr−1 in the tropics in South America. The results show that the highest annual transpiration occurs in evergreen broadleaf forests with the highest amount of precipitation and dense vegetation (see also Table 5). Figure 5c shows that GLEAM, in comparison to Gerrits' model, overestimates the transpiration in some regions and especially in the tropics in South America and central Africa. Figure 5b also shows that STEAM is different from Gerrits' model over some regions like India, western China, and North America as well as in the tropics. Table 5 (MBE and RE) also indicates that Gerrits' model underestimates transpiration in comparison to GLEAM and overestimates it in comparison to STEAM. The Taylor diagram (Fig. 6) shows that the global annual transpiration of Gerrits' model is closer to that of GLEAM than STEAM, showing that Gerrits' model is in more reasonable agreement with GLEAM for transpiration estimation.
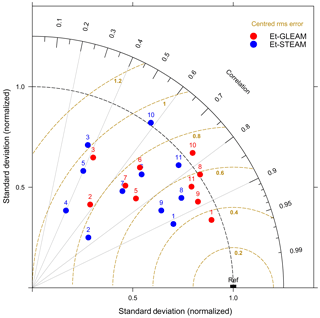
Figure 6Taylor diagram for mean annual transpiration estimated by Gerrits' model in comparison to STEAM (blue circles) and GLEAM (red circles) for all data (no. 1), evergreen needleleaf forest (no. 2), evergreen broadleaf forest (no. 3), deciduous needleleaf forest (no. 4), deciduous broadleaf forest (no. 5), mixed forest (no. 6), shrublands (no. 7), savannas (no. 8), grasslands (no. 9), croplands (no. 10), and croplands and natural vegetation mosaic (no. 11).
Moreover, the global transpiration ratio as estimated by Gerrits' model is 71 %, which is comparable to the ratio as estimated by other studies (e.g. 80 %; Miralles et al., 2011b, 69 %; Sutanto, 2015, 65 %; Good et al., 2015, 62 %; Maxwell and Condon, 2016, 62 %; Lian et al., 2018, 61 %; Schlesinger and Jasechko, 2014, 57 %; Wei et al., 2017, 52 %; Choudhury and Digirolamo, 1998, 48 %; Dirmeyer et al., 2006 and 41 %; Lawrence et al., 2007). Additionally, Coenders-Gerrits et al. (2014) found that based on the model of Jasechko et al. (2013) the transpiration ratio changes between 35 % and 80 %, which is in line with our current findings.
5.4 Analysing the results through the Budyko framework
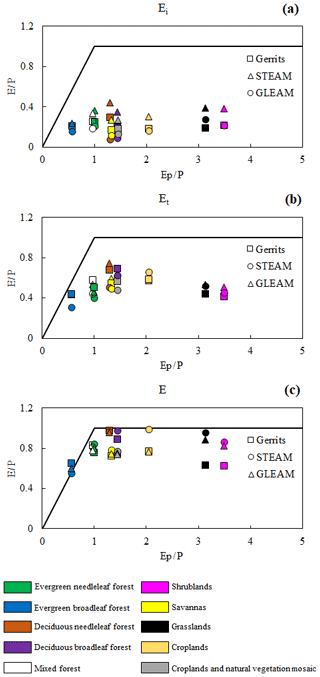
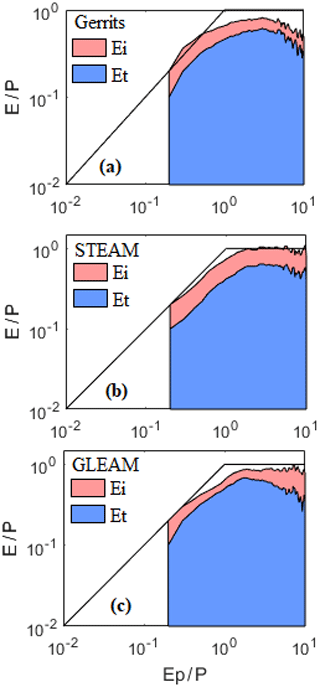
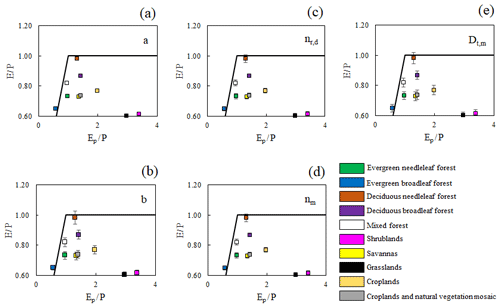
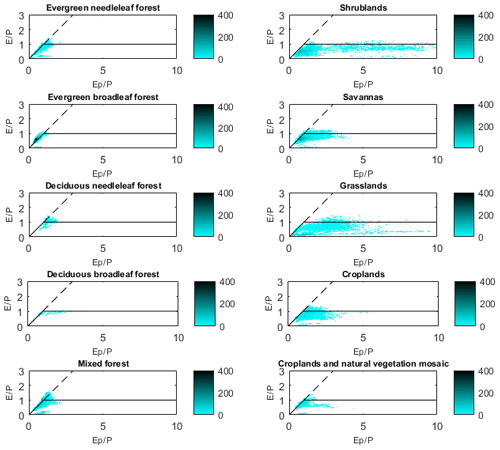
We evaluated the relation between the evaporation fluxes and the energy/water limitation in the Budyko framework as provided by Miralles et al. (2016) and Good et al. (2017) to see how our model can be related to the Budyko framework and how the energy and water limitations can be interpreted by our model. Figure 7 shows the density plot of versus within the Budyko framework. To calculate and for all models, precipitation and potential evaporation data are the same as used in this study. This figure indicates that, while Gerrits' model does not perform well in comparison to STEAM and GLEAM, it follows the framework in a reasonable manner. Furthermore, the results are comparable to the results of Miralles et al. (2016) (see Fig. 11 in their paper). The partition of evaporation related to the land cover within the Budyko framework is presented in Fig. 8. According to this figure, interception, as estimated by Gerrits' model, is closer to that of GLEAM rather than STEAM, but transpiration is close to both models. For mean annual total evaporation, Gerrits' model is more similar to GLEAM than STEAM for all land covers except for grasslands and shrublands. Moreover, the distribution of is comparable to that of Good et al. (2017) (Fig. 1a in their paper). Their results showed a unimodal distribution indicating that both increasing and decreasing aridity will result in a decline in the fraction of transpired rainfall by plants for growth and metabolism. This distribution is also seen in Fig. 9, where the plot is provided based on the average of for each aridity index (). This figure is also comparable to Fig. 1c in Good et al.'s (2017) paper.
Table 5Comparison of transpiration estimated by Gerrits' model to STEAM and GLEAM through average, RMSE, MBE, and RE per land cover type. Negative MBE and RE show Gerrits' model underestimates evaporation and vice versa. Average, RMSE, and MBE are in mm yr−1 and RE is in %.
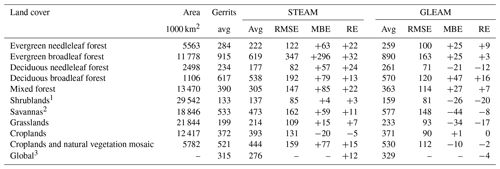
1 Including open and closed shrublands. 2 Including woody savannas and savannas. 3 For overlapped pixels with 1.5∘ × 1.5∘ resolution.
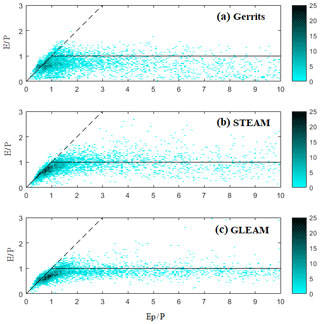
Figure 7Density plot of versus for comparison between models within the Budyko framework. The legend shows the frequency of pixels.
5.5 Sensitivity analysis
In our sensitivity analysis we investigated the sensitivity of the three parameters that are related to transpiration (constants a and b, and threshold Dt,m) and the effect of the number of rain days and rain months on the total evaporation calculation. All parameters were increased and decreased by 10 %. The analysis shows that the model is not too sensitive to parameter a, where a ±10 % change in a leads to a minor ±0.4 % change in (see Fig. 10a). Thus, the model is insensitive to changes in parameter a. Similar results were found for parameter b, where a ±10 % change in b resulted only in a ±3.5 % change in (Fig. 10b). Moreover, a ±10 % change in both nr,d and nr,m leads to a ±2.2 change in (Fig. 10c and d). The most sensitive parameter is Dt,m, where a ±10 % change in Dt,m resulted in a ±4 % change in (Fig. 10e). In conclusion, Dt,m and b are the most sensitive parameters for the estimation of ; however, it seems that the sensitivity is not that much different per land class, except for grasslands and shrublands, which may arise from the underestimation of interception in Gerrits' model for short vegetation. This underestimation is obtained because the relation between Smax and LAI might not be valid for short vegetation. This also might be due to the wide range of gridded points belonging to grasslands and shrublands as shown by the density plot of versus in Fig. 11.
In the current study, we revised and applied a simple evaporation model proposed by Gerrits et al. (2009) at the global scale. Instead of locally calibrated model parameters, we now only used parameters derived from remotely sensed data. Furthermore, we implemented in Gerrits' model a new definition of the root zone storage capacity from Gao et al. (2014).
Comparing our results for total evaporation to Landflux-EVAL estimates shows that Gerrits' model is in good agreement with Landflux-EVAL. The highest mean annual evaporation rates are found in evergreen broadleaf forests (1367 mm yr−1), deciduous broadleaf forests (796 mm yr−1), and savannas (695 mm yr−1), and the lowest ones are found in shrublands (203 mm yr−1) and grasslands (275 mm yr−1). Generally, Gerrits' model overestimates in comparison to Landflux-EVAL and GLEAM and underestimates in comparison to STEAM.
Gerrits' model underestimates interception in comparison to STEAM for all land covers. On the other hand, the model overestimates interception in comparison to GLEAM, since GLEAM does not include floor interception. Although we tried to correct for the different definitions of interception, the results may be biased. The relatively worse performance in forest ecosystems could be explained by the effect of the understory. This is not taken into account in Gerrits' model, while the understory can also intercept water. We could say that the constant value of 0.935 mm in Eq. (10) reflects the forest floor interception storage capacity, but since this number was derived for crops, it is likely an underestimation. Therefore, a better estimation of Smax to account for forest floor interception is recommended.
Estimated transpiration by Gerrits' model is in reasonable agreement with GLEAM and STEAM. Gerrits' model underestimates transpiration in comparison to GLEAM (RE = −4 %) and overestimates transpiration in comparison to STEAM (RE = +12 %). The scatter plots showed that, in comparison to GLEAM and STEAM, Gerrits' model performs well for all land cover types. Moreover, the transpiration ratio corresponded well in comparison to those of GLEAM and STEAM. The results also showed that the global transpiration ratio estimated by Gerrits' model (71 %) is approximately comparable to the other studies.
Our results are also related to the Budyko framework, and we found similarly to Good et al. (2017) that the distribution of is unimodal, indicating that both increasing and decreasing aridity will result in a decline in the fraction of transpired precipitation by plants for growth and metabolism.
By comparing all products, we found that, in general, there are considerable differences between STEAM, GLEAM, and Landflux-EVAL. The most convincing reason for this discrepancy lies in the different products for precipitation (and other global data sets), which have been used for the different models. Gerrits' model is sensitive to the number of rain days and months, especially for the higher rates of precipitation. Nonetheless, our sensitivity analysis of parameters a and b and nr,d, nr,m, and Dt,m shows that Dt,m and b are the most sensitive parameters for the estimation of .
Generally, it should be mentioned that the underlying reasoning of Gerrits' model is to recognize the characteristic timescales of the different evaporation processes (i.e. interception daily and transpiration monthly). In Gerrits et al. (2009) (and in the current paper as well), this has been done by taking yearly averages for the interception (Di,d, mm d−1) and transpiration threshold (Dt,m, mm per month) in combination with the temporal distribution functions for daily and monthly (net) rainfall. Hence, the seasonality is incorporated into the temporal rainfall patterns and not into the evaporation thresholds. This is a limitation of the currently used approach and could be the focus of a new study by investigating how seasonally fluctuating thresholds (based on LAI and/or a simple cosine function) would affect the results. This could be a significant methodological improvement of Gerrits' model, but will have mathematical implications for the analytical model derivation. It will improve the monthly evaporation estimates, but we expect that the consequences at the annual timescale (which is the focus of the current paper) will be less severe. The strength of Gerrits' model is that, in comparison to other models, it is very simple and, in spite of its simplicity, Gerrits' model performs quite well.
The model output of annual interception, transpiration and total evaporation can be found on Mianabadi et al. (2019) (https://doi.org/10.4121/uuid:f3afc700-1466-4b3f-92f1-989921536a57).
AM and MCG implemented the model on the global scale and analysed the data. PS helped with the code programming. AM and MCG prepared the manuscript with contribution from all the co-authors.
The authors declare that they have no conflict of interest.
This research was partly funded by NWO Earth and Life Sciences (ALW), Veni-project 863.15.022, the Netherlands. Furthermore, we would like to thank Iran's Ministry of Science, Research and Technology for supporting this research and the mobility fellowship. We also would like to thank Jie Zhou, Lan Wang-Erlandsson, Kamran Davary, Shervan Gharari, and Hubert Savenije for their kind help and comments.
This research has been supported by the NWO Earth and Life Sciences (grant no. 863.15.022).
This paper was edited by Nunzio Romano and reviewed by Stephen Good and one anonymous referee.
Allen, R., Pereira, L., Raes, D., and Smith, M.: Crop evapotranspiration: Guidelines for computing crop water requirements, FAO Irrig. Drain. Pap. 56, FAO, Rome, Italy, p. 300, 1998.
Arora, V. K.: The use of the aridity index to assess climate change effect on annual runoff, J. Hydrol., 265, 164–177, https://doi.org/10.1016/S0022-1694(02)00101-4, 2002.
Baird, A. J. and Wilby, R. L.: Eco-hydrology: Plants and Water in Terrestrial and Aquatic Environments, Routledge, London, 1999.
Blyth, E. and Harding, R. J.: Methods to separate observed global evapotranspiration into the interception, transpiration and soil surface evaporation components, Hydrol. Process., 25, 4063–4068, https://doi.org/10.1002/hyp.8409, 2011.
Budyko, M. I.: Climate and life, Academic Press, Orlando, Florida, 1974.
Channan, S., Collins, K., and Emanuel, W. R.: Global mosaics of the standard MODIS land cover type data, College Park, Maryland, USA, 2014.
Chen, X., Alimohammadi, N., and Wang, D.: Modeling interannual variability of seasonal evaporation and storage change based on the extended Budyko framework, Water Resour. Res., 49, 6067–6078, https://doi.org/10.1002/wrcr.20493, 2013.
Choudhury, B.: Evaluation of an empirical equation for annual evaporation using field observations and results from a biophysical model, J. Hydrol., 216, 99–110, https://doi.org/10.1016/S0022-1694(98)00293-5, 1999.
Choudhury, B. and Digirolamo, N. E.: A biophysical process-based estimate of global land surface evaporation using satellite and ancillary data I. Model description and comparison with observations, J. Hydrol., 205, 164–185, 1998.
Coenders-Gerrits, A. M. J., van der Ent, R. J., Bogaard, T. A., Wang-Erlandson, L., Hrachowitz, M., and Savenije, H. H. G.: Uncertainties in transpiration estimates, Nature, 506, E1–E2, https://doi.org/10.1038/nature12925, 2014.
de Boer-Euser, T., McMillan, H. K., Hrachowitz, M., Winsemius, H. C., and Savenije, H. H. G.: Influence of soil and climate on root zone storage capacity, Water Resour. Res., 52, 2009–2024, https://doi.org/10.1002/2015WR018115, 2016.
de Groen, M. M.: Modelling Interception and Transpiration at Monthly Time Steps: Introducing Daily Variability Through Markov Chains, PhD Dissertation, IHE Delft, Swets and Zeitlinger, Lisse, the Netherlands, 2002.
de Groen, M. M. and Savenije, H. H. G.: A monthly interception equation based on the statistical characteristics of daily rainfall, Water Resour. Res., 42, W12417, https://doi.org/10.1029/2006WR005013, 2006.
de Jong, S. M. and Jetten, V. G.: Estimating spatial patterns of rainfall interception from remotely sensed vegetation indices and spectral mixture analysis, Int. J. Geogr. Inf. Sci., 21, 529–545, https://doi.org/10.1080/13658810601064884, 2007.
Dirmeyer, P. A., Gao, X., Zha, M., Guo, Z., Oki, T., and Hanasaki, N.: GSWP-2: Multimodel analysis and implications for our per- ception of the land surface, B. Am. Meteorol. Soc., 87, 1381–1397, https://doi.org/10.1175/BAMS-87-10-1381, 2006.
Dolman, A. J.: Summer and winter rainfall interception in an oak forest: Predictions with an analytical and a numerical simulation model, J. Hydrol., 90, 1–9, 1987.
Dolman, A. J. and Gregory, D.: The Parametrization of Rainfall Interception In GCMs, Q. J. Roy. Meteorol. Soc., 118, 455–467, https://doi.org/10.1002/qj.49712051713, 1992.
Donohue, R. J., Roderick, M. L., and McVicar, T. R.: On the importance of including vegetation dynamics in Budyko's hydrological model, Hydrol. Earth Syst. Sci., 11, 983–995, https://doi.org/10.5194/hess-11-983-2007, 2007.
Donohue, R. J., Roderick, M. L., and McVicar, T. R.: Can dynamic vegetation information improve the accuracy of Budyko's hydrological model?, J. Hydrol., 390, 23–34, https://doi.org/10.1016/j.jhydrol.2010.06.025, 2010.
Fredlund, D. G., Rahardjo, H., and Fredlund, M. D.: Unsaturated Soil Mechanics in Engineering Practice, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2012.
Friedl, M. A., Sulla-Menashe, D., Tan, B., Schneider, A., Ramankutty, N., Sibley, A., and Huang, X.: MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets, 2001–2012, Collection 5.1, IGBP Land Cover, Boston, MA, USA, 2010.
Funk, C. C., Peterson, P. J., Landsfeld, M. F., Pedreros, D. H., Verdin, J. P., Rowland, J. D., Romero, B. E., Husak, G. J., Michaelsen, J. C., and Verdin, A. P.: A quasi-global precipitation time series for drought monitoring, US Geological Survey data series 832, Tech. rep., US Geological Survey, Reston, Virginia, p. 4, https://doi.org/10.3133/ds832, 2014.
Gao, H., Hrachowitz, M., Schymanski, S. J., Fenicia, F., Sriwongsitanon, N., and Savenije, H. H. G.: Climate controls how ecosystems size the root zone storage capacity at catchment scale, Geophys. Res. Lett., 41, 7916–7923, https://doi.org/10.1002/2014GL061668, 2014.
Gerrits, A. M. J., Savenije, H. H. G., Hoffmann, L., and Pfister, L.: New technique to measure forest floor interception – an application in a beech forest in Luxembourg, Hydrol. Earth Syst. Sci., 11, 695–701, https://doi.org/10.5194/hess-11-695-2007, 2007.
Gerrits, A. M. J., Savenije, H. H. G., Veling, E. J. M., and Pfister, L.: Analytical derivation of the Budyko curve based on rainfall characteristics and a simple evaporation model, Water Resour. Res., 45, W04403, https://doi.org/10.1029/2008WR007308, 2009.
Gerrits, A. M. J., Pfister, L., and Savenije, H. H. G.: Spatial and temporal variability of canopy and forest floor interception in a beech forest, Hydrol. Process., 24, 3011–3025, https://doi.org/10.1002/hyp.7712, 2010.
Good, S. P., Noone, D., and Bowen, G.: Hydrologic connectivity constrains partitioning of global terrestrial water fluxes, Science, 349, 175–177, https://doi.org/10.1126/science.aaa5931, 2015.
Good, S. P., Moore, G. W., and Miralles, D. G.: A mesic maximum in biological water use demarcates biome sensitivity to aridity shifts, Nat. Ecol. Evol., 1, 1883–1888, https://doi.org/10.1038/s41559-017-0371-8, 2017.
Guerschman, J. P., Van Dijk, A. I. J. M., Mattersdorf, G., Beringer, J., Hutley, L. B., Leuning, R., Pipunic, R. C., and Sherman, B. S.: Scaling of potential evapotranspiration with MODIS data reproduces flux observations and catchment water balance observations across Australia, J. Hydrol., 369, 107–119, https://doi.org/10.1016/j.jhydrol.2009.02.013, 2009.
Haddeland, I., Clark, D. B., Franssen, W., Ludwig, F., Voß, F., Arnell, N. W., Bertrand, N., Best, M., Folwell, S., Gerten, D., Gomes, S., Gosling, S. N., Hagemann, S., Hanasaki, N., Harding, R., Heinke, J., Kabat, P., Koirala, S., Oki, T., Polcher, J., Stacke, T., Viterbo, P., Weedon, G. P., and Yeh, P.: Multimodel Estimate of the Global Terrestrial Water Balance: Setup and First Results, J. Hydrometeorol., 12, 869–884, https://doi.org/10.1175/2011JHM1324.1, 2011.
Istanbulluoglu, E., Wang, T., Wright, O. M., and Lenters, J. D.: Interpretation of hydrologic trends from a water balance perspective: The role of groundwater storage in the Budyko hypothesis, Water Resour. Res., 48, W00H16, https://doi.org/10.1029/2010WR010100, 2012.
Jasechko, S., Sharp, Z. D., Gibson, J. J., Birks, S. J., Yi, Y., and Fawcett, P. J.: Terrestrial water fluxes dominated by transpiration, Nature, 496, 347–350, https://doi.org/10.1038/nature11983, 2013.
Lawrence, D. M., Thornton, P. E., Oleson, K. W., and Bonan, G. B.: The Partitioning of Evapotranspiration into Transpiration, Soil Evaporation, and Canopy Evaporation in a GCM: Impacts on Land–Atmosphere Interaction, J. Hydrometeorol., 8, 862–880, https://doi.org/10.1175/JHM596.1, 2007.
Leyton, L., Reynolds, R. C., and Thompson, F. B.: Forest hydrology, edited by: Sopper, E. W. and Lull, H. W., Pergamon Press, Oxford, 1967.
Lian, X., Piao, S., Huntingford, C., Li, Y., Zeng, Z., Wang, X., Ciais, P., Mcvicar, T. R., Peng, S., Ottlé, C., Yang, H., Yang, Y., Zhang, Y., and Wang, T.: CMIP5 models constrained by observations, Nat. Clim. Change, 8, 640–646, https://doi.org/10.1038/s41558-018-0207-9, 2018.
Martens, B., Miralles, D. G., Lievens, H., Van Der Schalie, R., De Jeu, R. A. M., Fernández-Prieto, D., Beck, H. E., Dorigo, W. A., and Verhoest, N. E. C.: GLEAM v3: satellite-based land evaporation and root-zone soil moisture, Geosci. Model Dev., 10, 1903–1925, https://doi.org/10.5194/gmd-10-1903-2017, 2017.
Maxwell, R. M. and Condon, L. E.: Connections between groundwater flowand transpiration partitioning, Science, 353, 377–380, 2016.
Mianabadi, A., Coenders-Gerrits, A. M. J., Shirazi, P., Ghahraman, B., and Alizadeh, A.: Data underlying the publication: A global Budyko model to partition evaporation into interception and transpiration. 4TU, Centre for Research Data, Dataset, https://doi.org/10.4121/uuid:f3afc700-1466-4b3f-92f1-989921536a57, 2019.
Milly, P. C. D.: An analytic solution of the stochastic storage problem applicable to soil water, Water Resour. Res., 29, 3755–3758, https://doi.org/10.1029/93WR01934, 1993.
Milly, P. C. D.: Climate, soil water storage, and the average annual water balance, Water Resour. Res., 30, 2143–2156, https://doi.org/10.1029/94WR00586, 1994.
Milly, P. C. D. and Dunne, K. A.: Macroscale water fluxes 2. Water and energy supply control of their interannual variability, Water Resour. Res., 38, 24-1–24-9, https://doi.org/10.1029/2001WR000760, 2002.
Miralles, D. G., Gash, J. H., Holmes, T. R. H., De Jeu, R. A. M., and Dolman, A. J.: Global canopy interception from satellite observations, J. Geophys. Res.-Atmos., 115, 1–8, https://doi.org/10.1029/2009JD013530, 2010.
Miralles, D. G., Holmes, T. R. H., De Jeu, R. A. M., Gash, J. H., Meesters, A. G. C. A., and Dolman, A. J.: Global land-surface evaporation estimated from satellite-based observations, Hydrol. Earth Syst. Sci., 15, 453–469, https://doi.org/10.5194/hess-15-453-2011, 2011a.
Miralles, D. G., De Jeu, R. A. M., Gash, J. H., Holmes, T. R. H., and Dolman, A. J.: Magnitude and variability of land evaporation and its components at the global scale, Hydrol. Earth Syst. Sci., 15, 967–981, https://doi.org/10.5194/hess-15-967-2011, 2011b.
Miralles, D. G., Jiménez, C., Jung, M., Michel, D., Ershadi, A., Mccabe, M. F., Hirschi, M., Martens, B., Dolman, A. J., Fisher, J. B., Mu, Q., Seneviratne, S. I., Wood, E. F., and Fernández-Prieto, D.: The WACMOS-ET project – Part 2: Evaluation of global terrestrial evaporation data sets, Hydrol. Earth Syst. Sci., 20, 823–842, https://doi.org/10.5194/hess-20-823-2016, 2016.
Monteith, J. L.: Evaporation and environment, in: Symp. Soc. Exp. Biol., vol. 19, chap. The State, Cambridge University Press, Swansea, 205–234, 1965.
Mu, Q., Zhao, M., and Running, S. W.: Improvements to a MODIS global terrestrial evapotranspiration algorithm, Remote Sens. Environ., 115, 1781–1800, https://doi.org/10.1016/j.rse.2011.02.019, 2011.
Mueller, B., Hirschi, M., Jimenez, C., Ciais, P., Dirmeyer, P. A., Dolman, A. J., Fisher, J. B., Jung, M., Ludwig, F., Maignan, F., Miralles, D. G., McCabe, M. F., Reichstein, M., Sheffield, J., Wang, K., Wood, E. F., Zhang, Y., and Seneviratne, S. I.: Benchmark products for land evapotranspiration: LandFlux-EVAL multi-data set synthesis, Hydrol. Earth Syst. Sci., 17, 3707–3720, https://doi.org/10.5194/hess-17-3707-2013, 2013.
Mulder, J. P. M.: Simulating Interception Loss Using Standard Meteorological Data, in: The Forest-Atmosphere Interaction, edited by: Hutchison, B. A. and Hicks, B. B., Reidel Publishing Company, Dordrecht, 177–196, 1985.
Ol'dekop, E. M.: On evaporation from the surface of river basins, Trans. Meteorol. Obs., 4, 200, 1911.
Pearce, A. J. and Rowe, L. K.: Rainfall interception in a multi-storied, evergreen mixed forest: estimates using Gash's analytical model, J. Hydrol., 49, 341–353, https://doi.org/10.1016/S0022-1694(81)80018-2, 1981.
Pike, J. G.: The estimation of annual run-off from meteorological data in a tropical climate, J. Hydrol., 2, 116–123, https://doi.org/10.1016/0022-1694(64)90022-8, 1964.
Porporato, A., Daly, E., and Rodriguez-Iturbe, I.: Soil water balance and ecosystem response to climate change, Am. Nat., 164, 625–632, https://doi.org/10.1086/521238, 2004.
Ruane, A. C., Goldberg, R., and Chryssanthacopoulos, J.: Climate forcing datasets for agricultural modeling: Merged products for gap-filling and historical climate series estimation, Agr. Forest Meteorol., 200, 233–248, https://doi.org/10.1016/j.agrformet.2014.09.016, 2015.
Rutter, A. J., Morton, A. J., and Robins, P. C.: A predictive model of rainfall interception in forests II. Generalization of the model and comparison with observations in some coniferous and hardwood stands, J. Appl. Ecol., 12, 367–380, 1975.
Savenije, H. H. G.: The importance of interception and why we should delete the term evapotranspiration from our vocabulary, Hydrol. Process., 18, 1507–1511, https://doi.org/10.1002/hyp.5563, 2004.
Schlesinger, W. H. and Jasechko, S.: Transpiration in the global water cycle, Agr. Forest Meteorol., 189–190, 115–117, https://doi.org/10.1016/j.agrformet.2014.01.011, 2014.
Schreiber, P.: About the relationship between the precipitation and the water management of the river in Central Europe, Meteorology, 21, 441–452, 1904.
Scott, R., Koster, R. D., Entekhabi, D., and Suarez, M. J.: Effect of a Canopy Interception Reservoir on Hydrological Persistence in a General Circulation Model, J. Climate, 8, 1917–1922, https://doi.org/10.1175/1520-0442(1995)008<1917:EOACIR>2.0.CO;2, 1995.
Senay, G. B., Bohms, S., Singh, R. K., Gowda, P. H., Velpuri, N. M., Alemu, H., and Verdin, J. P.: Operational Evapotranspiration Mapping Using Remote Sensing and Weather Datasets: A New Parameterization for the SSEB Approach, J. Am. Water Resour. Assoc., 49, 577–591, https://doi.org/10.1111/jawr.12057, 2013.
Shuttleworth, W. J.: Evaporation, in: Handbook of Hydrology, McGraw-Hill, New York, 4.1–4.53, 1993.
Sutanto, S. J.: Global transpiration fraction derived from water isotopologue datasets, J. Tek. Hidraul., 6, 131–146, 2015.
Taylor, K. E.: Summarizing multiple aspects of model performance in a single diagram, J. Geophys. Res., 106, 7183–7192, 2001.
Turc, L.: The water balance of the soil. Relationship between precipitation, evaporation and runoff, Ann. Agron., 5, 491–569, 1954.
University of East Anglia Climatic Research Unit, Harris, I. C., and Jones, P. D.: CRU TS3.22: Climatic Research Unit (CRU) Time-Series (TS) Version 3.22 of High Resolution Gridded Data of Month-by-month Variation in Climate (Jan. 1901–Dec. 2013), NCAS Br. Atmos. Data Cent., Norwich, UK, https://doi.org/10.5285/18BE23F8-D252-482D-8AF9-5D6A2D40990C, 2014.
Von Hoyningen-Huene, J.: Die Interzeption des Niederschlags in Landwirtschaftlichen Pflanzenbeständen, Arbeitsbericht Dtsch. Verband für Wasserwirtschaft und Kult. – DVWK, Braunschweig, 1981.
Wang, D.: Evaluating interannual water storage changes at watersheds in Illinois based on long-term soil moisture and groundwater level data, Water Resour. Res., 48, W03502, https://doi.org/10.1029/2011WR010759, 2012.
Wang-Erlandsson, L., Van Der Ent, R. J., Gordon, L. J. and Savenije, H. H. G.: Contrasting roles of interception and transpiration in the hydrological cycle – Part 1: Temporal characteristics over land, Earth Syst. Dynam., 5, 441–469, https://doi.org/10.5194/esd-5-441-2014, 2014.
Wang-Erlandsson, L., Bastiaanssen, W. G. M., Gao, H., Jägermeyr, J., Senay, G. B., van Dijk, A. I. J. M., Guerschman, J. P., Keys, P. W., Gordon, L. J., and Savenije, H. H. G.: Global root zone storage capacity from satellite-based evaporation, Hydrol. Earth Syst. Sci., 20, 1459–1481, https://doi.org/10.5194/hess-20-1459-2016, 2016.
Wei, Z., Yoshimura, K., Wang, L., Miralles, D. G., Jasechko, S., and Lee, X.: Revisiting the contribution of transpiration to global terrestrial evapotranspiration, Geophys. Res. Lett., 44, 2792–2801, https://doi.org/10.1002/2016GL072235, 2017.
Yang, D., Sun, F., Liu, Z., Cong, Z., and Lei, Z.: Interpreting the complementary relationship in non-humid environments based on the Budyko and Penman hypotheses, Geophys. Res. Lett., 33, 1–5, https://doi.org/10.1029/2006GL027657, 2006.
Yang, H., Yang, D., Lei, Z., and Sun, F.: New analytical derivation of the mean annual water-energy balance equation, Water Resour. Res., 44, W03410, https://doi.org/10.1029/2007WR006135, 2008.
Zhang, L., Dawes, W. R., and Walker, G. R.: Response of Mean Annual Evapotranspiration to Vegetationchanges at Catchment Scale, Water Resour. Res., 37, 701–708, 2001.
Zhang, L., Hickel, K., Dawes, W. R., Chiew, F. H. S., Western, A. W., and Briggs, P. R.: A rational function approach for estimating mean annual evapotranspiration, Water Resour. Res., 40, WR002710, https://doi.org/10.1029/2003WR002710, 2004.
Zhang, L., Potter, N., Hickel, K., Zhang, Y., and Shao, Q.: Water balance modeling over variable time scales based on the Budyko framework – Model development and testing, J. Hydrol., 360, 117–131, https://doi.org/10.1016/j.jhydrol.2008.07.021, 2008.
Zhu, Z., Bi, J., Pan, Y., Ganguly, S., Anav, A., Xu, L., Samanta, A., Piao, S., Nemani, R., and Myneni, R.: Global Data Sets of Vegetation Leaf Area Index (LAI)3g and Fraction of Photosynthetically Active Radiation (FPAR)3g Derived from Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) for the Period 1981–2011, Remote Sens., 5, 927–948, https://doi.org/10.3390/rs5020927, 2013.