Niger discharge from radar altimetry: bridging gaps between gauge and altimetry time series

The Niger River represents a challenging target for deriving discharge from spaceborne radar altimeter measurements, particularly since most terrestrial gauges ceased to provide data during the 2000s. Here, we propose deriving altimetric rating curves by “bridging” gaps between time series from gauge and altimeter measurements using hydrological model simulations. We show that classical pulse-limited altimetry (Jason-1 and Jason-2, Envisat, and SARAL/Altika) subsequently reproduces discharge well and enables continuing the gauge time series, albeit at a lower temporal resolution. Also, synthetic aperture radar (SAR) altimetry picks up the signal measured by earlier altimeters quite well and allows the building of extended time series of higher quality. However, radar retracking is necessary for pulse-limited altimetry and needs to be further investigated for SAR. Moreover, forcing data for calibrating and running the hydrological models must be chosen carefully. Furthermore, stage–discharge relations must be fitted empirically and may need to allow for break points.

1 Introduction

The Niger River, shared by Nigeria, Mali, Niger, Benin, and Guinea, represents the 14th largest river in the world, with a length of 4180 km. The Niger basin covers an area of 2.1 million square kilometers and provides water resources to more than 100 million inhabitants (Oyerinde et al., 2017). Mean annual discharge into the Niger Delta and the tropical Atlantic Ocean amounts to 5600 m³ s⁻¹, with peaks during September reaching 27 600 m³ s⁻¹ and low flow during winter and spring decreasing to 500 m³ s⁻¹ (Abrate et al., 2013). Seasonal variations are largely driven by the monsoon during June–August. During the wet season, the vast wetlands of the Inner Niger Delta with 36 000 km² regularly turn into a large lake, forming a unique ecosystem. However, interannual variability is large and decreased rainfall predominantly during the 1960s to the early 1980s led to droughts and famines, while floods have occurred more frequently during the last 25 years, leading to loss of life, infrastructure damage, and tremendous economic costs.

It is thus of obvious importance to water managers, planners, and scientists to better understand and quantify Niger flows, both at short timescales with near-real-time latency and at longer timescales where discharge responds to climate and land use change (Coulthard and Macklin, 2001; Legesse et al., 2003). At the largest spatial scale, discharge measurements would be required to close terrestrial water budgets, with observed or reanalysis precipitation and evapotranspiration data sets and total water storage variations observed with the GRACE satellite mission (Springer et al., 2017), and to improve estimates of freshwater forcing for understanding ocean dynamics (e.g., Papa et al., 2012). However, the gauge observation network along the Niger is not well developed in many locations due to periodical damage during floods, poor funding for maintenance, and armed conflict or unrest in some regions or because data are not automatically transmitted. As in most of Africa, the majority of stations ceased to provide daily discharge time series to global databases in the early 2000s.

Spaceborne radar altimetry, originally designed to monitor the world's oceans, has been suggested for a long time as a means to complement the declining gauge network (Koblinsky et al., 1993). The altimetry community has developed techniques to extract water levels from reprocessed (“retracked”) radar echoes with uncertainties down to a few centimeters for large lakes and a few decimeters to about 1 m for rivers, depending on width (see review in Biancamaria et al., 2017). Radar altimetry is hampered by the long repeat cycles of the satellites (generally 10 d and longer), and the large footprints of the altimeters render the processing less straightforward when compared to later altimetry. However, recent missions such as CryoSat-2 and Sentinel-3 have been shown to be able to capture more small river reaches due to their improved SAR (synthetic aperture radar) delay–Doppler measuring systems. For crossings of medium and large rivers, operational altimetric-level time series are provided as “virtual tide gauges” via public databases such as Hydroweb (Crétaux et al., 2011) or DAHITI (Schwatke et al., 2015).

Yet radar altimeters measure water levels, and converting them directly to discharge requires having a daily discharge time series from a real gauge near the virtual gauge – possible distances strongly depending on the river morphology – for an overlapping period of time. In the Niger basin, the largest obstacle in exploiting radar altimetry is that very few gauge time series are available nowadays. In fact, the only altimeter that provides a temporal overlap with the gauge time series is TOPEX/Poseidon, launched in 1993. However, TOPEX/Poseidon measured with a ground-track spacing of 270–300 km in western Africa, and water levels have lower accuracy compared to contemporary satellites due to less-accurate onboard tracking as well as ionosphere and troposphere corrections (Uebbing et al., 2015). Moreover, due to changes in river morphology, we can expect that stage–discharge relations based on data from the 1990s may not be applicable to contemporary data well.

In recent years, several approaches have been developed to convert radar-altimetric water levels into discharge; see Tarpanelli et al. (2013) or Paris et al. (2016) for an extended discussion. However, most of these techniques assume that a stage–discharge (“rating-curve”) relation can be derived empirically during an overlap period, and they can thus not be applied to the Niger River directly. Tarpanelli et al. (2017), for the Niger–Benue river, suggested forecasting flood discharge from altimetric water levels, MODIS river width, and rating-curve calibration, however with in situ measurements of water levels being available. Others have proposed simulating discharge using fully fledged calibrated and validated land surface modeling (Pedinotti et al., 2012; Casse et al., 2016; Fleischmann et al., 2018; Poméon et al., 2018), assimilating altimetric levels into elaborate hydrodynamic modeling (Munier et al., 2015), or interpolating discharge based on empirical dynamic models trained on gauge discharge (Tourian et al., 2017); however such models are not always available and are less straightforward to transfer to new regions. Therefore we propose combining simplified hydrological models with radar altimetry. The calibrated models serve to “bridge” time series between the gauge and altimeter era, and stage–discharge relationships are then derived using simulated discharge and altimeter data from four different missions. Our results show that altimetry subsequently can reproduce (simulated) discharge very well and effectively continue the gauge time series, albeit at a lower temporal resolution. However, we will confirm that (1) a careful choice of model forcing data sets is important, (2) radar retracking is key for obtaining meaningful time series (we have created virtual stations which either cannot be obtained from public databases or became available only very recently), and (3) fitting the empirical stage–discharge relation may need to allow for break points, where the river regime changes, for example, due to riverbank overflow.

This paper is organized as follows: in Sect. 2 we present the gauge, altimetry, and precipitation data that we use and our methods for discharge conversion. Section 3 contains results and statistics, while Sect. 4 concludes with a discussion and an outlook.

2 Methods and data

2.1 Study area and gauge data

We focus on the upper Niger (Sahelian) region shown in Fig. 1, which extends from Koulikoro (Mali) to Kandadji (Niger) and includes the Inner Niger Delta. Rainfall is typically around 800 mm a⁻¹. Hydrographs at Koulikoro exhibit sharp peaks around mid-September and are affected by operating the Sélingué Dam on the Sankarani River, a tributary of the Niger in southern Mali. Water moving along the Niger floods up to 25 000 km² of the inner delta during wet years and 2000 km² during dry years (Ibrahim et al., 2017). Downstream from the inner delta, hydrographs are significantly flattened (e.g., Olomoda, 2012) and peak discharge is delayed (e.g., Aich et al., 2014).

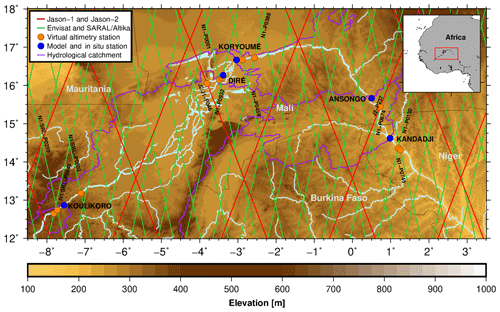
Figure 1 Study area, gauge and virtual gauge locations, altimeter ground tracks, and subbasin delineations (area: Koulikoro – 118 400 km², Diré – 362 000 km², Koryoumé – 378 800 km², Ansongo – 530 000 km², and Kandadji – 596 400 km²).

We select five gauging stations for this study (Koulikoro, Diré, Koryoumé, Ansongo, and Kandadji) based on the following criteria: (1) availability of daily discharge measurements, (2) temporal overlap with the data required to force our simple hydrological model, (3) distance to an altimeter crossing, and (4) minimum width of the river and crossing angle with respect to the altimeter track. Among the five stations, Koulikoro is the only one upstream from the inner delta and has the highest discharge. Diré is located in the Inner Niger Delta, and Koryoumé is right downstream from it. From Koryoumé, the Niger River flows 700 km until it reaches Ansongo and then approaches the country Niger, where the Kandadji station is located. The subbasins upstream from these gauges, for which we calibrate and run the simple lumped hydrological models (see Sect. 2.4), are shown in Fig. 1 with purple lines.

Figure 1 includes altimeter ground tracks and the locations of virtual gauges that we created (see Sect. 2.2) for the Envisat, Jason-1 and Jason-2, and SARAL/Altika satellite altimeters close to the five mentioned gauges. Water-level data from Envisat and SARAL/Altika became available very recently in the DAHITI database (Schwatke et al., 2015) close to all stations except Diré. They are used here only for validation. We have also generated recent water-level time series from Sentinel-3A (launched February 2016) data. A Sentinel-3A virtual gauge is located about 40 km upstream from Koulikoro; this crossing almost coincides with the Envisat pass 646 crossing. The second Sentinel-3A virtual gauge that we generated is close to Koryoumé, about 20 km upstream from the Envisat pass 459 crossing.

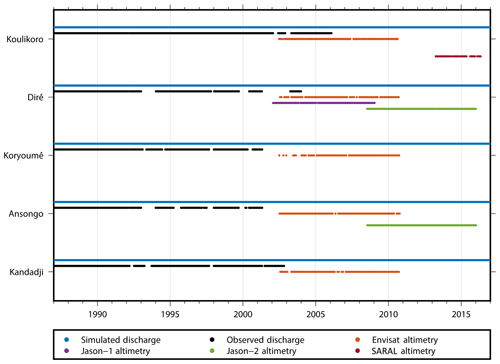
Figure 2 Time periods of available data. Blue: simulated discharge. Black: observed discharge from the GRDC. The other colors represent data periods for four different altimetry missions that are used in this work. Sentinel-3 altimetry data have been available since early 2016 and are used here for comparison only.

Daily gauge time series have been available via public archives since 1975 (Kandadji) and earlier and extend up to 2001 for Ansongo and Koryoumé, 2002 for Kandadij, 2003 for Diré, and 2006 for Koulikoro, albeit with gaps. Figure 2 shows data availability and overlap periods for the gauges, altimeters, and the model simulation. We used discharge data from the Global Runoff Data Centre (GRDC; 56068 Koblenz, Germany) and begin our analysis in 1988, since no reliable model forcing data are available prior to this date (see Sect. 2.4). It is unknown, however, which stage–discharge relations these discharge data are based on.

2.2 Deriving altimetric water levels

Radar altimeters map water levels by continuously emitting microwave pulses, whose nadir echoes are recorded and digitized aboard the satellite. From these “waveforms” one derives signal travel time and range as measured from the antenna to the water surface. Dense water-level profiles across river sections from one overflight at time t are then usually averaged into a single “gauge level”, H(t). The Jason-1 (2001–2013) and Jason-2 (2008–present) satellites have mapped water bodies with a 10 d repeat period and inter-track spacing of about 290 km in our study area. Jason-1 and Jason-2 followed TOPEX/Poseidon (1992–2006) but carried improved altimeter payloads. In the mean time, Jason-3 (launch 2016) continues this data set, and Jason-CS and Sentinel-6 (anticipated launch 2020) will take over in time. Relative altimeter errors (i.e., with respect to an arbitrary vertical reference) are thought to be at the level of a 20–80 cm root-mean-square error (RMSE) for Jason-2, dependent on river width (Papa et al., 2012; Seyler et al., 2013; Tourian et al., 2016). In addition, we used Envisat (2002–2013) and SARAL/Altika (2013–present) to benefit from their much higher spatial resolution (about 70 km in the area), but these satellites have repeat cycles of 35 d. Relative errors are believed to be in the 15–70 cm range (Sridevi et al., 2016; Tourian et al., 2016; Bogning et al., 2018). Absolute errors of altimetric water levels are generally larger due to biases in altimeter calibration and retracker biases.

In this study, we used the Jason-1 and Jason-2, Envisat, and SARAL/Altika 20 Hz data from the Sensor and Geophysical Data Record (SGDR) products, provided by Aviso (ftp://avisoftp.cnes.fr/AVISO/pub/, last access: 28 September 2019) and the ESA (https://earth.esa.int/, last access: 28 September 2019), with latency of around 30 d. We applied corrections for microwave signal delay due to the dry troposphere (ERA-Interim), wet troposphere (ERA-Interim), and ionosphere (NIC09) and for time-varying water-level changes due to solid-earth tides, pole tides, and (ocean) loading tides (GOT4.10).

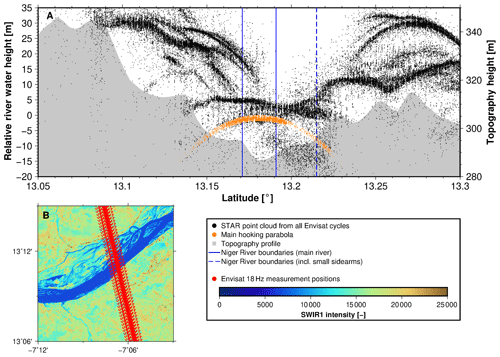
Figure 3 Hooking effect. (A) STAR point cloud from retracking all available Envisat cycles of P0259 crossing the Niger River. The main hooking parabola corresponding to the main river is marked in orange. (B) Virtual station of Envisat P0259 crossing the Niger River. The shortwave infrared (SWIR) information was extracted from Band 6 of a Landsat 8 image captured on 31 October 2018.

We “retrack” individual radar echoes received along the river crossings of the satellites following the STAR retracking method described in Roscher et al. (2017), which had led to much more useful ranges in coastal applications when compared to ranges obtained from the onboard tracker or from standard retrackers. Here, we make use of the “point-cloud” by-product of STAR in order to derive improved river heights. The signal returns from the Niger River are significantly stronger compared to the returns from the surrounding land surface, and consequently the altimeter will “see” the river off nadir when the satellite approaches or departs from the actual crossover location. This leads to the so-called “hooking effect” (Frappart et al., 2006; Santos da Silva et al., 2010; Boergens et al., 2016), a spurious parabolic profile in the along-track surface height measurements. To remove the hooking effect, we explore the water-level point cloud (e.g., Fig. 3A). The point cloud represents several possible surface heights for each measurement location; this is in contrast to other retracking techniques where typically a single best height estimate is provided. Then, for each crossover profile, we remove a “hooking parabola” (Fig. 3A) by fitting a 2nd-order polynomial to the point clouds from our retracker by using the random sample consensus (RANSAC) method (Fischler and Bolles, 1981). Due to the large number of “likely” water levels contained in the point clouds, it is possible to detect multiple hooking parabolas (Fig. 3A) and to remove the hooking effect particularly over narrow river crossings, smaller than 100 m. The final water level is then derived from the peak of the parabola. For wide river crossings, where several height measurements are located over the river itself, we derive the final height from simple averaging.

Sentinel-3 data, which have been available since about March 2016, are used here for comparison to Koulikoro and Koryoumé water levels derived from earlier altimeters. The level-two SAR data have been made available via the Copernicus Open Access Hub (https://scihub.copernicus.eu, last access: 28 September 2019) and through ESA's G-POD SARvatore Service (https://gpod.eo.esa.int/services/cryosat_sar, last access: 28 September 2019). In the Copernicus SAR data set, results from two retrackers applied to the SAR waveforms are available. The first is the standard Offset Centre of Gravity (OCOG; also named ice-1) retracker, which retrieves the range and backscatter coefficient. The second is a fully analytical SAR SAMOSA-2 retracker (Ray et al., 2015), which fits the theoretically modeled multi-look L1B waveform to the real L1B SAR waveform by using the Levenberg–Marquardt method and retrieving the geophysical variables range, backscatter coefficient, mispointing, and quality information. In the G-POD data set, the SAR SAMOSA+ retracker (Dinardo et al., 2017) was used, which includes application of a Hamming window and thus noise reduction (Moore et al., 2018). The hooking effect is thought to be negligible in SAR due to the smaller footprint and since only across-track off ranging will contribute to this error. Moreover, SAR echoes are more accurate compared to conventional altimetry due to the multi-looking property. Whether waveforms originate from water or land reflections is decided upon based on a static map, this should be improved in the future. At both Sentinel-3 crossings, the river width is about 400–500 m and the altimeter pass is about 700 m wide.

2.3 Stage–discharge relations

Stage–discharge relations represent the hydraulic behavior of a river channel section, thus changing with changing river morphology, and must generally be considered to be unknown. Since the river banks are not vertical and the water flows are faster at high stages, the relation is not linear. The most frequently used empirical expression for the stage–discharge relation is the simple rating curve (Lambie, 1978)

$$\begin{array}{}\text{(1)}& {\displaystyle }Q=a\cdot h^b.\end{array}$$

In the above equation, Q(t) represents the discharge (in m³ s⁻¹) and h(t) is the river depth (in m). The parameters a and b describe the hydraulic behavior. They can be computed from Manning's equation under idealized conditions (Paris et al., 2016); then usually $b=\mathrm{5}/\mathrm{3}$ (dimensionless; a in m^4∕3 s⁻¹). As a rule, a wide river leads to a large a, and shallow river banks lead to a large b. However, river width has been difficult to observe in the past, and other characteristics like river cross section and slope remain unknown, so the operational solution is that a and b are fitted to discharge and stage data observed during a calibration campaign.

Assuming that observed discharge and virtual gauge level data from altimetry are available during an overlap period, it is possible to estimate the rating-curve parameters a and b. However, spaceborne altimeters observe heights with respect to a global reference frame, which is realized through satellite orbit determination, while Eq. (1) requires water depth h as measured with respect to the riverbed. Therefore, Eq. (1) is reformulated as in Chin et al. (2001) and Kouraev et al. (2004):

$$\begin{array}{}\text{(2)}& {\displaystyle }Q=a\cdot (H-Z_{\mathrm{0}}{)}^b.\end{array}$$

The water depth is partitioned into the water level or elevation H observed with the altimeter and the elevation Z₀ of the riverbed, i.e., the elevation of zero flow. Z₀ needs to be calibrated alongside a and b.

The three parameters are obtained by applying a Monte Carlo approach. For any given Z₀, parameters a and b are estimated from observed pairs of Q and H via minimizing the sum of squared residuals of a the linear regression model, which reads, after log transformation (Chin et al., 2001; Leon et al., 2006),

$$\begin{array}{}\text{(3)}& {\displaystyle }\ln \left(Q\right)=\ln \left(a\right)+b\cdot \ln (H-Z_{\mathrm{0}}).\end{array}$$

This regression is repeated for a wide range of possible Z₀ values, and the final set of parameters is found as the RMSE minimizer with respect to the observed Q.

For some gauges along the Niger, we find that a single rating curve may not sufficiently represent the observed stage–discharge relation. This is most likely due to changes in the geometry of the riverbed at certain water stages. For stages above this level, the “break point”, we estimate an additional rating curve. For the Niger this is often required when the river bursts its banks. In our estimation of rating curves, possible break points are identified manually. When a break point is found, first the rating curve for lower heights is estimated, and subsequently the rating curve for higher stages (only a and b) is estimated with the constraint of yielding the same discharge exactly at the break point. Afterwards, stage and discharge are added back. The corresponding equation reads

$$\begin{array}{}\text{(4)}& \begin{array}{rl}& Q=\left\{\begin{array}{l}{a}_{\mathrm{1}}\cdot (H-Z_{\mathrm{0}}{)}^{b_{\mathrm{1}}},\\ a_{\mathrm{1}}\cdot (H_{\mathrm{b}}-Z_{\mathrm{0}}{)}^{b_{\mathrm{1}}}+a_{\mathrm{2}}\cdot (H-H_{\mathrm{b}}{)}^{b_{\mathrm{2}}},\end{array}\right.\\ & \mathrm{for}\begin{array}{l}H<H_{\mathrm{b}},\\ H>H_{\mathrm{b}},\end{array}\end{array}\end{array}$$

where H_b is the stage of the break point.

2.4 Simulating discharge

Simulating discharge in the Niger catchment using hydrological models is challenging, since precipitation data sets rely on few rain gauges and since it is difficult to determine evapotranspiration in the vast floodplains. In addition, dam operations affect discharge, and information about the management of the reservoirs is often not available. In order to bridge the gap between gauge and altimeter time series, two simple lumped hydrological models have been calibrated individually for each gauge. We decided to use GR4J (Perrin et al., 2003) and HBV Light (Seibert and Vis, 2012) for this purpose, which allows us to investigate the sensitivity of the approach with respect to the model choice. Furthermore, it is known that GR4J has limitations concerning the travel time within the catchment, and we will confirm that this limits its application to the Inner Niger Delta.

GR4J represents a daily four-parameter rainfall–runoff model, which has performed well in previous investigations for African river catchments (e.g., Bodian et al., 2018 and Kodja et al., 2018). Running GR4J requires area-averaged precipitation (P) and potential evapotranspiration (E) data for the subbasin upstream from the gauge. The model parameters x₁ to x₄ represent the maximum capacity of the “production store”, which is replenished from precipitation, the time lag between a rainfall event and its resulting discharge peak, the capacity of the routing store, and finally the catchment water exchange coefficient. The resulting discharge Q at time t can be written as

$$\begin{array}{}\text{(5)}& {\displaystyle }Q\left(t\right)=\underset{t-x_{\mathrm{4}}}{\overset{t}{\int }}f(P,E,x_i)\mathrm{d}\mathit{\tau }.\end{array}$$

For each gauge, the x_i values are calibrated against the discharge time series while optimizing the RMSE. We use the first 10 years of data for calibration, and the remainder of the available discharge data (3 to 8 years) are then used as the validation period. For both time periods, visual inspection is performed and the Nash–Sutcliffe coefficient (NSC; Nash and Sutcliffe, 1970) is derived.

Precipitation data products differ considerably in the Niger region (Awange et al., 2015; Poméon et al., 2017). For simulating discharge with GR4J, we evaluated four different gridded, daily precipitation data products, i.e., PERSIANN-CDR (Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks – Climate Data Record; Ashouri et al., 2015), CMORPH v1.0 CRT (Climate Prediction Center Morphing Technique; Xie et al., 2011), TMPA 3B42 v7 (Tropical Rainfall Measuring Mission – TRMM – Multi-satellite Precipitation Analysis; Huffman et al., 2007), and CPC Unified Gauge-Based Analysis of Global Daily Precipitation (Chen et al., 2008). CMORPH and TMPA are predominantly based on satellite data, are bias corrected with GPCC (Global Precipitation Climatology Centre) and CPC gauge data, and have only been available since 1998, so they serve comparison purposes here. PERSIANN-CDR contains 0.25^∘ data from 1983 onwards, while CPC has been available since 1979 on a 0.5^∘ grid.

First, mean daily precipitation for the five upstream basins associated with the Niger gauges is constructed from the gridded precipitation estimates. Time series (after annual smoothing) are shown in Fig. 4. The largest differences between the individual precipitation data sets can be observed at Koulikoro, the most upstream station, and are thus related to the smallest catchment area. When moving downstream (from top to bottom in the figure), the bias between the data sets becomes smaller. As the catchments associated with the downstream stations include the smaller Koulikoro subbasin, we observed how precipitation biases tend to average out. However, most striking is a prolonged (2001–2007) period of low precipitation in the CPC time series, which becomes most obvious at Koulikoro but can be observed for all five stations. We found that GR4J simulates unrealistically low discharge for this time period even at the more downstream stations. Therefore, we finally decided to use PERSIANN-CDR for calibrating GR4J. Although the time series starts in 1983, we discarded the first 5 years, where annual means are up to 32 % lower than in the following years, in order to prevent calibrating in the drier period that lasted from the 1960s to the earlier 1980s.

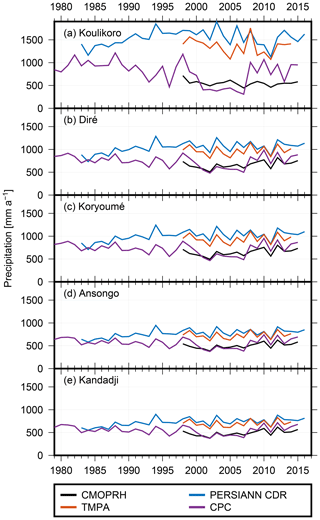
Figure 4 Comparison of precipitation from the data sets PERSIANN-CDR, CMORPH, TMPA, and CPC for the five study catchments.

For potential evapotranspiration, we chose the CRU (Climatic Research Unit, University of East Anglia) TS v. 4.01 data set (Harris and Jones, 2013), which contains monthly data from 1901 to 2016 on a 0.5^∘ grid. It is based on the analysis of over 4000 individual weather station records and mostly homogenized.

As the second model, HBV Light (Seibert and Vis, 2012) was applied to simulate discharge and evapotranspiration, using the same forcing data and calibration period as for GR4J. HBV Light represents a user-friendly version of the HBV model (Bergström, 1995). HBV Light includes an automatic parameter estimation routine that uses numerous quality measures and a Monte Carlo routine to perform automatic simulations for sensitivity analysis. Like GR4J, HBV belongs to the class of rainfall–runoff models and consists of three main components: a snow routine (not used in this study), a soil moisture routine used for computing actual evapotranspiration and groundwater recharge, and groundwater as well as river routines to simulate discharge at the observed gauging station. HBV Light is a semi-distributed model, meaning that different elevation and vegetation zones can be considered, which is important for our study region (Poméon et al., 2017). Furthermore, it offers the possibility of modeling lakes and can easily be adapted to the given geological situation by introducing up to three different groundwater zones. The actual version of the model is available at the website of the University of Zurich (https://www.geo.uzh.ch/en/units/h2k/Services/HBV-Model.html, last access: 28 September 2019). It offers a higher flexibility compared to GR4J but contains more calibration parameters (Seibert and Vis, 2012). HBV Light was applied here as a lumped model in the standard version, with nine calibration parameters.

3 Results and discussion

3.1 Simulated discharge

In Fig. 5, discharge simulated for the five Niger stations is shown together with observed discharge. For Koulikoro, Diré, and Koryoumé (Fig. 5a–c), observed and simulated discharge from both models are very close for most of the time (i.e., during calibration and validation periods). Even the peak flows are reproduced very well by the models. For Ansongo and Kandadji (Fig. 5d–e), GR4J-simulated discharge appears distinctly different from the observed data, especially regarding seasonal variability.

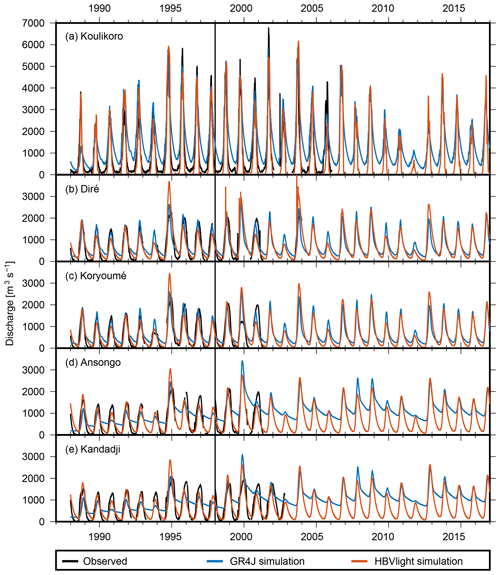
Figure 5 Observed and simulated discharge for the five Niger stations. The first 10 years of data serve as calibration period, marked by the vertical black line. The validation period starts after these 10 years.

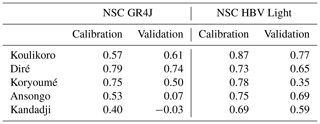
For a more quantitative analysis, the Nash–Sutcliffe coefficient (Table 1) is computed separately for the calibration and the validation period. As expected, the NSC is higher in the calibration period in every case except the GR4J simulation for Koulikoro, where it is almost equal. For GR4J, NSC values computed for Koulikoro, Diré, and Koryoumé are larger than 0.5, confirming the good prediction skills discussed above. For Ansongo and Kandadji, the NSC of the validation period is about zero, which indicates that GR4J is not suitable here. NSC values of the HBV Light simulation are larger than those for GR4J except for the validation period at Diré and Koryoumé. The HBV Light results in particular are surprisingly good for a rather simple model in a complex basin. Fleischmann et al. (2018) reported NSC numbers of 0.72, 0.82, and 0.79 for Koulikoro, Diré, and Ansongo, respectively, for their calibration period (2001–2014). Despite the use of a more sophisticated model (MGB; Collischonn et al., 2007), the numbers are not inferior to the HBV Light values, which underlines the utility of HBV Light. Tourian et al. (2017) used a stochastic process model, time-series densification (Tourian et al., 2016), and Kalman filtering – for assimilating altimetry data – and smoothing to estimate discharge in the whole Niger basin. They computed NSC values between 0.65 and 0.8 for Koulikoro, Diré, Koryoumé, and Ansongo. Only a few years of altimetry entered this validation; thus it is mainly based on the process model and the smoothing. In contrast to our method, however, they estimated daily values of discharge.

Table 1 Nash–Sutcliffe coefficients for calibration and validation periods and for both models (NSC = 1 means perfect agreement between observed and simulated discharge, NSC = 0 indicates that model predictions are as accurate as the mean of the observed data, and NSC < 0 indicates that the observed mean is a better predictor than the model).

3.2 Altimetric water-level time series

Time series of river levels, which we created from retracked altimetry, are provided in Fig. 6 for the virtual stations (VSs) near Koulikoro, Diré, Koryoumé, Ansongo, and Kandadji. Multiple VSs belong to one gauging station due to multiple ground track or river crossings nearby. Individual time series from Envisat and Jason agree well during their overlap time periods (Diré and Ansongo). Gaps occur when no observations are available, which can happen due to “loss of lock” of the altimeter instrument. Due to undulating terrain, the onboard tracker is then unable to follow the range and backscatter variations of the reflected echoes. Consequently, it loses track of the leading edge of the radar return, which serves as a reference for the data window that is transmitted to Earth.

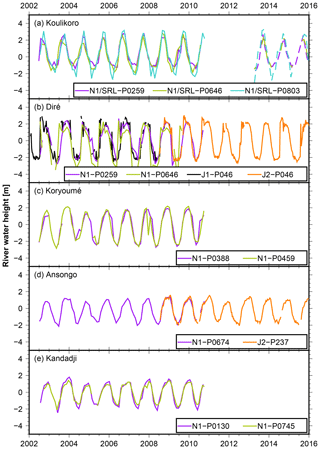
Figure 6 Time series of relative river heights for each investigated station. Legend composition: satellite (N1 for Envisat, SRL for SARAL/Altika, and J for Jason) and pass number (P).

We find good agreement between our reprocessed time series and the Envisat mission time series from the DAHITI archive (Schwatke et al., 2015), with correlations of up to 0.99 and root-mean-square (RMS) differences between 0.2 and 0.5 m for the stations Koulikoro, Koryoumé, Ansongo, and Kandadji; this is encouraging but does not provide a thorough validation. For Diré no external data from altimetric databases are available for validation.

For Koulikoro, water-level series from two neighboring Envisat and SARAL/Altika river crossovers with a distance of about 10 km (passes 259 and 646; see Fig. 1) match quite well. At the third crossover (pass 803) about 70 km downstream (and about 40 km downstream from the terrestrial gauge), the amplitude is larger by about 0.5–1 m.

Diré is located in the Inner Niger Delta, which is prone to frequent flooding events. It is thus a difficult area to derive river heights due to the various tributaries of the Niger River, which strongly influence the radar returns, resulting in overlapping hooking parabolas. One Jason-1 and Jason-2 and two Envisat crossovers are located within a 35 km stretch, and we observe water levels with annual variability of up to 5.5 m, with a RMS difference of 1.25 m between different missions and river crossovers.

For Koryoumé, two Envisat river crossovers with about 35 km distance are evaluated, and water levels with a RMS difference of 0.6 m between the two crossovers are observed.

Annual water-level variability at Ansongo and Kandadji is about 2 m amplitudes lower compared to the more upstream stations (amplitudes of about 3 m). Despite differing temporal resolution, the Envisat and Jason-2 data match quite well for Ansongo, since both cross the river at almost the exact same location (RMS difference of 0.25 m). For Kandadji, two Envisat crossovers at 8 km distance and with a temporal shift of 13 d provide similar water levels.

In Fig. 7, Sentinel-3A (S3A) river levels from the years 2016 to 2018 are compared to the Envisat data measured 10 years earlier (2006 to 2008).

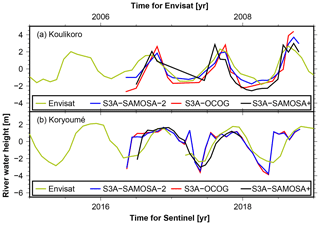
Figure 7 River water height anomaly from Sentinel-3A (S3A) at two stations compared to Envisat data (pass 646 for Koulikoro and pass 459 for Koryoumé) measured 10 years earlier (green). The S3A solutions (pass 87 for Koulikoro amd pass 244 for Koryoumé) are the Copernicus Hub Land (blue and red) and the G-POD solutions (black).

The Copernicus heights corresponding to the OCOG and SAMOSA-2 retrackers (red and blue, respectively) are very similar and in good agreement also with the SAMOSA+ heights (black). For Koulikoro, the S3A measurements show a slightly longer low water period and a higher amplitude than Envisat. This may well be due to river regime changes, but it could result from annual variations as well. Also, altimeter sampling effects cannot be excluded without further investigations. At the VS near Koryoumé, the S3A SAMOSA+ solution (black) shows a hydrograph which is very close to the time shifted Envisat measurements. Both Copernicus solutions (red and blue) are instead somewhat more different, with higher amplitudes and longer high water periods.

3.3 Altimetric rating curves and discharge

Figure 8 displays rating curves computed from simulated discharge and altimetric water levels as described in Sect. 2.3. Figure 9 shows simulated and altimetry-derived discharge. Altimetry rating curves are derived from the full overlap period between simulated discharge and the data period of each altimetry mission, which is limited from 2002 to 2010 in the case of Envisat and limited from 2013 to 2016 in the case of SARAL/Altika.

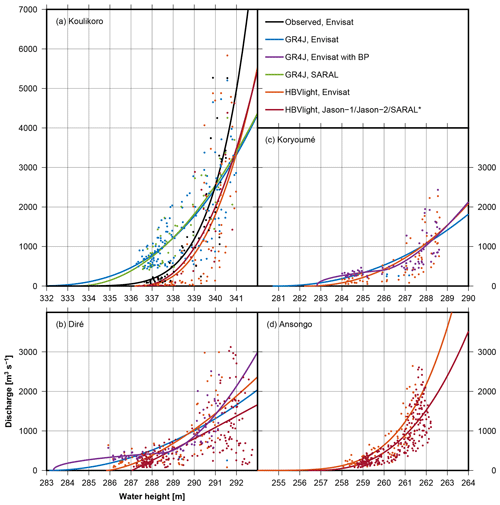
Figure 8 Rating curves for (a) Koulikoro, (b) Diré, (c) Koryoumé, and (d) Ansongo. The Kandadji station is omitted due to the insufficient amount of altimetry and discharge data. The points are the discharge values plotted against the altimetric water depth. The lines are the rating curves, which are fitted through the points. ^∗ The red rating curves are created with SARAL/Altika data for Koulikoro, Jason-1 for Diré, and Jason-2 for Ansongo.

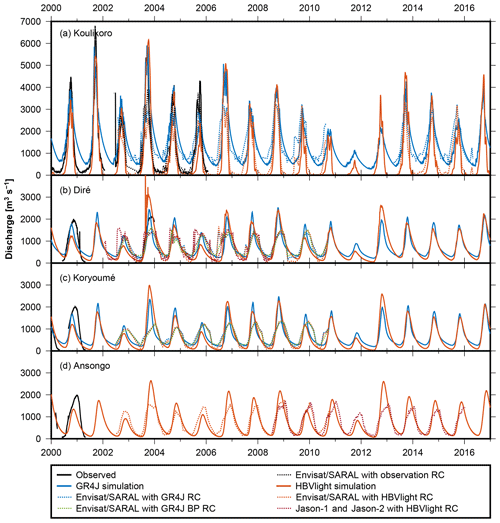
Figure 9 Altimetric discharge (dotted lines) together with observed and simulated discharge (solid lines). RC is the rating curve; BP is the break point. The Kandadji station is omitted due to the insufficient amount of altimetry and discharge data.

For Koulikoro, altimetric discharge is derived from the Envisat and SARAL/Altika missions at 35 d temporal resolution. We observed that for GR4J, the rating curves for the two different satellite data sets – i.e., Envisat (2002–2010; blue curve) and SARAL (2013–2016; green curve) – are almost parallel (Fig. 8a). Rating curves estimated from the HBV Light simulation differ from the rating curves from GR4J, but differences between the two HBV Light rating curves are again small (orange and red curve). Obviously, the choice of the hydrological model has a significant impact on the estimated rating curve. Figure 9a shows that altimetric discharge peaks (dotted lines) from Envisat (2002–2010) are often lower as compared to simulated discharge (solid lines); this is expected , since the stage–discharge relation is derived as a fit where we neither down-weighted peak nor low flows. Also, altimetric discharge inherits the 35 d temporal resolution given by altimeter revisit cycles and may thus simply miss peaks. Furthermore, it is obvious that the yearly peaks of the altimetric discharge time series are less variable than the peaks from discharge simulated by the hydrological models. This was expected due to the rather uniform annual amplitudes of the water-level time series (Fig. 6) and suggests that the hydrological models may overestimate such variability. For SARAL/Altika, it appears that the short overlapping period considered for estimating the rating curve does not lead to worse results compared to Envisat, and peaks of altimetric discharge are even closer to simulated discharge.

For Koulikoro, we have an overlapping period between observed discharge and Envisat water-level time series for a period of 4 years. As a check of our methodology, we estimated an alternative rating curve based on these observed data only (Fig. 8a; black curve). Again, the shortness of the period does not affect the result; measurements scatter less around the rating curve, and discharge from altimetry is close to observed discharge (cf. dotted and solid black lines in Fig. 9). Low flows from altimetry appear to be quite realistic. It is noticeable that the rating curve is close to the two rating curves estimated with HBV Light simulation, however with a different zero-flow (Z₀) estimate, which can be inferred from the x-axis intercept in the rating-curve figure. Getirana and Peters-Lidard (2013) point out that this procedure of rating-curve fitting may not necessarily converge for Z₀. The correctness of Z₀ is difficult to assess, but it is not of primary concern, since a Z₀ shift in the rating curve does not affect the resulting altimetric discharge.

We used the overlapping period for further assessing the validity of the approach. We compared the altimetric discharge from the “observed” and “HBV Light” rating curves (Fig. 9a; dotted black and orange lines, respectively) to the observed discharge. The comparison yields NSCs of 0.78 and 0.60. The latter value, albeit derived from only a short period, suggests a successful validation of our altimetric discharge against observed discharge.

At Diré (Fig. 8b), we observe for the GR4J simulation that estimating a rating curve with one break point (purple curve) indeed improves the estimation of Envisat-based discharge (the RMS difference between simulated and altimetric discharge can be reduced by 17 % when compared to a simple relation; see Fig. 9b). Altimetry still misses peak simulated discharge, but the discharge hydrographs are much closer and low to medium flows fit better. For the HBV Light simulation, different parameters are estimated for the rating curves, and introducing break points does not improve results. In summary, altimetry misses simulated peak flows by about 30 % but appears to reproduce the overall shape of the hydrograph well. However, comparisons against observed discharge are not possible, and we do not know the truth in this case.

We observe that for Koryoumé the situation is comparable to Diré; fitting a rating curve with GR4J simulation benefits from introducing a break point, and again altimetric (Envisat) discharge appears to be much more regular when compared to the simulated one. With the HBV Light simulation we find that adding a break point does not improve results. The rating curve without break point fits well and mostly agrees with the GR4J rating curve with a break point.

For Ansongo, we do not use the GR4J simulation (see Fig. 5). Discharge simulated by HBV Light overlaps with altimetry data from Envisat and Jason-2. The two estimated rating curves differ mostly by a Z₀ shift, leading to almost identical altimetric discharge. This can be seen in Fig. 9d in the overlap period of the two missions (2008–2010). Simulated discharge and altimetric discharge exhibit RMS differences for Envisat and Jason-2 of 328 and 348 m³ s⁻¹, respectively, and NSC values of 0.56 and 0.49. These values are comparable to the NSCs reported in Fleischmann et al. (2018) at virtual stations (0.37 to 0.75 if disregarding one outlier); however it should be noted that they computed the NSCs between water levels and not between discharge series. The Kandadji station is omitted in this discussion due to the insufficient amount of altimetry and discharge data.

In summary, we find that relatively large scatter renders the estimation of stage–discharge relations difficult. This may have been expected due to the challenging study region. Although one expects that with higher water levels, altimetry provides more reliable results (since the river is wider), the sensitivity of changes in water level with respect to discharge is higher. This characteristic can be observed well at the scattering points in Fig. 8d. Fitted stage–discharge relations will inevitably lead to “mean” peak and low flows.

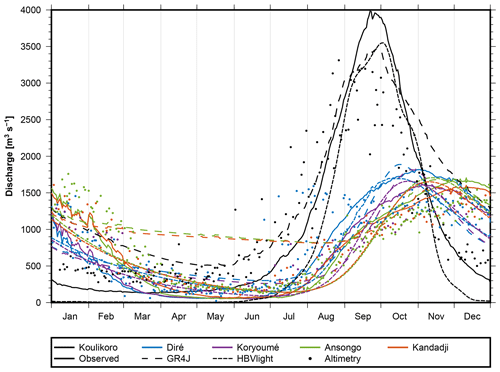
Figure 10 Mean annual hydrographs. The color indicates the station, and the line style indicates the discharge source.

Figure 10 visualizes the seasonal cycle of discharge for the five stations as obtained from gauge data, model simulations, and radar altimetry. The day of peak flow is listed in Table 2. We notice that modeled peak days are generally ahead of observed peaks except for Koulikoro; this points to the problem of representing travel time in the models. Low-flow and peak-flow times (and peak discharge) for Ansongo and Kandadji appear to nearly coincide; this is due to the short travel time between the two stations, which are only about 150 km apart. Between Diré and Koryoumé (about 80 km), a phase lag of a few days is identified in gauges and models but obviously misrepresented in altimetry (see Table 2). When computing the mean annual hydrographs with daily available observed or simulated discharge, there are multiple values for each day getting averaged. For altimetry, this is not necessarily the case due to the lower temporal resolution. Thus, peaks identified from altimetric data may refer to individual years rather than to mean annual values. After correcting this effect by fitting an annual signal per virtual gauge, we find the peak timings to be much closer to those of observed discharge.

Table 2 Dates of maximum flow. Altimetry averaging is done by fitting an annual signal through the points. The points and complete hydrographs can be seen in Fig. 10.

4 Conclusions

Radar altimetry enables one to observe water levels for larger rivers, although temporal resolution is generally low due to satellite revisit times. This study shows that careful processing of altimeter data, i.e., retracking and accounting for “hooking” effects due to the dominant river signal at off-nadir locations, allows one to generate reliable water-level time series also for river crossovers that are not contained in public databases, which operate automated processing chains. We found that comparisons between neighboring crossovers, i.e., from ascending and descending satellite passes and between different missions, fit usually quite well, although crossovers are located up to 70 km apart. This has been observed already by others, but we can confirm it here for a quite challenging region where a braided river with often multiple but narrow channels creates multiple echoes. The Sentinel-3 SAR data pick up the signal measured by earlier altimeters quite well. The altimetric hydrograph flattens out from Koulikoro to Kandadji as expected, but with little interannual variability between the years. With time, flooding and morphological changes add to altimetric noise, which appears in a range of several decimeter up to one meter and corresponds to the findings of other studies.

Since observed discharge time series generally are available only until the 2000s, we used simple hydrological models for simulating discharge after station-by-station calibration. We showed that this approach works generally well for most gauges. The HBV Light simulates discharge well for all gauges, while the GR4J model fails to reproduce low flows for some gauges, which is likely due to model shortcomings concerning travel time but is of course also related to the specific calibration parameters. A careful choice of climate forcing data has turned out to be essential. Future research may concentrate on more sophisticated models. However, all models depend on observed precipitation, for which different data sets differ greatly.

Converting observed altimetric levels into discharge requires adopting the stage–discharge relation derived at gauges. For temporally non-overlapping periods of data, where gauge and altimetric overpass may be tens of kilometers apart, deriving such a relation represents a challenging and still-unsolved problem. We find that discharge simulated by simple lumped rainfall–runoff models may aid in creating empirical altimetry-discharge rating curves, although it is difficult to assess the validity of the approach. Different models, although based on the same precipitation data and all calibrated, generate different rating curves. For five gauges along the central Niger, including the Inner Niger Delta, we find mixed results. Altimetry discharge exhibits generally much less interannual variability when compared to simulated discharge; this is most likely due to problems with the observed precipitation data set. Altimetric discharge also does not capture peak flows that the model predicts while low flows fit reasonably well; this appears to be related to the temporal resolution of the satellite overpasses. We have shown that rating curves may need to account for break points, presumably when the river inundates its banks, but again this depends on model simulations.

We find that, averaged over the entire study period, model simulations capture the observed timing of the annual peak flow mostly within 2 weeks. Deriving these peak days from altimetry necessitates interpolating the altimetric observations; fitting an annual signal enables one to reconstruct the peak timings as close to (earlier) gauge observations as the models do.

We suggest that future research could ultimately focus on combining model simulation and model parameter estimation with gauge and multi-mission altimetry observations within data-assimilating frameworks. Remote sensing of channel width (Elmi et al., 2015), which now provides greatly improved resolution due to, for example, Sentinel data, should be explored jointly with radar altimetry. Near-real-time altimetry could provide discharge with 3–5 h latency and would thus enable utilizing such frameworks for flood forecasting purposes, for example. On the other hand, deriving consistent and long discharge time series would enable one to close budgets together with GRACE water storage data, and, for example, assess biases in reanalysis or remote sensing precipitation and evapotranspiration data products (Springer et al., 2017).