Understanding the potential of climate teleconnections to project future groundwater drought

Predicting the next major drought is of paramount interest to water managers globally. Estimating the onset of groundwater drought is of particular importance, as groundwater resources are often assumed to be more resilient when surface water resources begin to fail. A potential source of long-term forecasting is offered by possible periodic controls on groundwater level via teleconnections with oscillatory ocean–atmosphere systems. However, relationships between large-scale climate systems and regional to local-scale rainfall, evapotranspiration (ET) and groundwater are often complex and non-linear so that the influence of long-term climate cycles on groundwater drought remains poorly understood. Furthermore, it is currently unknown whether the absolute contribution of multi-annual climate variability to total groundwater storage is significant. This study assesses the extent to which multi-annual variability in groundwater can be used to indicate the timing of groundwater droughts in the UK. Continuous wavelet transforms show how repeating teleconnection-driven 7-year and 16–32-year cycles in the majority of groundwater sites from all the UK's major aquifers can systematically control the recurrence of groundwater drought; and we provide evidence that these periodic modes are driven by teleconnections. Wavelet reconstructions demonstrate that multi-annual periodicities of the North Atlantic Oscillation, known to drive North Atlantic meteorology, comprise up to 40 % of the total groundwater storage variability. Furthermore, the majority of UK recorded droughts in recent history coincide with a minimum phase in the 7-year NAO-driven cycles in groundwater level, providing insight into drought occurrences on a multi-annual timescale. Long-range groundwater drought forecasts via climate teleconnections present transformational opportunities to drought prediction and its management across the North Atlantic region.

1 Introduction

Multi-annual variability detected in hydrometeorological datasets has long been associated with systems of atmospheric–oceanic (climatic) oscillation, such as the El Niño–Southern Oscillation (ENSO) and the North Atlantic Oscillation (NAO). Such periodic teleconnection signals have been detected in rainfall (Luković et al., 2014), evapotranspiration (Tabari et al., 2014), air temperature (Faust et al., 2016), and river flow (Su et al., 2017; Kingston et al., 2006); however, these periodicities are often weak when compared to the finer-scaled (daily to seasonal) variability that is typical of hydrometeorological processes (Meinke et al., 2005). By contrast, groundwater systems are expected to be particularly susceptible to multi-annual teleconnection influence, given their sensitivity to long-term changes in rainfall and evapotranspiration (Bloomfield and Marchant, 2013; Forootan et al., 2018; Van Loon, 2015; Folland et al., 2015) and their ability to filter fine-scale variability in recharge signals (Dickinson et al., 2014; Velasco et al., 2015; Townley, 1995). Consequently, recent studies have focused on the detection of long-term periodic cycles in groundwater levels in Europe (e.g. Holman et al., 2009, 2011; Folland et al., 2015; Neves et al., 2019), North America (e.g. Tremblay et al., 2011; Kuss and Gurdak, 2014), and globally (e.g. Wang et al., 2015; Lee and Zhang, 2011) and on their relationships with climatic oscillations. An understanding of multi-annual periodicity strength in groundwater level may provide an improvement in long-lead forecasting of hydrogeological extremes (Rust et al., 2018; Meinke et al., 2005; Kingston et al., 2006), in part by enabling such cyclical behaviour to be projected into the future. This is particularly apparent for groundwater drought, which is known to result from multi-annual moisture deficits (Van Loon, 2015; Van Loon et al., 2014; Peters et al., 2006). Therefore, it is critical to quantify the absolute strength of all periodicities within groundwater levels so that the strength of multi-annual cycles, the influence of teleconnections, and their contribution towards groundwater droughts can be understood.

Existing studies into groundwater teleconnections use quantitative methods to detect periodic behaviour in groundwater datasets and often their relationship with time series of climate indices (used to measure the strength and state of climate oscillations). Common quantitative methods range from temporal correlation analysis (Knippertz et al., 2003; Szolgayova et al., 2014) to more complex periodicity detection and comparison. These latter methods include Fourier transform (Nakken, 1999; Pasquini et al., 2006), singular spectrum analysis (SSA) (Kuss and Gurdak, 2014; Neves et al., 2019), and wavelet transformations (Fritier et al., 2012; Holman et al., 2011; Tremblay et al., 2011). The wavelet transform (WT) has been shown to be particularly skilful at detecting multi-annual periodic behaviour in noisy hydrogeological datasets, detecting the influence of the NAO, ENSO, and Atlantic Multidecadal Oscillation (AMO) on North American groundwater levels (Kuss and Gurdak, 2014; Velasco et al., 2015) and of the NAO, east Atlantic pattern (EA), and Scandinavian pattern on European groundwater level variability (Holman et al., 2011; Neves et al., 2019). However, in order to enhance multi-annual periodicity detection, many studies have used data processing methods that remove or suppress variability at the higher end of the frequency spectrum (e.g. winter or annual averaging or conversion of time series to cumulative departures from mean; Weber and Stewart, 2004). Due to this data modification, it is currently unknown whether the absolute contribution of multi-annual climate variability to total groundwater storage is significant. This limitation makes the assessment of systematic linkages between climatic oscillations and groundwater level response problematic (Rust et al., 2018). As a result, the fundamental question of whether multi-annual teleconnection cycles in groundwater level are sufficiently strong to influence hydrogeological drought remains largely unanswered. Given the potential for improved long-lead forecasting, quantification of multi-annual variability in groundwater level represents an opportunity to support efficient infrastructure investment, systems of water trading (Rey et al., 2018), and robust planning for groundwater drought.

The aim of this paper is to assess the extent to which periodic behaviour in groundwater level produced by teleconnections may be used as an indicator of the timing of groundwater droughts. In doing so, this paper develops and applies an improved method to describe and characterize the absolute strength of periodic behaviour in groundwater level and its drivers (rainfall and evapotranspiration). This aim will be met by addressing the following research objectives:

1. characterize dominant intra- and multi-annual periodicities in groundwater level records across a range of aquifer types;

2. quantify the absolute strength of these multi-annual periodic groundwater level oscillations compared to the total variability in groundwater levels;

3. qualitatively assess evidence for the control of climate teleconnections on identified multi-annual periods;

4. assess the extent to which the timing of the multi-annual periodic groundwater level oscillations aligns with recorded groundwater droughts.

These objectives will be implemented in UK hydrogeology records, given the considerable coverage of recorded groundwater level data in time and across the country (Marsh and Hannaford, 2008); however, the methodologies developed can be applied to any regions.

2 Data and methods

2.1 Groundwater data

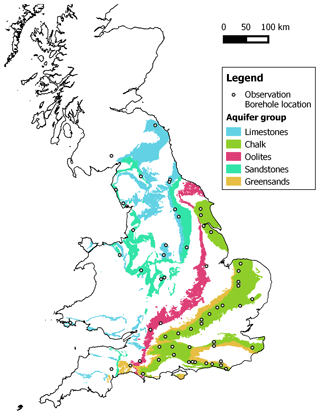
Groundwater level time series from 59 reference boreholes covering all of the major UK aquifers, with record lengths of more than 20 years and data gaps no longer than 24 months, have been assessed in the study. These recorded groundwater level hydrographs range from 21 to 181 years in length, with an average length of 53 years. The sites are part of the British Geological Survey's Index Borehole network and, in addition to their data coverage, have been chosen as they exhibit representative and naturalistic hydrographs with minimal impact from abstractions. They cover a range of unconfined and confined consolidated aquifer types and have been categorized into five main aquifer groups; 34 records in chalk, a limestone aquifer comprising a dual porosity system with localized areas where it exhibits confined characteristics; 8 records in limestone, characterized by fast-responding fracture porosity; 3 records in oolite characterized by highly fractured lithography with low inter-granular permeability; 12 sites in sandstone, comprised of sands silts and muds with principle inter-granular flow but fracture flow where fractures persist; and 2 records in greensands, characterized by inter-granular flow with lateral fracture flow depending on depth and formation (Marsh and Hannaford, 2008). The locations of the sites used in this study are shown in Fig. 1.

Figure 1 Location of the observation borehole locations used in this study. Boreholes within 0.5 km of another have been displaced and denoted by a grey circle for visibility.

2.2 Rainfall

Rainfall time series from the Centre of Ecology and Hydrology's CEH-GEAR 1 km gridded rainfall dataset (Tanguy et al., 2016), which is based on spatio-temporal interpolation of daily rain gauge totals between 1890 and 2017, was used. However, relatively few rainfall stations exist prior to 1950 that were used for this interpolation; as such, data prior to 1950 were not used in this analysis. Monthly rainfall series have been calculated for each borehole from the 1 km grid cell in which they are located, as geospatial data on areas of groundwater recharge connected to specific observation boreholes do not exist. This dataset may contain artefacts as a result of the spatio-temporal interpolation, in comparison to station data. However, the use of rainfall data in this study is to provide a broad understanding of rainfall periodicities to supplement those from groundwater level data. As such, this interpolated dataset is deemed appropriate.

2.3 Potential evapotranspiration (PET)

Monthly PET series for each borehole have been derived from the Centre of Ecology and Hydrology's CHESS-PE 1 km gridded dataset of calculated daily PET values. The PET values, between 1960 and 2015, were calculated using the Penman–Monteith equation, with meteorological data taken from the CHESS gridded meteorological dataset. Details on the underlying observation datasets and interpolation methods can be found in Robinson et al. (2016). These data have been used previously to study long-term trends in hydrological variability (Robinson et al., 2017).

2.4 Methods

2.4.1 Data preprocessing

In this study we use the continuous wavelet transform (CWT) to produce a time-averaged frequency spectrum for each borehole hydrograph and co-located rainfall and PET time series.

For all datasets, gaps of less than 2 years were infilled using a cubic spline to produce a complete time series for the CWT. This interpolated information was later removed from the time-frequency transformation (prior to time averaging) to ensure that the data infilling had minimal effect on the final spectrum. For time series with gaps greater than 2 years, the shortest time period before or after the data gap was removed to produce one complete record. Individual rainfall and PET time series were trimmed to match the length of the corresponding borehole level time series. All time series were centred on the long-term mean and normalized to the standard deviation to produce a time series of anomalies. Unlike most previous studies, no high- or low-band filtering was undertaken on the datasets, ensuring all information on periodic variability was preserved. This approach ensures that the proportion of a periodicity to the variance (standard deviation) of the original dataset is not modified.

2.4.2 Continuous wavelet transform

Following the data preprocessing steps, a CWT was applied to quantify the time-averaged frequency spectra of the rainfall, PET, and groundwater datasets. The CWT has been used to assess long-term trends and periodicities in many hydrological datasets including rainfall (Rashid et al., 2015), river flow (Su et al., 2017), and groundwater (Holman et al., 2011; Kuss and Gurdak, 2014). We use the package “WaveletComp” produced by Rosch and Schmidbauer (2018) for all transformations in this paper.

The continuous wavelet transform, W, consists of the convolution of the data sequence (x_t) with scaled and shifted versions of a mother wavelet (daughter wavelets):

$$\begin{array}{}\text{(1)}& W(\mathit{\tau },s)=\sum _t{x}_t{\displaystyle \frac{\mathrm{1}}{\sqrt{s}}}\mathit{\psi }\ast \left({\displaystyle \frac{t-\mathit{\tau }}{s}}\right),\end{array}$$

where the asterisk represents the complex conjugate, τ is the localized time index, s is the daughter wavelet scale, and dt is increment of time shifting of the daughter wavelet. The choice of the set of scales s determines the wavelet coverage of the series in its frequency domain. The Morlet wavelet was favoured over other candidates due to its good definition in the frequency domain and its similarity with the signal pattern of the environmental time series used (Tremblay et al., 2011; Holman et al., 2011).

The CWT produces a time-frequency wavelet power spectrum for each time series. Within the time-frequency spectra, a cone of influence (COI) is used to denote those parts that are affected by edge effects, where estimations of spectral power are less accurate. Therefore, only data from within COI were averaged over time to produce a time-average wavelet power spectrum for frequency bands from 6 months up to 64 years. Wavelet power spectra were then normalized to the maximum average wavelet value so that the frequency distribution of each site can be directly compared. The normalized average wavelet power spectra (herein referred to as the wavelet power spectra) provide a comparative measure of the strength of the range of periodicities within frequency space.

2.4.3 Significance testing

As Allen and Smith (1996) demonstrate, geophysical datasets can exhibit pseudo-periodic behaviour as a result of their lag-1 autocorrelation (AR1) properties. Datasets with greater AR1 tend to have spectra biased towards low frequencies; thus, they are described as containing red noise (Allen and Smith, 1996; Meinke et al., 2005; Velasco et al., 2015). In order to assess the likelihood that a periodic signal is the result of internal (red) noise within the data, the significance of the red noise null hypothesis was tested. For this, 1000 randomly constructed synthetic series with the same AR1 as the original time series were created using Monte Carlo methods. Wavelet spectra maxima from these represent periodicity strength that can arise from a purely red noise process. Wavelet powers from the original dataset that are greater than these “red” periodicities are therefore considered to be driven by a process other than red noise, thus rejecting the null hypothesis. Here, while a 95 % confidence interval (CI) ($<=\mathrm{0.05}$ α values) is identified, we report on the full range of alpha results to provide a detailed assessment of the likelihood of external forcing on periodic behaviour.

2.4.4 Time reconstruction

In order to assess the characteristics of periodicities over time, we employ a reversal of the wavelet transform (wavelet reconstruction) to convert selected periodic domains back into a time series of normalized anomalies. Period bands were selected where the frequency spectra identified shared wavelet power (and significance) between groundwater, rainfall and PET, indicating a widespread signal presence at these bands.

The reverse wavelet transform is given by

$$\begin{array}{}\text{(2)}& \left(x_t\right)={\displaystyle \frac{\mathrm{d}j\cdot \mathrm{d}{t}^{\mathrm{1}/\mathrm{2}}}{\mathrm{0.776}\cdot \mathit{\psi }\left(\mathrm{0}\right)}}\sum _s{\displaystyle \frac{Re\left(W\right(.,s\left)\right)}{s^{\mathrm{1}/\mathrm{2}}}},\end{array}$$

where dj is the frequency step and dt is the time step.

Negative phases of these time-reconstruction anomaly time series were compared to episodes of recorded wide-scale hydrogeological drought (provided by Marsh et al., 2007, and Todd et al., 2013), to assess the relationships between multi-annual variability in groundwater and groundwater droughts.

2.4.5 Periodicity strength quantification

While the wavelet power spectra from the CWT provide an estimate of the relative strength of periodicities compared to the total frequency spectra, they do not provide an absolute measure of a periodicity's contribution to total groundwater variability (which includes noise and non-periodic information). As such, the percentage contributions of each time reconstruction have been calculated. Since the datasets were normalized to the standard deviation of the raw data prior to the CWT, the standard deviations of the reconstructed anomaly time series represent the proportion of the original standard deviation as a decimal percentage.

3 Results

3.1 Time-averaged wavelet power and significance over red noise

Wavelet power spectra (frequency strength) and alpha values (significance) for each of the 59 groundwater level and rainfall time series are displayed in Figs. 2 and 3 respectively. Wavelet power is analogous to the strength of the periodicity compared to other frequencies. Periodicities with alpha values less than or equal to 0.05 (95 % CI) are highlighted. Bands of greater wavelet power and lower alpha values at periodicities of 1, ∼7, and 16–32 year(s) can be seen across the majority of the groundwater and rainfall spectra for the 59 sites (herein referred to as P1, P7, and P16–32 respectively). PET wavelet spectra were found to have no notable or significant periodicity beyond seasonality (indicative of the UK's temperate climate) and are displayed in the Supplement.

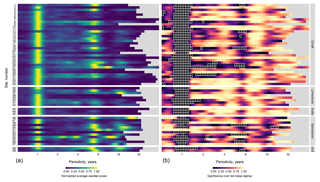
Figure 2 Normalized average wavelet power spectra (a) and wavelet power significance alphas (b) for monthly groundwater levels in the 59 index boreholes (grouped by aquifer type). In the right-hand figure, boxes outlined in white are those powers that are significant over red noise to a 95 % confidence interval ($a<=\mathrm{0.05}$).

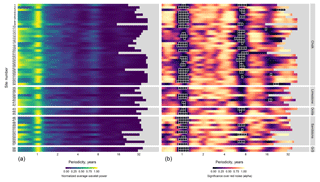
Figure 3 Normalized average wavelet power spectra (a) and wavelet power significance alphas (b) for monthly rainfall time series for co-locations of the 59 index boreholes. In the right-hand figure, boxes outlined in white are those powers that are significant over red noise to a 95 % confidence interval ($a<=\mathrm{0.05}$).

The annual cycle (P1) exhibited the greatest power across 43 of the 59 observation borehole spectra, with normalized wavelet powers ranging from 0.03 to 1 (mean of 0.84). Alpha values for P1 in the observation boreholes also showed the greatest likelihood of external forcing when compared to the other identified periodic domains (alpha values ranging from 0.00 to 0.94; mean of 0.017). All but one observation borehole (site 51) showed significant (95 %) alpha values for P1 wavelet power. Lower than average P1 wavelet powers were most prevalent in the sandstone lithology (6 out of 12 sandstone sites), greensands (1 out of 2 sites), and, to some extent, the chalk (6 out of 35 sites). It should be noted, however, that the relatively small sample sizes of greensand and oolite aquifers make interpretation of systematic differences at these lithographies difficult. P1 wavelet power was generally lower across all the corresponding rainfall time series, which is expected given rainfall's established bias towards high frequency (Meinke et al., 2005). Of those boreholes with lower P1 power in groundwater, most (e.g. 35, 59) show greater P1 powers in rainfall (and PET) indicating hydrogeological processes as the mechanism for weaker P1 periodicity. However, a small number (e.g. 38, 40, and 42) had similarly low P1 periodicity in the corresponding rainfall, indicating meteorological drivers for poor annual strength at these observation boreholes (considering that PET showed little variance in P1 strength across the observation boreholes). PET spectra and alpha values showed a universally high P1 wavelet power.

The second greatest wavelet power across the groundwater boreholes was between 6 and 9 years, roughly centred on the 7-year periodicity (P7). Maximum normalized groundwater wavelet powers ranging from 0.01 to 1 (average of 0.52) between boreholes were detected, as was a corresponding band of lower than average alpha values (ranging from 0.01 to 0.99; mean of 0.34), indicating that this periodicity is likely to be driven by an external variance. Average P7 wavelet power values were greatest for sandstone (0.68) and greensands (1.00) and lower for limestone (0.39) and oolite (0.17). Chalk showed intermediate strength with the greatest range (0.01 to 1.00; mean of 0.50). Ten groundwater sites showed significant (95 %) P7 wavelet powers (sites 1, 12, 14, 19, 26, 27, 49, 53, 55, and 59). While the P7 wavelet power in the corresponding rainfall data was considerably lower than those detected in groundwater levels (ranging from 0.014 to 0.35; mean of 0.16), the alpha values are comparable to the P7 signal strength in groundwater. This indicates that P7 signals in rainfall are weak but likely driven externally. Generally lower alpha values for P7 in rainfall, compared to groundwater, are also likely a result of rainfall's lower autocorrelation. Negligible wavelet powers and no significance was shown at the P7 band for corresponding PET data.

The final and second mode of common multi-annual wavelet power was the band between 16 and 32 years (P16-32). P16–32 had an average wavelet power of 0.28 across all boreholes, ranging between 0.01 and 1. Similar to P7, the greatest wavelet power of P16–32 was found in the sandstone (average of 0.58) and the greensand (average of 0.64) aquifer types, whereas chalk, limestone, and oolite showed relatively weaker signals (averages of 0.18, 0.32, and 0.03 respectively). Only one site in the groundwater (site 50) and five rainfall time series (sites 3, 11, 30, 34, 40) showed 95 % significance over red noise in this periodicity band.

3.2 Reconstructed anomaly time series

The three main common period domains identified by the wavelet transform (P1, ∼7, and 16–32 years) were reconstructed into anomaly time series using the reversed wavelet transform and are presented in Fig. 4 for groundwater levels and Fig. 5 for rainfall and PET. This was undertaken to allow the investigation and comparison of periodic behaviour over time and to assess how these reconstructed periodic signals, within multiple sites across multiple aquifers, align with periods of historical groundwater drought. The behaviour of the multiple reconstructed groundwater level, precipitation, and PET anomaly time series (in all three periodicity domains) were shown to be well-aligned in time, with positive (maxima) and negative (minima) phases occurring within a comparable time. The only exception to this pattern was seen between 1970 and 1980 in the P7 reconstructions, where phases in the P7 reconstructions become misaligned. This was predominantly apparent in groundwater and to a lesser extent in rainfall. Positive and negative phases of the P7 reconstructions in PET were well-aligned for the entire time series.

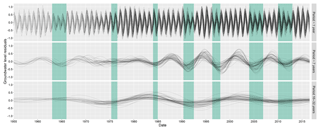
Figure 4 Overlaid reconstructions of the three key periodic domains found across the 59 groundwater wavelet spectra are shown. All periods (both significant and non-significant) within these bands have been displayed to allow for comparison of period strength and phase over time. Areas shaded green represent approximate periods of significant droughts in the UK. Only reconstructions between 1955 and 2017 are shown to allow clearer comparison.

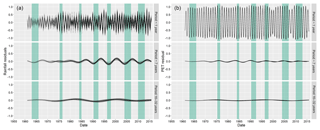
Figure 5 Overlaid rainfall (a) and PET (b) reconstructions of the three key periodic domains are shown. All periods (both significant and non-significant) within these bands have been displayed to allow for comparison of period strength and phase over time. Areas shaded green represent approximate periods of significant droughts in the UK. Only reconstructions between 1955 and 2017 are shown to allow clearer comparison.

Notable episodes of groundwater droughts in the UK were overlaid onto the reconstructed periods in Fig. 5 between 1955 and 2016. With the exception of the 1975–1976 event, every episode of drought in this time period coincides with a negative phase of the reconstructed P7 groundwater anomalies. The 1975–1976 drought (often used as a benchmark drought in the UK due to its wide-reaching impacts; Marsh et al., 2007) occurred at a time of notable minima/maxima misalignment of the P7 period across all groundwater sites and a period of negative anomaly in the P16–32 reconstructions. Most recorded major droughts in the UK appeared to occur irrespective of the state of the P16–32 anomaly, with droughts occurring in minima and maxima of this reconstruction.

3.3 Percentage standard deviation

The percentage of the standard deviation in the original groundwater level signal represented by each reconstructed periodicity band is shown in Fig. 6 for all the observation boreholes. The percentages are representative of the absolute strength of the periodicity compared to the recorded data variance (standard deviation).

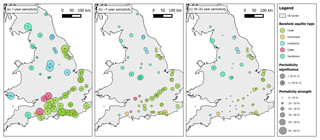
Figure 6 Maps showing strength (percentage of the original time series standard deviation) and significance of the (a) 1-year, (b) ∼7-year, and (c) 16–32-year periodicity bands. No periodicity strength was found to be above 60 % of the original signal.

P1 represents the greatest average contribution to groundwater variability across all the aquifer groups (chalk: 41 %; limestone: 40 %; oolite: 52 %; sandstone: 26 %; greensand: 28 %). While most sites show that P1 accounts for the greatest proportion of the standard deviation, P7 is the dominant periodicity at 11 of the 59 sites (5 within sandstone, 5 within chalk, and 1 within greensand) and P16–32 is the strongest cycle in 3 of the 59 sites (3 within sandstone and 1 within limestone). P1 strength in the chalk appears to be greatest in the south of England, with weaker strengths in the south-east and east. Aside from the chalk, there are no clear spatial patterns in P1 strength. P7 accounts for an average of 21.7 % of signal strength across all aquifer groups, ranging from 3.8 % to 40 % across the observation boreholes. Spatial variance in P7 signal strength is less when compared to P1, although there is a noted area of significance in the chalk of south-east England (e.g. the Chiltern Hills and Cambridgeshire) and a smaller cluster of P7 significance in the sandstone of central England, where the greatest P7 strengths are found. P16–32 strengths are spatially focused in eastern England for the chalk and central and north-western England for the sandstone. No clear patterns for the remaining aquifer groups are apparent for the 16–32-year periodicity band.

4 Discussion

4.1 Characterization of signal presence and strength in groundwater level

Many studies have focused on the role of seasonality in defining groundwater variability and the onset and severity of groundwater drought (Jasechko et al., 2014; Hund et al., 2018; Mackay et al., 2015; Ferguson and Maxwell, 2010). While we show that the annual cycle is an important component of groundwater response, it is often not representative of overall behaviour, accounting for (on average) less than half of total groundwater level variability. Conversely, we show that multi-annual periodicities form an unprecedented proportion of total groundwater variability, with 41 % of sites (24 out of 59) exhibiting multi-annual periodicity strength that is comparable to (within 10 %) or greater than seasonality. It is expected that the strength of multi-annual cycles in groundwater level will vary according to signal strength in recharge drivers (e.g. rainfall and evapotranspiration) and hydrogeological processes that lag or attenuate long-term changes in these recharge signals (Van Loon, 2013, 2015; Townley, 1995; Dickinson et al., 2014). These two processes may explain the local differences in signal strength between sites in aquifer types and geographically across the UK, as displayed in our results. For instance, pronounced multi-annual variability (significant 7-year cycles and stronger 16–32-year cycles) in the chalk sites is generally associated with catchments of thicker unsaturated zones, larger interfluves, or areas of weaker corresponding seasonality in rainfall (for example, the Chiltern Hills in south-east England). These catchment properties have been shown to dampen higher frequency variability between rainfall and groundwater response due to storage buffers, thereby producing a sensitivity to multi-annual variability (Peters et al., 2006; Van Loon, 2013). Multi-annual cycles are also generally strong for the granular-porosity aquifers (sandstone and greensand), which is to be expected given the influence of lower hydraulic diffusivity (typical of granular-porosity flow) on the suppression of high-frequency variability (Townley, 1995). This also agrees with Bloomfield and Marchant (2013), who document sensitivity to long-term accumulation in rainfall in UK sandstone aquifers. Conversely, the limestone and oolite aquifer types exhibit weaker multi-annual periodicities in groundwater level, with strong seasonality. Townley (1995) and Price et al. (2005) document that, due to their faster-responding fracture porosity with low storativity, limestone lithographies have a lower damping capacity of finer-scale variability in recharge, meaning they are able to respond in time to the strong seasonality in PET and rainfall. Our results typically show lower percentage contributions of multi-annual periodicities to total groundwater level variability than some previous international studies (Kuss and Gurdak, 2014; Neves et al., 2019; Velasco et al., 2015). This can be explained by potentially weaker periodicities driving climatic circulations over Europe compared to North America (as indicated by Kuss and Gurdak, 2014) or UK-specific hydrogeological properties such as smaller aquifer size compared to North America or continental Europe, which may affect teleconnection strength (Rust et al., 2018). However, we also expect lower percentage contributions of multi-annual periodicities due to our use of unmodified groundwater level datasets prior to spectral decomposition (wavelet transform). Using unmodified level data has enabled us to represent the absolute contribution of multi-annual variability to groundwater level behaviour at each site.

4.2 Evidence for teleconnection control on multi-annual groundwater variability

Here, we discuss the evidence that the multi-annual variability present in UK groundwater level records (as previously discussed) is the result of teleconnection influences with climatic oscillations. The conceptualization of groundwater teleconnections of Rust et al. (2018) suggests that a teleconnection between the oscillatory climate systems and groundwater level would be associated with

• a.

  an apparent and coherent multi-annual periodicity band within groundwater sites across a wide geographical area that aligns with known multi-annual variability in indices of climatic oscillations (for instance, the 7-year periodicity of the NAO (Hurrell et al., 2003);

• b.

  an increased likelihood that this periodicity band is the result of an external influence and not the result of internal red noise variability of the groundwater level time series (as indicated by Allen and Smith, 1996, and Meinke et al., 2005);

• c.

  comparable signals in rainfall as established drivers for multi-annual groundwater variability, and

• d.

  broad alignment of minima and maxima of time-reconstructed multi-annual periodicities. Some fine-scale misalignment in groundwater periodicities is expected as a result of unsaturated and saturated zone lags between rainfall and groundwater response (Van Loon, 2013; Peters et al., 2006; Dickinson et al., 2014; Cuthbert et al., 2019).

The majority of groundwater level hydrographs and corresponding rainfall profiles showed a coherent band of increased periodicity strength and periodicity significance principally around the 7-year frequency range and, to a lesser extent, the 16–32-year range. The 7-year periodicity closely compares to the principle 7-year periodicity documented in the strength of the NAO's atmospheric dipole, which has been associated with multi-annual periodicities in rainfall (Meinke et al., 2005) and groundwater globally (Tremblay et al., 2011; Kuss and Gurdak, 2014; Holman et al., 2011; Neves et al., 2019). Additionally, the time reconstructions show clear temporal alignment of minima (with the exception of the 1975–1976 period, which will be discussed later), indicating the widespread coherent influence of a climatic teleconnection. As such, we corroborate this with existing research that documents the control of the NAO on UK rainfall (Alexander et al., 2005; Trigo et al., 2004) and show new evidence of the widespread propagation of multi-annual variability in rainfall to spatio-temporal multi-annual groundwater variability, conceptualized by Rust et al. (2018).

While the NAO is known to be the dominant mode of winter climate variability in Europe (López-Moreno et al., 2011; Alexander et al., 2005; Hurrell and Deser, 2010), the second strongest is provided by the EA (Wallace and Gutzler, 1981). The EA is similar in frequency structure to the NAO but shifted southward; however, it has been shown to exhibit its own internal variability (Hauser et al., 2015; Tošić et al., 2016). Importantly, the EA has been shown to exhibit a 16–32-year periodicity (Holman et al., 2011) and therefore aligns with the second strongest mode of multi-annual variability in groundwater and rainfall documented in this study. As such, the increased strength, significance, and minima alignment of the 16–32-year periodicity range detected in groundwater levels in this paper may be explained through a teleconnection between the EA pattern and European winter climate variability. While the EA has received little focus in climate variability research compared to the NAO, our findings here support Krichak and Alpert (2005), who document a multi-decadal control on UK and European precipitation through shifting phases of the EA, and Holman et al. (2011), who detected weak relationships between the EA and groundwater levels in the UK. Comas-Brua and McDermotta (2014) suggest that much of the multi-decadal climate variability (temperature and precipitation) in the North Atlantic region can be explained by a modulation of the NAO by the EA, which may contribute to the spatial and temporal variability seen in both the ∼7- and 16–32-year reconstructions across the borehole sites. In summary, the modes of multi-annual variability detected in the majority of UK groundwater level hydrographs and rainfall time series appear to be best explained via a teleconnection with the NAO and EA's principle periodicities.

4.3 Teleconnections as indicators of groundwater extremes

The final objective of this paper was to assess the extent to which the timing of multi-annual periodic groundwater level oscillations align with the timing of recorded groundwater droughts. To achieve this, documented periods of groundwater drought have been compared to reconstructed periodicities within groundwater level. We show principally that every documented groundwater drought between 1955 and 2014 occurs during a negative phase of the ∼7-year cycle detected in the majority of UK groundwater boreholes, with the exception of the 1975–1976 drought.

Groundwater droughts are typically the result of multi-annual accumulation of rainfall deficits, with the specific timing and duration of drought (for a particular site) also driven by sub-annual rainfall and evapotranspiration (Van Loon et al. 2014; Peters, 2003). Marsh et al. (2007) identify a multi-annual decline in rainfall for the majority of droughts in the UK over the past 60 years, with rainfall deficits reaching a critical accumulation period of 2–3 years in the lead-up to drought commencement (Folland et al. 2015). It is therefore to be expected that the majority of droughts are captured within the negative phases of the ∼7-year cycle in the groundwater level anomalies, as this cycle (along with the 16–32-year cycle) represents groundwater's multi-annual response to the land–atmosphere water flux. The 1975–1976 drought does not fit this pattern as we show a clear disruption to the ∼7-year cycle during this period. This is of particular interest as this event is generally acknowledged to be anomalous for the UK. The severity of this event has been solely attributed to a short-term meteorological state (i.e. high-pressure atmospheric blocking) in the existing literature, with very little long-term decline in groundwater levels (Rodda and Marsh, 2011; Bloomfield and Marchant. 2013). It is therefore to be expected that the 1975–1976 drought did not occur during a coherent negative phase of the ∼7-year cycle detected in groundwater levels and that we see a more pronounced suppression of seasonality during this time. Furthermore, we note that most droughts do not perfectly align with the minima of this ∼7-year cycle. As previously stated, the commencement of a drought is dependent a combination of on multi-annual land–atmosphere water fluxes and particular sub-annual hydrological conditions (Van Loon et al., 2014). Therefore, this ∼7-year fluctuation could be considered a cycle of increased drought risk, where groundwater resources may be more sensitive to sub-annual hydrological conditions. The 16–32-year periodicity, while also a representation of groundwater's multi-annual response to moisture balance, represents a smaller proportion of total groundwater behaviour and as such appears less representative of drought timings. Despite this, it is likely that this signal still has a role in modulating the severity of the ∼7-year component.

The NAO and EA's control on long-term rainfall deficits in the UK and Europe has previously been identified by many studies (López-Moreno et al., 2011; Fowler and Kilsby, 2002; Hurrell, 1995). Here, we provide evidence to suggest that the NAO teleconnection with long-term rainfall volumes, in particular, propagates to detectable modes of groundwater level increased drought risk in line with the NAO's principle periodicity of approximately 7 years. While the effects of (non-) stationarity between the NAO, EA, and UK hydrogeology have not been assessed in this study, these detected cycles may yield improved foresight into future episodes of increased drought risk in the UK. This is especially important given the proportion of groundwater level variability these cycles represent. We also note that teleconnections are not persistent and can be disrupted, as exemplified by the 1975–1976 drought. Our findings here agree with Parry et al. (2012), who found no relationship between this drought and the NAO phase or strength. Peings and Magnusdottir (2014) suggest that atmospheric blocking prohibits the expected effects of the NAO on UK and European rainfall, which may explain both the 1975–1976 drought and the disruption to the 7-year periodicity in UK groundwater (Rodda and Marsh, 2011). This therefore further highlights the importance of atmospheric blocking in regulating groundwater variability in the UK (Shabbar et al., 2001).

5 Conclusions

This paper assesses the role of multi-annual variability and ocean–atmosphere systems in influencing groundwater drought. We quantify the absolute contribution of multi-annual cycles to groundwater variability and provide new evidence for the influence of the NAO's control of European rainfall on UK groundwater drought over the past 60 years.

The wavelet transformation was used to identify and evaluate bands of periodic external influence on UK groundwater level hydrographs. We document the strength of multi-annual behaviour that aligns with the NAO's principal periodicity (approximately 7 years) and the EA's principal periodicity (16–32 years). We find that seasonality accounts for an average of 39 % of groundwater level variance across boreholes, with a 7-year cycle accounting for an average of 21 % and 16–32 years accounting for 15 %. Furthermore, we show the majority of UK droughts align with negative phases of the 7-year cycle, indicating periods of increased drought risk as part of this periodicity. In the UK, the economic regulator has implemented several measures to promote the trading of water between water supply companies to enable a more robust water supply system (Water Trading, 2019; Deloitte LLP, 2015). Here, we show that recursive patterns in groundwater contribute to a considerable proportion of the total groundwater level variability and therefore may provide new insights to allow undertakers of water supply to trade water further into the future, depending on teleconnection sensitivities. Such forecasted planning could help to reduce the ecological and human impacts of groundwater drought by allowing more time to plan and organize the required water transfers from areas less susceptible to teleconnection-driven drought. It is clear from our results that long-range groundwater drought forecasts via climate teleconnections present transformational opportunities to drought prediction and its management across the North Atlantic region.