The ¹⁸O ecohydrology of a grassland ecosystem – predictions and observations

The oxygen isotope composition (δ¹⁸O) of leaf water (δ¹⁸O_leaf) is an important determinant of environmental and physiological information found in biological archives, but the system-scale understanding of the propagation of the δ¹⁸O of rain through soil and xylem water to δ¹⁸O_leaf has not been verified for grassland. Here we report a unique and comprehensive dataset of fortnightly δ¹⁸O observations in soil, stem and leaf waters made over seven growing seasons in a temperate, drought-prone, mixed-species grassland. Using the ecohydrology part of a physically based, ¹⁸O-enabled soil–plant–atmosphere transfer model (MuSICA), we evaluated our ability to predict the dynamics of δ¹⁸O in soil water, the depth of water uptake, and the effects of soil and atmospheric moisture on ¹⁸O enrichment of leaf water (Δ¹⁸O_leaf) in this ecosystem. The model accurately predicted the δ¹⁸O dynamics of the different ecosystem water pools, suggesting that the model generated realistic predictions of the vertical distribution of soil water and root water uptake dynamics. Observations and model predictions indicated that water uptake occurred predominantly from shallow (<20 cm) soil depths throughout dry and wet periods in all years, presumably due (at least in part) to the effects of high grazing pressure on root system turnover and placement. Δ¹⁸O_leaf responded to both soil and atmospheric moisture contents and was best described in terms of constant proportions of unenriched and evaporatively enriched water (two-pool model). The good agreement between model predictions and observations is remarkable as model parameters describing the relevant physical features or functional relationships of soil and vegetation were held constant with one single value for the entire mixed-species ecosystem.

1 Introduction

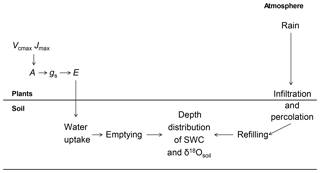
The stable oxygen isotope composition (δ¹⁸O) of meteoric water varies greatly in space and time. Meteoric waters impart their isotopic signal (δ¹⁸O_rain) to that of soil water (δ¹⁸O_soil), changing it as a function of refilling, exchange and percolation processes throughout the soil profile. The oxygen isotope composition of leaf water (δ¹⁸O_leaf) differs from that of the water taken up from the soil, as leaf water becomes ¹⁸O-enriched due to evaporative effects and morpho-physiological controls (Barbour, 2007). As a consequence, δ¹⁸O_leaf carries important environmental and physiological information that is imprinted on photosynthetic products and archived in long-lived cellular compounds such as cellulose in tree rings (Farquhar et al., 2007; Barbour, 2007; Treydte et al., 2014; Lehmann et al., 2018). The δ¹⁸O of leaf water also imprints the oxygen isotope compositions of atmospheric CO₂ and molecular oxygen, a property that can be used to estimate regional- and global-scale land primary productivity from seasonal to millennium timescales (Dole et al., 1954; Farquhar et al., 1993; Bender et al., 1994; Luz and Barkan, 2011; Wingate et al., 2009; Welp et al., 2011). A quantitative understanding of the hydrological and plant morpho-physiological mechanisms controlling δ¹⁸O_leaf is therefore fundamental to biological, Earth and environmental science disciplines (Barbour, 2007). This science, which explores relationships between the spatio-temporal dynamics of water in the soil–vegetation–atmosphere system with help of the dynamics of δ¹⁸O of water in the different components of the system, may be termed ¹⁸O ecohydrology.

Studies that deal with the δ¹⁸O in water and biomass compartments of grassland, the largest terrestrial biome after forest, are sparse (e.g. Flanagan and Farquhar, 2014; Webb and Longstaffe, 2003, 2006; Ramirez et al., 2009; Riley et al., 2002, 2003). To our knowledge, simultaneous observations of seasonal variations of the isotopic composition of the different water pools in a temperate grassland ecosystem over multiple years have not been reported so far. Only datasets covering short periods (e.g. Lai et al., 2008; Leng et al., 2013) or one single vegetation period (e.g. Wen et al., 2012) have been reported. In addition, our system-scale understanding of the propagation of the rainwater δ¹⁸O signal through soil water and plant xylem water to the leaf water has as yet not been verified for grassland. As a consequence, our quantitative knowledge of the drivers of δ¹⁸O_leaf in grassland ecosystems is limited.

The isotopic composition of the water taken up by plants (henceforth termed δ¹⁸O_stem) can vary over time through changes in the depth of soil water uptake by roots or direct changes in soil water isotopic composition. For example, summer rains in continental Europe are usually isotopically distinct (¹⁸O-enriched) relative to winter precipitation, generating intra-annual variations of δ¹⁸O_soil with soil depth. Apart from the temporal distribution of rainfall amounts and associated δ¹⁸O_rain, the relationship between δ¹⁸O_rain and δ¹⁸O_stem is affected by soil properties (that determine water storage, transport and mixing of rainwater with water stored at depth in the soil profile), the depth distribution of roots and their specific activities, and atmospheric conditions and vegetation properties (that determine transpiration as well as soil evaporation and associated enrichment of δ¹⁸O_soil near the soil surface). Assuming that root water uptake proceeds without ¹⁸O discrimination (Dawson et al., 2002), the comparison of δ¹⁸O_soil and δ¹⁸O_stem can help identify the depth of root water uptake (e.g. Durand et al., 2007) and how it changes during drought (e.g. Hoekstra et al., 2014; Nippert and Knapp, 2007a). So far, studies on potential shifts of root water uptake depth in C₃ grassland communities during drought were mainly conducted using rainout shelters and comparing the water uptake depth in droughted and control plots (Hoekstra et al., 2014; Prechsl et al., 2015). Thus it is still unclear how edaphic drought arising under natural conditions modifies the root water uptake depth in C₃ grassland communities over time, especially at a multi-seasonal timescale.

The mechanisms driving the isotopic enrichment of leaf water can be studied separately from those driving changes in δ¹⁸O_stem by expressing the isotopic composition of leaf water as enrichment above δ¹⁸O_stem; i.e. ${{\mathrm{\Delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{leaf}}={{\mathit{\delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{leaf}}-{{\mathit{\delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{stem}}$ if the δ¹⁸O of water entering the leaf is the same as that taken up by the root system as a whole. The process of evaporative enrichment was first modelled by Craig and Gordon (1965) for open water bodies and adapted to leaves by Dongmann et al. (1974). Many authors have since noted a discrepancy between the ¹⁸O enrichment at the evaporative sites predicted by the Craig–Gordon model (Δ¹⁸O_e) and leaf water enrichment (Δ¹⁸O_leaf) (Cernusak et al., 2016). This discrepancy has been interpreted conceptually with two different models called the two-pool model (Leaney et al., 1985; Yakir et al., 1994) and the Péclet model (Farquhar and Lloyd, 1993; Farquhar et al., 2007). In the two-pool model, leaf water is assumed compartmentalised between evaporatively ¹⁸O-enriched water (supposed to represent mainly mesophyll cells) and unenriched water (supposed to represent veins and associated ground tissues). In the so-called Péclet model, the mixing of water isotopes within the leaf lamina is assumed incomplete because of a limited back diffusion of heavy water from the evaporative sites to the remaining leaf lamina as a result of the high tortuosity of the path of water within the mesophyll. This incomplete mixing is characterised by a Péclet number p, defined as the ratio of advection to back diffusion (Farquhar and Lloyd, 1993; Cuntz et al., 2007). The two models predict a different effect of transpiration rate on the proportional difference (φ) between the ¹⁸O enrichment predicted by the Craig–Gordon model and the observed ¹⁸O enrichment of leaf water: $\mathit{\phi }=\mathrm{1}-{{\mathrm{\Delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{leaf}}/{{\mathrm{\Delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{e}}$ (Song et al., 2013; Cernusak et al., 2016). Because Δ¹⁸O_leaf, rather than Δ¹⁸O_e, imprints sugars (Barbour et al., 2000; Cernusak et al., 2003) and ultimately organic matter (Barbour and Farquar, 2000; Helliker and Ehleringer, 2002; Barbour, 2007), the choice of the model relating Δ¹⁸O_leaf and Δ¹⁸O_e has important implications. The Péclet model predicts an increase in φ with leaf transpiration while in the two-pool model φ does not respond to transpiration and is expected to be constant, at least on short (hourly to daily) timescales. Thus far, experimental and empirical studies on a large range of plant species have provided mixed results on these two alternative models of Δ¹⁸O_leaf, with some studies supporting the two-pool model and others the Péclet model (e.g. Barbour et al., 2000, 2004; Loucos et al., 2015; Song et al., 2015; Cernusak et al., 2016). The question as to which model is more appropriate for predicting the Δ¹⁸O of canopy-scale leaf water is particularly relevant for the modelling of Δ¹⁸O_leaf, and ultimately δ¹⁸O_leaf, at larger temporal and spatial scales.

In general, Δ¹⁸O_leaf responds strongly to changes in atmospheric humidity or the isotope composition of water vapour (e.g. Farquhar et al., 2007) and to changes in stomatal conductance (Wang and Yakir, 1995; Barbour and Farquhar, 2000; Helliker and Ehleringer, 2000; Xiao et al., 2012). However, it is generally not known whether edaphic drought, via its effect on stomatal conductance, indirectly affects the relative humidity response of leaf water enrichment. To our knowledge, the only study that reports a distinct effect of edaphic drought on Δ¹⁸O_leaf is that of Ferrio et al. (2012) on Vitis vinifera. Based on their results, and theoretical considerations regarding the effect of soil water availability on leaf stomatal closure and energy budget and associated ¹⁸O fractionation, one would expect a positive effect of edaphic drought on leaf water enrichment. Yet, whether or not drought exerts a measurable effect on Δ¹⁸O_leaf of grasslands, often found in climates with sporadic or prolonged drought periods, is not known.

The interpretation of the isotopic composition of water from samples collected in natural ecosystems is complicated by the fact that multiple environmental as well as site or plant morpho-physiological factors vary simultaneously, causing difficulties in disentangling the effect of different parameters on the water isotope composition. Hence, process-based ecosystem-scale models are key to aiding the interpretation of the water isotope signals in response to environmental and morphological parameters (e.g. Riley et al., 2003). Here we evaluate our system-scale ecohydrological understanding of the propagation of the δ¹⁸O signal of rainwater through soil water pools, root water uptake and ¹⁸O enrichment of leaf water in a drought-prone grassland ecosystem. For this, we systematically trace, predict and validate δ¹⁸O_soil, δ¹⁸O_stem and Δ¹⁸O_leaf and evaluate their sensitivity to input parameters. Specifically, we ask the following: what is the plant community's depth of root water uptake and does it shift in response to soil water scarcity? Is the two-pool model or the Péclet model more appropriate for describing Δ¹⁸O_leaf at the canopy scale? Does Δ¹⁸O_leaf respond to edaphic drought in grasslands? And, more generally, what is the sensitivity of soil, stem and leaf water δ¹⁸O to changes in soil and vegetation parameters that are suspected to alter ecosystem water dynamics? To explore these questions we compared predictions from the ¹⁸O-enabled soil–plant–atmosphere transfer model MuSICA (Ogée et al., 2003; Wingate et al., 2010; Gangi et al., 2015) with those observed in a unique, multi-annual dataset (7 years) of growing season (April to November), fortnightly samplings and δ¹⁸O analysis of soil water (at 7 and 20 cm depth), stem and midday leaf water, and atmospheric water vapour, along with rainfall amount and δ¹⁸O_rain data. The experimental site (Schnyder et al., 2006) was an intensively grazed Lolio-Cynosuretum (Williams and Varley, 1967; Klapp, 1965) community with Lolium perenne, Poa pratensis, Dactylis glomerata, Phleum pratense, Taraxacum officinale and Trifolium repens as the main species. Vegetation samples were taken as mixed-species samples, as described below.

2 Materials and methods

2.1 Study site

The study was performed inside pasture paddock no. 8 of the Grünschwaige Grassland Research Station near Freising, Germany (Schnyder et al., 2006). Mean annual air temperature from 2006 to 2012 was 9.3 ^∘C, and mean annual precipitation was 743 mm, as measured at the Munich airport meteorological station 3 km from the field site. The soil is a Mollic Fluvisol, with a shallow topsoil of low water holding capacity (66 mm plant-available field capacity) overlying coarse calcareous gravel. The depth to the groundwater table is around 1.5 m.

During the main vegetation period (mid-April to beginning of November) the paddock was grazed continuously by Limousin suckler cows (Schnyder et al., 2006). Animal stocking density was adjusted periodically to maintain a constant sward height of about 7 cm. This management system aimed at maintaining a constant sward state by continuously balancing pasture grass production and consumption by the grazing cattle.

2.2 Sampling

Precipitation water was collected following events during the vegetation periods of 2007 to 2012 and during winter 2007/2008 (see Methods S1 in the Supplement). Leaf, stem, soil, groundwater and atmospheric moisture samples were collected on non-rainy days, between 11:00 and 16:00 CEST (Central European Summer Time). Sampling occurred at approximately fortnightly intervals during the vegetation periods from April 2006 to September 2012. Samples were collected at random locations in an area of about 1 ha in the vicinity of an eddy flux tower installed near the centre of the paddock. On each date, two replicate samples of leaf, (pseudo-)stem and soil were collected. Soil samples were taken at two depths (7 and 20 cm) using an auger. Leaf and stem samples were obtained as mixed-species collections of the co-dominant species: four C₃ grasses (Lolium perenne, Poa pratensis, Phleum pratense, Dactylis glomerata), one rosette dicot (Taraxacum officinale) and one legume (Trifolium repens). Each leaf sample included all leaf blades, including the exposed part of the growing leaf but excluding senescing leaves (cf. Fig. 1 of Liu et al., 2017) from two vegetative tillers of D. glomerata and 16 vegetative tillers of L. perenne, P. pratensis and P. pratense, one half of a leaf blade of T. officinale (with the latter severed along, but not including, the midvein) and two trifoliate leaves of T. repens. This protocol ensured collection of the entire within-leaf evaporative ¹⁸O gradient of all sampled leaf blade tissue of the different species. Stem (xylem) samples comprised the midvein of T. officinale, the petioles of the two T. repens leaves and the basal part of the vegetative grass tillers, except for the outermost part that was removed as it could have been subject to evaporative enrichment (cf. pseudo-stem in Fig. 1 of Liu et al., 2017).

Atmospheric moisture was collected by pumping ambient air through a glass coil immersed in a dry ice–ethanol mixture at a flow rate of 1 L min⁻¹ over periods of 2–6 h around noon. Groundwater was sampled from a well located at about 100 m upstream of the ground water flow beneath paddock no. 8.

All plant and soil samples were immediately transferred to 12 mL Exetainer vials (Labco, High Wycombe, UK), sealed and covered with Parafilm. All samples were stored in a freezer at approx. −18 ^∘C until water extraction. Water was extracted for 2 h using a cryogenic vacuum distillation apparatus with sample vials placed in a water bath with a temperature set to 80 ^∘C (Liu et al., 2016).

2.3 Isotope analysis

Oxygen isotope composition was expressed in per mil (‰) deviation relative to a standard:

$$\begin{array}{}\text{(1)}& {\mathit{\delta }}^{\mathrm{18}}\mathrm{O}=(R_{\mathrm{sample}}/R_{\mathrm{standard}}-\mathrm{1}),\end{array}$$

where R_sample and R_standard are the ¹⁸O∕¹⁶O ratios of the sample and the V-SMOW standard (Vienna Standard Mean Ocean Water). Samples collected between 2007 and 2012 were analysed by cavity ring-down spectroscopy using previously described procedures (Liu et al., 2016). Water samples collected in 2006 were analysed with an IsoPrime isotope ratio mass spectrometer interfaced with a multi-flow equilibration unit (both GVI, Manchester, UK). Each sample was measured against a laboratory standard gas, which was previously calibrated against secondary isotope standards (V-SMOW, V-SLAP and V-GISP). Heavy and light laboratory water standards, which spanned the range of δ¹⁸O values in the dataset, were analysed every five samples. Analytical uncertainty was 0.2 ‰. δ¹⁸O measurements obtained by cavity ring-down spectroscopy were linearly related to those obtained by isotope ratio mass spectrometry (n=176; R²=0.99). In a previous study, we found no difference between the results from spectroscopy-based and pyrolysis-based measurements performed using a TC/EA HTC coupled to an isotope ratio mass spectrometer (see Liu et al., 2017).

2.4 MuSICA modelling

The isotope-enabled soil–plant–atmosphere model MuSICA (Ogée et al., 2003, 2009; Wingate et al., 2010; Gangi et al., 2015) was parameterised for the studied grassland based on data collected at the site or taken from the literature (for details and parameter values, see below and Methods S2 and Table S1).

The model was validated with latent energy flux (LE) data obtained from an eddy covariance station (EC) at the site. According to that comparison (Fig. S1), MuSICA estimates were unbiased (LE_MuSICA=0.997LE_EC; R²=0.59). Further, we compared MuSICA predictions of total plant-available soil water (PAW, mm) in the entire topsoil with PAW modelling and data for the same site presented in Schnyder et al. (2006). For the 2007–2012 data, this yielded the relationship ${\mathrm{PAW}}_{\mathrm{MuSICA}}=\mathrm{0.99}{\mathrm{PAW}}_{\mathrm{Schnyder}\mathrm{et}\mathrm{al}.\mathrm{2006}}+\mathrm{7.8}(R^{\mathrm{2}}=\mathrm{0.83})$.

Although the MuSICA model is capable of simulating δ²H of water pools in the soil–plant system, we excluded those data in the paper, as (1) we are primarily interested in the processes leading up to the δ¹⁸O of cellulose, (2) we had noticed discrepancies in the model–data agreement for ²H∕¹H indicating fractionation (including a surface effect on ²H∕¹H of soil water at the experimental site; Chen et al., 2016) that are currently not accounted for in the model, and (3) we did not want to overload the paper with extra figures and discussion. Issues of ²H∕¹H fractionation of water including data from this experimental site will be addressed in a separate paper.

2.4.1 Meteorological forcing and isoforcing

MuSICA was forced by half-hourly values of meteorological data and δ¹⁸O of water vapour (δ¹⁸O_vapour) and rainwater (δ¹⁸O_rain). Wind speed, precipitation, air temperature, relative humidity and air pressure data were obtained from the Munich airport meteorological station, located at about 3 km south of the experimental site. Radiation was calculated as the mean of two weather stations located 10 km west and 12 km east of the experimental site. CO₂ concentration was measured at the site by an open-path infrared CO₂∕H₂O gas analyser (LI-7500, LI-COR, Lincoln, USA). For δ¹⁸O_vapour and δ¹⁸O_rain, observations at the experimental site were used whenever available. Otherwise δ¹⁸O_vapour and δ¹⁸O_rain estimates were obtained from globally gridded reconstructions derived from the isotope-enabled, nudged atmospheric general circulation model IsoGSM (Yoshimura et al., 2011). The IsoGSM-predicted δ¹⁸O_vapour and δ¹⁸O_rain at the grid point relevant to our site were first corrected for their offset with observed data, as predictions were found to be more enriched by 2 ‰ and 1.3 ‰ on average compared to the δ¹⁸O_vapour and δ¹⁸O_rain measured at the site (Figs. S2–S4).

2.4.2 Soil parameters

Soil structural properties (proportion of quartz and organic matter) as well as hydraulic characteristics (water retention and hydraulic conductivity) were determined on soil core samples taken at the site (Methods S2 and Fig. S5). In MuSICA, the δ¹⁸O of soil water is predicted based on liquid- and vapour-phase water isotope transport in the soil column and evaporative enrichment during soil evaporation. MuSICA allows two alternative formulations of the liquid water and water vapour effective diffusivities through the soil matrix. In the first formulation, these effective soil diffusivities increase linearly with the soil volumetric content of the liquid or vapour phase (Penman, 1940), while in the other formulation, proposed by Moldrup et al. (2003), the influence of the pore-size distribution parameter and the total soil porosity is also taken into account. Here, we explore the consequences of using either the Penman or Moldrup soil diffusivity formulation on the prediction of the δ¹⁸O of soil, xylem and leaf waters.

2.4.3 Canopy and gas exchange parameters

Grassland vegetation at the experimental site was parameterised in terms of canopy structure, the gas exchange properties of leaves, and root distribution and hydraulic properties (Table S1). In theory, MuSICA could account for species mixtures and competition for water and light, but this would require parameters for every single species. As the mixed-species samples were dominated by L. perenne and P. pratensis with closely similar morpho-physiology, we treated the vegetation sample as one plant type, described with one parameter set (Table S1).

The mean leaf area index (LAI; 2.6±0.7 m² m⁻²) and the mean leaf zenithal angle (LZA; $\mathrm{58}{}^{\circ }\pm \mathrm{3}{}^{\circ }$, corresponding to a leaf inclination index (LII) close to zero, typical of a spherical leaf angle distribution) were estimated from compressed sward height measurements made throughout the 2005 to 2012 grazing seasons (n=74 dates with a total of more than 7000 measurements) and calibration functions obtained from parallel measurements of compressed sward height, uncompressed sward height (estimated with a ruler), LAI and leaf zenithal angle (both determined with a LAI-2000, LI-COR, Nebraska, USA) at the site. The vertical distribution of leaf area in the canopy was described based on Wohlfahrt et al. (2003) (Fig. S6). In the standard parameterisation, LAI and LII were set as constants, in agreement with the constant sward state imposed by management practices (see above). In the sensitivity analyses, we also tested the effect of observed variations of sward height, LAI and LII on modelled δ¹⁸O of the different water compartments.

Leaf turnover is generally high in grassland (Chapman and Lemaire, 1996), including at our experimental site (Schleip et al., 2013). Thus, the co-dominant species (L. perenne, P. pratensis, T. officinale and T. repens) had a short and very similar mean leaf life span of ∼460 growing degree days (GDD, with a base temperature of 4 ^∘C) throughout the vegetation period (Schleip et al., 2013). As leaf turnover is high, the photosynthetic characteristics of leaves were set constant in the standard parameterisation. Leaf photosynthesis was modelled according to the Farquhar–von Caemmerer–Berry model (Farquhar et al., 1980). Values for the maximum rate of carboxylation (V_cmax), the light-saturated potential rate of electron transport (J_max) and other photosynthetic parameters were all taken from literature (Table S1). Leaf respiration rate was estimated from measurements made in the dark at the site (Ostler et al., personal communication, 2018) and was assumed to be partly inhibited during the day (e.g. Atkin et al., 1997).

Under well-watered conditions, stomatal conductance for water vapour (g_s) was simulated according to the Ball–Woodrow–Berry (BWB) model (Ball et al., 1987). This model has two parameters: m_gs, a species-specific non-dimensional parameter that determines the composite sensitivity of g_s to net CO₂ assimilation and to relative humidity and CO₂ concentration at the leaf surface; and g₀, the basal (or minimal) stomatal conductance. Uncertainties exist regarding the slope parameter m_gs and the intercept g₀ (Miner et al., 2017, and references therein). Values for m_gs reported by Wohlfahrt et al. (1998) for 13 grassland species from differently managed sites ranged between 6.9 and 24.7, and values for the intercept g₀ (termed g_min in their work) ranged between 12 and 193 mmol m⁻² s⁻¹. Likewise, a considerable range of night-time stomatal conductance (g_night) has been reported for C₃ grasses: from 60 to 140 mmol m⁻² s⁻¹ (Ogle et al., 2012; Press et al., 1993; Snyder et al., 2003). Here, g_night (together with leaf water content W; see below) was manually adjusted by fitting MuSICA to diurnal measurements of leaf water δ¹⁸O (Fig. S7). In the standard simulation, we used m_gs=10, a commonly used value for C₃ vegetation (see Miner et al., 2017); g₀=10 mmol m⁻² s⁻¹; and g_night=30 mmol m⁻² s⁻¹. Although the diurnal pattern of δ¹⁸O_leaf (Fig. S7) indicated some nocturnal stomatal conductance, the model generally predicted very low night-time transpiration, in agreement with the eddy flux data (Fig. S1) and the generally high nocturnal relative humidity. Finally, we tested the sensitivity of model predictions to variations of m_gs and g₀ (see below).

The effect of edaphic drought on g_s was considered by scaling m_gs and g₀ with a function of predawn leaf water potential (Nikolov et al., 1995). This adds two extra model parameters whose values were sourced from the literature (Table S1) and results in a 50 % reduction of m_gs and g₀ at −1.5 MPa.

Characteristic dimensions of leaves and shoots for the calculation of boundary-layer conductance were estimated based on measurements on individual grass tillers. The width and length (0.1 and 7 cm, respectively) of the leaf blade of a 7 cm tall grass tiller were taken as minimum and maximum values for the leaf dimensions, and the average leaf dimension was estimated as the square root of the area of such a leaf blade (0.8 cm). Values for minimum, maximum and average shoot dimensions were taken from sward height measurements (see above). The shelter factor was varied between 1 and 3.5 (Monteith and Unsworth, 1990), with very little consequences on the results. Parameter values for leaf optical properties, rain interception and wind attenuation were taken from the literature (Table S1).

In the model, total rooting depth was equated with topsoil depth (37 cm), as in Schnyder et al. (2006). The vertical distribution of fine roots in the soil column was assumed to follow a beta distribution (e.g. Sadri et al., 2018) with a maximum at 7 cm belowground (Fig. S8). The total amount of roots (g m⁻² of soil) was obtained from soil core sampling. The proportion of live roots was derived from a 14 d long dynamic ¹³CO₂∕¹²CO₂ labelling experiment at the same site (Gamnitzer et al., 2009; Schleip, 2013; Ostler et al., 2016; Ostler et al., personal communication, 2018). Root mass data were converted to root lengths by assuming a specific root length of 100 m g⁻¹ (Picon-Cochard et al., 2012). Mean fine root radius was set to 0.15 mm (Picon-Cochard et al., 2012) and root xylem radial hydraulic resistance to 1.0×10¹² s m⁻¹.

2.4.4 Oxygen isotope composition of water pools

The steady-state ¹⁸O enrichment of leaf water at the evaporative site (Δ¹⁸O_e, ss) was calculated as (Farquhar and Lloyd, 1993; Farquhar and Cernusak, 2005)

$$\begin{array}{}\text{(2)}& {{\mathrm{\Delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{e},\mathrm{ss}}={\mathit{\alpha }}^{+}\left({\mathit{\alpha }}_{\mathrm{k}}\right(\mathrm{1}-h)+h({{\mathrm{\Delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{v}}+\mathrm{1}\left)\right)-\mathrm{1},\end{array}$$

where h is the air relative humidity, normalised at leaf temperature (estimated from the leaf energy budget); Δ¹⁸O_v represents the isotopic composition of atmospheric water vapour, expressed above that of xylem water; α⁺ is the isotope fractionation during liquid–vapour equilibrium at leaf temperature (Majoube, 1971); and α_k is the kinetic isotope fractionation during water vapour diffusion through stomata and leaf boundary layer. α_k was estimated at half-hourly time steps from stomatal and boundary-layer conductances for water vapour (g_s and g_b):

$$\begin{array}{}\text{(3)}& {\mathit{\alpha }}_{\mathrm{k}}=\mathrm{1}+{\displaystyle \frac{\mathrm{0.028}/g_{\mathrm{s}}+\mathrm{0.019}/g_{\mathrm{b}}}{\mathrm{1}/g_{\mathrm{s}}+\mathrm{1}/g_{\mathrm{b}}}}.\end{array}$$

Equation (3) uses the kinetic fractionation factor during molecular diffusion (28 ‰) reported by Merlivat (1978) and assumes laminar diffusion through the leaf boundary layer (Farquhar et al., 2007).

We modelled leaf water isotope enrichment at isotopic steady state (Δ¹⁸O_leaf, ss) using the two approaches introduced earlier. In the two-pool simulation, we used a constant value for φ of 0.39, which was chosen such that the observed Δ¹⁸O_leaf was on average predicted without bias. In the sensitivity analysis, φ was varied between −0.20 and 0.50 based on the range of values reported previously for a variety of grass species (Helliker and Ehleringer, 2000; Gan et al., 2003; see Sect. 4.3). In the Péclet simulation, Δ¹⁸O_leaf, ss was related to Δ¹⁸O_e, ss using the Péclet number, as described by Farquhar and Lloyd (1993):

$$\begin{array}{}\text{(4)}& {{\mathrm{\Delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{leaf},\mathrm{ss}}={{\mathrm{\Delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{e},\mathrm{ss}}{\displaystyle \frac{\mathrm{1}-e^{-p}}{p}},\end{array}$$

with p the Péclet number. The latter is calculated as $p=\mathrm{EL}/\left(\mathrm{CD}\right)$, where L (m) is the effective path length, E (mol m⁻² s⁻¹) is the leaf transpiration rate, C=55 500 mol m⁻³ is the molar density of liquid water and D (m² s⁻¹) is the diffusivity of ${\mathrm{H}}_{\mathrm{2}}^{\mathrm{18}}\mathrm{O}$ in liquid water (Farquhar and Lloyd, 1993; Cuntz et al., 2007). In line with the original notion of the Péclet model, one single value of L was applied to the dataset, which was again adjusted such that Δ¹⁸O_leaf was predicted without bias.

Two supplementary experiments were also conducted to directly test the relevance of the Péclet effect in the co-dominant pasture species L. perenne and D. glomerata. These are described in the Supplement.

As leaf water is not in isotopic steady state for extended periods of the day (Fig. S9), an equation for non-steady-state enrichment of leaf water was used in addition to Eqs. (2)–(4). Using isotopic mass balance of leaf water and assuming that Eq. (4) holds true also in the non-steady state (Farquhar and Cernusak, 2005), the time evolution of Δ¹⁸O_leaf was modelled as (see also Farquhar et al., 2007)

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{\mathrm{d}\left(W{{\mathrm{\Delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{leaf}}\right)}{\mathrm{d}t}}=\\ \text{(5)}& {\displaystyle }& {\displaystyle }-{\displaystyle \frac{E}{{\mathit{\alpha }}_{\mathrm{k}}{\mathit{\alpha }}^{+}\left(\mathrm{1}-h\right)}}{\displaystyle \frac{p}{\mathrm{1}-e^{-p}}}({{\mathrm{\Delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{leaf}}-{{\mathrm{\Delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{leaf},\mathrm{ss}}),\end{array}$$

where W (mol m⁻²) denotes leaf water content, expressed on a leaf area basis.

A 27 h time series of community-scale δ¹⁸O_leaf observed at the site in August 2005 (Fig. S7) was used to fine-tune the parameters controlling leaf water enrichment in MuSICA (leaf water content and night-time and minimum stomatal conductance) within the range of values expected for temperate grasslands (for parameter values see Table S1). Because MuSICA predicts different leaf-level variables (e.g. g_s, g_b, h, E, Δ¹⁸O_leaf, ss) for sunlit, shaded, wet or dry leaves at different levels within the canopy, water-volume-weighted canopy averages of δ¹⁸O_leaf and Δ¹⁸O_leaf were first calculated at every time step before performing comparisons with observed data.

2.5 Sensitivity analysis

A sensitivity analysis was conducted in order to quantify the responsiveness of predicted midday δ¹⁸O of leaf, stem and soil water to plant morpho-physiological parameters that were expected to affect those predictions based on theoretical considerations and/or observed parameter variation at the site. As the leaf water enrichment submodels are embedded in the process-based model MuSICA, the effect of parameters not included in the leaf water δ¹⁸O models per se could be evaluated. Based on the ceteris paribus principle, the sensitivity was tested by varying one parameter while keeping all other parameters the same as in the standard MuSICA parameter set (Table S1). For a sensitivity run, the parameter was not decoupled from the equations in MuSICA; hence changing one parameter value at the same time affected all equations containing this parameter and all dependent variables. Parameter effects (sensitivities) were quantified by two variables: (1) the mean sensitivity relative to the reference run, obtained as the mean differences from the reference run as ($\sum _{i=\mathrm{1}}^n({\mathit{\delta }}_{\mathrm{sens},i}-{\mathit{\delta }}_{\mathrm{ref},i}))/n$, with δ_sens, i the δ¹⁸O of a given water compartment (leaf, stem, or soil at 7 or 20 cm depth) in a sensitivity run and δ_ref, i that in the reference run, for a day i; and (2) the standard deviation of the sensitivity, obtained from the differences between δ_sens, i and δ_ref, i. The latter illustrated how strongly the effect of a parameter varied between sampling days and hence how strongly it depended on the conditions encountered on one specific day. Thus, the sensitivity variables reported if changes in parameter values caused systematic/general effects (shown by the mean sensitivity), or cancelling effects (shown by the standard deviations of the sensitivity), or combinations, or lack of the two.

The high and low parameter values for the sensitivity analyses were chosen according to the range observed for grasses or grassland species, as reported in the literature or observed at the site (see Supplement). Values for individual parameters of the sensitivity analysis were set at −0.20 and 0.50 for φ, 1 or 12 mol m⁻² for leaf water content (W), 7 or 25 for the slope of the BWB model (m_gs), 0 or 193 mmol m⁻² s⁻¹ for the intercept of the BWB model (g₀), 0.6 or 3.8 m² m⁻² for leaf area index (LAI), 3.6 or 11.7 cm for canopy height (h_canopy), 20 or 140 µmol m⁻² s⁻¹ for the maximum rate of carboxylation at 25 ^∘C (V_cmax), 32 or 224 µmol m⁻² s⁻¹ for potential rate of electron transport at 25 ^∘C (J_max), and 0.08 or 0.265 m for the mean of the vertical root distribution (μ_root). V_cmax and J_max were altered in tandem to keep the ratio J_max∕V_cmax at 1.6 (Medlyn et al., 2002), the same as in the standard simulation (Table S1). Apart from those plant morpho-physiological parameters, the effect of alternative submodels for the liquid and vapour effective diffusivity in the soil was tested by replacing the Moldrup formulation by the Penman one. In addition, we investigated the effect of using uncorrected IsoGSM-predicted δ¹⁸O_rain and δ¹⁸O_vapour data instead of local isotopic data (gap-filled with offset-corrected IsoGSM data; see Sect. 2.4.1) for the isoforcing of MuSICA. This served to illustrate the usefulness of having local rainwater δ¹⁸O data.

2.6 Statistics

For comparison of predicted and observed data, we calculated the mean bias error ($\mathrm{MBE}=\stackrel{\mathrm{‾}}{P}-\stackrel{\mathrm{‾}}{O}$, where $\stackrel{\mathrm{‾}}{P}$ is the mean predicted value and $\stackrel{\mathrm{‾}}{O}$ the mean observed value) between observed and predicted δ¹⁸O (or Δ¹⁸O), the mean absolute error ($\mathrm{MAE}=\left(\right(\sum _{i=\mathrm{1}}^n\mathrm{|}{P}_i-O_i\mathrm{|})/n$), where P_i is the predicted and O_i is the observed value at time i, and n is the number of values; Willmott and Matsuura, 2005), and R² values.

Simple and multiple linear regression analyses and Student t tests were performed in R, version 3.4.2 (R Core Team, 2017), and RStudio, version 1.1.383 (RStudio Team, 2017).

3 Results

3.1 Rainfall, δ¹⁸O of precipitation and vapour

Growing season rainfall amounts and distribution differed between years, with total precipitation in the main growing period (May to August) varying between 321 mm (2006) and 514 mm (2010) (Fig. 1a). The mean δ¹⁸O_rain signal tended to increase in the first half of the vegetation period and decrease later in the season (Fig. 1b). However, individual rain events sometimes differed markedly from the mean pattern, with excursions of up to +4.5 ‰ and −6.2 ‰ relative to the mean of the same month (Fig. 1b). The δ¹⁸O_vapour signal followed similar mean trends (Fig. 1c) and exhibited a significant correlation (P<0.001) with the δ¹⁸O of the previous rain event.

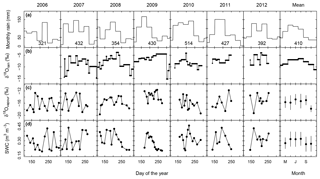
Figure 1 Multi-seasonal (2006–2012) and average patterns of monthly rainfall sums (a), δ¹⁸O of rain (δ¹⁸O_rain) (b), δ¹⁸O of atmospheric vapour (δ¹⁸O_vapour) (c), and volumetric soil water content (SWC, m³ water m⁻³ soil) at 7 cm depth as predicted by the standard MuSICA simulation (d). Permanent wilting point: 0.19 SWC; field capacity: 0.49 SWC. δ¹⁸O_vapour refers to measurements at the experimental site during the vegetation and soil sampling. δ¹⁸O_rain was determined following individual rains during the vegetation periods of 2007 to 2012. Rainfall data were taken from the DWD weather station of Munich airport, located at the same altitude ∼3 km south of the experimental site. The rainfall amount in the main growing period of each year (May to August) is given at the bottom of each panel in (a). Groundwater, at ∼1.5 m below the soil surface, had an average δ¹⁸O of 10.0 ‰ (±0.4 ‰ SD).

3.2 Soil water

The observed δ¹⁸O_soil was generally more enriched at 7 cm than at 20 cm belowground (Table 1; Fig. 2a, b). This relative enrichment with shallower depth was particularly large in the first half of the vegetation period and averaged 1.7 ‰ in the entire dataset. The total observed range of δ¹⁸O_soil differed somewhat between the two depths and was 7.8 ‰ at 7 cm, i.e. 16 % greater than at 20 cm (Table 1).

Table 1 Minimum, maximum, mean and range for the observed δ¹⁸O of grassland ecosystem water pools (soil water at 20 and 7 cm depth, and stem and bulk leaf water) and ¹⁸O enrichment of leaf water (Δ¹⁸O). Samples were collected at approximately fortnightly intervals during the vegetation periods of 2006–2012.

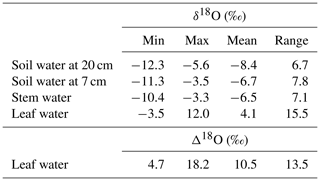
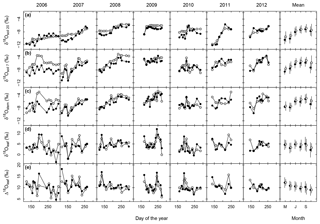
Figure 2 Multi-seasonal (2006–2012) and monthly average variation of δ¹⁸O in grassland ecosystem water pools: soil water at 20 (a) and 7 cm depth (b), stem (c) and leaf water (d), and ¹⁸O enrichment (Δ¹⁸O) of leaf water (e), as observed (closed symbols) or predicted by the standard MuSICA simulations including a two-pool leaf water model (light grey). The parameters for the standard MuSICA simulations are given in the Supplement (Table S1). The error bar in the monthly mean data displays the standard deviation.

In most years, δ¹⁸O_soil followed the rain pattern and increased during the course of the vegetation period at both depths (Fig. 2a, b). This increase was generally more pronounced at 7 cm than at 20 cm. Overall, the seasonal patterns of δ¹⁸O_soil were quite dynamic, with considerable differences between individual years.

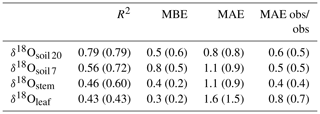
MuSICA simulations with the standard parameterisation (Table S1) predicted the multi-seasonal dynamics of δ¹⁸O_soil well (Fig. 2a, b) except in 2006 when local data of δ¹⁸O_rain were not available for the isoforcing (Fig. 1b) and δ¹⁸O_rain data were taken from the global atmospheric model IsoGSM, once corrected for the mean model–data offset (Figs. S2–S4). The seasonal trends and monthly fluctuations of observed δ¹⁸O_soil were reproduced with relatively small error (MAE of 1.1 ‰ and 0.8 ‰ at 7 and 20 cm, respectively). Also, the bias was small as MuSICA overestimated δ¹⁸O_soil by 0.8 ‰ and 0.5 ‰ at 7 and 20 cm, respectively.

Volumetric soil water content (SWC) predicted by MuSICA using the standard parameterisation (Table S1) exhibited strong seasonal and inter-annual variations. With SWC values (in m³ m⁻³) expected to vary between 0.19 (permanent wilting point) and 0.46 (field capacity), a SWC of less than 0.25 at 7 cm belowground corresponds to <25 % of the maximum plant-available water at this depth and is therefore a good indicator of edaphic drought. Each year, soil moisture at 7 cm fell below this threshold, but with a timing that differed from one year to the next (Fig. 1d).

3.3 Stem water

Observed δ¹⁸O_stem generally matched and followed that of δ¹⁸O_soil at 7 cm, independently of SWC, season and year (Figs. 2b, c, 3a and S10). Conversely, the relationship between δ¹⁸O_stem and δ¹⁸O_soil at 20 cm was generally weak, exhibiting large scatter and a significant offset between δ¹⁸O_stem and δ¹⁸O_soil at 20 cm for most of the data (Fig. 3c). Remarkably, for 90 % of all days on which the soil was classified as “dry” (predicted SWC<0.25), δ¹⁸O_stem was still closer to δ¹⁸O_soil at 7 cm than to δ¹⁸O_soil at 20 cm.

Barnard et al. (2006) showed that the δ¹⁸O of (pseudo-)stem water in grasses is very close to that of the water taken up by the root systems of grasses (see also Liu et al., 2017), meaning that root water uptake operates without ¹⁸O isotope fractionation. MuSICA simulations were based on this assumption and reproduced very similar relationships between δ¹⁸O_stem and δ¹⁸O_soil to those observed at both depths, with similar R², MBE and MAE (Figs. 2–3), thus showing a close agreement between observed and predicted data. Importantly, the close correspondence of δ¹⁸O_stem with δ¹⁸O_soil at 7 cm depth was not affected by changes in SWC predicted by MuSICA (Fig. 3). Again, the strongest disagreement between predicted and observed δ¹⁸O_stem occurred in 2006 (Fig. 2c), when observations of local δ¹⁸O_rain were unavailable.

3.4 Leaf water

Midday leaf water δ¹⁸O (δ¹⁸O_leaf) exhibited by far the greatest observed δ¹⁸O variations in the entire dataset (Table 1). Also, δ¹⁸O_leaf was unique in the way that it did not exhibit a general trend during the vegetation period (P=0.5; right panel in Fig. 2d). As on average δ¹⁸O_stem increased over the vegetation period while δ¹⁸O_leaf did not, Δ¹⁸O_leaf exhibited a significant decreasing trend over the vegetation period, with a decrease of 0.5 ‰ per month (P=0.01; right panel in Fig. 2e), in parallel with the increasing trend of relative humidity over the growing season (data not shown). Conspicuous short-term, parallel increases/anomalies of δ¹⁸O_leaf and Δ¹⁸O_leaf (i.e. changes in δ¹⁸O_leaf largely independent of variations of δ¹⁸O_stem) occurred occasionally in different years, e.g. in spring of 2008, late spring and early fall of 2009, and early summer of 2010.

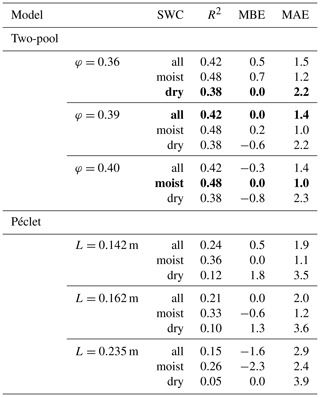
Predictions of Δ¹⁸O_leaf with MuSICA agreed best with observations using the two-pool model with φ=0.39 (R²=0.42; Table 2) in the standard MuSICA parameterisation. This result was robust for different soil water conditions. Unbiased predictions of Δ¹⁸O_leaf were best obtained by decreasing φ by 0.03 (i.e. setting φ to 0.36) under dry soil conditions (SWC<0.25) and increasing it by 0.01 (i.e. setting φ to 0.40) under moist soil conditions (SWC≥0.25), but this was an insignificant adjustment that did not change the overall coefficient of determination between observed and predicted Δ¹⁸O_leaf.

Table 2 R², mean bias error (MBE) and mean absolute error (MAE) for the comparison between predicted and observed δ¹⁸O_leaf, δ¹⁸O_stem and δ¹⁸O_soil at 7 cm (δ¹⁸O_soil 7) or 20 cm depth (δ¹⁸O_soil 20). Predictions were made with the standard MuSICA parameterisation given in Table S1. Values in parentheses exclude the data from year 2006. The last column presents the MAE between the replicate samples collected on the different dates. MBE and MAE values are given in per mil (‰).

The agreement between observed and predicted Δ¹⁸O_leaf was always weaker when using the Péclet model. Fixing the effective path length (L) at a certain value led to predictions that were systematically biased for either dry or moist soil conditions (Table 3). Unbiased predictions of Δ¹⁸O_leaf in conditions of different SWC were only obtained when increasing L (from 0.162 to 0.235 m) for dry soil conditions and decreasing L for moist soil conditions (from 0.162 to 0.142 m).

MuSICA predictions of δ¹⁸O_leaf and Δ¹⁸O_leaf obtained with the standard parameterisation agreed well with observations at all timescales (Figs. 2d, e, S7 and S9), with low or no bias (MBE of 0.3 ‰ and 0.0 ‰, respectively) and a MAE for δ¹⁸O_leaf of 1.6 ‰, i.e. 10 % of the total variation of δ¹⁸O_leaf in the entire dataset (Tables 1, 2). Also, the relationship between modelled transpiration rate and the proportional difference between the observed Δ¹⁸O_leaf and Δ¹⁸O predicted by the Craig–Gordon model (Fig. S11) was non-significant, revealing no evidence of a Péclet effect. This was also true when investigating that relationship with a subset of the data that included only the leaves that exhibited near-steady-state ¹⁸O enrichment. This subset was estimated using model output to identify the times when near-steady-state conditions were most likely and included about half of the data (results not shown).

Table 3 R², mean bias error (MBE) and mean absolute error (MAE) for the comparison between predicted and observed Δ¹⁸O_leaf obtained with different values of the proportion of unenriched leaf water (φ) in the two-pool model or effective path lengths (L) in the Péclet model for the prediction of Δ¹⁸O_leaf. Best predictions are highlighted in bold print. The agreement between predictions and observations was tested for the entire dataset (n=83) or the moist (SWC≥0.25; n=57) or dry soil subsets (SWC<0.25; n=26). The standard MuSICA parameterisation used a constant φ=0.39 for all conditions in all years. MBE and MAE values are given in per mil (‰).

3.5 Relationships between soil and atmosphere water status, transpiration, canopy conductance and ¹⁸O enrichment of bulk leaf water

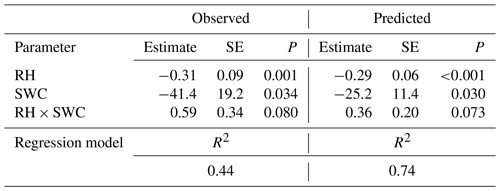
Multiple regression analysis demonstrated significant effects of air relative humidity (P<0.01) and SWC (P<0.05) on both observed and predicted Δ¹⁸O_leaf (Table 4). Δ¹⁸O_leaf increased with decreasing air relative humidity and SWC (Figs. 4a, b and 5a, b). The interaction effect of air relative humidity and SWC was close to significant for both observed (P=0.080) and predicted (P=0.073) Δ¹⁸O_leaf (Table 4). The effect of dry soil conditions on Δ¹⁸O_leaf was most evident at low air humidity (Figs. 4a, b and 5a, b) and was connected with a decrease in canopy conductance (g_canopy) (Fig. 5c).

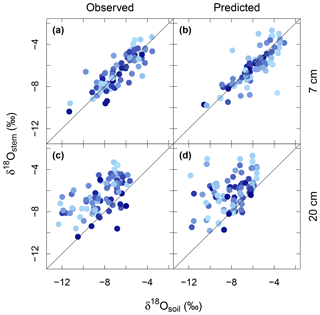
Figure 3 Correspondence between the δ¹⁸O of stem water and soil water at 7 cm (observed, a; and predicted, b) and at 20 cm depth (observed, c; and predicted, d). Colour strength indicates soil water content at 7 cm depth as predicted by MuSICA with standard parameterisation: light blue, dry soils; dark blue, soils near field capacity (for colour coding to SWC scale, see Fig. 4). The R², MBE and MAE for the relationship between δ¹⁸O_stem and the δ¹⁸O_soil at 7 cm depth were 0.69, 0.2 ‰ and 0.7 ‰ for the observed data (a) and 0.65, −0.2 ‰ and 0.7 ‰ for the predicted data (b). Conversely, the R², MBE and MAE values for the relationship between δ¹⁸O_stem and the δ¹⁸O_soil at 20 cm depth were 0.34, 1.9 ‰ and 2.1 ‰ for the observed data (a) and 0.17, 1.8 ‰ and 1.9 ‰ for the predicted data (b). The straight lines represent the 1:1 relationship.

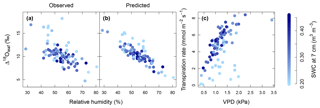
Figure 4 Relationship between relative humidity of air (RH) and observed Δ¹⁸O_leaf (a) and predicted Δ¹⁸O_leaf (b), and modelled response of transpiration to observed vapour pressure deficit (VPD) (c). Strength of blue colour from light to dark indicates the soil water content (SWC) at 7 cm depth as predicted by MuSICA with standard parameterisation. Permanent wilting point: 0.19 SWC; field capacity: 0.49 SWC. Predicted Δ¹⁸O_leaf data and transpiration rates were obtained with MuSICA in standard parameterisation and a two-pool leaf water model. Multiple regression analysis revealed effects of both RH and SWC on Δ¹⁸O_leaf (see Table 4).

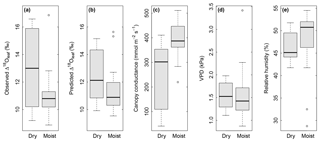
Figure 5 Box plots showing the effect of soil water content (“dry” in comparison with “moist”) on observed Δ¹⁸O_leaf (a), predicted Δ¹⁸O_leaf (b), and modelled canopy conductance, g_canopy (c), under conditions of low air relative humidity (<55 % RH). Differences between dry and moist soil conditions were significant at P=0.03 (a), 0.06 (b) and 0.003 (c). At the same time, observed air VPD (d) and relative humidity (e) did not differ between dry and moist soil for the displayed subset (RH<55 %). Dry soil was defined as <0.25 SWC (n=12) and moist soil as ≥0.25 SWC (n=29) at 7 cm depth. With a permanent wilting point of 0.19 SWC and a field capacity of 0.49, a SWC<0.25 corresponded to less than 25 % of the maximum plant-available water at 7 cm.

Table 4 Results of a multiple regression analysis of the effects of relative humidity (RH) and soil water content (SWC) on ¹⁸O enrichment of leaf water as observed and as predicted by MuSICA with standard parameterisation. SE, standard error; P, significance level.

The modelled dependence of transpiration on air VPD (vapour pressure deficit, the climatic driver of transpiration) was strongly modified by SWC (Fig. 4c). High air VPD drove high transpiration rates only under wet soil conditions (SWC≥0.25).

3.6 Sensitivity analysis

Increasing (decreasing) the proportion of unenriched leaf water (φ) and leaf water content (W) led to a strong reduction (increase) in δ¹⁸O_leaf (Fig. 6a, b). These changes in leaf-level parameters had no effect on δ¹⁸O_soil or δ¹⁸O_stem. Alterations of stomatal responsiveness (m_gs), minimum conductance (g₀), LAI or maximum carboxylation (V_cmax) and electron transport (J_max) rates had similar directional effects (reflected by the mean sensitivity in relation to the standard simulation) on predicted δ¹⁸O of soil, stem and leaf water. However, the strength of the effects differed for the different ecosystem water pools (Fig. 6). Stronger effects were found on δ¹⁸O_leaf and δ¹⁸O_soil at 20 cm, compared to δ¹⁸O_stem or δ¹⁸O_soil at 7 cm that tended to vary in close harmony. Generally, a change in the parameter value caused an opposite change in the predicted δ¹⁸O of a given pool. Moreover, these parameters caused strong cancelling effects, evidenced by large standard deviations of the sensitivity, particularly for δ¹⁸O_leaf. The sensitivity of δ¹⁸O_soil to plant morpho-physiological parameters was related to the effect of those parameters on plant transpiration rate (not shown), which in turn altered the residence time of soil water at the lower depth. For example, lower V_cmax and J_max values, not accompanied by a change in stomatal responsiveness m_gs, implied a decrease in transpiration rate and consequent increase in the percolation of growing season rain water to the lower part of the soil profile (Figs. 7a and 8). In comparison, the ¹⁸O-depleted (winter) signal persisted longer in the lower profile at intermediate (Fig. 7b) or high (Fig. 7c) V_cmax and J_max, as linked higher transpiration rates caused greater drying of the topsoil and reduced replenishment of deeper soil layers by summer rainfall.

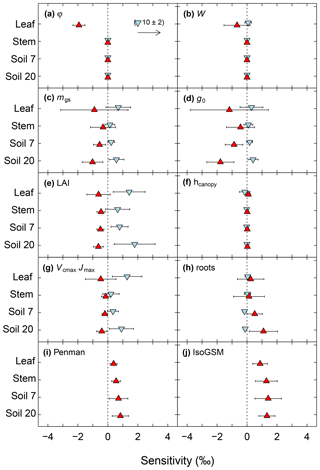
Figure 6 Sensitivity of modelled midday δ¹⁸O of leaf, stem and soil water at 7 and 20 cm depth to various parameters of the MuSICA model. The sensitivity was tested by varying one parameter while keeping all other parameters the same as in the standard MuSICA parameter set (Table S1), as detailed in 2.5. Sensitivity (parameter effect) was quantified by two variables: the mean (or average) sensitivity (in ‰) resulting from the change in a parameter value relative to the reference run, and the standard deviation of the sensitivity which captures the variability of the response to a parameter change for the different sampling times (displayed by error bars). Strong averaging (cancelling) effects resulting from the change in a parameter value are revealed by large standard deviations of sensitivities. Note that the sensitivity analysis revealed four different combinations of parameter effects: (1) strong mean sensitivities without cancelling effects, (2) strong mean sensitivities superposed with strong cancelling effects, (3) small mean sensitivities resulting from strong cancelling effects or (4) absence of sensitivities unrelated to cancelling effects. Parameter identity is given in the upper left corner of each panel. In (a) to (h), blue down-pointing triangles refer to the low parameter value and red up-pointing triangles to the high parameter value of a sensitivity run, based on the range of values observed at the site or – where such values were missing – the range of reported values for grasses or grassland in literature (see Sect. 2). In (i) the Moldrup submodel for the water vapour effective diffusivity in the soil was replaced by the Penman model. In (j) we used IsoGSM-predicted δ¹⁸O_rain and δ¹⁸O_vapour data instead of locally determined δ¹⁸O_rain and δ¹⁸O_vapour data for the isoforcing of MuSICA. Note that the low parameter value for Péclet number (a) predicted a far greater deviation of δ¹⁸O_leaf than any other parameter.

Apart from LAI, other shoot characteristics, such as canopy height (Fig. 6f), leaf inclination, shoot shelter factor, leaf size and shoot size (not shown), had a very small or no effect on predicted δ¹⁸O_leaf, δ¹⁸O_stem and δ¹⁸O_soil.

The formulation of the water vapour diffusivity through the soil matrix (Fig. 6i) and the average rooting depth (Fig. 6h) affected δ¹⁸O_soil (and more strongly so at the lower depth), while the effect on δ¹⁸O_stem and δ¹⁸O_leaf was much weaker. Not accounting for the pore-size soil particle distribution parameter in the soil diffusivity formulation caused a greater overestimation of δ¹⁸O_soil, especially at 20 cm belowground where the MBE reached 1.3 ‰, compared to 0.5 ‰ in the standard run. Shifting the root distribution closer to the soil surface had little effect on δ¹⁸O_soil at both depths. Conversely, shifting it towards greater depth (Fig. S8) led to an overestimation of δ¹⁸O_soil, especially at 20 cm (Fig. 6h), and increased MAE in the relationship between δ¹⁸O_stem and δ¹⁸O_soil at both soil depths (not shown).

We also tested the effect of the choice of the water isotope forcing of MuSICA (δ¹⁸O_rain and δ¹⁸O_vapour). In general, the agreement between predicted and observed ecosystem water pool δ¹⁸O was much better when MuSICA was forced using locally measured δ¹⁸O_rain and δ¹⁸O_vapour data (Fig. 6j). The MBE for the δ¹⁸O of the different water pools was 3.1 to 6.7-fold greater when using the IsoGSM-based isotope forcing, and the MAE was 1.5 to 2.6-fold higher.

4 Discussion

4.1 Model realism

An isotope-enabled, process-based soil–plant–atmosphere model, MuSICA, generated realistic predictions of multi-seasonal dynamics of δ¹⁸O in soil, (pseudo-)stem and midday leaf water, as well as of the ¹⁸O enrichment of leaf water in a drought-prone temperate grassland ecosystem. Throughout the vegetation periods of seven consecutive years (1) model bias (MBE) was low, (2) the range of δ¹⁸O variations of the different ecosystem water pools was similar in the predictions and observations, and (3) prediction error (MAE) was less than 15 % of the total observed range of δ¹⁸O in the different ecosystem water pools and about twice the size of the MAE for the duplicate samples of the different pools. The relationships between observed Δ¹⁸O_leaf and variables related to the water cycle such as SWC, air relative humidity, transpiration and canopy conductance were well captured by the model. Although MuSICA is a detailed and locally parameterised model, this general agreement between model predictions and observations is remarkable given that model parameters describing the relevant physical features or functional relationships of soil and vegetation were held constant with one single value for the entire mixed-species ecosystem. This is a striking outcome given that predicted δ¹⁸O were found to be sensitive to several (but not all) plant morpho-physiological parameters (Fig. 6). The greater scatter in the observed relationship between Δ¹⁸O_leaf and relative humidity compared to predictions (Fig. 4) likely resulted partly from sampling effects and error. Sampling effects could include small-scale spatial variation of soil properties, or spatio-temporal variation of LAI, nutrient levels and root distribution, a regular feature of grazed grassland (e.g. Schnyder et al., 2006, 2010). Also, Webb and Longstaffe (2003) observed differences of several per mil in δ¹⁸O_soil in the top 5 cm over distances of about 10 m in a sand dune grassland. Such spatial variations would inherently cause greater scatter in the observations compared to the model predictions.

Prediction of δ¹⁸O_stem at a given point in time is a real challenge, as δ¹⁸O_stem is influenced by numerous factors, including the temporal distribution of rainfall amounts and its associated isotopic composition, transport and mixing of rainwater with soil water, the depth distribution of root water uptake in the soil, and soil evaporation. These ecohydrological processes are described explicitly in MuSICA, and agreement between observations and predictions of δ¹⁸O_stem and δ¹⁸O_soil at 7 and 20 cm depth indicates that MuSICA is capable of simulating these ecohydrological processes including ¹⁸O of the different water pools. The ability of the model to generate realistic predictions of the δ¹⁸O dynamics at different depths in the soil (within the zone of most active root water uptake and just below that zone) suggests strongly that the ensemble of parameters dictating the spatio-temporal dynamics of soil water contents (including emptying and refilling dynamics) was described well in the model. That interpretation was also supported by the sensitivity analysis. Importantly, a better agreement between predicted and observed δ¹⁸O_soil at 7 cm and δ¹⁸O_stem was obtained when the δ¹⁸O of meteoric water was taken from local measurements rather than given by the isotope-enabled atmospheric model IsoGSM (Fig. 6j). This result is not surprising given the significant spatial and temporal variation of rainfall at weekly and sub-kilometre scales (Fiener and Auerswald, 2009) and the comparatively large grid size of the IsoGSM model simulations (ca. 200 km ×200 km). Our model sensitivity analysis also revealed a better predictive power of the soil diffusivity formulation proposed by Moldrup et al. (2003) over that proposed by Penman (1940) to reproduce the observed isotopic composition of all the ecosystem water pools (Fig. 6i). This superiority was likely related to the effect of accounting for the soil-pore-size distribution parameter for describing the effective liquid water and water vapour diffusivity through the soil matrix and estimating this parameter from the soil water retention curve parameters measured at the site.

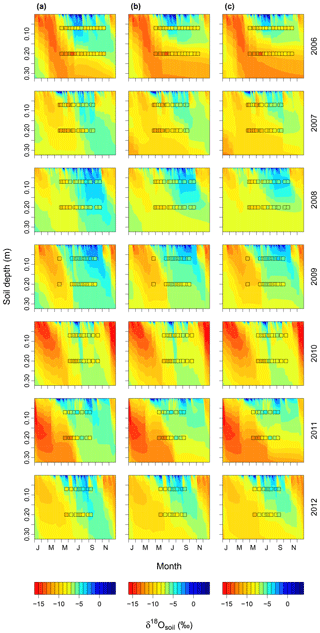
Figure 7 Soil water δ¹⁸O dynamics predicted for the studied period (2006–2012) with (a) low, (b) intermediate, and (c) high V_cmax and J_max. Values for low and high parameter values are given in the materials and methods. Observed values for δ¹⁸O_soil at 7 and 20 cm are displayed by squares. The same colour scheme is used for predicted and observed values and for each year and scenario. The abbreviations on the x axes indicate the months.

Figure 8 Flowchart illustrating how changes in photosynthetic parameters (V_cmax and J_max) affect soil water content (SWC) and isotopic composition (δ¹⁸O_soil).

4.2 Xylem water originates from shallow soil depths independently of season and soil water content

The comparison of observed δ¹⁸O_stem and δ¹⁸O_soil (Fig. 3a) strongly suggested that root water uptake occurred mainly at shallow depths (<20 cm) throughout the vegetation periods, largely independently of changes in SWC. This interpretation of observed data was based on comparison of δ¹⁸O_stem and δ¹⁸O_soil at two depths (7 and 20 cm) only, which provides limited spatial resolution and cannot inform precisely on the depth of root water uptake (Rothfuss and Javaux, 2017; Brinkmann et al., 2018). Such information can be improved by a locally parameterised, physically based, ¹⁸O-enabled ecohydrological model, as shown here. For instance, the standard MuSICA runs (Fig. 3b) indicated near-monotonous increases in δ¹⁸O_soil between 20 and 7 cm depth, matching well the observations in the majority of sampling dates (Fig. S13). Further, the simulations predicted a mean (uptake-weighted) depth of root water uptake above 15 cm in 90 % of all sampling dates, independently of SWC and observations of δ¹⁸O_soil (Figs. S12 and S13). Support came also from the MuSICA sensitivity analysis (Fig. 6h), showing that δ¹⁸O_stem was well predicted by the model only when root length density was maximum at shallow soil depth. The potential range of rooting depths is large in grassland, depending on site, species, climatic and management effects (Schenk and Jackson, 2002; Klapp, 1971). So, why would root water uptake be constrained to shallow depths in this drought-prone permanent grassland system? Several factors likely contributed: (1) the shallow topsoil overlying calcareous gravel (Schnyder et al., 2006); (2) the rapid shoot and root biomass turnover, which is associated with high phytomer dynamics leading to short leaf and root lifespan in intensively managed grassland (Schleip et al., 2013; Yang et al., 1998; Auerswald and Schnyder, 2009; Robin et al., 2010); (3) the high rates of shoot tissue (mainly leaves) losses that elicit a priority for assimilate (including reserve) allocation to shoot regeneration at the expense of the root system (e.g. Bazot et al., 2005); and (4) predominant placement of the root system near the soil surface dictated by the high need for nutrient interception and uptake (e.g. from excreta deposits), to compensate for the high rates of nutrient losses due to grazing (Lemaire et al., 2000). Importantly, (5) in a relatively high number of cases, the model predicted situations in which rainfall recharged mainly the topsoil, while SWC at depths >20 cm remained low (e.g. June–end of year 2006, April–October 2007, or May–end of year 2008; Fig. S12; see also below). Principally, however, factors (2)–(4) alone can explain why shallow rooting depth is a typical feature of intensively grazed grasslands (Troughton, 1957; Klapp, 1971). Also, Prechsl et al. (2015) did not find an increasingly deeper root water uptake upon soil drying in an alpine and a lowland grassland system in Switzerland. Similarly, grasses continued to rely on water in the uppermost soil layer during soil water scarcity in a mesic Savanna in South Africa, in which C₄ grasses were growing together with saplings and trees (Kulmatiski and Beard, 2013), and in a tallgrass prairie in the US dominated by C₄ grasses and C₃ shrubs and forbs (Nippert and Knapp, 2007a, b).

Predictions of δ¹⁸O_soil, particularly below the main zone of most water uptake, at 20 cm, were influenced markedly by estimates of LAI and by changes in V_cmax, J_max, and stomatal conductance responsiveness (m_gs) or minimal value (g₀). This resulted from the effect of those parameters on total canopy transpiration, which in turn altered the dynamics of soil water and hence of the mixing of ¹⁸O-depleted winter and ¹⁸O-enriched summer precipitation with soil water at different depths. For instance, an increase in transpiration rate caused by a high m_gs led to a decrease in δ¹⁸O_soil at 20 cm during the course of the growing season and a growing divergence between observations and predictions, particularly in years with low growing season precipitation (data not shown). This was likely caused by the fact that ¹⁸O-enriched summer rain mainly recharged the upper soil layer in this scenario, as this had been desiccated extensively because of the higher transpiration resulting from the higher m_gs. So, summer rains would contribute less to wetting of the lower profile. Conversely, if m_gs was set to a low value, predicted δ¹⁸O_soil at 20 cm increased throughout the vegetation period. According to the same mechanism, the effect of m_gs on δ¹⁸O_soil was negligible when growing season rainfall was high in 2010. The effects of changing V_cmax and J_max, LAI and minimum conductance on predicted δ¹⁸O_soil at 20 cm were very similar to m_gs, suggesting that these parameters acted via the same mechanism, that is canopy conductance for water vapour that is controlled largely by the (integrated) stomatal conductance of all leaves within the canopy. Thus, the effect of V_cmax and J_max was likely indirect, resulting from altered assimilation rates impacting stomatal conductance.

4.3 Evidence for a two-pool model of leaf water ¹⁸O enrichment

The Δ¹⁸O_leaf data were well predicted with a two-pool model and a constant fraction of unenriched water in bulk leaf water (φ≈0.39). This model was valid for a wide range of atmospheric and soil water conditions in seven consecutive growing seasons. Inclusion of a Péclet effect reduced the closeness of fit between measured and modelled Δ¹⁸O_leaf under all environmental conditions. We did not know if putative between-species differences in leaf water dynamics and associated ¹⁸O enrichment, or any other morpho-physiological effects for example associated with leaf ageing, could have led to a missing correlation between the proportional difference between measured leaf water ¹⁸O enrichment and that predicted by the Craig–Gordon model ($\mathrm{1}-{{\mathrm{\Delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{leaf}}/{{\mathrm{\Delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{e}}$) and transpiration rate. For these reasons, we explored this question with separate studies of L. perenne and D. glomerata, two species that also formed part of the present grazed grassland ecosystem. Again, these studies found no evidence for a Péclet effect and supported the two-pool model, as there was no relationship between the proportional difference between measured leaf water enrichment and that predicted by the Craig–Gordon model ($\mathrm{1}-{{\mathrm{\Delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{leaf}}/{{\mathrm{\Delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{e},\mathrm{ss}}$) and transpiration rate in either L. perenne plants grown in a controlled environment at different relative humidities and water availabilities, or D. glomerata leaves measured using an online transpiration isotope method (Notes S2 and Figs. S14, S15). A two-pool model was also suggested by the diurnal time courses of δ¹⁸O_leaf in this grassland (Fig. S7) and in a broadleaf and a coniferous tree species (Bögelein et al., 2017).

When interpreted with the Péclet model, the two-pool model implies a constant Péclet number and inverse variation of transpiration rate and effective path length (L). Dynamic changes in L in response to varying transpiration have been noted before, mainly in controlled conditions, and interpreted in terms of changing contributions of different paths (symplastic, apoplastic and transcellular) of water movements to the stomatal pore (Barbour and Farquhar, 2003; Kahmen et al., 2008; Song et al., 2013; Loucos et al., 2015; Cernusak et al., 2016). Increases in L in response to drought, as suggested in this work, have also been observed previously in Vitis vinifera by Ferrio et al. (2012) and were connected with variations in leaf lamina hydraulic conductance.

In principle, failure to detect a Péclet effect could be related to the presence of major veins and associated ground tissue of the grass leaves (Holloway-Phillips et al., 2016) or errors associated with non-steady-state effects on ¹⁸O enrichment of bulk leaf water (Cernusak et al., 2016). However, MuSICA predictions of Δ¹⁸O_leaf did account for non-steady-state effects and were generally consistent with observed Δ¹⁸O_leaf. The φ value used in our simulations is in the upper range of φ values reported for grasses. Liu et al. (2017) observed species-specific φ values ranging from −0.05 to 0.43 in two C₃ and three C₄ grasses, with no obvious effect of vapour pressure deficit on φ. Gan et al. (2003) presented φ values between ca. 0.16 and 0.41 in maize, with lower values coming from leaves with the midvein removed. Considering a similar effect of vein removal would move our observed φ to about 0.2. Such a value of φ for grasses is very similar to the mean φ reported for a wide range of non-grass species by Cernusak et al. (2016).

4.4 Atmospheric and edaphic effects on the ¹⁸O enrichment of leaf water

The strong response of Δ¹⁸O_leaf to air relative humidity has been observed and discussed previously (e.g. Farquhar et al., 2007; Cernusak et al., 2016), in addition to soil moisture (Ferrio et al., 2012). We are not aware of a previous study that disentangled the separate effects of atmospheric and soil humidity on Δ¹⁸O_leaf, either in field or controlled conditions. Notably, the responses observed in our work were corroborated by theoretical predictions as implemented in MuSICA. Modelled transpiration rate and stomatal conductance were greatly reduced under dry soil conditions, leading to higher kinetic fractionation α_k (Eq. 3) but lower α⁺ (Majoube, 1971) and relative humidity h, because of the warmer leaf temperatures. The net effect was a greater Δ¹⁸O_leaf predicted by MuSICA under dry soil conditions, in agreement with observations. This demonstrated that other vegetation parameters that affected the ¹⁸O enrichment in our sensitivity analysis (e.g. the unenriched fraction φ or the effective mixing length L, leaf water content W or LAI), but were not considered drought-sensitive, did not seem to be the main drivers of the enhancement of Δ¹⁸O_leaf during edaphic drought.