the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Evaluating the relative importance of precipitation, temperature and land-cover change in the hydrologic response to extreme meteorological drought conditions over the North American High Plains
Annette Hein
Laura Condon
Reed Maxwell
Drought is a natural disaster that may become more common in the future under climate change. It involves changes to temperature, precipitation and/or land cover, but the relative contributions of each of these factors to overall drought severity is not clear. Here we apply a high-resolution integrated hydrologic model of the High Plains to explore the individual importance of each of these factors and the feedbacks between them. The model was constructed using ParFlow-CLM, which represents surface and subsurface processes in detail with physically based equations. Numerical experiments were run to perturb vegetation, precipitation and temperature separately and in combination. Results show that decreased precipitation caused larger anomalies in evapotranspiration, soil moisture, stream flow and water table levels than increased temperature or disturbed land cover did. However, these factors are not linearly additive when applied in combination; some effects of multifactor runs came from interactions between temperature, precipitation and land cover. Spatial scale was important in characterizing impacts, as unpredictable and nonlinear impacts at small scales aggregate to predictable, linear large-scale behavior.
- Article
(10430 KB) - Full-text XML
- BibTeX
- EndNote
Improved understanding of drought is important to sustainably manage water resources and agricultural production worldwide. Agriculture depends on rainfall, especially in arid and semiarid regions, so large droughts can devastate global agriculture.
Because there are many ways to characterize drought, researchers often make a distinction between meteorological and hydrologic drought (Van Loon, 2015). Meteorological drought is defined as weather changes such as decreased precipitation or increased temperature. These changes may produce hydrologic drought, which is defined as impacts to the hydrologic system such as decreased runoff or soil moisture.
As climate continues to change, meteorological droughts are projected to occur more often and with greater severity than we have seen in the past. These meteorological changes will propagate to increased hydrologic drought as watersheds become increasingly stressed (IPCC, 2014; Diffenbaugh et al., 2017).
Within the US, the High Plains is a key agricultural region that is also drought-prone. Drought affected that region on many occasions during the 20th century, including the Dustbowl of the 1930s (Hong and Kalnay, 2000; Schubert et al., 2004) and the more recent 2012 drought that dried soils and lowered crop yields across most of the area (Otkin et al., 2016). Forecasts for the High Plains predict similar or worse droughts in the future (Cook et al., 2015) that could result in significant declines in crop yields (Glotter and Elliot, 2016). In the past, groundwater pumping has been used to buffer the region against hydrologic drought impacts, but groundwater is becoming depleted (Scanlon et al., 2012; McGuire, 2017). A better understanding of the effects of meteorological drought and the resulting hydrologic drought gained from modeling studies will be valuable for meeting future sustainability challenges.
Meteorological droughts are often characterized by some combination of decreased precipitation and increased temperature (Van Loon, 2015). Hydrologic drought occurs when these changes propagate through the watershed resulting in streamflow losses, changes in evapotranspiration (ET) and decreased soil moisture levels within a watershed. Sustained hydrologic drought can ultimately lead to crop failure for managed systems or changes in vegetation for natural systems.
There are a variety of pathways by which a meteorological drought can evolve to a hydrologic drought. When precipitation decreases, less water is available for any part of the water cycle, including ET. If the system is already wet (energy limited), this change may cause only minor impacts if the remaining water is still sufficient to supply potential ET. If the system is water limited, then a meteorological drought with a decrease in precipitation will cause a hydrologic drought in which ET and soil moisture both decrease. Some of the energy previously used to evaporate the water (latent heat of phase change) will instead go to sensible heat, causing a shift in the Bowen ratio (Eltahir, 1998; Seneviratne et al., 2010). Although feedbacks between the land surface and atmosphere are outside the scope of the current study, it should be noted that this change in the surface energy balance can carry over into atmospheric instability and changes to circulation (Eltahir, 1998), creating feedbacks to meteorology (Brubaker and Entekhabi, 1996) at a variety of timescales (Betts et al., 1996). In the present study area of the High Plains, an ensemble of climate models found a strong connection between soil moisture and the atmosphere (Koster et al., 2004).
In contrast to the precipitation decrease, temperature increases cause hydrologic drought more indirectly, through an increase in potential ET. In an energy-limited system, the available water will supply a higher actual ET (McEvoy et al., 2016). In a water-limited system, the increase in ET is bounded by the available water. Initially, ET can still increase, but as the soils dry ET is eventually expected to drop due to water limitations. This initial increase in ET is in the opposite direction of the effect predicted for precipitation decrease, so in a drought where both occur, there will be a competing effect on the hydrologic system (Livneh and Hoerling, 2016). If vegetation is disturbed, its buffering effect on the system is removed. Vegetation is expected to have a buffering effect against impacts to ET because it can reach deeper sources of water to satisfy ET demands when the surface soil moisture is depleted (Maxwell and Condon, 2016).
Many studies have used models to explore the driving factors and possible effects of future droughts. Otkin et al. (2016) examined US Department of Agriculture metrics and Noah, MOSAIC and variable infiltration capacity (VIC) models to show that hot and dry conditions in the 2012 drought dried High Plains soils within a few months. Gosling et al. (2017) used an ensemble of local and global hydrologic models and a variety of climate change scenarios to conclude there was no definite prediction for runoff in the upper Mississippi basin. Crosbie et al. (2013) also found no definite prediction for recharge in the High Plains under scenarios from 16 global climate models. Chien et al. (2013) predicted with a Soil Water Assessment Tool (SWAT) model that streamflow in Illinois watersheds will decrease under climate change. Naz et al. (2016) modeled hydrologic response to climate change across the entire continental US with a VIC model. They found large regional differences in runoff, SWE and the rain-to-snow ratio across the country under various Climate Model Intercomparison Project 5 model projections. Meixner et al. (2016) reviewed studies across eight representative aquifers in the US to anticipate effects of climate change on recharge. Recharge increased slightly in the northern High Plains and decreased in the south.
Modeling studies typically include some combination of temperature, precipitation and land cover changes as forcing factors to drought. However, since the preceding studies are either reconstructing a natural event or forecasting future droughts, they involve many simultaneous changes in forcing variables. Although the broad theoretical importance of each variable is clear, multiple simultaneous changes in one study obscure the details of exact mechanisms or interactions between factors. To address this limitation, other studies have taken the approach of isolating and comparing factors using numerical experiments instead of reconstructing real-world events.
Livneh and Hoerling (2016) argued that precipitation was more important than temperature in causing hydrologic drought impacts in the High Plains based on results from historical reconstruction and sensitivity experiments using VIC and the Unified Land Model (ULM). Maxwell and Kollet (2008) ran a ParFlow-CLM model over the Little Washita basin in Oklahoma and found that a 2.5 ∘C temperature increase reduced saturation and potential recharge. Effects were much more extreme with precipitation decreases than if temperature increased alone. They showed that this relationship was caused by shallow groundwater supported by lateral convergence in the subsurface, which allowed local regions of the model to maintain saturation and potential recharge regardless of the climate perturbations. These studies suggest that precipitation changes, typical of observed droughts, outweigh the effects of typical temperature or land cover changes in water-limited systems. However, if precipitation is stable, these secondary factors can be important; and when considered together with precipitation changes they may mitigate or exacerbate the effect of precipitation.
Previous work has identified precipitation and temperature as the most important controls of watershed drought response, with vegetation changes as a secondary impact. The studies reviewed here often reconstruct historical events, which does not allow for isolation of individual factors and their effects. Here we focus on isolating individual drought factors using an advanced and flexible hydrologic model to ensure that the results are as physically based as possible. This study builds on previous studies that compare different meteorological factors and their impact on hydrology by quantifying those impacts in detail. In particular, the project addresses three specific questions:
-
What is the relative importance of precipitation, temperature and land cover change in response of ET, runoff, soil moisture and water table levels to meteorological drought?
-
How do the hydrologic impacts of precipitation, temperature and land cover change differ when driving factors are considered together rather than in isolation?
-
How do impacts of the main drought factors and their interactions change across spatial scales?
This study explores how temperature, precipitation and land cover affect the water and energy balance of the High Plains through a series of numerical experiments where the driving factors (precipitation and temperature) and land cover are systematically perturbed. While land cover change can be viewed as a response to drought, it can also exacerbate system response to further drought. We include land cover change in our perturbations here to incorporate systemic watershed changes in addition to the meteorological forcing difference. The scenarios developed for these numerical experiments were modeled after an example of extreme drought in the region, the Dustbowl of the 1930s. The goal of the study is not to reconstruct the Dustbowl or produce operational forecasting, but rather to exploit the capabilities of large-scale modeling to illuminate major features of the hydrologic system using a real-world extreme drought as a test case.
The numerical simulations were conducted with ParFlow-CLM, an integrated hydrologic model. ParFlow-CLM was selected because it employs a more extensive and physically based representation of subsurface processes than many other hydrologic models and is therefore well suited to simulate the water and energy dynamics that occur during drought. Here we provide more details on the modeling platform (Sect. 2.1), study domain (Sect. 2.2), drought scenarios (Sect. 2.3) and metrics of analysis (Sect. 2.4). Selected model inputs and outputs are presented in the model data (Hein et al., 2018) on the Harvard Dataverse.
2.1 Model selection
The model was constructed using ParFlow, an integrated hydrologic modeling code, coupled to the Common Land Model (CLM), a land surface modeling code. The terminology “integrated hydrologic model” used here refers to the integration of variably saturated subsurface and overland flow processes and is not intended to imply that the model includes anthropogenic or biologic processes. ParFlow simulates saturated and unsaturated flow in three dimensions using Richards' equation, and relationships between pressure and relative saturation or permeability defined by the Van Genuchten pressure–saturation and pressure–relative-permeability relationships (Van Genuchten, 1980). Overland flow is modeled with the kinematic wave equation, with velocity found by Manning's equation. Energy and water balances at the surface are represented with CLM (Dai et al., 2003; Maxwell and Miller, 2005; Jefferson et al., 2017). CLM is coupled to ParFlow by passing the land surface water flux to ParFlow as a forcing in the top layer, and substituting ParFlow's computations for infiltration and streamflow routing within CLM (Maxwell and Miller, 2005).
ParFlow has a number of differences with commonly used models in other drought-related studies. It is instructive to compare ParFlow with the VIC model (Hamman et al., 2018; Liang et al., 1994) and the Soil Water Assessment Tool (SWAT, Neisch et al., 2011), not in order to criticize any model, but to illustrate the reasoning for model choice in this study. ParFlow allows any number of subsurface layers with any specified conductivity, and has vertical and lateral flow driven by pressure gradients. Soil moisture and groundwater are not distinguished; both are represented through pressure in a cell and solved for using Richards' equation. This three-dimensional variably saturated flow is the main difference between ParFlow and other models. While this detailed representation is an advantage for this study, it also leads to higher computational expense in ParFlow runs when compared to other models. VIC typically has three soil layers and does not simulate lateral flow between macroscale grid cells, although it includes a baseflow term for water leaving a cell to enter a stream. VIC is often applied to larger-scale modeling, while ParFlow can be used at any resolution. SWAT partitions groundwater into a “deep aquifer” which can have lateral flow to other subbasins and a “shallow aquifer” which contributes only to the stream. Soil moisture and groundwater are modeled separately. In contrast, ParFlow combines all of these processes at a variety of scales; in this model, scales are included from kilometer to subcontinental scale. (This does omit meter- and centimeter-scale processes such as biogeochemical cycles.) The detailed representation of subsurface processes makes ParFlow-CLM a suitable model to run numerical experiments whose results depend on physical processes and their interactions, as opposed to statistical fitting or simplified parameterizations.
2.2 Model configuration
The model domain covers the southern High Plains and Rocky Mountains, including portions of the Arkansas and Missouri river basins (Fig. 1) at a 1 km resolution. The domain is 1200 km by 1124 km and extends to a depth of 102 m, with five layers for a total of 6 744 000 computational cells. The lowest layer is 100 m thick and the other four layers are 1, 0.6, 0.3 and 0.1 m thick, listed from base to top. An overland-flow boundary condition, allowing free development of a stream network, was imposed at the top layer. A no-flow boundary condition was specified at the bottom and on all sides, with the exception of surface streams which can exit the domain. Due to computational expense, the runs in the present study were performed on the supercomputer Cori at the National Energy Research Scientific Computing Center (NERSC). In total, 1 year of the model required over 20 000 processor hours to calculate and this was completed in about a week of wall-clock time.
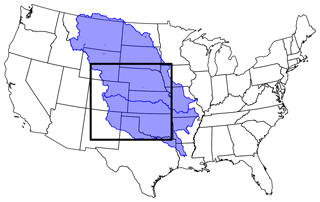
Figure 1The model domain (box) covers the southern High Plains of the US. Blue shading indicates the Missouri and Arkansas continental river basins.
Inputs for the study were developed from the previous work of Maxwell and Condon (2016), who modeled hydrology across the continental US (CONUS). The basic input data and initial conditions follow Maxwell and Condon (2016). Inputs include slopes, soil types, vegetation, attributes of soils and geologic units, and initial pressure conditions (see Fig. 2). The slopes in the x (east–west) and y (north–south) directions were derived from a digital elevation model and sink-filled to ensure the entire domain was connected. The simulations presented here use the kinematic wave approximation of the overland flow equations and therefore require a domain with a connected drainage network, as slopes control surface flow routing. While natural depressions in the landscape exist, the literature suggests that it is difficult to distinguish these natural depressions and sinks from noise within the processed DEM (e.g., Kenny et al., 2008). Soil types were taken from the SSURGO database. Important soil attributes include porosity, permeability, specific storage and van Genuchten parameters, which control saturated and unsaturated flow. Initial subsurface pressure conditions were taken from the original CONUS run, to increase spinup efficiency. The vegetation dataset was taken from the USGS land cover trends dataset (Soulard et al., 2014). Important vegetative parameters include leaf and stem area index, roughness length and displacement heights, rooting distribution parameters, and reflectance and transmittance for leaves and stems (Maxwell and Condon, 2016). While most inputs were drawn from Condon and Maxwell (2016), the geologic layer of that study contained features that were geologically less realistic at the scale of the High Plains. The geology of the base layer was updated for this project using local data from the US Geological Survey (USGS, 1998, 2005).
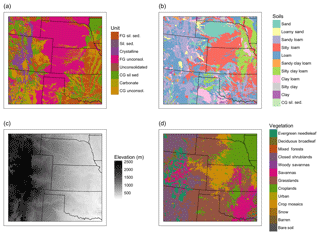
Figure 2Model inputs include (a) geology to characterize the bottom model layer, (b) soils to characterize upper layers, (c) topography for flow routing and (d) vegetation for surface energy and water exchanges.
It is important to note that water management such as groundwater pumping, surface water storage and diversion, and irrigation are not included in these simulations. This means that results of the project represent the system in a pre-development state not including anthropogenic impacts to the hydrology (Maxwell and Condon, 2016). The only management impact represented was land use and its changes applied by setting and changing the land cover type in the model. The use of modern-day vegetation is not temporally consistent with preindustrial water management (Hurtt et al., 2011). However, in this project, we are not reconstructing any specific historical drought, so it is less important in addressing the research questions to match all forcings and settings to one period of time. Additionally, different crops may affect the details of drought evolution in different ways, but this is not represented here because ParFlow-CLM is not an agricultural model. Each cell is assigned one vegetation type and all crops are represented as the same “croplands” vegetation type. Analyzing the details of crop type and its impact is outside the scope of the present study and not critical to address the study questions.
The initial conditions for the simulation were obtained from the existing continental-scale simulations (Maxwell and Condon, 2016) and include 4 additional years of spinup prior to this project. The pressure file was subset to the High Plains domain and the geologic layer was updated as described in the Appendix. The model was run repeatedly with water year 1984 North American Land Data Assimilation System (NLDAS-2) forcing until average subsurface storage change in 1 year was less than 1 % of precipitation (achieved after three repeated runs). Ajami et al. (2014) showed that change in subsurface storage is one of the most rigorous spinup metrics for integrated hydrologic modeling. Holding this value below 1 % of precipitation means that effects seen in numerical experiments can be interpreted as meaningful, i.e., something besides spinup noise if they exceed the threshold.
2.3 Numerical experiments
A suite of synthetic drought scenarios were developed to explore the importance of precipitation, temperature and land cover change on regional drought response in the High Plains. All simulations are developed using the hourly observed NLDAS-2 historical atmospheric forcings from Water Year 1984 as a baseline (precipitation, temperature, pressure, humidity, short wave radiation, long wave radiation, wind speed). The experiments are outlined in Tables 1 and 2 and include a baseline run, three one-perturbation experiments exploring the effect of precipitation, temperature and land cover changes in isolation, a combined experiment with both temperature and precipitation changes, and a worst-case scenario which also includes land cover changes.
Table 2Model scenarios including run name and perturbations applied relative to the baseline scenario.
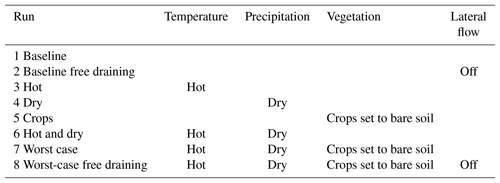
Two further runs were also conducted to explore the importance of lateral flow as a mechanism within the model as part of addressing the third research question on spatial scaling and complexity. Commonly used models including VIC and SWAT do not allow lateral flow within the model, and including this process makes the model computationally more expensive. Creating normal runs with lateral flow and free-draining runs (i.e., without lateral flow) allows exploration of how this process affects model results. To construct a free-draining run, the water table was set at the base of the domain and all overland and subsurface lateral flow processes were turned off, while vertical flow through the soil column and water table remained. (No separate spinup was conducted for the free-draining run, which has a lower water table than the other runs. To account for this, the free-draining drought run was compared to a free-draining baseline.) With these settings, ParFlow-CLM mimics a traditional land surface model as described in Maxwell and Condon (2016).
Definitions and specific implementation of each numerical experiment are shown in Table 2, and the exact perturbations used are quantified in Fig. 3. The baseline run and both free-draining runs were conducted for 1 year; the drought runs were conducted for 3 years of repeated drought forcing to simulate a transient time period a few years into a hypothetical severe drought. Although the simulation included 3 years, the analysis focuses on annually averaged results in the third and last year of model simulations in order to emphasize spatial scaling and factor interactions. Temporal evolution of drought is a large topic in itself and, while interesting, falls outside the scope of the present study.
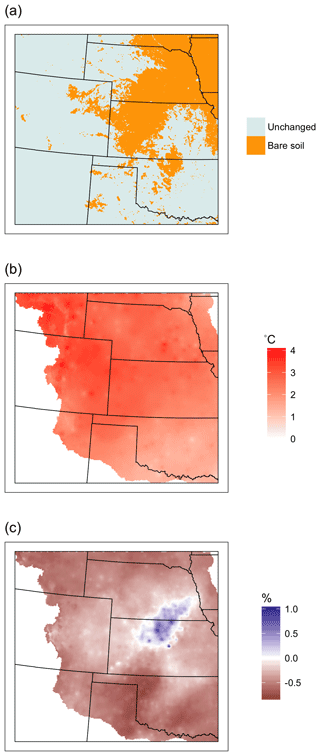
Figure 3Maps of the annual drought perturbations applied to the baseline scenario including (a) changes from cropland to bare soil, (b) absolute temperature increases and (c) relative precipitation increases.
These experiments are synthetic drought scenarios that are not an exact reconstruction of any historical drought, but rather an example of severe meteorological drought based on the Dustbowl drought of the 1930s. They begin with a baseline water year, then add perturbations singly and in combination, as shown in Table 1. We used NLDAS forcing from Water Year 1984 as the baseline because it is one of the most average water years in the United States in recent decades. We then increased temperature and decreased precipitation using examples drawn from a major drought in the region. Temperature and precipitation perturbations of the NLDAS forcing are based on PRISM reconstructions of the Dustbowl drought (the most extreme drought in the modern historical record) (PRISM Climate Group, 2017). Since PRISM data have a coarser resolution than the model grid, the PRISM rasters were resampled to the model grid before preparing forcing data.
Perturbations were applied at monthly timescale for each cell of the domain. To find these meteorological drought changes, a spatial map of changes was prepared for each month of water year 1934, one of the worst drought years historically recorded in the region, relative to the baseline decade of 1920–1929. Months of water year 1934 were taken to represent a “drought January”, “drought February” etc. Months of the 1920s were averaged to arrive at a baseline for that region at that time, a “non-drought January”, “non-drought February” etc. Then these months were subtracted to create anomalies. For example, “non-drought January” temperature was subtracted from “drought January” temperature to find the January temperature anomaly. The averaging and subtraction was done for each grid cell of the model grid, producing a spatial map for each month.
Lastly, these spatial maps were used to perturb the baseline and produce forcings for drought runs. Temperature was perturbed by adding an absolute temperature change to each cell of the hourly forcing for the relevant month. Precipitation was perturbed by multiplying each cell of the hourly forcing by a relative change for the appropriate month. Lastly, vegetation was disturbed for the crops runs by setting all crop or crop mosaic cells to bare soil (this approximation was inspired by the documented massive crop failure during the historic Dustbowl). Figure 3 shows plots of the resulting annual anomalies in temperature, precipitation and land cover which were used to drive the perturbed simulations.
In real droughts, we know that drought perturbations will not occur in isolation. For instance, changing temperature would generally accompany changes in radiation, humidity, etc. Additionally the vegetative changes could be more complex, as shifting temperature and rainfall patterns can produce a range of responses across several vegetative types. Finally, real droughts could exceed the ranges of drought simulated within the study (for example, if temperature was increased far enough, it could have a larger impact than a small precipitation change). However, in our simulations we are isolating the primary driving factors to perturb the model and we do not include such secondary effects. This is an approximation, but the forcing is still suitable to address the research questions in this paper because the goal is not to simulate a projected climate change (with, for example, a Global Climate Model prediction) nor to predict an actual hydrologic drought.
By making a single change at a time, the analysis can attribute any differences between the baseline and the perturbed run to the single variable that was perturbed. This is an advantage of modeling studies over real world observations, as we can assess process interaction with much greater precision and detail. Changing humidity and pressure with associated temperature changes would be modifying three things at once, which limit the linearity arguments and the strength of the experiment as such. For example, Maxwell and Kollet (2008) perturbed temperature without changing other meteorological variables for a study of drought in the Little Washita watershed. Rasmussen et al. (2011) also employed a simplified approach they called “pseudo-global warming”, adding estimated climate perturbations in temperature, vapor mixing ratio, boundary layer height and wind speed to a forcing dataset. Markovich et al. (2016) perturbed temperature alone in a similar study of climate change in California, and Pribulick et al. (2016) perturbed temperature and land cover in studying the impacts of vegetation change under global warming in a Colorado watershed. While changing one meteorological variable does not fully represent the physical system, it is a documented simplification used in multiple published papers. This study uses single-factor perturbations to the model (forcing, land cover) in a systematic way to better quantify system sensitivity and evaluate how watershed response varies between driving factors.
2.4 Metrics of drought analysis
Several metrics are applied to quantify drought impacts. First, standard anomalies were calculated for all drought scenarios relative to the baseline by simply subtracting the baseline values. The term anomaly is used in this discussion to describe changes to hydrologic processes resulting from the perturbations applied to the simulations. The subtraction produces a simple metric of the model impact. Averaging the anomaly across the domain produced a measure of the total impact of a given factor. The single-perturbation model runs allowed the calculation of average impacts (I) for each factor alone: I (temperature), I (precipitation) and I (land cover). The multiperturbation runs allowed calculation of the impacts for the combined factors: I(temperature + precipitation + land cover) and I(temperature + precipitation).
We acknowledge that these calculated anomalies are not equivalent to published drought metrics that are often used to define hydrologic drought. These calculations were chosen for this analysis in order to specifically evaluate the research questions being addressed, through specific focus on hydrological variables such as soil moisture, water table level, runoff and ET.
The individual run impacts make it possible to assess whether impacts were linearly additive. If impacts are linearly additive, then the impacts of multiperturbation runs (e.g., I(temperature + precipitation)) should equal the sum of the composite individual perturbation runs (e.g., I(temperature) + I(precipitation)). Here we quantify the nonlinearity in the combined drought response as a percent difference between the multiperturbation impact and the expected impact assuming linear addition.
In analyzing model results, it is important to note that these results do not constitute a direct prediction or reconstruction of a specific historical drought, therefore we do not directly validate the simulated drought impacts against observations. Comparison to data is an important and challenging step of model studies. There are observations that could be used to explore the same research questions that are addressed here; however, none of them are directly comparable to the present model because the present model is not a reconstruction of any historical drought. The findings of this model, therefore, cannot be taken as a direct prediction for central North America. Rather, their value lies in suggesting system-scale phenomena such as the nonlinear combination of factors.
Results are grouped into four sections. The first section provides a general overview of drought impacts in their spatial and temporal context. The second section focuses on attribution of drought impacts to specific factors of temperature, precipitation and land cover. The third part quantifies how these factors combine and interact in the multiperturbation simulations, with particular focus on whether the impacts are linearly additive. Lastly, the fourth section explores the importance of spatial scale to the predictability and linearity of impacts.
3.1 Description of simulated drought impacts
This section characterizes hydrologic drought impacts produced by the meteorological drought simulated in the hot and dry runs. Here we focus on ET and soil moisture impacts and put the simulated anomalies in the context of seasonal and spatial variability. The next section takes a broader approach to compare more runs and more variables, with less intensive detail.
Figure 4 shows that drought impacts on ET are relatively small compared to annual changes, but impacts to soil moisture are on the order of annual fluctuations. In the baseline year, ET is low in the fall, winter and early spring but becomes large in May–September, fluctuating between approximately 10 and 80 mm month−1. The annual change under meteorological drought is a hydrological drought impact to ET of −10.5 mm month−1 in the dry scenario, or +2.0 mm month−1 in the hot scenario. This average change also shows seasonal variation, with the largest impact occurring in May for the hot scenario and in June–August for the dry scenario. In the baseline year, soil moisture rises during fall, winter and spring and then decreases over the summer in response to high ET. The annual change under meteorological drought is a hydrological drought impact to soil moisture of −64 mm in the dry scenario, or −7 mm in the hot scenario. For soil moisture, the largest impact occurs in June for the hot scenario and in September–November for the dry scenario.
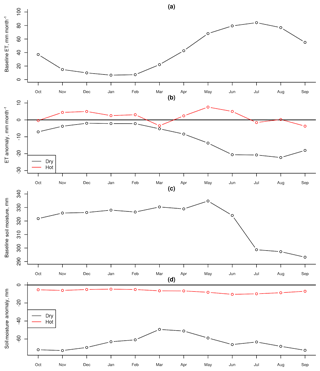
Figure 4Seasonal variability of ET and soil moisture. Panels (a) and (c) show the variables in the baseline runs, while (b) and (d) show hydrologic drought anomalies.
Figure 5 shows a map of ET and soil moisture anomalies in August for the dry run, when the anomalies were highest. The largest ET impacts were localized in the northeast and southeast area, with the west and central parts of the domain being much less affected. The largest soil moisture impacts were localized in the northeast and southwest parts of the domain. There was high variability in ET, with small-scale anomalies up to 10 times the domain average, and in soil moisture, with small-scale anomalies approximately double the domain average. However, while the largest impacts were localized, most of the domain was affected with impacts to ET or soil moisture caused by the meteorological drought forcing.
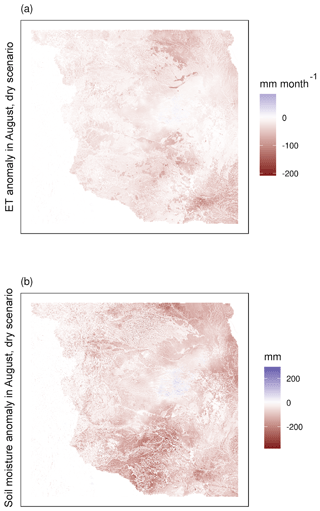
Figure 5Spatial snapshot of drought impacts in August. Panel (a) shows ET anomalies and (b) shows soil moisture anomalies.
This variability illustrates that the average annual temperature or precipitation anomaly is not representative of every snapshot in time, or each individual grid cell. The value of an annual average impact is to capture high-level information about the entire year and the whole domain in a single number which can be used to compare impacts between runs or variables.
3.2 Attribution of drought impacts
The simulated meteorological drought conditions applied in the hot and dry simulations as well as the prescribed land cover changes produced large hydrologic impacts to runoff, ET, soil water content and water table depth. Here we compare the hydrologic impacts of different perturbation combinations to evaluate the relative importance of temperature, land cover and precipitation changes in hydrologic drought impacts. Figure 6 shows domain-averaged annual values of runoff, ET, soil water content and water table depth. Relative to the baseline scenario, most of the drought scenarios have decreased runoff and ET, depleted soil water content, and lowered water tables (i.e., water tables that are further below the land surface), as would be expected in a drought. The exception is the hot and the crops runs, which have slightly higher ET, as discussed later. Figure 7 maps these anomalies across the domain and shows that impacts were typically most severe in the southern and eastern regions. In the central region where rainfall increased slightly (Fig. 3c), this extra water partly avoided the most severe impacts. For example, in the dry and hot–dry runs, soil moisture and runoff anomalies were smaller in this central region.
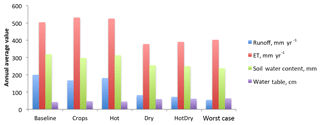
Figure 6Averages of runoff, ET, soil water content and water table depth, calculated on an annual basis across all cells in the model. Each color represents a different variable and each cluster is a different model run. The baseline, crops and hot runs are generally wetter than the others.
Comparison of single-perturbation runs and multiperturbation runs as shown in Fig. 7 allows the impacts of the drought run to be attributed to individual effects and associated mechanisms. For example, disturbances to land cover produced strong but localized effects. Changing cropland to bare soil stopped transpiration in the affected areas, but increased total ET. Setting plant-covered areas to bare soil stops all transpiration in those cells, but the missing transpiration was more than compensated for by higher ground evaporation in the same seasons. No extra water was available to the system, so (as Fig. 6 shows) the increase in ET was balanced by a small decline in runoff and a small drop in soil moisture and water table levels over the 2 years. Spatially, Fig. 7 shows that most effects were confined to the areas of vegetation change, with the exception of runoff, which decreased in downstream basins.
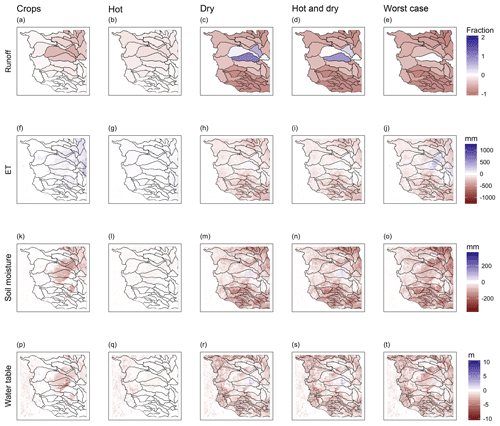
Figure 7Spatial maps of impacts to hydrologic variables, calculated by subtracting the baseline from each run. Each row represents one variable and each column is a different run. Panels (a–e) show runoff, (f–j) show ET, (k–o) show soil moisture and (p–t) show the water table.
(Basins in Fig. 7 are HUC-6 basins such as the North Platte, South Platte, Upper Cimarron, Republican, etc. The HUC or Hydrologic Unit Code system is used to classify drainages in the US.)
Increasing temperature produced small changes in several outputs across the domain. Hotter temperatures increased ET. The increase was limited by available water as many cells remained close to their baseline ET regardless of the temperature increase. Figure 7 showed that runoff decreased by about 10 % while soil moisture and water table levels remained almost the same as the baseline run.
Lowering precipitation drastically reduced all components of the water budget. Spatially, ET and soil moisture anomalies were largest where precipitation deficits were also largest. The exception was along riparian corridors where streamflow and lateral convergence of groundwater maintained local soil moisture and supported ET (Fig. 7). The larger impacts of precipitation relative to temperature are indicative of a water-limited system as would be expected for the High Plains.
It is important to note that the anomalies in the single-perturbation runs shown in Fig. 7 have high spatial variance. Variability in the sensitivity to the applied drought anomalies are illustrated in Fig. 8, which plots the response of individual grid cells to a given forcing change in temperature or precipitation. Variability in Fig. 8 shows that the same perturbation can result in a wide range of responses. Figure 8 also shows these anomalies do not follow a simple functional relationship, which suggests that the ET anomaly for any particular cell is influenced by many other variables. Since ET is controlled by soil and vegetative resistance, soil type and land cover would be possible controls. However, Fig. 8a and b show the anomaly colored by soil type, demonstrating that the wide range is not strongly correlated with soil type. Fig. 8c and d show the same for vegetative cover.
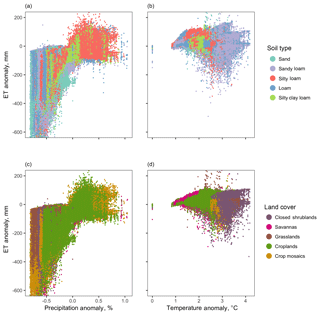
Figure 8Impacts for a given forcing span a wide range, independently of land cover, as shown in (a) and (b), or soil type, as shown in (c) and (d). In (a) and (c), annual anomalies from the dry run are plotted versus precipitation anomaly. In (b) and (d), annual anomalies from the hot run are plotted versus temperature anomaly.
Overall, this demonstrates that decreasing precipitation caused the largest anomalies of any of the single factors. Relative to precipitation, temperature produced minor changes, especially in runoff. Vegetation change from crops to bare soil had large impacts on the local areas, but an intermediate effect when averaged over the domain as a whole. This applies to the relative size of the changes studied; a 2 ∘C increase in temperature versus a 40 % drop in precipitation (when summed over the domain) and disturbance to land cover over about 30 % of the model area. For individual grid cells, anomalies followed the expected pattern, with heat causing ET to increase and dryness causing it to decrease. The size of the anomalies, however, were relatively unpredictable even when controlling for the forcing change, soil type and land cover.
3.3 Factor combinations
Section 3.1 presented the overall hydrologic impacts of individual and multiperturbation runs. This section quantifies how these factors combine and interact. In a completely linear system, the single-perturbation impacts would combine additively to equal the multiperturbation impacts; however, because hydrologic systems are non-linear and there are many system components interacting simultaneously, some part of that total may also be due to interactions between the factors. Consideration of important mechanisms includes land cover change and water-limited behavior. In general, individual factors can combine in a nonlinear way. For example, hotter temperatures occurring alone should increase ET, and drier weather alone should decrease ET, as detailed in the introduction. If hot and dry weather occurs, the total impact to ET could be a combination of the individual impacts. There could also be an interaction between the factors in which the change due to one perturbation depends on the level of the other factor. For example, the increase in ET due to temperature could depend on the amount of precipitation (which is a major control on available soil water) (e.g., Livneh and Hoerling, 2016).
Figures 9 and 10 compare the impacts of the single-perturbation runs with those in the multiperturbation runs. Each figure compares the result of a multiperturbation run with the combination of single-perturbation runs. In a perfectly linear system, the two results would be the same. Instead, the figures show that impacts of each multiperturbation run can be attributed to individual components, but not completely. For example, Fig. 9 shows that ET impacts predicted by adding the impact in the hot run (a 21 mm yr−1 increase) to the impact in the dry run (a 126 mm yr−1 decrease) predict a combined effect in the hot–dry run of 105 mm yr−1 decrease. This amounts to 93 % of the 114 mm yr−1 decrease that was actually modeled in the hot–dry simulation. Similar patterns hold for the other variables, with the dry run contributing more than the hot run to every anomaly, as observed qualitatively in the previous section. In Fig. 10, a similar analysis shows that the hot–dry run contributes almost three times as much as the crops run to each anomaly. The figures also show that the individual components do not account for the entire effect. For example, in Fig. 9 the hot–dry run is lacking 9 mm yr−1 of ET and keeps an extra 9 mm yr−1 of runoff compared to what would be expected by combining individual impacts calculated in the hot run and the dry run.
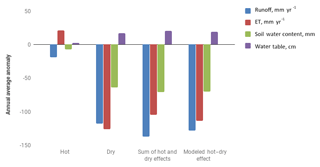
Figure 9Modeled anomalies between experimental runs and the baseline are shown for the hot–dry run, the hot run and the dry run. The anomalies in the hot–dry run are close to the sum of those in the hot run and the dry run. This linear behavior is most true for soil water content, less so for ET and runoff.
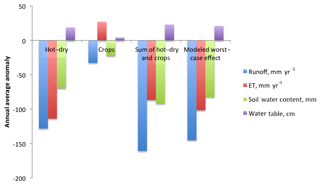
Figure 10Modeled anomalies between experimental runs and the baseline are shown for the worst-case run, the hot–dry run and the crops run. The anomalies in the worst-case run are close to the sum of those in the hot–dry run and the crops run; the largest difference is seen in runoff.
These runs show the impact of land use on hydrologic drought as it develops in response to meteorological drought. Figure 10 shows that the hot–dry run lowered ET by 114 mm yr−1 and dried soils by 70 mm on average, when drought occurred with no land use changes. However, in the worst-case run where meteorological drought was combined with removal of crops, ET was lowered less (102 mm yr−1) and soils were dried more (82 mm). The directions of these changes are consistent with the impact of land use alone: removing crops without drought increased ET by 27 mm yr−1 and dried soils by 22 mm. Vegetation removal exacerbates the drying effects of drought on soil because the presence of vegetation shields soil from evaporation, but since there is limited total moisture, the two effects do not add linearly and the soil moisture decrease is capped at 82 mm instead of 70 mm + 22 mm = 92 mm in the worst-case run. Similarly, vegetation removal tends to increase ET because more is evaporating from the soil, but drought decreases ET because less water is available in general. These water limitations may relate to nonlinear behavior as discussed later in the paper. The worst-case run has less impact on ET at the expense of drier soils when compared to the hot–dry run.
It is instructive to examine the mismatch between modeled anomalies and those predicted by linearity using spatial plots. Figure 11 maps this nonlinearity across the domain for runoff, ET, soil moisture and the water table. The left-hand column compares the hot–dry run to the individual hot and dry runs, and the right-hand column compares the worst-case run to the hot–dry and crops runs. The nonlinearity is calculated as a percent difference, as described in the Methods. Red colors mean that the multifactor impact was smaller than expected, while blue colors mean that it was larger. Gray denotes a small number of outlier grid cells. On average in the hot–dry run, ET generally decreased more than predicted by linearity, and runoff decreased less, while the water table and soil moisture decreased less in the center, and more in the north and south. Nonlinearity between the worst-case run compared to the hot–dry run was naturally localized to the areas of land cover disturbance (i.e., where there were differences between the two). Runoff changed in either direction, ET generally decreased more than predicted by single-factor runs, and soil moisture and water table levels decreased less than the combination of their single-factor run impacts. Importantly, the nonlinearity spans a wide range of variation, with simulated multiperturbation impacts being up to ±40 % from the expected values in a linear system.
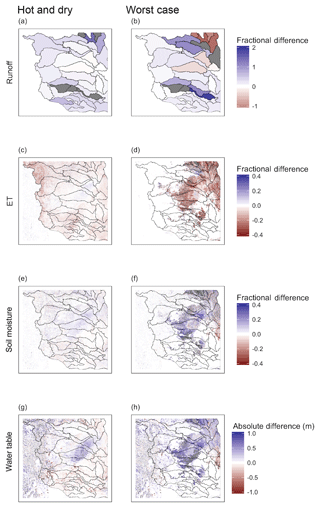
Figure 11Nonlinear behavior in both multiperturbation runs shows spatial patterns. Panels (a) and (b) show runoff, (c) and (d) show ET, (e) and (f) show soil moisture, and (g) and (h) show water table levels. Panels (a, c, e, g) compare the hot–dry run to the single-perturbation hot and dry runs. Panels (b, d, f, h) compare the worst-case run to the crops run and the hot–dry run.
Antecedent soil moisture and water-limited behavior may explain some of the nonlinearity shown in Fig. 11. Figure 12 shows the modeled ET anomalies versus antecedent soil moisture for a given forcing change (color scale), providing a general illustration of these mechanisms within the model. Figure 12a shows the dry run and Fig. 12b shows the hot run. In this figure, all cells are plotted regardless of soil texture. This is a slight simplification as soil texture changes water retention, so two soils with the same water content but different textures might have different amounts of water available for evaporation. Thus, in a few cases, the same water content might lead one cell to be energy limited but another to be water limited, as the demand for evaporation exceeds the available water. This does not change the overall finding that pre-existing soil moisture partially controls the response of model cells to forcing changes. The transition in both panels at about 350 mm of soil water content indicates the importance of antecedent soil moisture. Above this transition point, increasing temperature produces the largest increases in ET. Decreasing precipitation produces only small anomalies, because enough water is available in the wettest cells to supply the continued ET demand. Below this point, however, the system is water limited. In the presence of a temperature increase, soil water content limits the possible ET increase. These observations from the single-perturbation runs support a mechanism for the nonlinearities that has been suggested in previous research (e.g., McEvoy et al., 2016; Seniviratne et al., 2010): when precipitation decreases, there is less available water to supply ET demand even when a rising temperature increases potential ET. Thus the simulated multiperturbation ET is smaller (in other words, the deficit in ET is larger) than would be expected by simply combining factors.
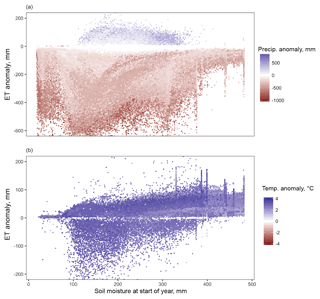
Figure 12Antecedent soil moisture is an important control on model ET response. The ET anomaly is plotted versus antecedent soil moisture and colored by model forcing. (a) shows data from the dry run (color scale is precipitation change) and (b) shows data from the hot run (color scale is temperature change). Each point is one model cell. Below about 350 mm of soil water content, the cells show water-limited behavior in which drought causes decreased ET depending on severity.
A final possible explanation is that the nonlinearity is an artifact of the modeling. This model captures important processes of the hydrologic cycle using physically based equations, as discussed in the Methods. Additionally, all runs were conducted with the same modeling environment and compared to a baseline from that model. However, we acknowledge there could be additional nonlinearities and feedbacks in the system that are not captured in our model.
3.4 Importance of spatial scale
This section examines the importance of scale in assessing these processes. Impacts of individual factors show less variability and more dependence on model forcing at larger scales. As was discussed in Sect. 3.1, impacts of individual factors can be more variable at small scales (Fig. 8); in other words, a given forcing change can produce a wide range of impacts to ET. Figure 13 shows that this variability is greatly reduced as soon as ET anomalies are aggregated to small (HUC-8) drainage basins. By the time the ET response is aggregated to subcontinental watersheds on the scale of the Arkansas or Red rivers, these spatial differences cancel out and variability is greatly reduced.
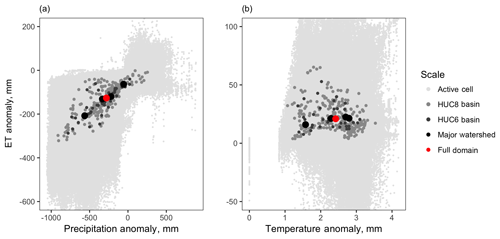
Figure 13Impacts of individual factors become less random at larger scales. (a) shows ET anomalies of the dry run and (b) shows ET anomalies of the hot run, plotted against their respective forcing anomalies. Impacts begin at the individual cell level and are aggregated to a series of larger scales.
Section 3.2 showed that nonlinearity (i.e., the portion of the response not accounted for by the linear combination of the individual perturbations) can span ±40 % for a given grid cell (Fig. 11) while being much less at the entire domain scale (Figs. 9 and 10).
Figure 14 examines this nonlinearity across a variety of spatial scales, comparing the multifactor hot–dry run to the single-factor hot and dry runs. The box plots show the spread of the data plotted in the left-hand column of Fig. 11, averaged at several different scales. Overall, Fig. 14 shows that the nonlinearity is much decreased in moderately sized (HUC-6) river basins, and small in subcontinental river basins. (HUC-8 basins are smaller basins that nest within HUC-6 drainages. The term major basins is used here to mean the Arkansas, Red and Missouri subcontinental basins.) This is especially important because it shows that treating the system as linear would fail to capture the most severe impacts occurring in individual grid cells. Closer inspection of Fig. 14 shows that the median nonlinearity becomes more positive for runoff and more negative for ET as scale increases. In a subcontinental basin as a whole, there is a small positive nonlinearity in runoff, meaning that the change in runoff under both temperature and precipitation increases is slightly larger than that due to the separate effects of temperature and precipitation. The interpretation that responses are more linear at larger scales focuses not on the median magnitude, but rather on the decreasing interquartile range of the box plots at larger scales.
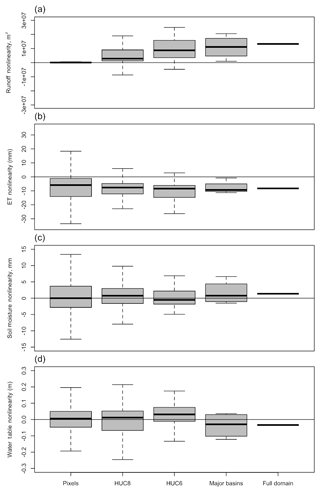
Figure 14Factors combine in a more linear way at larger scales. The multifactor hot–dry run is compared to the single-factor hot and dry runs. Each panel shows box plots that characterize deviations from linearity in the hot–dry run from model cell to subcontinental scales. Panel (a) shows runoff, (b) shows ET, (c) shows soil water content and (d) shows the water table.
The previous two figures may seem to contradict the message of earlier sections. They suggest that model responses at large scales are basically linear and predictable from the single-factor runs. If the impacts of individual factors are actually straightforward and combine in a basically linear way at subcontinental scales, perhaps simplified models would be adequate to answer big-picture questions at large scales without involving the full complexity of an integrated hydrologic model. The free-draining run provides insight to address this question by removing interactions between cells. Without lateral flow, a free-draining run can be considered as a package of single-column models, run across a spectrum of soil types, slopes and land cover.
The free-draining run allows us to directly test the impact of lateral flow on the simulated drought response across spatial scales. We find that the simulated changes from the land cover change simulation vary significantly between the standard and free-draining runs. As previously noted, ET tends to increase when croplands change to bare soil. Figure 15 compares ET in the worst-case simulation to a baseline in both the free-draining and typical configurations. Inspecting the area of crop disturbance in Fig. 15b confirms that in the normal model configuration, ET increases in the locations where crops change to bare soil. However, in the same area of the upper panel, exactly the same forcing changes cause ET to decrease for the free-draining run. This is largely explained by the nature of the free-draining run. In the normal configuration, lateral flow of groundwater can sustain ET and soil moisture, similar to the results found by Maxwell and Condon (2016). However, when no lateral flow is allowed, every grid cell is restricted to the soil moisture within it.
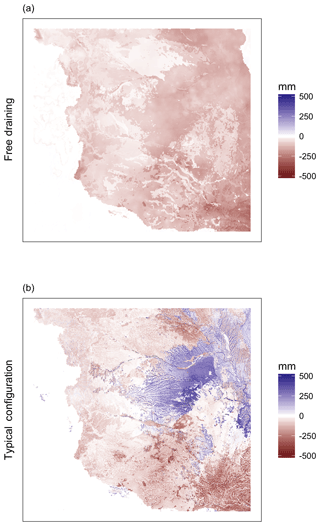
Figure 15Large-scale impacts of crop changes depend on representation of small-scale processes. Spatial maps are calculated by subtracting (a) the free-draining baseline (run 2) from the free-draining worst-case run (run 8) and (b) subtracting the baseline with lateral flow (run 1) from the worst-case run (run 7). Panel (a) shows the free-draining run where ET decreases in areas of land cover disturbance. Panel (b) shows the typical configuration for comparison, where ET increases in areas of land cover disturbance.
The difference may also be due to the differences in water table between the simulations, as the free-draining run did not use a constant water table or a separate spinup for the free-draining run, and therefore it has a lower water table than the other runs. (Impacts were calculated by comparison to the free-draining baseline run, which will partially adjust for this. However, it is still possible that a generally lower water table resulted in a water-limited system and decreased ET once plant transpiration stopped.) The results of the free-draining run relate to the third research question on spatial scaling and complexity by showing that even linear-seeming, large-scale predictions depend on representation of lateral flows and interactions within the model.
Overall, this section shows that nonlinear kilometer-scale impacts aggregate to large-scale changes which can be well predicted by linear combinations of single-factor simulations. The complexity of model response depends on the scale of the area of interest, with individual kilometer-scale grid cells being complex and aggregated subcontinental river basins response being much more simple. Responses at any scale nonetheless depend on representation of the processes and feedbacks at smaller scales. At coarse resolution, single-factor simulations may provide usable results; but as the resolution increases, accounting for the nonlinearities arising from multiple factors becomes more important. This means that coarser-scale simulations such as those often run on VIC may capture big-picture drought-related impacts, but may miss the finer-scale local variation.
This study explored impacts of drought-related drivers and relevant mechanisms through a series of numerical experiments using a ParFlow-CLM model. Meteorological and land cover perturbations are based on the example of the Dustbowl drought of the 1930s. Individually perturbed temperature, precipitation and land cover are followed by multiperturbation runs that combined these changes.
Attribution of drought effects to single factors showed that lowered precipitation caused more severe effects than increased temperature, within ranges of variation typical of major droughts. All impacts are ultimately due to forcing changes, but Sect. 3.2 and 3.3 showed that moisture limitations and scale also influenced responses and produced more complex behavior. Soil types and land cover had minimal effect. The complex behavior described above produced nonlinear impacts at small scales when comparing single-factor to multifactor simulations; however, these impacts combined more linearly at larger scales. Although large-scale behavior appears more simple than grid-scale responses, including complex small-scale processes such as lateral flow between cells was crucial to representing the large-scale responses.
In response to the first research question on the relative importance of precipitation, temperature and land cover change in hydrologic response to drought, we conducted single-factor simulations. The results show that precipitation is relatively more important than temperature or land cover change in hydrologic response to drought. The effects of precipitation are on the order of 3 times greater than the effects of temperature or land cover change, for ranges plausibly seen in extreme droughts. This is consistent with results of prior studies including Livneh and Hoerling (2016) and Maxwell and Kollett (2008). However, the exact effects of forcing change are still highly variable and this broad result may not hold true for individual grid cells.
Next we took these individual effects and combined them to see whether, and under what conditions, the impacts of the drought perturbations tested here (precipitation, temperature and land cover change) are linearly additive. We find that the effects can be linearly additive on a large scale for variables such as soil water content, but they are slightly less linear for variables such as ET or runoff. For individual model grid cells, the effects can be ±40 % of the expected value. This agrees with expected system feedbacks such as those described by Eltahir (1998) and expands on the results in Maxwell and Condon (2016).
Finally we evaluate how the impacts of the main drought factors and their interactions change across spatial scales. Results showed that highly variable and nonlinear impacts modeled at small scales aggregate to much less random, linear large-scale behavior, even though these large-scale predictions depend on representation of the small-scale processes and interactions. This extends the work of Maxwell and Condon (2016), which showed that lateral flow affects ET thresholds within the system.
Future studies could build on the work shown here by incorporating more detail. Including surface water management such as dams or irrigation diversions would make streamflow more representative of a present-day water year on the High Plains where streams are heavily managed. Inclusion of irrigation and groundwater pumping would allow for the study of human impacts to groundwater and surface energy balance. Further updates to the available geologic datasets would allow the model's existing detailed representation of subsurface processes to be based on better-supported parameters. Future studies could also combine an individual-factor approach, as done here, with a more realistic approach where meteorological variables like pressure or humidity change with temperature, or with complete future climate scenarios.
The results of this study indicate that when regional drought is occurring, local impacts may be many times smaller or larger. This matters because the most severe and costly impacts may occur in such small-scale, nonlinear responses. While the exact location and size of these small-scale anomalies is not predictable with a model like the present one, their general existence is. Even without specific predictions, plans for responding to regional drought will be more resilient and adaptive if they anticipate small-scale, severe impacts like those modeled here.
Selected model inputs and outputs are archived (Hein et al., 2018) on the Harvard Dataverse.
AH, RM and LC designed the analysis. AH conducted the simulations. LC and RM contributed data and analysis tools; in particular, RM provided high-performance computing resources. AH performed the analysis and wrote the paper with input from all coauthors.
The authors declare that they have no conflict of interest.
The simulations presented here were completed using resources of the National Energy Research Scientific Computing Center (NERSC), a US Department of Energy Office of Science User Facility operated under contract no. DE-AC02-05CH11231. Funding was provided by the National Science Foundation through its Water Sustainability and Climate (WSC) program and NSF award number 1204787. The authors thank the editor Niko Wanders, Peter LaFollette and two anonymous reviewers for their constructive comments.
This paper was edited by Niko Wanders and reviewed by two anonymous referees.
Ajami, H., McCabe, M. F., Evans, J. P., and Stisen, S.: Assessing the impact of model spin-up on surface water-groundwater interactions using an integrated hydrologic model, Water Resour. Res., 50, 2636–2656, 2014.
Betts, A. K., Ball, J. H., Beljaars, A. C., Miller, M. J., and Viterbo, P. A.: The land surface–atmosphere interaction: A review based on observational and global modeling perspectives, J. Geophys. Res.-Atmos, 101, 7209–7225, 1996.
Brubaker, K. L. and Entekhabi, D.: Analysis of feedback mechanisms in land-atmosphere interaction, Water Resour. Res., 32, 1343–1357, 1996.
Chien, H., Yeh, P. J. F., and Knouft, J. H.: Modeling the potential impacts of climate change on streamflow in agricultural watersheds of the Midwestern United States, J. Hydrol., 491, 73–88, 2013.
Cook, B. I., Ault, T. R., and Smerdon, J. E.: Unprecedented 21st century drought risk in the American Southwest and Central Plains, Sci. Adv., 1, e1400082, https://doi.org/10.1126/sciadv.1400082, 2015.
Crosbie, R. S., Scanlon, B. R., Mpelasoka, F. S., Reedy, R. C., Gates, J. B., and Zhang, L.: Potential climate change effects on groundwater recharge in the High Plains Aquifer, USA, Water Resour. Res., 49, 3936–3951, 2013.
Dai, Y., Zeng, X., Dickinson, R. E., Baker, I., Bonan, G. B., Bosilovich, M. G., Denning, A. S., Dirmeyer, P. A., Houser, P. R., Niu, G., and Oleson, K. W.: The common land model, B. Am. Meteorol. Soc., 84, 1013–1023, 2003.
Diffenbaugh, N. S., Singh, D., Mankin, J. S., Horton, D. E., Swain, D. L., Touma, D., Charland, A., Liu, Y., Haugen, M., Tsiang, M., and Rajaratnam, B.: Quantifying the influence of global warming on unprecedented extreme climate events, P. Natl. Acad. Sci. USA, 114, 4881–4886, 2017.
Eltahir, E. A.: A soil moisture–rainfall feedback mechanism: 1. Theory and observations, Water Resour. Res., 34, 765–776, 1998.
Glotter, M. and Elliott, J.: Simulating US agriculture in a modern Dust Bowl drought, Nature Plants, 3, 16193, https://doi.org/10.1038/nplants.2016.193, 2016.
Gosling, S. N., Zaherpour, J., Mount, N. J., Hattermann, F. F., Dankers, R., Arheimer, B., Breuer, L., Ding, J., Haddeland, I., Kumar, R., and Kundu, D.: A comparison of changes in river runoff from multiple global and catchment-scale hydrological models under global warming scenarios of 1 ∘C, 2 ∘C and 3 ∘C, Climatic Change, 141, 577–595, 2017.
Hamman, J. J., Nijssen, B., Bohn, T. J., Gergel, D. R., and Mao, Y.: The Variable Infiltration Capacity model version 5 (VIC-5): infrastructure improvements for new applications and reproducibility, Geosci. Model Dev., 11, 3481–3496, https://doi.org/10.5194/gmd-11-3481-2018, 2018.
Hein, A., Maxwell, R., and Condon, L.: Model data for Unravelling the impacts of precipitation, temperature and land cover changes for extreme drought over the North American High Plains, Harvard Dataverse, https://doi.org/10.7910/DVN/6PJDLG, 2018.
Hong, S. Y. and Kalnay, E.: Role of sea surface temperature and soil-moisture feedback in the 1998 Oklahoma–Texas drought, Nature, 408, 842–844, 2000.
Hurtt, G. C., Chini, L. P., Frolking, S., Betts, R. A., Feddema, J., Fischer, G., Hibbard, K., Houghton, R. A., Janetos, A., Jones, C. D., Kindermann, G., Kinoshita, T., Goldewijk, K. K., Riahi, K., Shevliakova, E., Smith, S., Stehfest, E., Thomson, A., Thornton, P., van Vuuren, D. P., and Wang, Y. P.: Harmonization of land use scenarios for the period 1500–2100: 600 years of global gridded annual land-use transitions, wood harvest, and resulting secondary lands, Climatic Change, 109, 117–161, https://doi.org/10.1007/s10584-011-0153-2, 2011.
IPCC: Summary for Policymakers, in: Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects, Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Field, C. B., Barros, V. R., Dokken, D. J., Mach, K. J., Mastrandrea, M. D., Bilir, T. E., Chatterjee, M., Ebi, K. L., Estrada, Y. O., Genova, R. C., Girma, B., Kissel, E. S., Levy, A. N., MacCracken, S., Mastrandrea, P. R., and White, L. L., Cambridge University Press, Cambridge, UK and New York, NY, USA, 1–32, 2014.
Jefferson, J. L., Maxwell, R. M., and Constantine, P. G.: Exploring the sensitivity of photosynthesis and stomatal resistance parameters in a land surface model, J. Hydrometeorol., 18, 897–915, 2017.
Kenny, F., Matthews, B., and Todd, K.: Routing overland flow through sinks and flats in interpolated raster terrain surfaces, Comput. Geosci., 34, 1417–1430, 2008.
Koster, R. D., Dirmeyer, P. A., Guo, Z., Bonan, G., Chan, E., Cox, P., Gordon, C. T., Kanae, S., Kowalczyk, E., Lawrence, D., and Liu, P.: Regions of strong coupling between soil moisture and precipitation, Science, 305, 1138–1140, 2004.
Liang, X., Lettenmaier, D. P., Wood, E. F., and Burges, S. J.: A simple hydrologically based model of land surface water and energy fluxes for general circulation models, J. Geophys. Res.-Atmos., 99, 14415–14428, 1994.
Livneh, B. and Hoerling, M. P.: The physics of drought in the US central great plains, J. Climate, 29, 6783–6804, 2016.
Markovich, K. H., Maxwell, R. M., and Fogg, G. E.: Hydrogeological response to climate change in alpine hillslopes, Hydrol. Process., 30, 3126–3138, 2016.
Maxwell, R. M. and Condon, L. E.: Connections between groundwater flow and transpiration partitioning, Science, 353, 377–380, 2016.
Maxwell, R. M. and Kollet, S. J.: Interdependence of groundwater dynamics and land-energy feedbacks under climate change, Nat. Geosci., 1, 665–669, 2008.
Maxwell, R. M. and Miller, N. L.: Development of a coupled land surface and groundwater model, J. Hydrometeorol., 6, 233–247, 2005.
McEvoy, D. J., Huntington, J. L., Hobbins, M. T., Wood, A., Morton, C., Anderson, M. and Hain, C.: The evaporative demand drought index. Part II: CONUS-wide assessment against common drought indicators, J. Hydrometeorol., 17, 1763–1779, 2016.
McGuire, V. L.: Water-level and recoverable water in storage changes, High Plains aquifer, predevelopment to 2015 and 2013–15, No. 2017-5040, US Geological Survey, Reston, VA, 2017.
Meixner, T., Manning, A. H., Stonestrom, D. A., Allen, D. M., Ajami, H., Blasch, K. W., Brookfield, A. E., Castro, C. L., Clark, J. F., Gochis, D. J., and Flint, A. L.: Implications of projected climate change for groundwater recharge in the western United States, J. Hydrol., 534, 124–138, 2016.
Naz, B. S., Kao, S. C., Ashfaq, M., Rastogi, D., Mei, R., and Bowling, L. C.: Regional hydrologic response to climate change in the conterminous United States using high-resolution hydroclimate simulations, Global Planet. Change, 143, 100–117, 2016.
Neisch, S. L., Arnold, J. G., Kiniry, J. R., and Williams, J. R.: Soil and Water Assessment Tool Theoretical Documentation Version 2009, Texas Water Resources Institute, College Station, Texas, 2011.
Otkin, J. A., Anderson, M. C., Hain, C., Svoboda, M., Johnson, D., Mueller, R., Tadesse, T., Wardlow, B., and Brown, J. Assessing the evolution of soil moisture and vegetation conditions during the 2012 United States flash drought, Agr. Forest Meteorol., 218, 230–242, 2016.
Pribulick, C. E., Foster, L. M., Bearup, L. A., Navarre-Sitchler, A. K., Williams, K. H., Carroll, R. W., and Maxwell, R. M.: Contrasting the hydrologic response due to land cover and climate change in a mountain headwaters system, Ecohydrology, 9, 1431–1438, 2016.
PRISM Climate Group: Oregon State University, available at: http://prism.oregonstate.edu, last access: December 2017.
Rasmussen, R., Liu, C., Ikeda, K., Gochis, D., Yates, D., Chen, F., Tewari, M., Barlage, M., Dudhia, J., Yu, W., and Miller, K. High-resolution coupled climate runoff simulations of seasonal snowfall over Colorado: A process study of current and warmer climate, J. Climate, 24, 3015–3048, 2011.
Scanlon, B. R., Faunt, C. C., Longuevergne, L., Reedy, R. C., Alley, W. M., McGuire, V. L., and McMahon, P. B.: Groundwater depletion and sustainability of irrigation in the US High Plains and Central Valley, P. Natl. Acad. Sci. USA, 109, 9320–9325, 2012.
Schubert, S. D., Suarez, M. J., Pegion, P. J., Koster, R. D., and Bacmeister, J. T.: On the cause of the 1930s Dust Bowl, Science, 303, 1855–1859, 2004.
Seneviratne, S. I., Corti, T., Davin, E. L., Hirschi, M., Jaeger, E. B., Lehner, I., Orlowsky, B., and Teuling, A. J.: Investigating soil moisture–climate interactions in a changing climate: A review, Earth-Sci. Rev., 99, 125–161, 2010.
Soulard, C. E., Acevedo, W., Auch, R. F., Sohl, T. L., Drummond, M. A., Sleeter, B. M., Sorenson, D. G., Kambly, S., Wilson, T. S., Taylor, J. L., Sayler, K. L., Stier, M. P., Barnes, C. A., Methven, S. C., Loveland, T. R., Headley, R., and Brooks, M. S.: Land cover trends dataset, 1973–2000, US Geological Survey Data Series 844, US Geological Survey, Reston, VA, p. 10, https://doi.org/10.3133/ds844, 2014.
USGS – US Geological Survey: Digital map of hydraulic conductivity for the High Plains Aquifer in parts of Colorado, Kansas, Nebraska, New Mexico, Oklahoma, South Dakota, Texas, and Wyoming, US Geological Survey Open-File Report 98-548, US Geological Survey, Reston, VA, 1998.
USGS – US Geological Survey: Preliminary Integrated Geologic Map Databases for the United States Central States: Montana, Wyoming, Colorado, New Mexico, Kansas, Oklahoma, Texas, Missouri, Arkansas, and Louisiana: Background Information and Documentation Version 1.0, US Geological Survey Open-File Report 2005-1351, US Geological Survey, Reston, VA, 2005.
Van Genuchten, M. T.: A closed-form equation for predicting the hydraulic conductivity of unsaturated soils, Soil Sci. Soc. Am. J., 44, 892–898, 1980.
Van Loon, A. F.: Hydrological drought explained, WIREs Water, 2, 359–392, 2015.






