Temporal- and spatial-scale and positional effects on rain erosivity derived from point-scale and contiguous rain data

Up until now, erosivity required for soil loss predictions has been mainly estimated from rain gauge data at point scale and then spatially interpolated to erosivity maps. Contiguous rain data from weather radar measurements, satellites, cellular communication networks and other sources are now available, but they differ in measurement method and temporal and spatial scale from data at point scale. We determined how the intensity threshold of erosive rains has to be modified and which scaling factors have to be applied to account for the differences in method and scales. Furthermore, a positional effect quantifies heterogeneity of erosivity within 1 km², which presently is the highest resolution of freely available gauge-adjusted radar rain data. These effects were analysed using several large data sets with a total of approximately 2×10⁶ erosive events (e.g. records of 115 rain gauges for 16 years distributed across Germany and radar rain data for the same locations and events). With decreasing temporal resolution, peak intensities decreased and the intensity threshold was met less often. This became especially pronounced when time increments became larger than 30 min. With decreasing spatial resolution, intensity peaks were also reduced because additionally large areas without erosive rain were included within one pixel. This was due to the steep spatial gradients in erosivity. Erosivity of single events could be zero or more than twice the mean annual sum within a distance of less than 1 km. We conclude that the resulting large positional effect requires use of contiguous rain data, even over distances of less than 1 km, but at the same time contiguously measured radar data cannot be resolved to point scale. The temporal scale is easier to consider, but with time increments larger than 30 min the loss of information increases considerably. We provide functions to account for temporal scale (from 1 to 120 min) and spatial scale (from rain gauge to pixels of 18 km width) that can be applied to rain gauge data of low temporal resolution and to contiguous rain data.

1 Introduction

Prediction of rain-induced soil erosion using models like the Universal Soil Loss Equation (USLE) requires quantification of the potential of rain to cause soil detachment and transport. This potential is called rainfall erosivity and is typically obtained from point rainfall measurements using rain gauges. For the conversion of erosivities from point to spatial information, isolines, interpolation techniques and relations to parameters such as the mean summer rainfall depth have been used (Rogler and Schwertmann, 1981; Wischmeier, 1959; Wischmeier and Smith, 1958, 1978). The characteristic relation between erosivity and rain depth of the same period was termed erosivity density and used in RUSLE2 (Dabney et al., 2012; USDA, 2013). It is recommended for areas with poor data availability (Nearing et al., 2017).

Rainfall is now able to be measured contiguously by radars and adjusted by rain gauges so that information about the spatio-temporal distribution of rain is combined with hyetographs measured at ground level. Several countries provide rain-gauge-adjusted radar data products with spatial resolutions of, for example, 1×1 km² (Bartels et al., 2004; Fairman et al., 2015), 2×2 km² (Koistinen and Michelson, 2002; Michelson et al., 2010) or 4×4 km² (Hardegree et al., 2008). Contiguous data of even coarser scale may result from other sources such as satellite data (Vrieling et al., 2010, 2014) or the output of regional climate models (e.g. Christensen et al., 2007; Flato et al., 2013).

Despite the important advantage that radar rain data are contiguous and temporally resolved, they cannot easily be used in place of rain gauge data for erosivity estimations because the scales of measurement differ a lot between both techniques. While rain gauges measure the rain near ground level at point scale (in Germany the collection area is 200 cm²), radars usually deliver rain measurements with an azimuthal resolution of approx. 1^∘ and a range of 125 to 1000 m. The data are then typically aggregated in grids of square pixels 1 to 16 km² in size. Rain intensity may differ greatly between point and grid measurements due to reduction in peak intensities with decreasing temporal and spatial resolution. Furthermore, sources of error differ between both measurement techniques. For radar measurements, errors may result from shading of rain cells by objects such as buildings, orographic elevations or hydrometeors and from the influence of the melting layer causing bright-band effects (Wagner et al., 2012). Major limitations of rain gauges are caused by adhesion, evaporation, wind drift and splashing (Habib et al., 2001). Finally, strong gradients can, in particular, be expected for thunderstorm cells of limited spatial extent. Thus, heterogeneity within pixels will be especially pronounced for erosive rains (Fiener and Auerswald, 2009; Fischer et al., 2016; Krajewski et al., 2003; Pedersen et al., 2010; Peleg et al., 2016). This heterogeneity cannot be resolved but needs to be quantified because it is the uncertainty that can be expected for predictions at a resolution higher than the pixel size. This uncertainty also applies in cases where a point measurement of rain erosivity is within a certain distance (e.g. 1 km) from the target area for which erosion is to be calculated. The resulting deviation between point measurement and grid pixel average will be called “positional effect” in the following. The positional effect also determines the uncertainty, caused by the spatial variability of rain, of soil loss predications in the proximity of a point rain measuring location. This positional effect should level out in long-term measurements as long as grid pixels are small enough not to include a consistent orographic pattern.

By definition in the USLE, erosivity is the product of a rain event's maximum 30 min intensity and its total kinetic energy (Wischmeier and Smith, 1958). Both factors depend on rain intensity; thus, intensity is squared in erosivity. Consequently, a difference in rain intensity of just 10 % would result in difference in erosivity of 21 %. Therefore, larger effects of variation in rain intensity can be expected for erosivity than for rainfall. In particular, an average of squares, as obtained from several point measurements within an area of non-uniform rainfall, will always be higher than the square of the average calculated from the same measurements. This difference between both squares caused by the difference in spatial scale of the measurements is expected to be a robust factor in the long run. We will call this the “spatial-scale effect”. A spatial-scale effect for erosivity, to the best of our knowledge, has not been studied. This is probably due to the novelty of operational radar measurements and the lack of long-term data sets required for erosivity estimations. Long-term and revised radar rain data now exist and can help to improve contiguous erosivity and soil loss estimations. Therefore, it is crucial to know to what extent erosivity, and subsequently also soil loss, is underestimated due to the spatial-scale effect by gridded rain data as provided by radar measurements and also by climate models or satellites that employ an even coarser spatial resolution than typical radars (Chen and Knutson, 2008; Vrieling et al., 2014). Rain intensities from radar may additionally be smoothed by measuring and subsequent processing procedures. The contribution of erosivity underestimation due to these procedures is called the “method effect” in the following. Thus, the difference in erosivity from rain gauge data and from radar data is caused by spatial-scale and method effects.

Another effect is induced by the temporal scale of the data used for erosivity calculations. With decreasing temporal resolution, maximum 30 min intensity and hence erosivity are increasingly underestimated. Therefore, temporal scaling factors are required to compensate for this underestimation (e.g. Auerswald et al., 2015; Agnese et al., 2006; Istok et al., 1986; Williams and Sheridan, 1991; Weiss, 1964; Yin et al., 2007). These are especially important for contiguous data, for which temporal resolution of rain data is decreased, often to 60 min, as a requirement for the adjustment to rain gauge data and to reduce the enormous amount of data caused by the high spatial resolution and wide spatial and temporal coverage.

We therefore hypothesize that (1) with decreasing temporal and spatial resolution of rain data, calculated erosivities decrease due to a smoothing of intensities; (2) radar measurements cause an additional underestimation of erosivities due to the measuring principle and the required calculation and correction steps; and (3) large uncertainty of erosivity within 1 km² is due to strong gradients of erosive rains as determined by the positional effect. The effects of hypotheses (1) and (2) have to be compensated for by changes in the calculation of erosivity, while the effect of hypothesis (3) quantifies uncertainty of erosivity of individual events at any location within an area of 1 km² around a rain gauge. We will quantify these effects and discuss their implications.

2 Material and methods

2.1 Data sets

To cover a wide range of spatial and temporal resolutions, several large and overlapping data sets had to be combined (for an overview see Table 1). The spatial resolution from point scale to 1 km pixel width (with an intermediate pixel width of 0.5 km) was covered by a high-density network of 12 rain gauges which operated over 4 years within an area of 1 km² (taken from Fiener and Auerswald, 2009; for location of the measuring site see Fig. 1a; for the spatial distribution of rain gauges see Fig. 1c). The data of the network comprised 542 events at point scale. The spatially integrated hyetographs at 0.5 or 1 km pixel width generated by the Thiessen polygon method (see Fig. 1c) will be referred to as “pseudo-radar” data.

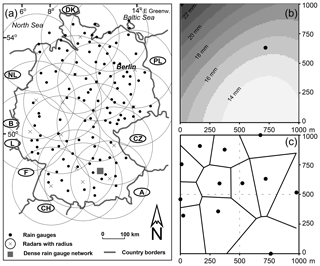
Figure 1 (a) Locations of the 115 rain gauges (dots), the coverage (circles) of the 17 weather radars (crosses) and the location of the 12 rain gauges used for the pseudo-radar data (square; size exaggerated) in Germany. (b) One rain gauge (dot) within one 1×1 km² pixel (bounding box) and isolines of rain depth (taken from Fiener and Auerswald, 2009) illustrating the variability of a single erosive rain event at 1×1 km² grid scale causing positional effects. (c) Distribution of the 12 rain gauges (dots) within an area of 1×1 km² (bounding box) and their corresponding Thiessen polygons. Dashed lines separate the area to a spatial scale of 0.5×0.5 km².

Point scale and 1 km pixel width were also compared for a much wider data set covering 16 years and the whole of Germany. Erosivities at 115 rain gauges were compared to erosivities obtained from radar data with 1 km resolution (for location of the rain gauges and the coverage of weather radars see Fig. 1a). Rain gauge data were taken from the Climate Data Center of the German Weather Service (Deutscher Wetterdienst: DWD; ftp://ftp-cdc.dwd.de/pub/CDC/, last access: 11 December 2018). DWD also provided the radar data, which were a revised version of the RADar OnLine ANeichung (RADOLAN) radar rain data product (Winterrath et al., 2012, 2017). This resulted in point–pixel pairs for >20 000 erosive rain events. For this data set the effect of temporal resolution was also evaluated. For spatial resolutions lower than 1 km pixel width (up to 18 km pixel width), a third data set was used. It comprised 1.9×10⁶ events at 1 km pixel width determined by radar measurements within an area of 800×600 km² (Table 1).

Table 1 Overview of the data used to determine the positional effect, the spatial-scale effect, the temporal-scale effect and the method effect.

Precipitation measurements of the DWD station network were conducted with OTT Pluvio weighing rain gauges (OTT Hydromet GmbH, Kempten, Germany) with a collector area of 200 cm², a measurement range of 0–1800 mm h⁻¹ and a 1 min resolution of 0.1 mm h⁻¹. The precipitation data passed a quality control system testing for completeness, carrying out climatological tests, and checking consistency over time as well as internal and spatial consistency (Spengler, 2002; Kaspar, 2013). The data were neither corrected for wind drift effects nor homogenized. A thorough overview of the precision of rain gauge measurements is given in Vuerich et al. (2009). Information on the stations' metadata can be found in the Climate Data Center (ftp://ftp-cdc.dwd.de/pub/CDC/observations_germany/climate/hourly/precipitation/historical/; last access: 11 December 2018) of DWD.

The DWD weather radar network underwent several upgrades during the analysis period. In the beginning of the considered time period five single-polarization systems (DWSR-88C, AeroBase Group Inc., Manassas, USA) operated without a Doppler filter, the latter being added between 2001 and 2004. Between 2009 and today, DWD has exchanged the network of C-band single-polarization systems of the next generation of type METEOR 360 AC (Gematronik, Neuss, Germany) and DWSR-2501 (Enterprise Electronics Corporation, Enterprise, USA) by modern dual-polarization C-band systems of type DWSR-5001C/SDP-CE (Enterprise Electronics Corporation), all equipped with a Doppler filter. During the time of exchange, a portable interim radar system of type DWSR-5001C was installed at some of the sites. Radar data underwent an operational quality control system. They were adjusted to gauge data within a reprocessing suite applying a consistent software version (version 2017.002) and optimized quality control algorithms with 5 min resolution (Winterrath et al., 2018a) and 60 min resolution (Winterrath et al., 2018b).

2.2 Erosivity calculation procedures

Following Wischmeier (1959) and Wischmeier and Smith (1978) erosivity of a single rain event (R_e) was calculated as the product of the maximum 30 min rain intensity (I_max30) and the kinetic energy (E_kin) (Eq. 1). A rain event is erosive by definition if it has a total precipitation (P) of at least 12.7 mm or a minimum I_max30 of 12.7 mm h⁻¹ (min(I_max30)).

$$\begin{array}{}\text{(1)}& R_{\mathrm{e}}=I_{max\mathrm{30}}\cdot E_{\mathrm{kin}}\end{array}$$

The E_kin,i per millimetre rain depth (in kJ m⁻² mm⁻¹) was calculated for intervals i of constant rain intensity I following Eq. (2a)–(2c). For all intervals i, E_kin,i was multiplied by the rain amount of this interval and then summed up to yield E_kin for the entire event.

$$\begin{array}{ll}{\displaystyle }{E}_{\mathrm{kin},i}=& {\displaystyle }\left(\mathrm{11.89}+\mathrm{8.73}\times {\log }_{\mathrm{10}}I\right)\times {\mathrm{10}}^{-\mathrm{3}}\\ \text{(2a)}& {\displaystyle }& {\displaystyle }\mathrm{\text{for}}\mathrm{0.05}\mathrm{mm}{\mathrm{h}}^{-\mathrm{1}}\le I<\mathrm{76.2}\mathrm{mm}{\mathrm{h}}^{-\mathrm{1}}\text{(2b)}& {\displaystyle }{E}_{\mathrm{kin},i}=& {\displaystyle }\mathrm{0}\text{for}I<\mathrm{0.05}\mathrm{mm}{\mathrm{h}}^{-\mathrm{1}}\text{(2c)}& {\displaystyle }{E}_{\mathrm{kin},i}=& {\displaystyle }\mathrm{28.33}\times {\mathrm{10}}^{-\mathrm{3}}\text{for}I\ge \mathrm{76.2}\mathrm{mm}{\mathrm{h}}^{-\mathrm{1}}\end{array}$$

When I_max30 was derived from data with intervals longer than 30 min, I_max30 was determined as the maximum rain intensity of the event. Erosive events are separated from each other by rain breaks of at least 6 h (Wischmeier and Smith, 1958, 1978). For example, using 60 min rain data, we defined events as being separate when five subsequent 60 min intervals without rain occurred. This assumes that rain events stop and start on average in the middle of the first and the last non-zero rain interval. The same concept was used for all data sets with temporal resolutions >60 min.

The annual erosivity of a specific year (R_y) is the sum of R_e of all n erosive events within this year. The long-term average annual erosivity (R) is then calculated as

$$\begin{array}{}\text{(3)}& R={\displaystyle \frac{\mathrm{1}}{k}}{\sum }_j^k({\sum }_i^n{R}_{\mathrm{e},i}{)}_j={\displaystyle \frac{\mathrm{1}}{k}}{\sum }_j^k{R}_{\mathrm{y},j},\end{array}$$

which is the average of R_y for a number of k years, in the case of this study 16 years.

While in the USA and other countries often the unit MJ mm ha⁻¹ h⁻¹ is used, we use N h⁻¹ for R_e, because it is the unit most often used in Europe and because of its simplicity. The units can be easily converted by multiplying the values in N h⁻¹ by a factor of 10 to yield MJ mm ha⁻¹ h⁻¹.

2.3 Determination of scale effects

The smoothing caused by decreasing resolution in time and space mainly decreases intensity, while the total amount of rainfall should, in principle, be unaffected. This decrease in intensity has two consequences. First, the intensity threshold min(I_max30) that defines an erosive event is less often met and thus has to be adjusted to arrive at the same number of erosive rains irrespective of resolution. Second, scaling factors for R_e are required. A temporal scaling factor t_τ,σ scales from temporal resolution τ to 1 min resolution at a certain spatial scale with pixel width σ. A spatial scaling factor s_σ scales from spatial resolution σ to point resolution (rain gauge). A method effect m may additionally occur, which quantifies the difference between erosivities obtained from rain gauges and from radar measurements at identical spatial and temporal scales. It is caused by the additional smoothing resulting from the radar technique and the adjustment and correction steps subsequently required. It may also include the errors of rain measurement that differ between the rain gauge and radar methods. The positional effect $p_{R_{\mathrm{e}}}$ describes the average relative deviation of erosivity of single events derived at 1 km resolution and at point scale from rain gauges located within the respective 1 km pixel including the spatial-scale and method effects. The positional effect cannot be used for correction, but it is a measure of variability within a certain pixel.

Adjusting the intensity threshold to account for smoothing at low resolution is appropriate only for the temporal resolution. With decreasing spatial resolution some areas will be included within a pixel that actually received erosive rain, while other areas within the pixel did not. Without adjustment of the intensity threshold the entire pixel may be classified as non-erosive, while adjustment of the threshold would then indicate an erosive event also in those areas within a pixel where no erosive rain had occurred. Adjusting the intensity threshold with decreasing spatial resolution could not correct both errors simultaneously. Even more important, the criterion of breaks that separate between events is biased for large areas. Any rain at some place within a large pixel abrogates an existing break even if it does not fall at a site that experienced an erosive rain event. The loss of a break with increasing pixel size decreases the number of events even when all events are considered. Adjusting the number of events in this case would be a wrong correction. Hence for the spatial resolution the threshold effect was included in s_σ, while for the temporal-scale effect the intensity threshold could be adjusted. As a result the number of erosive events can correctly be estimated at low temporal resolution with this adjustment at point scale, while for a spatial resolution lower than point scale the number of erosive events will be wrong compared to point scale. Only the sum of erosivities over a longer period of time (months, years or longer) can then be corrected with the spatial scaling factor.

The hyetographs of the high-density network of 12 rain gauges were spatially integrated to yield hyetographs at 0.5 or 1 km pixel width. The average deviation of annual erosivities calculated from hyetographs at point scale and from spatially integrated hyetographs at 0.5 or 1 km pixel width yielded the spatial scaling factors s_σ=0.5 and s_σ=1. The individual deviation of event erosivities at point scale from the average was due to the positional effect $p_{R_{\mathrm{e}}}$ (for an example see Fig. 1b). The average positional effect $p_{R_{\mathrm{e}}}$ was calculated as the geometric mean of the k ratios of R_e derived from rain gauge (σ=0) and 1 km²  pixel data (σ=1), for which neither rain gauge R_e nor pixel R_e was zero:

$$\begin{array}{}\text{(4)}& p_{R_{\mathrm{e}}}={\mathrm{10}}^{\left({\sum }_{i=\mathrm{1}}^k{\log }_{\mathrm{10}}\right(R_{\mathrm{e},\mathit{\sigma }=\mathrm{0}}/R_{\mathrm{e},\mathit{\sigma }=\mathrm{1}}{)}_i/k)}.\end{array}$$

The positional effects were determined separately for events with $R_{\mathrm{e},\mathit{\sigma }=\mathrm{1}}$ larger and $R_{\mathrm{e},\mathit{\sigma }=\mathrm{1}}$ lower than $R_{\mathrm{e},\mathit{\sigma }=\mathrm{0}}$. Rains that were erosive at only one of both spatial scales were excluded from the calculation of the geometric mean, and the percentages of these events were determined for both cases.

Erosivity at point scale and at 1 km²  pixel scale were also compared based on >20 000 erosive rain events at 115 locations distributed over Germany, where a rain gauge was situated within a radar pixel. The long-term (16 years) average deviation of R between point and pixel scale was due to the smoothing effects of the spatial-scale effect and the radar technique (method effect). The method effect was quantified by subtracting the spatial-scale effect, as obtained from the dense rain gauge network, from the combined effect, as obtained by comparing erosivities from rain gauges with radar-derived erosivities. The combined effects of spatial scale and method were also tested for seasonal variation.

For spatial resolution lower than 1 km pixel width, radar data were aggregated to yield pixel widths of up to 18 km. Erosivities were calculated from the aggregated rain data and compared to the erosivities at 1 km pixel width, which were averaged for the pixel width being examined. This comparison was carried out for radar data covering an area of 800×600 km² over 2 months (1.9×10⁶ events at 1 km pixel width; Table 1).

The temporal resolutions of the rain gauge data and the radar data differed (1, 5, 60 min). Erosivities derived from these data were adjusted to 1 min resolution with the appropriate temporal scaling factor. The temporal scaling factors were determined on two spatial scales, at point scale and at 1 km pixel width. To this end, 17 out of the 115 point–pixel pairs were selected randomly, and rain data for the period 2001 to 2016 (16 years) with 1 min resolution from rain gauges and 5 min resolution from radar measurements were used. The rain gauge data yielded a total of 4599 erosive events, for which rain data were aggregated to 2, 5, 10, 15, 30, 45, 60, 80, 100 and 120 min intervals, and R_e was determined as described in Sect. 2.1. The intensity threshold min(I_max30)_τ was adjusted until the annual number of erosive rain events at the respective temporal resolution τ was equal to that at τ=1 min. The temporal scaling factor ($t_{\mathit{\tau }=x,\mathit{\sigma }=y}$) for R_e was then obtained at point scale (σ=0) from

$$\begin{array}{}\text{(5)}& {\displaystyle }{t}_{\mathit{\tau }=x,\mathit{\sigma }=\mathrm{0}}={\sum }_{i=\mathrm{1}}^N(R_{\mathrm{e},\mathit{\tau }=\mathrm{1},\mathit{\sigma }=\mathrm{0}}{)}_i/{\sum }_{i=\mathrm{1}}^N(R_{\mathrm{e},\mathit{\tau }=x,\mathit{\sigma }=\mathrm{0}}{)}_i,\end{array}$$

which is the ratio of the sums of R_e derived from 1 min data and R_e derived from data with τ>1 min at point scale. Additionally, for 1 km pixel width $t_{\mathit{\tau }=x,\mathit{\sigma }=\mathrm{1}}$ was estimated by using an intermediate radar product of RADOLAN with a temporal resolution of 5 min that was recursively adjusted corresponding to the 60 min RADOLAN data (analogously to Fischer et al., 2016). This was done for the 17 grid pixels where the 17 rain gauges were located. The temporal scaling factors were derived from RADOLAN data as described above (Eq. 5) but relative to τ=5 min. The resulting factors were then multiplied by the scaling factor for τ=5 min obtained from the rain gauge data to yield scaling factors relative to a temporal resolution τ=1 min.

The temporal scaling factors $t_{\mathit{\tau }=x,\mathit{\sigma }=\mathrm{0}}$ were additionally determined for each month (January–December) and separately for rain gauges located in the northern and southern halves of Germany (7 and 10 rain gauges, respectively) to test for any seasonal or regional dependence of the factors.

Finally, the combined procedure of an adjusted intensity threshold and a temporal scaling factor was validated by comparing annual R_y obtained from 60 min RADOLAN data to R_y derived from RADOLAN data with 5 min resolution. This was done for the remaining 98 (115–17) grid pixels and 16 years, yielding a total of 1568 R_y.

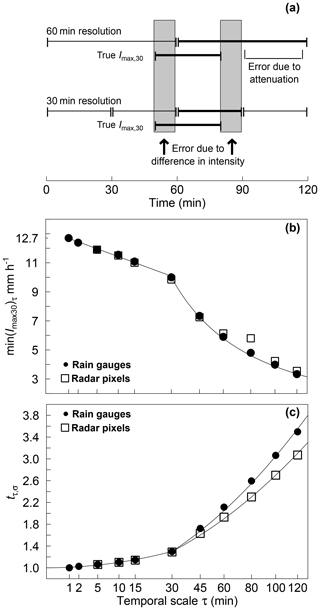
Figure 2 (a) Time periods influencing the underestimation of I_max30 when temporal resolution is 30 min (or higher) or when temporal resolution is 60 min (or any resolution >30 min). (b) Minimum threshold for I_max30 (min(I_max30)_τ) derived from rain gauge (solid circles) and radar data (open squares) required to obtain the same number of erosive events as with a temporal resolution of 1 min; lines show Eq. (6a) and (6b) (RMSE is 0.10 and 0.39). (c) Scaling factor t_τ,σ to scale R_e or R for temporal resolution τ when spatial resolution σ is either rain gauge scale (solid circles) or 1×1 km² (open squares), respectively; lines show Eq. (7a), (7b) and (7c) (for all RMSE ≤0.04). The x axes in (b) and (c) are square-root-scaled.

2.4 Statistics

We mainly used arithmetic means even though most distributions were strongly skewed. Arithmetic means are less robust than other measures like geometric means, but our huge sample size compensated for this. Using arithmetic means instead of robust measures is a requirement of the USLE, which sums up erosivities over 1 year or longer. The arithmetic mean provides an unbiased estimator of event erosivity that allows sums to be calculated over longer periods of time (e.g. 1 year). Otherwise different scaling factors would become necessary for individual events and for temporal sums depending on their temporal length.

Statistical spread is quantified by the standard deviation (SD) or the root mean squared error (RMSE), and the uncertainty of the scaling factors is quantified by their 95 % interval of confidence (CI). Validation included the calculation of the Nash–Sutcliffe efficiency (Nash and Sutcliffe, 1970).

3 Results

3.1 Temporal-scale effect

With 17 rain gauges operating at 1 min resolution, 4599 erosive events were determined in 16 years. R_e ranged from 0.1 to 178.4 N h⁻¹ with an average of 5.8 N h⁻¹. The number of events with P≥12.7 mm or $I_{max\mathrm{30}}>\mathrm{12.7}$ mm h⁻¹ decreased pronouncedly when resolution decreased from 1 min down to 120 min (by 1, 14 and 16 % at a resolution of 2, 60 and 120 min, respectively). To avoid this loss of events, min(I_max30)_τ was decreased continuously with decreasing temporal resolution (Fig. 2b). The decrease was less steep below a temporal resolution of 30 min than above:

$$\begin{array}{}\text{(6a)}& {\displaystyle }& {\displaystyle }min\left(I_{max\mathrm{30}}\right)=-\mathrm{0.59}{\mathit{\tau }}^{\mathrm{0.5}}+\mathrm{13.23}& {\displaystyle }\text{for}\mathit{\tau }\le \mathrm{30}\min ,\text{(6b)}& {\displaystyle }& {\displaystyle }min\left(I_{max\mathrm{30}}\right)=\mathrm{147}{\mathit{\tau }}^{-\mathrm{0.79}}& {\displaystyle }\text{for}\mathit{\tau }>\mathrm{30}\min .\end{array}$$

This change at a resolution of 30 min is because 30 min is the time interval in which the maximum is searched for. For resolutions higher than 30 min, there is a discrepancy between the true period of I_max30 and the period of I_max30 that is coerced by the temporal resolution (see grey bars in Fig. 2a). The error caused by this discrepancy only results from the difference in intensity immediately before and after true I_max30. When the temporal resolution becomes less than 30 min, attenuation caused by the period exceeding the 30 min interval additionally decreases in intensity (see 60 min resolution in Fig. 2a). This attenuation increases the lower the temporal resolution becomes, and it caused Eq. (6b) to be much steeper than Eq. (6a).

The decrease in min(I_max30)_τ was identical for both the rain gauge scale and the 1 km² scale (slope between both scales: 1.0067, r²=0.9858, n=9). For both scales combined, RMSE was only 0.10 and 0.39 for Eq. (6a) and (6b), respectively. Thus, both equations were valid for point scale and for a grid width of 1 km.

Rain erosivity also decreased with decreasing temporal resolution; in turn, the scaling factor t_τ,σ increased (Fig. 2c; Eq. 7a–7c). For intervals τ≤30 min, the increase was identical for rain gauge scale and for radar pixels of 1 km pixel width. The increase of t_τ,σ was much steeper when τ became longer than 30 min. This increase then depended on the spatial scale and was larger for rain gauge scale than for radar pixels of 1 km pixel width (Fig. 2c). The behaviour of t_τ,σ was caused by underestimating E_kin and underestimating I_max30. The underestimation of I_max30 was the stronger effect (data not shown). It prevailed for time intervals greater than 30 min and caused the break at a temporal resolution of 30 min, as already shown for min(I_max30)_τ. The identical behaviour of intensity with decreasing temporal resolution at rain gauge scale and at 1 km² radar pixel scale that was already evident for min(I_max30)_τ thus also led to identical t_τ,σ for both spatial scales as long as τ was less than 30 min. For τ>30 min the attenuation of intensity peaks came into play. This attenuation was less for the 1 km radar data than for the rain gauge data because the time a moving intensity peak remains in a 1 km² grid pixel is longer than the time it requires to pass a rain gauge. In consequence, three equations for t_τ,σ (Eq. 7a–7c) were necessary to adjust R_e, R_y or R to 1 min resolution at the respective spatial scale.

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\text{For}\mathit{\tau }\le \mathrm{30}\min \text{and point or}\mathrm{1}\times \mathrm{1}{\mathrm{km}}^{\mathrm{2}}\text{grid scale:}\\ \text{(7a)}& {\displaystyle }& {\displaystyle }{t}_{\mathit{\tau },\mathit{\sigma }}={\displaystyle \frac{\mathit{\tau }}{\mathrm{100}}}+\mathrm{1}{\displaystyle }& {\displaystyle }\text{For}\mathit{\tau }\ge \mathrm{30}\min \text{and point scale or}:\\ \text{(7b)}& {\displaystyle }& {\displaystyle }{t}_{\mathit{\tau },\mathit{\sigma }=\mathrm{0}}={\displaystyle \frac{\mathit{\tau }}{\mathrm{40}}}+\mathrm{0.55}{\displaystyle }& {\displaystyle }\text{For}\mathit{\tau }\ge \mathrm{30}\min \text{and}\mathrm{1}\times \mathrm{1}{\mathrm{km}}^{\mathrm{2}}\text{grid scale:}\\ \text{(7c)}& {\displaystyle }& {\displaystyle }{t}_{\mathit{\tau },\mathit{\sigma }=\mathrm{1}}={\displaystyle \frac{\mathit{\tau }}{\mathrm{50}}}+\mathrm{0.70}\end{array}$$

The RMSE of all three equations was less than 0.04. The validity of combining the effects of min($I_{max\mathrm{30}}{)}_{\mathit{\tau }=\mathrm{60}}$ and $t_{\mathit{\tau }=\mathrm{60},\mathit{\sigma }=\mathrm{1}}$ was supported by the close correlation of temporally scaled R_y derived from 5 and 60 min RADOLAN data, for which the Nash–Sutcliffe efficiency was 0.9483 (n=1568) while RMSE was 8.8 N h⁻¹ yr⁻¹.

Variation among monthly $t_{\mathit{\tau },\mathit{\sigma }=\mathrm{0}}$ was small, especially for τ≤60 min. The coefficient of variation among monthly $t_{\mathit{\tau },\mathit{\sigma }=\mathrm{0}}$ was ≤6 % for τ≤60 min and 11 % to 14 % for τ>60 min. It was not clear if there was seasonality in this variation because for some temporal resolutions $t_{\mathit{\tau },\mathit{\sigma }=\mathrm{0}}$ was higher for summer than for winter months, while for other resolutions the opposite was the case.

There was also a negligible regional variation for τ>30 min, while no difference could be found for τ≤30 min. For intervals longer than 30 min the scaling factor $t_{\mathit{\tau },\mathit{\sigma }=\mathrm{0}}$ increased slightly more in northern Germany (+4 %) than in southern Germany (−2 %), compared to the whole of Germany. This small difference will only become relevant if data of very low temporal resolution are used.

3.2 Spatial-scale effects

Erosivities from all data of rain gauge–radar pixel pairs were calculated by application of appropriate min(I_max30)_τ and temporal scaling factors to enable comparison. Annual erosivity R_y for the 0.5×0.5 km² pseudo-radar data set was 7.3 % lower than the average R_y of the rain gauges. This resulted in a factor s_σ=0.5 of 1.08 (CI: 1.00–1.16). This factor increased to $s_{\mathit{\sigma }=\mathrm{1}}=\mathrm{1.15}$ (CI: 1.04–1.26) when R_y was calculated from 1×1 km² pseudo-radar data (Fig. 3).

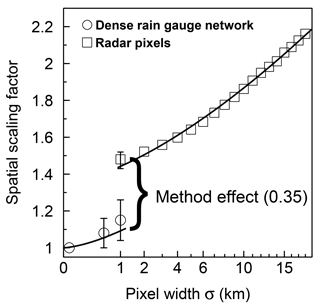
Figure 3 Spatial scaling factors for long-term average annual R. Open circles result from rain gauges aggregated to pseudo-radar pixels. Open squares result from radar and aggregation of radar data. Error bars represent the 95 % confidence interval. Lines denote a multiple regression (see text). The x axis is square-root-scaled to improve visibility at low pixel width.

For the rain gauges of the 115 rain gauge–radar pixel pairs, long-term average annual R varied between 42 and 223 N h⁻¹ yr⁻¹ over 16 years and was on average 90.2 N h⁻¹ yr⁻¹. For the radar pixels, R varied between 26 and 146 N h⁻¹ yr⁻¹ but was on average only 62 N h⁻¹ yr⁻¹ (Fig. 4). In this case the deviation was equal to a factor of 1.48 (CI: 1.43–1.52), which was considerably larger than s_σ=1 obtained from pseudo-radar data, for which no difference in measurement method occurred between point scale and pixel scale. This difference was hence assigned to a method effect (Fig. 3).

Table 2 Percentage of cases that were erosive at point (115 rain gauges) or pixel scale (115 radar pixels) relative to a total of 35 124 point–pixel pairs of rain events that were erosive on at least one of both scales.

The monthly comparison of the 115 rain gauge–radar pixel pairs over 16 years did not yield significant differences between months due to the large CI of the combined scale and method effects (CI between ±4 % and ±9 % for the individual months), but on average this combined effect was lower during the hydrological winter months (1.16; CI: 1.12–1.21) than during the hydrological summer months (1.42; CI: 1.30–1.53). This difference, despite being significant (p<0.001), was unimportant because of the small contribution of winter months to annual erosivity.

For the large and contiguous radar data set of 800×600 pixels, 1.9×10⁶ events were recorded at 1×1 km² scale. For these events, R_e was on average 5.1 N h⁻¹ and ranged from 0.5 to 1270 N h⁻¹. Aggregating these pixels to larger square pixels decreased R_e. At 18×18 km², R_e was on average 4.4 N h⁻¹ and ranged from 0.2 to 221.6 N h⁻¹. In consequence, the spatial scaling factor s_σ increased further (Fig. 3). The increase in scaling factors over the entire range from point scale to 18 km grid width could be described by a multiple regression (r²=0.9995, n=21) accounting for pixel width σ (in km) and the method effect m depending on the method μ (which is 0 for rain gauges and 1 for radar data):

$$\begin{array}{}\text{(8)}& {\displaystyle }m+s_{\mathit{\sigma }}=\mathrm{1}+\mathrm{0.35}\mathit{\mu }+\mathrm{0.092}{\mathit{\sigma }}^{\mathrm{3}/\mathrm{4}}.\end{array}$$

The CI was ±0.004 for the slope of σ and ±0.02 for the method effect.

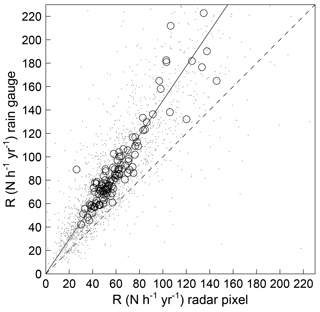
Figure 4 Annual erosivity R_y (grey points) and multi-annual mean erosivity R (black circles) derived from radar pixel and rain gauge data for 115 point–pixel pairs and 16 years. The difference in slope between the solid line and unity (dashed line) is due to the spatial scale and method effects.

On average for the pseudo-radar pixel, rain was erosive for only 10 out of 12 rain gauges. Hence only 83 % of the 1 km² pixel was covered by an erosive event. The fraction covered by the erosive event decreased further the larger the pixel size became (fraction =83 % $-\mathrm{10.3}\times \ln$(pixel size (km²)), r²=0.9974, n=18). On average only about 50 % of a 5×5 km² pixel and 25 % of a 17×17 km² pixel received an erosive rain event. This makes it increasingly difficult to detect erosive rains the larger pixel size becomes.This caused the strong increase in the spatial scaling factor and indicated a strong positional effect.

3.3 Positional effects

The positional effect as defined here describes the variability of R_e within 1×1 km². Using the pairs with the true radar data, 29 610 erosive rain events were recorded during 16 years at the 115 rain gauges. On average, R_e was 5.6 N h⁻¹ and ranged from 0.1 to 547.2 N h⁻¹. For the corresponding 115 radar pixels, 25 884 erosive events were recorded during the 16 years. Mean R_e was 4.4 N h⁻¹ and ranged from 0.2 to 318.9 N h⁻¹.

Combining all events of the 115 rain gauge–radar pixel pairs during 16 years that were at least erosive at rain gauge scale or at radar pixel scale resulted in 35 124 events. Only 57 % of them were erosive at both scales, while the criteria for an erosive event were met exclusively at pixel scale for 16 % of all events and exclusively at rain gauge scale for 27 % of all events (Table 2). The gradients of erosivity within 1 km² were huge. The largest event that was recorded at a rain gauge while the radar pixel indicated no erosive event was 156 N h⁻¹. The largest event for the opposite case, i.e. that radar recorded an erosive event while the rain gauge recorded no erosive event, was similarly high (180 N h⁻¹). The mean R_e of erosive events which were recorded for the radar pixel while R_e at the corresponding rain gauge was zero was 2.9 N h⁻¹ (SD: ±4.9 N h⁻¹). The mean R_e of events which were erosive at a rain gauge but not for the corresponding radar pixel was also 2.9 N h⁻¹ (SD: ±5.6 N h⁻¹).

The percentage of unpaired events was not significantly related to the geographical location, neither longitude ($r=-\mathrm{0.02}$, p=0.23) nor latitude ($r=-\mathrm{0.01}$, p=0.83). It was also independent of the distance to the adjacent radar station ($r=-\mathrm{0.02}$, p=0.79), which might be used as a proxy for increasing noise in the radar data. The percentage was higher in winter (October–March) with 34 % (SD: ±2.4 %) than in summer (April–September) with 25 % (SD: ±2.4 %). The probability of remaining just below the threshold of an erosive event on one of both scales was higher in winter than in summer as in general winter events are less intensive than summer events. Mean R_e in winter was only 35 % of mean R_e in summer.

Rain gauge R_e was larger than radar R_e for 74 % of those point–pixel pairs (points above the line of unity in Fig. 5) which were erosive on both scales (19 944 events). Mean $p_{R_{\mathrm{e}}}$ was 1.54 (CI: ±0.01) for these events. This value quantifies the mean deviation of all locations within a 1 km² pixel that experience a higher erosivity than the mean. For individual locations, the deviation can be much larger, which was already evident from the magnitude of the largest events that were recorded only on one of both scales. For individual locations with an erosive event on both scales, $p_{R_{\mathrm{e}}}$ could be considerably higher than 10 (see “outliers” in Fig. 5). Rain gauge R_e was lower than radar R_e for only 26 % of all events (points below the line of unity in Fig. 5), and $p_{R_{\mathrm{e}}}$ was 0.72 (CI: ±0.01). Again, the deviation of individual locations within 1 km² could be much larger.

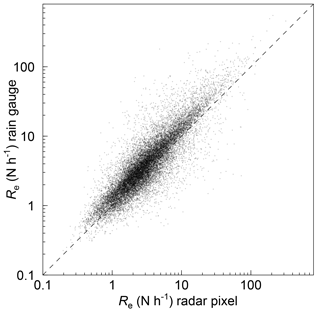
Figure 5 Comparison of event erosivity R_e calculated from radar data and R_e from rain gauge data for 115 radar pixels that enclose a rain gauge. Only events that were erosive at both scales (19 944 events) during the 16-year period are shown. The dashed line represents unity. Axes are log-scaled. Note that no spatial scaling factor or method factor was applied because these factors also included the effect of incomplete coverage of the pixel by an erosive rain cell.

For the dense rain gauge field used to create pseudo-radar data, 579 point–pixel pairs of events were at least erosive at rain gauge scale or at pseudo-radar pixel scale. For these 579 events, R_e derived from rain gauge data ranged from 0 to 45.5 N h⁻¹ (mean: 3.9 N h⁻¹), and R_e derived from pseudo-radar data ranged from 0 to 28.1 N h⁻¹ (mean: 3.4 N h⁻¹) (Fig. 6). For 9 % of these events, the event was not erosive with pseudo-radar but at the rain gauge, and for 6 % the opposite was true (Table 3).

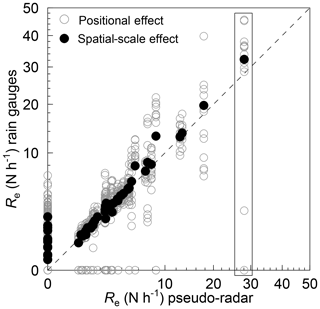
Figure 6 Event erosivity R_e at 12 rain gauges located within a 1 km² pixel vs. R_e based on pseudo-radar data calculated from the hyetographs of the 12 rain gauges (open grey circles). Filled black circles show the average R_e of all 12 rain gauges vs. the R_e from pseudo-radar rainfall. Note that the average R_e can be considerably larger than zero while the averaged rainfall of the pseudo-radar remains below the thresholds of erosivity (black circles along the y axis). Rectangular frame shows variation of R_e for a single day. Axes are square-root-scaled to improve resolution at low R_e.

Table 3 Percentage of cases that were erosive at point (rain gauge) or pixel scale, using the pseudo-radar data; in total 579 point–pixel pairs of rain events were erosive on at least one of both scales.

For 67 % of those events which were erosive at both scales, rain gauge R_e was larger than pseudo-radar R_e and $p_{R_{\mathrm{e}}}$ was 1.28 (CI: 1.25–1.30). For 33 % of these events, rain gauge R_e was lower than pseudo-radar R_e and $p_{R_{\mathrm{e}}}$ was 0.81 (CI: 0.77–0.85). Also in this case, where measurement errors could be excluded because rain gauge R_e and pseudo-radar R_e were calculated from the same data, the variation within 1 km² was again huge. For the single days with erosive events, R_e varied greatly between rain gauges. For an example see height of the rectangle in Fig. 6. Although this was the largest event in this data set, one rain gauge remained below the threshold and hence recorded no erosive event. This large variation was also reflected by the large coefficient of variation between rain gauge R_e for the same day (mean: 68 %).

4 Discussion

Our analysis showed pronounced effects of temporal scale, spatial scale, position and measuring method. These effects were all caused by the sensitivity of erosivity calculation to intensity peaks and because thresholds were used for the definition of erosivity. These strong effects call for using temporally and spatially highly resolved rain gauge measurements, like those used in the development of the USLE and most subsequent studies. Our study, however, also showed strong gradients in erosivity that were also caused by the sensitivity to intensity peaks and by the thresholds which earlier studies also showed (Fiener and Auerswald, 2009; Fischer et al., 2016; Krajewski et al., 2003; Pedersen et al., 2010; Peleg et al., 2016). Erosivity can thus reliably be recorded at the position of a rain gauge, but this information cannot even be extrapolated over a distance of only 500 m (half of our radar pixel widths). This was illustrated by the fact that, within this distance, R_e could be zero or >150 N h⁻¹, which is more than twice the annual erosivity in Germany (Auerswald, 2006; Sauerborn, 1994). It is also illustrated by the fact that the largest R_e that was recorded within only 2 months was 1270 N h⁻¹ when contiguous measurements were used, while the largest R_e that occurred during 16 years when the same region was covered by 115 rain gauges was only 547 N h⁻¹. Hence rain gauge measurements fail to record many erosive events that occur in their close vicinity (even <500 m). Erosivity determined by a rain gauge cannot be extrapolated to a small watershed, to farms or even to fields. Discrepancies between model predictions and measurements of erosion that can be found in many studies (Govers, 1991; Liu et al., 1997; Risse et al., 1993; Rüttimann et al., 1995; Zhang et al., 1996) probably originate in part from this strong positional effect. Such strong discrepancies during individual events even exist between replicates of bare plots (Nearing et al., 1999) or between replicated vegetated plots and cannot be explained by plot characteristics. They do not appear in subsequent runoff and soil loss observations (Wendt et al., 1986). Erosion prediction and model development are thus strongly limited by the unexplained variability caused by short-range erosivity gradients. Hence, there is no alternative to using contiguous rain measurements. Radar technology provides, for the first time, measurements that fulfil this need.

Contiguous measurements, on the other hand, suffer from the fact that they cannot be carried out at the same temporal and spatial scale as rain gauge measurements, and the method of measurement differs. Here we provide scaling factors that help to partly overcome this problem and that allow radar measurements to be used for erosivity calculations. These factors, however, do not solve the problem that contiguous measurements integrate over a certain space and time and thus that the information about the variation within these domains is lost. In particular, the positional effect can only be used to quantify uncertainty within a radar pixel, but it cannot be used to predict erosivity at specific locations within a pixel. This large uncertainty is probably also one of the main reasons for the discrepancy between observed soil loss and predicted soil loss based on radar rain data for individual fields, whereas this discrepancy disappeared as soon as many fields were grouped, irrespective of how this grouping was done (Fischer et al., 2018a; Auerswald et al., 2018). With future improvements in technology it may become possible to further improve temporal and spatial resolution of contiguous rain data and, thus, to reduce the uncertainty of event erosivities.

Temporal scaling factors had already been developed (Auerswald et al., 2015; Agnese et al., 2006; Istok et al., 1986; Williams and Sheridan, 1991; Weiss, 1964; Yin et al., 2007) because they are also required for rain gauge measurements of low temporal resolution (in data storage). Our temporal scaling factors were of a similar order of magnitude to those in other studies. However, our data showed that using a scaling factor is not sufficient because the intensity threshold also has to be adjusted in order to identify the correct number of erosive events. The existence of an erosive event and long-term sums of erosivity will otherwise be incorrect, even with a temporal scaling factor. To our knowledge our study provides, for the first time, a function that enables the intensity threshold to be adjusted according to the temporal resolution of the rain data. Adjustment of the total rain depth threshold is not necessary because total rain depth should be independent of the temporal resolution, as long as it is still short enough to identify the rain breaks that separate individual events.

Despite providing intensity thresholds and scaling factors for R_e, R_y and R for different temporal resolutions, we advocate using a high resolution in order to not lose information. All scaling factors can only represent average behaviour and cannot reflect the characteristic of an individual event. A high resolution is easier to achieve in the time domain than in the spatial domain. In particular, it is advantageous to have a temporal resolution that is higher than 30 min because scaling factors increased strongly for less resolved data. For shorter time increments, only compensation for the error that resulted from an imperfect identification of the period of I_max30 was necessary. Longer time increments than 30 min additionally attenuated I_max30 and thus blurred this information.

The spatial scale was more difficult to consider than the temporal scale due to the large positional effect. In particular, large parts of a pixel remained below the thresholds of an erosive event even when measurement errors could be excluded, like in the case of the pseudo-radar pixel that used rain gauge measurements. On average, 17 % of the rain gauges within a 1 km² pixel remained below the erosivity threshold while the other rain gauges recorded an erosive event. This percentage increased strongly with increasing pixel size. In consequence, the spatial-scale effect cannot be corrected for individual events but only for the averages of many events.

The spatial scaling factor is conceptually the inverse of the so-called areal reduction factors, which are used to reduce rain intensity from rain gauge measurements when scaled to catchment areas depending on the duration and return period of the rain event (Allen and DeGaetano, 2005; De Michele et al., 2001; Stewart, 1989). This conceptual difference is due to the difference in the intended purpose of contiguous rain data. While in catchment hydrology the average and the relative distribution of rain depth within a watershed is of interest (Asquith and Famiglietti, 2000), for erosion analysis rain intensities are important at point and field scale, where erosion occurs.

The method effect combines all differences in measurement and measuring errors (e.g. the wind effect in the case of rain gauges). It is thus highly dependent on the specific configuration of rain gauge measurements and radar measurements, including all subsequent data manipulation steps. These configurations are usually fairly standardized within a country (e.g. rain gauge height and diameter are usually defined) but differ from country to country. Our method effect may thus only be valid for Germany, whereas application to other countries, even if they use similar rain gauge and radar protocols (e.g. Goudenhoofdt and Delobbe, 2016; Koistinen and Michelson, 2002), should be done with care. The same is true for using satellite data or data of commercial microwave links, which recently have been identified as additional source for retrieving precipitation (Chwala et al., 2012; Overeem et al., 2013) and which will require the method effect to be adapted for this particular approach. The approach is based on analysing the signal attenuation that depends on rain intensity. These data are especially valuable in regions with sparse coverage by conventional measurement devices, e.g. in parts of the African continent, but may also improve high-resolution precipitation estimates and forecasts in hydrometeorological applications (Chwala et al., 2016).

As an example, for the new German RADOLAN product that recently became publicly available (spatial resolution: 1 km²; temporal resolution: 60 min) the I_max30 threshold has to be lowered to 5.79 mm h⁻¹, while the total precipitation threshold remains at 12.7 mm. The temporal scaling factor becomes t=1.9, and the spatial scaling factor becomes s=1.13, to which the method effect of m=0.35 has to be added. In total, the correction factor is $\mathrm{2.81}\left(\right(\mathrm{1.13}+\mathrm{0.35})\times \mathrm{1.9})$. Hence the change of the I_max30 threshold and the combined scaling factor are large, and ignoring both would considerably underestimate erosivity. The large change of the I_max30 threshold and the large temporal scaling factor also show that much information is lost when using data of 60 min resolution.

This loss of information can be either an advantage or a disadvantage. It would be a disadvantage in hindcasting, wherein usually the true pattern of erosivity is wanted. In this case a better-resolved product like 5 min data should be used. The I_max30 threshold would then be 11.9 mm h⁻¹, and the temporal scaling factor would only be t=1.05, indicating a minor loss of information. The spatial scaling factor is already rather low, and the method effect cannot be avoided.

On the other hand the loss of information would be an advantage in forecasting, which aims at the likely regional pattern of erosivity. The loss of information removes the influence of randomly occurring local events of extraordinarily high magnitude that add noise to the regional pattern of erosivity. The finding that the largest R_e within only 2 months was 1270 N h⁻¹ while the expected long-term average R was only about 70 N h⁻¹ yr⁻¹ (Sauerborn, 1994) shows that this single event would add 64 N h⁻¹ yr⁻¹ to a 20-year record of radar data. Even in a 100-year record this single event would still be detectable. Using data of 60 min resolution thus reduces the need for smoothing the map statistically to remove the influence of such local events.

5 Conclusions

Large gradients in event erosivity occur that can only be captured by contiguous rain data. Radar technology enables such contiguous rain data to be recorded but not at the same temporal and spatial scale as measurements from rain gauges. Using data of lower temporal and spatial resolution than rain gauges leads to a pronounced underestimation of erosivity. Here we provide a set of correction functions that enable this underestimation to be corrected. In particular, the intensity threshold has to be modified, and a temporal scaling factor, a spatial scaling factor and a factor accounting for measurement peculiarities have to be considered. In combination with contiguous radar rain data this could be a major step forward in erosion modelling.