Estimation of effective porosity in large-scale groundwater models by combining particle tracking, auto-calibration and ¹⁴C dating

Effective porosity plays an important role in contaminant management. However, the effective porosity is often assumed to be constant in space and hence heterogeneity is either neglected or simplified in transport model calibration. Based on a calibrated highly parametrized flow model, a three-dimensional advective transport model (MODPATH) of a 1300 km² coastal area of southern Denmark and northern Germany is presented. A detailed voxel model represents the highly heterogeneous geological composition of the area. Inverse modelling of advective transport is used to estimate the effective porosity of 7 spatially distributed units based on apparent groundwater ages inferred from 11 ¹⁴C measurements in Pleistocene and Miocene aquifers, corrected for the effects of diffusion and geochemical reactions. By calibration of the seven effective porosity units, the match between the observed and simulated ages is improved significantly, resulting in a reduction of ME of 99 % and RMS of 82 % compared to a uniform porosity approach. Groundwater ages range from a few hundred years in the Pleistocene to several thousand years in Miocene aquifers. The advective age distributions derived from particle tracking at each sampling well show unimodal (for younger ages) to multimodal (for older ages) shapes and thus reflect the heterogeneity that particles encounter along their travel path. The estimated effective porosity field, with values ranging between 4.3 % in clay and 45 % in sand formations, is used in a direct simulation of distributed mean groundwater ages. Although the absolute ages are affected by various uncertainties, a unique insight into the complex three-dimensional age distribution pattern and potential advance of young contaminated groundwater in the investigated regional aquifer system is provided, highlighting the importance of estimating effective porosity in groundwater transport modelling and the implications for groundwater quantity and quality assessment and management.

1 Introduction

The age of groundwater, i.e. the time elapsed since the water molecule entered the groundwater (Cook and Herczeg, 2000; Kazemi et al., 2006), is useful (i) to infer recharge rates (e.g. Sanford et al., 2004; Wood et al., 2017) and hence to sustainably exploit groundwater resources; (ii) to evaluate contaminant migration, fate and history (Bohlke and Denver, 1995; Hansen et al., 2012) and predict spread of pollutants and timescales for intrinsic remediation (Kazemi et al., 2006); (iii) to analyse aquifer vulnerability or protection to surface-derived contaminants (e.g. Manning et al., 2005; Bethke and Johnson, 2008; Molson and Frind, 2012; Sonnenborg et al., 2016) and indicate the advance of modern contaminated groundwater (Hinsby et al., 2001b; Gleeson et al., 2015; Jasechko et al., 2017) and groundwater quality in general (Hinsby et al., 2007); and (iv) to contribute to the understanding of the flow system, e.g. in complex geological settings (Troldborg et al., 2008; Eberts et al., 2012).

The groundwater science community (de Dreuzy and Ginn, 2016) has a continued interest in the topic of residence time distributions (RTDs) in the subsurface. Turnadge and Smerdon (2014) reviewed different methods for modelling environmental tracers in groundwater, including lumped parameter models (e.g. Maloszewski and Zuber, 1996), mixing-cell models (e.g. Campana and Simpson, 1984; Partington et al., 2011) and direct age models (e.g. Cornaton, 2012; Goode, 1996; Woolfenden and Ginn, 2009). Here, we focus on three different approaches with specific benefits and disadvantages that are commonly applied to simulate groundwater age in 3-D distributed groundwater flow and transport models (Castro and Goblet, 2005; Sanford et al., 2017). Particle-based advective groundwater age calculation utilizing travel time analysis is computationally easy, but neglects diffusion and dispersion. The full advection–dispersion transport simulation of a solute or an environmental tracer is computationally expensive and limited to the specific tracer characteristics (McCallum et al., 2015; Salmon et al., 2015), but accounts for diffusion, dispersion and mixing. The tracer-independent direct simulation of groundwater mean age (Goode, 1996; Engesgaard and Molson, 1998; Bethke and Johnson, 2002) includes advection, diffusion and dispersion processes and yields a spatial distribution of mean ages. A comparison of ages simulated using any of these methods with ages determined from tracer observations, referred to as apparent ages, is desirable as it can improve the uniqueness in flow model calibration and validation (Castro and Goblet, 2003; Ginn et al., 2009) and it potentially informs about transport parameters such as effective porosity, diffusion and dispersion that are otherwise difficult to estimate. However, the approach is far from straightforward as environmental tracers undergo non-linear changes in their chemical species (McCallum et al., 2015) and groundwater models only represent a simplification and compromise on structural and/or parameter heterogeneity. In a 2-D synthetic model, McCallum et al. (2014) investigated the bias of apparent ages in heterogeneous systems systematically. McCallum et al. (2015) applied correction terms, e.g. diffusion correction for radioactive tracers, on apparent ages to improve the comparability to mean advective ages. They concluded that with increasing heterogeneity the width of the residence time distribution increases and that apparent ages would only represent mean ages if this distribution is narrow and has a small variance. It is important here to distinguish between mean and radiometric ages, as defined by Varni and Carrera (1998) for example. The only way they can be directly compared in reality is if no mixing is taking place, i.e. if the flow field can be regarded as pure piston flow, which will give the kinematic age.

Flow and transport parameters such as hydraulic conductivity, conductance of streambeds and drains, recharge, and dispersivities have gained more and more focus in calibration of groundwater models, recently also on large scales, where of head, flow and tracer observations are widely used as targets (McMahon et al., 2010). However, effective porosity has not received nearly as much attention, and its spatial variability in particular is often neglected, except for Starn et al. (2014). The lack of focus on calibrating distributed effective porosity on a regional scale might be related to the common assumption that recharge in humid climates can be precisely estimated and porosity of porous media is relatively well known from the literature (Sanford, 2011). However, for steady-state flow (Ginn et al., 2009) in a layered aquifer system, Bethke and Johnson (2002) concluded that the mean groundwater age exchange between flow and stagnant zones is only a function of the volume of stored water (Harvey and Gorelick, 1995; Varni and Carrera, 1998). Thus, the groundwater age exchange is directly related to the porosity. Yet, the calibration of a spatially distributed porosity field and its application to simulate groundwater ages and infer capture zones has not gained much attention.

The uniqueness of the presented study lies in the calibration of a three-dimensional, spatially distributed, effective porosity field in a regional-scale complex multi-layered heterogeneous coastal aquifer system. The aims are as follows: (i) to use apparent ages inferred from dissolution- and diffusion-corrected ¹⁴C measurements from different aquifer units as targets in auto-calibration with PEST of seven unit-specific effective porosities in an advective (particle tracking) transport model – it would have been optimal to use RTD analysis (de Dreuzy and Ginn, 2016) to compare modelled and inferred groundwater ages in this study, but due to the rather complex nature of our hydrogeological flow model, the inherent uncertainties associated with inferring an apparent age from ¹⁴C analysis and the long computer runtimes, we have chosen to use the particle-based kinematic approach of simulating a mixed age at the well screen (or numerical cell with a screen); (ii) to assess the advective age distributions at the sampling locations to obtain information on the age spreading; (iii) to apply the estimated seven porosities in a direct age simulation (Goode, 1996) to gain insight in the three-dimensional age pattern of the investigation area; and (iv) to assess the effect of using the heterogeneous porosity model compared to a homogeneous porosity model for differences in capture zones via particle back-tracking, which is a water management approach to define wellhead protection areas or optimize pump-and-treat locations for remediation of pollution (Anderson et al., 2015).

2 Study area

The 1300 km² investigation area is located adjacent to the Wadden Sea in the border region between southern Denmark and northern Germany (Fig. 1). During the Last Glacial Maximum (LGM; 22 to 19 ka ago, Stroeven et al., 2016), the area was the direct foreland of the Scandinavian ice sheet. The low-lying marsh areas (with elevations below mean sea level) in the west were reclaimed from the Wadden Sea over the last few centuries and protected from flooding by a dike for the last ≈200 a. A dense network of drainage channels keeps the groundwater level constantly below the ground surface and thus mostly below sea level. The water divide near the Jutland ridge with elevations of up to 85 m a.s.l. defines the eastern boundary of the study area.

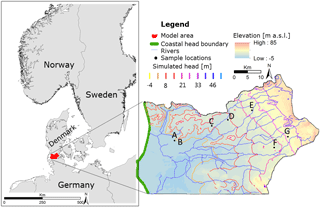
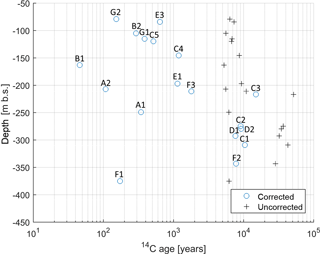
Figure 1 Investigation area at the border between Denmark and Germany. Simulated hydraulic heads are from the shallow aquifer (Meyer et al., 2018a). Topography, ¹⁴C sample locations (A–G), river network and coastal head boundary are indicated.

The aquifer systems are geologically complex and highly heterogeneous, spanning Miocene through Holocene deposits. The bottom of the aquifer system is defined by low-permeability Palaeogene marine clay. The overlying Miocene deposits consist of alternating marine clay and deltaic silt and sand (Rasmussen et al., 2010). The Maade formation, an upper Miocene marine clay unit, with a relatively large thickness in the west while thinning out to the east, is located below the Pleistocene and Holocene deposits. Buried valleys filled with glacial deposits, mainly from the Saalian glaciation, cut through the Miocene and reach depths up to 450 m below the surface. They are important hydrogeological features as they may constitute preferential flow paths and locally connect the Pleistocene and Miocene aquifers.

In our previous studies (Jørgensen et al., 2015; Høyer et al., 2017; Meyer et al., 2018a), the available geological and geophysical information including borehole lithology, airborne electromagnetic (AEM) and seismic data were assembled into a heterogeneous geological voxel model comprising 46 geological units with raster sizes of 100 m × 100 m × 5 m. Manual and automatic modelling strategies, such as clay fraction (CF), multi-point simulation (MPS) and a cognitive layer approach, were complementarily applied. Meyer et al. (2018a) investigated the regional flow system and identified the most dominant mechanisms governing the flow system, comprising geological features and land management that are visualized in a conceptual model in Fig. 2. Extensive clay layers separate the Miocene and Pleistocene aquifers; buried valleys locally cut through the Maade formation and connect Miocene and Pleistocene aquifers, allowing groundwater exchange and mixing. The large drainage network, established in the reclaimed terrain and keeping the groundwater table constantly below the sea level, acts as a large sink for the entire area. In the deeper aquifers, significant inflow from the ocean occurs at the coast near the marsh area as a result of a landward head gradient induced by the drainage.

3 Methods

The age simulation and calibration of effective porosities builds upon the calibrated regional-scale groundwater flow model (MODFLOW) of a highly heterogeneous coastal aquifer system by Meyer et al. (2018a). First, an advective transport simulation using MODPATH (Pollock, 2012) was used for the calibration of effective porosities of seven different geological units. ¹⁴C observations were corrected for carbon dissolution and diffusion and subsequently used as calibration targets during inverse modelling with PEST. It would have been optimal to use RTD analysis (de Dreuzy and Ginn, 2016) to compare modelled and inferred groundwater ages in this study. But, due to the rather complex nature of our hydrogeological flow model, the inherent uncertainties associated with inferring an apparent age from ¹⁴C analysis, and the long computer runtimes, we have chosen to use the particle-based kinematic approach of simulating a mixed age at the well screen (or numerical cell with a screen). Secondly, the analysis of advective age distributions at ¹⁴C sampling locations provided an insight in the ranges of travel times and distances and hereby the complexity of groundwater age mixing. Thirdly, the estimated effective porosities were used in a direct age simulation (Goode, 1996) in order to investigate the spatial groundwater age distribution in the regional aquifer system. Finally, the impact of using a seven-porosity model compared to a constant porosity model on capture zone delineation at two well locations was assessed.

3.1 ¹⁴C measurements

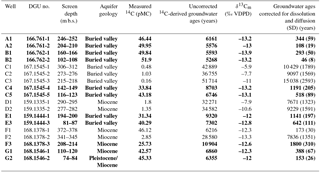
During a field campaign in February 2015, 18 groundwater samples were collected from wells at seven sites with screens at different depths and in different aquifers (Fig. 1, Table 1). The wells were pumped clean with 3 times their volume to prevent the influence of mixing with stagnant water. In situ parameters (pH, EC, O₂) were measured and, after they stabilized, samples for radiocarbon analyses were collected in 1 L opaque glass bottles. The 18 groundwater samples were analysed for δ¹³C_‰VPBD with an isotope ratio mass spectrometer (IRMS) and for ¹⁴C with an accelerator mass spectrometer (AMS) at the AGH University of Science and Technology, Kraków, Poland, and in the Poznań Radiocarbon Laboratory, Poznań, Poland, respectively, in September 2015.

3.1.1 ¹⁴C correction for dissolution and diffusion

The ¹⁴C activity (A_m) was measured in the dissolved inorganic carbon (DIC) content of the groundwater. Uncertainties arise from geochemical and hydrodynamic processes that change the ¹⁴C content in the aquifer (e.g. Bethke and Johnson, 2008; Sudicky and Frind, 1981). The dissolution of “dead” fossil (¹⁴C-free) carbon dilutes the ¹⁴C content in groundwater and results in lower ¹⁴C concentrations (Appelo and Postma, 2005). Diffusion into aquitards also reduces the ¹⁴C concentration in the aquifer (Sanford, 1997). Both processes reduce the ¹⁴C concentration and result in an apparent groundwater age that is older than the true age. Consequently, the measured ¹⁴C activities were corrected for carbonate dissolution as well as aquitard diffusion prior to use in the calibration.

A modified chemical correction was applied that takes into account the effect of dissolution as described by Boaretto et al. (1998). This method was successfully used in Danish geological settings similar to those investigated in the present study (Eq. 2; Boaretto et al., 1998; Hinsby et al., 2001a). The initial ¹⁴C activities were corrected for fossil carbon dissolution (Pearson and Hanshaw, 1970) assuming an atmospheric ¹⁴C activity (A₀) of 100 pMC (percent modern carbon) and a δ¹³C concentration of −25 ‰ in the soil CO₂, and a ¹⁴C activity of 0 pMC and δ¹³C concentration of 0 ‰ in the dissolved carbonate. With a decay rate constant (λ) of $\mathrm{1.21}\times {\mathrm{10}}^{-\mathrm{4}}$ a⁻¹ for the ¹⁴C decay, the dissolution-corrected age τ_C was calculated as (e.g. Bethke and Johnson, 2008)

$$\begin{array}{}\text{(1)}& {\displaystyle }{\mathit{\tau }}_{\mathrm{C}}={\displaystyle \frac{-\mathrm{1}}{\mathit{\lambda }}}\ln \left({\displaystyle \frac{A_m}{A_{\mathrm{0}}}}\right),\end{array}$$

with

$$\begin{array}{}\text{(2)}& {\displaystyle }{A}_{\mathrm{0}}={\displaystyle \frac{{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}{-\mathrm{25}}}\times \mathrm{100}.\end{array}$$

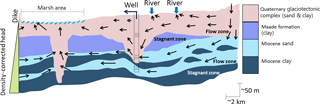
Figure 2 Conceptual regional model showing a simplified geology featuring buried valleys, groundwater flow and stagnant zones (as used for the diffusion correction). Arrows indicate general flow field of groundwater. Also shown are the boundary conditions, i.e. density corrected coastal boundary, drained marsh area, rivers.

Subsequently, a diffusion correction was made to take into account diffusion loss into low-permeability layers (Sanford, 1997). Aquitard diffusion is sensitive to porosity, diffusion coefficient and the thicknesses of the active flow (aquifer) and stagnant (aquitard) zones (Sudicky and Frind, 1981). Because of the geological complexity, the sand-to-clay ratio based on voxel lithology was used to calculate the relative aquifer ∕ aquitard ($a/b=\mathrm{0.72}$) thicknesses. Diffusion-corrected groundwater ages were calculated for three different diffusion coefficients (D): $\mathrm{1.26}\times {\mathrm{10}}^{-\mathrm{9}}$ m² s⁻¹ (Jaehne et al., 1987) representing the CO₂ diffusion in water, $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{10}}$ m² s⁻¹ as an average for clay deposits (Freeze and Cherry 1979; Sanford, 1997) and $\mathrm{2.11}\times {\mathrm{10}}^{-\mathrm{10}}$ m² s⁻¹ as calculated by Scharling (2011), using aquifer effective porosities (n_e) ranging from 0.16 to 0.35 and aquitard (b) thicknesses between 10 and 50 m. Based on the ranges of variables, an average corrected age and the corresponding standard deviation were obtained for each sample (Table 1). Corrected groundwater sample age (τ_D), also referred to as the apparent age, was calculated as

$$\begin{array}{}\text{(3)}& {\displaystyle }{\mathit{\tau }}_D={\mathit{\tau }}_{\mathrm{C}}\times \left({\displaystyle \frac{\mathit{\lambda }}{\mathit{\lambda }+{\mathit{\lambda }}^{\prime }}}\right),\end{array}$$

with

$$\begin{array}{}\text{(4)}& {\displaystyle }{\mathit{\lambda }}^{\prime }=\mathrm{2}\times \tanh \left[\left({\displaystyle \frac{b}{\mathrm{2}}}\right)\times {\left({\displaystyle \frac{\mathit{\lambda }}{D}}\right)}^{\frac{\mathrm{1}}{\mathrm{2}}}\right]\times {\displaystyle \frac{(\mathit{\lambda }D{)}^{\frac{\mathrm{1}}{\mathrm{2}}}}{n_{\mathrm{e}}a}}.\end{array}$$

Table 1 Sampling wells, uncorrected and corrected groundwater ages. Bold indicates samples used for calibration. Note that lower numbers of the wells indicate deeper locations (m b.s. = metres below ground surface, SD = standard deviation, pMC = percent modern carbon).

3.2 Groundwater flow model

Meyer et al. (2018a) simulated the 3-D steady-state regional groundwater flow using MODFLOW 2000 (Harbaugh et al., 2000). A brief description of the model set up and calibration results are presented here; further details can be found in Meyer et al. (2018a). The model was discretized horizontally by 200 m × 200 m in the west and 400 m × 200 m in the east and vertically by 5 m above 150 m b.s.l. and 10 m below 150 m b.s.l., resulting in 1.2 million active cells. The voxel geology was interpolated to the MODFLOW grid and 46 hydrogeological units were defined. No-flow boundaries were used along the flow lines in the north and south, along a water divide in the east and at the bottom, where the Palaeogene clay constitutes the base of the aquifer system. At the western coast a density-corrected constant head boundary was applied (Fig. 1; Guo and Langevin, 2002; Post et al., 2007; Morgan et al., 2012). Distributed net recharge, averaged over the years 1991–2010, was extracted from the national water resources model (Henriksen et al., 2003) and included as a specified flux condition. Internal specified boundaries include abstraction wells with a total flux of 26×10⁶ m³ year⁻¹ (averaged over the years 2000–2010, corresponding to 4 % of the total recharge) as well as rivers and drains.

Horizontal hydraulic conductivities (one for each hydrogeological unit), two anisotropy factors (K_h∕K_v, one for sand and one for clay units), and river and drain conductances were calibrated using a multi-objective regularized inversion scheme (PEST; Doherty, 2016) with head and mean stream flow observations as targets. The resulting head distribution is shown in Fig. 1. Horizontal hydraulic conductivities were estimated in a range of K_h ∈ [1 m d⁻¹; 83 m d⁻¹] for Pleistocene sand units, K_h ∈ [0.028 m d⁻¹; 0.19 m d⁻¹] for Pleistocene clay units, K_h ∈ [0.008 m d⁻¹; 0.016 m d⁻¹] for the Maade formation, K_h ∈ [16 m d⁻¹; 46 m d⁻¹] for Miocene sand and K_h ∈ [0.14 m d⁻¹; 0.23 m d⁻¹] for Lower Miocene clay.

The steady-state MODFLOW flow solution (calibration results summarized in Fig. 3; Meyer et al., 2018a, also contains an identifiability and uncertainty analysis of the estimated parameters as well as an evaluation and discussion of the non-uniqueness of the flow model) forms the basis for the advective transport simulation using MODPATH.

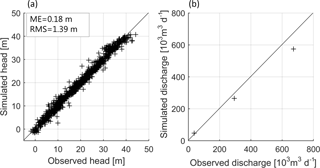
Figure 3 Calibration results of steady-state groundwater flow model that forms the basis for the advective transport model (modified after Meyer et al. (2018a). Panel (a): simulated versus observed hydraulic head; panel (b): simulated versus observed stream discharge. ME = mean error, RMS = root mean square.

3.3 Advective transport model

Advective transport simulation was performed using MODPATH (Pollock, 2012) in particle back-tracking mode. Hereby, the travel time of a particle, released in a cell, is calculated based on the MODFLOW cell-by-cell flow rates (q). The advective travel time (t) along the travel paths in 3-D (x) is calculated as

$$\begin{array}{}\text{(5)}& {\displaystyle }t\left(\mathit{x}\right)=\underset{{\mathit{x}}_{\mathbf{0}}}{\overset{\mathit{x}}{\int }}{\displaystyle \frac{n_e\left(\mathit{x}\right)}{\mathit{q}\left(\mathit{x}\right)}}\mathrm{d}\mathit{x}.\end{array}$$

In addition to the input data required by MODFLOW to generate the flow solution, MODPATH requires a value for effective porosity (n_e) to calculate the seepage velocity.

The groundwater age can be seen as the backward integration of travel times along the travel path back to its recharge location. Hence, the simulated groundwater age is a function of the ratio of flux to effective porosity and the travel distance. In this study, the total flux is controlled by prescribed recharge and heterogeneous distribution of hydrogeological parameters (e.g. hydraulic conductivity, porosity).

In order to ensure stability (Konikow et al., 2008), 1000 particles were distributed evenly in the cell of the well screen and their average simulated particle age was compared with apparent groundwater ages (derived from Eq. 3).

The corrected ¹⁴C ages were used as targets in the objective function (see below) of the simulated average travel time during calibration. The particle-based approach used in this study computes the kinematic age at a point. With 1000 particles released in each cell with a screen, we essentially get an age distribution of kinematic ages by perturbing the measurement location within the cell, reflecting the mixing of waters from different origins. The ¹⁴C ages have also been diffusion-corrected (Sect. 3.1.1) so that dilution or mixing due to loss of ¹⁴C into the stagnant zones have been accounted for.

3.3.1 Calibrating porosity

The flow solution of the calibrated flow model (Meyer et al., 2018a) constitutes the base for the 3-D advective transport model. Depending on the depositional environment and clay or sand content, effective porosities of seven units corresponding to two Pleistocene sand, two Pleistocene clay, one Miocene sand and two Miocene clay units were estimated using a regularized (Tikhonov) inversion with PEST (Tikhonov and Arsenin, 1977; Doherty, 2016). As the calibration approach is similar to the one of Meyer et al. (2018a), only additional characteristics are described in the following. Average corrected ¹⁴C groundwater ages from 11 samples with a ¹⁴C activity higher than 5 pMC (Table 1) were used as calibration targets. ¹⁴C activity lower than 5 pMC was not used as it was assumed that the boundary conditions of the flow model (e.g. sea level, recharge, head gradients) were not representative for pre-Holocene conditions. Moreover, the data from well F1 were excluded from calibration as an age inversion with F2 was observed here (Table 1), probably due to local heterogeneity or contamination of water with a higher ¹⁴C concentration, which cannot be reproduced by the model. The average uncertainty of apparent ages was estimated to be about 102 years. This value was based on the average of the standard deviation of the diffusion correction for the selected 11 samples and was used for weighting of the individual ages.

When Tikhonov regularization is applied, a regularized objective function (Φ_r) is added to the measurement objective function (Φ_m) in the form of the weighted least-squares of the residuals of preferred parameter values and parameter estimates. Within the limits of the user-defined objective function (PHIMLIM) and the acceptable objective function (PHIMACCEPT), the weight of the regularized objective function (μ) increases and the parameter estimates are directed towards the preferred values.

Calibration settings such as initial and preferred values and final parameter estimates are shown in Table 2. Values for PHIMLIM and PHIMACCEPT were set to 60 and 100, respectively. The total objective function (Φ_tot), minimized by PEST, is then the sum of the measurement objective function (Φ_m) and the regularized objective function (Φ_r):

$$\begin{array}{}\text{(6)}& {\displaystyle }{\mathrm{\Phi }}_{\mathrm{tot}}={\mathrm{\Phi }}_{\mathrm{m}}+{\mathit{\mu }}^{\mathrm{2}}{\mathrm{\Phi }}_{\mathrm{r}},\end{array}$$

with

$$\begin{array}{}\text{(7)}& {\displaystyle }{\mathrm{\Phi }}_{\mathrm{m}}=\sum {\left({\mathit{\omega }}_{\mathrm{a}}\left(a_{\mathrm{obs}}-a_{\mathrm{sim}}\right)\right)}^{\mathrm{2}},\end{array}$$

where a_obs and a_sim are observed and simulated groundwater ages, respectively, and the weight ω_a is the inverse of the standard deviation of the observed age. The calibration is evaluated based on the mean error (ME) and the root mean square (RMS) between apparent (corrected ¹⁴C ages) and advective groundwater ages. Parameter identifiability (Doherty and Hunt, 2009) is used to investigate to what extent the effective porosities were constrained through model calibration. Identifiability close to 1 means that the information content of the observations used during calibration can constrain the parameter. Parameters with an identifiability close to zero cannot be constrained.

3.4 Direct age

To visualize the mean groundwater age pattern in the regional 3-D aquifer system, direct simulation of mean groundwater age was performed with MT3DMS (standard finite difference solver with upstream weighting) and the chemical reaction package using a zeroth-order production term (Goode, 1996; Bethke and Johnson, 2008). Hereby, mean groundwater age is simulated in analogy to solute transport as an “age mass” (Bethke and Johnson, 2008). For each elapsed time unit (day) the water “age mass” increases by 1 day in each cell. Increases or decreases in ages are a result of diffusion, dispersion and advection (Bethke and Johnson, 2008). The transient advection–dispersion equation of solute transport of “age mass” in three dimensions and with varying density and porosity is given by Goode (1996):

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{\partial a{n}_{\mathrm{e}}\mathit{\rho }}{\partial t}}=n_{\mathrm{e}}\mathit{\rho }-\mathrm{\nabla }a\mathit{\rho }\mathbf{\text{q}}+\mathrm{\nabla }{n}_{\mathrm{e}}\mathit{\rho }\mathbf{D}\times \mathrm{\nabla }a+F,\end{array}$$

where F is an internal net source of mass age, q the Darcy flux (m d⁻¹), a the mean age (d), n_e the effective porosity, ρ the density of water (kg m⁻³) and D the dispersion tensor (m² d⁻¹), including molecular diffusion and hydrodynamic dispersion. The initial concentration of the “age mass” was set to zero, while a constant age of zero was assigned to the recharge boundary and the constant head boundary at the coast. Steady-state conditions were evaluated based on the change in mass storage in a 40 000-year simulation. The age mass storage (m) in the whole model was calculated for each time step as the sum of mass in each cell (m_i). The latter was calculated by multiplying the cell dimensions ($\mathrm{\Delta }z,\mathrm{\Delta }x,\mathrm{\Delta }y$) with porosity (n_e) and age (a_s):

$$\begin{array}{}\text{(9)}& {\displaystyle }m=\sum m_i,\end{array}$$

with

$$\begin{array}{}\text{(10)}& {\displaystyle }{m}_i=\mathrm{\Delta }z\times \mathrm{\Delta }x\times \mathrm{\Delta }y\times n_{\mathrm{e}}\times a_s.\end{array}$$

The percentage change in mass storage (Δm_t) per time step (Δt) was calculated as

$$\begin{array}{}\text{(11)}& {\displaystyle \frac{\mathrm{\Delta }{m}_t}{\mathrm{\Delta }t}}=\left({\displaystyle \frac{m_t-m_{t-\mathrm{1}}}{m_{t-\mathrm{1}}}}\right)\times \mathrm{100}.\end{array}$$

The integral of the change in mass storage over time was used to define quasi-steady-state conditions. This was reached when

$$\begin{array}{}\text{(12)}& {\displaystyle }\underset{t\mathrm{1}}{\overset{t}{\int }}\mathrm{\Delta }m\left(t\right)\mathrm{d}t\ge \mathrm{0.95}\times \underset{t\mathrm{1}}{\overset{\mathrm{\infty }}{\int }}\mathrm{\Delta }m\left(t\right)\mathrm{d}t.\end{array}$$

Dispersion experiments were carried out for longitudinal dispersivity α_L values of 0, 5, 20, 50 and 500 m, while the horizontal transversal α_TH and vertical transversal α_TV dispersivities were specified to 10 % and 1 % of α_L, respectively. A diffusion coefficient of $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{9}}$ m² s⁻¹ was used to account for self-diffusion of the water molecule at about 10 ^∘C (Harris and Woolf, 1980).

3.5 Capture zones

Well capture zones are used in water management to define areas of groundwater protection, where human actions, such as agricultural use, are restricted. Simulated by the uniform effective porosity and distributed effective porosities model, the capture zones of one existing well (Abild, abstraction rate 27 m³ d⁻¹) located in a buried valley and one virtual well (AW, abstraction rate 280 m³ d⁻¹) located in a Miocene sand aquifer were evaluated and compared for different back-tracking times using 100 particles per well. Given that the hydraulic conductivity field is unchanged, no differences in the area of the whole capture zone are expected as porosity does not impact the trajectory of the particle path (Hill and Tiedeman, 2007) and only affects the travel time. Hence, the capture zone areas at different times were compared.

4 Results

4.1 ¹⁴C corrections

Figure 4 shows the corrected and uncorrected ¹⁴C ages over depth. Except for well F, ages increase with depth at each multi-screen location. Otherwise, no clear trend between age and depth can be identified on the regional scale. Uncorrected ages range from 5000 to 50 000 years (Table 1). After correction, all ages decrease and the relative difference between the corrected ages increase, now within a range from 46 to 15 000 years. Hence, it is expected that the oldest water recharged the groundwater at the end of the last glacial period. The majority of the samples represent younger waters, with 12 out of 18 samples being less than 2000 years old.

Figure 4 Apparent groundwater ¹⁴C ages as a function of groundwater sampling depth: black crosses indicate ages without correction for dissolution and diffusion, blue circles show ages with correction. Labels indicate well location and screen number (see Fig. 1 and Table 1).

4.2 Calibration results

The match between the average of simulated groundwater ages (particle tracking with MODPATH) and corrected ¹⁴C ages is shown in Fig. 5a.

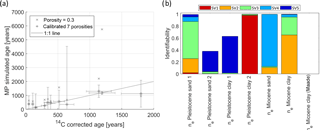
Figure 5 Calibration results: (a) “x” shows apparent ages simulated with MODPATH (MP) and a porosity of 0.3 as often used in porous media models and “+” shows MP ages simulated based on the seven calibrated porosities (Table 2); standard deviations based on MP and correction terms (see Sect. 3.1.1) are shown. (b) Parameter identifiability of effective porosities (warmer colours correspond to singular values (SV) of a lower index, cooler colour to SV of higher index) of the different geological formations; the identifiability of the Maade porosity is close to zero.

Results from the calibrated distributed effective porosities model were compared to those from a uniform effective porosity model with an effective porosity of 0.3, which is a typical textbook value for porous media (Hölting and Coldewey, 2013; Anderson et al., 2015) and often used in groundwater modelling studies (e.g. Sonnenborg et al., 2016). The calibrated distributed effective porosity model is able to match all the observations reasonably. This is not the case for the single effective porosity model, where one sample in particular is poorly simulated with an estimate of more than 5500 years, whereas the corresponding observation only reach about 1200 years. The ME and RMS of the calibrated distributed effective porosity model were −2.3 years and 267 years, respectively, which correspond to a reduction in ME of 99 % and RMS of 82 % compared to the single effective porosity model. Considering the uncertainties involved in estimation of apparent age (see uncertainty estimates in Table 1, column to the right), the match is found to be acceptable. Comparison of the average uncertainty in apparent ages used for calibration of 102 years with the achieved RMS of 267 years indicates that no overfitting occurred and that mismatches can be a result of small-scale heterogeneity below grid resolution, errors in the model structure or uncertainties of parameters, for example.

Table 2 Calibration settings and results: parameters with initial, preferred and estimated values for effective porosity.

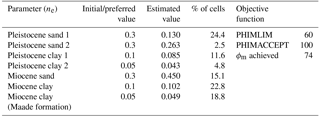
The estimated effective porosities of the seven hydrogeological units are listed in Table 2. Realistic values are found for all parameters and the values of the sand units are generally higher than those of the clay units. However, the effective porosity estimate of 0.13 for Pleistocene sand 1 is relatively low. This may be explained by the fact that this unit does not represent sand exclusively everywhere. The Pleistocene deposits in the area are highly heterogeneous (Jørgensen et al., 2015) and it is therefore difficult to identify units exclusively composed of sand, partly due to the difficulties in using AEM data to guide the distinction between sand and clay at a relatively small scale. Hence, Pleistocene sand 1 may to some extent represent a mixture of sand and clay. The relatively small effective porosities for clay units might be due to compaction as a result of glacial loading in the course of several glacial periods during the Pleistocene. Additionally, uncertainties in the estimates of hydraulic conductivity from Meyer et al. (2018a) will translate into errors in seepage flux and hence ages. Uncertainties and errors in hydraulic conductivity may therefore be partly compensated by estimates of effective porosity that are somewhat different from the expected value.

The parameter identifiability (Fig. 5b) shows that the corrected ¹⁴C ages may constrain four out of seven estimated effective porosities, i.e. of Pleistocene sand 1, Pleistocene clay 2, Miocene sand and Miocene clay. The warmer colours (red–yellow) indicate that the parameter is less influenced by measurement noise (Doherty, 2015, Fig. 5b). Where the parameter identifiability is relatively low (<0.8), i.e. for effective porosities of Pleistocene sand 2, Pleistocene clay 1 and Miocene clay (Maade), the estimated parameter value is more constrained by the regularization and hence stays close to the preferred value (Table 2). The low identifiability is a result of the distribution (or density) of observations compared to the particle travel paths. Figure 6 shows the pathlines of particle back-tracking (for better visualization only one path line is shown per well screen). As mentioned above, only ¹⁴C observations with an activity higher than 5 pMC (Table 1) were used, which excludes results from well screens C1, C2, C3, D1, D2, F1 and F2. The recharge area is mostly located to the east (Fig. 6). The Maade formation is more dominant towards the west while it is patchy in the east. Consequently, it does not affect the particle tracking as much in the east. Only effective porosities of geological units through which particles actually travel are well informed by the observations. The low-permeability Maade unit acts as an obstacle to the travel paths and since the particles circumvent the Maade formation the actual value of porosity has no impact on the age. The Maade unit significantly affects the age distribution due to its influence on travel paths, but no sensitivity to the porosity of the unit is found.

Pleistocene sand 2 represents less than 5 % of the total amount of cells (Table 2) and it occurs mostly in the west. Pleistocene clay 1 is mostly shallow, patchy and located far away from the well locations. Hence, the impact of these two geological units on the particle tracks is also relatively small and results in low identifiability (Fig. 5b).

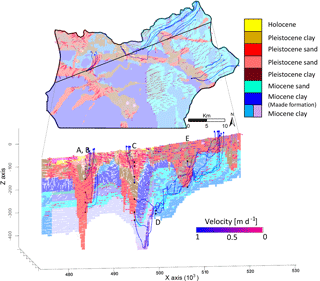
Figure 6 Horizontal geological cross section at an elevation of −100 m a.s.l. and a SW–NE cross section through sampling well locations (A–E). Bluish (cold) colours represent pre-Pleistocene sediments (dark blue = clay, light blue = sand), while warm colours represent Pleistocene deposits (red = sand, brown = clay). Also shown are MODPATH back-tracking lines (1 per cell) and groundwater flow velocity vectors. The units for the x and z axes are meters (m).

4.3 Advective age distribution at observation wells

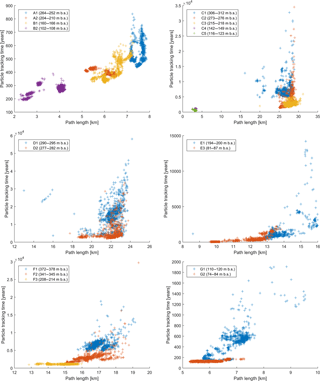
Figure 7 shows the simulated advective age distribution at the sampling locations (A–G, Fig. 1).

Table 3 Results of the analysis of particle age distributions and path lengths. Bold indicates well screens used for calibration.

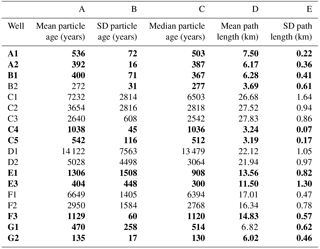
The results show a wide variety of mean particle ages (Table 3) and the shape of the age distributions is very different (Fig. 7). The well screens with mean particle ages less than 1000 years (except for C4 and F3 which have slightly higher mean particle ages) show particle age distributions that are mostly narrow and unimodal (except E3 and G1), which is also reflected in a small standard deviation (smaller than 20 % of the mean age, except E3 and G1), see column B in Table 3. The particle age distributions of older waters with a mean particle age higher than 1000 years (Table 3) tend to have broader and/or multi-modal shapes (Fig. 7c, d) and large standard deviations (Table 3, column B).

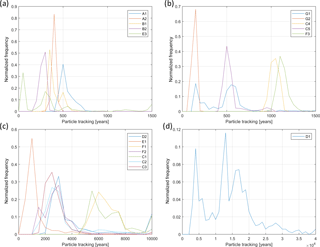
Figure 7 Particle age distributions at sampling wells A–G (see Fig. 1 for locations). Panels (a) and (b): young waters (bin size = 50 years) show a narrow, unimodal distribution; panel (c) old waters (bin size = 500 years) have broader and often multimodal distributions; panel (d): multi-modal age distribution at sample location D1 (bin size = 1000 years), which shows the longest travel times.

The mean distance that particles travel from their recharge points to the sampling well (Table 3, column D) ranges between 3 and 28 km. The younger waters (mean particle ages < 1000 years) show path lengths less than 10 km (except at well location E3 and F3; Fig. 8), while most of the older waters travel more than 20 km. However, the relation between path length and travel time is far from linear. At some well locations (e.g. well locations A2, B2, C4, C5) the relation between path length and travel time forms a few distinct small clouds without much spread, indicating that the particles follow alternative large-scale preferential flow paths. At other locations a larger and more diffusive spread is found, either in travel times (e.g. well locations C1, C2, C3, D1, E1) or path lengths (e.g. well locations F3, G2, E3). The large spread in travel times indicates that some particles travel slowly through clay units of various thicknesses. The large spread in path lengths originates from long and quick or short and slow travel paths through or around clay units and reflects the geological heterogeneity.

Figure 8 Particle tracking time over path length for the different well locations (see Fig. 1; the screen depth is indicated in parentheses).

4.4 Regional age distribution based on direct age simulation

Figure 9 shows the ME and RMS of the direct mean age and the apparent age (corrected ¹⁴C) for different α_L values (α_TH and α_TV are tied to α_L, see Sect. 3.4).

Mean error and root mean square

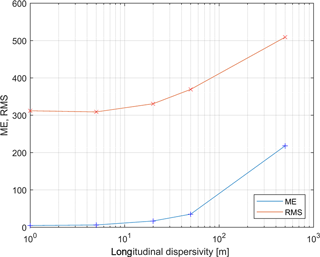
Figure 9 Mean error (ME) and root mean square (RMS) between corrected ¹⁴C ages (shaded in gray in Table 1) and directly simulated ages as a function of longitudinal dispersivity.

Minimum ME and RMS values are achieved for longitudinal dispersivities α_L<5 m. For lower α_L the effect on ME and RMS is insignificant as numerical dispersion is expected to dominate at this scale. With higher α_L values ME and RMS increase significantly. Other regional-scale studies (e.g. Sonnenborg et al., 2016) have used longitudinal dispersivity in the magnitude of tens of metres or more to account for geological heterogeneities at formation scale. The very detailed voxel geological model resolves heterogeneities at a scale of 200 m × 200 m. Hence, it is assumed that mixing at scales larger than 200 m is accounted for by the geological model. Therefore, the dispersivity should only describe the heterogeneity at a flow scale of several hundreds of metres, which justifies the use of a relatively small α_L. In accordance with Gelhar et al. (1992) flow scales of hundreds of metres result in α_L of magnitudes in the range of a few metres, which is also in line with studies in the Dutch polder system where dispersivity values of 2 m were applied in similar-sized models (e.g. Oude Essink et al., 2010; Pauw et al., 2012). Similar to Weissmann et al. (2002) and LaBolle and Fogg (2001) the simulations showed little sensitivity to local-scale dispersivity because at the modelling scale of tens of kilometres, dispersion is dominated by facies-scale heterogeneity, which is captured by the detailed, highly resolved geological model. On the grid scale of 200 to 400 m and with the standard difference solver for the advection–dispersion equation, a substantial numerical dispersion is expected. Choosing the TVD or MOC solver scheme for the advection–dispersion equation would have been more accurate in terms of less numerical dispersion, but would have required excessive running times, which made it impractical to use in this study. Since there is no sensitivity for lower α_L (numerical dispersion dominates at this scale), physical dispersivity was set to zero in the following simulations of direct age.

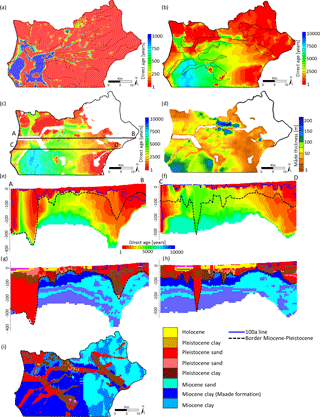
Figure 10 Directly simulated mean ages: (a) horizontal section at layer 2, also showing river network; (b) horizontal section at a depth of 100 m a.s.l. (buried valleys indicated with dotted lines); (c) horizontal section at the top of the Maade formation; (d) extent and thickness of the Maade formation; (e) cross sections A–B and (f) C–D; Pleistocene-Miocene boundary indicated with dashed lines (buried valleys), 100 year lines; (g) and (h) geological cross section and (i) horizontal geological section, main geological units indicated (a detailed geological description is given in Meyer et al., 2018a). Notice that the colour scheme in (a) is different in order to better resolve younger ages close to the surface.

The directly simulated mean age distribution on a regional scale (Fig. 10) shows a general age evolution from young water in the recharge area in the east towards older water in the west (Fig. 10b, e, f). Young water also enters the system through the coastal boundary in the west (Fig. 10b, e, f). The age distribution is strongly affected by geology and is therefore in good agreement with the interpretation of the flow system by Meyer et al. (2018a). Two main aquifers are present on a regional scale: a shallow Pleistocene sand aquifer and a deep Miocene sand aquifer, separated by the Maade formation and locally connected through buried valleys (conceptual model in Figs. 2, 10g, h). The regional mean age distribution also reflects this system. Younger waters dominate the shallow Pleistocene aquifers (Fig. 10a, e, f), where the flow regime can be described as mostly local and intermediate (Tóth, 1963). The separating Maade formation with its increasing thickness towards the west (Fig. 10d) acts as a stagnant zone where groundwater age increases (Fig. 10c). The underlying Miocene sand shows the mean age evolution from young water in the recharge areas in the east to older water towards the discharge zones in the west (Fig. 10b, e, f). Here the flow regime is dominated by regional flow (Tóth, 1963). Special features are the buried valleys where downward flow of young waters, upwelling of old waters and mixing occurs (Fig. 10e, f, g, h). At the coastal boundary in the west young water enters the system and due to the density-corrected head boundary a wedge is formed with young waters in the wedge and old water accumulating in the transition zone (Fig 10e, f). The two cross sections (Fig. 10e and f) differ in their geological connection to the sea boundary (compare geological sections in Fig. 10g and h). In (e) a buried valley connects the inland aquifer with the sea and here younger waters reach further inland due the relatively higher hydraulic conductivity and the inland head gradient as a result of the drainage system. Moreover, buried valleys constitute locations where the deep aquifer system, bearing old waters, connects with the shallow one, and here upwelling of older waters occurs due to the higher heads in the deep semi-confined (by the Maade aquitard) Miocene aquifer. In cross section (f) where the buried valley occurs further inland, the young ocean water penetrates the higher permeable Miocene aquifer but is impeded in the low permeable sections and hence does not reach as far inland. Another feature is the human land use change including an extensive drainage network with drain elevations below the sea level in the marsh area. There, old groundwater is forced upward, partly through buried valleys, before it could discharge to the sea.

4.4.1 Direct simulated mean age distribution in geological units

The steady-state distribution of direct simulated mean groundwater age was reached after 26 000 years. Over this time span the system has been exposed to transient stresses from human activity and climatic changes (glacial cover, sea level, etc.). Therefore, the steady-state assumption is a notable simplification, which is further discussed in Sect. 5.1.

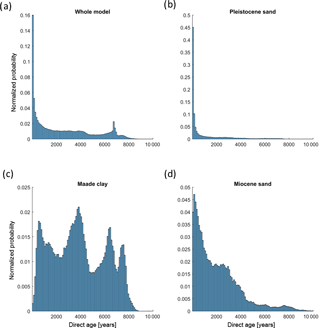
Figure 11 Frequency distributions (bin size = 100 years) of directly simulated groundwater ages in (a) the whole model, (b) the shallow Pleistocene aquifer, (c) the separating Miocene clay (Maade formation) and (d) the deep Miocene aquifer.

In Fig. 11 the normalized direct age distributions are shown for (a) the whole model, (b) the Pleistocene aquifer, (c) the Maade clay formation that acts as an aquitard and (d) the Miocene sand aquifer (compare the geological setting with conceptual model in Fig. 2). The directly simulated mean groundwater ages for the whole model, the Pleistocene sand, the Maade formation and the Miocene sand were determined by a moment analysis (Levenspiel and Sater, 1966) as 2574, 1009, 3883 and 2087 years, respectively. The shape of the age distribution in these units varies significantly. The Pleistocene sand shows a unimodal distribution with one peak at ≈100 years and a tail (Fig. 11b). The age distribution is governed by recharge of young water and discharge through rivers and drains, which are fed by the upwelling older groundwater (Fig. 10a). The age distribution in the Maade formation is multi-modal, with five peaks at about 600, 1400, 3900, 6500 and 7600 years (Fig. 11c). Comparison of Fig. 10c and d reveals a positive relation between age and thickness of the Maade formation. The age distribution in the underlying Miocene sand has one peak at 200 years followed by a plateau between 1600 and 3100 years and a small peak at 7800 years (Fig. 11d). This distribution is controlled by the overlying and separating Maade formation in the west and the inter-layering with Miocene clay.

4.4.2 Advective and directly simulated ages

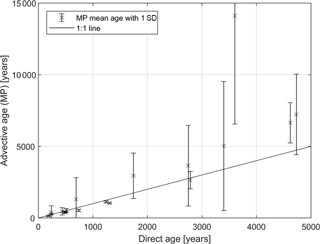
The comparison of the advective ages with the direct simulated ages at the sampling well locations shows a good match for advective ages with a small variance and worsens when the variance increases (Fig. 12). Older ages are generally associated with larger variances. Where the mismatch between advective and direct ages is large, the direct simulated mean ages are consistently lower than mean ages derived from particle back-tracking (see discussion below) because of diffusion into clay units. However, most of them lie within 1 standard deviation; but please observe that the standard deviation spans several thousands of years at some locations, where particle travel time distributions show a multi-modal shape.

Figure 12 Mean advective age (MODPATH (MP) particle backtracking) compared to directly simulated mean groundwater age at sampling well locations; error bars on advective age represent 1 standard deviation.

4.4.3 Capture zones: effect of porosity

Figure 11 shows the capture zones at the Abild well for 1500 and 2000 years and for the virtual well (AW) for 1000, 2000 and 3000 years for a constant effective porosity of 0.3 (solid line) and the calibrated distributed effective porosities model (dashed line), respectively. The capture zones of the two models vary both in extent and shape. The areas of the capture zone differ by up to 50 %. Interestingly, it is not always the same effective porosity model that has the smaller capture zone, but it changes due to the heterogeneity in the geological model and the assigned effective porosities. However, the results illustrate the importance of reliable estimates of effective porosity when delineating the capture zone of an abstractions well.

5 Discussion

¹⁴C observations were used to constrain the estimation of effective porosities of a large-scale coastal aquifer system using an approach similar to Konikow et al. (2008), Weissmann et al. (2002) and Starn et al. (2014). Advective transport modelling and direct age simulations were applied to gain insight into the regional age structure of this highly heterogeneous geological system. In the following, limitations, uncertainties and simplifications of the model structure as well as estimated parameters and resulting interpretations are discussed. A detailed description of the age distribution is provided to highlight the relevant physical processes and their interactions.

5.1 Uncertainties

5.1.1 Boundary conditions

Uncertainties in model results originate partly from simplifications in boundary conditions and geological heterogeneities that are not resolved at the grid scale. Groundwater recharge, drain levels, well abstractions and sea levels were assumed to be constant over time for practical reasons and to reduce computational time. However, Karlsson et al. (2014) showed that recharge has changed significantly in Denmark during the last centuries. Changes in recharge could result in different age patterns (Goderniaux et al., 2013). Similarly, sea level changes that were disregarded in this study would have an effect on the groundwater age distribution in the coastal areas (Delsman et al., 2014). Prescribing a vertical coastal age boundary of zero years is another simplification that neglects the vertical mixing and dispersion, which would result in an increase of age with depth (Post et al., 2013). However, since these physical processes were difficult to quantify, estimating age at this boundary would be highly uncertain. Thus, a constant age of zero years was applied.

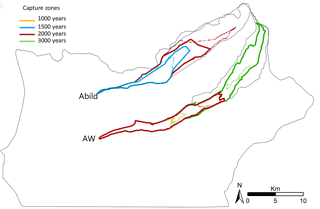
Figure 13 Capture zones at a well in Abild and a virtual well (AW) with a comparison of capture zones for a model with homogeneous porosity of 0.3 in all geological units (solid lines) and one with seven different porosities (dashed lines).

The area close to the coast has not only been affected by changing sea levels during the past thousands of years, but also by saltwater intrusion. In this study, the density effects on flow were accounted for in a simplified way by using a density-corrected constant head boundary at the coast. Both sea level changes and density effects would also have affected the age distribution. The impact on age calculations due to density effects would be largest close to the coast. However, most of the groundwater samples used for age estimations were collected several tens of kilometres inland and are therefore expected to be affected to a minor extent. To quantify the impact of boundary conditions and saltwater intrusion on the particle tracking, the differences of particle travel path lengths for a 200-year period, investigated based on the present model and a preliminary density-driven model (SEAWAT) accounting for non-stationary and density effects (similar to the one presented in Meyer, 2018), are computed. The relative differences are below 10 % (except at location A and B). Also, the uncertainties introduced by simplifying the density boundary effects are likely to be less important compared to other uncertainties associated, for example, with estimating the groundwater age by the procedures for correcting ¹⁴C activities. A solution would, of course, be to use a fully density-driven model such as SEAWAT as in Meyer (2018) or Delsman et al. (2014). But the very long computer runtimes for these kinds of models and the need for several thousand model runs during calibration made it infeasible to use a variable-density flow model.

5.1.2 Apparent age as calibration target

Uncertainties in the use of ¹⁴C as a groundwater dating tool and as calibration target arise at different levels. First, sampling of well screens with a length of 6–10 m would encompass a range of groundwater ages as a result of mixing of groundwater of different ages. Thereby younger waters, corresponding to DIC with a higher ¹⁴C content, would dominate older water (Park et al., 2002). The ¹⁴C content is measured in the DIC of the groundwater. In order to obtain a reliable age estimate, the origin of DIC in groundwater is important. For the different processes that can affect the DIC and change its ¹⁴C content (e.g. dissolution, precipitation, isotopic exchange) a variety of correction models exists (see overview of correction models in IAEA, 2013). For the investigated system, corrections for carbonate dissolution and diffusion were applied, but it cannot be ruled out that other chemical processes might also have changed the ¹⁴C content over the past few thousands of years. The ¹⁴C correction for diffusion into stagnant zones is sensitive to aquifer porosity, aquitard thickness and diffusion constant. The geology is highly complex and aquitard thickness and porosity distribution change spatially over the entire region, whereas the correction terms were based on the properties averaged over hydrogeological units. Hence, average values of diffusion corrections were applied with parameters varying in ranges realistic for an aquifer system at this scale. However, in reality a groundwater particle would have been exposed to a variety of aquifer and aquitard thicknesses and porosities along its flow path, implying smaller or larger diffusion. The correction results show that both carbonate dissolution and diffusion into stagnant zones reduce the apparent groundwater age considerably, both at a similar magnitude as observed by Scharling (2011) and Hinsby et al. (2001a).

As mentioned in the introduction, the apparent age (or radiometric age) is not equal to the mean particle-based kinematic age. This introduces additional, but unknown uncertainties. Ideally, one could develop an advection–dispersion equation for the second moment and solve for the variance of ages (Varni and Carrera, 1998) and use that together with the directly simulated mean age (or first moment) to establish a relation between radiometric and mean ages. This has not been pursued as we believe the benefits from this would be masked by uncertainty in age dating ¹⁴C (i.e. uncertainty on analyses, and corrections for effects of geochemical and physical processes). Finally, the calibration of effective porosity using an advective transport model relies on a calibrated 3-D flow solution that already bears uncertainties with respect to structure and parameters, as addressed by Meyer et al. (2018a). The number and position of the released particles contribute to the uncertainty, especially in heterogeneous systems, as pointed out by Konikow et al. (2008) and Varni and Carrera (1998). The use of a high number of particles – here 1000 particles were distributed in one cell – generally reduces the uncertainty and enhances stability of the solution. The arithmetic mean of the 1000 released particles evenly distributed in the sampling cells resulted in estimates of effective porosities in the range of 0.13 to 0.45 for sand and 0.043 to 0.1 for clay units, which is significantly different to porosities of 0.25 or 0.30 that are often used in porous media (e.g. Sonnenborg et al., 2016). The reliability of the estimated effective porosities was assessed through the identifiability that depends on the observation density (see Sect. 4.2) and is high for four out of the seven estimated porosities.

5.1.3 Commensurability

The comparison of groundwater ages, estimated from tracer concentration in a water sample, and simulated groundwater ages, either derived by particle tracking or direct age modelling, bears the problem of commensurability, the comparison of a point measurement relative to the modelling scale. The water sample represents the age distribution in the direct surrounding of the well screen, which only makes up a few percent of the water in one model cell.

The differences between mean advective ages and directly simulated mean ages as described in Sect. 4.4 can be related to the simulation methods. While particle tracking neglects dispersion, but allows an age distribution in a cell to be simulated (by perturbing the measurement location so to speak), direct age modelling allows for dispersion/diffusion to be accounted for, resulting in only the mean age at a cell. The mismatches between advective and direct age can be related to the diffusion and dispersion processes (here represented by numerical dispersion as dispersivity was set to zero), which are included in the direct age approach, but neglected in simulating advective ages.

5.2 Flow system and age distribution interpretation

5.2.1 Advective age distribution

The analysis of the advective age and travel distance distributions (Figs. 7 and 8, Table 3) revealed a larger variance of ages for waters with a higher mean age. Following the pathlines of wells with younger waters (e.g. Fig. 6, well locations A, B, C4, C5 and G), recharge areas are more proximal (path length <10 km, Fig. 8, Table 3). Consequently, the particles pass through fewer hydrogeological units and hence the flow path is less influenced by heterogeneous geology, which results in a smaller variance in ages and path lengths (Fig. 8, Table 3). Particles travelling to well locations C1, C2, C3, D, E and F (e.g. Fig. 6) have to travel through a variety of hydrogeological units, characterized by different hydraulic conductivities and effective porosities and hence showing a broader age distribution and larger variance as well as longer travel distances. Their broad and multi-modal age distributions reflect the up-gradient heterogeneity in fluxes, related to hydraulic conductivity and effective porosity. This behaviour is in accordance with conclusions by Weissmann et al. (2002), who investigated groundwater ages in a heterogeneous 3-D alluvial aquifer based on particle tracking and CFC-derived ages.

5.2.2 Regional age pattern

The regional age pattern derived from direct age simulation is consistent with the findings of Meyer et al. (2018a) about the flow system. The two-aquifer system is separated by a confining aquitard in the west. The shallow aquifer system consisting of glaciotectonically disturbed Pleistocene sands mixed with clays is dominated by local and intermediate flow regimes and contains water of younger ages. The confining aquitard (Maade formation) shows older waters and a positive relation between ages and aquitard thickness what agrees with Bethke and Johnson (2008). In the deep Miocene sand aquifer that is interbedded with Miocene clay, regional flow regimes dominate and groundwater ages vary from young waters in the recharge areas in the east, where the overlying confining aquitard does not exist, to very old waters (up to 10 000 years) in the west. The confining Miocene aquitard (Maade formation) influences the age distribution pattern in the underlying Miocene sand in two ways. First, it limits the ability of deeper groundwater to seep upward and mix with the younger waters in the shallow aquifer. Secondly, the age flux from the aquitard to the aquifer shows a positive correlation with the ratio between aquitard thickness and aquifer thickness (Bethke and Johnson, 2008).

At the buried valleys, groundwater exchange and hence age mixing occurs. Upwelling of the older groundwater from the deeper aquifer happens preferentially through these buried valleys. The dense drainage network in the west close to the coast acts as a regional sink, with younger groundwater flowing horizontally and older water flowing vertically and discharging to the drains. At the coastal boundary in the west, where a constant concentration of an “age mass” zero was assigned to the density-corrected constant head boundary, an age wedge characterized by waters of contrasting ages is established as a result of intruding young ocean water that meets old waters in the transition zone. This agrees with the findings by Post et al. (2013) based on simulation of synthetic groundwater age patterns in coastal aquifers using density-driven flow.

The results of our study differ significantly from findings by Sonnenborg et al. (2016), who investigated a regional aquifer system with a similar geological setting located a few hundred kilometres north of the present study area. Their direct simulation of groundwater ages shows a pattern of much younger water than here, rarely exceeding 700 years even in the deepest aquifers, while in our study ages exceeding 10 000 years occur. The discrepancies may arise from differences in the geological models. In the area of Sonnenborg et al. (2016) the thickness of the Miocene sand units decreases towards the west and disappears before reaching the west coast. Sonnenborg et al. (2016) conclude that rivers control the age distribution even in deep aquifers. Based on particle tracking they found that the flow regimes were dominated by local and intermediate flow (see Tóth, 1963), with flow lengths not exceeding 15 km. In contrast, in the study presented here, the Miocene sand extends to the coast and probably beyond. While the age pattern in the shallow aquifers is controlled by rivers and drains (similarly to Sonnenborg et al., 2016), the age pattern in the deep aquifers is dominated by the extent and thickness of the Maade formation, the marsh area as a location of preferred discharge and the occurrence of buried valleys as locations of groundwater exchange, especially upwelling of old groundwater. Particle path lengths reach up to 30 km and regional flow dominates in the Miocene aquifer.

5.3 Perspectives of using spatial and temporal groundwater age distributions in groundwater quantity and quality assessment and management

The groundwater age distribution in aquifers is closely related to the distribution of physical (e.g. hydraulic conductivity and porosity) and chemical parameters (e.g. concentrations of contaminants and natural geogenic elements) of the aquifers and aquitards. Hence, tracer- and model-estimated groundwater age distributions provide important information for the assessment of the hydraulic properties of the subsurface as demonstrated in this study, and as an indicator of groundwater quality and vulnerability (Hinsby et al., 2001a; Sonnenborg et al., 2016), including contaminant migration (Hinsby et al., 2001a), contents of harmful geogenic elements such as arsenic and molybdenum (Edmunds and Smedley, 2000; Smedley and Kinniburgh, 2002, 2017), and the risk of saltwater intrusion (MacDonald et al., 2016; Larsen et al., 2017; Meyer et al., 2018b). Groundwater age distributions in time and space are therefore important pieces of information for groundwater status assessment and the development of proper water management strategies that consider and protect both water resources quality and quantity (MacDonald et al., 2016). Water quality issues are often related to human activities such as contamination or over-abstraction (MacDonald et al., 2016) and are typically found in waters younger than 100 years to depth of about 100 m (Seiler and Lindner, 1995; Hinsby et al., 2001a), although deep subsurface activities may threaten deeper and older resources (Harkness et al., 2017). Deeper and older water is generally not contaminated or affected by human activities, but the impact of natural processes and contents of dissolved trace elements increases with depth and transport times (Edmunds and Smedley, 2000). Similarly, the risk of saltwater intrusion from fossil seawater in old marine sediments increases with depth in inland aquifers and reduces the amount of available high-quality groundwater resources (MacDonald et al., 2016; Larsen et al., 2017; Meyer et al., 2018b). Furthermore, old groundwater resources that are only slowly replenished are more vulnerable to over-exploitation, which leads to declining water tables, increasing hydraulic gradients and long-term non-steady-state conditions that change the regional flow pattern (Seiler and Lindner, 1995) and potentially result in contamination of deeper groundwater resources by shallow groundwater leaking downward. The presented modelling results show that the Miocene sand aquifer is protected by the overlying Maade formation over a wide area. The Miocene aquifer bears old waters (>100 a, see Fig. 10e, f) of high quality (Hinsby and Rasmussen, 2008), especially in the east and the central part of the area, as the risk of seawater intrusion increases towards the west. However, caution should be shown as the shallow and the deep aquifers are naturally connected through buried valleys, where groundwater exchange occurs in both direction (Meyer et al., 2018a). In these geological features, young and possibly contaminated water can be found to greater depth (Seifert et al., 2008; Fig. 10e). Moreover, deep, old waters are vulnerable to contamination by modern pollutants as a result of the construction of wells with long screens, connecting different aquifers separated by aquitards (Seiler and Lindner, 1995; Jasechko et al., 2017; Fig. 2).

6 Conclusions

The originality of this study comes from a 3-D multi-layer coastal regional advective transport model, where heterogeneities are resolved on a grid scale. The distributed effective porosity field was found by parameter estimation based on apparent ages determined from ¹⁴C activities, corrected for dissolution and diffusion. Based on regularized inversion seven effective porosities were estimated. Four of these were found to have high identifiability, indicating that they are well constrained by the age data. The remaining three have moderate to low identifiability, implying that they are less or poorly constrained by the data. In the latter case, parameter estimates close to the preferred values were obtained because of the use of Tikhonov regularization. By using a distributed effective porosity field, it was possible to match the observed age data significantly better than if effective porosity was assumed to be homogeneous and represented by a single value.

The advective age distributions at the well locations show a wide range of ages from a few hundred to several thousand years. Younger waters show narrower unimodal age distribution with small variances while older waters have wide age distributions and are often multi-modal with large variances. The variances in age distribution reflect the spatial heterogeneity encountered by the groundwater when travelling from the recharge location to the sampling point.

The estimated effective porosity field was subsequently applied in a direct age simulation that provided insight into the 3-D groundwater age pattern in a regional multi-layered aquifer system and the probable advance of modern potentially contaminated groundwater. Large areas in the shallow Pleistocene aquifer is dominated by young recharging groundwater (<200 a) while older water is upwelling into rivers and drains in the marsh area. Hence, the upper aquifer is prone to contamination. In large areas the deeper Miocene aquifer is separated and protected by the Maade formation bearing old water, whereas young and possibly contaminated water is located in the recharge area in the east and in the buried valleys where the shallow and deep aquifer systems are connected.

The study clearly demonstrates the governing effect of the highly complex geological architecture of the aquifer system on the age pattern. Even though there are multiple uncertainties and assumptions related to groundwater age and its use in calibration, the results demonstrate that it is possible to estimate transport parameters that contain valuable information for assessment of groundwater quantity and quality issues. This can be used in groundwater management problems in general, as demonstrated in an example of capture zone delineation where a heterogeneous distributed effective porosity field resulted in a 50 % change in the capture zone area compared to the case of homogeneous effective porosity. The adopted approach is easy to implement even in large-scale models where auto-calibration of transport parameters using models based on the advection–dispersion equation might be restricted by computer runtime.