the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Detecting dominant changes in irregularly sampled multivariate water quality data sets
Christian Lehr
Ralf Dannowski
Thomas Kalettka
Christoph Merz
Boris Schröder
Jörg Steidl
Gunnar Lischeid
Time series of groundwater and stream water quality often exhibit substantial temporal and spatial variability, whereas typical existing monitoring data sets, e.g. from environmental agencies, are usually characterized by relatively low sampling frequency and irregular sampling in space and/or time. This complicates the differentiation between anthropogenic influence and natural variability as well as the detection of changes in water quality which indicate changes in single drivers. We suggest the new term “dominant changes” for changes in multivariate water quality data which concern (1) multiple variables, (2) multiple sites and (3) long-term patterns and present an exploratory framework for the detection of such dominant changes in data sets with irregular sampling in space and time. Firstly, a non-linear dimension-reduction technique was used to summarize the dominant spatiotemporal dynamics in the multivariate water quality data set in a few components. Those were used to derive hypotheses on the dominant drivers influencing water quality. Secondly, different sampling sites were compared with respect to median component values. Thirdly, time series of the components at single sites were analysed for long-term patterns. We tested the approach with a joint stream water and groundwater data set quality consisting of 1572 samples, each comprising sixteen variables, sampled with a spatially and temporally irregular sampling scheme at 29 sites in northeast Germany from 1998 to 2009. The first four components were interpreted as (1) an agriculturally induced enhancement of the natural background level of solute concentration, (2) a redox sequence from reducing conditions in deep groundwater to post-oxic conditions in shallow groundwater and oxic conditions in stream water, (3) a mixing ratio of deep and shallow groundwater to the streamflow and (4) sporadic events of slurry application in the agricultural practice. Dominant changes were observed for the first two components. The changing intensity of the first component was interpreted as response to the temporal variability of the thickness of the unsaturated zone. A steady increase in the second component at most stream water sites pointed towards progressing depletion of the denitrification capacity of the deep aquifer.
- Article
(7156 KB) - Full-text XML
-
Supplement
(1191 KB) - BibTeX
- EndNote
Numerous high-frequency sampling studies unravelled the high temporal variability of stream water quality (e.g. Kirchner et al., 2004; Cassidy and Jordan, 2011; Halliday et al., 2012; Neal et al., 2012; Wade et al., 2012; Aubert et al., 2013; Kirchner and Neal, 2013; Tunaley et al. 2016; Rode et al., 2016; Blaen et al., 2017). Therefore, monitoring water quantity and quality on the timescale of the hydrological response of the catchment is a key requirement for understanding water quality dynamics and its driving processes in detail (Kirchner et al., 2004; Neal et al., 2012; Halliday et al., 2012). While the development of sensor technology, data loggers and transmission technology hopefully will help to significantly increase the number of high-frequency monitoring programmes in the future, most of the existing monitoring programmes so far applied a rather low sampling frequency. Nonetheless, there is common agreement that for short periods with high-frequency data, longer periods of low-frequency monitoring provide invaluable context (Burt et al., 2011; Neal et al., 2012; Halliday et al., 2012; Bieroza et al., 2014). This is especially true for existing long-term records which are required as reference to distinguish between natural short-term and long-term variability of the observed variables and the assessment of the effects of anthropogenic influence on water quality such as changes in land use in the catchment (Burt et al., 2008; Howden et al., 2011).
The intriguing temporal and spatial variability in water quality monitoring data sets can in most cases hardly be related to single causal factors. Instead, a variety of biogeochemical processes (e.g. Stumm and Morgan, 1996; Neal, 2004; Beudert et al., 2015), climatic (e.g. Neal, 2004) and hydrological (e.g. Molenat et al., 2008) variability and anthropogenic influences, for example agricultural (e.g. Basu et al., 2010, 2011; Aubert et al., 2013) or forestal (e.g. Neal, 2004) land use, land use change (e.g. Scanlon et al., 2007; Raymond et al., 2008) or urbanization (e.g. Kroeze et al., 2013), interact at different scales impeding identification of clear cause–effect relationships. Usually a single solute is affected by numerous different drivers at different scales (see e.g. Molenat et al., 2008; Lischeid et al., 2010; Schuetz et al., 2016 for ). Inversely, a single driver usually has an impact on various solutes (Massmann et al., 2004; Lischeid and Bittersohl, 2008). This suggests that trend analyses of single variables might easily be misleading with respect to the identification of driving factors. For this purpose techniques which are able to account for the interaction of multiple drivers and observed variables are preferable.
On the other hand, despite their complexity, catchments are highly constrained systems. Usually only a few dominant processes determine the main dynamics of streamflow, groundwater head or water quality (Grayson and Blöschl, 2000; Sivakumar, 2004; Lischeid et al., 2016). Using joint information from different solutes is an established way to derive hypotheses on processes or other causal factors that are dominant in the monitored data. For this purpose, dimension-reduction techniques, especially the linear principal component analysis (PCA), have been used in analyses of multivariate water quality data for a long time, mostly as an exploratory tool for descriptive process identification (e.g. Usunoff and Guzmán-Guzmán, 1989; Haag and Westrich, 2002; Cloutier et al., 2008) or for determining mixing ratios (e.g. Hooper et al., 1990; Capell et al., 2011). If the analysed data consist of time series of one or several variables observed at different sites, then the temporal features of the results of the dimension reduction can be analysed in a spatially explicit way, e.g. with respect to seasonal patterns or long-term developments at the monitored sites (Lischeid and Bittersohl, 2008; Lischeid et al., 2010).
However, many of the methods commonly used for analysing temporal developments in monitoring data sets require regularly sampled data. In practice the spatiotemporal design of sampling campaigns and monitoring networks often evolves during the sampling period in an irregular way. In order to obtain a regularly sampled data set, additional information with a different sampling design, e.g. from pilot studies or single sampling campaigns, might not be utilized in the analysis at all. Further irregularities in the spatiotemporal structure of environmental monitoring data sets arise typically during the monitoring itself from a variety of reasons such as failure of sensors or data loggers, measurement errors, loss of samples or periods of ice or drought. Thus, in environmental monitoring practice, data sets with gaps and periods with corrupted measurements are more the rule rather than the exception (see e.g. Zhang et al., 2018, for river quality data).
Lischeid et al. (2010) suggested a combination of exploratory data analysis methods to detect and analyse dominant processes and their temporal development in multivariate water quality data sets that is capable of dealing with irregular time series. We built on that and extended it towards the detection of “dominant changes” in time series of multivariate water quality data that are monitored at different sites, i.e. at different parts of a catchment or in different catchments within a region. In analogy to the dominant process concept (Grayson and Blöschl, 2000; Sivakumar, 2004), we use the term “dominant changes” in a broad and descriptive sense referring to systemic changes that clearly exceed the usual range of heterogeneities in the temporal, spatial or inter-variable structure of the observed water quality data. The changes we considered as dominant were those that concerned (1) main components of the multivariate water quality data set rather than single water quality variables (multivariate components), (2) behaviour at various sites rather than at single sites (multiple sites), and (3) long-term behaviour rather than short-term fluctuations or single events (long-term patterns).
To identify the dominant changes, we combined exploratory data analysis methods for non-linear dimension reduction, spectral analysis, linear and non-linear trend estimation, and a monotonic trend test in one exploratory framework. The suggested approach was tested with a multivariate water quality data set that has been sampled with a spatially and temporally irregular sampling scheme in northeast Germany from 1998 to 2009. In the following, we present and discuss the results of our case study according to the three aspects of dominant changes: (1) multivariate components, (2) multiple sites and (3) long-term patterns. We continue with a discussion of (4) effects of the irregular sampling and (5) methodological aspects of the exploratory framework.
2.1 Study area
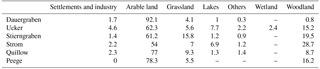
The study area is the upper part of the basin of the Ucker river located in the northeast of Germany, about 90 km north of Berlin, which drains to the Baltic Sea another 50 km further north. It is part of the Leibniz Centre for Agricultural Landscape Research (ZALF) long-term monitoring region AgroScapeLab Quillow, the LTER-D (Long Term Ecological Research Network, Germany) and the TERENO (Terrestrial Environmental Observatories, http://teodoor.icg.kfa-juelich.de, last access: 8 October 2017) Northeastern German Lowland Observatory. Water samples have been taken in the adjacent catchments of Dauergraben (78.9 km2), Stierngraben (104.8 km2), and Quillow (399.4 km2) with its subcatchments Strom (235.8 km2) and Peege (25.6 km2) (Fig. 1). At the ZALF weather station Dedelow, which is situated approximately 500 m northeast of Q_97 (Fig. 1a), a mean annual precipitation of 550 mm and a mean annual temperature of 8.9 ∘C was observed for the hydrological years within the study period (November 1997 to October 2009). The mean annual climatic water balance for this period, calculated from daily precipitation and potential evapotranspiration, was found to be −103 mm, exhibiting high interannual variability with −148 mm in the summer half year and +45 mm in the winter half year.
The topography of the region developed basically during the Pomeranian stage and the Mecklenburgian stage of the Weichselian ice age, i.e. 15 200 to 14 100 years before present. Altitude varies from 20 m in the lowlands of the Ucker river to more than 100 m above sea level in the southwestern part of the study area. During the Pleistocene, repeated advances and recessions of the ice sheet deposited highly heterogeneous unconsolidated sediments of about 150 to 200 m thickness. The base consists of a thick Oligocene clay layer which separates the upper freshwater groundwater system from saline groundwater underneath. Based on borehole surveys, up to seven aquifers divided by layers of till have been identified within the unconsolidated Quaternary sediments. In some parts of the region patches of halophilous plants are found in the lowlands, indicating local upwelling of saline groundwater from the underlying Tertiary aquifer through windows of the Oligocene clay layer.
Loamy and sandy loamy soils that developed from the till substrate prevail. Most of the region is intensively used as cropland, although the fraction of arable land differs between the catchments (Table 1). Forests comprise only a minor fraction of the area (Table 1). Land cover did not change within the study period from 1998 to 2009. The riparian zone of the catchments is mostly used as grassland, underlain by peat and organic and sandy fluvial deposits. The hummocky landscape includes about 1300 closed drainage basins and small ponds with an area of the water surface < 1 ha (Kalettka and Rudat, 2006; Lischeid et al., 2016). Many of the larger depressions have been connected by ditches to facilitate drainage. Partly, these ditches have later been replaced by underground pipes for land reclamation. In addition, agricultural soils are extensively drained by subsurface tile drainage systems. From the 13th century until the end of the 19th century, the energy of the natural water courses was also occasionally used to power mills. Today, those mills are not active any longer and have been replaced in most cases by weirs for water management or ramps. For more details on the study site, please see Merz and Steidl (2015).
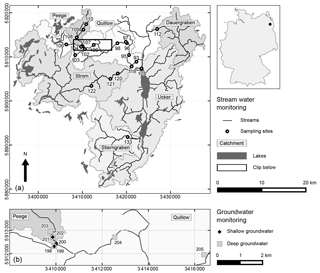
Figure 1Map of the study area. Coordinates of WGS84 ∕ UTM zone 33N are given in m. (a) Stream water monitoring sites and the location of the study area (upper Ucker river catchment) within Germany. (b) Section with the included groundwater monitoring sites. For better readability only the number of the ID of the monitoring sites is shown.
2.2 Sampling and analysis
The monitoring aimed to cover the spatial and temporal variability of water quality along the Quillow stream, its tributaries and the adjacent streams. The main focus of the monitoring was the Quillow catchment. Here, eight sampling sites were located along the main stream and another four at each of the two tributaries Peege and Strom (Fig. 1 and Supplement Table S1). At the streams Dauergraben and Stierngraben and at the Ucker river, stream water quality was monitored at one site respectively. Stream water sampling started in 1998 and was performed until 2009. Discharge data were only available at sites Q_93 and S_118 (Fig. 1a). Thus, we did not include it in the presented analysis. Groundwater quality was monitored in the Quillow catchment only, close to the middle reaches of the stream and close to the mouth of the Peege tributary, from 2000 to 2008 (Fig. 1b). At this site, an up to 15 m thick horizontal till layer separates a shallow and very heterogeneous unconfined aquifer from a mainly confined deep aquifer. The separating till layer crops out further downstream (Merz and Steidl, 2015). Both aquifers were monitored (Table S2). The deep aquifer is known to be confined except at well Gd_204. Groundwater level in the deep aquifer was measured daily with automatic data loggers at wells Gd_198, Gd_201, Gd_203 and Gd_204 (Merz and Steidl, 2014a).
Groundwater quality (Merz and Steidl, 2014b) and stream water quality (Kalettka and Steidl, 2014) monitoring in the Quillow catchment covers a wide range of water quality parameters. For the multivariate analysis in this study, we considered from the joint groundwater and stream water quality data set only the 16 variables with less than 5 % missing values, i.e. , , , , Na+, K+, Mg2+, Ca2+, Cl−, O2, pH, water temperature, redox potential (Eh), electric conductivity (EC), and dissolved organic carbon (DOC) (Table S3). Each sample contained measurements of all 16 variables. Those water samples for which more than 2 of the 16 monitored variables were missing were excluded from the analysis, resulting in a set of 1572 samples. In total, 0.69 % of the values in the data set were missing. In addition, we considered and Fe2+ concentration from the groundwater monitoring (Table S3).
The number of temporal replicates varied between one and 127 per site (Fig. 2). In general, streams were sampled at approximately monthly intervals, and groundwater samples were taken every 3 months. Median (mean) sampling intervals were 29 (38.7) days for stream water and 98 (125.3) days for groundwater. The one shorter sampling interval at site GdQ_198 was an exceptional sample taken during maintenance work. In total, sampling intervals between two consecutive samples varied between 9 and 714 days (Fig. 2). The sites were sampled roughly similarly across seasons (Fig. 2a). The most important systematic deviations from this rule were the Peege sites and the most upstream sites of the Quillow (Figs. 2a and 1), which often fall dry in summer (Merz and Steidl, 2015).
Further details on the data and measurement methods are provided by Merz and Steidl (2015). The selection of water quality data used in this article and the groundwater level data have been published under the CC-BY 4.0 license and can be found in Lehr et al. (2018) and Merz and Steidl (2014a) respectively.

Figure 2(a) Sampling dates at the sites for the whole monitoring period. (b) Box plots of the variability of sampling intervals during the monitoring period. For better readability, the maximum of the x axis is limited to 180 days. The median (red) and mean (blue) of sampling intervals are shown separately for the groundwater and stream water sites. Grey vertical lines mark the 1-day, 1-week and 1-month interval. (a, b) The dashed horizontal line separates groundwater sites (bottom) from stream water sites (top). Labels: P, Peege; Q, Quillow; S, Strom; St, Stierngraben; U, Ucker; D, Dauergraben; Gs, shallow groundwater; Gd, deep groundwater. The number of samples at each site is given in brackets. Names of the sites with more than 50 samples are printed bold.
3.1 Data preprocessing
Missing values were replaced by the median of the respective variable. This concerned at most DOC (3.44 % of the values) and (2.54 %), whereas the percentage of missing values was less than 2 % for each of the other 14 variables (Table S3). Values below detection limit were replaced by 0.5 times that limit. To achieve equally weighted variables the values were z-normalized to zero mean and unit standard deviation for each variable separately.
3.2 Exploratory framework
To identify the dominant changes, we firstly used the non-linear dimension-reduction technique isometric feature mapping (Isomap) to derive the main multivariate water quality components. To account for the interaction of groundwater and stream water, both groundwater and stream water samples have been analysed together in one joint analysis. Secondly, we studied differences between the sites with respect to median component values. Thirdly, we analysed the time series of the components at sites with more than 50 samples. Seasonal patterns were analysed with the Lomb–Scargle approach (Lomb, 1976; Scargle, 1982,, 1989) and – if significant – were subtracted from the series prior to trend analyses. Please note that the term “seasonal” refers to the annual cycle throughout the article. Linear trends were estimated with the Theil–Sen estimator and tested for significance with the Mann–Kendall test. Non-linear trends were depicted with the locally weighted regression (LOESS) approach (Cleveland, 1979; Cleveland and Devlin, 1988). We then related resulting low-frequency patterns to the long-term groundwater head dynamics, likewise determined as the LOESS smooth of the de-seasonalized series. Time series analysis at different sites allowed us to check whether long-term patterns were consistent, pointing to more general effects in the study area.
As the methods do not require regularly sampled data in space or time, we considered every sample as additional information of the spatiotemporal variability of the observed water quality in the study area rather than noise. Consequently, irrespective of irregularities of sampling intervals at a site or differences in sampling intervals and numbers of samples between the different sites, we included as many samples in the analysis as possible to increase the informative value and support the representativeness of the study in space and time. This might lead to a bias in the determination of the components, as well as in the estimation of the trends of the components and their significance, if deviations from a regular sampling scheme follow a systematic pattern. To check for that, we tested the distribution of sampling intervals at all sites with N > 50 (Table S1) for normality with the Shapiro–Wilk test and the temporal development of the lengths of the sampling intervals for the whole observation period for monotonic trends with the Mann–Kendall test. For all tested sites a Gaussian distribution of sampling intervals as well as a monotonic trend of the length of sampling intervals during the observation period was rejected.
3.3 Dimension reduction
Dimension-reduction methods aim to represent a data set with a given number of dimensions (here the number of measured hydrochemical variables) in a new data space with substantially fewer dimensions. This is achieved by projecting the data in a new ordination system which makes a more efficient use of the intrinsic structures of the data set than the original one. The axes of the new ordination system are usually called components or dimensions. In the following, we will use the term “components”. For the values of a component we will use the term “scores”. The reduction of the data set's dimensionality is achieved by considering only some of the new components for further analysis. The selection process is a trade-off between reduction of the dimensionality and minimizing the loss of potentially informative structures. Typically only the first few components are selected as they depict the main structures in the data set.
In the projection, different methods focus on different aspects of the data. For example PCA aims at maximizing variance on the first components, classical multidimensional scaling (CMDS) at preserving the inter-point distances of the input data in the projection and self-organizing maps (SOM) at preserving the neighbourhood relations (topology) of the input data in the projection (Lee and Verleysen, 2007). In the last years, a variety of non-linear dimension-reduction methods have been developed (Van der Maaten et al., 2009). Although being sensitive to noisy data, isometric feature mapping (Tenenbaum et al., 2000) was one of the best-performing approaches when applied to real-world data (Geng et al., 2005). It has been successfully applied in environmental research disciplines, e.g. biodiversity studies (Mahecha et al., 2007), soil sciences (Schilli et al., 2010), climatology (Gámez et al., 2004) and biogeochemistry (Weyer et al., 2014).
3.3.1 Principal component analysis
In our study, the well-established linear principal component analysis (PCA) served as benchmark for the non-linear isometric feature mapping. PCA is one of the most widespread dimension-reduction methods going back to research of Pearson (1901) and Hotelling (1933). For a brief introduction to PCA, please see for example Jolliffe and Cadima (2016) and for a comprehensive one see Jolliffe (2002). PCA aims to successively maximize the variance of the data set on the new calculated components. The scores of the components are calculated as weighted linear combinations of the original variables. The weights (loadings) of the linear combination define the axes of the data space in which the data are projected. The loadings are the eigenvectors derived from an eigenvalue decomposition of the covariance matrix of the analysed variables. If the analysed variables are z-normalized, as was done here, their covariance matrix is equivalent to the (Pearson) correlation matrix. The components are ordered with decreasing size of their eigenvalues. The share of variance that is assigned to a component is proportional to the size of its eigenvalue in relation to the sum of all eigenvalues. Thus, the ratio of total variance that is captured by the considered components gives a measure of performance of the PCA. PCA was performed in R (R Core Team, 2017) with the function “princomp” of the default package “stats”.
3.3.2 Isometric feature mapping
Isometric feature mapping (Isomap) is a non-linear extension of CMDS. It aims to approximate the global non-linearity in a data set by local linear fittings (Geng et al., 2005). This is done by mapping approximated geodesic inter-point distances to an Euclidean distance matrix via a neighbourhood graph G (Tenenbaum et al., 2000). The geodesic distance between two points is the distance along the surface of a (non-linear) manifold, in contrast to the straight-line Euclidean distance (Geng et al., 2005). The neighbourhood graph G consists of segments that connect every data point to its k nearest neighbours directly via Euclidean distances. For all unconnected points the shortest path along the neighbourhood graph G is computed as the smallest sum of connected segments via the Dijkstra algorithm (Dijkstra, 1959). This approximation of the geodesic distances allows the adaptation of G to the global non-linear structures in a data set. The only free parameter k has to be optimized by checking the performance of several runs. The more linear the data, the higher the optimum k will be. If k equals the possible number of connections of one data point to all other data points, the approximations of the geodesic distances are equal to the Euclidean distances and the Isomap results are congruent with those of CMDS and linear PCA (Gámez et al., 2004). Finally the neighbourhood graph G is embedded in the Euclidean space.
In contrast to PCA, assessing performance based on the eigenvalues of the components is not applicable for Isomap. Performance of the dimension reduction of the Isomap approach was assessed and compared to performance of the PCA by the squared Pearson correlation coefficient (R2) of the inter-point distances in the high-dimensional data space and in the low-dimensional projection spanned by selected components (Lischeid and Bittersohl, 2008; Lischeid et al., 2010). A perfect fit would yield a value of 1 and a value of 0 reflects no correlation between the distance matrices of the original data and of the projection. Please note that with this measure the contribution of single components to the overall performance does not necessarily decrease monotonically with increasing order of the components, as it is the case for the eigenvalue-based performance measure of PCA. For the local assessment of the representation of inter-point distances at the individual sites, only the data points from the respective sites were used. Because the selection of data points at a site is only a subset of the global data set for which the dimension reduction was performed, the performances regarding the representation of inter-point distances differ between the individual sites as well as compared to the overall performance for the global data set. At some sites it can even happen that adding more components does not improve the representation of inter-point distances in the low-dimensional projection for every component. Isomap and the determination of the distance matrices were performed with the R package “vegan” (Oksanen et al., 2017).
3.3.3 Interpretation of components
The analysis focused on those components that explained a major fraction of the total inter-point distances. The considered components were regarded to reflect dominant drivers influencing water quality. Here, the term “driver” was used for biogeochemical and hydrological processes as well as for anthropogenic influences affecting water quality. Correspondingly we formulated a hypothesis for each considered component. The interpretation of the components is based on analysing (i) the correlations between measured variables and component scores as well as (ii) spatial and temporal patterns of the scores.
Correlation between scores of a selected component cpx and values of single variables might be blurred due to the effects of other components on the same variable. We excluded those effects by analysing the relationships between scores of the selected component cpx and the residuals of the multiple linear regression (mlr) of the single variable vi at hand and the remaining other considered components CP\x (residuals):
where CP\x is the set of m considered components, without the selected component cpx; and β0 and βj are the intercept and coefficients of the regression
To assess the relationships between components and residuals we used bivariate scatterplots. To summarize the relationships between components and residuals we used the Spearman rank correlation, which enables us to consider non-linear relationships as well, as long as they are monotonic. In addition, it is less sensitive to extreme values than the Pearson correlation.
3.4 Time series analysis
At sites with more than 50 samples, time series of component scores were analysed for seasonal patterns, linear trends and non-linear trends. The sites were compared with respect to the identified long-term patterns to detect general patterns in the study area. The significance level for trend and frequencies in this study was set to p≤0.05. At each site, the fractions of variance of a time series that were assigned to its seasonal pattern, linear trend or non-linear trend were determined as the R2 of the respective pattern with the component series. In the case of significant seasonal patterns, the estimations of the trends were based on the de-seasonalized series. Accordingly, the fractions of variance assigned to the trends were determined as the R2 of the trend pattern with the de-seasonalized series. The decomposition of the time series in a seasonal component and a non-linear trend derived with LOESS was inspired by the seasonal-trend decomposition procedure based on LOESS (STL) of Cleveland et al. (1990).
3.4.1 Lomb–Scargle method
Standard Fourier analysis requires an equidistant time series, which was not given in our study. Therefore, the estimation of seasonal patterns in the time series was done with the Lomb–Scargle method, which is an extension of Fourier analysis to the unevenly spaced case genuinely invented in astrophysics (Lomb, 1976; Scargle, 1982). The application of the Lomb–Scargle method in this study follows to a large extent the workflow suggested by Glynn et al. (2006) as well as Hocke and Kämpfer (2009). Details are given in Appendix A. The implementation used in this paper can be accessed as an R script at https://doi.org/10.4228/ZALF.2017.340 (Lehr et al., 2018).
3.4.2 Theil–Sen estimator and Mann–Kendall test
The linear trend was estimated with the non-parametric Theil–Sen estimator, which is the median of all inter-point slopes in a time series (Theil, 1950a, b, c; Sen, 1968). The Mann–Kendall test (Mann, 1945; Kendall, 1990) was used to test for significant monotonic trends. Identified trends are not necessarily linear. Being based on rank correlation, data do not have to obey any specific distribution. Please note that we did not account for the effect of overestimation of the significance of trends with the Mann–Kendall test due to short-term autocorrelation (Yue et al., 2002). That would have required an assessment of the lag-1 autocorrelation which was hampered by the irregular sampling. Neither did we consider long-term memory and its effects on the statistical significance of the trends (Cohn and Lins, 2005; Zhang et al., 2018). Consequently, we did not consider the possible effects of the irregular sampling on the long-term memory (fractal scaling) of the water quality series either (Zhang et al., 2018). Due to the limited number of samples per year and non-equidistant sampling, the seasonal Mann–Kendall test was not applicable (Fig. 2). Instead, significant seasonal patterns according to the Lomb–Scargle approach were subtracted prior to trend analysis. The Mann–Kendall test was performed with the R package “Kendall” (McLeod, 2011).
3.4.3 Locally weighted regression (LOESS)
We assessed non-linear trends and low-frequency patterns with locally weighted regression (LOESS; Cleveland, 1979; Cleveland and Devlin, 1988), where the smoothing is done by local fitting of a second-order polynomial to each point x in the data set using weighted least squares. The weights for each value to be fitted are scaled to the range from 0 to 1 by the distance d(x) between x and its qth closest point. The ratio of q to the number n of all data points, i.e. the span of the local regression smoother, defines the degree of smoothing. We used the default smoothing span, which is a proportion of of x's nearest neighbours. Data points further away than the qth data point do not contribute to the regression. Within the range of the span, the weights wi of the neighbouring points xi in the least squares fit decrease with increasing distance of xi to x symmetrically around x according to the tricubic weighting function . Again, significant seasonal patterns according to the Lomb–Scargle approach were subtracted prior to trend analysis. For details about choosing different LOESS parametrizations, please see Cleveland (1979) as well as Cleveland and Devlin (1988). Local extrema of the LOESS smooth were identified with the R package “EMD” (Kim and Oh, 2009, 2014.).
4.1 Multivariate components
We achieved the best performance of the Isomap dimension reduction with k=1300 (Table 2). In the following, results are presented for the first four Isomap components representing 88 % of the inter-point distances of the total data set. For single sites (with more than 15 samples), between 29 % and 97 % of the respective inter-point distances were represented (Table S4).
The first component depicted 42 % of the inter-point distances of the total data set. Plotting residuals of the variables versus the first component showed strong positive correlations for , Na+, K+, Mg2+, Ca2+, Cl−, EC, , DOC and slightly weaker, but still positive, correlations for O2 and Eh. Temperature was the only variable correlating negatively with the first component (Fig. 3). Visualization of the component scores versus residuals of solute concentration revealed predominantly linear relationships (Fig. S1 in the Supplement).
The second component reflected 18 % of the inter-point distances in the data. It exhibited clear positive correlation with O2 concentration, pH and Eh, and weaker correlation with Na+, K+ and DOC. It was inversely correlated with Ca2+, EC and (Figs. 3 and S2). In the groundwater samples, and Fe2+ had been determined as well. Both solutes were negatively correlated with this component (Fig. 4a). concentration in the deep groundwater samples was very low (with 27 % of the samples below detection limit) and did not show any clear correlation with the second component. Low component scores in the groundwater came along with high Ca2+ and concentration.
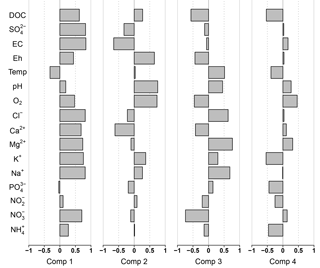
Figure 3Spearman rank correlation of a component and the residuals of the multiple linear regression of the measured variable and the remaining three other components.
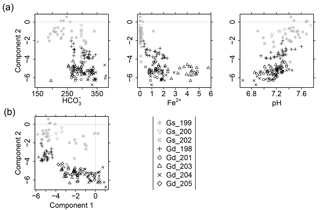
Figure 4(a) Selection of variables versus scores of component 2 for the groundwater samples. Concentration in mg L−1. (b) Scores of component 1 versus component 2 at the groundwater sites.
The relationship of scores of component one and two in the groundwater is shown in Fig. 4b. Except for the two shallow wells close to the Peege stream (Gs_200, Gs_202; see Fig. 1b), scores of the first and second component are negatively related (Fig. 4b).
The third component represented 6 % of the inter-point distances in the data set. The residuals exhibited positive correlation for Na+, Mg2+, Cl−, pH and temperature. Negative correlations were found for , Ca2+, O2, Eh and DOC (Figs. 3 and S3).
Another 22 % of the inter-point distances in the data were assigned to the fourth component. Residuals of the component scores showed negative correlation for , , K+, temperature, and DOC and positive correlation for O2 (Figs. 3 and S4). The range of component values was spanned mainly by single large values of , and K+ that cannot be explained with the preceding three components (Fig. S4). This highlights the importance of particular events for the fourth component.
4.2 Multiple sites
Median values of scores of the first component clearly differed between streams (Fig. 5a). At the Strom sites, the median score values were considerably lower than those from the other stream water sampling sites. The median values of scores of the sites at the Quillow and Stierngraben showed intermediate values followed by the Ucker site, the Peege sites and finally the Dauergraben with the highest median score value. Groundwater samples in general exhibited consistently low scores for the first component, but without clear differences between deep and shallow groundwater samples. Mixing of water from different streams was visible at site Q_93 downstream of the confluence of the Quillow (Q_95) and of the Strom stream (S_118), as well as at site Q_100 downstream of the confluence of Q_104, Q_102 and P_107 (Figs. 1 and 5a).
Stream water samples exhibited the highest scores of the second component, whereas low scores were limited to deep groundwater samples, and shallow groundwater samples were in an intermediate position (Fig. 5b). Median values of the stream water sites were approximately on the same level except for the sites Q_103, Q_106 and U_128, which exhibited noticeably higher median values than the other stream water sites, and the two Peege sites P_109 and P_108, which exhibited median values on the same level as the shallow groundwater sites Gs_199 and G_200. The scores in the deep groundwater clearly showed the largest absolute values, indicating the significance of deep groundwater for this component (Fig. 5b).
Scores of the third component in the deep groundwater were consistently higher than in shallow groundwater, while the stream water samples covered the whole range of values (Fig. 5c). The lowest scores of the third component were found at the Peege sites and in the shallow groundwater, and the highest scores were found at Ucker, Dauergraben and the deep groundwater. At the Quillow stream, scores tended to increase from the spring to the outlet. The effect of mixing of tributaries with different water qualities was visible along the course of the Peege and Quillow streams downstream of the respective confluences at the sites P_108, Q_95 and Q_93 (Figs. 1 and 5c).
The range of values of the fourth component was strongly biased towards negative values, caused by single events at some sites which exhibited very low values (Fig. 5d).
4.3 Long-term patterns
Time series of scores of the components were studied at sites with more than 50 temporal replicates. This applied for 13 stream water sites (Table S1). All dominant frequencies (for details, please see Appendix A) interpreted as seasonal patterns had a period length in the range between 350 and 380 days. For de-seasonalization these seasonal patterns were subtracted from the time series prior to analysis for linear and non-linear trends.
Most of the time series of the scores of the first component exhibited clear seasonal patterns with maximum scores during the winter season (Figs. 6 and 7). Between 30 % and 67 % of the variance was assigned to the seasonal pattern. At all sites we found significant negative monotonic trends (Fig. 6). The strongest decline was found at site D_112 and the weakest trend at site Q_97 (not shown). The linear trend comprised between 9 % and 48 % of the variance of the de-seasonalized time series (Fig. 6). In contrast, the LOESS smooth depicted 14 % to 57 % of the variance (Fig. 6). It showed a decrease until December 2004 approximately and an increase thereafter (Fig. 8). The de-seasonalized time series of groundwater heads showed a similar behaviour, with the minimum water level in June 2006 (Fig. 8). Timing of the minimum values of the scores of the first component varied between sites, spanning a range from 17 February 2004 to 17 March 2009 (Fig. 8). As an example, Fig. 7 gives the time series of scores of the first component at site Q_93, the seasonal pattern extracted from the series and the de-seasonalized time series with the non-linear trend estimated with the LOESS smoother.
Unlike for the first component, only 5 of the 13 considered time series of the second component exhibited a clear significant seasonal pattern, accounting for 17 % to 48 % of the variance (Fig. 6). The maxima of the seasonal patterns of the sites at Quillow and Ucker were in spring and at Stierngraben and Dauergraben in summer. In contrast, significant monotonic trends were found at most of the stream water sampling sites. All significant trends of the second component were positive. The linear trend comprised between 5 % and 16 % of the variance of the time series, while the LOESS smooth comprised between 4 % and 25 %.
Values of the third component showed a clear seasonal pattern with maxima in summer (Fig. 6). Between 30 % and 60 % of the variance was assigned to the seasonal signal. The only exception was site D_112 were the seasonal pattern was distorted by strong maxima in the winters of 2003, 2004 and 2007. Only at four sites were significant linear trends found. All of them were negative, comprising between 6 % and 13 % of the variance. The LOESS smooth depicted between 0 % and 21 % of the variance.
For the fourth component, significant seasonal patterns with maxima in summer were observed at 7 of the 13 analysed series, comprising between 17 % and 61 % of the variance (Fig. 6). Five sites showed a significant monotonic trend, comprising between 5 % and 10 % of the variance. A negative trend was observed at site St_133 only. Four sites showed a positive trend. The LOESS smooth depicted between 1 % and 16 % of the variance.
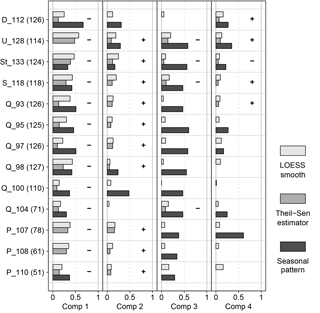
Figure 6Fraction of variance of the time series of the Isomap component scores of sites with N > 50 assigned to the seasonal pattern (dark grey) and the trend estimated by the linear Theil–Sen estimator (mid-grey) as well as the non-linear LOESS smooth (light grey). Fraction of variance is derived as the R2 of the scores of the respective component with the seasonal pattern or the estimated trend. Only significant seasonal patterns and linear trends are shown. The sign of the linear Theil–Sen estimator is given in the respective line. The number of samples at each site is given in brackets.
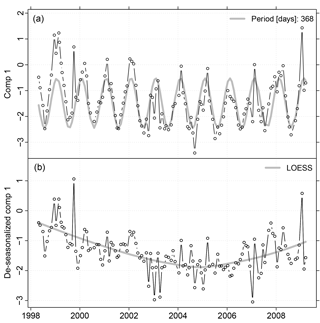
Figure 7(a) Time series of scores of the first component at site Q_93 (N=126) in black and the seasonal pattern estimated with Lomb–Scargle in grey. (b) The de-seasonalized series in black and the non-linear trend estimated with LOESS in grey.
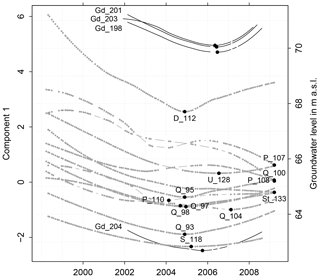
Figure 8Left y axis: LOESS smooth of time series of the first component at sites with N > 50 in grey. If a significant seasonal pattern was present, this was removed before smoothing. Right y axis: LOESS smooth of the de-seasonalized groundwater level at four sites in black. The black dots mark the minima of the LOESS-smoothed series.
5.1 Multivariate components
Non-linear Isomap performed in this study only slightly better with respect to the representation of inter-point distances than PCA (Table 2), suggesting that mainly linear relationships were of importance for the overall dynamics in the data set. As there were only minor differences, we will present in the following the results of Isomap only.
For PCA and Isomap, the first component represents by definition the correlation structure that predominantly can be extracted from the set of variables as a whole. If all the loadings of the first component of a PCA have the same sign, it is a weighted average of all the analysed variables (Jolliffe, 2002; Jolliffe and Cadima, 2016). The stronger the analysed variables are linearly correlated, the more the first component approximates the arithmetic mean of all variables (for examples with hydrometric data see Lischeid, et al., 2010; Lehr et al., 2015). Furthermore, the first component serves as reference for all the subsequent components.
In this study each sample of the multivariate water quality data set is uniquely defined by a sampling site and a sampling date. Thus, the first component depicted (a) for each sampling site the pattern that was most prominent in the time series of the variables correlating with the first component and (b) between the sampling sites the difference in concentration level of those variables. High values of the first component indicate synchronous appearance of relatively high Eh and EC together with relatively high concentration of , Cl−, , Na+, K+, Mg2+, Ca2+, DOC and O2 accompanied with relatively low temperature (Fig. 3).
The whole study region is characterized by relatively intense agriculture (Table 1). Thus, in addition to the natural background, we assume a general effect of the agricultural practice on the solute concentration level and the dynamics of the water quality series in the area. Enhanced concentration of , Cl−, and Ca2+ is typical for groundwater and stream water in regions with intense agriculture compared to forested areas (Broers and van der Grift, 2004; Fitzpatrick et al., 2007; Lischeid and Kalettka, 2012). Nitrogen and potassium are the main ingredients of mineral fertilizers. Cl− and are the dominating anions in potassium fertilizers. is a major ingredient of phosphorus fertilizers and in some nitrogen fertilizers. Calcite is present in some nitrogen fertilizers or is applied separately via liming. DOC might be leached from slurry application or via tile drains after mechanical destruction of topsoil aggregates during tillage (Graeber et al., 2012). In addition, cations from the soil matrix might be leached by an enhanced anion concentration (mainly ) (Jessen et al., 2017). Overall the application of fertilizers and other agricultural practices like tillage tend to enhance the solute concentration of seepage water (Pierson-Wickmann et al., 2009). Thus, we interpreted the first component as the enhancement of the natural background level of solute concentration due to agricultural practices.
Compared to the first component, the relationships of the second component with Eh, pH and O2 concentration were more clearly expressed (Figs. 3 and S2). The range of the scores of the second component was spanned by the lowest values in the deep groundwater and the highest values in the stream water (Fig. 5b), whereas shallow groundwater exhibited intermediate scores. This sequence corresponds to redox conditions expected in those water categories. Thus, we interpreted the second component as a redox-controlled component covering a sequence from reducing conditions in deep groundwater to post-oxic conditions in shallow groundwater and oxic conditions in stream water. O2 and concentration in deep groundwater samples usually was below the detection limit, which is a common feature in this region (Merz et al., 2009). in seepage and groundwater can be denitrified by microorganisms which use the oxidation of sulfides to sulfate as electron donor for denitrification (Massmann et al., 2003; Jørgensen et al., 2009). We ascribed the high and Fe2+ concentration to the oxidation of pyrite (Figs. 4a and S2). Pyrite and other sulfides are abundant in the Pleistocenic sediments of northern Germany (e.g. Weymann et al., 2010). Consequently, the pH decreases, calcite gets dissolved and the concentration increases. Part of the released Ca2+ replaces Na+ and K+ being sorbed to clay minerals.
We interpreted the clear separation in the third component between relatively low scores for the shallow aquifer and relatively high scores for the deep aquifer as a reflection of two opposing gradients (Fig. 5c). High concentration of , O2 and DOC and relatively high Eh values being negatively related to the third component (Fig. 3) are indicative of groundwater close to the surface, whereas enhanced concentration of the positively related solutes Na+, Mg2+ and Cl− is characteristic for local upwelling of saline groundwater from the underlying Tertiary aquifers at greater depth (Hannemann and Schirrmeister, 1998; Tesmer et al., 2007). The scores of the stream water samples, in turn, reflect the mixing ratio of groundwater from the two aquifers to the streamflow. We expect the baseflow maintained from the deep aquifer to be relatively enriched with geogenic solutes compared to the water that stems from the shallow aquifer or faster-responding flow components like tile drain discharge and surface runoff. Water from the shallow aquifer is expected to be relatively enriched with solutes originating from the surface compared to water that stems from the deep aquifer.
The range of values of the fourth component was dominated by single extremely low scores, reflecting samples with high concentration of , and K+ (Fig. S4). The catchments of the analysed streams are only sparsely populated and mainly characterized by intensive agriculture (Table 1). In agricultural landscapes slurry is a typical source in which those nutrients occur in high concentration (Hooda et al., 2000). We are not aware of any other high-concentration sources of this combination of nutrients in the region. The small number of scores with very low scores implied that there were merely single events occurring at some of the sites only. This fits the finding that the timing of slurry application is crucial for the amount of nutrient loss to the streams (Hooda et al., 2000; Cherobim et al., 2017). Thus, we interpreted the negative peaks of the fourth component as sporadic events of slurry application, being either unintentionally directly applied to the stream during the spreading of the slurry or being leached via surface runoff and tile drain discharge after application.
5.2 Multiple sites
The interpretation of the first component as an agriculturally induced enhancement of the natural background level of most of the water quality variables is consistent with the spatial pattern of median component scores at the different sites. The highest scores were found in the Dauergraben stream and in the Peege stream (Fig. 5a). Both catchments are characterized by intense agriculture, a relatively dense network of tile drains and hardly any buffer strips along the streams leading to a rapid transmission of solute-enriched waters from the fields to the streams. In contrast, the Strom stream exhibited the lowest scores among all streams. Compared to the other streams, the valley of the Strom stream is clearly deep cut. Therefore, the Strom stream is expected to receive along its whole length continuous and substantial groundwater inflow from the deep aquifer. In addition, the valley slopes are covered with forest and are not in agricultural use, acting as a buffer strip for the agricultural impact. Furthermore, the fraction of arable land in the Strom catchment is smallest and the fraction of woodland is largest compared to the other catchments (Table 1). Main parts of the Strom catchment are situated within a nature conservation area, furthermore limiting the agricultural impact in its riparian zone.
Deep groundwater, shallow groundwater and the stream water were well separated by the second component (Fig. 5b). Exceptions were the sites at the Peege stream, which are mainly supplied with water from tile drainage and the shallow aquifer and consequently yield median values similar to the shallow groundwater. The largest positive median values of the second component, being higher than those of the other stream water sites, were observed at sites with less than 13 samples (Q_103 and Q_106) and at the site U_128, which received at least partly waters from a different region than the other stream water sites (Figs. 1 and 5b). Thus, for the purpose of this study, we restricted our analysis on the spatial variability of the redox component to the categories of deep groundwater, shallow groundwater and stream water.
However, we took a closer look at the non-linear structure that became apparent for the deep groundwater samples in some of the residual plots of the second component (Fig. S2). In addition, we related the groundwater values of the second component to the first component and the and Fe2+ concentration (Fig. 4). The negative relationship between the second component and the first component in the deep groundwater suggests that the agricultural load represented by the first component acts as a driver for the sulfide oxidation represented by the second component. Among all deep groundwater wells, the deepest groundwater well Gd_198 exhibited the lowest scores of the first component (Fig. 5a) and the highest scores of the second component (Fig. 4b and Fig. 5b). This suggests that due to the relatively low agricultural load the oxidation of sulfides was the least pronounced among all deeper wells. Similar relationships between the extent of sulfate oxidation in the aquifer and agricultural input have been found in other studies (e.g. Zhang et al., 2009; Jessen et al., 2017, and references therein).
We expected the ratio of groundwater from the deep aquifer contributing to the streamflow to increase in general with increasing catchment size. The Peege stream is mainly fed by the shallow aquifer and yielded consequently median values of the third component similar to the shallow groundwater sites (Fig. 5c). In comparison the streams of Quillow, Strom and Stierngraben exhibited higher median values, indicating a larger proportion of groundwater from the deep aquifer contributing to runoff in comparison to the Peege stream. The sites U_128 and D_112 showed the highest median values of the third component among the stream water sites, being equal or even higher than those of the deep groundwater sites (Fig. 5c). Both sites have subsurface catchments that do not include the deep groundwater sampling sites in this study. Site D_112 is on the eastern side of the river Ucker, while all groundwater sampling sites are on the western side of it (Fig. 1a). In addition, its higher median value of the third component was partly due to several peaks during the winter time. Those coincide with high values of Cl−. These might indicate road salt application, but we did not investigate this further, as the winter peaks considered only this single site. Site U_128 is situated at the outlet of the lake Unteruckersee upstream of the confluence of the Quillow stream (Fig. 1a). There, we did not expect a contribution of the groundwater sampled in the Quillow catchment either.
All the stream water sampling sites with negative peaks of the fourth component are located near arable fields which are known to get fertilized by slurry (Fig. 5d). For example the two most affected sites Q_102 and Q_103 receive slurry input from a large pig farm close by (Gernot Verch, personal communication, 2018). Overall, only a few slurry input events accounted for 22 % of the representation of the inter-point distances of all the water quality samples of the water quality data set in the Isomap projection (Fig. 5d). However, the performance of the representation of the inter-point distances after adding the fourth component differed substantially between the different sites (Table S4). In the case of site S_121 the representation of inter-point distances with four components (R2=0.68) was even slightly worse than with three components (R2=0.66) (Table S4). This indicated an anomaly at this specific site compared to all other sites with respect to the fourth component, i.e. the solutes which mainly determine the fourth component. We traced this phenomenon back to one single sample from 25 May 2004 which comprised relatively high DOC values and at the same time relatively low values of K+, which is opposite the relationships indicative of the fourth component (Fig. 3). The deterioration of the representation of the inter-point distances after adding the fourth component at this site vanished in an Isomap analysis which was performed without this sample. We were not able to find an explanation for this exceptional sample. However, it underlined that by applying a dimension-reduction method every single sample is put into the perspective of the global features of the data set as depicted by the components. Overall, the fourth component underlines the necessity of developing and using methods in environmental data analysis, which enable us to consider non-linear processes as well as singular and site-specific events.
5.3 Long-term patterns
Dominant changes were observed for the first two components (Fig. 6). We interpreted the non-linear long-term trend of the first component at most stream water sites (Fig. 8) as the response of stream water quality to the interannual variability of depth to groundwater. An increase in the thickness of the unsaturated zone leads in general to longer residence time of seepage water, increasing retardation and buffering of topsoil seepage water, which reduces the solute concentration originating from the surface in the seepage water and consequently reduces the values of the first component.
Trends similarly shaped to the non-linear trend of the first component of stream water quality were observed for the water level in the deep groundwater. In general, the turning points of the deep groundwater head time series lag behind those of the scores of the first component of the stream water sites by approximately 1.5 years (Fig. 8). The earlier date of the turning point at groundwater gauge Gd_204 in October 2005 is most probably an artefact, caused by the effect of the large time gaps in 2006 and 2007 on the de-seasonalizing at this site and has to be considered with care.
We suggest that the time lag between stream water chemistry and water level in the deep aquifer is due to different response times to changes in the moisture conditions of the unsaturated zone. Compared to the relatively fast response of the stream water quality, the groundwater level in the deep aquifer reacts slower. In general, the overall trend of groundwater recharge reflects a relatively slow response to changes in the regional water balance. The velocity of seepage in the sediments of the upstream region of the Quillow catchment is estimated to be roughly 1 m per year.
The seasonal patterns, i.e. the annual variability, in the time series of the scores of the first component in the streams were ascribed to transient hydraulic decoupling of the mostly affected topsoils from the streams in summer. Usually there is hardly any seepage during the dry summer months at all. This leads often to drought in the uppermost stream reaches (Fig. 2a and Merz and Steidl, 2015). Thus, shallow groundwater and tile drain discharge, both sources with relatively high agricultural load, did not contribute to stream discharge during these periods and larger areas of the catchment got hydraulically decoupled from the stream network (Merz and Steidl, 2015). Similar effects of the seasonal variability of the hydrological connectivity of streams, groundwater and tile drainage in agricultural catchments on the concentration level of solutes originating from agriculture in the stream water have been reported, e.g. for in the Schaugraben study catchment in the north of Germany (Wriedt et al., 2007) and for and Cl− in the Kervidy-Naizin catchment in western France (Molenat et al., 2008; Aubert et al., 2013).
The other dominant change in stream water chemistry observed in this study was the continuous increase in the second component at most stream water sites (Fig. 6). All of the sampling sites with very low values of the second component were in the deep aquifer (Fig. 5b). The positive trends of the second component at most stream water sites were ascribed to changes in the chemistry of the baseflow originating from groundwater. Considering the interpretation of the second component, this translates into enhanced oxidation of geogenic sulfides in the deeper aquifer due to the continuous input of and DOC originating from agriculture and subsequent calcite dissolution. Geogenic sulfides, such as pyrite, serve as electron donors for denitrification. The consumption of the geogenic sulfides is irreversible and might lead to the depletion of the denitrification capacity in the deep aquifer in the long run (Merz et al., 2009; Zhang et al., 2009; Merz and Steidl, 2015). Consequently, buffering of surplus from agricultural land use is expected to decrease and concentration in the groundwater and the stream water is expected to increase. The hypothesized long-term development should be of concern for the water resources and environmental protection agencies with respect to future water quality and related international commitments, such as the Water Framework Directive (EU, 2000), the Groundwater Directive (EU, 2006) and the Nitrates Directive (EU, 1991) of the European Union. Substantial time lags have to be considered for the response of groundwater quality to measures that reduce leaching of (e.g. Pierson-Wickmann et al., 2009; Meals et al., 2010). In the Quillow catchment, we expect travel times in the order of magnitude of decades for the seepage water to reach the deep aquifer.
We did not observe dominant changes for the other two water quality components during the course of the observation period. The main temporal feature of the third component was a very distinct and steady seasonal pattern, as could be expected for the mixing ratio of groundwater from the deep aquifer. All stream water sites with n > 50, except for D_112, showed a distinct seasonal pattern with maximum scores in the summer, which is consistent with the assumption that the fraction of deep groundwater in the streams is highest during this period (Fig. 6). The seasonal pattern at site D_112 was disturbed by the winter peaks we ascribed to road salt application (Sect. 5.2).
Because of its strong dependence from single events (Fig. 5d), the results of the estimation of the seasonal patterns and the trends of the fourth component have to be considered with care. The maxima of the seasonal pattern in summer at some sites were interpreted as reduced nutrient inputs to the stream due to nutrient uptake of plants and maximum buffering capacity of the unsaturated zone in summer. There were no indications for any effects of those events that we ascribed to the direct effect of slurry application on samples taken on the subsequent sampling dates at the affected sites. This is presumably due to the width of the sampling interval (Fig. 2).
In the case of dependence of a component from single events, change might be also related to clustering of those events during certain parts of the series, either for series at single sites or sets of series. Most of the extreme events of the fourth component appeared during the first half of the observation period (not shown). However, because of the small number of clearly outstanding events, we did not investigate this further (Fig. 5d).
In this study, the presented analysis of changes in water quality was limited by the temporal resolution of the data. Aspects such as long-term memory effects, as indicated by fractal scaling of solute series (Kirchner et al., 2000) and the observed scale-crossing non-self-averaging behaviour of solute series (Kirchner and Neal, 2013), were not considered. However, we assume that the suggested use of multivariate components gives some robustness to the detected changes compared to the analysis of single solutes.
5.4 Effects of the irregular sampling
There was an obvious spatial bias with a focus on the Quillow catchment itself, conditioned by the focus of the monitoring (Sect. 2.2, Fig. 1). Stream sampling sites were only partly independent from each other, as the same streams had been sampled along different reaches. This needs to be considered in the interpretation of the components. In our exploratory approach, differences between subsequent stream reaches helped to identify the effects of tributaries or groundwater that recharged between the respective sampling sites. In that way, the stream was used as a measurement device for biogeochemical processes and water-borne solute transport in different parts of the catchment and the interlinkages of groundwater and stream water.
It is important to note that our approach does not require the same number of samples per site (Fig. 2). The derived components constitute a frame in which all samples are integrated independent of the number of samples per site. Thus, in our application we get the information of how those sites with very few samples group or behave in relation to the others. Even a few samples might indicate for example that the respective site behaves similar to other sites with respect to some components and very different with respect to other components. The influence of single samples for the integration of the different sites into the global pattern of the water quality relationships summarized by the fourth component is an illustrative example for that (Sect. 5.2). Thus, even occasional sampling at some sites helps in assessing the strength of effects of the respective drivers at these sites and might support or contradict hypotheses on spatial variability and related long-term patterns of those influences. This information would be lost if those samples would be excluded beforehand.
In addition, the approach followed here does not require identical temporal sampling resolution at all sites or synchronous sampling dates. Thus, a strictly regular sampling design, which is hardly feasible, is no prerequisite. Correspondingly, data from different monitoring programs could be used for a joint analysis. Sampling intervals at the sampling sites with N > 50 were not normally distributed and biased towards deviations that are longer than the median (Fig. 2b). Several series exhibited large time gaps. However, as sampling intervals did not change systematically throughout the monitoring period we assume that the effects on the results of the significance test with Mann–Kendall were negligible (Sect. 3.2). In comparison, the trend estimations with the Theil–Sen estimator and LOESS are more robust, as they incorporate the exact sampling dates explicitly in the calculations. Thus, we do not expect major effects on the sign of the Theil–Sen estimator or the general shape of the LOESS smooth at the given temporal resolution.
In general, the interpretation of the components should consider the temporal structure of the data set. For example in this study the drying out of the streams at the Peege sites and the most upstream sites of the Quillow in summer was the most important systematic deviation from an otherwise roughly similar sampling across seasons (Fig. 2a). This information was included in the interpretation of the first component (Sect. 5.3). If the monitoring would in general not have been performed roughly similarly across seasons, e.g. if one or more seasons would in general be missing, the estimation of the seasonality would not be applicable. If the monitoring would be such that there would be different seasons sampled in different years, this would have to be considered in the estimation of the trend.
5.5 Exploratory framework
The application of a dimension-reduction approach was motivated by the assumption that drivers influencing water quality usually affect more than one solute and that single solutes are affected by more than one driver. Like in preceding studies (e.g. Lischeid and Bittersohl, 2008; Lischeid et al., 2010), the representation of water quality data in low-dimensional space required only a few components to capture the main features of the data set.
Whether the relationships in the data set are mainly linear ones, as in this study, or whether there are considerably non-linear relationships as well is usually not known in advance. Thus, if the aim is to consider and check for possible non-linear relationships in the analysis we recommend using PCA as a linear benchmark for Isomap (demonstrated by Lischeid and Bittersohl, 2008). In a straightforward way this allows for (1) assessing whether the dominant correlation structures in the data set are mainly linear or non-linear and (2) identifying those components, samples, sites and periods deviating from the linear behaviour as captured by the PCA.
Based on the correlation of component scores and residuals, we formulated for each considered component a hypothesis on a dominant driver influencing water quality. Again, whether the relationships are linear, as they were for most of the global relationships in this study (Figs. S1–S4), is usually not known beforehand. Summarizing the relationships between residuals and components with Spearman rank correlation enables us to consider non-linear relationships between residuals and components as well, as long as they are monotonic. However, the main benefit in this study was that the Spearman rank correlation is less sensitive to extreme values compared to the Pearson correlation. This concerned especially the assessment of the relationships of the residuals of and Cl− with the second component and the residuals of and with the fourth component (Figs. S2 and S4), which were more strongly expressed with Pearson correlation due to a few single extreme values. The derived correlations differ from default loadings of PCA, which are defined as the coefficients of the linear combination of the analysed variables which is used to calculate the principal component scores. Those coefficients, scaled by the square root of the eigenvalue of the respective component, are equivalent to the Pearson correlation of PCA component scores and analysed variables. It is important to note that the differences in the evaluation of the correlations of components and the measured variables might lead to different interpretations of the components.
The treatment of censored values can substantially affect the derived components and the subsequent interpretation of the results and has to be considered carefully (Helsel, 2012, and references therein). For the application of Isomap, it is required to provide numerical values for the values below the detection limit. For simplicity, we here used half the detection limit as a maker for values below the detection limit. We checked for the effect of this substitution by comparing the Isomap results of the presented analysis with another Isomap analysis in which we excluded the two most affected variables, and (Fig. S4). The correlation of the Isomap scores of the interpreted components 1 to 4 of version 1 (with and ) versus version 2 (without and ) yielded R2 values of 0.99 for the first component, 0.98 for the second component, 0.97 for the third component and 0.64 for the fourth component. The comparison of the two versions with respect to the Spearman rank correlations of Isomap scores of the first four components and the residuals (please see Fig. 3 for the respective values of version 1) yielded R2 values of 0.98 for the first component, 0.99 for the second component, 0.99 for the third component and 0.88 for the fourth component. Thus, the first three components are virtually identical. The fourth component is affected, because is one of the important variables for this component (Fig. 3). Nevertheless, the similarity of the correlations of Isomap scores and the fourth component of both versions suggests that the characteristics of the fourth component were not merely introduced by the substitution of the values below the detection limit for . Thus, overall, the substitution did not substantially affect the interpretation of the considered components; however, we acknowledge that the replacement of censored data with some fraction of the reporting limit is not generally appropriate for dealing with censored data (Gilliom and Helsel, 1986; Singh and Nocerino, 2002; Helsel, 2005, 2006, 2012). For data sets which are more heavily affected by censored values, other dimension-reduction methods such as the rank-based approaches suggested by Helsel (2012) should be preferred.
For data sets in which the number of measured variables differs between the sites there is a trade-off between the number of considered variables versus the number of considered sites. Depending on the focus of the study different selections of the data set can be used. For example if the main focus of the study is to analyse the multivariate water quality dynamics in detail it might be worthwhile to disregard some sites to be able to include more variables. If the focus is to maintain the spatial coverage of the monitoring, like in this study, more sites might be of more value than additional variables. Depending on the available resources a third option would be to perform two analyses, one focusing on more variables, one on more sites and comparing the results. If it is possible to link the considered components, like we did in the preceding paragraph, this proceeding can be used for spatial extrapolation of the hypotheses derived from the version which included more variables. However, in our case the sketched trade-off was not dramatic. Thus, we excluded only the variables with more than 5 % missing values (Sect. 2.2) to keep the possible effect of any method of replacement rather low.
To prevent adding variables with little information gain it is recommendable to perform a correlation analysis beforehand and rule out highly correlated variables. For this purpose we recommend not to rely only on a numerical measure of correlation, but to visually examine the scatterplots of the respective variables to check for systematic deviations from the global relationship. There might be for example some sites or seasons in which the otherwise tight relationship gets weaker, pointing to local or temporal phenomena.
Technically it is possible to combine other data than solutes (e.g. sediment data and biological indicators) together with the solutes in one joined data set for the derivation of the components. However, the multivariate components derived by the dimension-reduction approach are the basis of the subsequent interpretation of the results. It has to be considered as well that all included variables are equally weighted due to the z scaling prior to the dimension reduction. Thus, including other types of data might in some cases complicate the interpretation. In general, we recommend not mixing variables with different scales of measures (e.g. nominal variables and ratio scaled variables) in the database for the derivation of the components.
Instead, data which were not used in the derivation of the components can be used as additional information for their interpretation. For example in this study we used in addition to the spatiotemporal features of the components other variables like groundwater level series, and concentration from the groundwater samples, the spatial distribution of land use and expert knowledge on the study area for the derivation of the hypotheses. A thorough testing of the hypotheses, for example through hydrochemical modelling or numerical experiments with virtual catchments, was out of the scope of this study.
However, an interpretation of the components as distinct drivers is no prerequisite for the further analysis of the components. In any case, the components constitute, and can simply be used as, a condensed representation of similar behaviour among the analysed variables according to the constraints of the used dimension-reduction method.
For PCA and Isomap each component describes subsequently the correlation structure that is most prominent in the remainder of what has not already been assigned to the higher-ranked components. This implies that each component has to be interpreted with respect to the higher-ranked components. Also, the consideration of the respective other components in the interpretation of a component can be helpful to carve out its characteristics as it was done here with the residuals of the multiple linear regression of the respective three other components and the measured variables (e.g. Fig. S1). Beyond that, it can be helpful to elucidate the interaction of the components as it was done here for example for scores of the first and second component (Fig. 4b).
The sites differed substantially with respect to the median values of the four analysed multivariate components (Fig. 5). However, these components comprised the largest fraction of the inter-point distances at any single site with more than 18 samples (Table S4). We conclude that our results identified major regional phenomena rather than site-specific peculiarities. This is consistent with the prior assumption that there are a few dominant drivers which determine the main stream water and groundwater quality dynamics in the region. This provides some confidence to hypothesize that these drivers presumably play a major role even in adjacent catchments that have not been sampled so far.
To detect and characterize the dominant changes in the multivariate water quality data we explored whether there were shifts in time in specific components, whether they were linear or non-linear in nature and whether trends occurred at many or only at single sites. For example for the scores of the first component, the Mann–Kendall approach identified monotonic trends at various stream water sampling sites (Fig. 6). However, the linear trend estimation failed to detect the non-linear trend that was observed at many series (Fig. 8). This reflects the well-known sensitivity of global linear trend estimation to low-frequency patterns that are not entirely covered by the observation period (Koutsoyiannis, 2006; Milliman et al., 2008; Lins and Cohn, 2011).
The LOESS smooths of the de-seasonalized series, on the other hand, did clearly reveal the similarity between the long-term behaviour of groundwater level in the deep aquifer and the series of the first component. In our exploratory approach, the LOESS smooth of the de-seasonalized series served as a descriptive tool for illustrating rather than for proving non-linear long-term patterns. No significance test was applied. The outcome of the LOESS smoother highly depends on the parameterization of the approach (i.e. the degree of smoothness) that would have to be justified prior to the testing of significance.
We suggested and tested an exploratory approach for the detection of dominant changes in multivariate water quality data sets with irregular sampling in space and time. The combination of the selected methods aimed to provide a broadly applicable exploratory framework for typical existing monitoring data sets, e.g. from environmental agencies, which are often characterized by relatively low sampling frequency and irregularities of the sampling in space and/or time. In the approach, we applied a dimension-reduction method to derive multivariate water quality components and analysed their spatiotemporal features with respect to changes that concerned more than single sites, short-term fluctuations or single events.
The components can be used irrespective of an interpretation as drivers influencing water quality. By definition, the components are a compact description of the common dynamics among the water quality variables. Thus, similar behaviour in space and time among the water quality variables as well as systematic changes in the multivariate water quality data can be addressed in a purely descriptive manner. This can be used for example to test the often implicit assumption of constant boundary conditions of scientific process and modelling studies. Furthermore, the components and their spatiotemporal features per se can serve as reference for further studies, e.g. detailed process studies with higher temporal resolution, and the assessment of future developments of water quality in an area. In this study, the components were used to develop hypotheses on dominant drivers influencing water quality and to analyse the temporal and spatial variability of those influences.
It is emphasized that the presented approach is readily applicable with data from common monitoring programs without specific requirements concerning sampling frequency or regular distribution of sampling sites, sampling dates and sampling intervals, except that there should be no systematic bias in the respective distribution. Even variables which have to be excluded from the derivation of the components, for example because of the amount of missing values or because they have been monitored only at subsets of the sampling sites, can be related to the components as additional information for their interpretation. For example in this study we used the concentration of Fe2+ and in the groundwater as additional information for the interpretation of the second component. Thus, the approach allows an efficient use of existing monitoring data as well as the consideration of often neglected irregular pieces of data from for example pilot studies or single sampling campaigns. Irregularities in the structure of a data set are not seen as a fundamental hindrance, but as an additional source of information. We see this as a major advantage for the analysis of comprehensive water quality monitoring programs, both from a scientific perspective and from a more applied point of view of for example water resources and environmental agencies. Therefore, we recommend the approach especially for the exploratory assessment of existing long-term low-frequency multivariate water quality monitoring data sets.
A selection of R scripts that covers the main steps of the exploratory framework is provided at https://doi.org/10.4228/ZALF.2017.340 (Lehr et al., 2018) under the CC-BY 4.0 licence. The selection of R scripts comes together with the water quality data used in this paper and some examples of exploratory plots not included in this paper. The groundwater level data used in this paper are provided at https://doi.org/10.4228/ZALF.2000.272 (Merz and Steidl, 2014a).
A given discrete time series Y(ti) with i=1, …, N and centred around zero can be described as a superposition from sin and cos terms with amplitudes a and b, time ti, angular frequency ω=2πf and a noise term ni.
Lomb (1976) introduced an additional factor τ to consider deviations from the evenly spaced case.
The constant scales the term to the centre of the period covered by the series for every frequency j. If the starting point of the series is set to zero, tave enables us to correct for offsets between the spectral components and thus allows us to correctly reconstruct the original series out of its spectral components (Hocke, 1998; Hocke and Kämpfer, 2009).
With these two extensions of the time term, Eq. (A1) can be rewritten as
with amplitude and phase .
The Lomb–Scargle periodogram PN(ω) (Eq. A4) normalized with the total variance of the data σ2 equals the linear least squares fit of the time series model in Eqs. (A1) and (A3) for a certain frequency (Lomb, 1976; Press et al., 2007).
The amplitudes a and b can be computed out of the square root of the corresponding sin and cos terms of the normalized Lomb–Scargle periodogram, which yields the normalized power spectral density at certain frequencies (Hocke and Kämpfer, 2009).
Different modified series can be reconstructed out of any set of spectral components. So the method might be used for example for band-pass filtering or gap filling of the analysed series (Hocke and Kämpfer, 2009).
The number of frequencies in which the series is decomposed is calculated with the empirical formula derived out of Monte Carlo simulations by Horne and Baliunas (1986) (Glynn et al., 2006; Press et al., 2007).
The false-alarm probability or statistical significance level p of the PN(ω) value at a certain frequency is calculated with equation (Scargle, 1982; Glynn et al., 2006; Press et al., 2007)
M is the number of test frequencies, which is here set to Nindep; and z is the tested value of PN(ω) at a certain frequency. To diminish aliasing, the highest test frequency is set to the Nyquist rate . Because of the irregular sampling, the sampling rate Δt is approximated here by the average sampling interval . The lowest test frequency is the inverse of the sampling range (Scargle, 1982; Press et al., 2007).
Although Nindep should be the number of independent frequencies in the signal it is possible that frequencies lying close to each other share the same underlying trigger. This leakage of power is promoted by the uneven sampling and oversampling of the frequency domain M>N (Scargle, 1989; Horne and Baliunas, 1986). In addition, the effect may be enhanced because of local high sampling density, autocorrelation in the data or very strong momentum of the underlying trigger.
With regard to these circumstances, which apply especially for the groundwater level series in this study, only the dominant frequencies were used to identify seasonal patterns. The term “dominant frequency” is used here for the peaks in between groups of significant frequencies. If such groups build “significance plateaus”, the median of this plateau is taken as dominant frequency.
The supplement related to this article is available online at: https://doi.org/10.5194/hess-22-4401-2018-supplement.
The authors declare that they have no conflict of interest.
The long-term monitoring program that provided the data for this study would
not have been possible without the diligent work of many colleagues. We would
like to thank Roswitha Schulz, Dorith Henning, Ralph Tauschke,
Joachim Bartelt†, Peter Bernd and Bernd Schwien for the
installation of sampling sites, including numerous groundwater wells, and for
performing the sampling program in spite of sometimes harsh field conditions.
In addition we acknowledge the painstaking work of Rita Schwarz†
and Melitta Engel in the chemical laboratory of the Institute of Landscape
Hydrology as well as of the staff of the central chemical laboratory of the
Leibniz Centre for Agricultural Landscape Research. We thank Gernot Verch of
the research station Dedelow for the information on the historical
development of agricultural land use in the study area. We thank the editor
Stacey Archfield for the smooth handling of the review process and the two
anonymous referees for their contributions and constructive comments,
especially the issue of censored values, which helped to improve the
manuscript. Christian Lehr received funding from the Leibniz Association
(SAW-2012-IGB-4167) within the International Leibniz Research School: aquatic
boundaries and linkages in a changing environment (Aqualink). We used free
software products under the GNU General Public Licence and thank the
respective communities. Maps and the determination of the catchments' areas
were carried out with Quantum GIS 2.14.5 (https://www.qgis.org/, last
access: 28 August 2016) and statistical analyses and the graphs were
performed using the R statistical software environment, version 3.4.1 (R Core
Team, 2017; http://www.r-project.org, last access:
8 October 2017).
Edited by: Stacey
Archfield
Reviewed by: two anonymous referees
Aubert, A. H., Gascuel-Odoux, C., Gruau, G., Akkal, N., Faucheux, M., Fauvel, Y., Grimaldi, C., Hamon, Y., Jaffrézic, A., Lecoz-Boutnik, M., Molénat, J., Petitjean, P., Ruiz, L., and Merot, P.: Solute transport dynamics in small, shallow groundwater-dominated agricultural catchments: insights from a high-frequency, multisolute 10 yr-long monitoring study, Hydrol. Earth Syst. Sci., 17, 1379–1391, https://doi.org/10.5194/hess-17-1379-2013, 2013.
Basu, N. B., Destouni, G., Jawitz, J. W., Thompson, S. E., Loukinova, N. V., Darracq, A., Zanardo, S., Yaeger, M., Sivapalan, M., Rinaldo, A., and Rao, P. S. C.: Nutrient loads exported from managed catchments reveal emergent biogeochemical stationarity, Geophys. Res. Lett., 37, L23404, https://doi.org/10.1029/2010GL045168, 2010.
Basu, N. B., Thompson, S. E., and Rao, P. S. C.: Hydrologic and biogeochemical functioning of intensively managed catchments: A synthesis of top-down analyses, Water Resour. Res., 47, W00J15, https://doi.org/10.1029/2011WR010800, 2011.
Beudert, B., Bässler, C., Thorn, S., Noss, R., Schröder, B., Dieffenbach-Fries, H., Foullois, N., and Müller, J.: Bark Beetles Increase Biodiversity While Maintaining Drinking Water Quality, Conserv. Lett., 8, 272–281, https://doi.org/10.1111/conl.12153, 2015.
Bieroza, M. Z., Heathwaite, A. L., Mullinger, N. J., and Keenan, P. O.: Understanding nutrient biogeochemistry in agricultural catchments: the challenge of appropriate monitoring frequencies, Environ. Sci.-Proc. Imp., 16, 1676–1691, https://doi.org/10.1039/C4EM00100A, 2014.
Blaen, P. J., Khamis, K., Lloyd, C., Comer-Warner, S., Ciocca, F., Thomas, R. M., MacKenzie, A. R., and Krause, S.: High-frequency monitoring of catchment nutrient exports reveals highly variable storm event responses and dynamic source zone activation, J. Geophys. Res.-Biogeo., 122, 2265–2281, https://doi.org/10.1002/2017JG003904, 2017.
Broers, H. P. and van der Grift, B.: Regional monitoring of temporal changes in groundwater quality, J. Hydrol., 296, 192–220, https://doi.org/10.1016/j.jhydrol.2004.03.022, 2004.
Burt, T. P., Howden, N. J. K., Worrall, F., and Whelan, M. J.: Importance of long-term monitoring for detecting environmental change: lessons from a lowland river in south east England, Biogeosciences, 5, 1529–1535, https://doi.org/10.5194/bg-5-1529-2008, 2008.
Burt, T. P., Howden, N. J. K., Worrall, F., and McDonnell, J. J.: On the value of long-term, low-frequency water quality sampling: avoiding throwing the baby out with the bathwater, Hydrol. Process., 25, 828–830, https://doi.org/10.1002/hyp.7961, 2011.
Capell, R., Tetzlaff, D., Malcolm, I., Hartley, A., and Soulsby, C.: Using hydrochemical tracers to conceptualise hydrological function in a larger scale catchment draining contrasting geologic provinces, J. Hydrol., 408, 164–177, https://doi.org/10.1016/j.jhydrol.2011.07.034, 2011.
Cassidy, R. and Jordan, P.: Limitations of instantaneous water quality sampling in surface-water catchments: Comparison with near-continuous phosphorus time-series data, J. Hydrol., 405, 182–193, https://doi.org/10.1016/j.jhydrol.2011.05.020, 2011.
Cherobim, V. F., Huang, C.-H., and Favaretto, N.: Tillage system and time post-liquid dairy manure: Effects on runoff, sediment and nutrients losses, Agr. Water Manage. 184, 96–103, https://doi.org/10.1016/j.agwat.2017.01.004, 2017.
Cleveland, R., Cleveland, W., McRae, J., and Terpenning, I.: STL: A seasonal-trend decomposition procedure based on loess, J. Off. Stat., 6, 3–73, 1990.
Cleveland, W. S.: Robust Locally Weighted Regression and Smoothing Scatterplots, J. Am. Stat. Assoc., 74, 829–836, https://doi.org/10.1080/01621459.1979.10481038, 1979.
Cleveland, W. S. and Devlin, S. J.: Locally Weighted Regression: An Approach to Regression Analysis by Local Fitting, J. Am. Stat. Assoc., 83, 596–610, https://doi.org/10.1080/01621459.1988.10478639, 1988.
Cloutier, V., Lefebvre, R., Therrien, R., and Savard, M. M.: Multivariate statistical analysis of geochemical data as indicative of the hydrogeochemical evolution of groundwater in a sedimentary rock aquifer system, J. Hydrol., 353, 294–313, https://doi.org/10.1016/j.jhydrol.2008.02.015, 2008.
Cohn, T. A. and Lins, H. F.: Nature's style: Naturally trendy, Geophys. Res. Lett., 32, L23402, https://doi.org/10.1029/2005GL024476, 2005.
Dijkstra, E. W.: A note on two problems in connexion with graphs, Numer. Math., 1, 269–271, https://doi.org/10.1007/BF01386390, 1959.
DLR-DFD and UBA (German Aerospace Centre-German Remote Sensing Data Centre and German Federal Environmental Agency): CORINE Land Cover 2000, Daten zur Bodenbedeckung – Deutschland (Data on land cover – Germany), published on DVD, 2004.
EU: Council Directive 91/676/EEC of 12 December 1991 concerning the protection of waters against pollution caused by nitrates from agricultural sources, Official Journal of the European Communities, 1–8, 1991.
EU: Directive 2000/60/EC of the European Parliament and of the Council of 23 October 2000 establishing a framework for Community action in the field of water policy, Official Journal of the European Communities, 1–70, 2000.
EU: Directive 2006/118/EC of the European Parliament and of the Council of 12 December 2006 on the protection of groundwater against pollution and deterioration, Official Journal of the European Union, 19–31, 2006.
Fitzpatrick, M., Long, D., and Pijanowski, B.: Exploring the effects of urban and agricultural land use on surface water chemistry, across a regional watershed, using multivariate statistics, Appl. Geochem., 22, 1825–1840, https://doi.org/10.1016/j.apgeochem.2007.03.047, 2007.
Gámez, A. J., Zhou, C. S., Timmermann, A., and Kurths, J.: Nonlinear dimensionality reduction in climate data, Nonlin. Processes Geophys., 11, 393-398, https://doi.org/10.5194/npg-11-393-2004, 2004.
Geng, X., Zhan, D.-C., and Zhou, Z.-H.: Supervised nonlinear dimensionality reduction for visualization and classification, IEEE T. Syst. Man Cy. B, 35, 1098–1107, https://doi.org/10.1109/TSMCB.2005.850151, 2005.
Gilliom, R. J. and Helsel, D. R.: Estimation of Distributional Parameters for Censored Trace Level Water Quality Data: 1. Estimation Techniques, Water Resour. Res., 22, 135–146, https://doi.org/10.1029/WR022i002p00135, 1986.
Glynn, E., Chen, J., and Mushegian, A.: Detecting periodic patterns in unevenly spaced gene expression time series using Lomb–Scargle periodograms, Bioinformatics, 22, 310–316, https://doi.org/10.1093/bioinformatics/bti789, 2006.
Graeber, D., Gelbrecht, J., Pusch, M. T., Anlanger, C., and von Schiller, D.: Agriculture has changed the amount and composition of dissolved organic matter in Central European headwater streams, Sci. Total Environ., 438, 435–446, https://doi.org/10.1016/j.scitotenv.2012.08.087, 2012.
Grayson, R. and Blöschl, G. (Ed.): Spatial patterns in catchment hydrology: observations and modelling, Cambridge University Press Cambridge, UK, 2000.
Haag, I. and Westrich, B.: Processes governing river water quality identified by principal component analysis, Hydrol. Process., 16, 3113–3130, https://doi.org/10.1002/hyp.1091, 2002.
Halliday, S. J., Wade, A. J., Skeffington, R. A., Neal, C., Reynolds, B., Rowland, P., Neal, M., and Norris, D.: An analysis of long-term trends, seasonality and short-term dynamics in water quality data from Plynlimon, Wales, Sci. Total Environ., 434, 186–200, https://doi.org/10.1016/j.scitotenv.2011.10.052, 2012.
Hannemann, M. and Schirrmeister, W.: Paläohydrogeologische Grundlagen der Entwicklung der Süss-/Salzwassergrenze und der Salzwasseraustritte in Brandenburg, Brandenburg Geowissenschaftliche Beiträge, 5, 61–72, 1998.
Helsel, D. R.: More Than Obvious: Better Methods for Interpreting Nondetect Data, Environ. Sci. Technol., 39, 419A–423A, https://doi.org/10.1021/es053368a, 2005.
Helsel, D. R.: Fabricating data: How substituting values for nondetects can ruin results, and what can be done about it, Chemosphere, 65, 2434–2439, https://doi.org/10.1016/j.chemosphere.2006.04.051, 2006.
Helsel, D. R.: Statistics for Censored Environmental Data Using Minitab and R, 2nd ed., John Wiley & Sons, 2012.
Hocke, K.: Phase estimation with the Lomb-Scargle periodogram method, Annales Geophysicae, 16, 356–358, 1998.
Hocke, K. and Kämpfer, N.: Gap filling and noise reduction of unevenly sampled data by means of the Lomb-Scargle periodogram, Atmos. Chem. Phys., 9, 4197–4206, https://doi.org/10.5194/acp-9-4197-2009, 2009.
Hooda, P. S., Edwards, A. C., Anderson, H. A., and Miller, A.: A review of water quality concerns in livestock farming areas, Sci. Total Environ., 250, 143–167, https://doi.org/10.1016/S0048-9697(00)00373-9, 2000.
Hooper, R. P., Christophersen, N., and Peters, N. E.: Modelling streamwater chemistry as a mixture of soilwater end-members – An application to the Panola Mountain catchment, Georgia, U.S.A., J. Hydrol., 116, 321–343, https://doi.org/10.1016/0022-1694(90)90131-G, 1990.
Horne, J. and Baliunas, S.: A prescription for period analysis of unevenly sampled time series, Astrophys. J., 302, 757–763, 1986.
Hotelling, H.: Analysis of a complex of statistical variables into principal components, J. Educ. Psychol., 24, 417–441, https://doi.org/10.1037/h0071325, 1933.
Howden, N. J. K., Burt, T. P., Worrall, F., and Whelan, M. J.: Monitoring fluvial water chemistry for trend detection: hydrological variability masks trends in datasets covering fewer than 12 years, J. Environ. Monitor., 13, 514–521, https://doi.org/10.1039/C0EM00722F, 2011.
Jessen, S., Postma, D., Thorling, L., Müller, S., Leskelä, J., and Engesgaard, P.: Decadal variations in groundwater quality: A legacy from nitrate leaching and denitrification by pyrite in a sandy aquifer, Water Resour. Res., 53, 184–198, https://doi.org/10.1002/2016WR018995, 2017.
Jolliffe, I.: Principal Component Analysis, 2nd ed., Springer, 2002.
Jolliffe, I. T. and Cadima, J.: Principal component analysis: a review and recent developments, Philos. T. R. Soc S.-A, 374, 20150202, https://doi.org/10.1098/rsta.2015.0202, 2016.
Jørgensen, J. C., Jacobsen, O. S., Elberling, B., and Aamand, J.: Microbial Oxidation of Pyrite Coupled to Nitrate Reduction in Anoxic Groundwater Sediment, Environ. Sci. Technol., 43, 4851–4857, https://doi.org/10.1021/es803417s, 2009.
Kalettka, T. and Rudat, C.: Hydrogeomorphic types of glacially created kettle holes in North-East Germany, Limnologica – Ecology and Management of Inland Waters, 36, 54–64, https://doi.org/10.1016/j.limno.2005.11.001, 2006.
Kalettka, T. and Steidl, J.: Measurement of stream water chemical ingredients, Quillow catchment, Germany, https://doi.org/10.4228/ZALF.1998.265, 2014.
Kendall, M.: Rank Correlation Methods, Charles Griffin Book Series, 1990.
Kim, D. and Oh, H.-S.: EMD: A Package for Empirical Mode Decomposition and Hilbert Spectrum, R J., 1, 40–46, 2009.
Kim, D. and Oh, H.-S.: EMD: Empirical Mode Decomposition and Hilbert Spectral Analysis, 2014.
Kirchner, J., Feng, X., and Neal, C.: Fractal stream chemistry and its implications for contaminant transport in catchments, Nature, 403, 524–527, 2000.
Kirchner, J., Feng, X., Neal, C., and Robson, A.: The fine structure of water-quality dynamics: the (high-frequency) wave of the future, Hydrol. Process., 18, 1353–1359, https://doi.org/10.1002/hyp.5537, 2004.
Kirchner, J. W. and Neal, C.: Universal fractal scaling in stream chemistry and its implications for solute transport and water quality trend detection, P. Natl. Acad. Sci., 110, 12213–12218, https://doi.org/10.1073/pnas.1304328110, 2013.
Koutsoyiannis, D.: Nonstationarity versus scaling in hydrology, J. Hydrol., 324, 239–254, https://doi.org/10.1016/j.jhydrol.2005.09.022, 2006.
Kroeze, C., Hofstra, N., Ivens, W., Löhr, A., Strokal, M., and van Wijnen, J.: The links between global carbon, water and nutrient cycles in an urbanizing world – the case of coastal eutrophication, Curr. Opin. Env. Sust., 5, 566–572, https://doi.org/10.1016/j.cosust.2013.11.004, 2013.
Lee, J. A. and Verleysen, M.: Nonlinear Dimensionality Reduction, Springer, 2007.
Lehr, C., Pöschke, F., Lewandowski, J., and Lischeid, G.: A novel method to evaluate the effect of a stream restoration on the spatial pattern of hydraulic connection of stream and groundwater, J. Hydrol., 527, 394–401, https://doi.org/10.1016/j.jhydrol.2015.04.075, 2015.
Lehr, C., Kalettka, T., Merz, C., Steidl, J., and Lischeid, G.: R scripts for the detection of dominant changes in irregularly sampled multivariate water quality data sets, https://doi.org/10.4228/ZALF.2017.340, 2018.
Lins, H. F. and Cohn, T. A.: Stationarity: Wanted Dead or Alive?, J. Am. Water Resour. As., 47, 475–480, https://doi.org/10.1111/j.1752-1688.2011.00542.x, 2011.
Lischeid, G. and Bittersohl, J.: Tracing biogeochemical processes in stream water and groundwater using non-linear statistics, J. Hydrol., 357, 11–28, https://doi.org/10.1016/j.jhydrol.2008.03.013, 2008.
Lischeid, G. and Kalettka, T.: Grasping the heterogeneity of kettle hole water quality in Northeast Germany, Hydrobiologia, 689, 63–77, https://doi.org/10.1007/s10750-011-0764-7, 2012.
Lischeid, G., Krám, P., and Weyer, C.: Tracing Biogeochemical Processes in Small Catchments Using Non-linear Methods, edited by: Müller, F., Baessler, C., Schubert, H., and Klotz, S., Springer, the Netherlands, 2010.
Lischeid, G., Kalettka, T., Merz, C., and Steidl, J.: Monitoring the phase space of ecosystems: Concept and examples from the Quillow catchment, Uckermark, Ecol. Indic., 65, 55–65, https://doi.org/10.1016/j.ecolind.2015.10.067, 2016.
Lomb, N.: Least-squares frequency analysis of unequally spaced data, Astrophys. Space Sci., 39, 447–462, 1976.
Mahecha, M. D., Martínez, A., Lischeid, G., and Beck, E.: Nonlinear dimensionality reduction: Alternative ordination approaches for extracting and visualizing biodiversity patterns in tropical montane forest vegetation data, Ecol. Inform., 2, 138–149, https://doi.org/10.1016/j.ecoinf.2007.05.002, 2007.
Mann, H. B.: Nonparametric Tests Against Trend, Econometrica, 13, 245–259, 1945.
Massmann, G., Tichomirowa, M., Merz, C., and Pekdeger, A.: Sulfide oxidation and sulfate reduction in a shallow groundwater system (Oderbruch Aquifer, Germany), J. Hydrol., 278, 231–243, https://doi.org/10.1016/S0022-1694(03)00153-7, 2003.
Massmann, G., Pekdeger, A., and Merz, C.: Redox processes in the Oderbruch polder groundwater flow system in Germany, Appl. Geochem., 19, 863–886, https://doi.org/10.1016/j.apgeochem.2003.11.006, 2004.
McLeod, A.: Kendall: Kendall rank correlation and Mann-Kendall trend test, available at: https://CRAN.R-project.org/package=Kendall (last access: 8 October 2017), 2011.
Meals, D. W., Dressing, S. A., and Davenport, T. E.: Lag Time in Water Quality Response to Best Management Practices: A Review, J. Environ. Qual., 39, 85–96, 2010.
Merz, C. and Steidl, J.: Measurement of groundwater heads, Quillow catchment, Germany, https://doi.org/10.4228/ZALF.2000.272, 2014a.
Merz, C. and Steidl, J.: Measurement of ground water chemical ingredients, Quillow catchment, Germany, https://doi.org/10.4228/ZALF.2000.266, 2014b.
Merz, C. and Steidl, J.: Data on geochemical and hydraulic properties of a characteristic confined/unconfined aquifer system of the younger Pleistocene in northeast Germany, Earth Syst. Sci. Data, 7, 109–116, https://doi.org/10.5194/essd-7-109-2015, 2015.
Merz, C., Steidl, J., and Dannowski, R.: Parameterization and regionalization of redox based denitrification for GIS-embedded nitrate transport modeling in Pleistocene aquifer systems, Environ. Geol., 58, 1587, https://doi.org/10.1007/s00254-008-1665-6, 2009.
Milliman, J. D., Farnsworth, K. L., Jones, P. D., Xu, K. H., and Smith, L. C.: Climatic and anthropogenic factors affecting river discharge to the global ocean, 1951–2000, Global Planet. Change, 62, 187–194, https://doi.org/10.1016/j.gloplacha.2008.03.001, 2008.
Molenat, J., Gascuel-Odoux, C., Ruiz, L., and Gruau, G.: Role of water table dynamics on stream nitrate export and concentration in agricultural headwater catchment (France), J. Hydrol., 348, 363–378, https://doi.org/10.1016/j.jhydrol.2007.10.005, 2008.
Neal, C.: The water quality functioning of the upper River Severn, Plynlimon, mid-Wales: issues of monitoring, process understanding and forestry, Hydrol. Earth Syst. Sci., 8, 521–532, https://doi.org/10.5194/hess-8-521-2004, 2004.
Neal, C., Reynolds, B., Rowland, P., Norris, D., Kirchner, J. W., Neal, M., Sleep, D., Lawlor, A., Woods, C., Thacker, S., Guyatt, H., Vincent, C., Hockenhull, K., Wickham, H., Harman, S., and Armstrong, L.: High-frequency water quality time series in precipitation and streamflow: From fragmentary signals to scientific challenge, Sci. Total Environ., 434, 3–12, https://doi.org/10.1016/j.scitotenv.2011.10.072, 2012.
Oksanen, J., Blanchet, F. G., Friendly, M., Kindt, R., Legendre, P., McGlinn, D., Minchin, P. R., O'Hara, R. B., Simpson, G. L., Solymos, P., Stevens, M. H. H., Szoecs, E., and Wagner, H.: vegan: Community Ecology Package, available at: https://CRAN.R-project.org/package=vegan, R-package version 2.4-4, last access: 8 October 2017.
Pearson, K. F.: LIII. On lines and planes of closest fit to systems of points in space, Philos. Mag., 2, 559–572, https://doi.org/10.1080/14786440109462720, 1901.
Pierson-Wickmann, A.-C., Aquilina, L., Martin, C., Ruiz, L., Molénat, J., Jaffrézic, A., and Gascuel-Odoux, C.: High chemical weathering rates in first-order granitic catchments induced by agricultural stress, Chem. Geol., 265, 369–380, https://doi.org/10.1016/j.chemgeo.2009.04.014, 2009.
Press, W., Flannery, B., Teukolsky, S., and Vetterling, W.: Numerical recipes, Cambridge University Press, 2007.
Raymond, P. A., Oh, N.-H., Turner, R. E., and Broussard, W.: Anthropogenically enhanced fluxes of water and carbon from the Mississippi River, Nature, 451, 449–452, https://doi.org/10.1038/nature06505, 2008.
R Core Team: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria, https://www.R-project.org/ (last access: 8 October 2017), 2017.
Rode, M., Wade, A. J., Cohen, M. J., Hensley, R. T., Bowes, M. J., Kirchner, J. W., Arhonditsis, G. B., Jordan, P., Kronvang, B., Halliday, S. J., Skeffington, R. A., Rozemeijer, J. C., Aubert, A. H., Rinke, K., and Jomaa, S.: Sensors in the Stream: The High-Frequency Wave of the Present, Environ. Sci. Technol., 50, 10297–10307, https://doi.org/10.1021/acs.est.6b02155, 2016.
Scanlon, B. R., Jolly, I., Sophocleous, M., and Zhang, L.: Global impacts of conversions from natural to agricultural ecosystems on water resources: Quantity versus quality, Water Resour. Res., 43, W03437, https://doi.org/10.1029/2006WR005486, 2007.
Scargle, J.: Studies in astronomical time series analysis. II-Statistical aspects of spectral analysis of unevenly spaced data, Astrophys. J., 263, 835–853, 1982.
Scargle, J.: Studies in astronomical time series analysis. III-Fourier transforms, autocorrelation functions, and cross-correlation functions of unevenly spaced data, Astrophys. J., 343, 874–887, 1989.
Schilli, C., Lischeid, G., and Rinklebe, J.: Which processes prevail?: Analyzing long-term soil solution monitoring data using nonlinear statistics, Geoderma, 158, 412–420, https://doi.org/10.1016/j.geoderma.2010.06.014, 2010.
Schuetz, T., Gascuel-Odoux, C., Durand, P., and Weiler, M.: Nitrate sinks and sources as controls of spatio-temporal water quality dynamics in an agricultural headwater catchment, Hydrol. Earth Syst. Sci., 20, 843–857, https://doi.org/10.5194/hess-20-843-2016, 2016.
Sen, P. K.: Estimates of the Regression Coefficient Based on Kendall's Tau, J. Am. Stat. Assoc., 63, 1379–1389, https://doi.org/10.1080/01621459.1968.10480934, 1968.
Singh, A. and Nocerino, J.: Robust estimation of mean and variance using environmental data sets with below detection limit observations, Chemometr. Intell. Lab., 60, 69–86, https://doi.org/10.1016/S0169-7439(01)00186-1, 2002.
Sivakumar, B.: Dominant processes concept in hydrology: moving forward, Hydrol. Process., 18, 2349–2353, https://doi.org/10.1002/hyp.5606, 2004.
Stumm, W. and Morgan, J.: Aquatic chemistry, Wiley, 1996.
Tenenbaum, J., Silva, V., and Langford, J.: A global geometric framework for nonlinear dimensionality reduction, Science, 290, 2319–2323, 2000.
Tesmer, M., Möller, P., Wieland, S., Jahnke, C., Voigt, H., and Pekdeger, A.: Deep reaching fluid flow in the North East German Basin: origin and processes of groundwater salinisation, Hydrogeol. J., 15, 1291–1306, https://doi.org/10.1007/s10040-007-0176-y, 2007.
Theil, H.: A rank-invariant method of linear and polynomial regression analysis I:, Proceedings of the Royal Netherlands Academy of Sciences, 53, 386–392, 1950a.
Theil, H.: A rank-invariant method of linear and polynomial regression analysis II:, Proceedings of the Royal Netherlands Academy of Sciences, 53, 521–525, 1950b.
Theil, H.: A rank-invariant method of linear and polynomial regression analysis III:, Proceedings of the Royal Netherlands Academy of Sciences, 53, 1397–1412, 1950c.
Tunaley, C., Tetzlaff, D., Lessels, J., and Soulsby, C.: Linking high-frequency DOC dynamics to the age of connected water sources, Water Resour. Res., 52, 5232–5247, https://doi.org/10.1002/2015WR018419, 2016.
Usunoff, E. J. and Guzmán-Guzmán, A.: Multivariate Analysis in Hydrochemistry: An Example of the Use of Factor and Correspondence Analyses, Ground Water, 27, 27–34, https://doi.org/10.1111/j.1745-6584.1989.tb00004.x, 1989.
Van der Maaten, L., Postma, E., and van den Herik, H.: Dimensionality Reduction: A Comparative Review, TiCC-TR 2009-005, 2009.
Wade, A. J., Palmer-Felgate, E. J., Halliday, S. J., Skeffington, R. A., Loewenthal, M., Jarvie, H. P., Bowes, M. J., Greenway, G. M., Haswell, S. J., Bell, I. M., Joly, E., Fallatah, A., Neal, C., Williams, R. J., Gozzard, E., and Newman, J. R.: Hydrochemical processes in lowland rivers: insights from in situ, high-resolution monitoring, Hydrol. Earth Syst. Sci., 16, 4323–4342, https://doi.org/10.5194/hess-16-4323-2012, 2012.
Weyer, C., Peiffer, S., Schulze, K., Borken, W., and Lischeid, G.: Catchments as heterogeneous and multi-species reactors: An integral approach for identifying biogeochemical hot-spots at the catchment scale, J. Hydrol., 519, 1560–1571, https://doi.org/10.1016/j.jhydrol.2014.09.005, 2014.
Weymann, D., Geistlinger, H., Well, R., von der Heide, C., and Flessa, H.: Kinetics of N2O production and reduction in a nitrate-contaminated aquifer inferred from laboratory incubation experiments, Biogeosciences, 7, 1953–1972, https://doi.org/10.5194/bg-7-1953-2010, 2010.
Wriedt, G., Spindler, J., Neef, T., Meißner, R., and Rode, M.: Groundwater dynamics and channel activity as major controls of in-stream nitrate concentrations in a lowland catchment system?, J. Hydrol., 343, 154–168, https://doi.org/10.1016/j.jhydrol.2007.06.010, 2007.
Yue, S., Pilon, P., Phinney, B., and Cavadias, G.: The influence of autocorrelation on the ability to detect trend in hydrological series, Hydrol. Process., 16, 1807–1829, https://doi.org/10.1002/hyp.1095, 2002.
Zhang, Y.-C., Slomp, C. P., Broers, H. P., Passier, H. F., and Cappellen, P. V.: Denitrification coupled to pyrite oxidation and changes in groundwater quality in a shallow sandy aquifer, Geochim. Cosmochim. Ac., 73, 6716–6726, https://doi.org/10.1016/j.gca.2009.08.026, 2009.
Zhang, Q., Harman, C. J., and Kirchner, J. W.: Evaluation of statistical methods for quantifying fractal scaling in water-quality time series with irregular sampling, Hydrol. Earth Syst. Sci., 22, 1175–1192, https://doi.org/10.5194/hess-22-1175-2018, 2018.