Dual-polarized quantitative precipitation estimation as a function of range

Since the advent of dual-polarization radar technology, many studies have been conducted to determine the extent to which the differential reflectivity (ZDR) and specific differential phase shift (KDP) add benefits to estimating rain rates (R) compared to reflectivity (Z) alone. It has been previously noted that this new technology provides significant improvement to rain-rate estimation, primarily for ranges within 125 km of the radar. Beyond this range, it is unclear as to whether the National Weather Service (NWS) conventional R(Z)-convective algorithm is superior, as little research has investigated radar precipitation estimate performance at larger ranges. The current study investigates the performance of three radars – St. Louis (KLSX), Kansas City (KEAX), and Springfield (KSGF), MO – with 15 tipping bucket gauges serving as ground truth to the radars. With over 300 h of precipitation data being analyzed for the current study, it was found that, in general, performance degraded with range beyond, approximately, 150 km from each of the radars. Probability of detection (PoD) in addition to bias values decreased, while the false alarm rates increased as range increased. Bright-band contamination was observed to play a potential role as large increases in the absolute bias and overall error values near 120 km for the cool season and 150 km in the warm season. Furthermore, upwards of 60 % of the total error was due to precipitation being falsely estimated, while 20 % of the total error was due to missed precipitation. Correlation coefficient values increased by as much as 0.4 when these instances were removed from the analyses (i.e., hits only). Overall, due to the lowest normalized standard error (NSE) of less than 1.0, a National Severe Storms Laboratory (NSSL) R(Z,ZDR) equation was determined to be the most robust, while a R(ZDR,KDP) algorithm recorded NSE values as high as 5. The addition of dual-polarized technology was shown to estimate quantitative precipitation estimates (QPEs) better than the conventional equation. The analyses further our understanding of the strengths and limitations of the Next Generation Radar (NEXRAD) system overall and from a seasonal perspective.

1 Introduction

In 2012, the National Weather Service (NWS) began upgrading the Next Generation Radar (NEXRAD) system from single to dual polarization. The potential benefits of this upgrade were investigated by the National Severe Storms Laboratory (NSSL) and the Cooperative Institute for Mesoscale Meteorological Studies. These advantages include, but are not limited to, (1) significant improvement in radar rainfall estimation (Ryzhkov et al., 2005; Gourley et al., 2010) through better representation of precipitation shape (Brandes et al., 2002; Gorgucci et al., 2000, 2006; Berne and Uijlenhoet, 2005); (2) discrimination between solid and liquid precipitation (Zrnic and Ryzhkov, 1996), allowing for better distinction between areas of heavy rain and hail (Park et al., 2009; Giangrande and Ryzhkov, 2008; Cunha et al., 2013); (3) identifying the melting layer position in the radar field (Straka et al., 2000; Park et al., 2009); (4) hardware calibration (Holleman et al., 2010; Hubbert et al., 2017); and (5) calculating drop-size distributions retrieved from measurements of reflectivity (Z), differential reflectivity (ZDR), and specific differential phase shift (KDP) as opposed to using ground-based point-located disdrometers (Zhang et al., 2001; Brandes et al., 2004; Anagnostou et al., 2008).

Rain-rate retrieval by weather radars is an estimation based upon the dielectric properties of the hydrometeors encountered in the atmosphere. Therefore, there is no direct measurement of rainfall, and this inherently introduces error. However, dual-polarized radar technology allows for in-depth analyses on the microphysics of precipitation that single polarization was incapable of conducting. In spite of this technology, conflicting studies report the benefits for quantitative precipitation estimation (QPE). For example, Gourley et al. (2010) and Cunha et al. (2015) reported that conventional R(Z) algorithms have significantly better bias than algorithms containing ZDR and/or KDP, while others (e.g., Ryzhkov et al., 2013; Simpson et al., 2016) report the opposite. This could be due, at least in part, to the fact that hydrometeor types (e.g., rain versus hail) vary on spatial scales that cannot be easily resolved by even densely gauged networks.

Multiple studies have found that the performance of radar rain-rate estimates decreases as range increases (Smith et al., 1996; Ryzhkov et al., 2003), which is caused, primarily, by degradation of beam quality with range. Furthermore, the researchers also discuss how the probability of detection (PoD) at larger ranges decreases, as the radar beam overshoots shallow, stratiform precipitation, especially winter precipitation (Kumjian, 2013b). Bright-banding can also play a crucial role in significantly increasing the amount of precipitation estimated by the radar, prompting many researchers to produce automated bright-band detection algorithms (e.g., Zhang et al., 2008; Zhang and Qi, 2010).

Despite these overall disadvantages, studies have shown that radar rain-rate algorithms seldom exceed absolute errors on the order of 10 mm h⁻¹ (Berne and Uijlenhoet, 2013). However, many of these studies have looked at a small sample of rain events (on the order of 10–50 h) (Kitchen and Jackson, 1993; Smith et al., 1996; Ryzhkov et al., 2003; Gourley et al., 2010; Cunha et al., 2013). Long-term performances of weather radar are becoming more common in recent years as the availability of data becomes more abundant (e.g., Haylock et al., 2008; Goudenhoofdt and Delobbe, 2012, 2016; Fairman et al., 2012). Additionally, few studies (e.g., Smith et al., 1996; Cunha et al., 2015; Simpson et al., 2016) quantified QPE errors including the probability of detection and false alarm ratio. In order to gain a better understanding of the performance of weather radars on rain-rate estimates, more data must be collected over a broad range of precipitation regimes in addition to an overall broader region of interest.

The overarching objective of the current study was to assess the performance of three different radars within the state of Missouri at various ranges from the radar, using terrestrial-based tipping bucket gauges as ground-truth data. Radar rain-rate estimation algorithms include 55 algorithms encompassing standard R(Z) relations as well as algorithms containing dual-polarization variables including differential reflectivity and the specific differential phase shift. A rain-rate echo classification algorithm was also tested for performance in correctly identifying the suitable rain-rate algorithm to choose based on the Z, ZDR, and KDP radar fields. The current work expands upon that of Simpson et al. (2016) such that a larger sample of data was analyzed (over 300 h of rainfall data from 46 separate days in 2014) to encompass multiple different precipitation regimes for both summer and winter, with several ground-truth tipping buckets to analyze the performance of three separate radars as a function of range, and further expanding upon the effects of erroneous precipitation estimates on the overall radar error. Objectives for this study included the following: (1) statistically analyze the performance of each radar at various ranges (compared against the gauges); (2) compute (a) the amount of precipitation incorrectly estimated by the radar (quantifying the probability of false detection, PoFD) and (b) the amount of precipitation incorrectly missed by the radar but measured by the rain gauge; (3) test the overall best radar rain-rate algorithm; and (4) perform objectives (1), (2), and (3) while the data are separated into warm and cool seasons, which have been shown to result in significantly different QPEs (Smith et al., 1996; Ryzhkov et al., 2003; Cunha et al., 2015).

2 Study area and methods

2.1 Study area

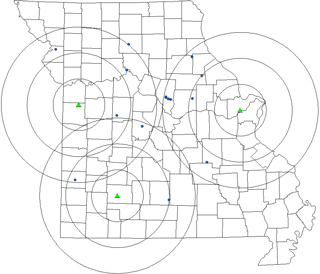
National Weather Service radars from St. Louis (KLSX), Kansas City (KEAX), and Springfield (KSGF), MO, are able to scan the majority of the state of Missouri. Because of this, the three aforementioned radars were used to assess overall performance in estimating precipitation for this study. Each radar covered a 200 km radius for which a different number of gauges were within their domains: KLSX, KEAX, and KSGF covered 9, 8, and 5 gauges, respectively (Fig. 1).

Missouri is characterized as a continental type of climate, marked by relatively strong seasonality. Furthermore, Missouri is subject to frequent changes in temperature, primarily due to its inland location and its lack of proximity to any large lakes. All of Missouri experiences below-freezing temperatures on a yearly basis. For example, the majority of the state typically registers 110 days with temperatures below freezing, while the Bootheel (i.e., southeast region) records, on average, 70 days of below-freezing day temperatures, emphasizing the typical northwest to southeast warming pattern of temperatures observed in the state. Because of the large variability in temperature, the warm and cool seasons were defined from an agronomic perspective, primarily taking probabilities of freezing into account. Based on the climatological averages of Missouri, from 1983 to 2013, November through April registered average minimum temperatures below freezing, which was considered the cool season, while May through October's minimum average temperatures were above freezing and constituted the warm season.

Figure 1 Study location (Missouri) with St. Louis (KLSX), Kansas City (KEAX), and Springfield (KSGF), MO, radars (triangles) overlaid with 50, 100, and 150 km range rings in addition to the 15 terrestrial-based precipitation gauges utilized as ground-truthed data.

2.2 Rainfall data

In order for the results to be comparable across the domains of the three radars it was necessary to select days on which rain was observed widely across the state. Although measurable rainfall occurs on more than 100 days of the year in Missouri with only 50 days typically recording greater than 0.254 mm, 2014 recorded 46 days with measurable rainfall throughout the state. Furthermore, occurrence of rain was defined as the observation of an amount greater than 0.5 mm (equivalent to two rain gauge tips) in an hour. This amounted to a total of approximately 300 h of rain across those 46 days. This represents a relatively standard year of rainfall for the state of Missouri. Furthermore, the days were chosen based on availability of data from the National Climate Data Center's (NCDC) Hierarchal Data Storage System (HDSS) for all three radars, in addition to error-free performance notes from each of the gauges used. The dates analyzed were split near evenly between the warm (May–October) and cool (November–April) seasons, therefore encompassing an overall performance of each of the radars throughout the year with no preferential bias towards rain or snow. Additionally, days were distributed evenly during the summer between convective and stratiform events with a threshold of 38 dBZ (Gamache and Houze, 1982).

Table 1 Terrestrial-based precipitation gauge locations used for the study in addition to the National Weather Service radars from Springfield, MO (KSGF), Kansas City, MO (KEAX), and St. Louis, MO (KLSX), used in conjunction with each gauge.

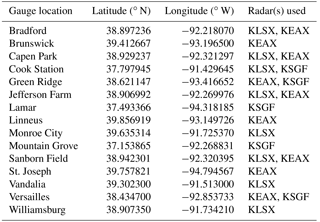
Terrestrial-based precipitation gauge data were collected from 15 separate weather stations within the Missouri Mesonet, established by the Commercial Agriculture Program of University Extension (Table 1). All precipitation data were aggregated in hourly intervals to match the temporal resolution of the gauges. Observed precipitation data were collected using Campbell Scientific TE525 tipping buckets located at each of the locations for the study (Table 1). The precipitation gauges have a 15.4 cm orifice which funnels to a fulcrum which registers 0.254 mm of rainfall per tip. For the current study, none of the day's average temperature values fell outside of the gauge's maximum performance range of 0 to 50 ^∘C. Accuracy in gauge measurements range between −1 and 1, −3 and 0, and −5 and 0 % for precipitation up to 25.4, 25.4 to 50.8, and 50.8 to 76.2 mm h⁻¹, respectively, which are, primarily, associated with local random errors and errors in tip-counting schemes (Kitchen and Blackall, 1992; Habib et al., 2001).

Each tipping bucket is located, approximately, 1 m above the ground in areas clear of buildings and properly maintained vegetation height to mitigate turbulence effects (Habib et al., 1999). Due to the well-maintained nature of the mesonet gauges, these errors were assumed negligible and, therefore, allowed for the gauges to be representative of the true rainfall rate. In spite of the non-homogeneous spacing of the gauges, unbiased statistics including the normalized mean bias (NMB) and normalized standard error (NSE) were utilized.

2.3 Radar data and radar rainfall algorithms

Next Generation Radar level-II data were retrieved from the NCDC's HDSS. Files were processed using the Warning Decision Support System – Integrated Information (WDSS-II) program (Lakshmanan et al., 2007a) to assess reflectivity (Z) in addition to dual-polarized radar variables including differential reflectivity and specific differential phase shift. Three other variables were also generated based on a KDP-based smoothing field (Ryzhkov et al., 2003) for reflectivity, differential reflectivity, and specific differential phase: DSMZ, DZDR, and DKDP, respectively. These were implemented to determine whether the additional KDP-smoothing fields tend to over- or underestimate QPEs (Simpson et al., 2016). A rain-rate echo classification variable (RREC) was also computed, which chooses whether an R(Z), R(KDP), R(Z,ZDR), or R(ZDR, KDP) algorithm is implemented in estimating rain rates based on the radar fields of Z, ZDR, and KDP (Kessinger et al., 2003) to determine whether a multi-parameter algorithm is superior to a single algorithm.

All seven variables (Z, ZDR, KDP, DSMZ, DZDR, DKDP, and RREC) were converted from their native polar grid to 256 × 256 1 km Cartesian grids, where the lowest radar elevation scans (0.5^∘) were used to mitigate uncalculated effects from evaporation and wind drift (Ciach, 2002). An average of 5 min scans were used for each of the variables, which were aggregated to hourly totals to be compared to the hourly tipping-bucket accumulations. In spite of previous reports suggesting 5 min to hourly aggregates can have significant effects on QPE (e.g., Fabry et al., 1994), Shucksmith et al.'s (2011) criterion of present accumulation exceeding 26 % for a pixel size of 1 km was not reached.

Table 2 List of single- and dual-polarimetric algorithms used for radar rainfall estimates.

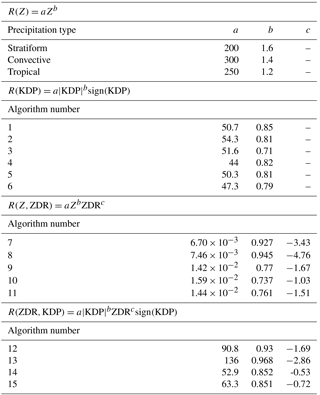
The latitude and longitude of each of the 15 gauges were matched with the radar pixel that corresponds to the Cartesian grid value of the seven radar variables which were then implemented in rain-rate calculations. These rain-rate calculations were calculated using the equations presented by Ryzhkov et al. (2005) (Table 2), which were gathered from multiple studies using disdrometers to derive a relationship between reflectivity, differential reflectivity, and specific differential phase (Bringi and Chandrasekar, 2001; Brandes et al., 2002; Illingworth and Blackman, 2002; Ryzhkov et al., 2003). Standard R(Z) algorithms were also included to test whether the addition of dual-polarized technology improves QPEs.

With the use of both (i) Z, ZDR, and KDP and (ii) DSMZ, DZDR, and DKDP fields produced by WDSS-II, the number of algorithms tested was 55. This includes the three standard single-polarized algorithms (stratiform, convective, and tropical) which were calculated using reflectivity R(Z) and then calculated as R(DSMZ), while algorithms 1–6 (R(KDP)) were also calculated as R(DKDP). Algorithms 7–11 (R(Z, ZDR)) were additionally calculated as R(Z, DZDR), R(DSMZ, ZDR), and R(DSMZ, DZDR), while the same four combinations of non- and KDP-smoothed fields were applied to the R(KDP, ZDR) algorithms (12–15). Quality controlling methods for the algorithms include mitigation of clutter, sun spikes, beam blockage, anomalous propagation, and removal of non-precipitation echoes (including biological and chaff returns) through w2qcnn the w2qcnndp algorithms (Lakshmanan et al., 2007b, 2010, 2014).

2.4 Statistical analyses

To test the performance of each algorithm, several statistical analyses were calculated. The average difference (Bias) was calculated as

$$\begin{array}{}\text{(1)}& \mathrm{Bias}={\displaystyle \frac{\sum (R_i-G_i)}{N}},\end{array}$$

where R_i is each hourly aggregated radar-estimated rainfall amount calculated from one of the 55 algorithms, G_i is the hourly aggregated gauge (observed) measurement, and N is the total number of observations which, for this study, was 300 h. A second statistical parameter, the normalized mean bias (NMB), was calculated as

$$\begin{array}{}\text{(2)}& \mathrm{NMB}={\displaystyle \frac{\mathrm{1}}{N}}{\displaystyle \frac{\sum (R_i-G_i)}{\sum G_i}}.\end{array}$$

The normalized mean bias is included in the analyses due to the fact that overestimations (i.e., radar estimates larger than gauge measurements) and underestimations (i.e., radar estimates smaller than gauge measurements) are treated proportionately. This is directly analogous to choosing the mean absolute error (MAE) opposed to the standard deviation as the MAE does not penalize smaller or larger errors, obscuring the overall results (Chai and Draxler, 2014). Bias measurements (Bias and NMB) were calculated to determine whether radar-derived rain rates were over- or underestimated in comparison to the gauges. However, to calculate the overall magnitude of error associated with the performance of the radars, the absolute values of Eqs. (1) and (2) were performed to yield the mean absolute error and normalized standard error, respectively.

Several other meteorological parameters were calculated, including the probability of detection (PoD), which was calculated as

$$\begin{array}{}\text{(3)}& \mathrm{PoD}={\displaystyle \frac{\sum \mathrm{|}{R}_i\cdot G_i>\mathrm{0}\mathit{\&}{R}_i>\mathrm{0}\mathrm{|}}{\sum \mathrm{|}{G}_i\mathrm{|}}},\end{array}$$

where the bullet (⋅) indicates “if”, to determine how accurate the radars were at correctly detecting precipitation. The probability of detection values range between 0.0 (radar did not detect any precipitation correctly) and 1.0 (radar detected the occurrence of all precipitation 100 % correctly). The probability of false detection (PoFD) takes into account the amount of precipitation the radars incorrectly estimated when the gauges recorded zero values, and it was calculated as

$$\begin{array}{}\text{(4)}& \mathrm{PoFD}={\displaystyle \frac{\sum R_i\cdot (G_i=\mathrm{0}\mathit{\&}{R}_i>\mathrm{0})}{\sum G_i}}.\end{array}$$

Quantitative measures including the missed precipitation amount (MPA) and the false precipitation amount (FPA) were defined such that

$$\begin{array}{}\text{(5)}& {\displaystyle }& {\displaystyle }\mathrm{MPA}=\sum R_i\cdot (G_i>\mathrm{0}\mathit{\&}{R}_i=\mathrm{0}),\text{(6)}& {\displaystyle }& {\displaystyle }\mathrm{FPA}=\sum R_i\cdot (G_i=\mathrm{0}\mathit{\&}{R}_i>\mathrm{0}),\end{array}$$

which analyzes the total amount of precipitation due to misses and false alarms. The total precipitation error was also recorded to assess the overall error from each radar.

3 Results and discussion

3.1 Overall algorithm performance

To test the overall performance of each radar, it was necessary to determine the overall best algorithm for each statistical measure. The best algorithm from each grouping of equations was determined to have the lowest normalized standard error, indicating the best performance relative to the gauge-recorded precipitation amount (Ryzhkov et al., 2005). This reduces the impact of bias inherent within the dataset between the warm and cool season, as well as between stratiform and convective events, and allows for statistical measurements in spite of the (typical) non-Gaussian behavior of precipitation (Kleiber et al., 2012; Alaya et al., 2017).

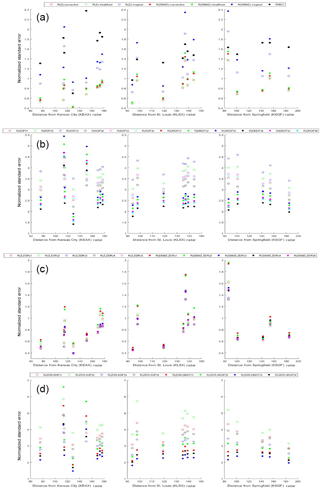
Figure 2 Normalized standard error values for the overall performance of the (a) 3 R(Z), 3 R(DSMZ), and RREC algorithms; (b) 6 R(KDP) and 6 R(DKDP) algorithms (algorithms 1–6 from Table 2); (c) 5 R(Z,ZDR) and 5 R(DSMZ,ZDR) algorithms (Eqs. 7–11 from Table 2); and (d) 4 R(ZDR,KDP) and 4 R(ZDR,DKDP) algorithms (Eqs. 12–15 from Table 2) for the three radars utilized for the current study.

From the results obtained, the three R(Z), three R(DSMZ), and RREC algorithms displayed a particular bias in favor of the R(Z)-convective algorithm for all three radars with R(Z)-stratiform displaying similar performance (Fig. 2a). This could be due, at least in part, to the near-equal stratiform and convective precipitation regimes throughout 2014. Although errors generally increased as range increased for KEAX and KLSX, the results were nebulous for KSGF. The lowest NSE values were, typically, closest to each of the radars (between 0.4 and 0.8), with the notable exception of the closest gauge to KSGF. In general, the RREC performed worst at the largest of ranges, potentially due to the algorithm's ability to incorrectly assess the hydrometeors present (Cifelli et al., 2010; Yang et al., 2016). Additionally, the poor performance by the R(DSMZ)-tropical equation is due to the lack of tropical precipitation within central Missouri. Overall, the KDP-smoothed reflectivity fields (DSMZ) performed worse than their counterparts, resulting in over-prediction of precipitation and, thus, larger errors (Simpson et al., 2016). Errors did not exceed 2.4 NSE units for any of these algorithms.

However, the performance of the KDP-smoothed KDP field (DKDP) performed better than the original specific differential phase shift field (Fig. 2b). For nearly all gauges for each of the three radars, R(DKDP)4 performed the best, with NSE values ranging from 1.4 to 4.1. The range of NSE values were largest at KEAX, while the spread was relatively small for KLSX and KSGF. In spite of this, the overall spread of the performance of the 12 KDP algorithms varied greatly (average of 2 NSE units), exhibiting the sensitivity of KDP estimates on QPE (Ryzhkov et al., 2005; Cunha et al., 2013). In general, the NSSL-derived R(KDP) equations (i.e., Eqs. 4–6) outperformed those from Bringi and Chandrasekar (2001, Eq. 1), Brandes et al. (2002, Eq. 2), and Illingworth and Blackman (2002, Eq. 3). Regardless, the magnitudes were all, approximately, more than 1 NSE unit than the performance of the R(Z) algorithms.

The algorithms with the lowest NSE values were Eqs. (7)–(11). For example, the overall lowest NSE was at a distance of 130 km from KEAX (0.3), with no locations exceeding NSE values of 2.0 (Fig. 2c). The large values at the closest location for KSGF (85 km, 1.3–1.9 NSE units) and the fifth closest gauge to KLSX (135 km, 1.3–1.8 NSE units), Cook Station, were similar to the R(Z) and R(DSMZ) results, indicating potential issues with reflectivity measurements. Additionally, these locations were the closest in performance to the R(KDP) and R(DKDP) NSE values. Observations from this gauge (Cook Station) indicated hail occurred during the evening of 1 August, for which KDP estimates would be more ideal than Z for QPE (Ryzhkov et al., 2005; Kumjian, 2013a; Cunha et al., 2015). In spite of this, the overall spread in performance of the R(Z,ZDR) equations was lower than the R(KDP) equations, demonstrating the robust performance of R(Z,ZDR) for QPE (Wang and Chandrasekar, 2010; Seo et al., 2015).

The R(ZDR,KDP) algorithms performed the worst, overall (Fig. 2d). In spite of the differential reflectivity being implemented, the overall NSE values increased in magnitude, exceeding six units for the second gauge analyzed by KEAX. Algorithms containing DKDP measurements performed better than simply KDP, demonstrating that, even with the scaling behavior of ZDR, DKDP is superior to KDP estimates. This provides a potential solution to the noisiness that tends to be exhibited in the KDP field (Ruzanski and Chandrasekar, 2012).

Due to the overall NSE values obtained, for the remainder of the analyses, Eq. (11) (i.e., R(Z,ZDR)5) and Eq. (13) (i.e., R(ZDR,KDP)2) will be utilized as the best and worst algorithms, respectively. Equations containing DZDR were not included in the following discussion due to the very large QPE errors for each radar.

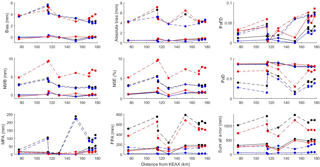
Figure 3 Values of analyses from the Kansas City radar. Dashed lines and points represent the analyses of the worst-performing algorithm (R(ZDR,KDP)), while the solid lines and points represent the analyses of the best-performing algorithm (R(Z,ZDR)). Red, blue, and black colors represent analyses conducted during the warm season, cool season, and overall, respectively.

3.2 KEAX

The overall bias showed that there was a positive bias, peaking near 5.5 mm h⁻¹ at the second gauge for KEAX, approximately 115 km from the radar for both the best- and worst-performing algorithms (Fig. 3). This corresponds well with the spike in the falsely detected precipitation recorded, which is canceled by the maximum in missed precipitation at the second distance of, approximately, 150 km. The overall worst algorithm, Eq. (13), an R(ZDR,KDP) relationship, revealed a decreasing trend in bias as the distance from the radar increased. For example, a bias of 4 mm h⁻¹ was observed at a distance of 75 km from the radar, whereas the bias reduced to 3 mm h⁻¹ at distances near 175 km. This could be due, at least in part, to the algorithm's utilization of KDP, which performs poorly in frozen (especially light) precipitation (Zrnic and Ryzhkov, 1996; Kumjian, 2013a), causing the overestimation. Conversely, the algorithm with the lowest bias was an R(Z,ZDR) algorithm (Eq. 11). There was a maximum in the bias calculations while utilizing Eq. (11) near 120 km, similar to Eq. (13); however, there was a more pronounced minimum in the data near 150 km. Furthermore, it appears the data oscillates around a bias value of 0 mm h⁻¹ when using Eq. (13). This could be due to ZDR's capability to respond to precipitation shape (Kumjian, 2013a), which helps to scale the reflectivity portion of the rainfall estimation algorithm to a more accurate value (Seo et al., 2015). In general, the cool season displayed a larger magnitude of error in terms of bias for both algorithms.

The normalized mean bias reveals the same trend in values for bias but with an overall decrease in magnitude. It is important to note, however, that the algorithms that tend to perform the worst (e.g., algorithms containing KDP) result in anomalous range responses which would be due, at least in part, to a stronger response to precipitation type (Kumjian, 2013c). This indicates that observations above the melting layer are dominant, for which QPEs tend not to be calculated (Cifelli et al., 2011; Seo et al., 2015), but are important for regions devoid of adequate radar coverage (Ryzhkov et al., 2003; Simpson et al., 2016).

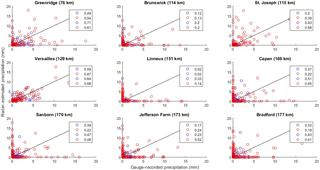
Figure 4 Correlation coefficient values for the nine locations analyzed by the Kansas City radar with the R(Z,ZDR) NSSL equation. Blue and red scatter points represent the cool and warm season data, respectively. The top two numbers on each plot indicate the overall R² value, whereas the bottom two numbers represent the R² when false alarms and misses are removed.

The absolute bias and normalized standard error shows the same maxima in the data at the second gauge (Brunswick) that was present in the bias data (6.2 mm h⁻¹ and 5.6, respectively). However, a second maxima is located at the fifth gauge at, approximately, 150 km (Linneus) with values of 5.9 mm h⁻¹ and 4.0, respectively. Bright-band issues are detected due, at least in part, to the increased missed precipitation amount (240 mm) at this particular distance for the R(ZDR,KDP) equation (i.e., worst-performing algorithm). There was also a pronounced minimum in the absolute bias and NSE results at the fourth gauge for equations 11 and 13, 4.0 and 0.8 mm h⁻¹, and 2.8 and 0.8, respectively, potentially indicating an idealized range of QPE for KEAX. Furthermore, the historical records at this particular gauge showed less issues (e.g., clogging) than any of the others analyzed by the KEAX radar. This highlights the importance of choosing ground-truth data, in particular tipping buckets which are prone to numerous errors (Ciach and Krajewski, 1999b).The largest contributions to the NSE and NMB were due to the warm season.

The probability of detection results indicate a large difference in algorithm choice for correctly detecting precipitation. The low PoD at, approximately 150 km, indicates overshooting of the beam. This is further evidenced by the MPA results, as about 225 mm of precipitation was missed by the radar at 150 km, whereas only 100 mm of precipitation was missed by the radar at the second gauge at 120 km. Although Eq. (11), an R(Z,ZDR) algorithm, was superior in terms of the bias, the same algorithm with a KDP-smoothed reflectivity value, R(DSMZ,ZDR), revealed the overall least amount of the falsely missed precipitation (by 10 mm). However, the summation of the amount of precipitation falsely detected (PoFD) by KEAX showed a larger source of error than the MPA in terms of magnitude. For example, at the second (fifth) gauge, only 100 (225) mm of precipitation was missed by the radar, but over 700 (725) mm of precipitation was incorrectly estimated by the radar.

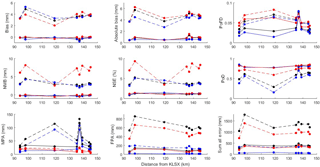
Figure 5 Values of analyses from the St. Louis radar. Dashed lines and points represent the analyses of the worst-performing algorithm (R(ZDR,KDP)), while the solid lines and points represent the analyses of the best-performing algorithm (R(Z,ZDR)). Red, blue, and black colors represent analyses conducted during the warm season, cool season, and overall, respectively.

Correlation coefficient (CC) values for any of the nine stations analyzed by KEAX range from 0.02 (Linneus, 151 km) to 0.93 for the cool season (St. Joseph, 115 km). The lowest R² values were due to a combination of false alarms and misses. For example, the CC values for the warm seasons at Sanborn (170 km) and Jefferson Farm (173 km) were 0.22 and 0.24, respectively, whereas when the instances of false alarms and misses were removed the CC values increased to 0.48 and 0.52. Few locations (Brunswick, 114 km; and Versailles, 129 km) saw little improvement in the CC values when only hits were analyzed (less than 0.1 increase), indicating the mean absolute error (in terms of hits) contributed the largest portion of error.

3.3 KLSX

Unlike the KEAX data, the gauges used for analyses for the KLSX radar span between 90 and 150 km. Furthermore, five out of the eight gauges were located within a 10 km of range from one another, near 140 km from the radar, limiting the data available for analyses between 100 and 140 km (Fig. 5).

The bias and NMB both show a relatively modest peak in values near the second gauge of 5 mm, which decreases to approximately 3.6 mm at the third gauge, 120 km from the radar. The worst-performing algorithm, Eq. (13), had the same R(ZDR,KDP) relation as the worst KEAX bias and NMB data. Additionally, the overall trend of decreasing bias and NMB as distance from the radar increases was noted, presumably due to overshooting effects similar to the KEAX data. Furthermore, the overall non-biased results from the R(Z,ZDR) equation demonstrates its robust capabilities in QPE, in spite of its sensitivity to calibration (Zrnic et al., 2005; Bechini et al., 2009; Gorgucci et al., 1992).

The double maxima in the absolute bias graph are present as with the KEAX data, but are not as pronounced. For example, the absolute biases at 95 and 140 km from KLSX were 5.9 and 4.9 mm for Eq. 13, while the values were 1.1 and 1.4 mm for Eq. 11, accordingly. Additionally, the overall minima in the absolute bias for both KEAX and KLSX are at, approximately, 125 km from the radar (3.9 and 1.0 mm h⁻¹, respectively, for Eqs. 13 and 11). The relative distance from the radars are the same, where the two maxima for KEAX were at 115 and 150 km, while the maxima were at, approximately, 100 and 140 km for KLSX. The overall best- and worst-performing algorithms at KLSX for the absolute bias and NSE were Eqs. (11) and (13), the R(Z,ZDR) and R(ZDR,KDP) algorithms, respectively.

The magnitude of error in terms of absolute bias, normalized mean bias, and normalized standard error all showed a decreasing pattern as distance from KLSX increased. This was due, primarily, from a maximum in the false precipitation amount at 95 km from the radar. Historical notes at this location indicate frequent clogging of the rain gauge, either due to bugs or leaves. From a particular series of events spanning from 1 to 4 April and 1 to 3 August 2014, over 130 mm of precipitation occurred during each period which was not captured by the gauge, resulting in a large amount of overall error. These results indicate the importance of dual gauges in the same vicinity (Krajewski et al., 1998; Ciach and Krajewski, 1999a). Interestingly, the cool season displayed a larger NSE (5 % for R(ZDR,KDP)) potentially due to the very low probability of detection (0.2) at this range of 118 km.

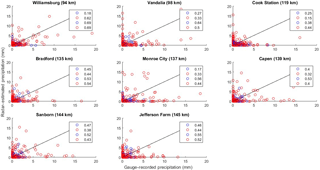
Figure 6 Correlation coefficient values for the eight locations analyzed by the St. Louis radar with the R(Z,ZDR) NSSL equation. Blue and red scatter points represent the cool and warm season data, respectively. The top two numbers on each plot indicate the overall R² value, whereas the bottom two numbers represent the R² when false alarms and misses are removed.

One of the main differences between the KLSX and KEAX data was the decreased probability of detection at 120 km for KLSX, while there was an increased probability of detection for KEAX. In general, the PoD values were worse for KLSX when compared to KEAX. For example, Eq. (11) had no PoD values below 0.90, whereas no PoD values exceeded 0.84 for KLSX. There was also a slight trend of increasing PoD values as distance from the St. Louis radar increased and, at one point near 140 km, the best algorithm, R(DSMZ)-convective, and the worst algorithm, KDP1, were not significantly different (p < 0.10). Additionally, the maxima in the PoD while utilizing KDP1 correspond to a minima in the R(DSMZ) detection percentage, which is well correlated by the similarly valued MPA results.

The missed precipitation amount (MPA) showed that the cool season contributed the most, whereas the warm season contributed the most amount of the false precipitation amount. The R(Z,ZDR) equation only registered, on average, 25 mm of MPA and 160 mm of FPA, whereas the R(ZDR,KDP) equation was very dependent upon range. For example, the FPA from R(ZDR,KDP) decreased as range increased from the radar from a maximum of, approximately, 850 to 620 mm. However, the fifth-furthest gauge (137 km from KLSX) displayed a sharp increase in the MPA for both cool seasons (above 100 mm).

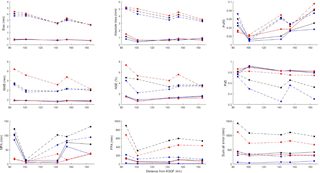
Figure 7 Values of analyses from the Springfield radar. Dashed lines and points represent the analyses of the worst-performing algorithm (R(ZDR,KDP)), while the solid lines and points represent the analyses of the best-performing algorithm (R(Z,ZDR)). Red, blue, and black colors represent analyses conducted during the warm season, cool season, and overall, respectively.

3.4 KSGF

In spite of the fact that the KLSX and KEAX data strongly suggest false precipitation errors near 100 km in addition to bright-banding near 150 km from the radars, the KSGF results reveal an overall smooth decrease (increase) of error with range (Fig. 7) for R(ZDR,KDP) and R(Z,ZDR), accordingly. One of the main reasons for this could be due to the fact that only five gauges were analyzed from KSGF (the fewest of the three radars analyzed), smoothing the overall trend lines.

The bias remained relatively constant near −0.3 mm for R(Z,ZDR), whereas the bias exhibited a sharp decrease from 4 to 2.7 mm over a distance of, approximately, 100 km. In general, the cool season displayed lower bias magnitudes when compared to the warm season, similar to the KEAX results. This may be due, at least in part, to the low PoFD values for the warm season close to the KSGF radar.

Similar to the bias, the absolute bias for R(Z,ZDR) was constant at all ranges (near 1 mm), whereas the R(ZDR,KDP) equation decreased from 5.2 to 3.8 mm. This is potentially due to the low cool season PoD values (below 0.6), while the warm season R(ZDR,KDP) values (near 0.8) remained constant. A larger contribution from more correctly detected precipitation in addition to the decreasing trends in the NMB and NSE would result in a lower absolute bias.

The closest location (90 km) typically displayed the largest errors for the R(ZDR,KDP) equation and then decreased in error magnitude as range increased. In spite of this, the PoFD results indicate both algorithms increased in PoFD values as range increased, with the warm season typically dominating, particularly due to the large convective clouds dominating in the warm season. False detection values as low as 0.01 for the cool season while utilizing R(Z,ZDR) were observed at distances near 100 and 140 km from the radar.

Normalized standard error values increased from 0.7 % at a distance of 105 km to 1.8 % at a distance of 185 km for R(Z,ZDR). Large NSE values for the warm season (7.5 %) were calculated for R(ZDR,KDP), which decreased to 3.8 % at 185 km from the radar. Furthermore, this was the only instance when the warm season was less than the cool season in terms of NSE. Otherwise, the overall NSE decreased from 5 to 3.9 % for R(ZDR,KDP). The NMB followed a similar trend for the KDP-containing algorithm, with a noticeable exception at the second gauge (105 km from KSGF), where the overall NSE was closer to the warm season than the cool season. This is due to the low PoFD values at this location, in addition to a smaller difference between the two algorithm's FPA measurements.

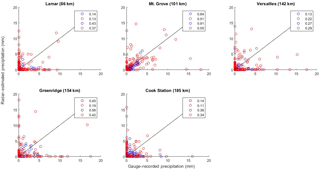
Figure 8 Correlation coefficient values for the five locations analyzed by the Springfield radar with the R(Z,ZDR) NSSL equation. Blue and red scatter points represent the cool and warm season data, respectively. The top two numbers on each plot indicate the overall R² value, whereas the bottom two numbers represent the R² when false alarms and misses are removed.

The MPA results, unlike for KEAX and KLSX, displayed a larger range of performance between seasons. However, the warm season still exhibited the overall best performance in terms of MPA, yet contributed the most to the FPA for both R(Z,ZDR) and R(ZDR,KDP). In spite of the MPA typically increasing as range increased, the FPA was more nebulous. For example, the second gauge (105 km from KSGF) had the overall lowest NSE (0.8 %), MPA (15 mm), and FPA (95 mm) for R(Z,ZDR). The third-furthest location (142 km) resulted in slightly larger errors, overall, while the fourth-furthest location had errors similar to the second gauge (105 km). Then, at the furthest tipping bucket location (185 km), NSE values increased, whereas FPA and MPA decreased. Therefore, the furthest location's errors are due, primarily, from discrepancies between precipitation magnitude between the gauge and radar.

Excluding Versailles (142 km from KSGF), the cool season exhibited larger R² values in comparison to the cool season (Fig. 8). Furthermore, CC values exceeded 0.9 when false alarms and misses were excluded from Mountain Grove (101 km) and were 0.84 when included. Otherwise, the other four stations analyzed by the Springfield radar displayed many counts of false alarms and misses, leading to low R² values.

Due to the relatively large ranges from the Springfield radar, most of the correlation coefficient values were low in comparison to either KLSX or KEAX. For the warm (cool) season without false alarms and misses, R² values ranged from 0.44 (0.38) to 0.34 (0.36) for KLSX and KSGF, respectively, at Cook Station (119 and 185 km). Similarly, the CC values ranged from 0.61 (0.71) to 0.42 (0.56) at Green Ridge (76 and 154 km) for KEAX and KSGF, accordingly.

4 Conclusions

Dual-polarization technology was implemented in the National Weather Service Next Generation Radar network in the spring of 2012 to, primarily, improve quantitative precipitation estimation and hydrometeor classification. The current study observed over 300 h of precipitation data with three separate radars in Missouri using 55 algorithms including the three conventional R(Z) radar rain-rate estimation algorithms (stratiform, convective, and tropical) along with a myriad of R(KDP), R(Z,ZDR), and R(ZDR,KDP) algorithms, which can be found in Ryzhkov et al. (2005). Additionally, a KDP-smoothing field of reflectivity, differential reflectivity, and the specific differential phase shift (DSMZ, DZDR, and DKDP, respectively) were measured and used for analyses. Unlike previous studies, the current work emphasizes the amount of precipitation correctly and incorrectly estimated by the radar in comparison to the terrestrial-based precipitation gauges through measurements of the missed and false precipitation amount.

For all three radars – Kansas City, St. Louis, and Springfield, MO – the majority of precipitation error (over 60 %) was contributed by the amount of precipitation falsely detected by the radar (up to 725 mm), while 20 % was due to the radar missing the precipitation (up to 225 mm) for KEAX. Similar magnitudes of error were reported for KLSX and KSGF, with an overall error in precipitation for each radar ranging between 250 mm for the best performing of the 55 algorithms, Eq. (11) (an R(Z,ZDR) algorithm), and up to 2000 mm for the worst-performing algorithms, R(ZDR,KDP) Eq. (13). The R(Z,ZDR) equation (an NSSL algorithm) was determined to be the most robust due to it registering the lowest NSE. These values of false precipitation amount and missed precipitation amount generally increased as range from the radar increased.

Most algorithms showed a degradation in the normalized standard error with range. In particular, the KDP-smoothed equations displayed larger biases and NSE values than their non-KDP counterparts, with the exception of R(KDP) algorithms themselves. Some larger errors were recorded at gauge locations close to the radar, potentially due to bright-banding effects which were determined to be due to the large false precipitation amount analyzed at these locations.

The data were divided into summer (May–October) and winter (November–April; 59 and 41 % of the entire data, respectively). Despite the winter data contributing less than the summertime data, they accounted for 20 % of the overall MPA and 40 % to the overall PoFD. The R² values were lower during the winter in comparison to the warm season, primarily due to the smaller magnitude of precipitation that occurred. Furthermore, CC values increased by as much as 0.4 when instances of hits and misses were removed from the analyses, resulting in the warm season outperforming the cool season CC values at particularly short ranges from the radar.

These results aid in our understanding of the possibilities for hydrometeorological studies. Nearly 50 % of the 300 h where precipitation occurred analyzed for the study consisted of either falsely estimated precipitation by the radar, or missed by the radar. Furthermore, these errors accumulate between 500 and 2000 mm of precipitation depending on the algorithms chosen. Although the overall performance increased when false alarms and misses were removed, correlation coefficient values still, typically, remained below 0.50 at ranges beyond 130 km.

Furthermore, results demonstrate the issues with analyzing QPE from a single gauge, explaining why the Community Collaborative Rain, Hail, and Snow Network (Kelsch, 1998; Cifelli et al., 2005; Reges et al., 2016) or other densely gauged networks (e.g., the Hydrometeorological Automated Data System, HADS; and the Meteorological Assimilation Data Ingest System, MADIS) tend to be more utilized since results have shown that measurements or quality-controlled techniques made by these organizations, especially CoCoRaHS (Community Collaborative Rain, Hail and Snow Network), are significantly more accurate than rain gauges (Simpson et al., 2017), especially for convective events (Moon et al., 2009).