the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Effects of microarrangement of solid particles on PCE migration and its remediation in porous media
Ming Wu
Jichun Wu
Bill X. Hu
Groundwater can be stored abundantly in granula-composed aquifers with high permeability. The microstructure of granular materials has important effect on the permeability of aquifers and the contaminant migration and remediation in aquifers is also influenced by the characteristics of porous media. In this study, two different microscale arrangements of sand particles are compared to reveal the effects of microstructure on the contaminant migration and remediation. With the help of fractal theory, the mathematical expressions of permeability and entry pressure are conducted to delineate granular materials with regular triangle arrangement (RTA) and square pitch arrangement (SPA) at microscale. Using a sequential Gaussian simulation (SGS) method, a synthetic heterogeneous site contaminated by perchloroethylene (PCE) is then used to investigate the migration and remediation affected by the two different microscale arrangements. PCE is released from an underground storage tank into the aquifer and the surfactant is used to clean up the subsurface contamination. Results suggest that RTA can not only cause more groundwater contamination, but also make remediation become more difficult. The PCE remediation efficiency of 60.01–99.78 % with a mean of 92.52 and 65.53–99.74 % with a mean of 95.83 % is achieved for 200 individual heterogeneous realizations based on the RTA and SPA, respectively, indicating that the cleanup of PCE in aquifer with SPA is significantly easier. This study leads to a new understanding of the microstructures of porous media and demonstrates how microscale arrangements control contaminant migration in aquifers, which is helpful to design successful remediation scheme for underground storage tank spill.
- Article
(2837 KB) - Full-text XML
- BibTeX
- EndNote
Groundwater is an essential natural resource for water supply to domestic, agricultural, and industrial activities as well as ecosystem health (Boswinkel, 2000; Valipour, 2012, 2015; Yannopoulos et al., 2015; Valipour and Singh, 2016). Unfortunately, with the rapid development of economic activities such as mining, agriculture, landfills and industrial activities (Bakshevskaia and Pozdniakov, 2016; Cui et al., 2016; H. Liu et al., 2016; An et al., 2016; Shen et al., 2017), more and more contaminants released from human activities are contaminating the precious groundwater resource and subsurface environment (Dawson and Roberts, 1997; Liu, 2005; Hadley and Newell, 2014; Carroll et al., 2015; Essaid et al., 2015; Huang et al., 2015; Y. Liu et al., 2016; Schaefer et al., 2016; Weathers et al., 2016). Among the contaminants detected in groundwater, dense nonaqueous phase liquids (DNAPLs) such as perchloroethylene (PCE) and other polycyclic aromatic hydrocarbons (PAHs), are highly toxic and carcinogenic (Dawson and Roberts, 1997; Hadley and Newell, 2014). When DNAPLs are released into aquifer from underground storage tanks, they will infiltrate through the entire aquifer and form residual ganglia and pools of DNAPLs due to their large densities, high interfacial tension, and low solubility. The residual ganglia and pools of DNAPLs can serve as long-term sources of groundwater contamination which are harmful to the subsurface environment and human beings (Bob et al., 2008; Liang and Lai, 2008; Liang and Hsieh, 2015). Consequently, it is very important to explore DNAPL migration in aquifers and associated remediation of groundwater contamination.
When DNAPLs migrate in aquifers on a macroscopic scale, the transport properties such as permeability, diffusivity and dispersivity are closely related to the aquifer's microstructures and can affect DNAPL behavior (Yu and Li, 2004; Yu, 2005; Yun et al., 2005; Feng and Yu, 2007; Yu et al., 2009). Therefore, characterizing the effect of microstructures on macroscopic properties is a key point of research on heterogeneity of porous media (Mishra et al., 2016). In the classical Kozeny–Carman equation, the permeability K is related to porosity n, surface area S and the Kozeny constant c, where c is affected by the porosity, solid particles and microgeometric structures (Bear, 1972; Yu et al., 2009). According to fractal theory, natural porous media can be treated as fractal objects (Pfeifer and Avnir, 1983; Katz and Thompson, 1985; Krohn, 1988). For example, the tortuosity of flow paths in porous media is deeply studied by various proposed fractal models (Yu and Cheng, 2002; Yu et al., 2009; Cai et al., 2010), indicating the effectiveness of fractal methods. Based on fractal concepts, mathematic models are proposed to depict the permeability and invasion of fluids in some special porous media (Yu and Cheng, 2002; Yu et al., 2009; Cai et al., 2010). Furthermore, fractal method is also used to explore the effect of microstructure of biological media on associated thermal conductivity while this kind of material has a complex randomly distributed vascular-tree structure at microscale (Li and Yu, 2013).
In this study, we focus on the effect of microarrangement of sand particles on macroscopic DNAPL migration and associated remediation for underground storage tank spills. With the help of fractal theory, the microstructures of two different microscale arrangements of sand particles are explored. Afterwards, the mathematical relationships between porosity, permeability, and entry pressure are derived for regular triangle arrangement (RTA) and square pitch microscale arrangement (SPA). An idealized heterogeneous contaminated site is generated using a sequential Gaussian simulation (SGS) method. An underground storage tank releases PCE into heterogeneous aquifer composed of granular material. After a long-term migration, PCE contamination is alleviated using a surfactant remediation method. A multicomponent, multiphase model simulator, UTCHEM, is then used to simulate the entire process of DNAPL migration and remediation. Effects of arrangements of sand particles on migration and remediation of DNAPLs are comparatively analyzed based on the simulations to reveal how the microstructure of porous media controls the contaminant migration and remediation on a macroscopic scale.
2.1 Fractal models of two different microscale arrangements of sand particles
The porous media can be treated as the bundle of tortuous capillary tubes, and the relationship between the diameter and the length of the capillary tube is as follows (Yu and Cheng, 2002):
where Ls is the straight length between the tortuous flow path's end point, λ is the diameter of the capillary tube, and Dt is the fractal dimension of tortuosity for porous media, (Yu and Cheng, 2002).
If an infinitesimal element consisting of a bundle of tortuous capillary tubes from porous media is selected, the total number of capillary tubes in infinitesimal element can be calculated by the power–law relation:
where Df is the fractal dimension for pore areas in porous media, (Yu and Cheng, 2002); λmax is the maximum diameter of capillary tubes.
Afterward, the derivative of Eq. (2) can be achieved:
The total number of capillary tubes in an infinitesimal element can be derived from Eq. (3):
where λmin is the minimum diameter of capillary tubes.
Dividing Eq. (3) by Eq. (4) can achieve the following:
where f(λ) is the probability density function, .
The probability density function satisfies the following relationship:
Considering , the above Eq. (6) becomes the following:
With regard to fluid flow in capillary tubes, the flow rate Q can be calculated by the Hagen–Poiseulle equation:
where μ is fluid's viscosity, and ΔP is the pressure gradient across the capillary tube.
The differentiation of flow rate of capillary tubes is as follows (Yu and Cheng, 2002):
Integrating the individual flow rate from λmin to λmax can achieve the total flow rate (Yu and Cheng, 2002):
Due to and , . Simultaneously, , . Therefore, Eq. (10) can be simplified as follows:
Substituting Darcy's law, , in Eq. (11) will obtain the permeability of porous media:
To obtain the fractal dimension of tortuosity Dt, the expression of tortuosity (τ) can be obtained from Eq. (1):
Then Dt is given by the following (Yu and Li, 2004):
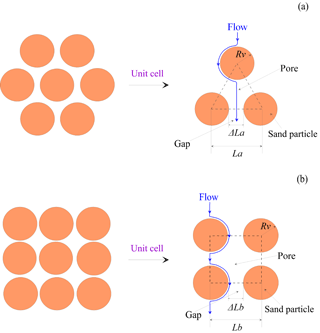
RTA and SPA are shown in Fig. 1. An equilateral triangle and a square are selected from the two microstructures as unit cells (Fig. 1a and b). The unit cell of the equilateral triangle is composed of three solid particles with the pore among them, while the unit cell of square is composed of four solid particles. For the unit cell of RTA in Fig. 1a, corresponding porosity is given by the following:
where n is porosity, Aa is the total area of equilateral triangle, and Rv is the average radius of solid particles. The total area of equilateral triangle can be achieved:
The side length of the equilateral triangle in Fig. 1a can be calculated as follows:
where La is the side length.
The area of irregular pore among solid particles is given by the following:
where Aap is the area of pore in the unit cell.
Approximate the pore in the equilateral triangle as a circle, then the maximum diameter of pore can be obtained:
where is the diameter of the capillary tube in equilateral triangle. The fluid does not only pass the central pore of the unit cell, but also flow through the gap between adjacent particles. The gap length and the average diameter of the capillary tube perpendicular to the plane of equilateral triangle are calculated as follows:
where ΔLa is the gap length between solid particles; λa is the average diameter of capillary tubes in the equilateral triangle.
Generally, the tortuosity of flow path in porous media is the ratio of the length of tortuous flow path to the straight length of flow path along the flow direction (Taiwo et al., 2016):
where Lt is the length of tortuous flow path, and Ls is the straight length of flow path along the flow direction.
For the flow path shown in Fig. 1a, Lt and Ls are respectively as follows:
where ho is the altitude of the equilateral triangle, .
Consequently, the tortuosity of RTA is yielded:
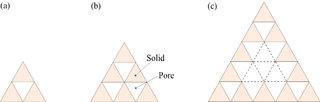
The Df is determined using Sierpinski gasket (Fig. 2) in fractal theory (Yu and Cheng, 2002). The shaded area represents solids of porous media and the white area represents pore. The pore area fractal dimensions in Fig. 2a–c are 0.000, 1.000 and 1.594, respectively (, , ). Based on the Sierpinski gasket, the dimensionless pore area in RTA (Fig. 1a) is approximated as follows:
where Aapd is the dimensionless pore area of RTA; . Equation (26) can be solved to achieve Df:
The porosity equals to the ratio of the dimensionless pore area of RTA (Aapd) to the dimensionless total area of RTA ():
where ; , .
From Eq. (28), the dimensionless pore area of RTA (Aapd) is given by the following:
The dimensionless total area of RTA () can be written as follows:
Afterward, is calculated as follows:
Substituting Eqs. (29) and (31) into Eq. (27) will derive Df of RTA:
For the unit cell of square shown in Fig. 1b, the porosity is as follows:
where Ab is the total area of the square. Equation (33) can also be expressed as the area of unit cell:
Again, the side length of the square is as follows:
Consequently, the area of an irregular pore in the square is given by the following:
where Abp is the area of pore in the square.
Using the following equation, the pore as a circle and obtain corresponding maximum diameter can be approximated:
where is the maximum diameter of the capillary tube perpendicular to the plane of the square. Similarly, fluid flows through the central pore in the square and the gap between adjacent particles. As a result, the gap and average diameter of the capillary tube are expressed as follows:
where ΔLb is the gap length between the adjacent two solid particles, and λb is the average diameter of the capillary tube.
For the tortuous flow path in Fig. 1b, Lt and Ls are respectively given by the following:
Afterward, the tortuosity of SPA yields the following:
The procedure of deriving Df of SPA is similar to the procedure of calculating Df of RTA. Similarly, the Df and porosity of SPA (Fig. 1b) are given by the following:
where Abpd is the dimensionless pore area of SPA, , is the dimensionless total area of SPA, and .
The dimensionless pore area of SPA (Abpd) can be yielded from Eq. (44):
can be calculated as follows:
Substituting Eqs. (45) and (46) into Eq. (43), Df of SPA can be derived:
The entry pressure of a tortuous capillary tube (Pc) is defined by Young–Laplace equation as follows (Ahn and Seferis, 1991):
where Pc is the entry pressure, λ is the diameter of the capillary tube, ω equals to Fσcosθ in which θ is the contact angle between fluid and solid, σ is the surface tension of the wetting fluid, and F is the form factor depending on the capillary tube alignment and the flow direction.
2.2 Dealing with the heterogeneity of porous media
In this study, SGS is used to generate random realization of a heterogeneous porosity field. SGS is a stochastic simulation method combining sequential principles and a Gaussian method. It assumes variable fit to a Gaussian random field. The Gaussian distribution function is constructed at each simulated spatial location based on the characteristics of variation function and afterward randomly selects a value as the variable at the location. In the SGS method, observation data are transformed to Gaussian distributions or normal distributions. Based on current sample data, the conditional probability distribution of points to be simulated is calculated by the SGS method and then simulation is performed based on a semivariogram model. Each simulated value, together with measured data and previous simulation data, becomes the conditional data set for the next step. As simulation proceeds, the conditional data set increases. Previous research suggests 50–400 realizations are required to obtain a statistically stable mean realization (Eggleston et al., 1996; Hu et al., 2007).
2.3 Modeling PCE migration and its remediation
The DNAPL migration and remediation are modeled using a multicomponent, multiphase, and multicomposition simulator named UTCHEM (University of Texas Chemical Compositional Simulator) (Delshad et al., 1996). As an extension to Delshad's work, UTCHEM was developed by the University of Texas as a comprehensive and practical tool. In numerous applications, UTCHEM has proved to be particularly useful in simulation of contaminant migrations and has been a popular multiphase-flow, multiconstituent, reactive transport model used widely in groundwater simulations. UTCHEM accounts for chemical, physical and biological reactions; complex non-equilibrium sorption; decay and geochemical reactions; and surfactant-enhanced solubilization and mobilization of DNAPLs. Moreover, heterogeneous properties of porous media are also considered. As a result, UTCHEM has been adapted for a variety of environmental applications such as surfactant-enhanced aquifer remediation (SEAR). In this study, DNAPL migration and remediation for cleaning up DNAPL contamination in idealized heterogeneous sites are simulated by UTCHEM.
3.1 Site description
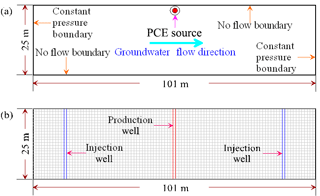
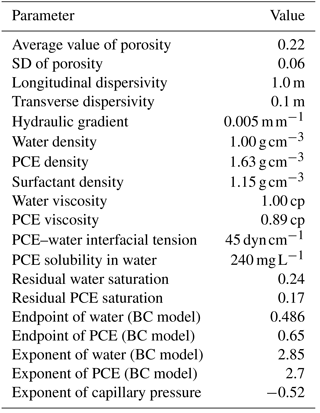
The idealized domain of synthetic application is a two-dimensional confined aquifer (Fig. 3). The length, width and depth of aquifer are 101, 25 and 25 m, respectively. Idealized aquifer is discretized into 101 grids horizontally and 25 layers vertically (Fig. 3b). The spacing of each grid is uniformly 1 m along x and z axes, and the longitudinal and transverse dispersivities are set as to 1.0 and 0.1 m, respectively. Horizontal and vertical correlation length values are each 5 m. The top and bottom borders of aquifer are defined as no-flow boundaries, while the left and right borders are defined as constant potential boundaries to create a groundwater flow from left to right under a low hydraulic gradient of 0.005 m m−1 (Liu et al., 2003; Liu, 2005; Qin et al., 2007). The porous media of idealized aquifer is assumed to be heterogeneous and mixed by different grades of sands.
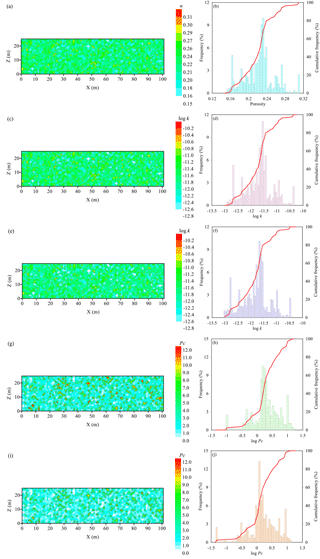
Figure 4(a) The individual porosity field generated by the sequential Gaussian simulation (SGS) method; (b) the frequency of an individual porosity field; (c) the individual permeability field of RTA obtained from an individual porosity field; (d) the frequency of individual permeability field for RTA; (e) the individual permeability field of SPA obtained from an individual porosity field; (f) the frequency of individual permeability field for SPA; (g) the obtained individual entry-pressure field of RTA; (h) the frequency of individual entry-pressure field of RTA; (i) the obtained individual entry-pressure field of SPA; and (j) the frequency of individual entry pressure of SPA.
The porosity of aquifer is assumed to be spatially and uniformly distributed with an average value of 0.220 and SD (standard deviation) of 0.060. In this study, porosity follows normal distribution and its SD represents the enhanced geological heterogeneity. A total of 200 realizations of the porosity field are generated using SGS. One of the 200 realizations of heterogeneous field is shown in Fig. 4a. Simultaneously, statistical assessment is undertaken on the individual realization of the porosity field, and corresponding histograms are shown in Fig. 4b. We find that the frequency of the individual realization of the porosity field is close to normal distribution, which conforms to the situation that most characteristics of natural aquifer can be expressed as a normal distribution (Montgomery et al., 1987). Based on the heterogeneous porosity field, the fractal dimension of tortuosity Dt, the fractal dimension for pore areas Df and the diameter of capillary tubes in porous media, permeability is obtained by Eq. (12). Figure 4c shows the individual heterogeneous permeability field selected from the 200 realizations of RTA, and the result of the associated frequency analysis is shown in Fig. 4d. The permeability field fits the lognormal distribution well, which has been presented by many studies which show that the parameter of aquifer penetrability follows lognormal distribution (Montgomery et al., 1987; Veneziano and Tabaei, 2004). Compared to the histogram of the porosity field in Fig. 4b, the shape of permeability is similar. The individual heterogeneous permeability field of SPA is shown in Fig. 4e. Corresponding frequency analysis of SPA reveals that the permeability field follows lognormal distribution, while some difference appears compared with RTA (Fig. 4f). The average permeability of individual realization of RTA is 2.012 × 10−12 m2, and the average permeability of individual realization of SPA is 1.618 × 10−12 m2. For 200 realizations, the average permeability of RTA and SPA are 2.120 × 10−12 and 1.706 × 10−12 m2, indicating the permeability of RTA is slightly bigger than SPA.
The average pore diameters of two different microscale arrangements of particles are derived using corresponding fractal models. In detail, the average diameter of RTA is calculated by Eq. (21) and the average diameter of SPA is calculated by Eq. (39). Consequently, the entry pressure of the two kinds of microscale arrangements can be obtained by Eq. (48). The individual entry-pressure fields of two microscale arrangements and associated frequency analysis are shown in Fig. 4g–j. From the frequency of entry pressure in Fig. 4h and j, the entry pressures of both RTA and SPA are the lognormal distributions. However, the average entry pressure of individual realization of RTA is 1.980 kPa, while the average entry pressure of SPA is 1.481 kPa. For 200 realizations of the entry-pressure field, the average entry pressure of RTA is 1.922 kPa and the average entry pressure of SPA is 1.442 kPa. The differences of average entry pressure between RTA and SPA imply the microstructure of aquifer has an effect on the macroscopic characteristics.
The purpose of this study is to explore the effects of microstructure of aquifer on DNAPL migration and remediation. A PCE spill event (the leaking of underground storage tank) occurs on the top of the aquifer and a surfactant remediation is designed to clean up the contaminated aquifer. The total duration of 300 days is divided into four stages: (1) 300 m3 PCE is released from underground storage tank into aquifer at the top layer of spill position shown in Fig. 3a during 0–30 days, (2) PCE migrates in aquifer freely during 30–100 days, (3) surfactant is injected into aquifer during 100–150 days, and (4) water is flushed during 150–300 days. In the first stage, PCE is released as a point pollution source in the center grid block at the top layer of the aquifer, in which spill is at a constant rate of 10 m3 day−1. After PCE coming into the heterogeneous aquifer, PCE is migrating freely under the effects of gravity and the natural hydraulic gradient condition. The PCE not only migrates downward through the aquifer, but can also be trapped by capillary forces as residual ganglia and globules. During the long-term PCE migration period, PCE is contaminating groundwater and expanding plume. To clean up the contaminated aquifer, 4 % surfactant solution is injected into aquifer through the two injection wells (Fig. 3b) at a constant rate of 80 m3 day−1, and, simultaneously, contaminated groundwater is extracted through production well at a constant rate of 160 m3 day−1. Surfactant can reduce the interfacial tension between the DNAPL and aqueous phase to promote solubilization and mobilization of DNAPL. After surfactant injection, the contaminated aquifer is flushed by water over a long period of 150 days. Based on the distributions of porosity, permeability and entry pressure of two microscale arrangements, the entire PCE migration and remediation process is simulated by a multicomponent, multiphase model simulator, UTCHEM (Delshad et al., 1996). The parameters used in the simulation are listed in Table 1. Simulation results of two different microscale arrangements are compared to reveal the effect of microstructure on the DNAPL migration and remediation.
3.2 Results and discussion
3.2.1 PCE migration and its remediation based on single realizations
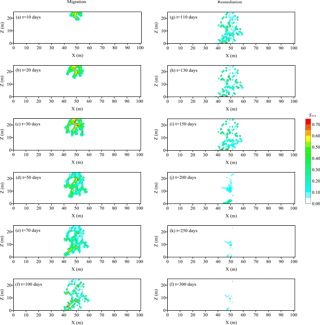
The simulation results of PCE migration for individual realization of the porosity field for RTA are shown in Fig. 5a–f. When PCE is released into an aquifer at the top layer of spill position, PCE almost infiltrates vertically under the effect of gravity (Fig. 5a). Due to the heterogeneity of the aquifer, some preferential flow appears and the PCE plume becomes irregular (Fig. 5b). After 30 days, PCE plume almost touches the bottom of aquifer (Fig. 5c). When the PCE leakage is stopped, PCE migrates continuously in aquifer for 70 days (Fig. 5d–f). The released PCE is migrating downward and entrapped by capillary forces as residual ganglia and globules. The heterogeneity of the aquifer makes PCE migrate along a preferential pathway. When the PCE plume touches the zones of low permeability and high entry pressure, it will bypass these zones and migrate continuously, which leads to an increasing variability in PCE distribution. After the PCE plume reaches the bottom of aquifer, PCE begin accumulate and form a contaminant pool at the bottom. At t = 100 days, a PCE pool is formed at the bottom of aquifer, moving toward the right boundary.
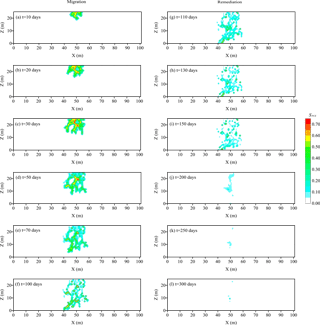
Figure 6Simulated PCE saturation for individual realization of SPA over the entire migration and remediation periods (0 ∼ 300 day).
Figure 6a–f show the simulated PCE saturation for individual realization of porous media for SPA during migration period. Under the effects of gravity and the natural hydraulic gradient, PCE is migrating and the contaminant plume becomes larger and larger. The heterogeneity of the aquifer significantly changes the migration paths and leads to irregular morphology of the PCE plume (Fig. 6a–c). However, due to the different microarrangements of the aquifer, the entry-pressure distribution is also different, which leads to some differences. After the PCE injection, the simulated PCE saturation in Fig. 6d–f indicates that further trapping and spreading of the PCE occurs during this period. Compared with the simulation results of RTA in Fig. 5, the PCE plume slightly seems similar in Fig. 6. Moreover, PCE infiltrates more quickly in porous media of RTA in Fig. 5. After 70 days, the PCE plume has touched the bottom for RTA (Fig. 5e), while the PCE plume based on SPA still keeps a significant distance from the bottom (Fig. 6e).
To clean up the DNAPL, 4 % surfactant solution is injected through two injection wells at a constant rate of 80 m3 day−1 over 50 days. Afterwards, water flushing is applied during 150–300 days. The locations of the injection and production wells are presented in Fig. 3b. The production well is rightly installed at the location of the PCE spill position and two injection wells are located 39 m to the left and right of the production well. Figure 5g–l show the PCE remediation results of individual realization for RTA. During the early remediation period, the effect of cleaning up DNAPL is not yet apparent (Fig. 5g–i). When the water flushing begins, the surfactant solution circulates throughout the contaminated aquifer (Fig. 5j–l). At t = 200 days, 237.01 m3 PCE is removed from contaminated aquifer, occupying 79.00 % of the total released PCE (Fig. 5j). As time goes on, 268.30 m3 PCE is removed from the aquifer and remediation efficiency reaches 89.43 %.
The same surfactant remediation is also conducted for individual realization of SPA. Compared with the remediation for RTA, the remediation effect is more apparent for SPA (Fig. 6g–l). As the remediation progresses, more DNAPL is removed and less DNAPL remains at the bottom of aquifer. At t = 200 days, 267.68 m3 PCE is removed from the contaminated aquifer and the corresponding remediation efficiency rises to 89.23 %. At t = 300 days, 285.32 m3 PCE is cleaned up and remediation efficiency reaches 95.11 %. From the results of remediation, it is obvious that microstructure has an effect on remediation for macroscopic-scale aquifer. Results suggest contaminated aquifer of RTA is hard to clean up by surfactant remediation while SPA can improve DNAPL remediation efficiency.
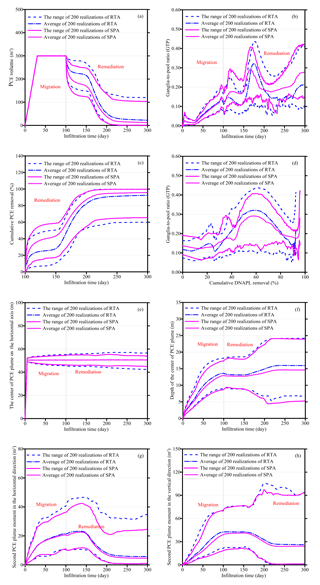
Figure 7(a) PCE volume in aquifer vs. time, RTA represents RTA and SPA represents SPA; (b) changes in GTP as a function of time; (c) cumulative DNAPL removal as a function of time; (d) variation of GTP value as a function of cumulative DNAPL removal percent; (e) the change of the center of PCE plume during the entire periods of migration and remediation; (f) the change of the depth of PCE plume center during the entire periods; (g) variation of second PCE plume moment on the horizontal axis; and (h) variation of second PCE plume moment in vertical axis.
3.2.2 PCE migration and SGS realizations
PCE migration and remediation processes are simulated for 200 realizations of the porosity field for porous media of RTA and SPA. The variations of contaminant mass, the ganglia-to-pool (GTP) ratio and moments of PCE plume vs. time are presented in Fig. 7a–h. During 0–30 days, the PCE in aquifer increases linearly at a constant rate of 10 m3 day−1 (Fig. 7a), which corresponds to the contaminant spill stage. Afterward, PCE volume keeps constant during the second stage (30–100 days), while PCE volume in aquifer is reduced when surfactant is injected into aquifer. After surfactant insertion and water flushing of the contaminated aquifer, most DNAPL is cleaned up. The residual DNAPL mass remained in aquifer of 0.67–119.89 m3 with a mean of 22.42 and 0.79–103.33 m3 with a mean of 12.51 m3 are achieved for 200 heterogeneous realizations based on the RTA and SPA, respectively. The average remediation efficiency of SPA is undoubtedly higher than RTA, indicating the aquifer of SPA is easier to clean up. PCE plume architectures are quantified by measuring the GTP ratio in Fig. 7b. Over entire periods, curves of GTP value show obvious oscillations. Surfactant has the ability to promote solubilization, and mobilization of DNAPL can reduce GTP value. As a result, when surfactant is injected at t = 100 day, the GTP value reduces quickly. When surfactant injection is ended and water flushing begins, the GTP value increases with steep flank slope. Finally, GTP values reach 0.10–0.41 with a mean of 0.21 and 0.15–0.42 with a mean of 0.28 for 200 heterogeneous realizations based on the RTA and SPA, respectively.
Figure 7c shows cumulative PCE removal from the contaminated aquifer vs. flushing time for RTA and SPA. During the surfactant injection period, 100–150 days, the DNAPL removal is not apparent. However, DNAPL is removed effectively and quickly during the water-flushing period. Through long-term remediation, the removal of PCE from the contaminated aquifer reached 179.89–298.98 m3 with a mean of 277.29 and 196.45–298.87 m3 with a mean of 287.21 m3 for 200 realizations based on RTA and SPA, respectively. Average remediation efficiency of SPA (95.83 %) is noticeably higher than average remediation efficiency of RTA (92.52 %).
Figure 7d shows the GTP value as a function of cumulative PCE removal for the contaminated aquifer. The GTP remains at a relatively low level before 30 % of the DNAPL is removed from the aquifer. When 40 % of the total 300 m3 PCE is removed, GTP values are increasing and corresponding curves appear as a wave crest because the high-saturation zones of the PCE plume are dissolved and turned into ganglia. After the wave crest, the GTP values decline quickly with steep flank slope due to PCE ganglia removal through water flushing. Finally, GTP values increase at the end of the remediation process for 200 realizations, indicating that most of PCE is removed and most of residual PCE turns into ganglia.
For the center of the PCE plume on the horizontal axis, associated variations vs. time are similar for 200 realizations based on RTA and SPA (Fig. 7e). Significantly, the PCE plume vertical-infiltration rate in aquifer of RTA is slightly faster than PCE infiltration in the aquifer of SPA for 200 realizations (Fig. 7f). Simultaneously, the second PCE plume moments in the horizontal direction of RTA are different from the second PCE plume moments in the horizontal direction of SPA (Fig. 7g). After PCE migration under natural conditions at t = 100 days, the second PCE plume moments in the horizontal direction are 10.61–40.50 m2 with a mean of 21.51 and 10.99–36.38 m2 with a mean of 20.75 m2 for 200 realizations based on RTA and SPA, respectively. At t = 300 day, the second PCE plume moments in the horizontal direction change to 0.81–34.88 m2 with a mean of 5.79 and 1.03–24.57 m2 with a mean of 4.64 m2 for RTA and SPA, respectively. The horizontal second moment of RTA is always larger than the horizontal second moment of SPA, indicating that the PCE plume in the aquifer of RTA is wider than the PCE plume in the aquifer of SPA, and RTA can cause more groundwater contamination. Similarly, the second moments in vertical direction for RTA are larger than the second moments in vertical direction for SPA.
This study takes an important step toward exploring how microscale arrangements control contaminant migration on a small-aquifer scale. Results are essential to the macroscopic aquifer composed of porous media without large heterogeneity, such as sandy aquifers containing rich groundwater resources. However, there are many problems associated with the upscaling of aquifers in real-world conditions (Dagan et al., 2013; Pacheco, 2013; Pacheco et al., 2015). Due to the large heterogeneity of natural aquifers, research results may be very different and can not be extrapolated to complex regional aquifer on a large scale. However, the finding in this study is absolutely applicable for natural aquifers with similar heterogeneities. If the heterogeneity and anisotropy of natural aquifers are very different, the effect of the microscale arrangements on the macroscopic contaminant migration and remediation will be different. Although real-world conditions are complex, the new findings achieved from this research are very significant for understanding the effect of microscale arrangement on contaminant behaviors on an aquifer scale. The upscaling problem of the results obtained on the simulation scale (100 m × 25 m × 25 m) is the basis and the upscaling problem with more complex heterogeneity conditions is needed to be further investigated. Various research on the upscaling problem is done through experiment and simulation (Wu et al., 2017a–d). Based on this research, the microstructure of porous media is developed and the contaminates migration in porous media is explored using fractal methods in this study, implying the experimental results are very significant for real-world problems on an aquifer scale. Our next procedure involves applying these models in a real-world aquifer with complex heterogeneity conditions and modifying our models and method according to realistic conditions.
The microstructure of aquifers has an important effect on macroscopic-scale characteristics of contaminant migration and remediation. In this study, we focus on the DNAPL migration and remediation in heterogeneous aquifers composed of granular porous media with RTA and SPA. The microscale models of RTA and SPA are developed to obtain the mathematical expressions of permeability and entry pressure using fractal methods. A total of 200 realizations of the porosity field are generated using the SGS method, and PCE is released from an underground storage tank into a heterogeneous aquifer. To clean up contamination caused by the underground storage tank spill, a surfactant remediation technique is used to remove contaminants in the aquifer. The entire process of DNAPL migration and remediation is simulated by a multicomponent, multiphase model simulator, UTCHEM. Results suggest RTA not only cause more groundwater contamination than RTA, but also the contaminated aquifer of RTA is harder to clean up compared with SPA. The second PCE plume moments in the horizontal direction are 10.61–40.50 m2 with a mean of 21.51 and 10.98–36.38 m2 with a mean of 20.75 m2 for 200 realizations based on RTA and SPA, respectively, after long-term migration at t = 100 days. Furthermore, the second PCE plume moments in the horizontal direction at t = 300 day are 0.807–34.88 m2 with a mean of 5.79 and 1.025–24.57 m2 with a mean of 4.64 m2 for RTA and SPA, respectively, after long-term remediation. Simultaneously, the residual DNAPL mass remaining in the aquifer is 0.67–119.89 m3 with a mean of 22.42 for RTA and 0.79–103.33 m3 with a mean of 12.51 m3 for SPA, indicating that the remediation efficiency of SPA (65.53–99.74 % with a mean of 95.83 %) is mostly higher than the remediation efficiency of RTA (60.01–99.78 % with a mean of 92.52 %). This study reveals that the microstructure of an aquifer has an important effect on contaminant movement and associated remediation efficiency on a macroscopic scale, which is very essential and significant for dealing with accidental underground storage tank spills and for identifying subsurface contaminant sources in the future.
Research data are available from Jianfeng Wu (jfwu@nju.edu.cn), Jichun Wu (jcwu@nju.edu.cn), or Ming Wu (wumingnanjing@gmail.com).
The authors declare that they have no conflict of interest.
This research was financially supported by the National Key Research and
Development Plan of China (2016YFC0402800), the National Natural Science
Foundation of China (41772254 and 41372235), and the National Natural Science
Foundation of China-Xianjiang (project U1503282). The authors are also
profoundly grateful to Pacheco Fla and an anonymous reviewer whose precious
suggestions and constructive comments helped to improve the paper
significantly.
Edited by: Sabine Attinger
Reviewed by: Fernando Pacheco and one anonymous referee
Ahn, K. J. and Seferis, J. C.: Simultaneous measurements of permeability and capillary pressure of thermosetting matrices in woven fabric reinforcements, Polym. Composite., 12, 146–152, 1991.
An, C. J., McBean, E., Huang, G. H., Yao, Y., Zhang, P., Chen, X. J., and Li, Y. P.: Multi-soil-layering systems for wastewater treatment in small and remote communities, J. Environ. Inform., 27, 131–144, 2016.
Bakshevskaia, V. A. and Pozdniakov, S. P.: Simulation of hydraulic heterogeneity and upscaling permeability and dispersivity in sandy-clay foormations, Math. Geosci., 48, 45–64, 2016.
Bear, J.: Dynamics of Fluids in Porous Media, Dover, New York, 1972.
Bob, M. M., Brooks, M. C., Mravik, S. C., and Wood, A. L.: A modified light transmission visualization method for DNAPL saturation measurements in 2-D models, Adv. Water Resour., 31, 727–742, 2008.
Boswinkel, J. A.: Information Note, International Groundwater Resources Assessment Centre (IGRAC), Netherland Institute of Applied Geoscience, Netherlands, in: UNEP (2002), Vital Water Graphics – An Overview of the State of the World's Fresh and Marine Waters, UNEP, Nairobi, Kenya, 2000.
Carroll, K. C., McDonald, K., Marble, J., Russo, A. E., and Brusseau, M. L.: The impact of transitions between two-fluid and three-fluid phases on fluid configuration and fluid-fluid interfacial area in porous media, Water Resour. Res., 51, 7189–7201, 2015.
Cai, J. C., Yu, B. M., Zou, M. Q., and Mei, M. F.: Fractal analysis of invasion depth of extraneous fluids in porous media, Chem. Eng. Sci., 65, 5178–5186, 2010.
Cui, Q. L., Wu, H. N., Shen, S. L., Yin, Z. Y., and Horpibulsuk, S.: Protection of neighbour buildings due to construction of shield tunnel in mixed ground with sand over weathered granite, Environ. Earth Sci., 75, 458, https://doi.org/10.1007/s12665-016-5300-7, 2016.
Dagan, G., Fiori, A., and Jankovic, I.: Upscaling of flow in heterogeneous porous formations: critical examination and issues of principle, Adv. Water Resour., 51, 67–85, 2013.
Dawson, H. E. and Roberts, P. V.: Influence of viscous, gravitational, and capillary forces on DNAPL saturation, Groundwater, 35, 261–269, 1997.
Delshad, M., Pope, G. A., and Sepehrnoori, K.: A compositional simulator for modeling surfactant enhanced aquifer remediation, 1 Formation, J. Contam. Hydrol., 23, 303–327, 1996.
Eggleston, J. R., Rojstaczer, S. A., and Peirce, J. J.: Identification of hydraulic conductivity structure in sand and gravel aquifers: Cape Cod data set, Water Resour. Res., 32, 1209–1222, 1996.
Essaid, H. I., Bekins, B. A., and Cozzarelli, I. M.: Organic contaminant transport and fate in the subsurface: evolution of knowledge and understanding, Water Resour. Res., 51, 4861–4902, 2015.
Feng, Y. J. and Yu, B. M.: Fractal dimension for tortuous streamtubes in porous media, Fractals, 15, 385–390, 2007.
Hadley, P. W. and Newell, C.: The new potential for understanding groundwater contaminant transport, Groundwater, 52, 174–186, 2014.
Hu, K., White, R., Chen, D., Li, B., and Li, W.: Stochastic simulation of water drainage at the field scale and its application to irrigation management, Agr. Water Manage., 89, 123–130, 2007.
Huang, J. Q., Christ, J. A., Goltz, M. N., and Demond, A. H.: Modeling NAPL dissolution from pendular rings in idealized porous media, Water Resour. Res., 51, 8182–8197, 2015.
Katz, A. J. and Thompson, A. H.: Fractal sandstone: implications for conductivity and pore formation, Phys. Rev. Lett., 54, 325–332, 1985.
Krohn, C. E.: Sandstone fractal and Euclidean pore volume distributions, J. Geophys. Res., 93, 3286–3296, 1988.
Li, L. and Yu, B. M.: Fractal analysis of the effective thermal conductivity of biological media embedded with randomly distributed vascular trees, Int. J. Heat Mass Tran., 67, 74–80, 2013.
Liang, C. and Hsieh, C. L.: Evaluation of surfactant flushing for remediating EDC-tar contamination, J. Contam. Hydrol., 177–178, 158–166, 2015.
Liang, C. and Lai, M. C.: Trichloroethylene degradation by zero valent iron activated persulfate oxidation, Envrion. Eng. Sci., 25, 1071–1077, 2008.
Liu, H., Li, Y. X., He, X., Sissou, Z., Tong, L., Yarnes, C., and Huang, X.: Compound-specific carbon isotopic fractionation during transport of phthalate esters in sandy aquifer, Chemosphere, 144, 1831–1836, 2016.
Liu, L.: Modeling for surfactant-enhanced groundwater remediation processes at DNAPLs-contaminated sites, J. Environ. Inform., 5, 42–52, 2005.
Liu, L., Hao, R. X., and Cheng, S. Y.: A possibilistic analysis approach for assessing environmental risks from drinking groundwater at petroleum-contaminated sites, J. Environ. Inform., 2, 31–37, 2003.
Liu, Y., Wang, S., McDonough, C. A., Khairy, M., Muir, D. C. G., Helm, P. A., and Lohmann, R.: Gaseous and freely-dissolved PCBs in the lower great lake based on passive sampling: spatial trends and air-water exchange, Environ. Sci. Technol., 50, 4932–4939, 2016.
Mishra, A. K., Kumar, B., and Dutta, J.: Prediction of hydraulic conductivity of soil bentonite mixture using Hybrid-ANN approach, J. Environ. Inform., 27, 98–105, 2016.
Montgomery, R.H ., Loftis, J. C., and Harris, J.: Statistical characteristics of ground-water quality variables, Ground Water, 25, 176–184, 1987.
Pacheco, F. A. L.: Hydraulic diffusivity and macrodispersivity calculations embedded in a geographic information system, Hydrolog. Sci. J., 58, 930–943, 2013.
Pacheco, F. A. L., Landim, P. M. B., and Szocs, T.: Bridging hydraulic diffusivity from aquifer to particle-size scale: a study on loess sediments from southwest Hungary, Hydrolog. Sci. J., 60, 269–284, 2015.
Pfeifer, P. and Avnir, D.: Chemistry in nonintegral dimensions between two and three. I. Fractal theory of heterogeneous surface, J. Chem. Phys., 79, 3558–3565, 1983.
Qin, X. S., Huang, G. H., Chakma, A., Chen, B., and Zeng, G. M.: Simulation-based process optimization for surfactant-enhanced aquifer remediation at heterogeneous DNAPL-contaminated sites, Sci. Total Environ., 381, 17–37, 2007.
Schaefer, C. E., White, E. B., Lavorgna, G. M., and Annable, M. D.: Dense nonaqueous-phase liquid architecture in fractured bedrock: implications for treatment and plume longevity, Environ. Sci. Technol., 50, 207–213, 2016.
Shen, J., Huang, G., An, C. J., Zhao, S., and Rosendahl, S.: Immobilization of Tetrabromobisphenol A by pinecone-derived biochars at solid–liquid interface_Synchrotron-assisted analysis and role of inorganic fertilizer ions, Chem. Eng. J., 321, 346–357, 2017.
Taiwo, O. O., Finegan, D. P., Eastwood, D. S., Fife, J. L., Brown, L. D., Darr, J. A., Lee, P. D., Brett, D. J. L., and Shearing, P. R.: Comparison of three-dimensional analysis and stereological techniques for quantifying lithium-ion battery electrode microstructures, J. Microsc.-Oxford, 263, 280–292, 2016.
Valipour, M.: Comparison of surface irrigation simulation models: full hydrodynamic, zero inertia, kinematic wave, J. Agr. Sci., 4, 68–74, 2012.
Valipour, M.: Future of agricultural water management in Africa, Arch. Agron. Soil Sci., 61, 907–927, 2015.
Valipour, M. and Singh, V. P.: Global Experiences on Wastewater Irrigation: Challenges and Prospects, in: Balanced Urban Development: Options and Strategies for Liveable Cities, edited by: Maheshwari, B., Singh, V., and Thoradeniya, B., Water Science and Technology Library, Springer, Cham, 72, 289–327, 2016.
Veneziano, D. and Tabaei, A.: Nonlinear spectral analysis of flow through porous media with isotropic lognormal hydraulic conductivity, J. Hydrol., 294, 4–17, 2004.
Weathers, T. S., Harding-Marjanovic, K., Higgins, C. P., Alvarez-Cohen, L., and Sharp, J. O.: Perfluoroalkyl acids inhibit reductive dechlorination of trichloroethene by repressing dehalococcoides, Environ. Sci. Technol., 50, 240–248, 2016.
Wu, M., Cheng, Z., Wu, J. F., and Wu, J. C.: Quantifying representative elementary volume of connectivity for translucent granular materials by light transmission micro-tomography, J. Hydrol., 545, 12–27, 2017a.
Wu, M., Cheng, Z., Wu, J. F., and Wu, J. C.: Estimation of representative elementary volume for DNAPL saturation and DNAPL-water interfacial areas in 2-D heterogeneous porous media, J. Hydrol., 549, 12–26, 2017b.
Wu, M., Wu, J. F., and Wu, J. C.: Simulation of DNAPL migration in heterogeneous translucent porous media based on estimation of representative elementary volume, J. Hydrol., 553, 276–288, 2017c.
Wu, M., Cheng, Z., Wu, J. F., and Wu, J. C.: Precise simulation of long-term DNAPL migration in heterogeneous porous media based on light transmission micro-tomography, Journal of Environmental Chemical Engineering, 5, 725–734, https://doi.org/10.1016/j.jece.2016.12.039, 2017d.
Yannopoulos, S. I., Lyberatos, G., Theodossiou, N., Li, W., Valipour, M., Tamburrino, A., and Angelakis, A. N.: Evolution of water lifting devices (pumps) over the centuries worldwide, Water, 7, 5031–5060, 2015.
Yu, B. M.: Fractal character for tortuous streamtubes in porous media, Chinese Phys. Lett., 22, 158–160, 2005.
Yu, B. M. and Cheng, P.: Fractal models for the effective thermal conductivity of bidispersed porous media, J. Thermophys. Heat Tr., 16, 22–29, 2002.
Yu, B. M. and Li, J. H.: A geometry model for tortuosity of flow path in porous media, Chinese Phys. Lett., 21, 1569–1571, 2004.
Yu, B. M., Cai, J. C., and Zou, M. Q.: On the physical properties of apparent two-phase fractal porous media, Vadose Zone J., 8, 177–186, 2009.
Yun, M. J., Yu, B. M., Zhang, B., and Huang, M. T.: A geometry model for tortuosity of streamtubes in porous media with spherical particles, Chinese Phys. Lett., 22, 1464–1467, 2005.