Review of gridded climate products and their use in hydrological analyses reveals overlaps, gaps, and the need for a more objective approach to selecting model forcing datasets

Climate forcing data accuracy drives performance of hydrologic models and analyses, yet each investigator needs to select from among the numerous gridded climate dataset options and justify their selection for use in a particular hydrologic model or analysis. This study aims to provide a comprehensive compilation and overview of gridded datasets (precipitation, air temperature, humidity, wind speed, solar radiation) and considerations for historical climate product selection criteria for hydrologic modeling and analyses based on a review and synthesis of previous studies conducting dataset intercomparisons. All datasets summarized here span at least the conterminous US (CONUS), and many are continental or global in extent. Gridded datasets built on ground-based observations (G; n= 20), satellite imagery (S; n= 20), and/or reanalysis products (R; n= 23) are compiled and described, with focus on the characteristics that hydrologic investigators may find useful in discerning acceptable datasets (variables, coverage, resolution, accessibility, and latency). We provide best-available-science recommendations for dataset selection based on a thorough review, interpretation, and synthesis of 29 recent studies (past 10 years) that compared the performance of various gridded climate datasets for hydrologic analyses. No single best source of gridded climate data exists, but we identified several common themes that may help guide dataset selection in future studies:

1. Gridded daily temperature datasets improved when derived over regions with greater station density.

2. Similarly, gridded daily precipitation data were more accurate when derived over regions with higher-density station data, when used in spatially less-complex terrain, and when corrected using ground-based data.

3. In mountainous regions and humid regions, R precipitation datasets generally performed better than G when underlying data had a low station density, but there was no difference for higher station densities.

4. G datasets were generally more accurate in representing precipitation and temperature data than S or R datasets, although this did not always translate into better streamflow modeling.

We conclude that hydrologic analyses would benefit from guided dataset selection by investigators, including justification for selecting a specific dataset, and improved gridded datasets that retain dependencies among climate variables and better represent small-scale spatial variability in climate variables in complex topography. Based on this study, the authors' overall recommendations to hydrologic modelers are to select the gridded dataset (from Tables 1, 2, and 3) (a) with spatial and temporal resolutions that match modeling scales, (b) that are primarily (G) or secondarily (SG and RG) derived from ground-based observations, (c) with sufficient spatial and temporal coverage for the analysis, (d) with adequate latency for analysis objectives, and (e) that includes all climate variables of interest (so as to better represent interdependencies).

1 Introduction

Hydrologists are faced with a dizzying variety of options when selecting climate data for water resource analyses. Climate drives hydrological processes, and accurate climate forcing data are essential for meaningful water resource investigations and modeling. However, it is arguable that no single source of climate data is universally appropriate, leading to a dearth of studies that make an effort to justify their dataset selection. Over recent decades, while ground-based observations from weather stations have decreased (Sun et al., 2018; Strangeways, 2006), gridded datasets built on ground-based observations, satellite imagery, and reanalysis products have increased.

A well-maintained, long-term weather station, although not error-free (Gebremichael, 2010; Strangeways, 2006), provides direct, in situ point measurements for a location. However, most hydrologic analyses address processes at locations and scales for which the point weather station data may not be representative. Gridded datasets offer several advantages over point station data (Essou et al., 2016a): gridded datasets are relatively easy to use, have uniform spatial coverage, provide consistent coverage over time (avoids the problem of non-reporting stations), and rarely have missing data. Uniform grids with temporal consistency allow simple averaging across a domain. However, gridded datasets often are not available in real time (i.e., data latency), which might pose limitations for some hydrologic analyses (e.g., snowmelt and runoff forecasting as well as operational water resource decision-making).

Many studies (29 of which are reviewed in Sect. 4 of this article) have intercompared the accuracy of particular subsets of these gridded climate datasets for various regions, settings, and time frames across the globe with various insights and conclusions. However, no cataloguing or synthesis of these studies has been completed to date, presenting an important knowledge gap that may hinder well-informed dataset selection. To address this need, we completed a search of “intercomparison” AND “gridded AND climate AND data”, which yielded 202 documents using Scopus. Excluding “climate change” reduced this to 100 documents, and excluding “CMIP” produced 77 documents. Even with these filters, most studies focus on a limited number of datasets, lack generalizable recommendations, and do not consider the functional implications of dataset limitations on end users' hydrologic analysis. The present study aims to provide a comprehensive compilation, overview, and considerations for selection of gridded datasets with an emphasis on selection for hydrologic modeling and analyses. Our focus is on historical datasets (not climate projections) at the conterminous US (CONUS) to global extents.

2 Gridded dataset sources

Gridded historical climate datasets can be categorized as ground-based (G), satellite-based (S), or reanalysis-based (R) according to the sources of data and methods used in their derivation. Many datasets integrate multiple data sources and methods in deriving the dataset; in this article, the primary data source/method for integrated datasets is listed first, followed by secondary method(s) (e.g., SR, RG, and RSG). We focus on gridded datasets available for five climatological variables that are essential to hydrological analyses: precipitation (P), air temperature (T), atmospheric moisture (relative humidity, rh; specific humidity, sh; dew-point T, T_dp; or vapor pressure, V_p), wind speed (u), and solar radiation (R_s) or associated metrics (cloud cover, cc, or sky cover, sc). Particular emphasis is on datasets that provide gridded P, a highly variable and critical driver in hydrological analyses. For more details, the reader is directed to an informative review of global P datasets, including a discussion of these dataset sources and estimation procedures (Sun et al., 2018).

Although the grid resolution of each data product is clear, the support scale is generally vague. That is, the grid centroid is often treated as a point, which is then interpolated or regionalized to obtain area-averaged values at the scale of hydrologic model resolution (e.g., a hydrologic response unit – HRU). However, if the gridded data represent grid-scale (e.g., 4 km × 4 km) areal averages, this should be considered during interpolation to the HRU scale. Scaling within and across grid cells has been explored for gridded soil moisture (Hoehn et al., 2017), but it remains an issue for gridded climate products. In this study, we mention this as a precaution but do not offer scaling solutions.

2.1 Ground-based (G) datasets

Ground-based gridded datasets (Table 1) are derived directly from observational data, typically from weather station networks. Various methods are used to interpolate data between stations and may account for orographic effects, lake effects, and other mesoscale meteorologic phenomena. These datasets benefit from direct application of data with relatively well-defined biases and uncertainty inherited from the instrumentation characteristics and errors. For example, P data collection has well-known errors at the station level from sources such as wind, evaporation, wetting, splashing, site location, instrument error, spatiotemporal variation in drop-size distribution, and frozen vs. liquid P (Sun et al., 2018). Interpolating these data to a grid adds additional uncertainty to the extent to which station density inadequately captures spatial variability in the climatic variable across the domain. Minimum recommended station densities vary by physiographic unit (e.g., mountains and plains) from one to four stations per 1000 km² (WMO, 2008). Essou et al. (2017) noted that most of the 316 watersheds in their comprehensive Canadian study had less than one station per 1000 km², indicating a wider global concern. Increased station density generally improves gridded dataset quality, but it may be impractical to adequately cover regions with complex topography, localized convective storms, heat islands, blowing snow, or other micrometeorological heterogeneity. For example, snow gauge undercatch due to high wind speeds is an especially pronounced phenomenon that challenges accurate characterization of water storage in snow-dominated basins (Fassnacht, 2004; Panahi and Behrangi, 2020). Station density and coverage also change over time as old stations are deprecated or new stations added, complicating interpolation schemes and often disproportionately diminishing coverage in remote areas. Sun et al. (2018) noted that the number of global stations in the GPCC v7 dataset changed from 10 900 stations in 1901 to a maximum of 49 470 in 1970, decreasing to 30 000 in 2005, and decreasing again to only 10 000 in 2012. This recent decline in station data not only impacts G datasets but also S and R datasets that rely on station data in their dataset development. Uncertainties associated with these temporal changes in sampling density are further complicated by the nonstationarity of climate and accelerated climate change in recent decades.

Table 1 Summary of ground-based (G) gridded datasets.

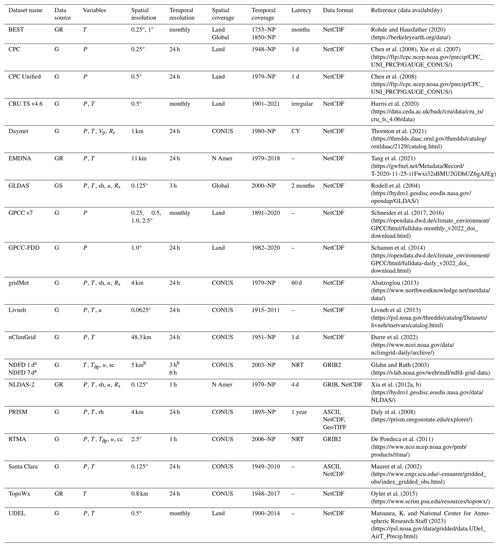
Data source: G – ground-based observations (with interpolation); S – satellite; R – reanalysis. Variables: P – precipitation; T – air temperature; rh – relative humidity; sh – specific humidity; T_dp - dew-point T; V_p – vapor pressure; u – wind speed; R_s – solar radiation; sc – sky cover; cc – cloud cover. Spatial resolution: 1.0° latitude = 111 km; 1.0° longitude = 111 km at 0° latitude and 85 km at 40° latitude. Spatial coverage: CONUS – conterminous US; N Amer – North America; Land – global land surfaces only (not ocean surfaces); Global – global land and ocean surfaces. Temporal coverage: NP – near present. Latency: NRT – near-real time; CY – available each calendar year; “–” – static dataset. Data format: NetCDF – Network Common Data Form; ASCII – American Standard Code for Information Interchange; GRIB – Gridded Binary; GeoTIFF – Georeferenced Tagged Image File Format. ^a NDFD provides 1–7 d lead-time forecasts. ^b NDFD spatial resolution changes to 2.5 km and 1 d forecast temporal resolution changes to 1 h after 19 August 2014. All links listed in the table were last accessed on 29 November 2024.

2.2 Satellite-based (S) datasets

Satellite-based gridded datasets (Table 2) are derived from various sensors aboard geostationary satellites (visible/infrared, IR, sensors) with rapid sampling frequency (30 min or less) and low-Earth-orbit satellites (visible/IR; passive microwave, MW; and active MW) with a lower temporal sampling frequency (Sun et al., 2018). Compared to G datasets, S datasets provide spatially homogenous coverage (the entire area within the coverage field has similar data density) and temporally continuous records, but they are limited in temporal coverage to the satellite era, with the first Television and IR Observation Satellite (TIROS) launched in 1960. Visible/IR methods detect cloud-top surface conditions and correlate colder/brighter cloud tops to greater convection and more P. Passive MW methods detect precipitation-sized particles, thereby providing a more-direct measure of P. Active MW methods allow measurement of the instantaneous three-dimensional structure of rainfall. Methods have been developed to merge these datasets to capitalize on the higher accuracy of MW methods and greater temporal frequency of visible/IR methods and increase overall product accuracy (Sun et al., 2018).

A review by Maggioni et al. (2016) described satellite instruments and compared many of the algorithms used in current satellite P datasets. They found that S datasets have a larger overestimation bias in the warm season and a lower positive bias in the cold season. Satellite datasets have high probability of capturing warm-season convective events; as a result, in the central US, for example, S datasets have better agreement with ground-radar products than rain gauge stations, which can miss localized convective storms. Satellite-based products tend to underestimate intense rainfall during extreme hurricane events; S also tends to underestimate light P at high elevations and overestimate P at low elevations in regions of complex topography in northwestern Mexico and the Appalachian Mountains, all of which may be attributed to IR sensors' lack of discrimination between raining and non-raining clouds.

Table 2 Summary of satellite-based (S) gridded datasets.

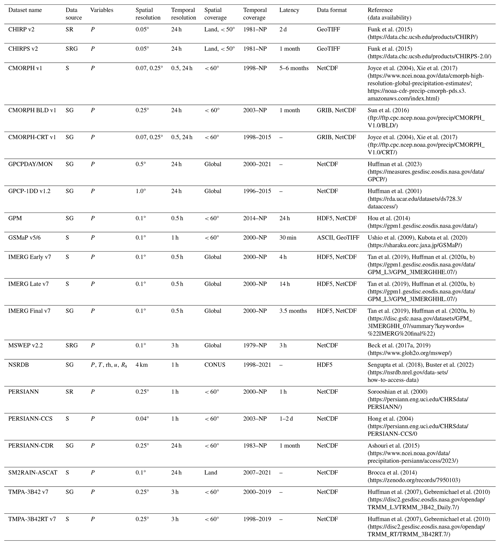
Data source: G – ground-based observations (with interpolation); S – satellite; R – reanalysis. Variables: P – precipitation; T – air temperature; rh – relative humidity; u – wind speed; R_s – solar radiation. Spatial resolution: 1.0° latitude = 111 km; 1.0° longitude = 111 km at 0° latitude and 85 km at 40° latitude. Spatial coverage: CONUS – conterminous US; N Amer – North America; Land – global land surfaces only (not ocean surfaces); Global – global land and ocean surfaces. Temporal coverage: NP – near present. Latency: “–” – static dataset. Data format: NetCDF – Network Common Data Form; HDF5 – Hierarchical Data Format 5; ASCII – American Standard Code for Information Interchange; GRIB – Gridded Binary; GeoTIFF – Georeferenced Tagged Image File Format. All links listed in the table were last accessed on 29 November 2024.

2.3 Reanalysis-based (R) datasets

Reanalysis-based gridded datasets (Table 3) are synthesized from process-based climate models, often together with G and/or S observational data, with the goal of generating gridded datasets with spatially homogenous data density that are temporally continuous. A precipitation forecast is generated from complex interactions of a priori predictions from a physically based, dynamical process model (that can often account for orographic effects in topographically complex regions) and ingested observational data. Reanalysis systems use various models, observational datasets, and assimilation methods; can generate many climate variables with interdependent variable consistency; and provide near-real-time datasets with latency periods from hours to months. Accuracy of R methods may be limited by the changing availability of observational data and biases in observations and models.

Reanalysis datasets have been found to better capture winter P resulting from large-scale systems than summer P with a greater influence of localized convective storms (Massmann, 2020; Beck et al., 2019). Similarly, Beck et al. (2017b) confirmed the conclusions of several other studies (Barrett et al., 1994; Xie and Arkin, 1997; Adler et al., 2001; Ebert et al., 2007; Massari et al., 2017) which demonstrated that reanalysis underperformed MW- and IR-based datasets in the tropics and outperformed them in colder regions (> 40° latitude). Reanalysis demonstrated reduced bias compared with S datasets, with greater ranges of bias among all datasets in areas with complex topography (the Rockies, Andes, and Hindu Kush) and arid regions (the Saharan, Arabian, and Gobi deserts) (Beck et al., 2017b).

Table 3 Summary of reanalysis-based (R) gridded datasets.

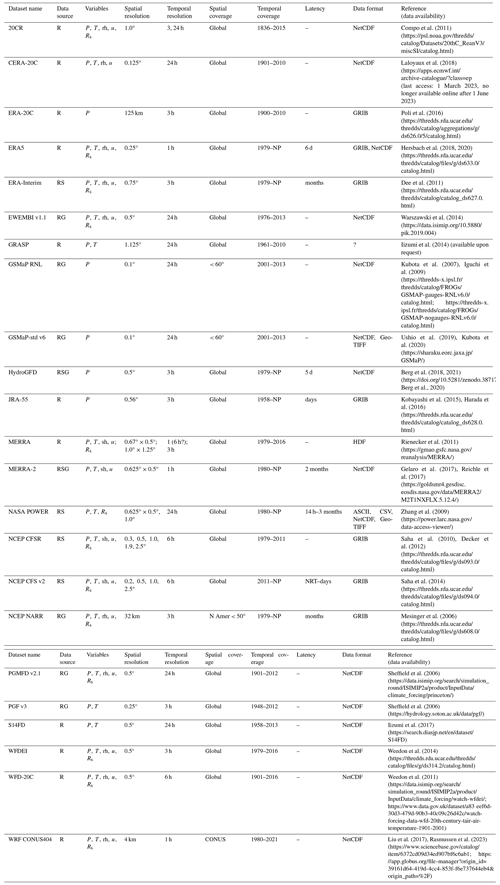
Data source: G – ground-based observations (with interpolation); S – satellite; R – reanalysis. Variables: P – precipitation; T – air temperature; rh – relative humidity; sh – specific humidity; u – wind speed; R_s – solar radiation. Spatial resolution: 1.0° latitude = 111 km; 1.0° longitude = 111 km at 0° latitude and 85 km at 40° latitude. Spatial coverage: CONUS – conterminous US; N Amer – North America; Land – global land surfaces only (not ocean surfaces); Global – global land and ocean surfaces. Temporal coverage: NP – near present. Latency: “–” – static dataset. Data format: NetCDF – Network Common Data Form; HDF5 – Hierarchical Data Format 5; ASCII – American Standard Code for Information Interchange; GRIB – Gridded Binary; GeoTIFF – Georeferenced Tagged Image File Format; CSV – comma-separated values; ? – unknown. All links listed in the table were last accessed on 29 November 2024.

2.4 Integrated products

Inherent limitations of individual data sources (G, S, or R) can be reduced by merging other data sources with complementary advantages to reduce errors or biases. Some reanalysis datasets are used independently or merge multiple reanalysis products (denoted by R in Table 3). Reanalysis datasets commonly ingest ground-based observational data (RG), satellite data (RS), or both (RSG). Some S datasets also integrate G data (denoted by SG in Table 2), reanalysis data (SR), or both (SRG) to enhance accuracy and reduce bias. Several data sources, such as CHIRP, CMORPH, IMERG, PERSIANN, and TMPA, offer multiple products with increasing data source complexity, often with increased latency and different spatial and temporal resolutions. Each dataset follows a different workflow in developing the integrated product; in general, the primary method (in this article, the first abbreviation letter) is enhanced somewhat sequentially with various interpolation or bias correction schemes using the secondary dataset(s).

3 Considerations for use of gridded dataset for hydrologic analyses

The gridded datasets summarized in Tables 1, 2, and 3 span 0.8 to 278 km spatial resolutions, 0.5 to 720 h (monthly) temporal resolutions, 0.02 (30 min) to 365 d latencies, CONUS to global spatial coverage, and 10- to 271-year periods of record, starting as early as 1753 (Fig. 1). Differences have emerged in the representation of G, S, and R datasets across many of these categories. G datasets have the finest spatial resolutions (1 km) and longest periods of record (> 240 years) and tend to have the longest latency (average for G = 86 d, compared with S = 29 d and R = 36 d). A greater proportion of G datasets have less-extensive spatial coverage (CONUS to North American continental in this study), whereas S and R datasets were typically global in extent. S datasets start no earlier than 1979 and comprise no greater than a 45-year period of record (through 2023). More R and S datasets have finer temporal resolution than G datasets, with average resolutions of 10 h for R and 9 h for S compared with 158 h for G.

No single best source of gridded climate data exists. Many characteristics of gridded datasets influence the best product for a given application or research question. We highlight several of the most important considerations in differentiating among the many possible gridded datasets. Most of these characteristics are detailed for each gridded dataset in Tables 1, 2, and 3.

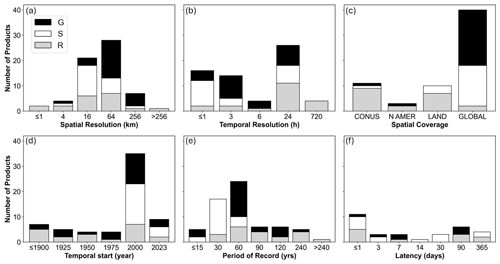
Figure 1 Distribution of (a) spatial resolution, (b) temporal resolution, (c) latency, (d) period start date, (e) period of record, and (f) spatial coverage for assessed ground-based (G), satellite-based (S), and reanalysis-based (R) gridded precipitation data sources. x-axis labels are the upper limits of each categorical bin, exclusive of other bins. The abbreviations used in the figure are as follows: CONUS – conterminous US; N AMER – North America; LAND – global land surfaces only (not ocean surfaces); GLOBAL – global land and ocean surfaces.

3.1 Variables and interdependencies

Hydrological investigations typically begin with selecting datasets for each important climate variable. Tables 1, 2, and 3 summarize the variables included in each gridded dataset. Datasets that include all climate variables of interest may inherently represent appropriate interdependencies or cross-correlations among the variables. For example, periods of time with P are associated with cloud cover; decreased R_s; and, often, higher humidity. Other types of dependency-related dilemmas may also occur in gridded datasets. Cold-air drainage can invert the minimum T (T_min)–elevation relationship in montane foothills, and daily T_min may not equal daily average T_dp in semiarid regions (T_min decoupled from 100 % rh), thus invalidating an assumption of commonly used schemes to spatially interpolate gridded T_dp data (McEvoy et al., 2014). Often the accurate representation of these interdependencies is important in hydrologic analyses.

3.2 Coverage

Gridded datasets have a range of spatial and temporal extents. All datasets summarized in this article span at least the CONUS, and many are continental or global in extent. General guidelines by the World Meteorological Organization require a 30-year minimum period of record to reasonably represent climate variability. Non-stationarity of climate makes it even more important to consider whether longer periods representing climatic trends or periods more heavily weighted toward recent data are preferable for a given hydrologic study. Periods of record may be dictated by investigations focused on specific events or periods, such as studies of the hydrologic effects of wildfire or other disturbance events, calculations of the recurrence interval of a flood of a given severity, or studies assessing hydrologic responses over specific periods.

3.3 Resolution

The spatial and temporal resolution of the dataset should be adequate to represent the variability in the climate variable given the representational scale of the hydrologic model. The simulated spatial and temporal resolution of evapotranspiration (ET), runoff, and other hydrological elements in hydrologic models can be relatively fine (< 1 km, subdaily), and model resolution is increasing in ways that capitalize on increasing computational power, process understanding, and data availability (Melsen et al., 2016). Hydrologic model output resolution and uncertainty are often limited by the spatial and temporal resolution of climate datasets. As such, the resolution of gridded climate datasets should be an important criterion to consider, especially in mountainous areas within complex terrain driving spatial heterogeneity in climate variables. Some gridded datasets sacrifice the representation of extremes, both wet and dry, to better represent mean climatic conditions. Alternatively, increased temporal resolution may come at the cost of reduced spatial resolution. Creation of spatially continuous and consistent gridded response surfaces can result in point data extremes being smoothed during interpolation. Gridded data interpolation schemes can also influence the representation of meteorologic variability; for example, Daymet uses a strict T–elevation relationship that limits its ability to represent T inversions relative to PRISM, which includes “climatologically aided interpolation” (McEvoy et al., 2014). Methods that create ensembles of multiple gridded datasets often better represent mean conditions across a domain at the expense of representing the full range of possible conditions within the domain.

3.4 Format and accessibility

Data format and accessibility dictate how easily and effectively a dataset can be accessed, processed, and analyzed for a specific hydrologic application. Several common data formats are described in Table A1. The data format must be compatible with software and tools used in the hydrologic analysis. Formats such as NetCDF and HDF5 are widely used in climate research because they are consistent with various processing tools and can efficiently store large multidimensional datasets. Adequate metadata are essential for understanding the dataset, including its origin, methodology, and any processing it has undergone. Investigators may consider the importance of datasets that can be compressed without significant data loss, are interoperable with the other datasets, and are freely available and easily accessible online. Some datasets have application programming interfaces (APIs) for automated data retrieval that can be useful.

3.5 Site and event characteristics

Preference may be given to datasets that reflect characteristic spatial and temporal dimensions of climatic processes in the domain, such as cool-air drainage patterns, orographic or convective P events, lake effects, and effects of altitude. Priority may be given to datasets that capture the most important aspects of climate variable magnitude and variability at appropriate scales, including daily/seasonal/annual averages, extreme event (high or low) magnitudes, or event sequences (continuous dry days, CDDs; continuous wet days, CWDs; etc.). For example, datasets with fine temporal resolution (∼1 h) may be required to capture hydrological functioning when P is dominated by high-intensity but short-duration convective events. In hydrologic models, spatiotemporal scales are interdependent, and source data should be considered in watershed delineation.

3.6 Process and model sensitivity and latency

Hydrologic processes are differentially sensitive to climatic variables and characteristics. For example, a snowmelt runoff modeling study may prioritize a dataset with accurate, fine-spatial-resolution T and accurate R_s, whereas a small-basin study of soil moisture or erosion dynamics may prioritize a fine-scale P dataset that maintains a full range of extreme events. A study focused on ET dynamics may prioritize a dataset that includes T, rh, u, and R_s and maintains appropriate inter-variable dependencies. Flood simulation may prioritize fine-temporal-resolution P data at a resolution matching the domain heterogeneity. Long-term water balance studies or large-scale river basin studies may prefer daily or monthly datasets with coarse spatial resolution. Often, the selected model formulation will constrain the required variables, their characteristics, and the preferred data format.

Latency, or the time lag in dataset availability, may also be an important consideration. Some modeling applications may require real-time or near-real-time results. Other applications designed to analyze historical trends or prior conditions can tolerate long data latency periods. Gridded datasets may implement additional processing steps intended to increase accuracy or resolution but that increase the latency before data become available for use. In the gridded datasets summarized in Tables 1–3, S datasets averaged the shortest latency periods (29 d), followed by R (36 d) and G (86 d).

3.7 Time zone considerations

When using climate and other hydrologic data from different sources, the data time period consistency is critical and too often overlooked. Particularly for data in a “daily” format, users must be cognizant of the zonal time period for each dataset. Station data vary with respect to the reporting period for G data (e.g., daily periods beginning at midnight, 07:00, or 08:00 standard time or local time, i.e., with spring and fall daylight savings time shifts). Gridded datasets may provide data for a standard time period (e.g., 24 h period from 00:00 GMT) or adjusted for a user-defined time zone. Hydrologic comparison datasets (e.g., streamflow) may be reported for 24 h starting at midnight standard or local time or for some other 24 h period. Mismatched datasets may lead to systematic analysis errors.

4 Review of gridded dataset performance

Appropriate selection from among the many available gridded meteorological datasets requires an understanding of how these datasets impact hydrologic modeling. To assist with the selection process, we conducted a thorough review and synthesis of the recent (past 10 years) literature comparing gridded meteorological datasets, with specific consideration of their influence on hydrologic modeling (Table 4). Studies were selected that (a) compared multiple gridded datasets, preferably including comparisons with different resolutions, scales, spatial contexts (topography, climate), goals, or hydrologic models; (b) compared the accuracy of those datasets to observed meteorological data; and (c) compared the performance of those datasets as forcing data for hydrologic model(s) or analyses. Most studies assessed and compared P datasets; some also assessed T datasets; and very few assessed rh, u, or R_s datasets. This relates, in equal measures, to the relative importance of P data in hydrologic analysis; the relative complexity of representing P in gridded datasets; and the relative availability of P, T, and other data across G, S, and R datasets (Tables 1, 2, 3).

Table 4 Summary of recent (10 years, 2014–2023) literature on gridded dataset comparisons for hydrologic modeling.

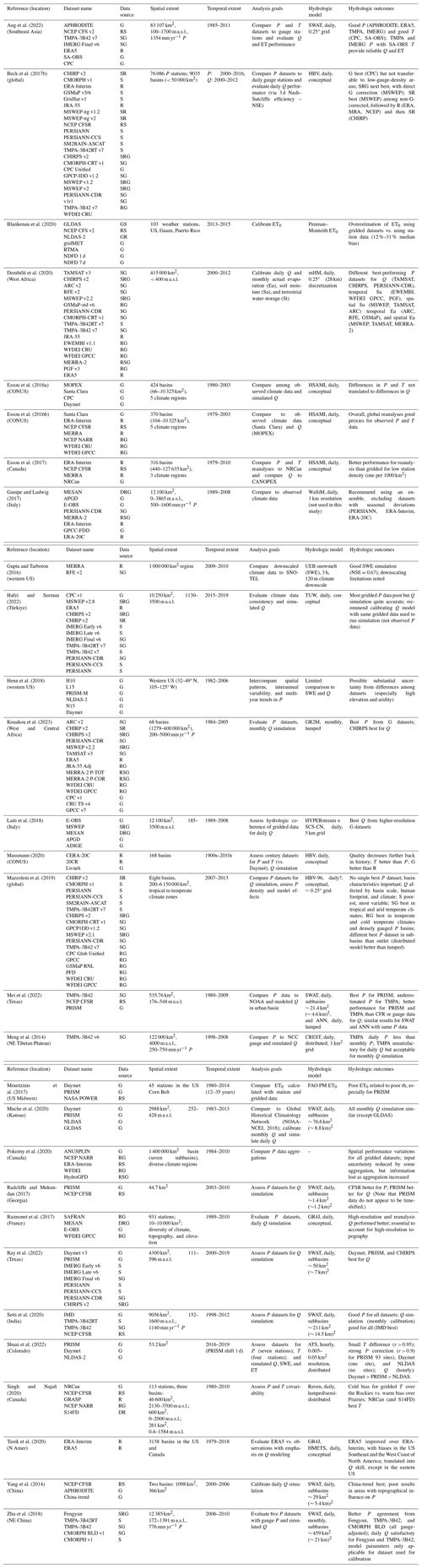
Reference (location): general region of study. Data source: G – ground-based observations (with interpolation); S – satellite; R – reanalysis; D – downscaling.

4.1 Humidity, wind, and solar radiation dataset assessment

A total of 2 of the 29 studies summarized in Table 4 assessed and compared humidity (rh, sh, T_dp, or V_p), wind speed (u), and/or solar radiation (R_s, sc, or cc) to station data or their effects on hydrologic analyses. Mourtzinis et al. (2017) assessed and compared G gridded datasets for rh (Daymet, derived from V_p, and PRISM derived from T_min and T_max) and R_s (Daymet, G; NASA POWER, RS) to observed data from 45 stations in the US Midwest. They found good agreement between daily R_s and station data (RMSE = 8 % for both datasets), with 98 % of data within 15 % of the measured data. However, daily rh agreement was poor for both Daymet (RMSE = 13 %) and PRISM (RMSE = 18 %). Blankenau et al. (2020) compared six G datasets to 3 years of data at 103 weather stations across the US, Guam, and Puerto Rico. For V_p, u, and R_s, performance was best for RTMA and NDFD 1 d forecasts and worst for NLDAS. High spatial resolution did not necessarily confer accuracy, as coarser GLDAS (28 km) and NCEP CFS v2 (22 km) datasets outperformed finer NLDAS (14 km). Bandaru et al. (2017) compared four gridded datasets (three G and one RG) to observed monthly data from five flux towers in the northwestern US and found different results for humidity (T_dp) and R_s. For T_dp, performance decreased in the following order: NCEP NARR (RG) to PRISM to Daymet to NLDAS (G). Conversely, for R_s, performance decreased in the following order: from NLDAS to Daymet (both with negative bias) to NCEP NARR (positive bias). McEvoy et al. (2014) compared P, T, and rh data from four G datasets to 14 stations in Nevada. Gridded datasets, particularly Daymet, had difficulty representing cold-air drainage in this mountainous terrain; PRISM incorporates methods to represent inversions and performed better across the 1-year comparison study. Finer resolution (PRISM: 800 m; Daymet: 1 km) had less bias than coarser resolution (PRISM and gridMet: 4 km) datasets. Also, the common assumption that daily T_min approximates T_dp (used by Daymet) was unrealistic in this semiarid environment.

Current literature is too limited to provide a consensus for humidity, u, or R_s gridded dataset selection. More studies are needed, both to assess the accuracy of available humidity, u, or R_s gridded datasets (Tables 1, 2, 3) and to assess their impacts on hydrologic model performance. A key conclusion was that analyses in which rh, u, and R_s are primary forcing variables (e.g., ET, airshed, snowpack, or surface soil moisture dynamic analyses) would benefit from an assessment of available dataset suitability (e.g., comparison of the gridded dataset to reference, ground-based weather stations in or around the study area) and a sensitivity analysis of the model (how responsive is the response variable to the noted gridded climate dataset uncertainty) prior to dataset selection. Hybrid data sources (station and gridded) need to be considered regarding both model skill for simulating hydrology and optimal model parameter sets, because effects of mixing data sources are generally unknown. Dependencies among climate variables (such as those discussed in Sect. 4.4 for P−T dependencies) may also be an important consideration for humidity, u, and R_s and lead to prioritizing a gridded dataset that represents covariances among variables of concern. As such, methods to retain coupling of climate variables in gridded datasets are needed.

4.2 Temperature (T) dataset assessment

Accuracy and agreement of gridded datasets of air temperature (T) at 2 m above the ground (Table 4), about crop canopy height, were dependent on many factors, including the spatial region of interest and topography. Essou et al. (2016b) found that T data from six R datasets were generally comparable to station data in 370 basins across the CONUS. Behnke et al. (2016) evaluated eight G datasets and found gridded T data to be highly correlated (r>0.9) with station data, although biased towards cooler T, across the CONUS; the best dataset differed by region, and spatial resolution was not an important factor. Massmann (2020) analyzed three datasets (two R and one G) with long (century) periods of record in 168 basins throughout the CONUS and found that T datasets were generally adequate across the US but were less adequate (lower daily rank correlation and higher long-term bias) in the Rocky Mountains. In the Rockies, Shuai et al. (2022) found a strong correlation (r>0.95) with measured station data in Colorado for G datasets (PRISM, Daymet, and NLDAS-2). In the US Midwest, Mourtzinis et al. (2017) found good agreement (RMSE < 5 %) for both PRISM and Daymet. Tercek et al. (2021) revealed a characteristic of G datasets tending to underrepresent higher-elevation point locations (e.g., mountain tops), which corresponded to gridded monthly maximum T data. McEvoy et al. (2014) found that G datasets (PRISM, Daymet, and gridMet) in montane regions underestimated inversion strength and T_min in foothills. As expected, datasets resulting from downscaling methods were constrained by the inherent inaccuracies of the original gridded T dataset (Gupta and Tarboton, 2016).

Several studies have specifically addressed the contribution of gridded T datasets to hydrologic model performance. A consensus across many studies was that T dataset selection was less influential on hydrologic simulation accuracy than P dataset selection (Dembélé et al., 2020; Essou et al., 2016a; Mei et al., 2022; Shuai et al., 2022). Laiti et al. (2018) evaluated five gridded daily T datasets covering a basin in the Italian Alps, with elevations ranging from 185 to 3500 m. They found that G datasets with higher resolution produced the best streamflow (Q) simulation and also suggested that T datasets from various sources (G, S, and R) can be used interchangeably, with negligible impacts on simulation results. The consensus from these nine studies (discussed in this section and cited in Table 4) suggests that gridded T datasets can generally be used interchangeably for hydrologic analyses in most parts of the CONUS or globally, although differences in hydrologic response may arise in areas of more complex (i.e., mountain) topography.

4.3 Precipitation (P) dataset assessment

Precipitation (P) datasets were less reliable than T datasets, both with respect to their accuracy and their performance forcing hydrologic models. P data often lack accuracy and spatial variability in complex, mountainous topography (Hafzi and Sorman, 2022; Henn et al., 2018) and need to be gauge-corrected (Raimonet et al., 2017; Mazzoleni et al., 2019; Laiti et al., 2018; Essou et al., 2017; Hafzi and Sorman, 2022). In mountainous regions and humid regions, R datasets generally performed better than G in areas with a low station density (less than one station per 1000 km²), but there was no difference in performance for higher station densities (more than three stations per 1000 km²) (Essou et al., 2017). Gampe and Ludwig (2017) and Essou et al. (2016b) found that R datasets show a great potential to provide reasonable P data in areas where the station location and density cause high errors and uncertainty, especially at higher elevations and in topographically complex regions. Ang et al. (2022) found that P data from G (APHRODITE), SG (TMPA-3B42 and IMERG), and R (ERA5) datasets all performed well (r>0.75) in a data-sparse region (less than three stations per 1000 km²) of Southeast Asia. Essou et al. (2016b) judged that differences between R and observed G data across the CONUS were small enough to allow direct use of R-based P and T data for hydrologic modeling without bias correction. Satellite datasets corrected with either R or G datasets increased P accuracy (Hafzi and Sorman, 2022). In hydrologic models, inputs of daily or hourly P are partitioned into rain (liquid) and snow (solid) based primarily on T (daily T_min), but little information exists on the relative accuracy of P for rain, snow, and rain–snow mixes. See Sect. 4.4 and 4.6 for P–T interactions and the estimation of the snow-water equivalent (SWE).

The G methods provided the most accurate gridded P data (Kouakou et al., 2023; Massmann, 2020), although performance of G datasets deteriorate in gauge-sparse regions (Beck et al., 2017b). With adequate station density, weather-station network data were superior at local to regional scales (Tarek et al., 2020; Meng et al., 2014; Yang et al., 2014). Datasets that directly integrated higher-temporal-resolution gauge data performed best, with decreasing performance from those incorporating daily gauge data (CPC Unified and MSWEP v1.2 and v2) compared with 5 d gauge data (CHIRPS v2), monthly gauge data (GPCP-1DD v1.2, TMPA-3B42 v7, and WFDEI CRU), or a monthly SG GPCP product (PERSIANN) (Beck et al., 2017b).

Global R datasets often were good proxies for P data (Essou et al., 2016b). Massmann (2020) found that R datasets were more appropriate for short-term P in the northwestern US, with some difficulties in representing P in the southern and eastern US. From a comparison of 18 gridded datasets, Mazzoleni et al. (2019) found no single best P dataset. The R datasets performed better than G datasets for a low station density (less than one station per 1000 km²); otherwise, little difference was observed (Essou et al., 2017; Tarek et al., 2020). Gampe and Ludwig (2017) found that higher-resolution P data performed better, but coarse-resolution data provided a close representation of overall, longer-term climate characteristics. Raimonet et al. (2017) demonstrated the importance of accounting for the impacts of high-resolution topography on P gridded data and that low-altitude, less-complex topographies were less sensitive to the choice of gridded dataset. Similar results were reported by Laiti et al. (2018), who added that simple bias correction cannot overcome P dataset deficiencies.

Overall, the literature suggests that the interaction of station density and basin characteristics, primarily topography, is of central importance and can drive performance. In regions with a high station density (more than three stations per 1000 km²), G datasets or those corrected using G data (SG, RG, SRG, and RSG) perform similarly. However, in areas with a lower station density (less than one station per 1000 km²), at higher elevations, and in topographically complex regions, R datasets perform better. Unadjusted S datasets, without G or R correction, were generally the least reliable. Other site and dataset considerations may also be important for specific hydrologic modeling applications and are discussed in the following sections.

4.4 P–T dependency

Climatological dependencies can exist between P and T. Gridded datasets decouple P and T, which can cause problems with hydrologic simulation (Singh and Najafi, 2020). For example, Singh and Najafi (2020) noted the failure of gridded datasets to represent warm–wet dependencies in north and southwest Canada and hot–dry dependencies in the spring and summer seasons in the Canadian Prairies that were present in the observed data. This led to inaccurate modeling of hydrologic processes (rain–snow partitioning and extreme events), which may be particularly important in representing hydrological reality under a changing climate. In response to this need for coupled P and T data, Raimonet et al. (2017) suggested a process for dynamically calibrating a conceptual hydrological model on meteorological datasets, which was able to assess the consistency of the meteorological datasets, including the covariance of P and T, as well as improve streamflow simulation performance. Again, these results suggest that methods to retain coupling of climate variables in gridded datasets are needed.

4.5 Streamflow (Q) modeling

Not surprisingly, as noted above, Q was more responsive to P than T (Dembélé et al., 2020; Essou et al., 2016a; Mei et al., 2022; Shuai et al., 2022). Most gridded P datasets were adequate for Q simulation at the monthly scale and at spatial scales ranging from 3000 to 122 000 km² (Ray et al., 2022; Meng et al., 2014; Muche et al., 2020; Setti et al., 2020). Some studies found that G-based P datasets were generally better than S or R datasets for hydrological modeling (Ray et al., 2022; Meng et al., 2014; Kouakou et al., 2023; Massmann, 2020), especially for high-spatial-resolution datasets (Laiti et al., 2018). In addition, hydrologic performance using G datasets was not affected by basin size, but the performance of the G datasets did improve slightly as the weather station density of their source data increased (Essou et al., 2017). However, total basin size did not influence Q performance (Tarek et al., 2020). In a study of eight large-scale basins globally, Mazzoleni et al. (2019) found that Q simulation was affected by the basin scale, human footprint, and climate: S datasets had the poorest performance and were the most variable; SG datasets were the best performers in tropical and arid temperate climates; and RG datasets were the best performers in temperate and cold temperate climates and within basins with densely gauged P.

In a study of nine gridded datasets applied with a conceptual hydrologic model to simulate streamflow in 9053 basins (< 50 000 km²) worldwide, Beck et al. (2017b) found that the MSWEP v2 P dataset provided consistently better performance than other products across North America, Europe, Japan, Australia, New Zealand, and southern and western Brazil, whereas CHIRPS v2 performed better than other products in Central America, and central and eastern Brazil, but no one dataset performed best everywhere. They also concluded, based on the good performance of CPC-United, CHIRPS v2, and MSWEP v1.2 and v2, that the incorporation of sub-monthly gauge data improved Q simulation.

Interestingly, the best P dataset was not always the best for Q modeling (Yang et al., 2014), and lower P and T performance did not always translate into lower Q performance (Essou et al., 2016a; Hafzi and Sorman, 2022). Similarly, Ang et al. (2022) found that S datasets corrected with G observations had better Q performance than other G or R datasets that performed similarly in comparison to observed P data.

Datasets with the best representation of temporal dynamics did not necessarily align with those with the best representation of spatial patterns, with more hydrologic uncertainty associated with misrepresenting spatial patterns than temporal dynamics (Dembélé et al., 2020). Hafzi and Sorman (2022) found that most gridded P datasets had low performance with respect to representing daily P over space and time, but some still had accurate Q simulation. Mazzoleni et al. (2019) found that the best P dataset for a basin outlet was not necessarily the best for its subbasins, which reflects the influence of scale and suggests a benefit to distributed hydrologic modeling over lumped modeling approaches.

Hydrologic model calibration approaches were also sensitive to the selection of gridded dataset. Ray et al. (2022) found that model parameter uncertainty decreased when calibrating the SWAT model using G-based P datasets. In addition, hydrologic models calibrated using one gridded dataset did not work as well when applied using forcings from other datasets (Zhu et al., 2018; Hafzi and Sorman, 2022).

Dependency between P and T did not appear to affect Q simulation. Shuai et al. (2022) found that intermixing T datasets among PRISM, Daymet, and NLDAS P datasets had little effect on Q.

4.6 ET and SWE modeling

Few studies were found that compared the effects of gridded datasets on the simulation of other spatially distributed hydrologic variables, such as ET or SWE. Mourtzinis et al. (2017) found that Daymet outperformed PRISM with respect to calculating the FAO Penman–Monteith reference ET (ET₀) in the US Midwest. Although both were similar in comparisons of P and T, ET₀ bias was less for Daymet (−4 mm) than for PRISM (+253 mm), and both had poor agreement in the high and low ranges of measured ET₀. Errors were related to poor agreement with rh, especially for PRISM. Similarly, ET₀ was generally overestimated (relative to ET₀ from weather station data) by all six G datasets evaluated by Blankenau et al. (2020), with median biases from 12 % to 31 %, consistent with the overestimation of T, u, and R_s and the underestimation of V_p. In a comparison of different gridded datasets forcing ET simulation in SWAT, Ang et al. (2022) found that using P from TRMM and IMERG with T from a Southeast Asia observational network (SA-OBS) outperformed other gridded datasets (P: Aphrodite, ERA5, and NCEP CFS v2; T: CPC) in this tropical region. Poor performance of gridded dataset P and T was credited to the poor ET simulation. Shuai et al. (2022) found little difference between the simulation of ET from PRISM, Daymet, and NLDAS in Colorado and assumed that the similarity was related to using the same R_s forcing. Shuai et al. (2022) also evaluated the effects of G datasets on SWE in Colorado. They found that a fine spatial scale helped PRISM (0.8 km) and Daymet (1 km) outperform NLDAS (12 km) with respect to simulating spatial SWE, with the highest correlation from PRISM. Gupta and Tarboton (2016) used spatially downscaled R datasets (MERRA data for T, rh, u, and R_s; RFE v2 data for P) and found good SWE simulation compared to SNOTEL data (mean NSE = 0.67 across eight sites). Key sources of discrepancies were from P and R_s data uncertainty. These results indicate that accuracy in climate data translated into accuracy in ET and SWE simulation and suggest that all gridded data be scrutinized, as well as possibly bias-corrected, before use in ET and SWE modeling.

4.7 P ensembles

Ensembles of gridded datasets have often been recommended to account for gridded dataset uncertainty and better represent overall climatology (Gampe and Ludwig, 2017; Pokorny et al., 2020), although with some caveats. For example, Gampe and Ludwig (2017) found that R data (compared with station data) showed fewer consecutive dry days (CDDs, P < 1 mm), more consecutive wet days (CWDs, P > 1 mm), and a lower contribution of heavy-P events (i.e., more low- but steady-P events) to annual P, which has the potential to impact hydrologic simulation (more infiltration, less streamflow, greater baseflow, fewer floods, etc.). They recommended identification and removal of such nonrepresentative datasets from ensembles. Pokorny et al. (2020) suggested that data should be assessed in relation to the target hydrologic model's spatiotemporal scale. Notably, ensembles dampen extreme events and decrease the frequency of low-P/high-P events, which can lead to nonrepresentative hydrological simulations (Pokorny et al., 2020). Laiti et al. (2018) demonstrated a hydrologic coherence test (HyCoT), essentially a metric-independent method of comparing gridded datasets according to their performance in a hydrologic model, to exclude meteorological data less capable of reproducing a hydrologic outcome.

4.8 Latency

The latency with which gridded datasets become available for use may be a critical factor in gridded dataset selection. Few studies have assessed latency effects. Hafzi and Sorman (2022) found that some real-time datasets that were available with short latency (e.g., 1 h lag, PERSIANN-CSS with 0.04°) sacrificed accuracy compared with coarser, longer-latency datasets, such as IMERG Late v6 (14 h lag, 0.1°), MSWEP v2.8 (a few months lag, 0.1°), and CHIRPS v2 (1-month lag, 0.05°).

5 Conclusions

This study summarized characteristics, primary references, and data availability of 63 gridded datasets from a CONUS to a global extent to assist with dataset selection by hydrologic investigators. Our review of information from 29 recent (past 10 years) intercomparison studies spans a wide range of gridded datasets, study settings and scales, and hydrologic modeling objectives. Readers are referred to these studies for a wealth of detail on their results and recommendations; we encourage a particular focus on studies with similar climatic setting and hydrologic objectives to the planned investigation. From this review and synthesis, we formulated interpretations and, where appropriate, guidelines that are outlined in the following.

No single gridded climate dataset or data source was universally superior for hydrologic analyses. Several common themes arose among the 29 studies reviewed. Gridded daily temperature (T) datasets improved when derived from greater station density, although they were relatively interchangeable in hydrologic analyses. Gridded daily precipitation (P) data were more accurate when derived from higher-density station data, when used in spatially less-complex terrain, and when corrected using ground-based (G) data. In mountainous or humid regions, reanalysis-based (R) gridded datasets generally performed better than G gridded datasets when the underlying station density was low; however, when station densities were higher, there was no difference. Ground-based (G) gridded P datasets generally performed better than satellite-based (S) or R datasets, although better P and T datasets did not always translate into better streamflow modeling. Hydrologic analyses would benefit from advances in creating gridded datasets that retain climate variable interdependencies and better represent climate variables in complex topography. The caveat that some studies were insensitive to using independent sources of P and T may not be a good rationale for ignoring possible cross-correlations between climate variables. Rather, this result may point to the insensitivity of hydrologic models that do not necessarily capture spatiotemporal process interactions within a watershed. Use of hybrids of gridded datasets and station data for a particular region remains a topic for further investigation, as there can be substantial differences between data at a particular station and the corresponding grid cell data.

Hydrologic studies rarely defend their selection of a particular dataset to address research questions, but investigators should justify their selection of a particular gridded dataset with full consideration of both the climatologic setting and the hydrologic analysis type and objectives. Via a thorough review of the recent literature, this study provides general consensus recommendations for dataset selection, although characteristics of a given hydrologic analysis or study may warrant more specific selection processes and criteria. The authors' overall recommendations to hydrologic modelers are to select the gridded dataset (from Tables 1, 2, and 3) (a) with spatial and temporal resolutions that match modeling scales; (b) that are primarily (G) or secondarily (SG and RG) derived from ground-based observations, especially in areas of high topographic relief; (c) with sufficient spatial and temporal coverage for the analysis; (d) with adequate latency for analysis objectives; and (e) that includes all climate variables of interest, so as to better represent interdependencies.

Appendix A

Table A1 Summary of different data formats, descriptions, and processing approaches for gridded climate datasets using programming languages and software.

All links listed in the table were last accessed on 29 November 2024.