Modelling runoff in a glacierized catchment: the role of forcing product and spatial model resolution

Glaciers are vital water resources, particularly in alpine regions, sustaining ecosystems and communities during dry summer months. Accurate glacio-hydrological models are essential for understanding water availability under climate change. However, these models face numerous challenges, including limited observations for model forcing, calibration and validation, as well as computational constraints at fine spatial resolutions. This study assesses the reliability of glacio-hydrological simulations in a glacierized catchment (39.4 km²) in Switzerland using the Glacier Evolution Runoff Model (GERM) at daily temporal resolution. Two experiments investigate how simulated glacier mass balance and runoff are affected by (1) varying meteorological forcing products, from point data to coarse grids, and (2) spatial model resolution, from 25 to 3000 m. We find that the forcing from different precipitation data sets has the largest effect on model results. In this study, model resolutions coarser than 1000 m fail to capture essential glaciological and topographic details, affecting the accuracy of small and medium-sized glaciers. Single-data calibration on geodetic glacier ice volume change can accurately reproduce annual glacier mass balance but lead to seasonal biases, driven by underestimating winter precipitation and compensatory parameter adjustments. Calibrating the model on multi-data, including geodetic glacier ice volume change and runoff, improves seasonal accuracy but is limited by temporally constant precipitation adjustments that cannot account for temporal forcing biases. These findings highlight the trade-offs between computational efficiency and model reliability, emphasizing the need for high-resolution forcing data, particularly precipitation amount and seasonal variability, and careful calibration strategies to capture glacio-hydrological processes accurately. While the results are derived for a single, well-instrumented catchment, they hint at broader implications for modelling glacierized catchments under data-scarce conditions.

1 Introduction

Glaciers are essential water reserves. Their contribution to water availability and variability is of increasing importance and uncertainty, especially in the context of climate change (Jost et al., 2012; Tarasova et al., 2016; Huss and Hock, 2018; Biemans et al., 2019; Immerzeel et al., 2020; Parmesan et al., 2022). In many mountainous and alpine regions, glaciers act as “water towers”, storing water as snow and ice on multiple timescales and gradually releasing it during warmer periods (Stahl and Moore, 2006; Pritchard, 2019; Immerzeel et al., 2020; van Tiel et al., 2020a). This glacial meltwater is crucial for downstream ecosystems and human populations. In regions where seasonal snowmelt has decreased, especially during late summer, glacier melt remains as the primary contributor to runoff. The importance of glacier melt contribution on downstream hydrology varies strongly, shaped by factors such as local climate, the proportion of glacial coverage, and altitude (Immerzeel et al., 2020).

Understanding the behaviour of water resources in glacierized catchments requires extensive observational data, such as temperature, precipitation, and runoff measurements. However, mountainous regions generally face a scarcity of these observations as complex and heterogeneous terrain demands a high density of monitoring for capturing the local variability accurately. In remote and high-altitude glacierized regions like the Himalayas and the Andes, with challenging terrain and limited infrastructure, this scarcity is particularly pronounced (Qin et al., 2009; Salzmann et al., 2013; Azam et al., 2021; Muñoz et al., 2021). Even in regions like the European Alps that are comparatively well-monitored, data from the highest elevations remains sparse. Glacio-hydrological models are an essential tool to address these data gaps, simulate processes in ungauged areas, and make future projections (Chen et al., 2017; van Tiel et al., 2020b). However, glacio-hydrological models are often limited by incomplete knowledge of the physical processes across scales. This makes calibration essential for improving the reliability of the models, especially in under-observed regions (Huss et al., 2014; van Tiel et al., 2020b; Schuster et al., 2023).

To apply these glacio-hydrological models to data-scarce environments, regional and global gridded climate model results are often used as forcing, instead of in situ (point) meteorological observations. Point data would require installing and maintaining high-altitude weather stations, ideally spread in a dense network over the entire region of modelling, to provide local and high-resolution model forcing. Gridded climate products, on the other hand, offer an alternative by providing meteorological information over large regions. They are typically generated through interpolation of available weather station measurements (e.g. Dorninger et al., 2008; Frei, 2014), or by estimating the conditions in non-monitored areas with numerical modelling in combination with the observed data from nearby stations (e.g. Muñoz Sabater, 2019; Hersbach et al., 2020). Alternatively, satellite observations can provide remote sensing estimates of precipitation and temperature with broad spatial and temporal coverage. For example, satellite precipitation products from missions such as the Integrated Multi-satellitE Retrievals for GPM (IMERG) (Huffman et al., 2014) or the Climate Hazards Group InfraRed Precipitation with Station data (CHIRPS) (Funk et al., 2015) rely on active and passive microwave sensors. However, both gridded climate products and satellite-derived estimates face important limitations in complex mountainous regions. Gridded products often have coarse spatial resolutions (typically 1–30 km or larger), which can lead to significant uncertainties in precipitation estimates due to unresolved orographic effects and local variability in precipitation patterns (Palazzi et al., 2013; Tarasova et al., 2016; Chen et al., 2021; Peña-Guerrero et al., 2022). Similarly, satellite-based products are affected by retrieval uncertainties in high-altitude regions, misclassification of the precipitation phase, and limited ground validation (Li et al., 2014; Nepal et al., 2024). In addition, satellite temperature products generally provide land surface temperature (e.g. Wan, 2006, MODIS) rather than near-surface (2 m) air temperature. For these reasons, and because no single satellite product consistently provides both precipitation and temperature variables, we opted not to use satellite-derived climate data as forcing in this study, but only the interpolation and reanalysis products. As all meteorological products come with their uncertainties, it is essential to understand how the choice of meteorological forcing products influences the accuracy of glacio-hydrological simulations.

Another uncertainty is the spatial model resolution of (glacio)-hydrological models that may hamper capturing fine-scale changes. At the catchment scale, high-resolution distributed models with grid resolutions of 10 to 100 m (e.g. Konz et al., 2007; Huss et al., 2008b; Immerzeel et al., 2012), or models based on Hydrological Response Units (HRUs) (e.g. Argentin et al., 2025; Schaffhauser et al., 2024), aim to account for local-scale factors such as complex topography or small glaciers in the catchment. However, for regional (glacio)-hydrological simulations, where computational demand increases, model resolutions are often coarsened to reduce computational efforts (e.g. Lutz et al., 2014; Singh et al., 2021). This coarsening, while reducing processing time, can lead to a loss of important terrain details such as topographic characteristics, including elevation, slope and curvature, and glacier hypsometry. These regional scale models, can go up to a 1 km resolution or even coarser (Ali et al., 2023; van Jaarsveld et al., 2024), potentially not able to capture fine-scale changes. A key question for applying (glacio)-hydrological models over broad regions or multiple catchments hence is whether coarser model resolution and reduced computational demands can still produce reliable simulations and capture the relevant processes and changes. Understanding this trade-off is crucial for scaling model applications efficiently, enabling the simulation across complex mountainous terrain.

Recent studies have examined some of these significant uncertainties in glacio-hydrological modelling at various scales. These include challenges related to the spatial distribution of precipitation, calibration approaches, and the limitation of model complexity and discretization. Tarasova et al. (2016) examined the effects of model discretization. They found that models with fewer spatial subdivisions can perform comparably well in certain data-scarce glacierized areas, depending on calibration methods. Chen et al. (2017) looked at precipitation forcing. They showed that while high-resolution precipitation datasets perform better at capturing orographic effects, their availability and accuracy are often limited in mountainous regions. Huss et al. (2014) analysed sources of uncertainty in 21st-century glacier runoff projections, finding that variations in climate models, calibration data quality, and assumptions about ice thickness are primary contributors to uncertainty, which strongly influence projected runoff changes. Furthermore, a study conducted in the Himalayas highlighted that uncertainties in precipitation estimates are a major source of model uncertainty, which affects runoff projections and the variability of seasonal runoff (Wang et al., 2024). Together, these studies underscore the need to advance understanding of meteorological forcing, model configuration, and calibration strategies to enhance model reliability.

In this study, we investigate the impact of meteorological forcing products and spatial model resolution on the reliability of simulated glacier mass balance and runoff within the well-instrumented Gletsch catchment, a 39.4 km² glacierized headwater basin of the Rhone River in the Swiss Alps. By using a catchment with robust data availability, we aim to assess how these modelling choices perform in a controlled setting and to provide insights relevant for data-limited, high-altitude regions. While the experiments are conducted in a well-instrumented Alpine catchment, the design of this study reflects the limitations commonly encountered in remote regions, such as the Himalayan mountain range for example. Understanding how the model performance is affected by the absence of high-resolution input or runoff data, and systematically quantifying the magnitude of performance loss, is crucial for evaluating the reliability of glacio-hydrological models under such constraints, especially when applied in ungauged or poorly monitored environments. More specifically, we aim at answering the following questions:

1. How does the choice of meteorological forcing product influence the reliability of simulated runoff and glacier mass balance?

2. How does the performance of the glacio-hydrological model change when coarsening the spatial distribution of the model?

3. How reliable is the model in simulating glacier mass balance and runoff, without having measured runoff data available for calibration?

To answer these questions, we simulate the glacier mass balance and runoff of the small-scale Gletsch catchment (44 % glacierized, Rhonegletscher) at daily resolution over a 22-year period, using the Glacier Evolution Runoff Model (GERM, Huss et al., 2008b; Farinotti et al., 2012). This catchment provides extensive, high-resolution data that allows for detailed analysis of the model's performance. We conduct two model experiments, Experiment 1 and 2, dedicated to the main research questions. In Experiment 1 we investigate the effects of using different meteorological forcing products, with point data and grid resolutions ranging from 1 to 30 km, on the model outcomes. In Experiment 2 we assess the impact of coarsening the spatial resolution of the model on the simulation results. For both experiments the study also explores whether accurate simulations can be achieved without measured runoff data for model calibration. This is done by applying and comparing two calibration procedures, which include a single-data and multi-data calibration. By systematically investigating the influence of meteorological forcing and spatial model resolution, this study aims to provide insights into the potential challenges and limitations in capturing the seasonal and annual variability of glacier mass balance, glacier area evolution, and runoff, particularly in regions where observational data is limited.

2 Study area and Data

2.1 Rhonegletscher and Gletsch catchment

Rhonegletscher and the Gletsch catchment (Fig. 1, Table 1), are situated in the central part of Switzerland within the Canton of Valais. The Gletsch catchment (39.4 km²) is the headwater of the Rhone River. The term “Rhonegletscher” in this study encompasses the main glacier (14.9 km² in 2016) along with 10 smaller glaciers (cumulative 1.8 km² in 2016) within the Gletsch catchment, all contributing to the hydrological dynamics of the region (Fig. 1). This glacier has been the subject of extensive research on e.g. glacier mass balance, hydrology, glacier dynamics, and the impacts of climate change (Wallinga and Van De Wal, 1998; Klok et al., 2001; Zappa and Kan, 2007; Jouvet et al., 2009; Huss et al., 2010; Farinotti et al., 2012). The availability of extensive datasets allows us to develop, calibrate and validate our glacio-hydrological model and explore its performance. A summary of the main characteristics of the catchment are found in Table 1.

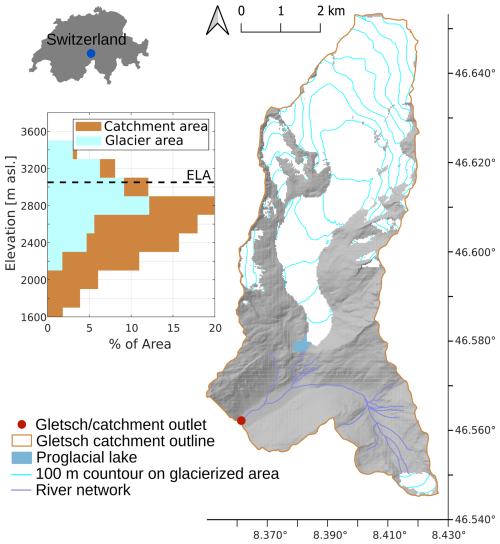
Figure 1 Gletsch headwater catchment. The blue dot in the upper-left inset marks the location of the catchment within Switzerland. The right panel shows the catchment area, with glacierized area (in white) and contour lines (100-meter intervals, in cyan) over the glacier for the year 2016 (based on: Swiss Glacier Inventory (SGI): Linsbauer et al., 2021). Contour lines are shown only for the glacierized area. The red dot marks the location of the catchment outlet and the gauging station at Gletsch. The river network and the proglacial lake shown on the map are taken from the HydroRIVERS (Lehner and Grill, 2013) and HydroLAKES datasets (Messager et al., 2016), respectively. The hypsometry (middle-left panel) represents the distribution of catchment area and glacier area across elevation bands based on data from 2016, with the equilibrium-line altitude (ELA) indicated as dashed black line. The ELA marks the elevation at which annual accumulation equals annual ablation, effectively dividing the glacier into zones of net mass gain and loss. The catchment outline is provided by the Federal Office for the Environment (FOEN).

Table 1 Summary of the catchment (Gletsch) and glacier (Rhonegletscher, including the main glacier and 10 small glaciers in the same catchment) characteristics. Glacierized area is based on the Swiss Glacier Inventory (SGI) 2016 (Linsbauer et al., 2021). Catchment area was provided by the Federal Office for the Environment, Switzerland (BAFU/FOEN) (2024). The bounding box specifies the outer coordinates defining the outline of the catchment, used for extracting the gridded meteorological forcing, and is based on the WGS 84 coordinate system, arranged in the order [North, West, South, East]. Area of the bounding box approximately 340 km².

2.2 Data

2.2.1 Meteorological data

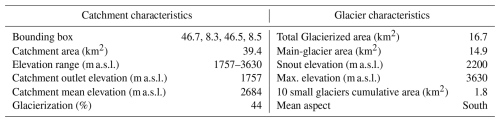
To test the reliability of the model when forced with different meteorological datasets, we applied four different datasets. These included in situ observational data from the Grimsel-Hospiz Automatic Weather Station (46.57° N, 8.33° E; 1980 m a.s.l., Fig. 2A, E), which provides daily temperature and precipitation data and is located approximately 5 km south-west of Rhonegletscher (MeteoSwiss, 2024a) and three gridded regional and global-scale meteorological products (Fig. 2B–D, F–H): (1) MeteoSwiss TabsD and RhiresD (MeteoSwiss, 2024b), (2) ERA5-Reanalysis (Hersbach et al., 2023), and (3) ERA5-Land (Muñoz Sabater, 2019). With these four continuous data products, we aim to cover a wide range of applicable data sets, ranging from in situ point scale, to high-resolution regional 1 km grid scale (MeteoSwiss) to coarse global 9–30 km grid scale (ERA5-Land and -Reanalysis). The characteristics of these datasets are summarized in Table 2 and Fig. 2. For simplification, in the following “Grimsel” refers to the Grimsel-Hospiz meteorological station and “MS_grid” to the gridded products from MeteoSwiss. Data of all four products was obtained for the period 2000–2022. Furthermore, we did not perform any additional bias correction to the gridded data products or the station data prior to their use as model inputs, in order to emulate a data-scarce environment. Bias adjustments are instead handled internally by the model through its parameters and lapse rates, as described in detail in Sect. 3.1.

MeteoSwiss (2024a)MeteoSwiss (2024b)Muñoz Sabater (2019)Hersbach et al. (2023)

Table 2 Details of the meteorological data compared in this study. The elevation for MS_grid, ERA5 Land, and ERA5 Reanalysis is aggregated and corrected to 2684 m a.s.l., representing the mean elevation of the catchment using the product-specific monthly constant temperature lapse rate and a constant precipitation lapse rate. Elevation is given in (m a.s.l.). Abbreviations: Temp. = Temporal; Obs = Observations; Interp = Interpolation; NMod = Numerical Modelling (Reanlysis); T =  Temperature; P = Precipitation; TabsD = Daily mean temperature; RhiresD = Daily Precipitation; 2 m T = Temperature of air at 2 m above the land surface.

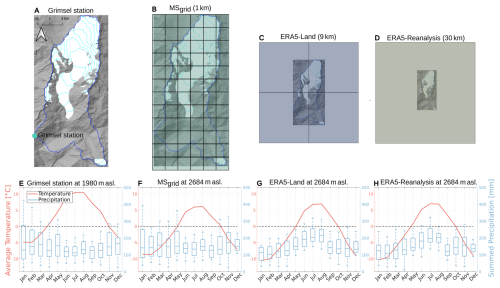
Figure 2 (A–D) Spatial visualization of the four applied meteorological datasets in reference to Gletsch. From left to right: Grimsel (point), MS_grid (1 km grid), ERA5 Land (9 km grid), ERA5 Reanalysis (30 km grid). (E–H) Average monthly temperature and precipitation for each dataset for the period of 2000–2022. Temperature and precipitation of the gridded products were spatially averaged over the catchment. Temperature was then corrected to the mean catchment elevation using a product-specific monthly constant temperature lapse rate (cf. Supplement Table S1) while precipitation is given as the mean catchment precipitation. For the box plots, the 22-year daily precipitation series was aggregated to mean monthly sums.

We used the gridded MeteoSwiss TabsD and RhiresD. TabsD provides daily mean temperatures at 2 m above the surface using data from about 90 long-term station series across Switzerland since 1961. The dataset applies a deterministic analysis method for high-altitude temperature interpolation with a spatial resolution of 1 km, capturing daily temperature variations (Frei, 2014). The interpolation procedure combines a two-dimensional lapse-rate regression to represent vertical temperature gradients with a subsequent horizontal interpolation to account for spatial variability (Frei, 2014). Precipitation data from the MeteoSwiss RhiresD product corresponds to daily precipitation totals from 06:00 UTC of day D to 06:00 UTC of day D+1, with a spatial resolution of 1 km (MeteoSwiss, 2021). The dataset incorporates high-resolution rain-gauge networks across Switzerland and neighbouring regions, with uniform gauge-station distribution, though high-altitude areas above 1200 m are less represented (MeteoSwiss, 2021). The second applied gridded dataset is the fifth generation of the European Centre for Medium-Range Weather Forecasts Reanalysis ERA5-Reanalysis (Hersbach et al., 2020). This takes into account meteorological observations from around the world combined with numerical modelling to generate a globally consistent dataset of past meteorological conditions, offering 137 vertical hybrid sigma/pressure levels, hourly temporal resolution, and a spatial resolution of approximately 30 km (Hersbach et al., 2020). For this study, daily 2 m temperature and hourly total precipitation data, aggregated into daily totals, were used. The third dataset, ERA5-Land, extends the ERA5-Reanalysis with a finer spatial resolution of 9 km, excluding oceanic regions (Muñoz Sabater, 2019). Similar to the ERA5-Reanalysis, daily 2 m temperature and hourly total precipitation data were aggregated into daily totals for use in this study.

2.2.2 Topography – model resolution

To describe the topography of the catchment, we use the SwissALTI3D Digital Elevation Model (DEM), a high-precision DEM provided by the Swiss Federal Office of Topography (Swisstopo, 2016) and referring to the year 2016. The DEM was downsampled from its 2 m native resolution (DEM accuracy: 0.3–0.5 m for below 2000 m a.s.l., 1–3 m for above 2000 m a.s.l., Swisstopo (2016)) to resolutions between 25 and 3000 m (Fig. 3). The input geometry was resampled by averaging the 2 m grid cells to reduce data volume while preserving spatial detail, followed by cubic convolution interpolation using the GDAL warp function to ensure smooth transitions and minimize artifacts (GDAL/OGR contributors, 2024).

Figure 3 Glacier and catchment representation across various model resolutions. The resolution is given at the top of each panel and ranges between 25 and 3000 m. Light blue represents the glacierized area, characterized by the light blue contour lines. For each case, the original (high-resolution) catchment outlines are drawn in blue for reference.

2.2.3 Geodetic mass balance

For model calibration, we relied on geodetically-derived glacier mass loss change between 2013 and 2021. The geodetic mass loss was determined by differentiating two high-resolution DEMs for Rhonegletscher acquired by dedicated monitoring flights on 21 August 2013 and 20 August 2021 (GLAMOS, 2024b). The resulting ice volume change of –0.1354 km³ was found for the respective time period referring to the main glacier in the catchment (Rhonegletscher). The ice volume change was converted to a mass change by assuming a density of volume change of 850 kg m⁻³ (Huss, 2013).

2.2.4 Measured glacier mass balance and catchment runoff

To evaluate model results, we used annual and seasonal glacier-wide mass balance measurements for Rhonegletscher, covering the period 2007–2022 (GLAMOS, 2024a). This data is based on spatially distributed in-situ measurements of snow accumulation and ice melt across the entire glacier surface both in late April and September. Winter observations from 150 up to 300 snow-sounding locations were converted to water equivalent using snow density measurements. Measurements of local annual mass balance at a network of 10 ablation stakes were extrapolated to the entire glacier surface with a model-based approach (Huss et al., 2021). Herein, a daily distributed mass balance model is optimized to match all point observations of winter and annual mass balance and thus extrapolates to unmeasured regions based on calibrated physical relations. Furthermore, the utilized approach provides a homogenization of arbitrary measurement dates to the fixed dates of the hydrological year. The so-obtained data set thus allows for straight-forward comparison to model results acquired in the present study.

For catchment runoff, we used continuous daily observations from the Rhone-Gletsch gauging station (LV95 coordinates: 2.670.831° E/1.157.201° N; altitude: 1759 m a.s.l.) operated by the Federal Office for the Environment, Switzerland (BAFU/FOEN) (2024). We use data for the period 2000–2022.

3 Methods

We apply the Glacier Evolution Runoff Model (GERM;  Huss et al., 2008b; Farinotti et al., 2012), a distributed glacio-hydrological model, to simulate glacier mass balance and runoff in the Gletsch catchment over the period 2000–2022. The model architecture of GERM incorporates several components essential for simulating glacier processes, including snow accumulation and its spatial distribution patterns, snow- and ice melt, evapotranspiration, and runoff routing across glacierized and non-glacierized areas within the catchment, classified as either ice, snow, vegetation, or rock surfaces (Huss et al., 2008b, 2010; Farinotti et al., 2012; Huss and Fischer, 2016). This setup enables GERM to simulate glacier geometry changes, glacier mass balance, and partitioned runoff at high spatial resolution. Detailed descriptions of the model components are provided in Huss et al. (2008b) and Farinotti et al. (2012) while the key model components and model calibration are described in the following sections.

Our workflow (Fig. 4) contains two main experiments performed with GERM. Experiment 1 assesses the impact of the choice of meteorological forcing data on model outputs. To do so, the model is forced using four distinct meteorological products, while maintaining a fixed model (GERM) geometry at 25 m resolution. Experiment 2 investigates how the models spatial resolution (i.e., the resolution of the input DEM) affects performance. This experiment uses the local Grimsel point-scale meteorological data as forcing while varying the model resolution from highly distributed (25 m) to much coarser resolutions, as coarse as 3000 m. Additionally, we apply and compare both experiments in settings where measured runoff data for calibration was unavailable (data-scarce, single-data calibration) and available (best-case, multi -data calibration). Further details on the calibration process are provided in Sect. 3.5.

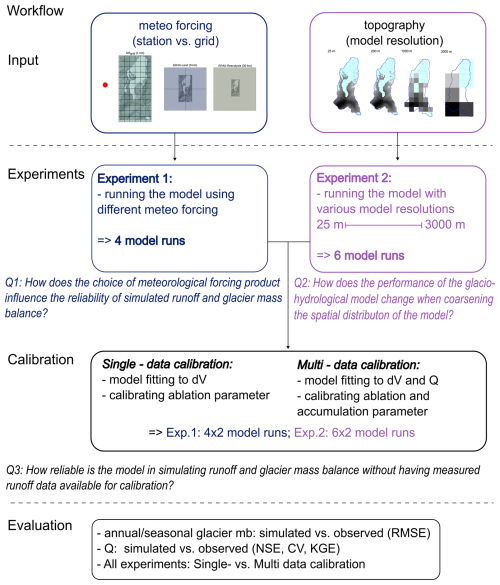
Figure 4 Workflow illustrating the basic methodology. Experiment 1 investigates the influence of different meteorological forcing products (station vs. gridded) on model performance, running four model simulations, while Experiment 2 explores the impact of varying DEM resolutions (from 25 to 3000 m) through six model simulations. Both experiments involve two calibration approaches: single-data calibration (fitting to glacier volume change dV and calibrating the ablation parameter) and multi-data calibration (fitting to both glacier volume change dV and runoff Q, while calibrating both ablation and accumulation parameters). Evaluation metrics include comparisons of simulated vs. observed glacier mass balance (mb) on an annual and seasonal basis using Root Mean Square Error (RMSE), and runoff (Q) validation using Nash-Sutcliffe Efficiency (NSE), Kling–Gupta efficiency (KGE) and Coefficient of Variation (CV).

3.1 Climate forcing

GERM is driven by a point time series of temperature and precipitation, either near or within the catchment area, which are subsequently distributed across the catchment using a monthly-averaged temperature lapse rate (cf. Table S1) and a constant precipitation lapse rate to every grid cell at the specified model resolution. For each meteorological product, temperature lapse rates were computed as monthly constants by performing a linear regression of air temperature against elevation of grid cells that fall within the catchment. For the ERA5 Reanalysis, neighbouring grid cells outside the catchment were also included, since the catchment itself is covered by only a single grid cell. For the Grimsel station data, we used observations from surrounding stations within a 50 km radius to perform the linear regression. These monthly lapse rates were then used to downscale the temperature time series across the model domain. Precipitation is distributed across the catchment by applying an overall correction factor (C_prec) and an annually fixed precipitation lapse rate (dP $/$ dz) based on regional literature values (e.g. Farinotti et al., 2012) and validated by in situ snow accumulation data over the glacier’s elevation range. For capturing the small-scale spatial variability of snow accumulation, a distribution matrix derived from terrain characteristics (slope and curvature) is superimposed on spatialized precipitation (Huss et al., 2008a). In this setup, the spatial distribution of precipitation within the original product has a limited effect on the catchment-averaged time series applied in the model. This was tested by upscaling the high-resolution products to a coarser resolution prior to extracting the catchment-averaged precipitation time series (cf. Supplement Figs. S1 and S2). Consequently, in our model configuration, the ability of the precipitation product to accurately capture total amounts and temporal variability is of greater importance than its spatial resolution.

3.2 Glacier surface mass balance

The annual glacier surface mass balance is quantified as the sum of solid precipitation (accumulation, A) and snow/ice melt (ablation, M) and only requires temperature and precipitation data as forcing. Accumulation A is estimated, in every grid cell (x,y) and day (d) as solid precipitation (P_solid), calculated as the amount of precipitation falling below a temperature threshold (T_thr) of +1.5 °C, with a linear transition range between +0.5 and +2.5 °C (Hock, 1999):

$$\begin{array}{}\text{(1)}& A(x,y,d)=P_{\mathrm{solid}}\left(d\right)\cdot C_{\mathrm{prec}}\cdot D(x,y)\end{array}$$

The parameter C_prec allows for the adjustment of measured precipitation sums to the catchment (Huss et al., 2014). The spatial distribution (D, at every grid cell x,y) of accumulation on the glacier surface is modelled by a simplified parametrization of snow redistribution processes, including snow drift and avalanches. This is achieved using curvature and slope assessments derived from the input DEM and the specified model resolution at every grid cell (Huss et al., 2008a). The snow distribution is then normalized across the catchment to a value of 1, ensuring that only the spatial distribution is affected, without altering the total amount of solid precipitation. Ablation is computed by using the distributed temperature-index model proposed by Hock (1999) that incorporates potential solar radiation. The surface melt rates M in every grid cell (x,y) and day (d) is computed by (Hock, 1999; Huss et al., 2008a):

$$\begin{array}{}\text{(2)}& \begin{array}{rl}& M(x,y,d)\\ & =\left\{\begin{array}{ll}\left(F_M+r_{\mathrm{ice}/\mathrm{snow}}I(x,y,d)\right)T(x,y,d)& :T(x,y,d)>\mathrm{0}\mathit{°}\mathrm{C}\\ \mathrm{0}& :T(x,y,d)\le \mathrm{0}\mathit{°}\mathrm{C}\end{array}\right.\end{array}\end{array}$$

In the equation, F_M is a melt factor, $r_{\mathrm{ice}/\mathrm{snow}}$ are two radiation factors for ice and snow, I is the potential clear-sky solar radiation at every grid cell and day calculated based the topography and solar angle based on Hock (1999), and T is the local air temperature.

3.3 Glacier area change

Glacier geometry and area are updated annually using the Δh-parametrization (Huss et al., 2010). It approximates changes in glacier surface elevation and glacier area in response to annual mass balance. This empirical approach redistributes net mass changes across the glacier based on a normalized elevation-dependent function (Δh) derived from observed surface elevation changes in the past. The parameterization is mass-conserving and reflects typical glacier behavior, producing the largest and smallest elevation changes in the ablation and accumulation area, respectively. It adjusts the glacier extent by removing glacier sections where the surface elevation falls below the bedrock. Albeit the Δh-parameterization does not explicitly simulate dynamic processes, it has been shown to closely replicate the results of a 3-D finite element flow model in terms of glacier volume, length, and area evolution over decadal scales (Huss et al., 2010). Since the Δh-approach allows the glacier to transiently adjust to the imposed climate forcing, no spin-up time was applied in our simulations.

3.4 Catchment runoff

GERM uses a runoff routing scheme that integrates meltwater and rainfall, with evapotranspiration subtracted at each time step (see Farinotti et al., 2012, for a detailed description of this model component). The scheme is structured around the concept of linear reservoirs (Langbein, 1958) and simulates the water balance of every grid cell and time step across diverse surface types – including ice, snow, rock, vegetation, and groundwater – by routing water through type-specific reservoirs with fixed retention constants. Each land surface type is assigned to a reservoir and associated with specific fixed retention and storage parameters, originally described in Huss et al. (2008b) and Farinotti et al. (2012). These parameters are not calibrated in this study but are based on validated applications of GERM to similar catchments, including the Gletsch basin (e.g. Farinotti et al., 2012). A detailed list of the parameter values used is provided in Table S3. This representation captures both rapid surface runoff and delayed subsurface flow components, which are particularly relevant during summer rainfall events and low-flow conditions. The total discharge is obtained by summing the outflows from all reservoirs at the catchment level, enabling a fully distributed, partitioned hydrograph simulation (Farinotti et al., 2012).

$$\begin{array}{}\text{(3)}& Q_d=P_{\mathrm{liq},d}+M_d-{\mathrm{ET}}_d-\sum _r\mathrm{\Delta }{S}_{r,d}.\end{array}$$

Here, d is the time step (days), Q_d total runoff, P_liq,d liquid precipitation, M_d snow/ice melt, ET_d evapotranspiration and ΔS_r,d the storage change of the reservoir r.

3.5 Model calibration

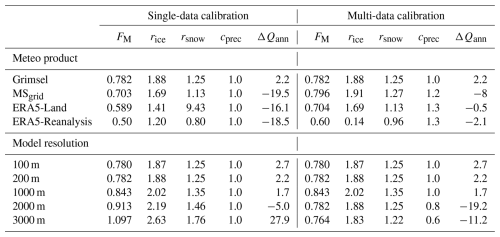
Besides the two Experiments 1 and 2, we also explore two calibration procedures to assess model performance under varying data availability scenarios. In both procedures, GERM’s calibration focuses on two main parameter groups: accumulation and ablation parameters. Geodetic glacier mass change serves as the primary constraint, and additional constraints can include measured runoff data. During the calibration process, the model adjusts the ablation parameter, which includes the melt factor (F_M) and the radiation factors for ice and snow ($r_{\mathrm{ice}/\mathrm{snow}}$) in an automated procedure. F_M and $r_{\mathrm{ice}/\mathrm{snow}}$ have a fixed relation to each other ($r_{\mathrm{ice}}/F_{\mathrm{M}}=\mathrm{0.024}$; $r_{\mathrm{snow}}/r_{\mathrm{ice}}=\mathrm{0.66}$). The ratio between the parameters was adopted from earlier applications of the same model, which demonstrated their suitability for glacierized catchments in the Swiss Alps (Farinotti et al., 2012). Thus, they can be handled as one parameter, which is optimized without setting a fixed parameter range. At the same time, the precipitation correction factor (C_prec) is optimized within bounds of [0.6, 1.5]. C_prec is a constant parameter, adjusting daily catchment precipitation – both liquid and solid – by a fixed percentage, thereby increasing or decreasing it uniformly over the modelling period. Since accumulation in GERM is entirely determined by solid precipitation, and C_prec directly scales this input, it effectively also controls the magnitude of accumulation in the model.

The two calibration procedures tested here differ in their use of constraints and the scope of parameter optimization. In the single-data calibration, only the ablation parameter (F_M, $r_{\mathrm{ice}/\mathrm{snow}}$) is optimized. In contrast, the accumulation parameter (C_prec) remains fixed at 1.0, and no measured runoff data is used as a constraint, only geodetic glacier ice volume change (Table 3, left column). This approach ensures that the total precipitation input remains unchanged. Thus, avoiding increases in runoff that might result solely from precipitation adjustments, overshadowing the effect of each forcing product on the model outcome. It simulates a data-scarce scenario where runoff data is unavailable for calibration. In contrast, the multi-data calibration involves optimizing both the ablation and accumulation parameters (Table 3, right column). In this case, geodetic volume change and measured annual runoff sums are constraints, representing a best-case scenario with additional data availability, allowing for more precise model tuning.

Table 3 Single- and multi- data calibration: Final best-calibrated parameter values for simulations Experiment 1 (top) Experiment 2 (bottom). The left side shows the parameter sets of the single-data calibration simulating the case where only geodetic ice volume change is available for calibration. The right side shows the multi-data calibration parameter sets, where both geodetic ice volume change and measured runoff are available for the calibration. Abbreviations: F_M = Meltfactor, $\left({\mathrm{10}}^{-\mathrm{3}}\mathrm{m}{\mathrm{d}}^{-\mathrm{1}}\mathit{°}{\mathrm{C}}^{-\mathrm{1}}\right)$; r_ice: radiation factor for ice/snow, $\left({\mathrm{10}}^{-\mathrm{11}}{\mathrm{m}}^{\mathrm{3}}{\mathrm{W}}^{-\mathrm{1}}{\mathrm{d}}^{-\mathrm{1}}\mathit{°}{\mathrm{C}}^{-\mathrm{1}}\right)$; r_snow: radiation factor for snow; C_prec = Precipitation correction; ΔQ_ann = annual runoff volume bias, (%).

In this study, model calibration was performed over the period 2013–2021, which aligns with the availability of high-resolution geodetic glacier volume change data. This period serves as the calibration window for both the single- and multi-data calibration approaches. Although it is becoming increasingly common to also include snow cover or snow depth observations as additional constraints during model calibration (e.g. Schaefli and Huss, 2011; Barandun et al., 2018; Cremona et al., 2025), we deliberately refrained from doing so in this study, as our aim is to replicate data-scarce conditions. In such settings, consistent and spatially representative snow observations are rarely available, whereas geodetic glacier volume change data are more accessible both locally and globally (e.g. GLAMOS, 2024b; Hugonnet et al., 2021). To maintain methodological consistency with these conditions, we based the model calibration solely on geodetic glacier volume change in the single-data calibration, complemented by runoff observations in the multi-data calibration setup. Model evaluation (Section 3.6) was then conducted over the simulation period (2001–2022), allowing assessment of long-term model performance, seasonal variability, and year-to-year consistency. This fixed calibration–evaluation approach was selected to maintain consistency across experiments.

3.6 Model evaluation

In our study, model accuracy refers to how well simulated glacier mass balance (annual and seasonal) and catchment runoff match corresponding observations over the historical evaluation period. Thus, to assess the influence of Experiment 1 and 2, and the effect of single versus multi-data calibration on the accuracy of the model results, we evaluate the simulated glacier mass balance and runoff against observational data for both. The runoff simulations are assessed against measured daily catchment runoff at Gletsch over the period 2001–2022, while glacier mass balance is evaluated using annual and seasonal measurements spanning 2007–2022. Note that, due to the spin-up of the hydrological storages (up to one year for groundwater in this catchment), the first simulation year was discarded from the runoff evaluation. The monthly and annual Nash–Sutcliffe efficiency (NSE), annual Kling–Gupta efficiency (KGE) and monthly relative difference (%) are used to quantify the agreement between observed and simulated runoff and capture seasonal variations. This model evaluation focuses on the melt season (April–September), when snow and glacier melt dominate the hydrological response. This period is most relevant to our study objectives, which centre on glacier-influenced hydrology. Winter runoff is excluded due to its limited relevance and higher associated uncertainty from low flows. Additionally, the partitioning of runoff into snow and ice melt is evaluated. Here we use the ice and snow runoff simulations forced with the Grimsel meteorological data as baseline to compare the other simulations with, as no measurements of these components are available. For glacier mass balance, the Root Mean Square Error (RMSE, in m w.e.) is calculated to evaluate the accuracy of simulated annual and seasonal mass balance relative to observations. We also evaluate the impact of single- versus multi-data calibration by comparing the model results from both calibration procedures.

4 Results

4.1 Impact on simulated glacier mass balance

The analysis of single-data simulations reveals distinct patterns in glacier mass balance across various scales and seasonal periods, with both the choice of forcing dataset and model resolution influencing the model results (Fig. 5A, B). In Experiment 1, the model runs utilizing ERA5-Land and MS_grid demonstrate the highest agreement for annual glacier mass balance (Fig. 5A), closely followed by the Grimsel dataset and ERA5-Reanalysis. All of them indicating an overall good model performance on the annual scale. However, winter glacier mass balance (Fig. 5B) is consistently underestimated relative to observational data, especially in simulations using gridded forcing products. This underestimation implies a compensatory underestimation effect on summer mass loss. For glacier area evolution (Fig. 5C), all datasets show a comparable rate of glacier retreat, although ERA5-Land forcing results in a lower glacier retreat rate.

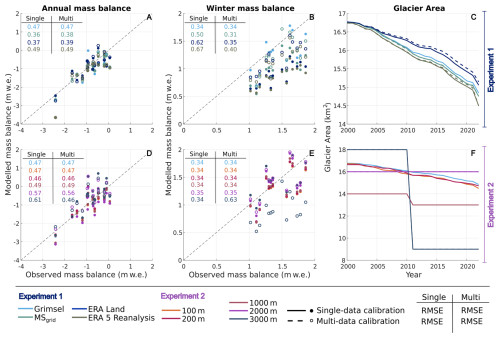
Figure 5 Simulated versus observed glacier mass balance for both annual (A, D) and winter (B, E) periods from 2007 to 2022. (A–C) Impact of different meteorological forcing products (Experiment 1). (D–F) Effect of varying model spatial resolutions (Experiment 2). The inset tables provide the RMSE (m w.e.) of the computed glacier mass balances for both single- and multi-data calibration. (C, F) Glacier area evolution from 2000 to 2022. For Experiment 2 (spatial resolutions from 25 to 1000 m), both mass balance and glacier area were identical for single- and multi-data calibrations.

Experiment 2 illustrates that simulations conducted at coarser model resolutions computed a more positive annual and winter mass balance than observed. Although the discrepancies are relatively limited (Fig. 5D, E), significant differences are noted regarding glacier area evolution (Fig. 5F). Model runs with a higher spatial resolution exhibit a gradual decline in glacier area, whereas coarser resolutions display, as expected, a more abrupt retreat, as much of the area is lost as soon as a glacier grid cell is removed. Furthermore, the initial glacier area in coarse-resolution simulations diverges from observed values by approximately ±2 km² (for the 1000 and 3000 m resolutions), while the glacier area for the 2000 m resolution remains constant.

Applying the multi-data calibration for Experiment 1 demonstrates no substantial changes at the annual scale, but significantly better agreement in winter for all simulations with different forcing products (Fig. 5). This improvement indicates that a more accurate (positive) winter mass balance leads to a correspondingly more negative summer mass balance (closer to observed levels) to ensure consistency with the annual mass balance. When analysing the glacier area evolution, the simulations performed with ERA5-Land still produce the slowest glacier retreat, with the retreat being even more limited than with the single-data calibration. For simulations performed with ERA5-Reanalysis the glacier retreat rate also slows down, compared to before with the single-data calibration.

In the simulations for Experiment 2, model agreement with observations slightly increases at the annual scale but no relevant improvement was found for winter mass balance (see Fig. 5). Specifically, at the 3000 m resolution, the agreement with winter mass balance is reduced, showing notably more negative values than the observations. This decline is not reflected in the evolution of glacier area. Whether single- or multi-data calibration is used, the outcomes remain the same. Thus, this emphasizes that regardless of the calibration method used here, the annual glacier mass balance does not change substantially. This consistency is primarily controlled by the calibration constrained with the geodetic ice volume change applied in both calibration procedures.

4.2 Impact on simulated catchment runoff

In Experiment 1 in combination with the single-data calibration, the summer catchment runoff is notably underestimated, no matter the applied forcing product, particularly in July and August (Fig. 6A, B). When forced with MS_grid and ERA5-Reanalysis, the model produces up to 20 % less ice melt than when forced with Grimsel (which yields the results that are most consistent with the observed total runoff). Simulation forced by ERA5-Land show the greatest underestimation at the onset of the melt season in May. It is important to note that, since these are relative values, even small differences during periods of low runoff (winter months) can result in high relative discrepancies. For snowmelt, simulations driven by ERA5-Land typically underestimate melt, while simulations driven by ERA5-Reanalysis tend to overestimate it when compared to Grimsel-forced results. The seasonal inconsistency in runoff totals is further underscored by the monthly NSE metric (Fig. 7), focusing on April to October when runoff data is sufficiently reliable, as low winter flows introduce uncertainties and even small absolute differences between modelled and simulated can translate into large relative differences. From April to June, NSE values gradually increase, reflecting challenges at the onset of the melt season. During the main melt period, from June to October, NSE values remain between 0.6 and 0.8 for all simulations, indicative of moderate performance. However, a sharp decline in NSE is observed in September across all simulations, followed by an increase towards the winter months. Ultimately, across seasonal and annual scales, the single-data calibration consistently underestimated runoff (Fig. 8). Similarly, the KGE values reflect a comparable fit, with the annual values indicating a bias primarily driven by the systematic underestimation of runoff. However, the year-to-year runoff variability was reasonably well captured, with simulated Coefficient of Variation (CV)-values slightly lower than the observed variability (Figure 7C). In the context of multi-data calibration, correcting the measured precipitation by +20 %–30 % (Table 3) significantly reduced the runoff underestimation and improved summer runoff estimates. Here, a similar NSE evolution is observed with generally higher NSE values, particularly during April and May, indicating better alignment with observed runoff data at the melt season’s onset.

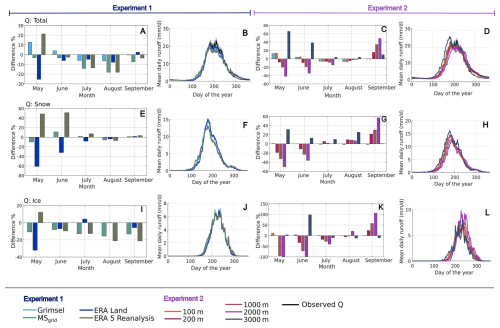
Figure 6 (A, C, E, G, I, K) Monthly percentage differences between simulated (Experiment 1 and 2, single-data calibration) and observed summer runoff for the period 2001–2022. The panels include total runoff (A, C), snow runoff (E, G), and ice runoff (I, K). Negative and positive values indicate model underestimation and overestimation, respectively. (B, D, F, H, J, L) Mean daily runoff hydrographs over the same period, showing both modelled results (coloured lines) and observed data (black line) with it's uncertainty (grey shade, ±0.9 % (Bernath, 1989)). Panels include depict catchment runoff (B, D), snow runoff (F, H) and ice runoff (J, L). In cases of snow and ice runoff, differences are relative to simulations forced by Grimsel station data.

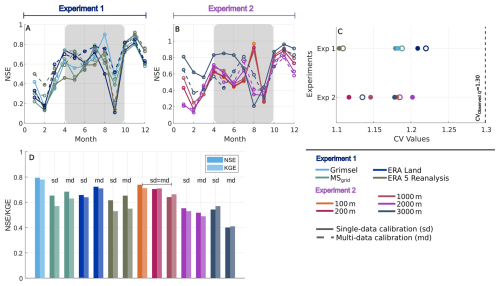
Figure 7 (A, B) Monthly NSE values for each experiment. Grey-shaded areas indicate the melt season (April–September), which is considered for model evaluation. This period aligns with the time of year when glacier- and snowmelt-driven runoff dominates. Winter runoff values are excluded due to both their high uncertainty and their limited contribution to annual discharge. (C) CV of the annual runoff sums for the two experiments, distinguishing between single- (empty dots) and multi-data (filled dots) calibration. Observed runoff CV of 1.30 is indicated with a dashed vertical line. (D) Annual NSE (left bar) and KGE (right bar) for each simulation. sd indicates a simulation performed with the single-data calibration, md with the multi-data calibration. For model resolutions finer than 2000 m, NSE, KGE and CV remain consistent across both calibration methods.

In Experiment 2, combined with single-data calibration, the findings indicate that as the model resolution coarsens, runoff becomes progressively too low and shifts temporally to later in the season (Fig. 6D). Analysing contributions from snow and ice melt underscores these patterns. At coarser resolutions (excluding 3000 m), ice melt is generally underestimated early in the season compared to high-resolution simulations (25 m). However, these coarser resolutions overestimate ice melt toward the end of the melt period, a trend mirrored in snowmelt behavior. The 3000 m resolution diverges significantly, consistently overestimating both total runoff and melt components, particularly during the early melt season, suggesting a temporal shift toward earlier melt timing. Monthly NSE-values from April to October further illustrate these seasonal trends (Fig. 7). For most resolutions (except 3000 m), NSE declines from April to June, likely due to a seasonal shift in runoff timing (i.e., a delayed onset of melting), then improves markedly from June to August, before dropping again in September. In contrast, the 3000 m resolution exhibits stable NSE values from April to July but shows an earlier decline in August, likely reflecting a premature shift in runoff timing. On the annual scale, the overestimated runoff produced with the 3000 m resolution is also evident, though the year-to-year variability is well captured (Fig. 8). In contrast, finer resolutions, up to 1000 m, align more closely with observed annual runoff in both magnitude and variability. When performing this Experiment in combination with the multi-data calibration, no notable improvement is observed for resolutions finer than 2000 m. However, for coarser resolutions (2000 m and above), simulated runoff increasingly underestimates annual totals, even with adjusted precipitation (Table 3 and Fig. 8). This suggests that finer resolutions effectively capture annual runoff patterns. In contrast coarser resolutions struggle with runoff dynamics due to heightened sensitivity to melt timing and precipitation distribution.

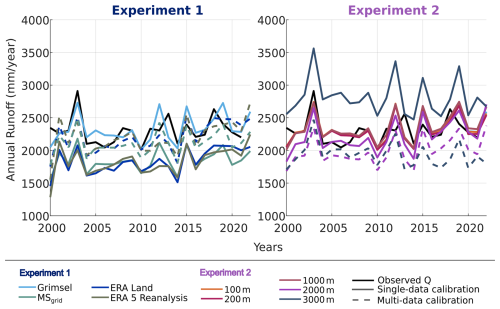
Figure 8 Annual catchment runoff observed and simulated using different (A) forcing products and (B) model resolutions. Simulations calibrated with the single-data (solid lines) and with the multi-data (dashed lines) calibration scheme are distinguished. For model resolutions < 2000 m, the annual runoff results are independent of the calibration method.

5 Discussion

5.1 Impact of meteorological forcing

The results of Experiment 1, combined with the single-data calibration, reveal a good agreement for annual glacier mass balance with all forcing products. However, consistent underestimation of winter snow accumulation on the glacier (Fig. 5), particularly when forced with either of the Reanalysis products, lead to inaccuracies in capturing seasonal glacier mass balances. This is attributed to their lower estimates of winter and annual precipitation for this catchment (Fig. 2G, H), consistent with studies documenting precipitation biases in other alpine regions (e.g. Chen et al., 2021; Monteiro and Morin, 2023; Dalla Torre et al., 2024). Schaefli and Huss (2011) similarly emphasized the importance of accurately capturing seasonal precipitation variability to represent snow accumulation processes in glacierized regions. The model compensates for winter precipitation deficits with a more positive summer glacier mass balance to maintain consistency with geodetic glacier ice volume change. This reflects findings by Konz et al. (2007), who noted that errors in precipitation inputs in glacierized catchments are often offset by compensatory adjustments in glacier melt estimates. The single-data calibration achieves satisfactory annual glacier mass balance results. Seasonal dynamics, however, are poorly represented, particularly in seasonal glacier mass balance and in summer runoff, which is consistently underestimated (Figs. 6, 8). This underlines the sensitivity of glacio-hydrological models to forcing data quality, as highlighted by Tarasova et al. (2016). They identified precipitation inaccuracies as a primary driver of errors in hydrological simulations. Nonetheless, the year-to-year variability of runoff is captured well throughout the simulation period (Fig. 8), which is mainly driven by temperature variability (Fountain and Tangborn, 1985; Chen and Ohmura, 1990; Schaefli and Huss, 2011). In line with the finding that meteorological variables are the main source of uncertainty the parameter sensitivity analysis of GERM by Farinotti et al. (2012) in the Gletsch catchment, showed that constant retention and storage capacity parameters have a relatively minor impact compared to temperature lapse rate, precipitation correction, and ablation parameters. This justifies the decision not to calibrate reservoir-specific parameters individually. Instead, calibration efforts are best focused on accurately estimating temperature gradients and ablation dynamics, which contribute most significantly to uncertainty in runoff projections.

Multi-data calibration improves the simulation of seasonal glacier mass balance and runoff. Introducing a second constraint to the calibration – in this case, measured runoff – and adjusting the precipitation correction factor (Table 3) results in better agreement with observations. Nevertheless, such corrections do not necessarily enhance the physical accuracy of modelled processes, as they rely on constant adjustments that fail to capture seasonal or spatial variability in precipitation patterns (Konz et al., 2007). Equifinality issues like these can obscure underlying deficiencies in the forcing data (Tarasova et al., 2016). Therefore, although the multi-data calibration improves the agreement with observations, it does not necessarily signify a more accurate representation of actual physical processes. It instead reflects the model's adjustment of forcing data and parameters to better align with the calibration data. However, the model’s representation of evapotranspiration provides a useful point of validation. While evapotranspiration plays a relatively small role in this high-alpine environment, it becomes relevant during summer in non-glacierized areas. Modelled annual evapotranspiration values (173–206 mm yr⁻¹) are consistent with the historical range of 131–240 mm yr⁻¹ reported by Bernath (1989) (Table S3), indicating that this process is well represented. This suggests that the main sources of uncertainty in summer runoff simulations are not due to evapotranspiration losses, but rather arise from reservoirs more directly affected by meteorological forcing – such as glacier and snow components – which are also more sensitive to calibration parameters. Similar to NSE, KGE values are highest for simulations forced with Grimsel data and decline when using gridded meteorological products (Fig. 7D). Multi-data calibration generally improves KGE values across all simulations. However, the ranking between forcing products remains consistent with that seen for NSE, reinforcing the conclusion that meteorological forcing quality impact the reliability of runoff simulations.

Furthermore, for all simulations a similar evolution of glacier area retreat between 2000 and 2022 is observed for all tested simulations. This is a gradual decrease in glacier area regardless of the calibration method. However, the magnitude of area change varies among simulations. For example, the model forced with ERA5-Land projects approximately 0.5 km² more glacier area remaining by the end of the simulation period compared to the average of other simulations, a difference that represents nearly one-third of the total glacier area change over the period. Variations stem primarily from differences in the calculated mean glacier mass balance, particularly before the calibration period. These are primarily driven by variations in the temperature and precipitation time series of each forcing product. These discrepancies in mean glacier mass balance affect the calculated glacier volume and result in divergent glacier area evolution across the various simulations. The spatial distribution of meteorological inputs over the glacier surface plays a critical role in driving the sensitivity of lower and higher-elevation areas to melt processes (Schaefli and Huss, 2011). Thus, simulated glacier area retreat can be disproportionally affected across extended periods by even small parameter combinations or meteorological forcing differences.

Capturing seasonal variability in precipitation inputs is one of the most important variables for accurately capturing glacier mass balance and runoff at various scales. While the application of the multi-data calibration procedure can improve seasonal accuracy, high-resolution and well-constrained forcing data are also needed to reduce unwanted parameter compensation. To further isolate the impact of the meteorological forcing, we conducted additional model runs without re-calibrating model parameters to each forcing product. The results (Figs. S3–S5) show that in the absence of calibration, the deviations between modelled and observed glacier area, mass balance, and runoff are even larger. Calibration reduces these differences but does not eliminate them, confirming that the choice of meteorological forcing product remains a primary driver of model performance.

5.2 Impact of spatial model resolution

In Experiment 2, the spatial resolution of the model does not significantly affect the computed annual glacier mass balance up to a resolution of 1000 m, while the winter glacier mass balance remains the same up to a resolution of 3000 m (Fig. 5). Similarly, no substantial differences are observed in the annual catchment runoff up to a resolution of 1000 m (Fig. 8B). The observed strong decline in KGE (Fig. 7D) values with coarser spatial model resolution, larger than 100 m, supports this interpretation. While NSE primarily reflects timing and shape agreement, KGE additionally accounts for deviations in runoff magnitude and variability. Thus, the decreasing KGE at coarser resolutions emphasizes that errors in total runoff volumes increase as spatial detail is lost. Seasonal shifts occur, however, as the resolution becomes coarser, particularly at resolutions of 200 m and coarser (Fig. 6D, L). These shifts are linked to a delayed onset of snow and ice melt caused by the compression of glacier and catchment areas to higher elevations in the coarser resolution models. With coarser resolutions the model also considers elevations outside of the original catchment and glacier area (Fig. 3), where colder temperatures prevail. Furthermore, the compression occurs, because lower glacier areas, which are typically glaciated to a smaller extent, tend to disappear as grid sizes become coarser, leaving only the extensively glaciated higher elevations. As a result, the mean glacier elevation shifts upward. One of the effects noticed from this, is the apparent glacier area stability observed for the 2000 m resolution. With an average higher glacier elevation, the low-lying ablation areas are under-represented, and the relative proportion of the accumulation area increases, leading to an unrealistically balanced mass budget and a stable glacier extent. At the coarsest resolution of 3000 m, the unexpected earlier onset of melt is likely a result of amplified ablation parameter adjustments necessary in the calibration procedure to compensate for these elevation biases, caused by the coarse spatial discretization, in both the single-data and multi-data calibration (Table 3).

Furthermore, large grid cells aggregate varying elevations into a single value creating “steps” in the elevation distribution. As temperatures rise, these coarse cells abruptly contribute melt all at once, unlike smaller grid cells that allow a gradual melt progression as the 0 °C isotherm moves across elevation bands. Konz et al. (2007) observed similar shifts in melt dynamics. Larger grid cells smooth out rapid hydrological responses, making the timing of runoff less accurate (Konz et al., 2007).

Glacier extent and area changes further highlight the impact of model resolution on the model output. Coarser resolutions progressively lose fine-scale glaciological and topographic details. These include altitude, slope, and glacier hypsometry (Fig. 3). At resolutions higher than 200 m, the model captures both the main glacier and ten smaller glaciers in the catchment. In contrast, at 1000 m, only one smaller glacier is resolved alongside the main glacier, and at 2000–3000 m resolution, only the main glacier remains, with smaller glaciers effectively excluded. This coarse representation limits the model’s ability to simulate the runoff contributions from smaller glaciated areas. Such limitations are particularly problematic in regions where small glaciers contribute significantly to seasonal runoff variability (Tarasova et al., 2016). Coarser spatial resolutions can sometimes provide a reasonable balance between model reliability and computational efficiency. However, the suitability of a model resolution depends heavily on the study objective and the glacier area within the catchment. Larger basins with more complex glacier dynamics may require higher resolutions or sub-grid parametrizations to ensure accurate projections of runoff and glacier volume changes (Shannon et al., 2019). Furthermore, abrupt glacier area change at coarse resolutions reflects the stepwise retreat of large grid cells. This effect might average out over time though, as glacier melt dynamics at different altitudes interact with the coarse grid's smoothing effects (Konz et al., 2007). However, future projections neglecting finer spatial details could lead to underestimating glacier melt and runoff contributions (Shannon et al., 2019).

The findings demonstrate that coarse model resolutions, while computationally efficient, can oversimplify critical glaciological processes, particularly for smaller glaciers. While the results are derived for a single, well-instrumented catchment, they hint at broader implications for modelling glacierized catchments under data-scarce conditions and with small glaciers.

5.3 Model limitations

The experiments presented in this study are subject to structural limitations of GERM. In the model, runoff is routed at the grid-cell level using a linear-reservoir approach (Farinotti et al., 2012). Each cell contains a set of reservoirs that represent different runoff components, depending on the local surface type. The runoff from each grid cell is computed individually and then aggregated at the catchment outlet. This structure allows for a spatially distributed simulation of runoff generation. At the same time, GERM uses some simplifications. Although spatial heterogeneity in the form of land-cover classes is explicitly represented, drainage networks and topographic flow pathways are not resolved (Farinotti et al., 2012). As a result, changes in spatial resolution primarily affect the mean catchment elevation and the distribution of land-cover classes, whereas flow directions, accumulation zones, and travel times remain unaffected. This is in contrast to fully distributed hydrological models, where resampling to coarser resolutions can significantly alter hydrological connectivity and runoff dynamics in complex terrain (Cao et al., 2021; Erdbrügger et al., 2021). In flat terrain, this resampling can affect flow directions (Erdbrügger et al., 2021). In contrast, in steep and spatially limited catchments such as Gletsch, this effect is expected to be minor – particularly at a daily temporal resolution – since most water reaches the outlet within a day. These simplifications do not diminish the value of the experiments, but they need to be considered when interpreting the results and when transferring the findings to other settings. In particular, applications in larger or more topographically complex basins may require model structures that explicitly resolve drainage pathways in order to capture the full sensitivity of the hydrological responses to spatial resolution.

6 Conclusions

This study investigated the impact of meteorological forcing and spatial model resolution on the accuracy of glacio-hydrological simulations in a small, well-monitored Alpine catchment in Switzerland. The findings underscored the importance of carefully selecting meteorological forcing products and spatial resolutions and the choice of calibration data to achieve reliable simulations.

While single-data calibrations can achieve good accuracy for annual glacier mass balance, they often fail to represent seasonal dynamics accurately due to biases in seasonal precipitation estimates and ablation and accumulation processes. Multi-data calibration improves seasonal accuracy but remains limited by the inability to capture temporal and spatial variability in precipitation. This emphasizes the critical role of high-quality forcing data.

Meteorological forcing, particularly precipitation variability, emerges as a dominant factor influencing model outcomes. The precipitation biases in the here applied forcing products, significantly affect the capability of GERM in capturing seasonal snow accumulation and consequently, melt processes accurately. The spatial resolution of the model also plays an important role, especially on the seasonal scale. Coarse resolutions introduce biases in melt onset and runoff timing, particularly by oversimplifying glaciological and topographic details and excluding smaller glaciers, which are critical contributors to seasonal runoff.

These findings hint at broader implications for data-scarce regions. In such regions, the absence of high-resolution observations and meteorological inputs amplify erroneous parameter compensations, potentially obscuring the true glacio-hydrological processes. Coarse spatial resolutions, although computationally efficient, exacerbate these issues, particularly in regions with diverse glacier scales and dynamics.

Overall, this study underscores the necessity of balancing computational efficiency with model reliability, particularly when scaling findings to poorly monitored regions. To address these challenges, future efforts must prioritize the development of high-resolution forcing based on in-situ observations and innovative calibration techniques that capture seasonal variability. Further research involving diverse catchments and various models-setups is essential to refine these insights, ensuring the robustness of glacio-hydrological model predictions under changing climate conditions.