Quantifying matrix diffusion effect on solute transport in subsurface fractured media

Matrix diffusion is an important process for solute transport in subsurface fractured media. The effect of matrix diffusion on solute transport depends on various fracture and matrix parameters as well as the underlying temporal-spatial scales. In the present study, we quantitatively analyze the dependency of matrix diffusion effect on these parameters through analytical solutions, and then propose a new unified parameter to quantify the significance of matrix diffusion effect. A comprehensive analysis is performed to verify the applicability of the unified parameter through both analytical and field/laboratory data. Compared with previous unified parameters, the new unified parameter exhibits a stronger capability in quantifying the strength of matrix diffusion. Based on the field/laboratory data, a threshold of the unified parameter is recommended as a criterion to assess whether matrix diffusion effect is significant or negligible. We also derive an equivalent solute release function to compensate for matrix diffusion so that a fracture-matrix coupled model could be simplified to a fracture-only model, largely mitigating the computational burden associated with solute transport modeling. Although the unified parameter and the equivalent solute release function are derived with 1D analytical solutions, they also show satisfactory performance in a 3D numerical model with a nonuniform fracture flow field. Results of the present study offer an accurate method to quantify matrix diffusion effect on solute transport in fractured media, and are particularly useful to improve the computational efficiency of solute transport modeling for prediction and inversion purposes.

1 Introduction

Solute transport in fractured media has been characterized as an essential phenomenon in various natural and anthropogenic subsurface processes such as contaminant transport (Tang et al., 1981; Berkowitz et al., 1988; Bear et al., 2012), nuclear waste disposal (Smith and Degueldre, 1993; MacQuarrie and Mayer, 2005; Zhang et al., 2022), CO₂ geological sequestration (Chen and Zhang, 2010; Viswanathan et al., 2022), tracer testing for reservoir characterization (Tsang, 1995; Berkowitz, 2002; Dentz et al., 2020; Wu et al., 2021a), to name a few. The primary physical mechanisms governing solute transport in fractures and surrounding rock matrix include advection, hydrodynamic dispersion, sorption (for sorptive solute) and degradation (for degrading solute). As fracture permeability is generally several orders of magnitude higher than matrix permeability, flow-dependent advection and hydrodynamic dispersion processes mostly occur in fractures, while rock matrix affects solute transport mainly through molecular diffusion driven by solute concentration contrast between fracture and matrix (Bodin et al., 2003; Geiger et al., 2010; Hyman et al., 2019).

A high-fidelity model that incorporates both fracture and matrix with finely resolved grid is therefore necessary to: (1) accurately predict contaminant/nuclear waste/CO₂ fate and transport for long-term risk management; (2) correctly interpret solute concentration data (for example, tracer breakthrough curves obtained from tracer testing) to infer fracture and matrix characteristics. Such a high-fidelity, finely resolved model is undoubtedly computationally expensive. Another challenge of such high-fidelity models is the inevitable uncertainties associated with reservoir and fracture parameters, such as matrix porosity and permeability as well as fracture geometry and aperture, which might be highly heterogeneous under complex geological conditions. Due to the technical and economic difficulties in drilling and directly measuring subsurface reservoirs, available geological and geophysical data are normally spatially scarce and far from adequate to constrain these parameter uncertainties. As a result, a reliable prediction of solute fate usually requires running numerous forward models under various scenarios/parameters to accommodate the inevitable reservoir uncertainties. The interpretation of solute concentration data confronts the same challenge as inversion algorithms normally involve a large number of forward model runs to achieve stable and satisfactory fitting results. For example, Wu et al. (2021b) used a stochastic inversion framework to interpret tracer recovery data from the EGS Collab testbed and infer fracture aperture distribution. A total of 50 000 tracer transport simulations were performed to obtain satisfactory fitting results, requiring substantial computational resources.

To alleviate the computational burden associated with solute transport prediction and solute data interpretation in subsurface fractured media, an effective and straightforward simplification method that has been used in previous studies is to ignore matrix diffusion effect so that a fracture-matrix coupled model can be simplified to a fracture-only model (Unsal et al., 2010; Somogyvári et al. 2017; Hyman et al., 2021; Wu et al. 2021a, b). The absence of matrix greatly reduces the degree of freedom of the model and thus substantially relieve the computational burden. In cases that only one fracture is involved, the original 3D fracture-matrix model directly reduces to a 2D fracture model. The hypothesis of such a simplification is that for low-permeability and low-porosity fractured media, solute transport is dominated by fractures and matrix diffusion only has a minor impact, especially for short time scales (Cacas et al., 1990; Tsang et al., 1991; Hyman et al., 2019; Zhang et al., 2022). Similar model simplifications have also been used in multiphase flow simulations to make numerical models computationally amenable (Unsal et al., 2010).

A comprehensive and quantitative understanding of matrix diffusion effect on solute transport is critical for assessing the rationality of ignoring matrix as well as evaluating the induced biases in solute fate prediction. As mentioned in some previous studies, matrix diffusion might become a key mechanism that retards solute transport, leading to delayed release and prolonged persistence of contaminants/nuclear waste/CO₂/tracers in subsurface fractured reservoirs (Shapiro and Nicholas, 1989; Maloszewski and Zuber, 1993; Jardine et al., 1999; Polak et al., 2003; Hyman et al., 2019). For contaminant remediation, understanding matrix diffusion-induced contaminant spread and persistence is essential for the design of long-term remediation strategy. For geological storage (nuclear waste, CO₂), matrix diffusion on one hand is an important retaining mechanism and on the other hand may lead to unexpected leakage pathways. Quantifying the long-term effects of matrix diffusion is critical for the optimization of containment systems and risk management. From the computational perspective, correctly assessing matrix diffusion effect could provide useful insights for the simplification of solute transport model for prediction and data interpretation. In fact, considerable efforts have been devoted to characterizing the effect of matrix diffusion on solute transport in fractured media through analytical solutions (Grisak and Pickens, 1980; Tang et al., 1981; Sudicky and Frind, 1982; Zhu and Zhan, 2018), lab and field experiments (Novakowski et al., 1985; Raven et al., 1988; Birgersson and Neretnieks, 1990; Becker and Shapiro, 2000), as well as numerical simulations (Liu et al., 2007; Zhou et al., 2018; Hyman et al., 2019) in the past several decades. A major understanding from these efforts is that the effect of matrix diffusion on solute transport depends not only on matrix properties (porosity and matrix diffusion coefficient), but also on fracture characteristics (aperture, dispersivity) and the spatial-temporal scales of solute transport processes (Carrera et al., 1998; Reimus and Callahan, 2007; Zhou et al., 2018; Hyman et al., 2019). Many sensitivity analyses indicated that matrix diffusion effect is more significant with larger matrix porosity, larger matrix diffusion coefficient, and smaller fracture aperture and flow velocity (Grisak and Pickens, 1980; Zhou et al., 2018).

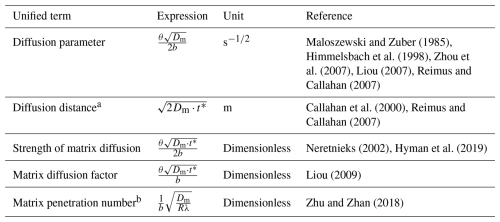
Nevertheless, although important insights have been gained from previous studies, there still exists some controversies regarding the effect of matrix diffusion under complex geological conditions. While low matrix porosity/permeability has been used as a main justification for the neglect of matrix in solute transport model, Bodin et al. (2003) pointed out that the role of matrix diffusion remained significant even for low matrix porosity. Cacas et al. (1990) performed field tracer tests in fractured rocks and indicated that for short time scales, solute transport was almost entirely due to advection in fractures and matrix diffusion could be neglected. However, Maloszewski and Zuber (1993) analyzed several field tracer testing data sets and achieved a contrary conclusion that matrix diffusion was not negligible and, in some cases, could be dominant even for short-time experiments in rocks with low matrix porosity. Some attempts have been made to propose a unified term that incorporates both fracture and matrix parameters to appropriately quantify matrix diffusion effect (Maloszewski and Zuber, 1985; Neretnieks, 2002; Reimus and Callahan, 2007; Liou, 2009; Dai et al., 2012; Zhu and Zhan, 2018). Most of such unified terms were proposed based on analytical solutions for solute transport in a single fracture-matrix system with ideal conditions such as uniform aperture and fracture flow field, as well as negligible solute advection process in rock matrix. Unfortunately, these unified terms generally lack a rigorous theoretical derivation and exhibit different forms in terms of the combination of fracture and matrix parameters. For example, Maloszewski and Zuber (1985) proposed a diffusion parameter to quantify matrix diffusion rate, considering the effect of rock porosity, matrix diffusion coefficient and fracture aperture. Neretnieks (2002) further incorporated mean residence time and defined a new matrix diffusion factor to quantify the strength of matrix diffusion. Another unified parameter from Zhu and Zhan (2018) mainly considered the effect of matrix diffusion coefficient and fracture aperture, and the parameter was used to characterize the diffusive length of solute into matrix. There is still a lack of consensus on such a unified term for matrix diffusion effect quantification.

In the present study, we endeavor to comprehensively quantify matrix diffusion effect on solute transport in subsurface fractured media. Analytical solutions of solute transport in fracture-matrix coupled and fracture-only models are compared to quantitatively analyze the effect of matrix diffusion under various matrix/fracture parameters and spatial-temporal scales. Based on the results, we identify scenarios in which matrix diffusion shows negligible effect and the fracture-only model is applicable for solute transport simulation, as well as scenarios in which matrix diffusion effect is significant and matrix should not be neglected. We also evaluate the feasibility of six unified terms in quantifying matrix diffusion effect, including five terms from the literature and a newly proposed term. For cases with non-negligible matrix diffusion effect, we further propose an equivalent solute release function to compensate for matrix diffusion effect in fracture-only models, so that the matrix can still be safely ignored without sacrificing any accuracy in solute transport simulation. A 3D numerical model with more realistic fracture flow field is developed to examine the effectiveness of the unified term in quantifying matrix diffusion effect and also the applicability of the proposed equivalent solute release function.

2 Matrix diffusion effect on solute transport in fractured media

2.1 Analytical solutions of solute transport

To focus on the analysis of matrix diffusion, we consider the transport of a conservative solute in a relatively simple 1D model with a smooth fracture located in an infinite matrix. The matrix is assumed impermeable and a constant flow velocity u is assumed in the fracture. Solute is released at the origin of the fracture and then transports along the flow direction (Fig. 1).

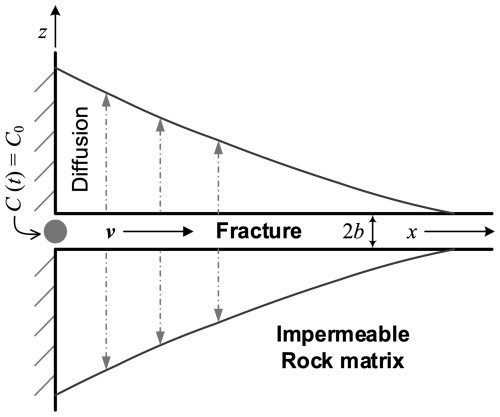
Figure 1 Conceptual model of solute in a fracture with impermeable matrix (adapted from Graf and Simmons, 2009).

The transport equation in the fracture and matrix are written:

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\partial C_{\mathrm{f}}}{\partial t}}+{\displaystyle \frac{u}{R_{\mathrm{f}}}}{\displaystyle \frac{\partial C_{\mathrm{f}}}{\partial x}}-{\displaystyle \frac{D_{\mathrm{f}}}{R_{\mathrm{f}}}}{\displaystyle \frac{{\partial }^{\mathrm{2}}{C}_{\mathrm{f}}}{\partial x^{\mathrm{2}}}}-{\displaystyle \frac{\mathit{\theta }{D}_{\mathrm{m}}}{b{R}_{\mathrm{f}}}}{\left.{\displaystyle \frac{\partial C_{\mathrm{m}}}{\partial z}}\right|}_{z=b}=\mathrm{0}\text{(2)}& {\displaystyle \frac{\partial C_{\mathrm{m}}}{\partial t}}-{\displaystyle \frac{D_{\mathrm{m}}}{R_{\mathrm{m}}}}{\displaystyle \frac{{\partial }^{\mathrm{2}}{C}_{\mathrm{m}}}{\partial z^{\mathrm{2}}}}=\mathrm{0}\end{array}$$

The analytical solution of solute breakthrough in the fracture has been derived in the literature as follows (Grisak and Pickens, 1980; Tang et al., 1981; Sudicky and Frind, 1982; Zou et al., 2016),

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{C_{\mathrm{f}}(x,t)}{C_{\mathrm{0}}}}=\left\{\begin{array}{ll}F\left(x,t\right)& \mathrm{0}\le t\le t_{\mathrm{0}}\\ F\left(x,t\right)-F\left(x,t-t_{\mathrm{0}}\right)& t>t_{\mathrm{0}}\end{array}\right.\text{(4)}& {\displaystyle }\begin{array}{rl}F\left(x,t\right)& ={\displaystyle \frac{\mathrm{2}}{\sqrt{\mathit{\pi }}}}{e}^{\frac{ux}{\mathrm{2}{D}_{\mathrm{f}}}}\underset{\sqrt{\frac{x^{\mathrm{2}}}{\mathrm{4}{D}_{\mathrm{f}}t}}}{\overset{\mathrm{\infty }}{\int }}{e}^{-{\mathit{\xi }}^{\mathrm{2}}-\frac{u^{\mathrm{2}}{x}^{\mathrm{2}}}{\mathrm{16}{D}_{\mathrm{f}}^{\mathrm{2}}{\mathit{\xi }}^{\mathrm{2}}}}\\ & \cdot \mathrm{erfc}\left({\displaystyle \frac{\frac{x^{\mathrm{2}}\mathit{\theta }\sqrt{D_{\mathrm{m}}}}{\mathrm{4}{D}_{\mathrm{f}}b{\mathit{\xi }}^{\mathrm{2}}}}{\mathrm{2}\sqrt{t-\frac{x^{\mathrm{2}}}{\mathrm{4}{D}_{\mathrm{f}}{\mathit{\xi }}^{\mathrm{2}}}}}}\right)\mathrm{d}\mathit{\xi }\end{array}\end{array}$$

in which C_f(x, t) is the solute concentration in the fracture at a distance of x from the solute release point, C₀ is the solute concentration at the release point, t₀ is the solute release duration, u is fluid velocity in the fracture, D_f is the fracture hydrodynamic dispersion coefficient, θ is the matrix porosity, D_m is the matrix diffusion coefficient, b is the half-aperture of the fracture, and ξ is an integral variable. F(x,t) denotes the solute concentration under continuous solute release condition. Note that D_f can be expressed as a function of longitudinal dispersivity in the fracture α_L, velocity u and molecular diffusion coefficient of solute in the fracture D*, i.e., $D_{\mathrm{f}}={\mathit{\alpha }}_{\mathrm{L}}\times u+D$*. Since D* is generally several orders of magnitude smaller than α_L×u, we ignore D* so that $D_{\mathrm{f}}={\mathit{\alpha }}_{\mathrm{L}}\times u$.

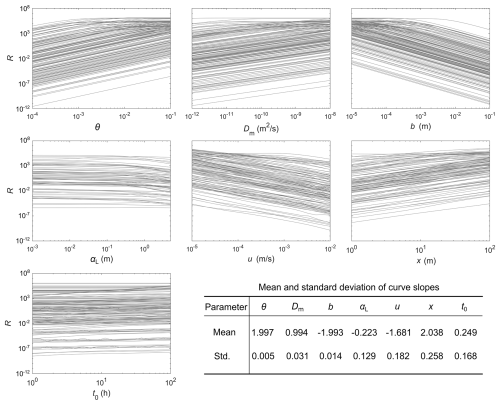
Figure 2 Relationship between matrix diffusion effect and model parameters. Each plot has 200 curves, corresponding to the randomly generated 200 parameter sets for the other six parameters (except the examined parameter). The mean and standard deviation of the slope of the curves for each parameter are annotated. Note that when matrix diffusion effect becomes significant under large θ, D_m and small b, u, the solute concentration from fracture-matrix coupled model within the calculating window is over three magnitudes smaller than that from fracture-only model, and the calculated R approaches to a maximum value, resulting in the non-linear relationship between the parameter and R. Therefore, we only select curves that exhibiting relatively linear relationships for the calculation of mean and standard deviation.

For a simplified model without matrix, the expression of F(x,t) is simplified as,

$$\begin{array}{}\text{(5)}& F\left(x,t\right)={\displaystyle \frac{\mathrm{2}}{\sqrt{\mathit{\pi }}}}{e}^{\frac{ux}{\mathrm{2}{D}_{\mathrm{f}}}}\underset{\sqrt{\frac{x^{\mathrm{2}}}{\mathrm{4}{D}_{\mathrm{f}}t}}}{\overset{\mathrm{\infty }}{\int }}{e}^{-{\mathit{\xi }}^{\mathrm{2}}-\frac{u^{\mathrm{2}}{x}^{\mathrm{2}}}{\mathrm{16}{D}_{\mathrm{f}}^{\mathrm{2}}{\mathit{\xi }}^{\mathrm{2}}}}\mathrm{d}\mathit{\xi }\end{array}$$

The difference between the solute breakthrough curves calculated from Eqs. (4) and (5) quantitatively denotes the matrix diffusion effect on solute transport. In this study, we use the normalized residual sum of squares between the two concentrations, denoted by R, to represent matrix diffusion effect,

$$\begin{array}{}\text{(6)}& R=\underset{\mathrm{0}}{\overset{T_{\mathrm{0}}}{\int }}{\left({\displaystyle \frac{C_{\mathrm{f}}-C_{\mathrm{mf}}}{C_{\mathrm{fmax}}}}\right)}^{\mathrm{2}}\mathrm{d}t\end{array}$$

in which C_f and C_mf denote solute concentrations calculated from fracture-only and fracture-matrix coupled models respectively, C_fmax is the peak solute concentration from the fracture-only model, and T₀ is the simulation time.

According to Eqs. (4) and (5), the matrix diffusion effect depends on seven parameters related to fracture, matrix, and spatial-temporal scale of the model, i.e., matrix porosity θ, matrix diffusion coefficient D_m, fracture half-aperture b, fracture longitudinal dispersivity α_L, fracture fluid velocity u, solute release time (t₀), and the distance between solute release and monitoring locations x. The last two parameters t₀ and x characterize the temporal and spatial scales of the problem.

2.2 Matrix diffusion effect

With the analytical solutions, we proceed to examine the impact of the seven parameters on matrix diffusion effect. We consider a relatively wide parameter range to include both lab and field scale scenarios (Table 1) according to previous studies in the literature (Grisak and Pickens, 1981; Novakowski et al., 1985; Shapiro and Nicholas, 1989; Himmelsbach et al., 1998; Jardine et al., 1999; Maloszewski et al., 1999; Reimus et al., 2003; Reimus and Callahan, 2007; Zhou et al., 2006). For each parameter being examined, we first generate 200 parameter sets for the other six parameters using the Latin-hypercube sampling (LHS) approach, with each individual parameter following a log-uniform distribution in its corresponding range. LHS is originally proposed by McKay et al. (1979) and has been widely used for sampling high-dimensional parameter spaces as it effectively ensures that all portions of the parameter space are sampled. For each generated parameter set, we then perform a sensitivity analysis to investigate the relationship between the parameter being examined and the matrix diffusion effect represented by R (Fig. 2).

Table 1 Parameter ranges for the analysis of matrix diffusion effect.

The positive relationship between R and parameters θ and D_m, and the negative relationship between R and parameters b and u are consistent with previous investigations in the literature (Grisak and Pickens, 1980; Zhou et al., 2018), that the matrix diffusion effect increases with the increase of θ and D_m, and decreases with the increase of b and u. The longitudinal dispersivity in fracture α_L exhibits a negative but relatively insignificant effect on matrix diffusion. The increase of R with the increase of t₀ and x indicates that larger temporal and spatial scales lead to a more significant matrix diffusion effect. A previous tracer modeling study from Zhou et al. (2018) reported similar results, that the decrease of tracer release duration led to a reduced sensitivity of tracer breakthrough curve to matrix diffusion coefficient. Another interesting observation corroborating the enhanced matrix diffusion effect in large scale problems is that matrix diffusion coefficients measured from field-scale tests were always larger than those measured from lab-scale tests (Shapiro, 2001; Andersson et al., 2004; Liu et al., 2004, 2007; Zhou et al., 2007).

We observe a nearly linear relationship between matrix diffusion effect and the seven parameters in a log-log coordinate (Fig. 2). According to the calculated mean slopes of the curves, the sensitivity of the matrix diffusion effect to matrix porosity and fracture aperture is almost double of that to matrix diffusion coefficient. Such a quantitative result of the sensitivity of matrix diffusion effect to matrix/fracture parameters happens to be consistent with the significance of these parameters reflected in previously proposed unified terms to characterize matrix diffusion (Table 2). The exponents of matrix porosity θ and fracture aperture 2b are two times of that of matrix diffusion coefficient D_m. We also note that the mean slopes for fracture longitudinal dispersivity α_L and solute release duration t₀ are much smaller than that of θ, 2b and D_m, justifying the omission of α_L and t₀ in these unified terms. However, the mean slopes for distance x and flow velocity u are similar to that of θ and 2b (Fig. 2), while their exponents in the unified terms are half of the exponents of θ and 2b.

Table 2 Unified terms proposed in previous studies to characterize matrix diffusion.

^a t^∗ denotes minimum advective travel time and can be calculated as $x/u$. ^b R and λ are retardation factor and first-order reaction rate constant respectively.

2.3 Evaluating matrix diffusion effect through unified parameters

As matrix diffusion effect depends on multiple matrix/fracture parameters, a unified parameter that lumps matrix/fracture parameters together is necessary to correctly quantify matrix diffusion. We further evaluate the effectiveness of the abovementioned unified parameters as well as the Peclet number in evaluating matrix diffusion effect. The Peclet number is a widely used dimensionless number to characterize the relative strength of advection to diffusion in solute transport problems. However, the conventional definition of Peclet number is $u\cdot x/D_{\mathrm{f}}$, which does not involve any matrix parameters, and therefore can only characterize the advection and hydrodynamic dispersion in the fracture. Wang et al. (2023) defined a different Peclet number expressed as $u\cdot \mathrm{2}b/D_{\mathrm{m}}$, which might be more appropriate in characterizing matrix diffusion. In the following analysis, we consider both the two Peclet numbers.

Similarly, we randomly generate 5000 parameter sets using Latin-hypercube sampling approach. For each parameter set, we calculate the unified parameters as well as the matrix diffusion effect represented by R (Fig. 3). The Peclet number that replaces x and D_f with 2b and D_m ($u\cdot \mathrm{2}b/D_{\mathrm{m}}$) shows a more remarkable correlation with matrix diffusion effect than the conventional Peclet number ($u\cdot x/D_{\mathrm{f}}$) does (Fig. 3a and b). However, the Pearson correlation coefficients between the Peclet numbers and R are relatively small, meaning that they might be unable to correctly quantify matrix diffusion effect. The performance of $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}}{\mathrm{2}b}$ and $\sqrt{\mathrm{2}{D}_{\mathrm{m}}\cdot t^{\ast }}$ is similar to the Peclet number $u\cdot \mathrm{2}b/D_{\mathrm{m}}$ (Fig. 3c and d). The unified parameter $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}\cdot x/u}}{\mathrm{2}b}$ shows the largest Pearson correlation coefficient and outperforms the other unified parameters in quantifying matrix diffusion effect as it incorporates all the five major parameters that affects matrix diffusion (Fig. 3e). As we mentioned before, according to the sensitivity of R to the parameters (reflected by the mean slopes) in Fig. 2, the significance of x and u in these previously proposed unified parameters is actually underestimated. Following the sensitivities in Fig. 2, we propose a new unified parameter according to the curve slopes of different parameters, which turns out to have a form of $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}x}}{\mathrm{2}bu}$, and then analyze its capability in quantifying matrix diffusion effect (Fig. 3f). A Pearson correlation coefficient of 0.99 is achieved. The almost linear relationship between R and $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}x}}{\mathrm{2}bu}$ indicates that the newly proposed unified parameter is likely a better indicator of matrix diffusion than the previously proposed unified parameters. We note that the proposed unified parameter is not dimensionless and has a unit of s${}^{\mathrm{1}/\mathrm{2}}$, indicating that the matrix diffusion effect is scale-dependent and increases with the advective travel time.

Based on the relationship between R and the unified parameters, a quantitative criterion or threshold could be suggested to evaluate whether or not matrix diffusion has a significant impact on solute transport. In fact, several such thresholds have been discussed in the literature. For $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}}{\mathrm{2}b}$, Raven et al. (1988) indicated that when the unified parameter is smaller than 10⁻⁴ s${}^{-\mathrm{1}/\mathrm{2}}$, matrix diffusion has a negligible effect on solute transport through fractures (Fig. 3d). For $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}\cdot x/u}}{\mathrm{2}b}$, Neretnieks (2002) proposed a threshold of 0.01, below which matrix diffusion effect could be neglected (Fig. 3e). To validate the unified parameters as well as the corresponding thresholds, we analyze and compile solute transport data from lab and field tests in fractured media reported in the literature, and select cases for which matrix diffusion effect (significant or negligible) has been explicitly discussed. According to the reported fracture/matrix parameters (Sect. S4 in the Supplement), we calculate the abovementioned unified parameters as shown in the bottom panel of each plot in Fig. 3. The majority of the selected cases was identified as exhibiting significant matrix diffusion effect according to the literature. Four unified parameters (the two Peclet numbers, $\sqrt{\mathrm{2}{D}_{\mathrm{m}}\cdot x/u}$ and $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}}{b}$) fail to correctly discriminate cases with significant matrix diffusion from that with negligible matrix diffusion, while the other two unified parameters ($\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}\cdot x/u}}{\mathrm{2}b}$ and the newly proposed $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}x}{\mathrm{2}bu}$) successfully separate the two scenarios (Fig. 3). For $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}\cdot x/u}}{\mathrm{2}b}$, the threshold of 0.01 from Neretnieks (2002) turns out to be relatively conservative as a case beyond 0.01 is identified as having negligible matrix diffusion (Fig. 3e). For the newly proposed $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}x}{\mathrm{2}bu}$, we find that the largest $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}x}{\mathrm{2}bu}$ value for the blue crosses (negligible matrix diffusion) and the smallest $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}x}{\mathrm{2}bu}$ value for the red circles (significant matrix diffusion) are both close to 5 s${}^{\mathrm{1}/\mathrm{2}}$. As a result, we recommend a threshold of 5 s${}^{\mathrm{1}/\mathrm{2}}$ (corresponding to a R value of approximately 50) as a reasonable criterion to determine whether matrix diffusion effect is significant or negligible (Fig. 3f).

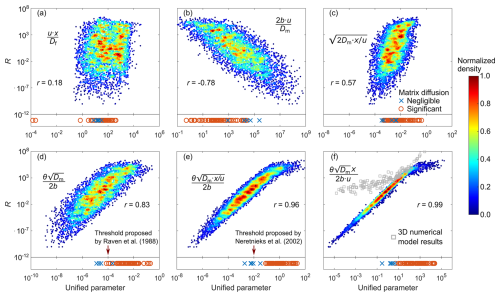
Figure 3 Relationship between matrix diffusion effect and unified parameters. All the 5000 data points are shown, with the color denoting the normalized density of data points. The Pearson correlation coefficients (r) are also annotated. In the bottom panel of each plot, we show 78 cases from the literature. For each case, the unified parameter is calculated and marked as a blue cross if matrix diffusion is identified as negligible in the literature, and a red circle if matrix diffusion is identified as significant. (a) Peclet number $u\cdot x/D_{\mathrm{f}}$. (b) Peclet number $u\cdot \mathrm{2}b/D_{\mathrm{m}}$. (c) Diffusion distance $\sqrt{\mathrm{2}{D}_{\mathrm{m}}}\cdot x/u$. (d) Diffusion parameter $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}}{\mathrm{2}b}$. Threshold proposed by Raven et al. (1988) is annotated. (e) Strength of matrix diffusion $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}\cdot x/u}{\mathrm{2}b}$. Threshold proposed by Neretnieks (2002) is annotated. (f) The newly proposed unified parameter $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}x}{\mathrm{2}bu}$. We also show the results (gray squares) from 3D numerical models with a point source for solute release.

2.4 Equivalent solute release function

For cases with non-negligible matrix diffusion, a following question is whether there is a way to accurately incorporate the effect of matrix diffusion in a fracture-only model, so that solute transport modeling can still employ the simplified model to avoid otherwise overwhelming computational burden. A straightforward approach is to upscale parameters that show positive impacts on matrix diffusion effect such as x, or downscale parameters that show negative impacts such as 2b and u. However, as these parameters have an integrative impact on matrix diffusion, it is difficult to derive an upscaling/downscaling equation for a single parameter to fully compensate for matrix diffusion effect. In the present study, we propose to tailor the solute release function to represent matrix diffusion effect in a fracture-only model.

We consider a typical solute release scenario with a constant release concentration of C₀. To simplify the actual fracture-matrix coupled model to a fracture-only model, we assume a time varying function C(t) as an equivalent solute release concentration. The goal is to determine C(t) so that the solute breakthrough curve calculated from the fracture-only model with a solute release concentration of C(t) is equal to that calculated from the fracture-matrix coupled model with a constant solute release concentration of C₀. The derivation of C(t) is provided in the Supplement (Sect. S3) and the expression is as follows,

$$\begin{array}{}\text{(7)}& {\displaystyle \frac{C\left(t\right)}{C_{\mathrm{0}}}}=\left\{\begin{array}{ll}\text{erfc}\left(\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}x}{\mathrm{2}bu\sqrt{t}}\right),& \mathrm{0}\le t\le t_{\mathrm{0}}\\ \text{erfc}\left(\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}x}{\mathrm{2}bu\sqrt{t}}\right)-\text{erfc}\left(\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}x}{\mathrm{2}bu\sqrt{t-t_{\mathrm{0}}}}\right),& t>t_{\mathrm{0}}\end{array}\right.\end{array}$$

By employing C(t) as the solute release function in the simplified fracture-only model, the obtained solute breakthrough curve is almost the same as that obtained from the fracture-matrix coupled model (solid blue and dashed red curves in Fig. 4a).

Interestingly, the coefficient within the complementary error functions in Eq. (7) is exactly identical to the newly proposed unified parameter $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}x}{\mathrm{2}bu}$, indicating that the equivalent solute release function C(t) depends solely on $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}x}{\mathrm{2}bu}$. Although the unified parameter is first empirically proposed based on the sensitivity analyses in Fig. 1, Eq. (7) provides a strong corroboration for the theoretical rationality of the unified parameter in quantifying matrix diffusion effect. The underlying logic of the equivalent solute release function is to consider matrix diffusion as a source/sink for fracture solute transport. when solute concentration in fracture is larger than that in matrix (during solute injection period), solute will diffuse into the matrix (matrix as a sink term), while when solute concentration in fracture is smaller than that in matrix (after solute injection), solute in the matrix gradually diffuses into the fracture (matrix as a source term). Essentially, the equivalent solute release function accurately compensates for matrix diffusion by delicately capture the source/sink effect of matrix on fracture solute transport processes.

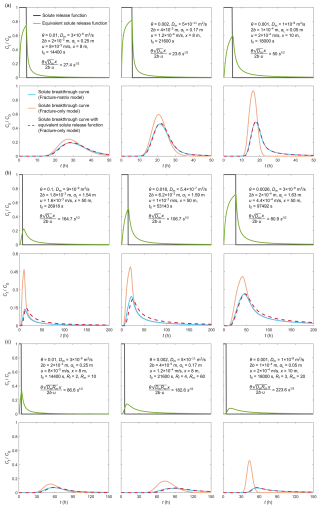
Figure 4 Compensation of matrix diffusion effect through the use of equivalent solute release function in fracture-only models. We randomly select three cases with relatively large $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}x}{\mathrm{2}bu}$ (as annotated) for analysis. (a) Results from the 2D analytical model for conservative solute. The upper row compares the original solute release function and the equivalent solute release function. The lower row compares solute breakthrough curves from three models, i.e., fracture-matrix and fracture-only models with the original solute release function, and fracture-only model with the equivalent solute release function. (b) Results from the 3D numerical model with point injection/production for conservative solute. (c) Results from the 2D analytical model for sorptive solute.

Figure 5 (a) A 3D numerical model with a horizontal fracture connecting an injection well and a production well. (b) The corresponding 2D fracture-only model.

3 Verification through a 3D numerical model

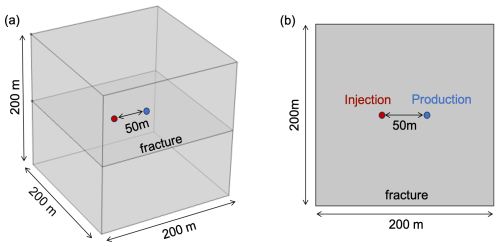
The above analyses demonstrate the effectiveness of the proposed unified parameter and the derived equivalent solute release function in quantifying and compensating for matrix diffusion effect on solute transport process respectively, for the relatively simple 2D model with a uniform flow velocity. In real-world problems, solute is generally released into/extracted from fractures through point sources, leading to a non-uniform fracture flow field. To verify the applicability of the unified parameter and equivalent solute release function in such realistic scenarios, we develop a 3D model ($\mathrm{200}\times \mathrm{200}\times \mathrm{200}$ m³) with a horizontal fracture located in the center of the model (Fig. 5a). Two wells with a distance of 50 m intersect the fracture, one for fluid injection and solute release, and the other one for fluid extraction and solute concentration measurement.

Similar as the above analysis, we randomly generate 150 parameter sets through Latin-hypercube sampling approach. Note that we fix the distance between solute release and extraction locations at 50 m, and each parameter set consists of θ, D_m, 2b, α_L, t₀, and flow rate q (with a range of 0.001–0.1 m³ s⁻¹). To examine the applicability of the derived equivalent solute release function, we also develop a 2D fracture-only model and then apply the equivalent solute release function (Fig. 5b). Solute transport simulations are then performed to obtain solute breakthrough curves for both the 3D and 2D models. We first simulate fracture flow field and then solve the advection-dispersion equation to simulate solute transport process (Grisak and Pickens, 1980; Tang et al., 1981; Wu et al., 2019). Both the 3D and 2D models are discretized with hexagonal elements, with 400 000 elements for the 3D model and 10 000 elements for the 2D model. A hydrostatic initial pressure is assumed in the model, and the pressure at the production well is fixed at its initial pressure. Fluid is injected into the fracture through the injection well with a flow rate of q, and solute is injected with a constant concentration of C₀ for a time period of t₀. Note that the production well acts as an open boundary for both fluid and solute, and the lateral boundaries of the 3D and 2D models are assumed impermeable for both fluid and solute. The advection-dispersion equation with the specified boundary and initial conditions are numerically solved using the finite element method implemented in COMSOL Multiphysics (Hu et al., 2020; Wang et al., 2023).

According to the calculated R and $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}x}{\mathrm{2}bu}$ (annotated by the gray squares in Fig. 3f), we find that although their relationship is not as linear as that for analytical solutions due to the non-uniform flow field, $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}x}{\mathrm{2}bu}$ still exhibits a strong ability to quantify matrix diffusion effect, indicating that the proposed unified parameter is also applicable to point source scenarios (Fig. 3f).

To apply the equivalent solute release function to the 2D fracture-only model, we first need to calculate a representative “average” flow velocity in the fracture. We tried three different methods: (1) Calculate solute mean residence time from solute breakthrough curve and divide well distance by the mean residence time to estimate average flow velocity. (2) Calculate average flow velocity from pressure difference between the two wells according to Darcy's law. (3) Divide well distance by the time difference between peak concentration time and half of solute injection time. By comparing the matrix diffusion compensation performance of the equivalent solute release functions using the three flow velocities, we find that the flow velocity calculated through the third method exhibits the best result (Sect. S2 in the Supplement). The solute breakthrough curve from the fracture-only model with equivalent solute release function matches well with that from the fracture-matrix coupled model, although not as perfect as that for the analytical model (Fig. 4b).

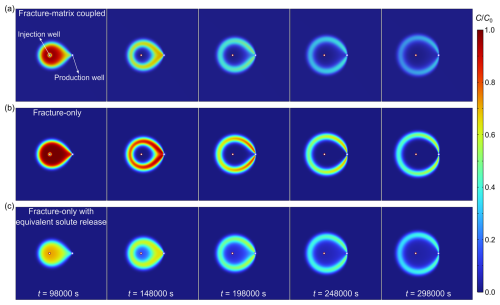
Figure 6 Distribution of solute concentration in the fracture. Parameters for this case are: θ=0.0026, $D_{\mathrm{m}}=\mathrm{3}\times {\mathrm{10}}^{-\mathrm{9}}$ m² s⁻¹, 2$b=\mathrm{2}\times {\mathrm{10}}^{-\mathrm{4}}$ m, α_L=1.63 m, $u=\mathrm{4.4}\times {\mathrm{10}}^{-\mathrm{4}}$ m s⁻¹, t₀=97492 s. (a) Results from the 3D fracture-matrix coupled model. (b) Results from the 2D fracture-only model. (c) Results from the 2D fracture-only model with equivalent solute release function.

We select the third case in Fig. 4b with a unified parameter of 80.9 s${}^{\mathrm{1}/\mathrm{2}}$ (i.e., significant matrix diffusion effect) to further compare the distribution of solute concentration from fracture-matrix coupled and fracture-only models. Compared with the results from the 3D fracture-matrix coupled model (Fig. 6a), the fracture-only model overestimates solute concentration in the fracture due to the neglect of matrix diffusion (Fig. 6b), and such an overestimation is largely corrected with the application of the equivalent solute release function (Fig. 6c). However, as the equivalent solute release function specifically aims to correct solute concentration at the production well, the concentrations at other locations are still slightly biased.

As aforementioned, the main purpose of simplifying the 3D fracture-matrix coupled model to 2D fracture-only model by applying the equivalent solute release function is to reduce the computational cost associated with solute transport modelling in subsurface fractured media. According to the above 150 3D and 2D simulations, the computational cost of 3D fracture-matrix coupled models is approximately 0.5–1 core hour, while 2D fracture-only models are generally completed within 10 s on a single core. The computational cost of the 2D fracture-only models is therefore only 0.28 %–0.56 % of the 3D fracture-matrix coupled models, corroborating the effectiveness of the equivalent solute release function in improving computational efficiency.

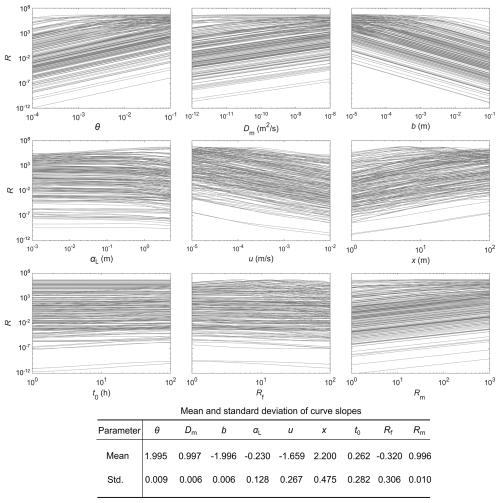
Figure 7 Relationship between matrix diffusion effect and model parameters for sorptive solute. Each plot has 200 curves, corresponding to the randomly generated 200 parameter sets for the other eight parameters (except the examined parameter). R_m and R_f denote retardation coefficient in matrix and fracture respectively. The mean and standard deviation of the slope of the curves for each parameter are annotated.

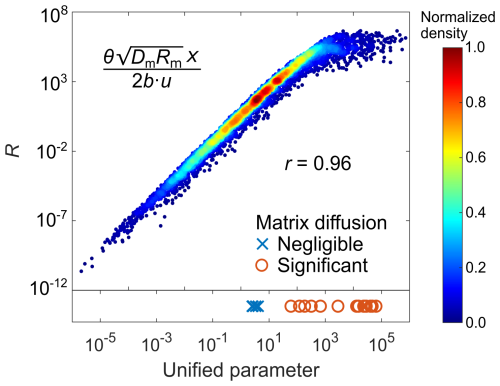
Figure 8 Relationship between matrix diffusion effect and the proposed unified parameter $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}{R}_{\mathrm{m}}x}{\mathrm{2}bu}$ for a sorptive solute. The color denotes the normalized density of data points. The Pearson correlation coefficient (r) is annotated. We show 21 cases from the literature in the bottom panel, with blue crosses denoting cases with negligible matrix diffusion and red circles denoting cases with significant matrix diffusion.

4 Application to sorptive and degradative solutes

4.1 Sorptive solute

The above analysis assumes a conservative solute. In real-world applications, sorptive solutes are also commonly encountered or used. For a sorptive solute, we perform the same analyses as that in Sect. 2 to understand matrix diffusion effect. Note that we assume an equilibrium sorption process (Tang et al. 1981; Dai et al., 2012). The retardation coefficient in matrix R_m shows a more significant on matrix diffusion effect than the retardation coefficient in fracture R_f does (Fig. 7). According to the sensitivity of the matrix diffusion effect to fracture/matrix parameters (Fig. 7), we propose a unified parameter to quantify matrix diffusion effect for sorptive solute, expressed as $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}{R}_{\mathrm{m}}}x}{\mathrm{2}bu}$. The unified parameter also performs satisfactorily in quantifying matrix diffusion effect with a Pearson correlation coefficient of 0.96 (Fig. 8). Similarly, we collect 21 sorptive solute transport field experiments performed in fractured media from the literature to validate the effectiveness of the proposed unified parameter in quantifying the significance of matrix diffusion effect (summarized in Sect. S5 in the Supplement). The unified parameter is able to discriminate cases with significant matrix diffusion from that with negligible matrix diffusion (Fig. 8), and a threshold of 10 s${}^{\mathrm{1}/\mathrm{2}}$ seems a reasonable criterion.

The equivalent solute release function for sorptive solute is derived based on analytical solutions for 2D fracture-matrix models (Tang et al., 1981; Dai et al., 2012), and can be expressed as,

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{C\left(t\right)}{C_{\mathrm{0}}}}=\left\{\begin{array}{ll}\text{erfc}\left(\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}{R}_{\mathrm{m}}}x}{\mathrm{2}bu\sqrt{t}}\right),& \mathrm{0}\le t\le t_{\mathrm{0}}\\ \text{erfc}\left(\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}{R}_{\mathrm{m}}}x}{\mathrm{2}bu\sqrt{t}}\right)-\text{erfc}\left(\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}{R}_{\mathrm{m}}}x}{\mathrm{2}bu\sqrt{t-t_{\mathrm{0}}}}\right),& t>t_{\mathrm{0}}\end{array}\right.\end{array}$$

For the three cases in Fig. 4a, we further assume retardation coefficients in fracture and matrix (as annotated in Fig. 4c), and calculate solute breakthrough curves from fracture-matrix coupled and fracture-only models. The comparison indicates that the derived equivalent solute release function is also able to correctly compensate for matrix diffusion effect in fracture-only models for sorptive solute (Fig. 4c).

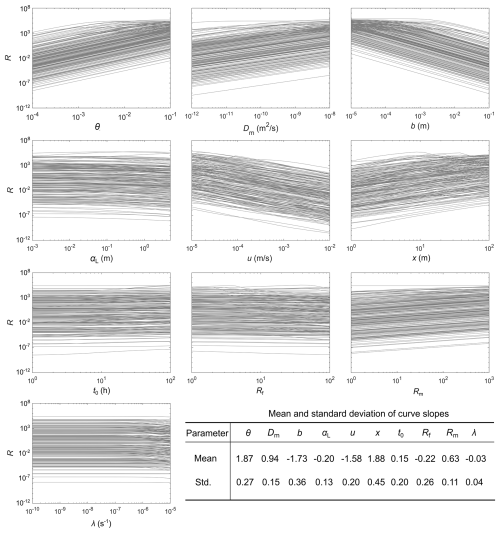
Figure 9 Relationship between matrix diffusion effect and model parameters for degradative solute. Each plot has 200 curves, corresponding to the randomly generated 200 parameter sets for the other eight parameters (except the examined parameter). R_m and R_f denote retardation coefficient in matrix and fracture respectively. The mean and standard deviation of the slope of the curves for each parameter are annotated.

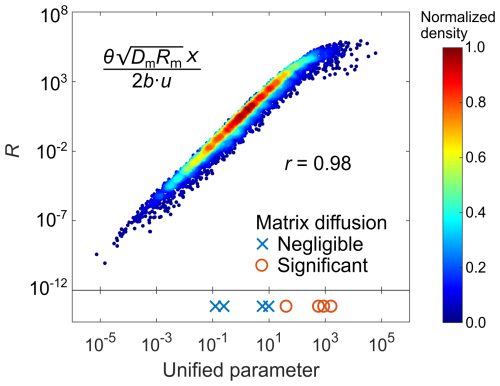
Figure 10 Relationship between matrix diffusion effect and the proposed unified parameter $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}}{R}_{\mathrm{m}}x}{\mathrm{2}bu}$ for a degradative solute. The color denotes the normalized density of data points. The Pearson correlation coefficient (r) is annotated. We show 10 cases from the literature in the bottom panel, with blue crosses denoting cases with negligible matrix diffusion and red circles denoting cases with significant matrix diffusion.

4.2 Degradative solute

In addition to conservative and sorptive solutes, degradative solutes like radionuclides, are also critical in real-world applications involving radionuclide transport in fractured media. To assess the matrix diffusion effect for degradative solutes, we perform analyses under the assumption of a first-order degradation process. The results indicate that the degradation coefficient λ has minimal impact on the matrix diffusion contribution (Fig. 9). This implies that the matrix diffusion effect for degradative solutes is primarily governed by the same fracture and matrix parameters as those for sorptive solutes. Therefore, the same unified parameter proposed for sorptive solutes, $\frac{\mathit{\theta }\sqrt{D_{\mathrm{m}}{R}_{\mathrm{m}}}x}{\mathrm{2}bu}$, is also suitable for quantifying the matrix diffusion effect for degradative solutes. This parameter exhibits a high quantification performance with a Pearson correlation coefficient of 0.98 (Fig. 10), validating its applicability to degradative solutes. We use data from 10 degradative solute transport field experiments in fractured media reported in the literature (summarized in Sect. S6 in the Supplement) to further confirm the reliability. The unified parameter effectively distinguishes cases with significant matrix diffusion from those with negligible diffusion (Fig. 10). The threshold value of 10 s${}^{\mathrm{1}/\mathrm{2}}$ for the unified parameter remains a reasonable criterion for evaluating matrix diffusion in degradative solute transport scenarios.

5 Discussions

5.1 Matrix diffusion effect for conservative, sorptive and degradative solutes

Conservative, sorptive and degradative solutes are three commonly encountered solute types in most subsurface reservoir applications. According to the above analyses on matrix diffusion for the three solute types, we find that matrix diffusion for conservative solute is mainly controlled by rock porosity (θ), rock diffusion coefficient (D_m), fracture aperture (2b) and mean residence time ($x/u$). For sorptive solute, retardation coefficient in matrix (R_m) is also an important controlling parameter, and its impact on matrix diffusion is similar to that of rock diffusion coefficient. A larger retardation coefficient leads to more significant matrix diffusion effect. For degradative solute, an interesting finding is that the degradation coefficient (λ) does not show significant impact on matrix diffusion. The proposed unified parameter is therefore the same for sorptive and degradative solutes. The relative strength of the effect of these parameters on matrix diffusion can be discussed based on the unified parameter. Rock porosity, mean residence time and fracture aperture exhibit stronger impact on matrix diffusion than rock diffusion coefficient and retardation coefficient. Although rock diffusion coefficient directly describes the diffusion rate of solute from fracture into matrix, its effect on the overall matrix diffusion effect is smaller than that of rock porosity, fracture aperture and solute mean residence time in fracture.

5.2 Field applicability of the unified parameter and equivalent solute release function

The current study uses a single-fracture model to derive the unified parameter and equivalent solute release function, which have relatively simple expressions and can be easily applied for matrix diffusion effect analysis. However, in real-world field applications, subsurface fractured media normally involve complex fracture characteristics such as multiple parallel fractures, heterogeneous fracture aperture distribution, discrete fracture networks, etc. For solute transport in such complex fracture scenarios, the application of the unified parameter and equivalent solute release function needs careful considerations. In cases with multiple parallel fractures, matrix diffusion around one fracture may affect matrix diffusion in adjacent fractures, and the interaction strength between two fractures depends on the distance between them. If the fracture distance is sufficiently large that the solute transport process in one fracture is independent of that in other fractures, then the unified parameter and equivalent solute release function are applicable for matrix diffusion analysis. On the contrary, if the fracture distance is relatively small, then it should be considered as an additional parameter that affects matrix diffusion, and future work is necessary to investigate how the distance could be incorporated in the unified parameter and equivalent solute release function.

In cases with heterogeneous fracture aperture or discrete fracture networks, flow and transport paths between solute release and monitoring points are normally highly channelized. The applicability of the unified parameter and equivalent solute release function is therefore compromised as they assume a uniform flow field, represented as u in Eq. (7). Nevertheless, the proposed unified parameter, as a practically convenient method, can still provide fast and quantitative estimations of matrix diffusion effect in complex field environments. The equivalent function should be able to at least partially offset the impact of ignoring matrix diffusion, but further investigations are required to improve its accuracy and applicability to such complex fracture characteristics.

6 Conclusions

In the present study, we provide a convenient and practical method to quantify matrix diffusion effect on solute transport in subsurface fractured media. We propose a unified parameter that incorporates matrix/fracture properties as well as spatial-temporal scales and demonstrate that the unified parameter shows better prediction capability of matrix diffusion effect than previously proposed unified parameters. Through a comprehensive analysis with lab and field data, we find that a threshold of 5 s${}^{\mathrm{1}/\mathrm{2}}$ of the unified parameter appears appropriate to evaluate whether matrix diffusion effect is significant or negligible. For cases with significant matrix diffusion effect, we derive an equivalent solute release function as an alternative of matrix diffusion. This function allows the simplification of a fracture-matrix coupled model to a fracture-only model, and is particularly useful for solute transport modeling efforts associated with contaminant remediation, geological storage and tracer testing because it can greatly improve computational efficiency without sacrificing accuracy.