Technical note: A simple feedforward artificial neural network for high-temporal-resolution rain event detection using signal attenuation from commercial microwave links

Two simple feedforward neural networks (multilayer perceptrons – MLPs) are trained to detect rainfall events using signal attenuation from commercial microwave links (CMLs) as predictors and high-temporal-resolution reference data as the target. MLP_GA is trained against nearby rain gauges, and MLP_RA is trained against gauge-adjusted weather radar. Both MLPs were trained on 26 CMLs and tested on 843 CMLs, all located within 5 km of a rain gauge. Our results suggest that these MLPs outperform existing methods, effectively capturing the intermittent behaviour of rainfall. This study is the first to use both radar and rain gauges for training and testing CML rainfall detection. While previous studies have mainly focused on hourly reference data, our findings show that it is possible to classify rainy and dry time steps with a higher temporal resolution.

1 Introduction

Commercial microwave links (CMLs) are radio links between telecommunication towers. By exploiting the relation between CML signal attenuation and rainfall intensity, it is possible to estimate the average rainfall intensity along the CML (Messer et al., 2006; Leijnse et al., 2007). As the signal is also attenuated by factors other than rain, such as air humidity, these non-rainy factors must be taken into account in what is often called the baseline attenuation. Rain-induced attenuation can then be estimated by subtracting the estimated baseline from the total loss. Since each CML can have a different baseline attenuation and because the baseline attenuation can change between different rainfall events, it is necessary to estimate the baseline attenuation for each rainfall event. A common approach is to use the signal attenuation from time steps that are temporally close to the rainfall period (Chwala and Kunstmann, 2019; Graf et al., 2020). This raises the need for algorithms that can separate the CML time series into rainy time steps, where the CML experiences signal attenuation due to rainfall, and dry time steps, where the CML signal level is not attenuated by rainfall. This task can be seen as a classification problem, where every time step is classified as either rainy or dry. The separation of the CML time series into rainy and dry time steps can also help to filter out events in the CML signal time series that show some of the same characteristics as rainfall events but that are not caused by rainfall. CML signal loss is recorded differently depending on the network operator and can, for instance, be available as instantaneous measurements every minute. Another popular format is to record the minimum and maximum signal loss over a period, typically 15 min. In this work, we focus on instantaneously sampled CML data as these data are becoming more available; see, for instance, Andersson et al. (2022) and Covi and Roversi (2024).

The CML signal experiences fluctuations during rain events. Based on this, a simple method for rain event detection was developed by Schleiss and Berne (2010). They suggested using these fluctuations to classify rainy periods by taking the standard deviation of a 60 min rolling window and setting time steps with values above a certain threshold to rainy. This threshold is different between CMLs but can be derived from local climate characteristics. Graf et al. (2020) expanded this method by recognising that climate characteristics are not necessarily valid for different locations; individual years; and, in particular, specific rainy periods that might be of interest. They proposed that one should estimate the threshold by computing the 80 % quantile of the 60 min rolling standard deviation for each CML and then multiply this number by a constant that was found to be similar for all CMLs in the study. A more data-driven approach was explored by Polz et al. (2020). They trained a convolutional neural network (CNN) to detect rainfall events using 800 CMLs in Germany. As a reference, they used the gauge-adjusted radar product RADOLAN-RW from Germany's National Meteorological Service (DWD), which has an hourly resolution. Another approach is to include the signal loss from nearby CMLs (Overeem et al., 2011). This method was shown to work for dense CML networks. The literature describes several other approaches (Habi and Messer, 2018; Reller et al., 2011; Rayitsfeld et al., 2012; Wang et al., 2012).

Although several of the mentioned approaches classify rainfall at a high temporal resolution, all large studies using instantaneously sampled CML data have been evaluated using hourly reference data. This might be a reasonable approach as rainfall detection is mostly used for estimating the baseline, which is typically set to be a constant throughout a rainfall event (Chwala and Kunstmann, 2019; Uijlenhoet et al., 2018; Messer and Sendik, 2015). However, existing methods are not optimised for estimating rainfall at a higher temporal resolution; thus, the estimates might not reflect the true intermittency of rainfall. Estimating too-long rainy periods could, in cases where the baseline attenuation drops during the rainfall event, result in a bias where the CML estimates rainfall during time steps where there is no rain. Further, a drawback of estimating too-long rainy periods is that some of the estimated rainy time steps could contain non-liquid precipitation. Because dry snow induces a very low signal attenuation, these time steps appear to be dry in the CML time series. Thus, correctly estimating rainy time steps is important because CML time steps that indicate no precipitation could contain dry snow.

In this study, we present two methods for detecting rainy time steps in CML time series data. The goal of both methods is to detect rainy time steps in the time series of a CML where the signal attenuation is provided every 1 min. This is done with a higher temporal resolution compared to existing methods so that short dry spells during rainy periods can be identified. One method is trained on radar reference data, and the other method is trained on rain gauge reference data. Both methods are tested against rain gauge and radar data, highlighting their differences. We also examine the performance of the developed methods in comparison to existing approaches, aiming to gain a clearer understanding of the differences between the two alternative methods.

2 Material and methods

2.1 Data

A large dataset with 3901 CMLs from Germany was used, providing transmitted and received signal levels with a temporal resolution of 1 min from 1 to 31 July 2021. The total signal loss (TL) was computed by subtracting the transmitted signal level from the received signal level. Each CML consists of two time series called sub-links, reflecting the signal loss in the beams going from location 0 to 1 and vice versa. More information on this dataset can be found in Graf et al. (2020). As the ground truth, two different sources were explored. The first used rain gauges near the CMLs provided by DWD. The rain gauge data were provided with a temporal resolution of 1 min and a volume resolution of 0.01 mm. We consider a minute to be rainy if the rain gauge records any rainfall. The other source was the radar product RADKLIM-YW (Winterrath et al., 2018). This product from DWD is a gauge-adjusted, climatologically corrected product with a temporal resolution of 5 min. For the comparison with CML data, the radar product was averaged over the CML path, with each grid value being weighted by the length of the CML path intersection in each grid cell. For a comparison of the path-averaged RADKLIM-YW reference and the CML rainfall estimates, RADKLIM-YW was resampled from a 5 min resolution to a 1 min resolution by linear interpolation and then dividing the rainfall sums by 5. To make it comparable to the rain gauges, minutes with rainfall above 0.01 mm were set to rainy.

Our study focused on CML–rain gauge pairs located less than 5 km from each other. This resulted in 882 CMLs where the CML lengths ranged from 0.3 to 22.9 km, with 90 % of the CMLs being longer than 2.4km. The CML frequencies ranged between 7 to 40 GHz, with most CMLs having a frequency above 15 GHz. Even though there are many CMLs in our dataset, we only have 429 unique rain gauges serving as references. This means that some CMLs use the same rain gauge for reference.

2.2 The MLP_RA and MLP_GA method

In our approach, we have used a simple feedforward neural network provided by the Python library scikit-learn (Pedregosa et al., 2011). This network consists of an input layer, fully connected hidden layers, and an output layer. Networks with a simple architecture of this type are often referred to as a multilayer perceptron (MLP). The MLP's job is to classify a time step in the CML time series as either rainy or dry. It does this by analysing the signal loss from the surrounding 40 time steps. In essence, the MLP acts like a sliding window, moving across 40 time steps at a time and determining whether each centred time step is rainy or dry. The predictor data – that is, the 40-time-step moving window – are organised in a so-called design matrix (Eq. 1), where tl${}_{s_{\mathrm{1}},t}$ and tl${}_{s_{\mathrm{2}},t}$ represent the total signal loss at time step t for sub-link 1 and sub-link 2, respectively.

$$\begin{array}{}\text{(1)}& \left[\begin{array}{cccccc}{\mathrm{tl}}_{s_{\mathrm{1}},t_{\mathrm{0}}-\mathrm{20}}& \mathrm{\dots }& {\mathrm{tl}}_{s_{\mathrm{1}},t_{\mathrm{0}}+\mathrm{20}}& {\mathrm{tl}}_{s_{\mathrm{2}},t_{\mathrm{0}}-\mathrm{20}}& \mathrm{\dots }& {\mathrm{tl}}_{s_{\mathrm{2}},t_{\mathrm{0}}+\mathrm{20}}\\ \mathrm{⋮}& & \mathrm{⋮}& \mathrm{⋮}& & \mathrm{⋮}\\ {\mathrm{tl}}_{s_{\mathrm{1}},t_i-\mathrm{20}}& \mathrm{\dots }& {\mathrm{tl}}_{s_{\mathrm{1}},t_i+\mathrm{20}}& {\mathrm{tl}}_{s_{\mathrm{2}},t_i-\mathrm{20}}& \mathrm{\dots }& {\mathrm{tl}}_{s_{\mathrm{2}},t_i+\mathrm{20}}\\ \mathrm{⋮}& & \mathrm{⋮}& \mathrm{⋮}& & \mathrm{⋮}\\ {\mathrm{tl}}_{s_{\mathrm{1}},t_n-\mathrm{20}}& \mathrm{\dots }& {\mathrm{tl}}_{s_{\mathrm{1}},t_n+\mathrm{20}}& {\mathrm{tl}}_{s_{\mathrm{2}},t_n-\mathrm{20}}& \mathrm{\dots }& {\mathrm{tl}}_{s_{\mathrm{2}},t_n+\mathrm{20}}\end{array}\right]\end{array}$$

We experimented with longer windows but could not find any improvements by increasing the window size beyond 40 time steps. There was also an improvement as a result of using both sub-links rather than one. This improvement could be because using two sub-links includes more information, which could help the MLP filter out noise.

As pre-processing, we subtracted the 12 h centred rolling median from the signal level for each CML. This removes longer trends from the signal level, making the time series stationary. We experimented with other detrending methods such as differencing but got poorer results.

Next, two approaches were explored, one where we trained the neural network against radar data (MLP_RA) and one where we trained the MLP against rain gauge data (MLP_GA). It must be noted that both references observe rainfall at different locations and different spatio-temporal aggregates as compared to the CML. In particular, the rain gauges observe time-aggregated point rainfall, whereas the CML observes instantaneous path-averaged rainfall. Thus, the references are just an approximation of the rainfall observed by the CML.

For testing, the optimal MLP_RA and MLP_GA were integrated into pycomlink, a Python library for CML processing (Chwala et al., 2024). Since the current pycomlink environment does not support sklearn, the weights and network architecture were exported to tensorflow using the Keras application programming interface (API) (Abadi et al., 2015). The final testing was performed by loading the exported MLPs from the pycomlink environment.

2.3 Reference methods

Two reference methods were used for comparing the MLP results from the σ₈₀ method of Graf et al. (2020) and from the CNN method of Polz et al. (2020). We note that, similarly to our MLP, the CNN method is also trained to use two sub-links, whereas the σ₈₀ method just uses one. Both methods are described in the Introduction and can be run from pycomlink.

2.4 Performance metrics

The performance of the methods was evaluated by recording the classified CML rainy and dry periods against the reference data (rain gauge or radar) in a confusion matrix. In our case, the confusion matrix is a 2×2 matrix listing the number of true positives (TPs), true negatives (TNs), false positives (FPs), and false negatives (FNs). Although no perfect performance metric exists, a balanced way of describing the confusion matrix as a single number can be done using the Matthews correlation coefficient (MCC) (Chicco and Jurman, 2020). The MCC is a diagnostic that gives a number between −1 and 1, where 1 represents a perfect classification, 0 is no better than a random guess, and −1 is a perfect disagreement with the reference.

2.5 Train–test split

In order to assess how well the models performed, the CML data were split into a training set and a test set. Due to, for instance, noisy CMLs, malfunctioning rain gauges, or spatio-temporal uncertainties, some CMLs showed a poor correlation with the rain gauges or the radar. As these pairs could result in poor training data, we opted to exclusively include pairs with high MCCs in our training set. We selected training pairs for MLP_RA and MLP_GA by estimating the CML rainy periods using the σ₈₀ method. The top 26 CML–radar pairs with the highest MCCs, evaluated using radar data as the ground truth, were chosen for MLP_RA. MLP_GA used the 26 CML–rain gauge pairs with the highest MCCs, evaluated using rain gauge data as the ground truth. As some of the CMLs share the same neighbouring rain gauge, simply selecting the pairs with the highest MCCs could make the training data too focused on very similar rainfall events. Thus, to ensure diversity in the training data, the training data used only unique rain gauges. The remaining 843 pairs were used for testing. A possible drawback of this approach is that the MLPs are not trained on noisy CMLs, hindering their effectiveness in dealing with erratic signal fluctuations. However, erratic CMLs are usually removed before the rain event detection step, for instance, by removing CMLs where the rolling standard deviation of the total loss exceeds 2 dB at least 10 % of the time or where the 1 h rolling standard deviation of the of the total loss exceeds 0.8 dB at least 33 % of the time (Graf et al., 2020; Blettner et al., 2023).

2.6 Hyperparameter estimation and cross-validation

During training, the MLP classifier can be tuned using several hyperparameters such as activation function, hidden layers, initial learning rate, and L2 regularisation. The optimal hyperparameters were found by using k-fold cross-validation over a grid search over the hyperparameter values listed in Table 1. We performed k-fold cross-validation by splitting the CMLs in the training data into five folds and iteratively trained the MLP on four folds of data and validated on the fifth fold using the MCC. The final score is the mean of all five validation MCC scores.

Table 1 MLP hyperparameters used in grid search.

The rainfall time series is characterised by extended periods of no rain, leading to an imbalance that can impede the effectiveness of neural network training. A common method to address this issue is random undersampling, where samples from the majority class are discarded to create a balanced dataset (Hoens and Chawla, 2013). However, rainfall time series often include short intermittent dry periods within longer events, which are of particular interest in our approach. If we were to use random undersampling, these events might be underrepresented in the training dataset. Recognising that the total signal loss moving window can include rainy time steps during dry periods close to rainy ones, we have adopted a modified undersampling strategy. Specifically, we only discard dry steps more than 30 min away from any rainfall events as detected by the reference methods.

3 Results and discussion

3.1 Training the MLP

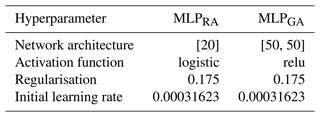
The performances (MCC) of MLP_RA and MLP_GA for the training and test datasets as a function of the increased number of neurons and hidden-layer sizes are shown in Fig. 1. For each hidden-layer configuration, the optimal regularisation and initial learning rate that yielded the highest mean MCC were selected and plotted together with the minimum and maximum of all five folds obtained from k-fold cross-validation.

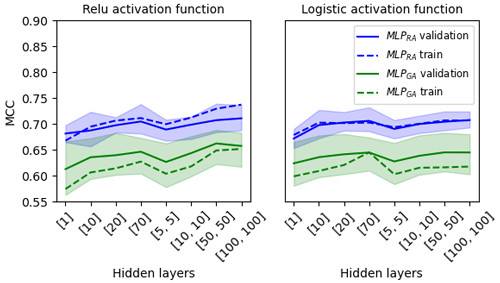
Figure 1 MCC as a function of network architecture for the relu and logistic activation function; [5, 5] means two layers with five neurons in each layer. The MLP was trained using k-fold cross-validation with five folds over 26 CML–rain gauge pairs using radar (MLP_RA) and rain gauge (MLP_GA) data as the reference. The solid line is the mean value of the five folds, while the shaded area shows the minimum and maximum score of the five folds.

We can observe that the MLP_GA generally has a lower score than the MLP_RA method. This could be because the rain gauges can be located up to 5 km away from the CMLs, causing errors related to spatial variability. For the radar data, this issue with spatial representation is most likely to be mitigated by the comparison based on CML path-weighted intersections. Another reason could be that the spatial averaging performed by the radar and CMLs produces less intermittent rainfall time series than what is the case for the rain gauges, resulting in better agreement between the CML and radar.

The relu activation function has a lower score for simple network architectures (for instance, [1]) but produces larger scores with increased network architecture compared to the logistic activation function. Further, for the relu activation function with larger networks ([70] and [100, 100]), MLP_RA shows a larger deviation between the training set and the validation set, indicating that the model is not generalising very well. MLP_RA has a smaller deviation between training and validation when the logistic activation function is used, indicating more general fits. Thus, MLP_RA seems to have a good compromise between model complexity and score when using a single layer with 20 neurons and the logistic activation function. MLP_GA, on the other hand, has a smaller deviation between the training and validation set and provides a good compromise between model complexity and score when using two layers with 50 neurons in each and the relu activation function. The optimal hyperparameters for MLP_RA and MLP_GA are shown in Table 2.

Table 2 Optimal hyperparameters for the MLP trained with the radar reference (MLP_RA) and the MLP trained with the rain gauge reference (MLP_GA).

3.2 Testing the MLP

The MCC scatter plot density for the MLP_RG and MLP_RA method compared with the benchmark methods σ₈₀ and CNN using the radar and rain gauge test data as the reference is presented in Fig. 2.

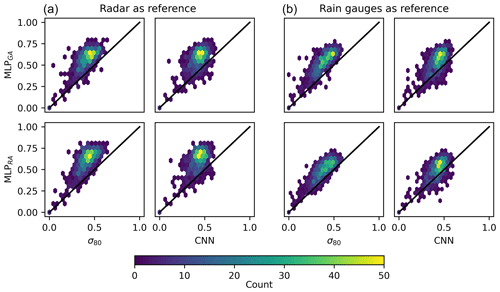
Figure 2 Scatter density plot of the MCC score for the MLP trained on the rain gauge reference (MLP_GA) and the MLP trained on the radar reference (MLP_RA) compared with the benchmark methods σ₈₀ and CNN. Panel (a) used the radar as the reference, and panel (b) used the rain gauges as the reference. CML, radar, and rain gauge data use a 1 min resolution. Scores were computed based on the test dataset.

For both radar and rain gauge references, we can observe that, for most data pairs, the MCC score is higher when using one of the MLP methods than when using one of the reference methods. Another observation is that MLP_GA performed slightly better (median MCC of 0.57) than MLP_RA (median MCC of 0.52) when the rain gauge was used as a reference. When the radar was used as a reference, MLP_RA scored slightly better (median MCC of 0.64) than MLP_GA (median MCC of 0.60). This difference could be explained by the inherent differences in the measurement methods, where the rain gauge captures the rainfall differently compared to the weather radar due to, for instance, wind.

3.3 CML time series

To illustrate how the MLPs perform in comparison to the CNN and σ₈₀ method, we have selected two events where the MLPs outperform the reference methods (Figs. 3 and 4) and one event where the MLP performs less well (Fig. 5). The figures show the CML signal loss as a function of time, as well as the estimated rainy periods for all methods and the ground truth. We also plot the confusion matrix and the corresponding MCC score for each method using the rain gauge as a reference.

Figure 3 (a) CML signal loss (TL) for a 10 h long interval for the CNN, σ₈₀, MLP_RA, and MLP_GA methods. The reference rainy periods for the rain gauge (RG) and gauge-adjusted radar (RA) were also plotted. The blue-shaded area marks the rainy periods, and the white marks the dry periods. (b) Confusion matrix and its corresponding MCC score for the 10 h period using the CNN, σ₈₀, MLP_RA, and MLP_GA methods with the rain gauge as a reference.

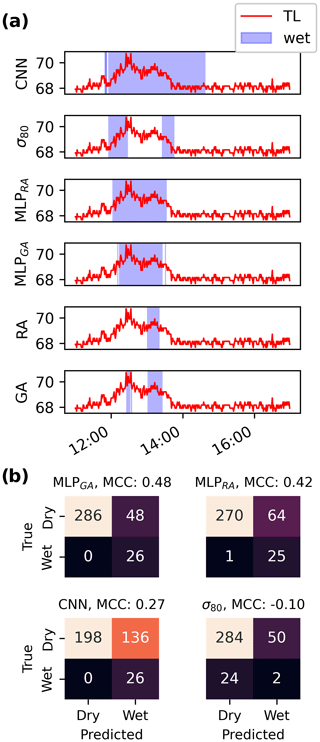
Figure 4 (a) CML signal loss (TL) for a 6 h long interval for the CNN, σ₈₀, MLP_RA, and MLP_GA methods. The reference rainy periods for the rain gauge (RG) and gauge-adjusted radar (RA) were also plotted. The blue-shaded area marks the rainy periods, and the white marks the dry periods. (b) Confusion matrix and its corresponding MCC score for the 6 h period using the CNN, σ₈₀, MLP_RA, and MLP_GA methods with the rain gauge as a reference.

Figure 3 shows the results from a 10 h long period for a CML where the MLP_RA method (MCC: 0.73) and MLP_GA method (MCC: 0.76) outperformed the CNN method (MCC: 0.08) and the σ₈₀ (MCC: 0.47). Looking at the CML total loss (TL), we can observe that the CML has a relatively constant baseline outside the rainy time steps. Around 06:00 UTC, the radar reference (RA) shows a short rainy period, while the rain gauge shows a longer highly intermittent rainy period. The intermittent behaviour of the rain gauge might be due to low-intensity rainfall or smaller droplets falling into the scale from the collector. MLP_GA was able to detect a short rainy period at this time, whereas MLP_RA did not. For the full 10 h, the CNN generally estimates a very long rainy period, missing several dry events and leading to a poorer MCC. This is not surprising as it was trained to detect rainy periods on an hourly basis. The σ₈₀ method was better in classifying the dry events but still estimated longer rainy periods than the MLPs. Further, MLP_RA tended to estimate rainy periods that started shortly before the CML TL started to rise, while the MLP_GA tended to estimate rainy periods shortly after the TL had started to rise; see, for instance, time step 01:00. This is an interesting feature and could be due to the rain gauges showing short breaks at the beginning of rainfall events due to low rainfall intensity. If the beginning of a rainy event has more dry minutes than rainy minutes, as seen by the rain gauge, this could lead MLP_GA to just estimate no rain on these occasions. This could also be caused by the radar observing rainfall before it is measured on the ground, making the MLP_RA estimate rainfall shortly before MLP_GA.

Figure 4 shows a 6 h case for a different CML. Like in Fig. 3, MLP_RA estimates a rainy period starting at 12:00, shortly before MLP_GA estimates a wet period. As in the previous case, the CNN estimates a very long rainy period, while the σ₈₀ estimates rain before and after the rain gauge and radar reference rainfall estimates. In this case, none of the CML rainfall detection methods can accurately estimate the radar or rain gauge reference rainy periods. Looking at the TL, we can see that it increases gradually over an extended period, suggesting a longer rainy period. In contrast, the reference data only indicate one or two short rainy events. This discrepancy may be attributed to very low rainfall rates, causing an elevated TL due to CML wet-antenna attenuation.

Figures 3 and 4 also raise some interesting questions. The final rainfall amount is often derived from a baseline that is typically estimated based on the values of the dry periods before the rainfall event. Since these baseline values are estimated differently for the different methods we have explored in this study, the resulting rainfall rates are expected to vary. For instance, if the MLP_GA is used, the baseline would be placed at a higher level than if the MLP_RA method was used, resulting in a lower rainfall rate estimate. Looking at Fig. 3 and the first and last rainfall events detected by MLP_GA (time steps 01:00 and 08:00), it is clear that MLP_GA estimates rainfall shortly after the TL has started to rise.

In Fig. 5 we have depicted the TL, as well as the estimated rainy periods and reference rainy periods, for a CML with more erratic signal fluctuations. For σ₈₀, multiple rainy periods are estimated. While these estimated rainy periods may seem plausible when observing the TL, the reference data reveal that there is no actual rainfall during this time. Therefore, the rainfall estimates likely stem from a noisy CML signal.

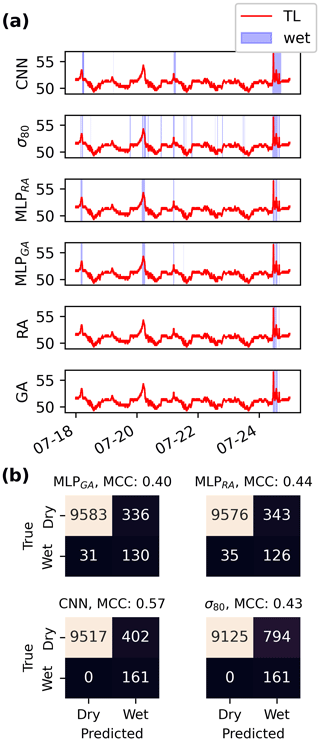
Figure 5 (a) CML signal loss (TL) for a 6 d long interval for the CNN, σ₈₀, MLP_RA, and MLP_GA methods. The reference rainy periods for the rain gauge (RG) and gauge-adjusted radar (RA) were also plotted. The blue-shaded area marks the rainy periods, and the white marks the dry periods. (b) Confusion matrix and its corresponding MCC score for the 6 d period using the CNN, σ₈₀, MLP_RA, and MLP_GA methods with the rain gauge as a reference.

3.4 General discussion

Our MLPs were trained using CML, weather radar, and rain gauge data from 26 CML–rain gauge pairs over 1 month. The trained MLPs were then tested on 843 CML–rain gauge pairs that were kept out of the training process. A possible limitation of our approach is that 1 single month might not adequately represent the different rainfall types associated with other months or different geographical locations. On the other hand, since our dataset covers the whole of Germany, the dataset contains widely different precipitation events. For instance, in addition to several smaller events, the dataset also captures the large precipitation event that happened in Germany between 13 and 15 July 2021. Moreover, to ensure convergence of the MLPs, the training data used only 26 CML–rain gauge pairs. Including more pairs, however, did not improve the results of the validation dataset, indicating that, in fact, the MLPs generalise to several different events.

Our results indicate that MLP_RA provides rainfall estimates that are more continuous and more consistent over time compared to the more intermittent estimates generated by MLP_GA (see, for instance, Fig. 3, time step 06:00). This could come from the fact that the rain gauges have a 1 min resolution, while the weather radar has a 5 min resolution, making the radar rainy periods more continuous. Another explanation could be that, at low rainfall rates, the rain gauge will not record any rainfall before the droplets have been transported to the scale, making the period seem more intermittent than it actually is. Further, while the rain gauges measure point rainfall close to the CML, the weather radar measures average rainfall along the CML. This path averaging blurs the rainy periods, making the rainy period more continuous, with fewer intermittent breaks. An interesting finding is that, even though the rain gauges do not represent the average rainfall along the CML, MLP_GA is able to capture more of the underlying intermittency as compared to MLP_RA. This is also reflected in the neural network configuration where the MLP_GA benefits from a more complex network architecture as compared to MLP_RA.

Both MLPs were trained using the 26 CML–reference pairs that showed the highest MCC estimated using the σ₈₀ method. This can be thought of as a pre-processing step, where the goal was to ensure training data with a good match between the reference and the CML. In our case, this was important for making the MLPs converge to approximately the same weights every time we trained the model. Since they, by selection, have a good correlation with their reference, these particular pairs might also contain little or no noise. Thus, the MLP training datasets might lack exposure to noisy CML time series, and, as a consequence, the MLPs might not handle noisy periods very well. On the other hand, from Fig. 2, we know that the MLPs still outperform the σ₈₀ and CNN method based on the 843 CMLs used in the test dataset, which was not subject to any noise filtering, suggesting that the MLPs can handle noise, at least to some extent. Moreover, very noisy CMLs are typically handled using pre-processing methods such as filtering out CMLs with strong diurnal cycles or plateaus, such as what is done in Graf et al. (2020) and Blettner et al. (2023).

Overall, it must be noted that, while the MCC is a useful and balanced metric, its score must be seen in relation to the reference chosen for evaluation. As weather radar provide average rainfall intensities for the entire radar grid cell, we expect that the radar rainfall estimates are less intermittent than what is observed by a rain gauge. This is supported by the findings in Fig. 3, where the weather radar rainfall events are less intermittent than what is the case for the rain gauges. The CML, like the weather radar, also measures spatially averaged rainfall. However, the CML measures rainfall closer to the ground and thus might be able to better capture the intermittency as seen by the rain gauge. In this study, MLP_GA was able to better detect rainfall events seen by the rain gauge than MLP_RA. This suggests that there is no single best reference or method for evaluating CML rainy periods. Rather, the CML rain event detection method must be seen in relation to its application.

4 Conclusions

In this technical note, we introduced two simple feedforward neural networks (MLPs) trained to detect rainy time steps in signal attenuation data from commercial microwave links (CMLs). The MLPs are trained and tested using reference data from rain gauges (MLP_GA) with a temporal resolution of 1 min and from gauge-adjusted radar (MLP_RA) with a temporal resolution of 5 min. Whereas existing methods tend to estimate longer continuous rainy periods, the MLPs estimate shorter rainy periods that more closely resemble the intermittent rainfall patterns that are observed by the rain gauges and weather radar. The performance of the MLPs is evaluated by comparing the MLP estimates with estimates produced by two existing methods using the Matthews correlation coefficient. Our results show that the MLPs outperform existing methods in almost all cases.

Interestingly, even if the rain gauges do not resemble the path-averaged rainfall as observed by the CML, MLP_GA was still able to learn the rainfall pattern in the CML time series. Moreover, MLP_GA better estimates rainy periods as recorded at the nearby rain gauges than what is the case for MLP_RA, while both methods perform equally well when radar data are used as the reference.

While MLP_RA tends to estimate rainy periods shortly before MLP_GA, both MLPs tend to estimate rainy periods after the CML total loss has started to increase. Thus, if the MLPs are used for baseline estimation, the user should consider using dry time steps at least 5 min away from the identified rainy time step for baseline estimation, similarly to Pastorek et al. (2022). Another possibility is to use the median value of a longer period before the rainy period.

Future work may involve further refining the model architecture and testing its robustness in terms of generalisation to other datasets. Another interesting topic could be to better understand how different wet and dry classifications affect the resulting baselines and the effect this has on rainfall rate estimation from CML data. Overall, MLP_RA and MLP_GA showed successful skill in the challenge of rainfall event detection in CML attenuation time series.