Experimental investigation of the interplay between transverse mixing and pH reaction in porous media

pH-induced reactive transport in porous environments is a critical factor in Earth sciences, influencing a range of natural and anthropogenic processes, such as mineral dissolution and precipitation, adsorption and desorption, microbial reactions, and redox transformations. These processes, pivotal to carbon capture and storage (CCS) applications to groundwater remediation, are determined by pH transport. However, the uncertainty in these macroscopic processes’ stems from pore-scale heterogeneities and the high diffusion value of the ions and protons forming the pH range. While practical for field-scale applications, traditional macroscopic models often fail to accurately predict experimental and field results in reactive systems due to their inability to capture the details of the pore-scale pH range. This study investigates the interplay between transverse mixing and pH-driven reactions in porous media. It focuses on how porous structure and flow rate affect mixing and chemical reaction dynamics. Utilizing confocal microscopy, the research visualizes fluorescently labeled fluids, revealing variations in mixing patterns from diffusive in homogeneous to shear-driven in heterogeneous media. However, pH-driven reactions show a different pattern, with a faster reaction rate, suggesting quicker pH equilibration between co-flowing fluids than predicted by transverse dispersion or diffusion. The study highlights the unique characteristics of pH change in water, which significantly influences reactive transport in porous media.

1 Introduction

The distribution of most chemical species in a porous environment is generally determined by both transport and biogeochemical reactions, as described by the term reactive transport (Holzbecher, 2005; Carrera et al., 2022). Reactive transport is involved in diverse processes occurring either naturally or anthropogenically, such as mineral dissolution and precipitation (Steefel and MacQuarrie, 1996; Noiriel and Soulaine, 2021; Stolze et al., 2022; Goldberg-Yehuda et al., 2022), adsorption and desorption (Carrillo‐González et al., 2006; Nützmann et al., 2005), microbial reactions (Stocks-Fischer et al., 1999; Thullner et al., 2005), and redox transformations (Thullner et al., 2005; Sposito, 2008). Reactive transport in porous media can be described with either pore-scale or Darcy-scale (macroscopic) models. Although pore-scale simulations have a solid physical foundation, they require knowledge of pore size distribution, geometry, tortuosity, and connectivity. These are seldom available and are impractical as predictive tools at scales that are orders of magnitude larger than the pore scale. Therefore, macroscopic models have developed to overcome these limitations (Battiato and Tartakovsky, 2011; Valocchi et al., 2019; Ghaderi Zefreh et al., 2019). Macroscopic representation is based on upscaling the porous medium by averaging it over space and timescales in a representative elementary volume (REV), which allows for the replacement of a solid-liquid domain with an equivalent continuum (Chiogna and Bellin, 2013). For the reaction to occur, both reactants must be in the vicinity of each other, and the process enabling them to ultimately react is the mixing, which is scale-dependent (Alhashmi et al., 2015; Acharya et al., 2007; Guadagnini et al., 2009; Dentz et al., 2011; Al-Khulaifi et al., 2017; Geurts, 2021). However, the pore-scale mixing impacts the larger-scale reactive transport behavior (Datta et al., 2013; Browne and Datta, 2023). Due to this mixing multiscale nature, there is still a lack of understanding of the integration between coupled transport and reactions at multiple scales of the porous medium, which poses a challenge in predicting mixing-driven reactions (Edery et al., 2015; Tartakovsky et al., 2009; Borgman et al., 2023). Thus, it is necessary to measure both mixing and reaction at the pore scale regarding pore properties. It is particularly essential to understand how mixing patterns at the pore scale affect pH-driven chemical reactions as these reactions are ubiquitous in porous media, such as soils and aquifers (Lai et al., 2015). Examples of such reactions are dissolution and precipitation of soil carbonates and sulfates (Sposito, 2008), nitrification and denitrification processes (Ward et al., 2011; Edery et al., 2011, 2021; Shavelzon and Edery, 2024), and protonation and deprotonation of carboxyl and phenolic groups in soil organic matter (Sparks et al., 2024). Soil pH has an enormous influence on soil biogeochemical processes as it influences the solubility of plant nutrients, phytotoxic elements, and pollutants and determines their biological availability and mobility (Penn and Camberato, 2019; Neina, 2019; Dehkharghani et al., 2019). Specifically for pH reactions, experimental data with a high Péclet value for transverse reaction are in good agreement with the advection–dispersion–reaction equation (ADRE), which uses a single diffusion coefficient for all species in a multispecies reactive system (Loyaux-Lawniczak et al., 2012), especially in stirred flow-cell reactors (Liu et al., 2011). Considering the coupling between mixing and reactive transport processes and how both scale with the heterogeneity, specifically in the context of pH reactions in heterogeneous soil, a set of experiments is proposed to observe if, indeed, the same coupling between mixing and reaction occurs for pH spread and reactions. These experiments focus on investigating how porous medium layouts ranging from homogeneous to heterogeneous affect pH-driven reactions by examining the pattern of transverse dispersion of co-flowing fluids for both mixing and pH. This is done by tracking the mixing and pH spread for two Péclet values using fluorescently labeled fluids imaged by a confocal microscope. The mixing experiments showed that transverse mixing varies from diffusive mixing in the homogeneous case to shear-driven mixing in the heterogeneous case. However, the pH measured in the pH experiments does not follow the pH value calculated from the mixing pattern. Instead, it shows a larger spread, suggesting that the co-flowing fluids' pH difference equilibrates faster than the mixing. We identify the proton transfer mechanism, which is comparatively faster than the transverse dispersion or diffusion, as the dominant mechanism, especially for a lower Péclet number. Pore-scale simulations agreed well with the mixing experiments and provided reasonable results for the pH experiments after considering the enhanced diffusion due to the proton transfer mechanism.

2 Methods

To investigate how the porous structure and flow rate influence the mixing and chemical reaction, three sets of experiments are employed to visualize the mixing and reaction in a porous medium. The first set is mixing experiments, where a conservative tracer is used to test the effect of different pore size variations (heterogeneities) with different flow rates on the local mixing dynamics. In the second set, a reactive experiment is employed under the same conditions as the conservative experiments, where the pH reactant is uniformly distributed at the flow cell and only the pH is unevenly distributed. And in the third set, both the pH and pH reactant are unevenly distributed in the cell to examine the effect of mixing on neutralization reaction dynamics, resulting in pH change, under the same conditions.

2.1 Experimental setup

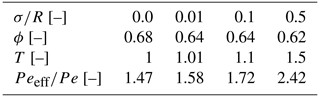
All sets of experiments, shown in Fig. 1a–c, were performed in a polydimethylsiloxane (PDMS) microfluidic flow cell, ∼ 4.5 mm × 1.3 mm × 0.05 mm in size. Each cell was composed of ∼ 300 cylindrical pillars (R= 50 µm), so the internal porosity of the cell was 60 %–70 % (see Table 1). The tracer moved only in the pore space among the pillars, which were set in four different arrangements within the cell to achieve four different levels of heterogeneity: from completely homogeneous, where the pillars' centers were set on a perfect lattice grid, with a normalized standard deviation of $\mathit{\sigma }/R=\mathrm{0}$ to the most heterogeneous arrangement, where the pillars centers were randomly moved in the x and y direction following a Gaussian distribution, with a normalized standard deviation of $\mathit{\sigma }/R=\mathrm{0.5}$ (see Fig. 1d).

Table 1 The porosity, tortuosity, and effective Péclet ratio for each heterogeneity.

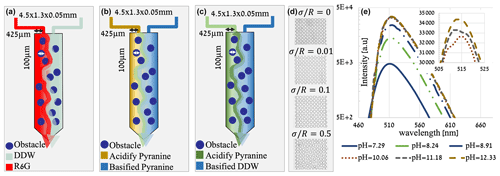
Figure 1 (a) An illustration of the mixing experiment setup. (b) An illustration of the reactive experiment setup (pH gradient only). (c) An illustration of the combined experiment setup (pyranine concentration gradient and pH gradient). (d) Four different pore size variations (heterogeneities) of the flow cell, from the homogeneous one ($\mathit{\sigma }/R=\mathrm{0}$) to the most heterogeneous ($\mathit{\sigma }/R=\mathrm{0.5}$). (e) Intensity of pyranine emission on a logarithmic scale versus wavelength for various pH values as measured by UV–vis and verified under the confocal. The inset is a blowup on a linear scale to present the relevant separation of the pH and intensity.

Each cell had two parallel inlets (right and left), each of them set at 425 µm from the edge of the cell, and one funnel-shaped outlet. At the two outlets, a syringe pump (Chemyx Fusion 200 two-channel model) with a small-diameter glass syringe (100 µL Hamilton glass syringe) allowed for a continuous movement of the motor and the piston with no oscillations for the applied fluxes (100 and 10 µL h⁻¹ flow rate, resulting in a Darcy velocity of v_d=0.142 and 0.0142 cm s⁻¹, respectively). These two velocities provided two Péclet numbers (Pe) as depicted by the following equation:

$$\begin{array}{}\text{(1)}& Pe={\displaystyle \frac{v_{\mathrm{d}}R}{D}}.\end{array}$$

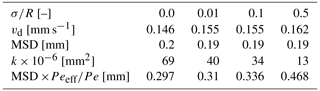
The Péclet number is a measure of the velocity magnitude (v_d) and the diffusion (D), which is an intrinsic property of the fluids over the mean pore size (R) (Bossis and Brady, 1987). While the mean pore size remains the same for all heterogeneity, there are small porosity (ϕ) variations (see Table 1 for details). However, the main heterogeneity effect is on the interface between the co-flowing fluids, forming a torturous path. To address this, we define an effective diffusion coefficient $D_{\mathrm{eff}}=\frac{D\mathit{\varphi }}{T}$, which scales the diffusion of the reactants in water as shown in many studies (Ray et al., 2018; Fogler, 2011; Guo et al., 2022; Kim et al., 1987; Quintard, 1993; Quintard and Whitaker, 1993; Beyhaghi and Pillai, 2011). The tortuosity can be directly calculated from the normalized standard deviation $\mathit{\sigma }/R$, which marks the range for the pillar center movement from a uniform grid using the relation $T=\mathrm{1}+\mathit{\sigma }/R$ (as shown in Eliyahu-Yakir et al., 2024) and leading to the effective Pe of

$$\begin{array}{}\text{(2)}& P{e}_{\mathrm{eff}}={\displaystyle \frac{v_{\mathrm{d}}RT}{D\mathit{\varphi }}}\end{array}$$

and scaling the Péclet number as depicted in Table 1.

The fluorescent conservative tracer used for the mixing experiments (Fig. 1a) is rhodamine 6G (R6G), which is widely used to visualize flow patterns, such as in the domain of environmental hydraulics (Barzan and Hajiesmaeilbaigi, 2018). Pyranine (8-hydroxypyrene-1,3,6-trisulfonate) is used for the reactive and combined experiments (Fig. 1b–c) as the pH reactant as its fluorescent emission spectra and intensity are highly dependent on medium pH (Avnir and Barenholz, 2005), therefore suitable for monitoring pH changes. Double-distilled water (DDW) purified by Milli-Q, with ≈18 MΩ cm⁻¹ at a lab temperature of 25 °C, is used in both the R6G and the reactive experiments. The R6G’s concentrations were 2 mg per 50 mL DDW (corresponding to 0.083 mM) and 9 mg per 50 mL DDW for the pyranine (corresponding to 0.347 mM). These concentrations had no measurable effect on the fluid viscosity and density in this experimental setup.

All the experiments' pH values used for the reactive experiments were 7.3 and 12.3, resulting in higher and lower emission intensities, respectively. As such, they are related to their respected tracer and background solution. To achieve the wanted pH, we added a strong acid or a strong base (hydrochloric acid and sodium hydroxide, respectively) to the pyranine aqueous solutions. When HCl is added, it ionizes to form the hydronium ion:

$$\begin{array}{}\text{(3)}& {\mathrm{HCl}}_{\left(\mathrm{aq}\right)}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\leftrightarrow {\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}_{\left(\mathrm{aq}\right)}^{+}+{\mathrm{Cl}}_{\left(\mathrm{aq}\right)}^{-}.\end{array}$$

When NaOH is added, it ionizes to form the hydroxide ion:

$$\begin{array}{}\text{(4)}& {\mathrm{NaOH}}_{\left(\mathrm{aq}\right)}\leftrightarrow {\mathrm{Na}}_{\left(\mathrm{aq}\right)}^{+}+{\mathrm{OH}}_{\left(\mathrm{aq}\right)}^{-}.\end{array}$$

When set together, the hydronium and hydroxide ions react to form water in a neutralization reaction:

$$\begin{array}{}\text{(5)}& {\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}_{\left(\mathrm{aq}\right)}^{+}+{\mathrm{OH}}_{\left(\mathrm{aq}\right)}^{-}\leftrightarrow \mathrm{2}{\mathrm{H}}_{\mathrm{2}}\mathrm{O},\end{array}$$

while the pyranine (ROH_(aq)) reaction is mainly with ${\mathrm{OH}}_{\left(\mathrm{aq}\right)}^{-}$ as the reactive experiment is performed under basic pH.

$$\begin{array}{}\text{(6)}& {\mathrm{ROH}}_{\left(\mathrm{aq}\right)}+{\mathrm{OH}}_{\left(\mathrm{aq}\right)}^{-}\leftrightarrow {\mathrm{RO}}_{\left(\mathrm{aq}\right)}^{-}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\end{array}$$

And, therefore, the intensity is mainly decreasing with the pH change (Fig. 1e).

To perform the mixing and reactive experiments, we saturate the flow cell with the background solution, i.e., DDW for the mixing experiments, and pyranine solution at a pH of 12.3 (which will be regarded as basified pyranine from here on) for the reactive experiments. Subsequently, a 100 µL glass syringe filled with the R6G or pyranine at a pH of 7.3 (which will be regarded as acidified pyranine from here on) is connected directly to the left inlet to reduce the experimental time until the R6G/acidified pyranine reaches the cell and forms an interface with the DDW/basified pyranine.

A picture of the cell filled with the background solution is taken before the insertion of the R6G/acidified pyranine, providing a base image for the image analysis calibration. Thereafter, both 100 µL syringes with the R6G/acidified pyranine and DDW/basified pyranine are placed in the same syringe pump with a pre-defined flow rate. This way, the DDW/basified pyranine flowed from the right inlet, and the R6G/acidified pyranine from the left inlet had the same flow rate while interfacing roughly in the middle of the cell.

Changes in color intensity of the R6G occurred due to mixing (or dilution) with the DDW, while for the acidified pyranine, the intensity change is due to a pH change followed by the neutralization reaction. Finally, the cell is saturated manually with the R6G/acidified pyranine for mixing/reactive experiments from both inlets to produce a high-intensity final image with a known concentration for the image analysis calibration. The third set of experiments combines both the concentration gradient and the pH gradient using DDW at a pH of 12.3 as the background solution (which will be regarded as basified DDW from here on) and acidified pyranine as the reactive tracer. pH values were achieved using NaOH and HCl, similarly to the reactive experiments. The combined experiments are made in the same process mentioned above but only within the completely homogeneous medium and the most heterogeneous one to present the effect of simultaneous migration of pyranine and pH.

2.2 Imaging setup

For both the R6G and the reactive experiments, a confocal microscope (Nikon Eclipse Ti2-FP) was used to visualize the intensity change due to the mixing and reaction within the flow cell. The R6G is excited by a 546 nm laser and tracked with the emission wavelength of 600 nm, while the pyranine is excited by a 405 nm laser and tracked with the emission wavelength of 550 nm. All experimental images taken by the confocal are taken by a Prime BSI camera with a 95 % quantum efficiency and 1e⁻ median noise and an exposure time of 500 ms, bit depth of 16 bits and magnification of ×2.

For the 100 µL h⁻¹ flow rate, a series of 50 pictures were taken 5 min after forming a stable interface between the fluids. Then, after an additional 5 min of delay, another series of 50 pictures is taken under the same conditions. The two series of images are compared to verify the stability of the interface. For the 10 µL h⁻¹ flow rate, the same imaging sequence was performed, with an initial time of 10 min and a subsequent delay time of 10 min. For both flow rates, i.e., each pixel intensity (marked as I_ij for location ij) at each 50-picture sequence, the variance of intensity per pixel did not exceed the 0.1 % white noise of the camera. To verify that the interface among image sequences is stable, the criteria were set so that the difference between the initial and later imaging sequence that exceeded the 0.1 % (white noise of the camera) was averaged in absolute terms, and the stability of the interface was established if the average difference was isotropic and smaller than 1 % (namely, $〈\frac{\left|I_{ij}\right(t=\mathrm{5})-I_{ij}(t=\mathrm{10}\left)\right|}{\left|I_{ij}\right(t=\mathrm{10}\left)\right|}>\mathrm{0.1}\mathit{\%}〉<\mathrm{1}\mathit{\%}$); a similar analysis was performed around the interface to verify that the 1 % difference is not the outcome of the bulk behavior. A MATLAB image processing program is developed to convert the image intensity received in the mixing experiments to normalized R6G concentration. Similarly, a program is developed to convert the image intensity received in the reactive experiments to its pH values. As such, this intensity analysis, which provides both the error bounds and the repeatability of the layout, is done for both the R6G and the pH experiment.

2.2.1 Imaging the mixing experiments

Conversion of image intensity to normalized R6G concentration is based on the Beer–Lambert law, dictating a linear relationship between the concentration and the absorbance of the solution (Barzan and Hajiesmaeilbaigi, 2018). The maximum and minimum intensity images are set to establish the scale between the maximum and minimum R6G concentration. The difference between each intermediate intensity and the minimal intensity is normalized to the difference between maximum and minimum intensities, yielding a unitless number between 0 to 1, i.e., the normalized R6G concentration:

$$\begin{array}{}\text{(7)}& C_{ij}={\displaystyle \frac{I_{ij}-I_{ij}\left(\min \right)}{I_{ij}\left(\max \right)-I_{ij}\left(\min \right)}}[-].\end{array}$$

Recall that I_ij is the image intensity at pixel ij, I_ij(min) is the intensity of the background solution image (DDW with no R6G), and I_ij(max) is the intensity of the R6G itself (DDW saturated with R6G) image. The validity of the method was verified for our setup as well as in other studies (Eliyahu-Yakir et al., 2024; Barzan and Hajiesmaeilbaigi, 2018).

The change in local normalized concentration (C_ij) for the R6G and DDW mixing can be transformed to pH and compared to the acidified and basified pyranine mixing. As the pyranine emission amplitude changes withOH⁻ groups, we base the calculation of pH on OH⁻ migration. This is done by the equation below:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{\mathrm{pH}}_{\mathrm{calculated}}=& -(\mathrm{14}-\log [C_{ij}\cdot {\mathrm{10}}^{-(\mathrm{14}-\mathrm{low}\mathrm{pH})}\\ & +(\mathrm{1}-C_{ij})\cdot {\mathrm{10}}^{-(\mathrm{14}-\mathrm{high}\mathrm{pH})}\left]\right),\end{array}\end{array}$$

where low pH and high pH are the pH values of the acidified and basified pyranine solutions.

2.2.2 Imaging the reactive experiments

Unlike the R6G experiment, the intensity change in the pyranine due to the pH does not scale linearly; thus, a scheme of the process of converting raw data to pH distribution is developed for this study (shown in Fig. 2). For the conversion of image intensity to pH, it was necessary to find a correlation between the two. To create a calibration curve, samples of pyranine dissolved in DDW (0.347 mM as in the experiments) at different pH values were made using HCl and NaOH. The flow cell was manually saturated with a sample with known pH, and an image of the cell was taken. The mean intensity of each image was then calculated.

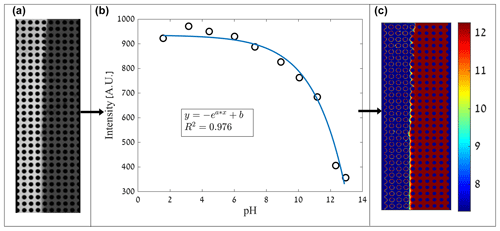
Figure 2 Scheme of the process of converting image intensity to pH distribution. (a) A raw image showing the intensity of acidified pyranine (0.347 mM) at a pH of 7.3 on the left and basified pyranine at pH of 12.3 on the right. (b) A calibration curve showing the mean intensity of pyranine (0.347 mM) at different pH values, excited at 405 nm, as measured within the flow cell. (c) An analyzed data image showing pH distribution.

The correlation between pH and mean image intensity was fitted (MATLAB Curve Fitting Toolbox application) in which a descending exponential function was set to fit the received calibration curve (R²=0.976), shown in Fig. 2b. The equation is as follows:

$$\begin{array}{}\text{(9)}& y=-e^{a\cdot x}+b,\end{array}$$

where y corresponds to the image mean intensity, x corresponds to the pH value, while a establishes the decedent rate (a=0.4977), b is the maximum intensity (b=935.7), and both are fitting parameters. This rapid exponential change in intensity due to pH marks the sensitivity of the pyranine to a narrow range of pH, which is reflected in the sharp transition between the pH values in Fig. 2c and the following experimental pH results. The consumption of OH⁻ by the pyranine will be negligible when changing the overall pH as the pyranine concentration is in equilibrium with the ions.

For the image analysis, we first fit a specific value of each of the parameters a and b in Eq. (9) to the intensity of each pixel composing the image. This is done by the two images produced at the beginning and the termination of each experiment by cell saturation with acidified/basified pyranine solution. Using image intensities of these two known pH values and Eq. (9), we find a and b for each separate experiment and for each pixel, which is subsequently used for the conversion of image intensity to pH.

2.3 COMSOL simulations

The results for both the mixing and the reactive experiments, described in Sect. 2.2 were simulated using the COMSOL multiphysics Stokes flow simulator. To that end, the AutoCAD file with the 2D design and dimensions of the flow cells was imported to the simulator with their dimensions and no-slip and no-flow boundary conditions for the pillars and walls. The inlet and outlet were defined as a Dirichlet boundary condition, corresponding to the constant flux condition imposed by the syringe pump. The simulation followed the following laminar flow equations for an incompressible fluid – namely, the continuity, mass conservation, and viscous stress, respectively:

$$\begin{array}{}\text{(10a)}& {\displaystyle }\mathit{\rho }{\displaystyle \frac{\partial \mathit{u}}{\partial t}}+\mathit{\rho }(\mathit{u}\cdot \mathrm{\nabla })\mathit{u}=\mathrm{\nabla }\cdot [-p\mathbf{I}+\mathbf{K}],\text{(10b)}& {\displaystyle }\mathit{\rho }\cdot \mathit{u}=\mathrm{0},\text{(10c)}& {\displaystyle }\mathbf{K}=\mathit{\mu }(\mathrm{\nabla }\mathit{u}+(\mathrm{\nabla }\mathit{u}{)}^T),\end{array}$$

where ρ is the fluid density; u is the velocity in vector form, aligned with and transverse (^T) to the principal flow direction; ∇p is the pressure drop over the determinant I; K is the stress tensor; and μ is the fluid viscosity. To account for the transport of the R6G and basified solution, the following transport equation is used to account for the concentration (C_n) of specific chemical species noted by n:

$$\begin{array}{}\text{(11a)}& {\displaystyle \frac{\partial c_n}{\partial t}}+\mathrm{\nabla }\cdot J_n+\mathit{u}\cdot \mathrm{\nabla }{c}_n=R_n,\text{(11b)}& {\displaystyle }{J}_n=-D_n\mathrm{\nabla }{c}_n,\end{array}$$

where J_n is the diffusive flux calculated for each chemical species by its corresponding diffusion coefficient, D_n, and the chemical retardation factor per species, R_n. The concentration, C_n, is inserted as mol M⁻³ at the inlets according to the experimental values and as a fixed boundary value.

The maximum and minimum element sizes within the adaptive mesh used for the solid boundaries in the simulation are 1070 and 49.3 µM, while the maximum and minimum element sizes for the fluid calculation are 101 and 4.5 µM for the adaptive mesh in the finite-element linearized calculation. The simulation begins with the introduction of either the R6G or the pH difference at the two inlets simultaneously and allowing the simulation to evolve up to the initial time frame in the experiment stated in Sect. 2.1 – namely, 5 and 10 min for the Darcy velocity of 1.42, and 0.142 mm s⁻¹, respectively – while the time discretization ranges between 5 and 15 s depending on the level of heterogeneity. The study state flow is achieved extremely fast within the simulation (1–2 simulated minutes), and therefore, there was no need to run it for another 5 and 10 min as in the experiment. These mesh sizes and temporal discretization were optimized to get the best results under the best stability, and simulations took about 5 min on a 10th generation Intel Core i5 computer with 16 GB of RAM. For each iteration, the concentration, velocity, and pressure were extracted, while the simulated 2D spatial distribution for the R6G and pH were compared with the experimental values using the 2D R² function in MATLAB.

3 Results and discussions

Firstly, we present the R6G experiments, showing how the heterogeneity level leads to various transverse mixing (Sect. 3.1), followed by the measured pH experiments (Sect. 3.2) and compared to the predicted pH as calculated by the measured mixing. The experimental part is concluded by the presentation of the combined experiments (Sect. 3.3). Finally, the results of the COMSOL simulations performed for the R6G and reactive experiments are presented (Sect. 3.4).

3.1 Mixing experiments

As the R6G is inserted into the left side of the flow cell with a given flow rate while the right side experiences the same flow rate with only DDW, we observe R6G migration between the sides due to the concentration gradient via diffusion and transverse dispersion. The maximum normalized R6G concentration (C_ij=1) is indeed on the left side, while the right side is at its minimum (C_ij=0), as shown in Fig. 3. However, the transition between the concentrations, representing the mixing due to diffusion and dispersion, varies according to the heterogeneity of the medium.

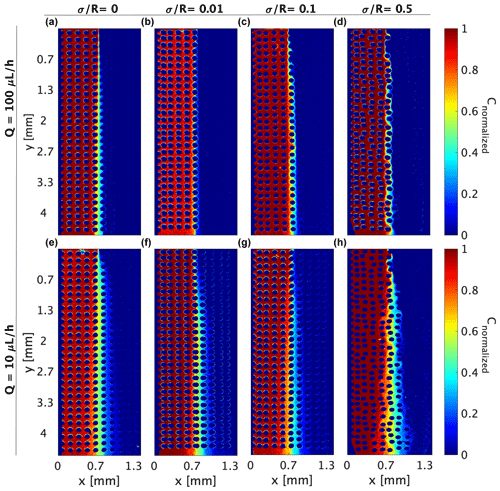
Figure 3 Mixing experiments depicting the distribution of the R6G normalized concentration for flow rate of (a–d) 100 µL h⁻¹ and (e–h) 10 µL h⁻¹ for various medium heterogeneities.

Both homogeneous and heterogeneous media show a relatively sharp interface between the R6G and the DDW near the flow-cell inlet; this interface gradually disperses down the flow as the diffusion and dispersion propagate and drive the mixing between the fluids. However, this mixing mechanism captured by the interface dispersion varies in size and character from the homogeneous medium (Fig. 3a and e) to the most heterogeneous one (Fig. 3d and h). While in the homogeneous media, mixing is symmetrical within the cell, in the heterogeneous medium, mixing is determined by the pillar's setting and moves between different pores.

This change in mixing pattern demonstrates the different mechanisms governing the mixing as affected by the variations in pore size: mixing in the homogeneous medium is controlled mainly by diffusion as shear forces effects are negligible, while in the heterogeneous medium, where pore size varies, forming tortoise route among pillars, mixing is dominated by shear forces acting on the fluid close to the obstacle’s boundaries. These forces result from the velocity gradient created due to the different pore sizes, where the smaller pores result in lower velocities and higher shear forces.

The Pe numbers calculated by Eq. (2) and presented in Table 1 are low yet still indicate that the velocity magnitude, which approximates the shear forces, has dominance over the diffusion in the pore scale, known to be critical in reactive transport (Nissan and Berkowitz, 2019). Mixing experiments results of the 10 µL h⁻¹ flow rate (Fig. 3e–h) show that in all medium heterogeneities, the interface between R6G and DDW is wider compared to the 100 µL h⁻¹ flow rate, demonstrating the increased dominance of diffusion as the flow rate descends. Comparing heterogeneities of $\mathit{\sigma }/R=\mathrm{0}$, $\mathit{\sigma }/R=\mathrm{0.01}$, and $\mathit{\sigma }/R=\mathrm{0.1}$ (Fig. 3e–g), we see the more significant effect of diffusion in the homogeneous and nearly homogeneous medium as mixing is apparent closer to the inlets. The most heterogeneous medium (Fig. 3h) also shows a more dispersive pattern that encompasses several pore lengths and points of the more dominant role of shear over diffusion.

3.2 Reactive experiments

Similarly to the mixing experiments and following the experimental procedure described in Sect. 2.2.2, we performed reactive experiments with flow rates of 100 µL h⁻¹ (Fig. 4a(a–d)) and 10 µL h⁻¹ (Fig. 4a(e–h)). The mixing experiments provide the distinction between the role of diffusion and shear forces, where the first is manifested in the homogeneous and low-velocity case and the latter is apparent in the heterogeneous and high-velocity case. However, the reactive experiments show that the pH reaction pattern does not necessarily follow the pH calculated from the normalized R6G concentration, particularly as the medium becomes more heterogeneous and the flow rate descends.

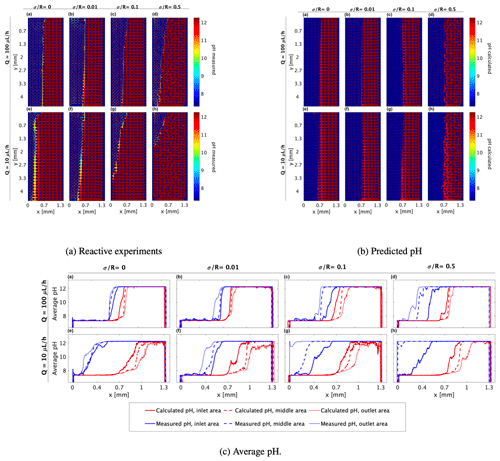
Figure 4 (a) pH values as indicated by the pyranine intensity distribution, (b) pH calculated from the normalized R6G concentration and received in the mixing experiments using Eq. (8) for (a–d) flow rate of 100 µL h⁻¹ at medium heterogeneities of $\mathit{\sigma }/R=\mathrm{0}$, $\mathit{\sigma }/R=\mathrm{0.01}$, $\mathit{\sigma }/R=\mathrm{0.1}$, and $\mathit{\sigma }/R=\mathrm{0.5}$, respectively, and (e–h) flow rate of 10 µL h⁻¹ at the marked medium heterogeneities, respectively, and (c1). The corresponding pH averaging of (a) and (b) along the x axis at three different sections of the flow cell (illustrated by the three, size-equal sections in c2): inlet area (continuous line), middle area (dashed line), and outlet area (dotted line), as calculated by the R6G concentration received in the mixing (red line) and as measured in the reaction (blue line).

Of all the tested conditions, the patterns received in the homogeneous and the slightly heterogeneous ($\mathit{\sigma }/R=\mathrm{0}$ and 0.01, respectively) media at a flow rate of 100 µL h⁻¹ in the reactive experiments (Fig. 4a(a–b)) and the pH predicted by the mixing (Fig. 4b(a–b)) are relatively similar. In these conditions, the interface is almost symmetrical within the cell although we do see a sharper gradient and a narrower interface when the reaction occurs. This sharp interface in pH value is probably due to the pyranine intensity exponential decay (Fig. 2) and the logarithmic scale at which concentration transforms to pH in Eq. (8).

Examining the reaction pattern at a flow rate of 100 µL h⁻¹ in the more heterogeneous media, i.e., $\mathit{\sigma }/R=\mathrm{0.1}$ and 0.5 (Fig. 4a(c–d)), clearly shows that the interface between the two fluids is not symmetrically distributed around the middle of the cell. Rather, it tends to migrate leftward as the flow proceeds, indicating that the reaction occurs earlier and closer to the area of the acidified pyranine (7.3). This interface migration due to the diffusive nature of OH⁻ ions from high to low concentration occurs for all medium heterogeneities and was reported in previous studies on precipitation of CaCO₃ (Katz et al., 2011; Tartakovsky et al., 2007, 2008), yet it becomes more dominant as the medium is more heterogeneous.

At a lower flow rate, sharper interfaces are received in the reactive experiments than those predicted by the mixing at all medium heterogeneities (Fig. 4a(e–h) and b(e–h), respectively). As seen in the 100 µL h⁻¹ flow rate, this tendency is more noticeable as the medium becomes more heterogeneous. However, as heterogeneity increases, it appears that reaction tends to occur closer to the inlet at the lower flow rate. This is demonstrated in Fig. 4a(c–d) in comparison with Fig. 4a(g–h), where the latter presents a stronger migration of the interface so that a larger volume of the cell is occupied by the basified pyranine. This substantial migration of pH towards the acidified solution (recall that the pyranine concentration is uniform throughout the cell and only the pH differs) cannot be the outcome of the initialization of solutions in the flow cell as these measurements were taken after 100 and 20 pore volumes for the 100 and 10 µL h⁻¹ flow rates, respectively.

The calculated pH at a 10 µL h⁻¹ flow rate (Fig. 4b(e–h)) predicts a somewhat asymmetrical pattern regarding the basified vs. acidified pyranine distribution and a slightly narrowing strip of the basified pyranine as fluids move towards the outlet zone, indicating that the reaction theoretically gets larger due to R6G diffusion. This increase is the outcome of the logarithmic scale of pH (see Eq. 8), where the molar value of the access OH⁻ ion is orders of magnitude higher on one side, which dominates over the cross-section. However, reactive experiments show that basified pyranine moves vertically along the cell significantly more than the calculated pH predicts and the volume of the basified pyranine is increased at the expense of the acidified pyranine. This demonstrates that the reaction does not necessarily follow the mixing pattern in porous media as the pH spreads faster than the R6G concentration predicts, an aspect that has a clearer representation in the following section.

3.2.1 Comparing the average pH transverse migration

Most studies and experiments do not have access to the pH or R6G spatial distribution, and, therefore, they rely on measuring the average values of pH in the system at a given volume. To reproduce this measurement, we further compare the averaged pH spread received in the reactive experiments with the averaged theoretical one we calculated according to the R6G concentration. Using a MATLAB program, we divided each analyzed image (of Fig. 4a and b) into three equal-size sections: inlet area, middle area, and outlet area (see Fig. 4c2). In each section, we calculated the average pH of each column of the matrix along the x axis. The plotted results, shown in Fig. 4c(a–h), clearly show how the transition in pH has a sharp interface for both the calculated and the measured pH, even when averaged spatially; yet they also emphasize that while the calculated pH is symmetric around the cell center, the experimental pH is very non-symmetrical and deviates significantly from the cell center, and this deviation between the calculated and experimental pH is worsened as the flow rate decreases.

The pH calculated from the mixing predicts that the average pH of the first section of the medium (continuous red line) starts to rise roughly in the middle of the cell. As we look at areas closer to the cell outlet, the average calculated pH (dashed and dotted red lines) starts to rise farther from the middle of the cell. However, the average pH measured in the reactive experiments shows a different tendency – the farther away from the cell inlet, the higher the pH value along the x axis.

Moreover, the pH calculated from mixing predicts a more moderate climb of the average pH as the flow rate descends from 100 to 10 µL h⁻¹, which we do see in the pH spread measured in the reactive experiment, particularly in the inlet area (blue continuous lines in Fig. 4c1, top vs. bottom row in the panel). However, at the lower flow rate, the pH spread starts significantly closer to the inlet in all the tested heterogeneities. This points to a diffusion-related mechanism that is scaled between the high and the low fluxes following the Péclet relation in Eq. (2), yet this effect is dominant for the pH spread and not the R6G mixing pattern with the DDW.

The diffusion dominance is especially apparent in the spread of basified pyranine at the expense of acidified pyranine for the lower flux, marking the rapid spread of low pH towards the high pH, yet the enhanced shear forces due to increased heterogeneity continue to play a role even in this low flux. Furthermore, the effect of heterogeneity on pH spread is also reflected in the rapid spread of the middle cell basified pyranine on the expense of acidified pyranine as the heterogeneity level increases, and with it, so are the shear forces. So, overall, although the neutralization reaction occurs faster than the R6G concentration gradient equilibrium, it appears to be affected by both the fluid flow rate and medium heterogeneity in a manner similar to that of the R6G.

3.2.2 The role of diffusion in pH transverse migration

While the logarithmically high OH⁻ concentration explains the sharp pH change, the rate of migration, which breaks the symmetry between R6G and the acidified–basified pyranine pH measurement, follows the high proton mobility in water (Agmon, 1995). It has already been well established that proton transfers are one of the fastest chemical processes, and even in the diluted solutions phase, where diffusion is limited, their rates exceed other known reactions (Donten et al., 2012). This is usually explained in terms of a sequence of proton transfer reactions between water molecules along a hydrogen-bonded network, known as proton hops, as described in the Grotthuss mechanism 200 years ago (Agmon, 1995; Hassanali et al., 2011; Wolke et al., 2016). Due to its tiny ionic radius and its strong polarization power, the proton cannot be isolated in equilibrium conditions. Instead, it immediately binds to an intact water molecule to form hydronium ions by creating covalent bonds (Thabet et al., 2020).

The Grotthuss mechanism was proposed to explain how the excess proton occurring as hydronium ion diffuses much faster than expected from its hydrodynamic radius. In this mechanism, the excess proton diffuses with a proton transfer from the hydronium to the neighboring water molecule or from a water molecule to a neighboring hydroxide (Hassanali et al., 2011).

The differences between the proton–hydronium diffusion rate to the R6G diffusion rate are reflected in their diffusion coefficients in water as the former is more than 1 order of magnitude larger than the latter, with a diffusion coefficient (D) of $\mathrm{9.3}\times {\mathrm{10}}^{-\mathrm{5}}$ cm² s⁻¹ (Amdursky et al., 2019; Zhang et al., 2021; Tuckerman et al., 2006) for hydronium vs. $\mathrm{4}\times {\mathrm{10}}^{-\mathrm{6}}$ cm² s⁻¹ (Gendron et al., 2008) for R6G and close to 1 order for OH⁻, shown in Table 2.

Table 2 Mapping of the various chemical components in our system, with their corresponding diffusion, ionic mobility, and Péclet value for both experimental fluxes. Details can be found in (1) Parkhurst and Appelo (2013), (2) Varcoe et al. (2014), (3) Himmelsbach et al. (1998), and (4) Gendron et al. (2008).

This high diffusion rate leads to a diffusion-dominated transverse flux captured by the pH enhanced spread as the applied flux reduces, forming a low Pe over the pore size. Calculating OH⁻ transverse migration from the diffusion mean square displacement over the 10 s it takes for the fluid to advance the length of the cell (4.5 mm) for the 10 µL h⁻¹ flow rate (recall that the v_d=0.0142 cm s⁻¹), the high diffusion advances OH⁻ by 0.2 mm. As diffusion is isotropic in nature, it not only occurs transversely to the flow but is also aligned with the flow, leading to a steady state of OH⁻ neutralized by the lower pH and marked by the acidified pyranine as seen in the homogeneous case (Fig. 4e). Multiplying this diffusion advancement by the Pe ratio reported in Table 1 brings this diffusion spread to 0.3 mm (see Table 3), nearly covering the full extent of the cell and remaining similar to the spread in Fig. 4e. However, for the same extent of time and Darcy velocity, the high shear in the heterogeneous case further mixes OH⁻, leading to full homogenization of the pH in the flow cell (see Fig. 4c(h), and Table 3). The shear increase with heterogeneity is marked by the reduction in the measured permeability presented in Table 3, which for fixed flow rate leads to higher shear. Yet the same increase in shear between the homogeneous and the heterogeneous case for the high flux/Pe produces a smaller relative effect on OH⁻ migration (Fig. 4c(a–d)).

Table 3 The Darcy velocity, mean square displacement (MSD), and MSD scaled by the effective Péclet ratio for each heterogeneity.

3.2.3 Calculating the ion concentration contribution to transverse migration

While the enhanced diffusion due to the Grotthuss mechanism being well established, the ionic nature of the proton/hydronium has the potential to form an electrical gradient that may affect the pH distribution. The contribution of this mechanism has been debated in the literature in the context of pH reaction, and it has been shown that it can be neglected for brine, where the ion ratio is minor compared to the background solution (Li et al., 2006; Lichtner and Kang, 2007; Li et al., 2007b). Simulations performed on experimental results from a Hele-Shaw cell (Huang et al., 2023; Almarcha et al., 2010) showed the importance of considering the Coulombic interaction via the Nernst–Plank equation and species-specific diffusion coefficient for density-driven flow in bulk. Additional simulations and experiments on porous media coupling the electrical gradient with various flow configurations while considering the different diffusion values for each reactive species were performed, yet for a high Péclet number, experiments pointed to the important role of Coulombic interactions during reactive transport (Rolle et al., 2018, 2013); it remains yet to be seen how relevant it is to the system presented in this study.

Following the Nernst–Planck equation (Bockris and Reddy, 1999), the flux of ions due to both diffusion and migration under an electric field is given by

$$\begin{array}{}\text{(12)}& \begin{array}{rl}{J}_{{\mathrm{OH}}^{-}}& =-D_{{\mathrm{OH}}^{-}}{\displaystyle \frac{\mathrm{d}{C}_{{\mathrm{OH}}^{-}}}{\mathrm{d}x}}+u_{{\mathrm{OH}}^{-}}{C}_{{\mathrm{OH}}^{-}}\cdot E\\ & =-D_{{\mathrm{OH}}^{-}}{\displaystyle \frac{\mathrm{\Delta }{C}_{{\mathrm{OH}}^{-}}}{\mathrm{\Delta }x}}+u_{{\mathrm{OH}}^{-}}{C}_{{\mathrm{OH}}^{-}}\cdot E,\end{array}\end{array}$$

where $J_{{\mathrm{OH}}^{-}}$ [mol cm⁻² s⁻¹] is the flux of the ion, $C_{{\mathrm{OH}}^{-}}$ [mol cm⁻³] is the concentration of the ion, u [cm² s ⁻¹ V⁻¹] is the ionic mobility, and E [V cm⁻¹] is the electric field. For OH⁻, $D_{{\mathrm{OH}}^{-}}=\mathrm{5.3}\times {\mathrm{10}}^{-\mathrm{5}}$ [cm² s⁻¹], $u_{{\mathrm{OH}}^{-}}\approx \mathrm{20}\times {\mathrm{10}}^{-\mathrm{4}}$ [cm² s⁻¹ V⁻¹] (see Table 2 for details and reference), and the concentration at both inlets and their distance is known (Δx=0.0475 cm): $E\approx -\mathrm{2.5693}$ [V cm⁻¹].

We repeated this calculation for the hydroxide ions (OH⁻), protons (H⁺), Cl⁻, and Na⁺, and for all cases, the diffusive flux (marked by the first term in Eq. (12) and scaling with $D_{{\mathrm{OH}}^{-}}$ [cm² s⁻¹]) was 2 to 3 orders of magnitude greater than the electric flux (marked by the second term in Eq. (12) and approximately $J_E\left({\mathrm{OH}}^{-}\right)\approx \mathrm{2}\times {\mathrm{10}}^{-\mathrm{7}}$ [mol cm⁻² s⁻¹]) due to the ion concentration, making them negligible for our study (see Bard et al., 2022 for details).

3.3 Combined experiments

In this study, we identify this neutralization reaction effect by setting fluids with the same reactive tracer concentration, so a concentration gradient is not present for the pyranine but only the pH gradient. To mimic the practice where pH indicators are locally introduced and allowed to diffuse according to their concentration gradient and flow, we perform combined experiments where the pyranine is introduced only with the high pH inlet, similarly to the basified pyranine; yet it will need to migrate towards the low pH area where only DDW is present (acidified DDW). The conversion of image intensity to pH is performed as in the experiments in Sect. 3.2. In this setup, the basified pyranine dispersion is the limiting reactant for the pH reaction, and as such, the role it has as a pH indicator is limited, since its dilution also acts as the limiting fluorescing factor as shown in Fig. 5.

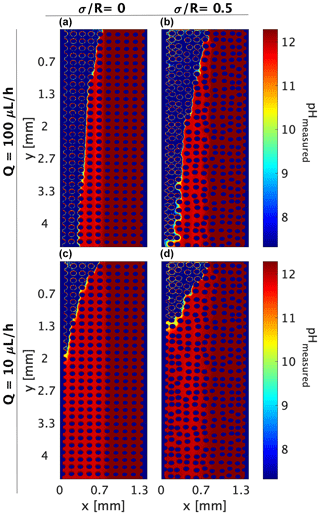
Figure 5 Combined experiments (both for a concentration gradient and pH gradient): pH values as indicated by the reactive tracer distribution, neglecting the tracer concentration gradient. (a, b) Flow rate of 100 µL h⁻¹ at medium heterogeneities of $\mathit{\sigma }/R=\mathrm{0}$ and $\mathit{\sigma }/R=\mathrm{0.5}$, respectively. (c, d) Flow rate of 10 µL h⁻¹ at medium heterogeneities of $\mathit{\sigma }/R=\mathrm{0}$ and $\mathit{\sigma }/R=\mathrm{0.5}$, respectively.

Although we should expect the same pH distribution within the porous media as for the R6G test, given that the basified pyranine diffusion is between the R6G and the OH⁻ value (see Table 2), the image analysis yields a different distribution than the one accepted for the R6G or the acidified–basified pyranine (Figs. 3 and 4a, respectively). While the pH change is only due to the occurring reaction, here, it is also wrongly accepted as a measure of the pyranine’s transverse diffusion/dispersion, leading to the pyranine dilution, which can be wrongly accounted for as the pH change. This is reflected in the measured pH of ∼11.5 we see in Fig. 5a–d, which does not appear in Fig. 4a and somewhat resembles the interface between the fluids around pH ∼ 11.5 and pH =12.3 in the pH pattern calculated from the R6G experiments.

Another interesting aspect is the fast migration of pyranine, which cannot be accounted for by pyranine diffusion. Calculating the transverse diffusion for the pyranine in the form of mean square displacement presents higher pH homogenization for the homogeneous case than the case where pyranine concentration is uniform in the cell, raising the question of if the OH⁻ concentration difference is facilitating migration in the form of osmotic pressure while fixing the pyranine excitation levels.

3.4 Simulating the tracer and reactive experiments

The 2D tracer and pH experiment results in Sect. 3.1 and 3.2, respectively (for convenience, presented again in Fig. 6(1) and 6(2), respectively), were reproduced using a COMSOL Multiphysics simulator (Fig. 6(3) and (4), respectively). This was done by importing the cell AutoCAD design to COMSOL so an exact Stokes flow simulation could be employed to solve the flow field as described in Sect. 2.3. The same parameters for the diffusion of the R6G and Darcy velocity were taken, and a forward solver was used to calculate the transverse dispersion. The simulation reproduced the initial invasion scheme for the experimental setup, and as in the experiment, the steady state was verified by comparing the output of consecutive time frames in the simulation. Comparing Fig. 6(1) with Fig. 6(3) shows that the simulation captures the transverse dispersion for all Pe values well although it somewhat enhances the dispersion for the low concentrations.

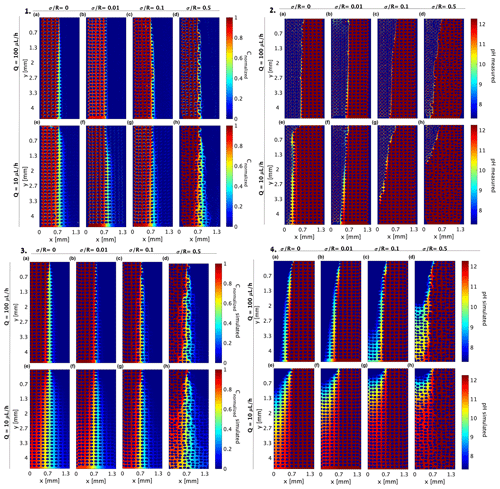
Figure 6 Distribution of (1) R6G normalized concentration, (2) pH measured by the pyranine, (3) simulated R6G normalized concentration, and (4) simulated pH provided for (a–d) flow rate of 100 µL h⁻¹ and (e–h) flow rate of 10 µL h⁻¹ at presented medium heterogeneities. The 2D R² for the R6G simulations was above 0.88 for all heterogeneities and flow rates, and 2D R² values ranged from 0.6 to 0.75 for the pH simulations, where the high heterogeneity and low flow rates portray lower 2D R².

As in the R6G experiment, we use the same Stokes flow solver for the reactive experiment and update the diffusion coefficient to the higher value of OH⁻ and H⁺ migration (Table 2), providing the pH value based on both ion and proton diffusion. As the pyranine emission intensity range is given by Eq. (9) and shown by the exponential decay in Fig. 2b, a similar exponential conversion was used in the COMSOL simulation to highlight this region. Comparing the experimental and simulated reactive case (Fig. 6(2) and (4), respectively) shows that the high Pe simulation produced similar results to the experimental values, yet the low Pe values proved more challenging. This difference between the simulation and experimental results, even when considering the pH exponential range, did not improve when we considered the Nernst–Planck equation (Eq. 12). We believe that the discrepancy stems from the fact that while diffusion is indeed higher, the neutralization reaction of OH⁻ ions and H⁺ proton, following their local concentration, requires a model that also considers both the diffusion and the local concentrations. Another aspect that is not considered in the COMSOL model is the Grotthuss mechanism and the strong polarization power leading to the immediate binding to an intact water molecule to form hydronium ions by creating covalent bonds, which is not considered in the enhanced diffusion directly. This mismatch between the model and the experimental setup clearly points to the need to incorporate these mechanisms in existing models.

4 Summary and conclusion

4.1 Summary

We experimentally investigated the effect of porous media heterogeneity and flow rate on transverse mixing and their effect on the pH-driven neutralization reaction. The experiments showed that transverse mixing is controlled by either diffusion or shear forces, with the former corresponding to the homogeneous medium and a lower flow rate and the latter corresponding to the heterogeneous medium and higher flow rate. Subsequent experiments followed the same flow rates and heterogeneity levels but with a pH reactive tracer, which provided the pH transverse dispersion. These pH reaction pattern does not necessarily follow the pH calculated by the mixing as the medium becomes more heterogeneous and the flow rate descends, and we trace this mismatch to the enhanced diffusion of pH. Another set of experiments were used to show how the measured pH can be wrongly interpreted once the tracer is not introduced uniformly in the domain. We simulated our system and showed that the mixing experiments matched flow simulations, yet the simulated pH experiments with the enhanced diffusion capture the trend of pH transverse advancement but not the local pH values.

4.2 Conclusion

The main conclusion from our experiments is that the pH gradient between the co-flowing fluids tends to equilibrate faster than the concentration gradient, so the reaction occurs earlier than predicted by the mixing pattern. The experiments demonstrate that the transition of a proton is considerably faster than that of diffusion and shear forces governing mixing. This can be accounted for by several mechanisms, resulting in the abnormally high proton mobility in water known as the Grotthuss mechanism. The experiments presented here show how important it is to consider the mechanism when incorporating pH-driven reactions in porous media. Even so, diffusion alone is not sufficient when considering neutralization reactions like pH, as is clear from the mismatch between the COMSOL simulations and the experimental results.

This difference in diffusion rate can be easily missed as in most experimental setups and in the field, pH is generally measured locally or with a pH indicator that migrates with the flow. The pH may equilibrate faster than the pH indicator diffusion due to the hydronium ion binding transition that does not require movement of the ion but only dissociation of the water, while the pH indicator and/or reactants should distribute slower in the porous media as they lack this mechanism. Moreover, to avoid the charged balance calculation between the various ions and cations in the reactive system, with their respective diffusion coefficients (Table 2), studies often assume that diffusion is uniform for all chemical species. This assumption may hold while the background salinity is high (namely, close to seawater), yet for low salinity water, this assumption becomes questionable (Lichtner and Kang, 2007; Li et al., 2007a; Lichtner, 1996).

As pH reactions are the most frequent and abundant reactions in soil and rock formation, considering the differences between pH migration and mixing is crucial to capturing the extent of reactions. Our findings raise questions on the assumption that the diffusion differences between chemical species for not only pH reactions specifically, but also various chemical species, as evident from the difference in transverse migration of the R6G and pyranine, are negligible. This assumption may be valid for a higher Péclet number or for specific chemical species, yet as typical flows in soil and rock generally follow a low Péclet number and involve pH reactions and/or rich ion composition, this assumption is rarely true.