Mangroves as nature-based mitigation for ENSO-driven compound flood risks in a large river delta

Densely populated coastal river deltas are very vulnerable to compound flood risks coming from both oceanic and riverine sources. Climate change may increase these compound flood risks due to sea level rise and intensifying precipitation events. Here, we investigate to what extent nature-based flood defence strategies, through the conservation of mangroves in a tropical river delta, can contribute to mitigate the oceanic and riverine components of compound flood risks. While current knowledge of estuarine compound flood risks is mostly focussed on short-term events such as storm surges (taking 1 or a few days), longer-term events, such as El Niño events (continuing for several weeks to months) along the Pacific coast of Latin America, are less studied. Here, we present a hydrodynamic modelling study of a large river delta in Ecuador aiming to elucidate the compound effects of El Niño-driven oceanic and riverine forcing on extreme high water level propagation through the delta and, in particular, the role of mangroves in reducing the compound high water levels. Our results show that the deltaic high water level anomalies are predominantly driven by the oceanic forcing but that the riverine forcing causes the anomalies to amplify upstream. Furthermore, mangroves in the delta attenuate part of the oceanic contribution to the high water level anomalies, with the attenuating effect increasing in the landward direction, while mangroves have a negligible effect on the riverine component. These findings show that mangrove conservation and restoration programmes can contribute to nature-based mitigation, especially the oceanic component of compound flood risks in a tropical river delta.

1 Introduction

Extreme sea levels (ESLs) are an enormous threat to coastal areas and are expected to increase in intensity and frequency due to climate change (Fox-Kemper et al., 2021; Tebaldi et al., 2021; Vousdoukas et al., 2018). ESLs typically occur when high tides coincide with surges, such as storm surges, which typically last for one or a few single high tides, or interannual climate fluctuations, such as El Niño events, which could last multiple months or years (Muis et al., 2016; Barnard et al., 2015). The flood hazards that these ESLs can cause might be intensified due to the co-occurrence of extreme river discharge events in estuaries and coastal deltas (Bevacqua et al., 2019; Wahl et al., 2015). As coastal areas typically host densely populated cities, ESLs are estimated to affect 5 % of the global population and 10 % of global gross domestic product by 2100 if no protective measures are taken (Hinkel et al., 2014). Consequently, in the face of continued climate warming and growing impacts of ESLs, the need for sustainable coastal defence strategies is increasing globally. As a complement to expensive engineered flood defence systems, nature-based solutions, such as the conservation and restoration of natural coastal wetlands, are being recognized more and more as ways to improve the sustainability of strategies to mitigate ESL-driven flood risks (Narayan et al., 2016; Temmerman et al., 2013, 2023).

The El Niño–Southern Oscillation (ENSO) is one of the most dominant interannual climate fluctuations on Earth that generates ESLs across the Pacific Ocean (Colas et al., 2008; Barnard et al., 2015; Widlansky et al., 2015; Chang et al., 2013). During the neutral phase of ENSO, westward trade winds pile up warm surface waters in the western Pacific, causing the upwelling of colder waters in the eastern Pacific in front of the Pacific coast of Latin America. During the warm phase of ENSO, referred to as El Niño, weakened trade winds reduce the upwelling of colder waters and therefore lead to warmer surface waters in the eastern Pacific (McPhaden et al., 2006). These positive sea surface temperature anomalies (SSTAs) trigger atmospheric convection, which further weakens the trade winds and reinforces the surface water warming (Timmermann et al., 2018). Likewise, the unusually warm surface waters cause sea levels to increase through thermal expansion for multiple months (Nerem et al., 1999), with sea level anomalies (SLAs) which can reach up to +40 cm in front of the Ecuadorian and Peruvian coasts, here further referred to as the oceanic forcing on El Niño-driven ESLs (Belliard et al., 2021; Colas et al., 2008). Simultaneously, the increased atmospheric convection leads to increased precipitation and hence increased river discharge for multiple months in coastal Ecuador and northern Peru (Takahashi, 2004; Tobar and Wyseure, 2018; Rollenbeck et al., 2022). Here, this is further referred to as the riverine forcing on El Niño-driven ESLs. Over the coverage of available data records (for both river discharge and tide gauges), eight El Niño events occurred for which four substantial discharge and sea level anomalies were recorded (Belliard et al., 2021).

For the case of river deltas and estuaries, several studies have demonstrated that when an ocean forcing, such as a storm surge, co-occurs with high riverine discharge events, the resulting flood risks could be much higher than that driven by a single forcing event, leading to so-called compound flood risks (Fang et al., 2021; Wahl et al., 2015; Gori et al., 2022; Bevacqua et al., 2019; Couasnon et al., 2020). Previous studies on estuarine compound flood risks suggest that the contribution of extreme tides and peak discharges to the resulting estuarine ESLs is strongly dependent on the location within the estuary. How far each forcing contribution reaches varies largely among estuaries due to a great dependence on the geometry of the estuary (Harrison et al., 2022). Furthermore, in estuaries with small watersheds (order of hundreds of squared kilometres or less), the hydrological response time between a rain event and the corresponding peak discharge tends to be short, and a storm-surge-driven ESL can be strongly amplified if it co-occurs with the peak discharge (Zheng et al., 2013; Robins et al., 2018). In estuaries with larger watersheds (order of thousands of squared kilometres or more), the response time tends to be much longer so that peak discharges may arrive in the tidal section of the estuary after the storm-surge-driven ESLs have occurred and no compound flood risks take place (Bevacqua et al., 2019; Hendry et al., 2019). However, in the case of a long-term intensification of precipitation (order of weeks to months, as in the case of strong El Niño events), risks for compound hazards also increase for larger estuaries (Dykstra and Dzwonkowski, 2021; Wu et al., 2021). So far there have been no studies on estuarine or deltaic ESL dynamics due to long-term (weeks to months) combined increases in both river discharge and sea level, such as during strong El Niño events. Although Belliard et al. (2021) demonstrated a landward amplification of El Niño-driven ESLs in an eastern Pacific tropical river delta, it remains uncertain as to what extent such landward amplification of ESLs is driven by compounding effects of both oceanic and riverine forcing.

The presence of coastal wetlands, such as mangroves in the tropics and tidal marshes in temperate regions, can contribute to reducing the peak water level of upstream propagating ESLs along estuarine or deltaic tidal channels (Temmerman et al., 2023). When the rising water levels exceed the elevation of channel banks, water can flow into the intertidal wetlands where it is temporarily stored, consequently contributing to lower upstream ESLs (Stark et al., 2015; Horstman et al., 2015). The landscape setting and network of channels and intertwining wetlands strongly affect the effectiveness of wetlands to attenuate extreme sea levels (Temmerman et al., 2023). Numerical hydrodynamic models explicitly consider the geometry of wetlands and channels (Smolders et al., 2015; Dominicis et al., 2023; Temmerman et al., 2023) in contrast to analytical approaches which typically describe wetlands as uniform un-channelized zones with increased friction (Montgomery et al., 2019) or a single channel (Van Rijn, 2011). Research on the capacity of mangroves to attenuate ESLs typically does not consider the interaction with increased river discharge. Conversely, studies on compound flooding do not consider the role of intertidal wetlands (Wu et al., 2021; Harrison et al., 2022; Cao et al., 2020). Hence, to what extent estuarine or deltaic mangroves can mitigate the risks of compound flood hazards is poorly known. This question is of high relevance to many tropical to subtropical estuaries and deltas, where mangrove conversion to human land use is a common practice, while mangrove conservation and restoration can be an effective nature-based strategy for flood risk mitigation (Gijsman et al., 2021; Temmerman et al., 2023).

Here, we present a hydrodynamic modelling study of a large delta in Ecuador, aiming to elucidate the compound effects of El Niño-driven oceanic and riverine forcing on ESL spatial dynamics. By analysing model scenarios in which we isolate the oceanic or the riverine forcing and combine both, we aim to identify their relative contributions and combined impacts on ESLs in the delta. Furthermore, all model scenarios are duplicated with and without the inclusion of large mangroves present in the delta to elucidate the capacity of mangroves to attenuate the landward amplification of El Niño-driven ESLs.

2 Methods

2.1 Study area

The Guayas delta is the largest river delta on the Pacific coast of South America, with a watershed of 32 300 km² (Frappart et al., 2017). In the upstream part of the delta plain, it accommodates the largest city and economic centre of Ecuador, Guayaquil (Fig. 1), home to about 3 million people and ranking fourth globally among the cities most vulnerable to coastal flooding (Hallegatte et al., 2013). More seaward from the city, the delta consists of a complex network of channels and mangroves, grown predominantly by Rhizophora mangle. As in many other tropical and subtropical river deltas and estuaries, large extents of mangroves have been replaced by aquaculture ponds such that only 63 % of the delta plain (about 1400 km²) is still covered by mangroves nowadays (Hamilton, 2019). The delta includes two major channel branches (Fig. 1). The eastern branch is fed by freshwaters from the Guayas river, which is formed at the confluence of the Babahoyo and Daule rivers. The discharge follows a strong seasonal variability ranging from 200 m³ s⁻¹ in the dry season (April–November) up to 1600 m³ s⁻¹ in the wet season (December–March). The western branch, Estero El Salado, does not receive any substantial freshwater discharge. At the seaside, the delta borders the Gulf of Guayaquil from where semidiurnal tides enter the delta with a mean tidal range of about 2 m. When propagating upstream through the delta, tides amplify, resulting in mean tidal ranges of about 5 m near the city of Guayaquil.

As in other regions in the eastern Pacific Ocean, El Niño is the main driver for ESLs in the Guayas delta (Belliard et al., 2021; Colas et al., 2008). For instance, during the particularly strong El Niño event of 1997–1998 that lasted over 18 months, the mean sea level increased up to 50 cm at the open coast, high water levels increased up to 90 cm above their normal values in the inner delta, and discharge values were 2.5 times higher than on average during the neutral phase of El Niño (Belliard et al., 2021).

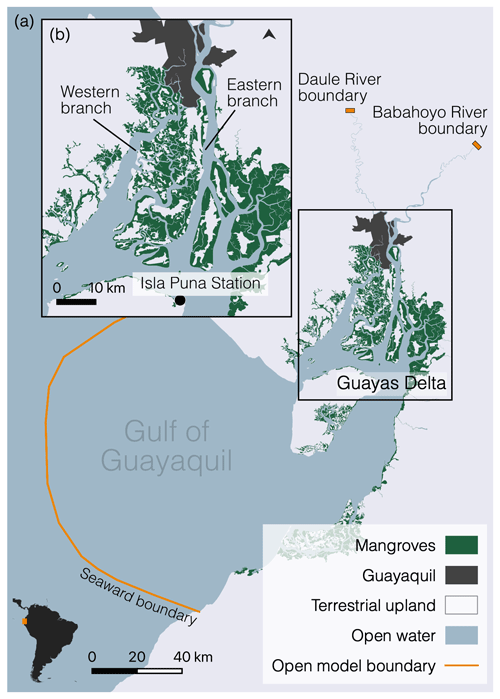
Figure 1 Map of the model domain (a), covering the Gulf of Guayaquil and the Guayas delta (b). The computational domain includes both the open water (in blue) and the mangrove areas (in green). The orange lines represent the open model boundaries: the seaward boundary downstream and two freshwater boundaries upstream in the Daule and Babahoyo rivers.

2.2 Model description

The present modelling study builds further on the work by Pelckmans et al. (2023), which presents the hydrodynamic model setup, calibration, and validation against observed tidal water levels for 11 tide gauge stations throughout the delta. The present paper focuses on the modelling of extreme high water levels under El Niño conditions, whereas Pelckmans et al. (2023) only accounted for ENSO-neutral conditions (i.e. without additional El Niño-driven forcing). Below, we briefly summarize the model setup by Pelckmans et al. (2023), to which we refer the reader for more details.

The model domain includes the entire Gulf of Guayaquil (Fig. 1), stretching from the edge of the continental shelf in the open ocean up to the landward boundaries, which approximately correspond to the upstream tidal limits along the Daule and Babahoyo rivers. Intertidal areas, consisting of vegetated mangroves and bare mudflats, are delineated through remote sensing (Sentinel-2 imagery) and are included in the domain. The mesh becomes finer (1) along the bathymetric gradient from the open sea towards the delta mouth area, (2) with decreasing channel width in the channels dissecting the delta, and (3) with decreasing distance to channels in the mangroves. Resulting mesh sizes range from 250 m at the open sea to 3 m in the narrowest channels. Mesh resolution in the main channel in the eastern branch of the delta does not exceed 75 m and has a minimum of 25 nodes per channel cross-section. The resulting mesh consists of 3 212 408 nodes and 6 425 420 elements.

The bathymetry is obtained from the General Bathymetric Chart of the Ocean in the open ocean and from the Oceanographic Institute of the Navy in Ecuador (INOCAR) inside the delta. The surface elevation of the mangrove forest is calibrated to match measured inundation levels (Belliard et al., 2021), and intertidal mudflat topographies were obtained through remote sensing.

The mangroves are characterized by a complex network of aerial roots, exerting a vegetation-induced drag in addition to the drag exerted by the bed. This vegetation-induced drag force is modelled as the drag force on random or staggered arrays of rigid vertical cylinders with uniform properties (Baptist et al., 2007; Horstman et al., 2021):

$$\begin{array}{}\text{(1)}& {\mathit{\tau }}_v={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\rho }{C}_{\mathrm{D}}DMh\mathit{\upsilon }\mathrm{|}\mathrm{|}\mathit{\upsilon }\mathrm{|}\mathrm{|},\end{array}$$

where C_D is the dimensionless bulk drag coefficient and equals 1 (Baptist et al., 2007), D is assumed to equal 3.5 cm and is the representative diameter of the mangrove prop roots, and M is set equal to 85 m⁻² as the representative density of prop roots. Values for the latter two are obtained from the literature on observations of Rhizophora trees in Australia and Japan (Mazda et al., 2005, 1997).

Bed friction in the channels is described by the Manning formulation where the Manning coefficient is calibrated to fit observed water levels at 11 tide gauge stations spread throughout the delta. To isolate uncertainties in the intertidal mangrove topography and vegetation-induced drag from the effects of the Manning coefficient in the subtidal channels, we calibrated the subtidal channel Manning coefficient during five consecutive high and low waters around a neap tide (22–24 September 2019), as mangroves in the Guayas do not flood during neap tides (Belliard et al., 2021). The tested Manning values ranged between 0.0075 and 0.02 (with an incremental step of 0.0025). The best model performance was obtained with a value of 0.0175 in the western branch and outer delta and a value of 0.0125 in the eastern branch. For the calibrated neap tides, simulated water levels resulted in a root mean square error of 0.11±0.06 m (average and standard deviation over the 11 tide gauge stations) on an observed tidal range between 1.49 and 2.88 m and a Nash–Sutcliffe model efficiency (Nash and Sutcliffe, 1970) of 0.98±0.02.

The model is validated against water levels at 11 tide gauge stations for four consecutive high and low waters during a spring tide on 28–30 October 2019. Model performance is considered excellent with a Nash–Sutcliffe model efficiency (Allen et al., 2007) of 0.85±0.10 m and a root mean square error of 0.18±0.09 m over the entire delta with tidal range between 2.74 and 4.72 m and root mean square error of 0.10±0.01 m for four tide gauge stations in the eastern branch with tidal range between 4.17 and 4.37 m.

2.3 Model boundaries

2.3.1 Seaward boundary

The El Niño seaward boundary condition, referred to as the El Niño oceanic forcing, corresponds to spring tides during the period 1–3 March 1998, which include the highest water levels for the 1997–1998 El Niño event. We generate this El Niño oceanic forcing following a stepwise procedure. In the first step, we obtained astronomical tidal water levels from the global tidal model TPXO9 (Egbert and Erofeeva, 2002). In a second step, because TPXO9 data do not include the local El Niño-driven sea level anomalies, we increased water levels by a constant value, calibrated against observed water levels at Isla Puna near the delta mouth (Figs. 1 and 2a). For scenarios not affected by El Niño conditions (i.e. referred to as neutral conditions) we estimated neutral water levels which do not necessarily coincide with the TPXO9 data. Therefore, in a third step, we calculated neutral ocean water levels by subtracting El Niño sea level anomalies from the water level data obtained in step 2. These anomalies were calculated by Belliard et al. (2021), who calculated anomalies by how much higher sea levels were due to the El Niño conditions as compared to neutral astronomical tidal conditions, based on tidal harmonic analysis.

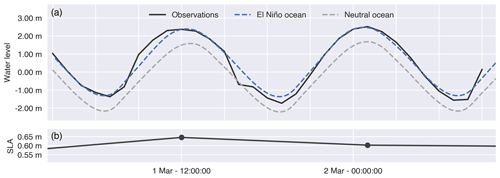
Figure 2 Time series of (a) observed water levels at Isla Puna station on 1–3 March 1998 (Observations) and simulated water levels under El Niño conditions (El Niño ocean) and neutral conditions (Neutral ocean). The latter are calculated by subtracting observed sea level anomalies (Belliard et al., 2021) (b) from the simulated water levels under El Niño conditions.

2.3.2 Landward boundary

The landward boundaries near the upstream tidal limits along the Daule and Babahoyo rivers were quantified based on observed river discharge data from INHAMI (Ecuador's national meteorological and hydrological institute). These data only cover 73 % of the watershed area which drains into the Guayas delta. Hence, we applied a precipitation-weighted linear extrapolation based on monthly precipitation data collected from OpenLandMap (Hengl and Parente, 2022), as similarly presented by Pelckmans et al. (2023). The El Niño-driven landward boundary conditions, referred to as the El Niño riverine forcing, were defined using the daily extrapolated discharge series from 1–3 March 1998. River discharge anomalies (i.e. the difference in river discharges between El Niño and neutral conditions) were calculated as the difference between the 30 d moving average of extrapolated discharges over March 1998 and the 30 d moving average of extrapolated discharges averaged over the neutral conditions observed in March 1993, 1995, 1999, and 2001 (i.e. the nearest 4 neutral years around 1998; Fig. 3a and b). We estimated neutral conditions by subtracting these discharge anomalies from the El Niño discharge series (Fig. 3c and d). As such, we defined the landward discharge boundary conditions (i.e. riverine forcing) for an El Niño and neutral scenarios.

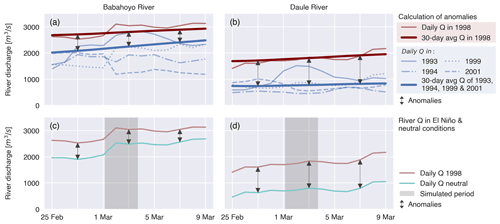
Figure 3 Calculation of river discharge (Q) anomalies from observed daily time series (a, b) and model input for daily river discharges for the El Niño and neutral scenarios (c, d) for the Babahoyo (a, c) and Daule rivers (b, d). The thick red line is a 30 d moving average of the daily river discharge time series observed during El Niño conditions in 1998 (thin red line). The thick blue line shows a 30 d moving average of the daily river discharge time series observed during neutral conditions in 1993, 1994, 1999, and 2001 (closest 4 years to 1998 without El Niño or La Niña events). River discharge anomalies are calculated as the difference between both 30 d moving means (a, b). Daily neutral river discharge values, as imposed at the upstream model boundaries, are calculated by subtracting the anomalies from the daily river discharges of 1998 (c, d).

2.4 Model scenarios

We set up 12 different model scenarios, with the aim of distinguishing (1) the effect of El Niño vs. neutral conditions prescribed as seaward and landward boundary conditions (i.e. ocean and riverine forcing), (2) the effect of including versus excluding the mangroves in the model domain (Table 1) on ESL spatial distribution along the delta, and (3) exploring the sensitivity of the strength of an El Niño event to the effect of mangroves. The first effect is studied by a scenario where we impose both increased sea levels and increased river discharge (referred to as “El Niño ocean & river” scenario in Table 1), a scenario where we only include increased sea level (“El Niño ocean”), a scenario where we only include increased river discharge (“El Niño river”), and a scenario where we impose neutral conditions to both land- and seaward boundaries (“Neutral”). These four scenarios are run either (1) including the mangrove areas in the domain (i.e. allowing them to flood) or (2) excluding the mangrove areas from the domain (i.e. preventing them from flooding by setting the mangrove platform elevation 10 m above the reference level). The latter scenarios, excluding mangroves, can be considered representative of mangrove conversion to aquaculture ponds. These aquaculture ponds are surrounded by high consolidated levees, which are assumed to be high enough to avoid overtopping during high water level events, and as such are completely excluded from the intertidal zone. Furthermore, we include four models similar to the “El Niño ocean & river” scenario where we have increased and decreased the sea level and discharge anomaly with 50 % and for each scenario included and excluded the mangroves (“El Niño ocean & river +50 %” and “El Niño ocean & river −50 %”). To compare all scenarios, we show high water levels along the eastern branch of the delta, while high water levels (HWLs) for the western branch are added in the Supplement (Figs. S1 and S2). In addition, high water level anomalies (HWLAs) are calculated as the difference between high water levels from a scenario including an El Niño forcing and the corresponding neutral scenario. HWLAs for the scenarios with mangroves are calculated using the neutral scenarios with mangroves, and HWLAs for scenarios without mangroves are calculated using the Neutral scenario without mangroves.

Table 1 Overview of the scenarios.

3 Results

3.1 Effect of El Niño forcings

The highest HWLs occur when including both the El Niño riverine and oceanic forcing (Fig. 4, Table 2). Including or excluding the oceanic forcing has a much larger effect than including or excluding the riverine forcing. When imposing the oceanic forcing, HWLs increase over the entire delta compared to the neutral scenario. In contrast, when imposing the riverine forcing, HWLs are only higher compared to the neutral scenario, upstream from the 100 km mark (Fig. 4).

When mangroves are included in the model, HWLAs are amplified upstream only if we impose the El Niño riverine forcing (Fig. 5). In all scenarios with mangroves, HWLAs remain constant in the first 60 km from the open sea before slightly decreasing in the central part of the delta (60–120 km), except for the scenario of El Niño-only riverine forcing. In the most upstream part of the delta (100–148 km), HWLAs continue to decrease without El Niño riverine forcing but increase again with El Niño riverine forcing.

3.2 Effect of mangroves vs. no mangroves

Excluding mangroves results in higher HWLs, regardless of the boundary conditions (Fig. 4, Table 2). The highest upstream HWLs were simulated when including both El Niño ocean and riverine forcing and when mangroves were excluded. In addition, the higher the HWLs are with mangroves, the higher the HWLs increase when removing the mangroves. In comparison with their respective scenarios with mangroves, HWLs are up to 40 cm higher with both El Niño ocean and riverine forcing, and up to 38 cm higher with El Niño oceanic forcing only. However, with neutral and El Niño riverine forcing, HWLs are only up to 21 and 22 cm higher, respectively, when mangroves are excluded.

Our simulations show that mangroves prevent the upstream amplification of HWLAs, while excluding mangroves causes HWLAs to increase upstream (Fig. 5). Furthermore, the effect of in- or excluding the mangroves ranges much further downstream than in- or excluding the riverine forcing. Similar to HWLs, the largest upstream HWLAs, and thus also the strongest increase in HWLAs, were simulated for the “El Niño ocean & river” scenario and when mangroves were excluded.

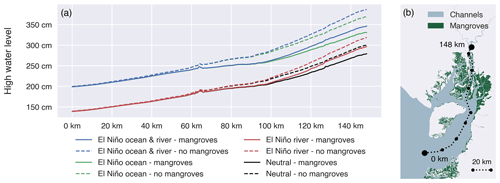
Figure 4 Maximum high water levels (a) during the simulated spring tides over a transect (b) running from the seaward boundary of the Gulf of Guayaquil through the eastern main branch of the Guayas river, receiving direct river discharge, for four scenarios, each one simulated with and without mangroves: a scenario with El Niño ocean and riverine forcing, with only El Niño oceanic forcing, with only El Niño riverine forcing, and with neutral conditions (without El Niño forcing) at both sea- and landward boundaries.

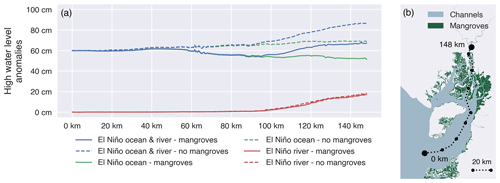
Figure 5 High water level anomalies (a) during the simulated spring tide over a transect (b) running from the seaward boundary of the Gulf of Guayaquil through the eastern main branch of the Guayas river, receiving direct river discharge, for three scenarios, each one simulated with and without mangroves: a scenario with El Niño ocean and riverine forcing, with only El Niño oceanic forcing, and with only El Niño riverine forcing. High water level anomalies are defined as the difference between each model scenario and the corresponding “Neutral” model scenario (without El Niño forcing).

3.3 Effect of strength of El Niño forcings

With stronger El Niño forcing, HWLAs increase over the entire delta (Fig. 6, Tables 2, S3 in the Supplement). The effect of excluding mangroves increases with forcing strength, where the scenario with a 50 % increase in El Niño forcings results in the largest difference between HWLAs with and without mangroves. Similarly, the smallest effect of mangroves results from the scenario where the forcings are lowered with 50 %. For all scenarios, the upstream increase in HWLAs is substantially lower for the scenarios with mangroves vs. scenarios without mangroves. The upstream increase in HWLAs for all scenarios with mangroves is similar for all scenarios, regardless of the strength of the El Niño forcings.

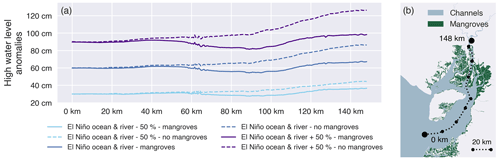
Figure 6 High water level anomalies (a) during the simulated spring tide over a transect (b) running from the seaward boundary of the Gulf of Guayaquil through the eastern main branch of the Guayas river, receiving direct river discharge, for three scenarios, each one simulated with and without mangroves: a scenario with 50 % of the El Niño ocean and riverine forcing (“El Niño ocean & river – 50 %”), with 100 % of the El Niño ocean and riverine forcing (“El Niño ocean & river”), and with 150 % of the El Niño ocean and riverine forcing (“El Niño ocean & river + 50 %”). High water level anomalies are defined as the difference between each model scenario and the corresponding “Neutral” model scenario (without El Niño forcing).

Table 2 Overview of the simulated increase in water level in the eastern branch. Differences between mangroves and no mangroves are shown in the bottom row for each meteorological forcing scenario.

4 Discussion

Current knowledge of estuarine compound flood hazards, coming from a combination of oceanic and riverine sources, is limited to short-term events such as storm surges and does not assess the capacity of intertidal wetlands, such as mangroves, to attenuate compound flood hazards (Wu et al., 2021; Harrison et al., 2022; Dykstra and Dzwonkowski, 2021; Sampurno et al., 2022). Here, we demonstrate that for an event during which both the river discharge and the mean sea level are increased for longer periods, such as during a strong El Niño event (continuing weeks to months) in an eastern Pacific river delta, HWLs are higher than if one such forcing were to occur. More specifically, while the oceanic forcing is the main contributor to HWLs over the entire delta (Fig. 4), the riverine forcing causes an upstream amplification of the HWLAs (Fig. 5). Furthermore, our results show that large extents of mangroves present in the delta attenuate part of the oceanic contribution to the HWLAs, with the attenuating effect increasing in the landward direction and increasing with the strength of the forcings (Fig. 5). However, the mangroves are not able to attenuate the riverine contribution to HWLAs.

4.1 Contributions of riverine and oceanic forcing

By comparing scenarios which combine and isolate the oceanic and riverine forcing, we identify the oceanic forcing as the most important driver of ESLs over the entire Guayas delta (Figs. 4 and 5). Nevertheless, we also show that the upstream amplification of ESLs, also identified by Belliard et al. (2021) from analyses of tide gauge records, is caused by the riverine forcing. Similarly, for storm surges, modelling studies have confirmed that increased river discharges have little effect in the downstream and central sections of a delta (Kumbier et al., 2018). There is typically, however, a tipping point from which an increased discharge adds to ESLs caused by the oceanic forcing in the upstream part (Gori et al., 2020). Such a tipping point is clearly visible in our simulation results at approximately 100 km along the studied transect (Fig. 4). For storm surges, the location of a tipping point depends on the relative strength of the oceanic vs. riverine forcing, with a seaward shift in case of more extreme discharge (Jane et al., 2022; Gori et al., 2020; Harrison et al., 2022). Therefore, the location of the tipping point in the Guayas delta is most likely to be specific to each El Niño event. As the magnitude of the oceanic and riverine forcing can vary largely between El Niño events (Belliard et al., 2021), the location of the tipping point will most likely vary accordingly.

Hence, in the most upstream part of deltas and estuaries, the co-occurrence of increased river discharges with increased sea levels can locally result in ESLs (Kumbier et al., 2018; Dykstra and Dzwonkowski, 2021). Despite only occurring in a limited area within a delta, such compound events can cause severe flooding of surrounding built-up areas (Olbert et al., 2017).

4.2 El Niño-driven compound flooding

We show for a large river delta (watershed of 32.200 km²) that the co-occurrence of El Niño-driven increased discharge and increased sea levels both add up to amplify ESLs (Fig. 4). For storm surges, however, previous studies have pointed out that compound flooding typically only occurs in small estuaries with a watershed smaller than 5000 km² (Bevacqua et al., 2019; Wahl et al., 2015). For estuaries with larger watersheds, the longer lag time between intense storm precipitations and estuarine peak discharges implies that the latter riverine forcing typically occurs later than the oceanic storm surge forcing (Dykstra and Dzwonkowski, 2020). The magnitude and frequency of compound floodings are therefore strongly dependent on the relative timing of peak river discharge, storm surge, and astronomical high tide (Olbert et al., 2013; Wahl et al., 2015). When the intensification of precipitation is driven by long-term climatic fluctuations, such as El Niño (continuing for several weeks to a few months), there is a higher likelihood that the resulting peak discharges are coinciding with ocean-driven ESLs (also continuing for several weeks to a few months) (Dykstra and Dzwonkowski, 2021; Wu et al., 2021). In the Guayas delta, El Niño causes sea levels and river discharges to increase for multiple months (Belliard et al., 2021). Consequently, the HWLAs in the delta resulting from the oceanic and riverine forcing occur simultaneously, and both contribute to ESLs in the delta.

4.3 Upstream increase in high water level anomalies and attenuation by mangroves

We found that the upstream increase in HWLAs is attributed to the riverine forcing (Fig. 5). This confirms the upstream amplification of HWLAs found from the analysis of tide gauge observations in the Guayas delta and the suggestion that this upstream amplification coincides with a shift from predominantly oceanic to riverine El Niño forcing on the HWLAs (Belliard et al., 2021). Our results suggest that without a riverine forcing, there is an upstream decrease in HWLAs (Fig. 5). The latter can be largely explained by the presence of intertidal wetlands such as mangroves, as our simulations without mangroves result in landward increasing HWLAs along the estuary, even without riverine forcing (Fig. 5). We show that large extents of mangroves in a delta can effectively attenuate a part of the oceanic contribution to the HWLAs and that this attenuating effect is increasing landwards.

When oceanically driven HWLs enter the delta and exceed the channel banks, water flows laterally into the fringing mangroves where it is spread out and temporarily stored, thus attenuating the upstream propagation of HWLs (Horstman et al., 2013; Smolders et al., 2015). Hence, when HWLs travel longer through channels fringed by mangroves, more water can be temporarily stored within the mangroves, which explains why this attenuation effect increases upstream. While the Guayas delta is predominantly covered by Rhizophora mangle, other tropical deltas might be covered by a wider variety of mangrove species with different morphologies and, consequently, different mangrove-induced drag. Nevertheless, previous studies have pointed out a low sensitivity of mangrove-induced drag on water levels in the channels (Pelckmans et al., 2023; Horstman et al., 2015; Hu et al., 2015). Instead, a developed channel network is essential to distribute the HWLs from the main estuarine channel into the wetlands, and as such, upstream HWL reduction is more sensitive to wetland topography and degree of channelization than the vegetation-induced friction (Pelckmans et al., 2023). In addition, as estuarine channels become narrower upstream, the total tidal prism decreases and, as such, the relative part of the tidal prism which is temporarily stored in the mangroves increases upstream. Consequently, upstream intertidal wetlands have a stronger attenuation effect than downstream intertidal wetlands of the same surface area (Smolders et al., 2015). Furthermore, with increasing El Niño forcings, the effect of the including or excluding mangroves increases. With higher water levels, a larger portion of the tidal prism is stored in the surrounding mangroves, causing lower upstream HWLs.

The capacity of mangroves to reduce upstream HWLs is also affected by the geometry and size of the delta. In shorter deltas, the HWLs travel less distance and for a shorter time through channels fringed by mangroves, and as such, less water can be temporarily stored in the surrounding mangroves. Hence, we expect lower attenuation rates in shorter mangroves. For wider deltas where the relative part of the tidal prism which is temporarily stored in the mangroves is lower, we also expect lower attenuation rates than described in this paper. Conversely, in longer deltas where HWLs travel for a longer time through channels fringed by mangroves and in narrow deltas where the relative part of the tidal prism, which is temporarily stored in the mangroves, we expect higher attenuation rates. Moreover, in wide estuaries or open bays where coastal wetlands only occupy a narrow strip relative to the width of the bay, the ESL attenuation provided by the wetlands is limited (Haddad et al., 2016; Cassalho et al., 2021; Temmerman et al., 2023).

HWLs are lower in our simulations with mangroves than without mangroves, also for the scenarios with only riverine forcing (Fig. 5). The mangroves also attenuate normal spring tides propagating from the sea during neutral conditions. However, the anomalies due to the riverine forcing are not affected by the presence of mangroves (Fig. 5). Indeed, the riverine discharge does not flow through mangrove-fringing channels upon arriving in the delta (Fig. 1), and therefore the increase in HWLs due to increased discharge is not affected by the mangroves. Moreover, we note that the complete removal of mangroves is likely to result in long-term morphodynamic changes, such as a reduction in tidal prism and consequent infilling and narrowing of tidal channels which is likely to further affect the tidal hydrodynamics and propagation/attenuation of extreme high water levels through the delta. However, modelling such long-term morphodynamic responses was beyond the scope of our scenario analysis. Instead, we aimed to illustrate that intertidal wetlands should be incorporated in compound flood risk assessments as they can be essential in protecting deltas against flood risks. Our results call for further research on what the optimal spatial configurations for mangrove conservation and restoration programmes are and also on the effects of restoring aquaculture ponds back to mangroves.

4.4 Mangrove loss due to ENSO

While we show that mangroves can mitigate El Niño-related extreme sea levels, ENSO-related climate extremes can cause extensive mangrove dieback event (Sippo et al., 2018). To our knowledge no studies have explored the role of ENSO in eastern Pacific mangrove dieback events. Nevertheless, Belliard et al. (2021) have shown that the opposite ENSO phase of El Niño, La Niña, can be associated with temporary drops in sea level and, as such, can create dry and increased saline conditions similar to during extensive mangrove dieback events in Australia (Duke et al., 2017; Lovelock et al., 2017). In addition, increased sea levels might result in excessive flooding of mangroves which might have similar effects as submergence under long-term sea level rise SLR and lead to loss of mangroves (Lovelock et al., 2015). With predicted increases in ENSO variability (Cai et al., 2022), mangrove dieback conditions are likely to increase as well. Further research is needed to assess the vulnerability of current mangroves to extreme ENSO events, especially in the eastern Pacific.

4.5 Implications

The co-occurrence of a riverine and oceanic forcing as typically taking place during an El Niño event at the Pacific coast of equatorial Latin America results in a landward amplification of HWLAs and associated flood risks. Storm-driven compound floods in the tropics are expected to decrease in frequency (Bevacqua et al., 2020), but we show that climatic fluctuations such as ENSO could also lead to ESLs in river deltas and thus should be taken into consideration when assessing future compound flood risks for densely populated cities.

Due to El Niño-driven ESL events, it is expected that an additional 30 % of the population of Ecuador, Peru, Panama, El Salvador, Guatemala, and Costa Rica will be exposed to coastal flooding, in comparison to coastal flooding due to long-term sea level rise only, by the end of the century (Reguero et al., 2015). However, due to the landward-increasing HWLAs and associated flood risks, upstream areas in river deltas can also be exposed to ESLs, and an even larger fraction of the population might be vulnerable to coastal flooding. Furthermore, recent studies point out a possible intensification of El Niño and the related oceanic and riverine forcing (Lee et al., 2021; Cai et al., 2022; Widlansky et al., 2015); therefore, an intensification of upstream compound flood risks may be expected.

In a large funnel-shaped estuary, mangroves have a landward increasing attenuation effect on HWLAs, and their role increases with the strength of the El Niño-related anomalies. As the compound effects of ESLs and increased discharge result in increasing flood risks particularly for inland cities in deltas or estuaries, there is also a larger potential for intertidal wetland conservation and restoration as a nature-based defence flood defence strategy (Temmerman et al., 2023). However, for many deltas and estuaries, there is strong economic pressure for conversion of mangroves into human land use such as aquaculture, agriculture, and urban lands (Thomas et al., 2017; Goldberg et al., 2020; Richards et al., 2020). In all countries along the Pacific coast of Central and South America which have been associated with increased coastal sea levels during past El Niño events (Hamlington et al., 2016), mangrove extent decreased between 1996 and 2020 according to the global mangrove watch (Bunting et al., 2018). Also for the Guayas delta, a third of the original mangrove forests have been replaced in favour of shrimp-producing aquaculture since the 1960s (Hamilton, 2019). Our study already indicates a substantial attenuation effect of the current mangrove extent, and therefore this attenuation effect has very likely decreased together with the mangrove extent in the past 6 decades. Especially in tropical and subtropical countries where large mangrove forests still remain, the conservation of mangroves can be an effective nature-based strategy to mitigate flood risks driven by ESL events, in addition to local engineered flood defences in inhabited areas along deltas and estuaries. While the potential for mangrove conservation as flood buffers has been addressed for coastal areas prone to storm surges (Temmerman et al., 2023), we want to extend this to other coastal regions, such as the Pacific coast of Central and South America. For deltas where mangrove forests have been converted in the past, mangrove restoration can potentially restore the flood attenuation capacity in addition to other ecosystem services such as carbon sequestration, fishery production, water quality regulation, and wood production (Su et al., 2021). However, mangrove conservation and restoration is not a one-size-fits-all solution to mitigate flood risks in tropical river deltas. For instance, attenuation rates attributed to mangroves can be expected in shorter and wider deltas, as described in Sect. 4.3. Nevertheless, we should note that in smaller estuaries wetlands can still provide protection against wind waves and local surge attenuation (Temmerman et al., 2023; Gijsman et al., 2021). We suggest future studies to include observations and numerical modelling of a wider variety of estuary and delta morphologies and scales.

Furthermore, there is still a limited understanding of how the mangrove-induced reduction in ESLs depends on the location and spatial configuration of mangrove conservation and restoration areas within a delta or estuary. Our results call for further advanced investigations of what is the most optimal spatial configuration of mangrove conservation and restoration programmes and investigations of the effects of restoring aquaculture ponds back to mangroves, depending on factors such as the spatial geometry of deltas or estuaries.