Deep learning for quality control of surface physiographic fields using satellite Earth observations

A purposely built deep learning algorithm for the Verification of Earth System ParametERization (VESPER) is used to assess recent upgrades to the global physiographic datasets underpinning the quality of the Integrated Forecasting System (IFS) of the European Centre for Medium-Range Weather Forecasts (ECMWF), which is used in both numerical weather prediction and climate reanalyses. A neural network regression model is trained to learn the mapping between the surface physiographic dataset, plus the main meteorologic fields from ERA5, and the MODIS satellite skin temperature observations. Once trained, this tool is applied to rapidly assess the quality of upgrades to the physiographic fields used by land surface schemes. Upgrades which improve the prediction accuracy of the machine learning tool indicate a reduction in the errors in the surface fields used as input to the surface parameterization schemes. Conversely, incorrect specifications of the surface fields decrease the accuracy with which VESPER can make predictions. We apply VESPER to assess the accuracy of recent upgrades to the permanent lake and glacier covers, as well as of planned upgrades to represent seasonally varying water bodies (i.e. ephemeral lakes). We show that, for grid cells where the lake fields have been updated, the prediction accuracy of VESPER in the land surface temperature (as quantified by the mean absolute error) improves by 0.37 K on average, whilst for the subset of points where the lakes have been completely removed and replaced with bare ground, the improvement is 0.83 K. We also show that updates to the glacier cover improve the prediction accuracy by 0.22 K. We highlight how neural networks such as VESPER can assist the research and development of surface parameterizations and their input physiography to better represent Earth’s surface coupled processes in weather and climate models.

1 Introduction

Accurate knowledge of the global surface physiography, including land, water and ice covers, and their characteristics, strongly determines the quality of surface and near-surface temperature simulations in weather and climate modelling. For instance, water bodies exchange mass and energy with the atmosphere, and their thermal inertia strongly influences the lower boundary conditions such as skin temperature and surface fluxes of heat and moisture near the surface. Globally, there are ∼ 117 million lakes – defined as inland waterbodies without lateral movement of water – making up around 3.7 % of the Earth's land surface (Verpoorter et al., 2014). Their distribution is highly non-uniform, with the majority of lakes located between 45–75^∘ N in the Boreal and Arctic regions. Lakes are highly important from the perspective of both numerical weather prediction and climate modelling as part of the EC-Earth model. For the latter, lakes generally influence the global carbon cycle as both sinks and sources of greenhouse gases; the majority of lakes are net heterotrophic (i.e. oversaturated with carbon dioxide, CO₂) as a result of in-lake respiration and so emit carbon into the atmosphere (Pace and Prairie, 2005; Tranvik et al., 2009). Total CO₂ emission from lakes is estimated to be 1.25–2.30 Pg of CO₂ equivalents annually (DelSontro et al., 2018), nearly 20 % of global CO₂ fossil fuel emissions, whilst lakes account for 9 %–24 % of CH₄ emissions, the second largest natural source after wetlands (Saunois et al., 2020). These rates of greenhouse gas emission are expected to rise further if the eutrophication (i.e. nutrient concentration increase) of the Earth's lentic systems continues. With regards to weather, freezing and melting of the lake surface modifies the radiative and conductive properties and consequently affects the heat (latent, sensible) exchange and surface energy balance (Franz et al., 2018; Huang et al., 2019; Lu et al., 2020). Considering particular examples, over Lake Victoria, convective activity is suppressed during the day and peaks at night, leading to intense, hazardous thunderstorms (Thiery et al., 2015, 2017); Lake Ladoga can generate low-level clouds, which can cause variability in the 2 m temperature of up to 10 K (Eerola et al., 2014); the Laurentian Great Lakes can cause intense winter snow storms (Notaro et al., 2013; Vavrus et al., 2013). Moreover, as a result of the increased temperatures due to climate change, lakes become more numerous due to the melting of glaciers and permafrost. Additionally, the higher temperatures mean that previously permanent lake bodies become seasonal or intermittent. There is then evidently a huge potential return in the ability to accurately model the location, morphology, and properties of lakes in weather and climate models.

The Integrated Forecasting System (IFS) at the European Centre for Medium Range Weather Forecasts (ECMWF) is used operationally for numerical weather prediction and climate modelling. Earth system modelling in the IFS can be broadly categorized into large-scale and small-scale processes. Large-scale processes can be described by numerically solving the relevant set of differential equations to determine e.g. the general circulation of the atmosphere. Conversely, small-scale processes such as clouds or land surface processes are represented via parameterization. Accurate parameterizations are essential for the overall accuracy of the model. For example, the parameterization of the land surface determines the sensible and latent heat fluxes, providing the lower boundary conditions for the equations of enthalpy and moisture in the atmosphere (Viterbo, 2002).

Lakes are incorporated in Earth system models via parameterization. At ECMWF, the representation of lakes via parameterization was first handled by introducing the Freshwater Lake model FLake (Mironov, 2008) into the IFS. FLake treats all resolved inland waterbodies (i.e. lakes, reservoirs, and rivers which are dominant in a grid cell) and unresolved or sub-grid water (i.e. small inland waterbodies and sea or ocean coastal waters which are present but not dominant in a grid cell). Its main input fields are lake location and lake mean depth. The broad impact of the FLake model (i.e. areas where it is active) and the important role that waterbodies play in human life can be illustrated by analysing ECMWF fields of the fractional land–sea mask and the inland-waterbody cover alongside the population density field (i.e. inhabitants per square kilometre) based on the population count for 2015 from the Global Human Settlement Layers (GHSL) Population Grid 1975–2030 (Freire et al., 2016; Schiavina et al., 2022) at 9 km horizontal resolution.

Globally, FLake is active over 11.1 % of the grid cells; considering only land grid cells, FLake is active over 32.4 % of the points. According to the population data, 64.5 % of densely populated areas (at least 300 inhabitants per square kilometre) are situated within a 9 km radius of a permanent waterbody (i.e. inland water or sea or ocean coast), with 31.2 % being in the vicinity of a waterbody of at least 1 km² – emphasizing how essential waterbodies are in human life. In some regions, this role may even be more crucial than in the others. For example, in North America, 45.7 % of the densely populated areas are close to a 1 km² waterbody; in Australia, where only 0.5 % of the land is populated, two-thirds of the population live within 9 km radius of a permanent waterbody of at least 1 km², with the majority of people living on the ocean coast.

It is a continuous enterprise to update the lake-related physiographic fields used as input by land surface schemes to better represent small-scale surface processes. It is, however, challenging to do it accurately as the majority of lakes which are resolved at a 9 km grid spacing have not had their morphology accurately measured, let alone monitored, whilst 28.9 % of land and coastal cells are treated for sub-grid (i.e. covering half or less of a grid cell) water. When introducing an updated lake representation, it is difficult a priori to determine the additional value gained through doing so. There are two key factors here:

• Are the updated fields closer to reality?

• Do the updated fields increase the accuracy of the model predictions?

The first point is straightforward; we want our fields to better represent reality. If the lake depth of some lake is updated from 10 to 100 m, we want to be sure that 100 m is closer to the true depth of the lake. For the second point, even if the updated fields are accurate, are they informative in the sense that they enable us to make more accurate predictions? For instance, the main target of lake parametrization is to reproduce lake surface water temperatures (and therefore evaporation rates). If lake parameterization input fields are updated to better represent different types of inland waterbodies, the time variability of inland waterbodies and/or the lake morphology fields use more in situ measurements. Does this additional information allow for more accurate predictions of the lake surface water temperatures? Is it therefore worthwhile to spend several person-months updating or creating a lake-related field? Since the resulting updated fields are ultimately used operationally, it is essential to ensure the accuracy of the fields and to prevent any potential degradation or instability of the model. This problem of quickly and automatically checking the accuracy and information gain of updated lake-related fields is the aim of this work.

Numerical weather prediction and climate modelling are domains that are inherently linked with large datasets and complex, non-linear interactions. It is therefore an area that is particularly well placed to benefit from the deployment of machine learning algorithms. At ECMWF, advanced machine learning techniques have been used for parameterization emulation via neural networks (Chantry et al., 2021), 4D-Var data assimilation (Hatfield et al., 2021), and the post-processing of ensemble predictions (Hewson and Pillosu, 2021). Indeed, the early successes of these machine learning methods have led to the development of a 10-year roadmap for machine learning at ECMWF (Düben et al., 2021), with machine learning methods looking to be integrated into the operational workflow and machine learning demands considered in the procurement of high-performance computing (HPC) facilities. The ongoing development of novel computer architectures (e.g. GPU, IPU, FGPA) motivates utilizing algorithms and techniques which can efficiently take advantage of these new chips and gain significant performance returns. In this work, we will demonstrate a new technique for the Verification of Earth System ParametERization (VESPER) based on a deep learning neural network regression model. This tool enables the accuracy of an updated waterbody-related field to be rapidly and automatically assessed and the added value that such updated fields bring to be quantitatively evaluated.

This paper is organized as follows. In Sect. 2 we describe the construction of the VESPER tool – the raw input data, the processing steps, and the construction of a neural network regressor. In Sect. 3, we then deploy VESPER to investigate and evaluate updated lake-related fields. A discussion and concluding remarks are made in Sects. 4 and 5, respectively.

2 Constructing VESPER

In order to rapidly assess the accuracy of new surface physiography fields and if their use in the model increases the accuracy with which we can make predictions, a neural network regression model (VESPER, hereafter) that can learn the mapping between a set of input features x and targets y is constructed. In this case, the features are the atmospheric and surface model fields, such as 2 m temperature from ERA5 reanalysis, and the surface physiographic fields, such as orography and vegetation cover used to produce ERA5 reanalysis. See Table 1 for the full list of variables used. The target is the satellite land surface temperature (LST; skin temperature from MODIS Aqua Day MYD11A1 v006 collection). Once trained, VESPER can then make predictions about the skin temperature given a set of input variables, i.e. atmospheric and surface model fields, and surface physiographic fields. In turn, these predictions can then be compared against observations, i.e. satellite skin temperature, and VESPER's accuracy can be evaluated. By varying the number, type, and values of the input features to VESPER and observing how the accuracy of its predictions change, some conclusions on if and how features can increase predictability of an actual atmospheric model can be drawn. Moreover, by isolating geographic regions where the predictions get worse with new or updated surface physiographic fields, areas where these fields might be erroneous or not informative enough can be identified. Due to the inherent stochasticity of training a neural network regression model, it is also possible for different models to settle in different local minimums, i.e. the network variance or noise. To understand the significance of this, every VESPER configuration was trained four times, each time with a different random seed.

In this section, we will now describe the data used for the features x and targets y in the neural network regression model, how various data types are joined together, and the details of VESPER’s construction.

2.1 Features and targets

VESPER's input feature selection (see Table 1) followed (i) permutation importance results for atmospheric and surface model fields – only fields with the highest importance were chosen – and (ii) expert choice for surface physiographic fields. As a first attempt, it was decided that testing of the current methodology for lake related information would be conducted; therefore, fields that could be most affected by the presence or absence of water were selected – e.g. if a lake had to be removed then some other surface had to appear, such as bare ground, high or low vegetation, glacier, or even ocean. Moreover the surface elevation had to change. Changes to the orographic fields will have important influences on temperature through e.g. wind or solar heating. Lake depth changes are similarly important, influencing how a lake freezes, thaws, and/or mixes and its overall dynamical range (i.e. changes of temperature and mixed-layer depth). VESPER's target selection followed globally available criteria, and the satellite LST is quite well observed globally and with a high temporal pattern, specifically daily or even several times a day, depending on the location.

Table 1 Input features used for training the neural network model VESPER; atmospheric model fields (time varying) were kept the same in all simulations, and surface physiographic fields (static) were updated when going from the original data based on GlobeCover2009/GLDBv1 (V15 field set) to GSWE/GLDBv3 (V20 field set); in brackets are the variable description (where needed), short name (according to the GRIB parameter database), and units.

2.2 Data sources

There are three main sources of data. The first is a selection of surface physiographic fields from ERA5 (Hersbach et al., 2020) and their updated versions (Choulga et al., 2019; Boussetta et al., 2021; Muñoz Sabater et al., 2021a), used as VESPER’s features. As a shorthand, we will refer to the original ERA5 physiographic fields as version V15 and the updated versions as V20. The second is a selection of atmospheric and surface model fields from ERA5, also used as VESPER’s features. The third is daytime LST measurements from the Moderate Resolution Imaging Spectroradiometer (MODIS) on board the Aqua satellite (GSFC, 2023), used as VESPER’s target variable.

2.2.1 Surface physiographic fields

Surface physiographic fields have gridded information of the Earth’s surface properties (e.g. land use, vegetation type, and distribution) and represent surface heterogeneity in the ECLand of the IFS. They are used to compute surface turbulent fluxes (of heat, moisture, and momentum) and skin temperature over different surfaces (vegetation, bare soil, snow, interception, and water) and then to calculate an area-weighted average for the grid box to couple with the atmosphere. To trigger all different parametrization schemes, the ECMWF model uses a sets of physiographic fields that do not depend on initial condition of each forecast run or the forecast step. Most fields are constant; surface albedo is specified for 12 months to describe the seasonal cycle. Depending on the origin, initial data come at different resolutions and different projections and are then first converted to a regular latitude–longitude grid (EPSG:4326) at ∼ 1 km at Equator resolution and secondly to a required grid and resolution. Surface physiographic fields used in this work consist of orographic, land, water, vegetation, soil, albedo fields, and their difference between initial V15 and updated V20 field sets. See Tables 1 and 2 for the full list of surface physiographic fields and their input sources; for more details, see IFS documentation (ECMWF, 2021). As this work is focused on assessing the quality of inland-water information, the main surface physiographic fields are lake cover (derived from land–sea mask) and lake mean depth (see Table 2).

(Liu et al., 2015)(Bontemps et al., 2011; Arino et al., 2012)(Liu et al., 2015)(Howat et al., 2014)(Slater et al., 2018)(GLIMS and NSIDC, 2005)(Pekel et al., 2016)(Amante and Eakins, 2009)(Kourzeneva et al., 2012)Choulga et al. (2019)(Weatherall et al., 2015)(Amante and Eakins, 2009)(Choulga et al., 2014)(Choulga et al., 2014)(FAO, 2003)(Schaaf et al., 2002)

Table 2 List of input datasets for the surface physiographic fields for V15 and V20 field sets. V15X and V20X are identical to V15 and V20, respectively, but with the addition of saline lake cover and monthly varying lake cover fields.

To generate V15 fractional lake cover, the GlobCover2009 global map (Bontemps et al., 2011; Arino et al., 2012) is used. This map has a resolution of 300 m, corresponds to the year 2009, and covers the latitudes 85° N–60° S; corrections outside these latitudes for the polar regions are included separately. In the Arctic, no land is assumed; in the Antarctic, data from the high-resolution Radarsat Antarctic Mapping Project digital elevation model version 2 (RAMP2; Liu et al., 2015) are used. To generate V20 fractional lake cover, more recent higher-resolution datasets and updated methods have been used (Choulga et al., 2019). The main data source is the Joint Research Centre (JRC) Global Surface Water Explorer (GSWE) dataset (Pekel et al., 2016). The GSWE is a 30 m resolution dataset from Landsat 5, 7, and 8, providing information on the spatial and temporal variability of surface water on the Earth since March 1984; here, only permanent water was used for lake cover generation as it provided a more accurate inland-water distribution on an annual basis (Choulga et al., 2019). Differences between V20 and V15 lake cover fields (see Fig. 1) are consistent with the latest global and regional information: (i) the increase in lake fraction in V20 compared to V15 over northern latitudes is due to permafrost melt leading to a new thermokarst lake emergence and due to a higher-resolution input source and its better satellite image recognition methodologies; (ii) the reduction in lake fraction in V20 compared to V15 can have several reasons, like anthropogenic land use change (e.g. the Aral Sea, which lies across the border between Uzbekistan and Kazakhstan, has been shrinking at an accelerated rate since the 1960s and started to stabilize in 2014 with an area of 7660 km², 9 times smaller than its size in 1960; GlobCover2009 describes the Aral Sea in 1998, when it was still only 2 times smaller than its 1960 extent, whereas GSWE provides a more up-to-date map.), the use of only permanent water (e.g. Australia, where GlobCover2009 over-represents inland water as most of these lakes are highly ephemeral, e.g. the endorheic Kati Thanda–Lake Eyre fills only a few times per century; the GSWE updates to this region therefore include only generally permanent water, removing all seasonal and rare ephemeral water.), and changes in the ocean and inland-water separation algorithm (e.g. northeast of Russia).

To generate V15 lake mean depth (see Fig. 2), the Global Lake DataBase version 1 (GLDBv1; Kourzeneva et al., 2012) is used. GLDBv1 has a resolution of 1 km and is based on 13 000 lakes with in situ lake depth information; outside this dataset, all missing data grid cells (i.e. over ocean and land) have a 25 m value; field aggregation to a coarser resolution is done by averaging. Overestimation of lake depth in the summer season can result in strong cold biases and in the winter season a lack of ice formation. To generate V20 lake mean depth, an updated version GLDBv3 (Choulga et al., 2014) is used. GLDBv3 has the same resolution of ∼ 1 km but is based on 1500 additional lakes with in situ depth information (in addition to bathymetry information over all Finnish navigable lakes), it introduces a distinction between freshwater and saline lakes (this information is currently not used by FLake), and it suggests the method to assess the depth of lakes without in situ observations using geological and climate type information; field aggregation to a coarser resolution is done by computing the most occurring value. Verification of GLDBv1 and GLDBv3 lake depths against 353 Finnish lake measurements shows that GLDBv3 exhibits a 52 % bias reduction in mean lake depth values compared to GLDBv1 (Choulga et al., 2019). For further details on lake distribution and depth and the representation of lakes by ECMWF in general, see Choulga et al. (2019) and Boussetta et al. (2021).

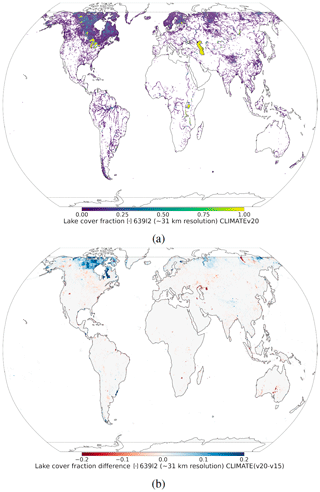
Figure 1 At ∼ 31 km resolution: (a) V20 fractional lake cover and (b) difference between V20 and V15 lake covers. Over northern latitudes, the inland-water increase in V20 compared to V15 is due to a higher-resolution input source and its better satellite image recognition methodologies, as well as thawing permafrost; the inland-water reduction in V20 compared to V15 is due to anthropogenic land use changes (e.g. Aral Sea) or due to the use of only permanent water (e.g. Australia), which was proven to better represent the inland-water distribution on annual basis.

To expand the V15 and V20 lake description (to V15X and V20X, respectively), their salinity and time variability information was generated. Even though static permanent water fits better to describe the inland-water distribution on average all year round, some areas (in the tropics especially) could benefit from having monthly varying information as they have a very strong seasonal cycle where the size, shape, and depth of a lake changes over the course of the year, leading to a significant change in modelling the lake temperature response. Similarly, saline lakes behave very differently to freshwater lakes since increased salt concentrations affect the density, specific heat capacity, thermal conductivity, and turbidity, as well as evaporation rates, ice formation, and ultimately the surface temperature. These two properties of time variability and salinity are often related; it is common for saline lakes to fill and dry out over the course of the season, which naturally also affects the relative saline concentration of the lake itself. To create a monthly varying lake cover, first, 12 monthly fractional land–sea masks based on JRC Monthly Water History v1.3 maps for 2010–2020 were created. Since the annual lake maps were created taking into account a lot of additional sources, the extra condition on the monthly maps that the monthly water is equal to or greater than permanent-water distribution from the fractional land–sea mask is enforced. To create an inland salt lake cover map, the GLDBv3 salt lake list was used. First, in order to identify separate lakes on a ∼ 1 km resolution lake cover (by lake cover we mean the maximum lake distribution based on 12 monthly varying lake covers), small sub-grid lakes and large lake coasts are masked, i.e. grid cells that have a water fraction less than 0.25. Next, the number of connected grid cells in each lake (i.e. connected with sides only) in the 1 km grid is computed. Then, only lakes that have 100 or more connected grid cells are vectorized¹ as, at the ERA5 resolution of ∼ 31 km, the grid cells are quite large and can include a mixture of freshwater and saline lakes. Finally, saline lake vectors are selected by filtering vectors which have no saline lake point from GLDBv3 – in total, there were 147 large salt lake vectors, which were further used to filter non-saline lakes at a 1 km resolution lake cover, finally aggregated to a 31 km resolution. In the future, it is planned to revisit this field and extend the list to include additional data. Note that all non-lake-related climate fields such as vegetation cover or orography were updated in the V20 field set compared to V15 only in relation to the changing lake fields (i.e. if the fraction of the lake in the grid cell increased then other fractions like vegetation or bare ground should have decreased accordingly).

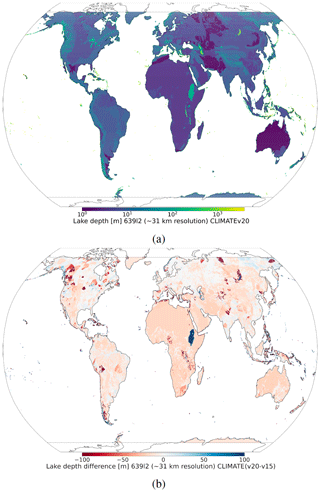
Figure 2 At ∼ 31 km resolution: (a) V15 lake mean depth in metres and (b) difference between V20 and V15 lake mean depths. In general, lake mean depth decreased in V20 compared to V15 due to the use of mean depth indirect estimates based on geological and climate information instead of default 25 m values over lakes without any information.

2.2.2 ERA5

Climate reanalyses combine observations and modelling to provide calculated values of a range of climactic variables over time. ERA5 is the fifth-generation reanalysis from ECMWF. It is produced via 4D-Var data assimilation of the IFS cycle 41R2 coupled to a land surface model (ECLand, Boussetta et al., 2021), which includes lake parametrization by FLake (Mironov, 2008) and an ocean wave model (WAM). The resulting data product provides hourly values of climatic variables across the atmosphere, land, and ocean at a resolution of approximately 31 km with 137 vertical sigma levels up to a height of 80 km. Additionally, ERA5 provides associated uncertainties of the variables at a reduced 63 km resolution via a 10-member ensemble of data assimilations (EDA). In this work, ERA5 hourly surface fields at ∼ 31 km resolution on a reduced Gaussian grid are used. The Gaussian grid’s spacing between latitude lines is not regular, but lines are symmetrical along the Equator; the number of points along each latitude line defines longitude lines, which start at longitude 0 and are equally spaced along the latitude line. In a reduced Gaussian grid, the number of points on each latitude line is chosen so that the local east–west grid length remains approximately constant for all latitudes (here, the Gaussian grid is N320, where N is the number of latitude lines between a pole and the Equator). The main field used from ERA5 is skin temperature (i.e. the temperature of the uppermost surface layer, which has no heat capacity and instantaneously responds to changes in surface fluxes), which forms the interface between the soil and the atmosphere. Skin temperature is a theoretical temperature computed by linearizing the surface energy balance equation for each surface type separately, and its feedback on net radiation and ground heat flux is included; for more information, see ECMWF (2021). ERA5 skin temperature verification against the MODIS LST ensemble (i.e. all four MODIS observations were used, namely Aqua day and night and Terra day and night) over the 2003–2018 period showed good correlation between two datasets; errors between ERA5 and the MODIS LST ensemble are quite small; i.e. the spatially and temporally averaged bias is 1.64 K, the root mean square error (RMSE) is 3.96 K, the Pearson correlation coefficient is 0.94, and the anomaly correlation coefficient is 0.75 (Muñoz Sabater et al., 2021b). ERA5 skin temperature verification against the Satellite Application Facility on Land Surface Analysis (LSA-SAF) product over the Iberian Peninsula showed a general underestimation of daytime LST and a slightly overestimate during the nighttime, relating the large daytime cold bias with vegetation cover differences between ERA5 surface physiography fields and the European Space Agency’s Climate Change Initiative (ESA-CCI) land cover dataset. The use of ESA-CCI low and high vegetation cover over ERA5 has been shown to lead to a complete reduction in the large maximum temperature bias during summer (Johannsen et al., 2019). ERA5 data are obtained via the Copernicus Climate Data Store (CDS; Munoz Sabater, 2019).

2.2.3 Aqua-MODIS

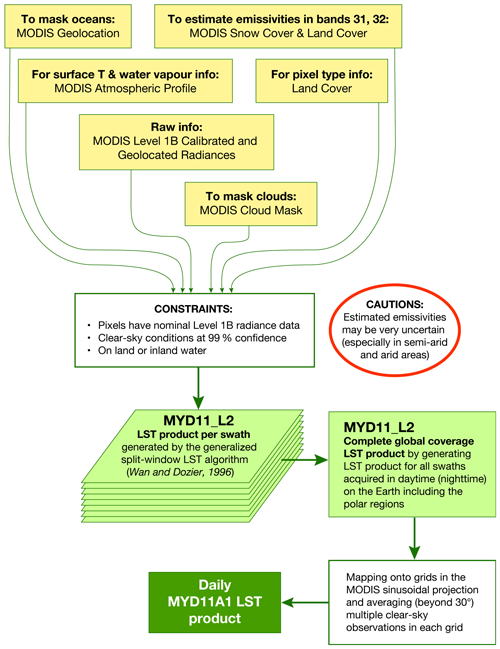
Aqua (Parkinson, 2003) is a NASA satellite mission which makes up part of the Earth Observing System (EOS). Operating at an altitude of 700 km, with an orbital period of 99 min, its orbital trajectory passes south to north with an Equatorial crossing time, in general, of 13:30 (local time, 01:30 pm). This post-meridian crossing time has led to it sometimes being denoted as EOS PM. Launched in 2002 with an initial expected mission duration of 6 years, Aqua has far exceeded its initial brief and, until recently, has been transmitting information from four of the six observation instruments on board. Here, we use information only from the MODIS instrument. MODIS can take surface temperature measurements at a spatial resolution of 1 km (the exact grid size is 0.928 km by 0.928 km), operating in the wavelength ranges of between ∼ 3.7–4.5 and ∼ 10.9–12.3 µm. In addition to surface temperature measurements that were used in this work, MODIS can take observations of cloud properties, water vapour, ozone, etc. Here, the MYD11A1 v006 (Wan et al., 2015) collection that provides daily LST measurements at a spatial resolution of 1 km on the sinusoidal projection grid SR-ORG:6974 (takes a spherical projection but a WGS84 datum ellipsoid) is exercised. Daily global LST data are generated by first applying a split-window LST algorithm (Wan and Dozier, 1996) on all nominal (i.e. 1 km at nadir)-resolution swaths (scenes) with a nominal coverage of 5 min of MODIS scans along the track acquired in the daytime and secondly by mapping results onto an integerized sinusoidal projection; for more details, see Wan et al. (2015) and Fig. 3. Validation of this product was carried out using temperature-based method over different land cover types (e.g. grasslands, croplands, shrublands, woody areas) in several regions around the globe (i.e. the United States, Portugal, Namibia, and China) at different atmospheric and/or surface conditions; the best accuracy is achieved over the United States sites, with an RMSE lower than 1.3 K (Duan et al., 2019). At large-view angles and in semi-arid regions, the data product may have slightly higher errors due to rather uncertain classification-based surface emissivities and heavy dust aerosols effects. In addition, the MODIS cloud mask struggles to eliminate all cloud- and/or heavy-aerosol-contaminated grid cells from the clear-sky ones (LST errors in such grid cells can be 4–11 K and larger). Validation of this product over five bare-ground sites in north Africa (in total, 12 radiosonde-based datasets were validated) showed that the mean LST error was within ±0.6 K (with the exception of one dataset, where the mean LST error was 0.8 K) and that the standard deviations of the LST errors were less than 0.5 K (Duan et al., 2019). In this work, to reduce the number of daily data to be stored and manipulated over multiple years, prior-use LST data are (i) filtered to contain only cloud-free data and (ii) averaged to a 4 km at the Equator resolution on a regular latitude–longitude grid, EPSG:4326 (note that only grid cells which have eight or more valid observations at 1 km resolution are averaged over; otherwise, they are classified as missing data).

Figure 3 A brief step-by-step explanation of the LST algorithm for the MYD11A1 v006 collection.

2.3 Joining the data

To join selected ERA5 global fields on a reduced Gaussian grid at ∼ 31 km resolution (information in UTC, 24 hourly maps per day) with Aqua-MODIS global LST data on a regular latitude–longitude grid at 4 km resolution (information in local solar time, one map per day), both datasets need to be in the same time space. First, it is necessary to determine the absolute time (i.e. UTC) at which the MODIS observations were taken. Since, in general, all Aqua observations are taken at 13:30 local solar time, it can be related to a UTC via observation longitude following Eq. (1):

$$\begin{array}{}\text{(1)}& \mathrm{UTC}=\mathrm{local}\mathrm{solar}\mathrm{time}-{\displaystyle \frac{\mathrm{longitude}}{\mathrm{15}}},\end{array}$$

where longitude is in degrees, and UTC is rounded to the nearest hour. This conversion is inexact since there is an additional correction as a function of the latitude, yet it is recommended by the official MODIS Products User’s Guide (Wan et al., 2015); given the short orbital period of Aqua, these additional higher-order corrections are expected to be typically small and, for our purposes, can be neglected. Also, the assumption that all Aqua observations are taken at 13:30 local solar time was checked (see Fig. 4). The annually averaged mean time difference at 31 km resolution (i.e. daily differences between local solar time of observations and 13:30 at 1 km resolution were first aggregated to 31 km resolution using averaging and were then aggregated in time over 1 year) is 0.16 h or 10 min, with the mean absolute error (MAE) being 0.46 h or 28 min and the RMSE being 0.61 h or 37 min (current values correspond to the 70^∘ N–70^∘ S region for the year 2019 but are confirmed to be approximately identical for each year of the 2016–2019 period). Since the temporal resolution of ERA5 data is hourly, the assumptions inherent to Eq. (1) are sufficiently accurate. Over the poles (i.e. 90–70° N and 70–90° S), satellite sweeps overlap significantly, and, in general, conversion becomes less accurate (daily time differences can reach more than ±3.5 h); thus, these areas were not included in the analysis.

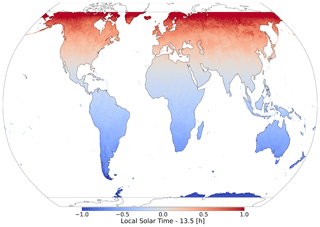
Figure 4 The annually averaged mean time difference of Aqua-MODIS and assumed local solar time of 13:30 for the year 2019 at 31 km resolution. Time differences are generally sub-hourly and grow at greater latitudes so data over 90–70° N and 70–90° S are excluded.

Once the Aqua-MODIS time of observation is converted to UTC, the Aqua-MODIS data at ∼ 4 km resolution are matched in time and space to ERA5 information in the following way:

1. Take a single Aqua-MODIS LST observation at a particular point on the MODIS grid.

2. Select the ERA5 global hourly map matching Aqua-MODIS LST observation time in UTC.

3. Find the nearest point on the ERA5 grid to that MODIS grid point.

4. Repeat the previous steps for every Aqua-MODIS observation.

5. Group matched data pairs with the ERA5 grid points, averaging over all the Aqua-MODIS observations that are associated with each ERA5 point.

At the end of this process, selected ERA5 fields are mapped to a single Aqua-MODIS time of observation, and Aqua-MODIS LST data are mapped (i.e. multiple Aqua-MODIS observations could be averaged over; see Fig. 5a) to a reduced Gaussian grid at 31 km resolution; averaged Aqua-MODIS observations are considered to be the ground truth (i.e. targets y) that VESPER is trying to predict. To better understand VESPER’s grid cell results at 31 km resolution, additional information was computed from Aqua-MODIS, namely (i) the total number of valid observations per month and year (see Fig. 5a) and (ii) the average LST error based on Aqua-MODIS quality assessment (i.e. quality flag; see Fig. 5b). Based on this additional information, it can be concluded that areas with a sparse number of observations in general have more uncertain LST values; exceptions are Alaska in the United States and in the Anadyrsky District in Russia (area 30^∘ east and west from 180^∘ E around 70–60^∘ N); the deserts of Australia; and the Kalahari Desert in Namibia, Botswana, and South Africa, where majority of the vast number of observations have only good or average quality.

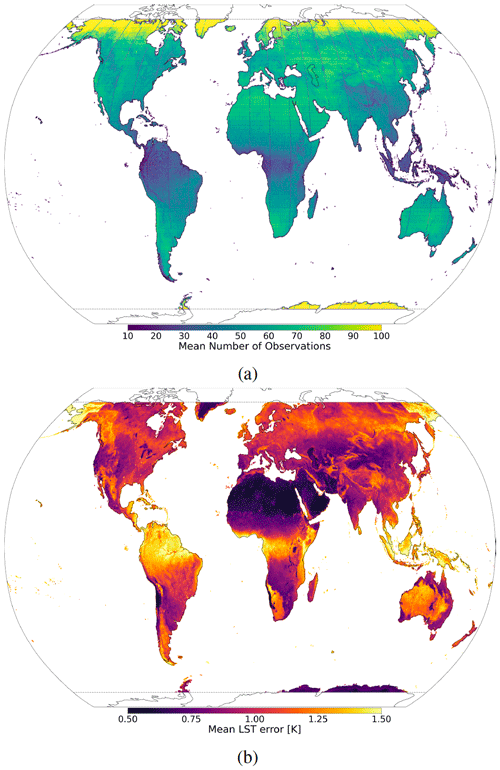
Figure 5 For 2019 at ∼ 31 km resolution: (a) mean daily number of Aqua-MODIS observations mapped to each ERA5 data point. The swath of the Aqua satellite is clearly visible, with more observations over the 70–60° N and 60–70° S areas as Aqua follows a polar orbit, south to north, and with fewer observations over the Equator, complex orography areas (such as the Himalayas, the Andes, and the Rocky Mountains), and the Siberian Tundra (due to increased cloud cover). (b) Average error in the Aqua-MODIS LST measurement. The raw Aqua-MODIS data at 1 km resolution provide categorical LST errors with bins of ≤ 1, 1–2, 2–3, and > 3 K. When averaging to the coarser resolution, a weighted average over the 1 km grid cells is computed, where the median bin value is used, and 5 K is used for the > 3 K bin. This information helps to understand that an abundant number of observations does not automatically mean a high quality of LST (e.g. Australia).

For step (3) in the joining process, we use a GPU-accelerated k nearest-neighbours algorithm (RAPIDS, 2022), where nearness on the sphere between two points is measured via the Haversine metric, i.e. the geodesic distance H, following Eq. (2):

$$\begin{array}{}\text{(2)}& H=\mathrm{2}\arcsin \left(\sqrt{{\sin }^{\mathrm{2}}\left({\displaystyle \frac{\mathit{\delta }\mathit{\theta }}{\mathrm{2}}}\right)+\cos {\mathit{\theta }}_{\mathrm{1}}\cos {\mathit{\theta }}_{\mathrm{2}}{\sin }^{\mathrm{2}}\left({\displaystyle \frac{\mathit{\delta }\mathit{\varphi }}{\mathrm{2}}}\right)}\right).\end{array}$$

This is applicable for two points with coordinates of latitude θ_1,2 and longitude ϕ_1,2 and $\mathit{\delta }\mathit{\theta }={\mathit{\theta }}_{\mathrm{2}}-{\mathit{\theta }}_{\mathrm{1}}$ and $\mathit{\delta }\mathit{\varphi }={\mathit{\varphi }}_{\mathrm{2}}-{\mathit{\varphi }}_{\mathrm{1}}$.

2.4 Constructing a regression model

VESPER is trained to learn the mapping between features x and targets y (i.e. mapping ERA5 to MODIS), a regression problem. For this purpose, a fully connected neural network architecture (also known as a multi-layer perceptron), implemented in TensorFlow (Abadi et al., 2016), was used. Whilst more advanced architectures are available, for the purposes of this work, the model is sufficient enough, exhibiting generally fast and dependable convergence. The networks built have differing numbers of nodes in the input layer, depending on the number of predictors (see Table 3). For all networks constructed, we use four hidden layers and a layer width that is half that of the input layer width. ADAM (Kingma and Ba, 2017) is used as an optimization scheme; the learning rate is set to $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{4}}$; and the default values for the exponential decay rate for the first- and second-moment estimates are set to 0.900 and 0.999, respectively. The network is not trained for a fixed number of epochs but is instead trained until the validation error reaches a minimum. Techniques for maximizing the performance of a network via hyperparameter optimization are now well established (Yu and Zhu, 2020; Bischl et al., 2021). However, for the purposes of this work, no attempt to tune hyperparameters was made; only some reasonable default values which were assumed to be good enough were applied. Some exploration of different hyperparameter configurations was undertaken, but for these data, the prediction accuracy is mostly independent of the hyperparameter configuration, subject to standard and reasonable hyperparameter choices. Whilst a more advanced automatic hyperparameter optimization method may have enabled a slightly higher performance of VESPER, our ultimate purpose is not to generate the most absolutely accurate prediction possible but is instead to have two predictive models which can be compared. In the Results section below, it will be shown that the variation in performance due to input feature modifications is far greater than the variation due to the hyperparameter choices.

VESPER was trained on selected atmospheric and surface model fields from ERA5 for 2016 (see Table 1), certain static version of the surface physiographic fields (see Table 2), and Aqua-MODIS LST for 2016. Once VESPER was fully trained, it was used to predict LST over the whole globe for 2019. Going forward, as a shorthand, we will refer to VESPER trained using the e.g. V15 field set as VESPER_V15 (in general, VM is a field set version, and VESPER_VM is a VESPER model trained using the fields from the VM field set). See Table 3 for an explicit definition of all the VESPER models. The training and test years were chosen simply as recent, non-anomalous years so that the updated surface physiographic fields could be checked. All VESPER versions are trained with ERA5 fields for 2016 and with the main surface physiographic fields from V15 field set. Then, depending on the version, some or all additional surface physiographic fields (see Table 1) are added. VESPER’s predictions can be compared to the initial ERA5 skin temperatures and actual Aqua-MODIS LST for 2019. Figure 6 shows the mean absolute errors (MAEs) globally in the VESPER_V15 LST predictions relative to the Aqua-MODIS LST, along with the corresponding MAEs in the predicted skin temperature from ERA5. We can see that VESPER_V15 was able to learn corrections to ERA5, especially in the Himalayas and sub-Saharan Africa, as well as Australia and the Amazon Basin, leading to the globally averaged MAE reduction for predicted LST; the MAE relative to Aqua-MODIS LST, averaged over all grid points, was 3.9 K for ERA5 and 3.0 K for VESPER_V15.

Table 3 List of input files for different VESPER versions; see Table 1.

Figure 6 Mean absolute error (MAE, δK) of LST predictions for 2019 at 31 km resolution based on differences between (a) ERA5 skin temperature and Aqua-MODIS LST and (b) between VESPER_V15 (i.e. VESPER trained with V15 surface physiographic fields) and Aqua-MODIS LST. It can be seen that VESPER_V15 managed to learn corrections over regions with complex surface fields such as the Himalayas (lots of orography), sub-Saharan Africa (lots of vegetation), and the Amazon Basin (lots of water + vegetation).

As the focus of this study is lake-related fields, and since lakes occupy only 1.8 % of the Earth’s surface and are distributed very heterogeneously (Choulga et al., 2014), analysis of the results was restricted to areas where there have been significant changes in the surface lake physiographic fields. By significant changes, we mean a change in any of the surface field when going from V15 to V20 (and to V15X or V20X) of ≥ 10 % (≥ 0.1 for fractional fields); for example, if lake or vegetation cover changed from 0.1 in V15 to 0.3 in the V20 field set, this change is classified as significant. The choice of ≥ 10 % as a significance cut-off was adopted as it proved to be a good trade off between having a sufficient number of grid points to inspect and the strength of the effect of changing the input field. As the cut-off percentage increases, fewer points are selected, albeit with more severe changes to their surface fields, whereas when the cut-off percentage decreases, more points are selected, but it becomes more difficult to disentangle the change in the prediction accuracy from VESPER’s training noise (training noise is discussed below). Alternative cut-off percentages were briefly explored, but conclusions in terms of the results remained broadly unchanged. All grid cells selected for the analysis can be classified according to how the surface fields are updated when going from V15 to V20:

• Lake updates. The changes in the lake cover cl and lake depth dl are significant, but the changes in ocean and glacier glm fractions are not. This corresponds to grid cells where lakes have been added or removed. Lake ground updates is a sub-category where the additional constraint that the change in the high or low vegetation fractions cvh or cvl are not significant is in place. This then corresponds to the exchange of lakes for bare ground or vice versa.

• Vegetation updates. The change in the high vegetation fraction cvh is significant, but the change in lake cover cl is not significant. This corresponds to grid cells where large features like forests and woodlands have been updated, exchanged for bare ground or low vegetation.

• Glacier updates. The change in the glacier cover glm is significant. This corresponds to any areas where the fraction of glacier ice has been updated.

The training of a neural network is inherently stochastic – the same model trained twice with the same data can settle in different local optima and so make different predictions. To make our conclusions robust against this training noise, each VESPER model is in turn trained four times. For each MODIS ground truth, we then have four LST predictions per model. We define the training noise as the standard deviation σ in the VESPER predictions for the same input fields; i.e. each VESPER_VM model will have a corresponding training noise σ_VM. To assess the changes in LST predictability due to the use of the updated surface physiographic fields instead of the V15 field set (default), we compare the mean absolute error (MAE) between different VESPER models using the simple metric δ_VM:

$$\begin{array}{}\text{(3)}& {\mathit{\delta }}_{\mathrm{VM}}={\mathrm{MAE}}_{\mathrm{VESPER}\mathrm{\_}\mathrm{VM}}-{\mathrm{MAE}}_{\mathrm{VESPER}\mathrm{\_}\mathrm{V}\mathrm{15}},\end{array}$$

where VM represents one of the field set versions V20, V20X, or V15X, and MAE is computed over the whole prediction period of 2019. In turn, the MAE is the error between the prediction of a VESPER model and the Aqua-MODIS LST, i.e.

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{\mathrm{MAE}}_{\mathrm{VESPER}\mathrm{\_}\mathrm{VM}}& ={\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N|{\mathrm{LST}}_{i,\mathrm{VESPER}\mathrm{\_}\mathrm{VM}}\\ & -{\mathrm{LST}}_{i,\mathrm{MODIS}}|,\end{array}\end{array}$$

for the total number of predictions N within a given grid cell classification. A negative δ_VM then indicates that the VESPER_VM LST prediction is more accurate than the VESPER_V15 prediction and vice versa.

3 Results

3.1 Evaluation of updated lake fields

To understand if there is a way to automatically and rapidly assess the accuracy of updated and/or new surface physiography fields and if their use in the atmospheric model increase predictability, we can compare the prediction accuracy of different VESPER_VM models. Generally, VESPER’s training noise is confirmed to be smaller than differences in LST predictions by different VESPER configurations so changes in LST predictability can be meaningfully attributed to the changes in surface physiographic fields. Particular situations where the training noise becomes significant are discussed below.

As a first attempt, lake-related information is assessed, namely lake cover (and land–sea mask and glacier cover as they are used for lake cover generation) and lake mean depth, which were created from scratch using new up-to-date high-resolution input datasets (see Table 2) for the V20 (and V20X) field set; other surface physiographic fields (see Table 1) were regenerated from the same input sources as in the initial V15 field set but taking into account that lake-related fields were changed. In cases when existing in V15 lake cover water was removed in V20, it could be replaced by the high or low vegetation, glacier, or bare ground. We now analyse the results for each of the four categories of grid cell in detail (see Table 4 for the results of each category aggregated over the whole globe).

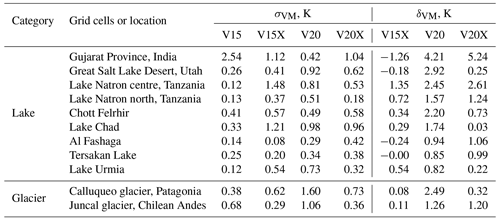
Table 4 Globally averaged differences δ_VM between mean absolute error (MAE) of VESPER_VM and VESPER_V15 LST for 2019 at  31km resolution (where M denotes V15X, V20, V20X field sets) per grid cell category. Negative δ_VM values indicate an increase in LST predictability due to the use of the updated surface physiographic fields instead of the V15 field set (default), and positive δ_VM values indicate a decrease in the LST predictability and suggest the presence of erroneous information in the surface physiographic fields. Training noise values σ_VM are generally much smaller than the variance between different VESPER configurations, indicating that changes in LST predictability are mainly due to changes in the surface physiographic fields. The quoted noise is the standard deviation of the prediction errors of Fig. 7.

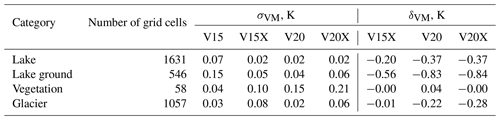
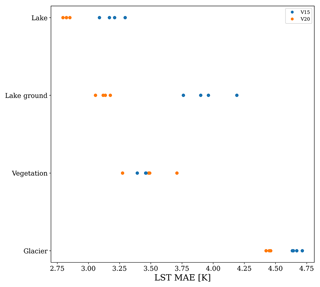
Figure 7 Distribution of prediction errors in the LST for each of the four grid point categories for each iteration of V15 and V20. For the lake, lake ground, and glacier categories, the improvement in V20 relative to V15 is much greater than the intrinsic model noise, with all V20 predictions outperforming all V15 predictions. For the vegetation category, the predictions of V15 and V20 are much more noisy, and it is difficult to draw any conclusions for the category as a whole.

Figure 8 Distribution of prediction errors in the LST for all grid points in the lake updates category for VESPER_V15 and VESPER_V20. Each prediction errors is in turn the average of four trained iterations of the VESPER model. The predictions of VESPER_V20 are evidently an improvement over VESPER_V15, especially for grid points with large LST errors.

3.1.1 Category: lake updates

The lake updates category shows significant improvements in LST predictability if using the V20 field set instead of the V15 – the prediction accuracy increased globally (over 1631 grid cells), on average, by 0.37 K. For the lakes category, the training noise in V20 was generally small with σ_V20∼0.02 K, with the V15 predictions being a little more noisy with σ_V15∼0.07 K, but this noise is much less than the improvement – as can be seen in Fig. 7, every V20 iteration significantly outperforms every V15 iteration. In Fig. 8, we plot the distribution of the mean LST error (averaged across each of the four trained VESPER iterations) for all lake grid points for both V15 and V20. Evidently, the V20 field significantly improved the high-tail behaviour relative to V15, as well as shifting the median of the distribution to lower errors. Particular regions where the V20 physiographic fields notably improved performance were in Australia and the Aral Sea (e.g. Fig. 9). These are two major regions where ephemeral lakes were removed and where the inland-water distribution was made to be up to date, as discussed in Sect. 2.2.1. In addition to the areas with a notable improvement in the prediction accuracy, there are some noteworthy regions where the predictions got worse (see red points in Fig. 9), suggesting inaccuracies or lack of information in the updated surface physiographic fields. A few of the most noteworthy grid cells (see red points highlighted with green circles in Fig. 9 and also Fig. 11) are as follows:

• Northern India. This grid cell lies in the state of Gujarat, India, close to the border with Pakistan. Here, ${\mathit{\delta }}_{\mathrm{V}\mathrm{20}}=+\mathrm{4.21}$, with σ_V15=2.54 and σ_V20=0.416. The lake fraction was increased from 0.59 in V15 to 0.71 in the V20 field set, along with the lake depth increase from 2.58 to 3.76 m. However, this point lies on a river delta within the Great Rann of Kutch, a large area of salt marshes (see Fig. 10a), known for having highly seasonal rainfall, with frequent flooding during the monsoon season and a long dry season. The surface itself also undulates with areas of higher sandy ground known as medaks and with greater levels of vegetation. It is evidently a complex and highly time-variable area, and an additional static fraction of fresh water provided via V20 field set is not sufficient.

• Salt Lake City, North America. This grid cell lies within the Great Salt Lake Desert, just to the west of the Great Salt Lake, Utah, US. Predictions of VESPER_V20 are worse than those of VESPER_V15, with ${\mathit{\delta }}_{\mathrm{V}\mathrm{20}}=+\mathrm{2.91}$ (σ_V15=0.26 and σ_V20=0.92). Whilst the training noise is significant here, it is less than the δ_V20 value, and we can see from Fig. 11 that the VESPER_V20 predictions consistently underperform compared to the VESPER_V15 predictions. The lake fraction was completely removed from over 0.50 in V15 to 0.00 in the V20 field set, meaning that the grid cell is fully covered with bare ground in the V20 field set. Whilst this area primarily is bare ground, satellite imagery also suggests the presence of a presumably highly saline lake (see Fig. 10b); in addition, the area has a large degree of orography and high elevation (∼ 1300 m), which probably further complicates the surface temperature response. A more accurate description that accounts for the seasonality of the surface water and the salinity is necessary here.

• Tanzania. There are two grid cells of interest at the centre and northern edge of Lake Natron, which itself lies southeast of Lake Victoria in Tanzania. For both of these points, VESPER_V20 predictions are less accurate than those of VESPER_V15; for the central point (${\mathit{\delta }}_{\mathrm{V}\mathrm{20}}=+\mathrm{2.45}$, σ_V15=0.12, and σ_V20=0.81; see also Fig. 10c), the lake fraction was increased from 0.04 in V15 to 0.39 in the V20 field set; for the northern edge point (${\mathit{\delta }}_{\mathrm{V}\mathrm{20}}=+\mathrm{1.57}$, σ_V15=0.13, and σ_V20=0.51), the lake fraction was also increased in V20 compared to in the V15 field set, along with a small decrease (∼ 0.1) in the low vegetation fraction. However, Lake Natron is a highly saline lake that often dries out, with high temperatures, high levels of evaporation, and irregular rainfall. It is a highly complex and variable regime that is not well described by simply increasing the fraction of permanent freshwater, and indeed, results suggest that, with the current lake parametrization scheme, it may be beneficial to keep the lake fraction low or to introduce an extra descriptor, e.g. salinity.

• Algeria. This grid point lies in Algeria, at the northern edge of the Chott Felrhir, an endorheic salt lake (${\mathit{\delta }}_{\mathrm{V}\mathrm{20}}=+\mathrm{2.20}$, σ_V15=0.41, and σ_V20=0.49). Similarly to the Great Salt Lake Desert, the lake fraction was completely removed, from 0.33 in V15 to 0.0 in V20. However, Chott Felrhir goes through frequent periods of flooding where the lake is filled by multiple large wadi and corresponding dry periods where the lake becomes a salt pan. As with the Great Salt Lake Desert, it is also a highly variable, complex area that may require additional consideration of the salinity and the seasonality.

• Lake Chad. This grid point contains Lake Chad, a freshwater endorheic lake in the central part of the Sahel (${\mathit{\delta }}_{\mathrm{V}\mathrm{20}}=+\mathrm{1.74}$, σ_V15=0.33, and σ_V20=0.98). Here, the lake fraction was modestly reduced from 0.63 to 0.47. However, Lake Chad is again a highly time-variable regime with seasonal droughts and wet seasons. It is a marshy wetland area, but the vegetation fractions in both V15 and V20 here are zero. Satellite imagery also shows a large fraction of the surface covered by water and vegetation (Fig. 10e).

• Al Fashaga. This grid point lies in a disputed region between Sudan and Ethiopia called Al Fashaga, close to a tributary of the Nile (${\mathit{\delta }}_{\mathrm{V}\mathrm{20}}=+\mathrm{0.94}$, σ_V15=0.14, and σ_V20=0.29). The updated V20 fields increased the lake fraction at this point from 0 to 0.14. The grid cell contains the Upper Atbara and Setit Dam Complex. However, the dam was only recently completed in 2018 – during the training period, the damn was still under construction. Consequently whilst the V20 field may be more accurate at the current time, during the period the model was training, the V15 field was more accurate since the damn was not yet built.

• Lake Tuz. This grid cell contains a large fraction of Lake Tuz, as well as the smaller Lake Tersakan, saline lakes in central Turkey (${\mathit{\delta }}_{\mathrm{V}\mathrm{20}}=+\mathrm{0.85}$, σ_V15=0.25, and σ_V20=0.34). Here, the updated physiographic field effectively removed all lake water, with the lake fraction decreasing from 0.14 to 0.005. Whilst the lake is shallow and does dry out in the summer, there is also a large fraction of surface water present (e.g. Fig. 10d), and it is an over-correction to completely remove all lake water at this point.

• Lake Urmia. This grid cell contains Lake Urmia, which is another saline lake in Iran (${\mathit{\delta }}_{\mathrm{V}\mathrm{20}}=+\mathrm{0.81}$, σ_V15=0.12, and σ_V20=0.73). The updated physiographic fields decreased the lake fraction at this point from 0.77 to 0.39. This was in response to the shrinking of Lake Urmia due to long-timescale droughts and the damming of rivers in Iran. However, this drought broke in 2019, and Lake Urmia is now increasing in size again – satellite imagery now shows a large fraction of the grid cell covered by water (Fig. 10f).

The lake ground updates sub-category, which restricts analysis to only points with no significant change in the vegetation, allows us to more clearly see the effect of adding or removing water to or from bare ground. This sub-category shows even larger improvements in LST predictability if using the V20 field set instead of V15 (see Table 4) – the prediction accuracy increased globally (over 546 grid cells), on average, by 0.83 K (σ_V15=0.15 and σ_V20=0.04; see also Fig. 7). This indicates that, whilst the updated lake fields are globally accurate and informative, providing, on average, over the globe over the course of a year nearly an extra Kelvin of predictive performance, the updates to the vegetation fields tamper this performance gain, indicating a potential problem with the vegetation fields.

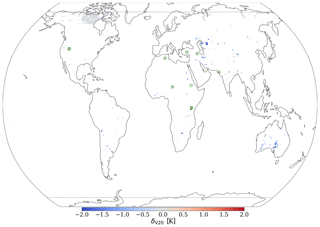
Figure 9 Differences in the prediction error MAE between VESPER_V20 and VESPER_V15, (i.e. δ_V20) for 2019 at 31 km resolution for the lake updates category (i.e. where lake cover changed significantly). Generally, VESPER_V20 LST predictions are more accurate, for example in the Aral Sea and Australia, indicating that the V20 field set is informative and accurate. Particular points where VESPER_V20 LST prediction gets notably worse compared to VESPER_V15 are highlighted with green circles and discussed in the text.

Figure 10 Satellite imagery of (a) Gujarat Province, India; (b) Great Salt Lake Desert, Utah; (c) Lake Natron, Tanzania; (d) Lake Tersakan and Lake Tuz; (e) Lake Chad; and (f) Lake Urmia. These are the problematic lake update points highlighted in Fig. 9, where the V20 predictions are worse than the V15 predictions. Generally the updated V20 fields remove water, only considering permanent water. However, these regions have highly time-variable waters, which are better captured, on average, by the V15 fields. The images are centred on the grid box coordinates.

Figure 11 As Fig. 7 for selected locations in the lakes grid point category where the added V20 data result in worse predictions when compared to V15.

3.1.2 Category: vegetation updates

The vegetation updates category restricts analysis to grid points with significant change in terms of high vegetation cover, where the high vegetation cover is substituted with either low vegetation or bare ground and vice versa. For this category, the prediction accuracy of V20 decreased globally (over 58 grid cells only), on average, by 0.04 K. However, this shift is much smaller than the training noise between successive VESPER iterations (σ_V15=0.04, σ_V20=0.15) and so it is hard to make definitive statements about the performance of the updated vegetation physiographic fields as a whole (see e.g. Fig. 13). The best we can say is that the updated V20 vegetation fields offer no global improvement in the LST prediction accuracy.

Figure 12 Satellite imagery of grid cells in (a) Siberut Island, Indonesia, and (b) South Island, New Zealand. For both grid cells, according to the updated V20 field set, there should be no vegetation, just bare ground. VESPER identified these erroneously updated areas.

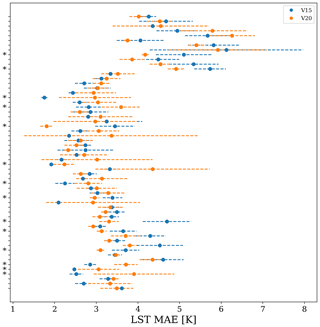
Figure 13 Distribution of prediction errors in the LST for VESPER_V15 and VESPER_V20 for all 58 grid points in the vegetation category. There is evidently a large degree of noise, with predictions from both generations of the VESPER model highly overlapping. Points with reduced training noise are highlighted with a ^*.

If we isolate our analysis to individual grid points where the training noise is small (highlighted by ^* points in Fig. 13), we can discern that there are multiple locations where the high vegetation fraction was decreased (often quite drastically to zero), specifying that there should just be bare ground, but thorough inspection of these areas with satellite imagery, it was revealed that they should in fact be covered with high vegetation (see e.g. Fig. 12) and that updating the V20 high vegetation cover was erroneous for these grid cells. Moreover, for this subset of less noisy grid points, the strength of the drop in LST predictability in VESPER_V20 compared to VESPER_V15 is approximately linearly dependent on the degree of reduction in high vegetation fraction, when the vegetation is replaced with bare ground (i.e. δ_V20 is maximally positive when the grid cell that was fully covered with forest becomes fully covered with bare ground – high vegetation cover is reduced to zero). These erroneous grid cells in V20 vegetation fields are likely to appear during the interpolation. The errors in these regions will in turn corrupt the LST predictions and mitigate the gain from a more accurate representation of the lake water. The majority of grid cells in this category (57 out of 58) are modified in this way, where the high vegetation fraction is severely reduced; however, due to the large degree of training noise and the small number of points, it is difficult to draw any definitive conclusions for the category as a whole.

3.1.3 Category: glacier updates

The glacier updates category in general shows an improvement in LST predictability in VESPER_V20 compared to in VESPER_V15 (see Table 4) – the prediction accuracy increases globally (over 1057 grid cells), on average, by 0.22 K (σ_V15=0.03, σ_V20=0.02), most notably around the Himalayas, on the land on either side of the Davis Strait, and in British Columbia and the Alaskan Gulf. Analogously to the lakes updates category, whilst the introduction of the V20 glacier cover generally improves LST predictions, there is a small selection of grid points where the prediction gets worse. These are heavily concentrated in the Southern Hemisphere, in particular on the southwestern edge of South America and the southern Shetland Islands (which lie closer to Antarctica) and some parts of the Himalayas. This deterioration in performance in these areas is not due to the erroneous update of V20 glacier cover but is related to the Aqua-MODIS data (i.e. sparse availability due to clouds and less certain due to orography; see Fig. 5a). Consequently, VESPER finds it difficult to make accurate predictions in this region, and for these points, there is often a large degree of training noise, with considerable overlap between VESPER_V15 and VESPER_V20. If grid cells with a scarce number of Aqua-MODIS observations (i.e. the mean number of Aqua-MODIS observations per day over the year per ERA5 grid cell is > 50) are removed from the analysis then the worst-performing grid cells become excluded, yet a few areas where VESPER_V20 underperforms compared to VESPER_V15 remain. For example, there is a grid cell in Chilean Patagonia that contains the Calluqueo glacier, close to Monte San Lorenzo, where δ_V20=2.49 (σ_V15=0.38, σ_V20=0.62). This grid cell has been updated in the V20 field set in comparison to V15 by strongly increasing glacier cover from 0.0 to 0.44), decreasing low vegetation cover (from 0.22 to 0.12) and high vegetation cover (from 0.16 to 0.09), as well as modestly decreasing lake cover (from 0.02 to 0.007). According to satellite imagery (see Fig. 14a), the glacier only occupies a small fraction of the overall grid cell, and the updated glacier cover may have been an over-correction. Moreover, this is a complex orographic area with snowy mountain peaks at high altitudes and deep valleys; therefore, the temperature response due to the glacier feature could be atypical compared to e.g. the Alaskan Gulf or the Davis Strait. There is also substantial vegetation cover in the valleys that may not be properly described. A similar point is in the Chilean Andes (see Fig. 14b), by the Juncal glacier, with δ_V20=1.26 (σ_V15=0.68, σ_V20=0.29). Here, the V20 glacier cover was increased to 0.25 compared to 0.00 in V15. Again, this may have been an over-correction as the glacier constitutes only a small fraction of the grid cell. As with the Calluqueo glacier, this is also an area with lots of orography and so could have an atypical temperature response. For both of these points, VESPER managed to identify potential inaccuracies in updated glacier cover and once again proved itself to be a useful tool for quality control of surface physiographic fields.

Figure 14 Satellite imagery of (a) Calluqueo glacier, Patagonia, and (b) Juncal glacier, Chile. In the updated V20 field set, the assumption for region (a) is that almost half is ice covered with little vegetation; for region (b), the assumption is that a quarter is covered with glacier. These assumptions seem to be insufficiently accurate or informative, as identified by VESPER.

3.2 Evaluation of new lake fields: monthly water and salt lakes

From the examples above, it is evident that VESPER enables the user to quickly identify regions where the update to surface physiographic fields was beneficial (e.g. Aral Sea) and where it was not (e.g. Lake Natron). In turn, areas where LST predictions do not improve as expected can be inspected, and erroneous or sub-optimal representations of the surface physiographic fields can be identified. This then provides key information on how and where to introduce additional corrections to better represent these more challenging or complex regions. Some of these problematic areas are now explored in more detail, and additional surface physiographic fields are introduced with the help of VESPER.

Particular regions where VESPER was struggling to make accurate LST predictions – especially with the updated V20 field set, which only includes permanent water – were either areas with a large degree of temporal variability (e.g. lakes which flood and dry out periodically) or areas with saline rather than freshwater lakes. Clearly, if the size, shape, and depth of a lake change over the course of the year, these are going to be hugely significant factors in modelling the lake temperature response. Similarly, saline lakes behave very differently to freshwater lakes since increased salt concentrations affect the density, specific heat capacity, thermal conductivity, and turbidity, as well as evaporation rates, ice formation, and ultimately the surface temperature. These two properties of time variability and salinity are often related; it is common for saline lakes to flood and dry out over the course of the season, which naturally also affects the relative saline concentration of the lake itself.

Currently, neither VESPER_V15 nor VESPER_V20 has any information regarding the salinity of the lakes or their time variability. Indeed, FLake is specifically a freshwater lake model! This information can be introduced by including a global saline-lake cover and monthly varying lake cover as additional VESPER input features and then using VESPER to rapidly assess the accuracy of these new surface physiography fields and to evaluate whether their use in the model increases LST predictability. We define additional models (see Table 3 for a summary of all VESPER models used in this work); VESPER_V20X uses the same field set and is the same as VESPER_V20 but with additional saline-lake cover and monthly varying lake cover. The results of this model in comparison with VESPER_V15 and VESPER_V20 are summarized in Tables 4 and 5. We will now explore the influence of the additional saline maps and monthly lake maps in more detail.

3.2.1 Category: lake updates

The lake updates category shows no significant difference in LST predictability globally when using the V20X field set instead of V20, with ${\mathit{\delta }}_{\mathrm{V}\mathrm{20}\mathrm{X}}={\mathit{\delta }}_{\mathrm{V}\mathrm{20}}=-\mathrm{0.37}$ (comparable training noise). For the lake ground category, there is a modest increase, with ${\mathit{\delta }}_{\mathrm{V}\mathrm{20}\mathrm{X}}=-\mathrm{0.84}$ compared to ${\mathit{\delta }}_{\mathrm{V}\mathrm{20}}=-\mathrm{0.83}$, but this is within the training noise. For some of the problematic lake grid cells highlighted in Table 5, the addition of saline maps and monthly lake maps does improve the LST predictability relative to VESPER_V20. For the Great Salt Lake Desert, Chott Felrhir, Lake Chad, and Lake Urmia, VESPER_V20X is a notable improvement over VESPER_V20, with δ_V20X = $\mathrm{0.248},\mathrm{0.726},\mathrm{0.029}$, and 0.22, respectively. The difference in δ_V20X and δ_V20 for these points is greater than the training noise. If we take as a case example the grid point in the Great Salt Lake Desert, the improvement from using VESPER_V20X over VESPER_V20 is 2.667 K  ± 1.10 K. At this point, there is a strong correction from the monthly lake maps (mean value 0.16) and the salt maps (mean value 0.56). This improvement is to be expected given the known strong salinity and time variability in the region, and so it is a nice confirmation to have these updated fields verified by VESPER. It is also notable that the variation in the monthly lake maps at this point is very large, with a standard deviation in the lake fraction over 12 months of 0.18. At the start of the year, the corrections from the monthly maps are very large; then, as the year progresses, the magnitude of the corrections generally decreases as the lake dries out. Such a large variation is again difficult to ever capture with a static field.

Table 5 As in Table 4 for specific grid points discussed in the text where the VESPER_V20 predictions are worse than VESPER_V15 (i.e. δ_V20 is positive).

It is, however, notable that, (a) for all of the problematic lake points that we have discussed, δ_V20X is positive, and (b) there are multiple points (e.g. Gujarat Province) where VESPER_20X exhibits no improvement over VESPER_V20 within training noise. Given all the extra information provided to the more advanced VESPER_20X model, this is unusual; it suggests that either (i) some of the additional information is erroneous in these regions, or (ii) the temperature response is atypical to the rest of the globe. For point (ii), this means that the additional information is not predictive in these regions. Including this additional information in our neural network increases the complexity of the model, which may in turn increase its training noise. This is likely the reason behind point (b) – the updated fields are not sufficiently informative but do increase the training noise, and so we see no improvement from using VESPER_V20X. For example, for Gujarat Province, σ_V20=0.416, but σ_V20X=1.04. In order to explore the hypothesis of point (i), we train one further model, VESPER_V15X (again, see Table 3 for a summary of all VESPER models used in this work). This VESPER iteration is analogous to VESPER_V20X, being simply the VESPER_V15 model with the additional monthly maps and salt lake fields included. Importantly, it does not have the updated physiographic correction fields from V20. Globally, this model performs worse than the V20 models, as we might expect – for example, in the lake updates category, δ_V15X=−0.20 (σ_V15X=0.02) compared to δ_V20=−0.37 K. However, VESPER_V15X does perform well at a number of the these problematic lake points (see Table 5). For seven out of the nine selected lake points, VESPER_V15X outperforms VESPER_V20X. For example, in Gujarat Province, the improvement from using V15X over V20X is 6.5 K ±1.53. This suggests that our hypothesis for point (i) is correct and that, for some grid points, the V20 fields are less accurate than the V15 fields. For a subset of points, VESPER_V15X also outperforms VESPER_V15 (e.g. for Gujarat Province, ${\mathit{\delta }}_{\mathrm{V}\mathrm{15}\mathrm{X}}=-\mathrm{1.26}$), but the difference is typically within or close to the training noise (e.g. for Gujarat, σ_V15X=1.12), and so it is hard to draw any strong conclusions. These examples illustrates again how VESPER can identify particular regions where the fields are inaccurate, as well as emphasizing the need, more generally, for accurate descriptions of seasonally varying inland water and saline-lake maps in Earth system modelling.

3.2.2 Category: vegetation updates

Whilst the vegetation updates category explicitly deals with areas where the lake fraction does not change when going from V15 to V20, many of the grid points in this category do contain some kind of waterbody, often lying close to the coast or else containing lakes or large rivers. Information on the salinity and temporal variability of these water bodies could then influence the prediction accuracy. By providing the additional information in VESPER_20X, the error relative to VESPER_V15 is reduced modestly to $-\mathrm{3}\times {\mathrm{10}}^{-\mathrm{4}}$, although, as we saw before with the vegetation category, the noise is large at σ_V20X=0.21, and so it is difficult to draw any further definitive conclusions. Similar arguments apply to VESPER_15X.

3.2.3 Category: glacier updates

We would expect the additional information provided by the V20X fields to be particularly effective for glacial grid points. Glacier ice is naturally found next to waterbodies which freeze and thaw over the year, and the salinity of water will also influence this freezing. Therefore, accurate additional information from the monthly lake maps and the saline maps should prove to be useful in these more time-variable regions. We do observe a small improvement globally, with ${\mathit{\delta }}_{\mathrm{V}\mathrm{20}\mathrm{X}}=-\mathrm{0.28}$ compared to ${\mathit{\delta }}_{\mathrm{V}\mathrm{20}}=-\mathrm{0.22}$; however, this difference is comparable to the training noise, with σ_V20X=0.06. This training noise could be slightly deceptive; three out of our four VESPER_V20X iterations outperform every VESPER_V20 iteration in the glacier updates category. The fourth VESPER_V20X iteration is somewhat anomalous – the increased network complexity could mean that the model did not converge well for that particular iteration for the glacier grid points. Since the updated V20 glacier fields are generally accurate globally, we saw no particular improvement in using VESPER_V15X to within the training noise. This suggests that the additional monthly lake maps are only useful if the underlying representation of static water is sufficiently accurate. Considering the particular glacier grid points we discussed previously in Sect. 3.1.3, the additional monthly lake maps were particularly useful for the Calluqueo glacier, with δ_V20X=0.32 compared to δ_V20=2.49 (σ_V20=1.59, σ_V20X=0.73). However we saw no improvement to within the training noise for the Juncal glacier

3.2.4 Time series

Thus far, we have been focusing mainly on the δ_VM metric averaged over the entire year of the test set. It is also of interest to explore how the prediction error for each of the three models varies with time. This is demonstrated in Fig. 15 for each of the four updated categories that we have discussed.

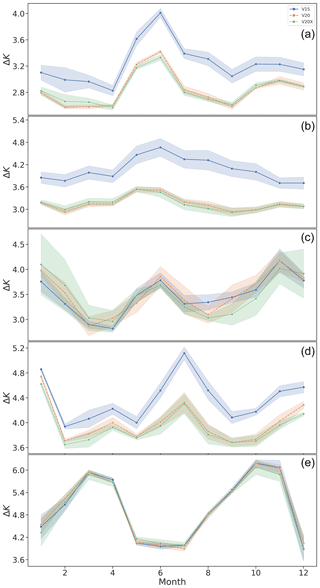
Figure 15 Mean prediction error in the surface temperature ΔK, averaged over all grid points, for each of the three models over the course of the test year for (a) lake updates; (b) lake ground updates; (c) vegetation updates; (d) glacier updates, Northern Hemisphere; and (e) glacier updates, Southern Hemisphere. The shaded regions show the 1σ training noises. For the lake categories, all models follow the same general profile, with the VESPER_V20 and VESPER_V20X models generally outperforming VESPER_V15 model over the year.

For the lake updates and lake ground updates, categories we can see that all the model predictions track the same general profile, with the error peaking in the Northern Hemisphere's summer months. This is a result of FLake modelling being the least accurate during the summer as the lake is not fully mixed, and so the mixed-layer depth for lakes is too shallow, resulting in skin temperatures with larger errors. Conversely, in the autumn and spring, the lake is fully mixed, and predictions have the smallest errors compared with observations. A clear hierarchy of models is evident; the VESPER_V20 and VESPER_V20X models consistently outperform VESPER_V15 across the year. This again is strong evidence, highlighted by VESPER, of the value of the updated fields, both static and seasonally varying. We discussed previously how the annually and globally averaged δ_VM values for the lake updates category were highly comparable for VESPER_V20 and VESPER_V20X. We can see from the top panel in Fig. 15 that this equivalence is not consistent over the year. Instead, during the winter months of the Northern Hemisphere, VESPER_V20 and VESPER_V20X are fairly equivalent; VESPER_V20 tends to outperform VESPER_V20X, but the difference is within the model training noise. However, in the central months of the year, VESPER_V20X starts to be slightly more accurate. This is likely for two reasons. Firstly, the monthly lake maps are in fact a climatology and are therefore insufficiently precise to detect the exact ice on–off dates during the winter months, where we have a large number of grid points at high latitudes which will be subject to freezing, nullifying any time variability. The second reason is due to the accuracy of the lake mean depth which strongly drives the freeze-up start dates due to its influence on the heat capacity of the lake. During the warmer months, when lakes thaw, the monthly maps are more accurate as the thawing of lake ice is mainly connected to the atmospheric conditions and not the lake depth, and so the information contained in them can be used to make more accurate predictions.

The lake ground updates time series broadly follows the same general profile as lake updates, but the errors are larger – those grid points where the lakes have been replaced with bare ground were particularly poorly described in V15. Additionally, for lake updates, we see two sharp decreases in the prediction error during ∼ April and September, which are not as strongly reflected in lake ground. This is due to the geographic location of the grid points in each of the two categories; for the lake updates category, the grid points are located primarily in the boreal zones and so are subject to freezing and thawing over the course of the year, leading to a strong seasonality due to the lake mixing that we have discussed. The sharp drop in April corresponds to a time where the lakes are unfrozen and fully mixed. However, the lakes in the lake ground sub-category are less concentrated and much more evenly distributed over the globe and so do not exhibit such a strong seasonality. Consistently with our previous discussion, the training noise makes it difficult to separate the predictions of the VESPER model for the vegetation category across the year. All generations of VESPER_VM follow the same general trend, with errors being maximal at the start and end of the year and minimal during the spring and autumn months.

For the glacier updates category, in order to deal with the separate warming and cooling seasonal cycles over the year, we separate grid points into the Northern and Southern hemispheres. For the Northern Hemisphere, the errors peak for all models in the summer, again due to the lakes not being fully mixed. There is also an uptick in the prediction error for all models during the winter when the freezing is greatest – this indicates how ice cover can strongly influence the LST response. The familiar hierarchy of models is recovered; VESPER_V15 is generally outperformed by the more updated models. In turn, VESPER_V20X shows a general improvement over VESPER_V20 throughout the year, especially during the winter months where the training noise is minimal. Since this is the time when freezing is greatest, this suggests that the additional monthly maps and salt lake maps are particularly useful during this time. For the Southern Hemisphere, the story is different. The errors are smallest during the middle of the year, when we expect the freezing to be greatest. During the spring and autumn, the errors are largest – this is correlated with a decrease in the number of observations, suggesting that this is due to poorer data quality due to cloud cover. In the summer, when the weather is clearer, the errors start to decrease again. Given this variation in the data quality due to cloud cover, it is difficult to draw any strong conclusions, and again, for a stronger performance, cloud-independent data should be used. What is obvious for the Southern Hemisphere glacier grid points is that the VESPER_V20 and VESPER_V20X models struggle to improve VESPER_V15, unlike in the Northern Hemisphere. This suggests that the updated V20 fields are still insufficiently accurate for southern latitudes.

We have also discussed previously particular grid points that will likely show a large degree of temporal variability, or the lakes are saline, and as a consequence the static physiographic V15 and V20 fields struggle to make accurate predictions (e.g. Table 5). In Fig. 16, we present time series for two of these points: the Great Salt Lake Desert, Utah, and Chott Felrhir, Algeria. Both these points were discussed in Sect. 3.1.1, 3.2.1. We can see that, for these two selected points, the hierarchy of models no longer holds. Whilst there is a large degree of variability, and there is no clear separation between models for some parts of the year, generally it can be seen that VESPER_V20 performs worse than VESPER_V15. For the Great Salt Lake, the inaccuracy when using the V20 physiographic fields is most pronounced during the summer months. April, May, and June are some of the wettest months in this region. But the updated V20 fields specify a much smaller lake fraction than in V15 (∼0.5 compared to 0.0). Consequently, during this time, the V20 fields are maximally inaccurate, and the prediction error of the VESPER_V20 model grows accordingly. This indicates again that the updated V20 fields are in fact over-corrections for this area. The inclusion of monthly lake maps and salt lake maps in VESPER_V20X notably reduces the error during these summer months. For Algeria, we can we can see that VESPER_V20 underperforms VESPER_V15 throughout the entire year. For this grid point, the lake was completely removed when updating the V20 fields, with the lake fraction being reduced from ∼0.35 to 0.0. This also appears to have been an over-correction. The separation between the models is most pronounced in the early months of the year; in the winter months, both the prediction error and the variance increase – this period is the wet season in Algeria where the wadi which feed Chott Felrhir fill up. Similarly to the Great Salt Lake Desert, the inclusion of the monthly lake maps in VESPER_V20X improves the prediction accuracy, most notably in the early months of the year. Again, later in the year, the training noise is much greater, and so it is harder to separate the predictions of the model, but on average, VESPER_V20X outperforms VESPER_V20 over the entire year, highlighting the value of these additional physiographic fields and monthly fields.

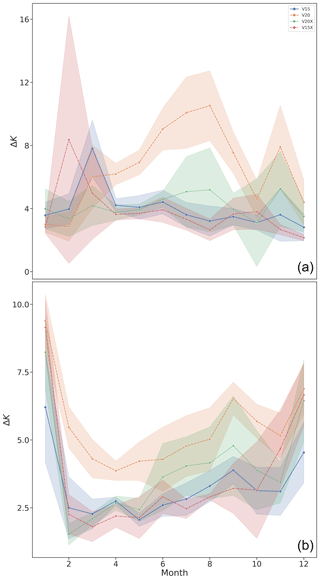
Figure 16 Variation in the prediction error for the grid points at Great Salt Lake, Utah (a), and Chott Felrhir, Algeria (b). There is a large degree of variability, but for both grid points, the VESPER_V20 model is generally less performant than VESPER_V15, indicating that the updated V20 fields are less accurate here. Corrections introduced by the augmented VESPER_V20X model with saline and monthly lake maps outperform those without, indicating the value of these fields in these regions. The shaded regions show the 1σ training noises.

4 Discussion

We have seen how VESPER can quantitatively evaluate the value of updates to the physiographic fields used by land surface schemes, as well as how it can identify areas where the updates are inaccurate. For the former, VESPER was able to show that the major regions where the lake surface parameterization fields were updated – such as the Aral Sea – enjoyed more accurate predictions, which verifies both the accuracy of the fields and their information content with respect to predicting skin temperatures. For the latter, VESPER was able to identify grid points where the predictions became worse with the updated fields, indicating that the updated fields were, in fact, less accurate. More generally, we have also seen how detailed knowledge of surface water fields (e.g. up-to-date permanent water distribution, seasonal water distribution, salt lake distribution) can notably improve the accuracy with which the skin temperature can be modelled; e.g. grid points with significant updates (i.e. where the field has changed by ≥ 10 %) to the lake fields show a mean absolute error reduction in skin temperature globally of 0.37 K (Table 4). Given the performance of VESPER, it may be possible in the future to update or correct the input fields at a high cadence, e.g. yearly or even more frequently.

There are multiple possible further extensions of this work. We have not currently included the errors of the MODIS observations into the VESPER model. During the matching-in-space step relating the ERA and MODIS data (Sect. 2.2), it could be a worthwhile extension to weight the averaged MODIS points by their corresponding errors (e.g. Fig. 5b) when deriving a single MODIS observation for a given ERA grid point. This would then provide a more accurate and confident representation of the true surface temperature at a particular space–time point. Due to the inherent stochasticity of training a model, we have seen that some grid points have a particularly large training noise. To better quantify this effect and to try to draw stronger conclusions for this subset of points, it would also be desirable to train an ensemble of models (ensemble learning) and to combine the predictions from multiple models to reduce this variance. Additionally, our examination of the value of the monthly lake maps is only a preliminary study. It would be of interest to follow seasonal lakes over a longer time period (e.g. decadal) beyond the 12 month maps that we use in order to better quantify their time variability, as well as the differences between years (e.g. if the lake fraction was particularly high in the January of one year but low in the subsequent year). It would also be of interest to try to quantify if VESPER and ECLand respond to changes in the input physiographic fields used by land surface schemes in the same way, which is key to being able to then apply the VESPER results to the full Earth system model development. Since VESPER is trained on ERA5, if we want to model the outputs of the IFS, we must assume that the statistical behaviour of the input fields does not change from ERA to IFS. This is a fair assumption, but it would be interesting to investigate this quantitatively in greater detail. We have focused here primarily on hydrological applications, our primary concern being the ability to evaluate the parameterized water body representation; however, the general application of the method for any updated fields that we want to assess could also be explored. Extension to non-lake hydrological fields like wetland extent or river bathymetry model parameters or even non hydrological fields such as orography would be an interesting further development. The development of a more mature, integrated pipeline for automatically evaluating updated parameterizations could also be a worthwhile pursuit.

Another natural and interesting extension of this work would be to use VESPER to perform a feature importance or sensitivity analysis for the various input fields of the neural network. Additionally, an approach which may prove to be fruitful in the enterprise for an improved parameterized representation of water bodies is to invert the problem and treat VESPER as a function to optimize. That is to say, VESPER can be thought of as a function which takes some inputs – in this case a lake parameterization – and returns a loss metric, i.e. how accurate the predictions are compared to the test set. Given this loss metric, it may then be possible to vary the inputs and use standard optimization techniques to learn the optimal parameterization. Whilst this may be an expensive technique as there are effectively two nested models over which to optimize (for every optimization step in the higher model, one must train the VESPER network from scratch), it could be possible given appropriate hardware or with reduced data focusing just on targeted locations (e.g. What is the best way to represent the lakes in this area?). The loss gradient information can also be used to tune individual features, informing us of whether an input variable should be larger or smaller.

5 Conclusion

Weather and climate modelling relies on accurate, up-to-date descriptions of surface fields, such as inland water, so as to provide appropriate boundary conditions for the numerical evolution. Lakes can significantly influence both weather and climate, but sufficiently accurate representation of lakes is challenging, and the natural changes in water bodies mean that these representations need to be frequently updated. A new method based on a neural network regressor for automatically and quickly verifying the updated lake fields – VESPER – has been presented in this work. This tool has been deployed to verify the recent updates to the FLake parameterization, which include additional datasets such as the GSWE and updated methods for determining the lake depth from GLDBv3. The updated parameterization fields were shown globally to be an improvement over the original fields; for a subset of grid points which have had significant updates to the lake fields, the prediction error in the skin temperature decreased by an MAE of 0.37 K. Conversely, VESPER also identified individual grid points where the updated lake fields were less accurate, such as through the incorrect removal of lake water and losing forests to bare ground, enabling these points to subsequently be corrected. Multiple further extensions of this work, including an extension to non-lake fields and the development of a more mature integrated pipeline, have been discussed.