Assimilation of airborne gamma observations provides utility for snow estimation in forested environments

An airborne gamma-ray remote-sensing technique provides a strong potential to estimate a reliable snow water equivalent (SWE) in forested environments where typical remote-sensing techniques have large uncertainties. This study explores the utility of assimilating the temporally (up to four measurements during a winter period) and spatially sparse airborne gamma SWE observations into a land surface model (LSM) to improve SWE estimates in forested areas in the northeastern US. Here, we demonstrate that the airborne gamma SWE observations add value to the SWE estimates from the Noah LSM with multiple parameterization options (Noah-MP) via assimilation despite the limited number of measurements. Improvements are witnessed during the snow accumulation period, while reduced skills are seen during the snowmelt period. The efficacy of the gamma data is greater for areas with lower vegetation cover fraction and topographic heterogeneity ranges, and it is still effective at reducing the SWE estimation errors for areas with higher topographic heterogeneity. The gamma SWE data assimilation (DA) also shows a potential to extend the impact of flight-line-based measurements to adjacent areas without observations by employing a localization approach. The localized DA reduces the modeled SWE estimation errors for adjacent grid cells up to 32 km distance from the flight lines. The enhanced performance of the gamma SWE DA is evident when the results are compared to those from assimilating the existing satellite-based SWE retrievals from the Advanced Microwave Scanning Radiometer 2 (AMSR2) for the same locations and time periods. Although there is still room for improvement, particularly for the melting period, this study shows that the gamma SWE DA is a promising method to improve the SWE estimates in forested areas.

1 Introduction

Seasonal snowpack is an important freshwater resource in snow-dominated regions, and thus accurate estimation of snow water equivalent (SWE) has been a pressing issue for managing water supply and forecasting snowmelt-driven flood events in a changing climate (Barnett et al., 2005; Cho et al., 2021; Musselman et al., 2021; Sturm et al., 2017). Due to its large variability, spatiotemporally continuous estimates of SWE cannot be generated by the existing in situ measurement network alone (e.g., Dozier, 2011). Large-scale distributions of SWE can be obtained from satellite remote-sensing techniques such as passive microwave sensors (Derksen et al., 2005; Vuyovich et al., 2014); however, these are subject to errors resulting from retrieval algorithm limitations and uncertainties in certain conditions (Kang et al., 2014). Spatiotemporally continuous snow estimates at large scales can be generated by land surface modeling, which however suffer from large uncertainties associated with model physics, parameterizations, and meteorological boundary conditions (Broxton et al., 2016b; Cho et al., 2022; Kim et al., 2021; Raleigh et al., 2015; Yoon et al., 2019). Given the limitations of each method, data assimilation (DA) has been considered a promising alternative to improve the SWE estimation skill as it systematically merges remote-sensing observations with land surface model (LSM) predictions (e.g., Durand et al., 2009; Forman et al., 2012; Kwon et al., 2019; Liu et al., 2013; Zhang et al., 2014).

Given the sensitivity to snow properties and long records of observations, passive microwave brightness temperature (T_B) observations have been used to retrieve SWE or snow depth (e.g., Chang et al., 1990; Derksen et al., 2010; Foster et al., 2005; Kelly et al., 2003; Kelly, 2009) and used within DA frameworks for the assimilation of T_B (e.g., Durand and Margulis, 2006, 2007; Durand et al., 2009; Kwon et al., 2015, 2017; Larue et al., 2018a, b) and T_B-based retrievals of SWE or snow depth (e.g., Dziubanski and Franz, 2016; Kumar et al., 2014). However, as mentioned above, T_B-based approaches are considered suboptimal for the following surface conditions: (1) deep snow, (2) wet snow, and (3) dense forest. Previous studies (e.g., Derksen et al., 2010; Kwon et al., 2019; Lemmetyinen et al., 2015) found that the T_B signal, especially at high frequency (e.g., 36.5 GHz), saturates in deep snowpacks (i.e., when SWE is greater than 100 to 200 mm), which hampers microwave T_B-based SWE estimations. In the presence of wet snow, the T_B sensitivity to SWE decreases because the liquid water of the snowpack dominates the T_B signal due to the high emissivity of liquid water (Clifford, 2010; Walker and Goodison, 1993). Thus, the quality of the T_B-based SWE estimates is degraded under wet snow conditions (Kwon et al., 2019). The T_B sensitivity to SWE also diminishes in forested areas (Roy et al., 2012) because the forest canopy blocks the microwave T_B emission from the snowpack and emits its own T_B signal (Foster et al., 1991), which adds considerable uncertainties in the T_B-based SWE estimates in forested areas (e.g., Kwon et al., 2016; Vuyovich et al., 2014). Vuyovich et al. (2014) showed specifically in the New England area that passive microwave retrievals underestimate SWE, though algorithms that account for the forest fraction show improved performance. Although many enhancements have been proposed for the use of T_B observations in estimating SWE, there are still significant limitations to overcome.

Recently, airborne remote-sensing approaches such as light detection and ranging (lidar) that have the potential to overcome existing challenges have been used within DA schemes to improve snow depth or SWE (e.g., Hedrick et al., 2018; Smyth et al., 2019, 2020). Hedrick et al. (2018) focused on enhancing snow depth estimations over the Tuolumne River basin in California by directly inserting the NASA Airborne Snow Observatory (ASO) lidar snow data into the iSnobal model (Mark et al., 1999). They found that agreement between the lidar snow depth and the updated modeled snow depth was improved as compared to the original modeled snow depth. Smyth et al. (2020) attempted to assimilate the ASO lidar snow depth observations into the Flexible Snow Model to improve snow density and SWE estimations. They showed that DA reduced snow density bias by over 40 % and SWE bias by over 70 % across eight climate zones in the western US and in both wet and dry years. However, the impacts of known limitations such as forest cover and wet snow (in the melting period) within a DA framework have not been widely examined, which were emphasized to be conducted in future research. Furthermore, most previous studies have mainly focused on the western US environments (e.g., mountainous regions), with limited investigations in other regions such as temperate forest environments over the northeastern US.

As a historically well-established remote-sensing technique, the airborne gamma radiation technique provides an opportunity to estimate reliable SWE, because the gamma approach uses the attenuation of the terrestrial gamma-ray emission by water in the snowpack (any phase) with minimal effects by wet snow and dense forest (Carroll, 2001; Carroll and Vose, 1984; Goodison et al., 1984; Tuttle et al., 2018). Since the early 1980s, airborne gamma radiation snow surveys operated by the National Oceanic and Atmospheric Administration (NOAA) Office of Water Prediction (OWP, formerly by the National Operational Hydrologic Remote Sensing Center – NOHRSC) have provided SWE observations to regional NOAA National Weather Service (NWS) River Forecast Centers (RFCs) and other agencies across the United States and southern Canada to support operational flood forecasting system and water supply outlooks (Carroll, 2001; Peck et al., 1980). Recently, Cho et al. (2020b) found that the long-term gamma SWE observations have a remarkable agreement with ground-based gridded SWE products, particularly in forest regions (R values = 0.73 and 0.72 and bias = 0.0 and −1.3 cm for mixed forest and deciduous forest, respectively), implying that the gamma-based SWE observations have the potential to be used in a DA framework to improve modeled SWE estimates. While the airborne gamma SWE products along with in situ snow depth and SWE and satellite-based snow cover areas are currently assimilated into the NWS SNOw Data Assimilation System (SNODAS) to provide the near-real-time, high-spatial-resolution (1 km² gridded) SWE information (Barrett, 2003), how much the gamma radiation SWE retrievals help improve the modeled SWE estimates is not well quantified, particularly in a forested region.

The objective of this study is to evaluate the potential of the airborne gamma SWE retrievals within a DA framework to enhance SWE estimates in a temperate forest environment in the northeastern US. More specifically, we aim to answer three research questions. (1) How much is the modeled SWE improved by assimilating the airborne gamma SWE into a model? (2) Do land surface characteristics such as forest density, slope, and elevation affect the assimilation performance? (3) Can the spatial sparseness of the gamma SWE observations be overcome by employing the localized DA approach? In this study, the Noah LSM with multi-parameterization options (Noah-MP) is used to assimilate the long-term airborne gamma radiation SWE observations with the ensemble Kalman filter (EnKF) scheme within the NASA Land Information System (LIS). This paper is organized as follows. Section 2 provides the study area with general land cover characteristics. Section 3 describes the datasets including the airborne gamma radiation survey, reference SWE data, tree cover fraction, and topographic feature variables. The description of the Noah-MP model with an assimilation scheme is included in Sect. 4. Section 5 presents evaluation results of DA SWE performances with a discussion of the similarities, differences, and new findings in the results with respect to previous studies. Conclusions and future perspectives are given in Sect. 6.

2 Study area

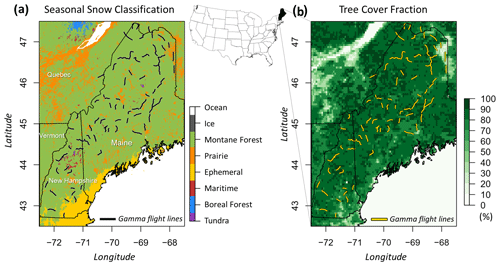
The study area comprises parts of the northeastern United States, including New Hampshire and Maine with heavily forested regions which remain a challenging region in the snow remote-sensing and modeling communities. The dominant seasonal snow class in this region is montane forest (Fig. 1a; Sturm and Liston, 2021). Land cover types are mainly deciduous broadleaf forest and mixed forest. Fractional tree cover over the study area ranges from 70 % to 100 % based on the Vegetation Continuous Field (VCF) map from the NASA Making Earth System Data Records for Use in Research Environments (Hansen and Song, 2018; Fig. 1b). The NOAA OWP airborne gamma snow surveys occur almost every year over the designated flight lines (yellow lines in Fig. 1b).

Figure 1 (a) Sturm and Liston's new seasonal snow classification (Sturm and Liston, 2021) and (b) tree cover fraction (Hansen and Song, 2018) maps of the study area over the northeastern United States with the NOAA airborne gamma flight lines.

3 Data

3.1 NOAA airborne gamma snow survey

The operational airborne gamma radiation snow and soil moisture survey operated by the NOAA's OWP has been conducted to observe near-real-time areal SWE (Carroll, 2001) throughout the United States and the Canadian provinces since 1979. The gamma SWE observations have been used by the NWS Hydrologic Services Program for spring flood forecasts and water supply outlook. The key principle of the gamma SWE technique is the attenuation of the natural gamma-ray signal due to the snowpack (Carroll, 2001; Peck et al., 1980). The gamma SWE values are estimated using the difference in the rates of gamma radioisotopes (⁴⁰K₀, ²⁰⁸Tl₀, and gross count, GC₀) between bare and snow-covered land surfaces (Cho et al., 2020a). The gamma-ray signals for designated flight lines are measured in the fall prior to freezing onset and are then revisited in the winter. A gamma radiation detector equipped on a low-flying aircraft observes the gamma-ray particles. This detector measures terrestrial gamma radiation naturally emitted from trace elements of the three radioisotopes in the upper 20 cm of the soil. The operational approach assumes that the gamma rates over bare ground from the fall survey remain constant during the winter surveys. A typical gamma flight footprint covers approximately 5 km² (300 m wide and 16 km long). The final gamma SWE value is generated as an area-mean value for each flight path. The airborne gamma SWE values are estimated using the equations below:

$$\begin{array}{}\text{(1)}& {\displaystyle }\begin{array}{rl}\mathrm{SWE}\left({}^{\mathrm{40}}\mathrm{K}\right)& ={\displaystyle \frac{\mathrm{1}}{A}}\cdot \left[\ln \left({\displaystyle \frac{\mathrm{40}{\mathrm{K}}_{\mathrm{b}}}{\mathrm{40}{\mathrm{K}}_{\mathrm{s}}}}\right)\right.\\ & \left.-\ln \left({\displaystyle \frac{\mathrm{100}+\mathrm{1.11}\cdot \mathrm{SM}\left(\mathrm{40}{\mathrm{K}}_{\mathrm{s}}\right)}{\mathrm{100}+\mathrm{1.11}\cdot \mathrm{SM}\left(\mathrm{40}{\mathrm{K}}_{\mathrm{b}}\right)}}\right)\right],\end{array}\text{(2)}& {\displaystyle }\begin{array}{rl}\mathrm{SWE}\left({}^{\mathrm{208}}\mathrm{Tl}\right)& ={\displaystyle \frac{\mathrm{1}}{A}}\cdot \left[\ln \left({\displaystyle \frac{\mathrm{208}{\mathrm{Tl}}_{\mathrm{b}}}{\mathrm{208}{\mathrm{Tl}}_{\mathrm{s}}}}\right)\right.\\ & \left.-\ln \left({\displaystyle \frac{\mathrm{100}+\mathrm{1.11}\cdot \mathrm{SM}\left(\mathrm{208}{\mathrm{Tl}}_{\mathrm{s}}\right)}{\mathrm{100}+\mathrm{1.11}\cdot \mathrm{SM}\left(\mathrm{208}{\mathrm{Tl}}_{\mathrm{b}}\right)}}\right)\right],\end{array}\text{(3)}& {\displaystyle }\begin{array}{rl}\mathrm{SWE}\left(\mathrm{GC}\right)& ={\displaystyle \frac{\mathrm{1}}{A}}\cdot \left[\ln \left({\displaystyle \frac{{\mathrm{GC}}_{\mathrm{b}}}{{\mathrm{GC}}_{\mathrm{s}}}}\right)\right.\\ & \left.-\ln \left({\displaystyle \frac{\mathrm{100}+\mathrm{1.11}\cdot \mathrm{SM}\left({\mathrm{GC}}_{\mathrm{s}}\right)}{\mathrm{100}+\mathrm{1.11}\cdot \mathrm{SM}\left({\mathrm{GC}}_{\mathrm{b}}\right)}}\right)\right],\end{array}\end{array}$$

where ⁴⁰K, ²⁰⁸Tl, and GC are uncollided gamma count rates in the top 20 cm of the soil, and SM(40K), SM(208Tl), and SM(GC) are the corresponding soil moisture values by weight (%). Subscripts “b” and “s” indicate bare and snow-covered grounds, respectively. The airborne gamma SWE (SWE_gamma; g cm⁻²) is a value weighted by multiplying the three independent SWE estimates by the weighting coefficients 0.346, 0.518, and 0.136 and summing the three calculated values as below (Carroll, 2001).

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{\mathrm{SWE}}_{\mathrm{gamma}}& =\mathrm{0.346}\cdot \mathrm{SWE}\left({}^{\mathrm{40}}\mathrm{K}\right)\\ & +\mathrm{0.518}\cdot \mathrm{SWE}\left({}^{\mathrm{208}}\mathrm{Tl}\right)+\mathrm{0.136}\cdot \mathrm{SWE}\left(\mathrm{GC}\right)\end{array}\end{array}$$

The final SWE value is reported in the Standard Hydrometeorological Exchange Format (SHEF) product through the NOHRSC website (https://www.nohrsc.noaa.gov/snowsurvey/, last access: 1 September 2023) (Carroll, 2001). In this study for dense forest environments, 1508 airborne gamma SWE observations covering 79 flight lines flown over densely forested environments in the northeastern United States are used from January 1985 to May 2017.

3.2 University of Arizona (UA) SWE

The UA SWE is the ground-observation-based 4 km gridded SWE product developed by consistently assimilating the snow telemetry (SNOTEL) SWE and NWS Cooperative Observer Program (COOP) snow depth measurements (which were first converted to SWE using a newly developed snow density parameterization) with Parameter-elevation Regressions on Independent Slopes Model (PRISM) temperature and precipitation data over the continental United States (Broxton et al., 2016a; Dawson et al., 2017; Zeng et al., 2018). In this study, the UA SWE is used as reference data to evaluate and compare the open-loop and assimilation results from the Noah-MP simulations. The accuracy and robustness of the UA SWE product have been proven by examinations of point-to-point and pixel-to-pixel interpolations (Broxton et al., 2016a, b) as well as evaluations against independent ASO lidar-based SWE and gamma radiation SWE measurements (Cho et al., 2020b; Dawson et al., 2018). Cho et al. (2020b) demonstrated that the UA SWE product strongly agreed with the airborne gamma SWE regardless of land cover type and snow classification over the continental US. This product has been used as a reference SWE for multiple purposes such as quantifying uncertainties in land-surface-modeled SWE (Kim et al., 2021; Zhang et al., 2022), characterizing extreme events (Welty and Zeng, 2021), and estimating extreme values for infrastructure design (Cho and Jacobs, 2020). The daily UA SWE product (version 1) from October 1984 to December 2017 is used in this study, which is publicly available from the National Snow and Ice Data Center website (https://nsidc.org/data/nsidc-0719, last access: 1 September 2023).

3.3 Advanced Microwave Scanning Radiometer 2 (AMSR2) passive microwave SWE

For comparison purposes, the existing satellite-based SWE retrievals from the AMSR2 were also assimilated into this study. The AMSR2 passive microwave sensor is the follow-on instrument to the Advanced Microwave Scanning Radiometer for Earth Observing System on board the Aqua satellite (AMSR-E; Imaoka et al., 2010). AMSR2 on board the Global Change Observation Mission – Water (GCOM-W1) satellite has measured daily scans at 01:30 and 13:30 local time at a 1–2 d revisit frequency since May 2012. The AMSR2 SWE product is calculated by using snow depth estimated from an empirical relationship between snow depth and T_B observations at 18.7 and 36.5 GHz along with higher and lower frequencies and snow density values for each snow class from Sturm's snow classification system (Kelly, 2009; Sturm et al., 2010). The L3 AMSR2 SWE products with the 10 km spatial grid were obtained from the JAXA Globe Portal System GCOM-W1 data-providing service (https://gportal.jaxa.jp/, last access: 1 September 2023). In this study, the AMSR2 data at a descending overpass (01:30) were only used to minimize the wet snow effect.

3.4 Tree cover fraction and topographic features

In this study, we used tree cover fraction (TCF) and topographic feature datasets to compare DA performance by the degrees of them. The NASA Making Earth System Data Records for Use in Research Environments (MEaSUREs) Vegetation Continuous Fields (VCF5KYR; version 1) provide annual global fractional vegetation cover maps with three layers, i.e., percent tree cover, percent bare ground, and percent non-tree vegetation, at 0.05^∘ spatial resolution from 1982 to 2016 (Hansen and Song, 2018). Among them, the percent tree cover was used. To account for the interannual variations in the fractional tree cover, annual TCF values were obtained for each gamma line. The elevation data (0.0083^∘ grid) used in this study were an aggregated map using the Shuttle Radar Topography Mission (SRTM) 90 m resolution elevation data (Farr et al., 2007). The slope and elevation range maps with the same spatial grid were obtained using the “raster” R package (“terrain function” in this package; Wilson et al., 2007). The elevation range, referred to as “topographic heterogeneity” in this paper, was calculated as the difference between the minimum and maximum elevation values in a given grid and its surrounding eight grids (total of nine grids). The three topographic features were computed by the areal-weighted average for each gamma flight footprint.

4 Model and methods

4.1 Noah-MP

Noah-MP (v3.6; Niu et al., 2011; Yang et al., 2011) was employed to simulate snow variables such as SWE and snow depth. Noah-MP was developed based on the original Noah LSM (Ek et al., 2003) with improved representations of biophysical and hydrological processes. A grid cell in Noah-MP consists of one vegetation canopy layer, up to three layers (depending on the whole snow depth) of snowpack, four soil layers (with thicknesses of 0.1, 0.3, 0.6, and 1.0 m from top to bottom), and an unconfined aquifer layer. Regarding snow processes, intercepted snow exists in Noah-MP as solid and liquid phases on the vegetation canopy, and melting–refreezing of intercepted snow, dew–evaporation, and frost–sublimation on the vegetation canopy are explicitly represented in the model. Snow depth and SWE are simulated by considering snow layer compaction by the weight of the overlying snow layers, snow metamorphisms (destructive and melt), and snowmelt–refreeze processes. The physical parameterization scheme options used in the current study are listed here: (1) dynamic vegetation for the vegetation option; (2) the Noah-type soil moisture factor for stomatal resistance (Chen and Dudhia, 2001); (3) the Ball–Berry canopy stomatal resistance scheme (Ball et al., 1987); (4) the TOPography-based hydrological MODEL (TOPMODEL)-based runoff scheme; (5) the simple groundwater scheme (SIMGM; Niu et al., 2007); (6) general Monin–Obukhov similarity theory (M–O; Brutsaert, 1982) for surface-layer drag coefficients; (7) the NY06 scheme (Niu and Yang, 2006) for supercooled liquid water (or ice fraction) in frozen soil; (8) the NY06 scheme (Niu and Yang, 2006) for frozen soil permeability; (9) the modified two-stream radiation transfer scheme (Yang and Friedl, 2003, Niu and Yang, 2004); (10) the Biosphere-Atmosphere Transfer Scheme (BATS) for snow albedo (Yang and Dickinson, 1996); (11) the Jordan91 scheme (Jordan, 1991) for partitioning precipitation into rainfall and snowfall; (12) the original Noah scheme for lower-boundary conditions of soil temperature; and (13) the semi-implicit snow and soil temperature time schemes. An ensemble of model initial conditions was constructed through a two-step spinup procedure. First, a single-member model simulation was run for 40 years from 1 January 1980 to 1 January 2020, driven by NASA Modern-Era Retrospective analysis for Research and Applications, version 2 (MERRA-2; Gelaro et al., 2017) forcing. Then, using a restart file generated in the first step, an additional 3-year spinup from 1 January 1981 to 1 March 1984 was conducted using 20 ensemble members to generate model uncertainty metrics for the DA. The open-loop (OL; without assimilation) and DA experiments were run from 1 March 1984 to 1 October 2017 using the 20-member ensemble initial conditions. A model simulation time step of 15 min was used, and daily mean outputs were evaluated.

4.2 Assimilation scheme

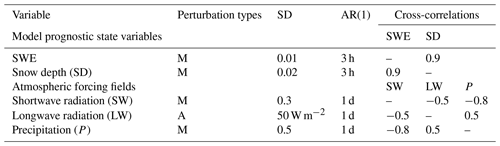
Data assimilation experiments were conducted within the NASA LIS (Kumar et al., 2006, 2008; Peters-Lidard et al., 2007). The EnKF scheme was applied (Reichle et al., 2002) to assimilate airborne gamma-radiation-based SWE retrievals into Noah-MP. In the EnKF scheme, model uncertainty is implicitly represented by the ensemble spread, and an ensemble size of 20 was used in this study. The ensemble spread was generated by perturbing meteorological forcing fields and prognostic model state variables with the assumption of a Gaussian distribution. Perturbation parameters applied during the OL and DA runs are presented in Table 1 and are suggested by Kwon et al. (2021) based on Forman et al. (2012), Kumar et al. (2009, 2014, 2016), and Reichle et al. (2008). When observations (i.e., airborne gamma SWE) are available, EnKF updates forecasted model state variables using the following equation:

$$\begin{array}{}\text{(5)}& M_i^{+}=M_i^{-}+K\left(\mathrm{Obs}-H{M}_i^{-}\right),\end{array}$$

where $M_i^{+}$ is the updated (after assimilation) model state (i.e., SWE), $M_i^{-}$ is the forecasted (before assimilation) model state (i.e., SWE), Obs is the gamma SWE retrievals, H is the observation operator (H=1 in this study), i denotes the ensemble member, and K is the Kalman gain given by

$$\begin{array}{}\text{(6)}& K=\mathrm{Cov}\left(M_i^{-},H{M}_i^{-}\right){\left\{\mathrm{Cov}\left(H{M}_i^{-},H{M}_i^{-}\right)+R\right\}}^{-\mathrm{1}},\end{array}$$

where Cov$\left(M_i^{-},H{M}_i^{-}\right)=\mathrm{Cov}\left(H{M}_i^{-},H{M}_i^{-}\right)$ is the covariance of the model-forecasted SWE and R is the covariance of the observation error. The gamma SWE retrieval error standard deviation of 23 mm was assumed based on realistic error values from previous studies such as Carroll and Vose (1984). Note that assimilation of gamma SWE updates only modeled SWE, and the amount of the SWE update is added to the ice content of the bottom snow layer. Then, snow layer variables such as thickness, snow ice and liquid water content, and the SWE of each snow layer are adjusted using the same methods as used in Noah-MP's snow layer compaction, combination, and subdivision procedures.

Table 1 Perturbation parameters applied to model prognostic state variables and atmospheric forcing fields during the OL and DA runs.

M: multiplicative; A: additive; AR(1): first-order autoregressive temporal correlation.

4.3 DA localization

Due to its sparsity in space, the airborne gamma-radiation-based SWE observations can be limited to use within the DA system. To quantify whether the spatially sparse gamma SWE observations can improve the SWE estimates in the surrounding areas, where the observations are not available, we apply a distance-based localization method to the assimilation procedure. The localization is applied in the assimilation by weighting distances from the flight lines (up to a specified localization distance; r) using the Gaussian decay-based localization method as follows:

$$\begin{array}{}\text{(7)}& W=\exp \left\{{\displaystyle \frac{-d^{\mathrm{2}}}{\mathrm{2}\cdot {\left(\frac{r}{\mathrm{2}}\right)}^{\mathrm{2}}}}\right\},\end{array}$$

where d is the distance between the updated grid cells (i.e., flight lines) and grid cells without observations within a specified localization radius r. The magnitude of the SWE DA adjustment for a grid cell from the assimilation is calculated using the localization weight (W), which is calculated based on the distance (d) from the updated grid cells overlapped by the flight line. If a grid cell is affected by multiple flight lines, an average of the updates is added to the prior SWE estimates of the grid cell. We apply a localization function with six different distances (e.g., 4, 8, 16, 24, 32, and 48 km from the lines). For an evaluation of the DA SWE with a given localization weight, the areal mean DA SWE time series are obtained for an effective area buffered by a specified distance around the gamma flight line. The areal mean OL and UA SWE time series are also obtained in the same way to compare with the corresponding OL and UA SWE values.

5 Results and discussion

5.1 Comparison between DA and OL SWE with airborne gamma SWE

To examine the updated SWE performance over the gamma lines by assimilating airborne gamma observations into Noah-MP, statistical metrics were compared between OL and DA SWE using UA SWE (Fig. 2). The values of the 1:1 slope were closer to 1 (the median slopes of OL and DA were 1.45 and 0.91, respectively) and RMSD values decreased by DA, even though negative biases were found. The absolute SWE bias was higher in the DA as compared to the OL simulation (Fig. 2). However, this was a consequence of the fact that in correcting the overestimated SWE during the accumulation season, the DA introduced a greater underestimation during the melt season (Figs. 3 and 4). The OL SWE largely deviated from the 1:1 linear relationship during the snow accumulation season (i.e., January, February, and March) and early in the snowmelt season (i.e., April). Figure 3 shows that the deviation was significantly reduced through the assimilation of the gamma SWE retrievals even though a reduced R value was obtained.

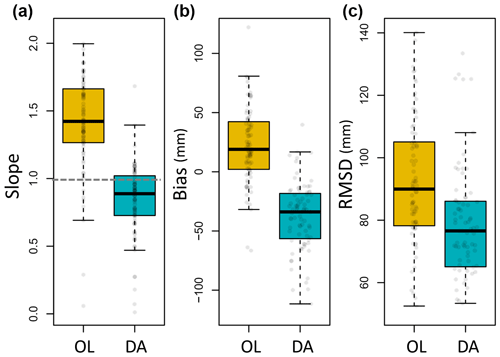
Figure 2 Comparison of statistics between the open-loop (OL) SWE and data-assimilated (DA) Noah-MP SWE estimates by using airborne gamma radiation SWE observations with the University of Arizona SWE from 1985 to 2017: (a) slope from the 1:1 plot, (b) bias, and (c) RMSD from a linear relationship between the estimated SWE and UA SWE.

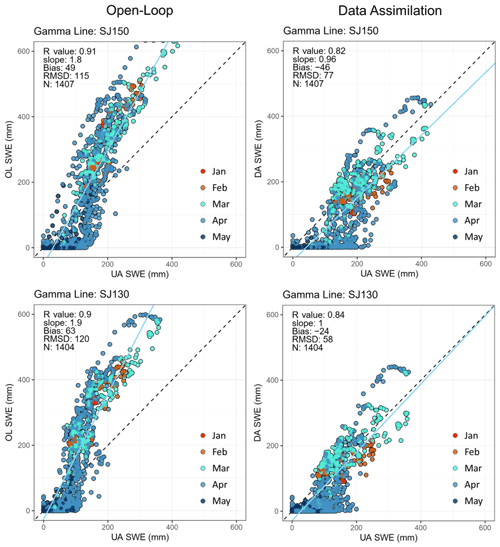
Figure 3 Examples of scatterplots of two gamma flight lines (SJ150 and SJ203) between the Noah-MP SWE estimates (from the OL and DA experiments; y axis) and the daily University of Arizona SWE (x axis) from October 1985 to May 2017 (total of 33 water years). The R value, slope, bias, RMSD, and number of data points (N) in the linear relationship are presented in the figures.

A promising aspect is that the assimilation of the temporally sparse (i.e., only one or two data points at the end of the snow accumulation period and/or early in the snowmelt period) airborne gamma SWE retrievals improved the model estimates of SWE, which was particularly noticeable in some lines and years, such as the gamma line SJ150 in WY1991 (Fig. 4). For comparison purposes, results of assimilating the AMSR2 SWE retrievals were also plotted (green solid line in Fig. 4). The AMSR2 SWE largely deviated (was underestimated) from the UA SWE in densely forested areas, and assimilating the AMSR2 SWE data led to degradation of the SWE estimates. This further emphasizes the effectiveness of the gamma SWE data in improving the model estimates of SWE via assimilation in forested areas, even with fewer available data compared to the AMSR2 SWE. However, the assimilation of the airborne gamma SWE measurements was not able to improve the snow ablation timing due to sparse gamma data during the spring in combination with the overall poor model performance during the melt season. As shown in Fig. 4, compared to the UA SWE, Noah-MP simulated earlier snow melt-out despite the overestimated snow accumulation, which may be attributed to the Noah-MP model structure and physics (e.g., simplified representations of snow layers), parameterization schemes, and/or atmospheric forcing. Also, the peak SWE cannot be corrected if a single gamma SWE flight exists only after the accumulation period. The availability of more frequent gamma observations during both the accumulation and melt seasons could lead to further improvements in estimating SWE in the ablation period, while the model and forcings need to be enhanced.

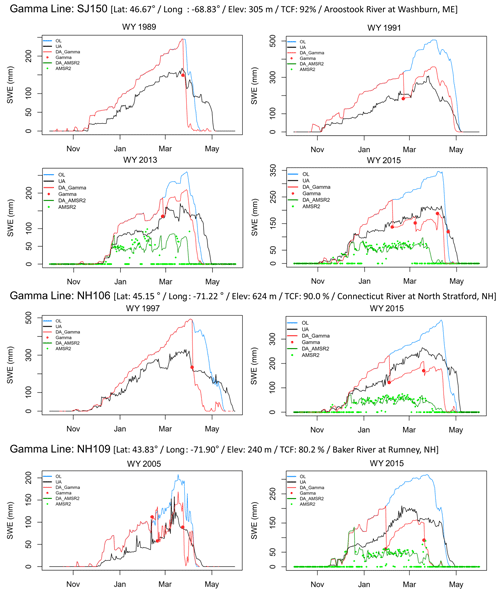
Figure 4 Examples of daily SWE time series of three gamma lines (SJ150, NH106, and NH109) with latitude (“Lat”), longitude (“Lon”), elevation (“Elev”), and tree cover fraction (“TCF”). for individual years including the OL and gamma-data-assimilated (DA_Gamma) Noah-MP SWE estimates along with the passive microwave SWE data from the Advanced Microwave Scanning Radiometer 2 (AMSR2) and AMSR2 data-assimilated SWE (DA AMSR2).

5.2 Effect of land surface characteristics on assimilation performance

To examine the effects of land surface characteristics on the DA performances as compared to the OL, the performances of the gamma SWE DA, presented as differences (i.e., DA minus OL) in the linear regression slope, bias, and RMSD, with the UA SWE were compared using four physical features: TCF, slope, elevation range (i.e., topographic heterogeneity), and elevation (Fig. 5). Two groups of each land surface characteristic were determined by dividing the gamma flight lines into two (i.e., low and high) groups of equal numbers of the flight lines. For TCF, DA SWE in a group with low TCF (less than 85 %) has a lower bias and a lower RMSD than OL SWE, while the DA led to a marginal improvement in the high TCF. Considering that the TCF values in the low group range from 31 % to 84 % (mean: 62 %), DA using airborne gamma SWE improved SWE over densely forested regions.

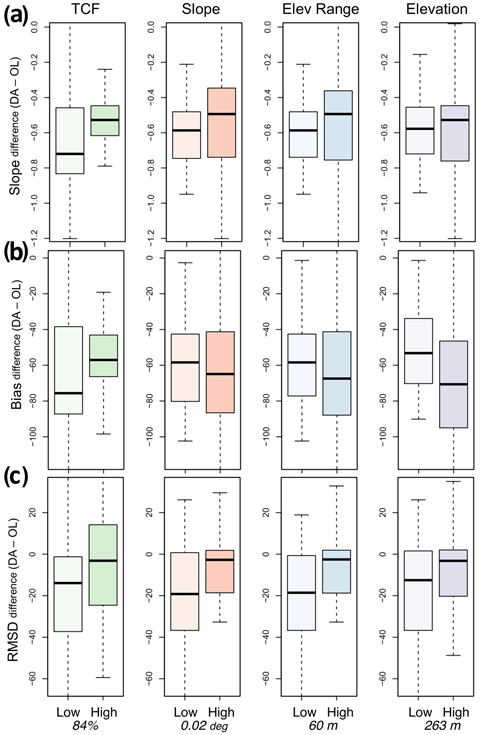
Figure 5 Boxplots of differences in (a) slope from the 1:1 plot, (b) bias, and (c) RMSD between the DA and OL cases (computed as DA minus OL) with respect to TCF, slope (^∘), elevation range (m), and elevation (m). The two groups (low and high) were divided into equal numbers of values. The bottom values are 50 % quantile values for each characteristic.

Differences in the DA performance between the low and high groups were observed for all surface characteristics. The 1:1 slope was improved by DA for both the low and high ranges of all surface characteristics. DA led to larger improvements in the 1:1 slope and RMSD for low TCF, slope, elevation range, and elevation. With respect to the bias, assimilation of the gamma SWE retrievals improved the group-averaged performance for both the low and high groups of the surface characteristics, with larger improvement in low TCF and high slope, elevation range, and elevation. For individual physical characteristics, the added value of the gamma SWE data on the model SWE estimates via assimilation was greater for the low-TCF range based on both bias and RMSD. It is worth noting that the low TCF ranges from 31 % to 84 %, and DA significantly improved the SWE, even for the high TCF (i.e., greater than 85 %). This implies that the gamma-based SWE estimates within DA frameworks can be a promising alternative to traditional T_B-based approaches in forested areas. Comparable DA performance patterns were also obtained for other land surface characteristics. Although the gamma SWE DA exhibited smaller RMSD improvements in areas with higher topographic heterogeneity than those with lower ranges, it was still effective at reducing error statistics.

5.3 Localized DA performance

One of the limitations of the airborne gamma SWE observations is a limited spatial coverage, which is typically 5–7 km² with a swath 300 m wide and 15–30 km long. It is necessary to assess whether the spatially sparse airborne gamma SWE observations can also improve the SWE estimates in areas surrounding the gamma flights via assimilation. Here, the DA experimental cases that employ a localization function with different distances (e.g., 4, 8, 16, 24, 32, and 48 km from the flight lines) are evaluated (Fig. 6). The OL and DA statistics in the figure are calculated using domain-averaged time series of OL and DA SWE over the effective surrounding areas by localization distances with the corresponding UA SWE. For the whole snow season that includes both accumulation and melting periods, the boxplot of the 1:1 slope shows that the localized DA SWE was improved as compared to OL. The slopes of the DA SWE are closer to 1 than the OL's slopes. The bias and RMSD boxplots also show that the DA SWE has lower errors than the OL SWE for all the localization distances, expect for a bias at 48 km which is too low (median: −23 mm). The OL's RMSDs slightly increased at distances up to 16 km (median: 72 mm) and decreased after that, while the DA's RMSD values continually decreased with increasing distances up to 48 km (median: 53 mm). When the statistics were calculated for the accumulation and melting periods separately, lower RMSDs and slopes closer to 1 of the localized DA SWE were found consistently. As previously discussed, the efficacy of assimilating the airborne gamma SWE is greater during the accumulation period, especially for bias and RMSD, than during the melting period. In the melting period, improvements in the RMSD and 1:1 slope with longer distances are achieved, even though biases were consistently negative due to early melting.

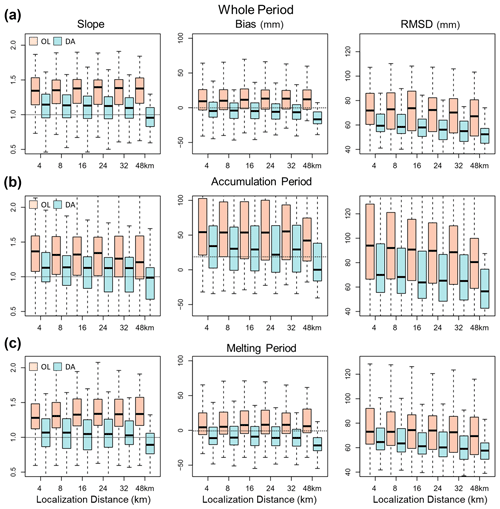
Figure 6 Localized DA and OL Noah-MP SWE performances as compared to the UA SWE with different localization distances (e.g., 4, 8, 16, 24, 32, and 48 km) for the whole (accumulation and melting periods), accumulation, and melting periods, respectively.

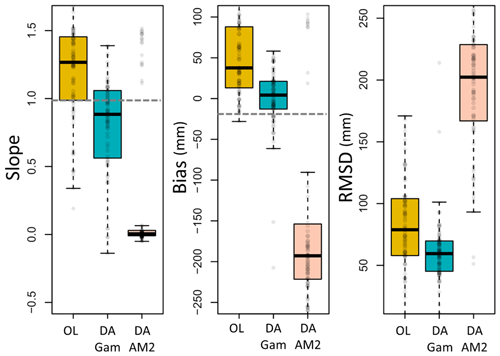
Figure 7 Comparison of the SWE estimation performance between the OL, gamma DA, and AMSR2 DA as compared to the UA SWE at the 16 km localization distance for the mutual DA effective accumulation periods.

To compare the AMSR2 DA outputs to localized gamma DA outputs, we chose the gamma DA outputs at the 16 km localization distance which have similar effective spatial coverages of DA around gamma flight lines (10 km AMSR2 resolution and 16 km localization; Fig. 7). Because the AMSR2 SWE was largely underestimated in the study domain (see Fig. 4), assimilating the AMSR2 SWE measurements did not improve the modeled SWE estimates. All error metrics of the AMSR2 DA SWE were degraded (e.g., median bias: −193 mm and RMSD: 202 mm) as compared to the OL (median bias: 38 mm and RMSD: 79 mm). The localized gamma DA SWE performance is clearly improved based on the error metrics (median bias: 4 mm and RMSD: 59 mm). The positive biases and high slopes of the OL SWE were improved, and the RMSD also decreased by approximately 20 mm.

Overall, we found that the localized DA using the airborne gamma SWE observations improved the model SWE up to 32 km distances, which is supported by the recent study that a single gamma SWE observation spatially represents up to 50 km even in dense temperature forest environments (Cho et al., 2022). The study found that there was strong agreement between the gamma SWE observations and in situ snow course transects (R value: 0.78; RMSD: 53 mm) at distances up to 50 km in the northeastern US. The results in this study indicate that, even though the airborne gamma SWE measurements exist with limited spatial coverages, the combined use of the physical model and DA with the gamma SWE has the potential to improve regional estimations of the SWE.

6 Discussion

We observed two issues associated with the Noah-MP SWE estimates in the study domain: (1) Noah-MP considerably overestimated SWE during the snow accumulation period, while (2) it underestimated SWE (i.e., early snowmelt) during the snow ablation period (see Fig. 4). The former issue was mitigated through the assimilation of the gamma SWE retrievals, whereas the latter issue was not. These issues can be attributed to parameterization schemes and/or atmospheric forcing employed in Noah-MP. Parameterization options for the precipitation-phase partitioning method, ground surface albedo, surface-layer drag coefficient, and snow–soil temperature time scheme can affect the snow simulations (You et al., 2020).

To further analyze the issues, we conducted additional experiments using different parameterization schemes and atmospheric forcing; i.e., the BATS scheme for partitioning precipitation into rainfall and snowfall, the CLASS scheme for snow albedo, the Chen97 scheme for the surface-layer drag coefficient, the fully implicit snow and soil temperature time scheme, and the bias-corrected MERRA-2 forcing were additionally tested. As shown in Fig. 8, the use of the BATS or CLASS snow albedo schemes does not make a significant difference in the SWE estimates as compared to the original OL results. Although the Chen97 or fully implicit schemes are effective at delaying the snow removal date, they add considerably more snow during the snow accumulation period and do not help capture the snowmelt start date (Fig. 8). Furthermore, the effectiveness of each parameterization scheme varies with flight lines and time periods within the study domain, as also emphasized by You et al. (2020). Figure 8 shows that the use of the bias-corrected MERRA-2 forcing is effective at improving the SWE estimates during the snow accumulation period but did not improve the issue of rapid snowmelt. The combined use of the bias-corrected MERRA-2 forcing and the fully implicit scheme leads to improved snow removal timing but largely overestimated SWE during the snow accumulation period. We originally used the uncorrected MERRA-2 forcing to demonstrate the feasibility of the gamma SWE DA for improving the model estimates of SWE, particularly in forested areas, using the atmospheric forcing as is (i.e., without bias correction), which is a typical case of operational prediction or monitoring systems. Here, it is worth noting that assimilation of the gamma SWE data provides similar SWE estimates to the case of using the bias-corrected forcing with a semi-implicit scheme when the gamma SWE observations are available during the snow accumulation period.

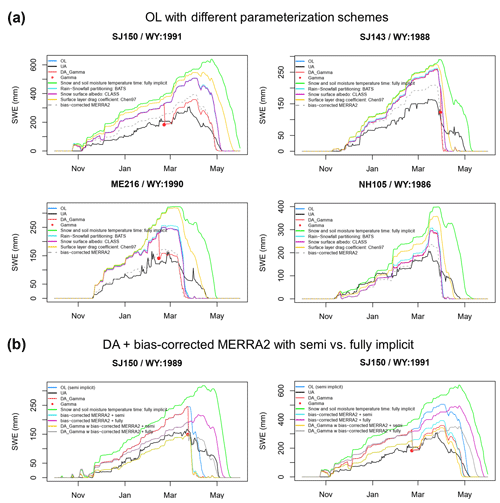
Figure 8 Examples of SWE time series including (a) the additional OL experiments using different parameterization schemes related to snow simulations such as the snow–soil temperature time scheme (semi-implicit vs. fully implicit), partitioning precipitation phase (Jordan91 vs. BATS), ground surface albedo (BATS vs. CLASS), and surface-layer drag coefficient (Monin–Obukhov (M–O) similarity theory vs. Chen97 – original Noah), together with (b) DA runs forced by original vs. bias-corrected MERRA-2 forcings with each snow–soil temperature time scheme, which is a parameterization option largely affecting snow simulations.

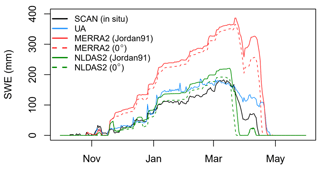
Figure 9 Comparison of SWE time series between four Noah-MP simulations and the Soil Climate Analysis Network (SCAN) ground-based observations at Hubbard Brook, New Hampshire, from 1 October 2002 to 31 May 2003 (https://wcc.sc.egov.usda.gov/nwcc/site?sitenum=2069, last access: 1 September 2023). The four Noah-MP SWE simulations were generated with the Jordan (1991) scheme, a single threshold of 0 ^∘C, and two meteorological forcings (MERRA-2, which is used for OL, and the North American Land Data Assimilation System – NLDAS2), respectively.

Many studies (e.g., Aoki et al., 2011; Augas et al., 2020; Cheng et al., 2008; Jennings et al., 2018; Kwon and Koo, 2014; Lecomte et al., 2011; Livneh et al., 2010; Saha et al., 2017; Suzuki and Zupanski, 2018) have emphasized the importance of the number of snow layers for accurate estimates of snowmelt timing because of its impact on the vertical snow temperature gradient. Augas et al. (2020) demonstrated that the accuracy of the SWE estimates increases with more snow layers, and Lecomte et al. (2011) showed that the agreement between the observed and modeled vertical snow temperature gradients is improved by adding more snow layers. The minimum threshold of the number of snow layers suggested by existing studies ranges from 3 to 20 depending on the locations, periods, and model setups. Different precipitation partitioning methods may lead to differences in the amount of snowfall and the subsequent snowpack (Jennings et al., 2018; Letcher et al., 2022; Suzuki and Zupanski, 2018; Xia et al., 2017), even though there were no significant differences in SWE between the two schemes. We used the scheme of Jordan (1991) in which total precipitation is fractionally divided into rainfall and snowfall using two thresholds of air temperature (i.e., there is no snowfall when T_air > 2.5 ^∘C, all precipitation is snow when T_air≤0 ^∘C, and there is fractional snowfall when 0 ^∘C < T_air≤2.5 ^∘C). However, Noah-MP uses a spatially uniform threshold of T_air. Jennings et al. (2018) found that rain–snow T_air thresholds exhibited significant spatial variability across the Northern Hemisphere, with the warmest thresholds in continental and mountain areas and the coolest thresholds in maritime areas and lowlands. This implies that the high T_air threshold (i.e., 2.5 ^∘C) used in Noah-MP may lead to the overestimated snowfall and subsequently the overestimated snow depth and SWE as the study area is characterized by the maritime snow class. Letcher et al. (2022) demonstrated that the use of cooler T_air thresholds in Noah-MP can improve the estimates of peak SWE in the northeastern US. To verify this, four Noah-MP SWE simulations with the Jordan (1991) scheme and a single threshold of 0 ^∘C with two different meteorological forcings (MERRA-2 and the North American Land Data Assimilation System – NLDAS2) are compared to ground-based SWE observations from 1 October 2002 to 31 May 2003 at Hubbard Brook, New Hampshire, which is within the study domain (Fig. 9). This supports the previous finding that the overestimated SWE with Jordan's scheme was reduced with a single threshold of 0 ^∘C for both forcings. This also shows that the use of regionally reliable meteorological forcings (e.g., precipitation) generates accurate SWE estimations. At the same time, further improvement in the modeled SWE during the melting season can be achieved by employing more sophisticated snow models since the sophisticated snow models with multiple layers of snowpack take into account meltwater infiltration and refreezing within the snowpack (Avanzi et al., 2016; Terzago et al., 2020).

While the model parameter calibration is not conducted here because it is outside the scope of the current study, we acknowledge that the parameter calibration procedure could further improve the model performance for regional applications. Cuntz et al. (2016) provided a sensitivity analysis of the Noah-MP parameters, including both the adjustable and hard-coded parameters that affect simulations of hydrological processes. Based on their analysis, some snow-related Noah-MP hydrological simulations exhibit high sensitivity to hard-coded parameters rather than tunable parameters. For example, snowmelt-induced surface runoff is sensitive to hard-coded snow-related parameters for surface resistance, partitioning of incoming radiation into direct and diffuse radiation, and snow thermal conductivity. Meanwhile, the current DA framework does not perform assimilation if one or more of the prior model ensemble members do not have snow. Thus, the gamma SWE retrievals could not add value to the SWE estimates during the snowmelt period. To address this issue, a rule-based approach (e.g., Kwon et al., 2019) that adds a thin snow layer when the model simulates snow-free conditions but observations have snow can be explored in a future study.

It is possible that the inherent uncertainties in the gamma radiation method limit the potential improvements through DA even though the airborne gamma radiation SWE was beneficial to enhancing SWE estimations by assimilation into Noah-MP land surface models. The potential sources of error in the gamma SWE retrievals have been explored in previous findings (Carroll and Carroll, 1989a, b; Glynn et al., 1988; Offenbacher and Colbeck, 1991). An impact of forest biomass on the accuracy of airborne gamma SWE measurements has been examined over forested watersheds (Carroll and Vose, 1984). Carroll and Vose (1984) showed that there was 23 mm of RMSE between airborne gamma SWE and in situ SWE for the moderate snowpack (20 to 470 mm of in situ SWE) in the Lake Superior and Saint John basins, New Brunswick, Canada. Spatial variability in elevations over the gamma flight footprint can cause larger errors in SWE (Cho et al., 2020b; Carroll and Carroll, 1989b; Cork and Loijens, 1980). Cho et al. (2020b) found that heterogeneous characteristics (e.g., elevation range and slope) within a flight line cause underestimations of gamma SWE as compared to UA SWE. Cork and Loijens (1980) discussed how the measurements of the attenuation of the gamma count rate over the snowpack with its large spatial variability were systematically underestimated, leading to the SWE underestimation. Because the results use the NOAA standard gamma radiation SWE retrievals without manual corrections, the DA results would be improved with the updated gamma SWE products in regions by correcting the existing potential errors. Lastly, the spatiotemporal sparseness of the airborne gamma SWE observations due to the operational costs is an inherent issue that may limit the widespread use of gamma SWE observations for DA work. However, as supported by our findings, effective uses of the gamma SWE (e.g., localization function) can enhance the utility of the gamma SWE in the DA framework.

7 Conclusion and future perspectives

In the snow hydrology community, DA has been used as a promising approach to improve SWE estimation at a large spatial scale by merging remote-sensing observations with LSM predictions. In densely forested regions, however, most remote-sensing techniques have limited performance of SWE due to attenuating and/or scattering radiation signals by canopy (e.g., passive microwave T_B and lidar), resulting in large uncertainty in DA outputs. The historically well-established, airborne gamma-radiation technique has provided strong potential in wet snow and dense forest conditions because the gamma approach uses an attenuation difference in the terrestrial gamma-ray emission by water in the snowpack (any phase) between snow-off and snow-on conditions. In this study, the airborne gamma SWE observations are assimilated with the Noah-MP model's SWE in densely forested regions in the northeastern US. We found that the assimilation of the airborne gamma SWE observations enhanced the model SWE estimates despite the limited number of measurements (up to four SWE values during a winter period). The added value of the gamma data on the model SWE estimates was greater for the relatively lower-TCF range. While the gamma-based DA SWE had relatively lower improvement in areas with higher topographic heterogeneity, the DA SWE with reduced errors was found as compared to the OL. We also found that the localized DA with the gamma SWE observations with distances up to 32 km reduced the model SWE's errors, indicating that the gamma SWE has the potential to improve regional estimations of the SWE and subsequently snowmelt runoff. Despite the accuracy of the gamma data on the DA framework, the improvements were limited by the spatial and temporal sparseness of the gamma measurements. With the enhanced physics in LSMs and optimal uses of the gamma data using enhanced DA or interpolation methods, future studies may achieve further improvement of the modeled SWE for larger areas where gamma flights do not exist.