HESS Opinions: Are soils overrated in hydrology?

Traditional hydrological theories are based on the assumption that soil is key in determining water's fate in the hydrological cycle. According to these theories, soil hydraulic properties determine water movement in both saturated and unsaturated zones, described by matrix flow formulas such as the Darcy–Richards equations. They also determine plant-available moisture and thereby control transpiration. Here we argue that these theories are founded on a wrong assumption. Instead, we advocate the reverse: the terrestrial ecosystem manipulates the soil to satisfy specific water management strategies, which are primarily controlled by the ecosystem's reaction to climatic drivers and by prescribed boundary conditions such as topography and lithology. According to this assumption, soil hydraulic properties are an effect rather than a cause of water movement. We further argue that the integrated hydrological behaviour of an ecosystem can be inferred from considerations about ecosystem survival and growth without relying on internal-process descriptions. An important and favourable consequence of this climate- and ecosystem-driven approach is that it provides a physical justification for catchment models that do not rely on soil information and on the complexity associated with the description of soil water dynamics. Another consequence is that modelling water movement in the soil, if required, can benefit from the constraints that are imposed by the embedding ecosystem. Here we illustrate our ecosystem perspective of hydrological processes and the arguments that support it. We suggest that advancing our understanding of ecosystem water management strategies is key to building more realistic hydrological theories and catchment models that are predictive in the context of environmental change.

1 A change in perspective

Soil is important in hydrology. Soil forms the substrate of the terrestrial ecosystem, and hence, it is a crucial element of the critical zone of life on Earth (Lin et al., 2006; Banwart et al., 2017). Through its porous structure, exercising capillarity against gravity, it provides water storage against droughts and nutrients for plant growth.

It has been argued that the soil forms an ecosystem in itself, full of microbiotic and macrobiotic life (Ponge, 2015; Weil and Brady, 2017). Fungi forming dense underground networks live in symbiosis with vegetation, exchanging nutrients for carbon, which makes them responsible for the larger part of subterranean carbon storage (Domeignoz-Horta et al., 2021). Soils are full of life. Above ground, life cannot survive without subsurface life; they are part of the same ecosystem.

Soils are embedded in the terrestrial ecosystems, which, through evolution and natural selection, have found ways to make best use of their resources. The processes and structure of a terrestrial ecosystem are mainly controlled by external factors which are largely prescribed. Among them, climate plays a major role as rainfall patterns and seasonal temperatures strongly affect the distribution of vegetation types; other external factors include topography, lithology (which determines parental material), and potential biota (Chapin et al., 2011). Given these boundary conditions, a terrestrial ecosystem adjusts its internal behaviour to satisfy its needs, and it manipulates the substrate on which it grows.

In particular, the soil is the result of a long-term evolution of terrestrial ecosystems given their boundary conditions. The classic clorpt model presented by Hans Jenny's famous 1941 book The Factors of Soil Formation states that $s=f(\mathrm{cl},o,r,p,t,\mathrm{\dots })$, where soil properties (s) are seen as a function of climate (cl), biotic effects (o for organisms), topography (r for relief), parent material (p), time (t), and additional factors such as fire (represented by the dots) (Huggett, 2023). This model suggests that soil properties are largely determined by the embedding ecosystems.

Managing water is an essential task of terrestrial ecosystems as water is essential to life. This is not a trivial task as it implies bridging dry-weather periods but also avoiding troubles caused by sustained or heavy rainfall, such as water stagnation or soil erosion. We argue that terrestrial ecosystems achieve this balance by manipulating key hydrological characteristics such as interception capacity, infiltration capacity, moisture storage capacity, preferential pathways to replenish moisture stocks and recharge, and subsurface drainage. According to this view, a terrestrial ecosystem manipulates the soil hydraulic properties to satisfy specific water management strategies.

Yet, the most established hydrological theories parameterize water fluxes using soil attributes such as texture, porosity, moisture retention capacity, wilting point, and plant-available moisture (e.g. Drewniak, 2019; Lu et al., 2019). These theories assume that soil properties control processes such as infiltration, drainage, or plant evaporation. But this is the wrong way around. Soil properties are the effect rather than the cause of water movement, which itself is governed by the behaviour of the embedding terrestrial ecosystem.

We therefore argue in favour of an ecosystem-based approach where the integrated hydrological behaviour of an ecosystem is inferred based on the water management strategies it needs to survive and grow without relying on internal-process descriptions. As we shall see, this is not a prohibitive task. The very existence of an ecosystem already provides many indications about its ability to manage its water resources.

This ecosystem-based approach has several beneficial consequences for hydrology. First, it provides a physical justification for the development of catchment-scale hydrological models that directly rely on the external factors that influence terrestrial ecosystems, such as climate, topography, and lithology. These models would be more realistic than soil-based models based on the correct cause–effect relationships. Moreover, they would be less data demanding and simpler as they would not require soil texture information and a detailed description of soil water dynamics. Second, it would allow us to dig into the small scale, if this is deemed necessary, exploiting the constraints that are imposed by the behaviour of the larger-scale system.

In the following, we first present the soil-centred hydrological perspective and its limitations (Sect. 2). We then argue that there is limited evidence that soil properties actually matter in catchment hydrology (Sect. 3). Next, we illustrate our terrestrial ecosystem perspective (Sect. 4) and provide an interpretation of why the soil-based modelling tradition has proliferated in hydrology (Sect. 5). Finally, we illustrate the limitations of our approach (Sect. 6) and present our conclusions (Sect. 7).

2 Limitations in the soil-centred hydrological perspective

2.1 Challenges in small-scale theories of soil water dynamics

It is a deeply rooted perception in hydrology that small-scale soil water dynamics are key in determining the integrated catchment behaviour at larger scales, such as the partitioning of rainfall between evaporation, drainage, and storage (Vereecken et al., 2022). For example, soil is assumed to control plant evaporation, as plant-available water content is often parameterized as a function of soil texture (Yang et al., 2016). Processes such as Hortonian overland flow, saturation excess overland flow, or percolation are often described in relation to water movement in the unsaturated zone using the laboratory-scale matrix flow theory developed by soil physicists. This theory describes flow in porous media based on equations that depend on soil hydraulic properties (e.g. porosity and hydraulic conductivity). Darcy's law describes matrix flow under saturated conditions through a porous medium under a head gradient. Richards' equation regards matrix flow under unsaturated conditions in the vadose zone, determining water flow direction and velocity. Numerous simplified semi-empirical soil infiltration equations were also derived to simulate the infiltration excess overland flow, such as the Philip and Horton equations (Schoener et al., 2021). The matrix flow theory is regarded as well-established, much like classical mechanics.

For a hydrological model to be considered physically based, it is generally assumed that it needs to be based on these small-scale theories. Land surface models (LSMs) are strongly based on these matrix flow equations (Freeze and Harlan, 1969; Lawrence et al., 2019), which determine soil water movement vertically and laterally (Duffy, 1996; Refsgaard et al., 2022). Even the representative elementary watershed (REW) approach (Reggiani et al., 1998), a physically based framework that describes catchment-scale processes, is based on the integration of small-scale conservation equations developed for porous media.

This soil-centred perspective is highly rated in the hydrological community. Some of the most prestigious hydrology awards exemplify the tribute of the hydrological community to this perspective, such as the Henry Darcy medal of hydrological sciences in the European Geosciences Union (EGU) and the Robert Horton American Geophysical Union (AGU) hydrological science medal, which are named after two hydrologists that pioneered the soil-centred approach.

Tracer field experiments, such as dye and isotope studies, have shown that matrix flow is rarely observed. Most soils contain crevices, preferential channels, and openings that transmit free water quite rapidly to the subsurface, which is termed preferential flow (Beven and Germann, 2013; McDonnell et al., 2007; Beven, 2018; Zehe et al., 2021). Hence, natural conditions do not resemble well-prepared homogenous soil that can be recreated in a laboratory.

In response to this criticism, soil water theories have become more complex, allowing for preferential flow, which required even more detailed soil characterizations. These challenges have stimulated the development of dual-continuum, dual-porosity, or dual-permeability modifications (Jarvis et al., 2016); however, most models are still based on matrix flow theory (Weiler, 2017). Because of the extreme complexity of soil preferential flow in nature, it is extremely hard to develop accurate models that describe it, even at the plot scale. The challenge is exponentially greater when upscaling preferential flow from the plot scale to hillslope or catchment scales (Davies et al., 2013; Germann, 2014; Or, 2020). At the global scale, hyper-resolution land surface models, which are deemed necessary for addressing critical water cycle science questions and applications, can have up to 10⁹ unknowns (Wood et al., 2011)!

From its establishment, preferential-flow theory was regarded as the main culprit challenging the foundation of physically based hydrological models. This avenue has led to models that require many space- and soil-dependent parameters that are difficult to measure; that require massive computational resources; and that, when calibrated, are prone to equifinality. Arguably, the avenue of building more complex models by increasingly detailed representation of soil water movement is a steep one. But is it a necessary one if the objective is to build a physically based model of catchment-scale hydrological processes?

2.2 Limitations in the pedotransfer functions approach

Soil-centred bottom-up hydrological models rely on estimates of soil hydraulic properties (SHPs), such as water retention characteristics and unsaturated and saturated hydraulic conductivity. As these properties are difficult to measure at appropriate scales, soil pedotransfer functions (PTFs) have been developed to express SHPs as a function of more accessible soil properties, such as soil texture (i.e. sand, silt, and clay content), organic matter, and bulk density (Fig. 1; van Looy et al., 2017; Or, 2020; Haghverdi et al., 2020; Gupta et al., 2021; Hohenbrink et al., 2023).

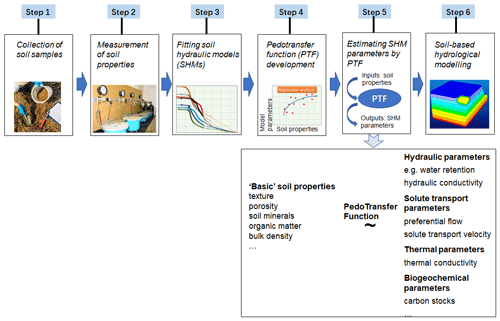
Figure 1 Schematic illustration of data collection, laboratory measurements, fitting soil hydraulic models (SHMs), pedotransfer function (PTF) development, and soil-based hydrological-modelling workflow (adapted from Van Looy et al., 2017, and Haghverdi et al., 2020).

There are several critical issues with the practicality and accuracy of this approach: (1) most soil property parameters are measured by pedologic surveys at great expense and effort (Van Looy et al., 2017); (2) PTFs are usually obtained by using measurements from uniform soil samples and by performing laboratory-scale experiments, which merely reflect disturbed and therefore unnatural conditions; (3) the parameters obtained at the laboratory scale are not necessarily the same as at the model scale, which requires upscaling assumptions that are difficult to verify or recalibrate, hampered by equifinality.

Unfortunately, readily available soil information (e.g. texture, bulk density, organic matter) correlates poorly with soil hydraulic properties. Gutmann and Small (2007) have shown that soil textural classes across a range of climates and vegetation covers merely explained 5 % of the variance of real SHPs. In another study, it was found that 95 % of the default soil hydraulic parameters in a state-of-the-art land surface model, largely based on soil textural data, were significantly different from region-specific observations (Kishné et al., 2017).

Recent studies showed that, in order to achieve more realistic estimates of soil hydraulic properties, it is necessary to include information about vegetation or biophysical activity (Or, 2020). For example, Bonetti et al. (2021) proposed soil structure corrections for pedotransfer functions, informed by remote sensing vegetation metrics and local soil texture. Additional studies rebalance the soil texture information and highlight the importance of soil structure originating from soil biophysical activity (Or, 2020; Fatichi et al., 2020). Not only the physically based models but also the empirical soil-based models, for example the soil conservation service (SCS) method in the SWAT model (soil water assessment tool), involve land use data to rebalance the soil-based curve number in catchment simulations (Arnold et al., 2012).

Building realistic pedotransfer functions requires detailed characterization of the soil, requiring a large number of parameters that are difficult to estimate. This approach, while feasible for a hillslope or a headwater catchment, becomes impractical at regional or global scales. For hydrological purposes, the ultimate goal is often to determine integrated fluxes of hydrological response at large scales. Hence, it is worth asking the following question: can this integrated behaviour be determined directly from observations without resorting to small-scale theories and upscaling assumptions?

3 Does soil variability matter in catchment hydrology?

3.1 Do soil-centred models reproduce hydrological variability?

A key objective of physically based models is to represent hydrological variability, such as spatial patterns of soil moisture, runoff, or evaporation. Figure 2 is a revealing illustration of how a physically based model that relies on detailed soil information can make inconsistent predictions under extreme circumstances (Beekman et al., 2014). On average, these models may function adequately, as almost all hydrological models do under average conditions, but the example of Fig. 2 shows how, during a relatively extreme drought in the Netherlands, the modelled evaporation is unrealistic.

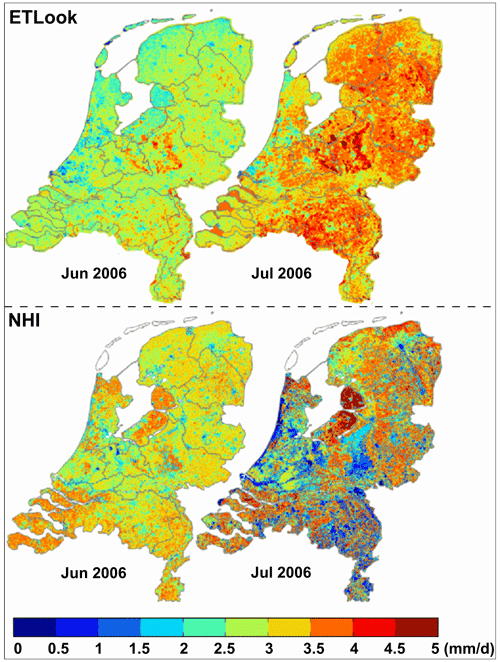
Figure 2 Evaporation during June (left) and July (right) of 2006 in the Netherlands. Remote-sensing-derived above, modelled with a physically based hydrological model below (from Beekman et al., 2014).

The top panels in Fig. 2 show remote-sensing-derived evaporation obtained by interpolation of eddy covariance and lysimeter observations using ETLook, an energy-balance-based evaporation product (Bastiaanssen et al., 2012). The bottom panels in Fig. 2 show evaporation modelled with the Netherlands Hydrological Instrument (NHI) distributed model, which heavily relies on detailed soil data. The two methods for estimating evaporation are independent, and arguably, the ETLook approach is more realistic as it is based on eddy covariance observations. The comparison is presented for two dry summer months in 2006: June (left panel) and July (right panel).

Two aspects of this comparison are striking. First, in terms of temporal dynamics, ETLook evaporation estimates show an increase in response to increased evaporative demand, whereas the NHI evaporation estimates decrease in response to water stress. Second, in terms of spatial patterns, ETLook estimates are more uniform in response to relatively uniform climatic conditions, whereas NHI estimates are highly variable, mimicking the variability of the soil maps used in the model, which are used to determine plant-available storage. The July 2006 picture in the bottom panel, in fact, mimics the soil map. Red (high evaporation) is seen on clay soils, and purple (almost no evaporation) is seen on sand.

It is interesting to observe that, according to ETLook (top right), the forested sandy part at the centre of the Netherlands was evaporating lushly, whereas, according to the hydrological model (bottom right), this ecosystem appeared to be dead. Apparently, the ecosystems continued to evaporate well during July 2006 in spite of the dry weather conditions. Our interpretation is that the ecosystems had prepared for this eventuality and had created enough root zone buffer to overcome this period of drought, compensating for the variability of soils.

Although such mismatches between distributed model outputs and remote-sensing-monitored patterns are not infrequent, they are typically not regarded as a challenge to the basic model assumptions but rather as a problem associated with the uncertainty in model inputs. Hence, such soil-centred hydrological models remain vivid under the hope that “novel, highly resolved soil information at higher resolutions than the grid scale of LSMs may help in better quantifying sub-grid variability of key infiltration parameters” (Vereecken et al., 2022). But is this a realizable hope?

3.2 Is soil a good predictor for streamflow spatial variability?

The top-down approach is a common way to infer internal catchment behaviour and its controlling factors from catchment response data (Sivapalan et al., 2003). For example, this approach has often been used to interpret spatial variability of streamflow based on controlling factors such as climate, vegetation, topography, geology, and soils. Interestingly, in these applications, soil properties are often a poor predictor of streamflow variability. For example, Addor et al. (2018) used 671 catchments in the USA and found that, compared to soil properties, landscape features, i.e. vegetation and topography, have stronger correlations with hydrologic signatures, not only for average streamflow but also for high-flow, low-flow, and streamflow seasonality (Fig. 3).

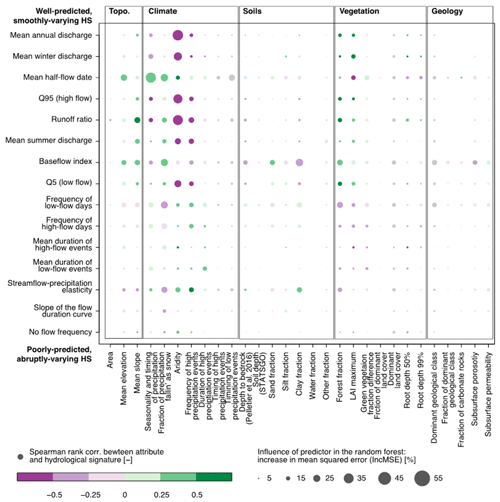
Figure 3 Comparison of the influence of catchment attributes and hydrological signatures for 671 US watersheds (from Addor et al., 2018). Large, brightly coloured circles imply strong correlations and high influence. Reprinted with permission of John Wiley and Sons.

One of the arguments in favour of high-resolution distributed models has been their ability for spatial extrapolation, such as capturing the spatial variability of streamflow. Such extrapolation ability cannot be achieved by lumped models that rely on the calibration of each individual catchment. However, there are now several examples of catchment-scale distributed models that describe the spatial variability of streamflow without relying on soil information (e.g. De Boer-Euser et al., 2016; Fenicia et al., 2016, 2022; Gao et al., 2019; Dal Molin et al., 2020). These models are clearly more complex than lumped models, but not more complex by any orders of magnitude, as they distribute parameters according to a small number of landscape units.

4 Putting the terrestrial ecosystem at the centre of hydrology

4.1 Ecosystem hierarchy

It has been shown that terrestrial ecosystems largely respond to external climate forcing and to the lower boundary conditions determined by topography and lithology (Chapin et al., 2011). With time, terrestrial ecosystems organize themselves to make best use of the available solar energy and resources. Hence, they adapt to the climate by developing vegetation types in response to rainfall patterns and seasonal temperatures. They also develop the soil given the climate, organisms, topography, and parental material, as suggested by the clorpt model (see Sect. 1).

Our view, consistent with this perspective, is that an ecosystem adjusts the soil hydraulic properties to fulfil specific water management criteria. Hence, understanding the water management strategies of the ecosystem is a prerequisite to understanding and modelling soil processes. This perspective is opposite to the classical soil-centred hydrological perspective presented in Sect. 2, which sees water fluxes, such as evaporation and drainage, as a function of soil properties.

Figure 4 further illustrates our ecosystem view and how it differs from the classical approach in hydrological science. The traditional view is represented by the four isolated circles in the left panel of Fig. 4. This view assumes that soil plays a central role in governing the terrestrial water cycle. In particular, depending on climate forcing, soil hydraulic properties will determine water availability for vegetation and water fluxes, such as percolation and surface runoff. According to this view, the understanding of soil water processes is a prerequisite to simulate vegetation dynamics and water fluxes. The circles are isolated from each other, reflecting that, in this view, soil properties, vegetation cover, and climate are seen as independent of each other and can independently influence hydrological processes. Indeed, hydrological models typically parameterize soil and vegetation independently from each other and from climate forcing.

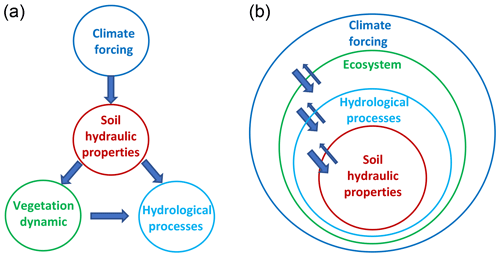
Figure 4 The isolated circles (a) represent the traditional soil-centred hydrological perspective. The nested circles (b) represent our view of ecosystem hierarchy and cause–effect relationships.

Our view is represented by the nested circles in the right panel of Fig. 4. Climate sets the boundaries for the terrestrial ecosystem, and in turn, the ecosystem manages its water resources, determining hydrological processes. Soil hydraulic properties are a function of the ecosystem water management strategies. The circles are nested to reflect the hierarchy between them in the sense that internal circles are dependent on the external ones. The double arrows indicate that there are feedbacks between these circles, but the influence of the external circles on the internal ones is much greater than vice versa. More specifically, local climate has a strong effect on an individual ecosystem, which intentionally adapts to it, developing strategies to grow, survive, and reproduce. In turn, an individual ecosystem cannot change the local climate significantly according to its needs. Hence, the feedback of an ecosystem on the climate is smaller and less intentional than the effect that the climate exerts on an ecosystem. Similarly, the control that the terrestrial ecosystem exerts on soil hydraulic properties, mediated by its water management strategies, is much greater and more purposeful than the control of the soil on the embedding ecosystem.

From our perspective, such a hierarchy and such interactions can reduce rather than add complexity and can facilitate hydrological-process understanding and modelling. For example, they provide a justification for the level of detail of catchment models. In many applications of catchment hydrology, the ecosystem circle represents the necessary level of detail, and as the effect of soil on the ecosystem is rather minor, it is unnecessary to dig into what happens within the soil water circle.

4.2 The ecosystem is the ultimate water manager

An ecosystem that results from a process of evolution contains traits that are functional to its survival. In this perspective, it is important to understand what the system is trying to achieve in order to explain and predict its behaviour. In the context of hydrology, this approach requires that we understand (i) which water management strategies the ecosystem needs to adopt in order to sustain itself and survive; (ii) how hydrological processes, such as interception, surface runoff (or lack thereof), and subsurface storm flow, contribute to satisfying the water needs of the ecosystem; and (iii) which physical characteristics the system needs to demonstrate to enable such processes. This evolutionary perspective considers the structure and internal processes of the ecosystem that are dependent on its overall behaviour, and it is contrary to the static approach which underlies typical descriptions of soil hydrology, where the system structure is seen as prescribed and where small-scale processes are assumed to determine overall system behaviour.

So, what are the water strategies of the ecosystem and how do they affect its structure and internal hydrological processes? Humans are well aware that water management is critical to their survival. For this reason, they have developed activities for optimum use of water resources such as flood control, water storage, water conservation, river regulation, irrigation, and water treatment. Similarly, a natural ecosystem can only survive if it organizes its water resilience. In other words, if an ecosystem does not organize its water resilience, it would not survive and would no longer exist. The very existence of an ecosystem tells us several aspects of its water management strategies.

• An ecosystem needs to provide sufficient moisture storage in the root zone (so that vegetation can overcome critical dry spells) but also sufficient infiltration capacity and subsurface drainage to maintain moisture levels between acceptable boundaries: not too wet and not too dry.

• Runoff, the excess water after precipitation has replenished the ecosystem's water deficit, needs to be drained as quickly and efficiently as possible.

• Preventing surface runoff is an essential need of an ecosystem; this serves to avoid soil erosion. Indeed, surface runoff is seldom observed on vegetated hillslopes. It does occur on bare rocks, where there is no vegetation, or on floodplains, where saturated overland flow does not cause significant erosion. Also, it occurs in disturbed ecosystems, such as urbanized areas, roads, paths, and ploughed agricultural fields. In rare cases, such as on the Loess Plateau in China, the failure of surface runoff prevention caused severe soil erosion at the local scale and disastrous sediment deposition and flooding in the lower Yellow River.

• The ecosystem needs to retain nutrients, soil particles, and water for plants. For this reason, it creates preferential flow paths that facilitate infiltration while retaining moisture and nutrients in retention zones. If there is too much water, then excess water bypasses the root zone, where it can recharge the groundwater or where it is evacuated through preferential subsurface drainage patterns on hillslopes. This type of drainage generates subsurface storm flow and recharges the groundwater system.

• Ecosystems will generally avoid catastrophic events such as death from drought, temperature stress, landslides, windthrows, or fires. If such disruptive events occur, it is generally on timescales longer than ecosystem memory. If disturbances occur more frequently, ecosystems generally develop resilience to them, such as in the case of frequent fires, where ecosystems can develop fire-resistant species or vegetation that can recover biomass more quickly (Chapin et al., 2011).

Considering hydrological processes in the context of their purpose from an ecosystem perspective can clarify cause–effect relationships and therefore help their conceptualization and modelling. For example, it can constrain plausible values of SHPs, which can be determined based on considerations of the overall system behaviour.

4.3 The root zone is the key element in hydrology

From a catchment hydrology perspective, a key objective is to determine the partitioning of precipitation between evaporation, drainage, and storage. This partitioning mostly takes place in the root zone. The vertical profile of the critical zone can be divided into different layers, i.e. canopy, litter layer, root zone, water transition zone, unconfined groundwater, and confined groundwater. The most significant phase change of water happens in the canopy, litter layer, and root zone. Once water overtakes these zones, evaporation is relatively small, and water is routed to the stream through various pathways. Globally, the vegetation interception storage capacity of terrestrial ecosystems is about 1–2 mm, as estimated by remote-sensing-based leaf area index (LAI) data (De Roo et al., 1996). The litter layer storage capacity differs among ecosystems, but it is likely to increase the total interception storage capacity to around 2–5 mm (Shi et al., 2004; Gerrits et al., 2010). Global average root zone storage capacity in vegetated regions is about 146–242 mm, as estimated by multiple approaches and datasets (Kleidon, 2004; Wang-Erlandsson et al., 2016), which is significantly larger than interception and litter layer water storage capacities. Therefore, the root zone storage is the one with the longest memory, which influences how much precipitation eventually becomes streamflow.

Referring to common hydrological models, the root zone storage can be assimilated to the production reservoir in the GR4J model (Perrin et al., 2003), the upper-zone reservoir in HBV (Hydrologiska Byråns Vattenbalansavdelning) (Lindström et al., 1997), the tension water storage in the Xinanjiang model (Zhao, 1992), or the soil moisture storage in the probability distributed model (PDM) (Moore, 2007). In these models, the size of this reservoir is typically obtained by calibration. This approach is clearly unsatisfactory from a theoretical point of view as it makes these models not predictive under environmental change.

From a soil-based perspective, the root zone storage is commonly estimated as a function of plant-available moisture and rooting depth (Yang et al., 2016). In our view, this approach is also not satisfactory as it considers plant-available moisture and rooting depth to be independent variables and root zone storage to be the dependent variable. We argue the reverse: plant-available moisture and rooting depth are a function of the root zone storage that is created by the ecosystem to fulfil its water management strategies. Moreover, the classical approach is impractical as obtaining the detailed spatio-temporal root and soil information at a global scale is virtually impossible (Or, 2020).

So how are we to determine root zone storage without resorting to calibration or in situ measurements? As mentioned in the previous section, our ecosystem approach would start with understanding the ecosystem water management strategies and using this understanding to figure out how the ecosystem needs to organize its internal behaviour. Vegetation will try to maintain evaporation close to its potential to maximize net carbon profit. It will therefore optimize its root zone water storage so that it is sufficiently large to overcome typical dry spells, much like humans size dams to sustain droughts (Gao et al., 2014). An approach that appeared to work well locally and globally for estimating the root zone storage capacity is the mass curve technique, originally developed for reservoir design at an acceptable probability of failure (Gao et al., 2014; Wang-Erlandsson et al., 2016). Here, the supply is represented by precipitation and the demand by potential evaporation. This technique is uniquely based on climate data. This technique has an important benefit over approaches based on calibration or field observations: it can also be used to describe how the root zone would evolve in response to climate change.

It is worth noting that root zone and soil have a strong connection but are essentially different things. The soil profile can reach depths over hundreds of metres, e.g. the Loess Plateau in China (Zhang et al., 2014), of which only the root zone is the active area, whereby the soil is merely the substrate of it. Root zone storage can also be larger than soil water storage – for example, in karst mountainous areas where soil is thin and discontinuous, bedrock storage serves as an important source of plant-available water (McCormick et al., 2021). In very dry climates, roots can even reach the deep groundwater; thus, in this case, the root zone also includes some part of the groundwater (see Singh et al., 2020). In cold regions, it is necessary to take account of the effects of snowmelt and soil freeze–thaw processes on root zone water storage and resulting hydrologic connectivity (Gao et al., 2020, 2022). In cropland, where irrigation provides an extra water supply to the root zone during dry seasons, the root zone water storage capacity is often smaller than under natural conditions with similar climate conditions (Xi et al., 2021).

4.4 Landscape-based model: the giant view of hydrology

A soil-based model of catchment-scale processes is like the ant's perspective, observing a complex world of heterogeneities and randomness (Savenije, 2010). According to this perspective, small-scale processes are the basis for integrated system behaviour. As a result, a model can be physically based only if it relies on small-scale physics.

Seeing the patterns of hillslope, landscape, and catchment is rather the giant's perspective as these patterns only become visible when we zoom out well beyond the microscale of the soil or the human scale (Savenije, 2010; Gao et al., 2018). Landscape, as the integration of topography and land cover, is seen as the long-term co-evolution of ecosystem, atmosphere, lithosphere, pedosphere, hydrosphere, and human activities (Wu, 2013; Troch et al., 2015). According to this perspective, a physically based model needs to be based on large-scale system behaviour.

Both approaches can produce models that provide good results. However, from our perspective, for catchment hydrology applications, it is the giant's perspective that wins. First, the giant's model captures the right cause–effect relationships and is therefore more satisfactory from a theoretical point of view. For example, it is a tool to test how an ecosystem would adapt to changes in climatic drivers. Second, landscape-based catchment models will generally be simpler than fragmented catchment models as a natural system exhibits emergent properties, which effectively enable a description of large-scale processes independent of what happens at the smaller scale. Such emergent properties are often characterized by simple laws, such as the fill-and-spill bucket model with thresholds and associated timescales (McDonnell et al., 2021) and the linear reservoir for groundwater at the hillslope and catchment scales (Savenije, 2010; Fenicia et al., 2011; Savenije and Hrachowitz, 2017). Interestingly, the groundwater system also appears to be self-organized and structured (Savenije, 2018). For example, the recession parameter k is around 45 d in worldwide catchments regardless of their climate, topography, soil, and geology (Brutsaert, 2008). Discovering these properties and related signatures benefits our understanding and prediction of the dynamic adaption of ecosystems to environmental change and the subsequent impacts on hydrology (Gharari et al., 2014; Jackisch et al., 2021).

This ecosystem perspective provides a physical justification for catchment-scale models that do not rely on small-scale physics as they are independent from what happens at the smaller scale. Moreover, they can provide a constraint to smaller-scale processes and therefore facilitate their representation. For example, the partitioning of water between the evaporation, storage, and release that characterize the larger-scale system can be used to constrain plausible values of difficult-to-measure soil properties such as rooting depth, plant-available moisture, and hydraulic conductivity. This can favour more accurate descriptions of soil water dynamics, which, although often unnecessary for typical catchment-scale applications, may be important for other purposes.

4.5 Proposed modelling steps in poorly gauged catchments

How can this approach be implemented in modelling an ungauged catchment? There are the following steps to be considered as a quick guide to model building.

The first thing is to classify the basin in terms of landscape and geology. This determines model structure. It defines the proportion between the major three fast-runoff mechanisms: rapid subsurface flow (for hillslope), saturation overland flow (for wetland), and Hortonian overland flow (for plateau and bare rock). The theory and application of landscape-based modelling are presented in numerous studies (e.g. Savenije, 2010; Gharari et al., 2011; Fenicia et al., 2011; Gao et al., 2014, 2018; De Boer-Euser et al., 2016; Hulsman et al., 2021a; Bouaziz et al., 2022).

Subsequently, it is necessary to classify landscape units in terms of ecosystem, land use, and climate. The climate and the ecosystem determine hydrological parameters such as root zone storage, interception capacity, infiltration capacity, and subsurface drainage. Spatial variability of root zone storage determines the beta function of the non-linear root zone reservoir (Gao et al., 2018). This results in hydrological-response units based on landscape and geology (defining model structure) and on ecosystem and climate (defining parameter values), which can be grouped per sub-basin.

Recession timescales can be derived from limited observations, if available, or they can otherwise be estimated; they do not affect the overall water balance. The longer timescales of groundwater recession may be derived from Gravity Recovery and Climate Experiment (GRACE) data, which can also be used to constrain groundwater dynamics (Winsemius et al., 2006; Hulsman et al., 2021b).

Minor calibration parameters remain, such as the splitter between fast subsurface runoff and recharge. These have a limited effect on the water balance and can be estimated if no observations are available.

5 Why is the soil-based modelling tradition so rooted in hydrology?

5.1 Agricultural bias

Since hydrology was born from chapters of agricultural and hydraulics textbooks (Rodríguez-Iturbe and Rinaldo, 2004), the agricultural bias has probably played a major role in overemphasizing the importance of soils. In agriculture, the focus is on seasonal crops. A seasonal crop has limited time to develop a root zone storage that can buffer for longer-term variability. At best, it can buffer for average dry spells that may occur within an average year. This is why modern agriculture requires water management by the farmer to buffer for natural fluctuations. In agriculture, ploughing destroys preferential infiltration and subsurface drainage. It also limits the root zone storage capacity to the relatively small soil layer above the plough pan. In such cases, it is indeed the moisture-holding capacity of the soil that determines the root zone storage capacity.

The widely used Penman–Monteith equation for estimating reference evaporation works well in agriculture, where the dominant evaporation is from crops. However, it is likely not to be appropriate for describing the land–atmosphere interaction of natural ecosystems. Unfortunately, this agricultural bias, only applicable in a small proportion of terrestrial area, has been dominant in most hydrological work. We argue that this deeply rooted soil-based perception may limit or even mislead the further development of hydrological science, especially for next-generation professionals.

Even in the Anthropocene, where human impacts on essential planetary processes have become profound and where hydrological processes are affected by human activities such as agriculture, urbanization, and deforestation, we believe it is still essential to emphasize the importance of ecosystem understanding. There are two reasons: (1) the majority of our Earth, and particularly the uphill-runoff-generating parts of catchments, is still dominated by natural ecosystems, although human modification has modified 14.5 % or 18.5 M km² of land (Theobald et al., 2020); and (2) for human-modified systems, the ecological approach also applies provided that the ecosystem is given sufficient time to become self-sufficient and to manage its own resources.

5.2 Unreliable intuition

Hydrologists intuitively see the soil as the critical agent. It may very well be the perspective of the ant that causes it. As people, we are biased by our perspective and the scale at which we observe processes. We are therefore just too small to perceive the larger-scale processes that dominate landscape hydrology. We tend to dig holes in the Earth and try to infer larger-scale behaviour from what we observe inside this hole. The human scale prevents us from seeing the larger picture. We need the giant's perspective to recognize the patterns present in the landscape.

At the human scale, assuming that soil properties such as texture and porosity matter makes intuitive sense. People tend to describe what they see, and if they see water flowing or disappearing in the ground, they think that it is because of such soil properties. The role of the ecosystem as the driver of the system is much more difficult to recognize, especially within its evolutionary history. It requires seeing the environment as a living organism which continuously evolves and adjusts to changing circumstances. It also implies that the hydrological properties are not constant over time. The root zone storage, the most critical control on rainfall–runoff processes, is continuously changing in response to changing climatic and human drivers (Nijzink et al., 2016; Bouaziz et al., 2022). Instead of describing the now as an invariant and static condition, with environmental properties as a given, we have to think of the history that determined these environmental conditions, which is much more difficult to realize.

6 Limitations

We stress that our ecosystem approach is subject to certain limitations. First, it applies at the so-called ecosystem scale. This spatial scale can vary depending on the environment. It can be a few square metres for grass, on the order of hectares for forests, and even larger for sparse vegetation. Catchment scales are usually larger than the ecosystem scale. Therefore, our approach is generally suited to scales that are typical in hydrological-modelling applications. Second, we are talking about ecosystems that have reached a certain level of equilibrium and are self-sustained. We are not limiting ourselves to natural ecosystems. They can also be artificially induced, but they do not need to rely on artificial help for their survival, such as irrigation or fertilization. Third, our arguments are mostly related to water fluxes, and they do not pertain to water chemistry. The variability of soils can have a pronounced influence on predicting water quality, solute transport, and transit times (Weiler et al., 2017; Sternagel et al., 2021).

7 Conclusions

Traditional hydrological theories place soil physical properties at the heart of hydrology, considering them to be the driver of water fluxes, which is misleading for both process understanding and model development. In contrast, we need an ecosystem-based approach, where the structure of the terrestrial ecosystem and its internal processes are seen as a consequence of the ecosystem water management strategies needed for its survival and growth. Hence, the ecosystem is the ultimate manager of the soil. We advocate a change in perspective that places the ecosystem and landscape at the heart of terrestrial hydrology and develop holistic and live-ecosystem-based hydrological models with a more realistic representation of hydrological processes.