Sources and mean transit times of stream water in an intermittent river system: the upper Wimmera River, southeast Australia

Determining the mean transit times (MTTs) and water sources in catchments at different flow conditions helps better understand river functioning, and manage river health and water resources. Despite being common in a range of environments, the MTTs and water sources in intermittent streams are much less well understood compared to perennial streams. Major ion geochemistry, stable isotopes, ¹⁴C, and ³H were used in this study to identify water sources and MTTs of the periodically intermittent upper Wimmera River from southeast Australia at different flow conditions, including zero-flow periods. The disconnected pool waters during the zero-flow period in the summer months of 2019 had ³H activities of 0.64 to 3.29 TU. These and the variations in total dissolved solids and stable isotopes imply that these pools contained a mixture of older groundwater and younger stream water impacted by evaporation. ³H activities during the high-flow period in July 2019 were 1.85 to 3.00 TU, yielding MTTs of up to 17 years. The ³H activities at moderate and low-flow conditions in September and November 2019 ranged from 2.26 to 2.88 TU, implying MTTs of 1.6 to 7.8 years. Regional groundwater near the Wimmera River had ³H activities of < 0.02 to 0.45 TU and ¹⁴C activities of 57 to 103 pMC, and was not recharged by the river at high flows. The Wimmera River and other intermittent streams in southeast Australia are sustained by younger catchment waters from relatively small near-river stores than comparable perennial streams, which have older deeper regional groundwater inputs. This results in these intermittent streams being more susceptible to short-term changes in climate and necessitates the protection of near-river corridors to maintain the health of the riverine systems.

1 Introduction

Understanding the timescales of water flow through catchments to rivers at different hydrological conditions is vital for effective water resources management, protecting riverine systems, and predicting the changes in river functioning due to climate variability, changes in land use, and water utilisation (Sophocleous, 2002; Cook, 2013; Van Dijk et al., 2013; Gleeson et al., 2016; Segura et al., 2019). Mean transit times (MTTs) represent the average time for precipitation to be transmitted from a recharge area through a catchment to where it discharges into rivers or streams (Cook and Bohlke, 2000; McDonnell et al., 2010; Morgenstern et al., 2010). Transit time distributions (i.e. the frequency of water of different ages in the sample) potentially provide better information on catchment processes than MTTs. In particular, they allow better understanding of finer-scale catchment processes (e.g. the release of water from different stores as catchments wet up and dry down) (Hrachowitz et al., 2010; Benettin et al., 2015; Birkel et al., 2015). However, MTTs are important for understanding broad catchment behaviour (McGuire and McDonnell, 2006; McDonnell et al., 2010; Blavoux et al., 2013; Duvert et al., 2016; Howcroft et al., 2018) such as the average age of the water stores contributing to streams at different flow conditions. Documenting MTTs is also important for understanding the resilience of catchments. Streams with long MTTs are sustained by larger volumes reservoirs of water from within the catchments (e.g. Morgenstern et al., 2010; Gusyev et al., 2016; Howcroft et al., 2018), and thus are less sensitive to short-term climate variability (e.g. droughts lasting years to decades). In addition, the MTTs may control water salinity, water temperature, microbial activity, and the attenuation and dispersion input of nutrients and other contaminants to rivers (Kirchner et al., 2000; Hare et al., 2021).

The water that sustains river flow may have residence times ranging from a few days to several centuries. Younger water may be derived from stores in the shallow near-river environment (such as surface runoff, water stored in the soil, and interflow), while regional groundwater represents a large store of older water (Soulsby et al., 2000; McGuire and McDonnell, 2006; Stewart et al., 2010; Cartwright and Morgenstern, 2015; Duvert et al., 2016; Jung et al., 2019). However, relatively little is known about the timescale of water flow in most catchments, and whether water of different ages and from different stores contributes to rivers at different flow conditions. Numerous studies have focused on perennial streams and have revealed the presence of long-lived water stores contributing to streamflow especially during low-flow periods (Rice and Hornberger, 1998; Soulsby et al., 2006; Hrachowitz et al., 2009; Cartwright and Morgenstern, 2015; Gusyev et al., 2016; Howcroft et al., 2018; Cartwright et al., 2020). There has been less attention on intermittent streams, which represent > 50 % of global rivers and are especially important in semi-arid areas (Datry et al., 2014; Costigan et al., 2015; Gutiérrez-Jurado et al., 2019; Shanafield et al., 2021). The connection between intermittent streams and regional groundwater may be less important than for perennial streams, especially during the periodic cease-to-flow times when the water table falls and water from near-river stores become dominant (e.g. Zimmer and McGlynn, 2017). Determining MTTs of intermittent streams will improve our understanding of groundwater–surface water interaction in these catchments.

1.1 Documenting mean transit times

Several approaches can be used to estimate MTTs in rivers. MTTs may be determined by using lumped parameter models (LPMs) that describe the distribution of water with different ages or tracer concentrations in homogeneous aquifers with simple geometries and consistent recharge rates (Małoszewski and Zuber, 1982; Maloszewski, 2000; Zuber et al., 2004; McGuire and McDonnell, 2006).

LPMs may be based on the attenuation of δ¹⁸O values or Cl concentration variabilities in rainfall at the catchment outlet. This approach requires frequent (generally at least monthly but preferably shorter spaced if the details of hydrological processes are to be captured) long-term tracer records in rainfall and stream water (Kirchner et al., 2004; McGuire and McDonnell, 2006), and such datasets are available only in a small number of catchments globally. Because intermittent streams only flow for part of the year, it is more difficult to use LPMs based on continuous ¹⁸O or Cl measurements than in perennial streams. In addition, this approach assumes that the catchment is at steady state, which is unlikely to be the case (Kirchner, 2016b). It is also not viable where MTTs are greater than 4 to 5 years due to attenuation of the input record to below the resolution at which the tracers can be measured (Stewart et al., 2010), which is commonly the case in southeast Australia (Cartwright et al., 2020). Techniques such as ensemble hydrographs (Kirchner, 2019; Knapp et al., 2019), flux tracking (Hrachowitz et al., 2013), and StoreAge Selection functions (Rinaldo et al., 2015) can determine transit times from shorter time-series and do not assume steady-state conditions. However, these methods still require frequent tracer data for rainfall and streams that are not commonly available.

Tritium (³H) has a half-life of 12.32 years and is part of the water molecule. Unlike tracers such as chlorofluorocarbons, and SF₆, ¹⁴C, and ³He, its abundance is not affected by degassing or geochemical or biogeochemical reactions. This allows ³H to be used to estimate MTTs of shallow groundwater, water from the unsaturated zone, and stream water (e.g. Morgenstern et al., 2010; Duvert et al., 2016; Jung et al., 2019). Due to atmospheric nuclear tests, ³H activities in rainfall reached a peak in the 1950s and 1960s (the “bomb pulse”). In the Southern Hemisphere, the remnant bomb pulse ³H activities are now lower than those in modern rainfall (Morgenstern et al., 2010; Tadros et al., 2014). This makes it possible to estimate MTTs from a single ³H measurement in a similar way to how other radioisotopes such as ¹⁴C and ³⁶Cl are used to determine residence times of older groundwater (e.g. Clark, 2015; Cartwright et al., 2017; Howcroft et al., 2019). Low-level ³H measurements allow MTTs of up to ∼ 150 years to be determined, although the relative precision of the estimates decreases at longer MTTs.

MTT estimates made using ³H have several uncertainties. The decline of the bomb pulse ³H activities in the Southern Hemisphere makes it impossible to assess the suitability of an LPM by time-series ³H measurements that commence now (Cartwright and Morgenstern, 2015). Assigning LPMs is therefore based on catchment attributes (e.g. the geometry of the flow system) or information from previous studies in similar catchments. Although it represents an uncertainty, MTTs are less sensitive to the choice of LPMs than in the Northern Hemisphere (Morgenstern et al., 2010; Blavoux et al., 2013). In addition, where multiple water sources (e.g. groundwater, soil water, or water from multiple tributaries) with different MTTs contribute to rivers (aggregation), it is difficult to estimate MTTs (Suckow, 2014; Kirchner, 2016a; Stewart et al., 2017). The heterogeneous hydraulic conductivities of aquifers also contribute to uncertainties in MTT calculations (Weissmann et al., 2002; McCallum et al., 2015). However, where the scale of heterogeneity is small relative to the size of the aquifer, the MTTs are similar to those predicted by the LPMs (Cartwright et al., 2018). Lastly, the seasonal variability of ³H activities in rainfall could lead to uncertainty in MTT estimates. Where strong seasonal recharge occurs, ³H activities of rainfall that recharges the catchment may be different from those of annual rainfall, which is usually used as the ³H input (e.g. Morgenstern et al., 2010). Although these factors introduce uncertainties in MTT calculations, water in the Southern Hemisphere with lower ³H activities invariably has longer MTTs, which allows relative relationships to be determined. This also permits the understanding of the changing sources of water contributing to streams during different flow conditions (Duvert et al., 2016; Howcroft et al., 2018; Cartwright et al., 2018, 2020).

Previous studies of perennial streams in southeast Australia (summarised in Cartwright et al., 2020) noted that the runoff coefficient (the proportion of annual rainfall exported by the stream) had an inverse correlation with MTTs. This relationship probably reflects the high evapotranspiration rates in some catchments which results in less of the rainfall being exported as runoff. Those catchments will also have low recharge rates and slower groundwater flow, and consequently the water discharging to the streams will have longer MTTs. The runoff coefficient represents a more viable first-order proxy for MTTs than catchment attributes such as slope, drainage density, or major ion concentrations in those catchments. Whether a similar relationship between MTTs and runoff coefficients occurs in intermittent catchment is not known.

1.2 Understanding water sources

As noted above, rivers are potentially fed by a range of water stores from within catchment, including soil water, interflow, bank return flow, shallow riparian groundwater, and deeper regional groundwater (e.g. Peters et al., 2014; Duvert et al., 2016; Cartwright and Morgenstern, 2018; Howcroft et al., 2019). Due to mineral dissolution, the breakdown of organic matter, and evapotranspiration, water stored within catchments commonly has a higher salinity than surface runoff (Herczeg et al., 2001; Edmunds, 2009). Variable operation of these processes may result in differences in major ion geochemistry between the water sources. For example, soil water may have high nitrate or organic carbon concentrations due to breakdown of organic matter. There may also be differences in the stable isotope geochemistry of these waters reflecting seasonal recharge, evapotranspiration, or long-term changes to rainfall stable isotope ratios (Hughes and Crawford, 2012). Not all catchments, however, contain water stores with distinct geochemistry. This is commonly the case in southeast Australia where high evapotranspiration rates mask the effects of mineral dissolution (Herczeg et al., 2001; Cartwright and Morgenstern, 2015; Howcroft et al., 2018; Barua et al., 2022). In those catchments, documenting MTTs allows the inputs of older and younger catchment water to be assessed.

1.3 Objectives

This study determines the mean transit time and water sources at different flow conditions (including zero flows) in the seasonally intermittent upper Wimmera River in southeast Australia using ³H, ¹⁴C, stable isotopes, and major ion geochemistry. A previous study (Zhou and Cartwright, 2021) used similar tracers to understand the locations of groundwater inflow to the river, however, did not specifically address the timescale of water flow in the catchment or the volumes of the water stores that sustain streamflow. We hypothesised that (1) mean transit times in the Wimmera River are younger than in comparable perennial streams from southeast Australia, (2) younger near-river water stores (such as shallow riparian groundwater and bank return flows) are more important than regional groundwater in sustaining the river at all flow conditions, and (3) due to the river containing alternate gaining and losing reaches, the runoff coefficient will not be a reliable indicator of mean transit times. As with many rivers globally (Shanafield et al., 2020; Messager et al., 2021), the upper Wimmera River has become more intermittent over recent years due to climate change. The results from this study are important in understanding and managing catchment behaviour in intermittent streams more generally. We also assess what tracers are useful in distinguishing between water sources, which will help inform studies on similar catchments.

2 Study area

Located in southeast Australia, the Wimmera River is an intermittent river in the southern Murray–Darling Basin. The Wimmera Catchment has an area of approximately 24 000 km², and the middle and lower parts of the river are important for agriculture (Fletcher, 2015; Department of Environment, Land, Water and Planning, 2021). In the summers of all but the wettest years, the Wimmera River ceases to flow and comprises a series of disconnected pools (Western et al., 1996). Since the 1980s, the Wimmera River has experienced a decline in streamflow and an increase in intermittency (Department of Environment, Land, Water and Planning, 2021) especially between 1996 to 2009 when southeast Australia experienced a large reduction in rainfall and streamflow during the Millennium Drought (Bureau of Meteorology, 2021). The study area is located in the upper Wimmera River catchment (Fig. 1) which has an area of approximately 3000 km². Dryland pasture with remnant native eucalypt woodlands is the dominant vegetation coverage in the upper catchment (Fletcher, 2015; Department of Environment, Land, Water and Planning, 2021), and there is only minor groundwater and river water use (Robinson et al., 2006; Wimmera Catchment Management Authority, 2013; Fletcher, 2015).

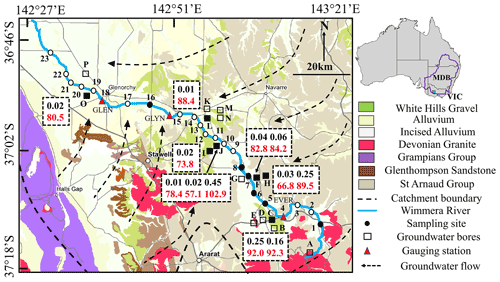
Figure 1 Summary geological and hydrogeological map of the upper Wimmera River. Stream water sampling sites and groundwater bores are indicated by numbers and letters, respectively. The sites that have radioactive isotope data are shown in solid symbols. Gauging stations with site number are Eversley (EVER; 415207), Glynwylln (GLYN; 415206), and Glenorchy (GLEN; 415201). Background geological map from Department of Jobs, Precincts and Regions (2021) (© State Government of Victoria 1996–2021); other information from Robinson et al. (2006), Department of Environment, Land, Water and Planning (2021), and Zhou and Cartwright (2021). Boxes show ¹⁴C (red) and ³H activities (black) of groundwater (data from Table 2).

The upper catchment of the Wimmera River comprises a Palaeozoic basement of metamorphosed shales and schists of the St Arnaud Group, indurated sandstones of the Glenthompson and Grampians Groups, and Devonian granites (Fig. 1, Department of Jobs, Precincts and Regions, 2021). Alluvial and lacustrine Palaeogene to Holocene sediments that were deposited by the precursors of the current rivers overlie the basement. These sediments consist of rounded gravels, coarse sands, silts, and clays (Robinson et al., 2006). The dominant topography in the upstream reaches of the upper Wimmera River is a broad valley while the downstream part is a flat alluvial flood plain (Robinson et al., 2006; Department of Environment, Land, Water and Planning, 2021).

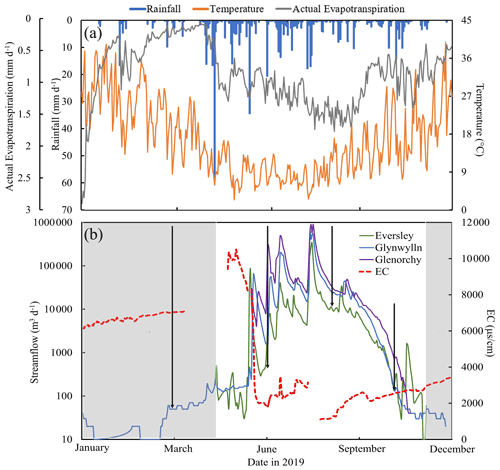
Figure 2 (a) Variations in daily rainfall, daily actual evapotranspiration, and temperature and (b) electrical conductivity (EC) at Glynwylln (missing data are caused by measurement errors of equipment) and streamflow at Eversley, Glynwylln, and Glenorchy (Fig. 1) in the upper Wimmera River in 2019. Variations in EC at Glynwylln (missing data are caused by measurement errors of equipment) and streamflow at Eversley, Glynwylln, and Glenorchy (Fig. 1) in the upper Wimmera River in 2019. Sampling times are indicated by arrowed lines. Shaded areas represent the zero-flow periods. Data from Department of Environment, Land, Water and Planning (2021) and Bureau of Meteorology (2021).

There is a decreasing trend of average annual rainfall from the southeast (709 mm) to northwest (505 mm) in this area (Bureau of Meteorology, 2021), and the winter and spring months (May to August) are the wettest (Fig. 2a). Evapotranspiration rates are also much higher in summer (up to 1.8 mm d⁻¹: Fig. 2a). The combination of rainfall and evapotranspiration variations leads to high river flows occurring in the winter and spring (Department of Environment, Land, Water and Planning, 2021; Fig. 2b).

Groundwater in the upper Wimmera recharges on the margins of catchment and flows northwards, with flow paths converging on the river (Radke and Howard, 2007; Fig. 1). River water geochemistry demonstrates that groundwater discharge locally occurs in the upper and middle reaches of the upper Wimmera River driven by relatively steep topography and high hydraulic gradients, whereas the lower reaches have lower groundwater inflows due to subdued topography (Zhou and Cartwright, 2021). From the downstream trends in Cl and ²²²Rn, and the high ³H activities, the study concluded that near-river stores were important contributors to streamflow.

3 Materials and methods

3.1 Sampling

Stream water samples (four rounds in total) were collected between March and November 2019 in the upper Wimmera River (Fig. 1, Table S1 in the Supplement). River samples were collected from the centre of the river ∼ 1 m below the surface, or just above the bed where the river was shallower, using an open sample collector. Fifteen samples of pool water were taken using an open sample collector in March 2019 when the river consisted of disconnected pools with small flowing sections. These samples were taken from isolated pools, not the flowing reaches. Twenty-three samples were collected in July, September, and November. July and September were high and moderate flow periods, respectively, whereas November was a low flow period just before the river ceased to flow again. Thirteen samples of near-river water (NRW) were taken from the top of the saturated zone within 3 m of the river. Due to Covid-19, the NRW samples were collected in April 2021 but the conditions were similar to March 2019. Groundwater samples were taken in November 2019 from groundwater-monitoring bores installed on the river bank and floodplain using an impeller pump (Fig. 1, Table S2). In excess of three volumes of water were extracted prior to sampling or the bores were pumped dry and allowed to recover.

There are three gauging stations along the river that continuously measure streamflow including Eversley, Glynwylln, and Glenorchy in Fig. 1. (Department of Environment, Land, Water and Planning, 2021). Linear interpolation and extrapolation were used to estimate intermediate streamflow data. Runoff coefficients (the percentage of rainfall that is exported annually by the stream) were estimated using 1993 to 2021 streamflow records from the three gauges (Department of Environment, Land, Water and Planning, 2021). Because insufficient rainfall data exist to calculate area-weighted rainfall amounts upstream of each gauge, runoff coefficients were calculated using the higher and lower annual rainfall from the catchment (505 and 709 mm; Bureau of Meteorology, 2021), which results in a 15 % uncertainty at each site. Here, the runoff coefficient is treated as a catchment attribute reflecting average flows rather than the flow at any one time.

3.2 Analytical techniques

³H activities were analysed at the Institute of Geological and Nuclear Sciences (GNS) in New Zealand by liquid scintillation in Quantulus ultra-low-level counters following vacuum distillation and electrolytic enrichment (Morgenstern and Taylor, 2009). ³H activities are expressed in tritium units (TUs) and the detection limit is 0.02 TU with relative uncertainties (1σ) of approximately ±2 %. ¹⁴C activities of groundwater were measured at GNS in New Zealand by accelerator mass spectrometer (AMS). CO₂ in groundwater was extracted using orthophosphoric acid and then converted into a graphite target after being purified under vacuum. ¹⁴C activities are expressed as percent modern carbon (pMC), where the ¹⁴C activity of modern carbon is 95 % of the ¹⁴C activity of the NBS oxalic acid standard in 1950 (Stewart et al., 2004).

EC values were measured in the field using a calibrated TPS meter and electrode. A Thermo Fischer quadrupole ICP–OES at Monash University was used to measure cation concentrations on samples that were filtered through 0.45 µm cellulose nitrate filters and acidified to pH < 2. Anion concentrations were measured using a Thermo Fischer ion chromatograph at Monash University on filtered, unacidified samples. Based on replicate analyses, the precision (σ) of major ion concentrations ranges from 2 % to 5 %. Stable isotope ratios were analysed at Monash University using a Thermo Finnigan Delta Plus Advantage mass spectrometer. δ¹⁸O values of water were measured in a Thermo Finnigan gas bench by equilibration with He-CO₂ at 32 ^∘C for 24–48 h. δ²H values of water were measured following reduction by Cr at 850 ^∘C in a Finnigan MAT H/Device. δ¹⁸O and δ²H values were normalised following Coplen (1988) and are expressed relative to V-SMOW (Vienna Standard Mean Ocean Water). Precision (σ) based on replicate analyses is 0.15 ‰ for δ¹⁸O and 1 ‰ for δ²H. The geochemistry data is in the Supplement.

3.3 Mean transit times

MTTs were calculated from single measurements of ³H using lumped parameter models (LPMs) implemented in the TracerLPM Excel workbook (Jurgens et al., 2012). The ³H activity of stream water at time t (C₀(t)) is related to the input of ³H (C_i) in rainfall overtime via the convolution integral:

$$\begin{array}{}\text{(1)}& C_{\mathrm{0}}\left(t\right)=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{C}_i\left(t-\mathit{\tau }\right)g\left(t\right)e^{-\mathit{\lambda }\mathit{\tau }}\mathrm{d}\mathit{\tau }.\end{array}$$

In Eq. (1), τ is the transit time, t−τ is the time that the water was recharged, λ is the decay constant of ³H (0.0563 yr⁻¹), and g(t) is a function that describes the distribution of flow paths and transit times in the flow system. The ³H input was from the annual weighted average ³H activities of rainfall in Melbourne (Tadros et al., 2014). Modern rainfall in central Victoria is predicted to have average annual ³H activities in the range of 2.8 to 3.2 TU (Tadros et al., 2014); measured ³H activities of rainfall in Victoria are within the range of the Tadros et al. (2014) estimates (Cartwright and Morgenstern, 2015; Cartwright et al., 2018; Howcroft et al., 2018; Barua et al., 2022).

Several LPMs were used. The dispersion model (DM) stems from the one-dimensional advection–dispersion transport equation and can be applied to a variety of aquifer configurations (Zuber and Maloszewski, 2001; McGuire and McDonnell, 2006; Jurgens et al., 2012). The dispersion parameter (DP), which is the ratio of dispersion to advection, needs to be defined when using this model. For kilometre-scale flow systems such as in this study, DP values of 0.05 to 0.5 are suitable (Maloszewski, 2000; Zuber and Maloszewski, 2001). The exponential mixing model (EMM) represents a flow system with a simple exponential distribution of flow paths. The exponential piston flow model (EPM) describes flow systems that have both exponential and piston-flow sections. It is an appropriate model for unconfined aquifers with vertical recharge through the unsaturated zone and exponential flow in the saturated zone (Maloszewski, 2000; Morgenstern et al., 2010; Howcroft et al., 2019). The EPM ratio is the relative contribution of piston to exponential flow, and values of 0.33 and 1, which represent 75 % and 50 % exponential flow, were used. MTTs were estimated by matching the ³H activities predicted by the LPMs to the measured ³H activities. While the estimates of MTTs are based on single samples, these LPMs have successfully reproduced long-term time-series ³H activities of stream water in other regions (Małoszewski and Zuber, 1982; Blavoux et al., 2013; Morgenstern et al., 2015).

The same lumped parameter models were used to calculate the predicted ¹⁴C vs. ³H trends and MTTs of groundwater. For ¹⁴C, the input function is based on activities of atmospheric CO₂ (McCormac et al., 2004; Reimer et al., 2013). Calcite in these aquifers is mainly cements and veins, which are likely to have variable δ¹³C values (Cartwright and Morgenstern, 2012; Cartwright et al., 2013; Clark, 2015; Meredith et al., 2016), precluding the use of isotope mass–balance to estimate the degree of closed-system calcite dissolution. However, the aquifers are siliceous and close-system calcite dissolution is expected to be minor (< 10 %) (Clark, 2015).

3.4 Volumes of groundwater

The groundwater volumes (V in m³) that contribute to the river are related to MTT and streamflow (Q in m³ yr⁻¹) via

$$\begin{array}{}\text{(2)}& V=Q\times \mathrm{MTT}.\end{array}$$

(Małoszewski and Zuber, 1982; Morgenstern et al., 2010).

4 Results

4.1 Streamflow

The variations of streamflow at the three gauging stations (Fig. 1) along the upper Wimmera River in 2019 are shown in Fig. 2b. Although streamflow of up to 50 m³ d⁻¹ was recorded at Glynwylln during the summer months (January to March), the river largely consisted of disconnected pools with only minor flowing sections. Based on the streamflow at this and the Eversley and Glenorchy gauges (Fig. 2b), the river is estimated to have commenced flowing continuously in early to mid-April. There was a significant increase in streamflow from June following autumn rains (Fig. 2a) and it reached a peak in August (up to 6.1 × 10⁵ m³ d⁻¹ at Glenorchy). Streamflow then decreased over spring and summer, and the river ceased to flow continuously in late November. Runoff coefficients have ranges of 4.0 % to 5.4 % at Eversley, 2.3 % to 3.2 % at Glynwylln, and 2.2 % to 3.0 % at Glenorchy.

4.2 EC and major ion geochemistry

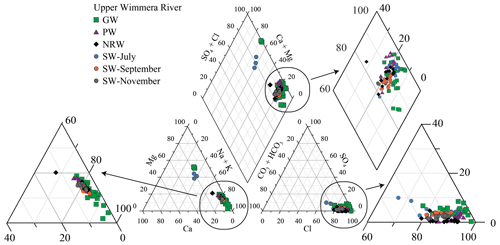
EC values in 2019 at the Glynwylln gauging station increased during the summer months, peaked at 10 500 µS cm⁻¹ in late May, and decreased to 1780 µS cm⁻¹ in June (Fig. 2b). Overall, EC values were broadly inversely correlated with streamflow. Total dissolve solid (TDS) concentrations of stream water in the upper Wimmera River varied from 360 to 2490 mg L⁻¹ (Table S1) and were also higher during the low flow period in November 2019. Na is the most abundant cation in the stream water (74 %–83 % on a molar basis) with lower abundances of Ca (3 %–7 %), Mg (12 %–19 %), and K (1 %–2 %). Cl is the most common anion (82 %–99 % on a molar basis) in the stream water (Fig. 3). During the zero-flow period in March 2019, the pool water was much more saline with EC values of 2430–15 330 µS cm⁻¹ and TDS concentrations (up to 11 420 mg L⁻¹) (Table S1). Near-river water (NRW) from the zero-flow period in 2021 had EC values of 1035 to 6080 µS cm⁻¹. TDS concentrations of regional groundwater from monitoring bores in this region ranged from 550 to 13 720 mg L⁻¹ (mean = 4900 ± 3770 mg L⁻¹: Table S2) and there is no correlation between TDS and depth. Na and Cl are again the dominant cations and anions in the groundwater (Fig. 3, Table S2). Overall, the major ion geochemistry of the groundwater, stream water from the different flow conditions, pool water, and NRW are similar (Fig. 3).

Figure 3 Trilinear diagram summarising molar major ion ratios of the different water sources in the upper Wimmera River (data from Tables S1 and S2). GW = groundwater; PW = pool water; NRW = near river water; SW = stream water. Inserts show details of the data.

4.3 Stable isotopes

The δ¹⁸O and δ²H values of the stream water differed between the sampling rounds (Tables S1 and S2, Fig. 4). The δ²H and δ¹⁸O values of the pool water were −24 ‰ to +37 ‰ and −3.3 ‰ to +10.3 ‰, respectively, and define an array to the right of Melbourne meteoric water line with a slope of 4.2 which implies that evaporation has occurred (Gonfiantini, 1986; Clark and Fritz, 1997). The pool water array intercepts the Melbourne meteoric water line at lower δ¹⁸O and δ²H values (−5.6 ‰ and −31 ‰) than those of average rainfall in Melbourne (δ¹⁸O = −4.98 ‰, δ²H = −28.4 ‰; Hollins et al., 2018), probably due to the Wimmera region being further inland. δ¹⁸O and δ²H values of river water in July and September cluster close to the Melbourne meteoric water line. δ¹⁸O and δ²H values in July 2019 were −3.6 ‰ to −7.2 ‰ (mean = −6.1 ± 0.7 ‰) and −29 ‰ to −43 ‰ (mean = −35 ± 3.8 ‰), respectively, whereas in September 2019, δ¹⁸O and δ²H values were −3.9 ‰ to −6.1 ‰ (mean = −5.3 ± 0.4 ‰) and −29 ‰ to −32 ‰ (mean = −31 ± 0.9 ‰), respectively (Table S1). δ¹⁸O and δ²H values during the low streamflow period in November 2019 ranged from −2.7 ‰ to −4.8 ‰ and −20 ‰ to −26 ‰, respectively, while those of the NRW were −0.5 ‰ to −3.1 ‰ and −8 ‰ to −29 ‰, respectively. Both the November river samples and the near-river waters define similar evaporative trends to the pool waters. Groundwater has δ¹⁸O and δ²H values of −4.4 ‰ to −6.7 ‰ (mean = −5.4 ± 0.6 ‰) and −28 ‰ to −38 ‰ (mean = −31 ± 2.7 ‰), respectively, that overlap with those of the stream water in July and September (Fig. 4; Table S1).

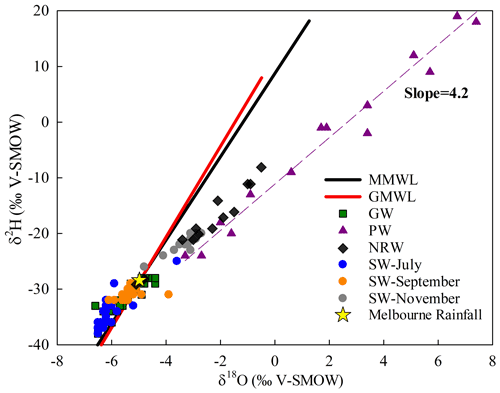
Figure 4 Stable isotope ratios of water samples in the upper Wimmera River. GMWL = global meteoric water line (δ²H = 8.2 × δ¹⁸O + 11.3 ‰, as defined by Rozanski et al., 1993); MMWL = Melbourne meteoric water line (δ²H = 7.4 × δ¹⁸O + 8.6 ‰, as defined by Hughes and Crawford, 2012). GW = regional groundwater; PW = pool water; NRW = near-river water; SW = stream water. The dashed line is the best fit for the pool water data. Data from Tables S1 and S2.

4.4 ³H and ¹⁴C activities

4.4.1 Regional groundwater

³H activities of regional groundwater were < 0.02 to 0.45 TU (Table 2), which are significantly lower than the predicted average ³H activity of annual modern rainfall in this area (3.0 ± 0.2 TU: Tadros et al., 2014). The higher ³H activities were from shallow groundwater (< 18 m depth) in the upper and middle catchment, whereas deep groundwater (> 30 m depth) had ³H activities < 0.02 TU. Groundwater close to the river does not generally have high ³H activities (Fig. 1). ¹⁴C activities of regional groundwater ranged between 57.1 and 103 pMC (Table 2). The highest ¹⁴C activities (up to 103 pMC) are again from the shallow groundwater in the upper and middle catchment. The trend of ³H vs. ¹⁴C activities (Fig. 5) are similar to those predicted for an aquifer system that does not show mixing between shallow younger groundwater and deeper older groundwater (i.e. where the activities of the two radioisotopes are controlled by their input functions and decay rates).

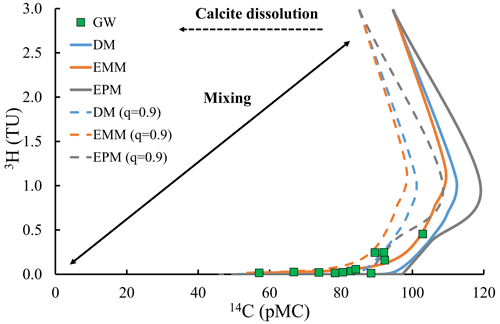
Figure 5 ³H activities vs. ¹⁴C activities of groundwater from the upper Wimmera River. Curved lines are the predicted covariance in the radioisotopes predicted by the exponential mixing, exponential piston (EPM ratio = 1), and dispersion (DP = 0.5) lumped parameter models. Solid arrowed lines show schematically the effects of mixing between old regional groundwater (low ¹⁴C and ³H free) and modern or recently recharged water (high ¹⁴C and ³H). Calcite dissolution lowers the predicted ¹⁴C activities (dashed lines are used to display 10 % calcite dissolution).

4.4.2 River water

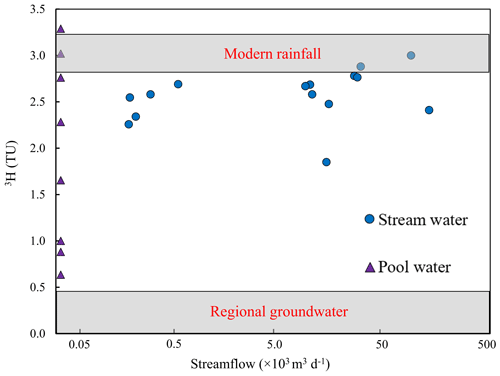
The ³H activities of pool water varied from 0.64 to 3.29 TU (Fig. 6; Table 1). The highest ³H activity (3.29 TU), which is higher than that of average annual rainfall, was from an area of subdued topography in the lower reaches. In contrast, ³H activities were lowest (down to 0.64 TU) where the river is located near steeper hillslopes and flows through coarse sediments. There is a strong positive correlation (R² = 0.94) between ³H activities of pool water and δ²H values (Fig. 6a). Pool waters have a wide range of ³H activities with variable TDS concentrations, ranging from 2237 to 4639 mg L⁻¹. The stream water was less saline with a range of TDS 433–2038 mg L⁻¹ (Fig. 6b).

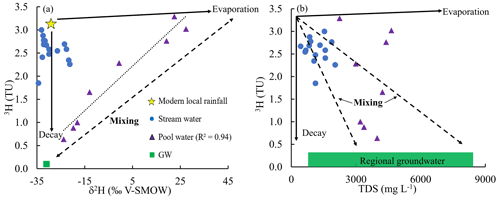
Figure 6 (a) Variation of ³H activities and δ²H values, and (b) ³H activities and TDS of stream water, pool water, and groundwater (GW) in the upper Wimmera Catchment. Arrows show trends expected from evaporation and mixing. Data from Tables S1 and S2.

Table 1 ³H activities and calculated mean transit times (MTTs) from pool water and stream water of upper Wimmera River.

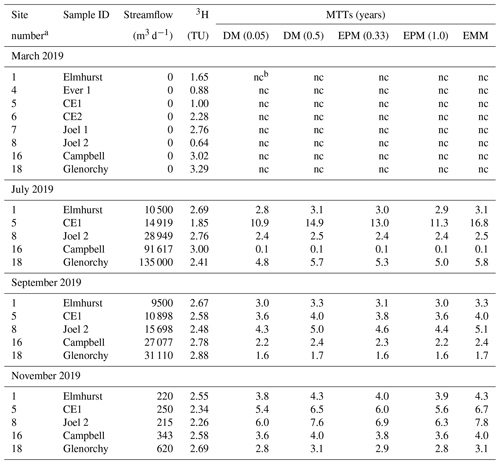
^a sites in Fig. 1. ^b nc = not calculated.

Table 2 ³H, ¹⁴C activities, and calculated MTTs by EPM (ratio = 0.33) of groundwater from the upper Wimmera River.

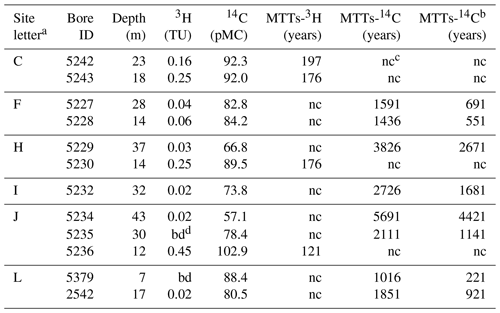
^a sites in Fig. 1. ^b MTTs estimated by ¹⁴C activities with 10 % calcite dissolutions. ^c nc = not calculated. ^d bd = below detection.

The ³H activities of stream water during the periods when the river was flowing were generally lower than those of rainfall and had a range of 1.85 to 3.00 TU in July, 2.48 to 2.88 TU in September, and 2.26 to 2.69 TU in November (Table 1). During the high streamflow in July, the ³H activities of river water were more variable than in September and November (Figs. 6, 7). Both lowest and highest values of ³H activities were recorded in the high flow period (Fig. 7).

Figure 7 Variation of ³H activities and streamflow. Pool water represents a time of zero streamflow. Shaded areas show ³H range of modern rainfall and regional groundwater. Data from Table 1.

5 Discussion

The combined streamflow, major ion geochemistry, and stable and radioactive isotopes allow the water sources contributing to streamflow and MTTs at different flow conditions to be understood.

5.1 Identification of water sources

Pool waters in summer months contain the last remnants of river water from when the river ceases to flow, and rainfall and/or groundwater discharging from the underlying aquifers (Cartwright and Morgenstern, 2016; Lamontagne et al., 2021). In the upper Wimmera River, most of the pools are perennial and have a wider range of ³H activities than stream water and groundwater (Fig. 7). The variation in ³H activities with δ²H (Fig. 6a) and TDS concentrations (Fig. 6b) most likely reflects the mixing between older regional groundwater (saline with lower ³H activities) and younger surface water with lower salinity and higher ³H activities. The variations between δ¹⁸O and δ²H values (Fig. 4), and ³H activities and δ²H values (Fig. 6a) imply that the surface-water-dominated pools have undergone higher degrees of evaporation than those with greater groundwater inflows. Conceivably, the pools that are better connected to the groundwater are throughflow systems, which would limit evaporation whereas other pools may trap surface water which then evaporates. Some of the pool water has higher ³H activities (up to 3.29 TU) than were recorded at the low flows that immediately precede the formation of the pools (Fig. 7). Summer rainfall in southeast Australia, however, generally has ³H activities close to the annual average (Tadros et al., 2014), and the input of summer rainfall cannot readily explain the locally high ³H activities. Late winter and spring rainfall has higher ³H activities than those of average rainfall due to stratosphere–to–troposphere moisture exchange (Tadros et al., 2014). The upper Wimmera River is locally losing at high streamflows, such as commonly occurring in late winter and early spring (Fig. 2) allowing bank storage to occur. Subsequent drainage of bank water back to the river potentially explains the local high ³H activities in the pools. Alternatively, these high ³H activities may reflect the input of young water from perched aquifers in the riparian zone as documented in intermittent streams elsewhere in western Victoria (Barua et al., 2022).

The ³H activities of stream water when the upper Wimmera River is flowing is much higher than that of groundwater (Figs. 6, 7), implying that the river is largely fed by young water. This is the case even during the low flow periods, which is when rivers are most likely to be sustained by long-lived water stores (e.g. Gusyev et al., 2016; Cartwright et al., 2020). The much lower TDS concentrations of the river water compared with the groundwater (Fig. 6b) and irregulated downstream trends in major ion concentrations (Table S1) are also consistent with the input of water from mainly near-river sources. The one lower ³H activity (1.85 TU) during high flow conditions in July 2019 (Table 1, Fig. 7) may reflect very local input of regional groundwater or older near-river waters being flushed into the stream during the early stages of rainfall by hydraulic loading. This has been documented in other Australian catchments (e.g. the Tambo River: Unland et al., 2015) and is a common feature in many river systems (sometimes referred to as the old water paradox: Kirchner, 2003; Cartwright and Morgenstern, 2018). Unlike in some catchments (Tsujimura et al., 2007; Birks et al., 2019; Jung et al., 2019), the major ion and stable isotope geochemistry of regional groundwater and near-river water are similar (Figs. 3 and 4; Tables S1 and S2). The geochemistry of the stream also does not vary with flow. This precludes using these tracers to distinguish water sources or as a proxy for ³H activities (e.g. Peters et al., 2014; Cartwright and Morgenstern, 2015; Beyer et al., 2016; Cartwright et al., 2020). The large difference in ³H activities between regional groundwater and rainfall, however, explicitly allows the input of older groundwater to be assessed.

5.2 Mean transit times of river water

The estimates of mean transit time assume that there is a single flow system within the catchment. The pool waters probably represent discrete mixing between older groundwater and younger water (Fig. 6). It is not possible to calculate the MTTs of these waters using a single LPM and there is insufficient data to use binary LPM calculations. In common with other studies of MTTs, it is assumed that when the river is flowing, it is sustained by a single store of water with MTTs that vary as the catchment dries down and wets up. As discussed above, most of the water sustaining the river when it is flowing is envisaged to be derived from near-river stores with little input from regional groundwater.

The MTTs in the upper Wimmera River when it was flowing ranged from < 1 to 17 years and are mostly less than 7 years (Table 1). The different LPMs yielded slightly different MTTs and the range of MTTs increases with decreasing ³H activities. The highest estimates of MTTs are from the EMM and the lowest are from the DM with D_p 0.05. During the high flow period in July 2019, MTTs were generally higher (< 1 to 16.8 years). By contrast, the range of MTTs at moderate and low flow conditions was 1.6 to 7.8 years (Table 1).

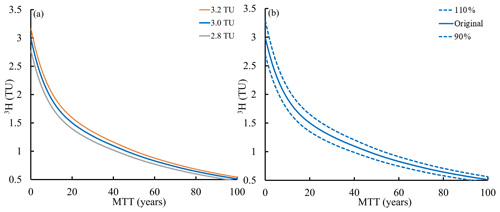
Figure 8 (a) Impacts of varying the ³H activity of modern rainfall from 2.8 to 3.2 TU on MTTs calculated using the exponential piston flow model (EPM ratio = 0.33). (b) Impacts of varying ³H activity of rainfall between 90 % and 110 % of its assumed values on mean transit time calculated using the exponential piston flow model (EPM ratio = 0.33).

The MTTs are subject to several uncertainties. The uncertainty arising from the choice of LPMs is greater at ³H activities < 2.5 TU with an average uncertainty of 22 % (Table 1). The influence of uncertainties in the ³H activities of modern rainfall (±0.2 TU: Tadros et al., 2014) may be demonstrated using the EPM with an EPM ratio of 0.33 (the effects are similar in other models) (Fig. 8a). Varying the ³H activities between 2.8 TU and 3.2 TU translates into uncertainties of ±6 % to 7 % (Fig. 8a). Applying a similar 10 % uncertainty to the entire ³H input function produces uncertainties of 9 % to 21 %, with the largest difference when ³H activities were greater than 1 TU (Fig. 8b). Uncertainties arising from the precision of the ³H analyses are < 0.8 years. Mixing of multiple water sources with different MTTs (aggregation) may result in actual MTTs being lower than calculated MTTs (Suckow, 2014; Kirchner, 2016a; Stewart et al., 2017). Aggregation has the most impact when there is binary mixing between water with very different MTTs. Mixing between multiple water stores with a range of MTTs has less impact on the MTTs calculated using ³H as that scenario is similar to what is modelled using the LPMs (Cartwright and Morgenstern, 2016). In the case of the upper Wimmera River, the smaller range of MTTs implies that aggregation may not be as significant as in other catchments in southeast Australia where the range of MTTs in the catchment waters is much larger. Considering the uncertainties from the different LPMs, the analytical uncertainty, and the tritium activities of modern and historical rainfall, the range of MTTs for a ³H activity of 1.5 TU was 15.2 to 25.5 years, which is a relative uncertainty of −24 % to +27 %. For water with 0.5 TU, the MTTs ranged 92.6 to 108 years, which is an uncertainty of −9 % to +15 %. Although these are substantial, it does not alter the conclusion that the upper Wimmera River is fed by relatively young water at all stages of flow.

The average annual rainfall ³H activities were used in the MTTs calculations. However, if there is strong seasonal recharge due to summer rainfall being lost by evapotranspiration, the ³H activities of the recharging water may be different to the average annual ³H activity (Morgenstern et al., 2010; Blavoux et al., 2013). Monthly variations in rainfall ³H activities are less than 1 TU and the ³H activities of summer rainfall are close to annual rainfall values (e.g. Tadros et al., 2014). Considering the general uncertainty in the ³H input function, uncertainties that originate from adopting the average annual ³H activity are minor.

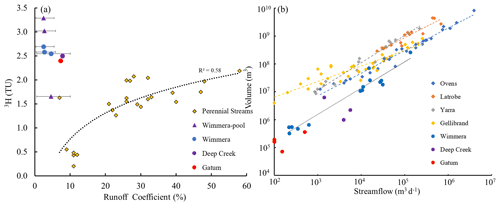
Figure 9 (a) Comparison of ³H activities and runoff coefficients at low and zero flow conditions, and (b) volumes of water sustaining streamflows between the upper Wimmera River and other intermittent and perennial streams in southeast Australia. Error bars represent the uncertainty of annual rainfall in the upper Wimmera Catchment. Perennial streams are the Ovens, Latrobe, Yarra, and Gellibrand (data from Cartwright et al., 2020); intermittent streams are Deep Creek and Gatum (data from Cartwright and Morgenstern, 2016 and Barua et al., 2022).

The volume of water store that sustained the streamflow calculated from the MTTs (Eq. 2) ranged from 3.2 × 10⁵ to 2.6 × 10⁸ m³ (Fig. 9b). The estimated volume of water stored in the riparian zone of the river is 3.1 × 10⁵ m³, which was calculated from the estimated river length (120 000 m), the width and depth of the riparian zone (6.5 and 2 m, respectively), and an assumed porosity of 0.2. This value is 3 orders of magnitude smaller than that of the calculated volume of water needed to generate streamflow during the high flow period, implying that the streamflow was generated from water derived from the broad landscape. By contrast, the volume of water in the riparian zone is similar to the volume needed to generate streamflow at low flow conditions, which indicates that it may be derived from near-river stores.

5.3 Groundwater transit times

Groundwater MTTs were calculated using the EPM model (EPM ratio = 0.33; Table 2). This model is applicable to groundwater flow systems where the bores sample deeper groundwater flow paths but not the short near-surface flow paths (Małoszewski and Zuber, 1982). MTTs of groundwater with ³H activities > 0.25 TU were calculated using ³H. For groundwater with lower ³H activities, the ¹⁴C activities were used. As discussed above, the proportion of dissolved inorganic carbon (DIC) from closed system calcite dissolution in these siliceous aquifers is likely to be minor, and MTTs were calculated assuming up to 10 % addition of ¹⁴C-free carbon. The estimated MTTs of groundwater were between 120 and 5690 years (Table 2). The relative uncertainties on these estimates are similar to those discussed above. Groundwater within a few tens to hundreds of metres of the river, such as at locality I and J in Fig. 1, had MTTs of up to 5690 years, and the ¹⁴C and ³H activities show little evidence of mixing (Fig. 5), implying that there is limited recharge of regional groundwater by stream water even when the river is losing. The large contrast between the MTTs of groundwater and river water also implies that the regional groundwater flow system is distinct from local near-river flow system.

5.4 Comparison with perennial streams

In southeast Australia, the ³H activities at low flows in the upper Wimmera River and other intermittent streams are higher than in perennial streams of comparable size from catchment with similar geology and land use (Fig. 9). Perennial streams elsewhere in Australia and New Zealand also locally have low ³H activities at low flows (Stewart et al., 2010; Duvert et al., 2016). This implies that intermittent streams at low streamflows are sustained by much younger water than perennial streams. This is concluded to be caused by a much weaker connection between intermittent streams and deeper older regional groundwater than is the case for perennial streams.

Because evapotranspiration rates, local vegetation types, and rainfall influence both how much of rainfall is exported via the stream and the MTTs, ³H activities in perennial streams from southeast Australia correlate with the runoff coefficient (Fig. 9a). There is a broad correlation (R² = 0.58) between ³H and runoff coefficients from multiple perennial catchments in southeast Australia (including the Ovens, Latrobe, Gellibrand, and Yarra catchments: Fig. 9a), and the correlations in individual catchments are higher (R² of 0.72 to 0.94: Cartwright et al., 2020). By contrast, the ³H activities in the Wimmera and other intermittent streams are much higher at comparable runoff coefficients and are poorly correlated (Fig. 9a). This may be due to the alternating gaining and losing conditions in intermittent streams.

The volumes of the stores of water in the catchment that contributes to streamflow in the upper Wimmera River (3.2 × 10⁵ to 2.6 × 10⁸ m³: Fig. 9b) are 1–2 orders of magnitude smaller at similar streamflows than those in perennial streams from southeast Australia (up to 8.3 × 10⁹ m³ in the Ovens Catchment) (Fig. 9b) but are similar to other intermittent streams (Deep Creek and Gatum catchments). These differences are also due to the intermittent streams being less well-connected to the deeper groundwater, which has larger volumes.

6 Conclusions

Currently about 51 % to 60 % of global rivers have ceased to flow at least one day per year and intermittency of streams is forecasted to increase due to climate change and rising water usage (Messager et al., 2021). Thus, investigation of intermittent streams that commonly occur in semi-arid regions with scarce surface water resources is vital. However, our understanding of the functioning of intermittent catchments remains incomplete (e.g. Datry et al., 2014; Shanafield et al., 2020, 2021). Integrating mean transit time estimates into studies of intermittent catchments will allow a better general understanding of this important group of rivers.

The upper Wimmera River and other intermittent streams in southeast Australia are connected to younger stores of near-river water with limited connections to deeper regional groundwater. Because those stores are smaller, intermittent rivers will be more vulnerable to short-term variability of rainfall and respond more quickly to land use changes than comparable perennial rivers. This is evident in the Wimmera River where flow has decreased and intermittency has increased following the onset of the Millennium Drought in the mid-1990s. In comparison, most of the perennial rivers summarised in Cartwright et al. (2020) currently have similar flow regimes as prior to the Millennium Drought. The fact that intermittent streams receive inputs from near-river water stores also has implications for their protection and management. They are probably less vulnerable to contamination via inputs of regional groundwater; however, protection of the near-river environment is crucial to maintain river health. The pools at zero flow conditions in the Wimmera and other intermittent streams have some groundwater inputs (Lamontagne et al., 2014, 2021; Cartwright and Morgenstern, 2016). Even where these are not substantial, connection with the regional groundwater is important for preventing the stream from drying up completely. Reduction in groundwater elevations due to climate change or pumping may have serious impacts on these pools that are commonly important water sources for local ecosystems in dry summers.

This study also illustrates the general use of radioisotopes such as ³H to understand water stores that contribute to river flow. Major ion geochemistry and stable isotopes may be able to discern the sources of river water; however, in many catchments (both intermittent and perennial), this is not possible. Estimating mean transit time estimates allows a direct understanding of where in the catchment the water is derived from. In the Southern Hemisphere, ³H allows mean transit times to be readily estimated in relatively large catchments and this will be the case in the Northern Hemisphere in the near future (Morgenstern et al., 2010).