the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Recession discharge from compartmentalized bedrock hillslopes
David E. Rupp
Jean-Raynald de Dreuzy
Laurent Longuevergne
Elizabeth R. Jachens
Gordon Grant
Luc Aquilina
John S. Selker
We used numerical modelling to explore the role of the vertical compartmentalization of hillslopes on groundwater flow and recession discharge. We found that, when hydraulic properties are vertically compartmentalized, streamflow recession behaviour may strongly deviate from what is predicted by groundwater theory that considers the drainage of shallow reservoirs with homogeneous properties. We further identified the hillslope configurations for which the homogeneous theory derived from the Boussinesq solution approximately holds and, conversely, for those for which it does not. By comparing the modelled recession discharge Q and the groundwater table dynamics, we identified the critical hydrogeological conditions controlling the emergence of strong deviations. The three main controls are (i) the contribution of a deep aquifer connected to the stream, (ii) the heterogeneity in hydraulic properties, and (iii) the slope of the interface between a shallow permeable compartment and deep bedrock one with lower hydraulic properties. Our results confirm that a correct physical interpretation of the recession discharge exponent b from the classical equation , and its temporal progression, requires knowledge of the structural configuration and heterogeneity of the aquifer.
- Article
(3716 KB) - Full-text XML
- BibTeX
- EndNote
Recent streamflow recession analyses have provided new insight into the spatial and temporal variability in hydrological behaviour across the globe (Fan, 2015; Tashie et al., 2020; Schmidt et al., 2020; Roques et al., 2021). These analyses have confirmed that the relationship between groundwater storage and stream discharge (hereafter called the storage–discharge function) may be highly nonlinear and deviate from what would be predicted from groundwater theory under the assumption of homogeneous subsurface properties. They have also shown that such nonlinearities in storage–discharge functions may be variable across different recharge events, suggesting dependencies on antecedent catchment conditions (Jachens et al., 2020; Tashie et al., 2020). In the current context where hydrological systems are increasingly impacted by more frequent and intense periods of drought, pushing aquifers and streams to new extremes (Gudmundsson et al., 2021; Famiglietti, 2014), it is urgent that we increase our understanding of the main controlling factors responsible for low-flow discharge dynamics (Fan et al., 2019; Blöschl et al., 2019).
Groundwater theory assuming homogeneous subsurface properties shows that the rate of change in discharge of the falling limb of the hydrograph may scale as a power law of the actual discharge Q, as follows:
The recession constants a and b arise from the geometric and hydraulic properties of the aquifer system. They are also highly sensitive to the predominant diffusive or kinematic flow conditions (Rupp and Selker, 2006). b is specifically defined as the constant of nonlinearity in the storage–discharge function (Kirchner, 2009). Large values of b are characteristic of resilient streams whose low flows decrease slowly with time (Jachens et al., 2020; Berghuijs et al., 2016; Kirchner, 2009). Models derived from solutions to the 1D Boussinesq equation, assuming homogeneous and horizontal aquifers, predict values from 1 to 1.5 under low-flow conditions (Brutsaert and Nieber, 1977). b ranges from b=1 for confined and thick unconfined aquifers (i.e. much thicker than the depth of the penetrating stream channel), whose saturated thickness only marginally changes, to b=1.5 for a relatively thin unconfined aquifer (Brutsaert and Nieber, 1977; Troch et al., 2013; Wittenberg, 1999). When b=1, the aquifer drainage is exponential, with a characteristic timescale . When b=1.5, the decrease in the transmissivity with head slows down the aquifer drainage. There is currently a dearth in the definition of contexts, where such simplified effective representations are likely to succeed or fail in accurately describing groundwater storage–discharge dynamics.
Indeed, observed values of b for low-flow conditions may exceed the theoretical values previously described and question the use of homogeneous groundwater flow theories (Tashie et al., 2020; Roques et al., 2017; Jachens et al., 2020; Roques et al., 2021). Previous authors have explored the processes that might be responsible. They include the effect of the spatial and vertical distribution of flow paths (Harman et al., 2009; Rupp and Selker, 2005; Clark et al., 2009), the influence of planform shape of elementary area on flow paths (Paniconi et al., 2003), the spatial variability in recharge and evapotranspiration (Tashie et al., 2020), and the storage from the unsaturated zone (Luo et al., 2018). Quantifying the relative contribution of all those factors in controlling the storage–discharge nonlinearity remains a major challenge in hydrology.
The storage–discharge function becomes nonlinear in catchments where geological heterogeneities affect the partitioning of groundwater flow. Heterogeneity may arise from the presence of different lithologies in the catchment with contrasted permeability. Another source of heterogeneity, which has been described in the referenced studies, is the general decrease of permeability with depth (Anderson, 2015; Boutt et al., 2010; St. Clair et al., 2015; Hencher et al., 2011; Welch and Allen, 2014; Guihéneuf et al., 2014). All conceptual models agree that (1) hydraulic conductivity decreases with depth in response to increasing confining stress and illuviation. Permeability data inferred from borehole tests show an exponential trend with depth that has been quantified in several studies around the world (Saar and Manga, 2004; Ingebritsen and Manning, 1999; Achtziger-Zupančič et al., 2017), and (2) hydraulic properties may be enhanced in the shallower part (up to a depth of 100 m), due to supergene weathering processes and the presence of elevated joint densities in response to unloading and topographic stresses (Harman and Cosans, 2019; Riebe et al., 2017; Rempe and Dietrich, 2014; Moon et al., 2017; Dewandel et al., 2006). Besides such evidence of the vertical compartmentalization of hillslopes, efforts aimed at modelling groundwater storage variations and streamflow discharge often simplify this heterogeneity by considering a homogeneous aquifer with effective hydraulic properties. Here we aim at identifying in which context this simplification may hold and, conversely, in which ones it could be a source of large uncertainty and error when estimating the storage–discharge functions of hillslopes.
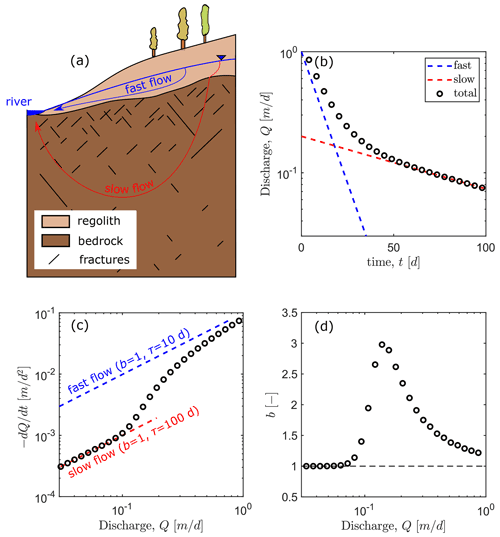
Figure 1(a) Conceptual model of a compartmentalized hillslope with groundwater flow distributed between fast flow within the shallow regolith/fractured aquifer and slow flow in the underlain bedrock. (b) Theoretical streamflow behaviour considering two linear reservoirs (b=1) in parallel with fast (blue line; τ=10 d) and slow (red line; τ=100 d) drainage timescales. (c) Resulting recession plot . (d) The evolution of b as a function of discharge identifying high values during the transitional flow regimes up to 3 in this case.
Storage–discharge functions with values of b larger than 1.5 during baseflow suggest that the resistance to drainage can be even stronger than the one induced by the decrease in transmissivity with the hydraulic head. The decrease in hydraulic conductivity with depth and vertical compartmentalization plays a significant role in the emergence of anomalous b values. From this perspective, Rupp and Selker (2005, 2006) derived analytical solutions for the case of horizontal (Rupp and Selker, 2005) and sloping (Rupp and Selker, 2006) aquifers, with a power law decrease of hydraulic conductivity with depth such that K≅zn, where z is the elevation, and n is the power law exponent (n>0). The authors showed that b is determined by n, according to for a horizontal aquifer, such that b is an increasing function of n with a lower limit of 1.5 for n near zero to an upper limit of 2 for large values of n. As expected, the stratification of the hydraulic conductivity increases b and slows down the drainage. In this approach, groundwater flows are constrained to the uppermost material, implicitly supposing that there is a shallow, impermeable boundary parallel to the topography. Although this may be a reasonable assumption in some cases, we hypothesize in this paper that, in other contexts, deeper aquifers may also significantly contribute to stream discharge (Fig. 1a). To test our hypothesis, we determine the recession discharge behaviour arising from the presence within the hillslope of a shallower compartment overlaying on a deeper one with contrasting hydraulic conductivities. This structure typically represents a permeable near-surface regolith aquifer underlain by a deeper, less permeable bedrock compartment (Fig. 1a). Such structures are expected to induce the two following effects. First, the aquifer discharge is expected to slow down progressively from the fast drainage of the permeable near-surface layer with low characteristic timescales (high value of a as shown in blue in Fig. 1b and c) to the drainage of the deeper less permeable compartment with consequently longer drainage timescale (lower value of a as shown in red in Fig. 1b and c). Second, the sloping interface between the two compartments conditions the shape of the water table profile and progressively modifies the partitioning of flows on either side of the interface. The transition between the trends given by each of the compartments is likely to cover a wide range of times and behaviours. For a simpler system of two parallel linear reservoirs (Fig. 1b–d), Gao et al. (2017) have shown a broad variety of transitioning flows and found that b may be written as a function of the ratio of the fast flow to the total flow and of the hydraulic conductivity ratio between the two compartments (Eq. 19 of their paper and in Appendix A). We will use the two parallel linear reservoirs theory as a reference to describe our results and explore in which context such a simplification might hold to describe storage–discharge functions of vertically compartmented hillslopes.
We investigate the time dependency of streamflow recession behaviours during the drainage of hillslopes where both shallow and deep compartments are involved (Fig. 1a). We specifically provide a thorough analysis of the respective controls of both geometrical and hydraulic properties in controlling storage–discharge nonlinearity in our two-compartment representation of the subsurface.
2.1 Model geometry and structure
We consider a 2-dimensional (2D) representation of the subsurface (Fig. 2a), which consists of a lower compartment with a horizontal impermeable base and a length of L=100 m from the stream location to the groundwater divide. The elevation z=0 is set at the river elevation located on the left boundary. The bottom of the model is at −ζ at x=0. We define an upper compartment of constant thickness D, leading to a total thickness (D+ζ) at x=0 that is equal to L and a slope angle , where e is the elevation of the interface at x=L.
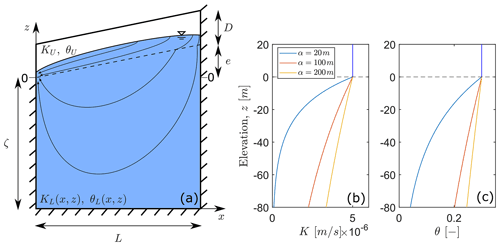
Figure 2(a) A 2D model cross section with the main geometrical parameters identified along with model boundaries and groundwater flow lines. Panels (b) and (c) are vertical profiles taken at x=0 of K and θ, respectively, for the different α values investigated.
In the lower compartment, the saturated hydraulic conductivity KL and the porosity θL decrease exponentially with depth (Fig. 2b and c), following the classically used relationship (e.g. in Cardenas and Jiang, 2010):
and
where zs=βx is the elevation of the interface between the two compartments, and α is the characteristic depth over which hydraulic properties decrease. Initial values of and were taken arbitrarily at m s−1 and 0.3, respectively. η is a coefficient related to the medium structure that we chose to be equal to 2, as commonly reported in the literature (Cardenas and Jiang, 2010; Bernabé et al., 2003). The upper layer has a homogeneous isotropic saturated hydraulic conductivity, KU, and a homogeneous porosity, θU. We explore contrasts in hydraulic conductivities between both compartments according to the ratio rK, as . The porosity of the upper compartment and the interface remain constant across simulations with .
The geometrical parameters β and D are varied in order to explore different hillslope configurations, with and = [0.0, 0.1, 0.2, 0.5]. The exponential decrease in hydraulic properties of the lower compartment is changed by varying α = [20, 100, 200] m in Eqs. (2) and (3). Finally, the contrast in hydraulic conductivities is explored over 2 orders of magnitude with rK = [1, 4, 16, 64, 256].
2.2 Groundwater flow simulation
We performed computational fluid dynamics (CFDs) simulations in the 2D hillslope. The flow for variably saturated porous media with incompressible fluid is modelled by solving the Richards' equations with a finite element approach implemented in COMSOL Multiphysics®. We set the vertical uphill boundary to no flow. The vertical downhill boundary is divided into a no-flow boundary below the river elevation and a fixed-head boundary on the top layer. The fixed-head boundary allows the groundwater to discharge into the stream at a rate that is driven by the head difference between the aquifer and the river and a conductance term. For simplicity, we set the head of the river to 0 m, meaning that no river stage variation is allowed in our model. We set the conductance between the aquifer and stream equal to the hydraulic conductivity of the uppermost aquifer KU to avoid any additional resistance at the boundary. We assume that the rock compressibility is negligible – by setting it equal to the water compressibility – implying that the storage coefficient only depends on the effective porosity.
The mesh is composed of tetrahedral elements. We imposed a finer mesh in the uppermost part of the model where the fastest changes in water table elevation and saturation occur. The initial conditions are of a fully saturated aquifer which then drains towards an asymptotically flat water table. We excluded the initial times of the simulations, until the water table progressed toward a free water table profile from the river to the uphill no-flow boundary. The case of a horizontal homogeneous shallow aquifer, i.e. without the deeper compartment, was checked against the analytical solution from Boussinesq (1904) to ensure accurate convergence, i.e. considering Eq. (1) for discharge per unit of river length Q, with a and b defined as follows:
3.1 Effect of the deep compartment in the case of a flat aquifer (β=0)
First, we review the numerical results for a horizontal homogeneous shallow aquifer overlying a deeper, less permeable, compartment, i.e. the case where . In order to identify the relative influence of the deep aquifer on the recession behaviour for the different values of rK, we compare in Fig. 3 our results with the predictions obtained from the classical analytical solution Eq. (1), with recession constants from Eq. (4), which consider only the drainage of a horizontal shallow aquifer with homogeneous hydraulic properties (Boussinesq, 1904). For a review of the different analytical solutions available, the reader is referred to Rupp and Selker (2006) and Dewandel et al. (2003).
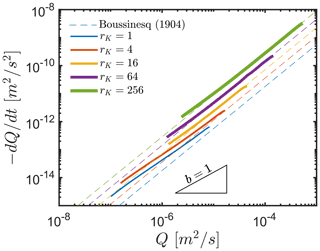
Figure 3Recession plots displaying vs. Q in a log–log space obtained for the horizontal interface, i.e. β=0, and different hydraulic conductivity ratios rK. D is fixed at 20 m and α at 100 m. The dashed lines show predictions for a flat and homogeneous aquifer, without the deep compartment combining Eqs. (1) and (4) (b=15; Boussinesq, 1904). The slope for b=1, characteristic of the drainage of a linear reservoir, has been drawn for reference.
The vs. Q recession curves shift upward as rK increases, i.e. increasing the rate of change in the discharge for the same discharge value as rK increases, which corresponds to an increase in the value of the recession constant a in Eq. (1). This is expected from Eq. (4), with a being directly proportional to . We found that the analytical solution provides accurate results for high values of rK(>16) for long portions of the recession, while deviations are seen when rK is smaller than 16. At late times, the analytical solution significantly underestimates , with b tending to lower values as recession progresses. For higher values of rK, the source of discharge is mainly the upper compartment, which satisfies the assumption of only considering the shallower flat aquifer. However, for lower values of rK, flow tends to be distributed over the full depth of the aquifer system, leading to higher , as the recession advances, than the ones predicted by the analytical solution.
We expect that, for low values of rK, b will take values close to 1, similar to the case of a thick aquifer with only marginal transmissivity variations with head. In contrast, for a high ratio rK, the change in transmissivity due to the fast drainage of the upper, more permeable, compartment satisfies the assumption of the Boussinesq solution for a relatively thin, unconfined aquifer over a large range in Q. This comparison allows us to identify the influence of the deeper compartment in shaping the recession hydrograph with respect to rK.
3.2 Effect of an inclined interface (β>0)
The variety of recession behaviours obtained by changing both rK and β is displayed in Fig. 4. Considering cases where β>0, and by increasing rK, values of increase near the onset of the recessions. With time, the water table progressively lowers below the interface, inducing a sharp reduction in the effective hydraulic conductivity that translates to larger values of b. Finally, the recession progressively converges to a value of a that is characteristic of the geometrical and hydraulic properties of the deeper compartment, i.e. the blue lines at late times for rK=1. The changes in local b values as a function of Q for each hillslope configuration bi are shown in Fig. 5. It is computed as follows:
where i and i+1 are indexes of the discharge range considered [Qmin:Qmax].
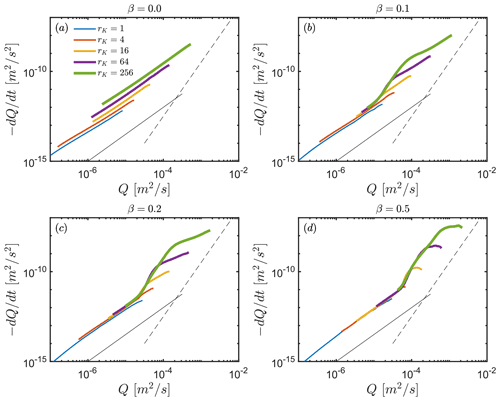
Figure 4Recession plots displaying vs. Q in a log–log space obtained for different hydraulic conductivity ratios rK and different slope angles of the interface between shallow and deep compartments β. D is fixed at 20 m and α at 100 m. Lines of b=3 and b=15 are drawn for reference.
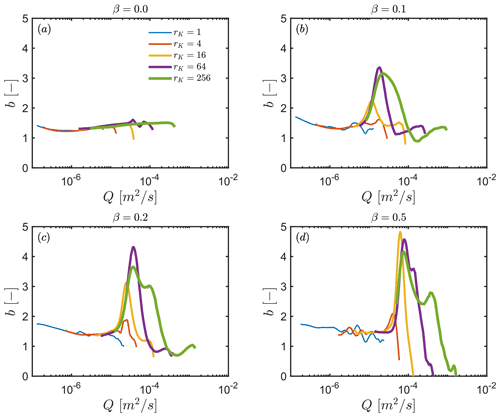
Figure 5Evolution of local b values as a function of discharge Q for the range of hydraulic conductivity ratios rK and different slope angles of the interface between shallow and deep compartments β. D is fixed at 20 m and α at 100 m.
Overall, sharp differences in recession behaviours are evident across all hillslope configurations. At late times, i.e. low discharge Q, all recessions show increasing b towards, and ultimately above, 1.5 when the flow is mostly controlled by the lower compartment. Theoretically, the drainage of a deep homogenous aquifer would lead to b=1, i.e. a negligible change in transmissivity during recession, whereas, in our simulations, the exponential decrease in hydraulic conductivity with depth results in b values > 1 at low Q. This latter result agrees qualitatively with the predictions made by Rupp and Selker (2005), showing how a permeability that decreases smoothly with depth increases b above the homogeneous case, up to a value of b=2. However, our configuration with a discontinuity of hydraulic conductivity also shows how b may not be constant during late times.
As expected from the solution considering the combined discharge from two parallel linear reservoirs (Fig. 1; Gao et al., 2017), the maximum values of b is strongly influenced by the contrast in hydraulic properties rK between the two overlapping compartments. Here we investigate the impact of hillslope structural configurations on recession discharge by comparing our simulated b with the ones predicted from the two parallel linear reservoirs. We derived the equation for the maximum value of b from the equation provided by Gao et al. (2017) used to predict the evolution of b as a function of discharge (see Appendix A). We found max(b) to only be a function of rK between the two parallel linear reservoirs with the following:
We compare, in Fig. 6, the progression of max(b) as a function of rK and, for different β, our simulations against the prediction from Eq. (6). Our two-compartment model shows a nonmonotonic behaviour. For rK≤4, max(b) remains close to the case of the horizontal interface, i.e. max(b) ranging from 1 to 2. However, increasing rK above 4 leads to a progressive increase in max(b) before decreasing back to lower values at high rK. For example, in the case of β=0.5, max(b) takes value of ∼5 at rK=16 before decreasing to approximately 4 at rK=256. This behaviour results from the different flow regimes involved.

Figure 6Maximum values of b as a function of rK. The different slope angles of the interface β are pictured by different symbols. The grey dashed line represents the Gao et al. (2017) model, predicting the evolution of maximum values of b as a function of rK, considering the drainage of two linear reservoirs in parallel.
We found that Eq. (6) (dashed line in Fig. 6) fails to predict the variety of behaviours arising from the different subsurface configurations investigated here. While it might be useful in the case of lateral heterogeneity (Harman et al., 2009; Gao et al., 2017), the parallel reservoir paradigm is not able to predict the recession dynamics involved in the case of a vertically compartmentalized hillslope.
3.3 Effect of changing thickness of the upper compartment, D, and characteristic length of permeability and porosity decrease with depth α
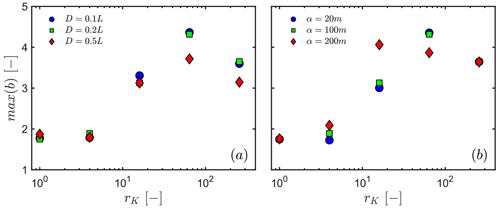
We display, in Fig. 7, the variability in the recession behaviours obtained by jointly changing rK, the upper compartment thickness D (Fig. 7a–c), and the characteristic length of permeability and porosity decrease with depth α (Fig. 7d–f). In this exploration, we fixed the value of β at 0.2. The results revealed that rK controls most of the variability in the recession behaviours obtained across the different hillslope configurations, while changing D and α only have little impact. This is confirmed by analysing the progression of max(b) as a function of rK for different D and α (Appendix B; Fig. B1), which generally shows low sensitivity to these parameters. However, one may note that the impact of both D and α appear not to be negligible when rK≥64. In this context, increasing the values of both parameters tends to lower the average and maximum values of b. This decrease in b is a consequence of the homogenization of the hydraulic properties when increasing D and α across the hillslope, which tends to simplify groundwater flow and diminish the nonlinearity in its storage–discharge functions.
3.4 Impact of transient flow regimes on b values with steep interfaces (β≫0): transition from gravity- to diffusion-controlled regimes
To illustrate the link between the transient pattern of the water table – and, consequently, the flow field – and its impact on the evolution of b, we show, in Fig. 8, the progression of the water table for two hillslopes under β=0.5, with rK=1 (Fig. 8a) and rK=64 (Fig. 8b). We also plot, in Fig. 8c, the progression of the average head gradient ∇H computed across the hillslope, normalized by the slope of the interface β, and, in Fig. 8d, the change in the saturation area in the upper compartment, νu, with respect to the total saturation area, ν, as a function of normalized discharge rates for the same hillslope configurations.
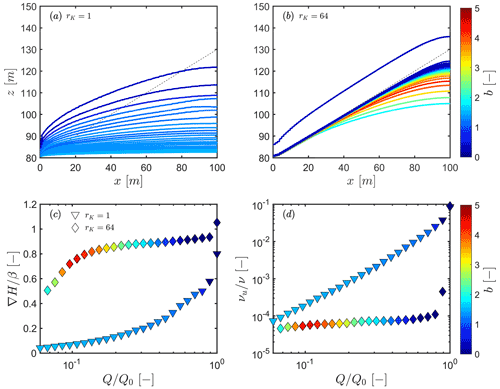
Figure 8The uppermost plots in panels (a) and (b) represent the groundwater table profiles taken at different during the recession, considering (a) β=0.5 and rK=1 and (b) β=0.5 and rK=64. The actual values of correspond to the ones used in the lowermost plots in panels (c) and (d). The upper–lower compartment interface is represented by the dashed black line in the background. Water tables are shown as a continuous line, with colours scaling with the corresponding b values. Panel (c) indicates the progression of the average head gradient ∇H, normalized by the slope of the interface β. In panel (d), the change in the saturation area of the upper compartment νu, with respect to the total saturation area ν, as a function of for the same hillslope configurations as in panels (a) and (b), is shown. The triangular symbols are for the case where rK=1, while diamond ones are for rK=64. The colours of the symbols show the magnitude of b during the recession.
The water table profile for a hillslope with rK=1 maintains a shape typical of diffusion-controlled drainage. This is confirmed by the linear decrease in the head gradient relative to discharge for rK=1, as expected from the Boussinesq equation (Fig. 8c is provided in linear scales in Fig. C1) and the progressive desaturation of the upper compartment (Fig. 8d). In the case of rK=64, the early stage of the recession follows almost constant with b tending toward values close to 0 (and even negative at the beginning of the recession) before increasing during a transition period (Fig. 5d). This first regime, where b is close to 0, or negative, suggests that drainage is controlled by a kinematic wave regime (Beven, 1982; Rupp and Selker, 2006), where the hydraulic head gradient mostly follows the slope interface, i.e. (Fig. 8c), and a constant or increasing rate of change in discharge is involved. This behaviour is visible in Fig. 8b, where the water table for rK=64 is mostly parallel to, and above, the interface near the start of the recession (). As the recession advances, the water table drops rapidly below the interface (Fig. 8b), with a low saturation of the upper compartment νu (Fig. 8d), whereby starts to decrease and discharge rates transition toward a diffusion-controlled regime. During the transition period, the hydraulic gradient remains steep, and the peak in b values occurs. Finally, at the late times, the water table progressively disconnects from the interface, and b values decrease back toward 1.5, as expected from the diffusion-controlled regimes under homogeneous conditions.
4.1 In which geomorphological context might vertical compartmentalization impact recession discharge?
Heterogeneity is ubiquitous in the subsurface, inherited from the interplay between tectonic, erosion, and weathering processes. For example, St. Clair et al. (2015) presented a high-resolution geophysical imaging of bedrock in three U.S. Critical Zone Observatories. They revealed a complex internal structure of hillslopes, with a clear differentiation between shallow permeable compartments overlying a deep and less permeable bedrock. There are multiple factors that may explain the presence of such a compartmentalization. Several authors have revisited the mechanical processes that may be responsible for such a compartmentalization (Moon et al., 2017; Martel, 2006; St. Clair et al., 2015) and argued that near-surface tectonic and topographic stresses could be the main drivers for the development of permeable fractures organized subparallel to the topographic surface, the so-called exfoliation joints. Similarly, in volcanic regions, basalt formations have been described as highly compartmentalized due to the presence of high densities of fractures formed during the cooling of the lava flow. Manga (1996), followed by several other works (Tague et al., 2008; Jefferson et al., 2006), has discussed the role of erosion and weathering in setting shorter drainage characteristic timescales in the Oregonian volcanic Cascades Range. It has also been shown that, when hillslopes are under critical stress conditions, the permeability of the shallower compartment may be enhanced by gravitational movements which favour the development of rock damage and fracture density (Wolter et al., 2020; Vallet et al., 2015). Consequently, increased permeability and storage capacities in the shallow subsurface are common characteristics in bedrock regions. Characterizing the depth and connectivity of such shallow compartments set during the evolution of the landscape and overprinted by current stress and hydrogeological conditions remains a main challenge (Riebe et al., 2017; Rempe and Dietrich, 2014; Dewandel et al., 2006; Guihéneuf et al., 2014; Worthington et al., 2016; Litwin et al., 2022).
While geophysics reveals the presence of such complexity with unprecedented details (Flinchum et al., 2018; St. Clair et al., 2015; Leone et al., 2020; Callahan et al., 2020), a challenge resides in attributing effective hydraulic properties to each compartment. This is classically achieved through borehole testing, which provides precious local estimates. As examples, we could cite the studies performed in India (Dewandel et al., 2006; Maréchal et al., 2004; Guihéneuf et al., 2014) and the Armorican Massif (Roques et al., 2014; Ayraud et al., 2008; Le Borgne et al., 2006) that have revealed contrasting hydraulic conductivities distributed over 2–3 orders of magnitude between shallow fractured/weathered aquifer and deeper, fresh bedrock. Yet the question remains in the representativity of these local estimates in the description of a hillslope to catchment-scale flow and transport processes.
4.2 To what extent does vertical heterogeneity impact the discharge behaviour of hillslopes?
Despite our simplification of the actual heterogeneity of hillslopes, we reveal a strong diversity of impacts on recession behaviour across the different hillslope configurations investigated here. We found that, when compartmentalization is accounted for in the vertical distribution of hydraulic properties, recession behaviour strongly deviates from what is predicted by groundwater theory that considers the drainage of shallow reservoirs with homogeneous properties. Results specifically demonstrate that the critical parameters in the emergence of anomalous behaviour are (i) the presence of a deep bedrock aquifer connected to the stream network, (ii) the contrast in hydraulic properties between shallow and deep compartments, and (iii) the slope of the interface (Fig. 1). Other parameters, such as the thickness of the shallow aquifer (D) and the decay exponent in hydraulic conductivity of the deeper compartment (parameter α in Eqs. 2 and 3), have less of an influence on the variability in recession exponent b obtained in our simulations (Fig. 7 and Appendix B). It is noteworthy that our exploration of the decay exponent in hydraulic conductivity and porosity remains restricted to a few cases of an exponential function. Other functions may deliver different results which would deserve a dedicated study.
In the case of hillslopes with a horizontal interface between shallow and deep compartments, we reveal that there exists a threshold in hydraulic conductivity ratio rK above which the assumption of only considering the drainage of a homogeneous shallow aquifer derived from the Boussinesq solution seems to hold. The assumption is satisfied when the lateral flow in the shallower compartment prevails, i.e. with only limited contribution from the deep bedrock to the discharge dynamics (when rK≥16 in our hillslope configuration). However, for lower values of rK, the continuity in hydraulic properties between shallow and deep compartments favours deeper flow partitioning. In this case, the recession behaviour deviates from the prediction of the Boussinesq equation. The values of b tend toward values close to 1, typical of the drainage of thick aquifers where the change in transmissivity involved by the desaturation during recession is negligible. At later times, b values were found to increase, which are again controlled by the decay in hydraulic conductivity, as shown in Fig. 5a, for m2 s−1 and rK=1 and 4. This shows the intrinsic variability in recession behaviour, even in a relatively simple configuration, which challenges the use of homogeneous groundwater theories.
Considering a steep slope interface, β=0.5, and a strong contrast in hydraulic conductivities, rK=64, sharp changes in flow regimes are involved when the water table transitions from the shallower compartment toward the deeper one with three separated phases (Fig. 8c and d). In the first phase, during high-flow regimes, when (i.e. the two first points on the left of Fig. 8c and d), the saturated volume drops by a factor of 4 with a minimal change in discharge rates (Fig. 7d). The upper zone drains quickly because of the combined effect of its higher conductivity and of the inclined interface. The slope has a strong control on the head gradient, causing high discharge rates and even achieving a kinematic flow regime. Flows occur predominantly in the upper compartment. In the second phase, discharge rates decrease sharply while transitioning to the lower compartment at an almost constant head gradient. The sharp increase in the value of b can be explained in the following way. As and Q∼HK∇H, for b to be large, K must be decreasing rapidly with the otherwise steady H∇H values. In the third phase, the head gradient decreases again with a flow mostly occurring in the lower compartment. The value of b decreases quickly with Q. The water table becomes parabolic uphill and remains influenced by the proximity of the interface close to the river (Fig. 8b), thus explaining the still significantly larger values of b than in the horizontal interface case (Fig. 8a). The presence and geometry of the interface between high and low permeable compartments and the decreasing trend of permeability with depth are keys in conditioning the emergence of complex groundwater flow processes and recession discharge behaviours. It is specifically true in this hillslope configuration for which the river channel fully penetrates the upper compartment. This can be considered as being a common case for landscapes under sufficient erosion rates to carve the weaker compartment, i.e. concerned by higher fracture density or higher porosity, until a more resistant fresh bedrock is reached. The case where high erosion rates may lead to the formation of gorges and canyons in the fresh bedrock may result in different behaviours. The impact of such specific configurations on recession behaviour remains to be explored.
With KL chosen at m s−1, simulated recession behaviours are typical of fractured igneous and metamorphic bedrock (Dewandel et al., 2006). Initial values of KL, and the porosity θL, may impact results and interpretation if different flow regimes are involved when increasing rK. Exploring different values of KL and θL typical of other lithologies is an important perspective of this work. Similarly, our experiment considers a constant value of porosity for the upper compartment across simulations. While this assumption neglects the coevolution of θU and KU during geomechanical and geochemically driven processes shaping the upper compartment of the aquifer, it allowed us to focus our interpretation on the impact of hydraulic conductivity enhancement. Investigating the impact of porosity contrast remains also to be explored.
4.3 Knowledge regarding the structural configuration and heterogeneity of the aquifer is crucial when interpreting discharge recession behaviours
Our results confirm that the exponent b and its temporal progression provide information that can only be interpreted with some amount of local geological knowledge. One of the main challenges in hydrology is to identify the relative contribution among climatic, geomorphological, geological, and land use factors in controlling spatial and temporal variabilities in discharge recession behaviour (Blöschl et al., 2019; Gnann et al., 2021; Hopp and McDonnell, 2009). Our results suggest that different recession behaviour is expected, depending on the structural configurations, the initial saturation condition, and location of the water table prior to recession. These are likely to be major factors in explaining the high variabilities in recession constants that have been observed in some catchments by recent works (Tashie et al., 2020; Roques et al., 2017, 2021) and for transit times and solute transport processes (Berghuijs and Kirchner, 2017; Ameli et al., 2016, 2021). We reveal that the temporal progression of the head gradient and the relative proportion of saturation volume in the upper compartment with respect to the deeper one are key indicators for predicting recession discharge behaviour. These indicators can be assessed through borehole logging and monitoring. The vertical compartmentalization is classically described through detailed core analysis and geophysical investigation (in hole and surface). The interface can also be approximated through the maximum depth of the boreholes in a region. Indeed, it is common that the drilling of a borehole is stopped when a less productive zone is reached, i.e. when airlift discharges stop increases with depth. While such methods will inform us about the geometry and heterogeneity of the hillslope, the pressure monitoring of a network of boreholes distributed along the hillslope will help us identify the different flow regimes involved during recession. It can specifically provide estimates of both the progression of head gradients and saturation distribution between upper and deeper compartments that, as we have shown here, are critical parameters to consider when interpreting streamflow recession dynamics.
While it is well accepted from structural and geophysical investigations that hillslopes settled in bedrock are compartmentalized, this consideration is often overlooked in hydrological models used to predict the evolution of groundwater storage and stream discharge dynamics (Blöschl et al., 2019; Clark et al., 2017; Stephens et al., 2021; Gnann et al., 2021). It is urgent to further develop knowledge on the role of such a vertical compartmentalization and its representation at the catchment scale to improve the prediction in stream baseflow regimes. Our results allow us to identify that both the slope interface between deep bedrock and a fractured/weathered shallow compartment and their contrast in hydraulic properties are key parameters to account for when modelling storage–discharge functions of hillslopes. Such a characterization, although demanding, is possible through geophysical investigation with combined surface and borehole techniques. While our approach assumes the continuity of the compartment along the hillslope, another key parameter influencing stream discharge dynamics during baseflow is related to the volume and spatial connectivity of shallow and deep compartments at the catchment scale. While mechanical and biogeochemical processes may increase the permeability and storage capacity of the bedrock, the spatial representation of this shallow permeable compartment might be highly heterogeneous, with poor connectivity at the catchment scale (Guihéneuf et al., 2014) and, consequently, display higher sensitivity to droughts.
We can define the total outflow from the drainage of two linear reservoirs as follows:
with subscripts f representing fast drainage and s slow drainage, respectively.
Linear reservoir theory defines the evolution of the discharge as a function of time, as follows:
and
with kf and ks as the recession constants of the fast and slow reservoirs, respectively, and Qf(0) and Qs(0) as the initial flow rates prior recession from the fast and slow reservoirs, respectively.
k is related to the geometrical and hydraulic properties of the reservoir by the following (Boussinesq, 1904):
Considering rf the ratio of fast flow to the total flow, we can write the following:
Rearranging to solve for rf(t) yields the following:
In Gao et al. (2017), the authors derived the solution for solving b as a function of rf(t), as follows:
If we replace rf(t) with Eq. (A6) and derive the solution for the maximum value of b, we find the following:
Considering that kf and ks are only differentiated by their hydraulic conductivities, we can write Eq. (A8) as a function of rK.
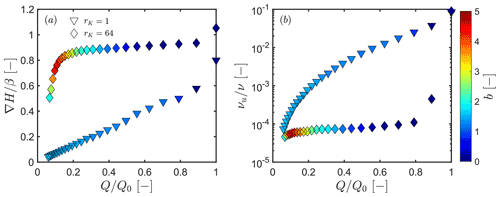
Figure C1(a) The progression of the average head gradient ∇H, normalized by the slope of the interface β. (b) The change in saturation area of the upper compartment νu with respect to the total saturation area ν, as a function of . Triangular symbols are for the case where rK=1, while diamond ones are for rK=64. The colours of the symbols show the magnitude of b during recession.
Model results are available in Roques (2022). The model results presented are found in HydroShare and are available at http://www.hydroshare.org/resource/882cbdcddfdf49ec9ba90c9e43c19cb0 (Roques, 2022). The MATLAB codes used to process the model results are available on request from the authors.
CR, DER, GG, ERJ, and JSS defined the initial research question. All co-authors were involved in conceptualization. CR developed the model, performed the simulations, and analysed the results. All co-authors participated in the interpretation of the results. CR created the figures. CR prepared the first draft, and all co-authors reviewed and edited the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Clément Roques acknowledges financial support from the Rennes Métropole research chair “Ressource en Eau du Futur”. This work has also been supported by the National Science Foundation (grant no. 1551483). We are grateful to the two anonymous reviewers and editor Patricia Saco, whose comments have greatly improved the content of this paper.
This research has been supported by the National Science Foundation (grant no. 1551483) and the European project WATERLINE (grant no. CHIST-ERA-19-CES-006; https://www.chistera.eu/projects/waterline, last access: 25 August 2022).
This paper was edited by Patricia Saco and reviewed by two anonymous referees.
Achtziger-Zupančič, P., Loew, S., and Mariéthoz, G.: A new global database to improve predictions of permeability distribution in crystalline rocks at site scale, J. Geophys. Res.-Solid, 122, 3513–3539, https://doi.org/10.1002/2017JB014106, 2017.
Ameli, A. A., McDonnell, J. J., and Bishop, K.: The exponential decline in saturated hydraulic conductivity with depth: a novel method for exploring its effect on water flow paths and transit time distribution, Hydrol. Process., 30, 2438–2450, https://doi.org/10.1002/hyp.10777, 2016.
Ameli, A. A., Laudon, H., Teutschbein, C., and Bishop, K.: Where and When to Collect Tracer Data to Diagnose Hillslope Permeability Architecture, Water Resour. Res., 57, e2020WR028719, https://doi.org/10.1029/2020WR028719, 2021.
Anderson, R. S.: Pinched topography initiates the critical zone, Science, 350, 506–507, https://doi.org/10.1126/science.aad2266, 2015.
Ayraud, V., Aquilina, L., Labasque, T., Pauwels, H., Molenat, J., Pierson-Wickmann, A. C., Durand, V., Bour, O., Tarits, C., Le Corre, P., Fourre, E., Merot, P., and Davy, P.: Compartmentalization of physical and chemical properties in hard-rock aquifers deduced from chemical and groundwater age analyses, Appl. Geochem., 23, 2686–2707, https://doi.org/10.1016/j.apgeochem.2008.06.001, 2008.
Berghuijs, W. R. and Kirchner, J. W.: The relationship between contrasting ages of groundwater and streamflow, Geophys. Res. Lett., 44, 8925–8935, https://doi.org/10.1002/2017GL074962, 2017.
Berghuijs, W. R., Hartmann, A., and Woods, R. A.: Streamflow sensitivity to water storage changes across Europe, Geophys. Res. Lett., 43, 1980–1987, https://doi.org/10.1002/2016GL067927, 2016.
Bernabé, Y., Mok, U., and Evans, B.: Permeability-porosity Relationships in Rocks Subjected to Various Evolution Processes, Thermo-Hydro-Mechanical Coupling Fract, Rock, 160, 937–960, https://doi.org/10.1007/978-3-0348-8083-1_9, 2003.
Beven, K.: On subsurface stormflow: Predictions with simple kinematic theory for saturated and unsaturated flows, Water Resour. Res., 18, 1627–1633, https://doi.org/10.1029/WR018i006p01627, 1982.
Blöschl, G., Bierkens, M. F. P., Chambel, A., Cudennec, C., Destouni, G., Fiori, A., Kirchner, J. W., McDonnell, J. J., Savenije, H. H. G., Sivapalan, M., Stumpp, C., Toth, E., Volpi, E., Carr, G., Lupton, C., Salinas, J., Széles, B., Viglione, A., Aksoy, H., Allen, S. T., Amin, A., Andréassian, V., Arheimer, B., Aryal, S. K., Baker, V., Bardsley, E., Barendrecht, M. H., Bartosova, A., Batelaan, O., Berghuijs, W. R., Beven, K., Blume, T., Bogaard, T., Borges de Amorim, P., Böttcher, M. E., Boulet, G., Breinl, K., Brilly, M., Brocca, L., Buytaert, W., Castellarin, A., Castelletti, A., Chen, X., Chen, Y., Chen, Y., Chifflard, P., Claps, P., Clark, M. P., Collins, A. L., Croke, B., Dathe, A., David, P. C., de Barros, F. P. J., de Rooij, G., Di Baldassarre, G., Driscoll, J. M., Duethmann, D., Dwivedi, R., Eris, E., Farmer, W. H., Feiccabrino, J., Ferguson, G., Ferrari, E., Ferraris, S., Fersch, B., Finger, D., Foglia, L., Fowler, K., Gartsman, B., Gascoin, S., Gaume, E., Gelfan, A., Geris, J., Gharari, S., Gleeson, T., Glendell, M., Gonzalez Bevacqua, A., González-Dugo, M. P., Grimaldi, S., Gupta, A. B., Guse, B., Han, D., Hannah, D., Harpold, A., Haun, S., Heal, K., Helfricht, K., Herrnegger, M., Hipsey, M., Hlaváčiková, H., Hohmann, C., Holko, L., Hopkinson, C., Hrachowitz, M., Illangasekare, T. H., Inam, A., Innocente, C., Istanbulluoglu, E., Jarihani, B., et al.: Twenty-three unsolved problems in hydrology (UPH) – a community perspective, Hydrolog. Sci. J., 64, 1141–1158, https://doi.org/10.1080/02626667.2019.1620507, 2019.
Boussinesq, J.: Recherches théoriques sur l'écoulement des nappes d'eau infiltrées dans le sol et sur le débit des sources, Journal de mathématiques pures et appliquées, 10, 5–78, 1904.
Boutt, D. F., Diggins, P., and Mabee, S.: A field study (Massachusetts, USA) of the factors controlling the depth of groundwater flow systems in crystalline fractured-rock terrain, Hydrogeol. J., 18, 1839–1854, https://doi.org/10.1007/s10040-010-0640-y, 2010.
Brutsaert, W. and Nieber, J. L.: Regionalized drought flow hydrographs from a mature glaciated plateau, Water Resour. Res., 13, 637–643, https://doi.org/10.1029/WR013i003p00637, 1977.
Callahan, R. P., Riebe, C. S., Pasquet, S., Ferrier, K. L., Grana, D., Sklar, L. S., Taylor, N. J., Flinchum, B. A., Hayes, J. L., Carr, B. J., Hartsough, P. C., O'Geen, A. T., and Holbrook, W. S.: Subsurface Weathering Revealed in Hillslope-Integrated Porosity Distributions, Geophys. Res. Lett., 47, 1–10, https://doi.org/10.1029/2020GL088322, 2020.
Cardenas, M. B. and Jiang, X. W.: Groundwater flow, transport, and residence times through topography-driven basins with exponentially decreasing permeability and porosity, Water Resour. Res., 46, 1–9, https://doi.org/10.1029/2010WR009370, 2010.
Clark, M. P., Rupp, D. E., Woods, R. A., Tromp-van Meerveld, H. J., Peters, N. E., and Freer, J. E.: Consistency between hydrological models and field observations: linking processes at the hillslope scale to hydrological responses at the watershed scale, Hydrol. Process., 23, 311–319, https://doi.org/10.1002/hyp.7154, 2009.
Clark, M. P., Bierkens, M. F. P., Samaniego, L., Woods, R. A., Uijlenhoet, R., Bennett, K. E., Pauwels, V. R. N., Cai, X., Wood, A. W., and Peters-Lidard, C. D.: The evolution of process-based hydrologic models: Historical challenges and the collective quest for physical realism, Hydrol. Earth Syst. Sci., 21, 3427–3440, https://doi.org/10.5194/hess-21-3427-2017, 2017.
Dewandel, B., Lachassagne, P., Bakalowicz, M., Weng, P., and Al-Malki, A.: Evaluation of aquifer thickness by analysing recession hydrographs. Application to the Oman ophiolite hard-rock aquifer, J. Hydrol., 274, 248–269, https://doi.org/10.1016/S0022-1694(02)00418-3, 2003.
Dewandel, B., Lachassagne, P., Wyns, R., Maréchal, J. C., and Krishnamurthy, N. S.: A generalized 3-D geological and hydrogeological conceptual model of granite aquifers controlled by single or multiphase weathering, J. Hydrol., 330, 260–284, https://doi.org/10.1016/j.jhydrol.2006.03.026, 2006.
Famiglietti, J. S.: The global groundwater crisis, Nat. Clim. Change, 4, 945–948, https://doi.org/10.1038/nclimate2425, 2014.
Fan, Y.: Groundwater in the Earth's critical zone: Relevance to large-scale patterns and processes, Water Resour. Res., 51, 3052–3069, https://doi.org/10.1002/2015WR017037, 2015.
Fan, Y., Clark, M., Lawrence, D. M., Swenson, S., Band, L. E., Brantley, S. L., Brooks, P. D., Dietrich, W. E., Flores, A., Grant, G., Kirchner, J. W., Mackay, D. S., McDonnell, J. J., Milly, P. C. D., Sullivan, P. L., Tague, C., Ajami, H., Chaney, N., Hartmann, A., Hazenberg, P., McNamara, J., Pelletier, J., Perket, J., Rouholahnejad-Freund, E., Wagener, T., Zeng, X., Beighley, E., Buzan, J., Huang, M., Livneh, B., Mohanty, B. P., Nijssen, B., Safeeq, M., Shen, C., Verseveld, W., Volk, J., and Yamazaki, D.: Hillslope Hydrology in Global Change Research and Earth System Modeling, Water Resour. Res., 55, 1737–1772, https://doi.org/10.1029/2018WR023903, 2019.
Flinchum, B. A., Steven Holbrook, W., Rempe, D., Moon, S., Riebe, C. S., Carr, B. J., Hayes, J. L., Clair, J. S., and Peters, M. P.: Critical zone structure under a granite ridge inferred from drilling and three-dimensional seismic refraction data, J. Geophys. Res.-Earth, 123, 1317–1343, https://doi.org/10.1029/2017JF004280, 2018.
Gao, M., Chen, X., Liu, J., Zhang, Z., and Cheng, Q. B.: Using two parallel linear reservoirs to express multiple relations of power-law recession curves, J. Hydrol. Eng., 22, 1–12, https://doi.org/10.1061/(ASCE)HE.1943-5584.0001518, 2017.
Gnann, S. J., Mcmillan, H. K., Woods, R. A., Howden, N. J. K., and Nicholas, J. K.: Including Regional Knowledge Improves Baseflow Signature Predictions in Large Sample Hydrology, Water Resour. Res., 57, 1–22, https://doi.org/10.1029/2020WR028354, 2021.
Gudmundsson, L., Boulange, J., Do, H. X., Gosling, S. N., Grillakis, M. G., Koutroulis, A. G., Leonard, M., Liu, J., Müller Schmied, H., Papadimitriou, L., Pokhrel, Y., Seneviratne, S. I., Satoh, Y., Thiery, W., Westra, S., Zhang, X., and Zhao, F.: Globally observed trends in mean and extreme river flow attributed to climate change, Science, 371, 1159–1162, https://doi.org/10.1126/science.aba3996, 2021.
Guihéneuf, N., Boisson, A., Bour, O., Dewandel, B., Perrin, J., Dausse, A., Viossanges, M., Chandra, S., Ahmed, S., and Maréchal, J. C.: Groundwater flows in weathered crystalline rocks: Impact of piezometric variations and depth-dependent fracture connectivity, J. Hydrol., 511, 320–334, https://doi.org/10.1016/j.jhydrol.2014.01.061, 2014.
Harman, C. J. and Cosans, C. L.: A low-dimensional model of bedrock weathering and lateral flow coevolution in hillslopes: 2. Controls on weathering and permeability profiles, drainage hydraulics, and solute export pathways, Hydrol. Process., 33, 1168–1190, https://doi.org/10.1002/hyp.13385, 2019.
Harman, C. J., Sivapalan, M., and Kumar, P.: Power law catchment-scale recessions arising from heterogeneous linear small-scale dynamics, Water Resour. Res., 45, 1–13, https://doi.org/10.1029/2008WR007392, 2009.
Hencher, S. R., Lee, S. G., Carter, T. G., and Richards, L. R.: Sheeting joints: Characterisation, shear strength and engineering, Rock Mech. Rock Eng., 44, 1–22, https://doi.org/10.1007/s00603-010-0100-y, 2011.
Hopp, L. and McDonnell, J. J.: Connectivity at the hillslope scale: Identifying interactions between storm size, bedrock permeability, slope angle and soil depth, J. Hydrol., 376, 378–391, https://doi.org/10.1016/j.jhydrol.2009.07.047, 2009.
Ingebritsen, S. E. and Manning, C. E.: Geological implications of a permeability-depth curve for the continental crust, Geology, 27, 1107–1110, https://doi.org/10.1130/0091-7613(1999)027<1107:GIOAPD>2.3.CO;2, 1999.
Jachens, E. R., Rupp, D. E., Roques, C., and Selker, J. S.: Recession analysis revisited: Impacts of climate on parameter estimation, Hydrol. Earth Syst. Sci., 24, 1159–1170, https://doi.org/10.5194/hess-24-1159-2020, 2020.
Jefferson, A., Grant, G., and Rose, T.: Influence of volcanic history on groundwater patterns on the west slope of the Oregon High Cascades, Water Resour. Res., 42, 1–15, https://doi.org/10.1029/2005WR004812, 2006.
Kirchner, J. W.: Catchments as simple dynamical systems: Catchment characterization, rainfall-runoff modeling, and doing hydrology backward, Water Resour. Res., 45, 1–34, https://doi.org/10.1029/2008WR006912, 2009.
Le Borgne, T., Bour, O., Paillet, F. L., and Caudal, J. P.: Assessment of preferential flow path connectivity and hydraulic properties at single-borehole and cross-borehole scales in a fractured aquifer, J. Hydrol., 328, 347–359, https://doi.org/10.1016/j.jhydrol.2005.12.029, 2006.
Leone, J. D., Holbrook, W. S., Riebe, C. S., Chorover, J., Ferré, T. P. A., Carr, B. J., and Callahan, R. P.: Strong slope-aspect control of regolith thickness by bedrock foliation, Earth Surf. Proc. Land., 3010, 2998–3010, https://doi.org/10.1002/esp.4947, 2020.
Litwin, D. G., Tucker, G. E., Barnhart, K. R., and Harman, C. J.: Groundwater affects the geomorphic and hydrologic properties of coevolved landscapes, J. Geophys. Res.-Earth, 127, e2021JF006239, https://doi.org/10.1029/2021jf006239, 2022.
Luo, Z., Shen, C., Kong, J., Hua, G., Gao, X., Zhao, Z., Zhao, H., and Li, L.: Effects of Unsaturated Flow on Hillslope Recession Characteristics, Water Resour. Res., 54, 2037–2056, https://doi.org/10.1002/2017WR022257, 2018.
Manga, M.: Hydrology of spring-dominated streams in the Oregon cascades, Water Resour. Res., 32, 2435–2439, https://doi.org/10.1029/96WR01238, 1996.
Maréchal, J. C., Wyns, R., Lachassagne, P., and Subrahmanyam, K.: Vertical anisotropy of hydraulic conductivity in the fissured layer of hard-rock aquifers due to the geological patterns of weathering profiles, J. Geol. Soc. India, 63, 545–550, 2004.
Martel, S. J.: Effect of topographic curvature on near-surface stresses and application to sheeting joints, Geophys. Res. Lett., 33, 1–5, https://doi.org/10.1029/2005GL024710, 2006.
Moon, S., Perron, J. T., Martel, S. J., Holbrook, W. S., and St. Clair, J.: A model of three-dimensional topographic stresses with implications for bedrock fractures, surface processes, and landscape evolution, J. Geophys. Res.-Earth, 122, 823–846, https://doi.org/10.1002/2016JF004155, 2017.
Paniconi, C., Troch, P. A., Van Loon, E. E., and Hilberts, A. G. J.: Hillslope-storage Boussinesq model for subsurface flow and variable source areas along complex hillslopes: 2. Intercomparison with a three-dimensional Richards equation model, Water Resour. Res., 39, 1317, https://doi.org/10.1029/2002WR001730, 2003.
Rempe, D. M. and Dietrich, W. E.: A bottom-up control on fresh-bedrock topography under landscapes, P. Natl. Acad. Sci. USA, 111, 6576–6581, https://doi.org/10.1073/pnas.1404763111, 2014.
Riebe, C. S., Hahm, W. J., and Brantley, S. L.: Controls on deep critical zone architecture: a historical review and four testable hypotheses, Earth Surf. Proc. Land., 42, 128–156, https://doi.org/10.1002/esp.4052, 2017.
Roques, C.: Model results presented in HESS-2022-7, HydroShare [code], http://www.hydroshare.org/resource/882cbdcddfdf49ec9ba90c9e43c19cb0, 2022.
Roques, C., Aquilina, L., Bour, O., Maréchal, J.-C., Dewandel, B., Pauwels, H., Labasque, T., Vergnaud-Ayraud, V., and Hochreutener, R.: Groundwater sources and geochemical processes in a crystalline fault aquifer, J. Hydrol., 519, 3110–3128, https://doi.org/10.1016/j.jhydrol.2014.10.052, 2014.
Roques, C., Rupp, D. E., and Selker, J. S.: Improved streamflow recession parameter estimation with attention to calculation of , Adv. Water Resour., 108, 29–43, https://doi.org/10.1016/j.advwatres.2017.07.013, 2017.
Roques, C., Lacroix, S., Leith, K., Longuevergne, L., Leray, S., Jachens, E. R., Rupp, D. E., DeDreuzy, J.-R., Cornette, N., de Palezieux, L. B., Oestreicher, N., Boisson, A., Grant, G., and Selker, J. S.: Geomorphological and geological controls on storage-discharge functions of Alpine landscapes: evidence from streamflow analysis in the Swiss Alps and perspectives for the Critical Zone Community, Earth Space Sci. Open Arch., 39, 1–39, https://doi.org/10.1002/essoar.10506976.1, 2021.
Rupp, D. E. and Selker, J. S.: Drainage of a horizontal Boussinesq aquifer with a power law hydraulic conductivity profile, Water Resour. Res., 41, 1–8, https://doi.org/10.1029/2005WR004241, 2005.
Rupp, D. E. and Selker, J. S.: On the use of the Boussinesq equation for interpreting recession hydrographs from sloping aquifers, Water Resour. Res., 42, 1–15, https://doi.org/10.1029/2006WR005080, 2006.
Saar, M. O. and Manga, M.: Depth dependence of permeability in the Oregon Cascades inferred from hydrogeologic, thermal, seismic, and magmatic modeling constraints, J. Geophys. Res.-Solid, 109, 1–19, https://doi.org/10.1029/2003JB002855, 2004.
Schmidt, A. H., Lüdtke, S., and Andermann, C.: Multiple measures of monsoon-controlled water storage in Asia, Earth Planet. Sc. Lett., 546, 116415, https://doi.org/10.1016/j.epsl.2020.116415, 2020.
St. Clair, J., Moon, S., Holbrook, W. S., Perron, J. T., Riebe, C. S., Martel, S. J., Carr, B., Harman, C., Singha, K., and De Richter, D. B.: Geophysical imaging reveals topographic stress control of bedrock weathering, Science, 350, 534–538, https://doi.org/10.1126/science.aab2210, 2015.
Stephens, C. M., Lall, U., Johnson, F. M., and Marshall, L. A.: Landscape changes and their hydrologic effects: Interactions and feedbacks across scales, Earth-Sci. Rev., 212, 103466, https://doi.org/10.1016/j.earscirev.2020.103466, 2021.
Tague, C., Grant, G., Farrell, M., Choate, J., and Jefferson, A.: Deep groundwater mediates streamflow response to climate warming in the Oregon Cascades, Climatic Change, 86, 189–210, https://doi.org/10.1007/s10584-007-9294-8, 2008.
Tashie, A., Pavelsky, T., and Emanuel, R. E.: Spatial and Temporal Patterns in Baseflow Recession in the Continental United States, Water Resour. Res., 56, 1–18, https://doi.org/10.1029/2019WR026425, 2020.
Troch, P. A., Berne, A., Bogaart, P., Harman, C., Hilberts, A. G. J., Lyon, S. W., Paniconi, C., Pauwels, V. R. N., Rupp, D. E., Selker, J. S., Teuling, A. J., Uijlenhoet, R., and Verhoest, N. E. C.: The importance of hydraulic groundwater theory in catchment hydrology: The legacy of Wilfried Brutsaert and Jean-Yves Parlange, Water Resour. Res., 49, 5099–5116, https://doi.org/10.1002/wrcr.20407, 2013.
Vallet, A., Bertrand, C., Fabbri, O., and Mudry, J.: An efficient workflow to accurately compute groundwater recharge for the study of rainfall-triggered deep-seated landslides, application to the Séchilienne unstable slope (western Alps), Hydrol. Earth Syst. Sci., 19, 427–449, https://doi.org/10.5194/hess-19-427-2015, 2015.
Welch, L. A. and Allen, D. M.: Hydraulic conductivity characteristics in mountains and implications for conceptualizing bedrock groundwater flow, Hydrogeol. J., 22, 1003–1026, https://doi.org/10.1007/s10040-014-1121-5, 2014.
Wittenberg, H.: Baseflow recession and recharge as nonlinear storage processes, Hydrol. Process., 13, 715–726, https://doi.org/10.1002/(SICI)1099-1085(19990415)13:5<715::AID-HYP775>3.0.CO;2-N, 1999.
Wolter, A., Roques, C., Gröble, J., Ivy-Ochs, S., Christl, M., and Loew, S.: Integrated multi-temporal analysis of the displacement behaviour and morphology of a deep-seated compound landslide (Cerentino, Switzerland), Eng. Geol., 270, 105577, https://doi.org/10.1016/j.enggeo.2020.105577, 2020.
Worthington, S. R. H., Davies, G. J., and Alexander, E. C.: Enhancement of bedrock permeability by weathering, Earth-Sci. Rev., 160, 188–202, https://doi.org/10.1016/j.earscirev.2016.07.002, 2016.
- Abstract
- Introduction
- Methodology
- Results
- Discussion
- Conclusion
- Appendix A: The two parallel linear reservoirs theory
- Appendix B: Sensitivity to parameter D and α
- Appendix C: Figure 8c and d displayed with a linear scale for
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Methodology
- Results
- Discussion
- Conclusion
- Appendix A: The two parallel linear reservoirs theory
- Appendix B: Sensitivity to parameter D and α
- Appendix C: Figure 8c and d displayed with a linear scale for
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References