The era of infiltration

Inspired by a quotation from Howard Cook in 1946, this paper traces the evolution of the infiltration theory of runoff from the work of Robert Horton and LeRoy Sherman in the 1930s to the early digital computer models of the 1970s and 1980s. The reasons for the popularity of the infiltration theory are considered and its impact on the way in which hydrological responses were perceived by several generations of hydrologists. Reconsideration of the perceptual model for many catchments, partly as a result of the greater appreciation of the contribution of subsurface flows to the hydrograph indicated by tracer studies, suggests a more precise utilisation of hydrological terms and, in particular, that the use of runoff and surface runoff should be avoided.

1 The background to the era of infiltration

This quotation from Howard L. Cook has stimulated this paper, which has the aim of trying to understand why the infiltration theory of runoff came to have such an impact on hydrological understanding and analysis from the 1930s onwards, particularly in the work of American hydrologists such as Robert Elmer Horton¹, LeRoy Kempton Sherman², Waldo Smith³, Cook himself, and many others. In particular, this paper aims to consider the question of why, when in many parts of the United States overland flow is just not observed that often, the infiltration theory of runoff achieved such a widespread acceptance both in the US and elsewhere. The literature in relation to infiltration and surface runoff is, however, vast, and a complete review is not possible. I hope to have brought out the most important points and references relevant to this question, particularly from some of the earlier publications.

We will take the start of the era of infiltration as being the 1933 paper “On the role of infiltration in the hydrological cycle” in the Transactions of the American Geophysical Union by Robert Horton. That was not the start of infiltration studies in the United States. Before that, there had been experimental studies of infiltration, particularly in relation to irrigation practices (e.g. Muntz et al., 1905) and at the plot scale (e.g. Houk, 1921), as well as the model of infiltration of Green and Ampt (1911). In the 1933 paper, however, Horton sets out a particular perceptual model of catchment response in an often-cited quotation.

Infiltration divides rainfall into two parts, which thereafter pursue different courses through the hydrologic cycle. One part goes via overland flow and stream-channels to the sea as surface-runoff; the other goes initially into the soil and thence through ground-water flow again to the stream or else is returned to the air by evaporative processes. The soil therefore acts as a separating surface, and the author believes that various hydrologic problems are simplified by starting at this surface and pursuing the subsequent course of each part of the rainfall as so divided, separately. This has not hitherto, in general, been undertaken. (Horton, 1933, p. 446–447)

This last sentence (not so often cited) suggests that this provides a good starting point. More than a decade later, the context of the Cook quotation was the report of the AGU Committee for Infiltration for 1946, chaired by George W. Musgrave, who worked in the Soil Conservation Service at that time. This committee had a number of subcommittees, including on infiltration and the physics of soil moisture and of the infiltration process, infiltration in relation to ground water, infiltration in relation to snow and its physical properties, infiltration in relation to surface runoff, infiltration in relation to irrigation, and infiltration in relation to evapotranspiration and the consumptive use of water. Infiltration was therefore considered to be both central and fundamental to hydrological understanding. The following preface to the Cook article provided by Musgrave is pertinent to our question:

In the early phases of the development of a new concept, it is common to find considerable diversity of thought among the workers in that field. Subsequently, through the exchange of ideas, and particularly through the development of factual evidence, abstract ideas are crystallized into specific entities. Progress in the development of the field is increased, and practical application of ideas that originally were abstract now proceeds with greater and greater success.

The concept of infiltration as a factor modifying runoff phenomena is still relatively new. Discussions quite diverse in their conclusions abound in the literature. Is it not true that at least some of the diversity of thought is due to diverse interpretations of terms and definitions? Indeed, it would seem that there is need for re-examination of some of the very fundamentals of the problem.

Many have realized during the past several years that there is great need for clarification of thought in this relatively new phase of hydrology. Many have realized that whatever may be done to promote thinking and expression in terms that are specific and are understood by all other workers is certain to result in improved research and improved application of research findings.

This paper should do much in the way of promoting unanimity in use of terms, of opinion as to their significance, and of clarity of concept. (Musgrave, 1946a, p. 726)

The subcommittee on infiltration in relation to surface runoff was chaired by Howard Cook, with the other members being Wesley Winans Horner, Richard Adin Hertzler, Gail A. Hathaway, and Walter B. Langbein⁴. Cook had been one of the principal assistants of Robert Horton at the Horton Hydrological Laboratory in Voorheesville, New York⁵.

2 The popularity of the infiltration theory

Following the quotation at the head of this paper, Cook started his outline of the subject by considering why the infiltration concept had become so popular:

There have, of course, been logical reasons for this remarkable interest in the subject. As in all sciences, many have been attracted to it simply because of its newness. Another class – and the one that has participated most eagerly – is composed of those intrepid practicing engineers who are obliged to make the runoff estimates upon which depend the failure or success of costly flood control, water supply, and similar works. Still another group has been intrigued by a purely scientific interest, sharpened by the fact that the calculation of runoff is the central problem of the science of hydrology and involves all phases of the hydrologic cycle. Among these are scientists in the fields of soils, plants, and meteorology. As a result of these various motivations, vast amounts of labor have been expended – much of it misdirected – and many exaggerated claims have been made, to be countered, naturally, by the disparaging murmurs of the “old guard”, and other important lines of investigation have been temporarily slighted. But real progress has been made. Better estimates of runoff are now possible than could be made previously. Problems that would not yield at all to earlier methods are now soluble, albeit the solutions are sometimes only rough approximations. The inescapable conclusion is that a tool of considerable practical value has been added to the equipment of the hydrologist. (Cook, 1946, p. 727)

This quotation already reveals some quite modern elements of the sociology of an inexact science. The infiltration concept provided a new paradigm for thinking about runoff. It did so in a rational way, “simply by providing a physically correct concept of the runoff process” (Cook, 1946, p. 730), but which also provided the engineer with a tool that could be usefully applied to provide better estimates of runoff for design purposes (even if sometimes only rough approximations). I do wonder if any of that old guard were murmuring “ … but should you not be able to see the surface runoff occurring during storms to apply this type of analysis properly?”

3 Surface and subsurface runoff

Cook, in fact, almost immediately recognises the difficulty in applying the concept in practice in a section on surface and subsurface runoff. In the following, he notes that:

The runoff from an area is the water flowing from it over the surface of the Earth, either in streams or as overland flow. Part of this water has never been below the surface. This is called surface runoff. Another part has previously passed into the Earth and subsequently returned to the surface. This is called subsurface runoff … .(Cook, 1946, p. 728)

He continues as follows:

(1) Only surface runoff can be directly determined from infiltration data. (2) When runoff contains subsurface flow, the gauged discharge cannot be used to derive infiltration data for the area unless the surface runoff can be separated from the total. (3) In general, there is no way of separating surface and subsurface runoff when only records of the rates of flow are available. (Cook, 1946, p. 728)

In the following, there is also an interesting comment that:

A normal stream carries both surface and subsurface flow in proportions varying widely from time to time. During floods most of the water discharged from deep-soiled drainage basins is ordinarily made up of surface runoff. However, in areas of low storage capacity (such as thin-soiled basins) a large proportion of the flood water may consist of subsurface runoff. (Cook, 1946, p. 728)

The reasoning behind this statement is not totally clear. It implies an expectation that catchments with thin soils and small storage capacities would be associated with higher infiltration capacities and higher downslope transmissivities such that there could be a greater contribution of subsurface stormflow. However, the reasoning might have run more along the lines that high storage capacity will mean a longer mean residence time so that any infiltrated water would simply not be able to contribute within the timescale of the hydrograph. Cook also notes later that, in deeper soils when water tables are low in summer, infiltrating water may not actually reach the saturated zone.

In fact, the role of subsurface runoff production was being promoted more generally at this time. Charles R. (Chuck) Hursh⁶, director of the Coweeta watershed experiments in North Carolina, had long been promoting the idea that, in places where overland flow was only rarely seen, such as in the forests of the Appalachians, the hydrograph was necessarily dominated by direct channel precipitation and subsurface flows, with only slow responses observed in boreholes (Hursh, 1936, 1944; Hursh and Brater, 1941). It is also not as if hydrologists did not realise that in different parts of the US there was less expectation of overland flow. In a national review of flood runoff published during the era of infiltration, Hoyt and Langbein (1939) noted, with some surprise, that: “To those who are acquainted with the flood-producing possibilities of isolated storms of from 10 to 12 inches [250–300 mm] in humid areas, the absence of flood-runoff under single storm-experiences of the same magnitude on steep mountain slopes of parts of the southern coast range [in California] is amazing” (p. 172). In the following, they continue:

Although the small plots may indicate the absence of direct run-off and the differences between rainfall and runoff an absorption of between 15 and 20 inches [375–500 mm], there is a rapid passage of a part of the infiltrated water into stream channels, either through the relatively shallow earth-mantle or through the upper parts of the shattered bedrock. To the extent that the observations and deductions are correct, the flood-hydrograph in these areas is composed largely of ground-water which has concentrated very quickly as to time, superimposed on which is a small amount of direct runoff with irregularities closely following irregularities in the maximum rates of precipitation. This condition may also apply to other parts of the country where floods occur although studies on small areas indicate very high infiltration capacities. (Hoyt and Langbein, 1939, p. 174)

That the infiltration concept was used much more widely, however, was undoubtedly due to a number of factors. The first was that it claimed to be rational or physically based; the second was the simplicity of calculating amounts of runoff, given information about rainfalls and infiltration capacities; the third was the strong and rather combative character of Robert Horton.

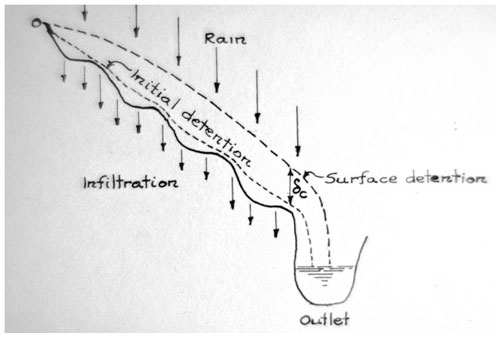
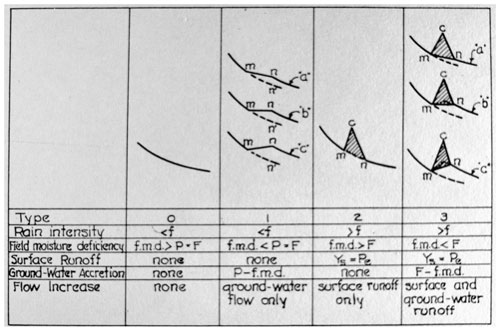
Figure 1 Half-section of a small drainage basin illustrating runoff phenomena (vertical scale greatly exaggerated). Source: Horton (1935), with original caption).

In the 1933 paper, Horton appears to completely buy in to the idea that storm hydrographs are produced by overland flow. This is also clear from his 1935 monograph on Surface Runoff Phenomena, from which Fig. 1 is taken. This is perhaps an example of the pragmatics of applications outweighing the information from direct observations (Horton was working as a consultant by the 1930s). This is also evidenced in his paper on “Remarks of Hydrologic Terminology” later published in the Transactions of the AGU in 1942. He starts by saying the following:

When a science is advancing rapidly, as is hydrology today, especially when it is changing from an adolescent or qualitative to an adult or quantitative basis, new terms are needed in particular for the following two purposes: (1) To give expression to new ideas and concepts; (2) to give more definite, specific, quantitative meaning to terms and concepts heretofore chiefly qualitative. (Horton, 1942, p. 479)

However, in what follows it is clear that Horton's primary purpose is to favour his own terminology over that of others. There are a number of entries of this type (infiltration rate v. infiltration capacity; recharge v. accretion; plot v. plat⁷), but in the current context the one on subsurface runoff is of most interest. Thus, in the following:

Subsurface and concealed-surface runoff. Cases arise where surface-runoff may take place in such a manner as not to be visible, as, for example, where it occurs through a layer of coarse material, sometimes through a thick matting of grass or mulch-cover; through a layer of plant roots close to the soil-surface and under forest-litter; or even, in some cases, (through a network of sun-cracks in the soil-surface. This has sometimes been called “subsurface-runoff”, sometimes “ground-water flow”. The term “subsurface-runoff” would not be objectionable were it not for the fact that it is likely to be confused with true ground-water flow. The term “ground-water flow” applied to this class of flow is highly objectionable on several counts; flow occurring close to the surface in the manner described has little in common with true ground-water flow. It is mostly turbulent flow, while true ground-water flow is mostly laminar. It persists only during rainfall-excess or for a short time thereafter, measured in hours or at the most in days, whereas ground-water flow persists on perennial streams at all times. Furthermore, surface runoff follows the same laws and behaves in the same manner whether it actually occurs visibly on the ground surface, or is concealed and invisible, taking place just below the soil-surface where it is sustained by temporary detention below the soil-surface. Nevertheless, it may be desirable to distinguish between the two cases and, if so, flow which is essentially surface-runoff but which is concealed from view in some one of the ways described, may appropriately be called “concealed-surface runoff”. (Horton, 1942, p. 481)

Thus, by definition, water contributing to the hydrograph is allowed to be hidden from view and treated as surface runoff as if it was in excess of the infiltration capacity of the soil, at least if no longer a laminar flow. An example, taken from the boxes of Horton's papers in his analysis of downslope flow through Sun cracks (see Fig. 2). Again, perhaps underlying this is an interpretation that laminar subsurface flow velocities were far too slow to allow significant contributions to the hydrograph (although, interestingly, observations from the Horton Hydrological Laboratory did show some examples of fast borehole responses; see Beven, 2004c).

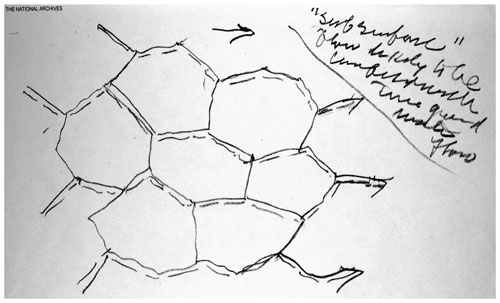
Figure 2 Figure explaining lateral, subsurface flow in Sun cracks as concealed surface runoff. Source: drawing in Horton's hand from Box 71 of the Horton Papers in the US National Archives.

We should remember that the tracer information that revealed that in many catchments hydrographs are composed largely of pre-event water was not available in the 1930s and 1940s, but Beven (2004a) shows that, by comparing rainfall frequency data and Horton's own infiltration observations, it is unlikely that he would have observed widespread overland flow on his own research catchment near Voorheesville more than 1 in 2 to 1 in 5 years (unless, of course, it was concealed!). Walter et al. (2003) had come to similar conclusions in an analysis of a number of sites in the New York State.

4 The complexity of infiltration processes

Horton's perceptual model of the response of catchments was, however, much more sophisticated than he is generally given credit for. This was revealed in the 94 boxes of his papers that were classified by Walter Langbein (who had also worked with Horton) and deposited in the US National Archives in 1949 (see the discussions in Beven, 2004a–c). Horton argued, for example, that infiltration capacities would be primarily controlled at the soil surface by what he called extinction phenomena, such as compaction of the surface by rain splash and blocking of larger pores by displaced fine particles. It was these extinction phenomena that led to the gradual decline in infiltration capacities with time, as described by his well-known infiltration equation that first appears in Horton (1939)⁸. He also recognised that bioturbation and agricultural practices would change the surface between events, resulting in a recovery of infiltration capacities. There could also be marked seasonal changes, something that he observed in his own infiltration observations, and strong variability in space. He recognised the role of macropores and surface microtopography in concentrating water and allowing the escape of air, which he had shown to be a control on infiltration by experiment (see Beven, 2004b). He also understood that, while it was possible to make local predictions of infiltration excess on different land units (effectively producing a distributed model of surface runoff production), it was not possible to calculate the different contributions given only hydrograph contributions.

Horton was also not alone in recognising the complexity of infiltration processes in this period. In the discussion of a physics-based paper on infiltration by Willard Gardner (1946), George W. Musgrave commented as follows:

However, we have before us a type of problem which particularly requires caution in extending and applying laboratory-findings to natural field-soils. At least insofar as the structure of the laboratory-sample differs from that of the natural soil, caution is warranted. Most soils of natural structure contain crevices, channels, and openings that transmit free water rather rapidly, though locally, to some depth. It appears from many observations in the field that in some cases at least, a very large portion of the infiltrating water is thus transmitted. Where a dye is used and the soil-profile is dissected following application, the highly irregular nature of the downward moving water becomes evident. Dry “islands” are bypassed and left with their air–water interfaces intact, at least temporarily. The channels conducting free water act as feeders laterally for capillary water, often for a considerable time. The forces of gravity and capillarity are not always acting in conjunction. One wonders whether other forces such as thermal gradients are involved, and if so, to what extent they are effective. (Musgrave, 1946b, p. 135)

5 Surface runoff and baseflow separation

This then created a problem for the infiltration theory of runoff because, as noted earlier, Cook points out that there was no way of separating surface runoff and subsurface contributions to the hydrograph. But, in order to derive the apparent infiltration characteristics from hydrographs and pluviographs, it was necessary to do so. The concept of baseflow separation and recession analysis has continued to exercise hydrologists ever since (see Hall, 1968; Tallaksen, 1995; Beven, 1991; Arnold et al., 1995; Chapman, 1999; Eckhardt, 2005), right to the present day (Ladson et al., 2013; Lott and Stewart, 2016; He et al., 2016; Duncan, 2019). Some of these methods allowed for an increase in baseflow during an event, arguing that there would be some accretion to the water table during the timescale of the event (e.g. Horton, 1935; Hursh and Brater, 1941, based on borehole observations at Coweeta; Hewlett and Hibbert, 1967; the digital filters of Nathan and McMahon, 1990; Furey and Gupta, 2001; and Aksoy et al., 2009).

Both Horton (1935) and Cook (1946) suggest the strategy of continuing the past groundwater depletion or recession curve as an indicator of baseflow, with all the flow above that curve being treated as if it was infiltration excess surface runoff but only for “the special case when the subsurface flow is derived entirely from the zone below the permanent groundwater table, and no groundwater accretion occurs, a satisfactory estimate of subsurface flow can be made simply by extending the groundwater depletion curve” (Cook, 1946, p. 728).

But simply continuing the recession curve results in a problem for the method of calculating the volume of surface runoff for an event, since the previous recession will always be below the recession of the current event. Thus, there was also a pragmatic need to allow for a baseflow contribution to rise to meet the falling recession limb of an event. Horton (1935) had earlier wanted to allow for the accretion of groundwater due to infiltration and specifies a method for deciding when the field moisture deficit of the soil has been satisfied, after which a line can be drawn to where the form of the recession matches the groundwater depletion curve. He notes that this might occur above or below the point of initial hydrograph rise (Fig. 3). Hewlett and Hibbert (1967) suggested using a standard slope for this rise of 0.05 cfs mi⁻² h⁻¹ (or 0.0567 L s⁻¹ km⁻² h⁻¹), starting from beneath the hydrograph peak, but this was based only on discharge and borehole data from some small catchments at Coweeta. Somehow, it became a standard that was used around the world, regardless of soils, vegetation, or geology. Others suggested that the end of surface runoff would be marked by a break between straight line segments on a semi-logarithmic plot of the recession, indicating a transition to a process with a slower time constant⁹. In essence, Cook was correct; there is no satisfactory way of separating surface from subsurface flow in this way (see also the discussion in Beven (1991)¹⁰).

Figure 3 Classification of stream rises, with Type 3 showing how to separate groundwater runoff. Source: Horton (1935).

6 Derivation of infiltration indices from the hydrograph

Both Horton and Cook recognised that there was a difference between predicting surface runoff locally, given information about rainfall and infiltration capacity curves for a soil, and deriving apparent infiltration information from rainfalls and an estimate of surface runoff. In the first case, the local variability of soils, vegetation, and management practices could be taken into account (given the infiltration characteristics of each) on what Cook calls soil cover complexes, which are the equivalent of modern-day hydrological response units. Such an approach can, in principle, also allow for the type of time variability of observed infiltration rates described by Horton (1940). However, I have found no real recognition at that time of the difference in scale between the point and plot scale, at which observations are possible, and the soil cover complex scale, at which the calculations might be applied.

The second case is more challenging in that it is not possible to obtain more than an index of catchment-wide apparent infiltration. Cook gives two examples of such indices that can be obtained by matching the observed volume of surface runoff to the observed pattern of rainfall, both of which still appear in texts today. The first is based on assuming an average declining infiltration capacity to produce an average infiltration capacity (the f_av or W index) with a special case after significant wetting equivalent to a final constant infiltration capacity W_min. The second is assuming a constant infiltration capacity (the ø index). He demonstrates that, for this latter index, a dependence on rainfall intensity should be expected where there are multiple soil cover complexes in a catchment “because the higher the intensity the greater the proportion of the area producing runoff throughout the rain, not because infiltration capacity increases with intensity of rainfall” (Cook, 1946, p. 738). He, therefore, already recognises the possibility of partial contributing areas of runoff production (but, again, not how scale issues might affect the outcome).

Further problems arise when there is intermittent rainfall, or where rainfall intensity intermittently falls below the infiltration capacity of the soil, and there might be the possibility of some recovery of infiltration capacities between bursts of rainfall. He goes into some detail to explain how different cases might be handled. He does not include, however, the suggestion of using time condensation (now more commonly known as the time compression assumption). This had been introduced 3 years earlier by LeRoy Sherman (1943) and then modified by Heggie Nordahl Holtan (1945)¹¹. Holtan (1961) was also the first person to suggest an infiltration equation that was expressed directly in terms of cumulative infiltrated water, thereby implicitly incorporating a time compression assumption.

7 Infiltration equations

Application of the infiltration theory is easiest on a single soil cover complex, given rainfall and information about infiltration capacities of the soil. Quantitative estimation of runoff is easier if the infiltration capacities can be represented as a mathematical function (although in the 1930s and 1940s, when the calculations were made by hand, it could actually be faster to read values off a graph or from a table than to do the calculation, and many papers from that time give examples of hand-worked calculations; e.g. Sherman, 1936, 1943).

The Green and Ampt (1911) infiltration equation (Table 1), based on a piston-like wetting front approximation to Darcy's law, had been available for some time. Horton (1939, 1940) developed his own form of this equation¹². As noted earlier, he argued that this represented surface controls rather than profile controls on the infiltration capacity. Cook mentions only the Horton equation in his exposition of the infiltration theory, but there were other empirical infiltration equations suggested, such as the power law form suggested independently by A. N. Kostiakov (1932) and Mortimer Reed Lewis (published in 1937 but, according to Swarzendruber (1993), proposed in 1926), the Soil Conservation Service (SCS) curve number method that first appeared in 1954 (SCS, 1954), and, later, that of Holtan (1961). The idea of solving the Darcy–Richards equation was picked up again in the 1950s, most notably by John Philip (1954),¹³ and then in a series of papers for the infiltration problem (Philip, 1957). Given the nonlinearity of the governing equation, this was a mathematical challenge for soil physicists and set off a variety of solutions for different types of diffusivity function and boundary conditions that continued into the 21st century (e.g. Ogden et al., 2015). A summary of some of these infiltration equations is given in Table 1. Comparison of the behaviours of different equations has been given by, for example, Wilson et al. (1982), Davidoff and Selim (1986), Mishra et al. (2003), and Chahinian et al. (2005).

Table 1 Selected 20th century infiltration equations with f(t) as infiltration capacity, F(t) as cumulative infiltration, and K_s as saturated hydraulic conductivity (other symbols defined under comments).

The SCS curve number method is of particular interest in terms of its common interpretation as an infiltration equation. Horton frequently clashed with the SCS and seems to have had a low opinion of their engineers (the SCS insisted on interpreting infiltration capacity as a volume rather than as a rate, for example¹⁴). This originally derives from the work of Mockus (1949), who plotted estimates of storm rainfall against the volume of surface runoff, as previously suggested by Sherman (1943). From this analysis, Mockus suggests a relationship between them of the following form:

$$\begin{array}{}\text{(1)}& Q=P\left[\mathrm{1}-(\mathrm{10}{)}^{-bP}\right],\end{array}$$

with a multiple regression used to estimate the coefficient b based on data for 50 storms collected from catchments “of field size or larger” (Mockus, 1949, p. 41). The soil, crop, season, and antecedent precipitation indices used in the regression were derived by an analysis of data from nine USDA research stations. Nowhere does he specify how the amounts of surface runoff were derived. The resulting surface runoff was routed through a dimensionless unit hydrograph to derive hydrograph peaks (Mockus, 1949, also mentions how a triangular unit hydrograph could be used to approximate the dimensionless unit hydrograph).

The methods were tested “by estimating total runoff for storms on single- and mixed-cover watersheds” (Mockus, 1949), by which he seems to mean the total volume of surface runoff. The results were better for large storms than small storms and for mixed-cover rather than single-cover catchments. Better results were obtained by breaking long-duration storms into parts. He notes that rainfall spatial variability and direction of movement might be important for obtaining better estimates.

The SCS curve number method took the data of Mockus (1949), and also a large number of infiltration capacity measurements on different soil types and land covers in the US, and postulated a proportionality between retention and runoff such that, in the following:

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{F}{S_{\mathrm{CN}}}}={\displaystyle \frac{P-Q}{S_{\mathrm{CN}}}}={\displaystyle \frac{Q}{P}},\end{array}$$

where F is the cumulative infiltration, S_CN is the storage capacity of the soil (here given a subscript to distinguish from the sorptivity of the soil), Q is the total runoff, and P is the total precipitation for an event. According to an interview with Vic Mockus, he had fixed on this functional relationship after dinner one evening, having tried many others, because it best fit the data (Ponce, 1996). An initial abstraction loss, I_a, was also introduced which, on the basis of data from catchments of 10 acres or less, was made proportional to S_CN as I_a=λS. While 50 % of these observations showed values of λ in the range 0.095 to 0.38, a value of 0.2 was chosen as being at the centre of the data (though Mockus, 1949, allows that other values might be valid). Combining these equations, an expression for Q can be derived as follows:

$$\begin{array}{}\text{(3)}& Q={\displaystyle \frac{{\left(P-\mathrm{0.2}{S}_{\mathrm{CN}}\right)}^{\mathrm{2}}}{P+\mathrm{0.8}{S}_{\mathrm{CN}}}},\end{array}$$

with only the one parameter S_CN. For convenience in engineering applications, this was then scaled to a non-dimensional curve number, CN, such that (for S_CN in units of inches), in the following:

$$\begin{array}{}\text{(4)}& S_{\mathrm{CN}}={\displaystyle \frac{\mathrm{1000}}{\mathrm{CN}}}+\mathrm{10},\end{array}$$

where CN has the range of 0 to 100 and is tabulated for different soil classes, land covers, and antecedent conditions. The soils information was simplified to only four classes for simplicity of use by George W. Musgrave (Ponce, 1996). It is clear from the literature associated with the curve number methodology that the SCS interpreted the output Q as a volume of surface runoff in excess of the infiltration capacity of the soil (Table 1). Thus, in module 103 of the SCS training manual it is stated that: “Runoff is that part of the precipitation that makes is way towards stream channels, lakes, or oceans as surface flow” (1989, p 1). The manual also provides definitions of interflow and baseflow as subsurface contributions to streams but suggests that interflow “is not usually considered in SCS methods of estimating runoff” (1989, p. 3).

There have since been many other interpretations of the SCS curve number relationships. Chen (1982) showed how the SCS curve number method could be related to the Holtan infiltration equation, which also allows for a maximum storage capacity, while Mishra and Singh (1999, 2002, 2003) showed how the Mockus relationship could be analytically related to the SCS curve number equation and also to the Horton infiltration equation (for the case where the long time infiltration capacity f_c can be assumed negligible). They refer to what is being estimated as direct surface runoff. It seems that, given the relationship to infiltration equations they derive, they mean by this overland flow to the stream. Steenhuis et al. (1995) suggested that the method could also be interpreted as a saturation excess variable contributing area function, which was later verified by Dahlke et al. (2012), while Yu (1998) suggested that it was equivalent to the partial area surface runoff that would be generated on a statistical distribution of soil infiltration characteristics. In all these cases, however, it retains the preconception of representing surface runoff as overland flow. It is important to note, however, that this may not have been the case for the original small catchment observations from which the method was derived (see also the results from Horton's runoff plat experiment reported in Beven, 2004a, where the runoff rate was significantly higher than the observed rainfall intensity). More recently, Ogden et al. (2017) argued that it is really time to move beyond the curve number method, suggesting that “sixty-five years of use and multiple reinterpretations have not resulted in improved predictability using the method.”

8 Surface detention, channel storage, and the unit graph

Horton and others in the era of infiltration recognised that, in both analysis and prediction, it was not enough to simply calculate the excess of precipitation over the infiltration capacity of the soil. As Horton (1935) put it, “A striking fact about surface runoff is the manner in which a jagged, irregular rain intensity graph is often transformed into a smoothly rounded runoff graph … . This is the result of regulation by surface detention and channel storage” (p. 1). By thinking in terms of a unit strip of hillslope (for which he credits a suggestion of LeRoy Sherman), Horton (1935) analyses the velocities expected for both laminar and turbulent sheet flow, with hydraulic radius assumed equal to the flow depth for a shallow flow, in terms of the Hagan power law equation as follows:

$$\begin{array}{}\text{(5)}& q=k_H{\mathit{\delta }}_c^m{s}^n,\end{array}$$

where q is the flow per unit width, δ_c is the depth of flow averaged across the width of the slope segment, s is the slope of the surface, and k_H, m, and n are parameters. Horton notes the theoretical values of m and n for laminar and turbulent flows but also gives an analyses of flume data provided by M. R. Lewis and E. H. Neal¹⁵ of the Idaho Agricultural Experiment Station that suggest values of m of 0.85 and n of 0.74, suggesting mixed laminar and turbulent flow. He also uses this to derive a profile of overland flow depths under a steady distributed input rate equal to the rainfall rate – a constant infiltration capacity (essentially making the kinematic wave assumption).

He also recognised the effect of routing through channel storage, both in predicting hydrographs and in the analysis of observed hydrographs to derive infiltration parameters. He suggested a method of routing through a nonlinear (power law) storage based on the storage discharge curve for the channels, but noted that “in applying this method for correction for channel storage it is important that groundwater flow, if any exists, should be eliminated from the hydrograph in advance” (Horton, 1935, p. 41).

It might be that Horton felt compelled to provide a method of routing runoff because, a few years earlier, LeRoy Sherman (1932) had already proposed a more general method as an abstraction of the time area approach that he called the unit graph method (see the discussion of Beven, 2020). This was then developed into the unit hydrograph theory, with its many variants in terms of mathematical representation, methods of fitting, and parameters related to catchment characteristics. In its classical form, the unit hydrograph is used to route estimates of the water contributing to the storm hydrograph after baseflow separation as appropriate (although modern transfer function methods can also be used to predict the complete hydrograph; e.g. Young, 2013). It was thus easy to combine the unit hydrograph with the infiltration theory as if all that water was overland flow in excess of the infiltration capacity of the soil. This provided a convenient engineering procedure that is still in widespread use in many countries.

9 Surface runoff, direct runoff, and stormflow

The infiltration theory essentially defines that proportion of the rainfall that will produce surface runoff and contribute to the storm hydrograph. But part of the problem here is what is actually meant by surface runoff. Even going back to the original definitions of Horton and Cook, we have seen how surface runoff is what is measured in a stream hydrograph, but that might have reached the stream as either overland flow or subsurface stormflow. We have seen already how Robert Horton suggested that some of this contribution might be concealed surface runoff and how Howard Cook allowed that effective infiltration rates could not be inferred if there was a significant contribution to the hydrograph from subsurface flows.

It is also clear that the runoff data analysed by Mockus (1949), and that were used in evolving the SCS-CN model, were not necessarily produced entirely by overland flow, despite the common interpretation of the SCS-CN function as an infiltration model. Yet, in setting out the definitions for his analysis, Mockus (1949) defines surface runoff as overland flow. He distinguishes between surface runoff, subsurface flow contributing to the hydrograph but which will quickly cease to contribute to streamflow, and groundwater flow which “may first appear in the stream channels during or after the storm, and may continue for a relatively long time” (p. 2). He then defines the term direct runoff as being the sum of surface runoff and subsurface flow “combined in unknown proportions” (Mockus, 1949, p. 2). However, having set out these definitions, he proceeds to outline methodologies for estimating surface runoff alone based on nomograms that allow for soil, crop, antecedent conditions, storm duration, and seasonal effects. In his use of direct runoff, Mockus (1949) was following Franklin F. Snyder, who, a decade earlier in a glossary of terms associated with his “A conception of runoff-phenomena”, defined surface runoff as being:

Usually defined as the runoff reaching the surface drainage-channels without penetrating the ground-surface. As actually used, surface-runoff usually includes considerable subsurface storm-flow and might be better termed direct runoff, since it consists of the discharge in excess of a base or ground-water flow which passes a gauging station within a rational period of time subsequent to the storm causing the rise. (Snyder, 1939, p. 736)

Note how this differs from the definition cited earlier in the SCS (1989) training module 103. Later usage was also mixed, and there does not seem to have been a real history of development in the use of the different terms for runoff. To give just a few examples, Leach et al. (1933) use both stormflow and surface runoff; Langbein (1940) uses direct runoff, as do Hursh and Brater (1941), who specifically say that storm runoff as overland flow has not been observed at the study watershed at Coweeta and give examples of hydrographs dominated by channel precipitation. Hoover and Hursh (1943), however, revert to using storm runoff. Marston (1952) equates storm runoff to overland flow, but Reinhart (1964) includes subsurface stormflow in storm runoff, and in the study of Whipkey (1969), essentially all the storm runoff is subsurface stormflow. Hamon (1963) refers to direct runoff in relation to that predicted by the SCS curve number method, whereas others have continued to use storm runoff as equivalent to overland flow, especially in semi-arid catchments (e.g. Fogel and Duckstein, 1970).

If we turn to the latest issue of the World Meteorological Organization (WMO) International Glossary of Hydrology (2012) we find runoff being defined as that part of the precipitation which flows towards a river on the ground surface (surface runoff) or within the soil (subsurface runoff or interflow). Direct runoff (or direct flow or storm runoff) is defined simply as water that enters a watercourse without delay (and without any process interpretation). Infiltration index, however, is defined as being an average rate of infiltration, such that precipitation in excess of that value equals the volume of storm runoff (implying that the infiltration theory concept still persists – if only in an index form). In his glossary for “Hillslope hydrology”, Chorley (1978) also defines direct runoff with respect to time, adding that it comprises the sum of channel precipitation, overland flow, and subsurface stormflow. His definition of surface runoff is limited to flow over the soil surface, and for quickflow, storm runoff, and stormflow he says, “see direct runoff” (Chorley, 1978).

There is, thus, some continuing ambiguity about the use of these terms, particularly surface runoff. This is in part a process issue because, however water flows into a stream, by either surface or subsurface flow processes, once in the stream it is measured as a surface runoff (as was the case for the fields and small catchments in the data used by Mockus, 1949). The problem is that the word runoff still induces a perception of an overland flow, as in running off over the land surface. This is reinforced by the use of surface runoff, even if the ambiguity recognised by Snyder, Cook, and Mockus of the unknown mix of surface and subsurface contributions to the hydrograph cannot be easily resolved. This mix, defined by them as being direct runoff (and now sometimes referred to as storm runoff, stormflow, or quickflow), is more commonly what is estimated by the use of hydrograph separation, but it should not then be interpreted as runoff in excess of the infiltration capacity of the soil. That is, perhaps, why the WMO glossary refers to an infiltration index to match the volume of storm runoff, even if this perpetuates the perception of runoff as an overland flow. On the other hand, the convenient alliteration of rainfall–runoff modelling is generally used to indicate a mix of surface and subsurface processes (except in models that are still limited to predicting only overland flows).

Given these ambiguities, it might be better to avoid the use of the terms runoff and surface runoff (and concealed surface runoff) altogether and instead refer to stormflow, or storm discharge when no process interpretation is inferred, and refer explicitly to overland flow and subsurface stormflow when there is evidence for making a process interpretation¹⁶. There is also no reason why the general term hydrological model should not replace the ambiguity of rainfall–runoff model. This might (just perhaps) lead to a greater appreciation and greater thought about the perceptual model of hydrological processes relevant to particular catchments of interest (Beven, 2001; Beven and Chappell, 2020).

10 Persistence of the era of infiltration and perceptual model failures

When Cook was writing in 1946, he noted that the infiltration theory of surface runoff was still young and needed to be developed further, such that “before it can be generally employed, many problems must be solved and large quantities of data published” (1946, p. 743). He notes that, in particular, it would only be valid for cases where subsurface runoff could be neglected, and that infiltration indices derived from hydrograph data would only be satisfactory if there was only one soil cover complex, otherwise “the physical significance is obscure” (Cook, 1946, p. 743). His final statement is to suggest that, because of these issues, all infiltration data should be accompanied by a statement of how they were derived, so that they would not be misused. It can be said, therefore, that Howard Cook had a rather realistic understanding of the limitations of the infiltration theory.

It seems that in the years following, however, the pragmatic utility of the methodology to provide estimates of the volume of storm discharge dominated any concerns about the validity of the assumptions. That volume could be combined with the time distribution of the Sherman (1932) unit graph (and later representations of the unit hydrograph) to allow the prediction of hydrographs and of hydrograph peaks for design applications. The methodology came to dominate hydrological practice, even well into the computer age, when there were many models essentially based on predicting and routing effective or excess rainfall based on infiltration equations (see, for example, Beven, 2012).

However, from the late 1960s onwards, the general applicability of the infiltration theory started to be questioned. Cappus (1960) and Moldenhauer et al. (1960) suggested that not all of a catchment would contribute surface runoff, while Betson (1964) concluded that the generally wetter conditions at the base of hillslopes would result in a relatively consistent partial contributing area (see also the consequent partial area model of Betson and Marius, 1969). Hewlett and Hibbert (1967) proposed that the contributing area would be dynamic, varying with antecedent conditions and storm rainfalls (see also Dickinson and Whitely, 1970).

However, particularly after the geochemical hydrograph separation of Pinder and Jones (1969) and the environmental isotope hydrograph separation of Sklash and Farvolden (1979), there was a more general realisation that subsurface processes were necessarily important in stormflow generation in many catchments because of the high proportion of pre-event water that appeared to be displaced in the event (something that was later called a double paradox by Kirchner, 2003). Thus, even if there was some overland flow, much of the water in the hydrograph had to be displaced from the soil or deeper layers (Sklash and Farvolden, 1979, reported that, at one site, samples of overland flow were indicative of event water in one sampled storm and pre-event water in another). Thus new concepts of runoff generation were required. At Coweeta, where overland flow is rare, except in the immediate riparian area (but runoff coefficients can be small), John Hewlett¹⁷ had continued the work of Hursh in trying to understand the role of subsurface flow in hydrograph generation. The idea of runoff and return flow to dynamic saturated areas had appeared in the work of Dunne and Black (1970), a concept later claimed by Hewlett (1974). However, at around the same time, computer models such as the Huggins and Monke (1968) model, the KINEROS (KINematic runoff and EROSion) model that developed from Smith and Woolhiser (1971), the partial area quasi-physically based rainfall–runoff model (QPBRRM) model of Engman and Rogowski (1974), also included in the study of Loague and Freeze (1985),¹⁸ and the CASC2D model of Downer et al. (2002) were all based on the infiltration theory (and there were many others). Of course there are still catchments where the infiltration theory might indeed match the perceptual model of overland flow as the dominant process, but it still took time for the perceptual model of how catchments function to recognise the important contribution of subsurface water to stormflow in many catchments.

A really instructive case in this respect is the history of modelling the R5 catchment at Coshocton by Keith Loague and his colleagues. This is only a small catchment area (0.1 km²), and it started out as a study of the effect of the variability in infiltration rates in space on runoff generation, making use of the extensive database of infiltration measurements collected by Sharma et al. (1980). It was included in the study of Loague and Freeze (1985), using the QPBRRM computer model. Loague and Gander (1990) added a further 247 infiltration measurements, and Loague and Kyriakidis (1997) used kriging interpolation to produce a fully distributed spatial pattern of infiltration characteristics. Using this information, however, produced less satisfactory hydrograph simulations than the original Loague and Freeze (1985) calibrated model. Various things were tried to improve the results, including allowing for temperature effects in the original infiltration measurements and taking averages over stochastic fields of parameters consistent with the kriging estimates. It was suggested that there were still limitations in the resolution when representing the surface runoff pathways and effects of run-on and reinfiltration. However, improvements in predictions of the peak and time to peak came with a change of model to the finite-element-based Integrated Hydrology Model (InHM) that included the effects of subsurface flow pathways (VanderKwaak and Loague, 2001; Loague et al., 2005). Following this change in perceptual model from a simple infiltration theory concept, R5 has continued to be used as a case study for the application of integrated models (Heppner et al., 2007; Mirus et al., 2011; Mirus and Loague, 2013).

Another case is reported in Beven (2002). I was a visiting scientist at the ARS laboratory in Fort Collins, Colorado, working with Dave Woolhiser and Roger Smith, and helped in an experiment looking at runoff generation on shallow restored soils over mine tailings near Steamboat Springs, Colorado, in 1981. The perceptual model in designing the experiment was that the runoff generation would be produced by an infiltration excess mechanism. Thus, many dual ring infiltrometer measurements were done, and replicate 25 m by 5 m sloping plots were watered using a sprinkler system supplied from a large impermeable container of rubberised fabric. Unfortunately, during the experiment, the supply started to be limited by the movement of the container as it emptied, but some overland flow was generated and collected. It was, however, localised on the surface and rapidly fell to zero. Meanwhile, in the shallow trench that had been dug to take the collected overland flow from the measurement flume to a small channel, subsurface flow from beneath the collectors continued for some 90 min, and at the bankside of the channel, there were two outflows from preferential flow pathways through otherwise unsaturated soil. It appeared as if there had been a form of a percolation excess process taking place at the boundary between the mine tailings and topsoil, and that the resulting subsurface flow was somehow being channelled within the soil that had been replaced over the mine waste. The volumes of subsurface flow were not measured but were clearly much greater than the surface runoff collected. This was also an instructive case in which the perceptual model based on the infiltration theory used in designing the experiment was clearly not correct and needed to be revised.

There is, therefore, no doubt that the infiltration theory concept led to many misconceptions or perceptual model failures of how the response of particular catchments was dominated by surface flow. There were, of course, many other catchments where subsurface contributions to the hydrograph had been studied in more detail and qualitative perceptual models developed, such as Hursh, Hewlett and others at Coweeta, North Carolina, as mentioned above, and Mosley (1982) and McDonnell (1990) at Maimai, New Zealand, with later additions by Brammer and McDonnell (1996) and McGlynn et al. (2002). These more complete perceptual models, however, tend to be complex and subject to limitations of knowledge of hydrological processes in the subsurface. In addition, there remains a need to simplify when applying quantitative predictive models in practice (Beven and Chappell, 2020). In that respect, infiltration theory still provides an approximate engineering solution that is simple to apply, as already recognised in the “rough approximations” of Cook (1946).

This is perhaps the main explanation of the question posed at the beginning of this paper as to why the infiltration theory of the runoff concept has persisted so widely in applications. It still underlies many current hydrological models in one form or another, including the SCS-CN or alternative Green–Ampt methods for estimating direct flow in the Soil and Water Assessment Tool (SWAT). In this way, the era of infiltration theory continues, in part because of the convenience of applying the SCS-CN method for practical applications without thinking too much about whether that is appropriate in any particular catchment. In fact, since we do not know too much about the processes in the catchments on which the analysis of Mockus (1949) that led to the SCS-CN method were based, this approach could be more defensible (if only for the range of conditions for which the data were available) as a predictor of total direct runoff at the scale of interest than the use of point infiltration equations to predict purely overland flow (especially if the heterogeneity of soil characteristics, the commensurability issues of scale of infiltration measurements against scale of applications, and run-on effects are neglected).

It does, however, seem surprising that more than 70 years after Howard Cook announced the era of infiltration, and 50 years after tracer information showed that hydrographs could be dominated by pre-event water, we should still be left with so much ambiguity about how to describe what is actually being observed and estimated in catchment hydrographs. Cook's observation that it is impossible to separate surface and subsurface contributions to the hydrograph when only records of the rates of flow are available still holds. Learning from tracer separations is not yet standard practice and does not provide unambiguous information about flow pathways. Yes, we understand that there are limitations to the knowability of what goes on in the subsurface, but such an ambiguity means that there have been no real attempts to define the limits of validity of the infiltration theory, and there is much confusion about its use. It seems that some of the old guard might still have a reason to grumble.